Acquiring High-Quality Oil Casing Steel 26CrMoVTiB under Optimal Continuous Casting Process Conditions
Abstract
:1. Introduction
2. Methods
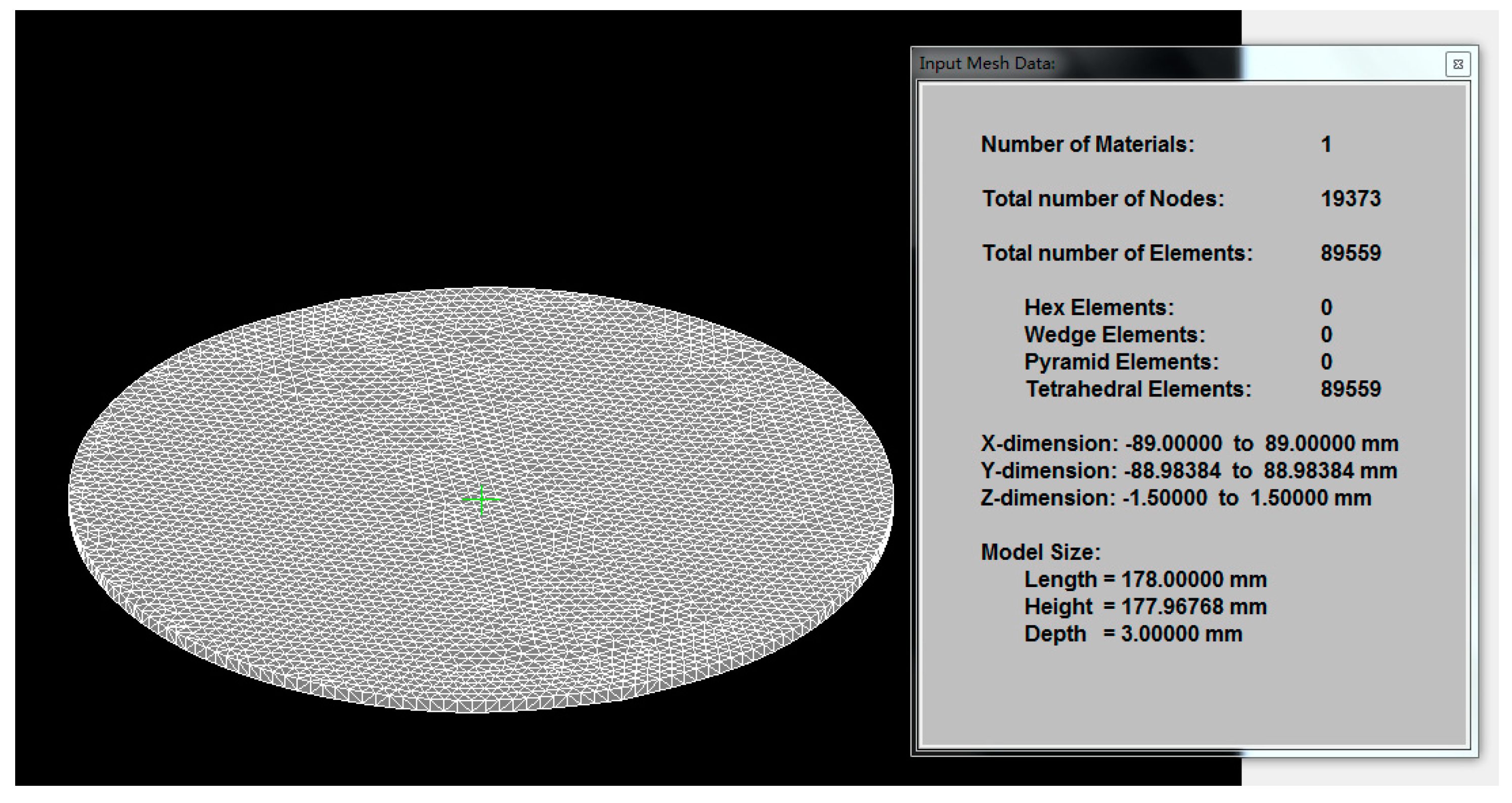
2.1. Mathematical Model
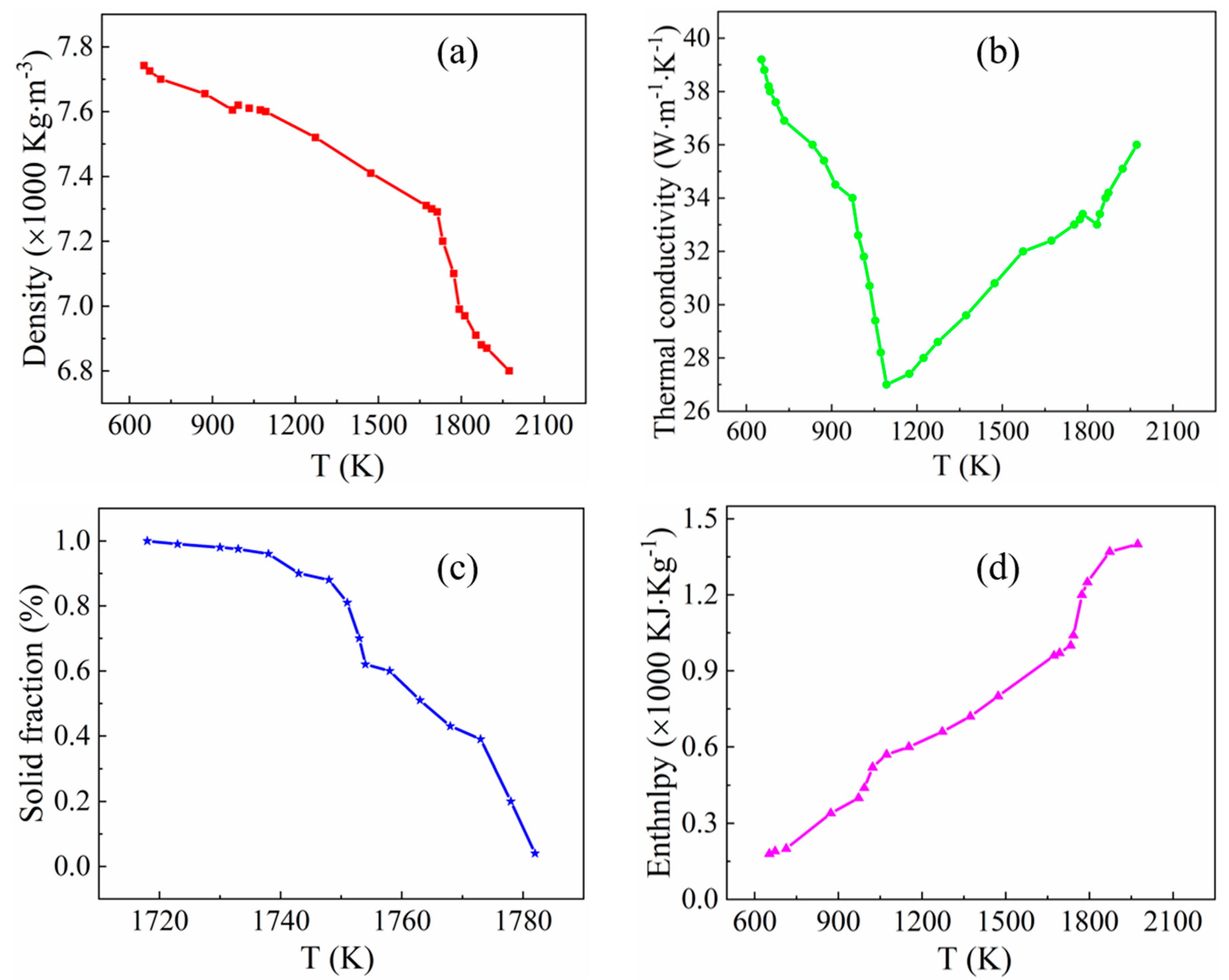
2.2. Thermo-Physical Properties
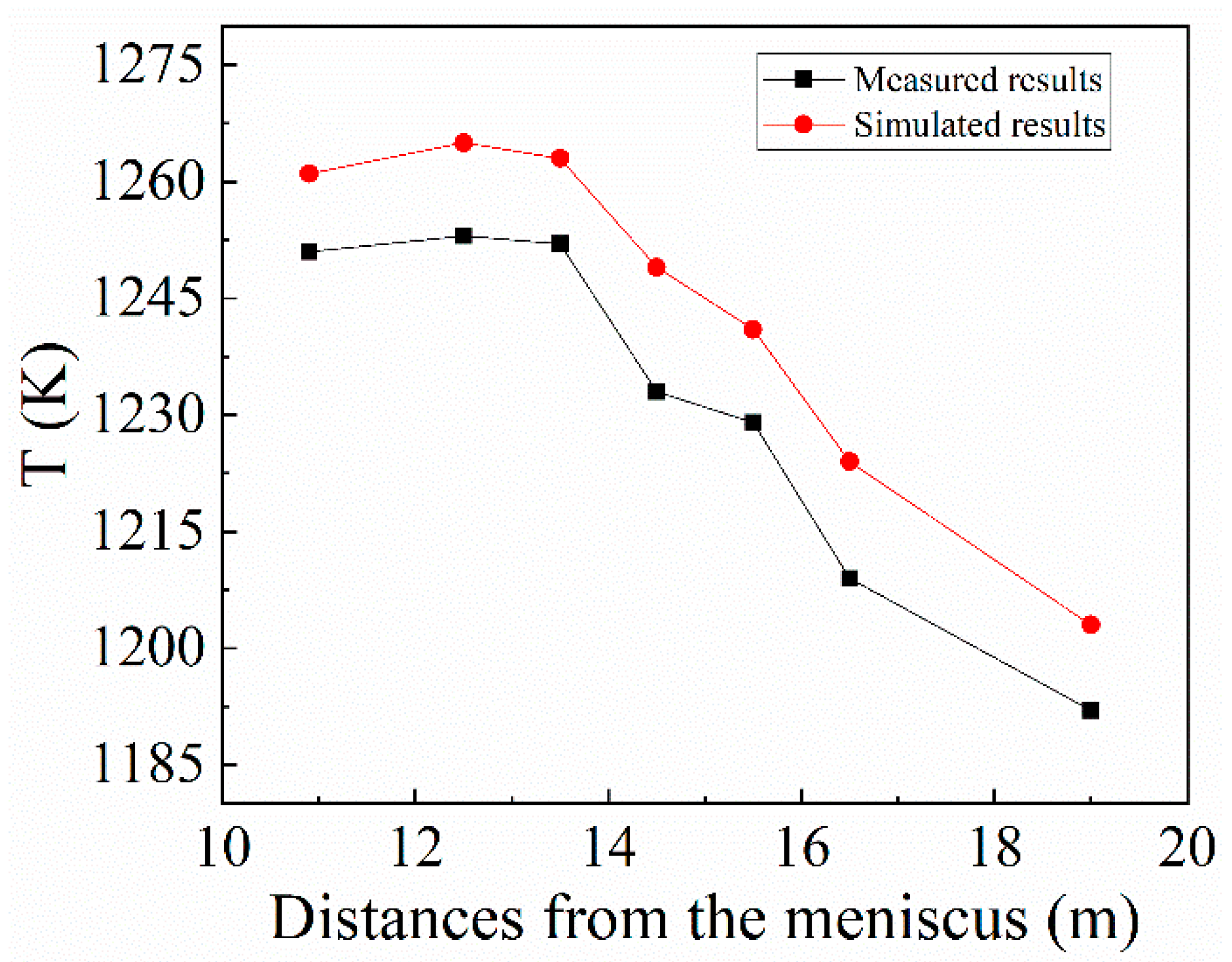
2.3. Model Verification
2.4. Industrial Trial Production
3. Results and Discussion
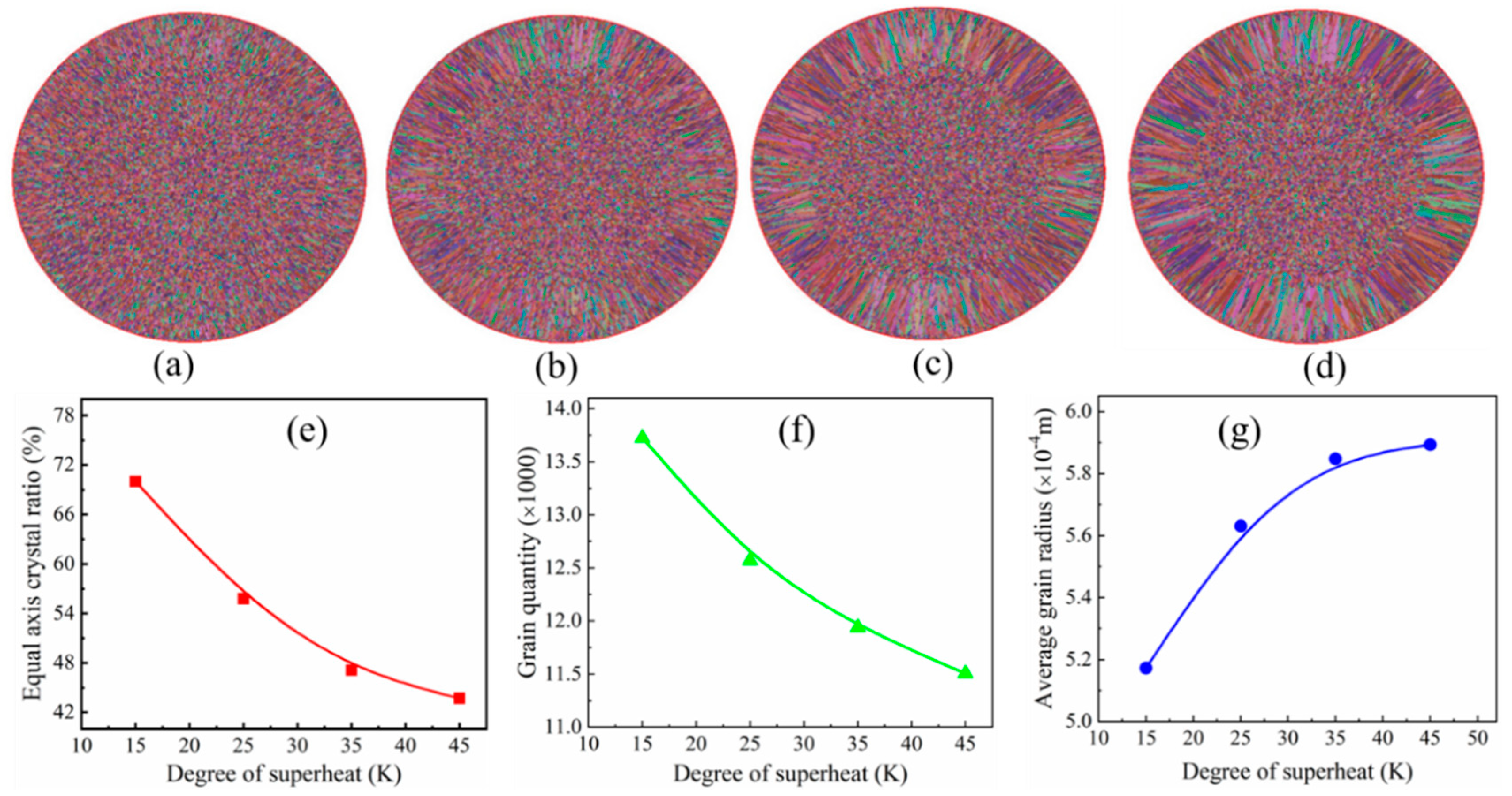
3.1. Influence of the Superheat Degree on the Solidification Structure
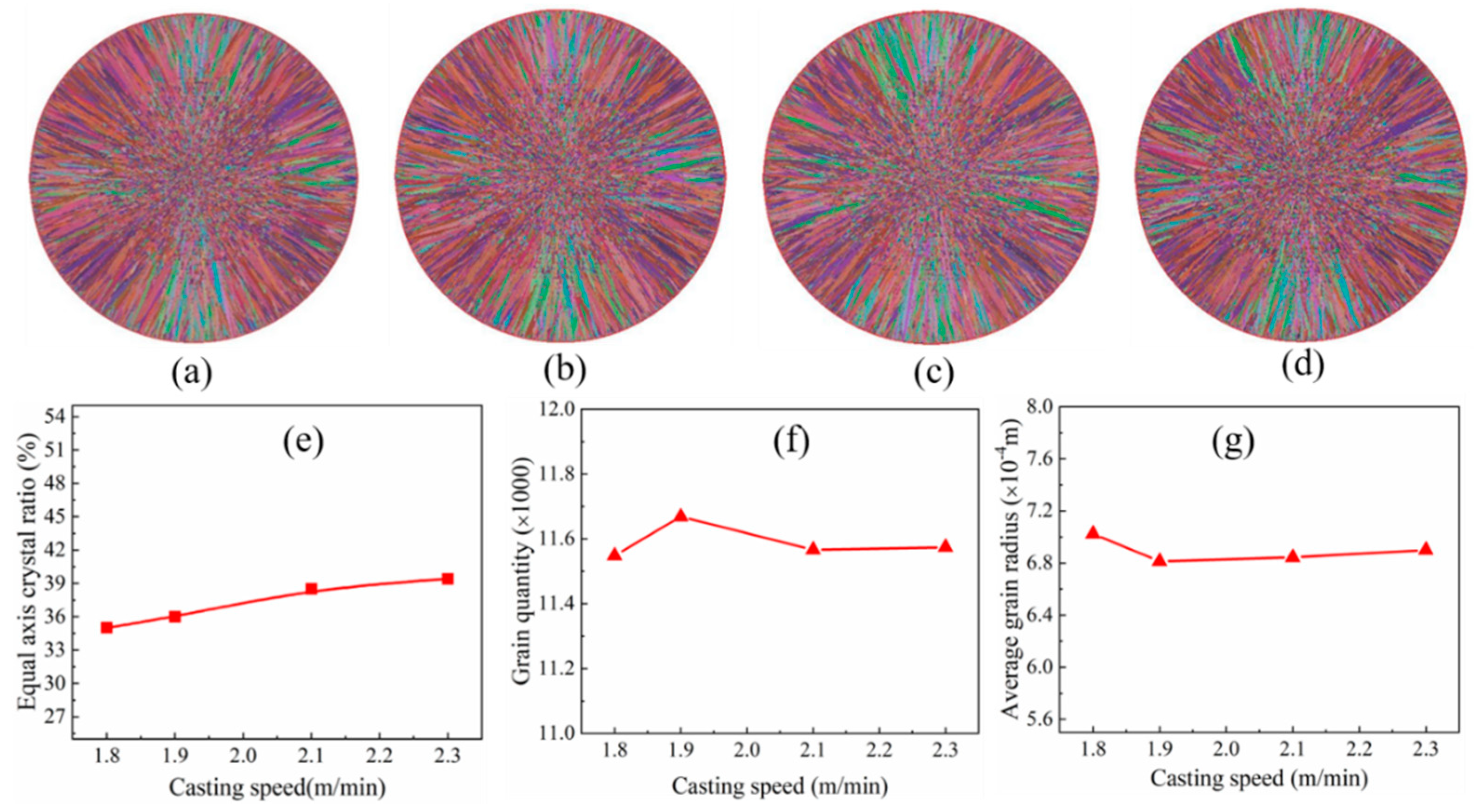
3.2. Influence of the Casting Speed on the Solidification Structure
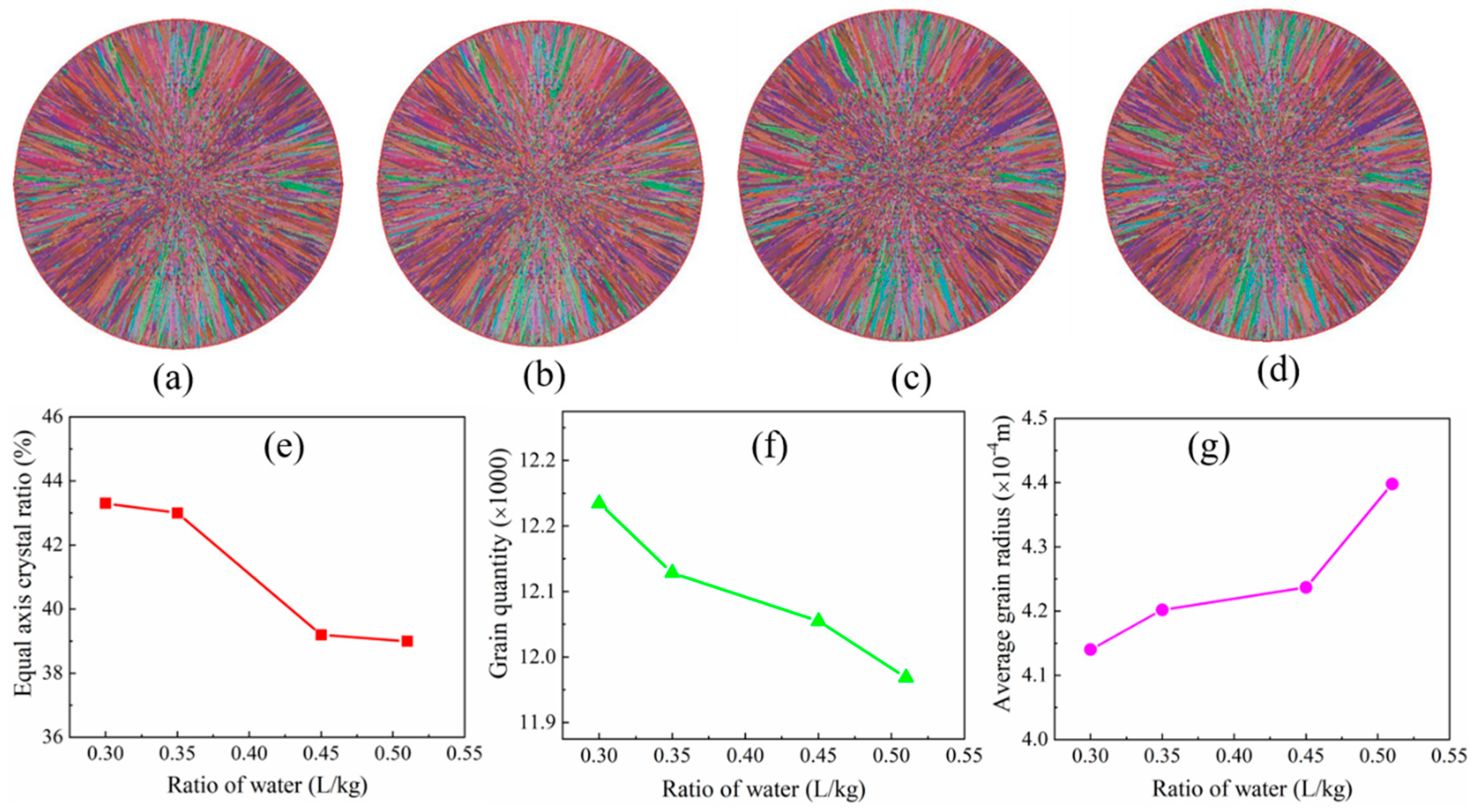
3.3. Influence of the Secondary Cooling Intensity on the Solidification Structure
3.4. Industrial Trial Production Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, H.-Y.; Li, Y.-H.; Wei, D.-D.; Liu, J.-J.; Wang, X.-F. Constitutive equation to predict elevated temperature flow stress of V150 grade oil casing steel. Mater. Sci. Eng. A 2011, 530, 367–372. [Google Scholar] [CrossRef]
- Thomas, B.G. Modeling of the continuous casting of steel-past, present, and future. Met. Mater. Trans. B 2002, 33, 795–812. [Google Scholar] [CrossRef]
- Mauder, T.; Stetina, J. High Quality Steel Casting by Using Advanced Mathematical Methods. Metals 2018, 8, 1019. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, H.; Tang, Q.; Pan, S.; Rettenmayr, M.; Zhu, M. Microstructural evolution during temperature gradient zone melting: Cellular automaton simulation and experiment. Comput. Mater. Sci. 2018, 146, 204–212. [Google Scholar] [CrossRef]
- Luo, S.; Zhu, M.Y. A two-dimensional model for the quantitative simulation of the dendritic growth with cellular automaton method. Comput. Mater. Sci. 2013, 71, 10–18. [Google Scholar] [CrossRef]
- Gandin, C.-A.; Desbiolles, J.-L.; Rappaz, M.; Thevoz, P. A three-dimensional cellular automation-finite element model for the prediction of solidification grain structures. Metall. Mater. Trans. A 1999, 30, 3153–3165. [Google Scholar] [CrossRef]
- Thévoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Wang, C.Y.; Beckermann, C. Prediction of Columnar to Equiaxed Transition during Diffusion-Controlled Dendritic Alloy Solidification. Metall. Mater. Trans. A 1994, 25, 1081–1093. [Google Scholar] [CrossRef]
- Bai, L.; Wang, B.; Zhong, H.; Ni, J.; Zhai, Q.; Zhang, J. Experimental and Numerical Simulations of the Solidification Process in Continuous Casting of Slab. Metals 2016, 6, 53. [Google Scholar] [CrossRef]
- Chen, S.; Chen, J. Micromodel of Simulation on Twin-Roll Continuous Casting Thin Strip Solidification Structure. Rare Metall. Mater. Eng. 2013, 1, 14–18. [Google Scholar]
- Fang, Q.; Ni, H.; Zhang, H.; Wang, B.; Liu, C. Numerical Study on Solidification Behavior and Structure of Continuously Cast U71Mn Steel. Metals 2017, 7, 483. [Google Scholar] [CrossRef]
- Zhu, H.-C.; Jiang, Z.-H.; Li, H.-B.; Zhu, J.-H.; Feng, H.; Zhang, S.-C.; Zhang, B.-B.; Wang, P.-B.; Liu, G.-H. Effect of Solidification Pressure on Compactness Degree of 19Cr14Mn0.9N High Nitrogen Steel Using CAFE Method. Steel Res. Int. 2017, 88, 1600509. [Google Scholar] [CrossRef]
- Zhai, Y.; Ma, B.; Li, Y.; Jiang, Z. Analysis of 13Cr bloom solidification structure using CA-FE model. J. Cent. South Univ. 2016, 23, 10–17. [Google Scholar] [CrossRef]
- Hou, Z.; Cheng, G.; Jiang, F.; Qian, G. Compactness Degree of Longitudinal Section of Outer Columnar Grain Zone in Continuous Casting Billet Using Cellular Automaton-Finite Element Method. ISIJ Int. 2013, 53, 655–664. [Google Scholar] [CrossRef] [Green Version]
- Cailiang, J.; Zhigang, X.; Ying, W.; Wanjun, W. Simulation on solidification structure of 72A tire cord steel billet using CAFE method. China Foundry 2012, 9, 53–59. [Google Scholar]
- Hou, Z.; Jiang, F.; Cheng, G. Solidification Structure and Compactness Degree of Central Equiaxed Grain Zone in Continuous Casting Billet Using Cellular Automaton-Finite Element Method. ISIJ Int. 2012, 52, 1301–1309. [Google Scholar] [CrossRef]
- Luo, Y.Z.; Zhang, J.M.; Wei, X.D.; Xiao, C.; Hu, Z.F.; Yuan, Y.Y.; Chen, S.D. Numerical simulation of solidification structure of high carbon SWRH77B billet based on the CAFE method. Ironmak. Steelmak. 2012, 39, 26–30. [Google Scholar] [CrossRef]
- Louhenkilpi, S.; Laitinen, E.; Nieminen, R. Real-time simulation of heat transfer in continuous casting. Metall. Trans. B 1993, 24, 685–693. [Google Scholar] [CrossRef]
- Thomas, B.G.; Najjar, F.M. Finite element modelling of turbulent fluid flow and heat transfer in continuous casting. Appl. Math. Model. 1991, 15, 226–243. [Google Scholar] [CrossRef]
- Tieu, A.K.; Kim, I.S. Simulation of the continuous casting process by a mathematical model. Int. J. Mech. Sci. 1997, 39, 185–192. [Google Scholar] [CrossRef]
- Li, C.; Thomas, B.G. Thermomechanical finite-element model of shell behavior in continuous casting of steel. Met. Mater. Trans. B 2004, 35, 1151–1172. [Google Scholar] [CrossRef]
- Han, H.N.; Lee, J.-E.; Yeo, T.; Won, Y.M.; Kim, K.; Oh, K.H.; Yoon, J.-K. A Finite Element Model for 2-Dimensional Slice of Cast Strand. ISIJ Int. 1999, 39, 445–454. [Google Scholar] [CrossRef]
- Choudhary, S.K.; Mazumdar, D. Mathematical Modelling of Transport Phenomena in Continuous Casting of Steel. ISIJ Int. 1994, 34, 584–592. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R.K. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 5, 823–830. [Google Scholar] [CrossRef]


| Element | Mass Fraction (wt %) | Liquidus Slope in Binary Fe-X System | Partition Coefficient | Self-Diffusion Coefficient (m2/s) |
|---|---|---|---|---|
| C | 0.255 | −84.9 | 0.23 | 14.7 × 10−9 |
| Si | 0.25 | −17.9 | 0.65 | 1.4 × 10−9 |
| Mn | 0.48 | −3.3 | 0.45 | 1.6 × 10−9 |
| P | 0.01 | −32.6 | 0.09 | 3.1 × 10−9 |
| V | 0.10 | −36.7 | 0.98 | 11.0 × 10−9 |
| S | 0.001 | −5.1 | 0.01 | 0.7 × 10−9 |
| Cr | 0.50 | −0.6 | 0.47 | 1.6 × 10−9 |
| Mo | 0.75 | −5.7 | 0.80 | 1.1 × 10−9 |
| Parameter | Value |
|---|---|
| Crystallizer length (mm) | 900 |
| Crystallizer water volume (L/min) | 1700 |
| Cast billet size (mm) | Φ178 |
| Superheat degree (K) | 40 |
| Casting speed (m/min) | 1.9 |
| Specific water flow (L/Kg) | 0.64 |
| Cooling water ratio in the secondary cooling segment | 24:17:16:13 |
| Continuous Casting Process Plan | Superheat Degree (K) | Casting Speed (m/min) | Specific Water Flow (L/Kg) |
|---|---|---|---|
| Original process | 40 | 1.9 | 0.64 |
| Scheme I | 30 | 2.0 | 0.40 |
| Scheme II | 25 | 2.1 | 0.35 |
| Scheme III | 35 | 1.9 | 0.45 |
| Scheme | Original Process | I | II | III |
|---|---|---|---|---|
| Equiaxed crystal ratio (%) | 37.0 | 41.8 | 45.2 | 39.6 |
| Improvement (%) | 0 | 4.8 | 8.2 | 2.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, Y.; Pan, K.; Wu, D. Acquiring High-Quality Oil Casing Steel 26CrMoVTiB under Optimal Continuous Casting Process Conditions. Metals 2019, 9, 993. https://doi.org/10.3390/met9090993
Zhai Y, Pan K, Wu D. Acquiring High-Quality Oil Casing Steel 26CrMoVTiB under Optimal Continuous Casting Process Conditions. Metals. 2019; 9(9):993. https://doi.org/10.3390/met9090993
Chicago/Turabian StyleZhai, Yingying, Kefeng Pan, and Dapeng Wu. 2019. "Acquiring High-Quality Oil Casing Steel 26CrMoVTiB under Optimal Continuous Casting Process Conditions" Metals 9, no. 9: 993. https://doi.org/10.3390/met9090993




