Simulation of Thermal Stress and Fatigue Life Prediction of High Speed Steel Work Roll during Hot Rolling Considering the Initial Residual Stress

Abstract

Considerable residual stress is produced during heat treatment. Compressive residual stress at the shell is conductive to improving the thermal fatigue life of a work roll, while tensile stress in the core could cause thermal breakage. In hot rolling, thermal stress occurs under the heating-cooling cycles over the roll surface due to the contact with the hot strip and water spray cooling. The combination of thermal stress and residual stress remarkably influences the life of a work roll. In this paper, finite element method (FEM) simulation of hot rolling is performed by treating the residual stress as the initial stress. Afterwards, the effects of the initial roll temperature and cooling conditions on thermal stress considering the initial residual stress are discussed. Lastly, the thermal fatigue life of a work roll is estimated based on the strain life model. The higher initial roll temperature causes a higher temperature but a lower compressive thermal stress at the roll surface. The surface temperature and compressive stress increase significantly in the insufficient cooling conditions, as well as the center tensile stress. The calculation of the fatigue life of a work roll based on the universal slopes model according to the 10% rule and 20% rule is reasonable compared with experimental results.

1. Introduction

The surface deterioration of work rolls used for hot strip rolling mills constitutes a significant constraint on the operation of hot mills, as the mill efficiency and rolled product quality are greatly influenced by the performance of the surface condition of the work rolls in service. The work roll surface in hot rolling is subjected to the combined effects of thermal and mechanical loadings. They are residual stresses produced during the roll manufacturing, thermal stress caused by the strip heating and water cooling, and mechanical stress induced by rolling pressures and contact actions with backup rolls. Considerable residual stress is introduced into work rolls due to the high temperature gradient and phase transformation during heat treatment. This stress is expressed as compression at the shell and tension at the core [1]. The severe temperature gradient is localized in a thin layer near the roll surface during hot rolling, since work rolls undergo cyclic heating and cooling due to their contact with the hot strip and water cooling in each revolution [2,3]. In the bite region, the temperature differences between the surface and roll body are adequately great, large compressive thermal stress is induced in the surface. In the cooling region, the surface is cooled by water spray, and the large tensile thermal stress is also induced. Thus, tensile and compressive stress states alternate on the roll surface. In hot rolling, thermal stresses are usually comparable to, or even larger than, mechanical stress, especially in the initial mill stands [3,4]. The thermal stress resulting in thermal fatigue is generally more important than the fatigue caused by purely mechanical stress [5,6]. Therefore, in this paper, only the thermal stress was investigated considering the initial residual stress. Surface cracking caused by thermal fatigue and abrasion is accepted as the two main factors on roll wear in hot strip rolling. Several studies have been conducted to investigate the relationship between the thermo-mechanical fatigue behaviour of the roll and roll wear [4,7]. In addition, thermal stress is combined with residual stress and impacts the service life of a work roll. Generally, compressive residual stresses, deliberately introduced through an adequate heat treatment, will suppress crack initiation and growth, as well as stress corrosion and fatigue [5,8]. However, tensile residual stress is added to tensile thermal stress in the roll core, causing thermal fractures to emerge in the roll centre and break out to the surface [9]. Therefore, an investigation on thermal stress considering the initial residual stress in the work roll during hot rolling is important for the clarification of the roll failure mechanism and to conduct a roll fatigue life evaluation.

Various methods have been used to investigate the thermal behavior of high speed steel (HSS) work rolls during hot rolling. Gao et al. studied temperature variations of HSS work rolls to determine the thermal crown in the rolls and compared their findings with the results of a high-Cr roll using the FEM model [10]. Deng et al. investigated the temperature and thermal stress fields to evaluate the oxidation behaviour of HSS work rolls [11,12]. Dünckelmeyer et al. proposed an analytical model to predict the surface temperature and thermal stresses in HSS work rolls [13]. Ryu et al. conducted thermal fatigue tests at temperature ranging from 200 to 600 °C to estimate the thermal fatigue property of high speed steel used for work roll [14]. A series of tests were performed on HSS rolls and high-carbon, high-chromium rolls by Mercado-Solis et al. with a stand-alone twin-disc machine to simulate the thermal fatigue of work rolls [15]. Then, similar experiment was carried out by Garza-Montes-de-Oca, who simulated the thermal damage of high speed steel caused by thermal cycling [16]. However, few studies have considered the combination of residual stress and thermal stress in work rolls during the hot rolling process. Additionally, the fatigue life of HSS work rolls using the practical hot rolling parameters has not been studied yet. Although the residual stress in work rolls has been investigated, these studies were limited to investigating quenching or tempering, while the thermal stress during hot rolling was not taken into account [17,18]. In our previous studies, the simulation of thermal stress and residual stress were performed on the basis of a simplified thermo-elastic model [19]. In fact, the compressive thermal stress is high enough to cause yielding with plastic deformation in the bite region, and tensile yield stress may develop if the roll surface is cooled sufficiently in the cooling region. The thermo-plastic behavior of the roll surface is the dominant factor of roll thermal fatigue.

In this paper, the thermo-mechanical coupled simulations of heat treatment and hot rolling are performed using the elastic-plastic finite element method (FEM). Firstly, the simulation of heat treatment is conducted for a better understanding of the generation mechanism of residual stress in the work roll. Subsequently, temperature simulation of work roll in the early stage of front finishing stands is performed using a 2D finite element model to avoid modeling the deformed strip and backup rolls. The effects of rotating heating and cooling thermal conditions of an actual hot rolling were applied on roll surface through the ambient temperature and the heat transfer coefficients. It should be noted that strip plastic deformation, as well as mechanical loads and friction at the interface between work roll and, respectively, strip and backup roll, are not included in the analysis. Then thermal stress considering the initial residual stress is compared with the thermal stress without considering the initial residual stress to clarify the combination of residual stress and thermal stress during hot rolling. Then, effects of the initial roll temperature and cooling conditions are discussed in relation to temperature and thermal stress within the work roll during hot rolling. Finally, the thermal fatigue life of the work roll is estimated using the strain-life model.

2. FEM Simulations

2.1. FEM Model Description

The work roll used in this study, composed of high speed steel (HSS) as the shell material and ductile casting iron (DCI) as the core material, is manufactured by the centrifugal casting method. HSS work rolls are widely used in hot rolling because of their excellent hardness, wear resistance, and high temperature properties. The chemical compositions of the HSS and DCI of the work roll and the material properties at room temperature are given in

Table 1. Chemical composition of the high speed steel (HSS) work roll, wt%.

Material	C	Si	Mn	P	S	Ni	Cr	Mo	Co	V	W	Mg
HSS	1–3	<2	<1.5			<5	2–7	<10	<10	3–10	<20	<10
DCI	2.5–4	1.5–3.1	-	<0.1	<0.1	0.4–5	0.01–1.5	0.1–1	-	-	-	0.02–0.08

and

Table 2. Mechanical and thermal properties of the HSS work roll at room temperature.

Property	HSS	DCI
Young’s modulus/GPa	233	173
Poisson’s ratio	0.3	0.3
Density/kg m−3	7600	7300
Thermal expansion coefficient/K−1	12.6 × 10−6	13.0 × 10−6
Thermal conductivity/W (m K)−1	20.2	23.4
Specific heat/J (kg K)−1	461	460
Tensile strength/MPa	1280	415

, respectively.

As illustrated in Figure 1a, the whole roll was heated up to a uniform temperature and the temperature was kept for several hours before the quenching process. Then, the roll temperature dropped rapidly through air cooling. Afterwards, the roll was put into the furnace again and maintained to prevent excessive stress caused by a high thermal gradient. After this maintenance period, the roll was cooled down slowly to room temperature. After the quenching process, the tempering process, including heating, maintenance and cooling, was performed twice to release the residual stress and obtain a stable microstructure. During hot rolling, the roll surface was heated in the bite region and cooled by air and water spray. Figure 1b shows the thermal boundary conditions along the circumferential direction of the work roll during one revolution. Region 1–2 involves high heat flow between the work roll and hot strip; regions 2–3, 5–7, and 9−1 involve natural air cooling without the strip radiation at the entrance and exit, as well as the heat exchange between work roll and backup roll; regions 3–4 and 8–9 involve wiper cooling; regions 4–5 and 7–8 involve water spraying cooling.

During the heat treatment process, the surface temperature along the circumferential direction was heated and cooled symmetrically; thus, the FEM model in the axial plane of a half-length of the work roll using a four-node axisymmetric quad element was used to simulate the temperature and residual stress. As shown in Figure 1c, the thermal isolation conditions and displacement boundary conditions were applied to z = 0 and y = 0 due to the geometric symmetry of the work roll. This thermo-elastic-plastic model was consisted of 4680 elements and considered the Von Mises yield criterion and isotropic strain hardening rule. The simulation of heat treatment was carried out by imposing the experimental measured surface temperature on the roll surface of the FEM model. It should be noted that the surface temperature during hot rolling is asymmetric due to the heat transfer along the circumferential direction. Generally, a 3D model of the work roll is justified for the thermo-mechanical analysis of hot rolling, while it also needs multiplied computational effort and time. Therefore, a 2D model in the circumferential plane was applied for temperature evaluation of the work roll during hot rolling [12,19]. As shown in Figure 1d, a mesh refinement was imposed near the surface along both the circumferential and radial directions to capture the great thermal gradient there. In the hot rolling, a very large thermal gradient in a very short time was imposed on the roll surface within a thin layer. Therefore, the computational mesh condition of a work roll leads to large influence on its temperature accuracy during hot strip rolling process. In this paper, the 360 elements with an angular distance of 1° along the circumferential direction were meshed [3]. In order to obtained optimal mesh size in radial direction, a series of mesh sensitivity tests was conducted to investigate the accuracy of FEM model in terms of the maximum temperature at the roll surface and the computational time. The results of the mesh sensitivity test illustrated that the maximum roll surface temperature became higher with fining the mesh to 22 elements within 1% of the roll radius (total elements of work roll was 23,400), and then did not increase with further meshing. By contrast, the computational time increased rapidly. However, a 2D model in the circumferential plane was not applicable to the thermal stress evaluation considering a non-uniform temperature in the axial direction. In this study, the surface temperature obtained from the 2D model in the circumferential plane was applied to the axial plane model shown in Figure 1c and used for the simulation of thermal stress. In the temperature simulation of the work roll during hot rolling, a uniform initial temperature of 30 °C was assumed for the work roll by neglecting the temperature variation along the axial direction. It should also be noted that the heat generation caused by strip deformation, friction, and radiation of the hot strip at the entrance and exit are ignored because of their slight effects on the work roll temperature. Since the temperature variation range (about 20–1100 °C) is very large for both heat treatment and hot rolling, temperature-dependent material properties were used for the simulation to ensure the accuracy of the FEM results. The test specimens were cut from HSS work roll after tempering and the material properties of HSS and DCI used in this study were measured experimentally at room temperature and 100–600 °C with an interval of 100 °C [20].

2.2. Heat Transfer Coefficients of the Work Roll during Hot Rolling

Heat transfer coefficients vary on different parts of the work roll surface and are usually difficult to obtain, because they are closely related to many rolling parameters including the initial temperature and material of the work roll and hot strip, the nozzle spraying cooling condition, the oxidation layer, and so on [21,22,23]. In previous decades, many researchers have tried to clarify the heat transfer coefficients of the work roll by theoretical calculations or experimental measurements. However, reports on the heat transfer coefficients have been inconsistent. The heat transfer coefficients used in this study were calculated based on the practical industrial hot rolling parameters of the first stand of hot strip finishing rolling given in

Table 3. Parameters of the work roll during hot rolling.

Parameters	Surface Region	Value
Velocity of the work roll/m·s−1 Rolling pressure [kN]	-	1.2419990
Roll diameter/mm	-	830
Rolling reduction	-	43.6%
Initial work roll temperature/°C	-	30
Entry strip temperature/°C	-	1030
Air/water temperature/°C	-	30
Entry strip temperature/°C	-	1030
Entry strip width/mm	-	1040
Water pressure/MPa	-	1.47
Water flow/L·min−1	-	2500
Heat transfer coefficient/W (m2·K)−1	Bite region	45,000
	Wiper cooling	14,600
	Water cooling	32,600
	Air cooling	5

. The calculation methods of heat transfer coefficients for the HSS work roll during hot rolling used in this study were as follows.

In the bite region (1–2), the heat transfer coefficient h_con was calculated using an empirical equation considering the rolling pressure and the surface flow stress of the work piece derived by Hlady et al. [24]:

$$h_{\mathrm{con}}=\frac{k}{C}(\frac{P_r}{\mathsf{\sigma }(T_s,\overline{\dot{\mathsf{\epsilon }}})})$$

(1)

$$k=k_r{k}_s/(k_r+k_s)$$

(2)

where C = 35 × 10⁻⁶ is a general roughness term; k_s is the thermal conduction of the strip; P_r is the rolling pressure; and σ is the flow stress of strip calculated using the equation derived by Shida [20,25].

In the air cooling regions (2–3, 5–7, and 9–1), the heat transfer coefficients h_air were calculated using the following equation [26,27]:

$$h_{\mathrm{air}}=1.456{(T_{\mathrm{s}}-T_{\mathrm{a}})}^{1/3}$$

(3)

where T_a is the air temperature. A different h_air was applied to the simulation because of the higher roll surface temperature in zone 2−3 and the lower temperature in zones 5–7 and 9–1.

In the wiper cooling regions (3–4 and 8−9), similar calculation equations of heat transfer coefficients were proposed in [11,27]:

$$h_{\mathrm{wiper}}=0.023R_{\mathrm{e}}^{0.8}{P}_{\mathrm{rcw}}^{0.4}{k}_{\mathrm{cw}}/l_c$$

(4)

$$R_e={\mathsf{\nu }}_w{l}_c/{\mathsf{\upsilon }}_{cw}$$

(5)

$$P_{\mathrm{rcw}}={\rho }_{\mathrm{cw}}{c}_{\mathrm{cw}}{\mathsf{\upsilon }}_{\mathrm{cw}}/k_{\mathrm{cw}}$$

(6)

where R_e is the Reynolds number, P_rcw is the water Prandtl number, k_cw is the water thermal conductivity, l_c is the contact arc length along the roll surface of the wiper region, v_r is the roll velocity, υ_cw is the water kinematic viscosity, ρ_cw is the water density, and c_cw is the water specific heat.

In the spray cooling regions (4−5 and 7−8) the heat transfer coefficients considering the roll temperature can be given by [11,27]:

$$h_{\mathrm{cw}}=6870\times Q^{0.19}{P}_{\mathrm{sp}}^{0.27}(T_r\le 100 °\mathrm{C})$$

(7)

$$h_{\mathrm{cw}}=2.9\times {10}^6\times Q^{0.08}{P}_{\mathrm{sp}}^{0.05}\frac{B}{200-T_{\mathrm{wa}}}\times \frac{4815.5}{3600}(T_r\ge 100 °\mathrm{C})$$

(8)

$$\begin{array}{l}B={(T_{\mathrm{wa}}/16)}^{-0.17}(Q\ge 10,000(\mathrm{l}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}))\\ B=1.0(Q\le 10,000(\mathrm{l}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}))\end{array}$$

(9)

where Q = V_sp/A_sp is the water flow per unit area, V_sp is the water flow, A_sp is the water flow area, P_sp is the water pressure, and T_wa is the cooling water temperature.

3. Residual Stress in Work Rolls during Heat Treatment

3.1. Generation Mechanism of Residual Stress in the Work Rolls during Heat Treatment

Since the residual stress is the initial stress of the hot rolling simulation, the heat treatment simulation was performed first. During heat treatment, residual stress in work rolls can be attributed to the combined effects of thermal stress, transformation stress, and the material difference between the shell and core. In order to understand the generation mechanism of residual stress in the work rolls, the simulation was performed on a single material model with/without considering phase transformation (PT) and on a composite material model with/without considering phase transformation. It should be noted that the core material was applied to the simulation of single material models.

The thermal stress caused by the thermal gradient was simulated by single or composite material model without phase transformation while the surface underwent the quenching process shown in Figure 1a. As shown in Figure 2a, during the early stage of rapid cooling (from t₀ to t₁), the roll surface temperature dropped faster than the center temperature. Hence, the temperature differences between the center and surface continually increased. As a result, the tensile stress appeared at the roll surface and compressive stress appeared in the roll center. As the temperature decreased (from t₁ to t₂), the core temperature dropped faster than the surface temperature, leading to continuing decrease in the temperature differences. Thus the tensile stress in the roll surface and the compressive stress in the roll center were reversed to compressive and tensile stress, respectively. During the maintenance process (from t₂ to t₃), the surface temperature firstly rose and the temperature difference decreased to approximately zero. In this period, the stresses of the surface and center decreased slightly. At the beginning of cooling (from t₃ to t₄), since the surface temperature dropped faster than that in the center, the surface tensile stress started to increase slightly. At the last cooling period (from t₄ to t₅), the temperature difference gradually decreased but the stresses at the surface and center gradually increased. The tensile stresses reached 378 MPa in the roll center and the compressive stresses reached −354 MPa at the roll surface for the single material model. It can be seen that the higher thermal stresses appeared in the composite material model compared with the results of single material model. Since the thermal expansion coefficient of the shell material was smaller than the core material, the difference in thermal shrinkage of the composite model was larger than that in the single material model. Hence, the stress of composite material without PT increased underwent the same temperature difference.

In order to rule out the effect of the thermal gradient on transformation stress, slow cooling with a very small thermal gradient was carried out as shown in Figure 1a. The effect of transformation stress on residual stress was simulated by single and composite material models with phase transformation. As shown in Figure 2b, the maximum temperature difference was only 88 °C during the whole cooling process. At the beginning of slow cooling (from $t_0^{\prime }$ to $t_1^{\prime }$), the surface temperature dropped faster than the center temperature, leading to compressive stress at the surface and tensile stress at the core. During the cooling period (from $t_1^{\prime }$ to $t_2^{\prime }$), the pearlite transformation happened from the surface and expanded to the inner part of the rolls. Phase transformations with volume expansion resulted in compressive stress generation. As a result, compressive stress rapidly increased at the surface and the tensile stress rapidly decreased in the center. Then, the compressive stress gradually decreased when phase transformation expanded to the roll core (from $t_2^{\prime }$ to $t_3^{\prime }$). After the pearlite transformation (from $t_3^{\prime }$ to $t_6^{\prime }$), the stress at the surface and center was almost unchanged. Finally, the transformation stress reached 138 MPa in the surface and −205 MPa in the center for a single material. Compared with the results of the single material with PT, the pearlite transformation of the roll core was constrained by the shell material; thus, the center stress changed slightly (from $t_1^{\prime }$ to $t_2^{\prime }$). After the pearlite transformation (from $t_3^{\prime }$ to $t_4^{\prime }$), the stresses at the surface and center of the composite material remarkably increased because of difference in thermal shrinkage. During bainite transformation at the shell (from $t_4^{\prime }$ to $t_5^{\prime }$), the surface tensile stress rapidly decreased. Contrary to the single material models with phase transformation, the compressive stress and the tensile stress appeared in the surface and the center of the composite material model, respectively.

3.2. Residual Stress Distribution in Work Rolls after Heat Treatment

Figure 3 shows the distributions of the z-, r-, and $\theta$-component residual stresses in the work roll during the heat treatment process shown in Figure 1a. After the quenching process, a compressive stress of −660 MPa appeared at the surface and the tensile stress of 483 MPa appeared in the center under the integrated effects of thermal stress and transformation stress. It was found that high tensile stress was introduced into the roll center during quenching compared with the yield strength (415 MPa) of the core material. The residual stress after tempering is also indicated in Figure 3 as a comparison with the results after quenching. It can be seen that the maximum tensile residual stresses decreased significantly from 483 to 253 MPa at the roll center after the second tempering process and uniformly distributed at the core, but the large compressive residual stress of −617 MPa was retained at the roll surface. Therefore, the tempering was contributed to the decrease of high tensile stress in the roll core and the maintenance of enough compressive stress in the roll shell. This residual stress after the heat treatment was applied in the FEM simulation of hot rolling as the initial stress condition.

4. Thermal Stress Considering the Initial Residual Stress in the Work Rolls during Hot Rolling

4.1. Generation Mechanism of Thermal Stress in the Work Rolls during Hot Rolling

In order to validate the reliability of the temperature prediction model, the simulation was performed using the hot rolling conditions published by Stevens et al. [28] who measured the temperatures of a cast iron work roll using thermocouples at different depths from the roll surface. Figure 4a shows a comparison of temperatures between the simulated results and the measured results during the first revolution. It can be observed that the simulated surface temperature agreed well with the measured surface temperature. However, the measured temperatures at the depth of 3.6 mm and 6.8 mm increased slowly compared with the FEM results. This can be attributed to experimental errors caused by the operations and sensitivity of the thermocouples as well as the temperature independent material used in the simulation model.

In this paper, a hot rolling process consisting of ten strips was simulated. Figure 4b shows the temperature histories at the different depths from the roll surface during the first strip rolling process. R means the roll radius and r means the distance from the roll center. In this study, temperature variations of r/R = 1, 0.99, 0.98, and 0.95 were investigated to reveal the temperature changes in the radial direction of work roll. It should be noted that the temperature history during the first revolution is enlarged in Figure 4 to clearly display the temperature changes. Due to the heat transfer from the hot strip to the roll surface in the bite region, the surface temperature rose rapidly and the maximum surface temperature reached 587 °C (from 1 to 2). In the subsequent cooling region, the surface temperature dropped to 289 °C (from 2 to 5) due to the air convection and heat transfer inward. However, the slight increase of the surface temperature was observed instead of decrease (from 5 to 7) due to the heat transferred from subsurface where temperature was higher than the surface temperature. Then, further decrease of the surface temperature was attributed to the following water and wiper cooling (from 7 to 8). At last, the surface temperature slightly rose in the air-cooling region (from 9 to 1) and reached 56 °C. In the following revolutions, the maximum surface temperature gradually increased until reaching a stable value of 605 °C after ten revolutions due to the heat flowing into the roll surface and the heat flowing out of the roll surface reached a dynamic balance. A similar trend in temperature was observed at the subsurface at the depths of r/R = 0.99, 0.98, and 0.95. However, the temperature rising rate of subsurface lagged behind the surface because the heat transfer from the surface to inner needed a process. In addition, the amplitudes of temperature decreased significantly as the depth from the roll surface increased. During the hot rolling, the surface heating and cooling was alternate in a very short time. Thus, the great thermal gradient was limited to a very thin layer of the roll surface. Compared with the surface temperature reaching a stable maximum temperature, the temperature at the subsurface showed an upward tendency during the first strip rolling. Therefore, in the initial stage of the hot rolling process, the roll temperature presented a dynamic change trend. In particular, the subsurface temperature changed continually in the early stage of the hot rolling. Therefore, the products with lower product quality requirements could be rolled in the initial stage of hot rolling.

Figure 5a shows the histories in thermal stress ${\sigma }_z$ considering the initial residual stress at the different depths from the roll surface during the first strip rolling process. Since the surface temperature increased, causing volume expansion, the expansion of the surface element was constrained by the elements underneath which were at a lower temperature. Therefore, the compressive thermal stress rapidly increased in the bite region. As shown in Figure 5a, the maximum compressive stress increased to −1256 MPa considering the initial residual stress of −617 MPa (from 1 to 2). In the subsequent cooling region, the compressive stress decreases gradually due to the surface temperature decreasing (from 2 to 5). The compressive stress increased slightly corresponding to slight increase of the surface temperature (from 5 to 7). At point 8, which had the minimum temperature, the minimum compressive stress reached −338 MPa. In the following revolutions, the maximum surface compressive stress gradually increased until a stable value of −1301 MPa was reached after 10 revolutions due to the surface temperature reaching a steady state. Similar to the temperature variations at the subsurface, the stresses at the depths of r/R = 0.99, 0.98, and 0.95 were much smaller than that at the surface. In the hot rolling, heating of the roll surface caused compressive stress that was sufficiently high to exceed the yield stress in the roll surface and, thus, deform the roll surface plastically. When the roll was cooled, the surface contraction should initiate reverse plastic yielding. However, yielding did not occur in the reverse direction because the ductility of the roll material was not sufficient when the roll surface was cooled, and the roll material cannot withstand the high tensile stress during cooling. Therefore, plastic deformation occurred only in the heating period, but cyclic plastic strain did not develop in the cooling period as shown in Figure 5b. It can be found that large plastic strain occurred at the early revolutions and decreased continuously with every revolution, and became to pure elastic strain after 10 revolutions. The pure elastic strain denoted a steady state of the hysteresis loop, which means no further accumulation of plastic strains. This result can be observed clearly in Figure 5c. The plastic strain range in the z-component was 0.098% in the first revolution, but it reduced to 0.011% in the second revolution.

In order to investigate the combination of the initial residual stress and thermal stress during hot rolling, the thermo-elastic and thermo-plastic simulations of hot rolling without considering the initial residual stress were conducted. As shown in Figure 5c, in the thermal-plastic analysis without considering the initial residual stress, the maximum compressive stress reached −576 MPa and the maximum tensile reached 348 MPa. Note that this tensile stress appearing in the cooling region contradicted previous studies. The previous studies showed that tensile stress was generated when the initial work roll temperature was 100–200 °C [23,29], and tensile stress was not observed when the initial work roll temperature was 30 °C [2,11]. This disagreement can be attributed to the plastic deformation produced in this study. With regard to the HSS work roll considering plastic deformation, the tensile stress was also observed in the work roll when the initial work roll temperature was 30 °C [13]. Compared with the thermo-plastic results without considering the initial residual stress, in the case of the thermo-elastic analysis, a larger maximum compressive stress of −926 MPa was reached without plastic yield, and no tensile stress was produced in the cooling region.

Figure 6 shows the distributions of the temperature and thermal stress considering the initial residual stress at the roll surface along longitudinal direction with the rolling time. However, it should be noted that these stresses were not the final stress states after rolling; but were just the transient values at the ending of a strip rolling. As shown in Figure 6a, a uniform temperature was seen at the contact area between the work roll and hot strip, while the temperatures near the roll body edge were almost unchanged. Hence, a great thermal gradient appeared at the contact boundary between the work roll and hot strip. Compared with the maximum surface temperature which reached a stable value, the surface temperature at the end of a strip rolling increased slightly with time due to the temperature increase of subsurface. As shown in Figure 6b, the initial residual stress distributed uniformly near the cross section of the work roll and decreased rapidly close to the roll body edge. The residual stress at the roll surface along the axial direction in this paper agreed well with the experimental measurements using magnetic Barkhausen noise method described in [30]. Compared with the initial residual stress, the stress decreased uniformly in the contact area at the ending of hot rolling. The stress near the roll body edge was almost unchanged, because the heat was not transferred to the roll body edge. In addition, it should be noted that the stresses decreased from −320 to −240 MPa when the rolling time increased from after two strips rolling to 10 strips rolling. This result can be attributed to the decrease in temperature difference between the surface and core with the continuous rolling.

Figure 7 shows the distributions of temperature and thermal stress considering the initial residual stress along the radial direction with the rolling time. It can be found that the maximum temperatures appeared at 6 mm below the roll surface. However, very slight increase (only 5 °C) was observed after six strips rolling, thus it can be assumed that the maximum subsurface temperature reached a stable state. Since the idling process was not considered in this paper, the surface heat was transferred continuously to the roll core, leading to the depth of thermal penetrations increasing over time. As shown in Figure 7b, compared with the initial residual stress, the thermal stresses at the shell changed significantly near the surface, while the tensile stresses at the core increased gradually during the whole rolling and reached 367 MPa after ten strips rolling. The high tensile stress at the roll core is the main factor in thermal breakage originating from the roll center once the tensile stress exceeds the material strength. The tensile stress of 376 MPa after ten strips rolling was close to the core material strength of 415 MPa. Therefore, the high throughput of hot strips can cause high tensile stress at the roll core in the early stage of hot rolling.

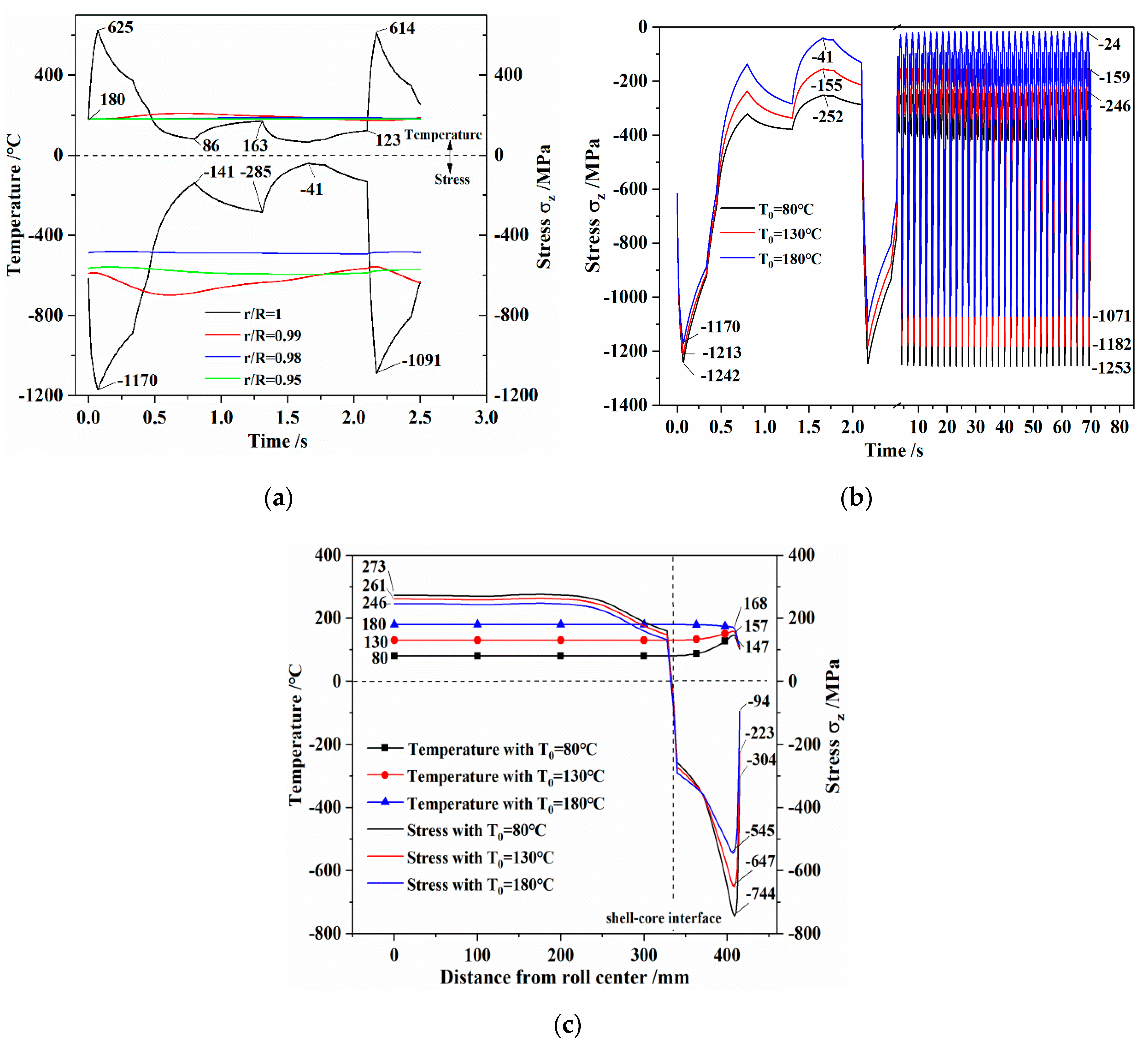
4.2. Effects of the Initial Work Roll Temperature and Cooling Conditions on Thermal Stress in Work Rolls during Hot Rolling

4.2.1. Effect of the Initial Temperature of Work Rolls on Thermal Stress during Hot Rolling

The temperature distribution in work rolls, especially the maximum temperature difference between the roll surface and roll center, has a very serious impact on the service life of work rolls. In this study, the temperature difference induced by the initial roll temperature and cooling conditions was simulated to investigate their effects on thermal stress. The initial roll temperatures of 80, 130, and 180 °C were compared with the results at 30 °C. In fact, the initial temperature of 30 °C is only available for the early stage of hot rolling, while 180 °C is usually difficult to reach in practical hot rolling processes. Since this paper aimed to reveal the thermal stress considering the initial residual stress, a large initial roll temperature was considered to obtain an evident influence.

Figure 8a shows the variations in temperature and thermal stress with the initial roll temperature of 180 °C during the first revolutions. Compared with the temperature at the initial roll temperature of 30 °C, a higher maximum temperature of 625 °C was reached, while an approximate temperature of 86 °C was observed at the end of the first revolution when the initial roll temperature is 180 °C. As has been introduced in Figure 4, the maximum temperature increased with every revolution until a stable maximum temperature was reached after 10 revolutions when the initial roll temperature was set to 30 °C. However, a different result is found when the initial roll temperature is 180 °C. As shown in Figure 8a, the maximum temperature decreased from 625 °C to 614 °C in the second revolution, and then a stable value of 611 °C was reached after six revolutions. With the increase of the initial roll temperature, the surface temperature can reach a higher maximum temperature when the same heat flowing into roll. Compared with the result at the initial roll temperature of 30 °C, the maximum compressive stress decreased from −1256 to −1170 MPa when the initial roll temperature was set to 180 °C, owing to the decrease in temperature difference between the initial temperature and maximum temperature. Instead, the minimum compressive stress decreased from −338 to −41 MPa due to the increase in temperature difference between the maximum temperature and the minimum temperature. The tensile stress of 576 MPa prevailed on the roll surface in the cooling region when the initial residual stress was not considered. In the linear elastic case, the thermal stress components in the roll surface which underwent temperature action were estimated by [31]:

$${\mathsf{\sigma }}_{\mathrm{r}}=0,{\mathsf{\sigma }}_{\mathrm{z}}={\mathsf{\sigma }}_{\mathsf{\theta }}=-\frac{\mathsf{\alpha }E\Delta T}{1-\mathsf{\nu }}$$

(10)

where α is the thermal expansion coefficient, E is the Young’s modulus, ν is the Poisson’s ratio, ΔT is the temperature difference between the surface and core. Compressive stress will be generated if ΔT > 0; otherwise, tensile stress will be generated. Since the core temperature of 180 °C was larger than the surface temperature, the tensile stress must be developed during cooling region. Figure 8c shows the distribution of temperature and stress with different initial roll temperatures after one strip rolling. Similar to the results with the initial roll temperature of 30 °C, the maximum compressive stress appeared at subsurface when the initial roll temperature was set to 80 °C or 130 °C. With an increase in the initial roll temperature, the tensile stress in the roll center decreased due to the temperature difference between the shell and core decrease.

4.2.2. Effect of Cooling Conditions on Thermal Stress during Hot Rolling

Although a considerable tensile stress of 367 MPa appeared at the roll center when considering the initial residual stress during hot rolling, the excessive tensile stress causing roll damage (e.g., fire crack, saddle spalls, and even thermal breakage) may be promoted under poor cooling conditions or mill stall. Under the poor cooling conditions, the roll surface cannot be cooled sufficiently, leading to the heat penetrating deeper into the roll body and intensifying the tensile stress in the core [32]. In the case of a mill stall, the work roll can remain in contact with the hot strip for a considerable amount of time and the roll surface temperature can increase rapidly. Since this paper aimed to reveal the effect of cooling conditions on thermal stress instead of optimizing the cooling conditions, three extreme cases were investigated as follows: complete cooling, without water spray cooling and mill stop. Complete cooling means that the surface regions, except for the bite region, were cooled by water spray. Without water spray cooling means that all of the surface regions were cooled by air. Mill stall means that the roll surface was in constant contact with the hot strip in the localized area.

Figure 9 shows the distributions of temperature and thermal stress considering the initial residual stress in the work roll after one strip rolling under different cooling conditions. Compared with the temperature of normal cooling conditions, the surface temperature decreased from 104 to 35 °C and the tensile stress increased slightly in the complete cooling condition. During a without water spray cooling condition, the surface temperature cannot be cooled sufficiently, which leaded to a high temperature was remained at the end of the rolling. As shown in Figure 9, the maximum temperature of 583 °C appeared at the surface and the maximum tensile stress increased to 370 MPa at the center. During a mill stall or a sudden stop of the rolling mill, the hot strip was in contact with the work roll surface for an extended period of time. The contact time can reach at least several minutes, which only 70 s, was simulated in this study. Due to extended holding of rolls at high temperatures of 1030 °C, the local overheating of work rolls appeared and the maximum temperature reached 1013 °C at the end of the rolling. During that time, the overheated surface expands in radial direction and contracts in axial and tangential direction, thus a large compressive stress of −1552 MPa appeared at the surface. When the remaining stresses exceed the yield strength of the material, the stall band fire cracks could appear at the surface with netlike shape. In addition, the tensile stress in the roll center increased significantly to 445 MPa due to increasing temperature difference between the surface and center.

5. Prediction of the Thermal Fatigue Life of Work Rolls during Hot Rolling

It is generally accepted that the thermal fatigue of a work roll is the typical low cycle thermal fatigue, since the accumulation of plastic strain under high thermal stress exceeds the elastic range of the shell material [14,15,16]. The strain-based fatigue life method is widely used in low-cycle fatigue life prediction, which represents the relationship between the strain amplitude and fatigue life. Basquin’s equation is the most commonly accepted, which could be expressed with the true elastic strain amplitude and fatigue life as follows [33]:

$${\mathsf{\epsilon }}_{\mathrm{e}}=\frac{{\mathsf{\sigma }}_{\mathrm{f}}^{\prime }}{E}{(2N_{\mathrm{f}})}^b$$

(11)

where ε_e is the elastic strain amplitude, ${\mathsf{\sigma }}_{\mathrm{f}}^{\prime }$ is the fatigue strength coefficient, E is the elastic modulus, N_f is the fatigue life, and b is the fatigue strength exponent. Afterwards, the plastic strain amplitude was taken into account by Manson and Coffin, which could be expressed as [34]:

$${\mathsf{\epsilon }}_{\mathrm{p}}={\mathsf{\epsilon }}_{\mathrm{f}}^{\prime }{(2N_{\mathrm{f}})}^c$$

(12)

where ${\mathsf{\epsilon }}_{\mathrm{p}}$ is the plastic strain amplitude, ${\mathsf{\epsilon }}_{\mathrm{f}}^{\prime }$ is the fatigue ductility coefficient, and c is the fatigue ductility exponent. This equation is widely used in fatigue life prediction of the work roll during hot rolling. For example, the fatigue life of a work roll is estimated by Stenvens et al., Williams and Boxall, Corral, and Sun et al. using the hoop plastic strain range [7,23,28,29]. However, Equation (12) has a drawback, that is, it can only be applied to a uniaxial state of the roll surface by neglecting the contribution of the elastic strain. It also can be found that the lack of a cyclic plastic strain range in the cooling region would make a fatigue life estimation based on Equation (12) somewhat problematic. Therefore, the total strain range instead of only plastic strain range should be taken into account.

The relationship between the total strain amplitude and fatigue life proposed by Manson and Coffin is most widely accepted as being represented by the following equations [35]:

$$\frac{\mathsf{\Delta }\mathsf{\epsilon }}{2}={\mathsf{\epsilon }}_{\mathrm{a}}={\mathsf{\epsilon }}_{\mathrm{e}}+{\mathsf{\epsilon }}_{\mathrm{p}}=\frac{{\mathsf{\sigma }}_{\mathrm{f}}^{\prime }}{E}{(2N_{\mathrm{f}})}^b+{\mathsf{\epsilon }}_{\mathrm{f}}^{\prime }{(2N_{\mathrm{f}})}^c$$

(13)

where ε_a is the total strain amplitude. In this equation, the fatigue life is correlated with the total strain amplitude instead of computing the relative amplitude of elastic and plastic strain. Generally, the fatigue parameters can be obtained through uniaxial fatigue tests. However, uniaxial fatigue tests are usually time-consuming and high cost. The situation becomes even more difficult if the loading condition is multi-axial [36]. An alternative method, which relates strain and cycles to low cycle fatigue, is the Universal Slopes equation, which assumes that the elastic and plastic lines have unique slopes (b = −0.12 and c = −0.6, respectively) for all materials [37,38]:

$$\mathsf{\Delta }\mathsf{\epsilon }={\mathsf{\epsilon }}_{\mathrm{e}}+{\mathsf{\epsilon }}_{\mathrm{p}}=3.5\frac{{\mathsf{\sigma }}_{\mathrm{uts}}}{E}{N}_{\mathrm{f}}^{-0.12}+D^{-0.6}{N}_{\mathrm{f}}^{-0.6}$$

(14)

where σ_uts is the ultimate tensile strength and $D=-\ln (1-\mathsf{\Psi })$ is the ductility, which is related to the area reduction in a tensile test. In this paper, the ultimate tensile strength (σ_uts = 1100 MPa) and the area reduction (Ψ = 16%) obtained from the tensile tests of the shell material at the room temperature were used for the fatigue life calculation.

This strain-life equation assumes the development of uniaxial stress in the direction of the applied longitudinal total strain. When stress is multi-axial, the uniaxial strain corrected as the equivalent strain range has to be calculated to apply the strain-life equation:

$${\mathsf{\Delta }\mathsf{\epsilon }}_{\mathrm{eq}}=\frac{\sqrt{2}}{3}\sqrt{{\left[\Delta ({\mathsf{\epsilon }}_1-{\mathsf{\epsilon }}_2)\right]}^2+{\left[\Delta ({\mathsf{\epsilon }}_2-{\mathsf{\epsilon }}_3)\right]}^2+{\left[\Delta ({\mathsf{\epsilon }}_3-{\mathsf{\epsilon }}_1)\right]}^2}$$

(15)

where $\Delta ({\mathsf{\epsilon }}_i-{\mathsf{\epsilon }}_j)$ is the range of the difference in principal strain. Consequently, the elastic part in strain-life equations must be shifted downward and the final relation combining the Manson−Coffin and Universal Slopes equations is [37]:

$${\mathsf{\Delta }\mathsf{\epsilon }}_{\mathrm{eq}}=\left[\frac{2}{3}(1+\mathsf{\nu })\right]3.5\frac{{\mathsf{\sigma }}_{\mathrm{uts}}}{E}{N}_{\mathrm{f}}^{-0.12}+D^{-0.6}{N}_{\mathrm{f}}^{-0.6}$$

(16)

For a rough thermo-mechanical analysis in the very thin layer of the work roll, the total strain (i.e., the sum of the thermal strain and mechanical strain) in the axial, circumferential, and radial directions can be given by [31]:

$$\begin{array}{l}{\mathsf{\epsilon }}_{\mathsf{\theta }}=\frac{1}{E}({\mathsf{\sigma }}_{\mathsf{\theta }}-{\mathsf{\nu }\mathsf{\sigma }}_{\mathrm{z}})+\mathsf{\alpha }\Delta T\\ {\mathsf{\epsilon }}_{\mathrm{z}}=\frac{1}{E}({\mathsf{\sigma }}_{\mathrm{z}}-{\mathsf{\nu }\mathsf{\sigma }}_{\mathsf{\theta }})+\mathsf{\alpha }\Delta T\\ {\mathsf{\epsilon }}_{\mathrm{r}}=\frac{1}{E}({\mathsf{\sigma }}_{\mathrm{r}}-{\mathsf{\nu }(\mathsf{\sigma }}_{\mathsf{\theta }}+{\mathsf{\sigma }}_{\mathrm{z}}))+\mathsf{\alpha }\Delta T\end{array}$$

(17)

Figure 10 shows the difference in principal strain at the roll surface during the first strip rolling. It can be seen that the difference of ${\mathsf{\epsilon }}_{\mathsf{\theta }}-{\mathsf{\epsilon }}_{\mathrm{z}}$ is nearly zero due to the total strain ${\mathsf{\epsilon }}_{\mathsf{\theta }}={\mathsf{\epsilon }}_{\mathrm{z}}=0$ by substituting the thermal stresses given by Equation (10) into Equation (17). In addition, it also can be obtained that the strain difference is $\left|{\mathsf{\epsilon }}_{\mathrm{z}}-{\mathsf{\epsilon }}_{\mathrm{r}}\right|=\left|{\mathsf{\epsilon }}_{\mathrm{r}}-{\mathsf{\epsilon }}_{\mathsf{\theta }}\right|=0.007$.

The fatigue life of 35,145 cycles at the roll surface was calculated using the Universal Slopes model given in Equation (12). However, the fatigue life calculated on the basis of strain-life method only represents the life until crack initiation. The total fatigue life of the work roll consists of the crack initiation life and the crack propagation life which will be studied in the future. Thermal fatigue life obtained in this paper seems larger than the results reported in previous studies. Thermal fatigue tests of high speed steel used for work roll with cylindrical specimens showed that the fatigue life greatly reduced from 3000 to 70 cycles when the maximum temperature changed from 580 to 600 °C at a constant minimum temperature of 200 °C [14]. The fatigue tests conducted by Garza-Montes-de-Oca pointed out that the early formation stage of cracks can be observed after 300 cycles when the specimens subject to the thermal cycling in the range 30–655.6 °C [16]. However, a much longer fatigue life was also observed by Mercado-Solis et al. with a stand-alone twin-disc machine which was more in line with the actual rolling situation. Some examples of cracking were observed after 6280 cycles under a SEM analysis [15]. Due to the complicated operating conditions of the work roll during hot rolling, the test conditions in the laboratory can hardly match the actual hot rolling conditions. Despite the difference in experimental results, the range of the low cycle fatigue life of the work roll during hot rolling was given. In addition, it should be noted that the fatigue life is computed based on strain-life equations at the room temperature. However, creep and high temperature are known to reduce fatigue life by up to 90% [39]. Thus, a further correction of the Universal Slopes equation with the 10% rule of Manson and Halford for thermal fatigue problems at high temperatures is suggested. The 10% rule estimates that, at high temperatures, only 10% of the life computed by the Universal Slopes equation will actually be achieved. Thus, Universal Slopes equation gives the upper bound life, while the 10% rule gives the lowest expected life, i.e., the lower bound life. The average mean fatigue life, estimated as twice the lower bound (20% rule), was also suggested [39,40]. Using the suggestions of the 10% rule and 20% rule, the thermal fatigue life of the work roll reduced to 41 cycles and 175 cycles, respectively. The thermal fatigue life based on the 10% rule and 20% rule is more reasonable for the fatigue life prediction of the work roll compared with the mentioned experimental results.

6. Conclusions

In this paper, simulations of the temperature and stress of high speed steel work roll during heat treatment and hot rolling were performed by means of thermo-elastic-plastic FEM. The generation mechanisms of residual stress and thermal stress were clarified. The effects of different initial roll temperatures and cooling conditions on thermal stress considering the initial residual stress were discussed. The thermal fatigue life of the work rolls was estimated based on the strain-life model. The results of the current study can be summarized as follows:

(1)

During the quenching process, compressive residual stress appeared at the surface and tensile residual stress appeared at the center, induced by the integrated effects of thermal stress and transformation stress; during the tempering process, the tensile stress decreased uniformly, while the compressive stress was almost unchanged.

(2)

During the hot rolling process, stable maximum temperature and compressive stress were reached at the roll surface after 10 revolutions, while the temperature at the subsurface increased gradually with the small variation amplitude.

(3)

Considering the initial residual stress, the compressive stress caused plastic deformation at the roll surface in the bite region, while the tensile stress did not appear in the cooling region; the thermal stresses at the shell changed significantly near the surface, while the tensile stresses at the core increased gradually during the whole rolling and reached 367 MPa after rolling of ten strips.

(4)

Increasing of the initial roll temperature resulted in a higher temperature but lower compressive thermal stress at the roll surface; the complete cooling condition reduced the roll temperature and compressive thermal stress at the roll surface, while the surface temperature and compressive thermal stress increased significantly in the condition of without water spray cooling and mill stall, as well as the center tensile stress.

(5)

The thermal fatigue life of the work roll during hot rolling was calculated to be 35,145 cycles based on the Universal Slopes model and this reduced to 41 cycles and 175 cycles, respectively, according to the 10% rule and 20% rule.