Abstract
Frequency is an important factor influencing the fatigue behavior. Regarding to the dwell fatigue, it corresponds to the effect of rise and fall time, which is also an important issue especially for the safety evaluation of structure parts under dwell fatigue loading, such as the engines of aircrafts and the pressure hulls of deep-sea submersibles. In this paper, the effect of rise and fall time (2 s, 20 s, 110 s, and 200 s) on the dwell fatigue behavior is investigated for a high strength titanium alloy Ti-6Al-2Sn-2Zr-3Mo-X with basket-weave microstructure. It is shown that the dwell fatigue life decreases with increasing the rise and fall time, which could be correlated by a linear relation in log–log scale for both the specimen with circular cross section and the specimen with square cross section. The rise and fall time has no influence on the crack initiation mechanism by the scanning electron microscope observation. The cracks initiate from the specimen surface and all the fracture surfaces present multiple crack initiation sites. Moreover, the facet characteristic is observed at some crack initiation sites for both the conventional fatigue and dwell fatigue tests. The paper also indicates that the dwell period of the peak stress reduces the fatigue life and the dwell fatigue life seems to be longer for the specimen with circular cross section than that of the specimen with square cross section.
1. Introduction
The dwell fatigue in titanium alloys has drawn great attention [,,,,,] since it was detected in Rolls-Royce RB211 engines on Lockheed Tristar aircraft in the early 1970s [,]. It has been shown that the dwell period at the peak stress significantly reduces the fatigue life of titanium alloys in comparison with the fatigue life under the conventional fatigue loading and that the crack initiation region has the characteristic of cleavage or quasi-cleavage facets [,,].
Loading frequency is an important factor influencing the fatigue behavior of metallic materials. The lower frequency usually increases the crack growth rate [,] and reduces the fatigue strength or fatigue life [,]. Regarding to the dwell fatigue, it corresponds to the effect of rise and fall time, which is also a very important issue especially for the safety evaluation of structure parts under dwell fatigue loading. As an example for the deep-sea submersibles, it frequently dives, works, and floats during the service life, and correspondingly its key component—the pressure hull is subjected to a relative long time (~tens of minutes) loading and unloading by the changing sea water pressure for each mission. However, the existing studies are mainly focused on the effect of dwell period on fatigue life, crack initiation, and crack propagation, and there is no report on this issue.
Further, the component parts are generally of very different size and shape with the specimens tested in laboratory. The specimen size and shape usually have great influence on the fatigue life or fatigue strength in conventional fatigue [,,]. For dwell fatigue of titanium alloys, it has been shown that the smaller round bar specimens showed shorter fatigue life than that of the larger round bar specimens []. However, there are few reports available for the effect of specimen shape on the dwell fatigue behavior.
In this research, the axial loading dwell fatigue test with different rise and fall times is first performed for the specimen with circular cross section and the specimen with square cross section of a high strength titanium alloy Ti-6Al-2Sn-2Zr-3Mo-X which could be used in the key components of deep-sea equipment such as submersibles. Then, the effect of rise and fall time and the effect of specimen shape on the dwell fatigue behavior are investigated. The dwell fatigue behavior is also compared with the conventional fatigue behavior for the specimen with circular cross section.
2. Materials and Methods
The material used here is a high strength titanium alloy Ti-6Al-2Sn-2Zr-3Mo-X cut from a forged flat plate parallel to the rolling direction. The tensile strength and yield strength are 1072 MPa and 978 MPa, respectively, which are obtained by the tensile test on three cylindrical specimens with diameter of 5 mm. The microstructure of the material is basket-weave, as shown in Figure 1. Two kinds of specimens are used, one is the specimen with circular cross section (C-specimen), and the other is the specimen with square cross section (S-specimen), as shown in Figure 2. In this paper, the size of the cross-sectional area is the same for both the C-specimen and the S-specimen in order to minimize the effect of size of the specimen. The experimental section surfaces of all the tested specimens are ground and polished to eliminate the machine scratches before fatigue test.

Figure 1.
Microstructure of Ti-6Al-2Sn-2Zr-3Mo-X alloy.
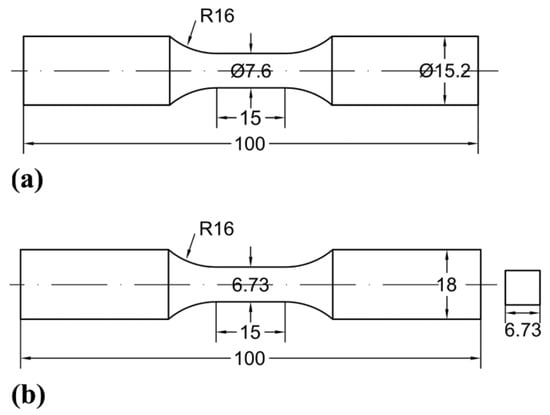
Figure 2.
(a) Specimen with circular cross section (in mm) for conventional fatigue test and dwell fatigue test; (b) specimen with square cross section (in mm) for dwell fatigue test.
The conventional fatigue test and the dwell fatigue test are conducted on a same Landmark servohydraulic test system (MTS Systems Corporation, Eden Prairie, MN, USA) at room temperature in air, the loading waveforms of which are shown in Figure 3. The maximum stress (i.e., peak stress) is 929.1 MPa for both the conventional fatigue test and the dwell fatigue test, which is 0.95 of the yield stress. The stress ratio R is −1. For conventional fatigue test, different rise and fall times 2 s, 20 s, and 200 s (i.e., different frequencies 0.25 Hz, 0.025 Hz, and 0.0025 Hz) are used. For dwell fatigue test, different rise and fall times 2 s, 20 s, 110 s, and 200 s are used, and the dwell time is 60 s for the peak stress. The fall time equals to the rise time for all the dwell fatigue tests.
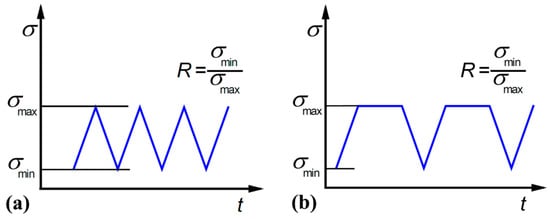
Figure 3.
(a) Schematic of loading waveforms for conventional fatigue test; (b) schematic of loading waveforms for dwell fatigue test.
The fracture surfaces of failed specimens are observed by a scanning electron microscope (SEM) (JEOL, Tokyo, Japan).
3. Results and Discussions
The variation of fatigue life with the rise and fall time is shown in Figure 4 for both the conventional fatigue test and the dwell fatigue test. The loading information and the associated fatigue life of specimens are given in Table 1. It is seen from Figure 4 that the fatigue life is scattered at a fixed rise and fall time. The rise and fall time has important influence on the dwell fatigue life. The dwell fatigue life decreases with the increase of the rise and fall time, which is very similar to the effect of rise and fall time (i.e., frequency) on the conventional fatigue life. A possible explanation for this is that the dislocations have more time to overcome obstacles via thermal activation under the larger rise and fall time than that under the smaller one [], which increases the amount of plastic strain accumulation and results in the shorter fatigue life. Figure 4 indicates that it will be very dangerous for the dwell fatigue life evaluation of specimens or structural parts under longer rise and fall time by using the dwell fatigue life data under shorter rise and fall time. Further, it is found that the effect of rise and fall time on the fatigue life under both dwell fatigue test and conventional fatigue test could be correlated by a linear relation in log–log scale, i.e.,
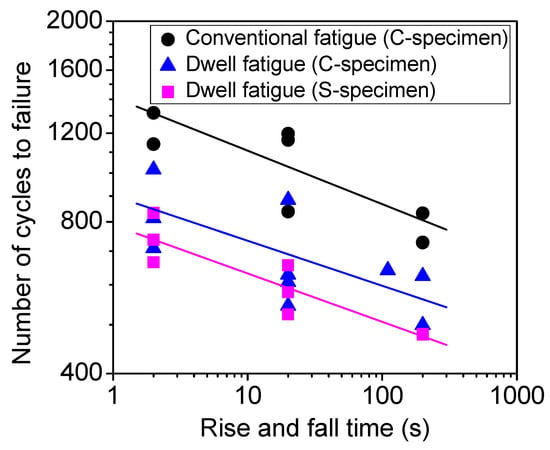
Figure 4.
Variation of fatigue life with the rise and fall time for both the conventional fatigue test and the dwell fatigue test, in which the lines denote the linear regression results of the fatigue life with the rise and fall time in log–log scale.

Table 1.
Loading information and the associated fatigue life of specimens in Figure 4.
The correlation coefficients are −0.68, −0.91, and −0.81 for Equations (1)–(3), respectively. According to the research in reference [], the correlation is significant for the dwell fatigue of C-specimen, highly significant for the dwell fatigue of S-specimen, and significant for the conventional fatigue of C-specimen.
Equations (1)–(3) indicate that the slope of the fatigue life with the rise and fall time under the dwell fatigue test is very close to that under the conventional fatigue test, namely that the effect of rise and fall time on the dwell fatigue life might be approximately obtained by that on the conventional fatigue life.
Figure 4 also indicates that the dwell fatigue life is shorter than the conventional fatigue life for the same rise and fall time, i.e., the dwell period of the maximum stress reduces the fatigue life of titanium alloys. This might be due to that the creep induced by the maximum stress during the dwell period in room temperature increases the strain accumulation compared with the conventional fatigue test [,], which accelerates the damage in specimens and results in the shorter fatigue life under dwell fatigue test.
SEM observations indicate that all the tested specimens fail from the specimen surface and all the fracture surfaces present multiple crack initiation sites for both the conventional and the dwell fatigue tests. Moreover, it is found that some crack initiation sites have the facet characteristic (A-3 and D-3 in Figure 5) for both the dwell fatigue of C-specimens and S-specimens at different rise and fall times. This indicates that the rise and fall time has no influence on the crack initiation mechanism of the dwell fatigue. The facet characteristic (A-3 in Figure 6) is also found at some crack initiation sites under the conventional fatigue test at different rise and fall times, indicating that the dwell period has no influence on the crack initiation mechanism compared with the conventional fatigue test.
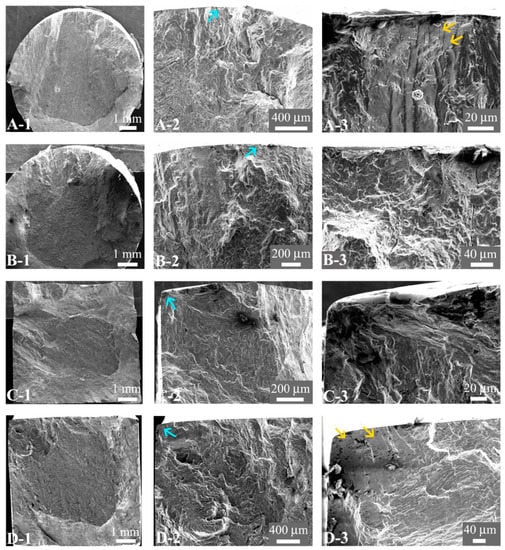
Figure 5.
Fracture surface morphology of failed specimens under dwell fatigue test. A-1 ~ A-3: C-specimen with Nf = 1016 for rise and fall time 2 s; B-1 ~ B-3: C-specimen with Nf = 709 for rise and fall time 2 s; C-1 ~ C-3: S-specimen with Nf = 833 for rise and fall time 2 s; D-1 ~ D-3: S-specimen with Nf = 665 for rise and fall time 2 s. A-2, B-2, C-2, and D-2 are close-ups of A-1, B-1, C-1, and D-1, respectively; A-3, B-3, C-3, and D-3 are close-ups of the crack initiation regions where the arrows point to in A-2, B-2, C-2, and D-2, respectively; the arrows pointing to in A-3 and D-3 denote the facets.

Figure 6.
Fracture surface morphology of failed specimens under conventional fatigue test. A-1 ~ A-3: Specimen with Nf = 1141 for rise and fall time 2 s; B-1 ~ B-3: Specimen with Nf = 728 for rise and fall time 200 s. A-2 and B-2 are close-ups of A-1 and B-1, respectively; A-3 and B-3 are close-ups of the crack initiation regions where the arrows point to in A-2 and B2, respectively.
For the effect of specimen shape on the dwell fatigue life, the linear regression result of the dwell fatigue life with the rise and fall time is compared for the C-specimens and S-specimens due to the scatter of the fatigue life. It is seen from Figure 4 that the dwell fatigue life is related to the specimen shape and it seems to be longer for the C-specimen than that of the S-specimen. SEM observation indicates that the main cracks for S-specimen usually initiate from the edges or very near the edges of the experimental section. Therefore, it is thought that the edges of the experimental section for the S-specimen favor the crack initiation and lead to a shorter fatigue life compared with the C-specimen. However, the specimen shape has no influence on the crack initiation mechanism from the SEM observation. Both the dwell fatigue of C-specimens and S-specimens fail from the multiple crack initiation sites of the specimen surface and some crack initiation sites present the facet characteristic (A-3 and D-3 in Figure 5).
4. Conclusions
This paper investigates the effect of rise and fall time on the dwell fatigue behavior of a high strength titanium alloy Ti-6Al-2Sn-2Zr-3Mo-X for the specimen with circular cross section and the specimen with square cross section under axial loading. It is shown that the dwell fatigue life is related to the rise and fall time, which decreases with increasing the rise and fall time. Moreover, the effect of rise and fall time on the dwell fatigue life could be correlated by a linear relation in log–log scale, the scope of which is very close to that of the effect of rise and fall time on the fatigue life under the conventional fatigue test. The crack initiation mechanism of the present titanium alloy is independent of the rise and fall time and the specimen shape. The dwell period of the peak stress reduces the fatigue life, but has no influence on the crack initiation mechanism compared with the conventional fatigue test. The paper also indicates that the specimen shape has influence on the dwell fatigue life, which appears to be longer for the specimen with circular cross section than that of the specimen with square cross section. The present results are essential for understanding the dwell fatigue behavior of high strength titanium alloys.
Author Contributions
Conceptualization, C.S. and Q.S.; methodology, C.S. and Y.L.; formal analysis, Q.S., Y.L., and L.W.; investigation, Q.S. and R.H.; data curation, C.S., L.W., and R.H.; writing—original draft preparation, Q.S., R.H., and C.S.; writing—review and editing, Q.S, C.S., and Y.L.; supervision, C.S.; funding acquisition, C.S., Y.L., and L.W.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2017YFC0305500, and the National Natural Science Foundation of China, grant number 91860112.
Acknowledgments
The authors would like to thank Fuping Gao at the Institute of Mechanics, Chinese Academy of Sciences, for the help in preparing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bania, P.J.; Eylon, D. Fatigue crack propagation of titanium alloys under dwell-time conditions. Metall. Trans. A 1978, 9, 847–855. [Google Scholar] [CrossRef]
- Lefranc, P.; Sarrazin-Baudoux, C.; Doquet, V.; Petit, J. Investigation of the dwell period’s influence on the fatigue crack growth of a titanium alloy. Scr. Mater. 2009, 60, 281–284. [Google Scholar] [CrossRef]
- Wang, F.; Cui, W. Experimental investigation on dwell-fatigue property of Ti-6Al-4V ELI used in deep-sea manned cabin. Mater. Sci. Eng. A 2015, 642, 136–141. [Google Scholar] [CrossRef]
- Qiu, J.; Ma, Y.; Lei, J.; Liu, Y.; Huang, A.; Rugg, D.; Yang, R. A Comparative study on dwell fatigue of Ti-6Al-2Sn-4Zr-xMo (x = 2 to 6) alloys on a microstructure-normalized basis. Metall. Mater. Trans. A 2014, 45, 6075–6087. [Google Scholar] [CrossRef]
- Shen, W.; Soboyejo, W.O.; Soboyejo, A.B.O. An investigation on fatigue and dwell-fatigue crack growth in Ti-6Al-2Sn-4Zr-2Mo-0.1Si. Mech. Mater. 2004, 36, 117–140. [Google Scholar] [CrossRef]
- Zheng, Z.; Balint, D.S.; Dunne, F.P.E. Mechanistic basis of temperature-dependent dwell fatigue in titanium alloys. J. Mech. Phys. Solids 2017, 107, 185–203. [Google Scholar] [CrossRef]
- Song, Z.; Hoeppner, D.W. Dwell time effects on the fatigue behavior of titanium alloys. Int. J. Fatigue 1988, 10, 211–218. [Google Scholar] [CrossRef]
- Bache, M.R. A review of dwell sensitive fatigue in titanium alloys: The role of microstructure, texture and operating conditions. Int. J. Fatigue 2003, 25, 1079–1087. [Google Scholar] [CrossRef]
- Evans, W.J.; Gostelow, C.R. The effect of hold time on the fatigue properties of a β-processed titanium alloy. Metall. Trans. A 1979, 10, 1837–1846. [Google Scholar] [CrossRef]
- Bache, M.R.; Cope, M.; Davies, H.M.; Harrison, G. Dwell sensitive fatigue in a near alpha titanium alloy at ambient temperature. Int. J. Fatigue 1997, 19, S83–S88. [Google Scholar] [CrossRef]
- Evans, W.J. Time dependent effects in fatigue of titanium and nickel alloys. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 543–557. [Google Scholar] [CrossRef]
- Takezono, S.; Satoh, M. Effect of stress frequency on fatigue crack propagation in titanium. J. Eng. Mater. Technol. ASME 1982, 104, 257–261. [Google Scholar] [CrossRef]
- Dahal, J.; Maciejewski, K.; Ghonem, H. Loading frequency and microstructure interactions in intergranular fatigue crack growth in a disk Ni-based superalloy. Int. J. Fatigue 2013, 57, 93–102. [Google Scholar] [CrossRef]
- Morrissey, R.J.; McDowell, D.L. Frequency and stress ratio effects in high cycle fatigue of Ti-6Al-4V. Int. J. Fatigue 1999, 21, 679–685. [Google Scholar] [CrossRef]
- Guennec, B.; Ueno, A.; Sakai, T.; Takanashi, M.; Itabashi, Y. Effect of the loading frequency on fatigue properties of JIS S15C low carbon steel and some discussions based on micro-plasticity behavior. Int. J. Fatigue 2014, 66, 29–38. [Google Scholar] [CrossRef]
- Beretta, S.; Ghidini, A.; Lombardo, F. Fracture mechanics and scale effects in the fatigue of railway axles. Eng. Fract. Mech. 2005, 72, 195–208. [Google Scholar] [CrossRef]
- Furuya, Y. Specimen size effects on gigacycle fatigue properties of high-strength steel under ultrasonic fatigue testing. Scr. Mater. 2008, 58, 1014–1017. [Google Scholar] [CrossRef]
- Sun, C.; Song, Q. A method for predicting the effects of specimen geometry and loading condition on fatigue strength. Metals 2018, 8, 811. [Google Scholar] [CrossRef]
- Song, Z.; Hoeppner, D.W. Size effect on the fatigue behaviour of IMI 829 titanium alloy under dwell conditions. Int. J. Fatigue 1989, 11, 85–90. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Yang, L.; Liu, J.; Chen, Z.; Wang, Q.; Yang, R. Effect of loading waveform on fatigue damage behavior of Ti-60 alloy. Chin. J. Nonferrous Metals 2010, 20, S487–S490. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).