Research on Four-Point Air Bending Process and Contour Detection Method for JCO Forming Process of LSAW Pipes
Abstract
:1. Introduction
2. Four-Point Air Bending for JCO Forming Process of LSAW Pipes
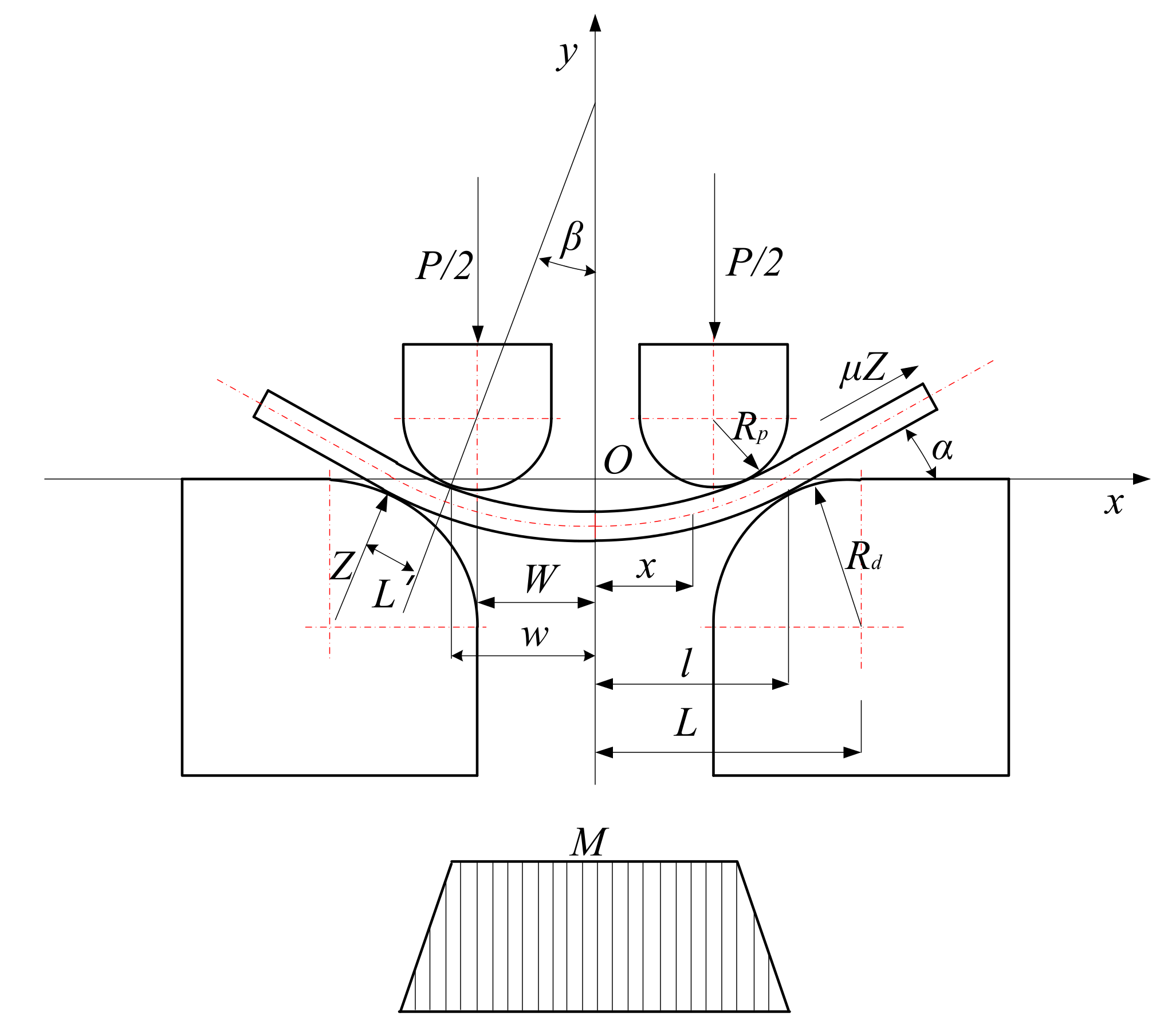
3. Establishment and Analysis of the Mechanical Model
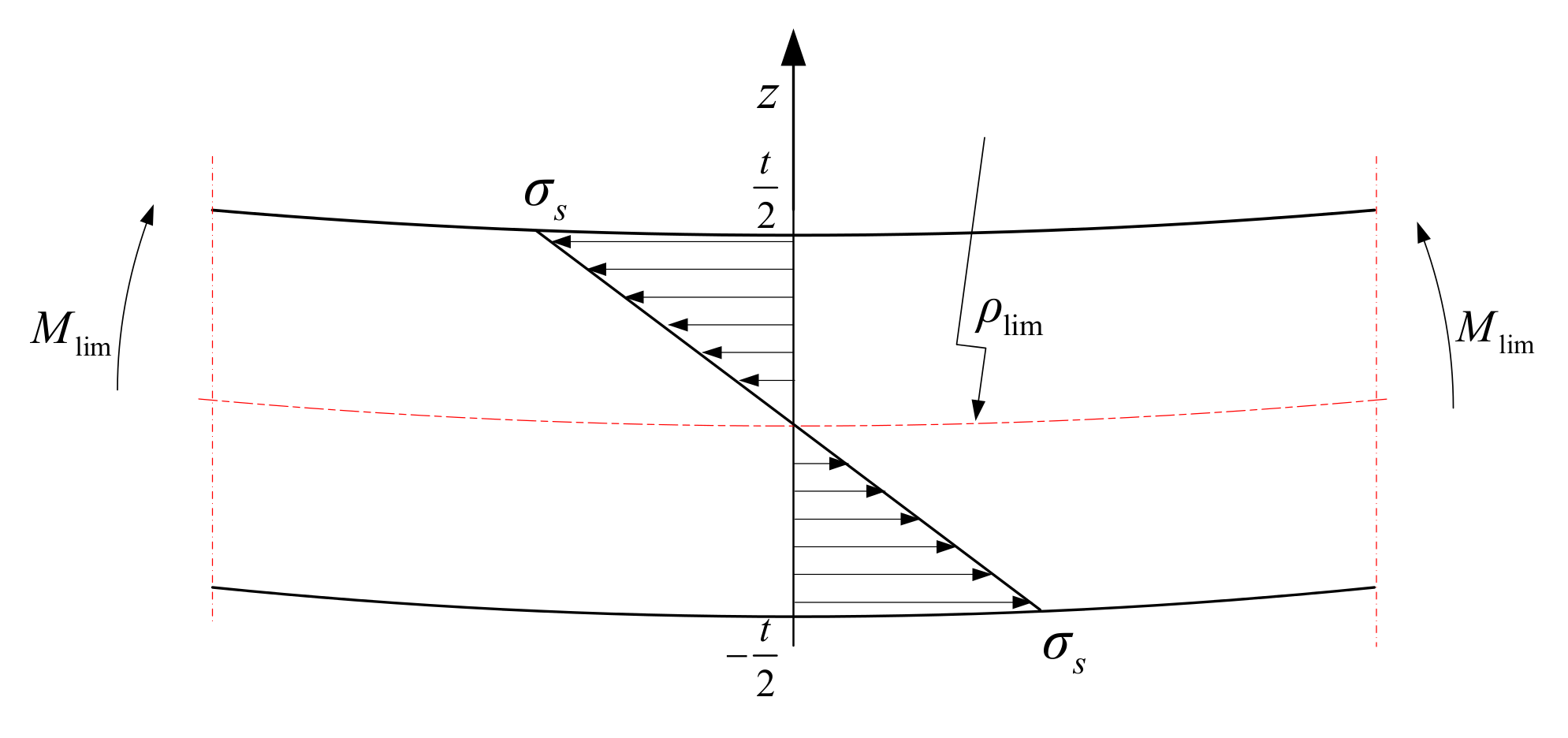
3.1. Static Analysis (Bending Moment)
3.2. Elastic–Plastic Analysis
3.2.1. Basic Assumptions
- (1)
- Pure bending assumption: the static bending process is considered to be a pure bending process, which means to ignore the influence of normal stress causes and to consider the bending strains only.
- (2)
- Neutral layer coinciding assumption: the strain neutral layer, stress neutral layer, and geometric neutral layer always coincide during the deforming process.
- (3)
- Bilinear hardening material model assumption: Effects of initial strain and change of material properties are neglected. The relationship between strain and stress iswhere is Young’s modulus, is yield strength of material, and is plastic tangent modulus.
- (4)
- Plane section assumption: any plane section remains plane after deforming and no aberrance occurs, so the strain distribution on any section is linear. The strain is expressed aswhere is strain, is the distance from the neutral layer, and is the curvature of neutral layer after loading.
- (5)
- Uniaxial stress state assumption: any particle on the sheet is uniaxially stretched or compressed when a deformation occurs.
3.2.2. Bending Process and Springback Analysis
4. Finite Element Simulation and Parameters Formulation
4.1. Finite Element Model
4.2. Analysis of Simulation Results
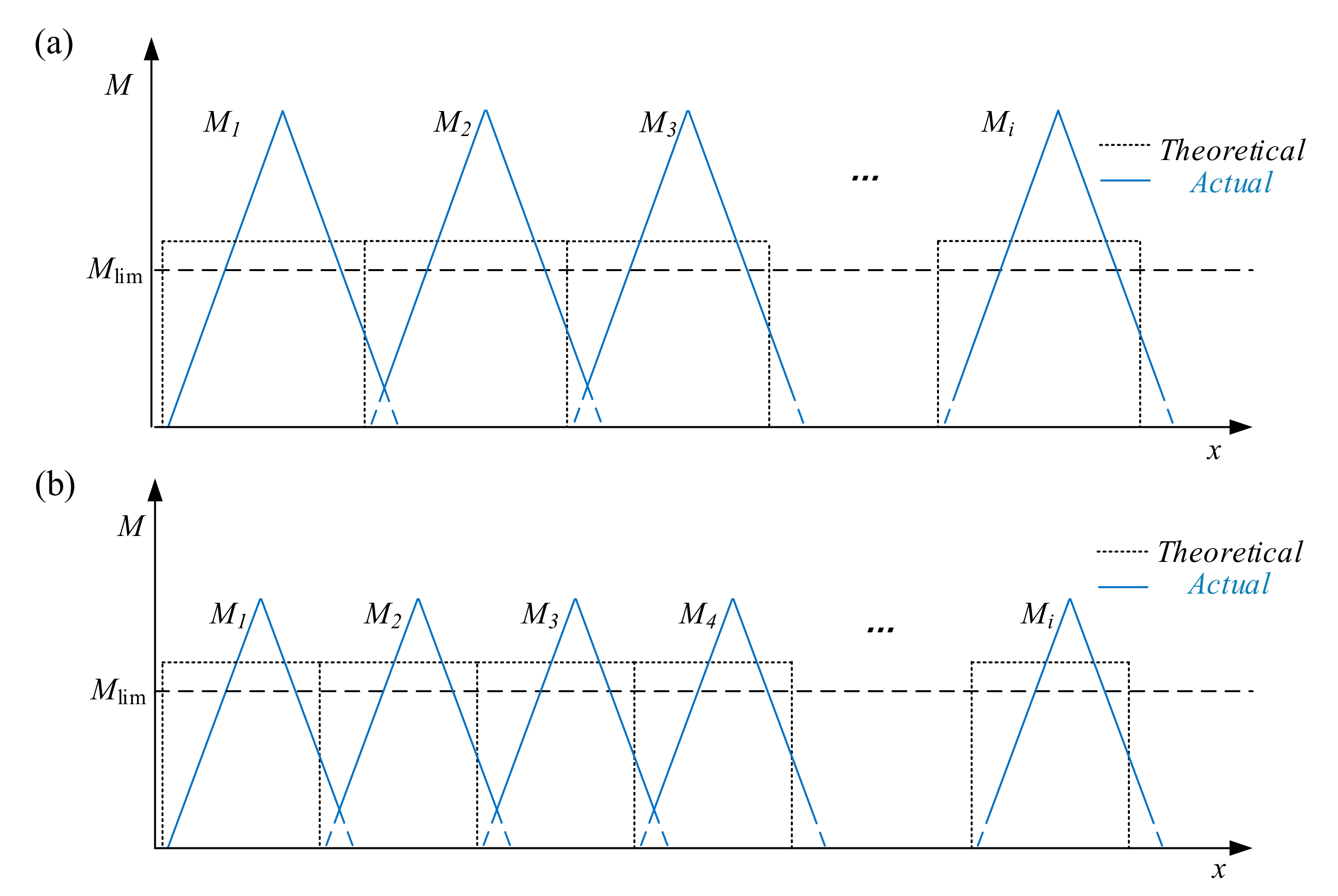
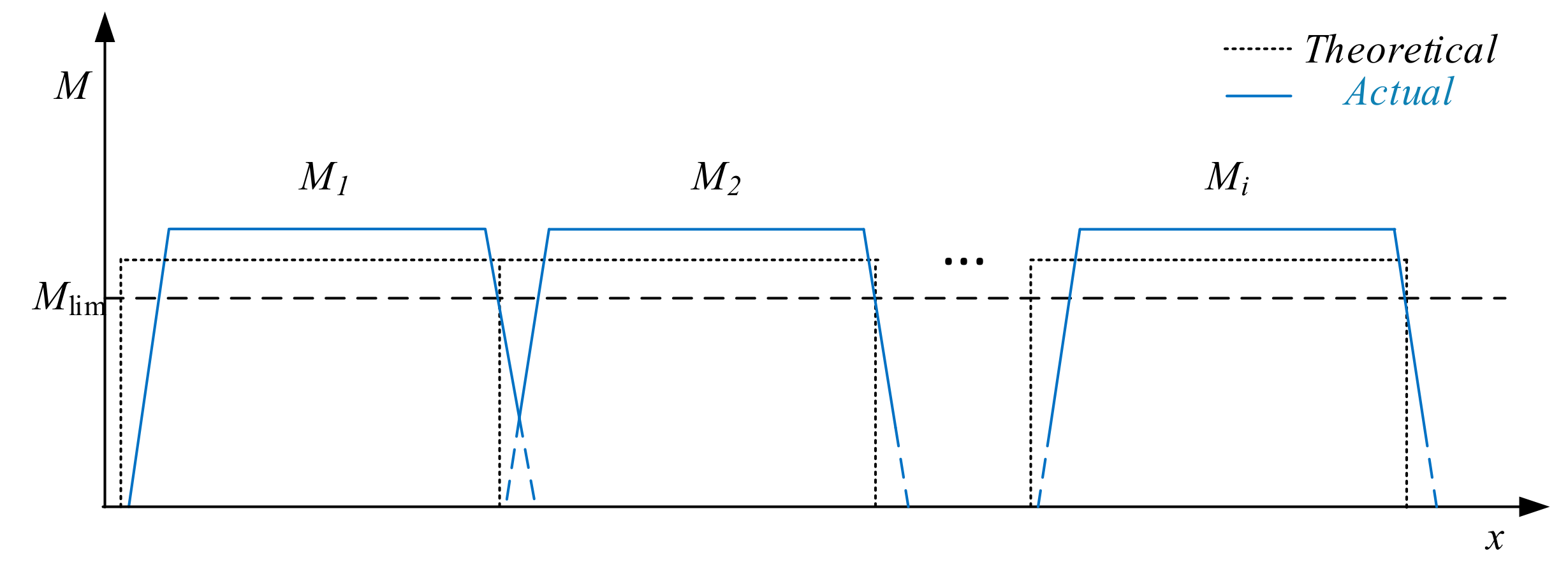
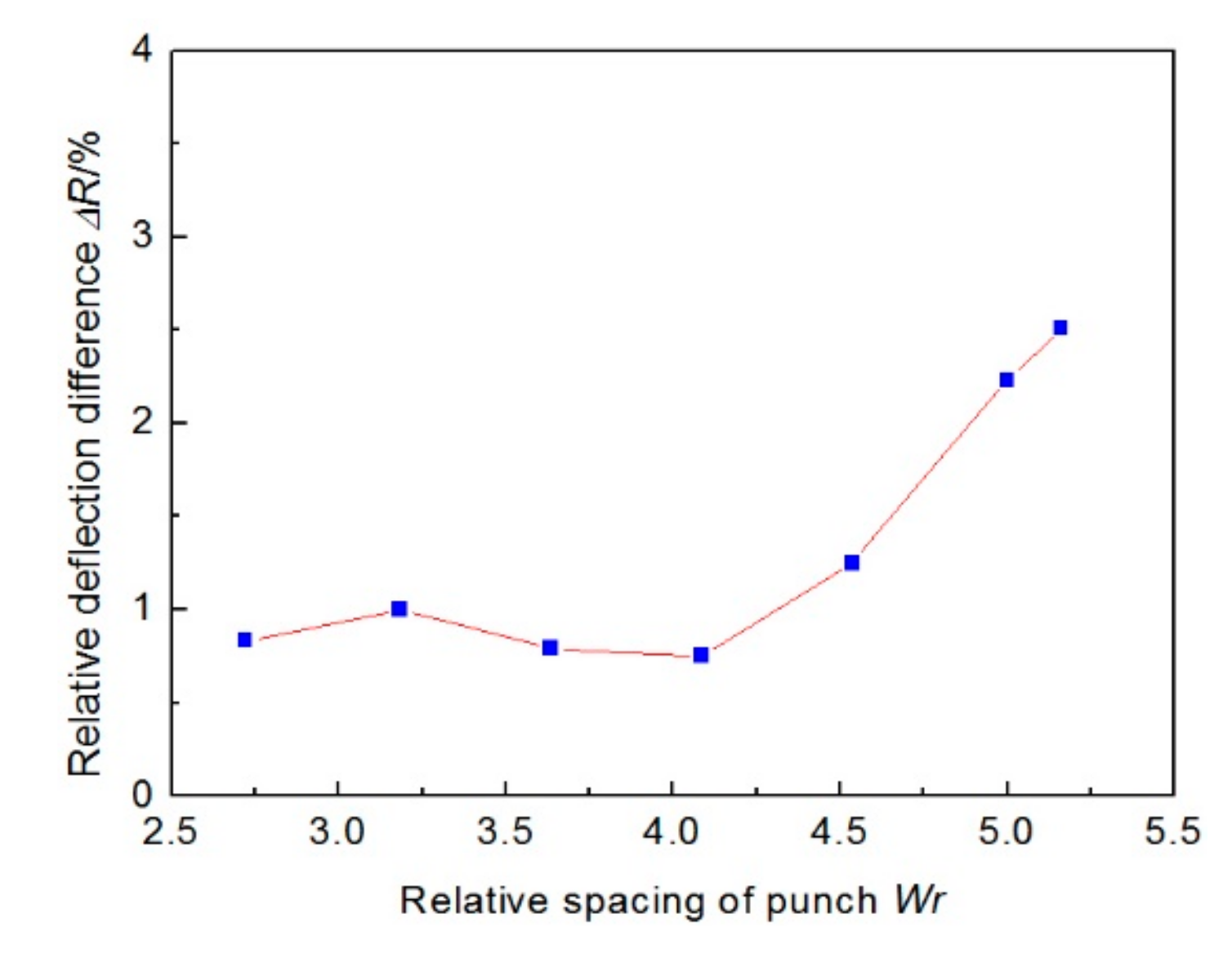
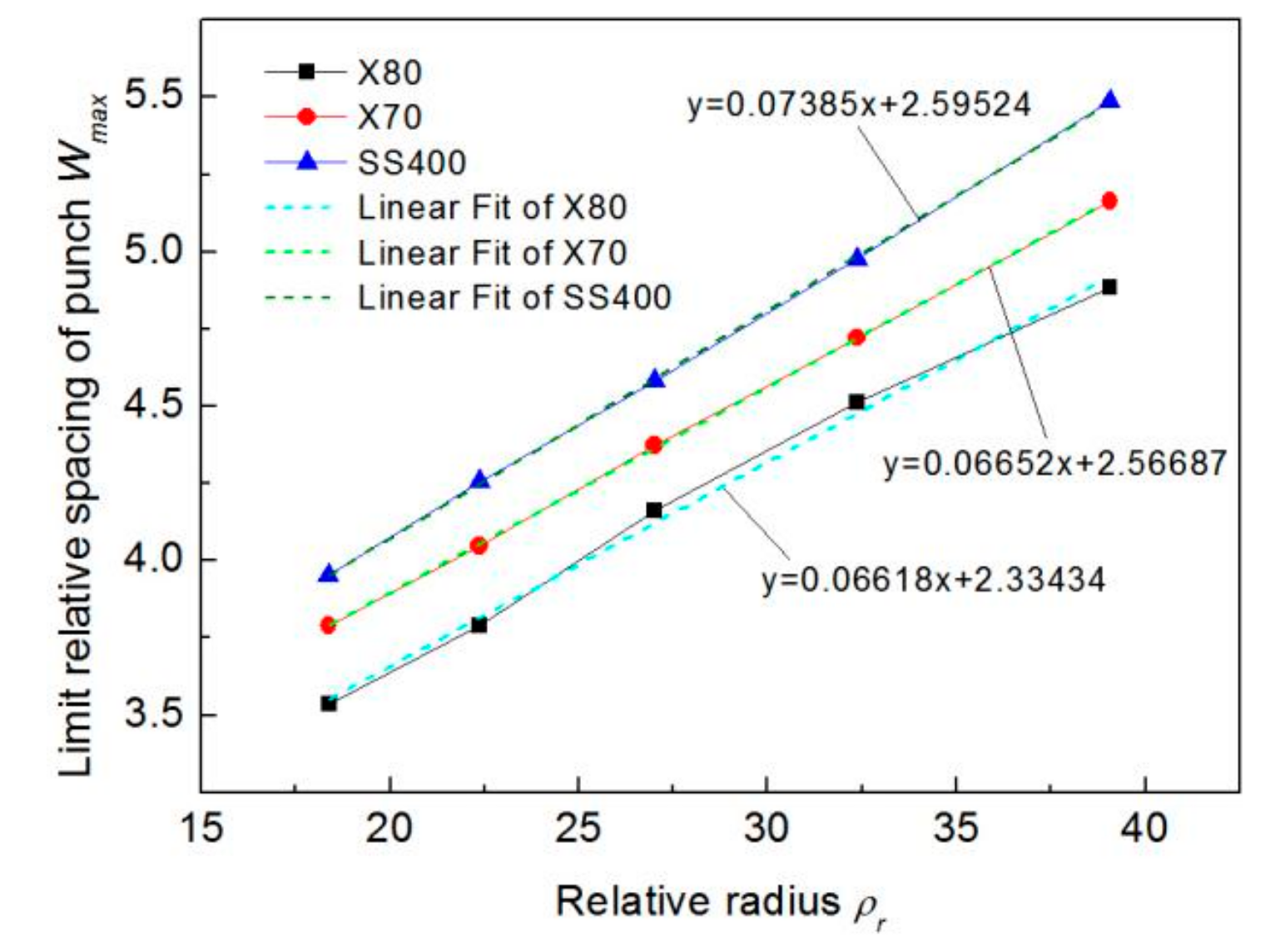
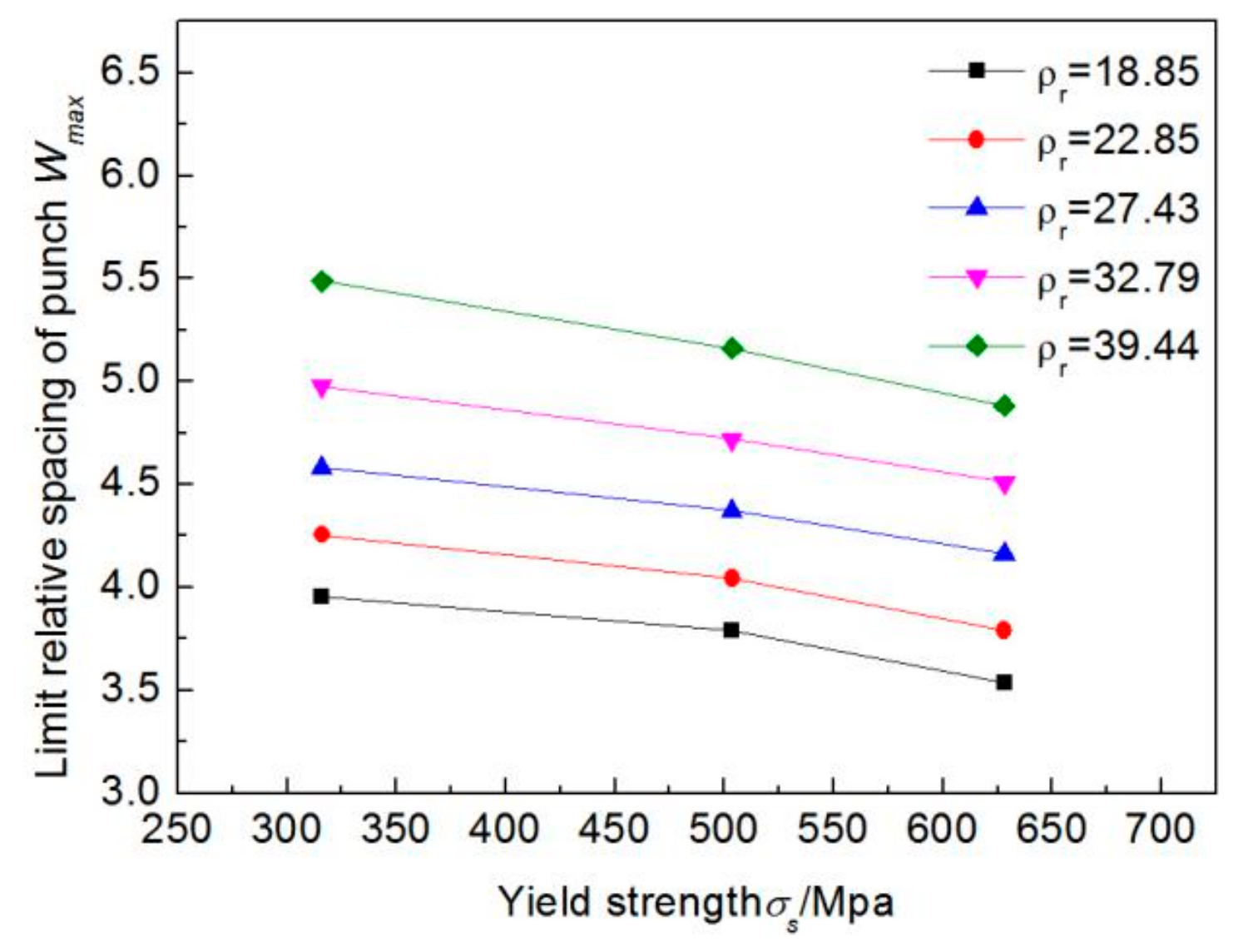
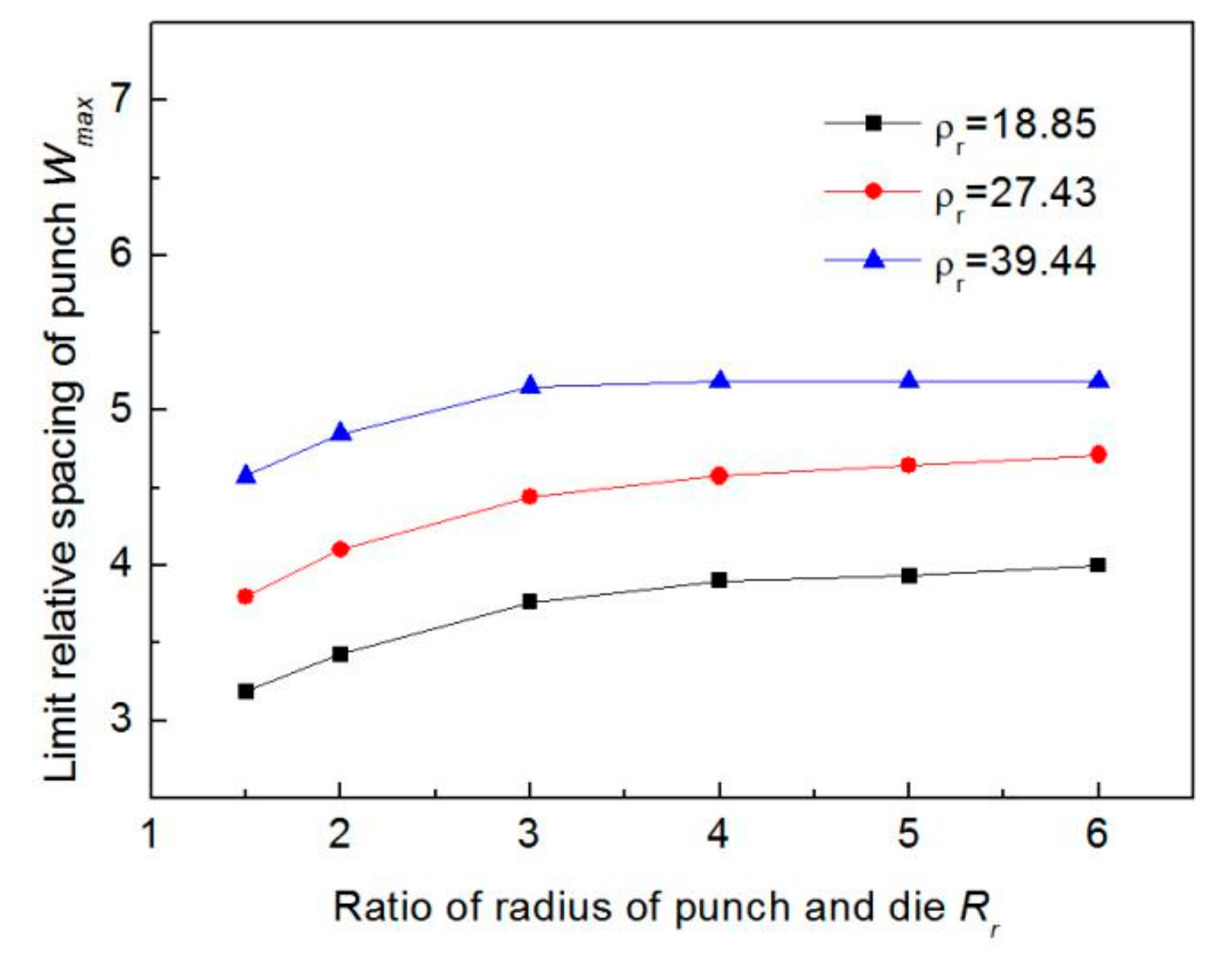
4.2.1. Radius Error Analysis
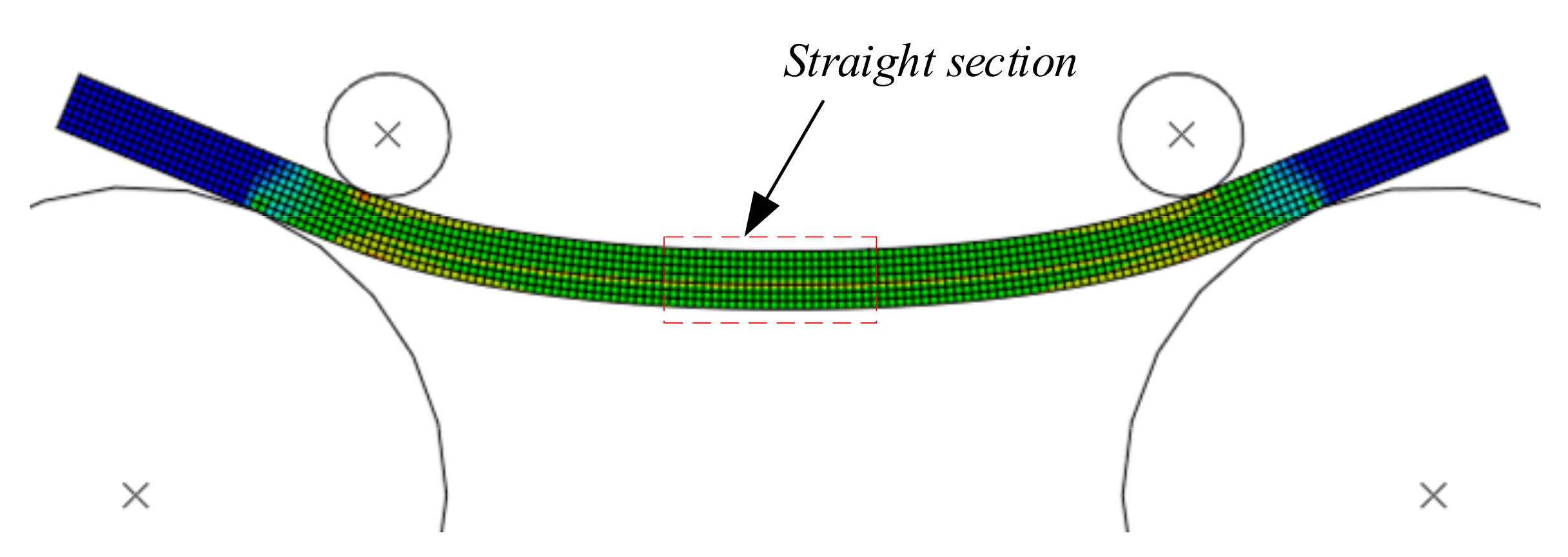
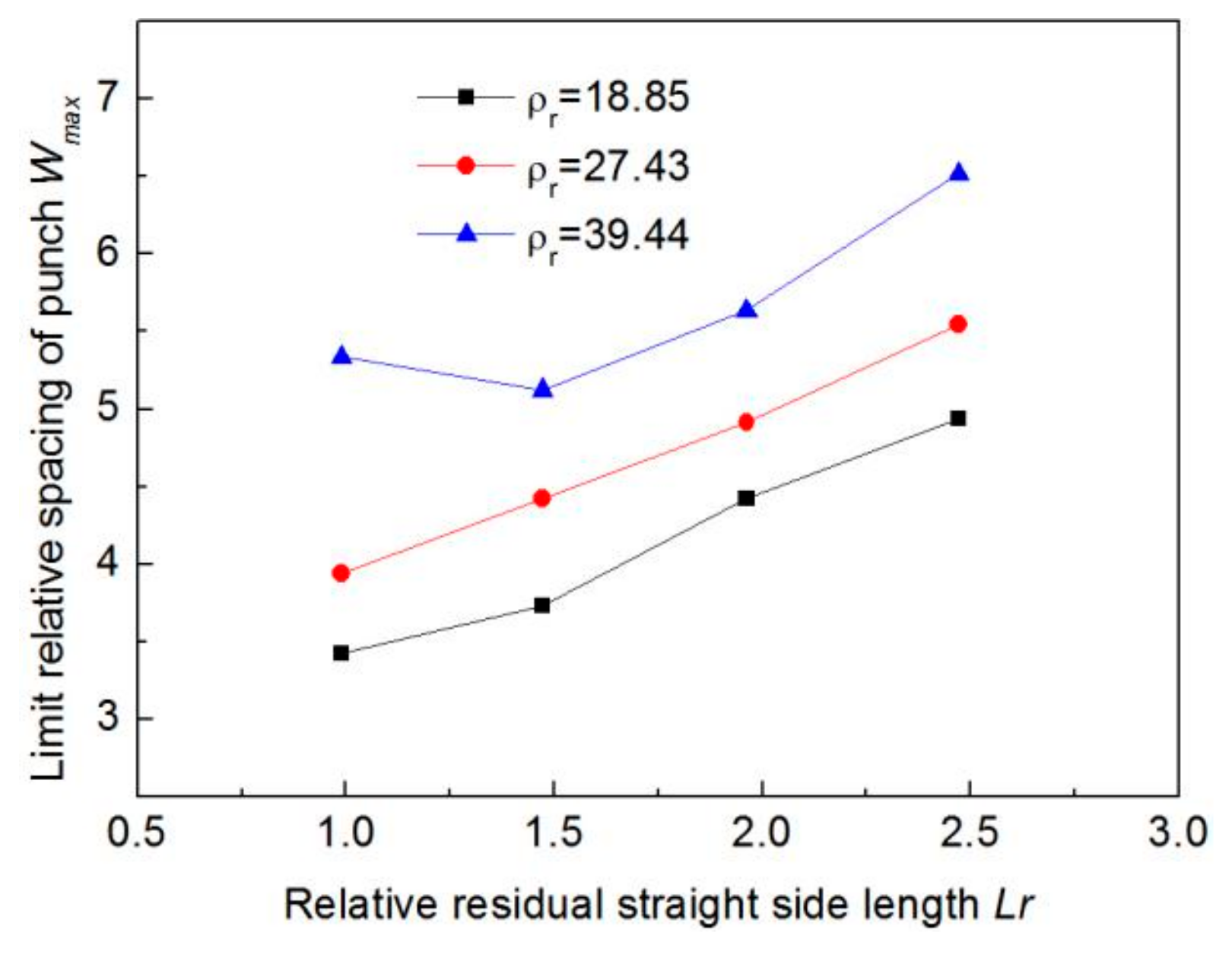
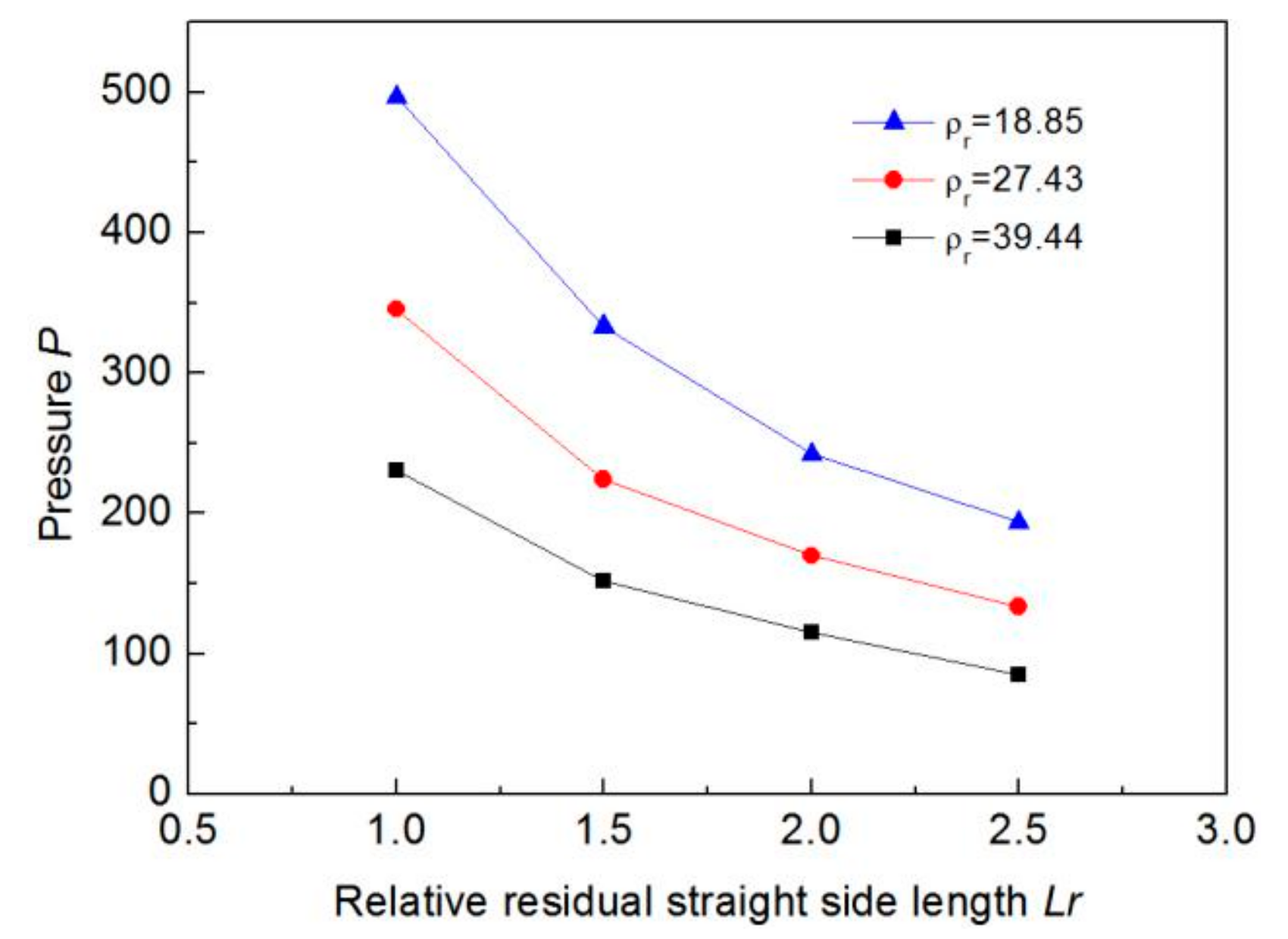
4.2.2. Residual Straight Segment Length Analysis
4.2.3. Dimension Analysis
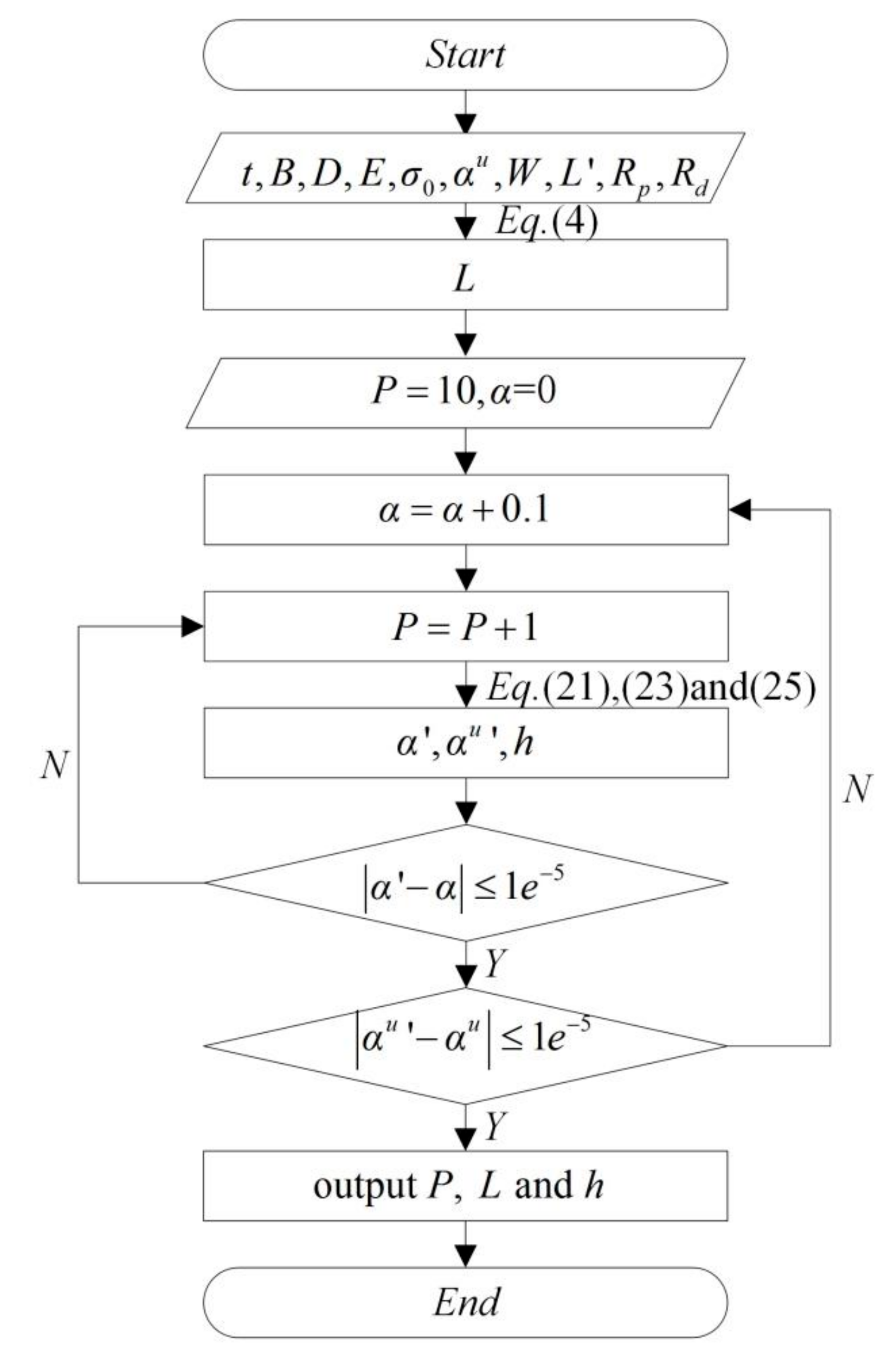
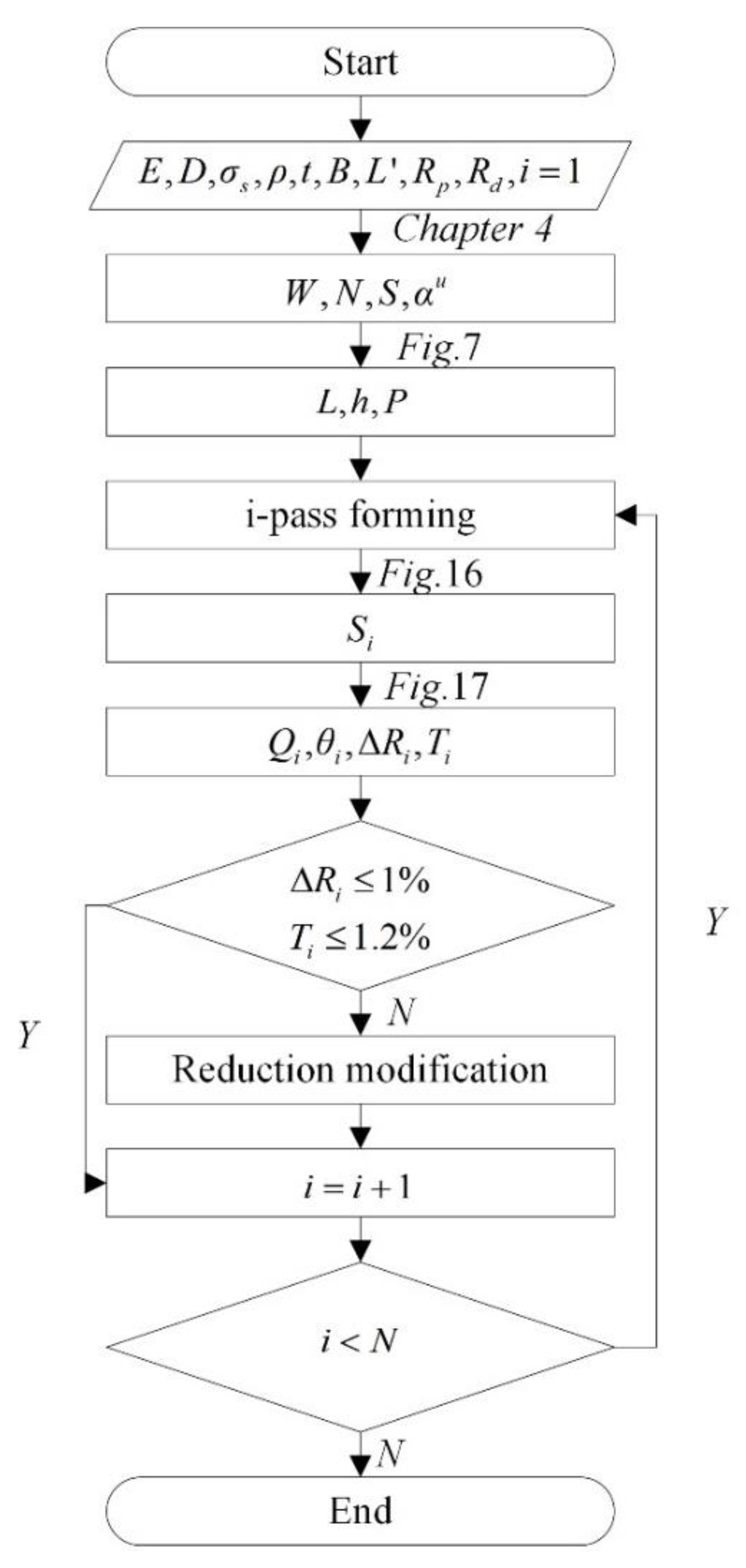
4.3. Formulation of Process Parameters
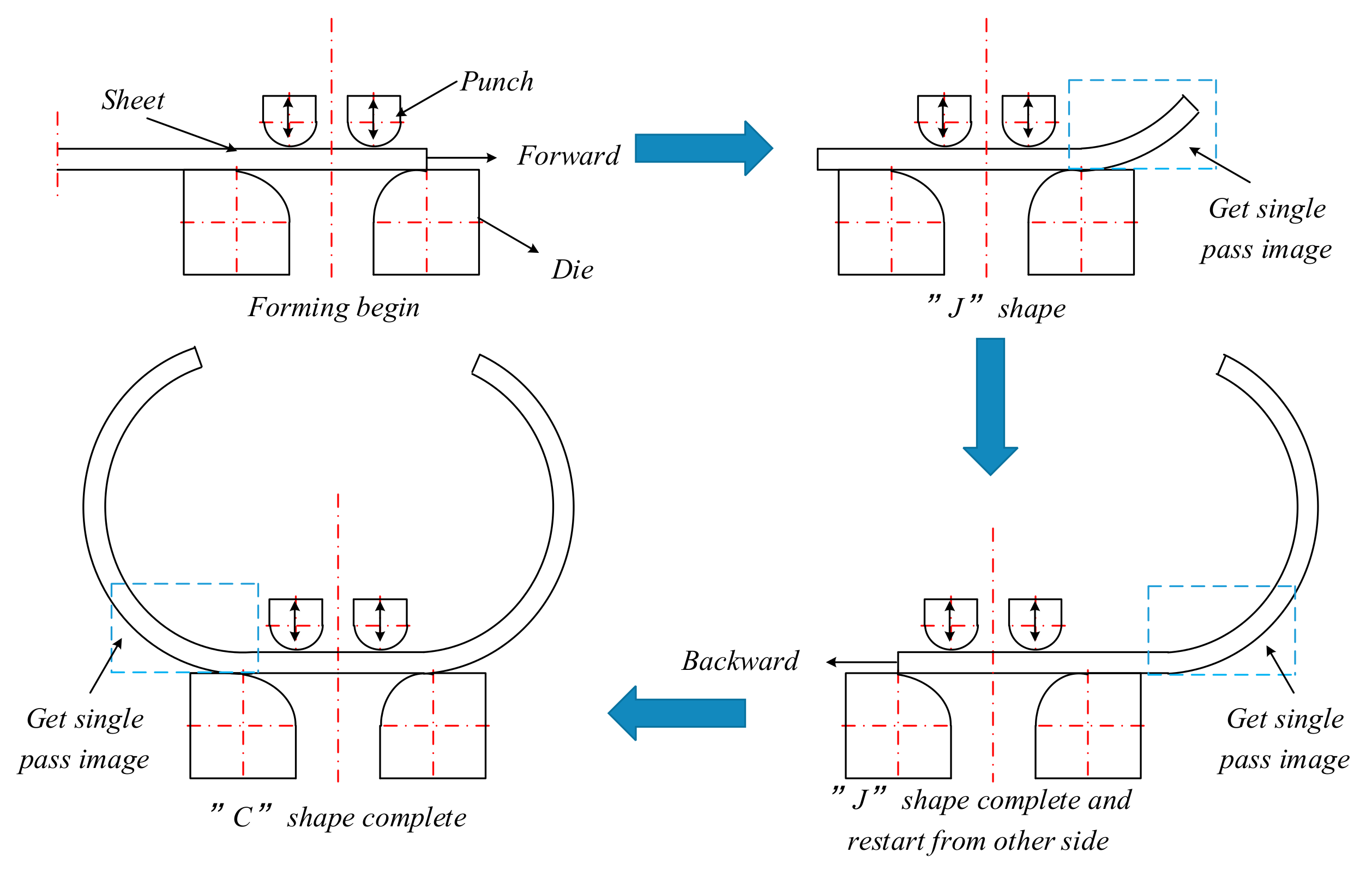
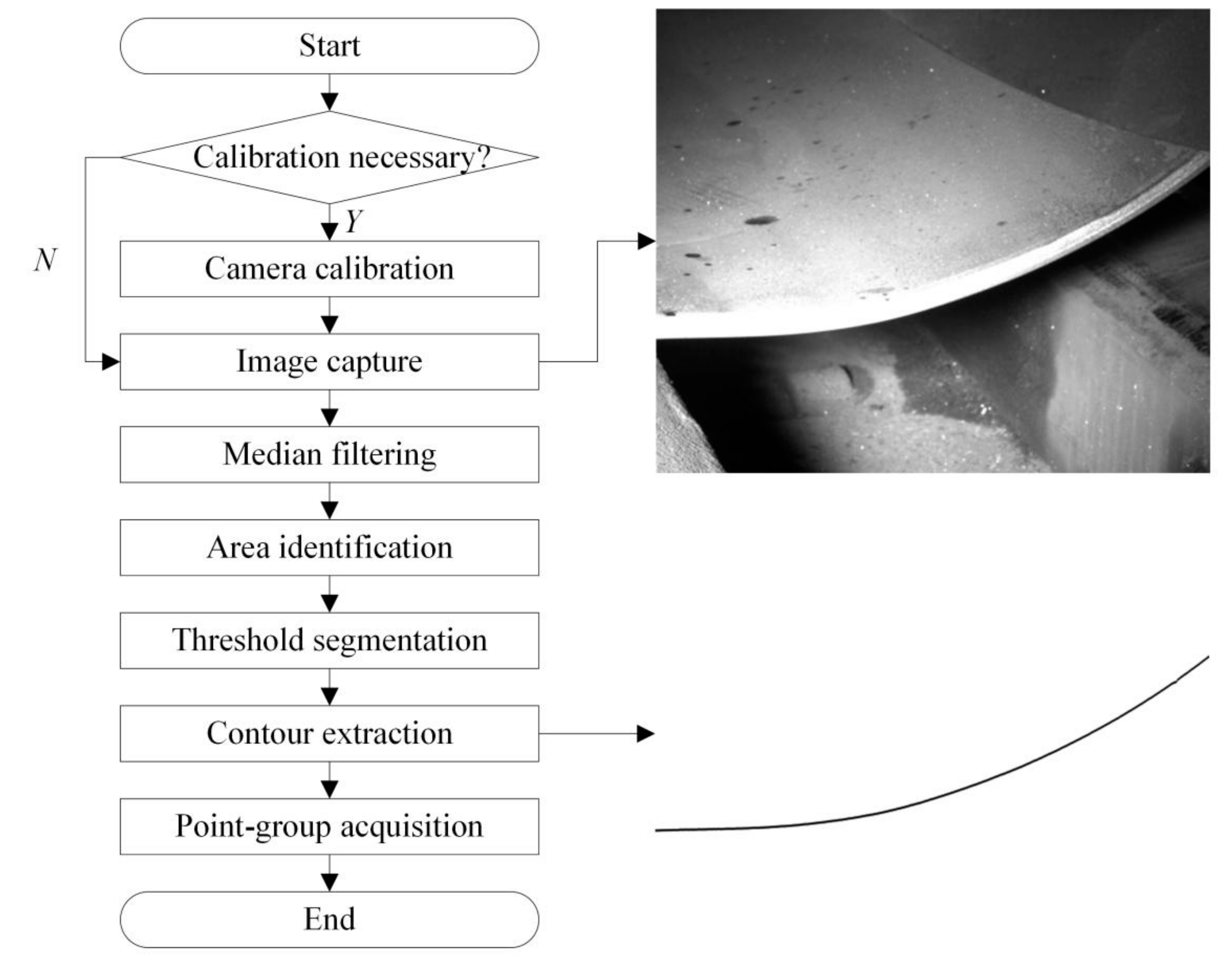
5. Contour Detection Method Based on Machine Vision
5.1. Formulation of Process Parameters
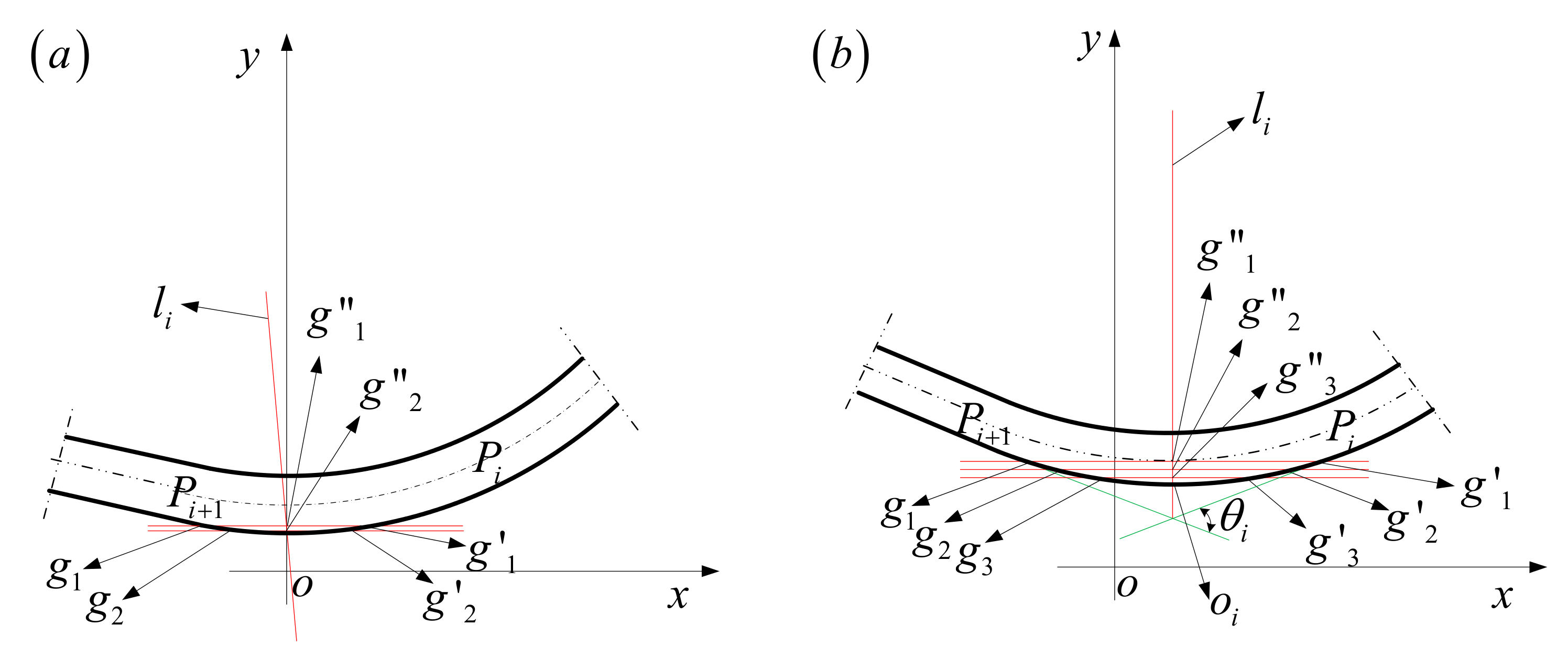
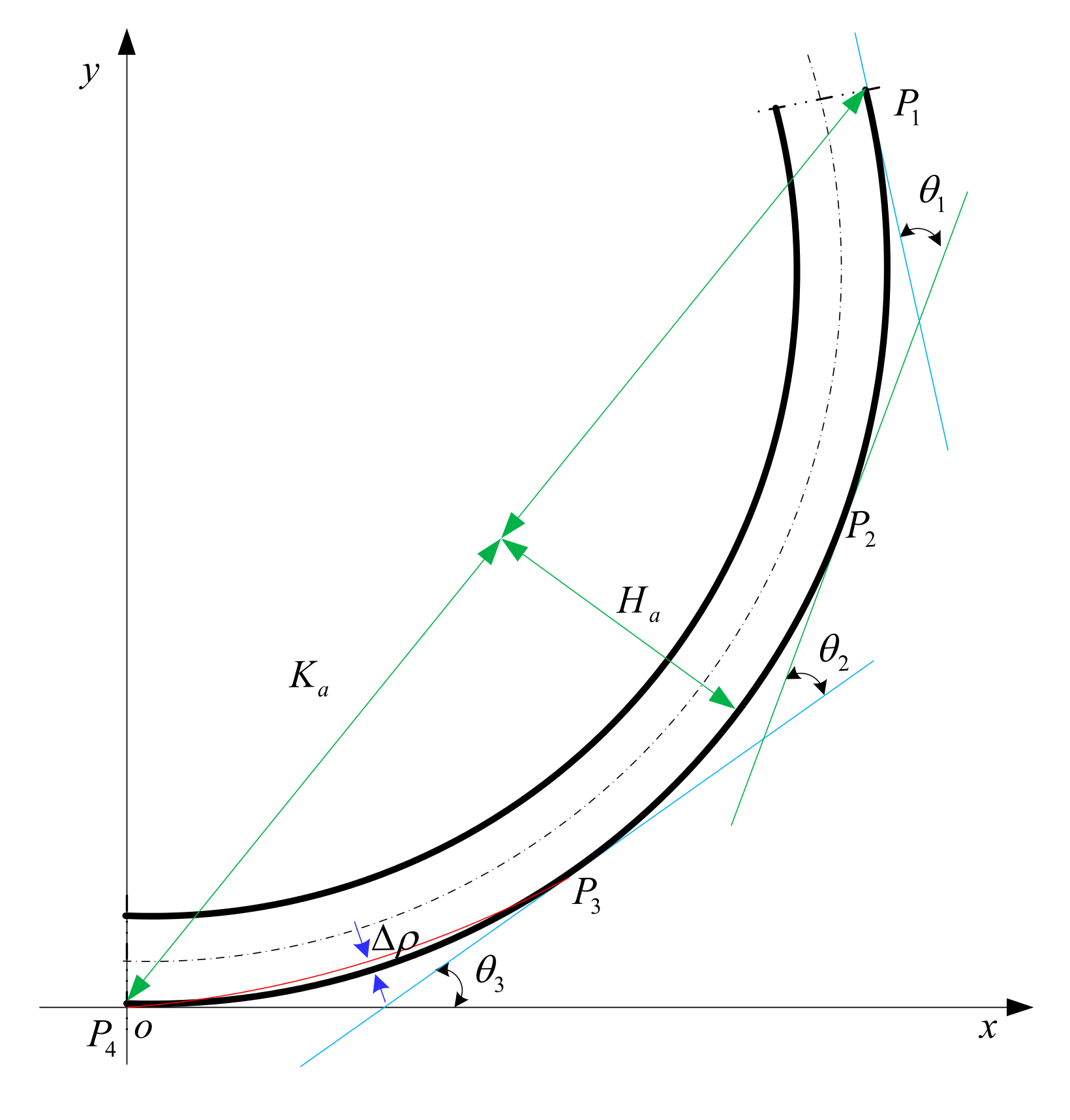
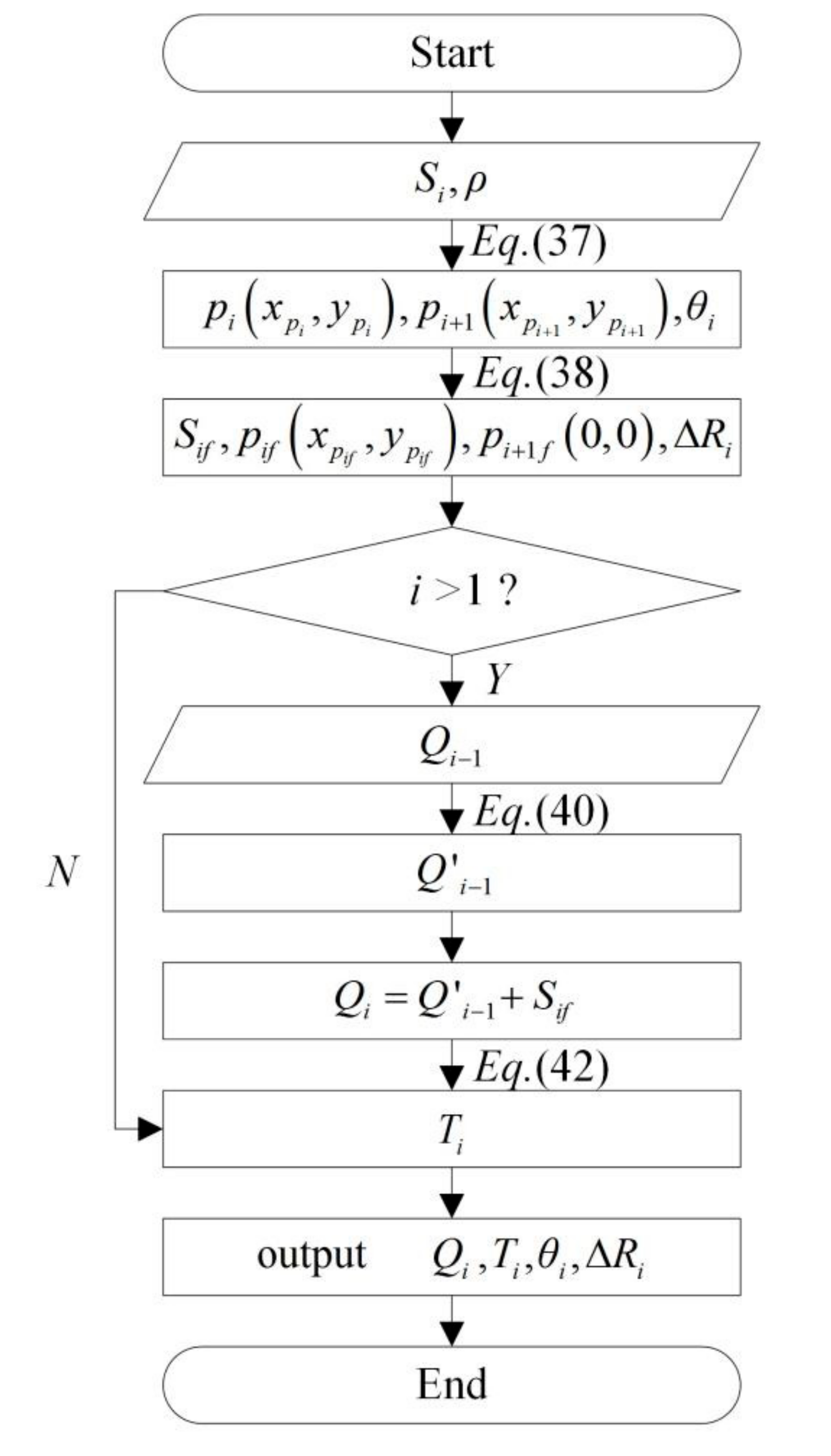
5.2. Splicing Algorithm for the Overall Contour
6. Experiment Design
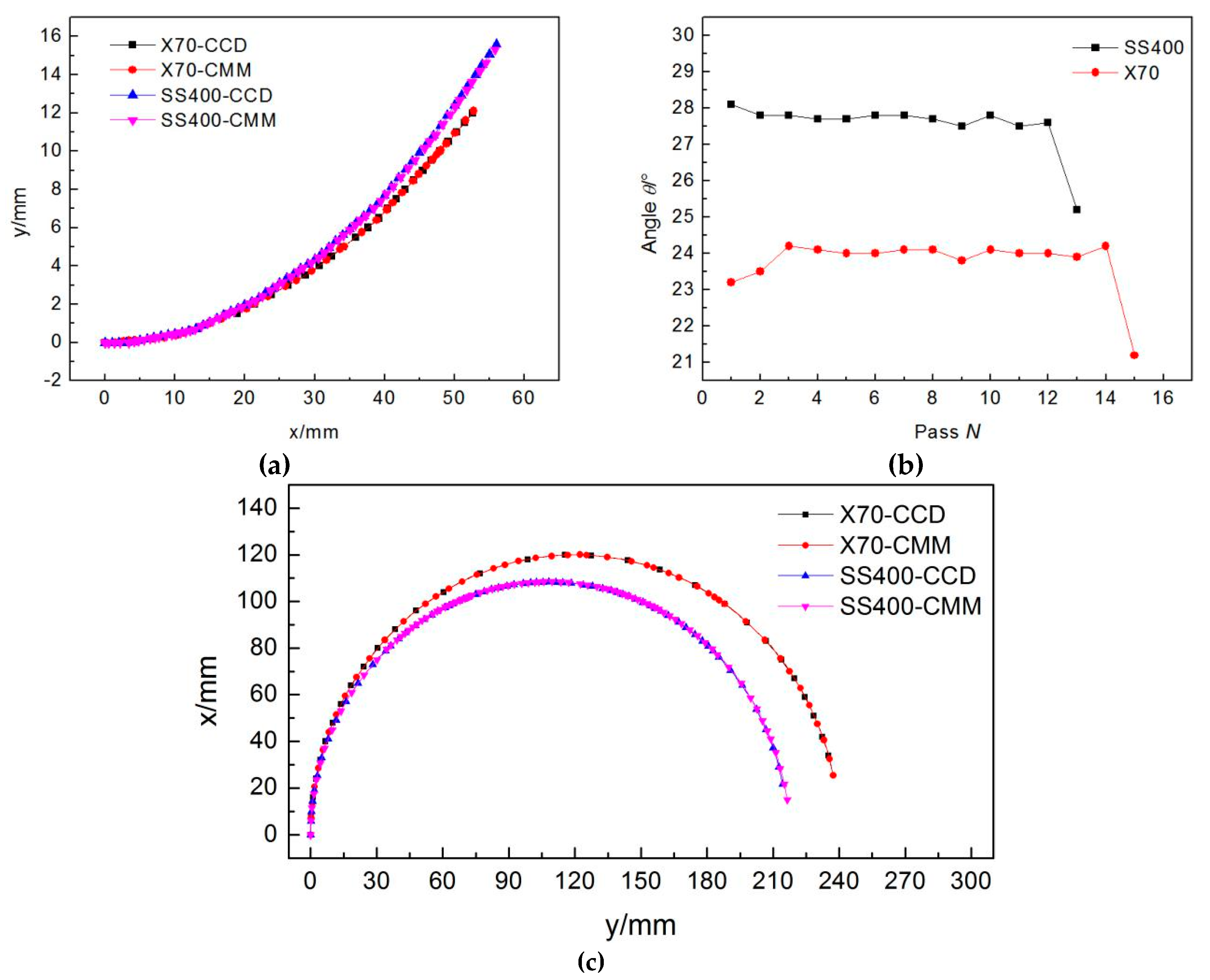
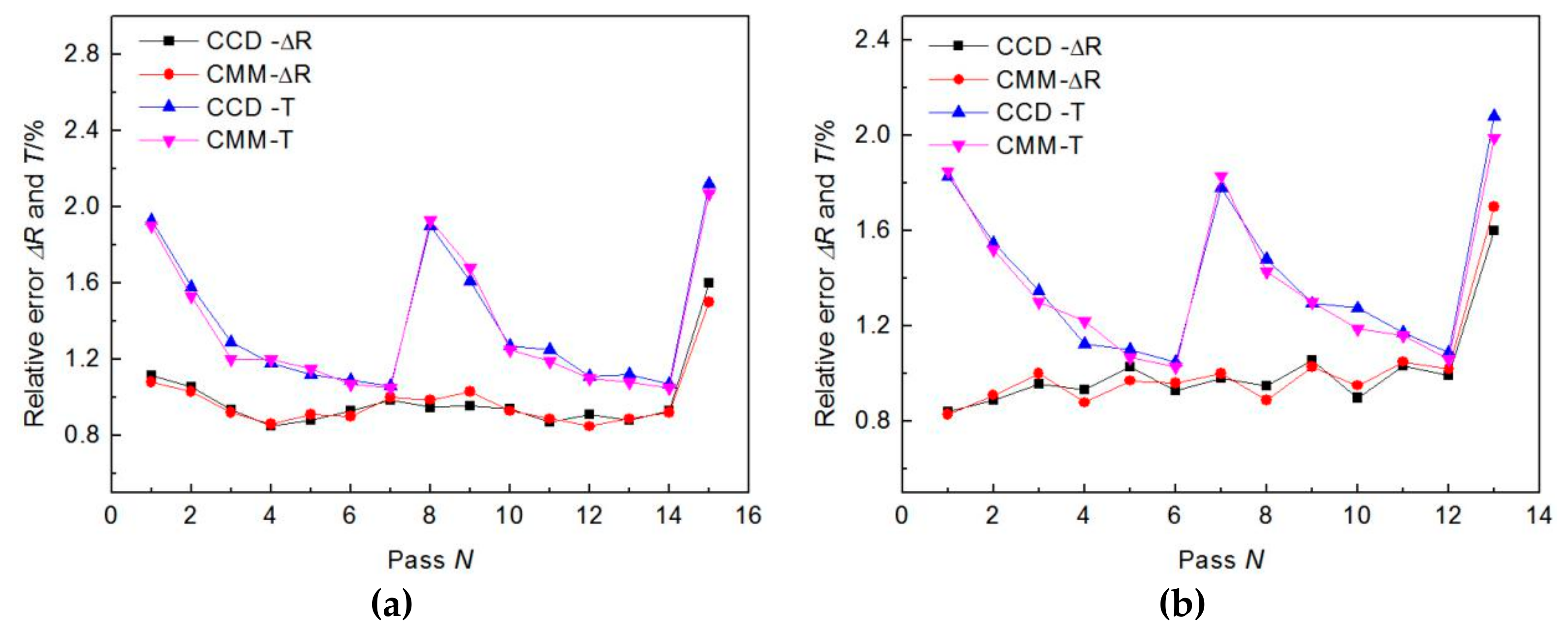
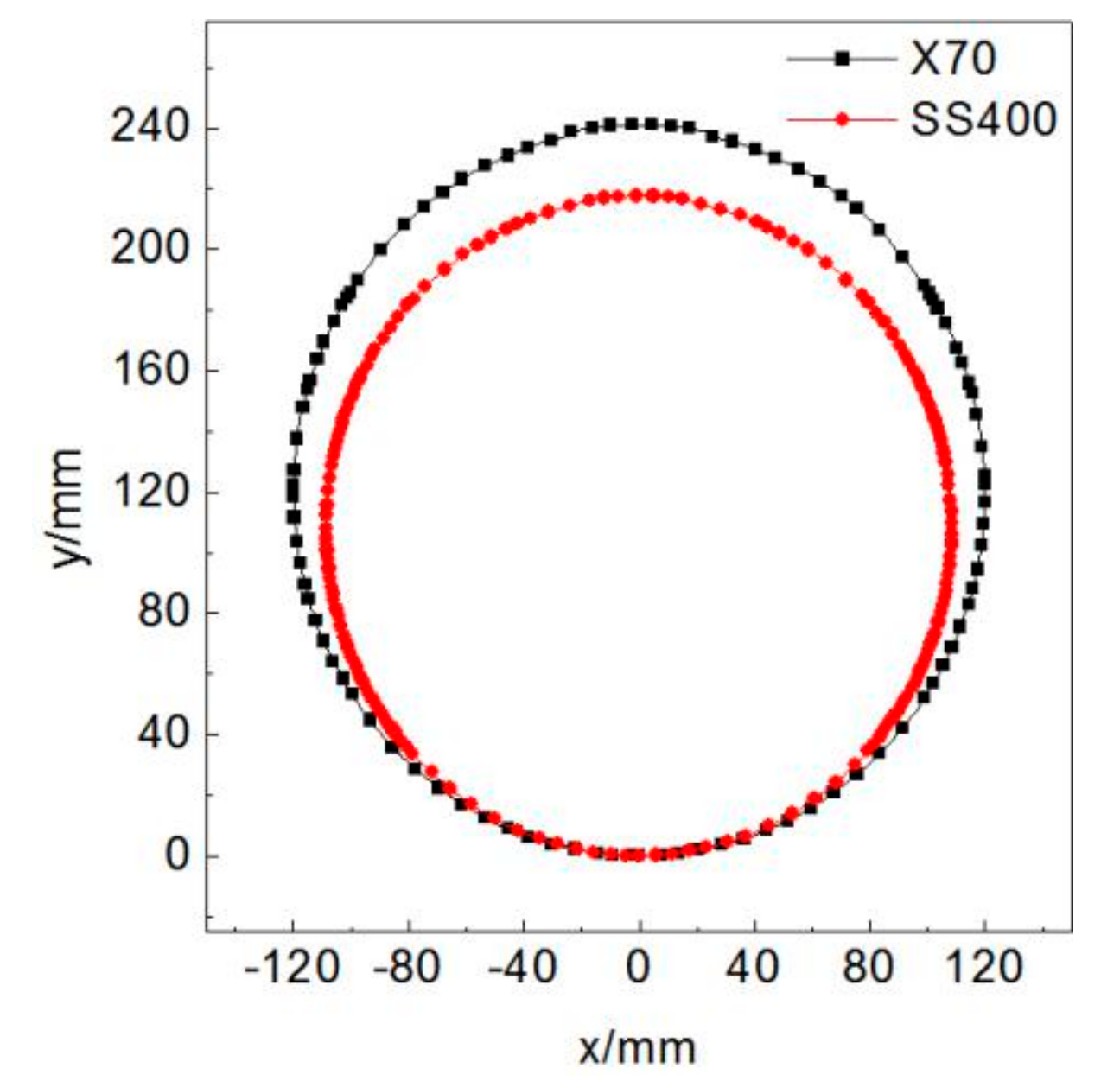
7. Experimental Results Analysis
8. Conclusions
- (1)
- The bending moment in the four-point bending process is evenly distributed between punch points, producing an arc with uniform curvature for the LSAW pipes.
- (2)
- The steel sheet does not need to crimp the edge before JCO forming process, which improves efficiency and reduces cost.
- (3)
- The pressure and reduction can be calculated based on the mechanical model of the four-point bending process, the material properties and process parameters.
- (4)
- The simulation results show that there is a limit to the relative spacing of punch for the pipe with certain geometrical dimensions and mechanical properties; based on this, the other process parameters are further determined.
- (5)
- The contour detection method based on the CCD camera can be used to detect the forming status of single pass, and the contour splicing method is proposed at the same time to obtain the overall contour of the formed part. These new methods take less time and have higher accuracy than previous detection methods.
- (6)
- Aiming at the four-point bending JCO forming process and the new contour detection method, the experiments were carried out. The two pipes required 13 and 15 passes, respectively, and the roundness of pipes are less than 1.1%, which is significantly less than the three-point bending JCO forming process. In addition, the contour detection system seems to run stably and accurately.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.; Yu, G.; Wang, W.; Zhao, J. Deflection detection and curve fitting in three-roll continuous straightening process for lsaw pipes. J. Mater. Process. Tech. 2017, 255, 150–160. [Google Scholar] [CrossRef]
- Genser, B.; Kleinjans, B. L-SAW large-diameter pipe production. Top quality is what counts Where are the trends leading? What are the benefits of UOE and JCOE®, Baosteel BAC; Shanghai Scientific and Technological Literature Publishing House: Shanghai, China, 2008; pp. 89–93. [Google Scholar]
- Specification for Line Pipe: API Specification 5L, 2018 Forty-Sixth Edition; American Petroleum Institute: Washington, DC, USA, 2018.
- Fu, Z.; Mo, J.; Wang, Y.; Ma, Z. Punch design’s springback prediction and geometrical parameter inverse of air-bending forming of sheet metal. J. Huazhong Univ. of Sci. Tech. 2009, 37, 86–89. [Google Scholar]
- Osadchii, V.Y.; Gaas, E.A.; Zvonarev, D.Y.; Kolikov, A.P. Shaping of thick sheet in the production of welded large-diameter pipe. Steel Transl. 2014, 44, 63–66. [Google Scholar] [CrossRef]
- Kumar, A.; Panangipalli, V.K.; Mahesh, K.; Swati, M. Prediction of springback in v-bending and design of dies using finite element simulation. Int. J Mater. Prod. Technol. 2010, 39, 291–301. [Google Scholar] [CrossRef]
- Fan, L.F.; Gao, Y.; Yan, J.X.; Yun, J.B. Effects of simulation parameters on springback in air bending of JCO forming. App. Mech. Mater. 2014, 623, 117–120. [Google Scholar] [CrossRef]
- Wang, F.; You, Y.P. Study on springback control of v-bending process of metal sheet. Mater. Sci. Tech. 2012, 20, 35–38+44. [Google Scholar]
- Vorkov, V.; Aerens, R.; Vandepitte, D.; Duflou, J.R. On the identification of a loading scheme in large radius air bending. Key Eng. Mater. 2015, 639, 155–162. [Google Scholar] [CrossRef]
- Zhao, J.; Yin, J.; Ma, R.; Ma, L.X. Springback equation of small curvature plane bending. Sci. China. Tech. Sci. 2011, 54, 2386–2396. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Qu, X.; Wang, G.; Sun, H.; Ma, R. Study on intelligent control technology for forming steel pipe of pipeline with JCO process. Sci. Chin. Technol. Sci. 2011, 10, 2754–2759. [Google Scholar] [CrossRef]
- Thome, M.; Vochsen, J.; Gotsis, V. Calculation tool and closed loop control for the JCO® pipe forming process. Procedia Eng. 2017, 207, 1605–1610. [Google Scholar] [CrossRef]
- Ayub, M.A.; Mohamed, A.B.; Esa, A.H. In-line inspection of roundness using machine vision. Procedia Tech. 2014, 15, 808–817. [Google Scholar] [CrossRef]
- Min, Y.; Wang, H.; Kang, F.; Dang, J. Study on rail gauge detection systems based on image sensors. Laser Tech. 2015, 39, 344–348. [Google Scholar]
- Li, J.; Zhao, J.; Ma, R. Precise bending pipeline steel pipes with JCO forming. Opt Precis Eng. 2010, 18, 638–645. [Google Scholar]
- Jia, L.; Wang, J.; Yin, Z.; Zheng, Z.; Li, S. Profile matching method for the measurement of steep conformal optics. Chin. Mech Eng. 2009, 20, 1159–1162. [Google Scholar]
- Fan, S. A new extracting formula and a new distinguishing means on the one variable cubic equation. Nat Sci J Hainan Teach Coll. 1989, 2, 91–98. [Google Scholar]




| Material | Yield Strength | Young’s Modulus E/MPa | Plastic Tangent Modulus D/MPa | Poisson’s Ratio |
|---|---|---|---|---|
| SS400 | 316 | 205,160 | 1870 | 0.3 |
| X70 | 504 | 200,007 | 2690 | 0.3 |
| X80 | 628 | 206,000 | 2660 | 0.3 |
| Diameter of Pipe d/mm | 1206.8 | |||||
| Thickness t/mm | 15.3 | 18.4 | 22 | 26.4 | 27.5 | 32 |
| 1 | 1.5 | 2 | 2.5 | |
|---|---|---|---|---|
| Radius of punch /mm | 20 | 40 | 60 | 80 |
| Radius of die /mm | 80 | 120 | 160 | 240 |
| Thickness t/mm | Punch Radius | Die Radius | Limit Relative Spacing of Punch | |
|---|---|---|---|---|
| 15.3 | 40 | 80 | 2 | 4.80 |
| 15.3 | 60 | 120 | 2 | 4.79 |
| 15.3 | 20 | 120 | 6 | 5.12 |
| 15.3 | 40 | 240 | 6 | 5.14 |
| 22 | 40 | 80 | 2 | 4.09 |
| 22 | 60 | 120 | 2 | 4.05 |
| 22 | 20 | 120 | 6 | 4.64 |
| 22 | 40 | 240 | 6 | 4.68 |
| 32 | 40 | 80 | 2 | 4.33 |
| 32 | 60 | 120 | 2 | 4.41 |
| 32 | 20 | 120 | 6 | 3.99 |
| 32 | 40 | 240 | 6 | 4.00 |
| Material | E/MPa | D/MPa | /mm | t/mm | B/mm | |
|---|---|---|---|---|---|---|
| SS400 | 316 | 205,160 | 1870 | 108.5 | 4.7 | 100 |
| X70 | 504 | 200,007 | 2690 | 120 | 4 | 100 |
| Material | Punch Radius | Die Radius | Punch Spacing /mm | Die Spacing /mm | Passes N | Pass Length /mm | Reduction /mm | |
|---|---|---|---|---|---|---|---|---|
| SS400 | 1.5 | 7.5 | 25 | 23.59 | 39.34 | 13 | 52.44 | 3.72 |
| X70 | 1.5 | 7.5 | 25 | 22.87 | 36.33 | 15 | 50.26 | 3.25 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, H.; Yu, G.; Zhao, J. Research on Four-Point Air Bending Process and Contour Detection Method for JCO Forming Process of LSAW Pipes. Metals 2019, 9, 859. https://doi.org/10.3390/met9080859
Zhang Z, Wang H, Yu G, Zhao J. Research on Four-Point Air Bending Process and Contour Detection Method for JCO Forming Process of LSAW Pipes. Metals. 2019; 9(8):859. https://doi.org/10.3390/met9080859
Chicago/Turabian StyleZhang, Zhiyuan, Haoran Wang, Gaochao Yu, and Jun Zhao. 2019. "Research on Four-Point Air Bending Process and Contour Detection Method for JCO Forming Process of LSAW Pipes" Metals 9, no. 8: 859. https://doi.org/10.3390/met9080859
APA StyleZhang, Z., Wang, H., Yu, G., & Zhao, J. (2019). Research on Four-Point Air Bending Process and Contour Detection Method for JCO Forming Process of LSAW Pipes. Metals, 9(8), 859. https://doi.org/10.3390/met9080859








