Probabilistic Modeling of Slip System-Based Shear Stresses and Fatigue Behavior of Coarse-Grained Ni-Base Superalloy Considering Local Grain Anisotropy and Grain Orientation
Abstract
1. Introduction
- Uniaxial stress states in each grain with global uniaxial load
- No influence of the deformation behavior of the surrounding grains
- Only Young’s modulus and Schmid factor in direction of a uniaxial stress were considered
- Homogeneous resolved shear stress field at slip system within the grain.
2. Materials and Methods
2.1. Material
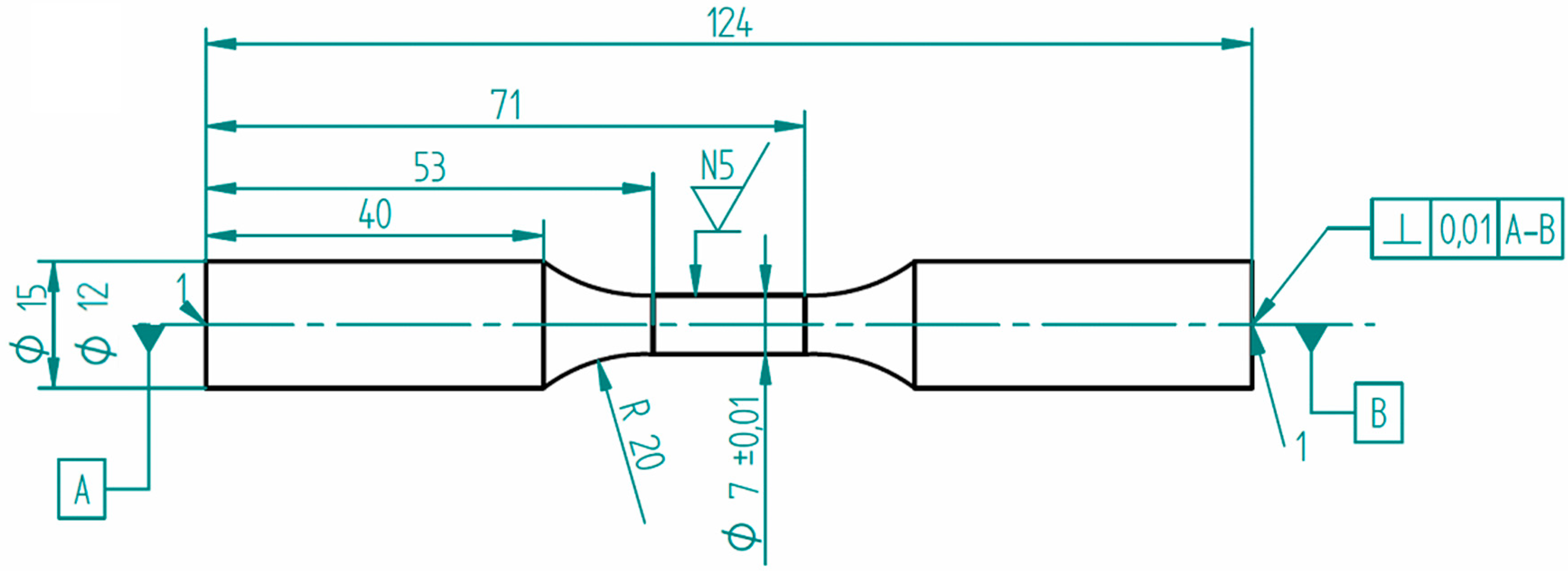
2.2. Experimental Isothermal LCF Testing
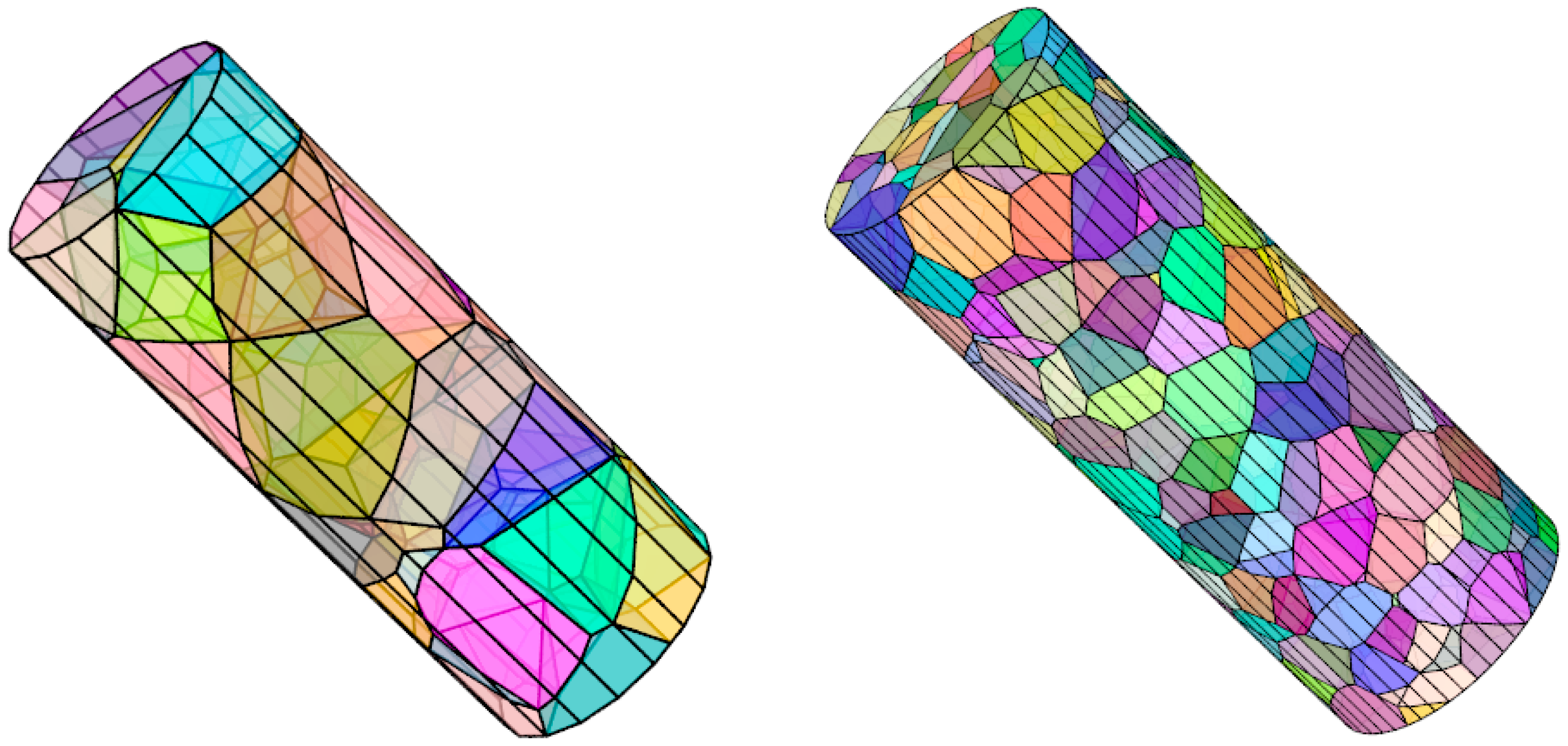
2.3. FEA Models for Polycrystalline Microstructure Modelling
2.4. Derivation of the Schmid Factor Distribution
2.5. Calibration of the Probabilistic LCF Fatigue Model and the Cyclic Material Strength Model
3. Results
3.1. Microscopic Material Examinations and Orientation Distributions
3.2. Results of the Isothermal LCF Tests at 850 °C
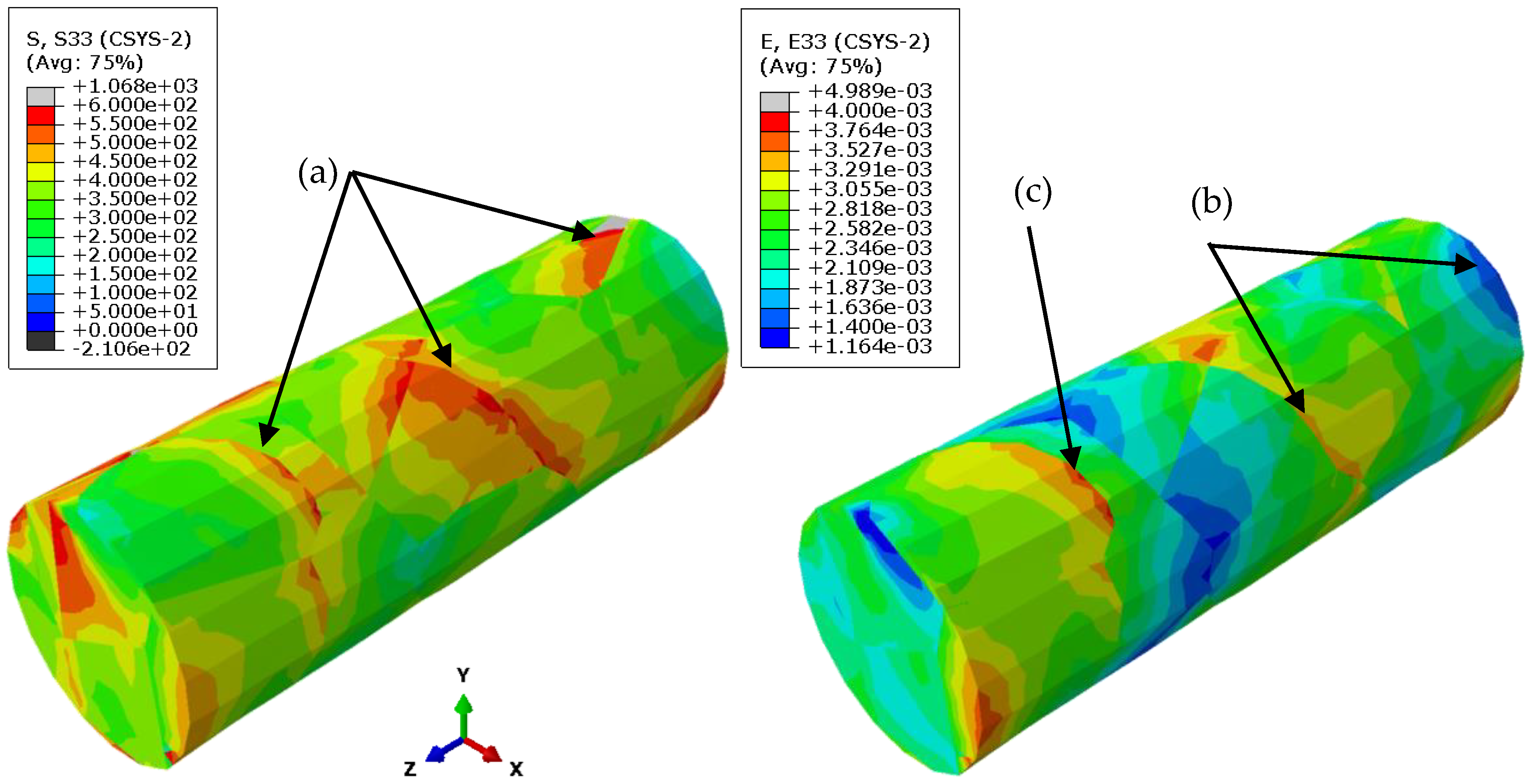
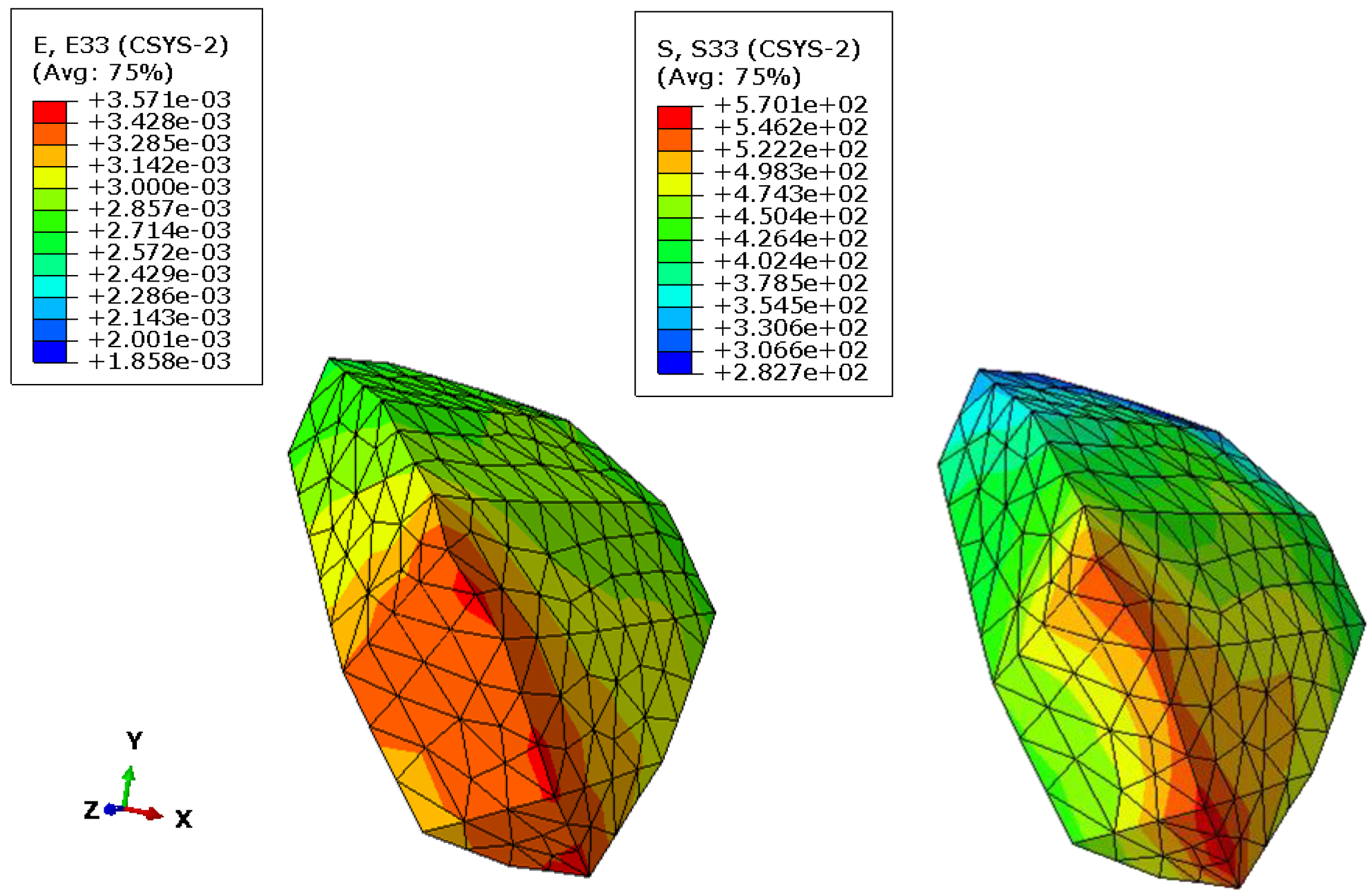
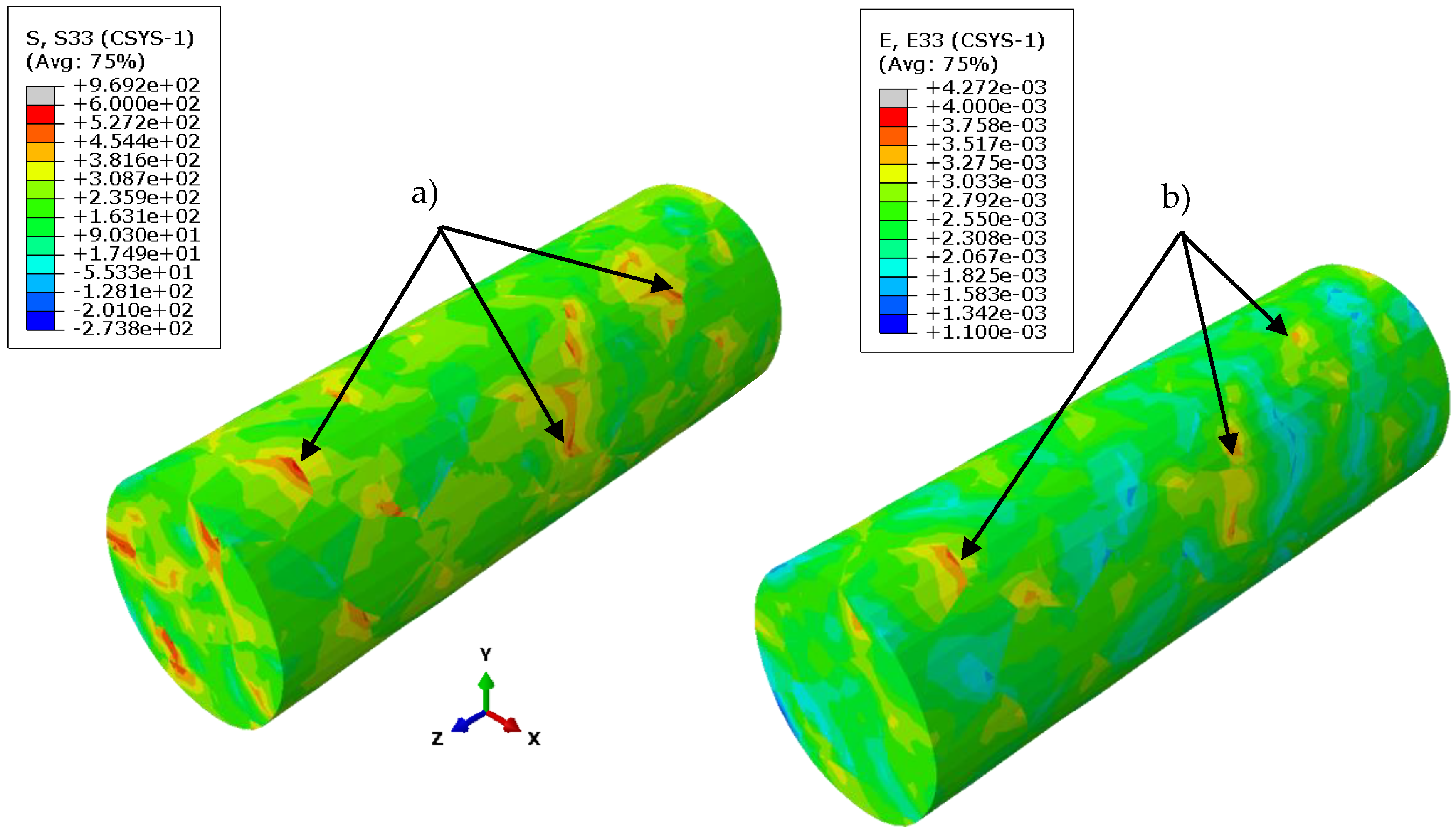
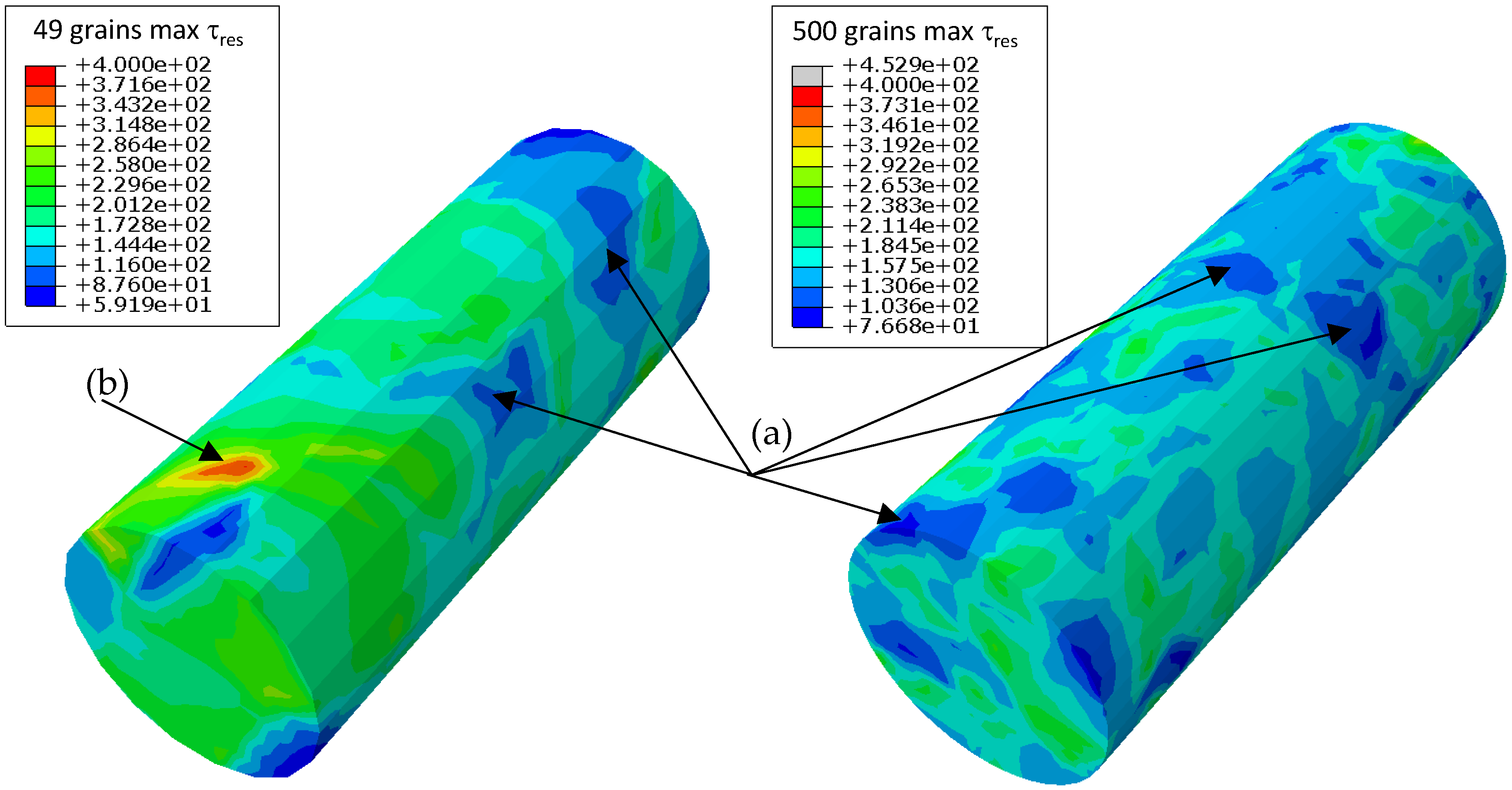
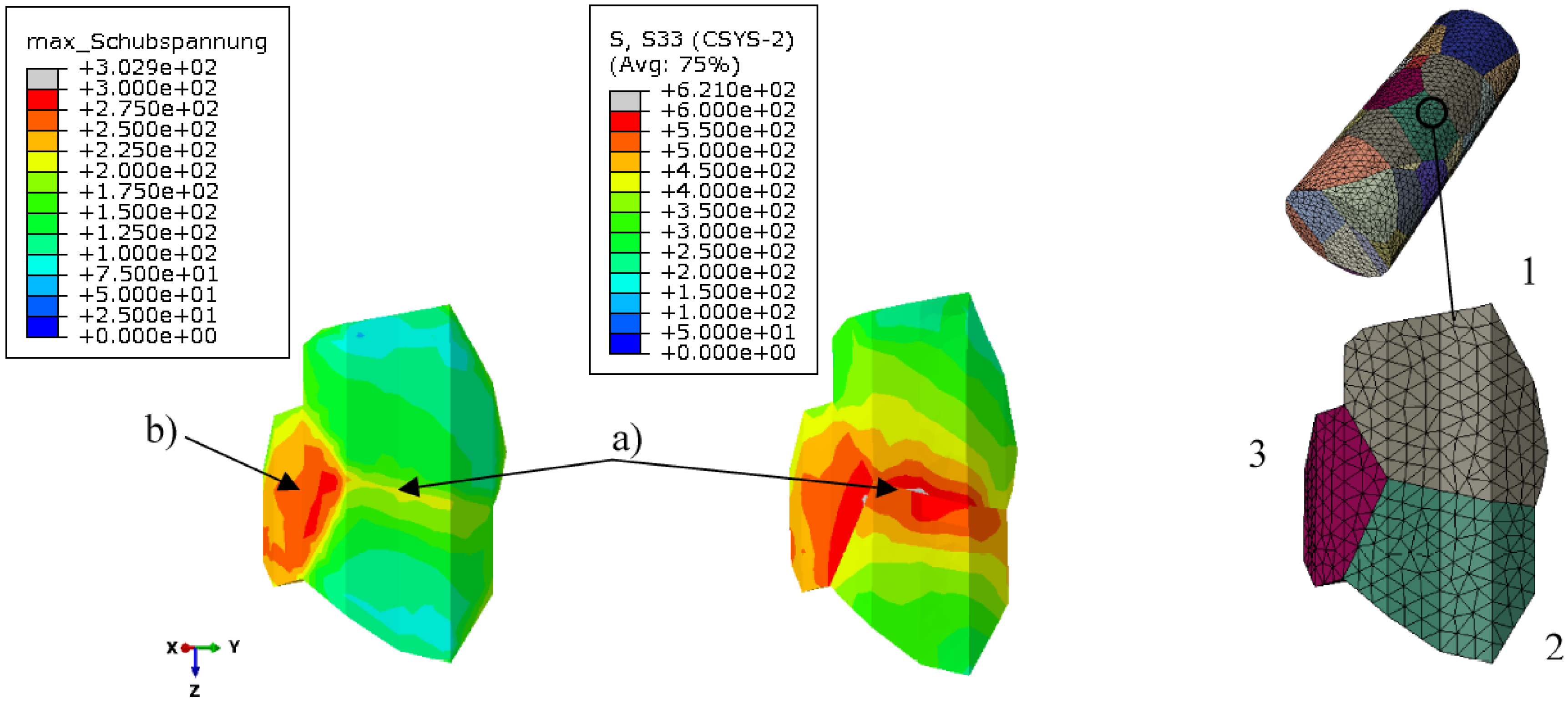
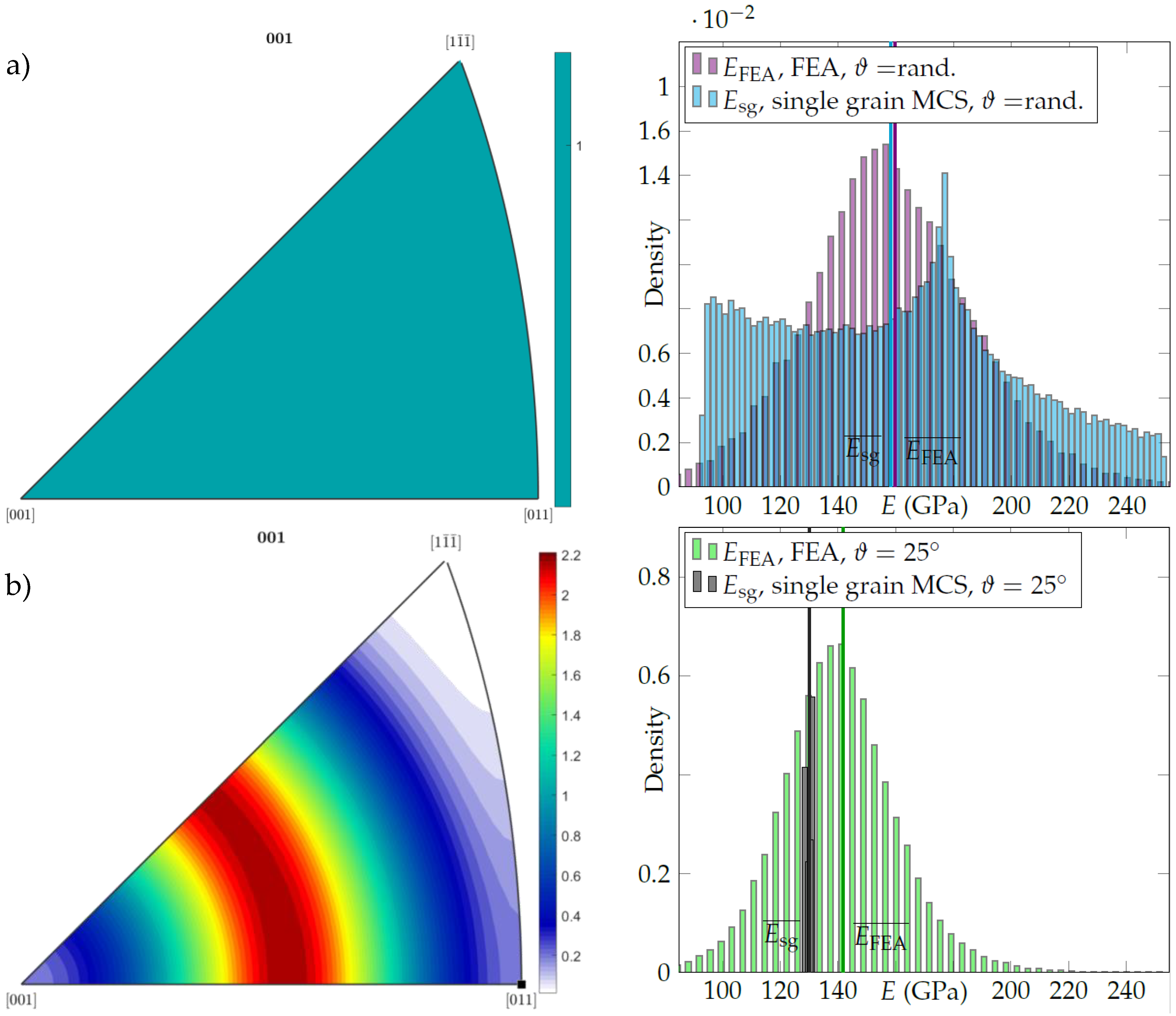
3.3. Results of the Finite Element Simulation
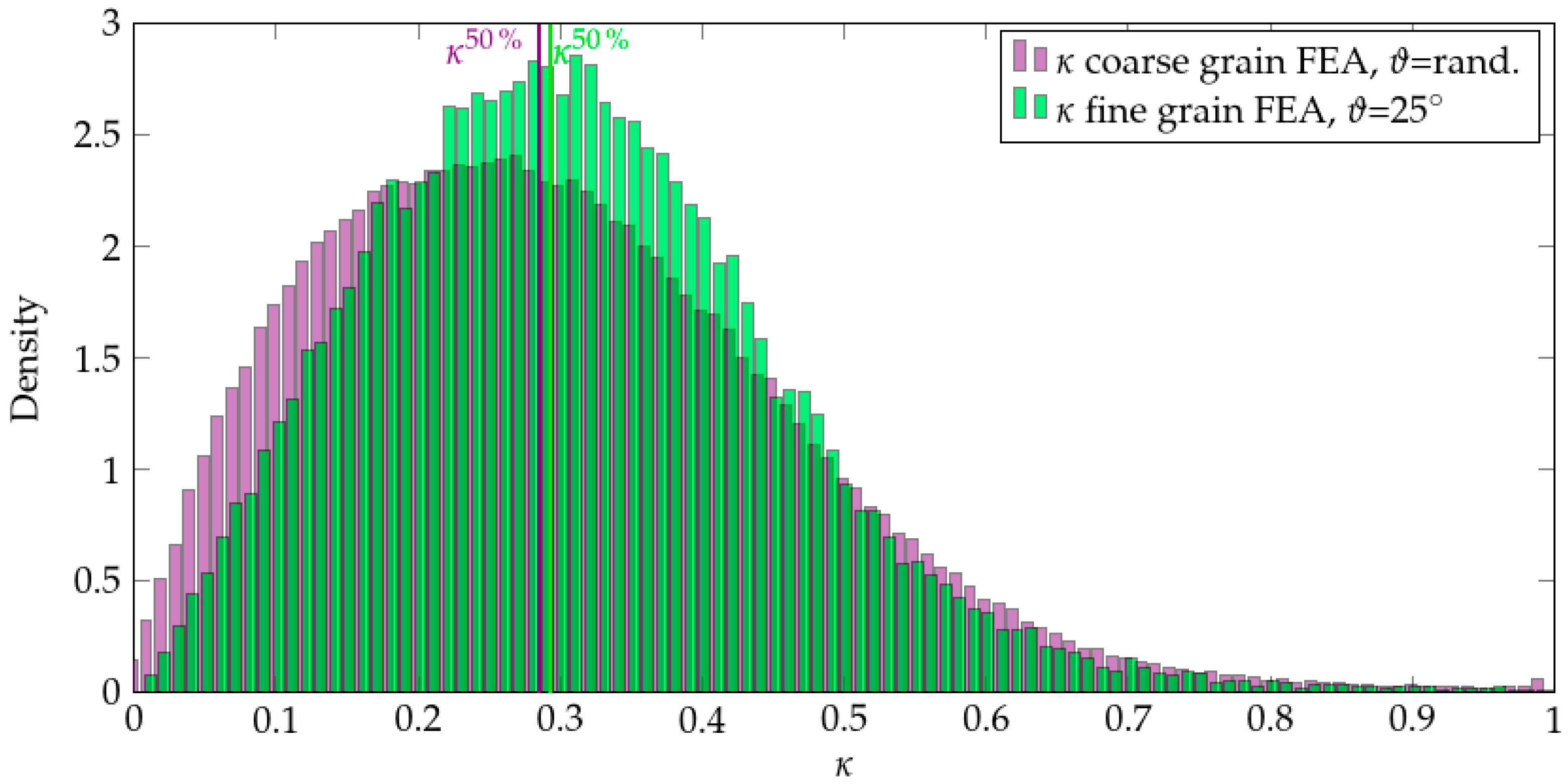
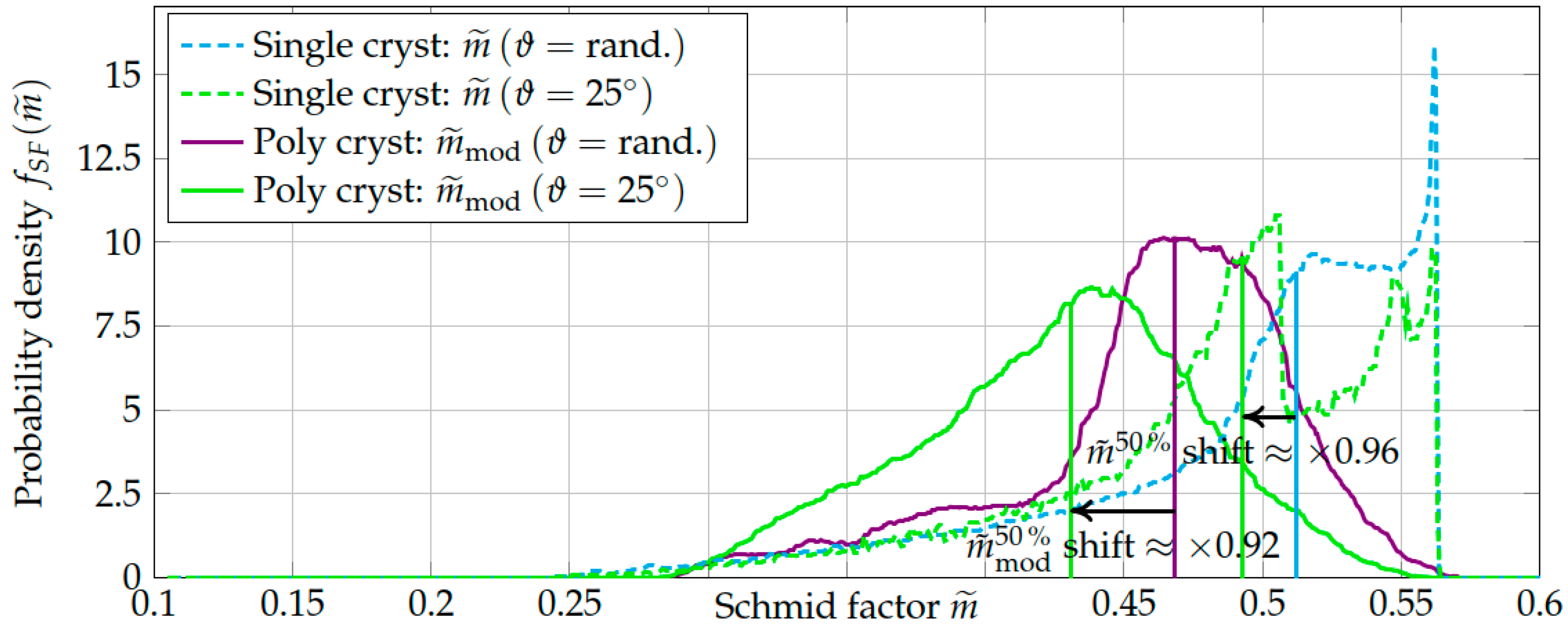
3.4. Results of the Schmid-Factor Distribution Calculations
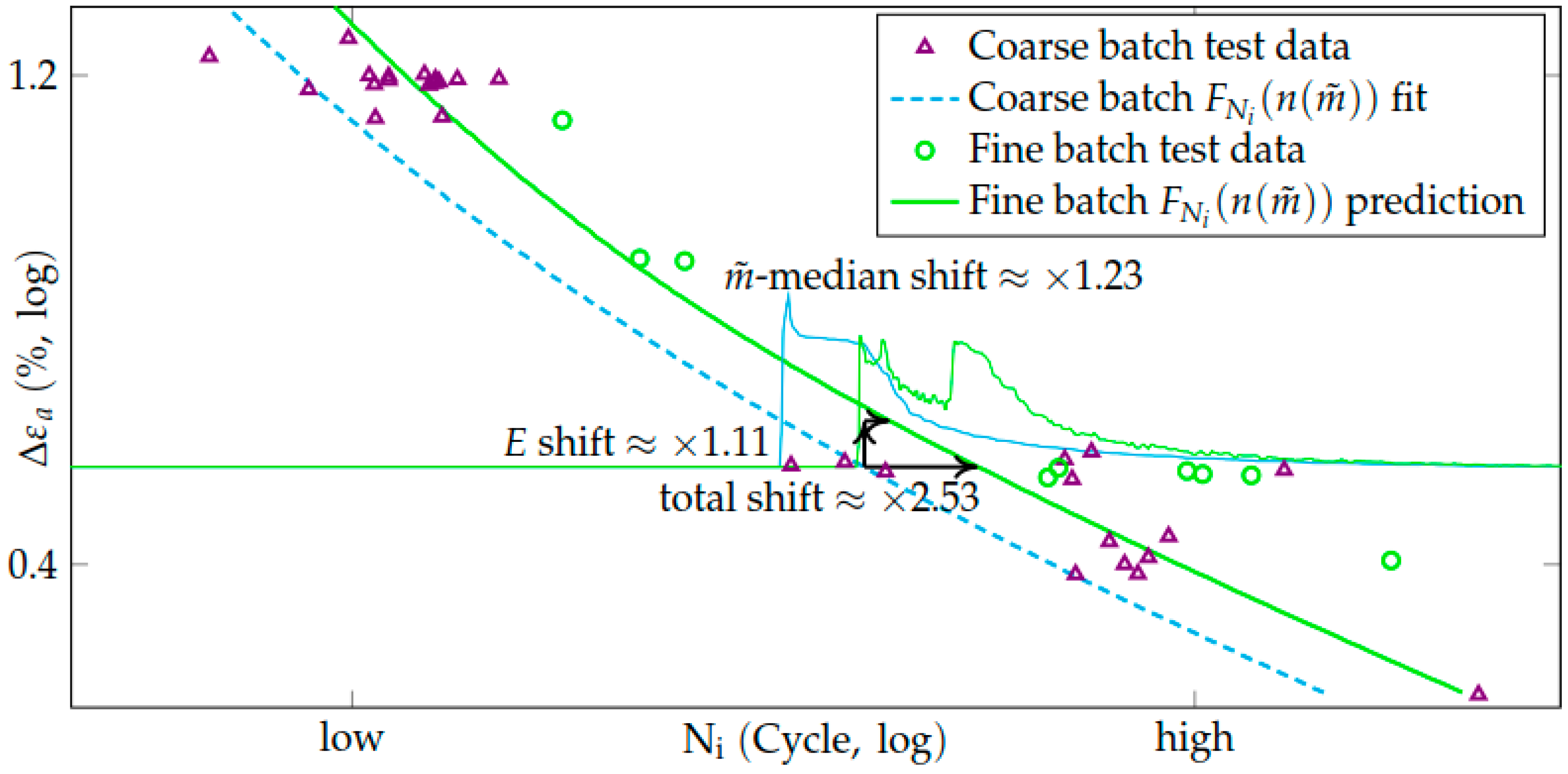
3.5. Procedure of the LCF Life Calibration and Prediction
Prediction of the Wöhler Curve from a Weibull Distribution
Prediction of the Wöhler Curve from the Single Grain Schmid Factor Distribution
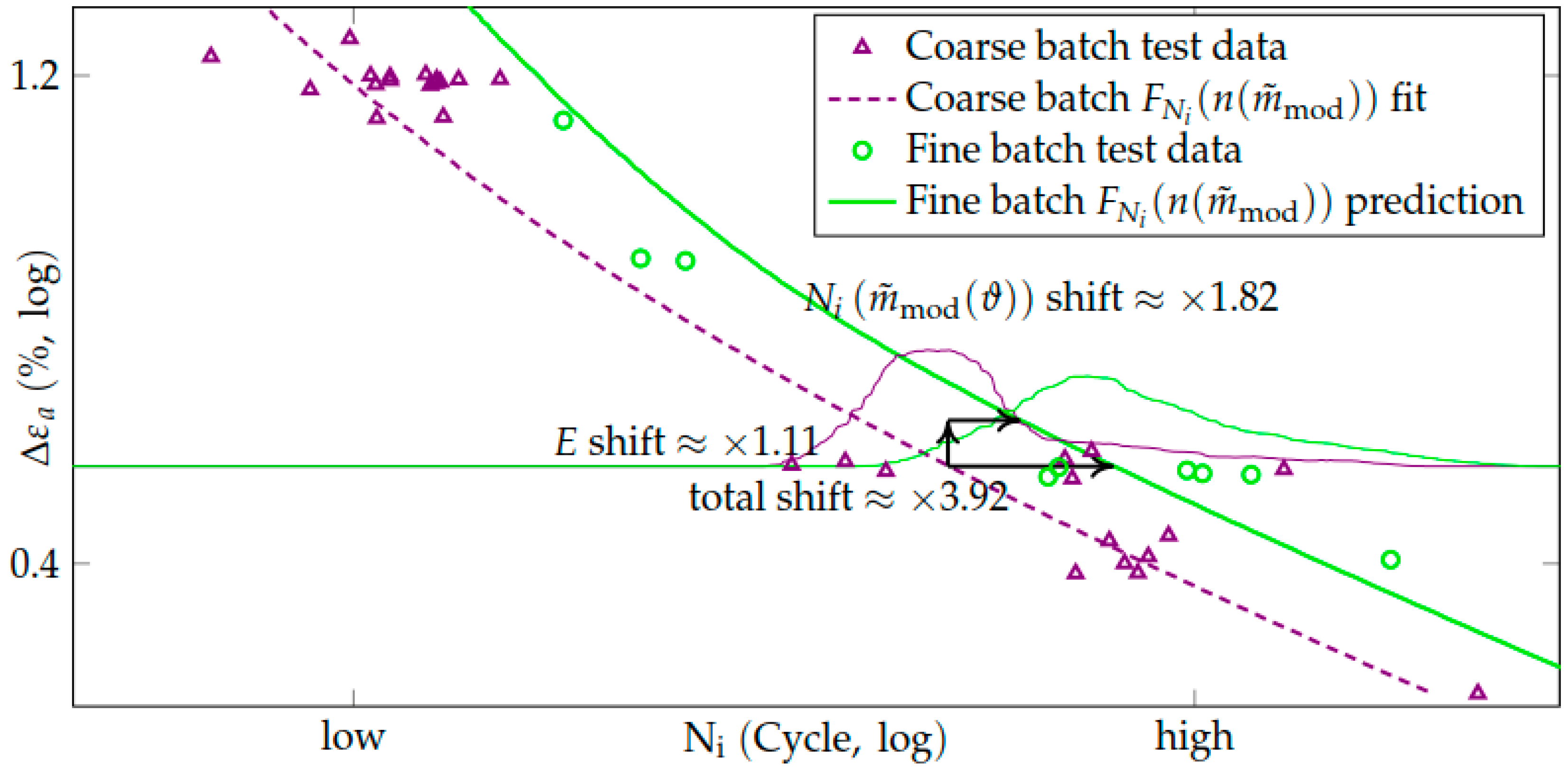
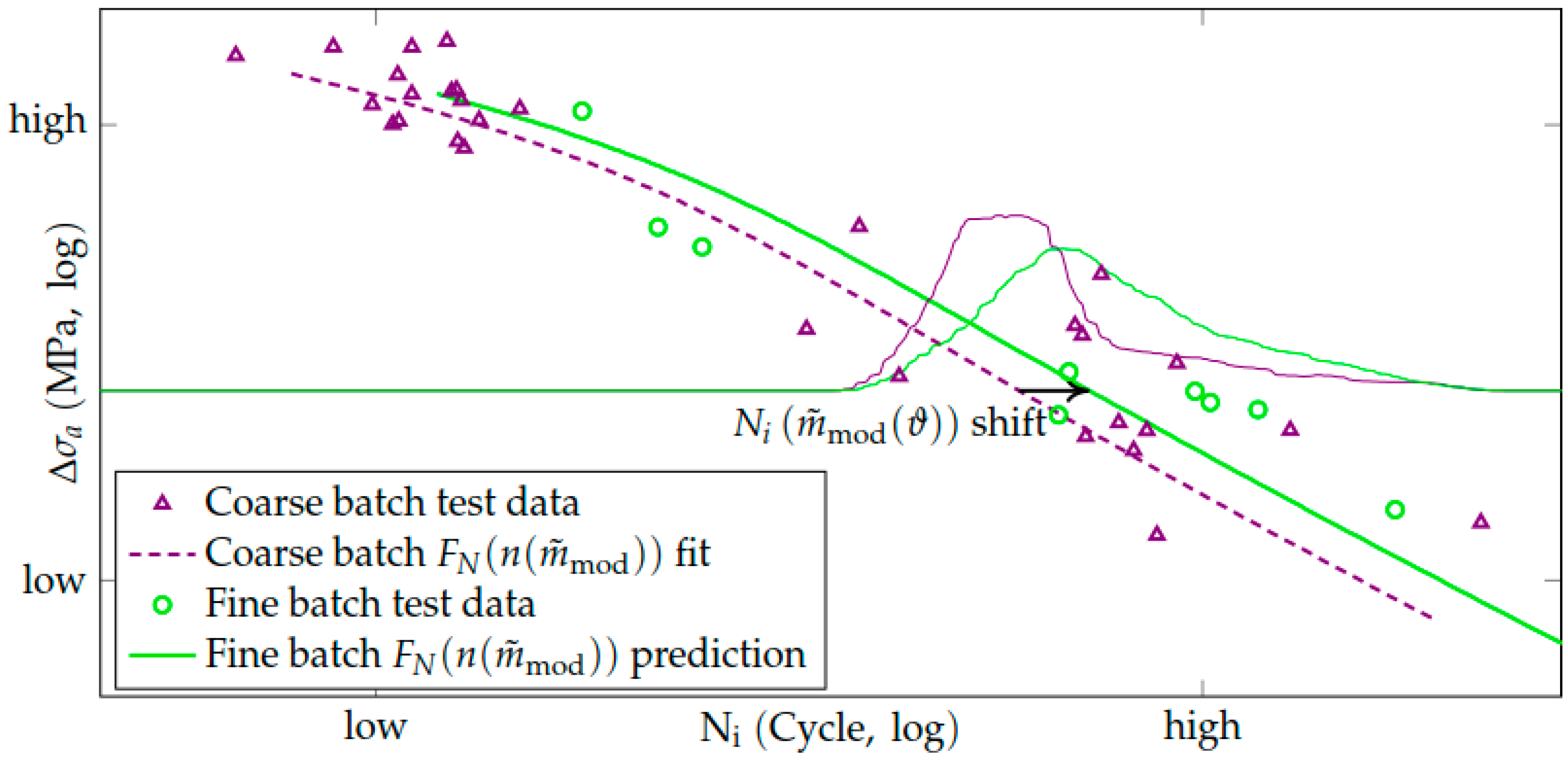
Prediction of the Wöhler Curve from the Modified Schmid factor Distribution
4. Discussion
4.1. Influence of the Grain Orientation Distribution on the Mechanical Properties
4.2. Influence of Grain Orientation Distribution on the Fatigue Behavior
4.3. Comparison of Fit and Prediction Quality of Probabilistic Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bussac, A.; Lautridou, J. A probabilistic model for prediction of lcf surface crack initiation in pm alloys. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 861–874. [Google Scholar] [CrossRef]
- Grison, J.; Remy, L. Fatigue failure probability in a powder metallurgy Ni-base superalloy. Eng. Fract. Mech. 1997, 57, 41–55. [Google Scholar] [CrossRef]
- Brückner-Foit, A.; Jäckels, H.; Quadfasel, U. Prediction of the lifetime distribution of high-strength components subjected to fatigue loading. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 891–908. [Google Scholar] [CrossRef]
- Pineau, A.; Antolovich, S.D. Probabilistic approaches to fatigue with special emphasis on initiation from inclusions. Int. J. Fatigue 2016, 93, 422–434. [Google Scholar] [CrossRef]
- Böhm, J.; Heckel, K. Die Vorhersage der Dauerschwingfestigkeit unter Berücksichtigung des statistischen Größeneinflusses. Materialwissenschaft und Werkstofftechnik 1982, 13, 120–128. [Google Scholar] [CrossRef]
- Zheng, X.-L.; Lü, B.; Jiang, H. Determination of probability distribution of fatigue strength and expressions of P-S-N curves. Eng. Fract. Mech. 1995, 50, 483–491. [Google Scholar] [CrossRef]
- Hertel, O.; Vormwald, M. Statistical and geometrical size effects in notched members based on weakest-link and short-crack modelling. Eng. Fract. Mech. 2012, 95, 72–83. [Google Scholar] [CrossRef]
- Okeyoyin, O.A.; Owolabi, G.M. Application of Weakest Link Probabilistic Framework for Fatigue Notch Factor to Turbine Engine Materials. World J. Mech. 2013, 03, 237–244. [Google Scholar] [CrossRef]
- Zok, F.W. On weakest link theory and Weibull statistics. J. Am. Ceram. Soc. 2017, 100, 1265–1268. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens Litografiska Anstalts Foìrlag: Stockholm, Sweden, 1939. [Google Scholar]
- Schijve, J. A normal distribution or a weibull distribution for fatigue lives. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 851–859. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue predictions and scatter. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 381–396. [Google Scholar] [CrossRef]
- Xiulin, Z. Prediction of probability distribution of fatigue life of 15MnVN steel notched elements under variable-amplitude loading. Int. J. Fatigue 1996, 18, 81–86. [Google Scholar] [CrossRef]
- Schijve, J. Statistical distribution functions and fatigue of structures. Int. J. Fatigue 2005, 27, 1031–1039. [Google Scholar] [CrossRef]
- Karolczuk, A.; Palin-Luc, T. Modelling of stress gradient effect on fatigue life using weibull based distribution function. J. Theor. Appl. Mech. 2013, 51, 297–311. [Google Scholar]
- Rechnerischer Festigkeitsnachweis für Maschinenbauteile aus Stahl, Eisenguss-Und Aluminiumwerkstoffen, 6th ed.; Rennert, R., Ed.; VDMA-Verlag: Frankfurt am Main, Germany, 2012; ISBN 9783816306054. [Google Scholar]
- Fiedler, M.; Varfolomeev, I. Rechnerischer Festigkeitsnachweis unter Expliziter Erfassung Nichtlinearen Werkstoff-Verformungsverhaltens, Final Report; VDMA-Verlag: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Fiedler, M.; Wächter, M.; Varfolomeev, I.; Vormwald, M.; Esderts, A. Richtlinie Nichtlinear. Rechnerischer Festigkeitsnachweis unter Expliziter Erfassung Nichtlinearen Werkstoffverformungsverhaltens; für Bauteile aus Stahl, Stahlguss und Aluminiumknetlegierungen, 1. Auflage; VDMA Verlag GmbH: Frankfurt am Main, Germany, 2019; ISBN 3816307299. [Google Scholar]
- Schmitz, S.; Seibel, T.; Beck, T.; Rollmann, G.; Krause, R.; Gottschalk, H. A probabilistic model for LCF. Comput. Mater. Sci. 2013, 79, 584–590. [Google Scholar] [CrossRef]
- Schmitz, S.; Gottschalk, H.; Rollmann, G.; Krause, R. Risk Estimation for LCF Crack Initiation. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3 June 2013; ASME: New York, NY, USA, 2013; p. V07AT27A007, ISBN 978-0-7918-5526-3. [Google Scholar]
- Hell, M.; Wagener, R.; Kaufmann, H.; Melz, T. Fatigue Design with Respect to Component Related Cyclic Material Behaviour and Considerations of Size Effects. Procedia Eng. 2015, 133, 389–398. [Google Scholar] [CrossRef]
- Mäde, L.; Schmitz, S.; Gottschalk, H.; Beck, T. Combined Notch and Size Effect Modeling in a Local Probabilistic Approach for LCF. Comput. Mater. Sci. 2017, 142, 377–388. [Google Scholar] [CrossRef]
- Maede, L.; Kumar, K. Evaluation of component-similar rotor steel specimens with a local probabilistic approach for LCF.—Under Review. Comput. Mater. Sci. 2019. [Google Scholar]
- Siebörger, D.; Knake, H.; Glatzel, U. Temperature dependence of the elastic moduli of the nickel-base superalloy CMSX-4 and its isolated phases. Mater. Sci. Eng. A 2001, 298, 26–33. [Google Scholar] [CrossRef]
- Engel, B.; Beck, T.; Moch, N.; Gottschalk, H.; Schmitz, S. Effect of local anisotropy on fatigue crack initiation in a coarse grained nickel-base superalloy. MATEC Web Conf. 2018, 165, 4004. [Google Scholar] [CrossRef]
- Hermann, W.; Sockel, H.G.; Bertram, A. Elastic Properties and Determination of elastic Constants of Nickel-base Superalloy by Free-Free Beam Technique. In Proceedings of the 11th International Symposium on Superalloys, Champion, PA, USA, 22–26 September 1996; p. 229. [Google Scholar] [CrossRef]
- Schmid, E.; Boas, W. Plasticity of Crystals. With Special Reference to Metals; Chapman & Hall: London, UK, 1968. [Google Scholar]
- Gottschalk, H.; Schmitz, S.; Seibel, T.; Rollmann, G.; Krause, R.; Beck, T. Probabilistic Schmid factors and scatter of low cycle fatigue (LCF) life. Materialwissenschaft und Werkstofftechnik 2015, 46, 156–164. [Google Scholar] [CrossRef]
- Seibel, T. Einfluss der Probengröße und der Kornorientierung auf die Lebensdauer Einer Polykristallinen Ni-Basislegierung bei LCF- Beanspruchung. Ph.D. Thesis, Forschungszentrum Jülich, Jülich, Germany, 2014. [Google Scholar]
- Moch, N. From Microscopic Models of Damage Accumulation to Probability of Failure of Gas Turbines. Ph.D. Thesis, Bergische Universität Wuppertal, Wuppertal, Germany, 2018. [Google Scholar]
- Engel, B. Einfluss der Lokalen Kornorientierung und der Korngröße auf das Verformungs- und Ermüdungsverhalten von Nickelbasis Superlegierungen. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2018. [Google Scholar]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Computer Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]
- Ghazvinian, E.; Diederichs, M.S.; Quey, R. 3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing. J. Rock Mech. Geotech. Eng. 2014, 6, 506–521. [Google Scholar] [CrossRef]
- Quey, R.; Renversade, L. Optimal polyhedral description of 3D polycrystals: Method and application to statistical and synchrotron X-ray diffraction data. Comput. Methods Appl. Mech. Eng. 2018, 330, 308–333. [Google Scholar] [CrossRef]
- Aghaie-Khafri, M.; Farahany, S. Creep Life Prediction of Thermally Exposed Rene 80 Superalloy. J. Mater. Eng. Perform. 2010, 19, 1065–1070. [Google Scholar] [CrossRef]
- Antolovich, S.D.; Liu, S.; Baur, R. Low cycle fatigue behavior of René 80 at elevated temperature. Met. Trans. A 1981, 12, 473–481. [Google Scholar] [CrossRef]
- Buchholz, B. Entwicklung eines Werkstoffmodells für Isotherme und Anisotherme Ermüdung der Nickelbasislegierung René80. Ph.D. Thesis, TU Dresden, Dresden, Deutschland, 2012. [Google Scholar]
- Neidel, A.; Riesenbeck, S.; Ullrich, T.; Völker, J.; Yao, C. Hot cracking in the HAZ of laser-drilled turbine blades made from René 80. Mater. Test. 2005, 47, 553–559. [Google Scholar] [CrossRef]
- Österle, W.; Krause, S.; Moelders, T.; Neidel, A.; Oder, G.; Völker, J. Influence of heat treatment on microstructure and hot crack susceptibility of laser-drilled turbine blades made from René 80. Mater. Charact. 2008, 59, 1564–1571. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. für die reine und angewandte Mathematik (Crelle’s J.) 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphère vide. A la mémoire de Georges Voronoï. Bulletin de l’Académie des Sciences de l’URSS. Classe Des Sciences Mathématiques Et Na 1934, 6, 793–800. [Google Scholar]
- León, C.A.; Massé, J.-C.; Rivest, L.-P. A statistical model for random rotations. J. Multivar. Anal. 2006, 97, 412–430. [Google Scholar] [CrossRef]
- Engel, B.; Beck, T.; Schmitz, S. (Eds.) LCF 8; High Temperature Low-Cycle-Fatigue of the Ni-Base Superalloy René80; Dresden, Deutschland, 2017. [Google Scholar]
- Rösler, J.; Harders, H.; Bäker, M. Mechanisches Verhalten der Werkstoffe, 5th ed.; Springer Vieweg: Wiesbaden, Germany, 2016; ISBN 978-3-8348-2241-3. [Google Scholar]
- Siredey, N.; Denis, S.; Lacaze, J. Dendritic growth and crystalline quality of nickel-base single grains. J. Cryst. Growth 1993, 130, 132–146. [Google Scholar] [CrossRef]
- Nitz, A.; Nembach, E. The critical resolved shear stress of a superalloy as a combination of those of its γ matrix and γ′ precipitates. Met. Mater. Trans. A 1998, 29, 799–807. [Google Scholar] [CrossRef]
- Österle, W.; Bettge, D.; Fedelich, B.; Klingelhöffer, H. Modelling the orientation and direction dependence of the critical resolved shear stress of nickel-base superalloy single crystals. Acta Mater. 2000, 48, 689–700. [Google Scholar] [CrossRef]
- Jöchen, K. Homogenization of the Linear and Non-Linear Mechanical Behavior of Polycrystals. Ph.D. Thesis, KIT, Karlsruhe, Deutschland, 2013. [Google Scholar]
- Gollmer, M. Schadensakkumulationsverhalten der Superlegierung René 80 unter Zweistufiger Low Cycle Fatigue Beanspruchung. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2018. [Google Scholar]





| Element | Ni | Cr | Co | Ti | Mo | W | Al | C | B | Zr | Ta | Nb | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| René80 | Bal. | 14.04 | 9.48 | 5.08 | 4.03 | 4.02 | 2.93 | 0.17 | 0.015 | 0.011 | - | - | - |
| IN 738 LC | Bal. | 16 | 8.3 | 8.7 | 3.4 | 1.8 | 2.7 | 3.4 | 0.11 | - | 1.9 | 0.9 | 0.1 |
| Distribution | Modeling Approach |
|---|---|
| Monte-Carlo sampling of statistically distributed orientations of a single crystal, i.e., single grain. Maximum normalized resolved shear stresses calculated at global uniaxial stress state. Explicit consideration of elastic stiffness anisotropy. | |
| Monte-Carlo sampling of statistically distributed orientations of single crystals in polycrystalline FEA simulations. Maximum normalized resolved shear stresses calculated at all FEA nodes from local (multiaxial) stress states. Explicit consideration of elastic stiffness anisotropy. |
| Value | Random Orientation | Preferential Orientation | Shift |
|---|---|---|---|
| 160 GPa | 142 GPa | ||
| Standard deviation | ±1.5 GPa | ±0.3 GPa | - |
| Schmid Factor | Random Orientation | Preferential Orientation | Shift |
|---|---|---|---|
| Model Nr. | Distribution Approach | Distribution Density Visualization |
|---|---|---|
| 1 | Weibull distributed life |  |
| 2 | Life distribution from (Schmid factors) in single grain, | 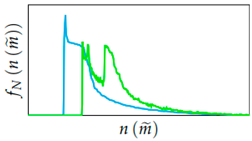 |
| 3 | Life distribution from (Schmid factors) in polycrystalline FEA, | 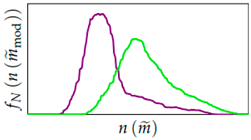 |
| Model Combination: Scale Model + Life Distribution | Neg. Log-Likelihood per Data Point at Calibration | Neg. Log-Likelihood per Data Point at Prediction |
|---|---|---|
| CMB + Weibull distribution | 10.7 | 8.7 |
| CMB + Schmid factor-corrected life distribution | 0.87 | 12.38 |
| CMB + modified Schmid factor-corrected life distribution | 0.57 | 0.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Engel, B.; Mäde, L.; Lion, P.; Moch, N.; Gottschalk, H.; Beck, T. Probabilistic Modeling of Slip System-Based Shear Stresses and Fatigue Behavior of Coarse-Grained Ni-Base Superalloy Considering Local Grain Anisotropy and Grain Orientation. Metals 2019, 9, 813. https://doi.org/10.3390/met9080813
Engel B, Mäde L, Lion P, Moch N, Gottschalk H, Beck T. Probabilistic Modeling of Slip System-Based Shear Stresses and Fatigue Behavior of Coarse-Grained Ni-Base Superalloy Considering Local Grain Anisotropy and Grain Orientation. Metals. 2019; 9(8):813. https://doi.org/10.3390/met9080813
Chicago/Turabian StyleEngel, Benedikt, Lucas Mäde, Philipp Lion, Nadine Moch, Hanno Gottschalk, and Tilmann Beck. 2019. "Probabilistic Modeling of Slip System-Based Shear Stresses and Fatigue Behavior of Coarse-Grained Ni-Base Superalloy Considering Local Grain Anisotropy and Grain Orientation" Metals 9, no. 8: 813. https://doi.org/10.3390/met9080813
APA StyleEngel, B., Mäde, L., Lion, P., Moch, N., Gottschalk, H., & Beck, T. (2019). Probabilistic Modeling of Slip System-Based Shear Stresses and Fatigue Behavior of Coarse-Grained Ni-Base Superalloy Considering Local Grain Anisotropy and Grain Orientation. Metals, 9(8), 813. https://doi.org/10.3390/met9080813






