Study on Sulfur Transfer Behavior during Refining of Rejected Electrolytic Manganese Metal
Abstract
1. Introduction
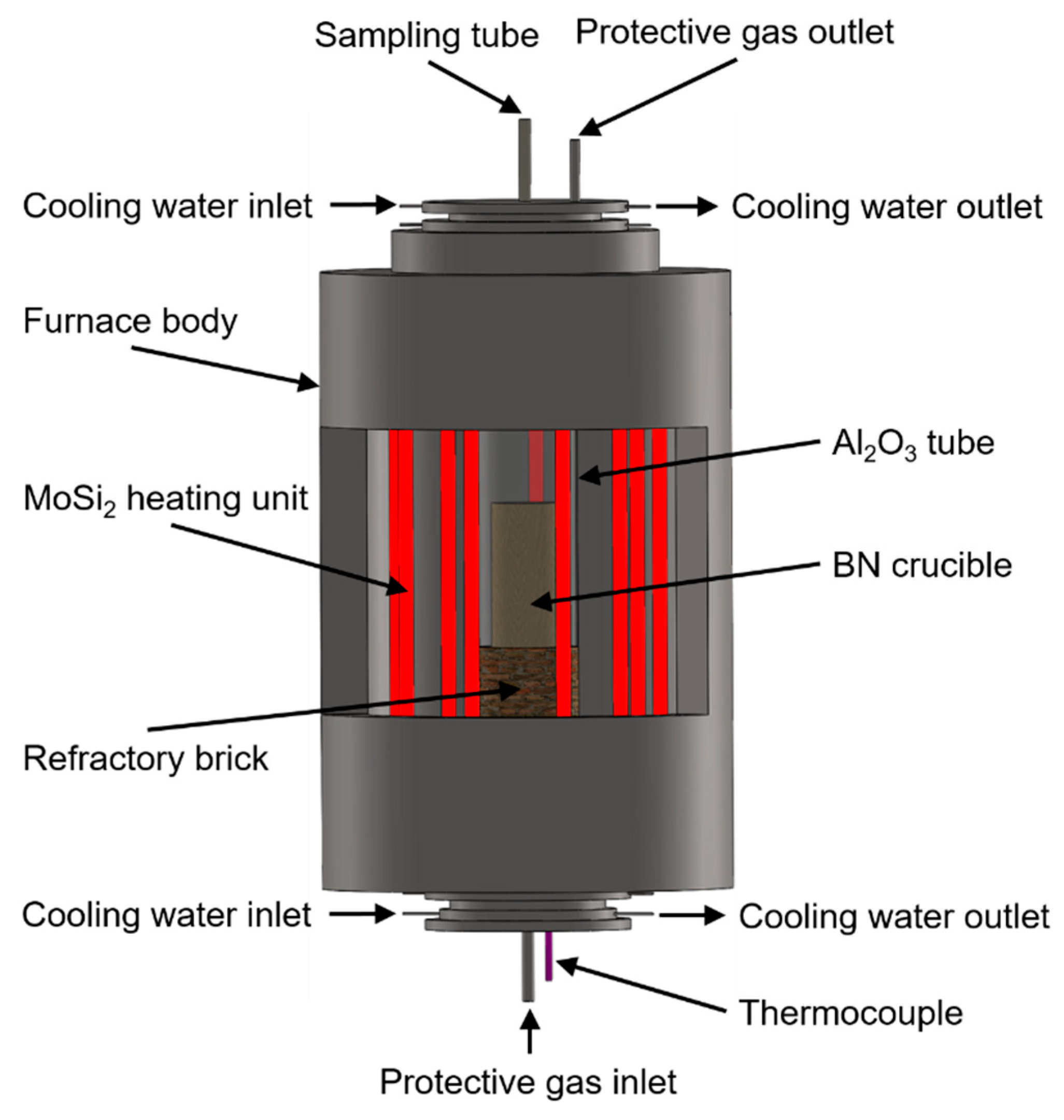
2. Experiment
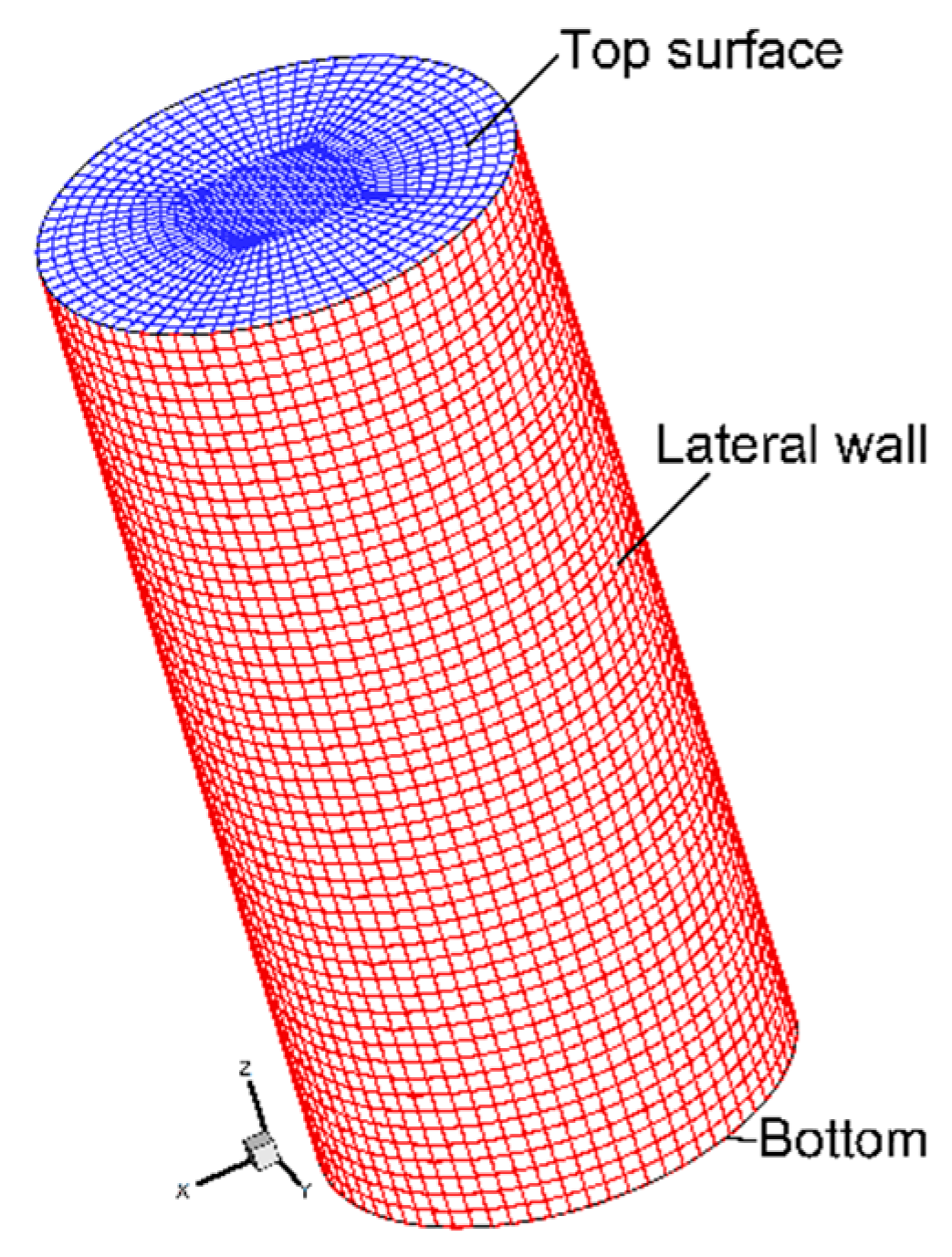
3. CFD Modeling Framework
4. Boundary Conditions
5. Numerical Procedure
6. Results and Discussion
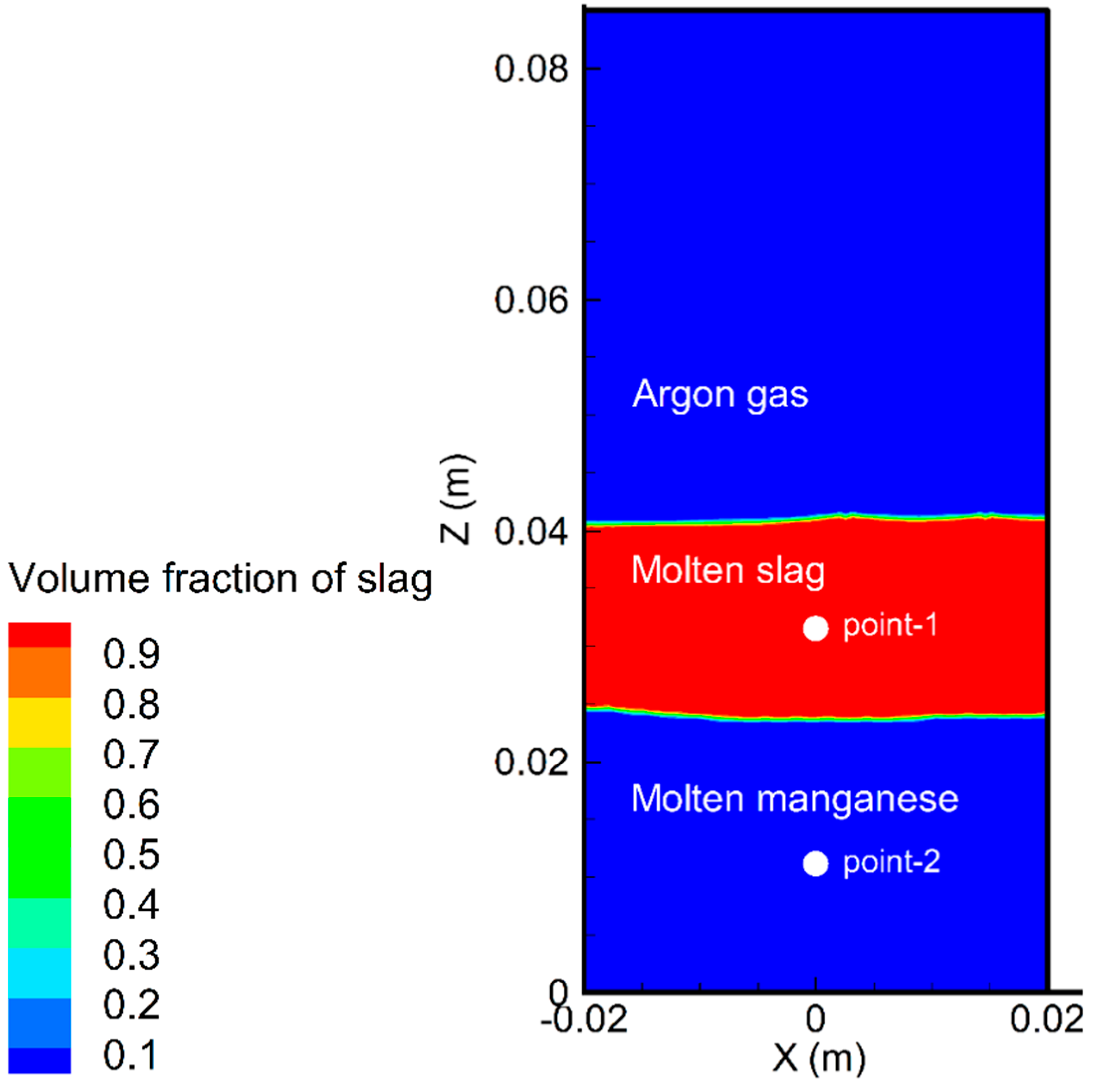
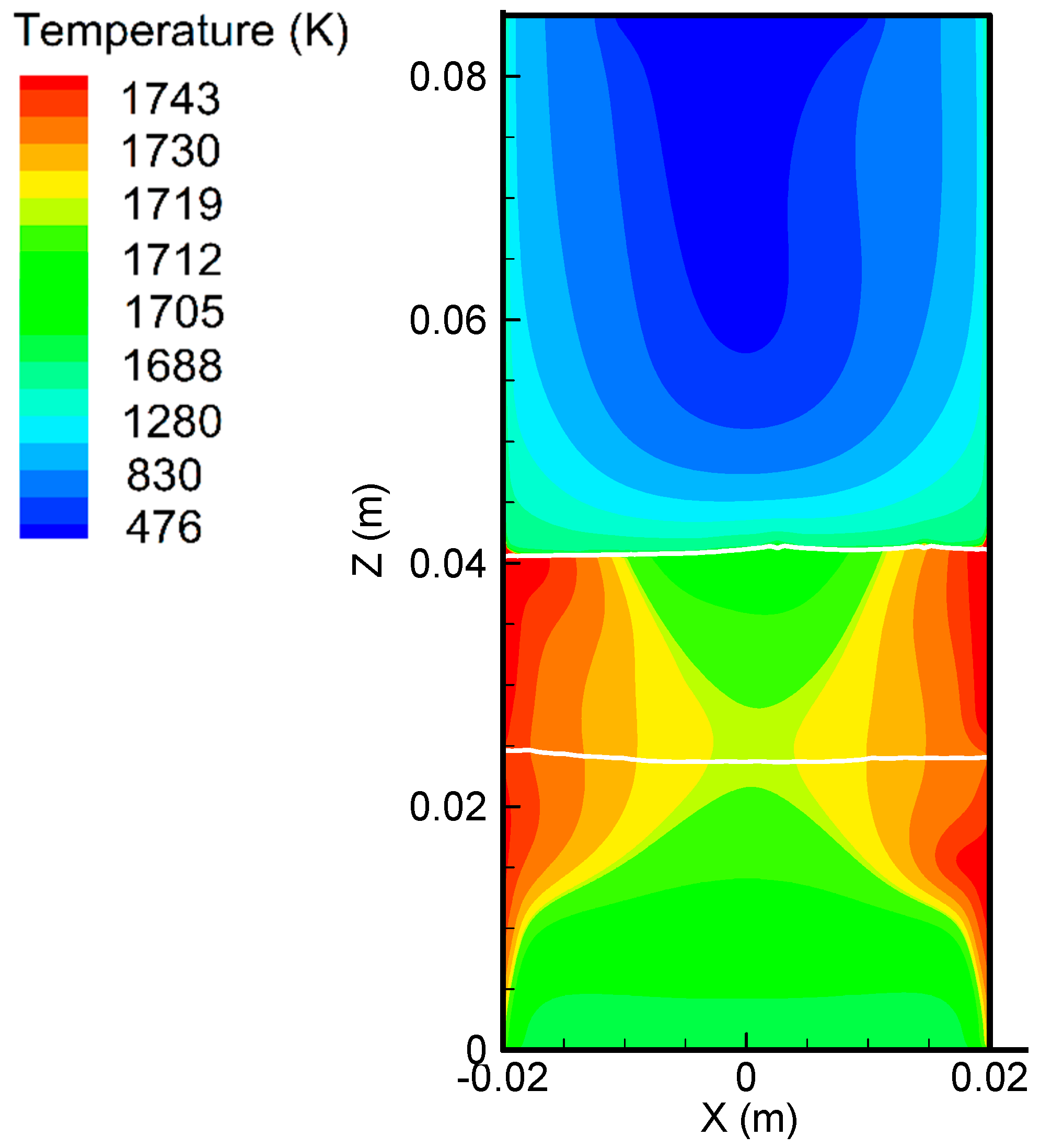
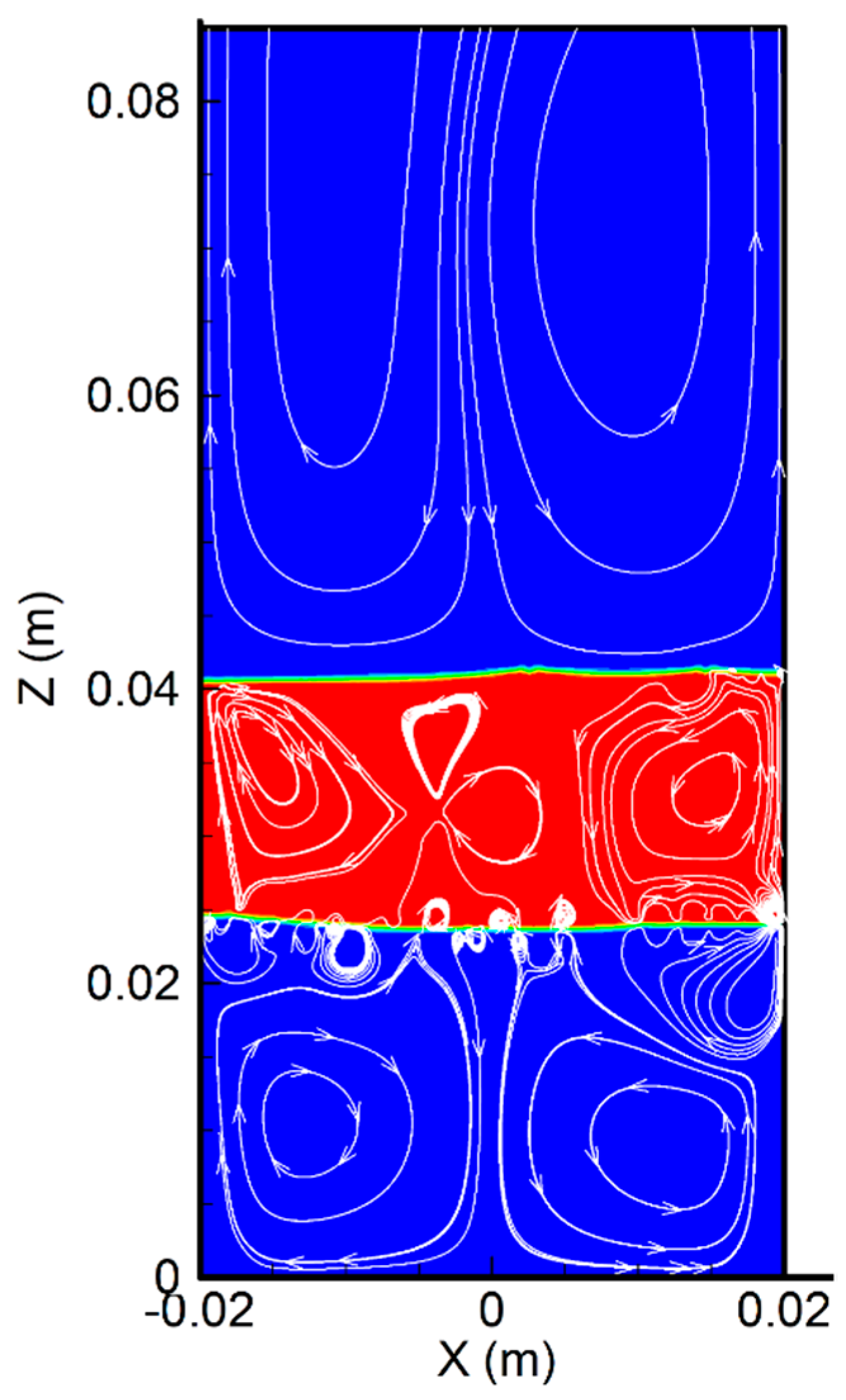
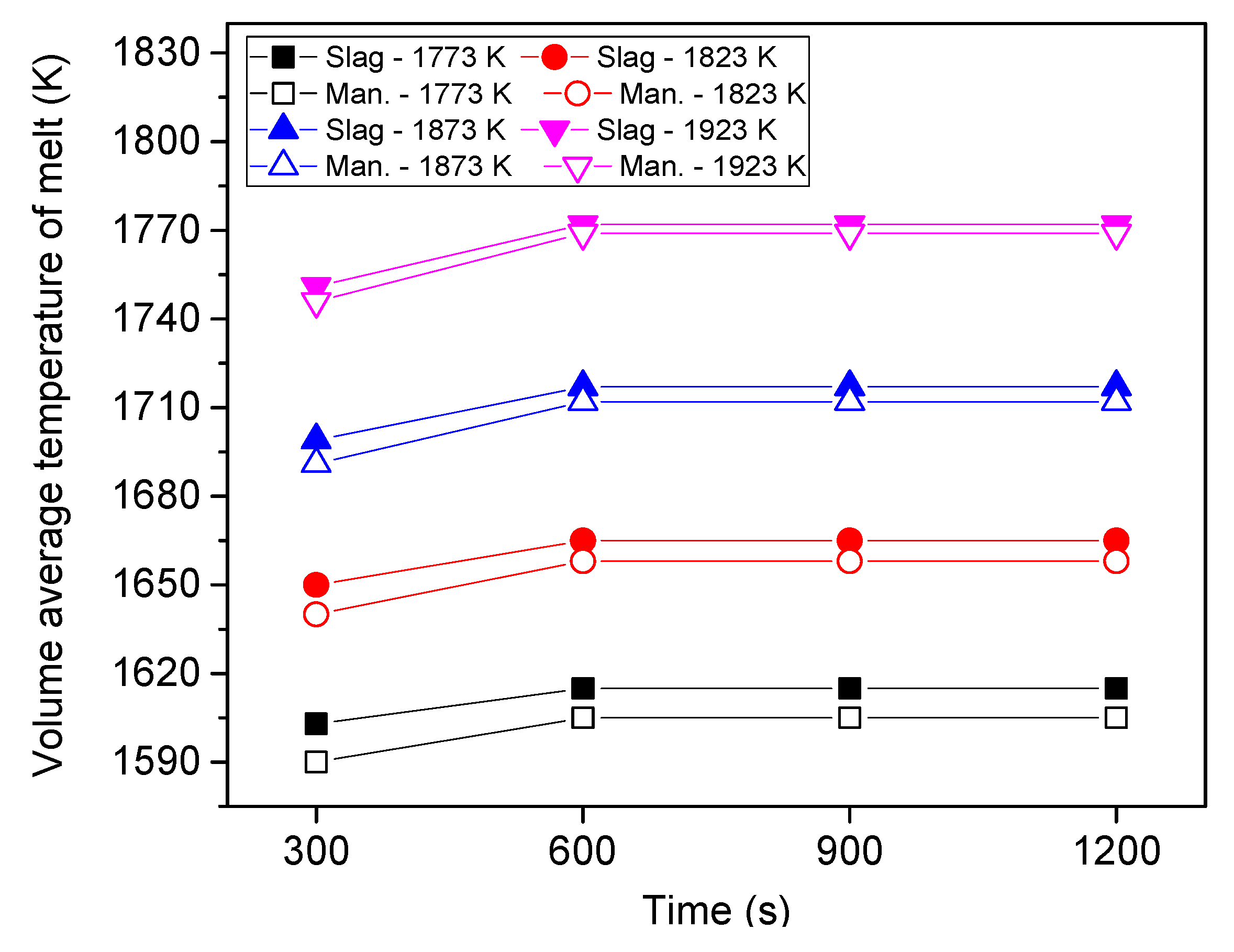
6.1. Flow Pattern and Temperature Distribution
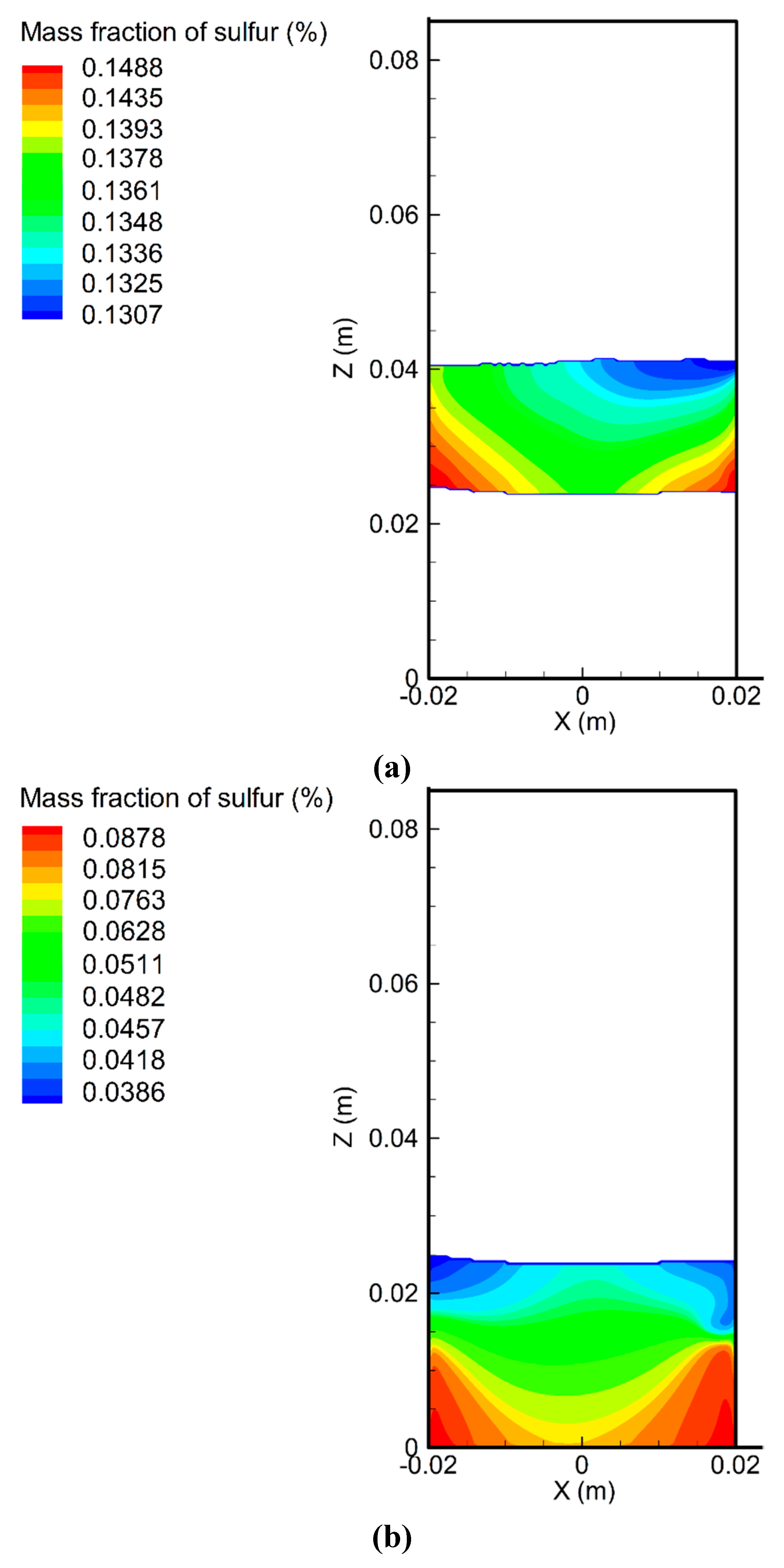
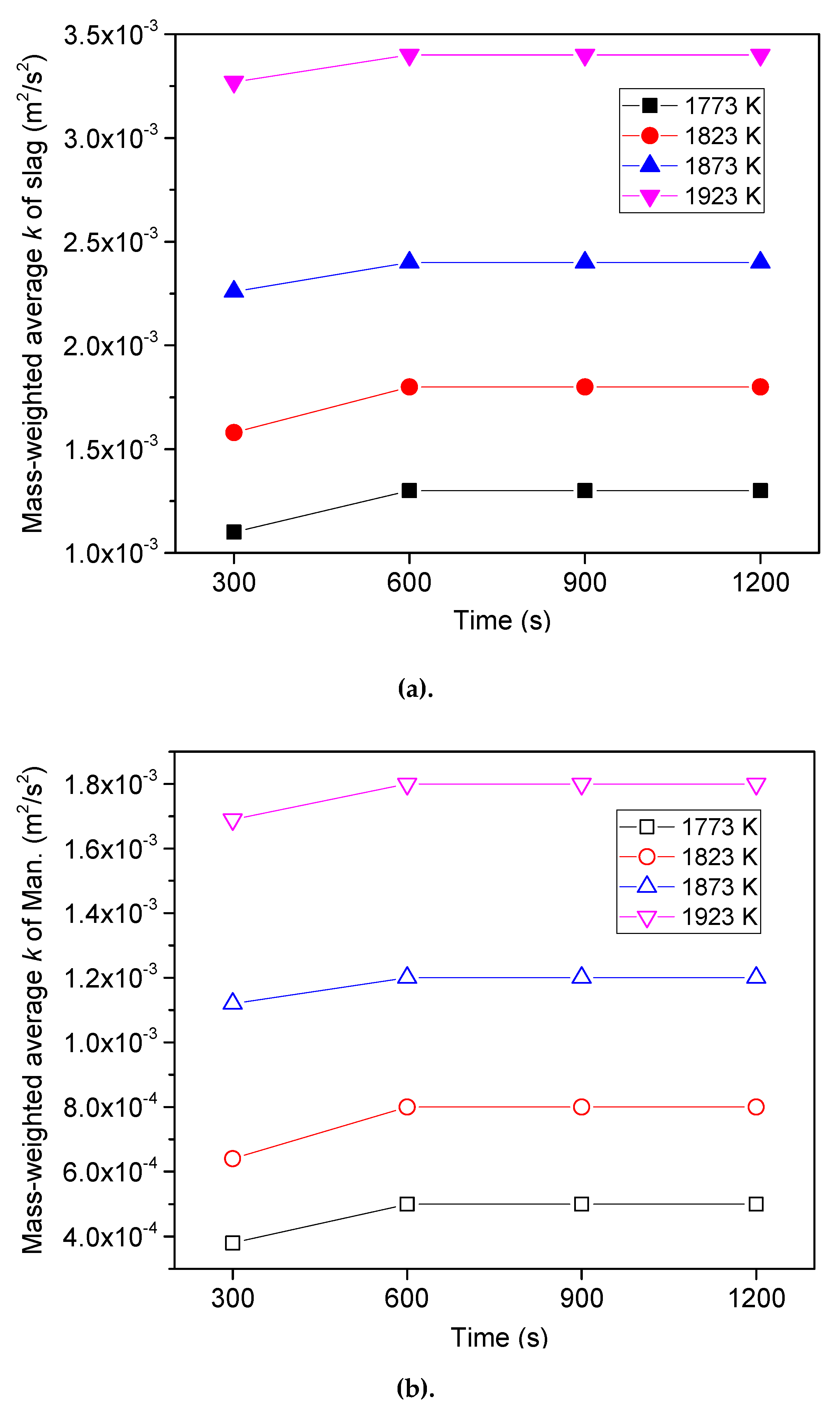
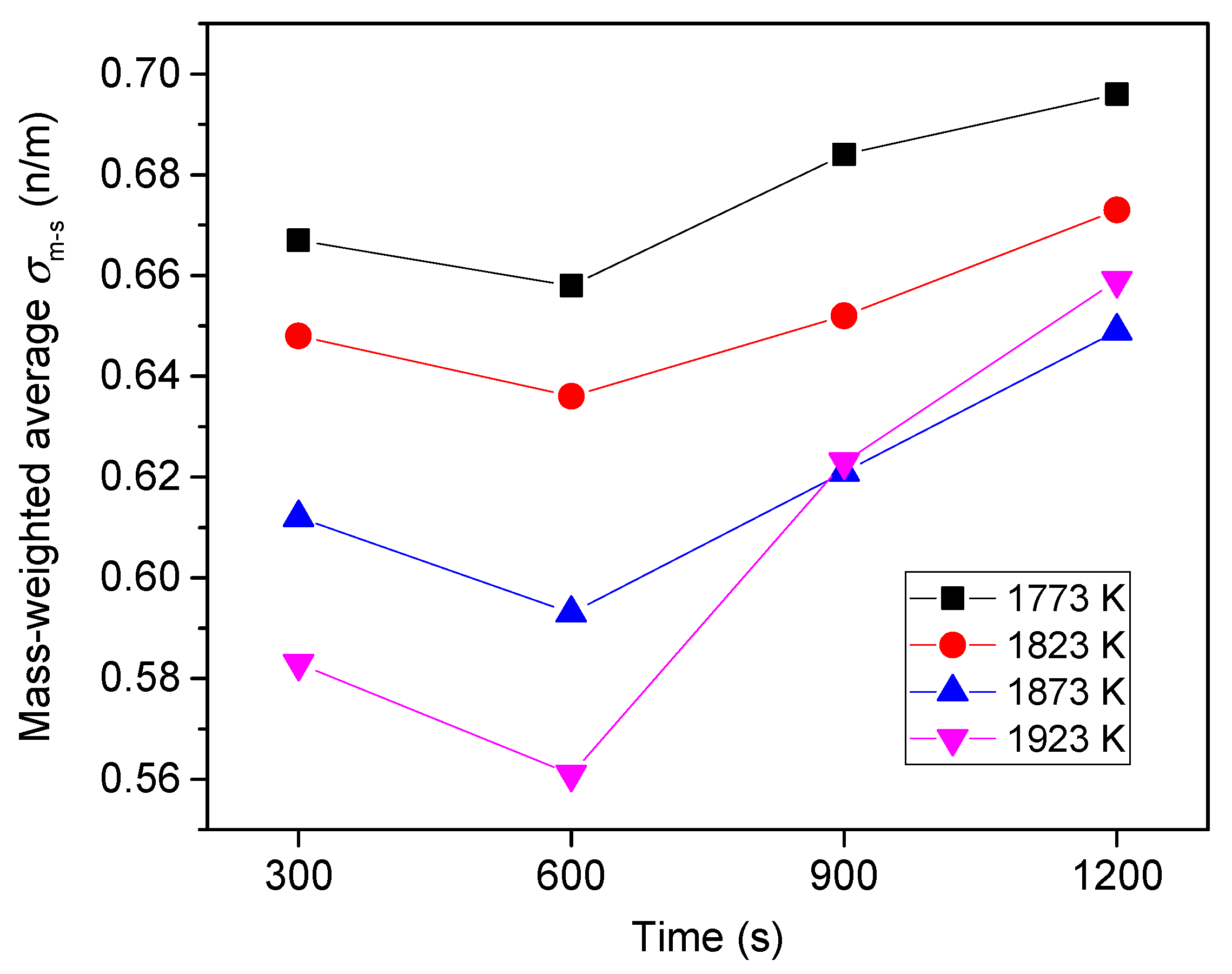
6.2. Variation of Sulfur Concentration
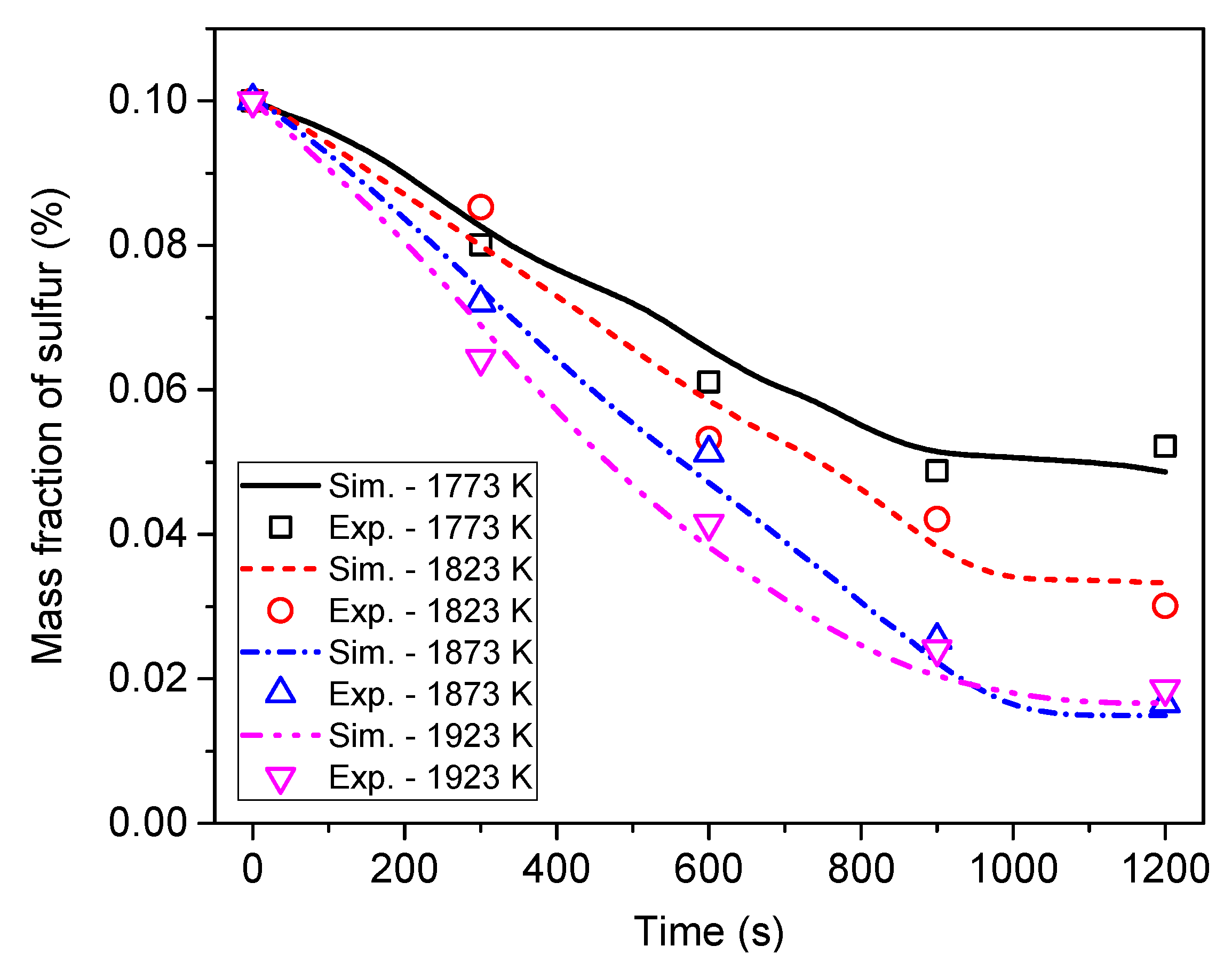
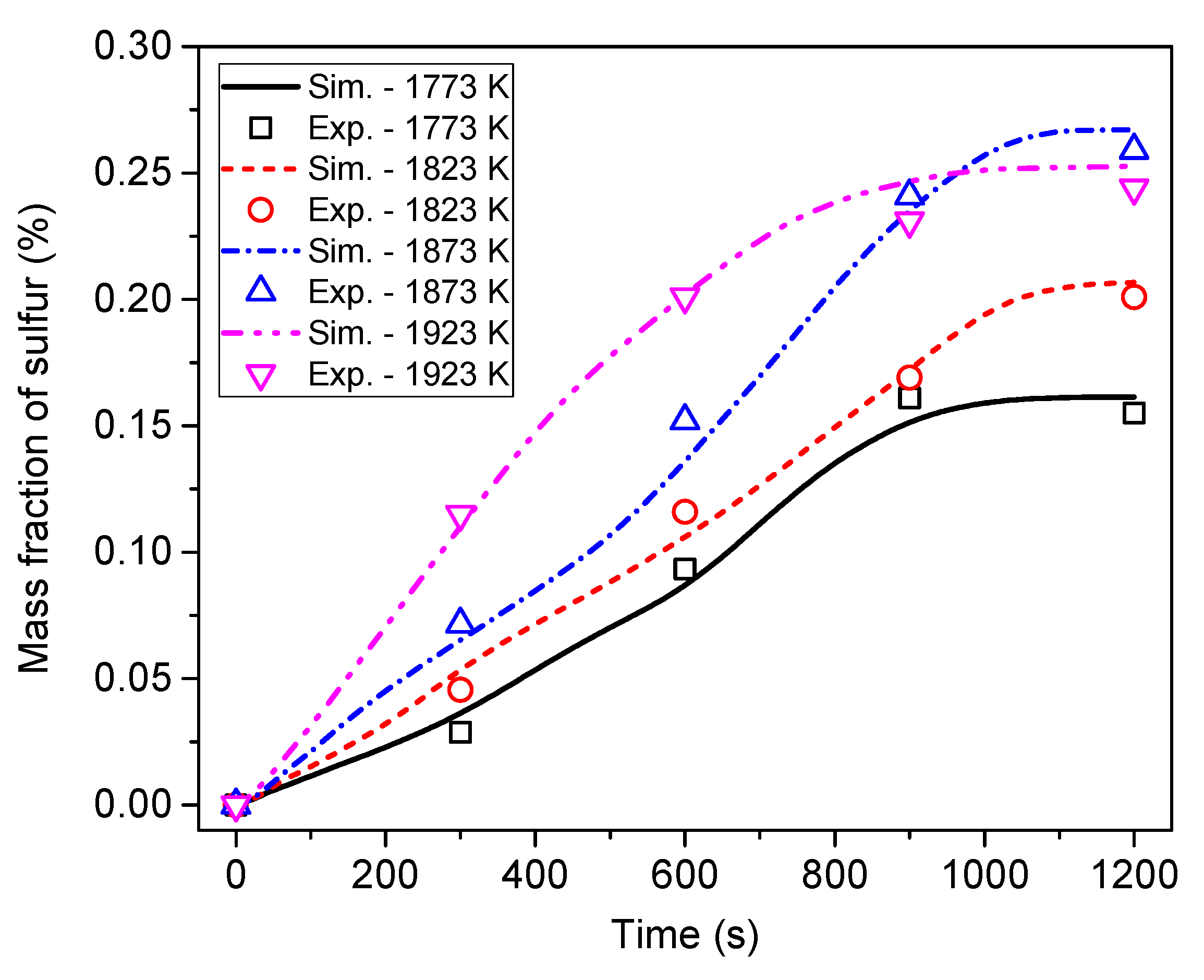
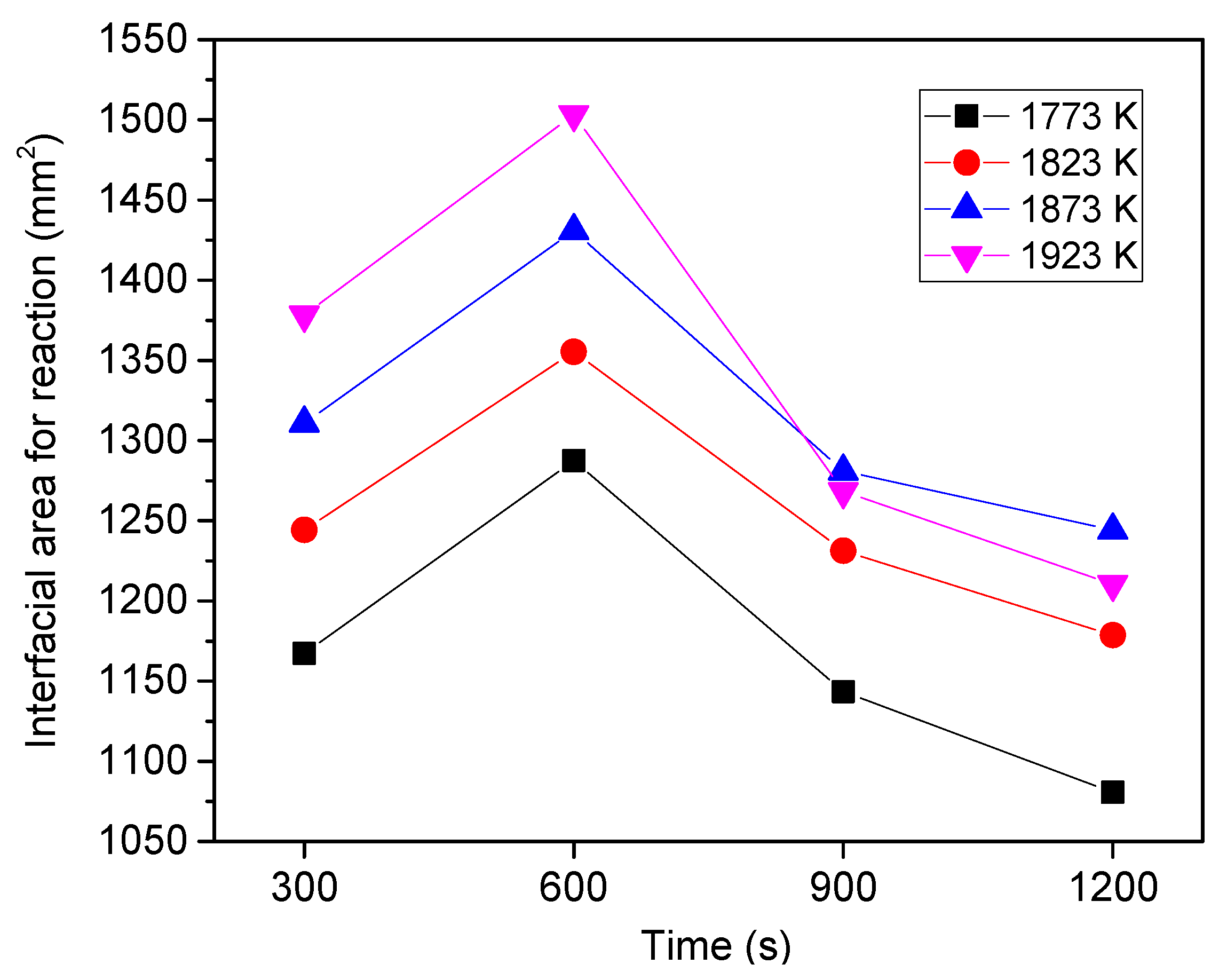
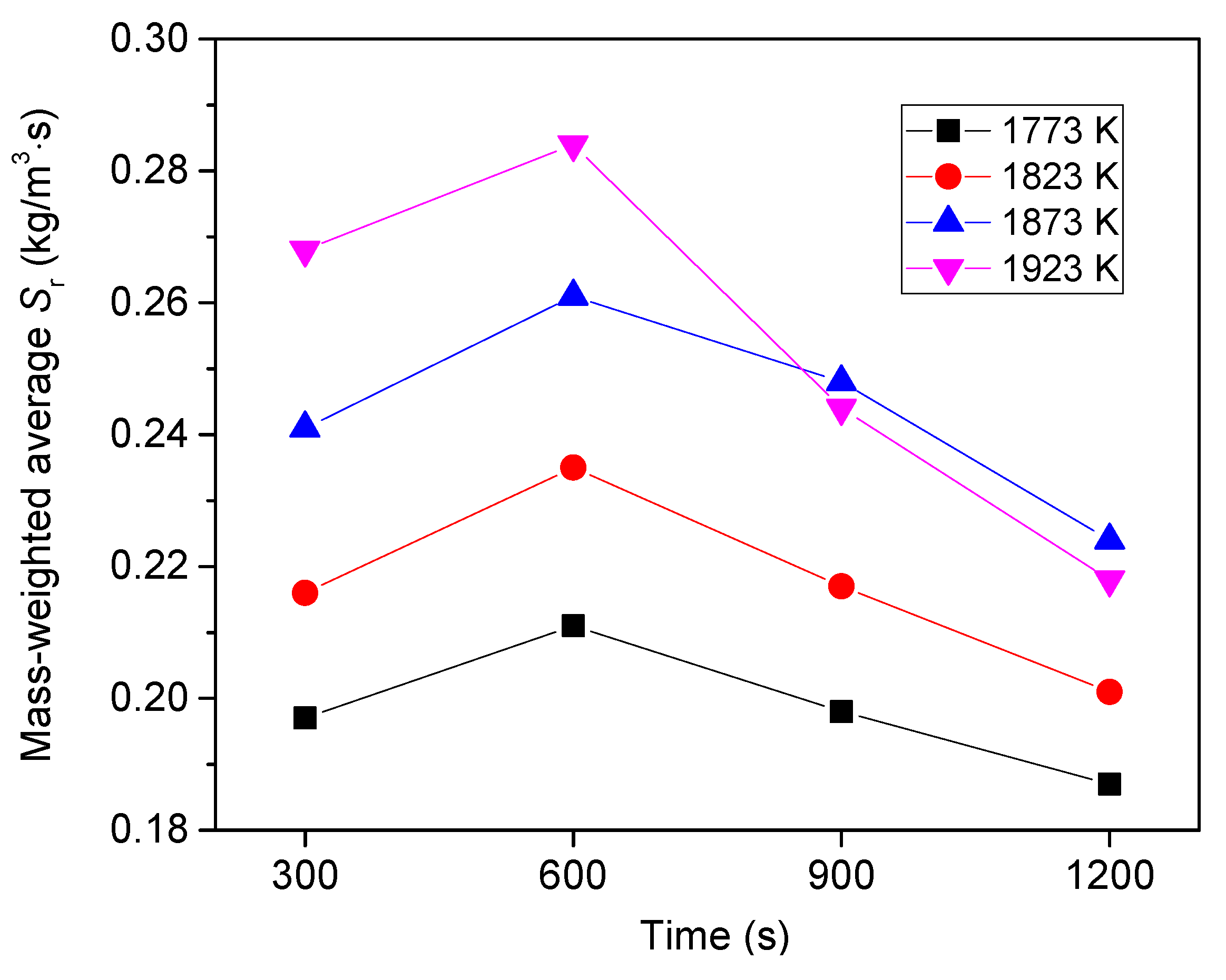
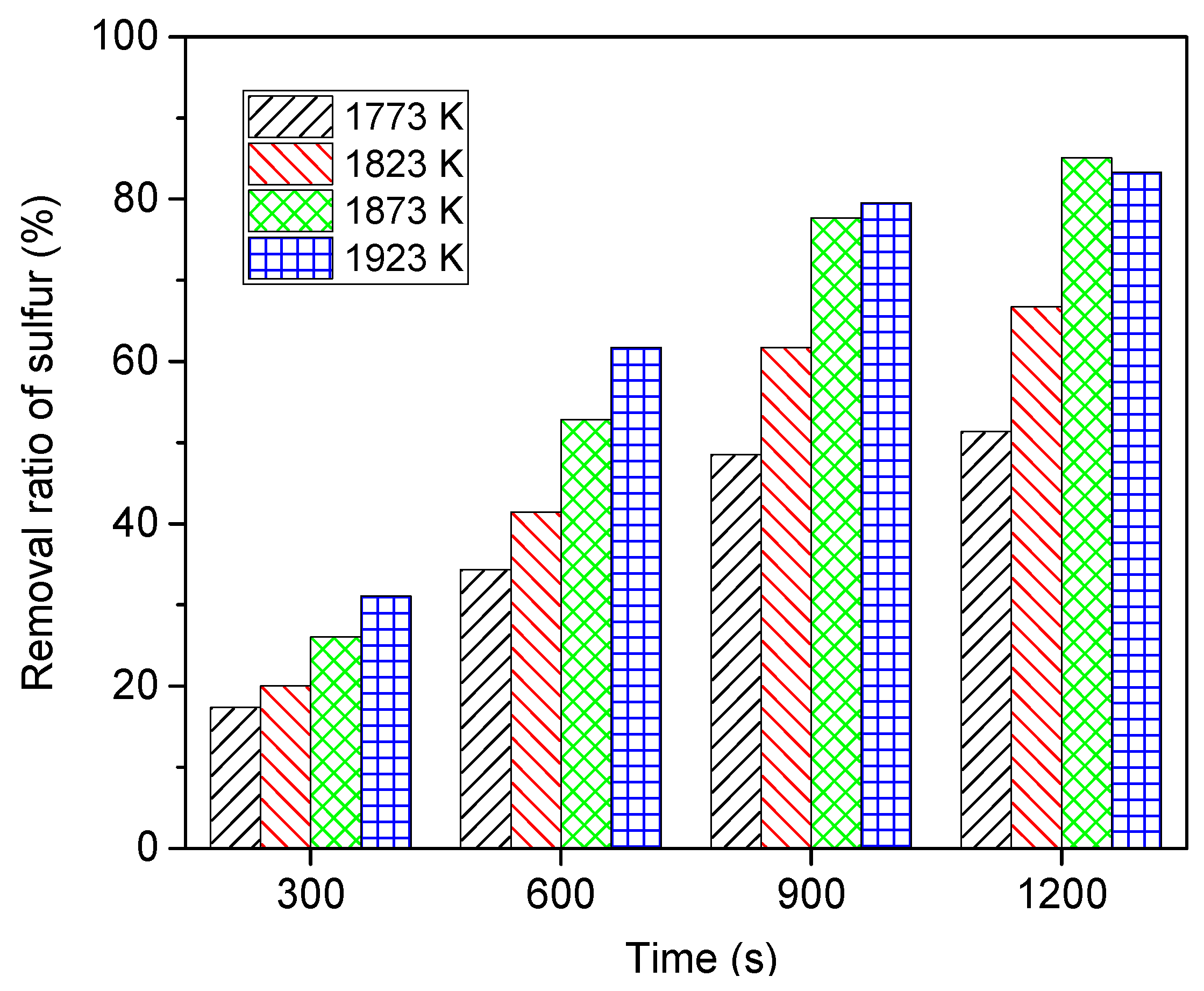
6.3. Effect of Heating Temperature
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cui, J.; Zhang, L.F. Metallurgical recovery of metals from electronic waste: A review. J. Hazard. Mater. 2008, 158, 228–256. [Google Scholar] [CrossRef] [PubMed]
- Duan, N.; Dan, Z.G.; Wang, F.; Pan, C.X.; Zhou, C.B.; Jiang, L.H. Electrolytic manganese metal industry experience based China’s new model for cleaner production promotion. J. Clean. Prod. 2011, 19, 2082–2087. [Google Scholar] [CrossRef]
- Lu, J.M.; Dreisinger, D.; Glück, T. Manganese electrodeposition—A literature review. Hydrometallurgy 2014, 141, 105–116. [Google Scholar] [CrossRef]
- Xu, F.Y.; Dan, Z.G.; Zhao, W.N.; Han, G.M.; Sun, Z.H.; Xiao, K.; Jiang, L.H.; Duan, N. Electrochemical analysis of manganese electrodeposition and hydrogen evolution from pure aqueous sulfate electrolytes with addition of SeO2. J. Eelectroanal. Chem. 2015, 741, 149–156. [Google Scholar] [CrossRef]
- Schrama, F.N.H.; Beunder, E.M.; Berg, B.V.D.; Yang, Y.X.; Boom, B. Sulphur removal in ironmaking and oxygen steelmaking. Ironmak. Steelmak. 2017, 44, 333–343. [Google Scholar] [CrossRef]
- Iwamasa, P.K.; Fruehan, R.J. Effect FeO in the slag and silicon in the metal on the desulfurization of hot metal. Metall. Mater. Trans. B 1997, 28, 47–57. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kim, D.J.; Lee, H.G. Reaction kinetics of desulfurization of molten pig iron using CaO-SiO2-Al2O3-Na2O slag systems. ISIJ Int. 2001, 41, 216–224. [Google Scholar] [CrossRef]
- Hiraki, T.; Kobayashi, J.; Urushibata, S.; Matsubae, K.; Nagasaka, T. Removal of sulfur from CaF2 containing desulfurization slag exhausted from secondary steelmaking process by oxidation. Metall. Mater. Trans. B 2012, 43, 703–709. [Google Scholar] [CrossRef]
- Alba, M.; Jung, S.H.; Kim, M.S.; Seol, J.Y.; Yi, S.J.; Kang, Y.B. Desulfurization of liquid steel by passing steel droplets through a slag layer. ISIJ Int. 2015, 55, 1581–1590. [Google Scholar] [CrossRef]
- Jönsson, P.G.; Jonsson, L.T.I. The use of fundamental process models in studying ladle refining operations. ISIJ Int. 2001, 41, 1289–1302. [Google Scholar] [CrossRef]
- Taniguchi, Y.; Sano, N.; Seetharaman, S. Sulphide capacities of CaO-Al2O3-SiO2-MgO-MnO slags in the temperature range 1673–1773 K. ISIJ Int. 2009, 49, 156–163. [Google Scholar] [CrossRef]
- Cho, M.K.; Cheng, J.; Park, J.H.; Min, D.J. Hot metal desulfurization by CaO-SiO2-CaF2-Na2O slag saturated with MgO. ISIJ Int. 2010, 50, 215–221. [Google Scholar] [CrossRef]
- Lou, W.T.; Zhu, M.Y. Numerical simulation of desulfurization behavior in gas-stirred systems based on computation fluid dynamics-simultaneous reaction model (CFD–SRM) coupled model. Metall. Mater. Trans. B 2014, 45, 1706–1722. [Google Scholar] [CrossRef]
- Jonsson, L.; Du, S.C.; Jönsson, P.G. A new approach to model sulphur refining in a coupled CFD and thermodynamic model. ISIJ Int. 1998, 38, 260–267. [Google Scholar] [CrossRef]
- Park, Y.J.; Ha, J.K.; Kim, J.M.; Lee, J.W.; Kim, J.S.; Kim, B.N. The effect of flux addition to Eu2+-doped Ca-α-SiAlON phosphor. J. Ceram. Soc. Jpn. 2013, 121, 498–501. [Google Scholar] [CrossRef]
- Murthy, A.S.; Medvedeva, J.E.; Isheim, D.; Lekakh, S.L.; Richards, V.L.; Van Aken, D.C. Copper precipitation in cobalt-alloyed precipitation-hardened stainless steel. Scr. Mater. 2012, 66, 943–946. [Google Scholar] [CrossRef]
- Yang, J.; Kuwabara, M.; Okumura, K.; Sano, M. Prevention of resulfurization in desulfurization process with magnesium vapor produced in situ by aluminothermic reduction of magnesium oxide. ISIJ Int. 2005, 45, 1795–1803. [Google Scholar] [CrossRef][Green Version]
- Nasch, P.M.; Steinemann, S.G. Density and thermal expansion of molten manganese, iron, nickel, copper, aluminum and tin by means of the gamma-ray attenuation technique. Phys. Chem. Liq. 1995, 29, 43–58. [Google Scholar] [CrossRef]
- Valencia, J.J.; Quested, P.N. Thermophysical properties. In ASM Handbook; Casting ASM Handbook Committee: Novelty, MO, USA, 2008; Volume 15, pp. 468–481. [Google Scholar]
- Wang, Q.; Liu, Y.; Wang, F.; Li, G.Q.; Li, B.K.; Qiao, W.W. Numerical study on the effect of electrode polarity on desulfurization in direct current electroslag remelting process. Metall. Mater. Trans. B 2017, 48, 2649–2663. [Google Scholar] [CrossRef]
- Keene, B.J. Review of data for the surface tension of pure metals. Int. Mater. Rev. 1993, 38, 157–192. [Google Scholar] [CrossRef]
- Hanao, M.; Tanaka, T.; Kawamoto, M.; Takatani, K. Evaluation of surface tension of molten slag in multi-component systems. ISIJ Int. 2007, 47, 935–939. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, F.; Li, G.Q.; Gao, Y.M.; Li, B.K. Simulation and experimental studies of effect of current on oxygen transfer in electroslag remelting process. Int. J. Heat Mass Transf. 2017, 113, 1021–1030. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Kim, S.K.; Wang, W.L.; Kang, Y.B. Modeling surface tension of multicomponent liquid steel using modified quasichemical model and constrained Gibbs energy minimization. Met. Mater. Int. 2015, 21, 765–774. [Google Scholar] [CrossRef]
- Choi, J.Y.; Lee, H.G. Thermodynamic evaluation of the surface tension of molten CaO-SiO2-Al2O3 ternary slag. ISIJ Int. 2002, 42, 221–228. [Google Scholar] [CrossRef]
- Nakamoto, M.; Tanaka, T.; Holappa, L.; Hämäläinen, M. Surface tension evalution of molten silicates containing surface-active components (B2O3, CaF2 or Na2O). ISIJ Int. 2007, 47, 211–216. [Google Scholar] [CrossRef]
- Tanaka, T.; Goto, H.; Nakamoto, M.; Suzuki, M.; Hanao, M.; Zeze, M.; Yamamura, H.; Yoshikawa, T. Dynamic changes in interfacial tension between liquid Fe alloy and molten slag induced by chemical reactions. ISIJ Int. 2016, 56, 944–952. [Google Scholar] [CrossRef]
- Cramb, A.W.; Jimbo, I. Calculation of the interfacial properties of liquid steel-slag systems. Steel Res. Int. 1989, 60, 157–165. [Google Scholar] [CrossRef]
- Wang, Q.; He, Z.; Li, G.Q.; Li, B.K.; Zhu, C.Y.; Chen, P.J. Numerical investigation of desulfurization behavior in electroslag remelting process. Int. J. Heat Mass Transf. 2017, 104, 943–951. [Google Scholar] [CrossRef]
- Byon, C. Numerical study on the phase change heat transfer of LNG in glass wool based on the VOF method. Int. J. Heat Mass Transf. 2014, 88, 20–27. [Google Scholar] [CrossRef]
- Fincham, C.B.J.; Richardson, F.D. The behavior of sulphur in silicate and aluminate melts. Proc. R. Soc. Lond. Ser. A 1954, 223, 40–62. [Google Scholar]
- Young, R.W.; Duffy, J.A.; Hassall, G.J.; Xu, Z. Use of optical basicity concept for determining phosphorus and sulphur slag-metal partitions. Ironmak. Steelmak. 1992, 19, 201–219. [Google Scholar]
- Ichise, E.; Moro-Oka, A. Interaction parameter in liquid alloys. Trans. ISIJ 1988, 28, 153–163. [Google Scholar] [CrossRef]
- Wang, J.; Li, G.Q.; Yang, X.P.; He, Z.; Li, B.K. Change of slag composition during electroslag remelting process and prediction of the dissolved oxygen content in steel. J. Iron Steel Res. 2015, 27, 18–23. (In Chinese) [Google Scholar] [CrossRef]


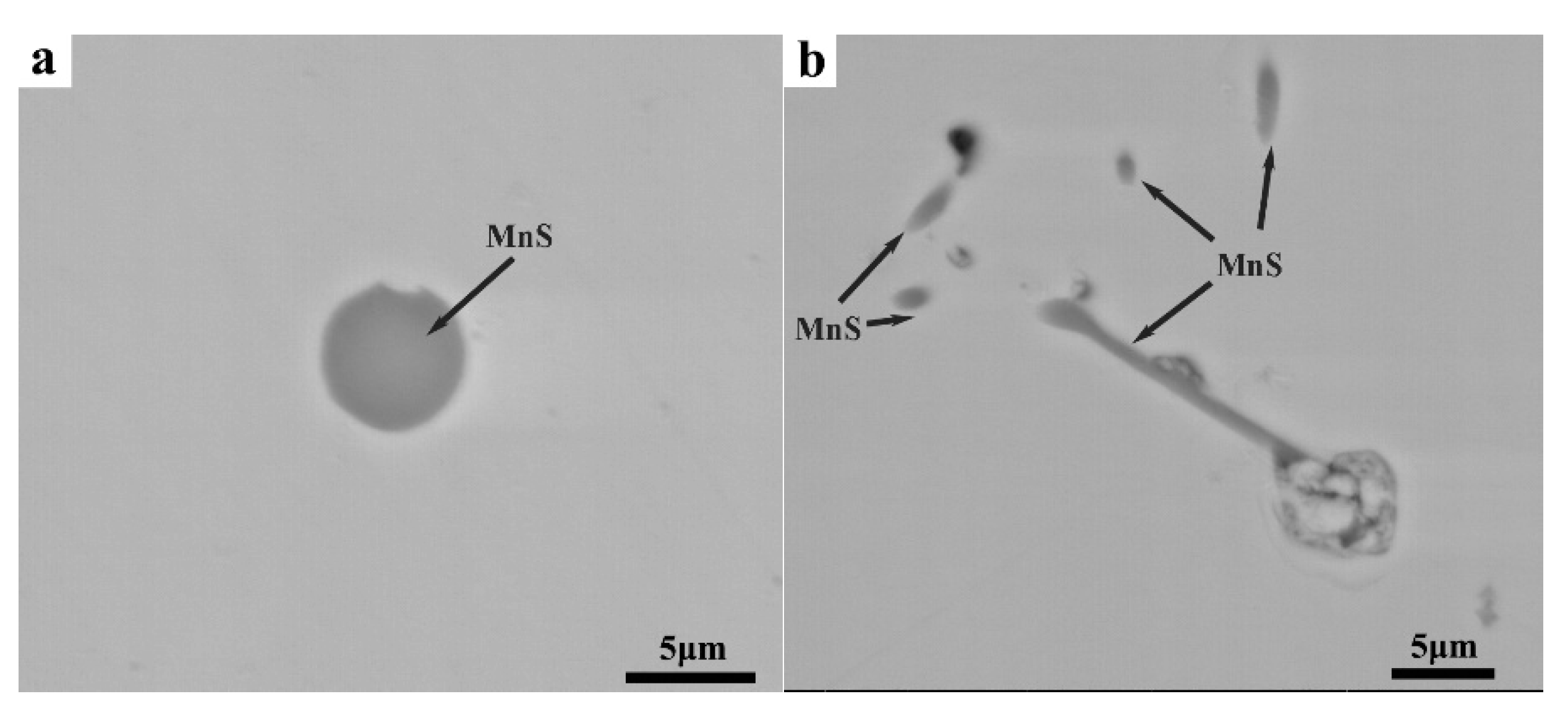
| Mn | Se | P | S | C | Si |
|---|---|---|---|---|---|
| 99.457 | 0.056 | 0.171 | 0.100 | 0.013 | 0.020 |
| CaF2 | Al2O3 |
|---|---|
| 70 | 30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Liu, Y.; Wang, F.; Cao, Y.; Li, G. Study on Sulfur Transfer Behavior during Refining of Rejected Electrolytic Manganese Metal. Metals 2019, 9, 751. https://doi.org/10.3390/met9070751
Wang Q, Liu Y, Wang F, Cao Y, Li G. Study on Sulfur Transfer Behavior during Refining of Rejected Electrolytic Manganese Metal. Metals. 2019; 9(7):751. https://doi.org/10.3390/met9070751
Chicago/Turabian StyleWang, Qiang, Yu Liu, Fang Wang, Yulong Cao, and Guangqiang Li. 2019. "Study on Sulfur Transfer Behavior during Refining of Rejected Electrolytic Manganese Metal" Metals 9, no. 7: 751. https://doi.org/10.3390/met9070751
APA StyleWang, Q., Liu, Y., Wang, F., Cao, Y., & Li, G. (2019). Study on Sulfur Transfer Behavior during Refining of Rejected Electrolytic Manganese Metal. Metals, 9(7), 751. https://doi.org/10.3390/met9070751







