Improvement of Damping Property and Its Effects on the Vibration Fatigue in Ti6Al4V Titanium Alloy Treated by Warm Laser Shock Peening
Abstract
1. Introduction
2. Materials and Methods
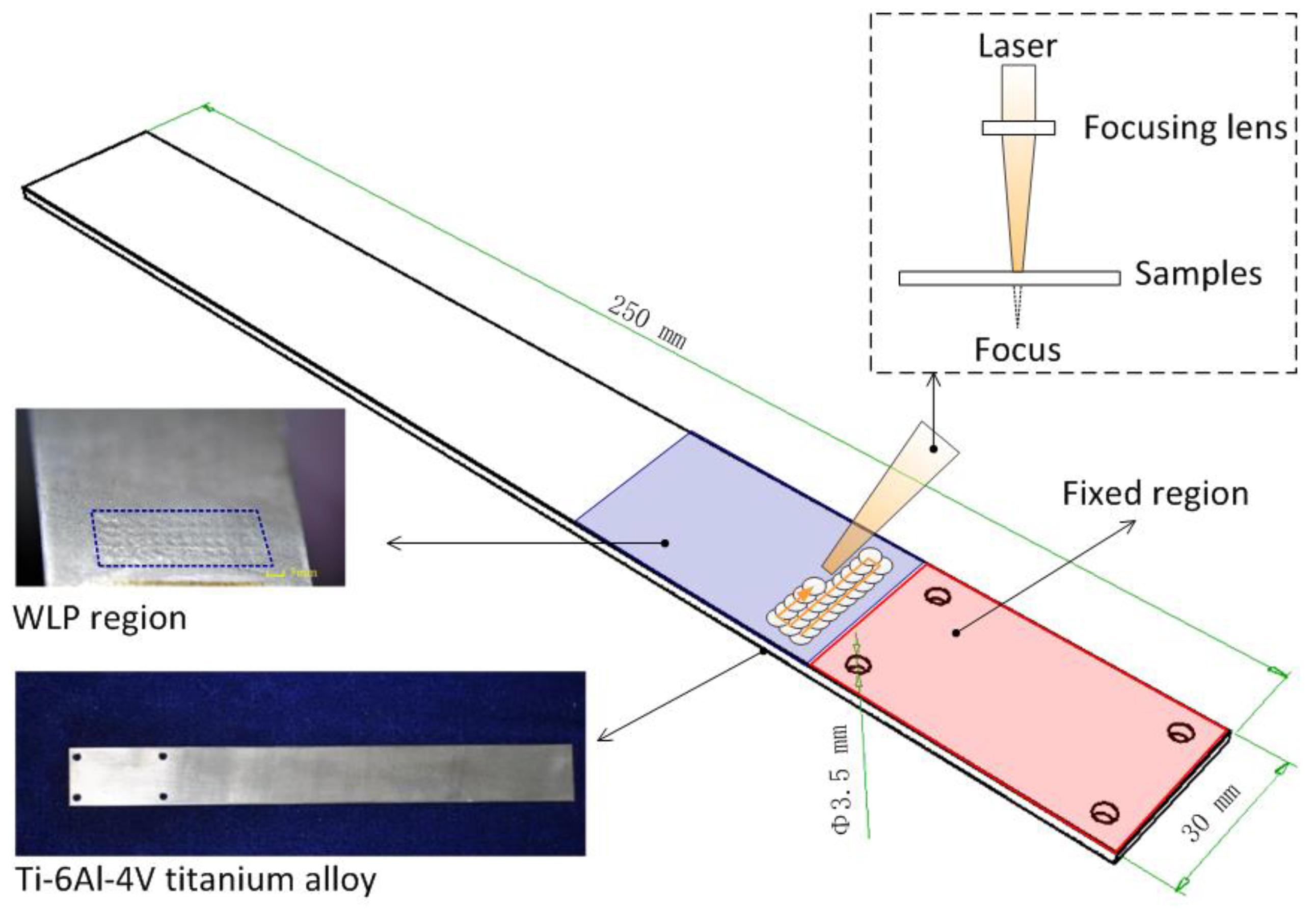
2.1. Materials and Specimens
2.2. RT-LSP and WLSP Processing
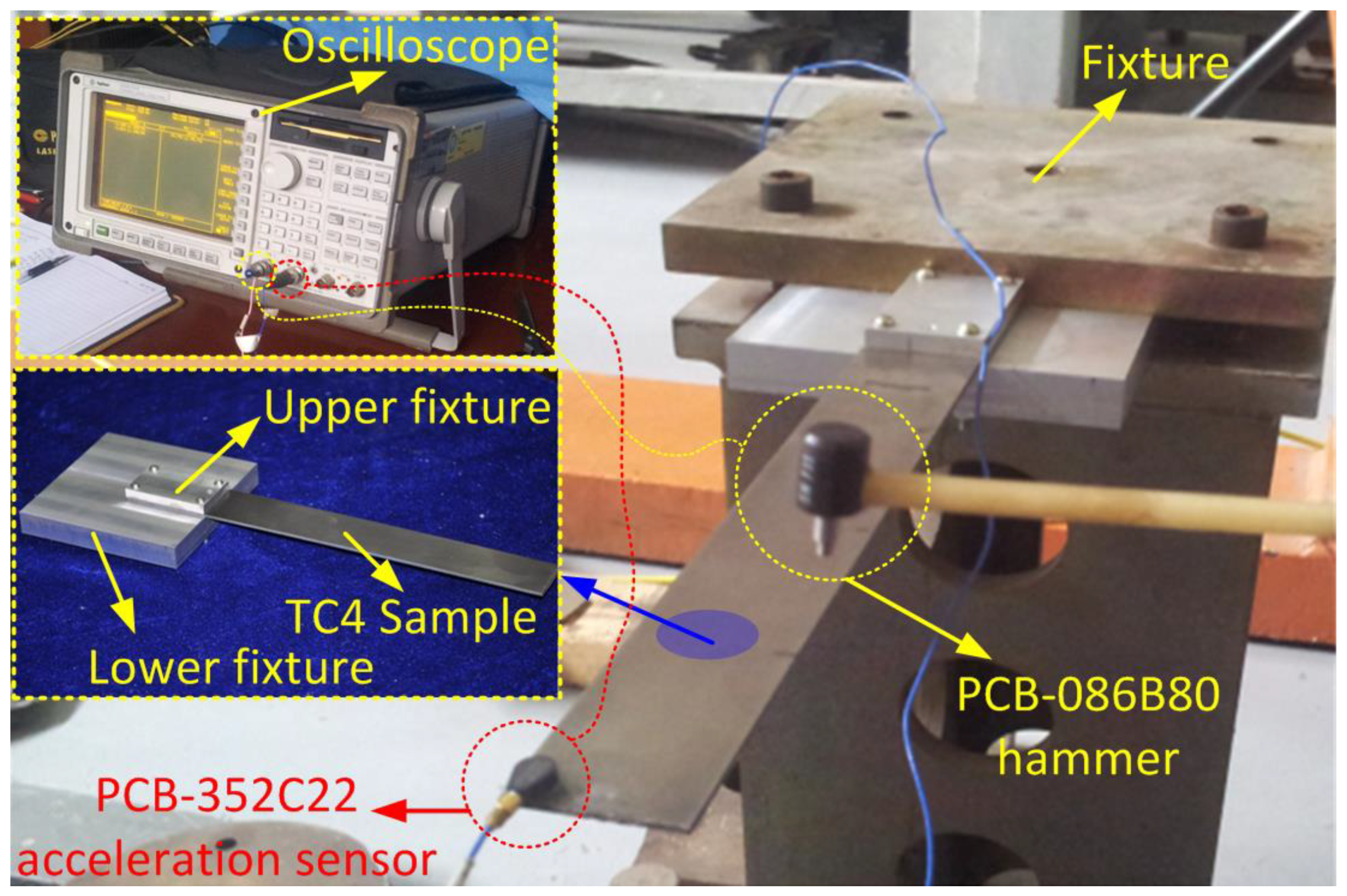
2.3. Impact Modal Tests
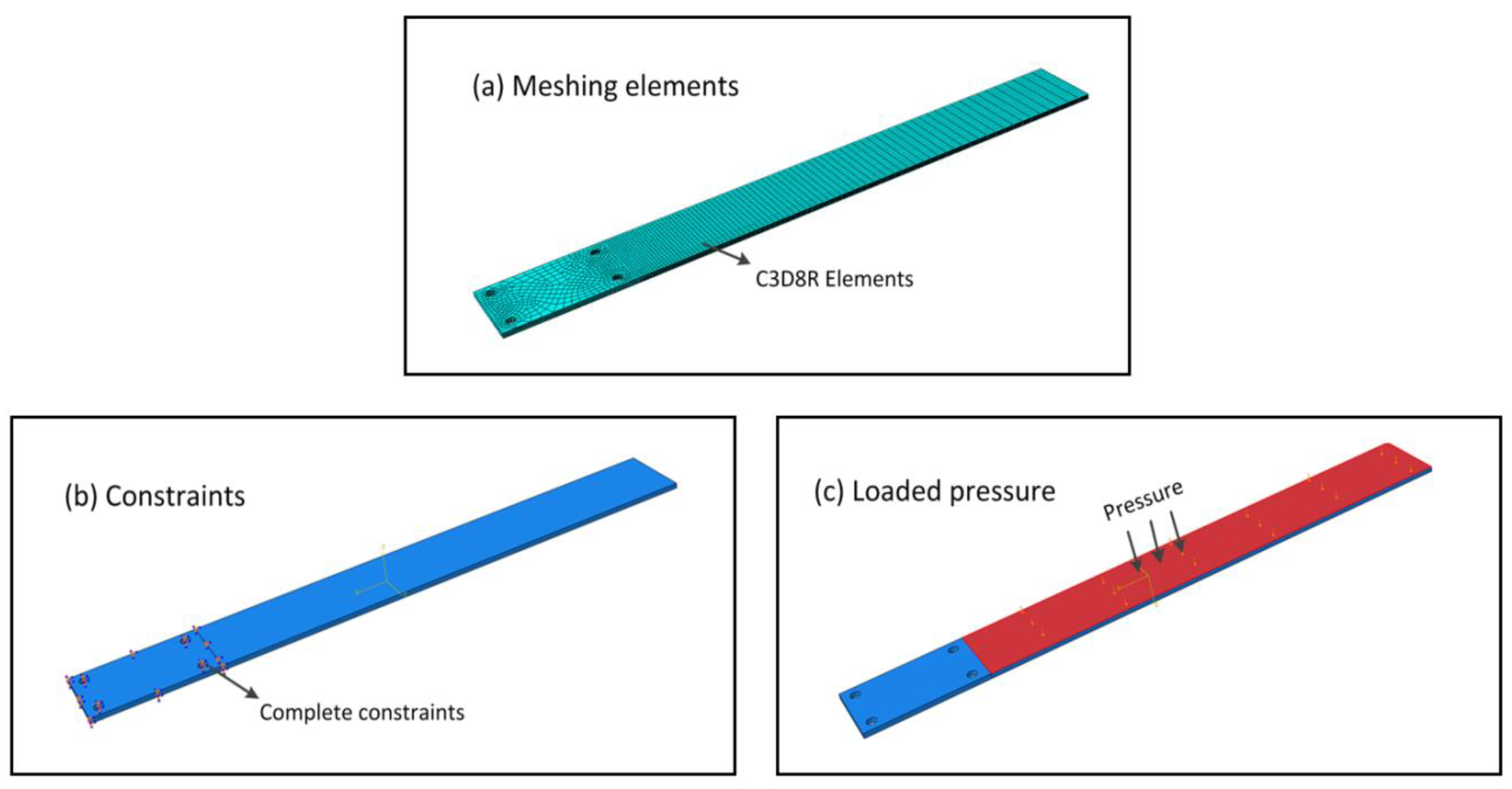
2.4. Frequency Response Simulations
2.5. Residual Stress Measurement
2.6. Vibration Fatigue Tests
3. Results and Discussion
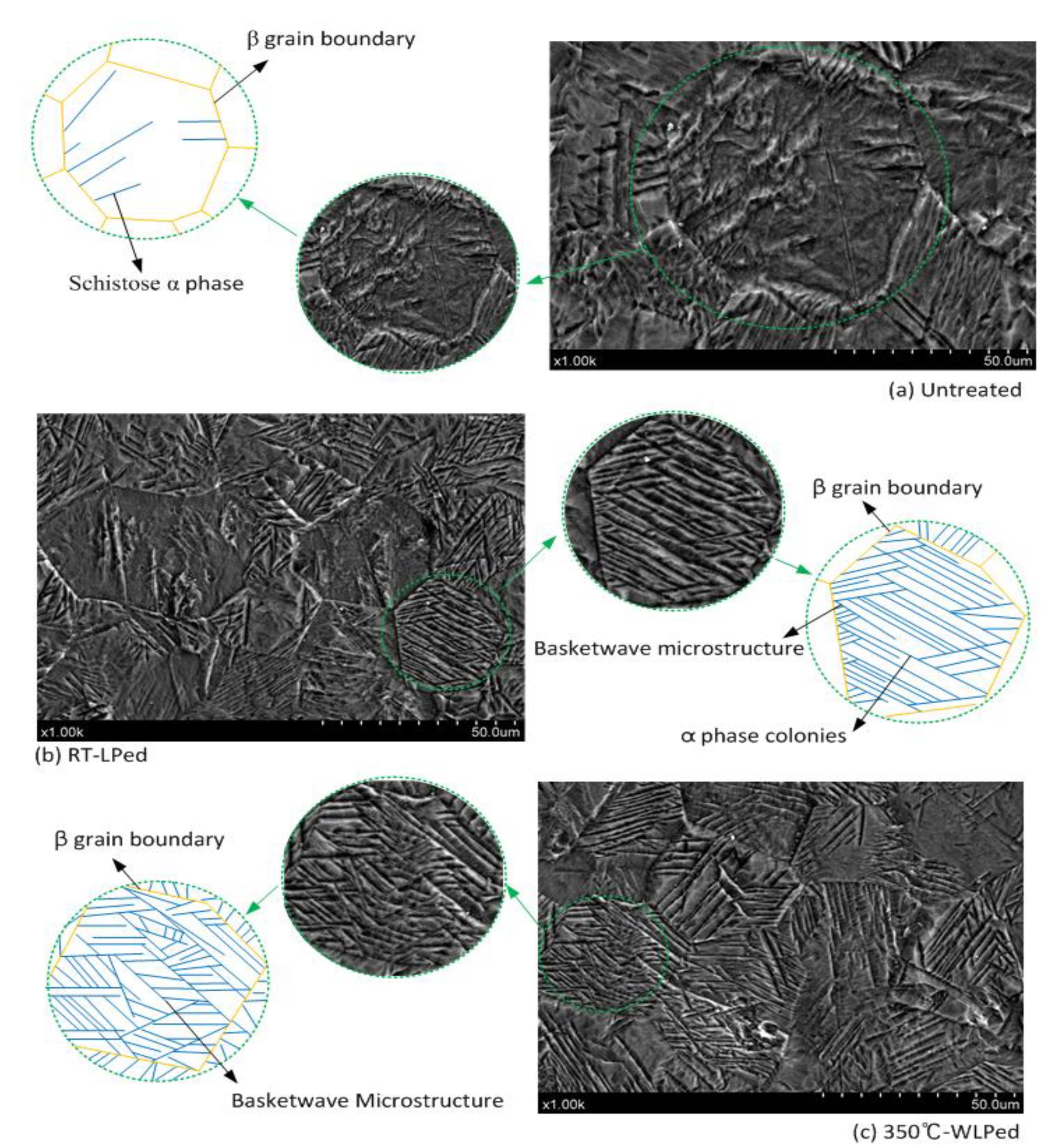
3.1. Microstructure in Ti6Al4V Titanium
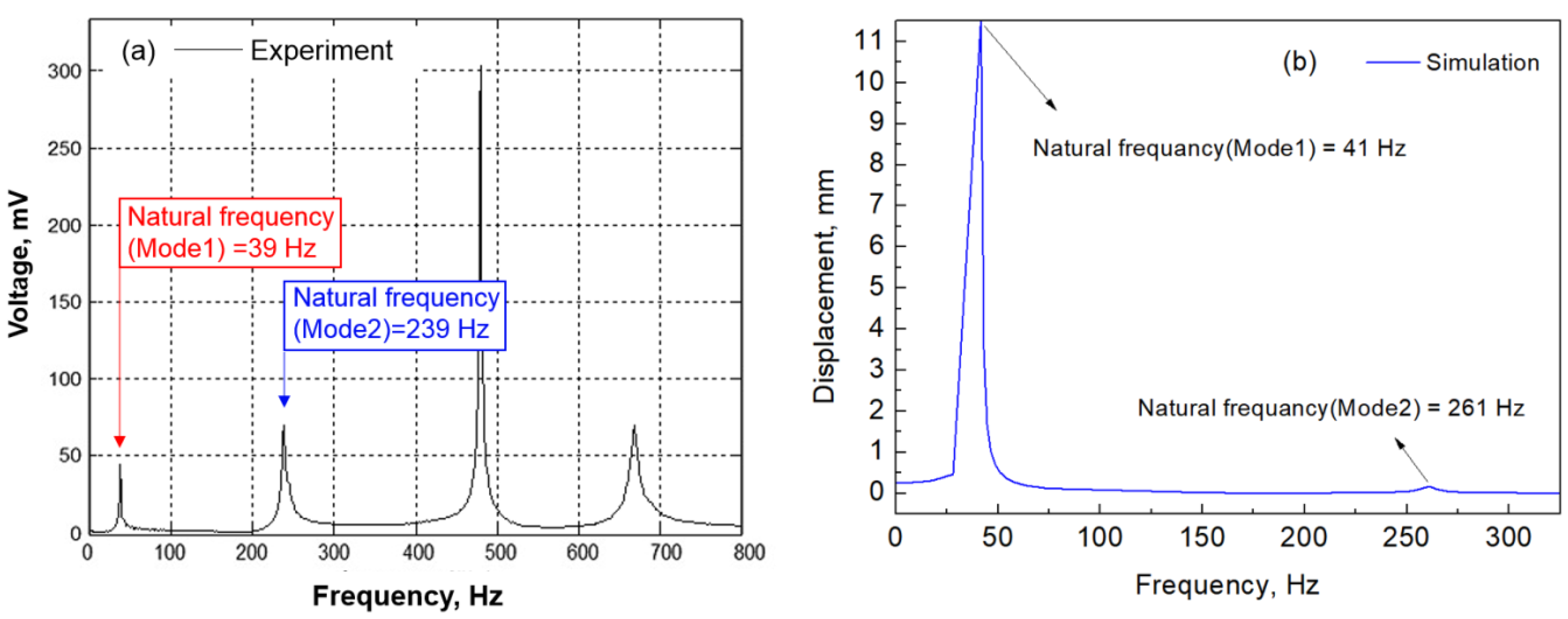
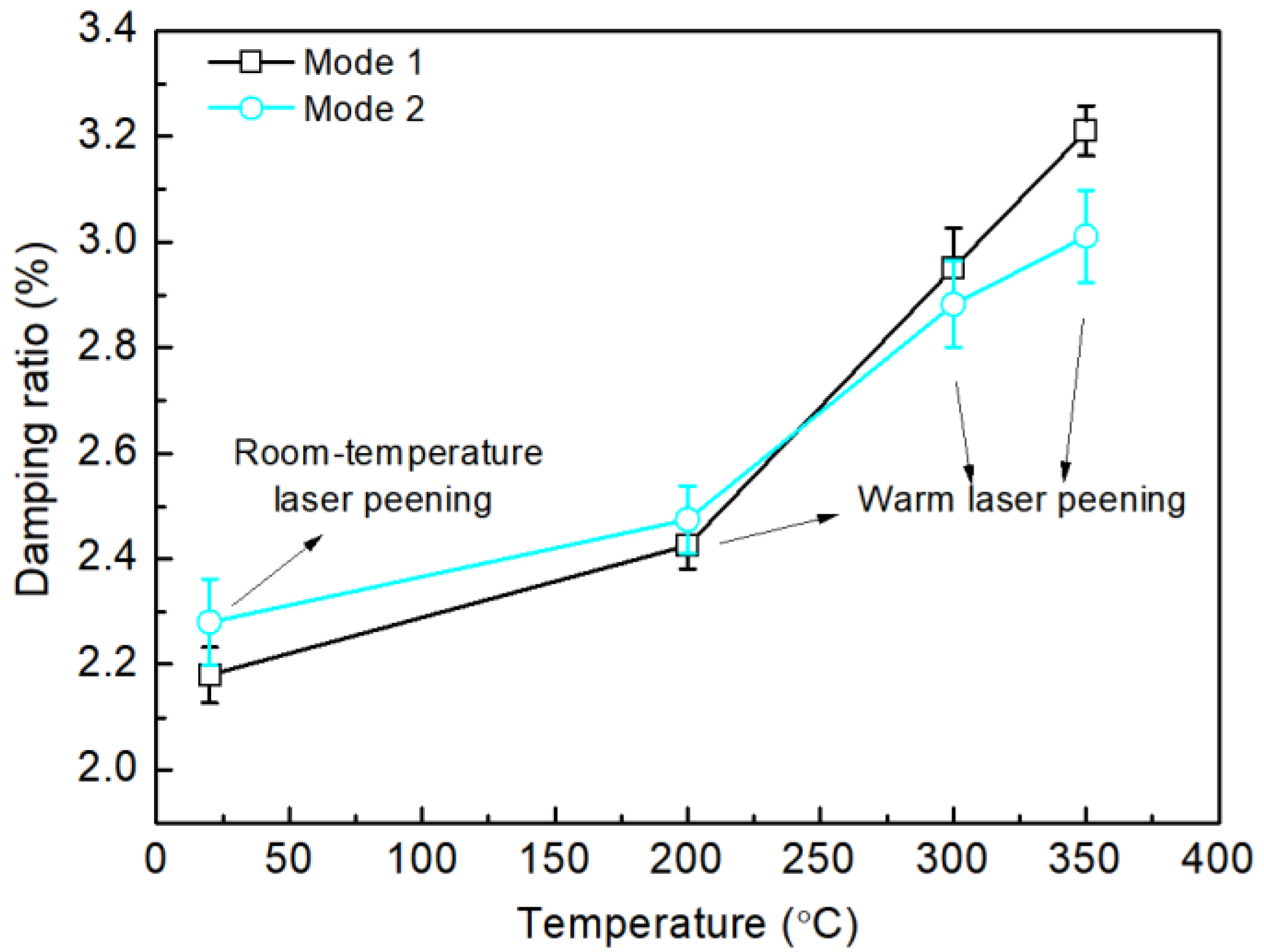
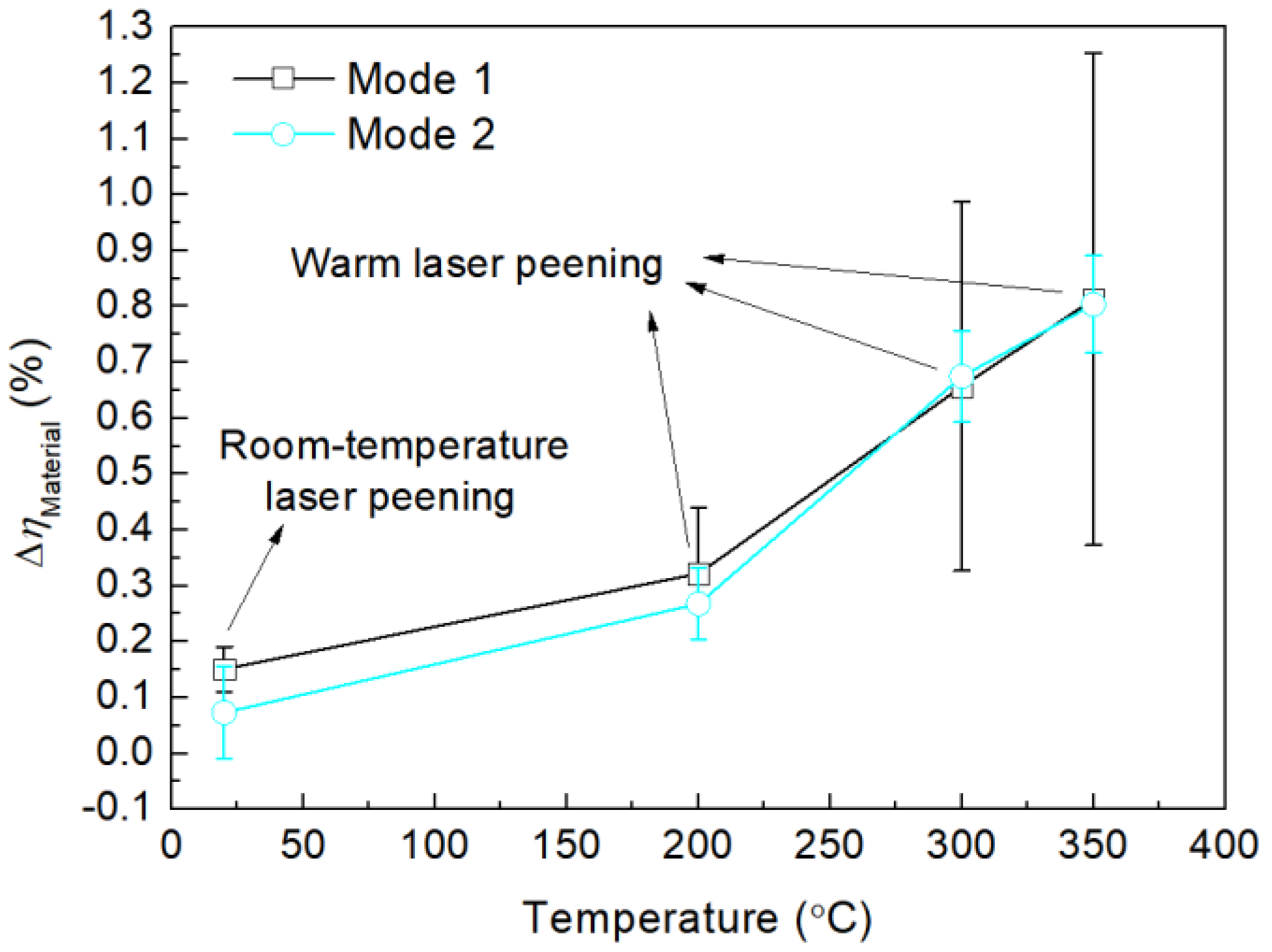
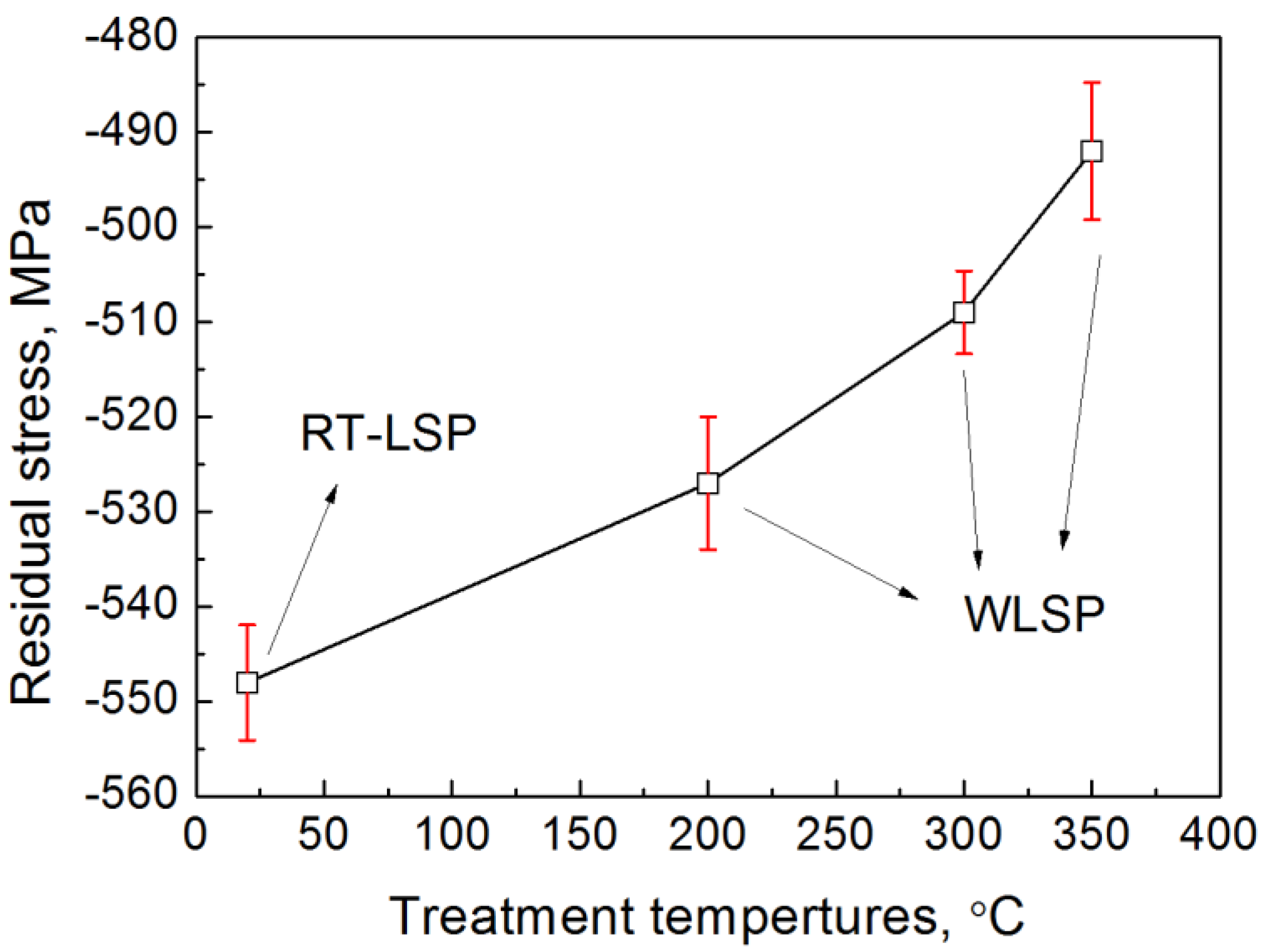
3.2. Damping Ratio and Residual Stress
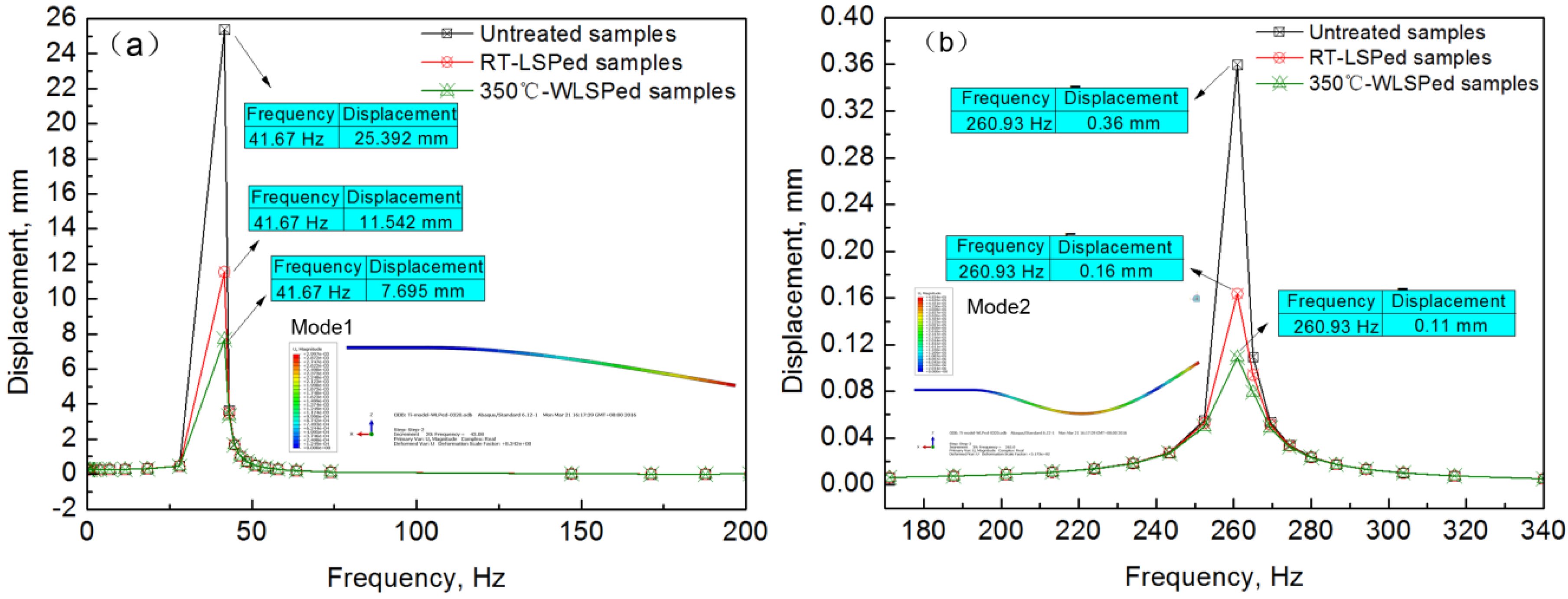
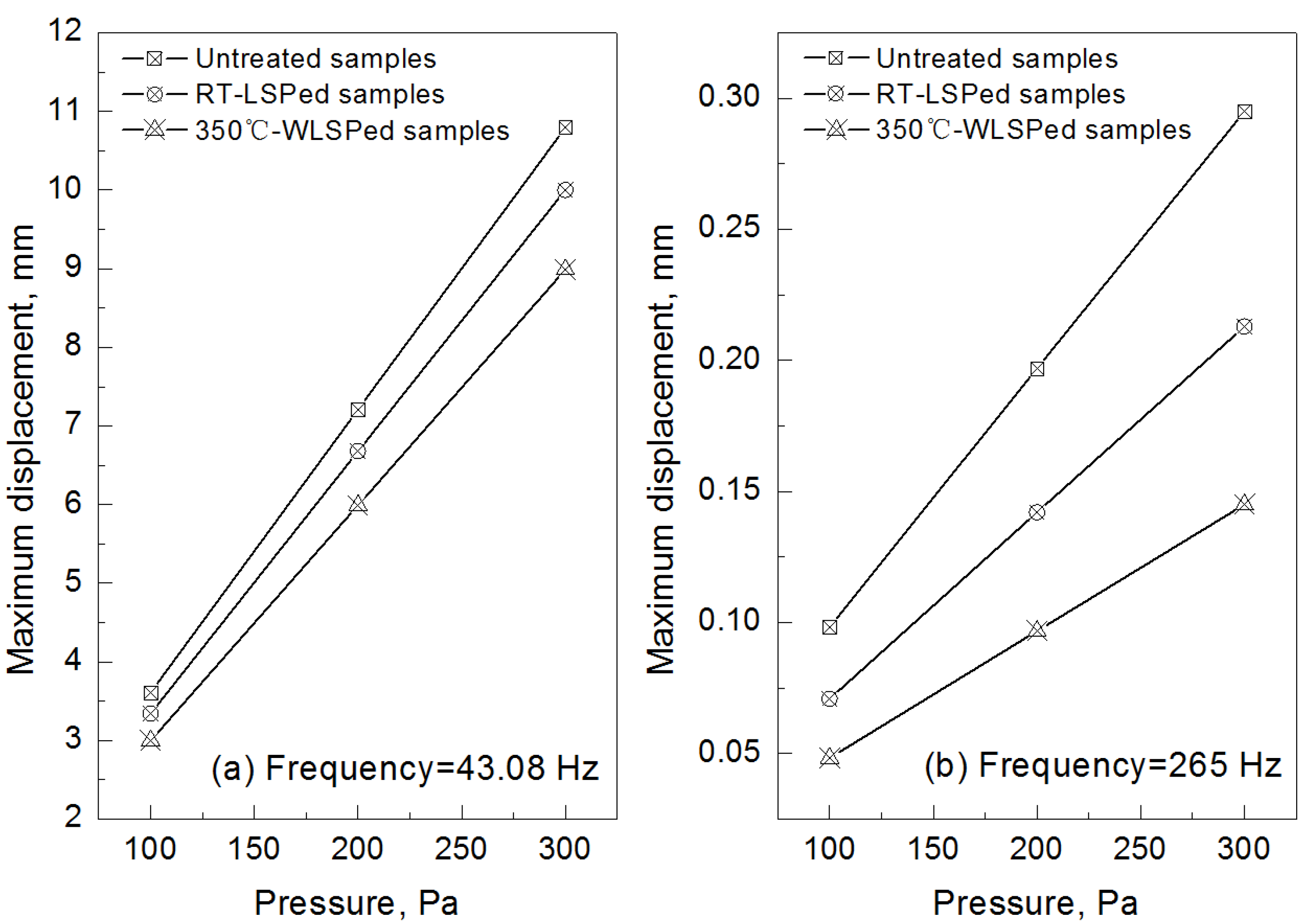
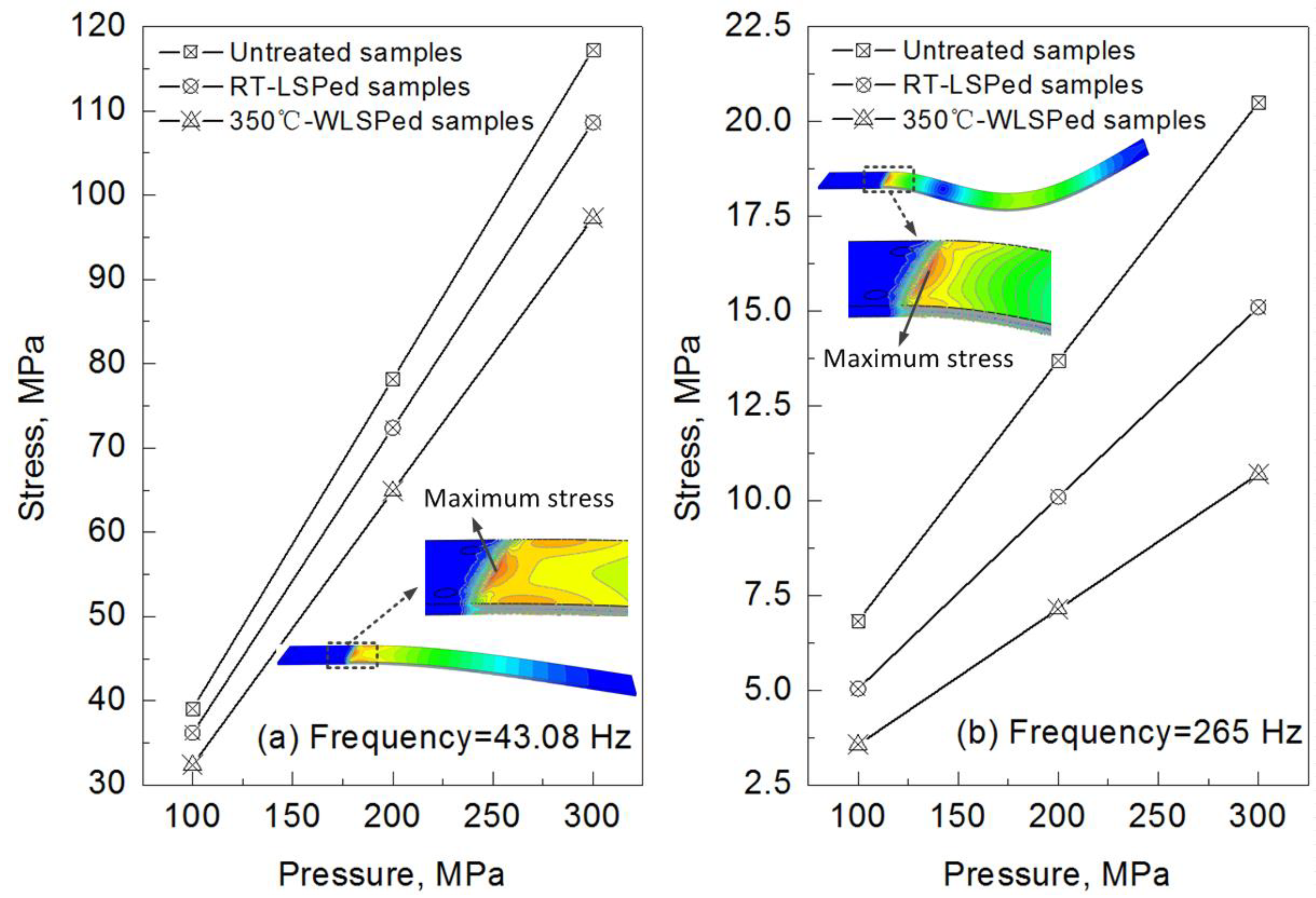
3.3. Vibration Displacement and Stress
3.4. Vibration Fatigue Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jha, A.K.; Singh, S.K.; Kiranmayee, M.S.; Sreekumar, K. Failure analysis of titanium alloy (Ti6Al4V) fastener used in aerospace application. Eng. Fail. Anal. 2010, 17, 1457–1495. [Google Scholar] [CrossRef]
- Sugianto, A.; Narazaki, M.; Kogawara, M. Failure analysis and prevention of quench crack of eccentric holed disk by experimental study and computer simulation. Eng. Fail. Anal. 2009, 16, 70–84. [Google Scholar] [CrossRef]
- Lingamanaik, S.N.; Chen, B.K. Microstructural and thermo-mechanical analysis of quench cracking during the production of bainitic–martensitic railway wheels. Eng. Fail. Anal. 2014, 40, 25–32. [Google Scholar] [CrossRef]
- Zhou, W.F.; Ren, X.D.; Liu, F.F.; Ren, Y.P.; Li, L. Nanocrystallization in the duplex Ti-6Al-4V alloy processed by multiple laser shock peening. Metals 2016, 6, 297. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhang, Y.K.; Lu, J.Z. Improvement of fatigue life of Ti–6Al–4V alloy by laser shock peening. Mater. Sci. Eng. A 2010, 527, 3411–3415. [Google Scholar] [CrossRef]
- Rubio-González, C.; Felix-Martinez, C.; Gomez-Rosas, G. Effect of laser shock processing on fatigue crack growth of duplex stainless steel. Mater. Sci. Eng. A 2011, 528, 914–919. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Lu, J.Z.; Luo, K.Y. Residual stress distribution and microstructure at a laser spot of AISI 304 stainless steel subjected to different laser shock peening impacts. Metals 2015, 6, 6. [Google Scholar]
- Qiao, H. Experimental investigation of laser peening on Ti17 titanium alloy for rotor blade applications. Appl. Surf. Sci. 2015, 351, 524–530. [Google Scholar]
- Kim, J.C.; Cheong, S.K.; Noguchi, H. Residual stress relaxation and low- and high-cycle fatigue behavior of shot-peened medium-carbon steel. Int. J. Fatigue 2013, 56, 114–122. [Google Scholar] [CrossRef]
- Dalaeia, K.; Karlssona, B.; Svensson, L.E. Stability of residual stresses created by shot peening of pearlitic steel and their influence on fatigue behaviour. Procedia Eng. 2010, 2, 613–622. [Google Scholar] [CrossRef]
- Basu, I.; Al-Samman, T. Deformation, Recrystallization and Grain Growth Behavior of Large-Strain Hot Rolled Binary Mg-1Dy Alloy// Magnesium Technology 2014; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Zhou, J.Z.; Meng, X.K.; Huang, S.; Sheng, J.; Lu, J.Z.; Yang, Z.R.; Su, C. Effects of warm laser shock peening at elevated temperature on the low-cycle fatigue behavior of Ti6Al4V alloy. Mater. Sci. Eng. A 2015, 643, 86–95. [Google Scholar] [CrossRef]
- Chen, H.S.; Zhou, J.Z.; Sheng, J.; Meng, X.K.; Huang, X.; Xie, X.J. Effects of Warm laser shock peening on Thermal Stability and High Temperature Mechanical Properties of A356 Alloy. Metals 2016, 6, 126. [Google Scholar] [CrossRef]
- Liao, Y.L.; Ye, C.; Kim, B.J. Nucleation of highly dense nano-scale precipitates based on warm laser shock Peening. J. Appl. Phys. 2010, 108, 063518. [Google Scholar]
- Ye, C.; Sergey, S.; Kim, B.J. Fatigue performance improvement in AISI 4140 steel by dynamic strain aging and dynamic precipitation during warm laser shock peening. Acta Mater. 2011, 59, 1014–1025. [Google Scholar] [CrossRef]
- Vázquez Jiménez, C.A.; Gómez Rosas, G.; Rubio González, C. Effect of laser shock processing on fatigue life of 2205 duplex stainless steel notched specimens. Optics Laser Technol. 2017, 97, 308–315. [Google Scholar] [CrossRef]
- Meng, X.K.; Zhou, J.Z.; Su, C. Residual stress relaxation and its effects on the fatigue properties of Ti6Al4V alloy strengthened by warm laser shock peening. Mater. Sci. Eng. A 2016, 680, 297–304. [Google Scholar] [CrossRef]
- Nie, X.F.; He, W.; Zhou, L. Experiment investigation of laser shock peening on TC6 titanium alloy to improve high cycle fatigue performance. Mater. Sci. Eng. A 2014, 594, 161–167. [Google Scholar] [CrossRef]
- Zhang, L. Modal Analysis and Experiments; Tsinghua University Press: Beijing, China, 2011. [Google Scholar]
- Postnikov, V.S.; Pavlov, V.S.; Turkov, S.K. Internal friction in ferroelectrics due to interaction of domain boundaries and point defects. J. Phys. Chem. Solids 1970, 31, 1785–1791. [Google Scholar] [CrossRef]
- Zhou, Z.; Bhamare, S.; Ramakrishnan, G.; Mannava, S.R.; Langer, K.; Wen, Y.; Qian, D.; Vasudevan, V.K. Thermal relaxation of residual stress in laser shock peened Ti–6Al–4V alloy. Surf. Coat. Technol. 2012, 206, 4619–4627. [Google Scholar]
- Pant, B.K.; Pavan, A.H.V.; Prakash, R.V. Effect of laser shock peening and shot peening on fatigue striations during FCGR study of Ti6Al4V. Int. J. Fatigue 2016, 93, 38–50. [Google Scholar] [CrossRef]

| Material | Young Modulus (GPa) | Yield Stress (MPa) | Ultimate Stress (MPa) | Elongation at Fracture |
|---|---|---|---|---|
| Ti6Al4V titanium | 110 | 826 | 1050 | 9.6% |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Operation material | Nd:YAG | Frequency (Hz) | 1–5 |
| Wavelength (nm) | 1064 | Power distribution | Flat |
| Pulse power (J) | <16 | Spot shape | Circle |
| Pulse width (ns) | <12 | Focus size (mm) | Φ3–8 |
| BPP (mm·mrad) | <20 | TEM mode | 00 |
| Pulse Energy (J) | Spot Diameter (mm) | Export Stability | Pulse Width (ns) | Laser Wavelength (nm) | Frequency (Hz) |
|---|---|---|---|---|---|
| 9 | 3 | <5% | 10 | 1064 | 1 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Exciting frequency (Hz) | 5–4500 | Exciting force (N) | 2940 |
| Maximum acceleration (m/s2) | 980 | Maximum peak-peak displacement (mm) | 40 |
| Carrying capacity (kg) | <120 | Maximum speed (m/s) | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Zhao, Y.; Lu, J.; Huang, S.; Zhou, J.; Su, C. Improvement of Damping Property and Its Effects on the Vibration Fatigue in Ti6Al4V Titanium Alloy Treated by Warm Laser Shock Peening. Metals 2019, 9, 746. https://doi.org/10.3390/met9070746
Meng X, Zhao Y, Lu J, Huang S, Zhou J, Su C. Improvement of Damping Property and Its Effects on the Vibration Fatigue in Ti6Al4V Titanium Alloy Treated by Warm Laser Shock Peening. Metals. 2019; 9(7):746. https://doi.org/10.3390/met9070746
Chicago/Turabian StyleMeng, Xiankai, Yaomin Zhao, Jinzhong Lu, Shu Huang, Jianzhong Zhou, and Chun Su. 2019. "Improvement of Damping Property and Its Effects on the Vibration Fatigue in Ti6Al4V Titanium Alloy Treated by Warm Laser Shock Peening" Metals 9, no. 7: 746. https://doi.org/10.3390/met9070746
APA StyleMeng, X., Zhao, Y., Lu, J., Huang, S., Zhou, J., & Su, C. (2019). Improvement of Damping Property and Its Effects on the Vibration Fatigue in Ti6Al4V Titanium Alloy Treated by Warm Laser Shock Peening. Metals, 9(7), 746. https://doi.org/10.3390/met9070746





