Abstract
In the continuous-casting process, mold-level control is one of the most important factors that ensures the quality of high-efficiency continuous casting slabs. In traditional mold-level prediction control, the mold-level prediction accuracy is low, and the calculation cost is high. In order to improve the prediction accuracy for mold-level prediction, an adaptive hybrid prediction algorithm is proposed. This new algorithm is the combination of empirical mode decomposition (EMD), variational mode decomposition (VMD), and support vector regression (SVR), and it effectively overcomes the impact of noise on the original signal. Firstly, the intrinsic mode functions (IMFs) of the mold-level signal are obtained by the adaptive EMD, and the key parameter of the VMD is obtained by the correlation analysis between the IMFs. VMD is performed based on the key parameter to obtain several IMFs, and the noise IMFs are denoised by wavelet threshold denoising (WTD). Then, SVR is used to predict each denoised component to obtain the predicted IMF. Finally, the predicted mold-level signal is reconstructed by the predicted IMFs. In addition, compared with WTD–SVR and EMD–SVR, VMD–SVR has a competitive advantage against the above three methods in terms of robustness. This new method provides a new idea for mold-level prediction.
1. Introduction
In the modern steel industry, high-efficiency continuous casting technology has become the most internationally competitive key technology [1]. The continuous casting process is a complex and continuous phase change process. Many factors affect the quality of slabs. The research into the key technology in the high-quality steel continuous-casting process is mainly focused on mold-level precision, as well as the segment and secondary cooling dynamic control [2].
At present, mold-level control is mainly based on the principle of predictive control, which combines prediction and control to improve the timeliness of prediction, but affects its accuracy. In view of the large mold-level disturbance, Guo et al. [3] used the prediction method in mold-level control. Aiming at the nonlinear characteristics of mold-level data, Tong et al. [4] carried out a constrained generalized prediction method based on the genetic algorithm. Aiming at the strong mold-level coupling characteristics, Qiao et al. [5] proposed an auto-disturbance suppression algorithm based on neural network tuning. However, these prediction methods have not effectively overcome the effects of mold-level noise.
Precise mold level monitoring is regarded as the key to improving continuous casting production quality, as shown in Figure 1 [2,3,4]. It is an important source of reference data for casting speed control, segment roll gap control, mold-cooling water control, and stopper rod opening control. If the mold level fluctuates too much, the following will occur. First, it will cause impurities on the surface of the mold. Surface defects and internal defects of the slab are generated which affect the surface and internal quality of the slab. Second, it will affect the casting speed, affecting productivity and the production rhythm. Eventually, it will cause the slab and the continuous casting machine to stick together, damage the tundish slide, and even cause downtime. Accurate prediction of the mold level occupies an important position in the continuous casting production process. This paper proposes an advanced mold level signal denoising method to prepare accurate data input for future mold level prediction, realize the purpose of predictive control, and greatly reduce the occurrence of accidents affecting quality and safety in the continuous casting production process.
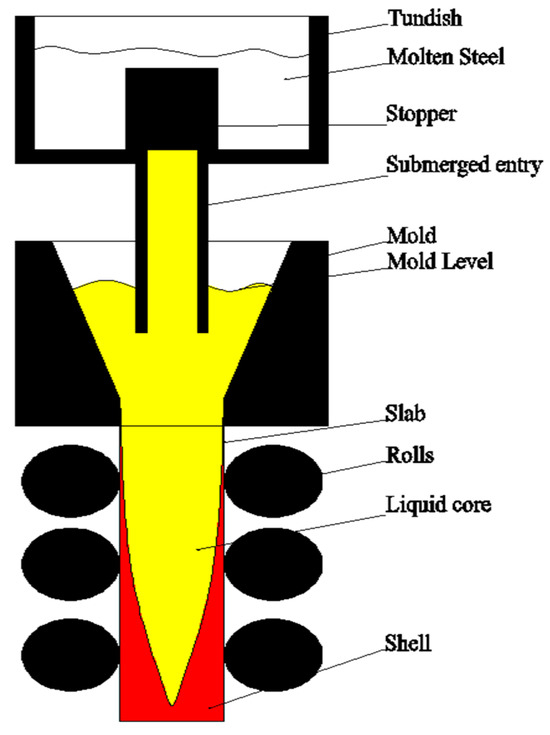
Figure 1.
Mold-level model.
A data-driven method for mold-level prediction is proposed in this paper, which provides a new idea for mold-level control. The method takes variational mode decomposition (VMD) and support vector regression (SVR) as its core ideas, and creates mold-level predictions driven by data to overcome the influence of white noise caused by the casting speed and strong mold-level coupling.
Recent studies have shown that although there are many methods in the field of signal processing, none of them is applicable to all signal data. Wavelet transform (WT)-based signal processing methods are widely used, but wavelet denoising methods are limited by the selection of the wavelet basis function and affect the generalization ability of the wavelet. Although the method based on empirical mode decomposition (EMD) is widely used for the adaptability of its decomposition [6], the EMD method has serious pattern aliasing and boundary effects which seriously affect the signal decomposition. Especially in the process of signal noise processing, high-frequency components are often removed directly, resulting in loss of effective information. Signal processing techniques based on the VMD method have been widely used in recent years [7]. Compared with the EMD method, VMD effectively avoids mode aliasing and boundary effects and can realize the frequency domain splitting of signals and effective separation of components, which results in better noise and sample rate robustness.
For the prediction of time series, various prediction methods have appeared in the past several decades. Traditional time-series prediction methods, such as regression analysis and grey prediction [8], have some shortcomings, and the prediction accuracy of signals with large fluctuations needs to be improved [9]. The numerical weather prediction model for predicting future wind speed using mathematical models [10], multiple regression, exponential smoothing, the autoregressive moving average model (ARMA), and many others are used for wind-speed prediction, power prediction, stock-trend prediction, etc. Traditional time-series prediction methods have low precision and poor robustness to nonlinear disturbances. Mold level is non-linear and non-stationary in terms of the time scale and does not satisfy Gaussian normal distribution. Traditional time-series prediction methods are not suitable for mold-level prediction.
In recent years, with the rapid development of science and technology, artificial intelligence technology has been widely used and introduced into the prediction of time series, and good prediction results have been achieved [11]. Artificial neural networks (ANN) [12] and SVR [13] methods are the main tools for dealing with non-linear, non-stationary time series. SVR is a small-sample machine-learning method based on statistical learning theory, Vapnik–Chervonenkis (VC) dimension theory, and the minimum structural risk principle. Based on limited sample information, it seeks the best compromise between model complexity and learning ability to achieve the best promotion effect [14,15]. Liu and Gao [16] established a method for the online prediction of the silicon content in blast-furnace ironmaking processes. Compared with other soft sensors, the superiority of the proposed method is demonstrated in terms of the online prediction of the silicon content in an industrial blast furnace in China. Existing studies have shown that the ANN method takes a long time to calculate and is prone to localized minimization [17,18,19,20], leading to overfitting and poor prediction results. SVR is more robust to overfitting than ANN. The parameters of SVR can be improved by means of global optimization. It can be used to improve the prediction performance of SVR.
This paper focuses on the use of a hybrid algorithm for a time-series prediction model, and it is used for mold-level prediction. After comparing and discussing the hybrid algorithm for mold-level prediction, a new idea for continuous-casting process improvement is proposed. Firstly, the model uses EMD to decompose the original mold-level signal into several intrinsic mode functions (IMFs), and the key parameter of the VMD is obtained by the correlation analysis between the IMFs. VMD is performed based on the key parameter to obtain several IMFs, and the noise IMFs are denoised by wavelet threshold denoising (WTD). Then, SVR is used to predict each denoised component to obtain the predicted IMF. Finally, the predicted IMF reconstructs the predicted mold-level signal. The rest of this paper is organized as follows. The VMD algorithm is introduced in Section 2. VMD–SVR algorithms are introduced in Section 3. The performance of the three algorithms is compared through experiments in Section 4. Section 5 concludes this paper and makes recommendations.
2. Basic Algorithm Research
2.1. Variational Mode Decomposition
VMD is a new type of signal decomposition method. This method redefines an amplitude modulation-frequency modulation signal as an IMF, whose expression is
where ϕk(t) ≥ 0 is the phase, Ak(t) is the amplitude, Ak(t) ≥ 0, , and ωk(t) is the frequency.
In the interval range of [t − δ, t + δ], uk(t) can be regarded as a harmonic signal with amplitude Ak(t) and frequency ωk(t), and , where the prime denotes differentiation with respect to t.
The difference between VMD and EMD is that VMD is based on solving the variational problem and uses the variational model principle in the process of obtaining the IMFs, so that the sum of the estimated bandwidths of each IMF is minimized. The optimal solution of the constrained variational model is solved. The center frequency and bandwidth of the IMF are updated in the process of solving the variational model. The signal band is adaptively segmented based on the frequency domain of the signal itself. Further, a narrowband IMF is obtained.
The variational constraint model is as follows:
where ; is the number of IMF; is the frequency center of each IMF; and is the sum of all modes. is the square of the 2-norm.
We introduce the Lagrange function as
where α is the penalty factor and λ is the Lagrange multiplier. is the second penalty. is the integral mean of the variables.
The problem of solving the original minimum value can be transformed into the saddle point of the extended Lagrange expression by the alternating direction method, which is the optimal solution of the below formula:
where is the convergence condition; n is the number of iterations; and τ is the update parameter.
Therefore, the original signal can be decomposed into K IMFs.
The calculation process of the VMD algorithm is as follows:
- Step 1:
- Initialize , , λ1 and n to zero;
- Step 2:
- n = n + 1, execute the entire loop;
- Step 3:
- Execute the loop k = k + 1 until k = K, update uk: ;
- Step 4:
- Execute the loop k = k + 1, until k = K, update ωk: ;
- Step 5:
- Use to update λ;
- Step 6:
- Given the discrimination condition ε > 0, if the iteration stop condition is satisfied, all the cycles are stopped and the result is output, and K IMFs are obtained.
2.2. Support Vector Machine
SVM can not only solve the classification problem, but also solves the regression problem; the basic model is the largest linear classifier defined in the feature space. SVM aims to achieve a distinction between samples by constructing a hyperplane for classification so that the sorting interval between the samples is maximized and the sample to the hyperplane distance is minimized.
Set a training data set for a feature space D = {(x1, y1), (x2, y2), …, (xm, ym)}, , , i = 1, 2, …, N, where xi is the i-th feature vector, yi is the class tag of xi.
The corresponding equation of the classification hyperplane is
where x is the input vector, ω is the weight, and b is the offset.
The classification decision function is
Sign(h(x))
The support vector machine is implemented to find ω and b when the interval between the separation hyperplane and the nearest sample point is maximized. When the training set is linearly separable, the sample points belonging to different classes can be separated by one or several straight lines with the largest interval. The maximum interval is solved by the following formula:
where γ is the geometric interval. Thus, we can obtain the linear separable support vector machine optimization problem.
In the actual data set, there are many specific points, making the data set linearly inseparable; in order to solve this problem, we introduce a slack variable for each sample point ξi ≥ 0, so that
For each slack variable ξi, pay a price ξi, and the optimization problem becomes
where C > 0 is the penalty factor.
Most of the data are linearly inseparable; therefore, these data should be mapped to a high-dimensional feature space through non-linear mapping, letting the non-linear problem be transformed into a linear problem. The linear indivisible problem is transformed into a linearly separable problem.
Introduce kernel functions:
where the value of the kernel equals the inner product of two vectors, xi and xj.
At this point, we obtain
where α is the Lagrangian multiplier, αi ≥ 0, i = 1, 2, …, N, and N is the number of samples.
In this paper, the radial basis function (RBF) is chosen as the SVR kernel function, and the expression is
where g is the kernel function coefficient.
At this point, the classification function becomes
2.3. Empirical Mode Decomposition
EMD is an adaptive signal processing technique suitable for non-linear and non-stationary processes [21]. In 1998, Huang et al. [6] proposed the empirical mode decomposition technology. Based on time scales, EMD local features such as local maxima, local minima, and zero-crossings, we decompose the signal into several IMFs and a residual; the IMFs are orthogonal to each other. Modal decomposition is determined by the signal itself.
EMD satisfies the following basic assumptions:
- (1)
- In the entire data set, the number of extreme values and the number of zero crossings must be equal or at most have one point of difference.
- (2)
- At any point, the average defined by the local maximum envelope and the minimum envelope is zero.
Finally, the original signal is decomposed into
where x(t) is the original signal, ci is the IMF, N is the number of IMFs, and rN is the residual.
2.4. Wavelet Threshold Denoising
Suppose the model of denoising based on wavelet transform is
where x is the noise signal; c is the effective signal; e is the noise component in the noise signal; and σ is the noise intensity.
The wavelet transform and its denoising process are carried out in the following steps [22]:
- (1)
- The noisy signal is transformed by wavelet transform. A wavelet basis is selected to determine the level N of the wavelet decomposition at the same time, and then the signal x is decomposed by the N-level wavelet.
- (2)
- The wavelet coefficients are thresholder. In order to keep the overall shape of the signal unchanged and keep the effective signal, the hard threshold, soft threshold or other threshold methods are used to quantify the sparseness of each layer after decomposition.
- (3)
- The inverse wavelet transform is performed, and the signal is reconstructed.
In this paper, a hard threshold denoising function is selected. Hard threshold processing compares the absolute value of wavelet transform coefficients with the threshold value. The coefficients smaller than or equal to the threshold value become zero, and the coefficients larger than the threshold value remain unchanged [23]. This method has better amplitude-preserving characteristics [24] and its expression is as follows:
where T is the threshold, and s is the wavelet decomposition coefficient.
3. Hybrid Algorithm Research
Mold-level prediction accuracy is influenced by many factors. In order to improve mold-level prediction accuracy, firstly, the noise in the original signal should be removed as much as possible. Then, we improve the prediction accuracy by using advanced prediction algorithms such as SVR. Thus, a prediction model based on the VMD–SVR algorithm for mold-level prediction is proposed in this paper. A hybrid algorithm flow chart is shown in Figure 2.
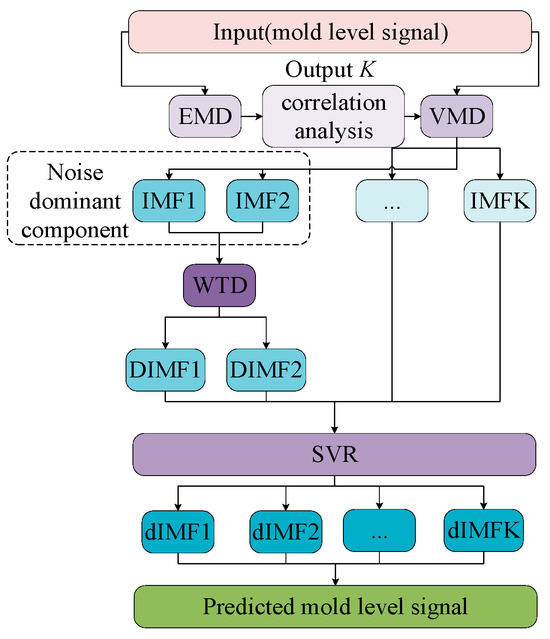
Figure 2.
Hybrid algorithm flow chart. EMD—empirical mode decomposition; VMD—variational mode decomposition; IMF—intrinsic mode functions; WTD—wavelet threshold denoising; SVR—support vector regression.
Firstly, the original mold-level signal is subjected to data preprocessing to remove singular points. Then, all data are marked in the range of 0 to 1 to improve computational efficiency. Finally, the hybrid model is used for data prediction.
The hybrid algorithm flow is as follows:
- Step 1:
- Adaptively decompose the mold-level data based on the EMD algorithm to obtain several IMFs;
- Step 2:
- The K value of the key parameter of the VMD is obtained by the correlation analysis between the IMFs;
- Step 3:
- Perform VMD decomposition on the original signal based on K to obtain K IMFs;
- Step 4:
- Denoise the noise related component;
- Step 5:
- Perform SVR on the denoised IMFs and other IMFs to obtain the predicted IMFs;
- Step 6:
- Reconstruct the predicted component and obtain the predicted signal.
First, the mold-level signal is decomposed into several IMFs by the EMD, and the modal parameter K of the VMD is determined by correlation analysis between the IMFs. Then, the mold-level signal is decomposed into K IMFs by VMD, and the IMFs are analyzed to identify the noise dominant component, and the signal dominant component uses correlation analysis between the IMFs. Afterwards, in order to avoid the loss of effective information, the noise-related component is denoised by the WTD algorithm, and the effective information is effectively retained. SVR is performed on the denoised IMFs and other IMFs to obtain the predicted IMFs. Finally, the predicted IMFs are reconstructed to obtain the predicted signal.
The IMFs are obtained by adaptively decomposing the original mold-level data based on the novel VMD–SVR hybrid algorithm, the main purpose of which is to distinguish the noise-dominant IMFs and information-dominant IMFs. In order to preserve as much valid information as possible in the original mold-level data, denoising the noise-dominant IMFs can effectively remove the effects of white noise. Then, SVR is performed on all IMFs, the predicted IMFs are obtained for signal reconstruction, and the predicted mold-level data is obtained.
4. Experimental Studies
4.1. Problem Prescription
This paper presents a mold-level prediction model. This model is important for mold-level control and propose new ideas to improve continuous-casting automatic control. In order to clearly express the applicability, superiority, and generalization capability of the model application, the mold-level data of actual process parameters, collected from the continuous casting machine developed by the China National Heavy Machinery Research Institute Co., Ltd. (Xi’an, China), are used in this paper. We used an eddy current sensor to collect the mold-level signal at a steady cast speed. There are many uncertain disturbance factors in the mold-level control process, and the disturbance may change constantly at any time. Most of the disturbances are non-linear and non-stationary, and the long-term prediction model is difficult to establish.
A continuous casting production process data acquisition graph is presented in Figure 3. The time interval ∆t = 0.5 h, and the sampling frequency was 2.7 Hz.

Figure 3.
Mold level. The unit of the mold level is mm, while m is the number of points.
The main technical parameters of the continuous casting machine are shown in Table 1.

Table 1.
Main technical parameters of the continuous casting machine.
4.2. Mold-Level Prediction Based on VMD–SVR Model
The VMD decomposition number is artificially determined, not adaptive. EMD is an adaptive decomposition method. Therefore, in order to minimize the interference of human factors, we decomposed the original data using EMD, and through the calculation of the correlation coefficient, a component having the largest correlation coefficient with the original signal was obtained as a boundary line between the high-frequency signal and the low-frequency signal, the high-frequency signal was integrated into one component, and the remaining components were retained to determine the number K of VMD decomposition.
First, the original data was subjected to EMD decomposition; the EMD decomposition results are shown in Figure 4.
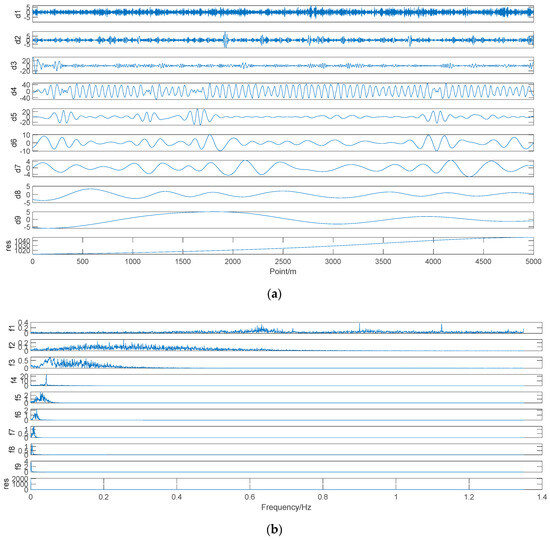
Figure 4.
(a) Mold-level data EMD results; (b) spectrogram after EMD of the mold-level data; di is the i-th IMF, the unit of di is mm, m is the number of points, res is the residual, and fi is the spectrum corresponding to the i-th IMF.
After the mold-level data is decomposed by the EMD as shown in Figure 3, the correlation coefficient between the original mold-level signal and the IMFs after EMD was determined, as shown in Table 2; IMFs 1–3 were seen to be weakly correlated with the original mold-level signal. There was a strong correlation between the original mold-level signal and the fourth IMF. We used IMFs 1–3 as a K value in the VMD decomposition, which is considered to be a high-frequency component of IMFs 1–3, and took the remaining IMF as 6 K values, thus obtaining K = 7, and performing VMD decomposition based on K = 7, which is not a simple direct merger of IMFs 1–3.

Table 2.
The correlation coefficient between the original mold-level signal and the IMFs after EMD.
The VMD decomposition of the mold-level data was based on K = 7. The decomposition result is shown in Figure 5.
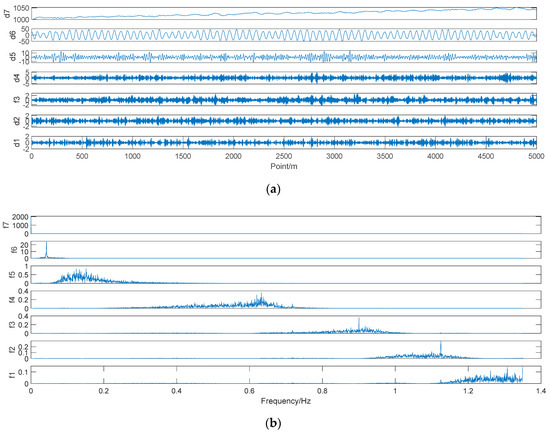
Figure 5.
(a) Mold-level data VMD results; (b) spectrogram after VMD of the mold-level data; di is the i-th IMF, the unit of di is mm, m is the number of Point, and fi is the spectrum corresponding to the i-th IMF.
It can be seen from Figure 4 that the mold-level data could clearly distinguish the center frequency of each IMF based on K = 7 decomposition, and no pattern aliasing occurred.
After the mold-level data was decomposed by the VMD, as shown in Figure 5, the correlation coefficient between the original mold-level signal and the IMFs after VMD was calculated, as shown in Table 3; IMFs 1–5 were weakly correlated with the original mold-level signal. There was a strong correlation between the original mold-level signal and the fourth IMF. Therefore, IMF 6 was a boundary line between the high-frequency signal and the low-frequency signal; high-frequency signals may also contain a small amount of effective information, and so, in order to minimize the loss of effective information, we performed wavelet threshold denoising on high-frequency signals (IMFs 1–5) instead of directly deleting them.

Table 3.
The correlation coefficient between the original mold-level signal and the IMFs after VMD.
It can be seen from Figure 6 that the noise reduction effect for IMFs 1–5 was very obvious. Both the main frequency and the amplitude had a large reduction.
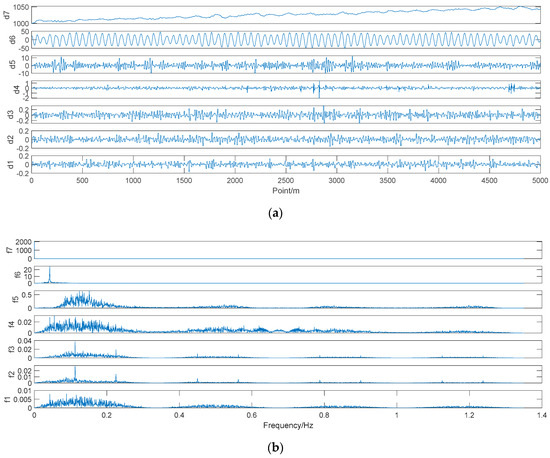
Figure 6.
(a) Denoising result of IMFs 1–5; (b) spectrogram of the mold-level data after denoising; di is the i-th IMF, the unit of di is mm, m is the number of points, and fi is the spectrum corresponding to the i-th IMF.
Then, SVR was performed on the all IMFs. In this section, the genetic algorithm was still used to globally optimize the model parameters C and g, so that the SVR model was determined. C was 15.2768 and g was 0.2018. The first 20 min of mold-level data was used as a training set, while the last 10 min of mold-level data was used as a test set in order to verify the prediction effect of the model. This method has high computational efficiency, high calculation accuracy, and can be run in real-time.
The optimization results of C and g are shown in Figure 7; fitness was the hit rate of the genetic algorithm. The predicted data of VMD–SVR are shown in Figure 8, and the VMD–SVR prediction error is shown in Figure 9.

Figure 7.
C and g optimization results. C is the penalty coefficient, g is the parameter of kernel function.

Figure 8.
Comparison of VMD–SVR prediction results with original mold-level data. m is the number of points.

Figure 9.
VMD–SVR prediction error. m is the number of points.
5. Prediction Results and Analysis
In this section, the performance of the three hybrid prediction algorithms is verified by the following four statistical indicators, which are the general purpose of the machine learning domain verification algorithm, and the optimal hybrid prediction model suitable for the mold steel level of the mold is selected.
Correlations between the original data and the predicted data, which is characterized by correlation coefficients (R):
CC is defined as a statistical indicator and is used to reflect the close relationship between variables; the larger the CC, the better the algorithm performance.
Root mean square error (RMSE)
RMSE is defined to reflect the degree of dispersion of a data set and to measure the deviation between the observed value and the true value; the smaller the RMSE, the better the algorithm performance.
Mean absolute error (MAE)
MAE is defined as the average value of absolute error, better reflecting the actual situation of predicted error; the smaller the MAE, the better the algorithm performance.
Mean absolute percentage error (MAPE)
MAPE can be used to measure the outcome of a model’s predictions; the smaller the MAPE, the better the algorithm performance.
In Formulas (23)–(26), where Pi and Ai are the i-th predicted and actual values, respectively, and n is the total number of predictions.
From the test results in Table 4 and Figure 10, comparing the four indicators of the three algorithms, the test results of the average error in the algorithm described in this paper are inferior to the other two algorithms. However, in the test results of the other three indicators, the RMSE index is improved by 36.1%, the MAPE index is improved by 37.5%, the R is improved by 3%, and the MAE index is improved by 37.6%. Compared with WT and EMD, the VMD algorithm has shown great superiority, which not only rejects the dependence of the wavelet transform on basis function, but also avoids the boundary effect and pattern aliasing of empirical mode decomposition and improves the robustness of the algorithm and generalization ability.

Table 4.
Test results comparison of prediction model. R is correlation coefficients; RMSE is root mean square error; MAE is mean absolute error; MAPE is mean absolute percentage error.

Figure 10.
Prediction error between VMD–SVR and other methods. m is the number of points.
6. Conclusions
This paper proposes a prediction method based on VMD–SVR, which is suitable for mold-level prediction in continuous casting. In this method, the original mold-level data are adaptively decomposed by the EMD algorithm to obtain the effective IMF number K, via correlation coefficient analysis between the original mold-level signal and IMFs. The VMD decomposition of the original mold-level data is performed based on K, and the IMFs are obtained. Time-series prediction is performed for each IMF via SVR, and the VMD reconstruction is performed on the prediction result to obtain the final predicted mold-level signal. In order to verify the effectiveness of the proposed method, we compared the four statistical indicators of three algorithms; the conclusions are as follows.
- (1)
- The VMD–SVR algorithm can be used to establish the prediction model, removing noise while retaining the effective information in the data, with good denoising performance and sampling rate robustness;
- (2)
- In comparison with the results of the other two algorithms, the three indicators of the VMD–SVR algorithm are significantly better than those of the other two algorithms. The RMSE index is improved by 36.1%, the MAPE index are improved by 37.5%, the R is improved by 3%, and the MAE index is improved by 37.6%;
- (3)
- The use of mold-level prediction methods in the research on mold prediction control represents a future research direction. Accurate mold-level prediction provides a new idea for mold-level prediction control, which has important practical significance;
- (4)
- Using the accurately predicted mold-level data for mold-level control, the sliding nozzle and roller pressure disturbances can be well restrained. The anti-interference ability of the mold level control system is enhanced.
The potential feedback between the mold level controller and the mold level prediction will improve the accuracy and efficiency of the prediction model, which will be the focus of further research in a future paper.
Author Contributions
W.S. conceived and designed the experiments, Z.L. performed the experiments, L.Y. provided mold-level data, Q.H. analyzed the data, and Z.L. wrote the paper.
Funding
This work was financially supported by the National Natural Science Foundation of China, grant number 51575429.
Acknowledgments
Q.G., X.L., H.Z., B.H., and Y.Z. are acknowledged for their valuable technical support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ataka, M. Rolling technology and theory for the last 100 years: The contribution of theory to innovation in strip rolling technology. ISIJ Int. 2015, 55, 89–102. [Google Scholar] [CrossRef]
- Jin, X.; Chen, D.F.; Zhang, D.J.; Xie, X. Water model study on fluid flow in slab continuous casting mould with solidified shell. Ironmak. Steelmak. 2011, 38, 155–159. [Google Scholar] [CrossRef]
- Guo, G.; Wang, W.; Chai, T. Predictive mould level control in a continuous casting line. Control Theory Appl. 2011, 18, 714–717. [Google Scholar]
- Tong, C.; Xiao, L.; Peng, K.; Li, J. Constrained generalized predictive control of mould level based on genetic algorithm. Control Decis. 2009, 24, 1735–1739. [Google Scholar]
- Qiao, G.; Tong, C.; Sun, Y. Study on Mould level and casting speed coordination control based on ADRC with DRNN optimization. Acta Autom. Sin. 2007, 33, 641–648. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A-Math. Phys. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Konstantin, D.; Dominique, Z. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar]
- Lee, W.J.; Hong, J. A hybrid dynamic and fuzzy time series model for mid-term power load predicting. Int. J. Electr. Power Energy Syst. 2015, 64, 1057–1062. [Google Scholar] [CrossRef]
- Dai, S.; Niu, D.; Li, Y. Daily peak load predicting based on complete ensemble empirical mode decomposition with adaptive noise and support vector machine optimized by modified grey wolf optimization algorithm. Energies 2018, 11, 163. [Google Scholar] [CrossRef]
- Lynch, P. The origins of computer weather prediction and climate modeling. J. Comput. Phys. 2008, 227, 3431–3444. [Google Scholar] [CrossRef]
- Gaudioso, M.; Gorgone, E.; Labbe, M.; Rodríguez-Chía, A.M. Lagrangian relaxation for SVM feature selection. Comput. Oper. Res. 2017, 87, 137–145. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP neural network algorithm in traditional hydrological model for flood predicting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- He, F.; Zhang, L. Mold breakout prediction in slab continuous casting based on combined method of GA-BP neural network and logic rules. Int. J. Adv. Manuf. Technol. 2018, 95, 4081–4089. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Hong, W.C.; Sun, F. Electric load predicting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Nie, H.; Liu, G.; Liu, X.; Wang, Y. Hybrid of ARIMA and SVMs for short-term load predicting, 2012 international conference on future energy, environment, and materials. Energy Procedia 2012, 16, 1455–1460. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Z. Enhanced just-in-time modelling for online quality prediction in BF ironmaking. Ironmak. Steelmak. 2015, 42, 321–330. [Google Scholar] [CrossRef]
- Shen, B.Z.; Shen, H.F.; Liu, B.C. Water modelling of level fluctuation in thin slab continuous casting mould. Ironmak. Steelmak. 2009, 36, 33–38. [Google Scholar] [CrossRef]
- Hong, W.-C. Chaotic particle swarm optimization algorithm in a support vector regression electric load predicting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Ganguly, S.; Chattopadhyay, P.P.; Datta, S. Effect of copper and microalloying (Ti, B) addition on tensile properties of HSLA steels predicted by ANN technique. Ironmak. Steelmak. 2009, 36, 125–132. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.-L. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef]
- Lei, Y.G.; Lin, J.; He, Z.J.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Sig. Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Tomic, M. Wavelet transforms with application in signal denoising. Ann. DAAAM Proc. 2008, 1401–1403. [Google Scholar]
- El B’charri, O.; Latif, R.; Elmansouri, K.; Abenaou, A.; Jenkal, W. ECG signal performance de-noising assessment based on threshold tuning of dual-tree wavelet transform. Biomed. Eng. Online 2017, 16, 26. [Google Scholar] [CrossRef] [PubMed]
- Varady, P. Wavelet-Based Adaptive Denoising of Phonocardiographic Records. In Proceedings of the 23rd Annual International Conference on IEEE-Engineering-in-Medicine-and-Biology-Society, Istanbul, Turkey, 25–28 October 2001; pp. 1846–1849. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).