Investigation of Bipolar Plate Forming with Various Die Configurations by Magnetic Pulse Method
Abstract
:1. Introduction
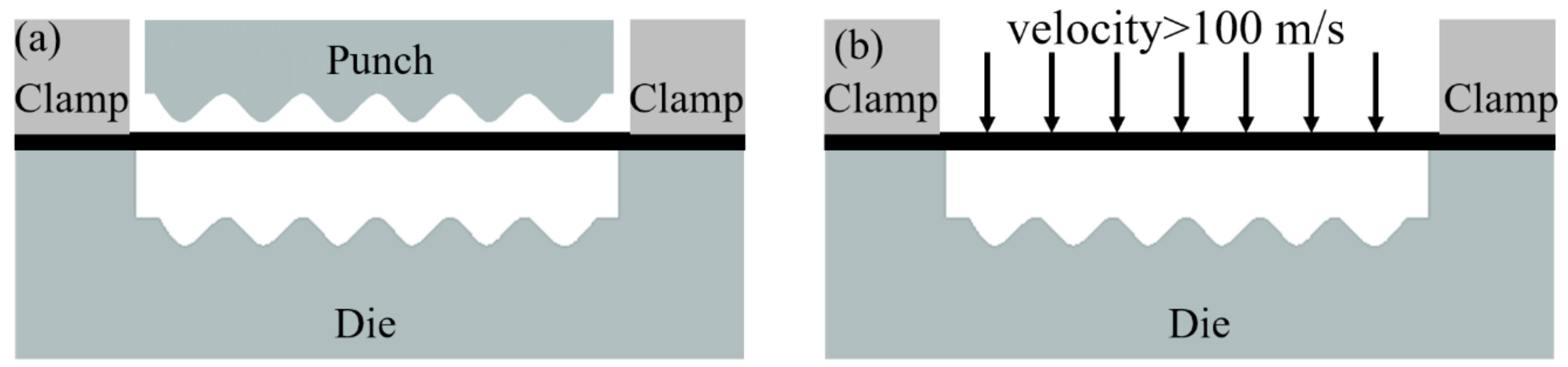
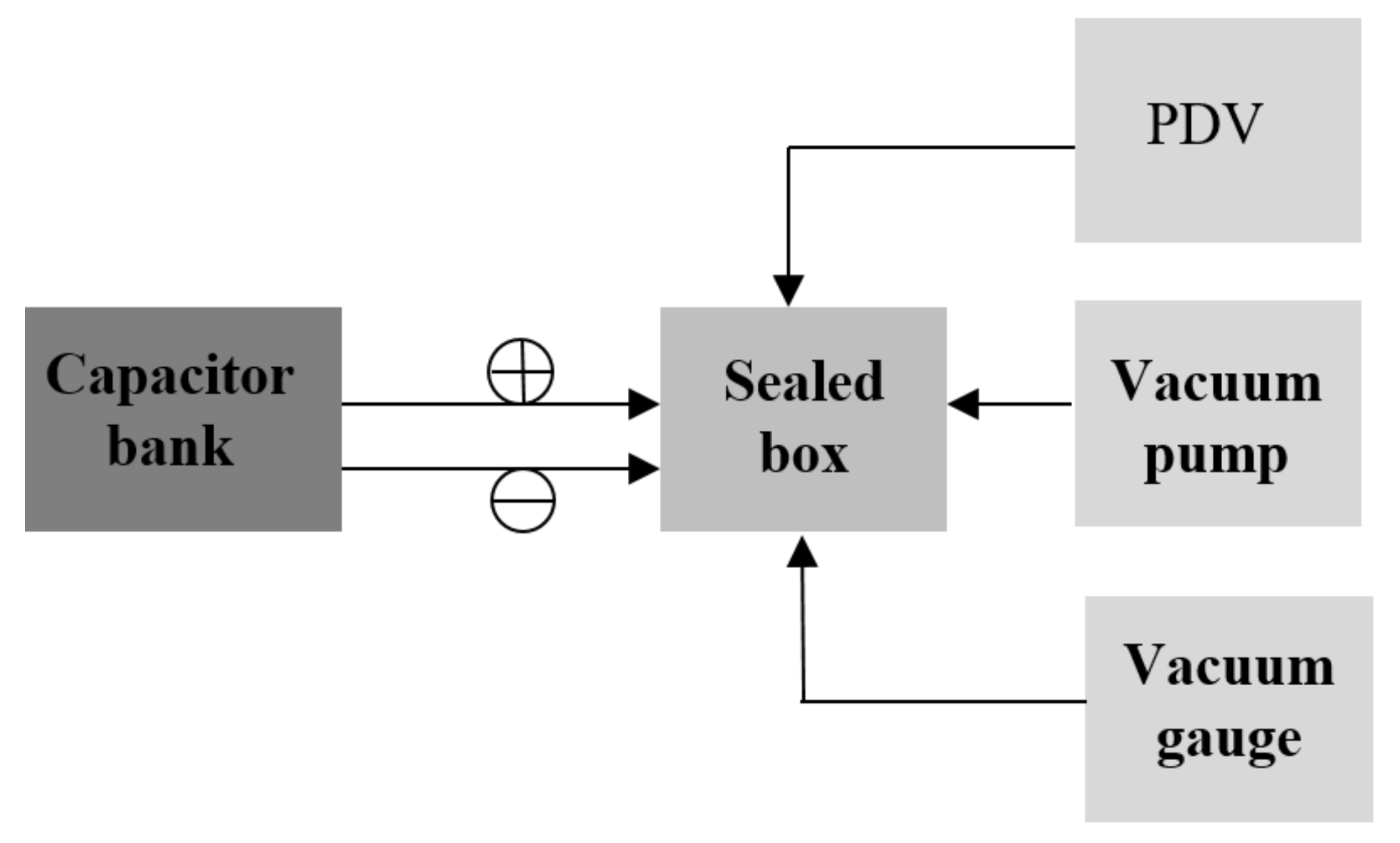
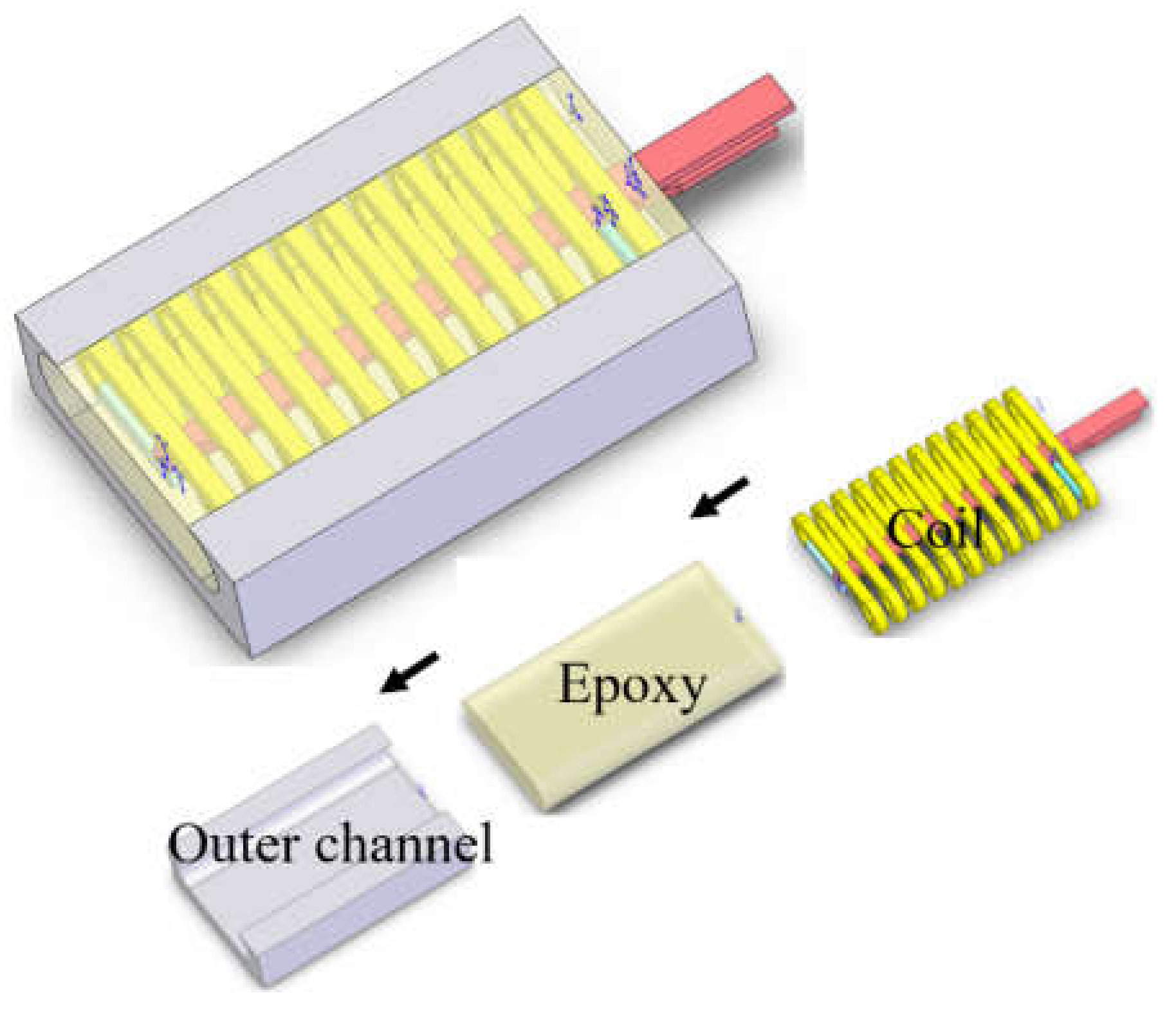
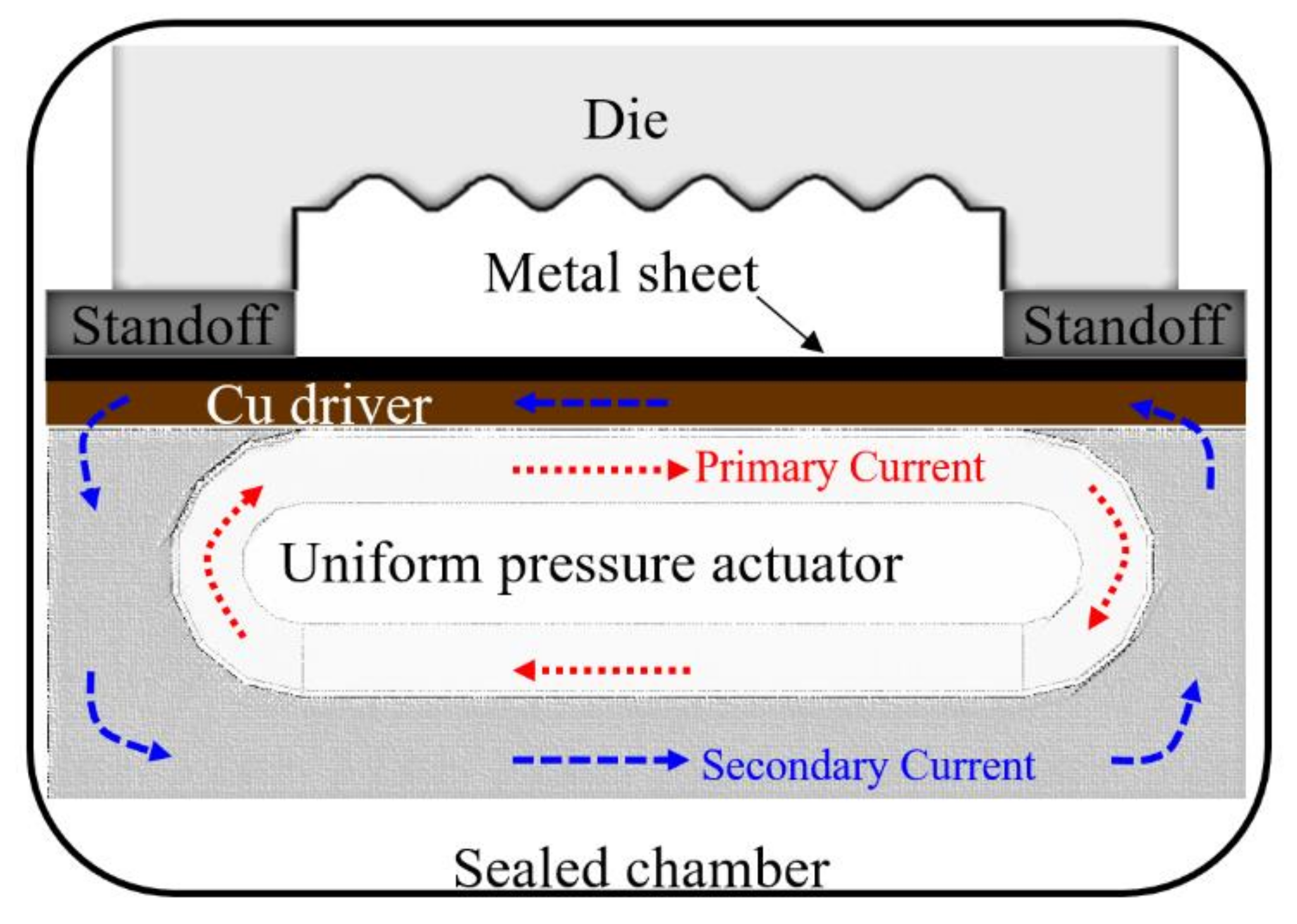
2. Experimental Setup
3. Results and Discussion
3.1. Experimental Results with the Bipolar Plate Die
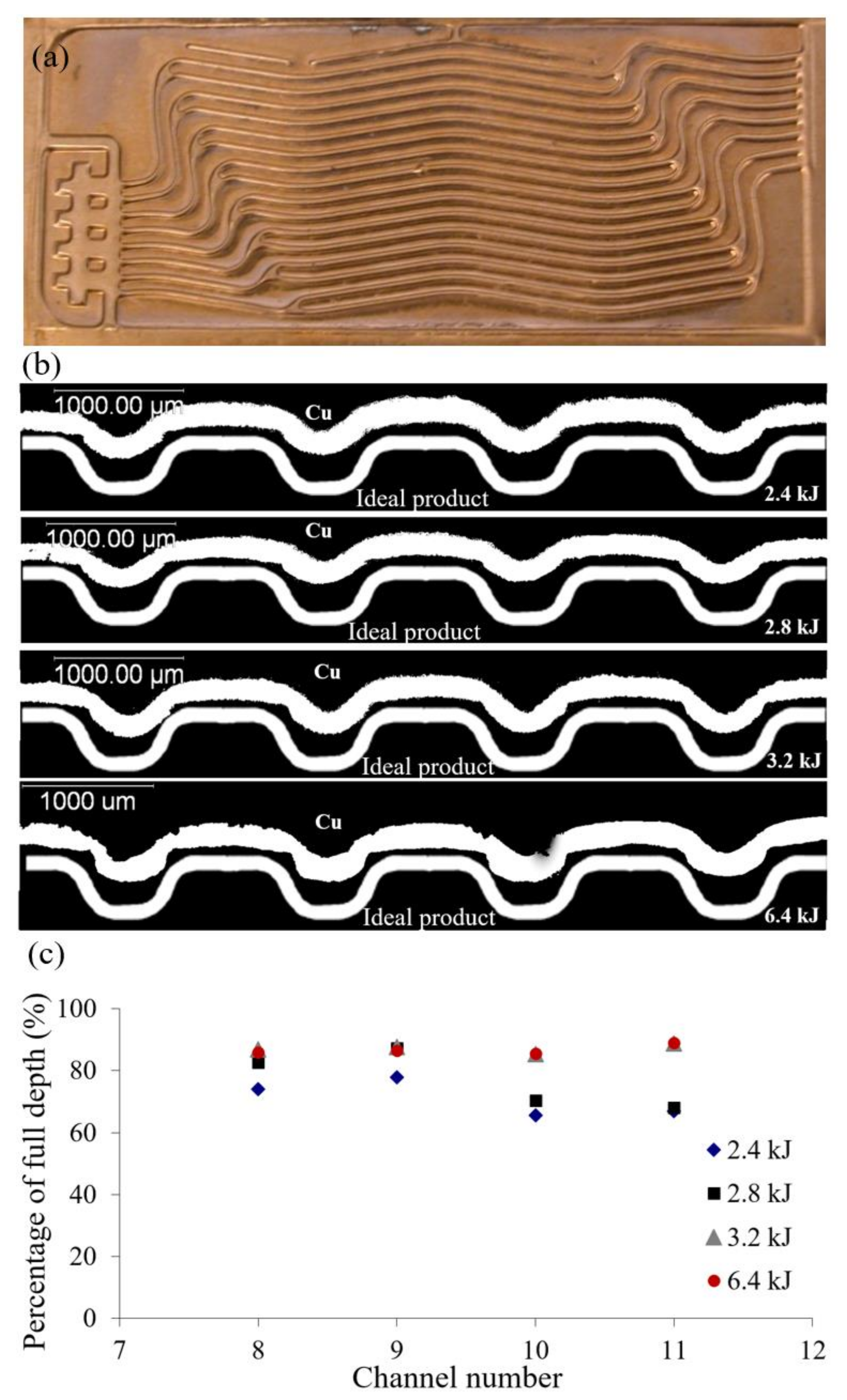
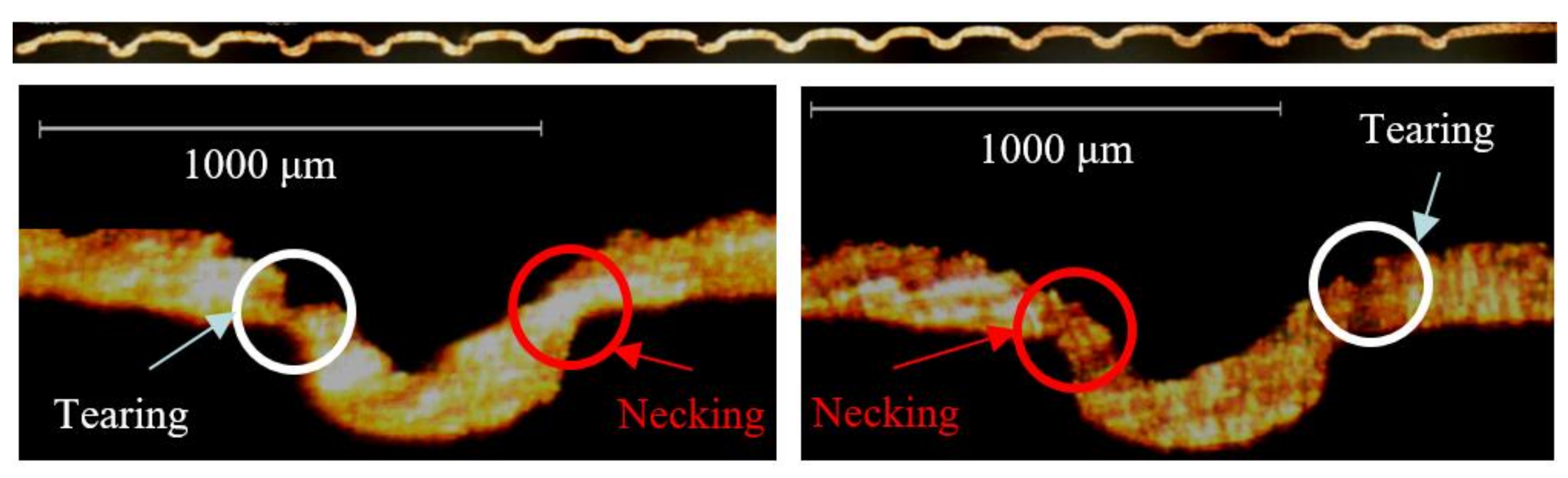
3.1.1. Cu110 as the Workpiece
3.1.2. Titanium as the Workpiece
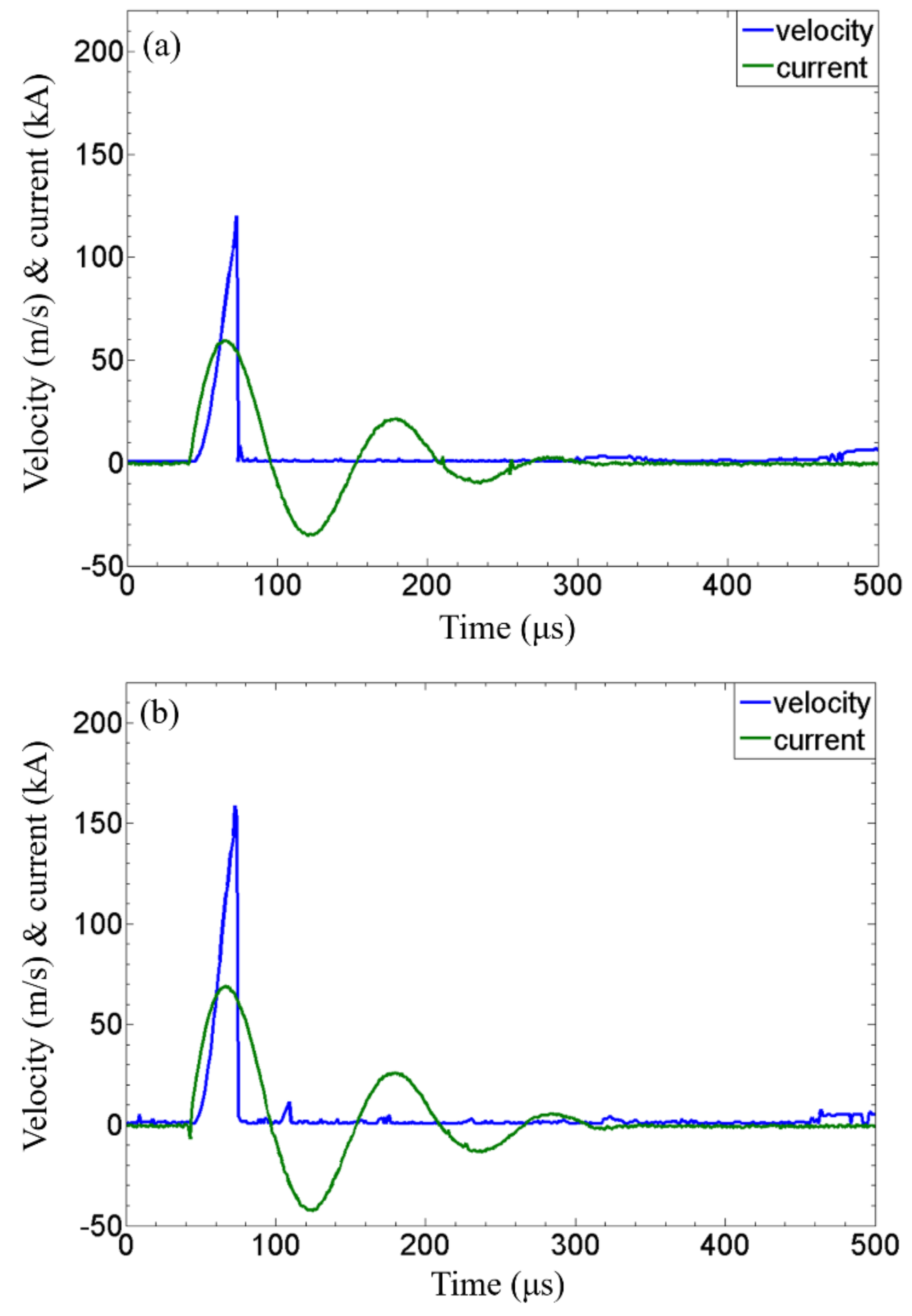
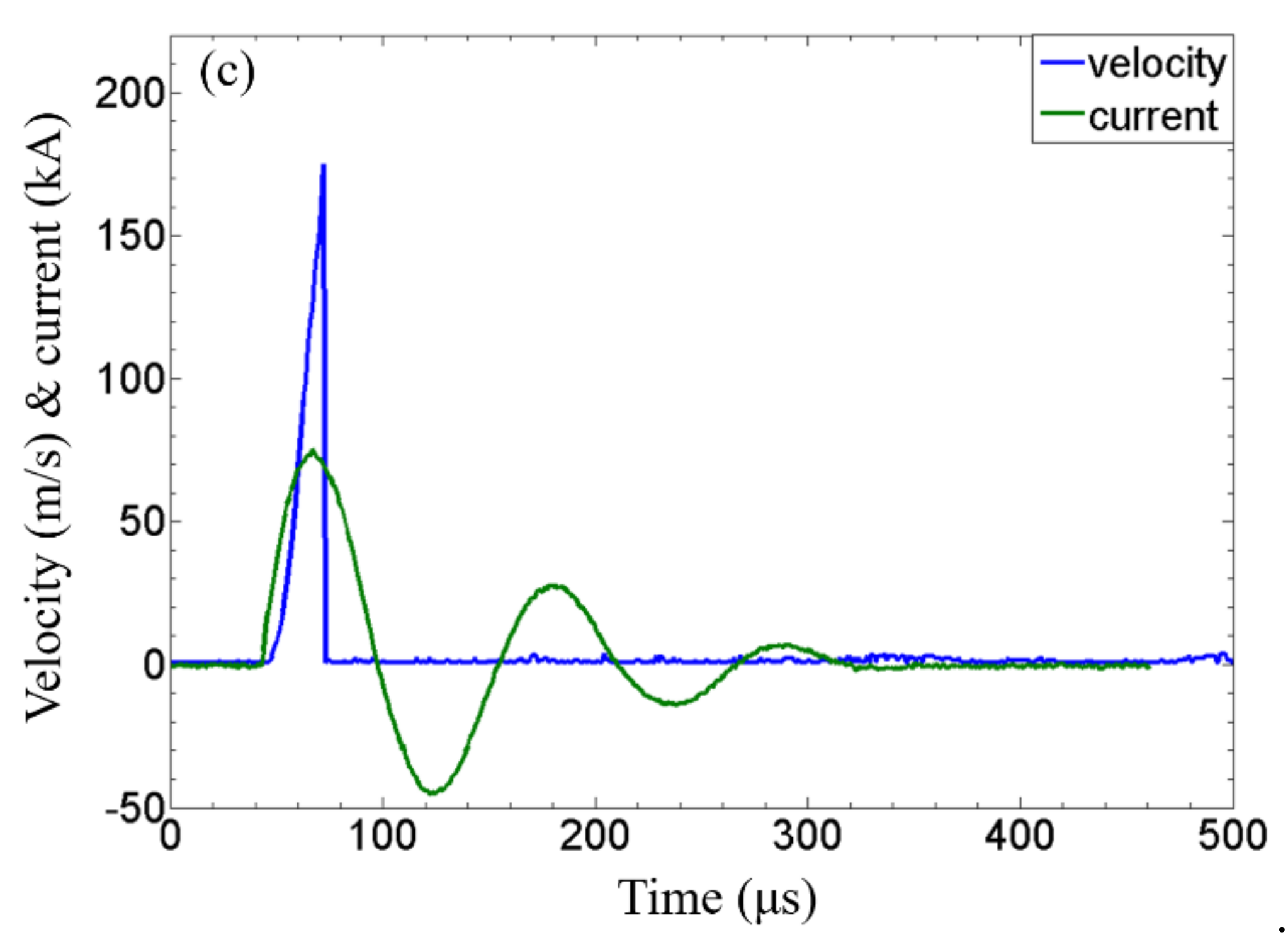
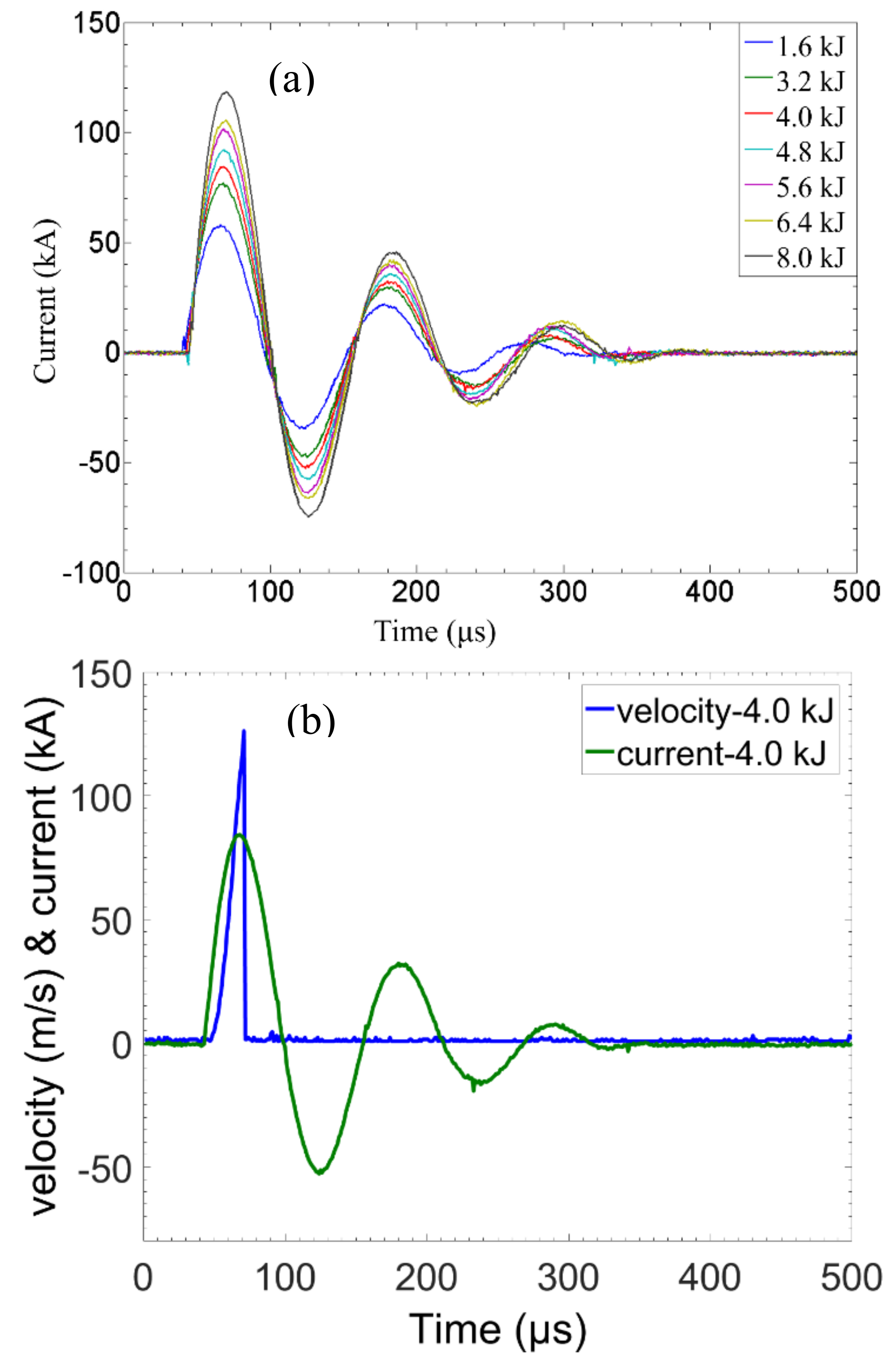
3.1.3. Primary Current and Flyer Velocity Measurement
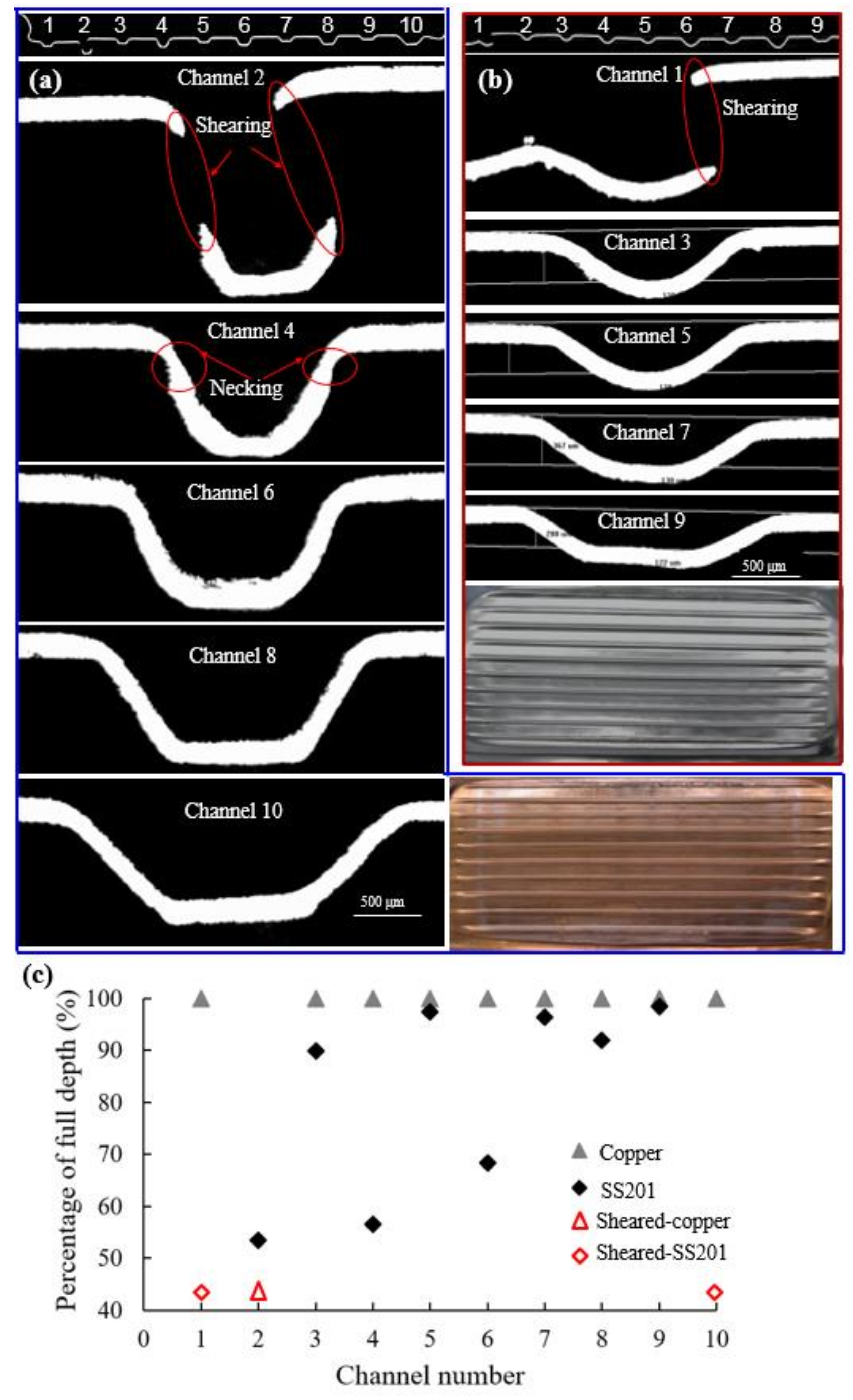
3.2 Experimental Results with 10-Channel Die
3.3. Discussion
4. Conclusions
- 1.
- With the current bipolar plate die, the maximum average channel depth with a Cu110 sheet was 86% at a capacitor bank energy 6.4 kJ, while the maximum average channel depth with a Ti sheet was 54% at a capacitor bank energy of 8.0 kJ.
- 2.
- For a Cu110 sheet, the increase of the capacitor bank energy from 3.2 kJ to 6.4 kJ resulted in the increase of the average depth percentage from 84% to 86%, but severe tearing and necking appeared at 6.4 kJ. For a Ti sheet, the increase of the capacitor bank energy from 6.4 kJ to 8.0 kJ caused the increase of the average depth percentage from 51% to 54%. For both metal sheets, the increase of the channel depth over the current maximum values would require much higher capacitor bank energies. Therefore, the current bipolar plate die would be optimized for full penetration with the magnetic pulse method.
- 3.
- Both the primary current and flyer velocity increased with the capacitor bank energy. When Cu110 was the driver, the primary current was not affected by the addition of Ti to the “flying part”, but the flyer velocity was reduced due to the weight increase of the “flying part”.
- 4.
- With the 10-channel die, a full penetration was achieved for channels with proper die parameters with both a Cu110 sheet and an SS201 sheet, which provided valuable information for the optimization of the bipolar plate die. The draft angle had a significant effect on the replication of the die surface. For a Cu110 sheet, the minimum draft angle was 23° for a channel with a depth of 0.762 mm and a width of 1 mm. For an SS201 sheet, the full replication was achieved for a channel with a depth of 0.381 mm, a width of 1 mm, and a draft angle of 90°.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Momirlan, M.; Veziroglu, T.N. Current status of hydrogen energy. Renew. Sustain. Energy Rev. 2002, 6, 141–179. [Google Scholar] [CrossRef]
- Cropper, M.A.J.; Geiger, S.; Jollie, D.M. Fuel cells: A survey of current developments. J. Power Sources 2004, 131, 57–61. [Google Scholar] [CrossRef]
- Hermann, A.; Chaudhuri, T.; Spagnol, P. Bipolar plates for PEM fuel cells: A review. Int. J. Hydrogen Energy 2005, 30, 1297–1302. [Google Scholar] [CrossRef]
- Bar-On, I.; Kirchain, R.; Roth, R. Technical cost analysis for PEM fuel cells. J. Power Sources 2002, 109, 71–75. [Google Scholar] [CrossRef]
- Steele, B.C.H.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Jeong, M.G.; Jin, C.K.; Hwang, G.W.; Kang, C.G. Formability evaluation of stainless steel bipolar plate considering draft angle of die and process parameters by rubber forming. Int. J. Precis. Eng. Manuf. 2014, 15, 913–919. [Google Scholar] [CrossRef]
- Jin, C.K.; Jeong, M.G.; Kang, C.G. Fabrication of titanium bipolar plates by rubber forming and performance of single cell using TiN-coated titanium bipolar plates. Int. J. Hydrogen Energy 2013, 39, 21480–21488. [Google Scholar] [CrossRef]
- Tawfik, H.; Hung, Y.; Mahajan, D. Metal bipolar plates for PEM fuel cell-A review. J. Power Sources 2007, 163, 755–767. [Google Scholar] [CrossRef]
- Elyasi, M.; Khatir, F.A.; Hosseinzadeh, M. Manufacturing metallic bipolar plate fuel cells through rubber pad forming process. Int. J. Adv. Manuf. Technol. 2017, 89, 3257–3269. [Google Scholar] [CrossRef]
- Elyasi, M.; Ghadikolaee, H.T.; Hosseinzadeh, M. Fabrication of metallic bipolar plates in PEM fuel cell using semi-stamp rubber forming process. Int. J. Adv. Manuf. Technol. 2017, 92, 765–776. [Google Scholar] [CrossRef]
- Kamal, M.; Daehn, G.S. A Uniform Pressure Electromagnetic Actuator for Forming Flat Sheets. J. Manuf. Sci. Eng. 2007, 129, 369–379. [Google Scholar] [CrossRef]
- Daehn, G. High velocity metal forming. In Metalworking: Sheet Forming; ASM Handbook Volume 14B; ASM International: Materials Park, OH, USA, 2006; pp. 405–418. [Google Scholar]
- Balanethiram, V.S.; Hu, X.; Altynova, M.; Daehn, G.S. Hyperplasticity: Enhanced formability at high rates. J. Mater. Process. Technol. 1994, 45, 595–600. [Google Scholar] [CrossRef]
- Shang, J.; Daehn, G. Electromagnetically assisted sheet metal stamping. J. Mater. Process. Technol. 2011, 211, 868–874. [Google Scholar] [CrossRef]
- Wang, H.; Vivek, A.; Wang, Y.; Viswanathan, G.; Daehn, G. High strain rate embossing with copper plate. Int. J. Mater. Form. 2017, 10, 697–705. [Google Scholar] [CrossRef]
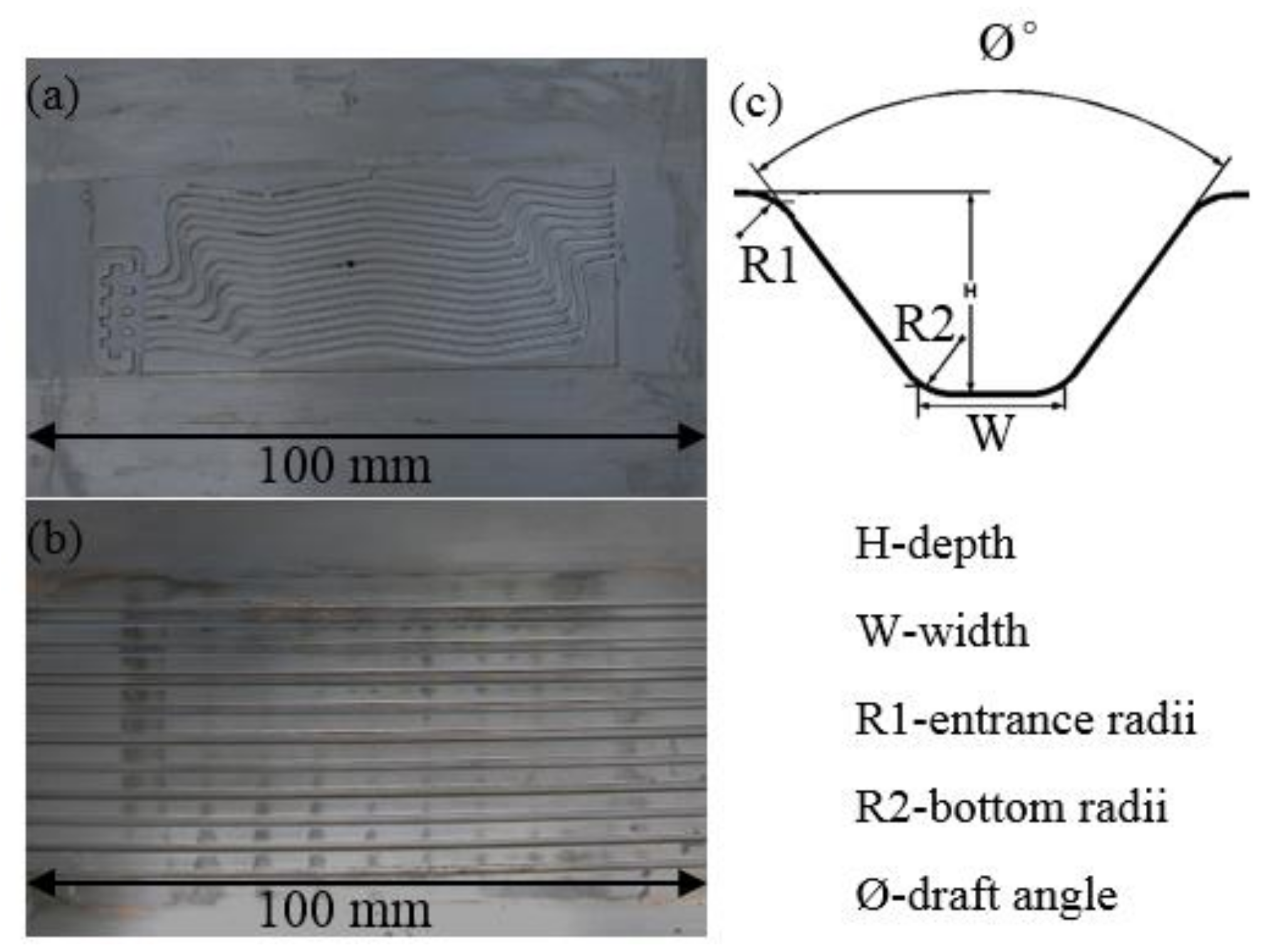

| Number | Depth(mm) | Width(mm) | Entrance Radii | Bottom Radii | Draft Angle |
|---|---|---|---|---|---|
| 17 channels | 0.325 | 0.8 | 0.2° | 0.2° | 40° |
| Channel 1 | 0.381 | 1.0 | 0.2° | 0.2° | 0° |
| Channel 2 | 0.762 | 1.0 | 0.2° | 0.2° | 0° |
| Channel 3 | 0.381 | 1.0 | 0.2° | 0.2° | 23° |
| Channel 4 | 0.762 | 1.0 | 0.2° | 0.2° | 23° |
| Channel 5 | 0.381 | 1.0 | 0.2° | 0.2° | 45° |
| Channel 6 | 0.762 | 1.0 | 0.2° | 0.2° | 45° |
| Channel 7 | 0.381 | 1.0 | 0.2° | 0.2° | 68° |
| Channel 8 | 0.762 | 1.0 | 0.2° | 0.2° | 68° |
| Channel 9 | 0.381 | 1.0 | 0.2° | 0.2° | 90° |
| Channel 10 | 0.762 | 1.0 | 0.2° | 0.2° | 90° |
| Material | Cr | Cu | Fe | Mn | Si | C | Ni | Ti |
|---|---|---|---|---|---|---|---|---|
| Cu 110 | - | 99.9 | - | - | - | - | - | |
| Grade 2 Ti | - | - | 0.3 | - | - | - | - | 99.2 |
| SS 201 | 16.0–18.0 | - | Balance | 5.5–7.5 | <1.0 | <0.15 | 3.5–5.5 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, Y. Investigation of Bipolar Plate Forming with Various Die Configurations by Magnetic Pulse Method. Metals 2019, 9, 453. https://doi.org/10.3390/met9040453
Wang H, Wang Y. Investigation of Bipolar Plate Forming with Various Die Configurations by Magnetic Pulse Method. Metals. 2019; 9(4):453. https://doi.org/10.3390/met9040453
Chicago/Turabian StyleWang, Huimin, and Yuliang Wang. 2019. "Investigation of Bipolar Plate Forming with Various Die Configurations by Magnetic Pulse Method" Metals 9, no. 4: 453. https://doi.org/10.3390/met9040453
APA StyleWang, H., & Wang, Y. (2019). Investigation of Bipolar Plate Forming with Various Die Configurations by Magnetic Pulse Method. Metals, 9(4), 453. https://doi.org/10.3390/met9040453





