A Review of Multi-Scale Computational Modeling Tools for Predicting Structures and Properties of Multi-Principal Element Alloys
Abstract
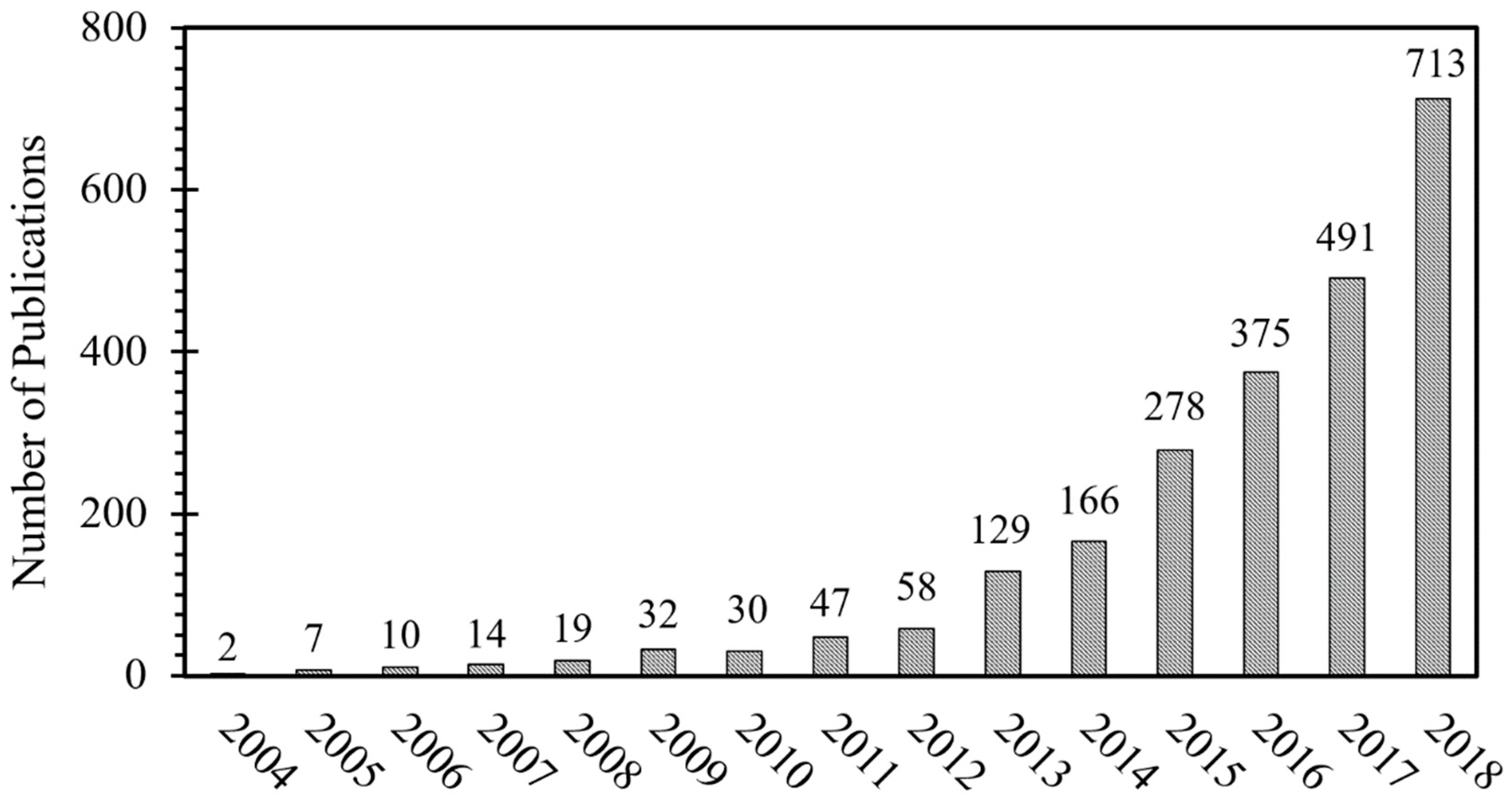
1. Introduction
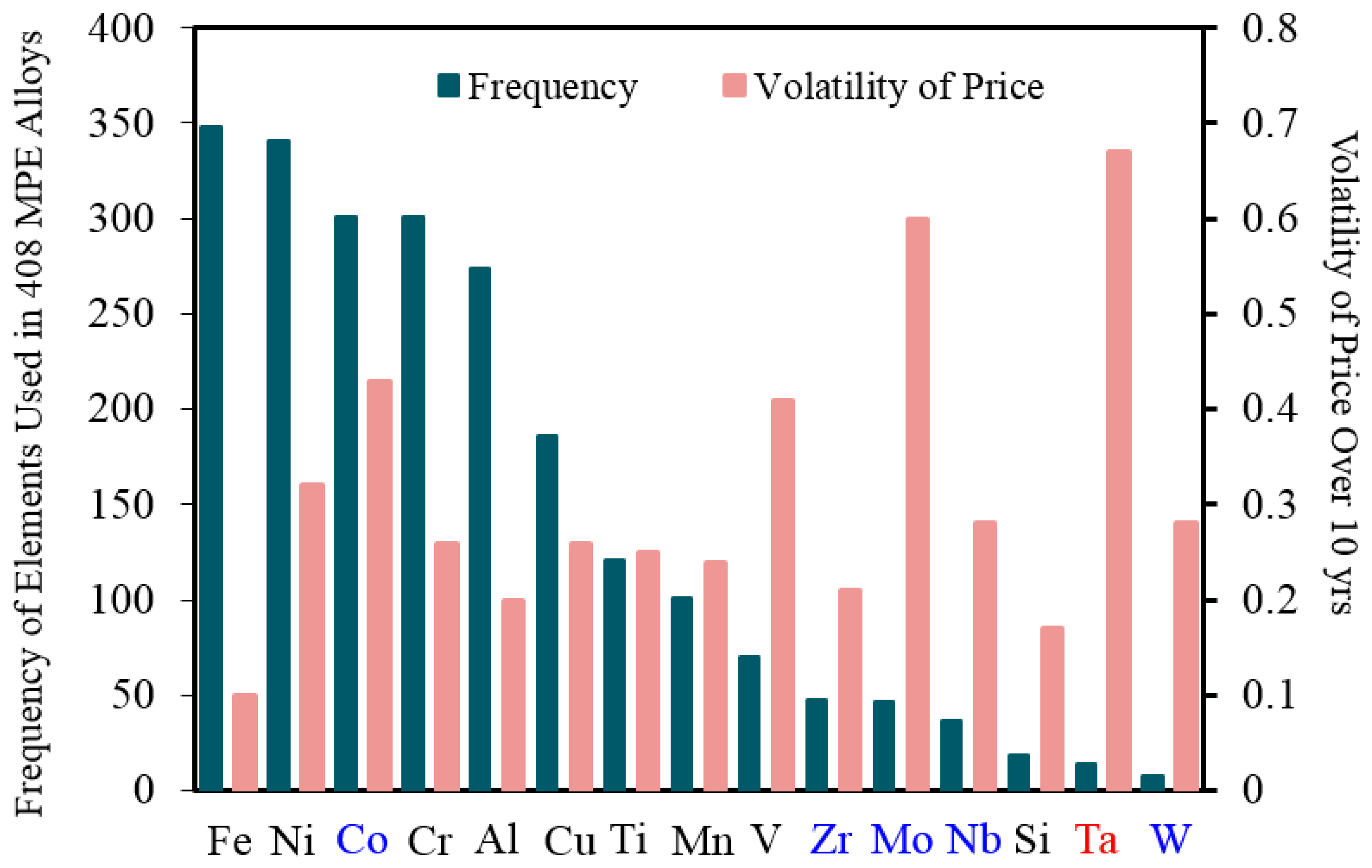
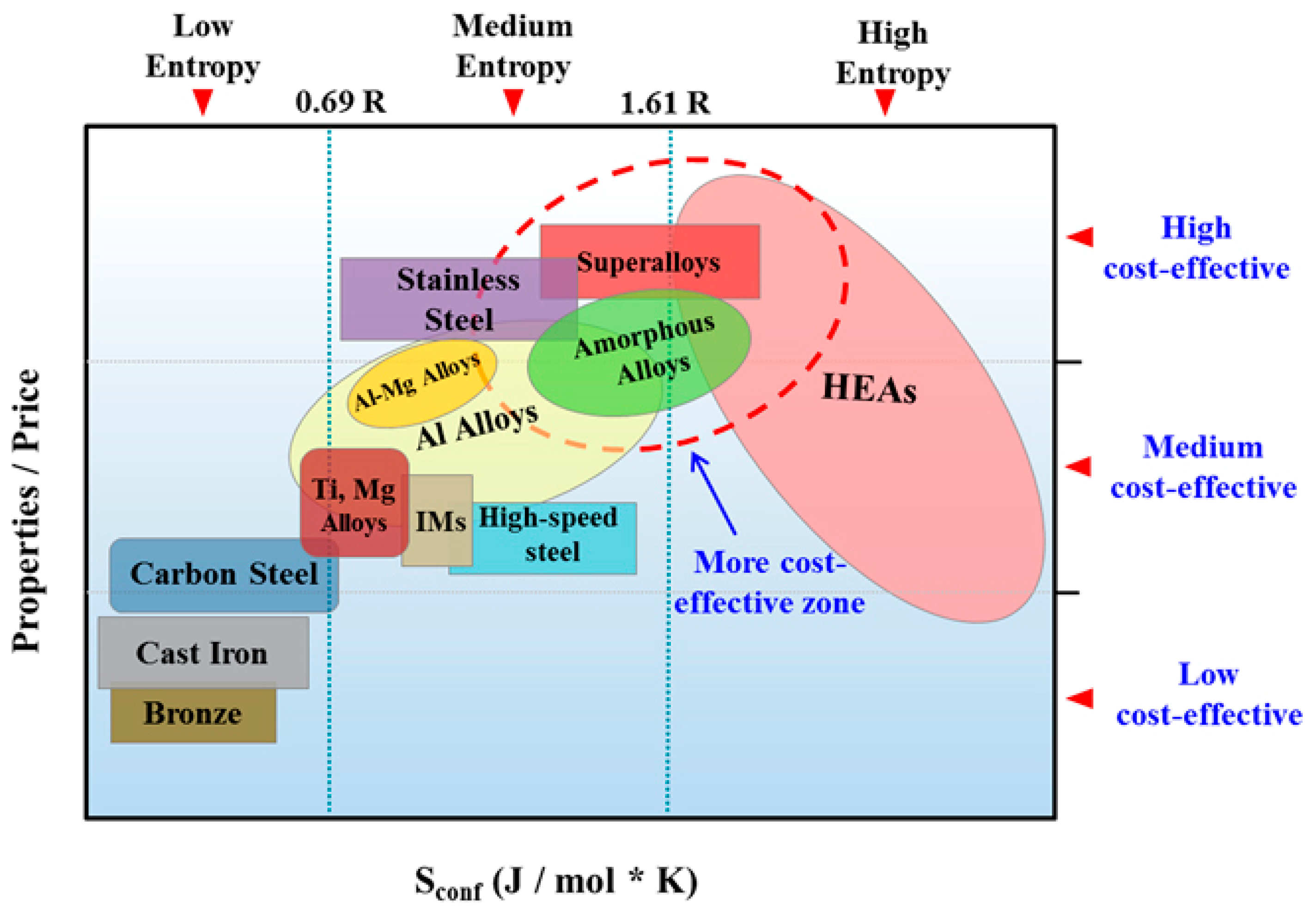
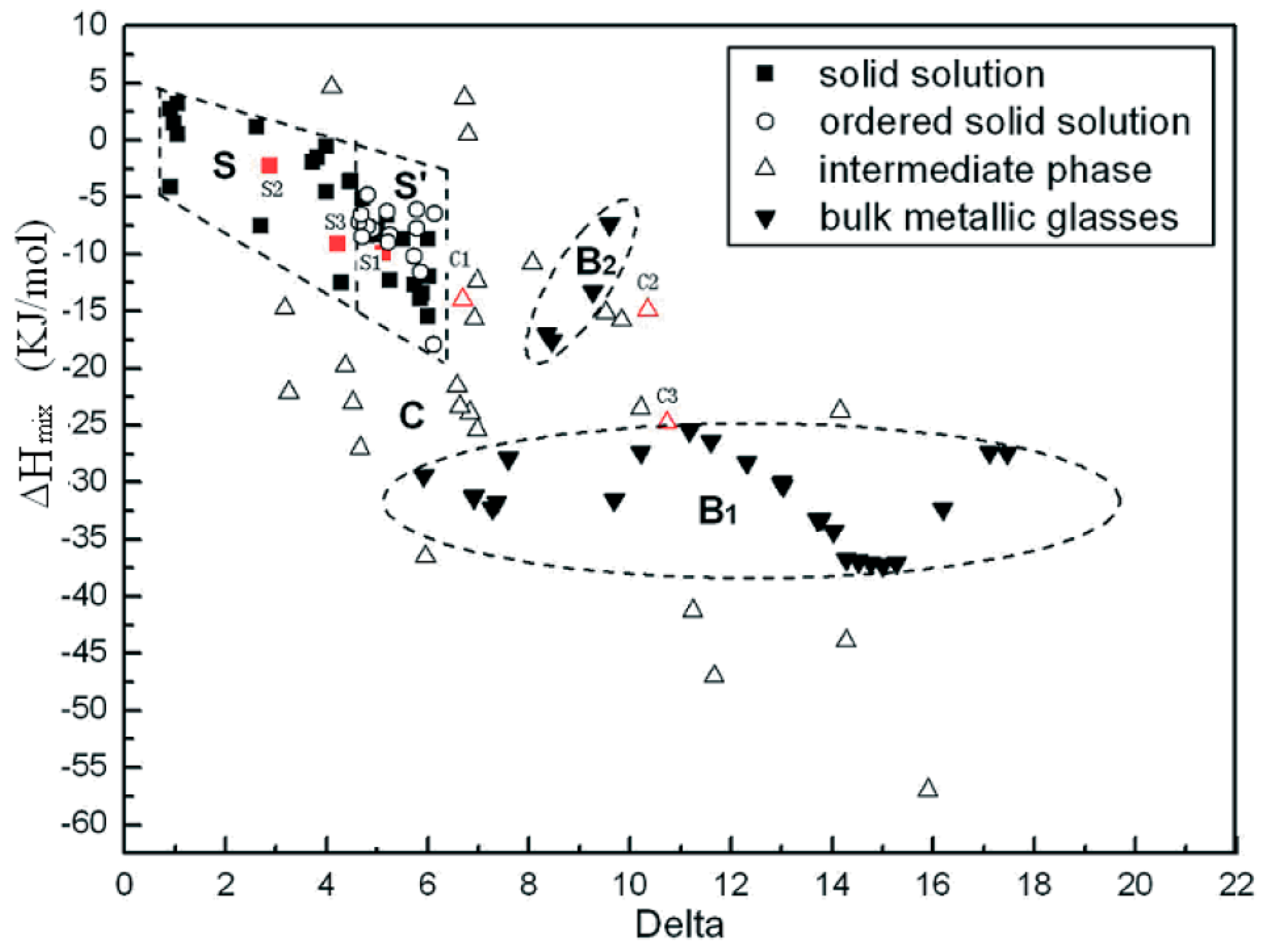
2. Phase Equilibria and Crystal Structures of MPE Alloys
3. Properties of MPE Alloys
3.1. Mechanical Properties
3.1.1. Elastic Properties
3.1.2. Plastic Deformation
3.1.3. Solute Strengthening
3.2. Thermo-Chemical Properties
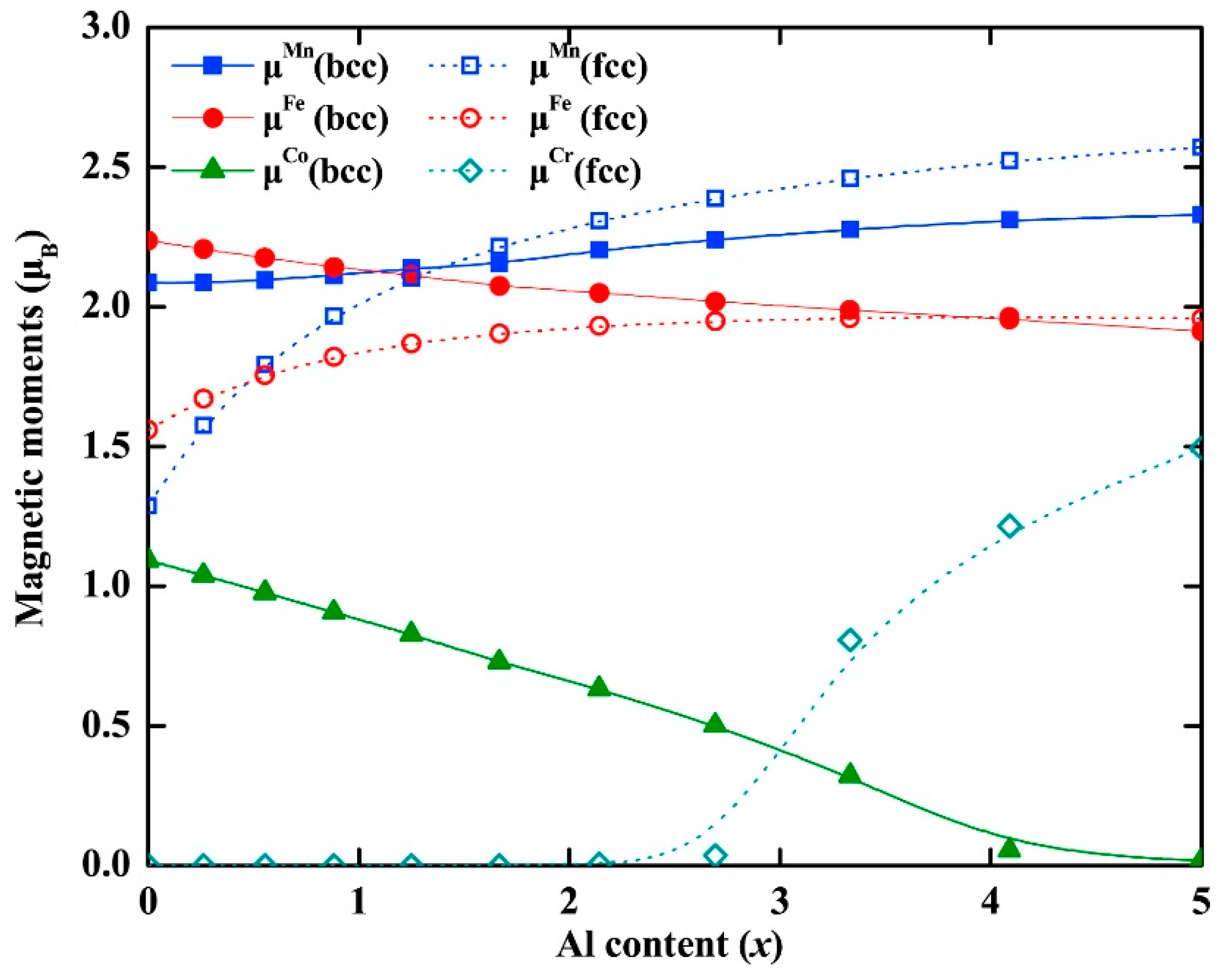
3.3. Magnetic Properties
4. Summary
Author Contributions
Conflicts of Interest
References
- Miracle, D.; Senkov, O. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.-W.; Ranganathan, S. High-Entropy Alloys; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Zhang, C.; Zhang, F.; Chen, S.; Cao, W. Computational thermodynamics aided high-entropy alloy design. JOM 2012, 64, 839–845. [Google Scholar] [CrossRef]
- Yeh, J.-W. Alloy Design Strategies and Future Trends in High-Entropy Alloys. JOM 2013, 65, 1759–1771. [Google Scholar] [CrossRef]
- Tsai, K.-Y.; Tsai, M.-H.; Yeh, J.-W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater. 2013, 61, 4887–4897. [Google Scholar] [CrossRef]
- Wu, Z.; Parish, C.; Bei, H. Nano-twin mediated plasticity in carbon-containing FeNiCoCrMn high entropy alloys. J. Alloy. Compd. 2015, 647, 815–822. [Google Scholar] [CrossRef]
- Wang, Z.; Baker, I. Interstitial strengthening of a fcc FeNiMnAlCr high entropy alloy. Mater. Lett. 2016, 180, 153–156. [Google Scholar] [CrossRef]
- Li, Z.; Tasan, C.C.; Springer, H.; Gault, B.; Raabe, D. Interstitial atoms enable joint twinning and transformation induced plasticity in strong and ductile high-entropy alloys. Sci. Rep. 2017, 7, 40704. [Google Scholar] [CrossRef]
- Laurent-Brocq, M.; Sauvage, X.; Akhatova, A.; Perrière, L.; Leroy, E.; Champion, Y. Precipitation and Hardness of Carbonitrides in a CrMnFeCoNi High Entropy Alloy. Adv. Eng. Mater. 2017, 19. [Google Scholar] [CrossRef]
- Beyramali Kivy, M.; Kriewall, C.S.; Zaeem, M.A. Formation of chromium-iron carbide by carbon diffusion in Al X CoCrFeNiCu high-entropy alloys. Mater. Res. Lett. 2018, 6, 321–326. [Google Scholar] [CrossRef]
- Fu, X.; Schuh, C.; Olivetti, E. Materials selection considerations for high entropy alloys. Scr. Mater. 2017, 138, 145–150. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, Q.; Zhao, Y.; He, Q.; Lu, J.; Yang, Y. Elemental segregation in solid-solution high-entropy alloys: Experiments and modeling. J. Alloy. Compd. 2016, 681, 167–174. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, X.; Ma, J.; Lu, Z.; Zhao, Y. Compositional gradient films constructed by sputtering in a multicomponent Ti–Al–(Cr, Fe, Ni) system. J. Mater. Res. 2018, 33, 3330–3338. [Google Scholar] [CrossRef]
- Sheng, G.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Natl. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar]
- Pickering, E.; Jones, N.G. High-entropy alloys: A critical assessment of their founding principles and future prospects. Int. Mater. Rev. 2016, 61, 183–202. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-Solution Phase Formation Rules for Multi-component Alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Mizutani, U. The Hume-Rothery Rules for Structurally Complex Alloy Phases, in Surface Properties and Engineering of Complex Intermetallics; World Scientific: Singapore, 2010; pp. 323–399. [Google Scholar]
- Guo, S.; Ng, C.; Lu, J.; Liu, C. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Tsai, M.-H.; Tsai, K.-Y.; Tsai, C.-W.; Lee, C.; Juan, C.-C.; Yeh, J.-W. Criterion for sigma phase formation in Cr-and V-containing high-entropy alloys. Mater. Res. Lett. 2013, 1, 207–212. [Google Scholar] [CrossRef]
- Tsai, M.-H.; Yeh, J.-W. High-entropy alloys: A critical review. Mater. Res. Lett. 2014, 2, 107–123. [Google Scholar] [CrossRef]
- Morral, J.; Chen, S.-L. High Entropy Alloys, Miscibility Gaps and the Rose Geometry. J. Phase Equilib. Diffus. 2017, 38, 319–331. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams. With Special Reference to Refractory Metals; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Kroupa, A. Modelling of phase diagrams and thermodynamic properties using Calphad method—Development of thermodynamic databases. Comput. Mater. Sci. 2013, 66, 3–13. [Google Scholar] [CrossRef]
- Kattner, U.R. The thermodynamic modeling of multicomponent phase equilibria. JOM 1997, 49, 14–19. [Google Scholar] [CrossRef]
- Bale, C.; Bélisle, E.; Chartrand, P.; Decterov, S.; Eriksson, G.; Hack, K.; Jung, I.-H.; Kang, Y.-B.; Melançon, J.; Pelton, A. FactSage thermochemical software and databases—Recent developments. Calphad 2009, 33, 295–311. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. First principles study of structural and thermodynamic properties of zirconia. Mater. Today Proc. 2014, 1, 44–54. [Google Scholar] [CrossRef]
- Chen, H.-L.; Mao, H.; Chen, Q. Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 2018, 210, 279–290. [Google Scholar] [CrossRef]
- CompuTherm, L. Pandat 8.0-Phase Diagram Calculation Software for Multi-Component Systems; CompuTherm LLC: Madison, WI, USA, 2008; Volume 53719. [Google Scholar]
- Idury, K.S.; Murty, B.; Bhatt, J. Thermodynamic modeling and composition design for the formation of Zr–Ti–Cu–Ni–Al high entropy bulk metallic glasses. Intermetallics 2015, 65, 42–50. [Google Scholar] [CrossRef]
- Idury, K.S.; Murty, B.; Bhatt, J. Identifying non-equiatomic high entropy bulk metallic glass formers through thermodynamic approach: A theoretical perspective. J. Non-Cryst. Solids 2016, 450, 164–173. [Google Scholar] [CrossRef]
- Tang, Z.; Gao, M.C.; Diao, H.; Yang, T.; Liu, J.; Zuo, T.; Zhang, Y.; Lu, Z.; Cheng, Y.; Zhang, Y. Aluminum alloying effects on lattice types, microstructures, and mechanical behavior of high-entropy alloys systems. JOM 2013, 65, 1848–1858. [Google Scholar] [CrossRef]
- Sonkusare, R.; Janani, P.D.; Gurao, N.; Sarkar, S.; Sen, S.; Pradeep, K.; Biswas, K. Phase equilibria in equiatomic CoCuFeMnNi high entropy alloy. Mater. Chem. Phys. 2018, 210, 269–278. [Google Scholar] [CrossRef]
- Saal, J.E.; Berglund, I.S.; Sebastian, J.T.; Liaw, P.K.; Olson, G.B. Equilibrium high entropy alloy phase stability from experiments and thermodynamic modeling. Scr. Mater. 2018, 146, 5–8. [Google Scholar] [CrossRef]
- Yao, H.; Qiao, J.; Gao, M.; Hawk, J.; Ma, S.; Zhou, H.; Zhang, Y. NbTaV-(Ti, W) refractory high-entropy alloys: Experiments and modeling. Mater. Sci. Eng. A 2016, 674, 203–211. [Google Scholar] [CrossRef]
- Feng, R.; Gao, M.C.; Lee, C.; Mathes, M.; Zuo, T.; Chen, S.; Hawk, J.A.; Zhang, Y.; Liaw, P.K. Design of light-weight high-entropy alloys. Entropy 2016, 18, 333. [Google Scholar] [CrossRef]
- Stepanov, N.; Yurchenko, N.Y.; Skibin, D.; Tikhonovsky, M.; Salishchev, G. Structure and mechanical properties of the AlCrxNbTiV (x = 0, 0.5, 1, 1.5) high entropy alloys. J. Alloy. Compd. 2015, 652, 266–280. [Google Scholar] [CrossRef]
- Gwalani, B.; Gorsse, S.; Choudhuri, D.; Styles, M.; Zheng, Y.; Mishra, R.S.; Banerjee, R. Modifying transformation pathways in high entropy alloys or complex concentrated alloys via thermo-mechanical processing. Acta Mater. 2018, 153, 169–185. [Google Scholar] [CrossRef]
- Abu-Odeh, A.; Galvan, E.; Kirk, T.; Mao, H.; Chen, Q.; Mason, P.; Malak, R.; Arróyave, R. Efficient exploration of the High Entropy Alloy composition-phase space. Acta Mater. 2018. [Google Scholar] [CrossRef]
- Tancret, F.; Toda-Caraballo, I.; Menou, E.; Díaz-Del, P.E.J.R. Designing high entropy alloys employing thermodynamics and Gaussian process statistical analysis. Mater. Des. 2017, 115, 486–497. [Google Scholar] [CrossRef]
- Gorsse, S.; Tancret, F. Current and emerging practices of CALPHAD toward the development of high entropy alloys and complex concentrated alloys. J. Mater. Res. 2018, 33, 2899–2923. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, S.; Gao, M.C.; Zhang, C.; Zhang, T.; Yang, H.; Wang, Z.; Qiao, J. Tribological properties of AlCrCuFeNi2 high-entropy alloy in different conditions. Metall. Mater. Trans. A 2016, 47, 3312–3321. [Google Scholar] [CrossRef]
- Haase, C.; Tang, F.; Wilms, M.B.; Weisheit, A.; Hallstedt, B. Combining thermodynamic modeling and 3D printing of elemental powder blends for high-throughput investigation of high-entropy alloys–Towards rapid alloy screening and design. Mater. Sci. Eng. A 2017, 688, 180–189. [Google Scholar] [CrossRef]
- Arslan, H.; Dogan, A. Thermodynamic investigations on the component dependences of high-entropy alloys. Russ. J. Phys. Chem. A 2016, 90, 2339–2345. [Google Scholar] [CrossRef]
- Eshed, E.; Larianovsky, N.; Kovalevsky, A.; Popov, V., Jr.; Gorbachev, I.; Popov, V.; Katz-Demyanetz, A. Microstructural Evolution and Phase Formation in 2nd-Generation Refractory-Based High Entropy Alloys. Materials 2018, 11, 175. [Google Scholar] [CrossRef] [PubMed]
- Beyramali Kivy, M.; Zaeem, M.A.; Lekakh, S. Investigating phase formations in cast AlFeCoNiCu high entropy alloys by combination of computational modeling and experiments. Mater. Des. 2017, 127, 224–232. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Wróbel, J.; Nguyen-Manh, D.; Perez, P.; Rivera-Díaz-del-Castillo, P. Simulation and modeling in high entropy alloys. JOM 2017, 69, 2137–2149. [Google Scholar] [CrossRef]
- Kresse, G.; Marsman, O.; Furthmuller, J. VASP the Guide. Available online: http://cms.mpi.univie.ac.at/vasp/vasp.pdf (accessed on 24 April 2016).
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Ma, D.; Grabowski, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 2015, 100, 90–97. [Google Scholar] [CrossRef]
- Niu, C.; Zaddach, A.; Koch, C.; Irving, D. First principles exploration of near-equiatomic NiFeCrCo high entropy alloys. J. Alloy. Compd. 2016, 672, 510–520. [Google Scholar] [CrossRef]
- Yalamanchili, K.; Wang, F.; Schramm, I.; Andersson, J.; Jöesaar, M.J.; Tasnadi, F.; Muecklich, F.; Ghafoor, N.; Odén, M. Exploring the high entropy alloy concept in (AlTiVNbCr) N. Thin Solid Films 2017, 636, 346–352. [Google Scholar] [CrossRef]
- Jiang, C.; Uberuaga, B.P. Efficient ab initio modeling of random multicomponent alloys. Phys. Rev. Lett. 2016, 116, 105501. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Vitos, L. Predicting single phase CrMoWX high entropy alloys from empirical relations in combination with first-principles calculations. Intermetallics 2017, 83, 9–16. [Google Scholar] [CrossRef]
- Li, Z.; Körmann, F.; Grabowski, B.; Neugebauer, J.; Raabe, D. Ab initio assisted design of quinary dual-phase high-entropy alloys with transformation-induced plasticity. Acta Mater. 2017, 136, 262–270. [Google Scholar] [CrossRef]
- Heidelmann, M.; Feuerbacher, M.; Ma, D.; Grabowski, B. Structural anomaly in the high-entropy alloy ZrNbTiTaHf. Intermetallics 2016, 68, 11–15. [Google Scholar] [CrossRef]
- Mu, Y.; Liu, H.; Liu, Y.; Zhang, X.; Jiang, Y.; Dong, T. An ab initio and experimental studies of the structure, mechanical parameters and state density on the refractory high-entropy alloy systems. J. Alloy. Compd. 2017, 714, 668–680. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, S.; Jin, K.; Bei, H.; Popov, D.; Park, C.; Neuefeind, J.C.; Weber, W.J.; Zhang, Y. Pressure-induced fcc to hcp phase transition in Ni-based high entropy solid solution alloys. Appl. Phys. Lett. 2017, 110, 011902. [Google Scholar] [CrossRef]
- Tian, F.; Delczeg, L.; Chen, N.; Varga, L.K.; Shen, J.; Vitos, L. Structural stability of NiCoFeCrAl x high-entropy alloy from ab initio theory. Phys. Rev. B 2013, 88, 085128. [Google Scholar] [CrossRef]
- Middleburgh, S.; King, D.; Lumpkin, G.; Cortie, M.; Edwards, L. Segregation and migration of species in the CrCoFeNi high entropy alloy. J. Alloy. Compd. 2014, 599, 179–182. [Google Scholar] [CrossRef]
- Takaki, T.; Ohno, M.; Shibuta, Y.; Sakane, S.; Shimokawabe, T.; Aoki, T. Two-dimensional phase-field study of competitive grain growth during directional solidification of polycrystalline binary alloy. J. Cryst. Growth 2016, 442, 14–24. [Google Scholar] [CrossRef]
- Leong, Z.; Wróbel, J.S.; Dudarev, S.L.; Goodall, R.; Todd, I.; Nguyen-Manh, D. The effect of electronic structure on the phases present in high entropy alloys. Sci. Rep. 2017, 7, 39803. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, M.; Rodriguez, G.; Bozzolo, G.; Mosca, H. Melting temperature of CoCrFeNiMn high-entropy alloys. Comput. Mater. Sci. 2018, 148, 69–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Stocks, G.M.; Jin, K.; Lu, C.; Bei, H.; Sales, B.C.; Wang, L.; Béland, L.K.; Stoller, R.E.; Samolyuk, G.D. Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat. Commun. 2015, 6, 8736. [Google Scholar] [CrossRef] [PubMed]
- Pielnhofer, F.; Schöneich, M.; Lorenz, T.; Yan, W.; Nilges, T.; Weihrich, R.; Schmidt, P. A Rational Approach to IrPTe–DFT and CalPhaD Studies on Phase Stability, Formation, and Structure of IrPTe. Z. Anorg. Allg. Chem. 2015, 641, 1099–1105. [Google Scholar] [CrossRef]
- Mathieu, R.; Dupin, N.; Crivello, J.-C.; Yaqoob, K.; Breidi, A.; Fiorani, J.-M.; David, N.; Joubert, J.-M. CALPHAD description of the Mo–Re system focused on the sigma phase modeling. Calphad 2013, 43, 18–31. [Google Scholar] [CrossRef]
- Bigdeli, S. Developing the Third Generation of Calphad Databases: What Can ab-Initio Contribute? KTH Royal Institute of Technology: Stockholm, Sweden, 2017. [Google Scholar]
- Ikeda, Y.; Grabowski, B.; Körmann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2018, 147, 464–511. [Google Scholar] [CrossRef]
- Yao, Q.; Shang, S.-L.; Wang, K.; Liu, F.; Wang, Y.; Wang, Q.; Lu, T.; Liu, Z.-K. Phase stability, elastic, and thermodynamic properties of the L1 2 (Co, Ni) 3 (Al, Mo, Nb) phase from first-principles calculations. J. Mater. Res. 2017, 32, 2100–2108. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Guo, S.; Qiao, J.; Hawk, J. High-entropy alloys in hexagonal close-packed structure. Metall. Mater. Trans. A 2016, 47, 3322–3332. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Yang, S.; Guo, S. Senary refractory high-entropy alloy HfNbTaTiVZr. Metall. Mater. Trans. A 2016, 47, 3333–3345. [Google Scholar] [CrossRef]
- Choi, W.-M.; Jo, Y.H.; Sohn, S.S.; Lee, S.; Lee, B.-J. Understanding the physical metallurgy of the CoCrFeMnNi high-entropy alloy: An atomistic simulation study. npj Comput. Mater. 2018, 4, 1. [Google Scholar] [CrossRef]
- Sharma, A.; Deshmukh, S.A.; Liaw, P.K.; Balasubramanian, G. Crystallization kinetics in AlxCrCoFeNi (0 ≤ x ≤ 40) high-entropy alloys. Scr. Mater. 2017, 141, 54–57. [Google Scholar] [CrossRef]
- Mooney, C.Z. Monte Carlo Simulation; Sage Publications: Thousand Oaks, CA, USA, 1997; Volume 116. [Google Scholar]
- Anzorena, M.S.; Bertolo, A.; Gagetti, L.; Kreiner, A.; Mosca, H.; Bozzolo, G.; del Grosso, M. Characterization and modeling of a MoTaVWZr high entropy alloy. Mater. Des. 2016, 111, 382–388. [Google Scholar] [CrossRef]
- Feng, W.Q.; Zheng, S.M.; Qi, Y.; Wang, S.Q. Periodic Maximum Entropy Random Structure Models for High-Entropy Alloys. Mater. Sci. Forum 2017, 898, 611–621. [Google Scholar] [CrossRef]
- Widom, M. Modeling the structure and thermodynamics of high-entropy alloys. J. Mater. Res. 2018, 33, 2881–2898. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, Q.; Li, J.; Liu, B.; Liu, Y. Effect of lattice distortion on solid solution strengthening of BCC high-entropy alloys. J. Mater. Sci. Technol. 2018, 34, 349–354. [Google Scholar] [CrossRef]
- del Grosso, M.; Bozzolo, G.; Mosca, H. Modeling of high entropy alloys of refractory elements. Phys. B Condens. Matter 2012, 407, 3285–3287. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Rivera-Díaz-del-Castillo, P.E. Modelling and design of magnesium and high entropy alloys through combining statistical and physical models. JOM 2015, 67, 108–117. [Google Scholar] [CrossRef]
- Kucza, W.; Dąbrowa, J.; Cieślak, G.; Berent, K.; Kulik, T.; Danielewski, M. Studies of “sluggish diffusion” effect in Co-Cr-Fe-Mn-Ni, Co-Cr-Fe-Ni and Co-Fe-Mn-Ni high entropy alloys; determination of tracer diffusivities by combinatorial approach. J. Alloy. Compd. 2018, 731, 920–928. [Google Scholar] [CrossRef]
- Fernández-Caballero, A.; Fedorov, M.; Wróbel, J.S.; Mummery, P.M.; Nguyen-Manh, D. Configurational Entropy in Multicomponent Alloys: Matrix Formulation from Ab Initio Based Hamiltonian and Application to the FCC Cr-Fe-Mn-Ni System. Entropy 2019, 21, 68. [Google Scholar] [CrossRef]
- Fernandez-Caballero, A.; Wróbel, J.; Mummery, P.; Nguyen-Manh, D. Short-range order in high entropy alloys: Theoretical formulation and application to Mo-Nb-Ta-VW system. J. Phase Equilib. Diffus. 2017, 38, 391–403. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef]
- Andersen, O.; Jepsen, O.; Krier, G. Exact Muffin-Tin Orbital Theory. In Lectures on Methods of Electronic Structure Calculations; World Scientific: Singapore, 1994; pp. 63–124. [Google Scholar]
- Vitos, L.; Skriver, H.L.; Johansson, B.; Kollár, J. Application of the exact muffin-tin orbitals theory: The spherical cell approximation. Comput. Mater. Sci. 2000, 18, 24–38. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Shen, J.; Vitos, L. Calculating elastic constants in high-entropy alloys using the coherent potential approximation: Current issues and errors. Comput. Mater. Sci. 2016, 111, 350–358. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Chen, N.; Shen, J.; Vitos, L. Ab initio design of elastically isotropic TiZrNbMoVx high-entropy alloys. J. Alloy. Compd. 2014, 599, 19–25. [Google Scholar] [CrossRef]
- Li, X.; Irving, D.L.; Vitos, L. First-principles investigation of the micromechanical properties of fcc-hcp polymorphic high-entropy alloys. Sci. Rep. 2018, 8, 11196. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Ni, X.; Tian, F.; Varga, L.K.; Vitos, L. Ab initio study of AlxMoNbTiV high-entropy alloys. J. Phys. Condens. Matter 2015, 27, 075401. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Tian, F.; Schönecker, S.; Zhao, J.; Vitos, L. Ab initio-predicted micro-mechanical performance of refractory high-entropy alloys. Sci. Rep. 2015, 5, 12334. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Schönecker, S.; Li, W.; Varga, L.K.; Irving, D.L.; Vitos, L. Tensile and shear loading of four fcc high-entropy alloys: A first-principles study. Phys. Rev. B 2018, 97, 094102. [Google Scholar] [CrossRef]
- Ge, H.; Song, H.; Shen, J.; Tian, F. Effect of alloying on the thermal-elastic properties of 3d high-entropy alloys. Mater. Chem. Phys. 2018, 210, 320–326. [Google Scholar] [CrossRef]
- Zheng, S.-M.; Feng, W.-Q.; Wang, S.-Q. Elastic properties of high entropy alloys by MaxEnt approach. Comput. Mater. Sci. 2018, 142, 332–337. [Google Scholar] [CrossRef]
- Tian, F.; Wang, D.; Shen, J.; Wang, Y. An ab initio investgation of ideal tensile and shear strength of TiVNbMo high-entropy alloy. Mater. Lett. 2016, 166, 271–275. [Google Scholar] [CrossRef]
- Qiu, S.; Miao, N.; Zhou, J.; Guo, Z.; Sun, Z. Strengthening mechanism of aluminum on elastic properties of NbVTiZr high-entropy alloys. Intermetallics 2018, 92, 7–14. [Google Scholar] [CrossRef]
- Sharma, A.; Balasubramanian, G. Dislocation dynamics in Al0. 1CoCrFeNi high-entropy alloy under tensile loading. Intermetallics 2017, 91, 31–34. [Google Scholar] [CrossRef]
- Zaddach, A.; Niu, C.; Koch, C.; Irving, D. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. JOM 2013, 65, 1780–1789. [Google Scholar] [CrossRef]
- Senkov, O.; Miller, J.; Miracle, D.; Woodward, C. Accelerated exploration of multi-principal element alloys with solid solution phases. Nat. Commun. 2015, 6, 6529. [Google Scholar] [CrossRef] [PubMed]
- Lucas, M.; Belyea, D.; Bauer, C.; Bryant, N.; Michel, E.; Turgut, Z.; Leontsev, S.; Horwath, J.; Semiatin, S.; McHenry, M. Thermomagnetic analysis of FeCoCr x Ni alloys: Magnetic entropy of high-entropy alloys. J. Appl. Phys. 2013, 113, 17A923. [Google Scholar] [CrossRef]
- Dirras, G.; Lilensten, L.; Djemia, P.; Laurent-Brocq, M.; Tingaud, D.; Couzinié, J.-P.; Perrière, L.; Chauveau, T.; Guillot, I. Elastic and plastic properties of as-cast equimolar TiHfZrTaNb high-entropy alloy. Mater. Sci. Eng. A 2016, 654, 30–38. [Google Scholar] [CrossRef]
- Dirras, G.; Gubicza, J.; Heczel, A.; Lilensten, L.; Couzinié, J.-P.; Perrière, L.; Guillot, I.; Hocini, A. Microstructural investigation of plastically deformed Ti20Zr20Hf20Nb20Ta20 high entropy alloy by X-ray diffraction and transmission electron microscopy. Mater. Charact. 2015, 108, 1–7. [Google Scholar] [CrossRef]
- Štamborská, M.; Lapin, J. Effect of anisotropic microstructure on high-temperature compression deformation of CoCrFeNi based complex concentrated alloy. Kov. Mater. 2017, 55, 369–378. [Google Scholar]
- Lu, Y.; Dong, Y.; Jiang, L.; Wang, T.; Li, T.; Zhang, Y. A criterion for topological close-packed phase formation in high entropy alloys. Entropy 2015, 17, 2355–2366. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, Y.; He, Q.; Zhuang, Y.; Wang, S.; Shi, S.; Hu, A.; Fan, J.; Yang, Y. Atomic-scale distorted lattice in chemically disordered equimolar complex alloys. Acta Mater. 2018, 150, 182–194. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, C.; Yang, Y. A geometric model for intrinsic residual strain and phase stability in high entropy alloys. Acta Mater. 2015, 94, 152–161. [Google Scholar] [CrossRef]
- Kivy, M.B.; Asle Zaeem, M. Generalized stacking fault energies, ductilities, and twinnabilities of CoCrFeNi-based face-centered cubic high entropy alloys. Scr. Mater. 2017, 139, 83–86. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Huang, S.; Li, W.; Lu, S.; Tian, F.; Shen, J.; Holmström, E.; Vitos, L. Temperature dependent stacking fault energy of FeCrCoNiMn high entropy alloy. Scr. Mater. 2015, 108, 44–47. [Google Scholar] [CrossRef]
- Pei, Z.; Eisenbach, M. Acceleration of the Particle Swarm Optimization for Peierls–Nabarro modeling of dislocations in conventional and high-entropy alloys. Comput. Phys. Commun. 2017, 215, 7–12. [Google Scholar] [CrossRef]
- Choudhuri, D.; Gwalani, B.; Gorsse, S.; Komarasamy, M.; Mantri, S.A.; Srinivasan, S.G.; Mishra, R.S.; Banerjee, R. Enhancing strength and strain hardenability via deformation twinning in fcc-based high entropy alloys reinforced with intermetallic compounds. Acta Mater. 2019, 165, 420–430. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Fang, Q.; Liu, B.; Zhang, L. Investigation into nanoscratching mechanical response of AlCrCuFeNi high-entropy alloys using atomic simulations. Appl. Surf. Sci. 2017, 416, 470–481. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Liu, B.; Liu, Y. Transformation induced softening and plasticity in high entropy alloys. Acta Mater. 2018, 147, 35–41. [Google Scholar] [CrossRef]
- Smith, T.; Hooshmand, M.; Esser, B.; Otto, F.; McComb, D.; George, E.; Ghazisaeidi, M.; Mills, M. Atomic-scale characterization and modeling of 60 dislocations in a high-entropy alloy. Acta Mater. 2016, 110, 352–363. [Google Scholar] [CrossRef]
- Zaddach, A.; Scattergood, R.; Koch, C. Tensile properties of low-stacking fault energy high-entropy alloys. Mater. Sci. Eng. A 2015, 636, 373–378. [Google Scholar] [CrossRef]
- Liu, S.; Wu, Y.; Wang, H.; He, J.; Liu, J.; Chen, C.; Liu, X.; Wang, H.; Lu, Z. Stacking fault energy of face-centered-cubic high entropy alloys. Intermetallics 2018, 93, 269–273. [Google Scholar] [CrossRef]
- Ventelon, L.; Lüthi, B.; Clouet, E.; Proville, L.; Legrand, B.; Rodney, D.; Willaime, F. Dislocation core reconstruction induced by carbon segregation in bcc iron. Phys. Rev. B 2015, 91, 220102. [Google Scholar] [CrossRef]
- Tsuru, T.; Chrzan, D. Effect of solute atoms on dislocation motion in Mg: An electronic structure perspective. Sci. Rep. 2015, 5, 8793. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Qi, L.; Tsuru, T.; Traylor, R.; Rugg, D.; Morris, J.; Asta, M.; Chrzan, D.; Minor, A.M. Origin of dramatic oxygen solute strengthening effect in titanium. Science 2015, 347, 635–639. [Google Scholar] [CrossRef] [PubMed]
- Varvenne, C.; Leyson, G.; Ghazisaeidi, M.; Curtin, W. Solute strengthening in random alloys. Acta Mater. 2017, 124, 660–683. [Google Scholar] [CrossRef]
- Varvenne, C.; Curtin, W.A. Strengthening of high entropy alloys by dilute solute additions: CoCrFeNiAlx and CoCrFeNiMnAlx alloys. Scr. Mater. 2017, 138, 92–95. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Rivera-Díaz-del-Castillo, P.E. Modelling solid solution hardening in high entropy alloys. Acta Mater. 2015, 85, 14–23. [Google Scholar] [CrossRef]
- Toda-Caraballo, I. A general formulation for solid solution hardening effect in multicomponent alloys. Scr. Mater. 2017, 127, 113–117. [Google Scholar] [CrossRef]
- Walbrühl, M.; Linder, D.; Ågren, J.; Borgenstam, A. Modelling of solid solution strengthening in multicomponent alloys. Mater. Sci. Eng. A 2017, 700, 301–311. [Google Scholar] [CrossRef]
- Labusch, R. A statistical theory of solid solution hardening. Phys. Status Solidi 1970, 41, 659–669. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Wróbel, J.; Dudarev, S.; Nguyen-Manh, D.; Rivera-Díaz-del-Castillo, P. Interatomic spacing distribution in multicomponent alloys. Acta Mater. 2015, 97, 156–169. [Google Scholar] [CrossRef]
- Huang, S.; Vida, Á.; Heczel, A.; Holmström, E.; Vitos, L. Thermal Expansion, Elastic and Magnetic Properties of FeCoNiCu-Based High-Entropy Alloys Using First-Principle Theory. JOM 2017, 69, 2107–2112. [Google Scholar] [CrossRef]
- Löffler, A.; Zendegani, A.; Gröbner, J.; Hampl, M.; Schmid-Fetzer, R.; Engelhardt, H.; Rettenmayr, M.; Körmann, F.; Hickel, T.; Neugebauer, J. Quaternary Al-Cu-Mg-Si Q Phase: Sample Preparation, Heat Capacity Measurement and First-Principles Calculations. J. Phase Equilib. Diffus. 2016, 37, 119–126. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, W.; Xu, Y.; Lu, Z.; Li, D. The thermal-mechanical behavior of WTaMoNb high-entropy alloy via selective laser melting (SLM): Experiment and simulation. Int. J. Adv. Manuf. Technol. 2018, 96, 461–474. [Google Scholar] [CrossRef]
- Rahul, M.; Samal, S.; Venugopal, S.; Phanikumar, G. Experimental and finite element simulation studies on hot deformation behaviour of AlCoCrFeNi2. 1 eutectic high entropy alloy. J. Alloy. Compd. 2018, 749, 1115–1127. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.-H.; Ferreira, L.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Ding, X.; Feng, Y.; Liu, X.; Liu, K.; Lu, Z.; Li, D.; Li, Y.; Liu, C.; Chen, X.-Q. Vacancy formation enthalpies of high-entropy FeCoCrNi alloy via first-principles calculations and possible implications to its superior radiation tolerance. J. Mater. Sci. Technol. 2018, 34, 355–364. [Google Scholar] [CrossRef]
- Schneeweiss, O.; Friák, M.; Dudová, M.; Holec, D.; Šob, M.; Kriegner, D.; Holý, V.; Beran, P.; George, E.P.; Neugebauer, J. Magnetic properties of the CrMnFeCoNi high-entropy alloy. Phys. Rev. B 2017, 96, 014437. [Google Scholar] [CrossRef]
- Huang, S.; Holmström, E.; Eriksson, O.; Vitos, L. Mapping the magnetic transition temperatures for medium-and high-entropy alloys. Intermetallics 2018, 95, 80–84. [Google Scholar] [CrossRef]
- Körmann, F.; Ma, D.; Belyea, D.D.; Lucas, M.S.; Miller, C.W.; Grabowski, B.; Sluiter, M.H. “Treasure maps” for magnetic high-entropy-alloys from theory and experiment. Appl. Phys. Lett. 2015, 107, 142404. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, H.; Lu, S.; Ding, X.; Wang, Y.; Vitos, L. Phase selection rule for Al-doped CrMnFeCoNi high-entropy alloys from first-principles. Acta Mater. 2017, 140, 366–374. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, S.; Gao, M.; Liaw, P.; Zhang, Y. A Successful Synthesis of the CoCrFeNiAl0. 3 Single-Crystal, High-Entropy Alloy by Bridgman Solidification. JOM 2013, 65, 1751–1758. [Google Scholar] [CrossRef]
- Zuo, T.; Gao, M.C.; Ouyang, L.; Yang, X.; Cheng, Y.; Feng, R.; Chen, S.; Liaw, P.K.; Hawk, J.A.; Zhang, Y. Tailoring magnetic behavior of CoFeMnNiX (X = Al, Cr, Ga, and Sn) high entropy alloys by metal doping. Acta Mater. 2017, 130, 10–18. [Google Scholar] [CrossRef]
- Calvo-Dahlborg, M.; Cornide, J.; Tobola, J.; Nguyen-Manh, D.; Wróbel, J.; Juraszek, J.; Jouen, S.; Dahlborg, U. Interplay of electronic, structural and magnetic properties as the driving feature of high-entropy CoCrFeNiPd alloys. J. Phys. D Appl. Phys. 2017, 50, 185002. [Google Scholar] [CrossRef]

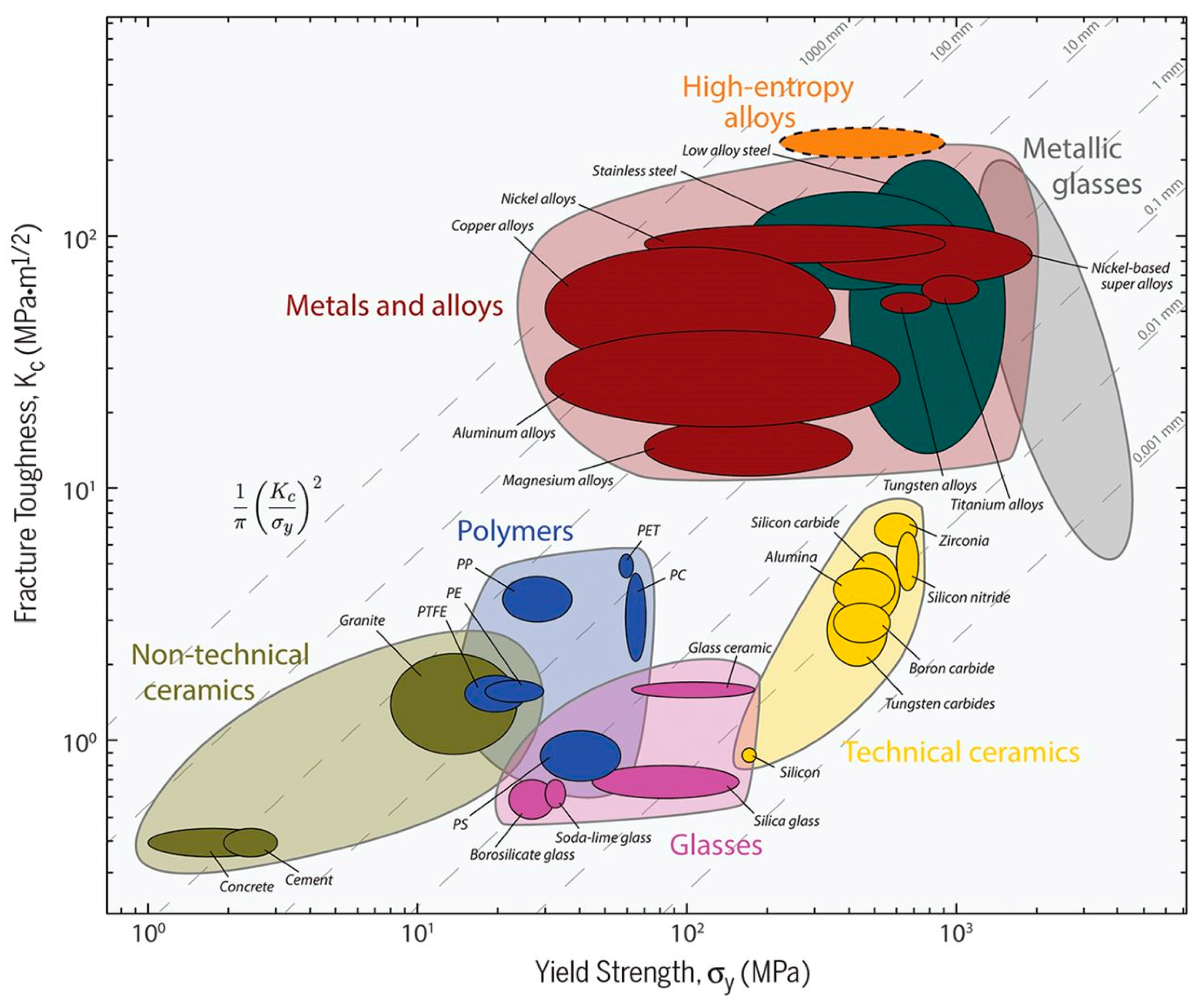
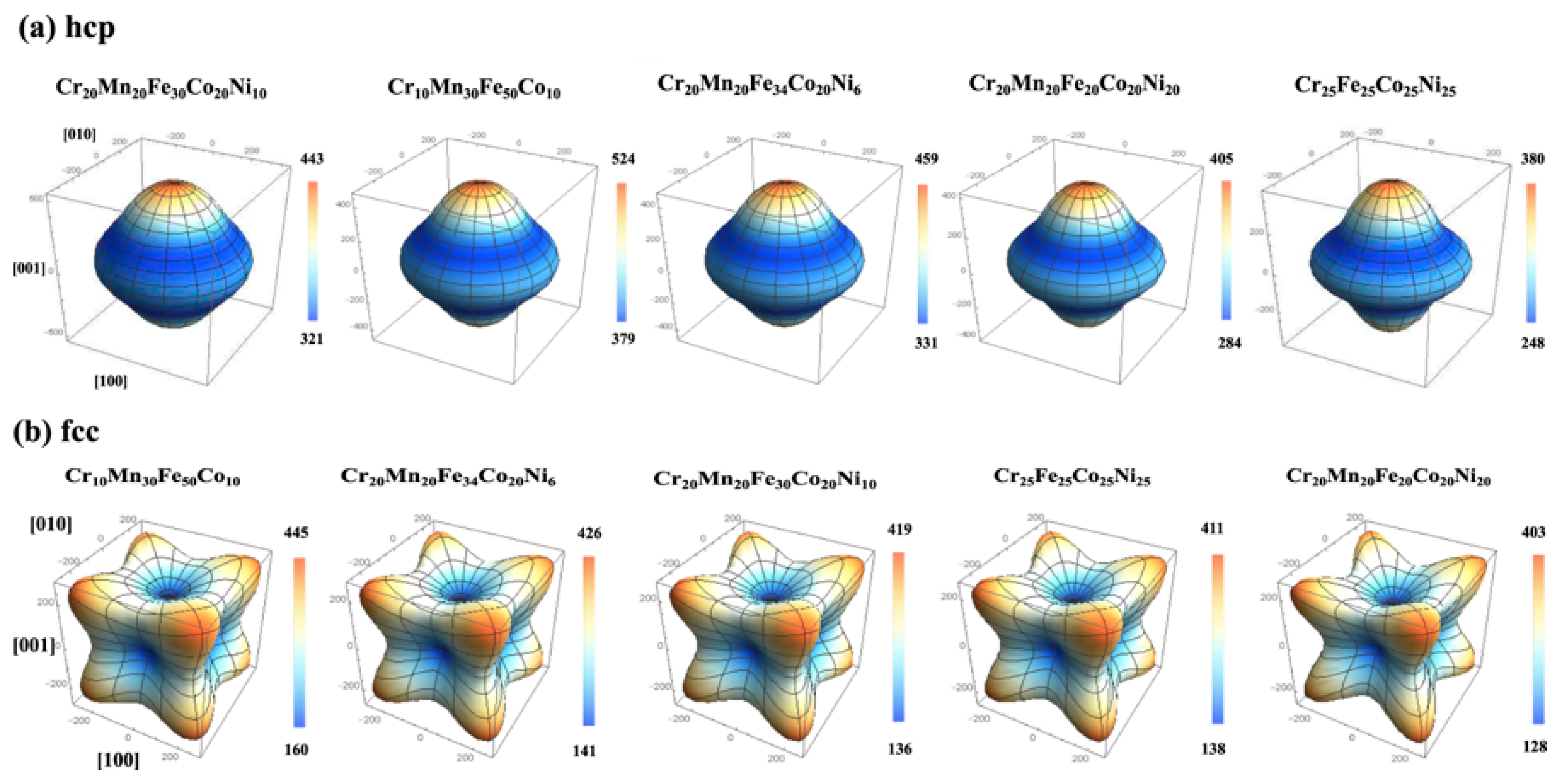
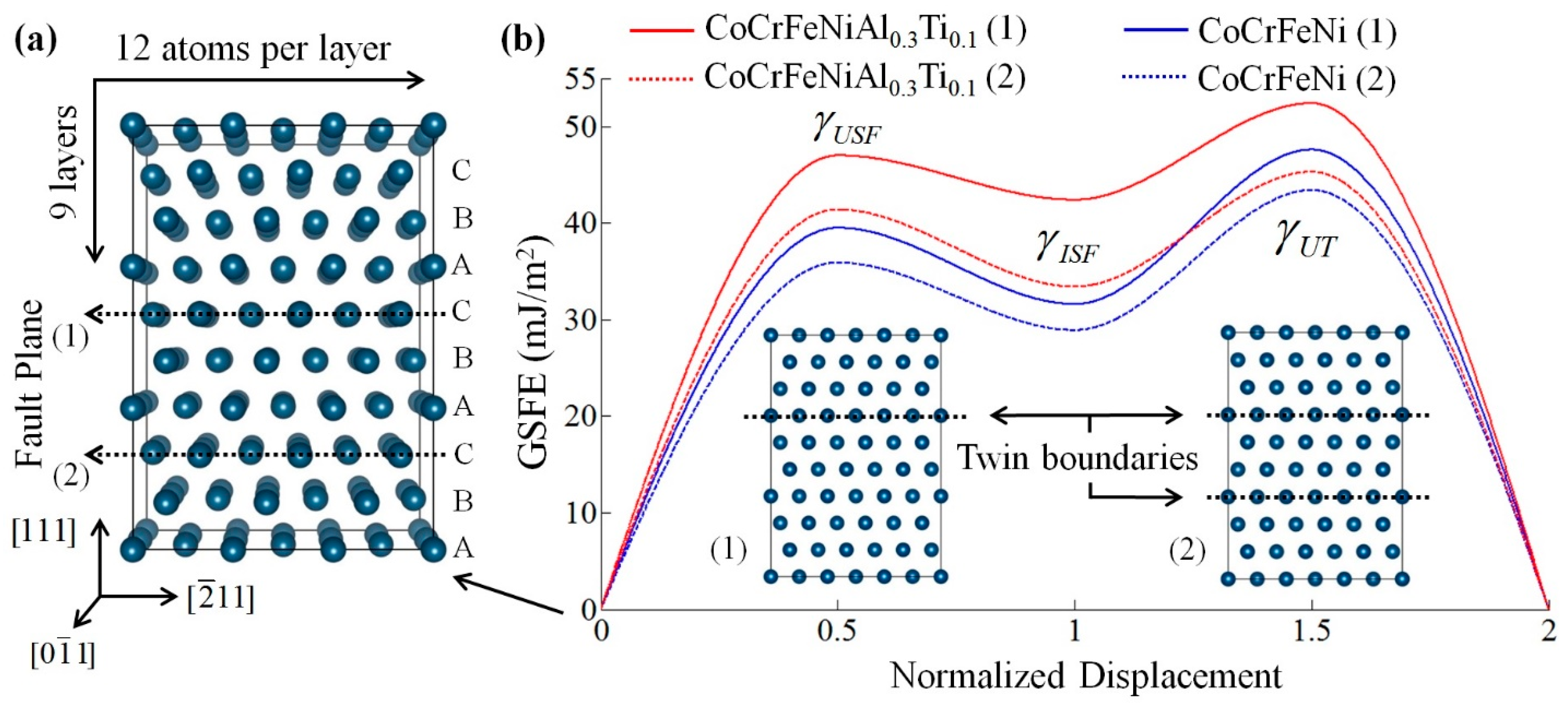
| Alloys | EDFT | EMD | Eexp. |
|---|---|---|---|
| Al0.1CoCrFeNi | - | 199 [99] | 203 [99] |
| CoCrFeNi | 275.7 [94], 274.1 [89], 225 [100], 196 [100] | - | 226 [101] |
| CoCrMnNi | 265.6 [89] | - | 171 [100] |
| CoFeMnNi | 267.2 [95] | - | - |
| CoCrFeMnNi | 262.4 [94], 279.7 [95], 207 [100] | - | 215 [102], 137 [100] |
| Cr10Mn40Fe40Co10 | 328.1 [94] | - | - |
| TiZrVMoTaNb | 71.9 [59] | - | - |
| TiZrVMoTaNbCr | 130.9 [59] | - | - |
| TiZrVMoTaNbCrW | 166.7 [59] | - | - |
| NbVTiZrAl | 118.0 [98] | - | - |
| ZrNbHf | 95.4 [93] | - | - |
| ZrVTiNb | 95.1 [98], 117.5 [93] | - | 80 [103], 101 [104] |
| ZrTiNbHf | 88.9 [93] | - | - |
| ZrVTiNbHf | 97.1 [93] | - | - |
| TiZrNbMoVx | 141.1 (x = 1) [90], 127.8 [96] | - | - |
| AlxMoNbTiV | 174.4 (x = 1) [92], 185.4 [96] | - | - |
| TaNbHfZrTi | 185.4 [96] | - | 78.5 [103], 87 [104] |
| NbTaTiWV | 257.3 [96] | - | - |
| WNbMoTaV | 218.0 [96] | - | - |
| MoNbTaTiV | 130.5 [96] | - | - |
| MoTiZrNbHfTa | 136.6 [96] | - | - |
| Alloys | γSFE-DFT | γSFE-MD | γSFE-exp |
|---|---|---|---|
| FeCrCoNiMn | 21 [111], 27.3 [100], 29.7 [109] | - | 25 [117], 26.5 [118], 19 [100] |
| CoCrFeNi | 31.6 [109], 31.7 [100] | - | 27 [118] |
| CoCrFeNiCu0.5 | 29.0 [109] | - | - |
| CoCrFeNiCu | 27.5 [109] | - | - |
| CoCrFeNiCuAl0.5 | 32.0 [109] | - | - |
| CoCrFeNiCuTi0.5 | 37.4 [109] | - | - |
| CoCrFeNiAl0.3 | 35.2 [109] | - | - |
| CoCrFeNi | 31.6 [109] | - | 26.8 [117] |
| CoCrFeNiCu0.5 | 29.0 [109] | - | - |
| CoCrFeNiCu | 27.5 [109] | - | 49.0 [115] |
| CoCrFeNiCuAl0.5 | 32.0 [109] | - | - |
| Co20Cr26Fe20Ni14Mn20 | - | - | 3.5 [117] |
| Co15Cr20Fe20Ni25Mn20 | - | - | 38 [118] |
| Co26Cr18.5Fe18.5Ni18.5Mn18.5 | - | - | 9.7 [100] |
| (CoCrFeNi)86Mn14 | - | - | 29 [118] |
| (CoCrFeNi)94Mn6 | - | - | 28 [118] |
| FeCrNi | - | 20 [114] | - |
| Method | First-Principles | Monte-Carlo | MD | Microscale (e.g., PFM simulations) | FEM | Thermodynamics | |
|---|---|---|---|---|---|---|---|
| Structures/ Phases | a | b | c | × | × | d | |
| Properties | Mechanical | e | × | f | × | g | × |
| Thermo-Chemical | h | × | × | × | i | × | |
| Magnetic | j | × | × | × | × | × | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beyramali Kivy, M.; Hong, Y.; Asle Zaeem, M. A Review of Multi-Scale Computational Modeling Tools for Predicting Structures and Properties of Multi-Principal Element Alloys. Metals 2019, 9, 254. https://doi.org/10.3390/met9020254
Beyramali Kivy M, Hong Y, Asle Zaeem M. A Review of Multi-Scale Computational Modeling Tools for Predicting Structures and Properties of Multi-Principal Element Alloys. Metals. 2019; 9(2):254. https://doi.org/10.3390/met9020254
Chicago/Turabian StyleBeyramali Kivy, Mohsen, Yu Hong, and Mohsen Asle Zaeem. 2019. "A Review of Multi-Scale Computational Modeling Tools for Predicting Structures and Properties of Multi-Principal Element Alloys" Metals 9, no. 2: 254. https://doi.org/10.3390/met9020254
APA StyleBeyramali Kivy, M., Hong, Y., & Asle Zaeem, M. (2019). A Review of Multi-Scale Computational Modeling Tools for Predicting Structures and Properties of Multi-Principal Element Alloys. Metals, 9(2), 254. https://doi.org/10.3390/met9020254






