Multiaxial Fatigue Life Prediction of GH4169 Alloy Based on the Critical Plane Method
Abstract
1. Introduction
2. The Critical Plane Method
2.1. Determination of the Critical Plane of a Smooth Specimen
2.2. Determination of the Critical Plane of a Notched Specimen
3. Multiaxial Fatigue Life Prediction Model
3.1. Considering Additional Enhanced Multiaxial Damage Parameters
3.2. Mean Strain Correction
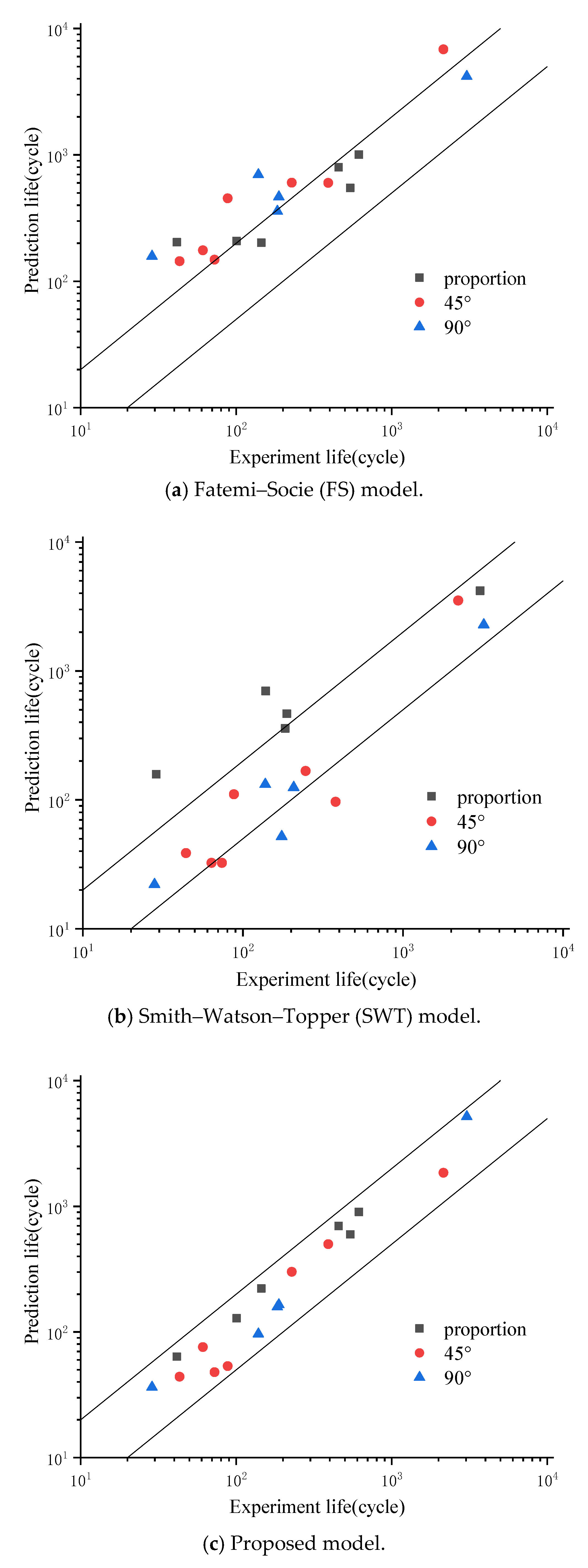
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brandão, P.; Infante, V.; Deus, A.M. Thermo-mechanical modeling of a high pressure turbine blade of an airplane gas turbine engine. Procedia Struct. Integrity 2016, 1, 189–196. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Yu, Z.Y.; Liu, Y. Fatigue reliability analysis of a turbine disc under multi-source uncertainties. Procedia Struct. Integrity 2017, 5, 967–972. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Zhou, J.; Yu, Z.Y. Fatigue reliability assessment of turbine discs under multi-source uncertainties. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1291–1305. [Google Scholar] [CrossRef]
- Calvente, M.M.; Blason, S.; Canteli, A.F. A probabilistic approach for multiaxial fatigue criteria. Frattura ed Integrita Strutturale 2017, 11, 160–165. [Google Scholar] [CrossRef]
- Correia, J.; Apetre, N.; Arcari, A.; Jesus, A.D.; Muñizcalvente, M.; Rui, C.; Berto, F.; Fernándezcanteli, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liu, Q.; Lei, Q.; Wang, Q. Probabilistic fatigue life prediction and reliability assessment of a high pressure turbine disc considering load variations. Int. J. Damage Mech. 2017, 27, 1569–1588. [Google Scholar] [CrossRef]
- Das, J.; Sivakumar, S.M. Multiaxial fatigue life prediction of a high temperature steam turbine rotor using a critical plane approach. Eng. Fail. Anal. 2000, 7, 347–358. [Google Scholar] [CrossRef]
- Gates, N.R.; Fatemi, A. On the consideration of normal and shear stress interaction in multiaxial fatigue damage analysis. Int. J. Fatigue 2017, 100, 322–336. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, Z.C.; Wang, X.G.; Zhang, Z.; Long, X.Y. A structural stress-based critical plane method for multiaxial fatigue life estimation in welded joints. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 372–383. [Google Scholar] [CrossRef]
- Jin, D.; Tian, D.J.; Li, J.H.; Sakane, M. Low-cycle fatigue of 316l stainless steel under proportional and nonproportional loadings. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 850–858. [Google Scholar] [CrossRef]
- Kamal, M.; Rahman, M.M. Multiaxial fatigue life modelling using hybrid approach of critical plane and genetic algorithm. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 479–490. [Google Scholar] [CrossRef]
- Brnić, J.; Turkalj, G.; Čanađija, M.; Lanc, D.; Kršćanski, S.; Brčić, M.; Li, Q.; Niu, J. Mechanical properties, short time creep and fatigue of an austenitic steel. Materials 2016, 9, 298. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, H.; Wang, Q.; He, J. A fatigue life prediction method based on strain intensity factor. Materials 2017, 10, 689. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Liu, Y. A critical plane-energy model for multiaxial fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1973–1983. [Google Scholar] [CrossRef]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A new nonlinear fatigue damage model based only on s-n curve parameters. Int. J. Fatigue 2017, 103, 327–341. [Google Scholar] [CrossRef]
- Brown, M.W.; Miller, K.J. A theory for fatigue failure under multiaxial stress-strain conditions. Proc. Inst. Mech. Eng. 2006, 187, 745–755. [Google Scholar] [CrossRef]
- Chu, C.C. Fatigue damage calculation using the critical plane approach. J. Eng. Mater. Technol. 1995, 117, 41–49. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Correia, J.A.F.O.; Jesus, A.M.P.D.; Calçadac, R. Computational framework for multiaxial fatigue life prediction of compressor discs considering notch effects. Eng. Fract. Mech. 2018, 202, 423–435. [Google Scholar] [CrossRef]
- Gates, N.; Fatemi, A. Notch deformation and stress gradient effects in multiaxial fatigue. Theor. Appl. Fract. Mech. 2016, 84, 3–25. [Google Scholar] [CrossRef]
- Gates, N.R.; Fatemi, A. A simplified cyclic plasticity model for calculating stress-strain response under multiaxial non-proportional loadings. Eur. J. Mech. A/Solid 2016, 59, 344–355. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W.; Huh, H.; Chao, Q.; Song, J.H. Correlation of the maximum shear stress with micro-mechanisms of ductile fracture for metals with high strength-to-weight ratio. Intl. J. Mech. Sci. 2018, 146, 583–601. [Google Scholar] [CrossRef]
- Luo, P.; Yao, W.; Susmel, L.; Wang, Y.; Ma, X. A survey on multiaxial fatigue damage parameters under non-proportional loadings. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1323–1342. [Google Scholar] [CrossRef]
- Ma, S.; Markert, B.; Yuan, H. Multiaxial fatigue life assessment of sintered porous iron under proportional and non-proportional loadings. Int. J. Fatigue 2017, 97, 214–226. [Google Scholar] [CrossRef]
- Romanowicz, P. Numerical assessment of fatigue load capacity of cylindrical crane wheel using multiaxial high-cycle fatigue criteria. Arch. Appl. Mech. 2017, 87, 1–20. [Google Scholar] [CrossRef]
- Shang, D.G.; Sun, G.Q.; Chen, J.H.; Cai, N.; Yan, C.L. Multiaxial fatigue behavior of ni-based superalloy gh4169 at 650 c. Mat. Sci. Eng. A Struct. 2006, 432, 231–238. [Google Scholar] [CrossRef]
- Pan, J.; Nicholas, T. Effects of mean stresses on multiaxial fatigue life prediction based. Int. J. Fatigue 2001, 23, 87–92. [Google Scholar] [CrossRef]
- Brown, M.W.; Surer, D.K.; Wang, C.H. An analysis of mean stress in multiaxial random fatigue. Fatigue Fract. Eng. Mater. Struct. 2010, 19, 323–333. [Google Scholar] [CrossRef]
- Ge, J.; Sun, Y.; Zhou, S. Fatigue life estimation under multiaxial random loading by means of the equivalent lemaitre stress and multiaxial s–n curve methods. Int. J. Fatigue 2015, 79, 65–74. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, Q.; Shi, X.; Fei, B. Effect of mean shear stress on torsion fatigue failure behavior of 2a12-t4 aluminum alloy. Int. J. Fatigue 2014, 67, 173–182. [Google Scholar] [CrossRef]
- Marciniak, Z.; Rozumek, D.; Macha, E. Verification of fatigue critical plane position according to variance and damage accumulation methods under multiaxial loading. Int. J. Fatigue 2014, 58, 84–93. [Google Scholar] [CrossRef]
- Spear, A.D.; Hochhalter, J.D.; Cerrone, A.R.; Li, S.F.; Lind, J.F.; Suter, R.M.; Ingraffea, A.R. A method to generate conformal finite-element meshes from 3d measurements of microstructurally small fatigue-crack propagation. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 737–751. [Google Scholar] [CrossRef]
- Susmel, L.; Taylor, D. A critical distance/plane method to estimate finite life of notched components under variable amplitude uniaxial/multiaxial fatigue loading. Int. J. Fatigue 2012, 38, 7–24. [Google Scholar] [CrossRef]
- Fatemi, A.; Socie, D.F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 2010, 11, 149–165. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. A path-independent parameter for fatigue under proportional and non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 2010, 16, 1285–1297. [Google Scholar] [CrossRef]
- Smith, K.N. A stresss train function for the fatigue metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Wu, Z.R.; Li, X.; Fang, L.; Song, Y.D. Multiaxial fatigue life prediction based on nonlinear continuum damage mechanics and critical plane method. J. Mater. Eng. Perform. 2018, 1–9. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, S.-P.; Hao, Y.-Z.; Liao, D. Critical plane–based multiaxial fatigue life prediction of turbine disk alloys by refining normal stress sensitivity. J. Strain Anal. Eng. 2018, 53, 719–729. [Google Scholar] [CrossRef]
- Ranganathan, R.M. An improved, automated finite element analysis for fatigue life predictions of notched components. Int. J. Mater. Prod. Technol. 2004, 21, 539–554. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, S.; Hao, Y.; Liao, D. Multiaxial fatigue life prediction of an hpt disk based on critical plane-damage parameters. Acta Aeronautica et Astronautica Sinica 2018, 39, 221930. (In Chinese) [Google Scholar]

| Material | K′/MPa | n′ | E/GPa | σy/MPa | b | c | ||
|---|---|---|---|---|---|---|---|---|
| GH4169 at 650° | 1933 | 0.1483 | 182 | 626.4 | 1476 | 0.162 | −0.086 | −0.58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Z.; Li, B.; Lang, S. Multiaxial Fatigue Life Prediction of GH4169 Alloy Based on the Critical Plane Method. Metals 2019, 9, 255. https://doi.org/10.3390/met9020255
Liu J, Zhang Z, Li B, Lang S. Multiaxial Fatigue Life Prediction of GH4169 Alloy Based on the Critical Plane Method. Metals. 2019; 9(2):255. https://doi.org/10.3390/met9020255
Chicago/Turabian StyleLiu, Jianhui, Zhen Zhang, Bin Li, and Shanshan Lang. 2019. "Multiaxial Fatigue Life Prediction of GH4169 Alloy Based on the Critical Plane Method" Metals 9, no. 2: 255. https://doi.org/10.3390/met9020255
APA StyleLiu, J., Zhang, Z., Li, B., & Lang, S. (2019). Multiaxial Fatigue Life Prediction of GH4169 Alloy Based on the Critical Plane Method. Metals, 9(2), 255. https://doi.org/10.3390/met9020255




