A Simulation Study on the Flow Behavior of Liquid Steel in Tundish with Annular Argon Blowing in the Upper Nozzle
Abstract
:1. Introduction
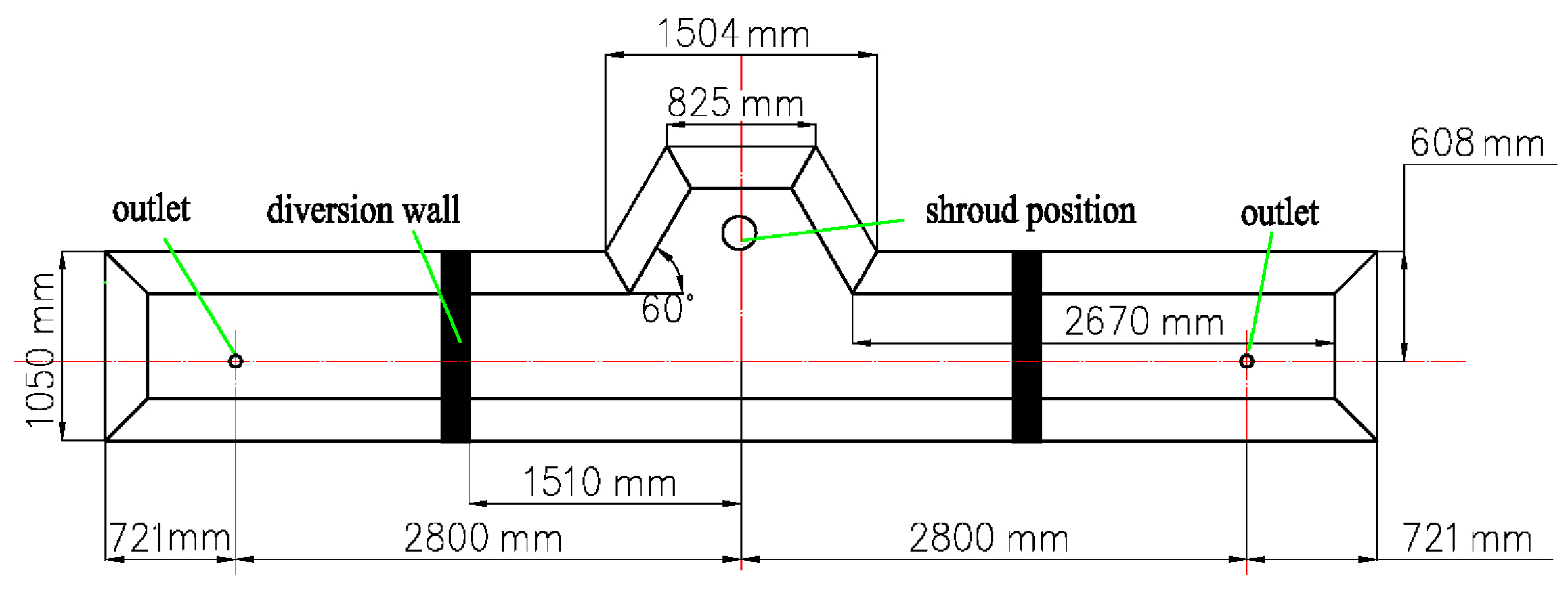
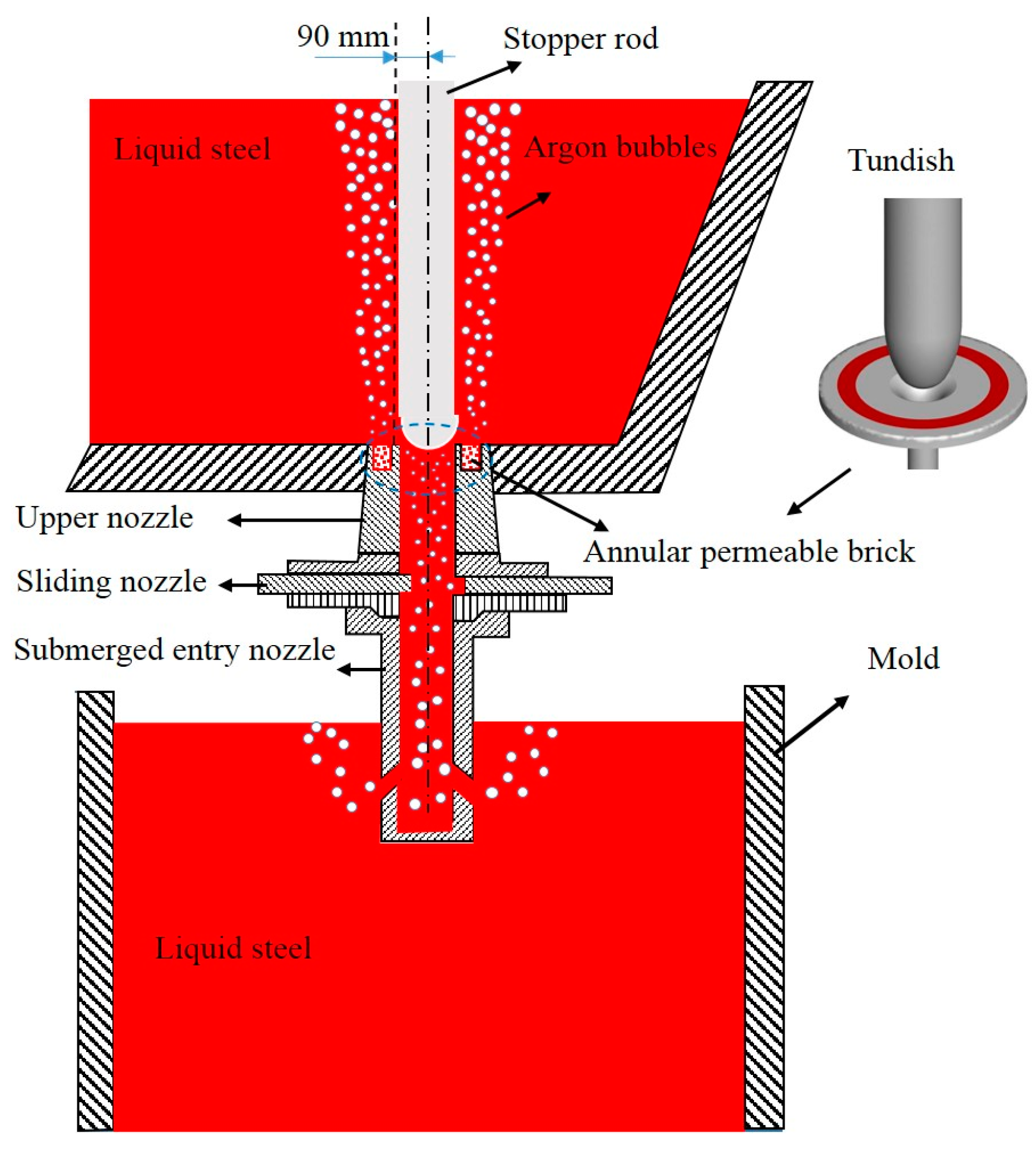
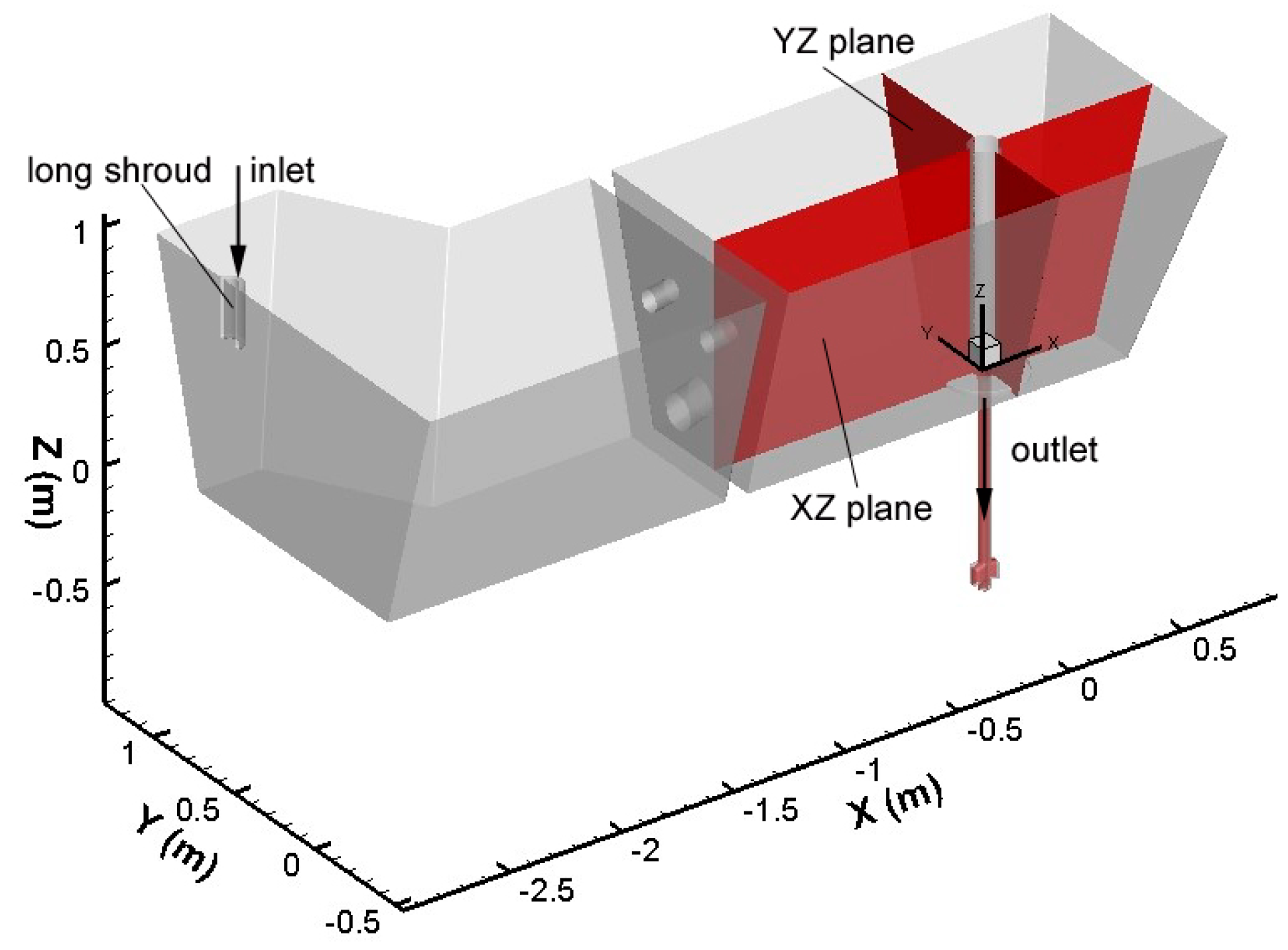
2. Model Description
2.1. Model Assumption
2.2. Governing Equations
2.3. Boundary Conditions
2.4. Numerical Method
3. Comparison of Flow Behavior in Mathematical Model and Water Model
4. Results and Discussion
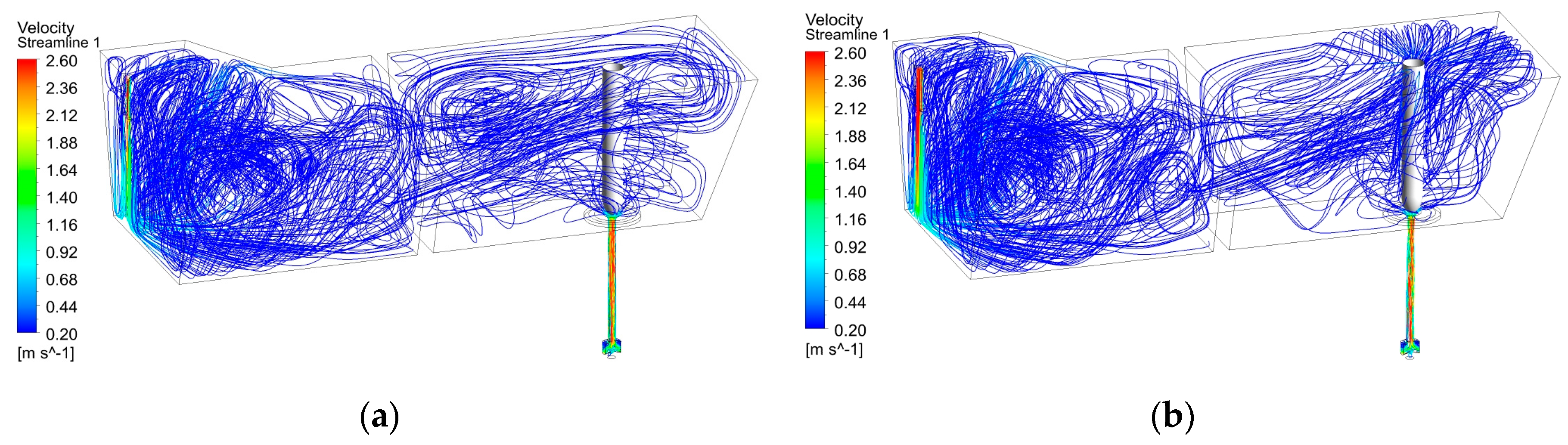
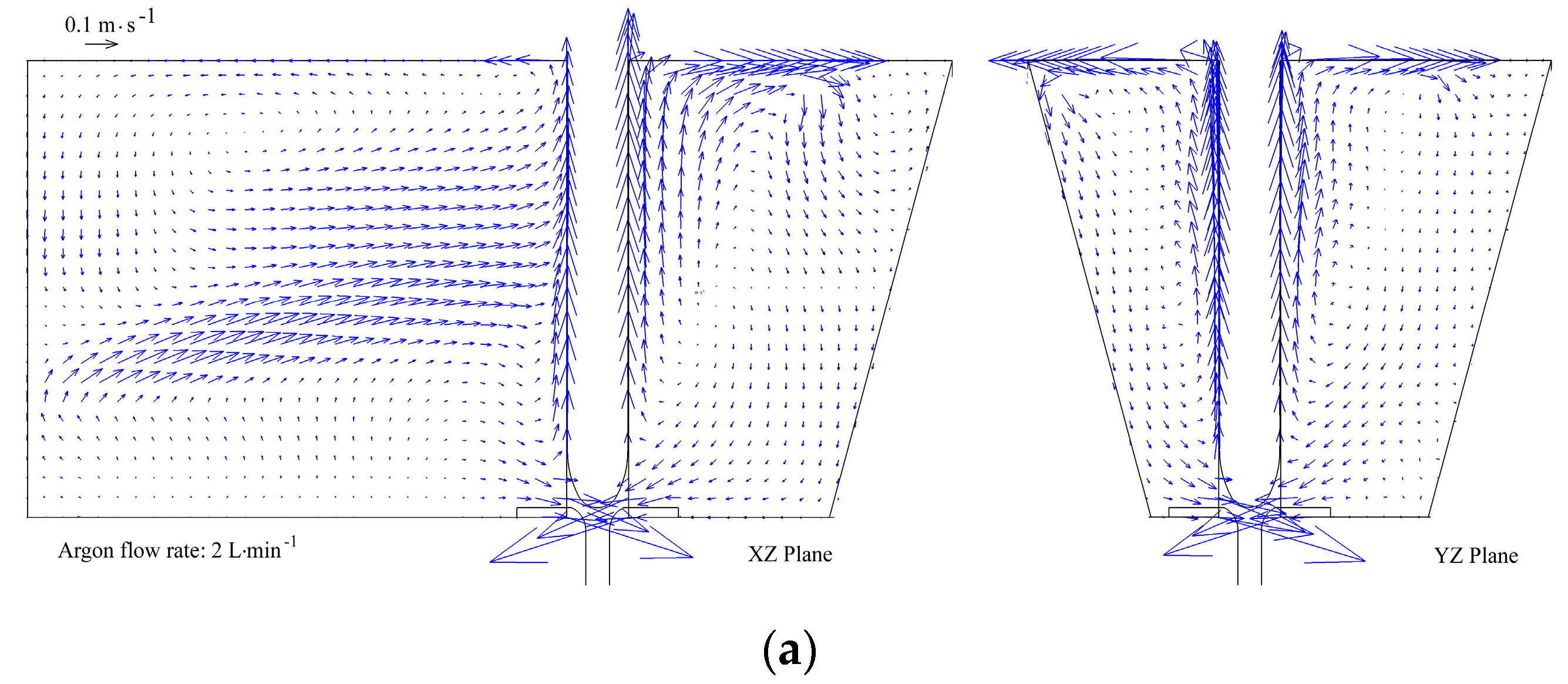
4.1. Typical Flow Behavior of Liquid Steel in the Tundish with Annular Argon Blowing in the Upper Nozzle
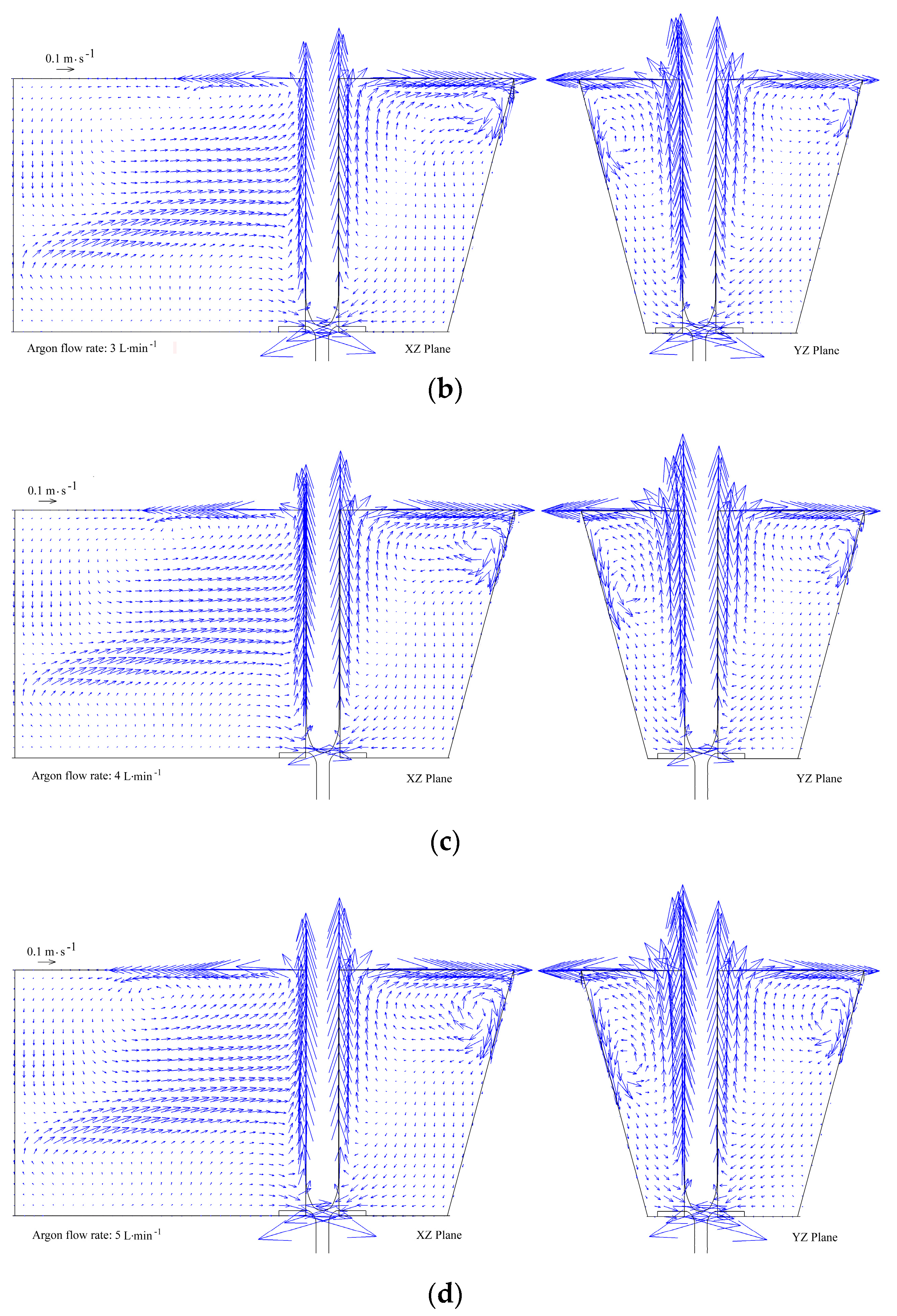
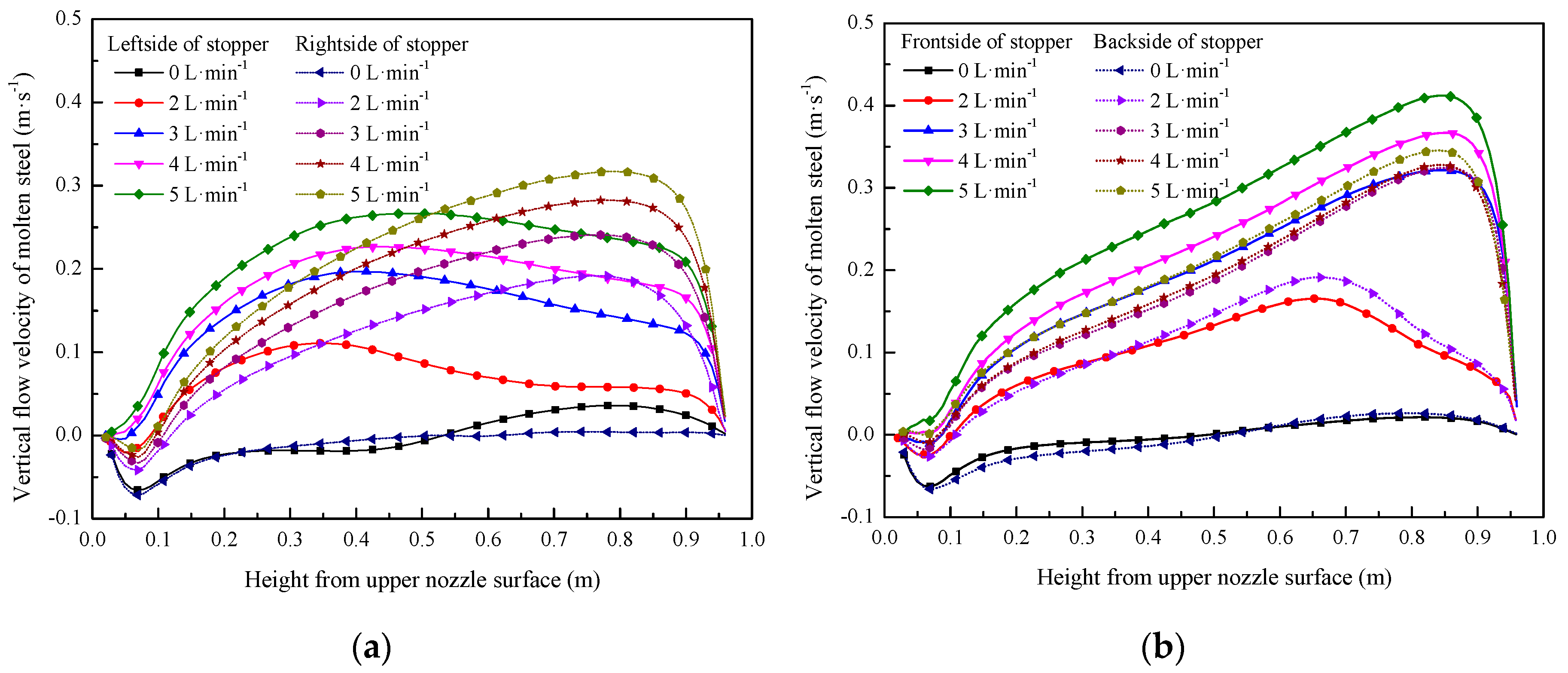
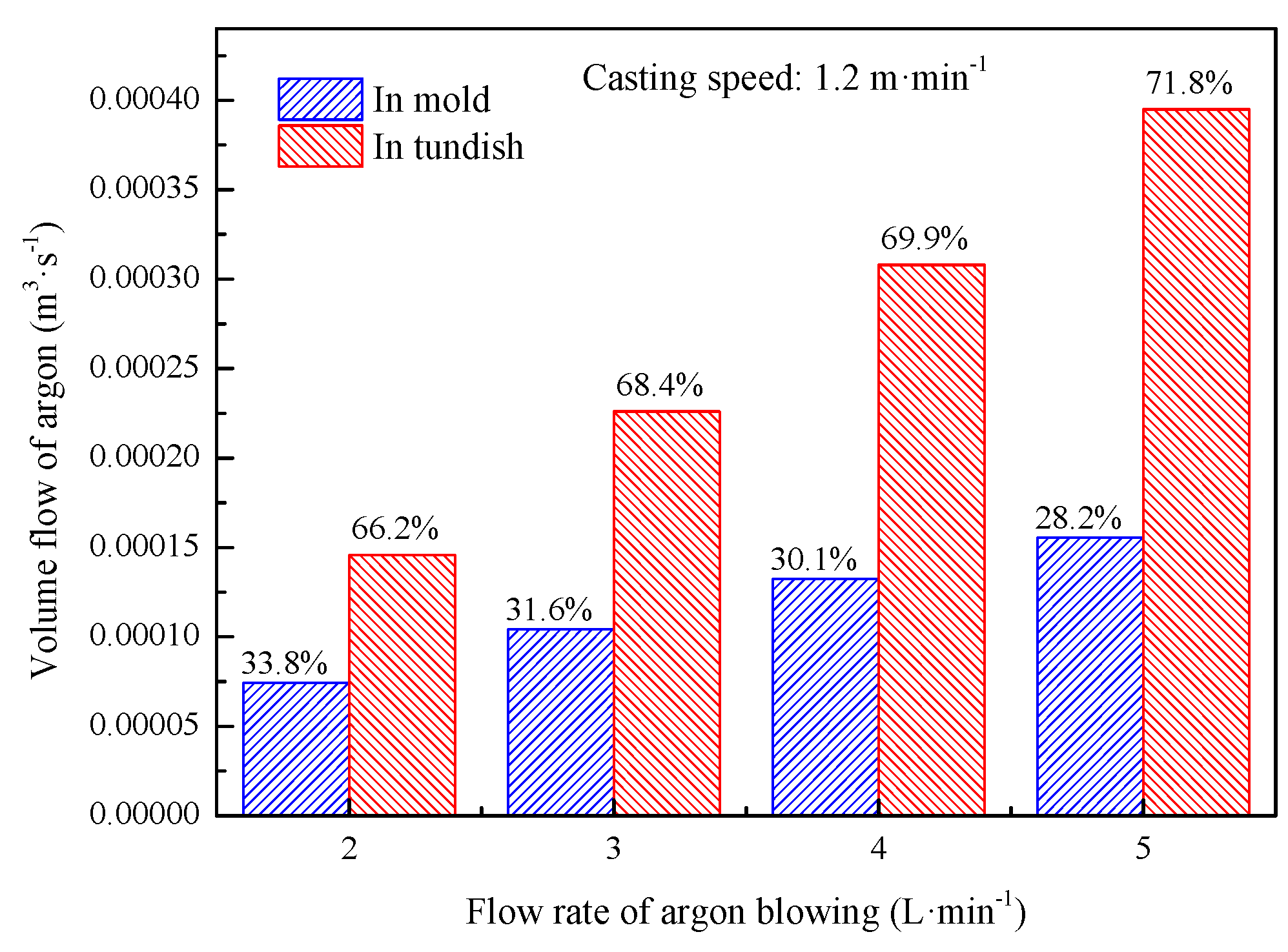
4.2. Effect of Flow Rate of the Argon Blowing on the Flow Behavior of Liquid Steel in the Tundish
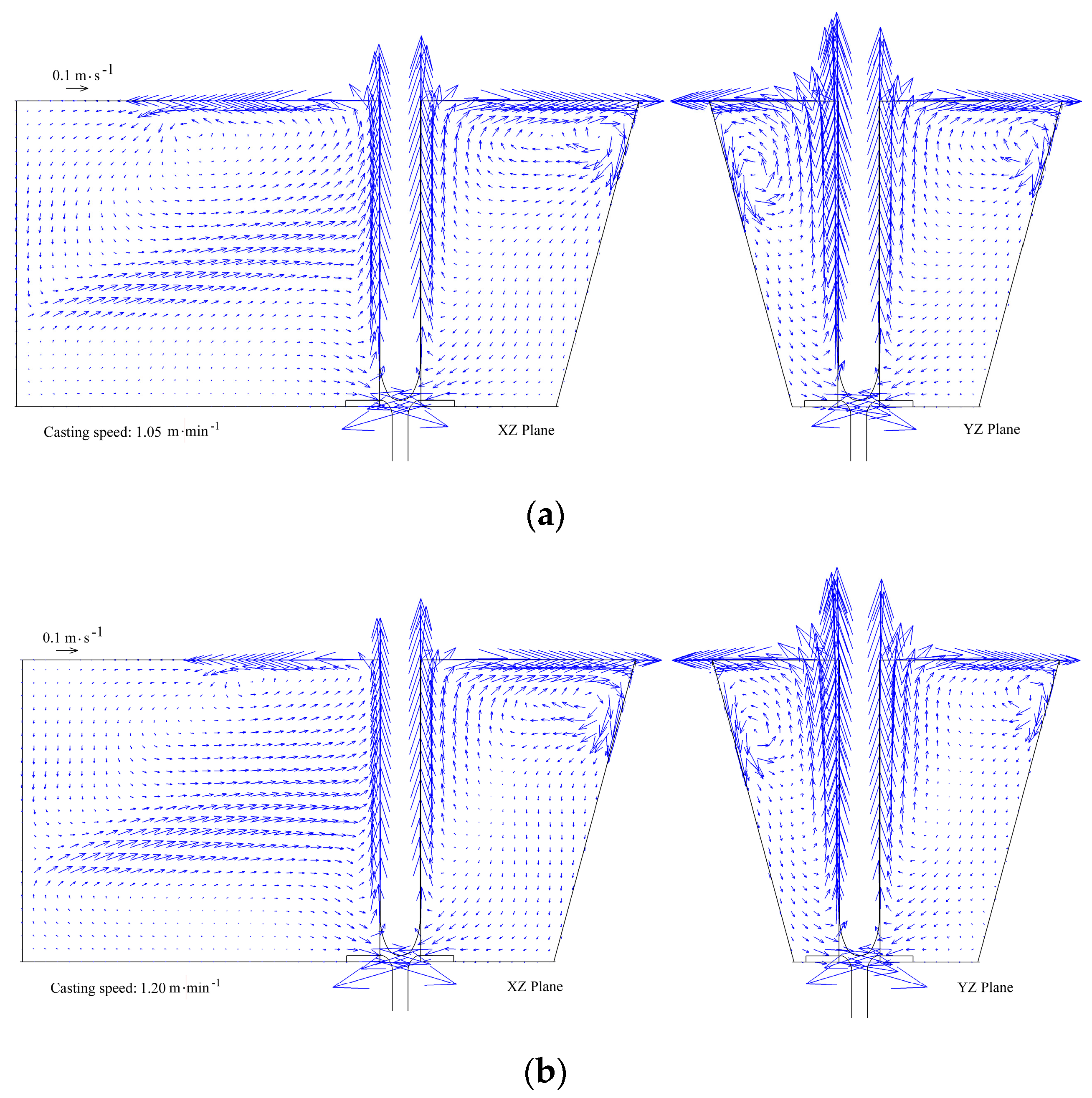
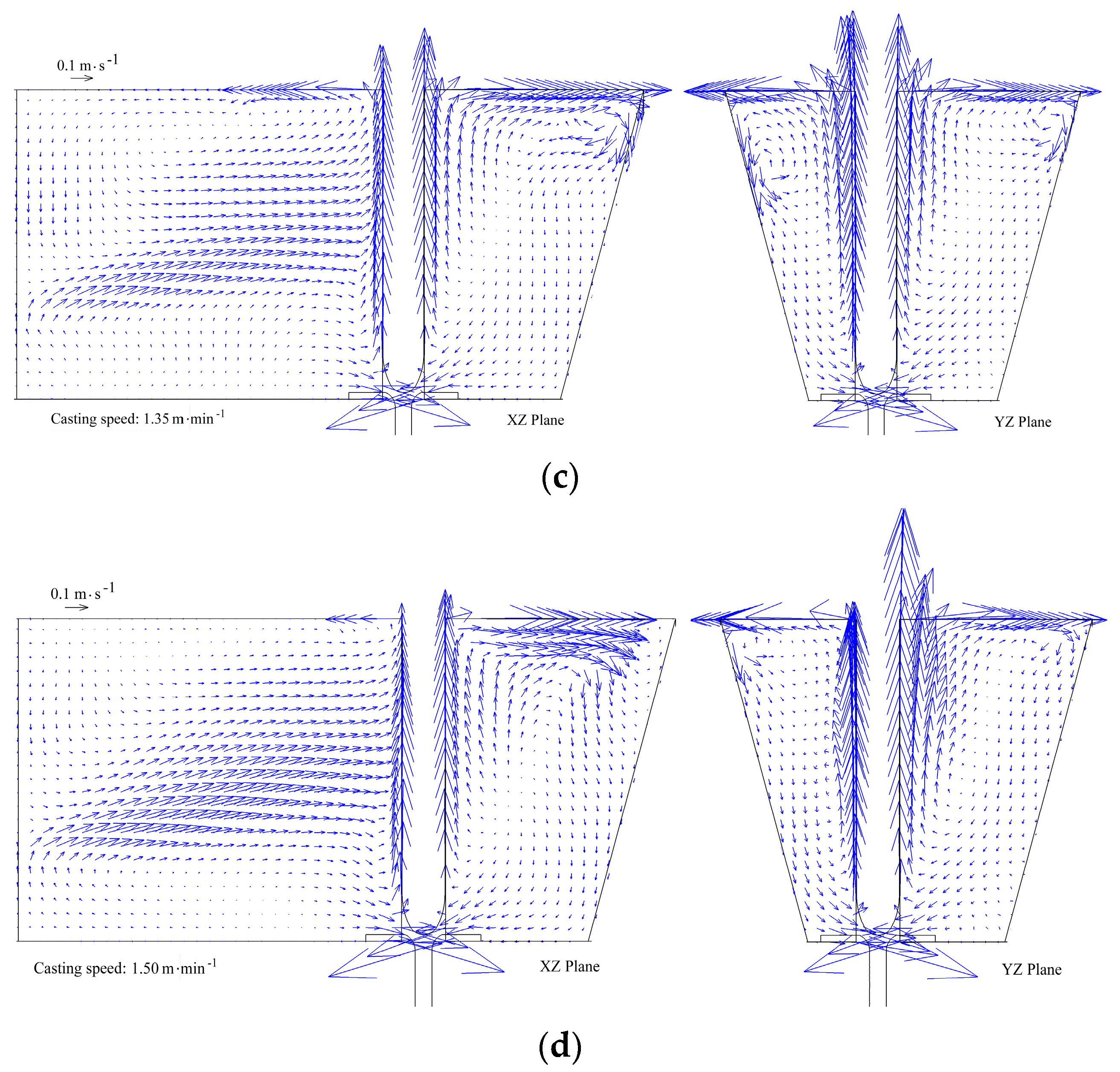
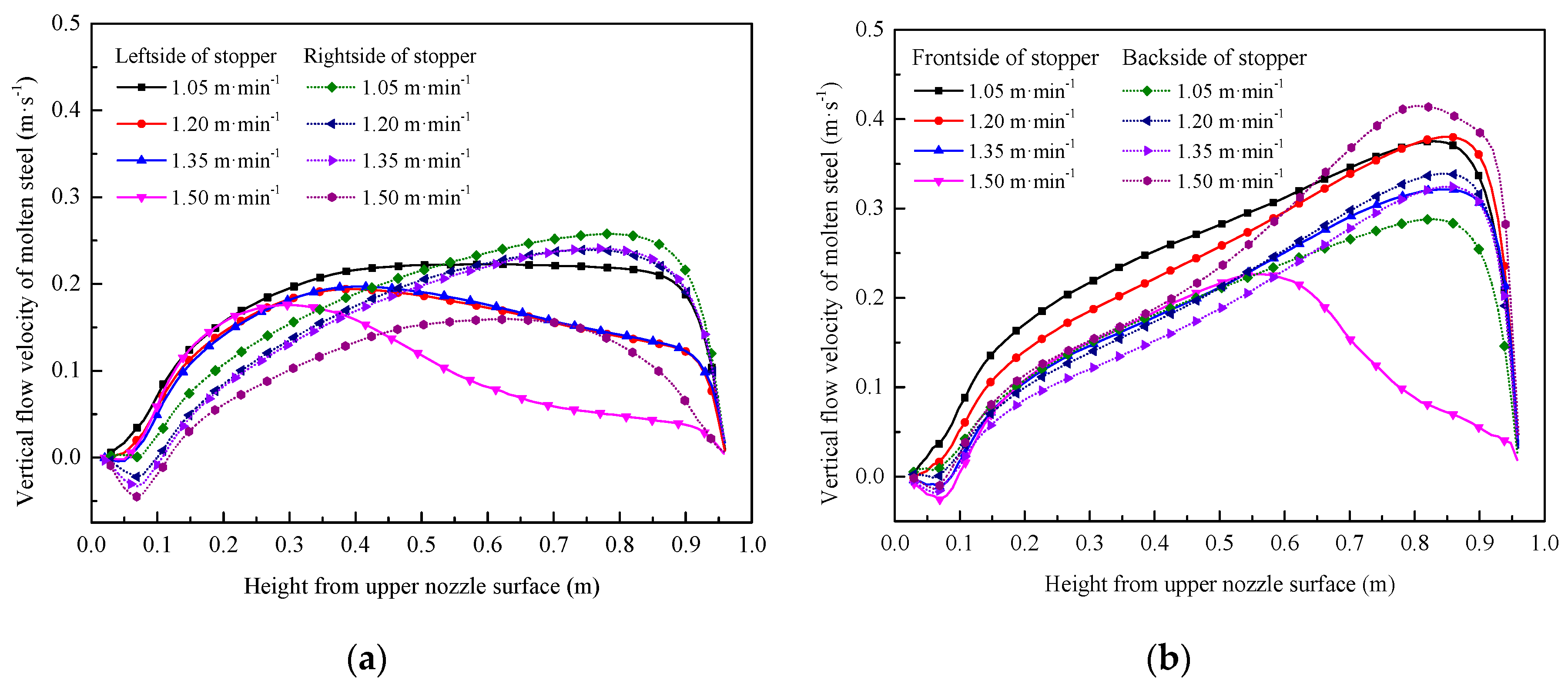
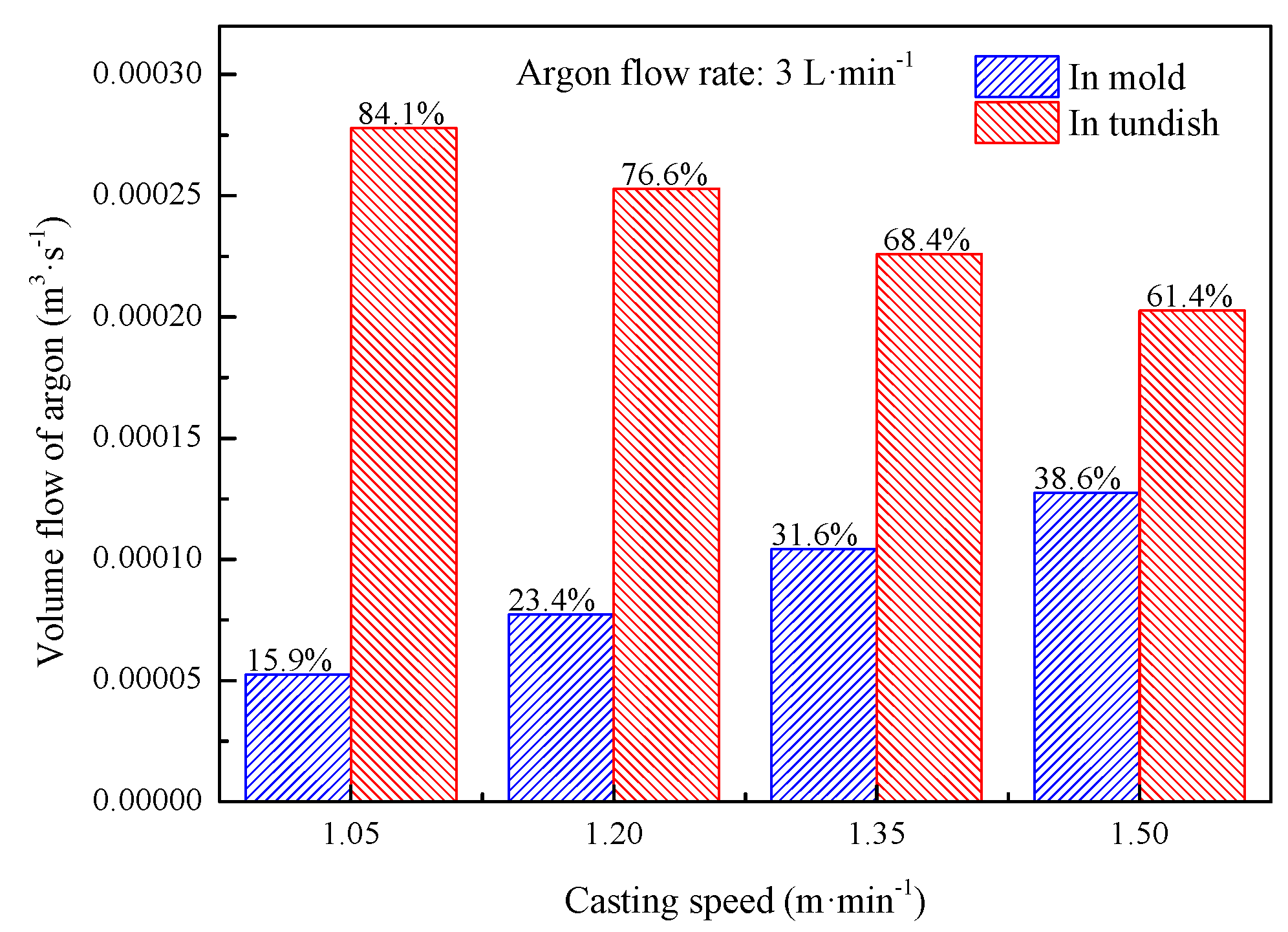
4.3. Effect of Casting Speed on the Flow Behavior of Liquid Steel in the Tundish
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moumtez, B.; Bellaouar, A.; Talbi, K. Numerical investigation of the fluid flow in continuous casting tundish using analysis of RTD curves. J. Iron Steel Res. Int. 2009, 16, 22–29. [Google Scholar]
- Ding, N.; Bao, Y.P.; Sun, Q.S. Optimization of flow control devices in a single-strand slab continuous casting tundish. Int. J. Miner. Metall. Mater. 2011, 18, 292–296. [Google Scholar] [CrossRef]
- Jin, Y.; Dong, X.S.; Yang, F. Removal mechanism of microscale non-metallic inclusions in a tundish with multi-hole-double-baffles. Metals 2018, 8, 611. [Google Scholar] [CrossRef]
- Tripathi, A. Numerical investigation of electro-magnetic flow control phenomenon in a tundish. ISIJ Int. 2012, 52, 447–456. [Google Scholar] [CrossRef]
- Chang, S.; Cao, X.; Zou, Z. Micro-bubble formation under non-wetting conditions in a full-scale water model of a ladle shroud Tundish system. ISIJ Int. 2018, 58, 60–67. [Google Scholar] [CrossRef]
- Chatterjee, S.; Li, D.; Chattopadhyay, K. Modeling of liquid steel/slag/argon gas multiphase flow during Tundish open eye formation in a two-strand Tundish. Metall. Trans. B 2018, 49, 756–766. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Hasan, M.; Isac, M. Physical and mathematical modeling of inert gas-shrouded ladle nozzles and their role on slag behavior and fluid flow patterns in a delta-shaped, four-strand tundish. Metall. Trans. B 2010, 41, 225–233. [Google Scholar] [CrossRef]
- Cwudziński, A. Numerical and physical modeling of liquid steel flow structure for one strand tundish with modern system of argon injection. Steel Res. Int. 2017, 88, 1–14. [Google Scholar] [CrossRef]
- Cwudziński, A. Numerical and physical modeling of liquid steel behaviour in one strand tundish with gas permeable barrier. Arch. Metall. Mater 2018, 63, 589–596. [Google Scholar]
- Jin, Y.L.; Shen, C.; Zhang, J.P. Study on process technology of gas bubbling curtain substituting dam in the tundish of slab casting. J. Iron Steel Res. Int. 2011, 18, 256–262. [Google Scholar]
- Chen, D.; Xie, X.; Long, M. Hydraulics and mathematics simulation on the weir and gas curtain in tundish of ultrathick slab continuous casting. Metall. Trans. B 2014, 45, 392–398. [Google Scholar] [CrossRef]
- Vargas-Zamora, A.; Palafox-Ramos, J.; Morales, R.D. Inertial and buoyancy driven water flows under gas bubbling and thermal stratification conditions in a tundish model. Metall. Trans. B 2004, 35, 247–257. [Google Scholar] [CrossRef]
- Zhong, L.; Li, L.; Wang, B. Water modelling experiments of argon bubbling curtain in a slab continuous casting tundish. Steel Res. Int. 2006, 77, 103–106. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, M.Y.; Zhou, H.B. Fluid flow and interfacial phenomenon of slag and metal in continuous casting tundish with argon blowing. J. Iron Steel Res. Int. 2008, 15, 26–31. [Google Scholar] [CrossRef]
- Terzija, N.; Yin, W.; Gerbeth, G. Electromagnetic inspection of a two-phase flow of GaInSn and argon. Flow Meas. Instrum. 2011, 22, 10–16. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Turbulent flow of liquid steel and argon bubbles in slide-gate tundish nozzles: Part 1. Model development and validation. Metall. Trans. B 2001, 32, 253–267. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Turbulent flow of liquid steel and argon bubbles in slide-gate tundish nozzles: Part II. Effect of operation conditions and nozzle design. Metall. Trans. B 2001, 32, 269–284. [Google Scholar] [CrossRef]
- Mohammadi-Ghaleni, M.; Zaeem, M.A.; Smith, J.D. Computational fluid dynamics study of molten steel flow patterns and particle–wall interactions inside a slide-gate nozzle by a hybrid turbulent model. Metall. Trans. B 2016, 47, 3056–3065. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, C.G.; Yang, M.L. Behavior characteristics of argon bubbles on inner surface of upper tundish nozzle during argon blowing process. Metals 2018, 8, 590. [Google Scholar] [CrossRef]
- Smirnov, A.N.; Efimova, V.G.; Kravchenko, A.V. Design of a permeable annular refractory injection block for the tundish refining of steel. Refract. Ind. Ceram. 2014, 55, 173–178. [Google Scholar] [CrossRef]
- Smirnov, A.N.; Efimova, V.G.; Kravchenko, A.V. Flotation of nonmetallic inclusions during argon injection into the tundish of a continuous-casting machine. Part 1. Steel Transl. 2013, 43, 673–677. [Google Scholar] [CrossRef]
- Smirnov, A.N.; Efimova, V.G.; Kravchenko, A.V. Flotation of nonmetallic inclusions during argon injection into the tundish of a continuous-casting machine. Part 2. Steel Transl. 2014, 44, 11–16. [Google Scholar] [CrossRef]
- Smirnov, A.N.; Efimova, V.G.; Kravchenko, A.V. Flotation of nonmetallic inclusions during argon injection into the tundish of a continuous-casting machine. Part 3. Steel Transl. 2014, 44, 180–185. [Google Scholar] [CrossRef]
- Raghavendra, K.; Sarkar, S.; Ajmani, S.K.; Denys, M.B.; Singh, M.K. Mathematical modelling of single and multi-strand tundish for inclusion analysis. Appl. Math. Modell. 2013, 37, 6284–6300. [Google Scholar] [CrossRef]
- Pfeiler, C.; Wu, M.; Ludwig, A. Influence of argon gas bubbles and non-metallic inclusions on the flow behavior in steel continuous casting. Mater. Sci. Eng. A 2005, 413–414, 115–120. [Google Scholar] [CrossRef]
- Merder, T.; Warzecha, M. Optimization of a six-strand continuous casting tundish: Industrial measurements and numerical investigation of the tundish modifications. Metall. Trans. B 2012, 43, 856–868. [Google Scholar] [CrossRef]
- Ramirez, O.S.D.; Torres-Alonso, E.; Banderas, J.Á.R. Thermal and fluid-dynamic optimization of a five strand asymmetric delta shaped billet caster tundish. Steel Res. Int. 2018, 89, 1700428. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, R.H.; Fang, Q. Numerical simulation of transient multiphase flow in a five-strand bloom tundish during lable change. Metals 2018, 8, 146. [Google Scholar] [CrossRef]
- Lei, H. New insight into combined model and revised model for RTD curves in a multi-strand tundish. Metall. Trans. B 2015, 46, 2408–2413. [Google Scholar] [CrossRef]
- Tang, D.T.; Li, Y.L.; Tian, Z.H. Numerical and physical simulation of bottom blowing gas rate effect on liquid steel fluidity feature in tundish. Shanghai Met. 2012, 34, 49–52. (In Chinese) [Google Scholar]


| Parameters | Value |
|---|---|
| Liquid steel density (kg·m−3) | 7000 |
| Liquid steel viscosity (Pa·s) | 0.0065 |
| Argon gas density (kg·m−3) | 0.27 |
| Working liquid surface height of tundish (mm) | 960 |
| Inner and outer diameter of the shroud (mm) | 70/120 |
| Immersion depth of the shroud (mm) | 250 |
| Diameter of the stopper (mm) | 127 |
| Inner diameter of the upper nozzle (mm) | 50 |
| Sectional dimensions of the slab (mm × mm) | 1235 × 175 |
| Case | Casting Speed (m·min−1) | Argon Flow Rate (L·min−1) | Inner and Outer Diameter of Annular Permeable Brick (mm) |
|---|---|---|---|
| Case 1 | 1.35 | 2, 3, 4, 5 | 220/280 |
| Case 2 | 1.05, 1.20, 1.35,1.50 | 3 | 220/280 |
| Argon Flow Rate (L·min−1) | Minimum Bubble Diameter (mm) | Maximum Bubble Diameter (mm) | Average Bubble Diameter (mm) | Distribution Index |
|---|---|---|---|---|
| 2 | 0.6 | 2.85 | 1.6 | 2.82 |
| 3 | 0.65 | 2.90 | 1.8 | 4.61 |
| 4 | 0.7 | 2.95 | 2.0 | 5.08 |
| 5 | 0.80 | 3.0 | 2.2 | 7.96 |
| Process Condition | Average Residence Time (s) | Volume Fraction of Plug Flow (%) | Volume Fraction of Dead Zone (%) | Volume Fraction of Mixed Flow (%) |
|---|---|---|---|---|
| without argon | 592.12 | 30.91 | 12.75 | 56.34 |
| with argon | 593.56 | 31.59 | 12.53 | 55.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Cheng, C.; Li, Y.; Zhang, C.; Zhang, J.; Jin, Y. A Simulation Study on the Flow Behavior of Liquid Steel in Tundish with Annular Argon Blowing in the Upper Nozzle. Metals 2019, 9, 225. https://doi.org/10.3390/met9020225
Qin X, Cheng C, Li Y, Zhang C, Zhang J, Jin Y. A Simulation Study on the Flow Behavior of Liquid Steel in Tundish with Annular Argon Blowing in the Upper Nozzle. Metals. 2019; 9(2):225. https://doi.org/10.3390/met9020225
Chicago/Turabian StyleQin, Xufeng, Changgui Cheng, Yang Li, Chunming Zhang, Jinlei Zhang, and Yan Jin. 2019. "A Simulation Study on the Flow Behavior of Liquid Steel in Tundish with Annular Argon Blowing in the Upper Nozzle" Metals 9, no. 2: 225. https://doi.org/10.3390/met9020225
APA StyleQin, X., Cheng, C., Li, Y., Zhang, C., Zhang, J., & Jin, Y. (2019). A Simulation Study on the Flow Behavior of Liquid Steel in Tundish with Annular Argon Blowing in the Upper Nozzle. Metals, 9(2), 225. https://doi.org/10.3390/met9020225





