Abstract
The present work provides validation of the ultimate tensile strength computational models, based on full-scale lamellar graphite iron casting process simulation, against previously obtained experimental data. Microstructure models have been combined with modified Griffith and Hall–Petch equations, and incorporated into casting simulation software, to enable the strength prediction for four pearlitic lamellar cast iron alloys with various carbon contents. The results show that the developed models can be successfully applied within the strength prediction methodology along with the simulation tools, for a wide range of carbon contents and for different solidification rates typical for both thin- and thick-walled complex-shaped iron castings.
1. Introduction
Nowadays, there is a great need to further improve both the material properties and the prediction models for optimization of the heavy truck engine components aimed to fulfil the rigorous environmental legislations, sustainability goals, and customer demands. Cylinder blocks and cylinder heads are the primary components of these engines, and the majority of them are composed of lamellar graphite iron (LGI). The ultimate tensile strength (UTS) of LGI is an essential material property that determines the engine performance and the fuel consumption. The complex geometry and variation of the wall thickness in the cylinder blocks result in different solidification times through the component, and thus, different tensile properties.
A number of investigators [1,2,3,4,5,6] underlined the major influence of the graphite flake size on the strength of LGI. It is believed that under stress, the graphite flakes are dispersed in the metal matrix act as notches that decrease the material strength. Modified Griffith and Hall–Petch models were introduced for the prediction of UTS in LGI, where the maximum graphite length was considered as the maximum defect size [3,7,8,9]. Recently, it was found that the maximum defect size can never be larger than the interdendritic space between the primary austenite dendrites formed during the solidification process [10]. The length scale of the interdendritic space was characterized by the hydraulic diameter of the interdendritic phase (), which proved to be the most suitable parameter to express the detrimental effect of the graphite lamella in the metallic matrix. Thus, the parameter was introduced as the maximum defect size in the modified Griffith and Hall–Petch equations [10,11].
Over the past decades, computer simulations of LGI solidification were carried out by several researchers [7,8,9,12,13] to describe the thermal history and the microstructure evolution of LGI castings. The main objective of these studies was prediction of the UTS. Macroscopic heat flow modeling, coupled with growth kinetic equations, was introduced in [7] to predict various microstructure features of LGI. Consequently, a modified Griffith fracture relation was applied to determine the UTS of a commercial LGI alloy. A similar solidification model was developed in [8], where a microstructure evolution model was employed together with the modified Hall–Petch equation for calculation of the UTS. Note that in [8], two different cooling rates resulted in two different relationships between the UTS and the maximum graphite flake length. Similar observations were made in [10], where three different cooling rates led to providing three different linear dependencies between the eutectic cell size (direct proportional to the maximum graphite length) and the UTS.
The present work provides validation of the UTS computational models against experimental data, based on full-scale pearlitic LGI gravity casting process simulation. We investigated whether the models recently developed in [10,11] can be applied within the UTS prediction methodology, along with the simulation tools, for different alloy compositions and for different solidification rates. The novel methodology for UTS prediction, presented in this paper, involves as the key morphological parameter, along with the pearlite lamellar spacing. These parameters are dependent on solidification time, cooling rate, and alloy composition. The proposed approach bears simplicity compared to the microstructure modelling methods [7,8]. The methodology is validated to include analytical formulation of the UTS prediction models and robust experimental thermal analysis, to obtain latent heat of solidification and solid-state transformation as input data for the simulation. First, the UTS modeling methods are elaborated followed by the details on the experimental setup and alloy composition. Casting simulation model is then introduced, as well as the simulation procedure. The results are discussed in comparison with the temperature and UTS measurements, followed by conclusions regarding applicability and limitations of the proposed UTS prediction methodology.
2. UTS Modeling
The modified Griffith fracture relation is given by Equation (1) [3], and the modified Hall–Petch strengthening model is represented by Equation (2) [8].
where is the ultimate tensile strength, α is the maximum defect size, and kt is the stress intensity factor of the metallic matrix, k1 and k2 are the contributions from other strengthening mechanisms, and d is the grain size. The maximum defect size and grain size, α and d, are provided in μm, parameters kt and k2 are in MPa, , and k1 is in MPa.
It was found in [10] that is the dominant factor that reduces the UTS in lamellar graphite iron alloys. A modified Griffith equation was obtained in [10] as result of the linear regression analysis of the experimental data, Equation (3).
According to this model, if a tensile force is applied on the microstructure, a crack will start to form at a certain stress level. The crack will propagate relatively easily through the numerous interconnected graphite particles that are embedded in the metallic matrix of the eutectic cell. When the crack reaches the metallic matrix (pearlite) that was originated from the primary austenite (dendritic phase), the relatively rapid crack extension will be halted, due to the fact that much larger stresses are required for the fracture of this phase. The magnitude of the additional stress is proportional to the pearlite lamellar spacing (λpearlite). Based on this assumption, it becomes apparent that the effect of λpearlite on the UTS must be taken into consideration. Thus, linear multiple regression analysis was made to determine the simultaneous influence of the and the λpearlite on the UTS. The model obtained is based on the modified Hall–Petch relation, and is expressed by Equation (4) [11].
The parameter was found to be related to the solidification time (ts) and the fraction of primary austenite (fγ), as seen from Equation (5) [14].
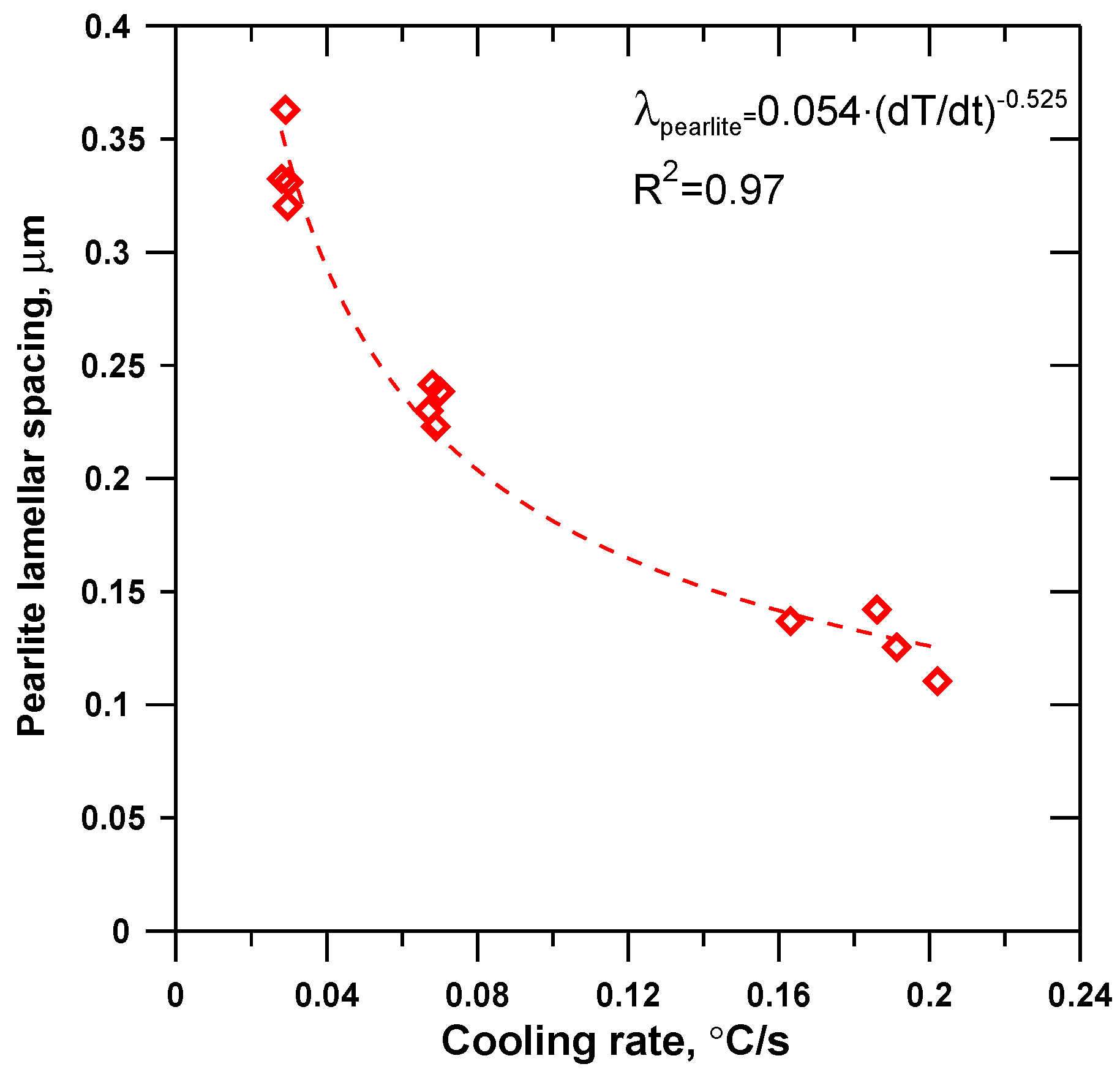
The λpearlite parameter at room temperature was assumed to be dependent on the cooling rate in the eutectoid transformation region. The empirical relationship between λpearlite at room temperature, and the cooling rate at the temperature intervals between 700 and 740 °C, is shown in Figure 1. The experimentally derived relation Equation (6) was used for investigating the effect of different λpearlite prediction models on simulated UTS. The measurements techniques, the microstructure and thermal data that resulted in Equation (6), are presented elsewhere [11,12]. Briefly, the pearlite lamellar spacing was measured using SEM and a linear intercept method. The minimum value was considered to be the correct spacing (perpendicular to the lamellae). The distance between 11 adjacent ferrite lamellas was measured and divided by 10 for estimation of a single interlamellar spacing.
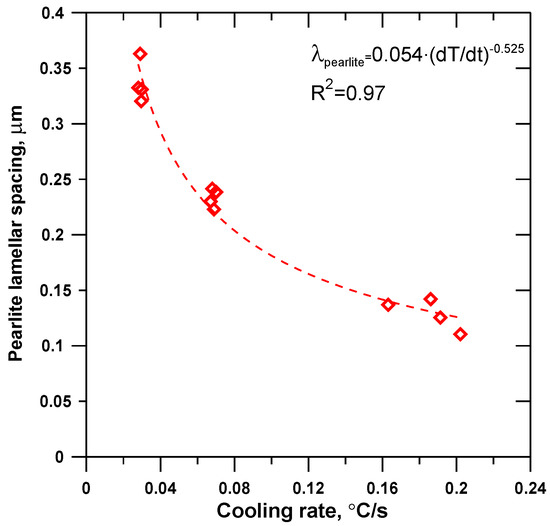
Figure 1.
Pearlite lamellar spacing as function of cooling rate between 700 and 740 °C.
3. Materials and Methods
3.1. Cylindrical Castings
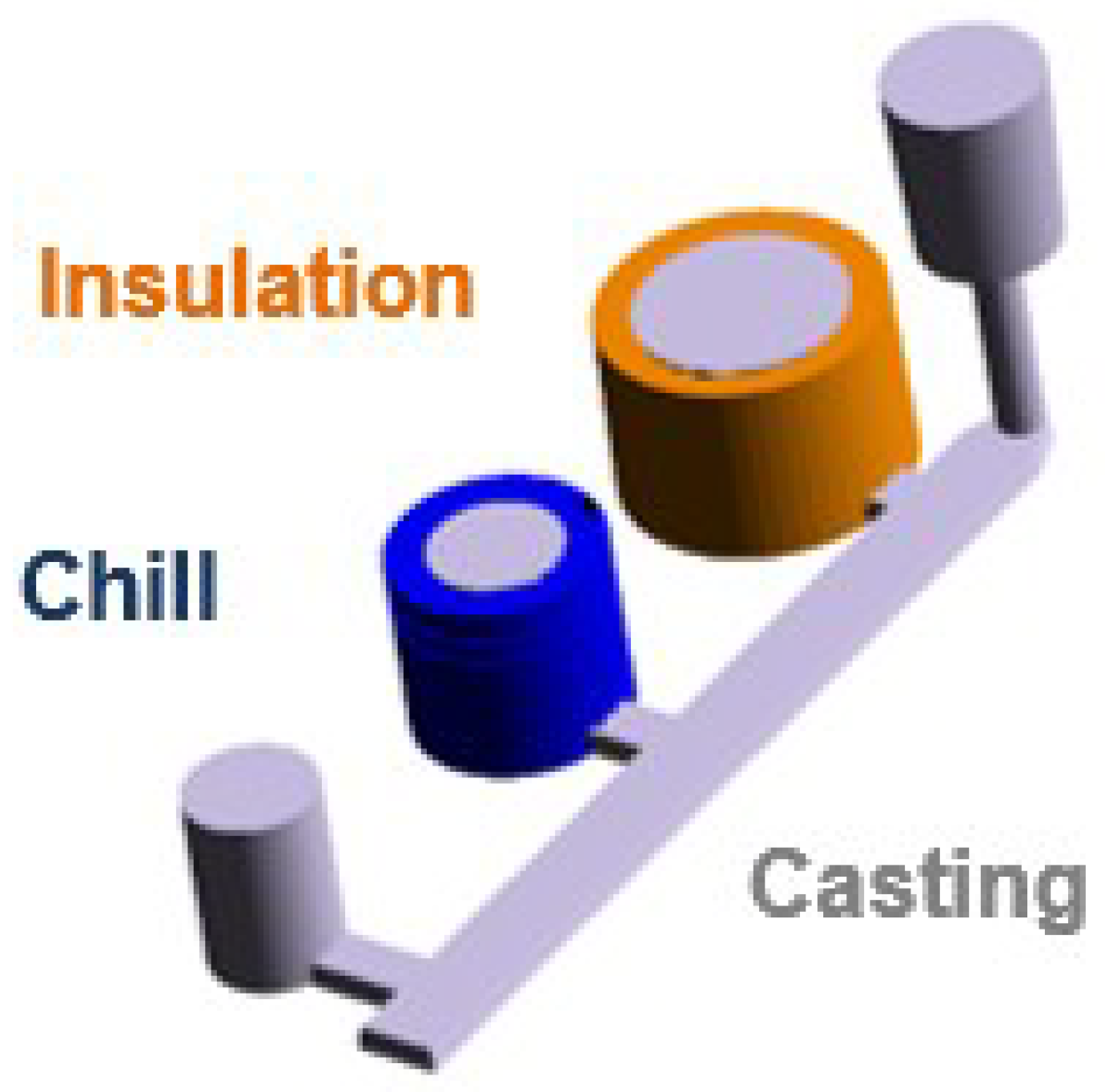
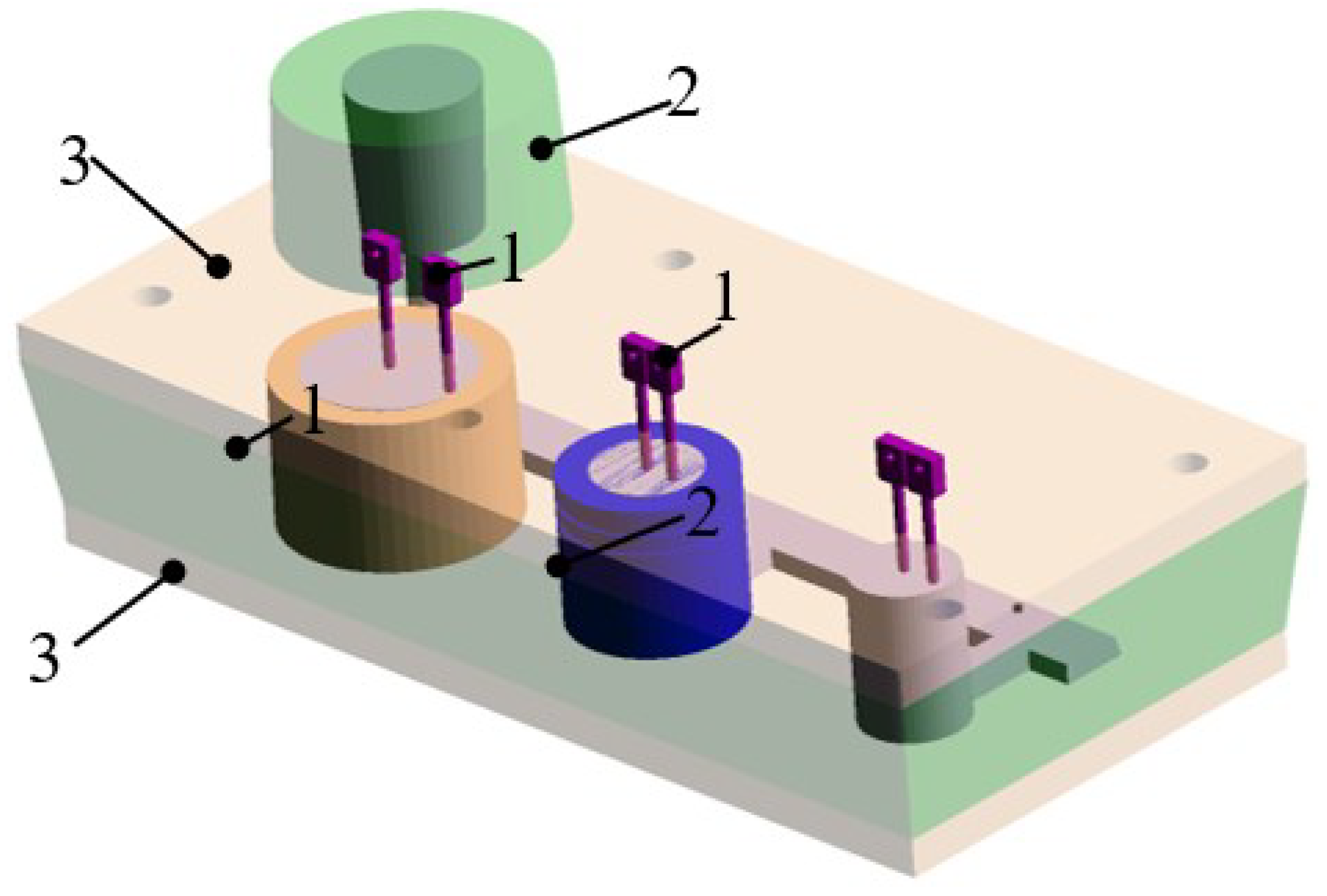
The experimental layout contained three cylindrical cavities, each one surrounded by a different material (steel chill, sand, and insulation) intended to provide three different cooling rates. The entire assembly was enclosed by a furan-bounded sand mold. The dimensions of the cylinders surrounded by sand and chill were ∅50 × 70 mm, and the insulated cylinder dimensions were ∅80 × 70 mm. A lateral 2-D heat flow condition was induced by placing an insulation plate at the top and bottom of the cylindrical castings. The design of the cylindrical castings and arrangement of the experimental layout are shown in Figure 2 and Figure 3, respectively.
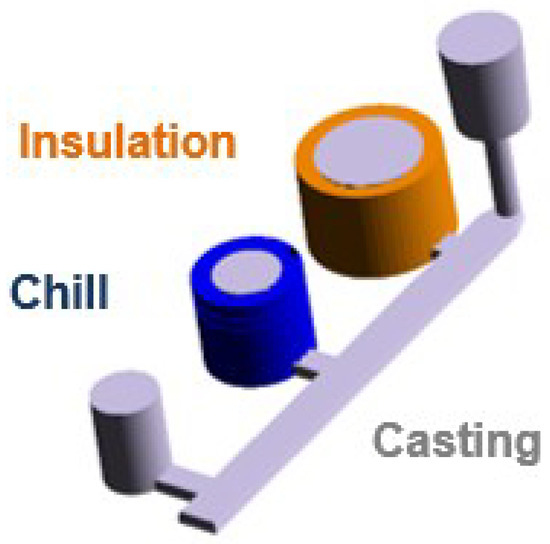
Figure 2.
Cylindrical castings with the insulation and chill.
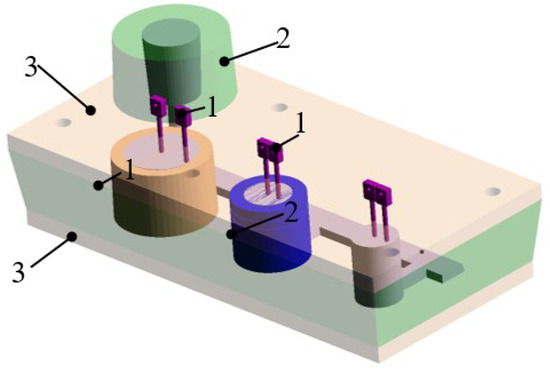
Figure 3.
The experimental layout. (1) Thermocouples, (2) sand mold, and (3) insulation plates.
Two type S thermocouples with glass tube protection were embedded in every cylindrical casting. A central thermocouple was located on the central axis of the cylinder. The distance between the central and the lateral thermocouple was 20 mm for the ∅50 mm cylinder and 30 mm for the ∅80 mm cylinder. The thermocouples were placed at the mid-height of each cylinder and the temperatures were recorded at approximately 0.2 s interval. A 16-bit resolution data acquisition system with the sampling rate 100 Hz was employed [12].
The mold-filling time was 12 s. The solidification times of the metal in the chill, sand, and insulation were roughly 80, 400, and 1500 s, respectively. An electric induction furnace was utilized for melting of the charge material. The cast iron base alloy was inoculated with a constant level of a standard Sr-based inoculant. Four hypoeutectic lamellar graphite iron heats with varying carbon contents were produced. The alloy with the higher carbon content was cast first, and steel scraps were added to the furnace for the adjustment of the carbon content in the following casting. Coin-shaped specimens were extracted for chemical analysis. The chemical compositions of the four different alloys are presented in Table 1. All the castings had a fully pearlitic microstructure.

Table 1.
Chemical composition (wt %) and carbon equivalent (Ceq = %C + %Si/3 + %P/3).
Tensile strength measurements were performed using a dog bone-shaped specimen with 6 mm diameter in the gauge section, 35 mm gauge length, and a 3 μm surface finish. The tests were conducted at a strain rate of 0.035 mm/s and at room temperature. The experimental tensile samples were machined at the distance ~10 mm (sand, chill) and ~20 mm (insulation) from the cylinder axis. The load cell error of the tensile testing machine was <0.5%.
3.2. Simulation Model and Assumptions
A CFD software (Flow-3D CAST, v.5.0 from Flow Science, Inc., Santa Fe, NM, USA) [15] was employed to develop a full-scale 3D model of the casting process for the experimental layout. Mold filling and the cooling/solidification stages were simulated, and local UTS computations were performed on the customized models. Mold-filling time was 12 s, and the laminar flow model was applied. The casting temperature was 1360 °C, and the metal input diameter was 3 cm. The ambient temperature was set to 20 °C. Symmetry boundary conditions were used on the faces of the computational domain, except for the upper face, where the pressure boundary condition was applied. A computational grid of cubical control elements was generated with the cell size 3 mm. The computational grid had a total of ~1 million cells. Different grid densities were tested, and grid-independent results were obtained. The explicit solver was employed during the mold filling, whereas the implicit solver was used for heat transfer simulation in the solidification phase. Since the focus was on heat transfer and the UTS computation methodology, shrinkage and micro-porosity models were not included in the solidification phase.
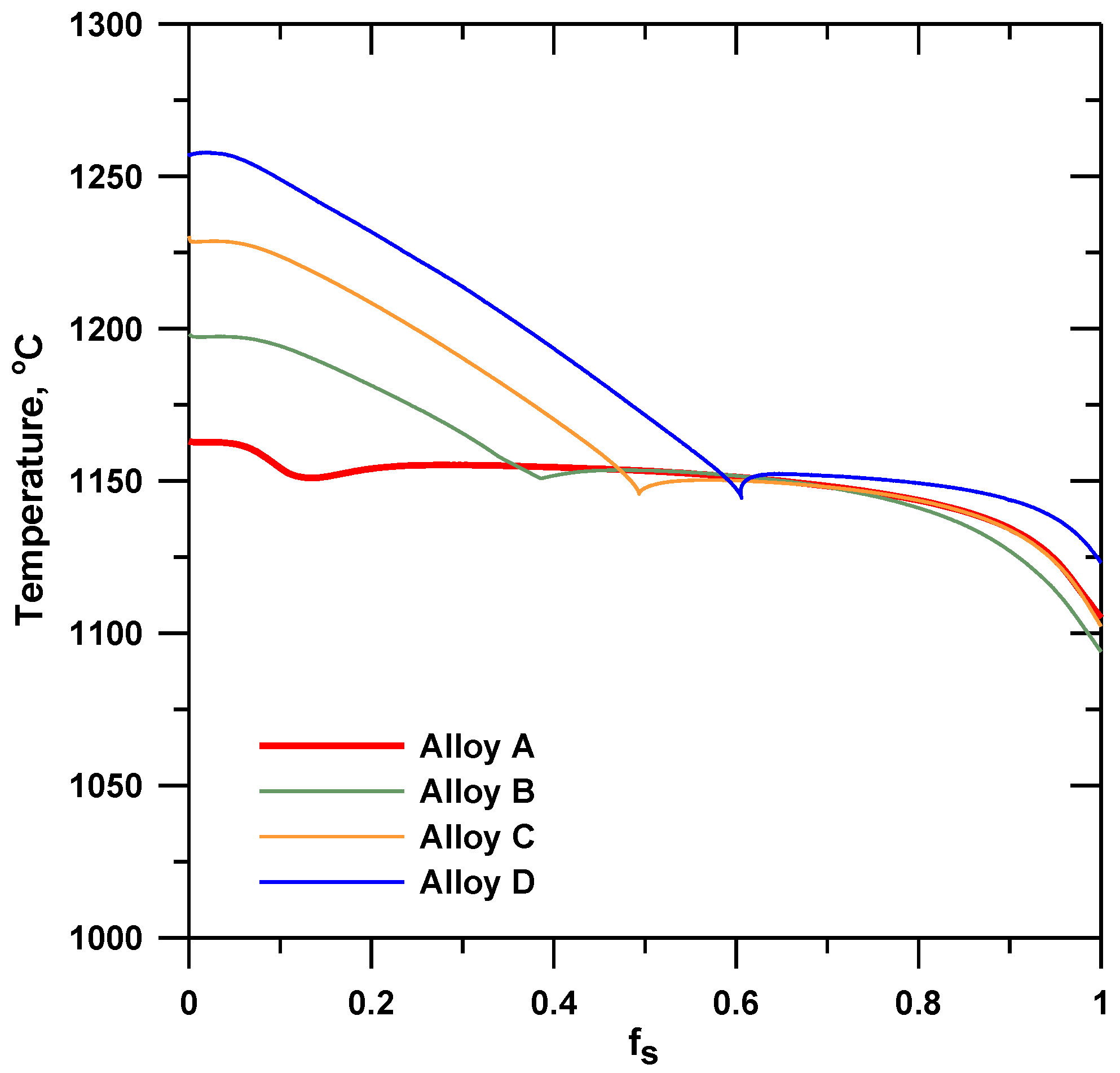
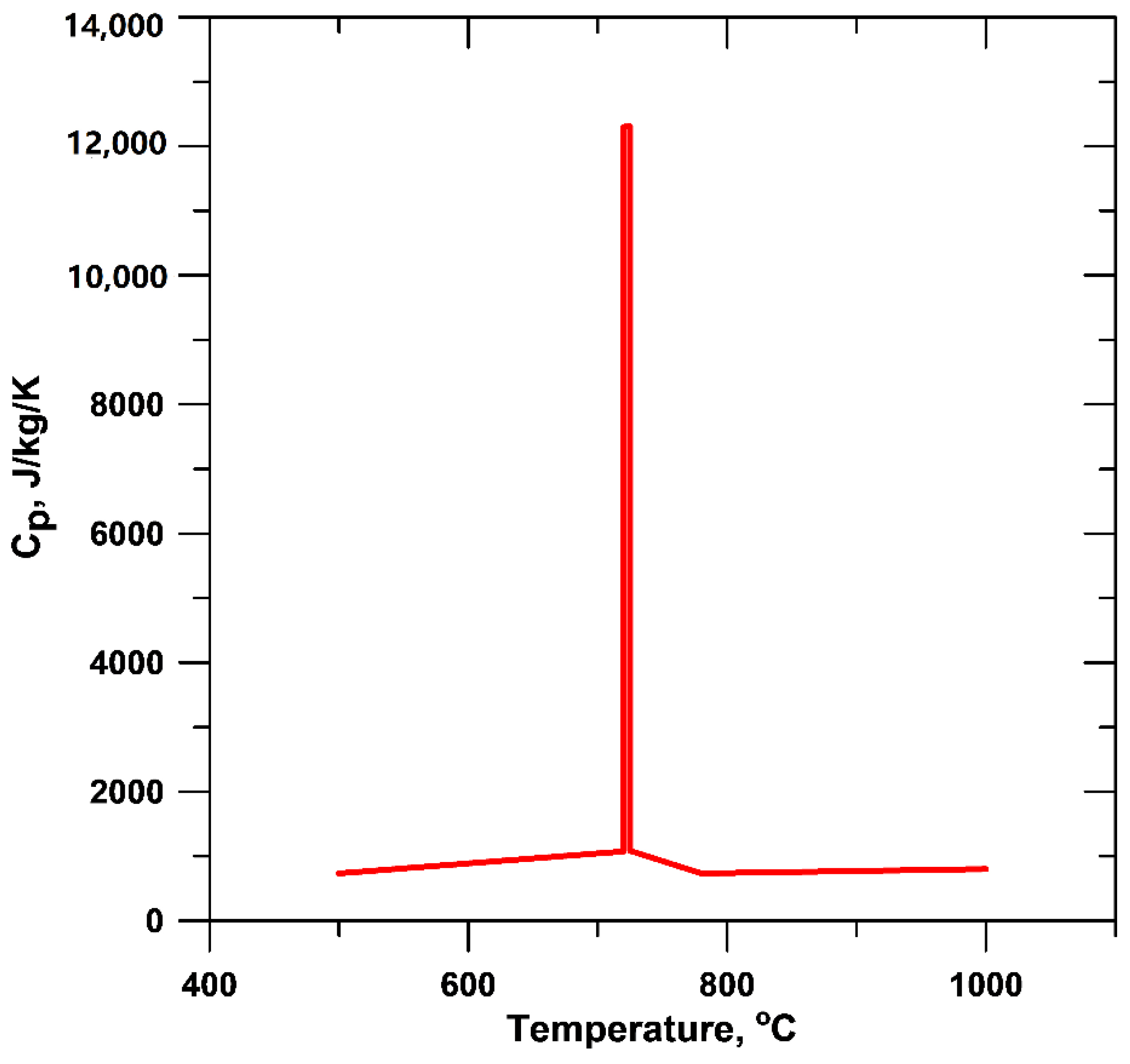
In this work, the amount of latent heat release due to solidification was related to the solid fraction curves, seen in Figure 4, for the studied alloys. These curves were calculated from the registered experimental cooling curves by using the Fourier thermal analysis method [16,17]. The latent heat of solidification was considered equal to 240 kJ/kg for all studied alloys [18]. Fourier thermal analysis was also applied on cooling curves for the determination of the latent heat release during the eutectoid transformation. The latent heat releases at the eutectoid transformation was found to be similar for all alloys and were incorporated into the specific heat curve as it is shown in Figure 5. The temperature dependent cast iron thermophysical properties [12], and the calibrated heat transfer coefficients applied in the simulation are presented in Table 2.
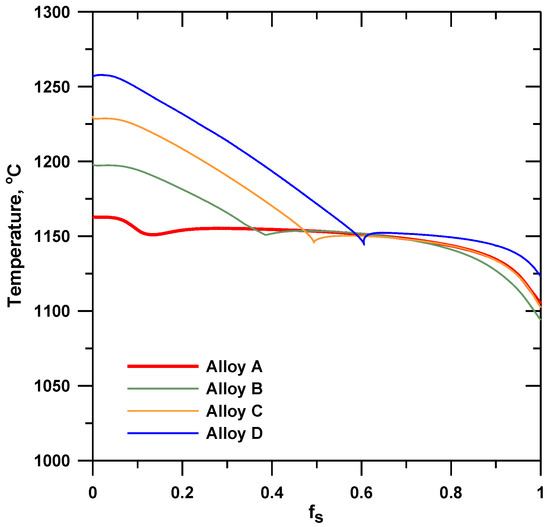
Figure 4.
Solid fraction variation with temperature.
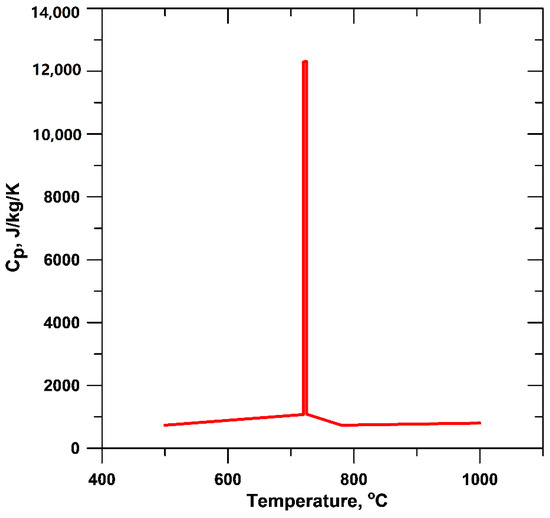
Figure 5.
Specific heat as function of temperature.

Table 2.
Temperature dependent properties of the cast iron and heat transfer coefficients *.
3.3. Simulation Procedure
The simulation procedure consisted of model calibration with respect to the experimental cooling curves available at the location of the central thermocouple. Correct reproduction of the experimental cooling curves is the key for the UTS computation methodology, and one is free to choose methods for model calibration. In this work, the calibration was done by adjustment of the typical heat transfer coefficients between the metal and the insulation, sand, and chill. The UTS calculations for the cylinders were performed during post-processing, by applying local solidification times, local cooling rates in the eutectoid transformation region, and the experimentally determined fraction of primary austenite (fγ) for each alloy: 0.3 for alloy A, 0.4 for alloy B, 0.51 for alloy C, and 0.61 for alloy D [16].
4. Results and Discussion
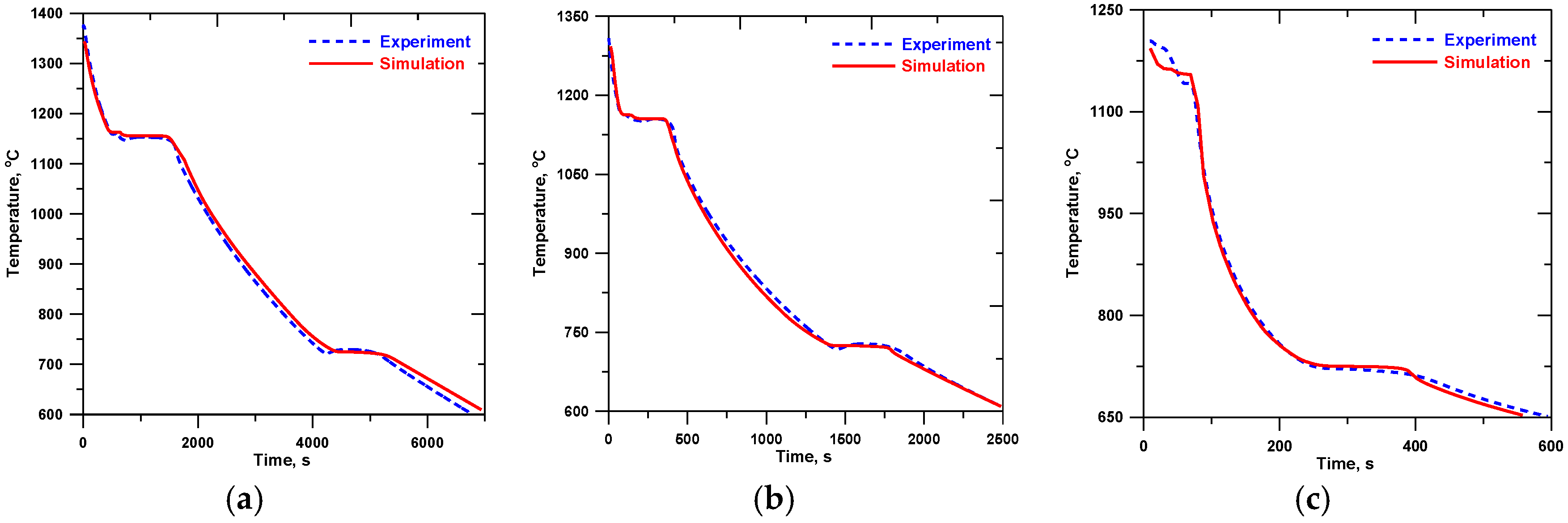
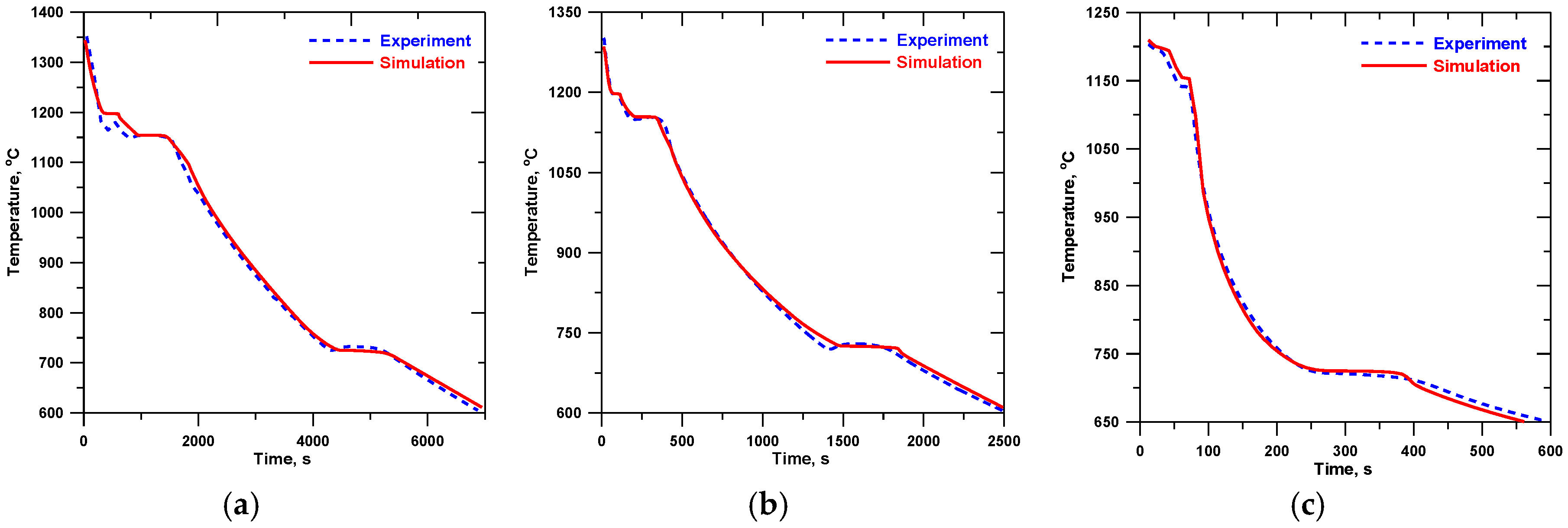
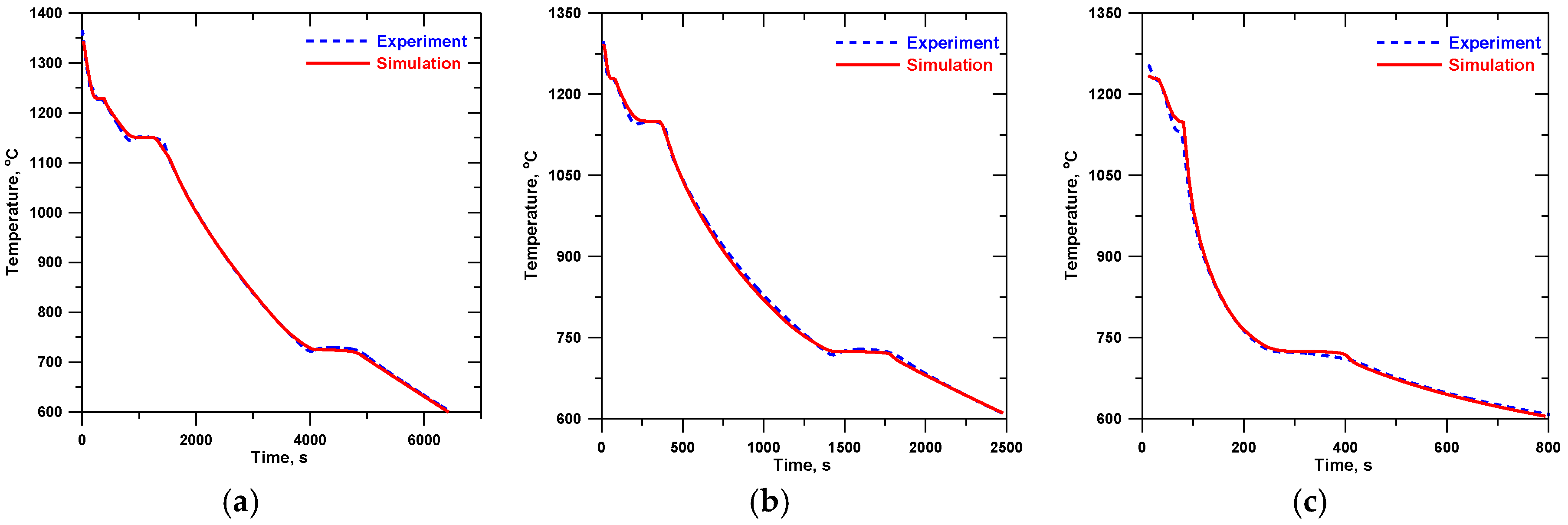
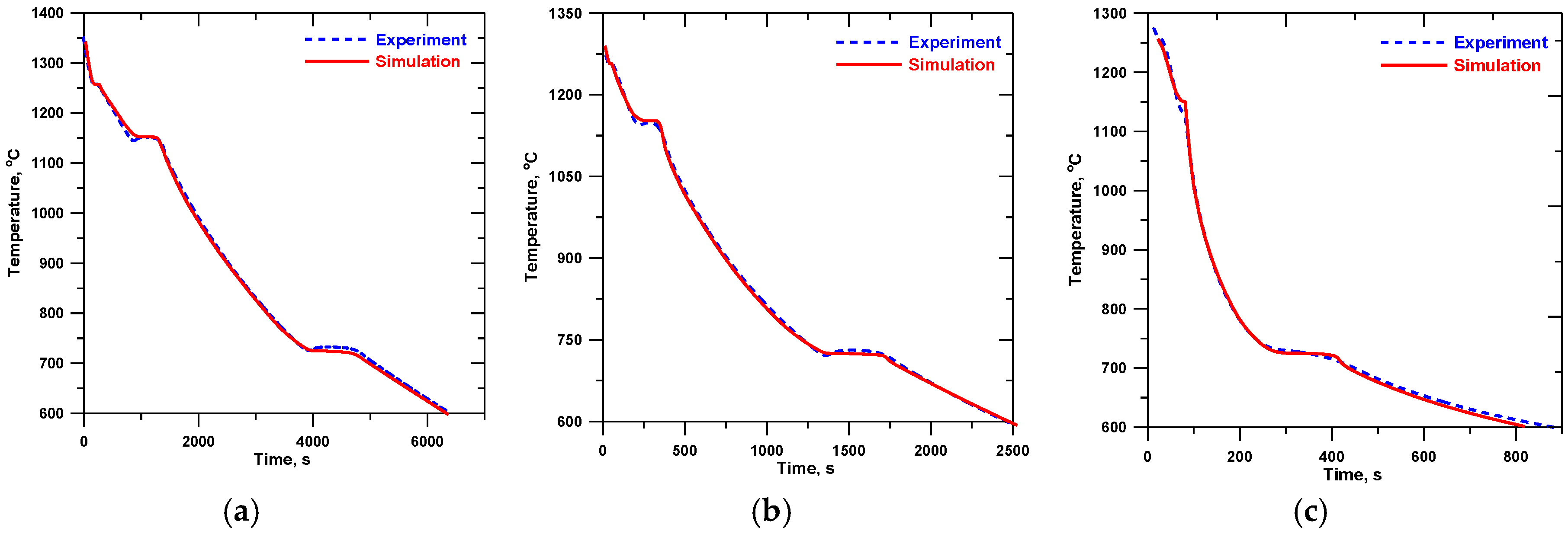
The general agreement within 7% was achieved between the simulated and measured cooling curves for insulation-, sand-, and chill-encapsulated cylinders; see Figure 6, Figure 7, Figure 8 and Figure 9. The larger differences were observed in the solidification region of the chill castings where the eutectic reaction was predicted at higher temperature than measured. This is because the solid fraction-temperature curves were derived from the sand-casting thermal histories, where the undercooling was much lower. Moreover, the solidification model in the simulation used the enthalpy method [19] and ignored the kinetics of phase transformation and, therefore, the undercooling and recalescence of solidification were not predicted. However, the simulated solidification times were in good agreement with the experiment.
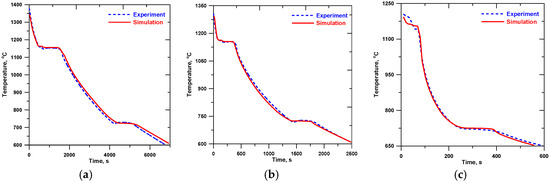
Figure 6.
Simulated and experimental cooling curves (central thermocouple) for alloy A: (a) insulation, (b) sand, and (c) chill.
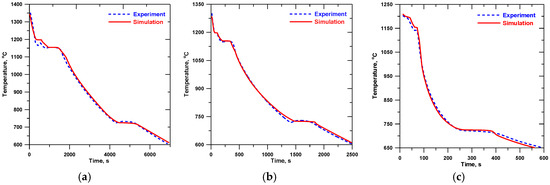
Figure 7.
Simulated and experimental cooling curves (central thermocouple) for alloy B: (a) insulation, (b) sand, and (c) chill.
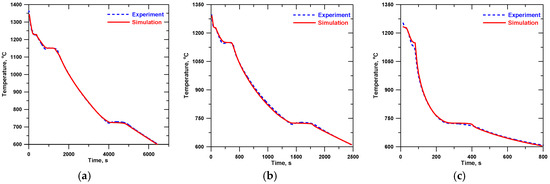
Figure 8.
Simulated and experimental cooling curves (central thermocouple) for alloy C: (a) insulation, (b) sand, and (c) chill.
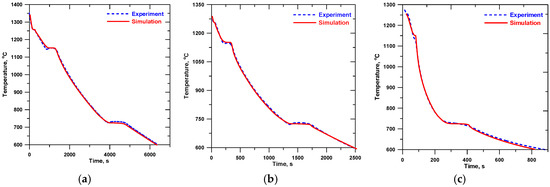
Figure 9.
Simulated and experimental cooling curves (central thermocouple) for alloy D: (a) insulation (b) sand, and (c) chill.
The measurement accuracy of the type S thermocouples was ±1.5 °C. It is worth noting that some of the thermocouples inserted in the melt could be slightly displaced from their intended positions during the solidification, which created an additional source of the measurement error; this can be seen clearly, e.g., from the solidification part of the experimental cooling curve for the insulated cylinder in Figure 7.
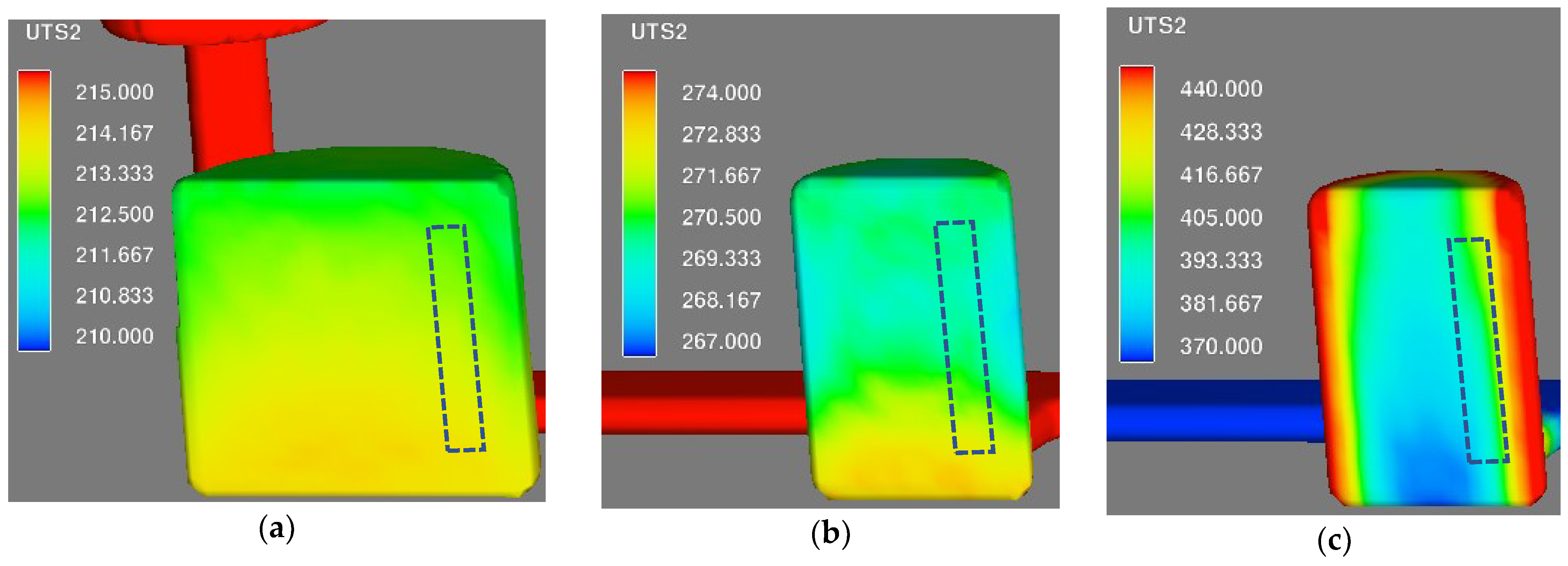
The simulated solidification times and cooling rates were used in Equations (3) and (4) for the calculation of UTS. The predicted UTS distribution, substituted in the middle cross-section of the alloy B casting, is shown in Figure 10. The figure illustrates the inhomogeneous material strength in the casting. It is directly related to the temperature gradient and the cooling rate distribution during solidification and solid-state transformation. The reduced UTS is the result of the microstructure coarseness that is related to the solidification time and the cooling rate. Moreover, large UTS gradients on the chilled cylinder can be explained by the large temperature gradients at high solidification rate. Intermediate and slow solidification rates on sand- and insulation-encapsulated cylinders resulted in more uniform distribution of UTS values, due to the smaller temperature gradients during solidification. It should be noted that the variation of UTS magnitude within the tensile bar positions (shown with dashed lines) complicates the model validation.
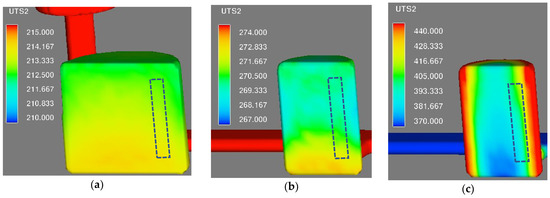
Figure 10.
Distribution of ultimate tensile strength (UTS) calculated from Equations (4) and (6) for alloy B: (a) insulation-, (b) sand-, and (c) chill-encapsulated cylinder; the dashed lines indicate the position of the tensile bars.
The obtained values were compared to the measured UTS. Table 3 presents the experimental and simulated UTS results for different cooling rates and for each alloy. The simulated UTS values in Table 3 were picked from the mid-height locations of the tensile bar regions, indicated in Figure 10 with dashed lines. This would correspond to the failure location in the tensile test. However, the exact fracture location might be influenced by several other factors, such as microporosities, graphite flakes that are in contact with the casting surface, or other casting impurities. All of these can cause the crack initiation at positions where the theoretical material strength is not the lowest. Apparently, the fracture analysis is out of scope of the present work. There are quite small differences between simulated and measured UTS values, with the exception of the intermediate and slow cooling rates (sand and insulation) for alloy A, where all the models predicted the UTS with less accuracy. Relatively high, but still acceptable average percentage errors are also observed for the insulated cylinders cast of alloys C and D.

Table 3.
Experimental and simulated UTS.
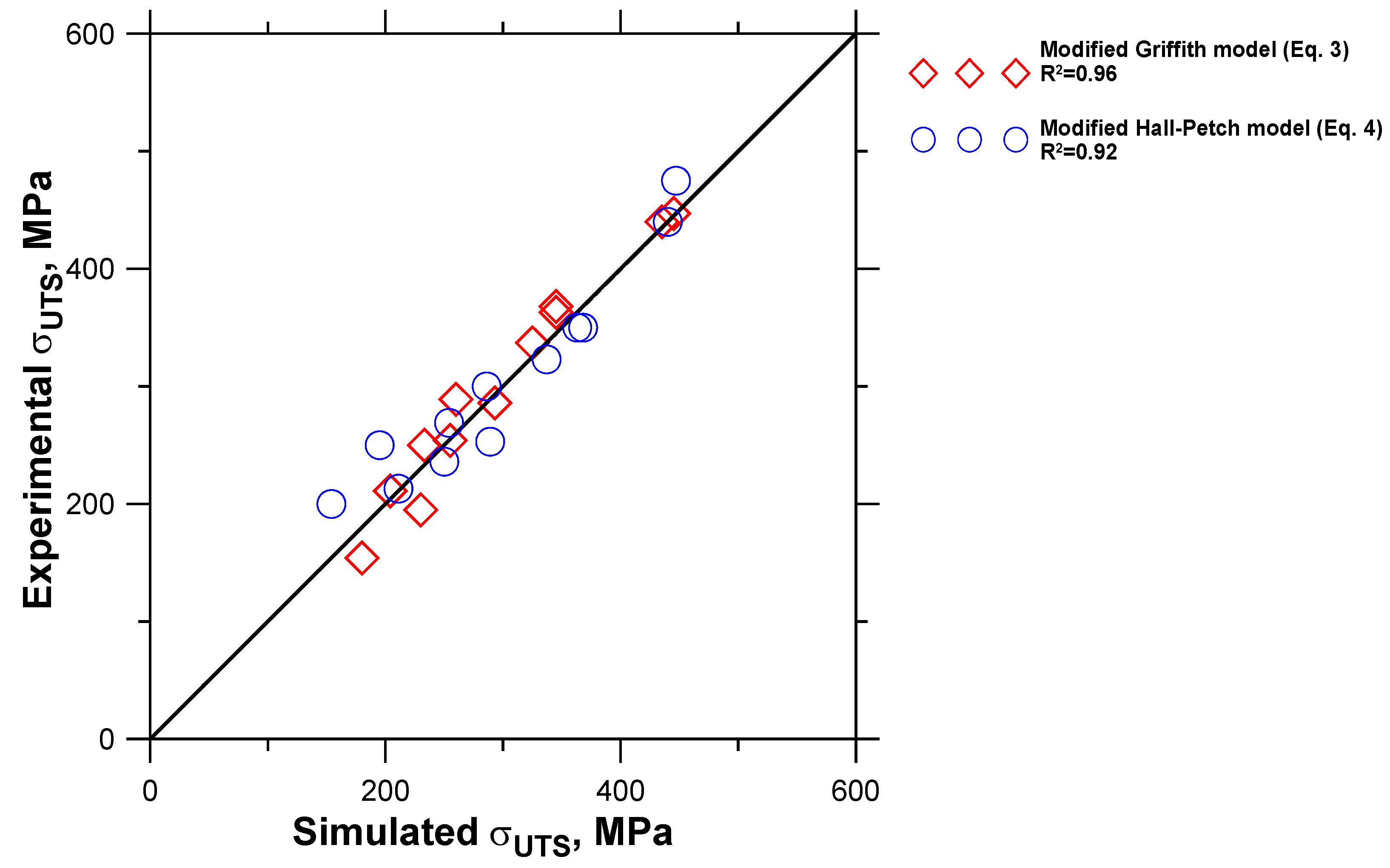
Comparisons between the calculated and the measured data are demonstrated in Figure 11. The graph reveals a relatively strong correlation between the measured and computed UTS. The R2 values show that Equation (3) predicts the UTS with better accuracy than Equation (4). This indicates the need to develop further the model for prediction of the λpearlite parameter.
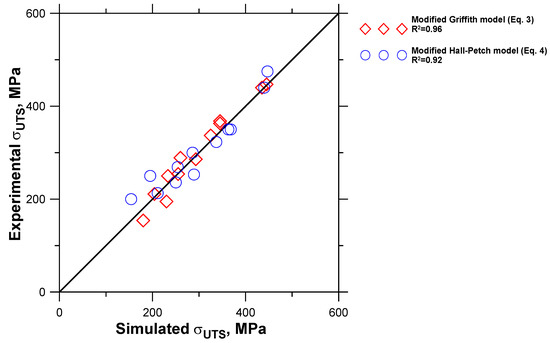
Figure 11.
Correlation between measured and simulated UTS values.
The observed deviations between the simulated and measured UTS can be also attributed to the limited number of tensile specimens [10] and to uncertainties regarding the measurements accuracy of the parameter, especially for the low cooling rate samples [20] that were used to develop the UTS models.
The presented results should be related to two fundamental publications on computer simulations of LGI solidification coupled with the Griffiths and Hall–Petch models [7,8]. The models for UTS calculation utilized in these works were based on a narrow carbon content interval, and on a limited cooling rate variation, in comparison. Moreover, growth kinetic equations were employed in [7,8]. On the contrary, the latent heat release model by the “enthalpy method” [19] was adopted for the solidification simulation in the present work. Furthermore, the presented way to determine the key parameters and incorporate them into material property prediction is novel. In [7,8], the key parameter was the eutectic cell diameter. It is evident that the modified Griffith and Hall–Petch equations are applicable once the eutectic diameter can be predicted, as well as the pearlite lamellar spacing in the Hall–Patch equation. A completely different approach validated in this work involved the hydraulic diameter as the key morphological parameter, along with the pearlite lamellar spacing introduced in [8]. The presented methodology to calculate the UTS features the simplicity of determining the key parameters by simulation (solidification time, cooling rate, and composition dependent). While [7] and [8] introduce complex microstructure models valid for small process intervals (with respect to composition and cooling condition), the current methodology lays back to a robust experimental thermal analysis [16], providing accurate input data (latent heat of both solidification and solid-state transformation) for the simulation. A robust iteration process for tuning up the heat transfer coefficient results in the accurately predicted cooling rate.
5. Conclusions
The novel UTS prediction methodology for fully pearlitic LGI alloys presented in this paper involves hydraulic diameter as the key morphological parameter, along with the pearlite lamellar spacing. It is characterized by simplicity, in comparison to the microstructure modelling methods. The methodology includes analytical formulation of the UTS prediction models, and robust experimental thermal analysis. The latter provides the latent heat of solidification and solid-state transformation as input data for the solidification simulation. In turn, the simulation delivers the solidification time and cooling rates for the UTS prediction models.
Microstructure models for the prediction of hydraulic diameter and the pearlite lamellar spacing, combined with modified Griffith and Hall–Petch equations, were incorporated into casting simulation software for the prediction of UTS in fully pearlitic LGI alloys. Overall, the simulation UTS results were found to be in good agreement (within 9% on the average) with the measurements. However, high average percentage errors were observed for the intermediate and slow cooling rates (sand and insulation) for the alloy with the higher carbon content (alloy A). This study revealed the necessity for development of a more advanced model for the prediction of the λpearlite parameter. The results demonstrated the applicability of the novel UTS prediction models for different chemical compositions and cooling conditions.
Further development of the microstructure modelling would enable determination of the key parameters (hydraulic diameter and pearlite lamellar spacing). However, it seems not to be critical for the presented novel UTS prediction methodology which is valid for the wide process interval.
Author Contributions
A.D. designed the experiment and supervised the work, I.B. performed the simulations, V.F. analyzed the data and wrote the paper, A.D. and I.B. reviewed the paper.
Funding
This research received no external funding.
Acknowledgments
This work was performed within the Swedish Casting Innovation Centre. Cooperating parties are Jönköping University, Scania CV AB, Swerea SWECAST AB and Volvo Powertrain Production Gjuteriet AB. Participating persons from these institutions/companies are acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Collini, L.; Nicoletto, G.; Konecná, R. Microstrucure and mechanical properties of pearlitic lamellar cast iron. Mater. Sci. Eng. A 2008, 488, 529–539. [Google Scholar] [CrossRef]
- Ruff, G.F.; Wallace, J.F. Effects of solidification structure on the tensile properties of lamellar iron. AFS Trans. 1977, 56, 179–202. [Google Scholar]
- Bates, C. Alloy element effect on lamellar iron properties: Part II. AFS Trans. 1986, 94, 889–905. [Google Scholar]
- Nakae, H.; Shin, H. Effect of graphite morphology on tensile properties of flake graphite cast iron. Mater. Trans. 2001, 42, 1428–1434. [Google Scholar] [CrossRef]
- Baker, T.J. The fracture resistance of the flake graphite cast iron. Mater. Eng. Appl. 1978, 1, 13–18. [Google Scholar] [CrossRef]
- Griffin, J.A.; Bates, C.E. Predicting in-situ lamellar cast iron properties: Effects of the pouring temperature and manganese and sulfur concentration. AFS Trans. 1988, 88, 481–496. [Google Scholar]
- Goettsch, D.D.; Dantzig, J.A. Modeling microstructure development in gray cast irons. Metall. Trans. A 1994, 25, 1063–1079. [Google Scholar] [CrossRef]
- Catalina, A.; Guo, X.; Stefanescu, D.M.; Chuzhoy, L.; Pershing, M.A. Prediction of room temperature microstructure and mechanical properties in lamellar iron castings. AFS Trans. 2000, 94, 889–912. [Google Scholar]
- Urrutia, A.; Celentano, J.D.; Dayalan, R. Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection used in Smelting Processes. Metals 2017, 7, 549. [Google Scholar] [CrossRef]
- Fourlakidis, V.; Diószegi, A. A generic model to predict the ultimate tensile strength in pearlitic lamellar graphite iron. Mater. Sci. Eng. A 2014, 618, 161–167. [Google Scholar] [CrossRef]
- Fourlakidis, V.; Diaconu, L.; Diószegi, A. Strength prediction of Lamellar Graphite Iron: From Griffith’s to Hall-Petch modified equation. Mater. Sci. Forum 2018, 925, 272–279. [Google Scholar] [CrossRef]
- Diószegi, A. On the Microstructure Formation and Mechanical Properties in Grey Cast Iron. In Linköping Studies in Science and Technology; Dissertation No. 871; Jönköping: Jönköping, Sweden, 2004; p. 25. ISBN 91-7373-939-1. [Google Scholar]
- Leube, B.; Arnberg, L. Modeling gray iron solidification microstructure for prediction of mechanical properties. Int. J. Cast Metals Res. 1999, 11, 507–514. [Google Scholar] [CrossRef]
- Fourlakidis, V.; Diószegi, A. Dynamic Coarsening of Austenite Dendrite in Lamellar Cast Iron Part 2—The influence of carbon composition. Mater. Sci. Forum 2014, 790–791, 211–216. [Google Scholar] [CrossRef]
- Barkhudarov, M.R.; Hirt, C.W. Casting simulation: Mold filling and solidification—Benchmark calculations using FLOW-3D. In Proceedings of the 7th Conference on Modeling of Casting, Welding and Advanced Solidification Processes, London, UK, 10–15 September 1995. [Google Scholar]
- Diószegi, A.; Diaconu, L.; Fourlakidis, V. Prediction of volume fraction of primary austenite at solidification of lamellar graphite cast iron using thermal analyses. J. Therm. Anal. Calorim. 2016, 124, 215–225. [Google Scholar] [CrossRef]
- Svidró, P.; Diószegi, A.; Pour, M.S.; Jönsson, P. Investigation of Dendrite Coarsening in Complex Shaped Lamellar Graphite Iron Castings. Metals 2017, 7, 244. [Google Scholar] [CrossRef]
- Diószegi, A.; Hattel, J. An inverse thermal analysis method to study the solidification in cast iron. Int. J. Cast Met. Res. 2004, 17, 311–318. [Google Scholar]
- Hattel, J.H. Fundamentals of Numerical Modelling of Casting Processes, 1st ed.; Polyteknisk Forlag: Lyngby, Denmark, 2005. [Google Scholar]
- Diószegi, A.; Fourlakidis, V.; Lora, R. Austenite Dendrite Morphology in Lamellar Cast Iron. Int. J. Cast Met. Res. 2015, 28, 310–317. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).