Abstract
The high temperature creep behaviors of a Zr-based bulk metallic glass (BMG) are studied by uniaxial tensile creep experiments under applied stresses of 50–180 MPa at temperatures of 660–700 K. The microstructural observations of the BMG samples after creep tests show that crystalline phases can be detected under high temperature or high applied stress. Constitutive models for predicting the high temperature creep behaviors of the studied Zr-based BMG are established based on the θ projection method. The creep activation energy and stress exponent are also calculated to establish the creep model. The parameters of the established models are found to be closely associated with the applied stress and temperature. The results show an excellent agreement between the measured and predicted results, confirming the validity of the established model to accurately estimate the high temperature creep curves for the Zr-based BMG. Moreover, based on the classical diffusion creep theory, a schematic model is proposed to describe the creep behaviors of BMGs from the framework of free volume theory.
1. Introduction
Bulk metallic glasses (BMGs) have attracted considerable attention due to their high strength, high elastic strain limit, excellent corrosion resistance, and unique processing capabilities, stemming from the lack of grain boundaries and crystal defects [1,2]. However, BMGs usually exhibit no macroscopic tensile plasticity at room temperature [3,4,5]. Over the past decades, many researchers have studied the mechanical behaviors and intrinsic plastic deformation mechanism of BMGs. Creep behavior is a critical issue of practical engineering significance for the applications of BMGs. Recently, the creep behaviors of BMGs have been reported using compression tests and nanoindentation technology [6,7,8,9,10,11,12,13,14,15]. Huang et al. studied the room temperature creep behaviors of a Fe41Co7Cr15Mo14C15B6Y2 BMG using the nanoindentation technique and found that the creep exponent varied with the peak load or loading rate, which has been interpreted based on the shear transformation zone theory [6]. Yu et al. suggested that the nanoindentation creep behaviors of Co56Ta9B35 metallic glass could be described by a Kelvin model [7]. However, it should be noted that the nanoindentation creep is sensitive to the ambient environment, and the different holding times used in creep tests in previous literature have caused paradoxical results. The compressive creep and stress relaxation experiments of Zr-based BMGs at high temperatures were also performed [15].
It has been noticed that previous works have mainly focused on room temperature creep by using nanoindentation technology or uniaxial compressive tests. In particular, nanoindentation has received increasing interest in recent years, owing to its versatility regarding the testing conditions and the significantly higher flexibility in sample geometry compared to the more standardized uniaxial compression or tensile creep experiments. However, the evaluation of creep characteristics through constant rate load and constant load holding nanoindentation creep experiments usually suffers from the strong impact of the loading rate during the constant loading segment as well as the maximum load during the subsequent holding period [16]. These disadvantages, along with the difficulties of accurate high temperature nanoindentation experiments limit the exploration of creep behaviors for BMGs. Apart from the scientific interests, nanoindentation and compression are not suitable for practical industrial applications. The tensile creep behaviors are critical to the service lifetime of engineering materials in practical applications. However, no work has been dedicated to the high temperature tensile creep behavior of BMGs. Galano et al. studied the creep behavior of a FeSi-based amorphous ribbon containing nanocrystals during tensile creep tests at stresses of 100–800 MPa and temperatures of 723–753 K and established a composite model based on the volume fraction rule to explain the changes in viscosity [17]. Thus, it is necessary to study the creep behaviors of BMGs at high temperatures.
In previous past decades, many constitutive models have been established to describe the creep behaviors of materials, such as power-law equation, the continuum damage equation, and the θ projection concept [18]. Among these models, the θ projection concept is a valid method for establishing the constitutive models describing the creep curves of materials [18]. The θ projection method could shed more insight on the interpolation and extrapolation of creep properties. It works by mathematically describing the conventional creep curves and then projecting those curves to different stresses and temperatures. It also allows the short-term data derived from tests lasting less than three months to predict the full creep strain and creep lifetime characteristics of complex alloys for 10 years or more. Up until now, the θ projection method has been proven to accurately predict the creep curves of Al alloy, steel, and Ti alloy [19,20,21,22,23,].
In present work, the Zr50.7Cu28Ni9Al12.3 (at %) alloy, which has a critical diameter of 14 mm for glass formation [24], was selected as the model material. Its creep behavior was studied through tensile tests. The microstructures of the alloy samples after the creep tests were studied in detail. Furthermore, constitutive models for predicting the high temperature creep behaviors of the Zr-based BMG were established based on the θ projection method, and the validity of the established creep models was confirmed. This work aims to investigate the creep behaviors and further predict the creep lifetime of the ZrCuNiAl glassy alloy below the Tg, which ensures that the Zr-based alloy remains in the amorphous state. The present work also provides the experimental and theoretical cornerstones for extending the applications of BMGs as structural materials.
2. Materials and Methods
The master alloy ingots were prepared by arc melting a mixture of Zr, Cu, Ni, and Al (each with a purity >99.9 wt %) in a Ti-gettered argon atmosphere. To achieve compositional homogeneity, the master alloys were remelted at least four times, followed by drop casting into a copper mold. The obtained as-cast cylindrical alloy samples had dimensions of Ф10 mm × 80 mm. Figure 1 illustrates the details of the geometry of creep samples. The amorphous structure of the as-cast samples was confirmed by X-ray diffraction (XRD, D8, Bruker, Karlsruhe, Germany) using Cu Kα radiation. The thermal parameters for the samples before creep tests were examined by differential scanning calorimetry (DSC, Perkin-Elmer Corp., Norwalk, CT, USA) at a constant heating rate of 0.67 K/s. The BMG samples of the creep tests were electrical discharge machined from the as-cast samples and then carefully ground and polished before testing. According to ASTM E139, testing temperatures of 660–700 K which were below the glass transition temperature, Tg, and applied stresses of 50–180 MPa were selected for 24 h creep tests in a high temperature creep fatigue testing apparatus (CRIMS RPL, Changchun, China). Tensile tests were carried out at different temperatures on an Instron type tensile machine (Instron Corp., Norwood, MA, USA) at an initial strain rate of 5 × 10−2 s−1. The microstructures of the samples after creep tests were examined by scanning electron microscopy (SEM, Quanta 200FEG, FEI, Hillsboro, OR, USA) and transmission electron microscopy (TEM, TECNAI G2, FEI, Hillsboro, OR, USA). The TEM samples were prepared by mechanical polishing, followed by twin-jet electropolishing.
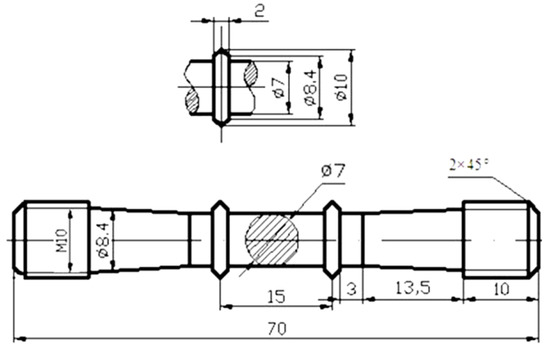
Figure 1.
Details of the geometry of creep specimen (units: mm).
3. Results and Discussion
Figure 2a shows the DSC curve of the studied Zr-based BMG sample at a constant heating rate of 0.67 K/s. The alloy exhibited an endothermic event, characteristic of the glass transition, and a distinct supercooled liquid region, followed by an exothermic peak due to crystallization. The Tg and crystallization temperature, Tx, were determined to be 715 K and 790 K, respectively. The inset of Figure 2a shows the XRD patterns of the as-cast Zr-based BMG alloy samples. A broad halo diffraction peak was observed, denoting a fully glassy phase. Figure 2b demonstrates the tensile stress-strain curves at different temperatures. The values of fracture stress were determined to be 1743 MPa, 1074 MPa, 887 MPa, and 788 MPa for 293 K, 660 K, 680 K, and 700 K, respectively. It is interesting to notice that the strength decreases remarkably from 1743 MPa to 788 MPa, following the temperature increases from 293 K to 700 K. It has been reported that the concept of shear transformation zones (STZs) can be introduced into the deformation mechanism of amorphous metals by argon [25]. In STZ theory, STZ is considered to be a basic shear unit in an amorphous metallic alloy. The cooperative rearrangement of atomic-scale STZs under applied stress results in the macroscopic shear deformation. Johnson and Samwer [26] suggested that the yield strength of a metallic glass can be determined by the cooperative shear motion of STZs, as follows:
where is the yield stress at finite T, while is the yield stress at T = 0 K, β is a constant, k is the Boltzmann constant, C is a dimensionless constant of order unity, ω0 is the attempt frequency, and is the shear strain rate. The ratio of G0T/G0Tg is a factor that incorporates the weak dependence of G on the thermal expansion of a fixed glass configuration, and t = T/Tg. The shear strength, τ, can be converted into the fracture strength, σ, according to the following equation [27]:
where θ is the fracture angle for the BMG, and n . According to Equations (1) and (2), σ can be approximately expressed as follows
where σ0 is the strength at T = 0 K, and , which can be considered to have a constant value. It is apparent, following the above relationship, that the strength of the bulk metallic glass decreases with an increasing testing temperature, which is consistent with previous reports [28,29,30].
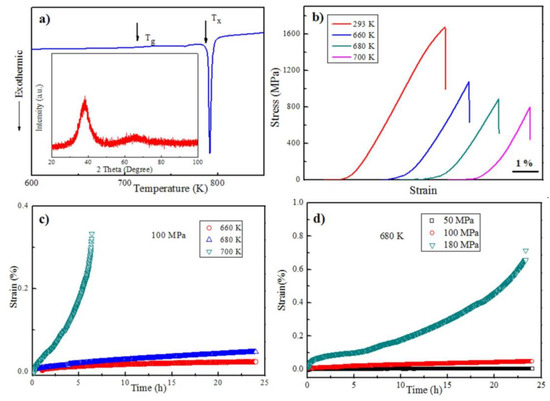
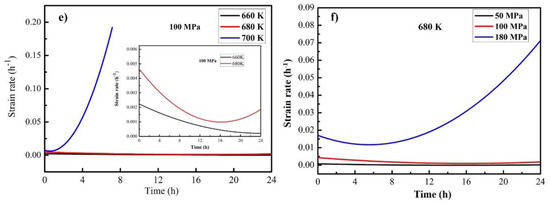
Figure 2.
(a) Differential scanning calorimetry (DSC) curve; (b) tensile stress-strain curves at different temperatures; (c,d) tensile creep curves; and (e,f) the corresponding strain rate-time curves of the Zr-based BMG alloy with different creep parameters.
Creep is the time-dependent plastic strain at constant testing temperature and applied stress [31,32,33]. For conventional metallic materials, time-dependent elevated temperature creep deformation can be represented by the creep strain-time curve, which is usually distinguished by primary, secondary and tertiary stages. Upon loading, the creep rate quickly decreases during the primary stage and then reaches a steady stage, i.e., the secondary stage, before dramatically increasing due to the formation of cracks during the tertiary stage, leading to the final fracture [31,32,33]. Figure 2c,d demonstrate the tensile creep curves of the studied Zr-based BMG under different creep parameters. It was found that the creep behaviors of the studied Zr-based alloy were dependent on the testing temperature and the applied stress. By increasing the creep temperature or the applied stress, the creep rate increased dramatically. Under an applied stress of 100 MPa, the creep curves exhibited no tertiary stage below 680 K, giving steady state creep rates of 1.52 × 10−7 s−1 and 3.9 × 10−7 s−1 at 660 K and 680 K, respectively. The secondary stage was greatly shortened, and the creep rate reached up to 6.83 × 10−6 s−1 when the creep temperature was 700 K. The tertiary stage at 700 K started after 5 h, and the fracture happened at 6.3 h with a creep strain of 0.34%. Figure 2d demonstrates the creep behaviors of the BMG at 680 K under different applied stresses. No tertiary stage appeared below 100 MPa, and the steady state creep rates at the secondary stages were 5.1 × 10−7 s−1 and 3.9 × 10−7 s−1 for 50 MPa and 100 MPa, respectively. For the case of the 180 MPa applied stress, after 1 h creep, the creep curve entered the secondary stage with a steady creep rate of 1.96 × 10−6 s−1 and lasted for 20 h. The tertiary stage began after 20 h. The total creep strain was ~0.7% for 24 h. The corresponding strain rate curves are shown in Figure 2e,f. For the case of 100 MPa applied stress, higher temperatures caused higher strain rates for the studied BMG sample. For the 680 K testing temperature, a higher applied stress resulted in a higher strain rate.
Figure 3 shows the SEM and TEM micrographs of the samples after the creep tests at 680 K with different applied stresses. It can be seen that the applied stress had a crucial effect on the microstructures of the tested samples. For the 50 MPa and 100 MPa applied stresses, no crystallization occurred during the creep tests, as shown in Figure 3a,b. The insets of Figure 3a,b show the bright field TEM images and corresponding selected area electron diffraction (SAED) patterns of the samples. There were no contrasts in the crystalline phases in the samples after the creep tests. The SAED patterns show clearly diffuse halo rings, which are the typical fingerprint of an amorphous structure. All of the above observations confirm that the Zr-based BMG maintained its amorphous structure after creep tests at 680 K with 50 MPa and 100 MPa applied stresses. For an applied stress of 180 MPa (Figure 3c), however, numerous crystals embedded in the glassy matrix were observed in the tested sample. The inset of Figure 3c shows the bright field TEM images and corresponding SAED patterns taken from the crystals. These crystalline phases were identified by TEM observations as the hexagonal Ni3Zr phase.

Figure 3.
SEM and TEM images, together with the selected area electron diffraction (SAED) patterns of the samples after creep tests at 680 K with different applied stresses: (a) 50 MPa; (b) 100 MPa; and (c) 180 MPa.
Figure 4 shows the SEM and TEM micrographs of the samples after the creep tests at 100 MPa under different temperatures. Similar to the results from Figure 3, for the 660 K and 680 K testing temperatures, no crystallization took place during the creep tests, as shown in Figure 4a,b, which confirms that the Zr-based BMG maintained its amorphous structure. At 700 K, numerous crystals were observed in glassy matrix, as shown in Figure 4c. The inset of Figure 4c shows the bright field TEM images and corresponding SAED patterns taken from the crystals. These crystalline phases can be identified by TEM observations as Al3Ni and Al4Zr5 intermetallics. Previous experiments [34] on the crystallization of the studied BMG above Tg under thermal annealing have shown the same crystalline phases precipitated from the glassy matrix as those formed in the present creep experiments. It has been reported that nanocrystalline phases, identical to those formed during annealing, can be induced by nanoindentation at room temperature. The observed rapid formation of crystalline phases is a direct consequence of dramatic enhancement of atomic diffusional mobility [35]. In the present work, though 680 K and 700 K were below the Tg, the external load with a duration of 24 h induced the occurrence of nanocrystallization. The different crystalline phases could be attributed to the different levels of atomic diffusional mobility at different temperatures and applied loads.

Figure 4.
SEM and TEM images, together with the SAED patterns of the samples after creep tests at 100 MPa with different temperatures: (a) 660 K, (b) 680 K, and (c) 700 K.
The stress exponent (n) and creep activation energy (Q) for the creep can be calculated according to the Norton-Baily law, given as follows [36,37]:
where is the steady state creep rate in s−1, A is the material constant, n is the stress exponent, Q is the creep activation energy in kJ/mol, R is the gas constant (8.31 J·mol−1·K−1), and T is the absolute temperature in K.
According to Equation (4), the stress exponent (n) and creep activation energy (Q) can be calculated from the slope of the best-fit line to the variation of ln versus lnσ at a constant temperature and ln versus 1/T at a constant applied stress, respectively. The stress exponent was calculated to be ~4.21 at a constant temperature of 680 K. The corresponding creep activation energy was calculated to be ~377 kJ/mol under a constant applied stress of 100 MPa.
The material parameters of the constitutive models established with the θ projection concept are closely associated with applied creep stress and temperature. The equation of a given creep strain at a time, t, is given by the following form [38,39]:
where θ1 and θ3 are the primary and tertiary strains, respectively, and θ2 and θ4 are rate parameters governing the curvatures of the primary and tertiary components, respectively. This expression can be divided down into two parts, as shown in Figure 5a. The expression, , represents the primary creep, where θ1 is the total primary strain while θ2 determines the shape of the primary creep component. Likewise, represents the tertiary creep with θ3 scaling tertiary creep strain, and θ4 determines the curvature of tertiary creep. Therefore, θ1 and θ3 are termed ‘scale’ parameters, while θ2 and θ4 are termed ‘rate’ parameters. The relationships between the θ parameters, temperature, and applied stress can be expressed with the following [40]:
where Gi and Hi are material constants, R is the universal gas constant, T is the absolute temperature, Q is the activation energy of creep deformation, and σy represents the initial yield stress under different creep temperatures, as shown in Figure 2b.
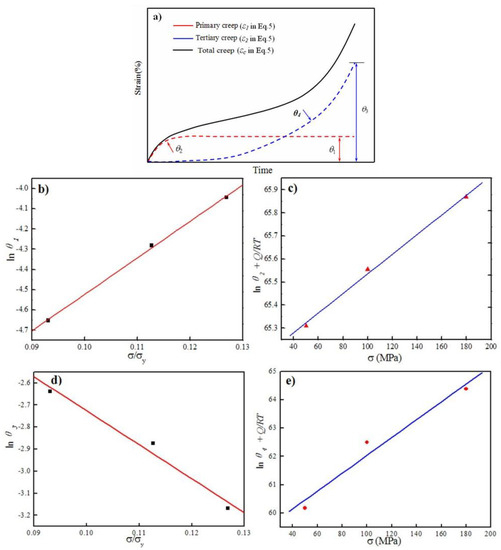
Figure 5.
(a) Schematic creep curve based on the θ projection concept. Relationships of (b) lnθ1 − σ/σy; (c) (lnθ2 + Q/RT) − σ; (d) lnθ3 − σ/σy and (e) (lnθ4 + Q/RT) − σ.
The values of the four θ parameters can be determined for each creep strain-time curve using a non-linear least-squares fitting, and the following expression was used to minimize the fitting error:
where εthe and εexp are the theoretical and experimental strains, respectively, and m represents the number of data points on each creep curve. Using the non-linear least-squares fitting method and a computer program based on “MATLAB”, the values of θ1 and θ2 under all the testing conditions were obtained based on the experiment results, as shown in Table 1.

Table 1.
Values of the total primary strain θ1, tertiary strain θ3, and rate parameters governing curvatures of the primary (θ2) and tertiary (θ4) components at different creep parameters.
Taking the logarithm of both sides of Equations (6) and (7), the following equations were obtained:
Based on the material properties and the values of θ1 and θ2 at different testing conditions, as shown in Table 1, the values of lnθ1 and lnθ2 can be easily evaluated. Meanwhile, the activation energy of this alloy can be obtained from the above results. Therefore, the values of lnθ2 + Q/RT under different applied stresses can be also calculated. The relationship between θ parameters (θ1 and θ2), creep temperatures and applied stresses is plotted in Figure 5. Obviously, it can be seen that there are excellent linear relationships between the θ1, θ2 parameters and the applied stresses. Then, the values of H1 and H2 were calculated to be 18.05 and −24.13, respectively, from the slopes of the lnθ1 − σ/σy and (lnθ2 + Q/RT) − σ plots, respectively. The values of G1 and G2 were calculated to be e−6.32 and e65.11, respectively. Thus, the constitutive model of Zr-based alloys during the primary creep stage can be expressed as follows:
Similarly, based on the values of θ3 and θ4 under different testing conditions, the relationship, lnθ3 − σ/σy and (lnθ4 + Q/RT) − σ, is also be shown in Figure 5. The values of G3, H3, G4 and H4 were calculated to be e−1.18, −15.42, e58.87 and −169.3 by an identical method, respectively. Therefore, the creep constitutive models during the secondary and tertiary creep stages for the studied Zr-based BMG can be expressed as
So, the total creep curves of Zr-based BMG, according to the θ projection concept can be achieved as follows:
Figure 6 shows the measured and predicted creep curves by Equation (15) over 48 h for different creep parameters. The predicted results agree well with the experimental ones, confirming the validity of the established creep constitutive models to predict the high temperature creep curves of BMGs.
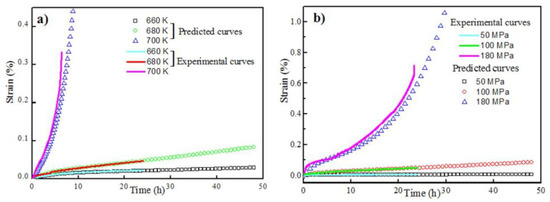
Figure 6.
Comparisons between the experimental curves and predicted curves: (a) 100 MPa for different temperatures and (b) 680 K for different applied stresses.
For crystalline materials, Nabarro-Herring creep is a mode of deformation of crystalline materials that occurs at low stresses and is maintained at elevated temperatures in fine-grained materials. The grain boundary of a crystalline metal acts as source of vacancies that assist in the diffusional motion of atoms through the lattice. Macroscopic deformation is induced by the diffusion of atoms through the lattice to the grain boundaries approximately parallel to the tensile axis, while there is a corresponding counterflux of vacancies perpendicular to the tensile axis [41], as shown in Figure 7a. For BMGs, which lack long-range order in their atomic configurations, their deformation is physically different from that of conventional crystalline solids. So far, the deformation mechanisms of BMGs have been approached by numerous theories, such as the shear transformation zone (STZ) theory [25,26,42], the fictive stress model [43], and the directional structural relaxation model [44] and so on. The free volume model developed by Spaepen and Turnbull is the most widely used to interpret the deformation of BMGs [45]. Free volume is often frozen into the structure because of the non-equilibrium processing during rapid solidification and can be introduced during deformation as well [25]. Argon introduced the concept of STZ into the deformation mechanism based on the free volume model. The collective operation of STZs triggers the formation and propagation of a shear band [46,47]. Li et al. [48] studied the structure in shear bands under high resolution transmission electron microscopy (HRTEM, TECNAI G2, FEI, Hillsboro, OR, USA) by using Fourier-filtering and adjusting the contrast and revealed the presence of numerous nanovoids in shear bands. Moreover, the density of the nanovoids resulting from the coalescence of free volume is higher in the shear band of the tensile region than that of the compressive region [49]. This means that there may be a concentration gradient region of the free volume surrounded by shear bands during deformation. It is also accepted that the diffusive atomic motion of BMGs occurs by the motion of free volume or “holes” dispersed in the supercooled liquid. This mechanism is similar to the case of metallic crystals, where the motion of vacancies or empty lattice sites controls the diffusive jumps of atoms [50,51]. This shear band is similar to the role of the grain boundary as a vacancy source and sink in crystalline metals, demonstrating its Nabarro-Herring creep behavior. Due to these reasons, the Nabarro-Herring creep model has been selected to elucidate the underlying creep mechanism of Zr-based BMG in the present work.
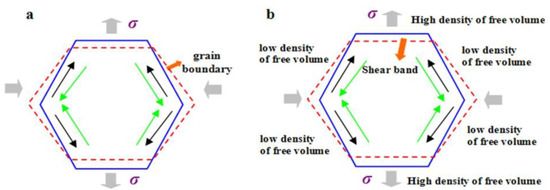
Figure 7.
Schematic diagram of (a) Nabarro-Herring creep model (black arrows: atom diffusion; green arrows: vacancy diffusion) [38], and (b) creep model for bulk metallic glass (BMGs) (black arrows: atom diffusion; green arrows: free volume movement).
Figure 7b shows the schematic diagram for the creep deformation model of BMGs during tension tests. The arrows in Figure 7b represent the direction of free volume movement. The density of the free volume in the shear band depends on the applied stress state, as proposed by Jiang and Atzmon [52]. When an external tensile stress is applied, the shear band nearly perpendicular to the applied stress will have high density of free volume, while the shear band under the compressive stress state will have low density of free volume. This density variation results in a concentration gradient region of free volume surrounded by the shear bands, which acts as a driving force for atomic motion and free volume movement at high temperatures. Under the fixed applied stress of 100 MPa, the amount of free volume increases with an increase in testing temperature, causing the larger concentration gradient region of free volume surrounded by the shear bands. Easier atomic movement happens, favoring creep deformation. However, the free volume increases continuously at high temperatures, such as, 700 K and evolves to cracks, leading to final fracture of the sample, as shown in Figure 1c. Under a fixed testing temperature of 680 K, the increase in the free volume caused by the temperature rise can satisfy the space required for the atomic motion at low applied stresses of 50 MPa and 100 MPa. Indeed, under a larger external force, the deformation rate of the amorphous phase increases. The process involves a large number of atoms involved in deformation. However, the increase in the free volume caused by the temperature rise cannot satisfy the space required for the atomic movement. At this moment, a new free volume is generated to support the atomic movement [53]. At high applied stress of 180 MPa, the new free volumes might continuously generate. The atomic diffusion perpendicular to the loading force constantly fills the new free volume, causing a high creep strain and high steady state creep rate, as shown in Figure 2.
Here, it should be mentioned that the mechanical properties of metallic glass are strongly dependent on the sample size and the stiffness of the testing machine [54,55,56,57,58]. Han et al. [54] suggested that catastrophic failure is dominated by a shear-band instability index which is proportional to the sample size and inversely proportional to the machine stiffness. This index can provide more understanding about the plastic deformation mechanism of BMGs and is helpful for designing glass-forming alloy systems which possess plasticity/ductility [54]. Ghidelli et al. [55] stated that the fracture strain of a Zr65Ni35 glassy film is closely related to both the sample size and the stability of the test device. Huang et al. [56] reported a dramatic effect of sample size on the compressive plastic strain of a TiZrNiCuBe metallic glass, i.e., the smaller the sample size, the higher the plastic strain, suggesting a “smaller is softer” trend. For the present work, BMG samples of a single diameter (10 mm) and creep fatigue testing apparatus with a fixed stiffness were selected for the creep tests. The effects of the applied stress and testing temperature on the creep behaviors were studied. The sample size and machine stiffness might have important effects on the creep behaviors of BMGs, but this is beyond the research topic of this work.
4. Conclusions
In summary, the high temperature creep behavior of Zr-based BMGs was studied. The microstructure observations showed that many Ni3Zr, Al3Ni and Al4Zr5 phases exist in a glassy matrix at high temperatures and high applied stresses. The creep activation energy and stress exponent were calculated to be 377 kJ/mol and 4.21, respectively. The parameters of the established models based on the θ projection method, θi, Gi and Hi (i = 1, 2, 3 and 4), at different testing conditions were calculated by non-linear least-squares and linear fitting methods. It was found that the established models were closely associated with the applied stress and temperature. The creep curves of Zr-based BMGs predicted by the proposed models were consistent with the experimental curves, verifying the validity of the established models to predict the creep behaviors of BMGs. The concentration gradient region resulted from the density variation of free volume acts as a driving force for atomic motion and free volume movement. A schematic model was proposed to describe the high temperature creep deformation of BMGs based on the diffusional motion of free volume within a glassy matrix surrounded by shear bands. Higher testing temperatures cause easier atomic movement, favoring creep deformation. Meanwhile, larger applied stresses increase the deformation rate of the BMG. The atomic diffusion perpendicular to the loading force constantly facilitates the formation of a new free volume, resulting in higher creep strain and a higher steady state creep rate.
Author Contributions
Y.H. conceived and designed the experiments. G.W., X.S., W.C. and M.H. wrote the article. D.P. finished the simulation and calculation part.
Funding
This work was funded by the National Natural Science Foundation of China [grant numbers 51704001 and 51671070], Key Research and Development Plan of Anhui Province [grant number 1704a0902056], Key Project of Natural Science of Education Department of Anhui Province [grant number KJ2018A0860], and Talent Project of Anhui Polytechnic University [grant number 2017yyzr08]. The financial supports from the Academy of Finland are also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, W.L. Bulk Glass-Forming Metallic Alloys: Science and Technology. MRS Bull. 1999, 24, 42–56. [Google Scholar] [CrossRef]
- Zhang, Z.F.; He, G.; Eckert, J.; Schultz, L. Fracture Mechanisms in Bulk Metallic Glassy Materials. Phys. Rev. Lett. 2003, 91, 045505. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Fan, H.B.; Huang, Y.J.; Shen, J.; Chen, Z.H. A new TiCuHfSi bulk metallic glass with potential for biomedical applications. Mater. Des. 2014, 54, 251–255. [Google Scholar] [CrossRef]
- Liang, D.D.; Wei, X.S.; Chang, C.T.; Li, J.W.; Shen, J. Effect of W addition on the glass forming ability and mechanical properties of Fe-based metallic glass. J. Alloy. Compd. 2018, 731, 1146–1150. [Google Scholar] [CrossRef]
- Li, J.C.; Chen, X.W.; Huang, F.L. On the mechanical properties of particle reinforced metallic glass matrix composites. J. Alloy. Compd. 2018, 737, 271–294. [Google Scholar] [CrossRef]
- Huang, Y.J.; Shen, J.; Chiu, Y.L.; Chen, J.J.J.; Sun, J.F. Indentation creep of an Fe-based bulk metallic glass. Intermetallics 2009, 17, 190–194. [Google Scholar] [CrossRef]
- Yu, P.F.; Feng, S.D.; Xu, G.S.; Guo, X.L.; Wang, Y.Y.; Zhao, W.; Qi, L.; Li, G.; Liaw, P.K.; Liu, R.P. Room-temperature creep resistance of Co-based metallic glasses. Scr. Mater. 2014, 90–91, 45–48. [Google Scholar] [CrossRef]
- Gong, P.; Jin, J.S.; Deng, L.; Wang, S.B.; Gu, J.L.; Yao, K.F.; Wang, X.Y. Room temperature nanoindentation creep behavior of TiZrHfBeCu(Ni) high entropy bulk metallic glasses. Mater. Sci. Eng. A 2017, 688, 174–179. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Wei, D.; Dai, L.H. Extraordinary creep relaxation time in a La-based metallic glass. J. Mater. Sci. 2018, 53, 2956–2964. [Google Scholar] [CrossRef]
- Zhang, T.H.; Ye, J.H.; Feng, Y.H.; Ma, Y. On the spherical nanoindentation creep of metallic glassy thin films at room temperature. Mater. Sci. Eng. A 2017, 685, 294–299. [Google Scholar] [CrossRef]
- Chen, Y.H.; Huang, J.C.; Du, X.H.; Wang, X. Time-dependent creep behavior of amorphous ZrCu and nanocrystalline Zr thin films—A comparison. Intermetallics 2016, 68, 101–106. [Google Scholar] [CrossRef]
- Wang, C.; Cao, Q.P.; Wang, X.D.; Zhang, D.X.; Qu, S.X.; Jiang, J.Z. Time-dependent shear transformation zone in thin film metallic glasses revealed by nanoindentation creep. J. Alloy Compd. 2017, 696, 239–245. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M.; Blandin, J.J.; Gravier, S. High temperature deformation in a lanthanum based bulk metallic glass showing a pronounced secondary relaxation. Mater. Sci. Eng. A 2013, 586, 57–61. [Google Scholar] [CrossRef]
- Zhang, C.; Qiao, J.C.; Pelletier, J.M.; Yao, Y. Thermal activation in the Zr65Cu18Ni7Al10 metallic glass by creep deformation and stress relaxation. Scr. Mater. 2016, 113, 180–184. [Google Scholar] [CrossRef]
- Kassner, M.E.; Smith, K.; Eliasson, V. Creep in amorphous metals. J. Mater. Res. Technol. 2015, 4, 100–107. [Google Scholar] [CrossRef]
- Li, F.C.; Xie, Y.; Song, M.; Ni, S.; Guo, S.F.; Liao, X.Z. A detailed appraisal of the stress exponent used for characterizing creep behavior in metallic glasses. Mater. Sci. Eng. A 2016, 654, 53–59. [Google Scholar] [CrossRef]
- Galano, M.; Rubiolo, G.H. Creep behaviour of a FeSi-base metallic glass containing nanocrystals. Scr. Mater. 2003, 48, 617–622. [Google Scholar] [CrossRef]
- Omprakash, C.M.; Kumar, A.; Srivathsa, B.; Satyanarayana, D.V.V. Prediction of creep curves of high temperature alloys using θ projection concept. Proccdia Eng. 2013, 55, 756–759. [Google Scholar] [CrossRef]
- Alipour, R.; Farokhi Nejad, A. Creep behaviour characterisation of a ferritic steel alloy based on the modified theta-projection data at an elevated temperature. Int. J. Mater. Res. 2016, 107, 406–412. [Google Scholar] [CrossRef]
- Xie, L.J.; Ning, D.; Yang, Y.Z. Experimental study on creep characterization and lifetime estimation of RPV material at 723-1023 K. J. Mater. Eng. Perform. 2017, 26, 643–652. [Google Scholar] [CrossRef]
- Kim, W.G.; Kim, S.H.; Lee, C.B. Long-term creep characterization of Gr.91 steel by modified creep constitutive equations. Metall. Mater. Int. 2011, 17, 497–504. [Google Scholar] [CrossRef]
- Lin, Y.C.; Xia, Y.C.; Ma, X.S.; Jiang, Y.Q.; Chen, M.S. High temperature creep behavior of Al-Cu-Mg alloy. Mater. Sci. Eng. A 2012, 550, 125–130. [Google Scholar] [CrossRef]
- Lin, Y.C.; Xia, Y.C.; Chen, M.S.; Jiang, Y.Q.; Li, L.T. Modeling the creep behavior of 2024-T3 Al alloy. Comp. Mater. Sci. 2013, 67, 243–248. [Google Scholar] [CrossRef]
- Sun, Y.J.; Qu, D.D.; Huang, Y.J.; Liss, K.-D.; Wei, X.S.; Xing, D.W.; Shen, J. Zr–Cu–Ni–Al bulk metallic glasses with superhigh glass-forming ability. Acta Mater. 2009, 57, 1290–1299. [Google Scholar] [CrossRef]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Johnson, W.L.; Samwer, K. A universal criteria for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys. Rev. Lett. 2005, 95, 195501. [Google Scholar] [CrossRef] [PubMed]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Huang, Y.J.; Shen, J.; Sun, J.F.; Zhang, Z.F. Enhanced strength and plasticity of a Ti-based metallic glass at cryogenic temperatures. Mater. Sci. Eng. A 2008, 498, 203–207. [Google Scholar] [CrossRef]
- Jiang, W.H.; Jiang, F.; Liu, F.X.; Choo, H.; Liaw, P.K.; Qiu, K.Q. Temperature dependence of serrated flows in compression in a bulk-metallic glass. Appl. Phys. Lett. 2006, 89, 261909. [Google Scholar] [CrossRef]
- Yu, P.; Chan, K.C.; Chen, W.; Xia, L. Low-temperature mechanical properties of Ce68Al10Cu20Co2 bulk metallic glass. Philos. Mag. Lett. 2011, 91, 70–77. [Google Scholar] [CrossRef]
- Jiang, W.C.; Zhang, Y.C.; Luo, Y.; Gong, J.M.; Tu, S.T. Creep analysis of solid oxide fuel cell with bonded compliant steel design. J. Power Source 2013, 243, 913–918. [Google Scholar] [CrossRef]
- Yang, B.; Xuan, F.Z. Creep behavior of subzones in a CrMoV weldment characterized by the in-situ creep test with miniature specimens. Mater. Sci. Eng. A 2018, 723, 148–156. [Google Scholar] [CrossRef]
- Zhao, J.F.; Gong, J.D.; Saboo, A.; Dunand, D.C.; Olson, G.B. Dislocation-based modeling of long-term creep behaviors of Grade 91 steels. Acta Mater. 2018, 149, 19–28. [Google Scholar] [CrossRef]
- Miresmaeili, S.M.; Nami, B. Impression creep behavior of Al–1.9%Ni–1.6%Mn–1%Mg alloy. Mater. Des. 2014, 56, 286–290. [Google Scholar] [CrossRef]
- Wilshire, B.; Burt, H. Creep data prediction for Aluminium air frame alloy. Mater. Sci. Forum 2003, 426–432, 261–266. [Google Scholar] [CrossRef]
- Tian, S.G.; Lv, X.X.; Yu, H.C.; Wang, Q.; Jiao, Z.H.; Sun, H.F. Creep behavior and deformation feature of TiAl-Nb alloy with various states at high temperature. Mater. Sci. Eng. A 2016, 651, 490–498. [Google Scholar] [CrossRef]
- Evans, R.W. A constitutive model for the high-temperature creep of particle-hardened alloys based on the θ projection method. Proc. R. Soc. A Math. Phys. 2000, 456, 835–868. [Google Scholar] [CrossRef]
- Williams, S.J.; Bache, M.R.; Wilshire, B. 25 Year Perspective Recent developments in analysis of high temperature creep and creep fracture behaviour. Mater. Sci. Technol. 2010, 26, 1329–1336. [Google Scholar] [CrossRef]
- Zheng, W. Dynamic Mechanical Behavior of ZrCuNiAl Bulk Metallic Glass. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Kim, J.J.; Choi, Y.; Suresh, S.; Argon, A.S. Nanocrystallization during nanoindentation of a bulk amorphous metal alloy at room temperature. Science 2002, 295, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Na, Y.S.; Lee, J.H. Interpretation of viscous deformation of bulk metallic glasses based on the Nabarro–Herring creep model. J. Mater. Proc. Technol. 2007, 187–188, 786–790. [Google Scholar] [CrossRef]
- Argon, A.S.; Shi, L.T. Development of visco-plastic deformation in metallic glasses. Acta Metall. 1983, 31, 499–507. [Google Scholar] [CrossRef]
- Kato, H.; Kawamura, Y.; Chen, H.S.; Inoue, A. A fictive stress model calculation of nonlinear viscoelastic behaviors in a Zr-based glassy alloy: Stress growth and relaxation. J. Appl. Phys. 2000, 39, 5184–5187. [Google Scholar] [CrossRef]
- Khonik, V.A. The kinetics of irreversible structural relaxation and homogeneous plastic flow of metallic glasses. Phys. Status Solidi A 2000, 177, 173–189. [Google Scholar] [CrossRef]
- Spaepen, F.; Turnbull, D. A mechanism for the flow and fracture of metallic glasses. Scr. Metall. Mater. 1974, 8, 563–568. [Google Scholar] [CrossRef]
- Lund, A.C.; Schuh, C.A. The mohr-coulomb criterion from unit shear processes in metallic glass. Intermetallics 2004, 12, 1159–1165. [Google Scholar] [CrossRef]
- Greer, A.L.; Cheng, Y.Q.; Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R Rep. 2013, 74, 71–132. [Google Scholar] [CrossRef]
- Li, J.; Spaepen, F.; Hufnagel, T.C. Nanometre-scale defects in shear bands in a metallic glass. Philos. Mag. A 2002, 82, 2623–2630. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.L.; Hufnagel, T.C. Characterization of nanometer-scale defects in metallic glasses by quantitative high-resolution transmission electron microscopy. Phys. Rev. B 2002, 65, 144201. [Google Scholar] [CrossRef]
- Nieh, T.G.; Wadsworth, J. Homogeneous deformation of bulk metallic glasses. Scr. Mater. 2006, 54, 387–392. [Google Scholar] [CrossRef]
- Yavari, A.R.; Moulec, A.L.; Inoue, A.; Nishiyama, N.; Lupu, N.; Matsubara, E.; Botta, W.J.; Vaughan, G.; Michiel, M.D.; Kvick, A. Excess free volume in metallic glasses measured by X-ray diffraction. Acta Mater. 2005, 53, 1611–1619. [Google Scholar] [CrossRef]
- Jiang, W.H.; Atzmon, M. Mechanically-assisted nanocrystallization and defects in amorphous alloys: A high-resolution transmission electron microscopy study. Scr. Mater. 2006, 54, 333–336. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Han, Z.; Wu, W.F.; Li, Y.; Wei, Y.G.; Gao, H.J. An instability index of shear band for plasticity in metallic glasses. Acta Mater. 2009, 57, 1367–1372. [Google Scholar] [CrossRef]
- Ghidelli, M.; Idrissi, H.; Gravier, S.; Blandin, J.-J.; Raskin, J.-P.; Schryvers, D.; Pardoen, T. Homogeneous flow and size dependent mechanical behavior in highly ductile Zr65Ni35 metallic glass films. Acta Mater. 2017, 131, 246–259. [Google Scholar] [CrossRef]
- Huang, Y.J.; Shen, J.; Sun, J.F. Bulk metallic glasses: Smaller is softer. Appl. Phys. Lett. 2007, 90, 081919. [Google Scholar] [CrossRef]
- Huang, Y.J.; Chiu, Y.L.; Shen, J.; Sun, Y.; Chen, J.J.J. Mechanical performance of metallic glasses during nanoscratch tests. Intermetallics 2010, 18, 1056–1061. [Google Scholar] [CrossRef]
- Huang, Y.J.; Shen, J.; Chen, J.J.J.; Sun, J.F. Critical cooling rate and thermal stability for a Ti–Zr–Ni–Cu–Be metallic glass. J. Alloy. Compd. 2009, 477, 920–924. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).