An Analysis of Electroplated cBN Grinding Wheel Wear and Conditioning during Creep Feed Grinding of Aeronautical Alloys
Abstract
:1. Introduction
1.1. State of the Art
1.1.1. Electroplated cBN Wheel Surface Characterization
1.1.2. Electroplated cBN Grinding Wheel Conditioning
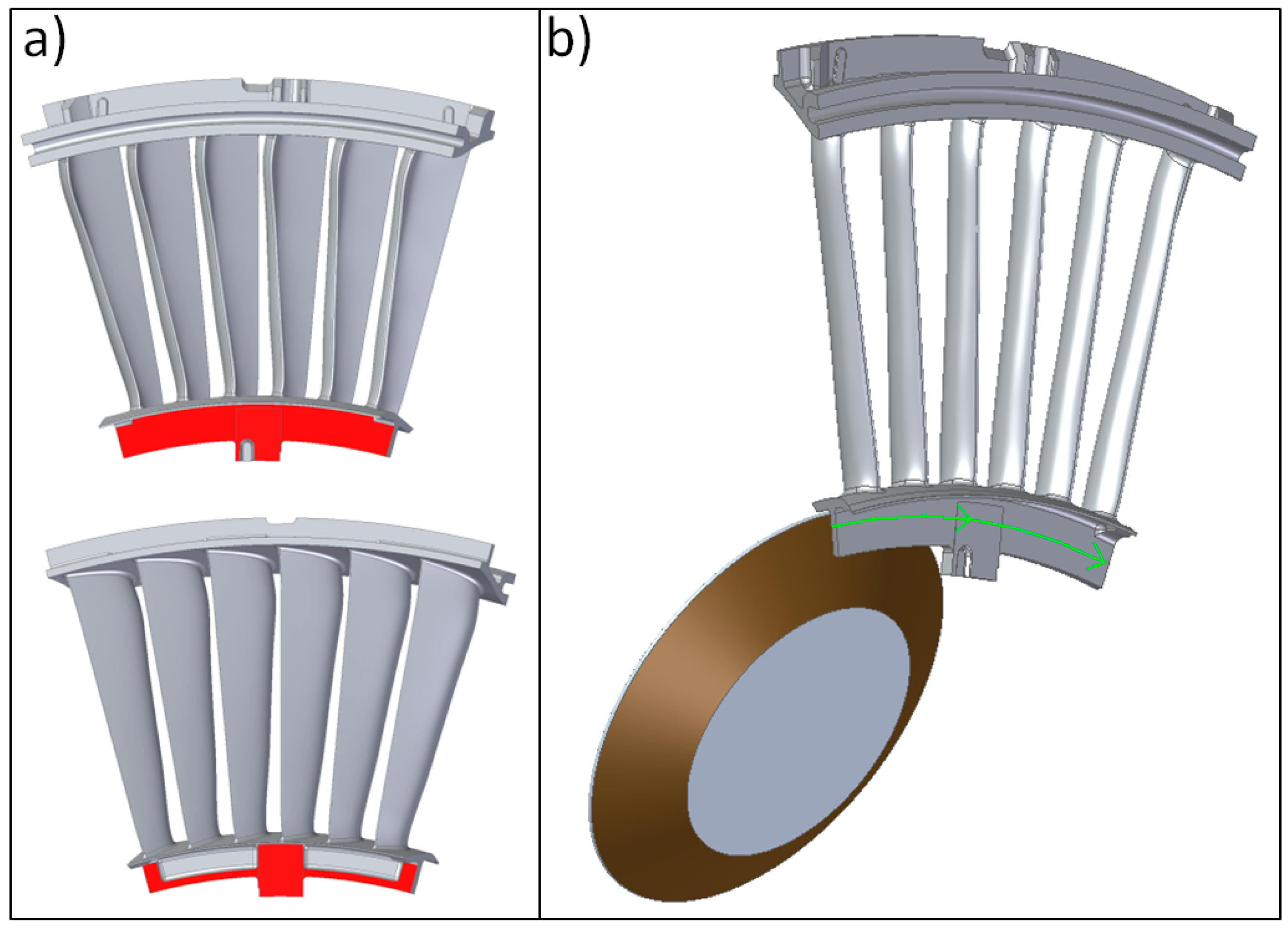
2. Materials and Methods
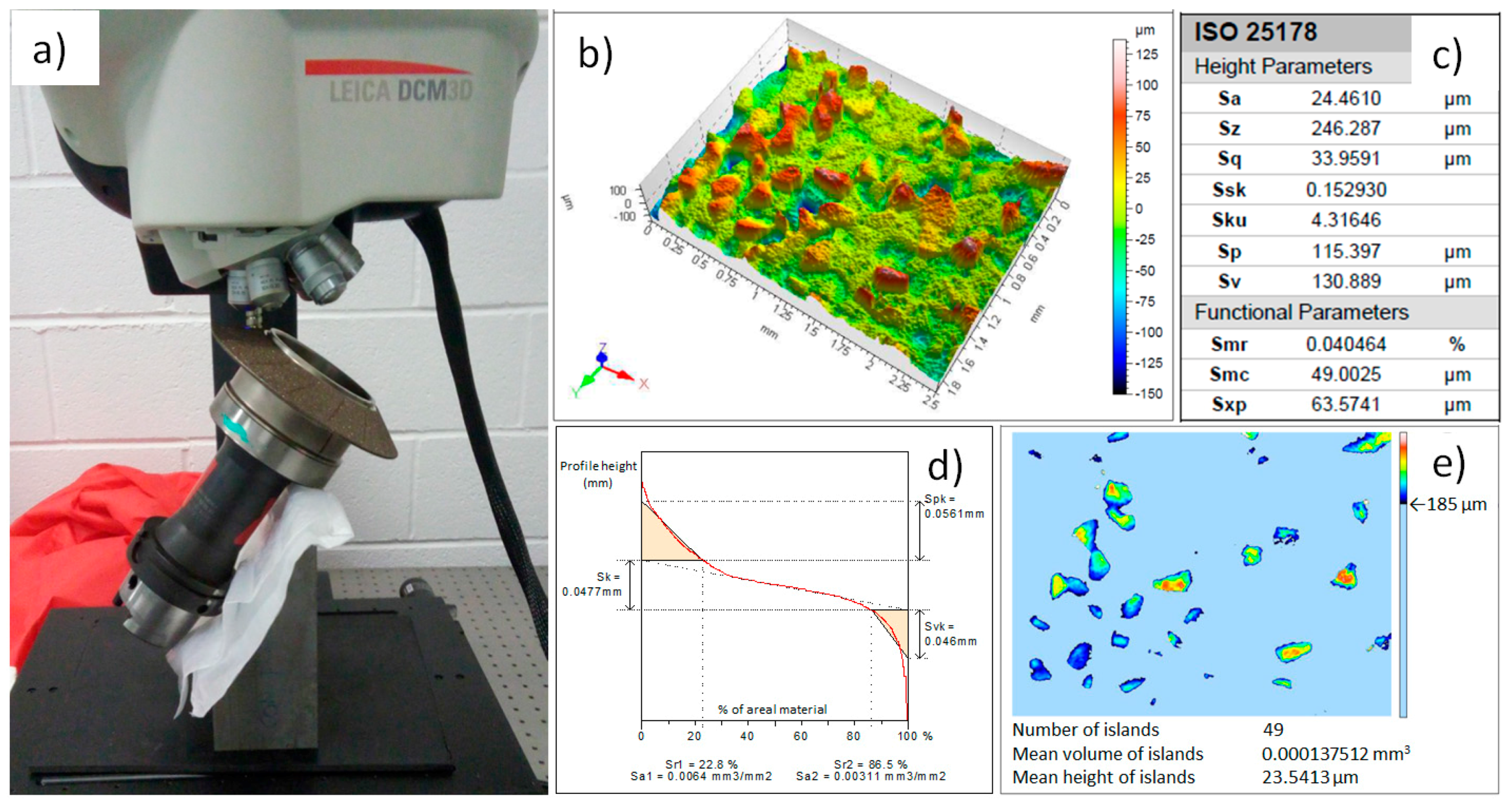
2.1. Wheel Surface Characterization during CFG
2.2. Roughness Parameters Analysis
- k = 1: Corresponds to 68%.
- k = 2: Corresponds to 95%.
- k = 3: Corresponds to 99.7%.
2.3. Wheel Conditioning
3. Results
3.1. Wheel Wear Analysis
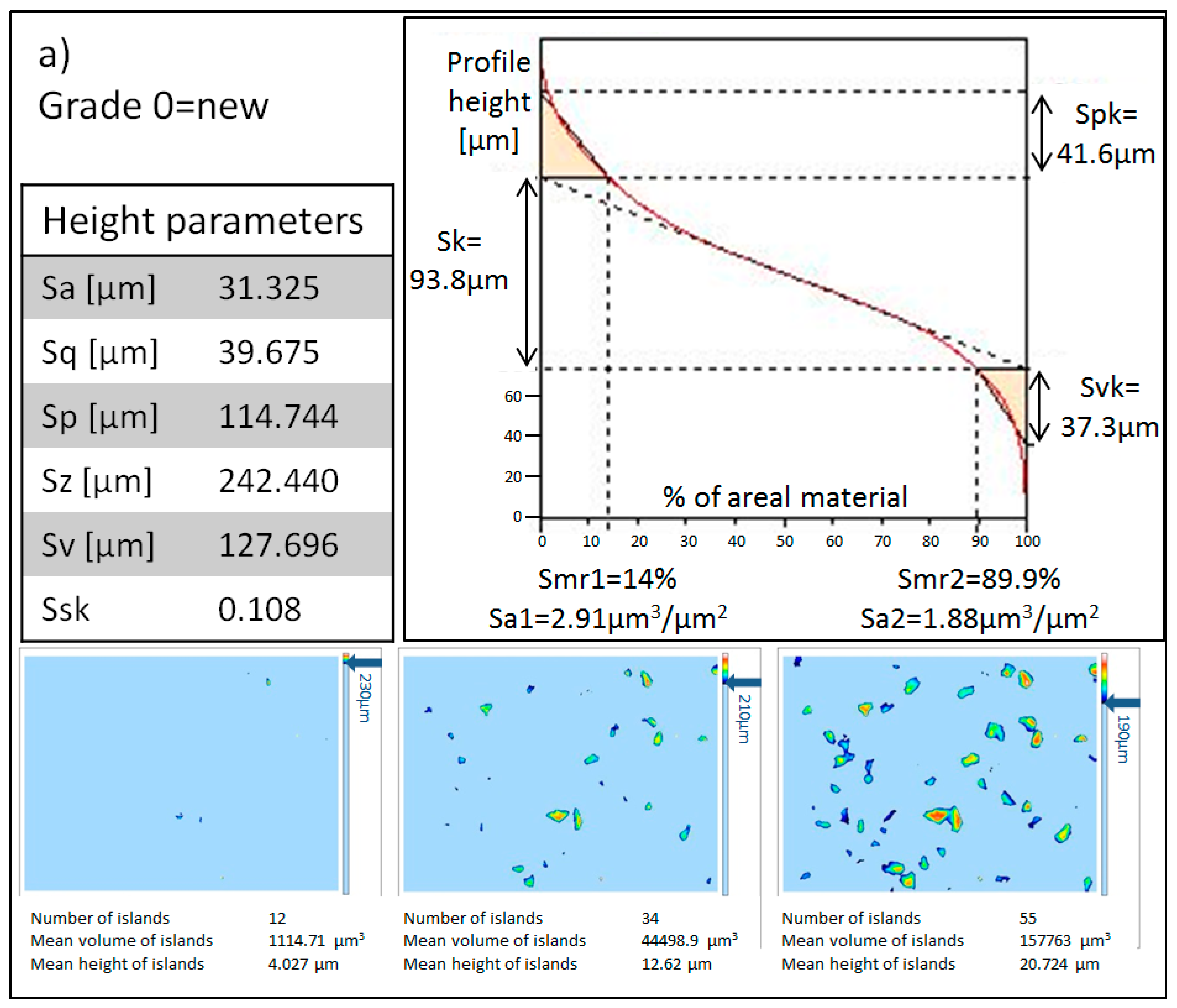
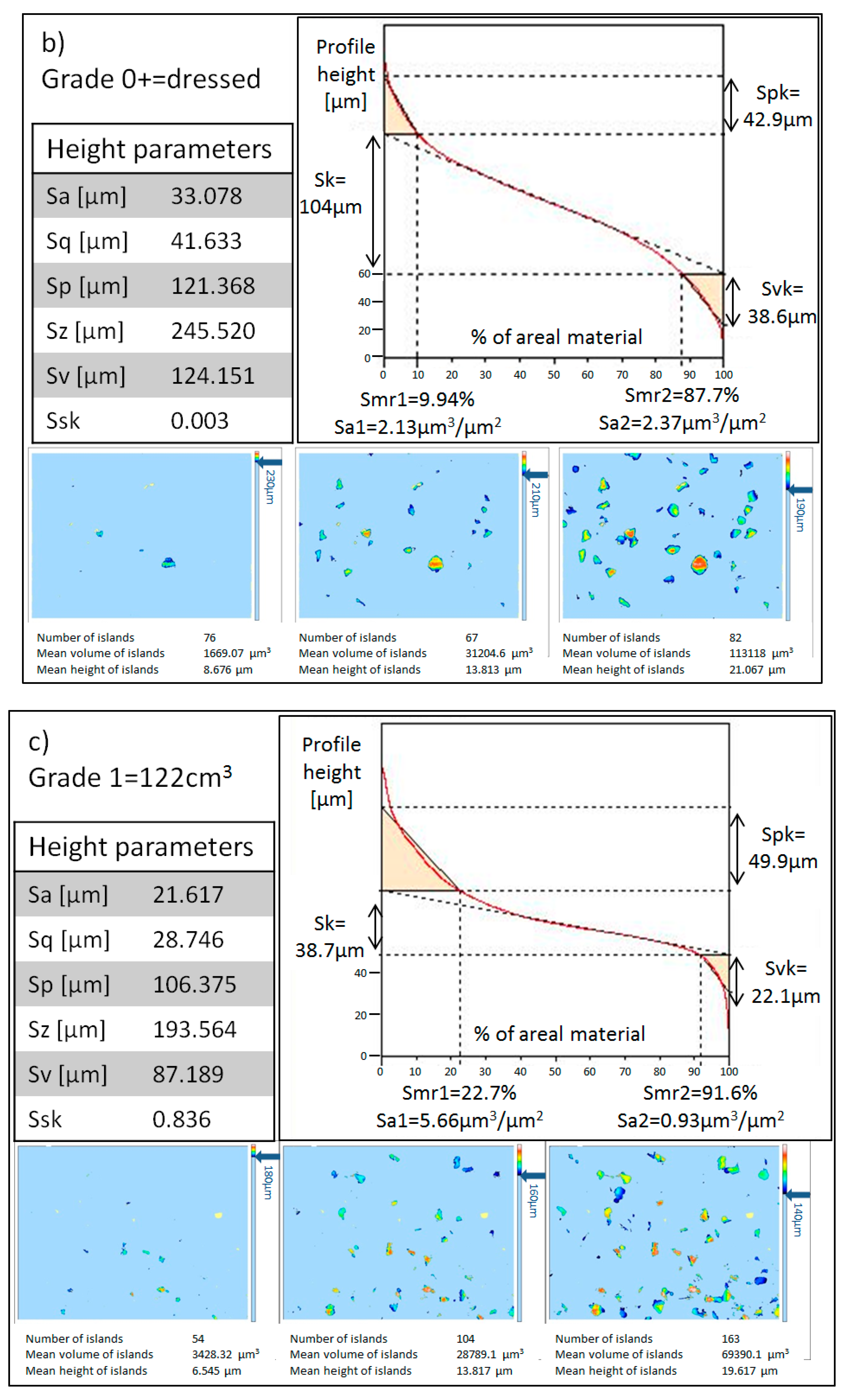
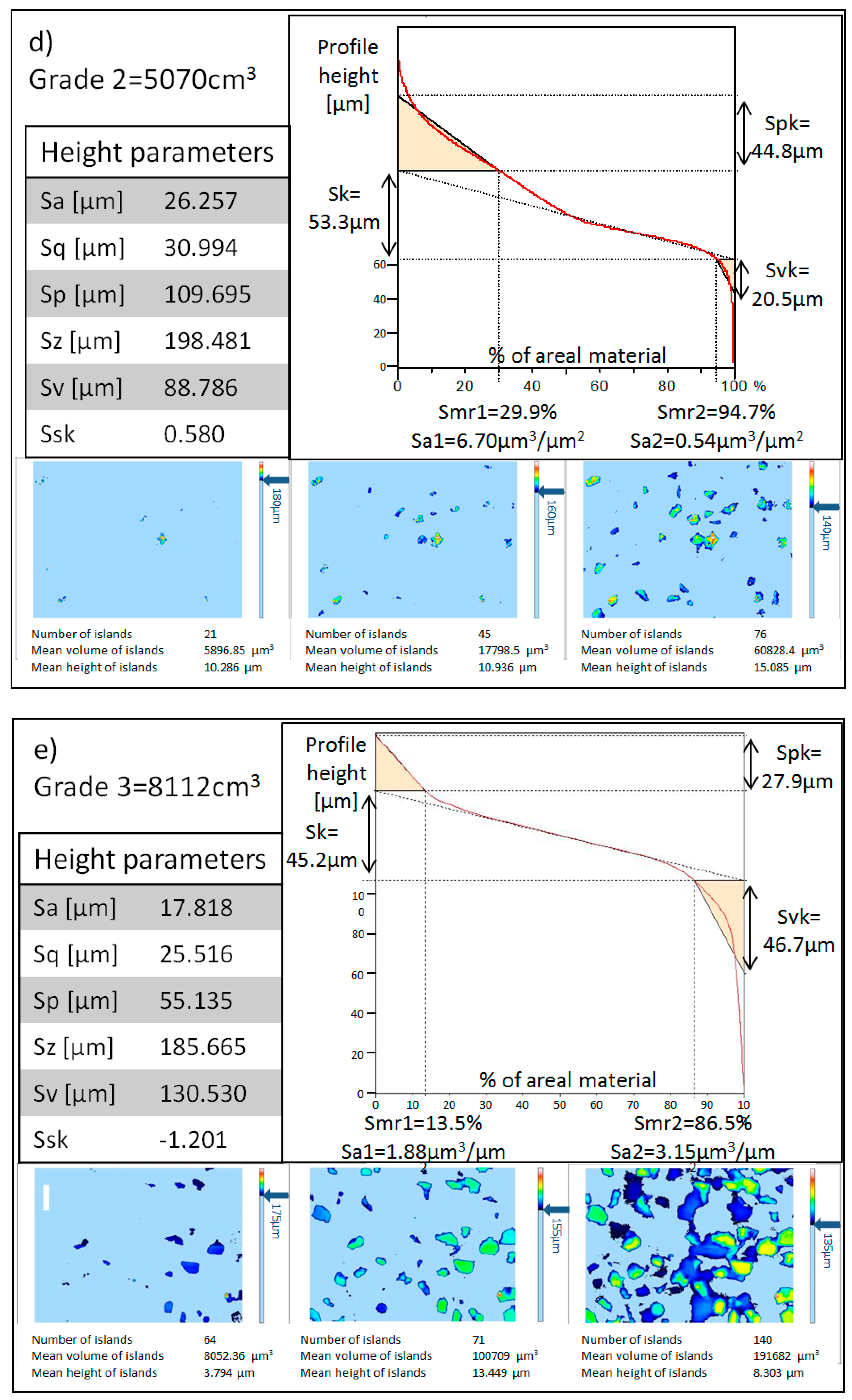
3.1.1. Qualitative Analysis
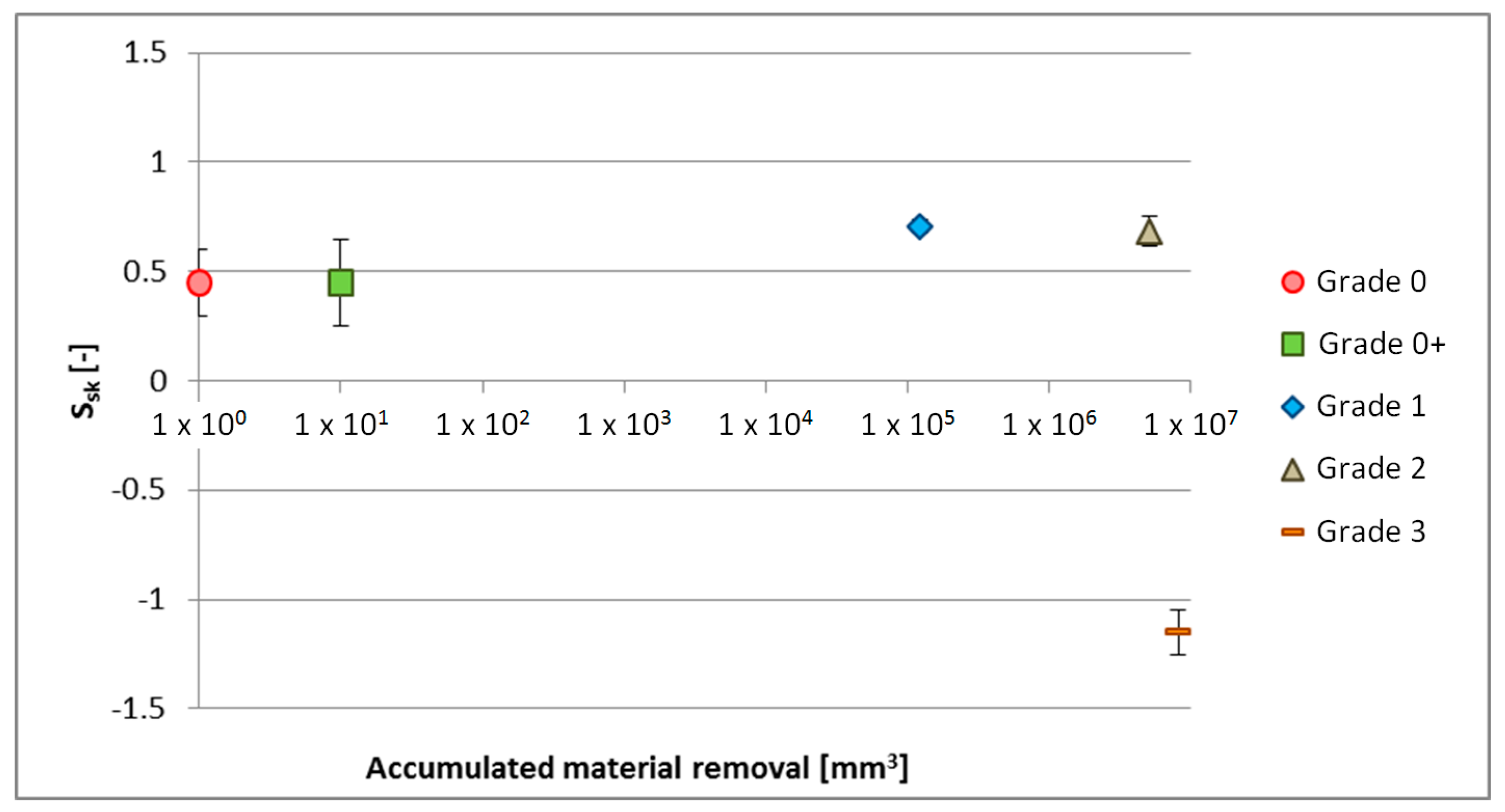
3.1.2. Quantitative Analysis
- Sa.
- This parameter is called the Average Roughness. It provides an overall measure of the surface.
- Sq.
- This parameter is called the Root Mean Square roughness and it is equivalent to the standard deviation of heights.
- Sp.
- This is the Maximum Peak Height above the mean line.
- Sz.
- This is the Maximum Height of the surface.
- Sv.
- This is called Maximum Valley Depth below the mean line.
- Ssk.
- This parameter is called Skewness and it is a measure of the symmetry of the profile. A profile where peaks are more predominant than valleys would present a positive Ssk value, while a surface with predominantly valleys would have a negative value.
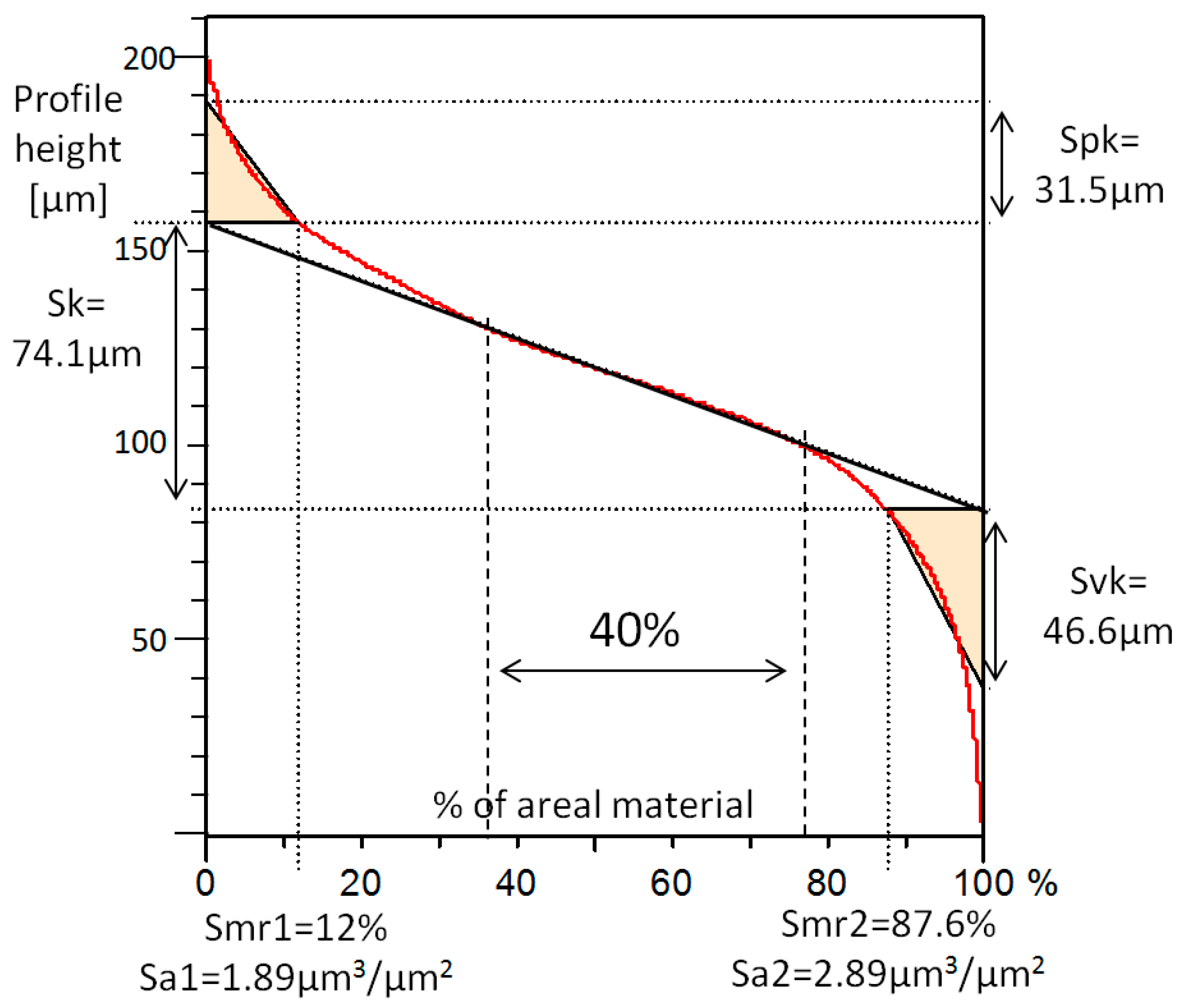
- Spk.
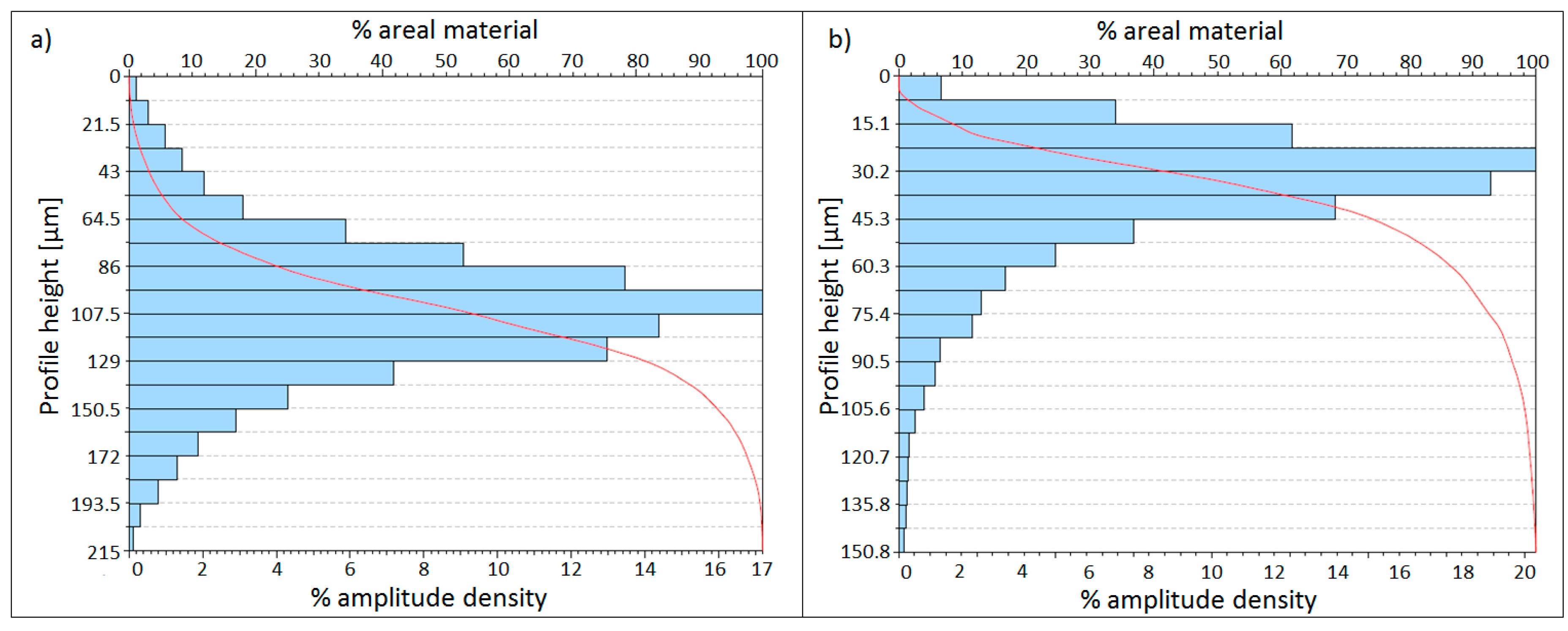
- The Reduced Peak Height, calculated from the Abbott–Firestone curve. This is the height of the triangle drawn above Sk in Figure 7. The area of the triangle is the same as the area covered by the red curve above the upper limit of Sk. Taking into account that the base of the triangle is the Smr1, the height of the triangle is adjusted in order to have the same area in both.
- Sk.
- The Core Roughness, calculated through the equivalent straight line. According to the ISO 25178 standard, the equivalent straight line is the one with the lowest slope that cuts the Abbott–Firestone curve in two points, distancing each other by 40% of the material. If there is more than one line with the same minimum slope, the equivalent line closer to 0% of the material, that is, the left vertical axis, must be chosen. See an example in Figure 7.
- Svk.
- The Reduced Valley Depth, calculated in a similar way to Spk. In this case, the height of the triangle must be adjusted for obtaining the same area as the area left between the red curve and the lowest limit of the Sk.
- Smr1.
- The Peak Material Portion, indicating the percentage of the areal material at the upper limit of Sk.
- Smr2.
- The Valley Material Portion, indicating the percentage of the areal material at the lower limit of Sk.
- Sa1.
- The Upper Area [27]. This is the area of the triangle formed by Spk and Sr1. The physical meaning of this parameter is the volume of material per unit of material surface above Sk.
- Sa2.
- The Lower Area. This is the area of the triangle formed by Svk and Sr2. Similar to Sa1, the physical meaning of this parameter is the volume of void space per unit of void surface below Sk.
3.2. Wheel Conditioning Analysis
3.2.1. Topographical Analysis
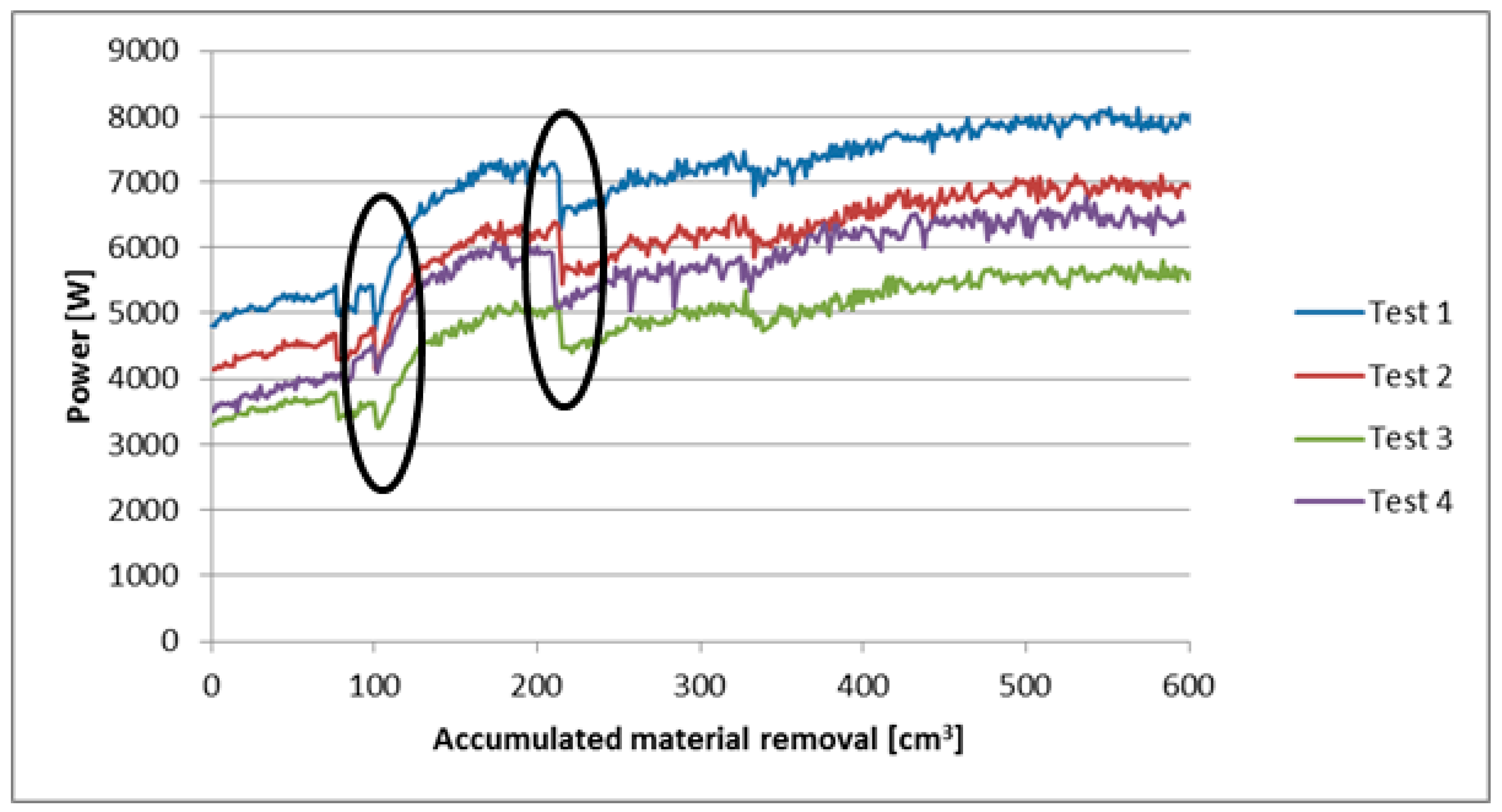
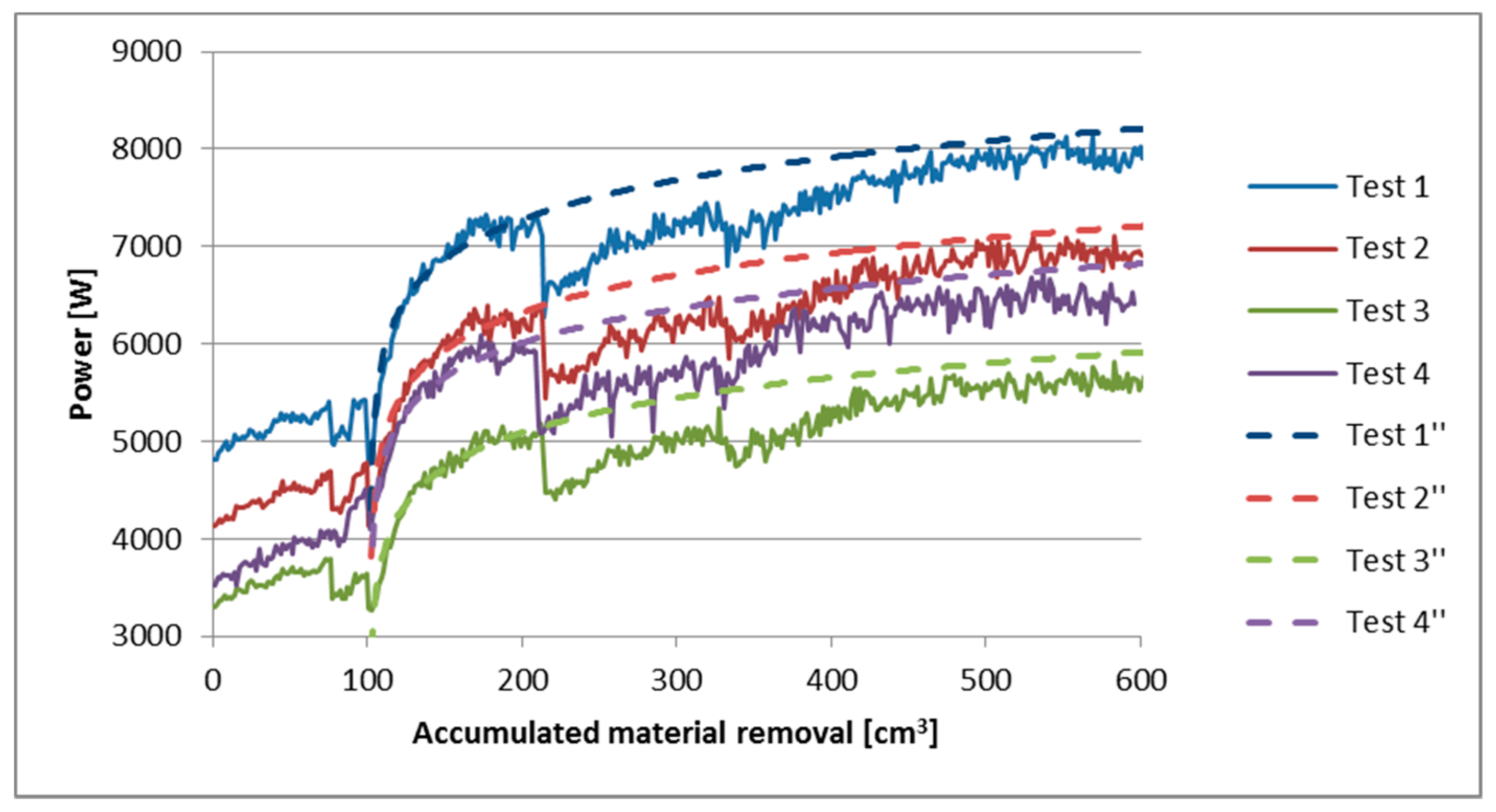
3.2.2. Power Consumption
- Test1 = 0.58 µm;
- Test2 = 0.53 µm;
- Test3 = 0.53 µm;
- Test4 = 0.58 µm.
4. Conclusions
Author Contributions
Acknowledgements
Conflicts of Interest
References
- Boyer, R. Aircraft Materials. In Encyclopedia of Materials: Science and Technology, 2nd ed.; Elsevier: New York, NJ, USA, 2001; pp. 66–73. ISBN 978-008-043152-9. [Google Scholar]
- Giampaolo, T. The Gas Turbine Handbook: Principles and Practice, 3rd ed.; The Fairmont Press: Lilburn, GA, USA, 2003; ISBN 0881735159. [Google Scholar]
- Marinescu, I.; Hitchiner, M.; Uhlmann, E. Handbook of Machining with Grinding Wheels; Taylor & Francis Group: Boca Raton, FL, USA, 2006; ISBN 9781574446715. [Google Scholar]
- Marinescu, I.D.; Rowe, W.B.; Dimitrov, B.; Inasaki, I. Tribology of Abrasive Machining Processe; William Andrew: Norwich, NY, USA, 2004; ISBN 0-8155-1490-5. [Google Scholar]
- Ding, W.; Barbara, L.; Zhu, Y.; Li, Z.; Fu, Y.; Su, H.; Xu, J. Review on monolayer cBN superabrasive wheels for grinding metallic materials. Chin. J. Aeronaut. 2017, 30, 109–134. [Google Scholar] [CrossRef]
- Wegener, K.; Hoffmeister, H.W.; Karpuschewski, B.; Kuster, F.; Hahmann, W.C.; Rabiey, M. Conditioning and monitoring of grinding wheels. CIRP Ann. Manuf. Technol. 2011, 60, 757–777. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Werner, F. Monitoring of Grinding Wheel Wear. CIRP Ann. Manuf. Technol. 1992, 41, 373–376. [Google Scholar] [CrossRef]
- Furutani, K.; Ohguro, N.; Hieu, N.T.; Nakamura, T. In-process measurement of topography change of grinding wheel by using hydrodynamic pressure. Int. J. Mach. Tools Manuf. 2002, 42, 1447–1453. [Google Scholar] [CrossRef]
- Furutani, K.; Trong Hieu, N.; Ohguro, N.; Nakamura, T. Automatic compensation for grinding wheel wear by pressure based in-process measurement in wet grinding. Precis. Eng. 2003, 27, 9–13. [Google Scholar] [CrossRef]
- Sutowski, P.; Plichta, S. An investigation of the grinding wheel wear with the use of root-mean-square value of acoustic emission. Arch. Civ. Mech. Eng. 2006, 6, 87–98. [Google Scholar] [CrossRef]
- Liao, T.W.; Tang, F.; Qu, J.; Blau, P.J. Grinding wheel condition monitoring with boosted minimum distance classifiers. Mech. Syst. Signal Process. 2008, 22, 217–232. [Google Scholar] [CrossRef]
- Blunt, L.; Ebdon, S. The application of three-dimensional surface measurement techniques to characterizing grinding wheel topography. Int. J. Mach. Tools Manuf. 1996, 36, 1207–1226. [Google Scholar] [CrossRef]
- Butler, D.; Blunt, L.; See, B.; Webster, J.; Stout, K. The characterisation of grinding wheels using 3D surface measurement techniques. J. Mater. Process. Technol. 2002, 127, 234–237. [Google Scholar] [CrossRef]
- Shi, Z.; Malkin, S. Wear of Electroplated cBN Grinding Wheels. J. Manuf. Sci. Eng. 2006, 128, 110. [Google Scholar] [CrossRef]
- Upadhyaya, R.P.; Fiecoat, J.H. Factors Affecting Grinding Performance with Electroplated cBN Wheels. CIRP Ann. Manuf. Technol. 2007, 56, 339–342. [Google Scholar] [CrossRef]
- Guo, C.; Shi, Z.; Attia, H.; McIntosh, D. Power and Wheel Wear for Grinding Nickel Alloy with Plated cBN Wheels. CIRP Ann. Manuf. Technol. 2007, 56, 343–346. [Google Scholar] [CrossRef]
- Ding, W.F.; Xu, J.H.; Chen, Z.Z.; Su, H.H.; Fu, Y.C. Wear behavior and mechanism of single-layer brazed cBN abrasive wheels during creep-feed grinding cast nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2010, 51, 541–550. [Google Scholar] [CrossRef]
- Yu, T.; Bastawros, A.F.; Chandra, A. Experimental Characterization of Electroplated Cbn Grinding Wheel Wear: Topology Evolution and Interfacil Toughness. In Proceedings of the ASME 2014 International Manufacturing Science and Engineering Conference, Detroit, MI, USA, 9–13 June 2014; pp. 1–8. [Google Scholar]
- Ye, R.; Jiang, X.; Blunt, L.; Cui, C.; Yu, Q. The application of 3D-motif analysis to characterize diamond grinding wheel topography. Meas. J. Int. Meas. Confed. 2016, 77, 73–79. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, A.K. Experimental investigation on performance of touch-dressed single-layer brazed cBN wheels. Int. J. Mach. Tools Manuf. 2007, 47, 1206–1213. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, A.K. On cumulative depth of touch-dressing of single layer brazed cbn wheels with regular grit distribution pattern. Mach. Sci. Technol. 2007, 11, 259–270. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, B. Ultra-precision grinding of optical glasses using mono-layer nickel electroplated coarse-grained diamond wheels. Part 1: ELID assisted precision conditioning of grinding wheels. Precis. Eng. 2015, 39, 56–66. [Google Scholar] [CrossRef]
- Kitzig, H.; Tawakoli, T.; Azarhoushang, B. A novel ultrasonic-assisted dressing method of electroplated grinding wheels via stationary diamond dresser. Int. J. Adv. Manuf. Technol. 2016, 86, 487–494. [Google Scholar] [CrossRef]
- Dold, C.; Transchel, R.; Rabiey, M.; Langenstein, P.; Jaeger, C.; Pude, F.; Kuster, F.; Wegener, K. A study on laser touch dressing of electroplated diamond wheels using pulsed picosecond laser sources. CIRP Ann. Manuf. Technol. 2011, 60, 363–366. [Google Scholar] [CrossRef]
- Pfaff, J.; Warhanek, M.; Huber, S.; Komischke, T.; Hänni, F.; Wegener, K. Laser Touch Dressing of Electroplated cBN Grinding Tools. Procedia CIRP 2016, 46, 272–275. [Google Scholar] [CrossRef]
- Leach, R. Characterization of Areal Surface Texture; Springer: London, UK, 2013; ISBN 978-3-642-36458-7. [Google Scholar]
- Arantes, L.J.; Fernandes, K.A.; Schramm, C.R.; Silveire Leal, J.E.; Piratelli-Filho, A.; Domingues Franco, S.; Valdes Arancibia, R. The roughness characterization in cylinders obtained by conventional and flexible honing processes. Int. J. Adv. Manuf. Technol. 2017, 93, 635–649. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Grinding Technology: Theory and Application of Machining with Abrasives; Industrial Press Inc.: New York, NY, USA, 2008; ISBN 978-0-8311-3247-7. [Google Scholar]
- Mayer, J.E.; Fang, G.P.; Kegg, R.L. Effect of Grit Depth of Cut on Strength of Ground Ceramics. CIRP Ann. Manuf. Technol. 1994, 43, 309–312. [Google Scholar] [CrossRef]





| Wheel diameter | 150 mm | |||
| cBN grain size | 250 µm | |||
| Grain density | ≈14 grains/cm2 | |||
| Workpiece material | C1023 (nickel base superalloy) | |||
| Grinding speed | 80 m/s | |||
| Test name | Test1 | Test2 | Test3 | Test4 |
| Depth of cut (mm) | 0.4 | 0.3 | 0.15 | 0.15 |
| Feed rate (mm/min) | 630 | 605 | 850 | 1040 |
| heq (µm) | 3.15 | 2.27 | 1.6 | 1.95 |
| Cutting fluid | Oil-based high pressure | |||
| SiC grain size | 68 μm | |||
| k = 1 | k = 2 | k = 3 | |||
|---|---|---|---|---|---|
| Parameters | Significance | Parameters | Significance | Parameters | Significance |
| Ssk (-) | 6.396 | Ssk | 4.776 | Ssk | 3.157 |
| Sa1 (µm3/mm2) | 1.143 | Sa1 | 0.642 | Smr1 | 0.384 |
| Sa2 (µm3/mm2) | 1.010 | Smr1 | 0.610 | Svk | 0.262 |
| Smr1 (%) | 0.837 | Sa2 | 0.514 | Sp | 0.230 |
| Spk (µm) | 0.630 | Svk | 0.444 | Sa1 | 0.140 |
| Svk (µm) | 0.625 | Sp | 0.400 | Sa2 | 0.018 |
| Sp (µm) | 0.570 | Spk | 0.127 | Smr2 | −0.021 |
| Sa (µm) | 0.111 | Smr2 | 0.033 | Sa | −0.179 |
| Smr2 (%) | 0.087 | Sq | −0.130 | Sz | −0.329 |
| Sz (µm) | 0.058 | Sz | −0.136 | Spk | −0.375 |
| Sq (µm) | 0.013 | Sv | −0.323 | Sv | −0.559 |
| Sv (µm) | −0.088 | Sku | −0.329 | Sk | −0.753 |
| Sk (µm) | −0.232 | Sk | −0.492 | Sku | −0.761 |
| k = 1 | k = 2 | k = 3 | |||
|---|---|---|---|---|---|
| Parameters | Significance | Parameters | Significance | Parameters | Significance |
| Sv | 0.074 | Sz | −0.064 | Smr2 | −0.102 |
| Sz | 0.060 | Smr2 | −0.066 | Sz | −0.188 |
| Sp | −0.020 | Sku | −0.112 | Sv | −0.238 |
| Smr2 | −0.031 | Sp | −0.166 | Sp | −0.311 |
| Spk | −0.079 | Spk | −0.277 | Spk | −0.474 |
| Sq | −0.154 | Sq | −0.334 | Sq | −0.515 |
| Sa | −0.158 | Sa | −0.359 | Sa | −0.560 |
| Svk | −0.194 | Smr1 | −0.482 | Smr1 | −0.754 |
| Smr1 | −0.210 | Sk | −0.488 | Sk | −0.757 |
| Sk | −0.219 | Svk | −0.520 | Svk | −0.845 |
| Sa2 | −0.304 | Sa2 | −0.784 | Sa2 | −1.263 |
| Sa1 | −0.626 | Sa1 | −1.412 | Sa1 | −2.198 |
| Ssk | −1.351 | Ssk | −4.000 | Ssk | −6.650 |
| Parameters | rGB |
|---|---|
| Sa | 0.812 |
| Sk | 0.800 |
| Sz | 0.744 |
| Smr1 | 0.739 |
| Svk | 0.685 |
| Smr2 | 0.632 |
| Sq | 0.625 |
| Sv | 0.448 |
| Sp | 0.164 |
| Sa1 | 0.126 |
| Ssk | −0.095 |
| Spk | −0.129 |
| Sa2 | −0.211 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidal, G.; Ortega, N.; Bravo, H.; Dubar, M.; González, H. An Analysis of Electroplated cBN Grinding Wheel Wear and Conditioning during Creep Feed Grinding of Aeronautical Alloys. Metals 2018, 8, 350. https://doi.org/10.3390/met8050350
Vidal G, Ortega N, Bravo H, Dubar M, González H. An Analysis of Electroplated cBN Grinding Wheel Wear and Conditioning during Creep Feed Grinding of Aeronautical Alloys. Metals. 2018; 8(5):350. https://doi.org/10.3390/met8050350
Chicago/Turabian StyleVidal, Gorka, Naiara Ortega, Héctor Bravo, Mirentxu Dubar, and Haizea González. 2018. "An Analysis of Electroplated cBN Grinding Wheel Wear and Conditioning during Creep Feed Grinding of Aeronautical Alloys" Metals 8, no. 5: 350. https://doi.org/10.3390/met8050350
APA StyleVidal, G., Ortega, N., Bravo, H., Dubar, M., & González, H. (2018). An Analysis of Electroplated cBN Grinding Wheel Wear and Conditioning during Creep Feed Grinding of Aeronautical Alloys. Metals, 8(5), 350. https://doi.org/10.3390/met8050350






