Hydrogen Embrittlement Mechanism in Fatigue Behavior of Austenitic and Martensitic Stainless Steels
Abstract
:1. Introduction
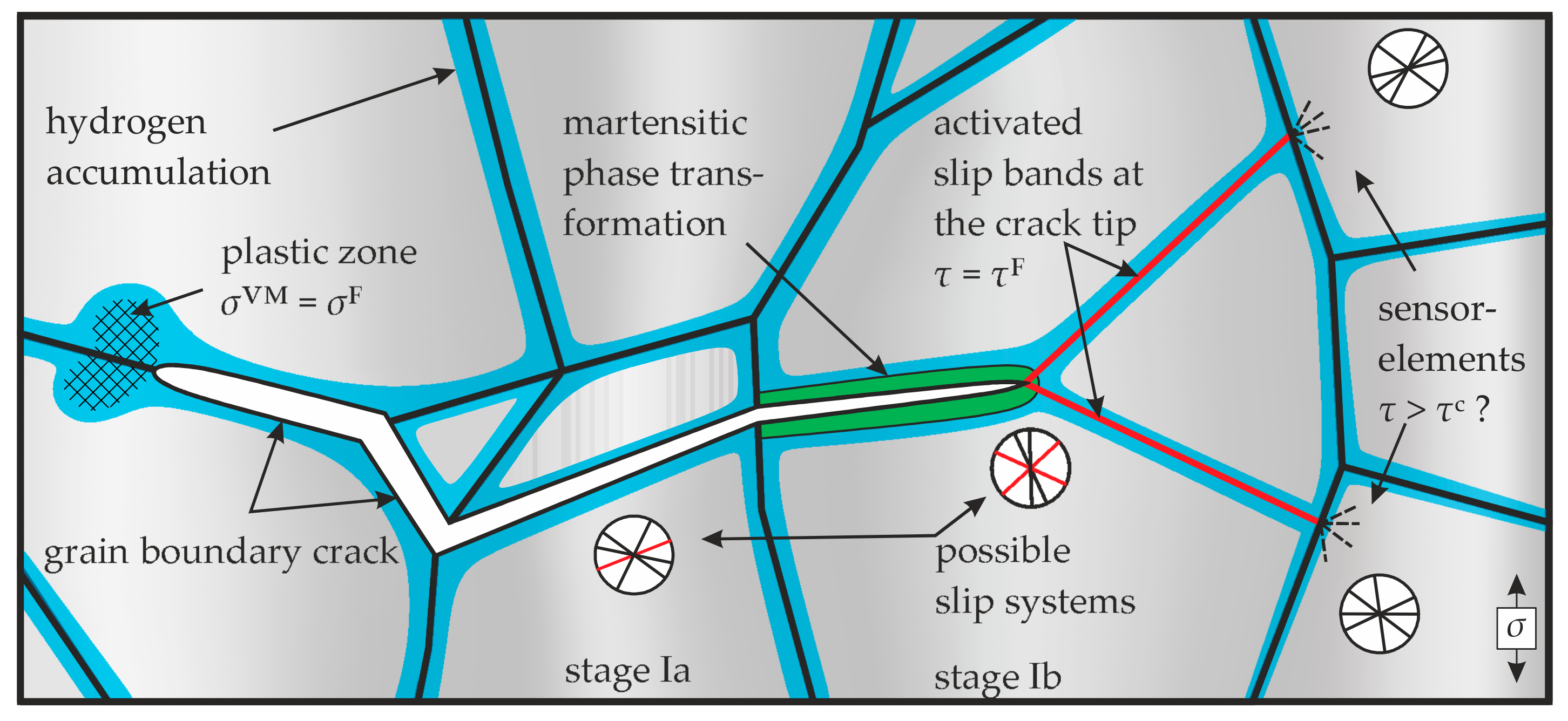
2. Hydrogen Embrittlement Mechanisms
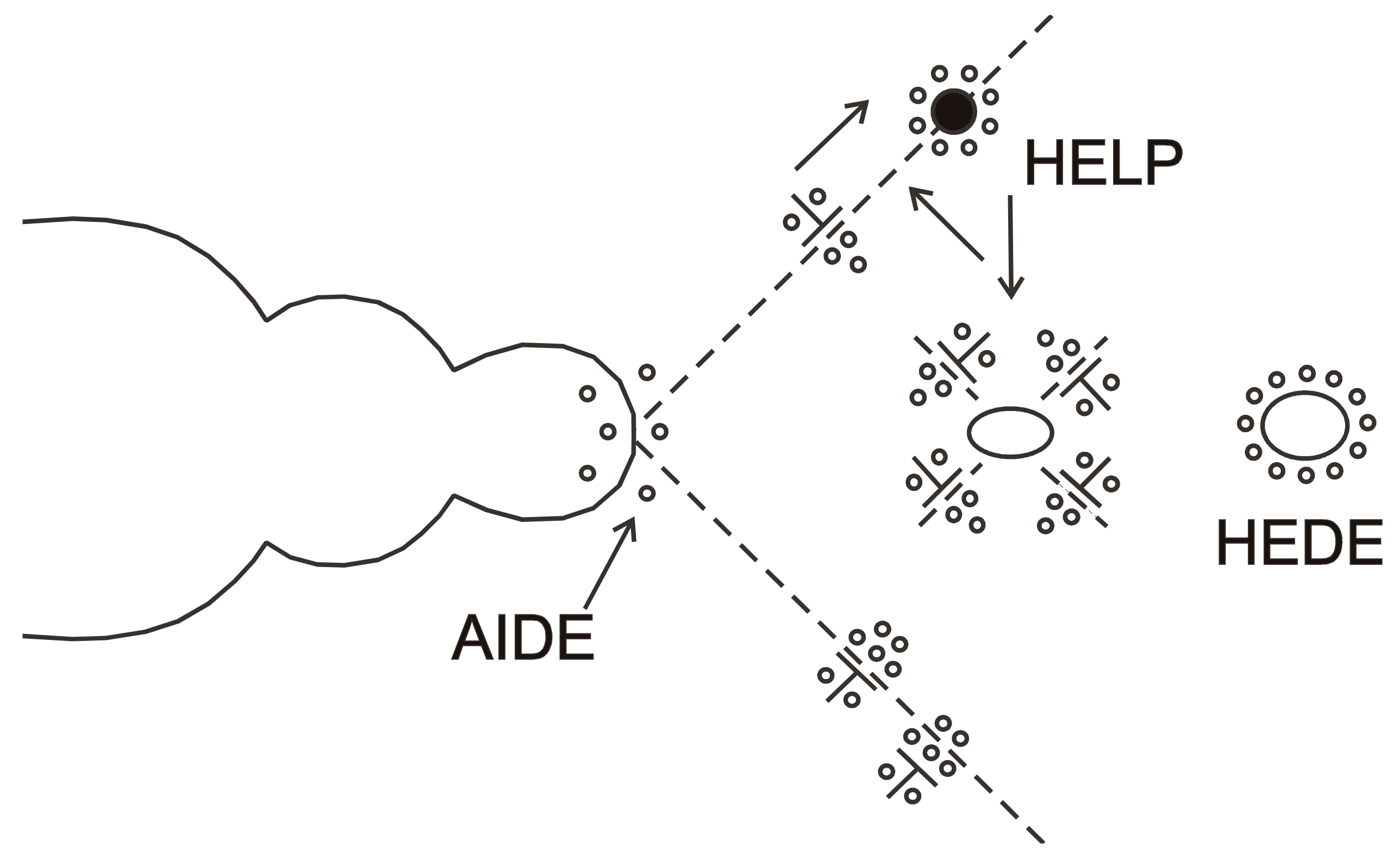
2.1. Hydrogen-Enhanced Localized Plasticity (HELP)
2.2. Hydrogen-Enhanced Decohesion (HEDE)
2.3. Adsorption-Induced Dislocation Emission (AIDE)
3. Materials and Methods
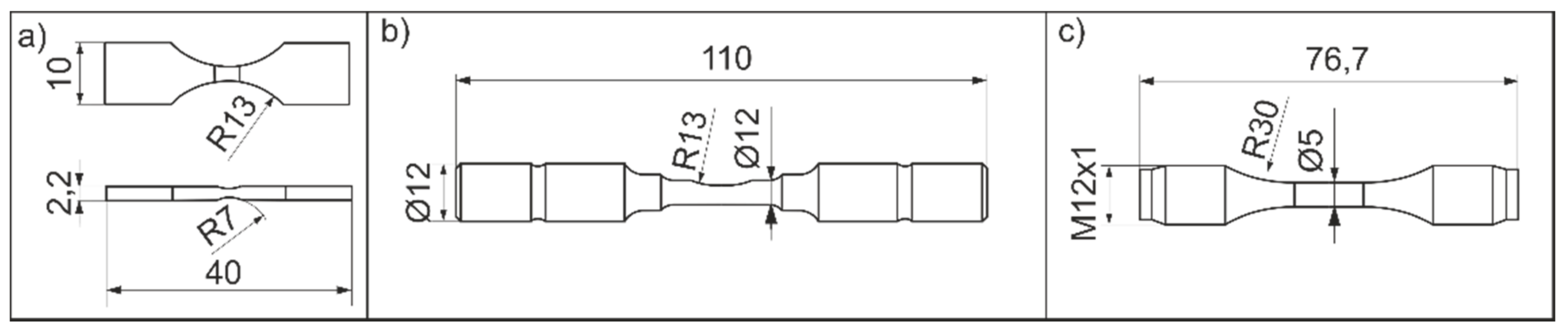
3.1. Materials
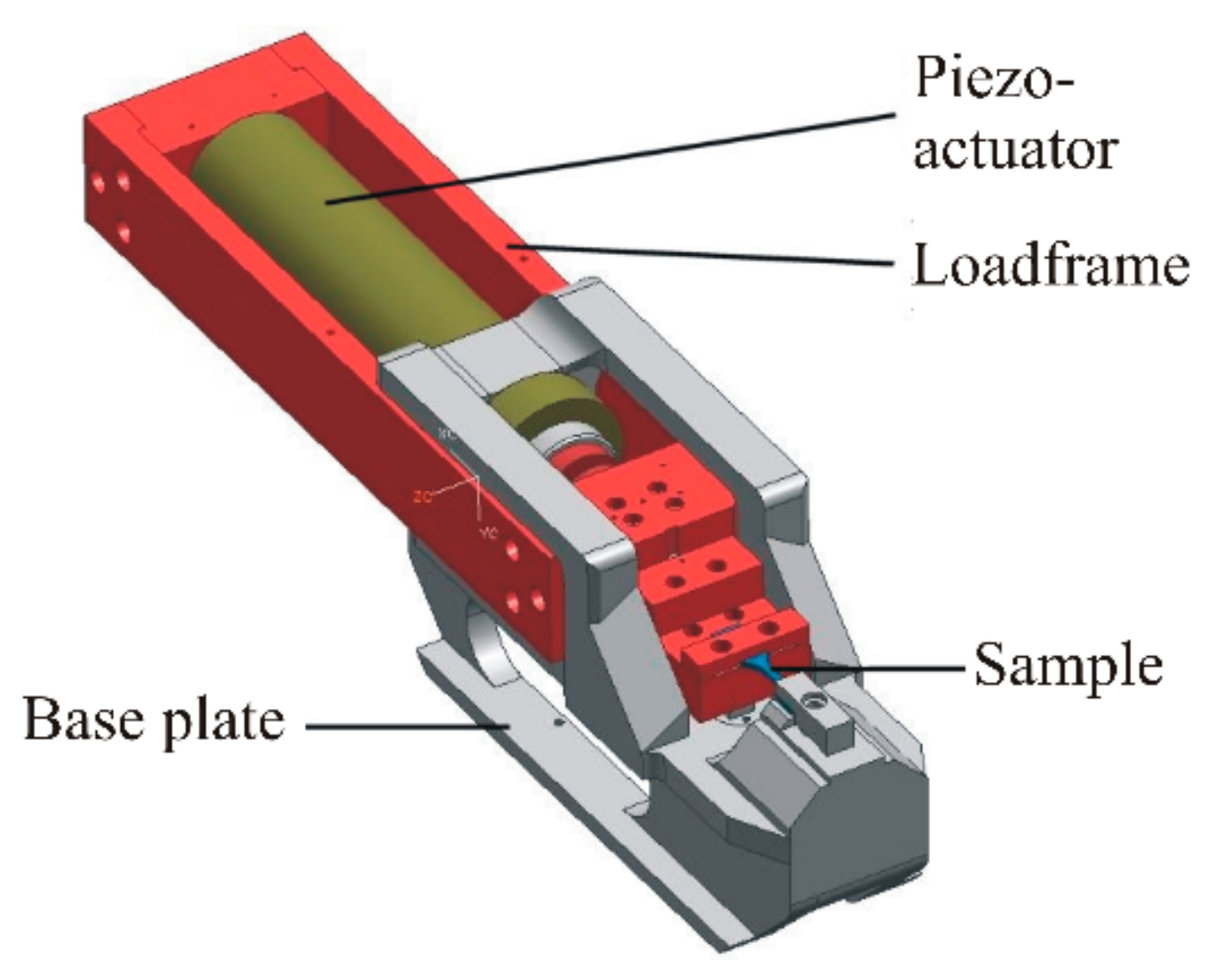
3.2. Testing Machines
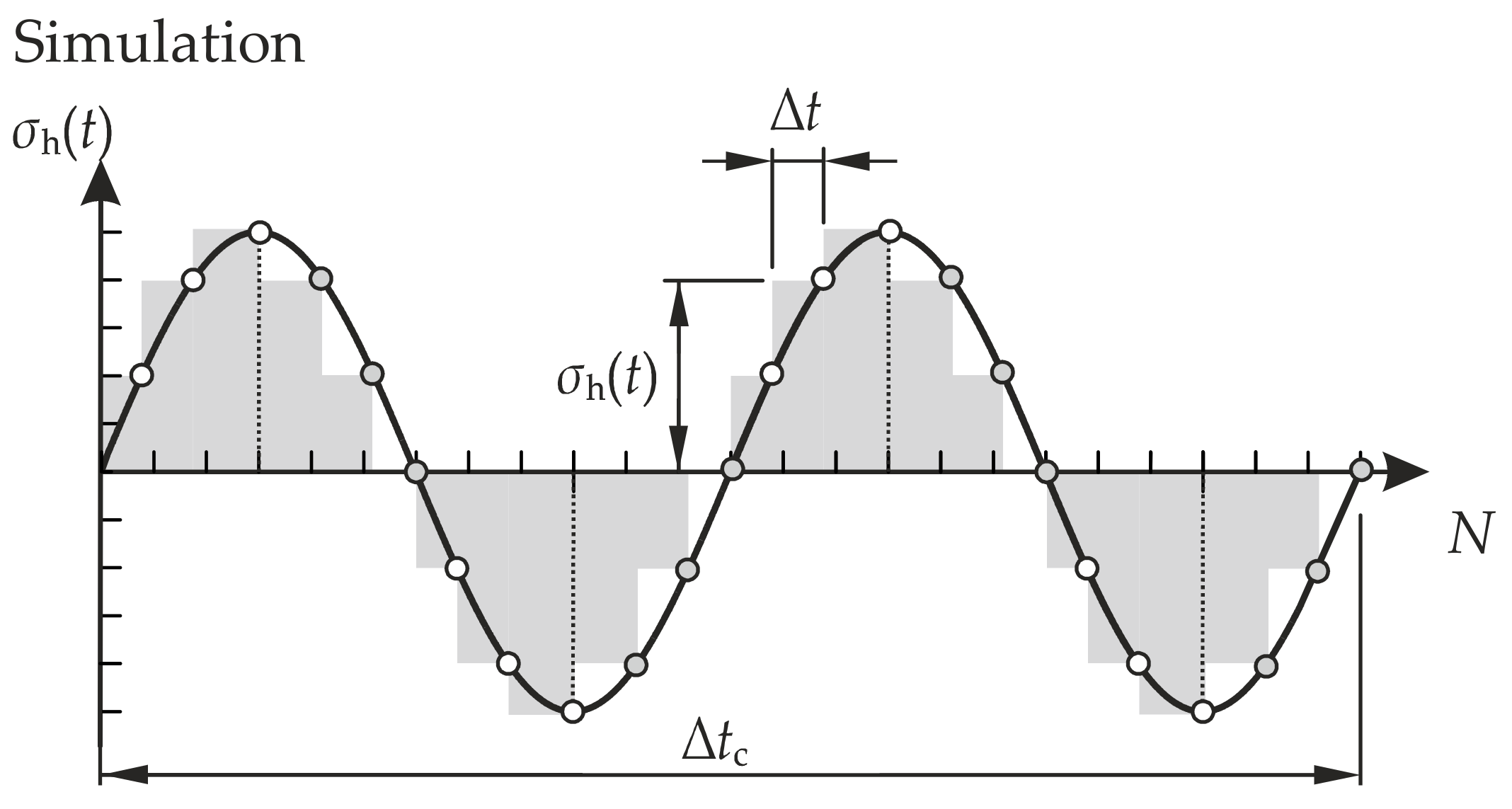
3.3. Modelling the Influence of Hydrogen on Short Fatigue Crack Propagation
3.3.1. Description of the Diffusion Model
3.3.2. Determination of the Material Parameters in the Model
4. Experimental Results
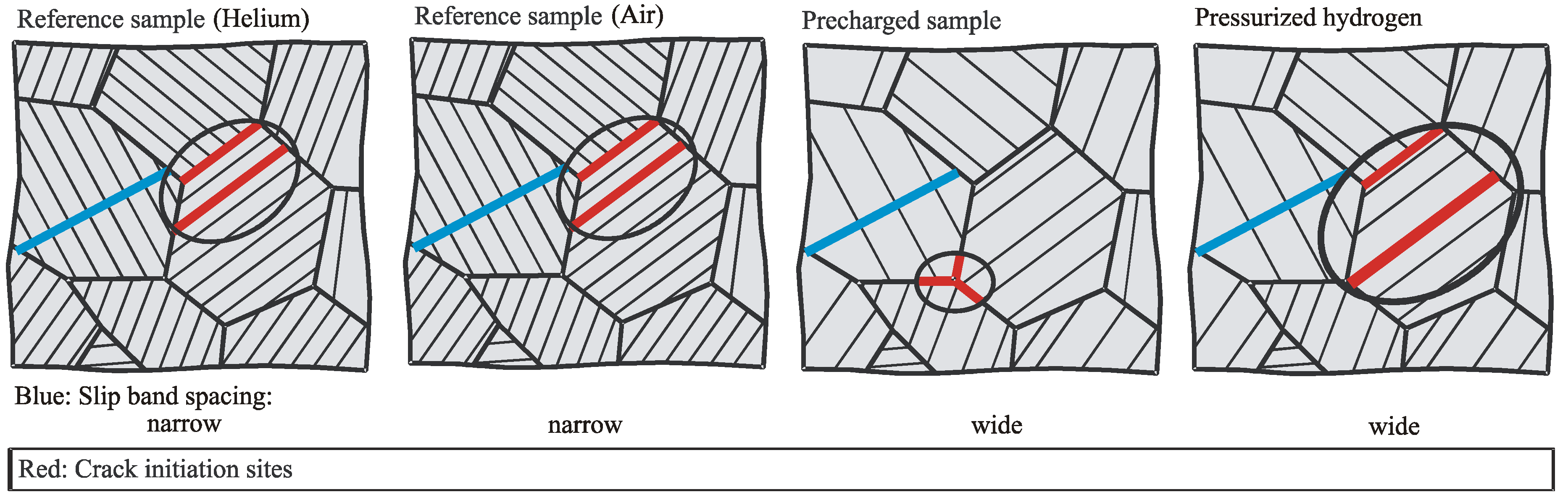
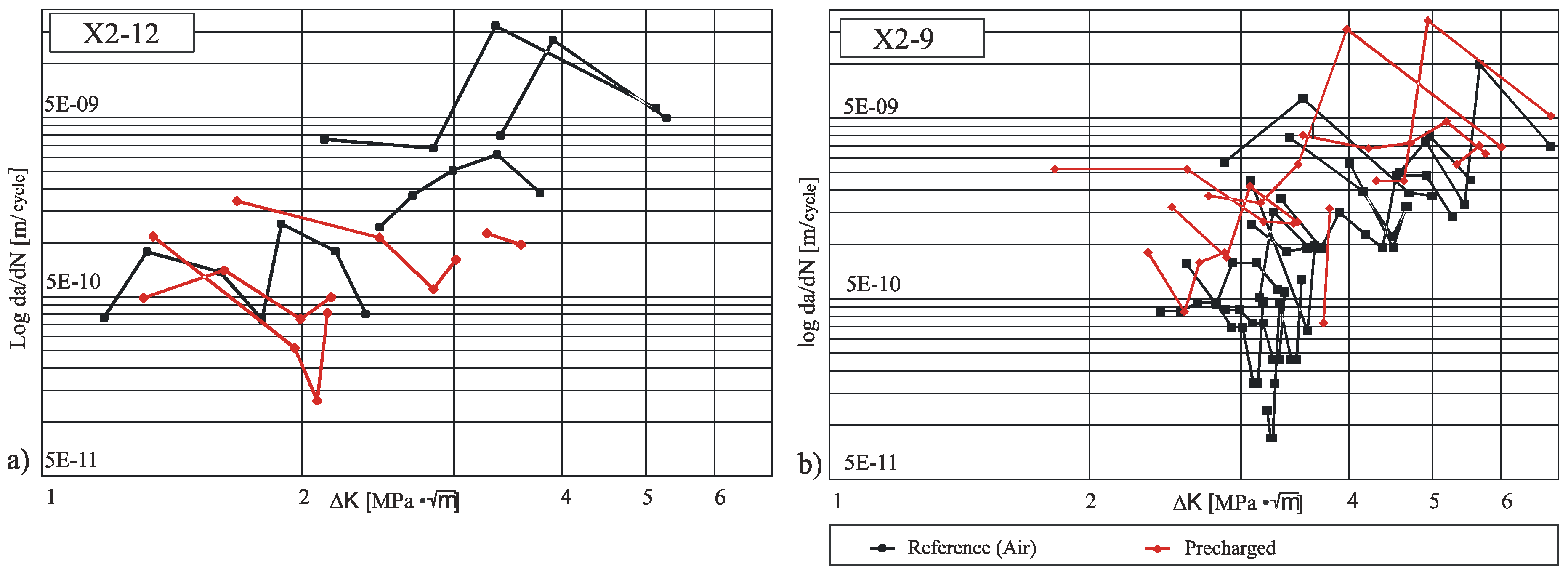
4.1. Investigations on the Metastable Austenitic Stainless Steels X2–12 and X2–9
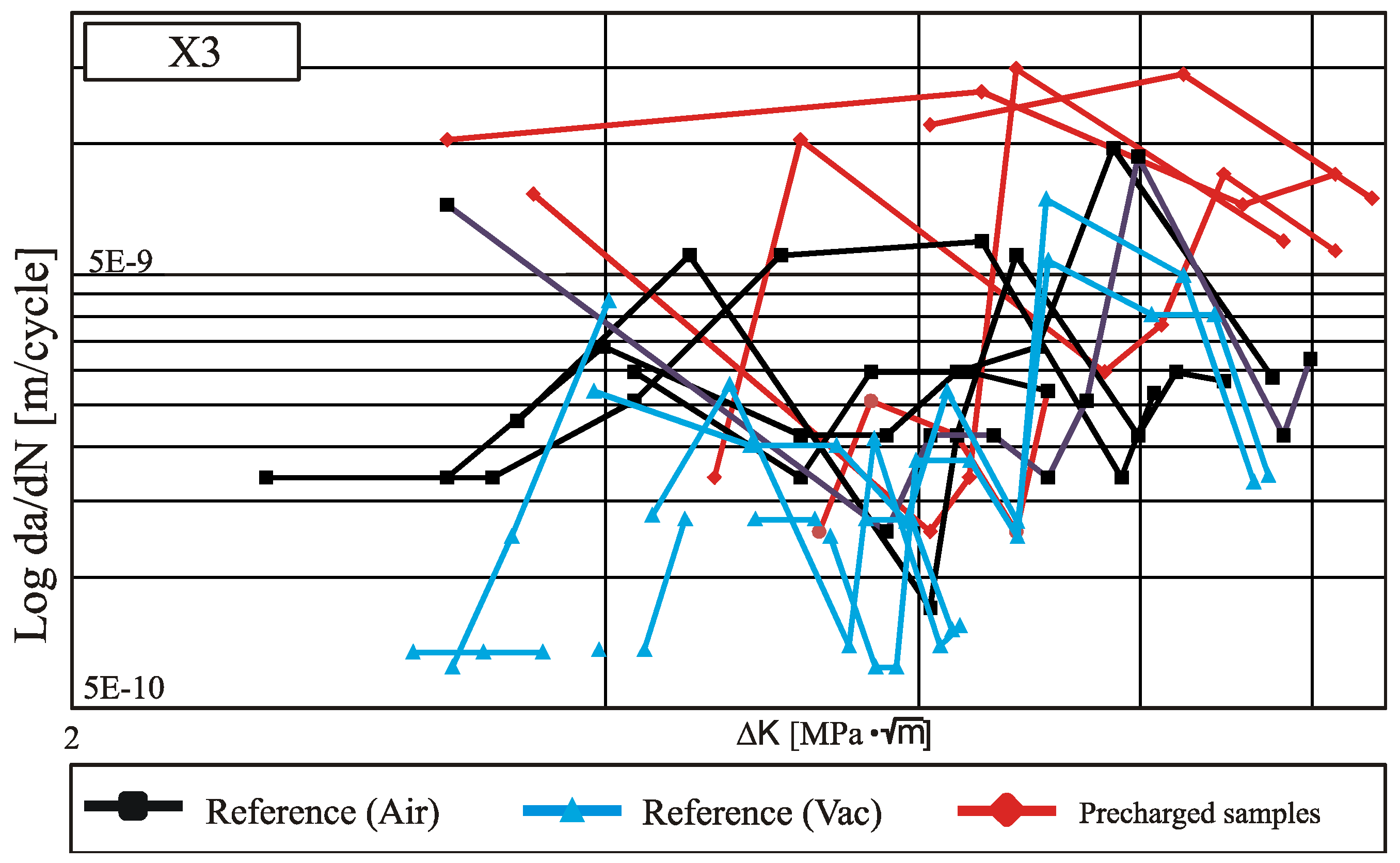
4.2. Investigations on the Martensitic Stainless Steel X3
4.3. Conclusion Experimental Results
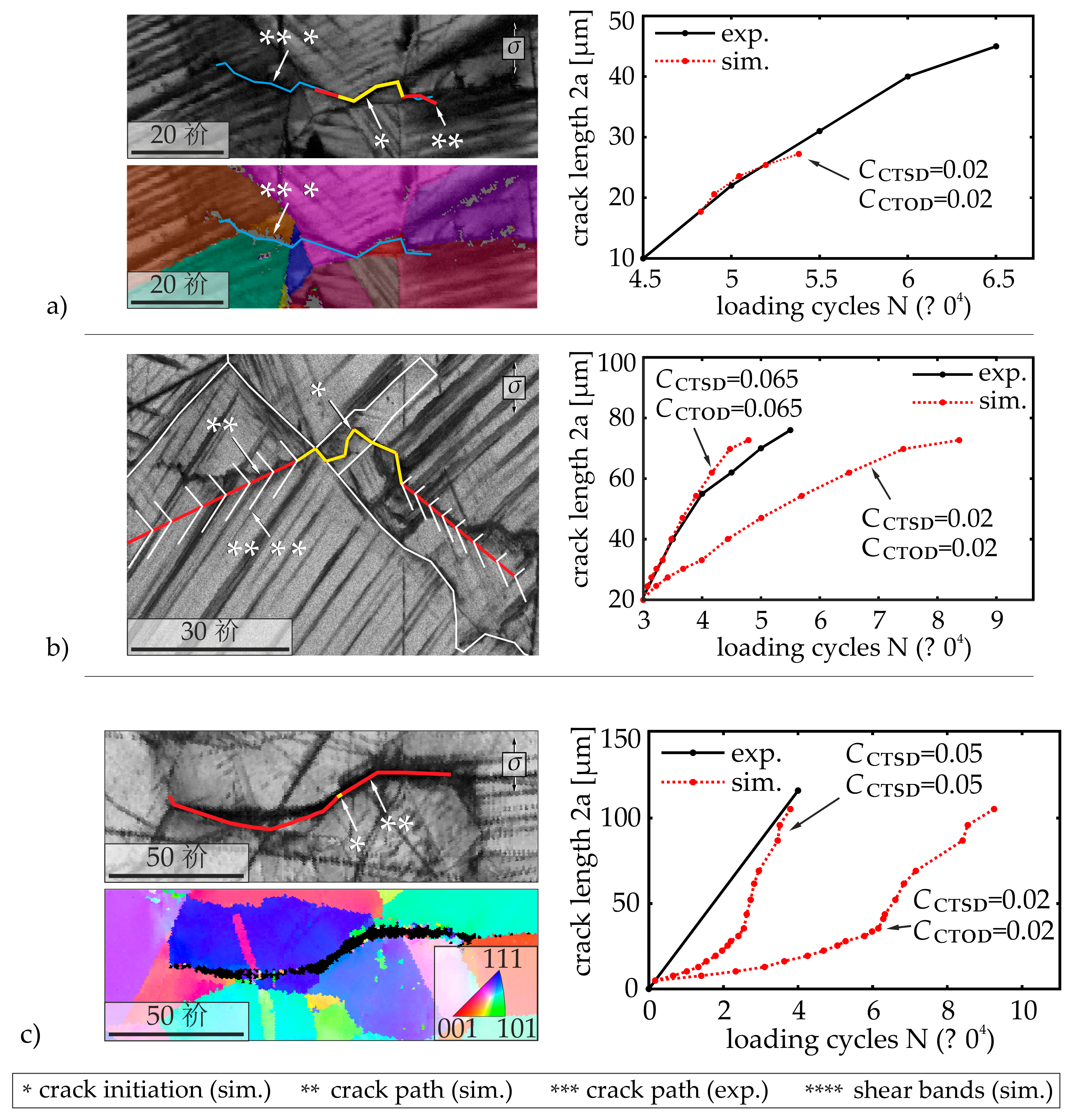
5. Results on the Simulation of Short Crack Propagation in a Metastable Austenitic Stainless Steel X2CrNi19-12
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Nibur, K.A.; Gibbs, P.J.; Foulk, J.W.; SanMarchi, C. Notched Fatigue of Austenitic Alloys in Gaseous Hydrogen. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference Volume 6B: Materials and Fabrication, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Takakuwa, O.; Yamabe, J.; Matsunaga, H.; Furuya, Y.; Matsuoka, S. Recent Progress on Interpretation of Tensile Ductility Loss for Various Austenitic Stainless Steels with External and Internal Hydrogen. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference Volume 6B: Materials and Fabrication, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Murakami, Y.; Kanezaki, T.; Mine, Y. Hydrogen Effect against Hydrogen Embrittlement. Metall. Mater. Trans. 2010, 41, 2548–2562. [Google Scholar] [CrossRef]
- Skipper, C.; Leisk, G.; Saigal, A.; San Marchi, C. Effect of internal hydrogen on fatigue strength of type 316 stainless steel. In Proceedings of the 2008 International Hydrogen Conference, Grand Teton National Park, WY, USA, 7–10 September 2008; Somerday, B., Sofronis, P., Jones, R., Eds.; ASME Press: New York, NY, USA, 2009; pp. 139–146. [Google Scholar]
- San Marchi, C.; Michler, T.; Nibur, K.A.; Somerday, B.P. On the physical differences between tensile testing of type 304 and 316 austenitic stainless steels with internal hydrogen and in external hydrogen. Int. J. Hydrog. Energy 2010, 35, 9736–9745. [Google Scholar] [CrossRef]
- Yagodzinski, Y.; Saukkonen, T.; Andronova, E.; Rissanen, L.; Hänninen, H. Hydrogen-induced cracking of metastable austenitic stainless and high-strength carbon steels. In Proceedings of the 2008 International Hydrogen Conference, Moran, WY, USA, 7–10 September 2008; Somerday, B., Sofronis, P., Jones, R., Eds.; ASME Press: New York, NY, USA, 2009; pp. 123–130. [Google Scholar]
- Künkler, B. Mechanismenorientierte Lebensdauervorhersage unter Berücksichtigung der Mikrostruktur—Modellentwicklung, Verifikation und Anwendung. Dissertation, Universität Siegen, Siegen, Germany, 2007. [Google Scholar]
- Kübbeler, M. Simulation der Mikrostrukturbestimmten Kurzrissausbreitung unter dem Einfluss Lokaler Phasenumwandlung. Dissertation, Universität Siegen, Siegen, Germany, 2017. [Google Scholar]
- Tabata, T.; Birnbaum, H.K. Direct observations of the effect of Hydrogen on the behaviour of dislocations in iron. Scr. Metall. 1983, 17, 947–950. [Google Scholar] [CrossRef]
- Oriani, R. A mechanistic theory of hydrogen embrittlement of steels. Phys. Chem. 1972, 76, 848–857. [Google Scholar]
- Petch, N.J.; Stables, P. Delayed Fracture of Metals under Static Load. Nature 1952, 169, 842–843. [Google Scholar] [CrossRef]
- Lynch, S.P. Mechanisms of hydrogen assisted cracking—A review. In Proceedings of the International Conference on Hydrogen Effects on Material Behaviour and Corrosion Deformation Interactions, Moran, WY, USA, 22–26 September 2002; pp. 449–466. [Google Scholar]
- Roth, I. Untersuchungen zum Ausbreitungsverhalten Mikrostrukturell kurzer Ermüdungsrisse in Metastabilem Austenitischen Edelstahl. Dissertation, Universität Siegen, Siegen, Germany, 2012. [Google Scholar]
- Brück, S.; Schippl, V.; Schwarz, M. Untersuchung des Einflusses einer Wasserstoffvorbeladung auf die Ermüdungskurzrissausbreitung in einem austenitischen Edelstahl. In Tagungsband zur Werkstoffprüfung; Borsutzki, M., Düsseldorf, G., Eds.; Moninger: Karlsruhe, Germany, 2015. [Google Scholar]
- Hilgendorff, P.-M. Mechanismenbasierte Modellierung und Simulation des VHCF-Wechselverformungs-Verhaltens Austenitischer Edelstähle. Dissertation, Universität Siegen, Siegen, Germany, 2017. [Google Scholar]
- Wilkinson, A.J.; Roberts, S.G. A dislocation model for the two critical stress intensities required for threshold fatigue crack propagation. Scr. Mater. 1996, 35, 1365–1371. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. A mechanism for the strain-induced nucleation of martensitic transformation. J. Less Common Met. 1972, 28, 107–118. [Google Scholar] [CrossRef]
- Köster, P. Mechanismenorientierte Modellierung und Simulation der Mikrostrukturbestimmten Kurzrissausbreitung unter Berücksichtigung ebener und Räumlicher Aspekte. Dissertation, Universität Siegen, Siegen, Germany, 2015. [Google Scholar]
- Rios, E.R.; Sun, Z.Y.; Miller, K.J. A theoretical and experimental study of environmental hydrogen-assisted short fatigue crack growth in an Al-Li alloy. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 1459–1474. [Google Scholar] [CrossRef]
- Von Pezold, J.; Lymperakis, L.; Neugebauer, J. Hydrogen-enhanced local plasticity at dilute bulk H concentrations: The role of H–H interactions and the formation of local hydrides. Acta Mater. 2011, 59, 2969–6980. [Google Scholar] [CrossRef]
- Kotake, H.; Matsumoto, R.; Taketomi, S.; Miyazaki, N. Transient hydrogen diffusion analyses coupled with crack-tip plasticity und cyclic loading. Int. J. Press. Vessels Pip. 2008, 85, 540–549. [Google Scholar] [CrossRef]
- Li, J.C.M.; Oriani, R.A.; Darken, L.S. The Thermodynamics of Stressed Solids. Z. Phys. Chem. 1966, 49, 271–290. [Google Scholar] [CrossRef]
- Brooks, A.N.; Hughes, T.J.R. Streamline Upwind Petrov-Galerkin Formulation for Convection-Dominated Flows with Particular Emphasis on the Incompressible Navier-Stokes Equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Navarro, A.; de los Rios, E.R. Short and long fatigue crack growth—A unified model. Philos. Mag. A 1988, 57, 15–36. [Google Scholar] [CrossRef]
- Müller-Bollenhagen, C.; Zimmermann, M.; Christ, H.-J. Very high cycle fatigue behaviour of austenitic stainless steel and the effect of strain-induced martensite. Int. J. Fatigue 2010, 32, 936–942. [Google Scholar] [CrossRef]
- Ratte, E. Wasserstoffinduzierte verzögerte Rissbildung austenitischer Stähle auf CrNi(Mn)- und Mn-Basis. Dissertation, Universität Aachen, Aachen, Germany, 2007. [Google Scholar]
- Kramer, D.; Brager, H.R.; Rhodes, C.G.; Pard, A.G. Helium embrittlement in type 304 stainless steel. J. Nucl. Mater. 1968, 25, 121–131. [Google Scholar] [CrossRef]
- Aubert, L.; Saintier, N.; Olive, J.M. Crystal plasticity computation and atomic force microscopy analysis of the internal hydrogen-induced slip localization on polycrystalline stainless steel. Scr. Mater. 2012, 66, 698–701. [Google Scholar] [CrossRef]
- Gangloff, R.P. Gaseous Hydrogen Embrittlement of Materials in Energy Technologies; Woodhead Publishing: Sawston, UK, 2012; ISBN 978-1-84569-677-1. [Google Scholar]
- Robertson, I.M.; Lillig, D.; Ferreira, P.J. Revealing the fundamental processes controlling hydrogen embrittlement. In Proceedings of the 2008 International Hydrogen Conference, Grand Teton National Park, WY, USA, 7–10 September 2008; Somerday, B., Sofronis, P., Jones, R., Eds.; ASME: New York, NY, USA, 2009; pp. 22–37. [Google Scholar]
- San Marchi, C.; Somerday, B. Technical Reference for Hydrogen Compatibility of Materials; Sandia Report SAND2012-7321; Sandia National Laboratories: Albuquerque, NM, USA, 2012.
- Düber, O. Untersuchungen zum Ausbreitungsverhalten Mikrostrukturell kurzer Ermüdungsrisse in Zweiphasigen Metallischen Werkstoffen am Beispiel eines Austenitisch-Ferritischen Duplexstahls. Dissertation, Universität Siegen, Siegen, Germany, 2007. [Google Scholar]
- Schwarz, M.; Brück, S.; Schippl, V.; Zickler, S.; Weihe, S. Hydrogen influence on fatigue life and short crack growth of X3CrNiMo13-4 and modified X2Crni19-11. In Proceedings of the 2016 International Hydrogen Conference, Materials Performance in Hydrogen Environment, Grand Teton National Park, MY, USA, 11–14 September 2016; Somerday, B.P., Sofronis, P., Eds.; ASME Press: New York, NY, USA, 2017; pp. 263–269. [Google Scholar]
- Nagumo, M.; Nakamura, M.; Takai, K. Hydrogen thermal desorption relevant to delayed-fracture susceptibility of high-strength steels. Metall. Mater. Trans. A 2001, 32, 339–347. [Google Scholar] [CrossRef]
- Schippl, V.; Brück, S.; Fritzen, C.-P.; Christ, H.-J.; Schwarz, M.; Weihe, S. Numerical simulation of the influence of hydrogen on small fatigue crack growth mechanisms in AISI304L. In Proceedings of the 2016 International Hydrogen Conference, Materials Performance in Hydrogen Environment, Grand Teton National Park, MY, USA, 11–14 September 2016; Somerday, B.P., Sofronis, P., Eds.; ASME Press: New York, NY, USA, 2017; pp. 620–627. [Google Scholar]





| Alloy | C | Si | Mn | P | S | Cr | Ni | Mo | Nb | Ti | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X3 | 0.023 | 0.42 | 0.61 | 0.018 | 0.001 | 12.38 | 4.41 | 0.368 | - | 0.004 | - |
| X2–9 | 0.014 | 0.53 | 1.71 | 0.010 | 0.009 | 18.05 | 9.07 | 0.02 | 0.01 | 0.005 | 0.0016 |
| X2–12 | 0.016 | 0.48 | 1.75 | 0.012 | 0.008 | 17.78 | 12.36 | 0.02 | 0.01 | 0.005 | 0.017 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brück, S.; Schippl, V.; Schwarz, M.; Christ, H.-J.; Fritzen, C.-P.; Weihe, S. Hydrogen Embrittlement Mechanism in Fatigue Behavior of Austenitic and Martensitic Stainless Steels. Metals 2018, 8, 339. https://doi.org/10.3390/met8050339
Brück S, Schippl V, Schwarz M, Christ H-J, Fritzen C-P, Weihe S. Hydrogen Embrittlement Mechanism in Fatigue Behavior of Austenitic and Martensitic Stainless Steels. Metals. 2018; 8(5):339. https://doi.org/10.3390/met8050339
Chicago/Turabian StyleBrück, Sven, Volker Schippl, Martina Schwarz, Hans-Jürgen Christ, Claus-Peter Fritzen, and Stefan Weihe. 2018. "Hydrogen Embrittlement Mechanism in Fatigue Behavior of Austenitic and Martensitic Stainless Steels" Metals 8, no. 5: 339. https://doi.org/10.3390/met8050339
APA StyleBrück, S., Schippl, V., Schwarz, M., Christ, H.-J., Fritzen, C.-P., & Weihe, S. (2018). Hydrogen Embrittlement Mechanism in Fatigue Behavior of Austenitic and Martensitic Stainless Steels. Metals, 8(5), 339. https://doi.org/10.3390/met8050339




