The Scrap Collection per Industry Sector and the Circulation Times of Steel in the U.S. between 1900 and 2016, Calculated Based on the Volume Correlation Model
Abstract
1. Introduction
2. Input Data
2.1. Scrap Collection
2.2. Steel Consumption
3. Calculation Procedure
4. Results and Discussion
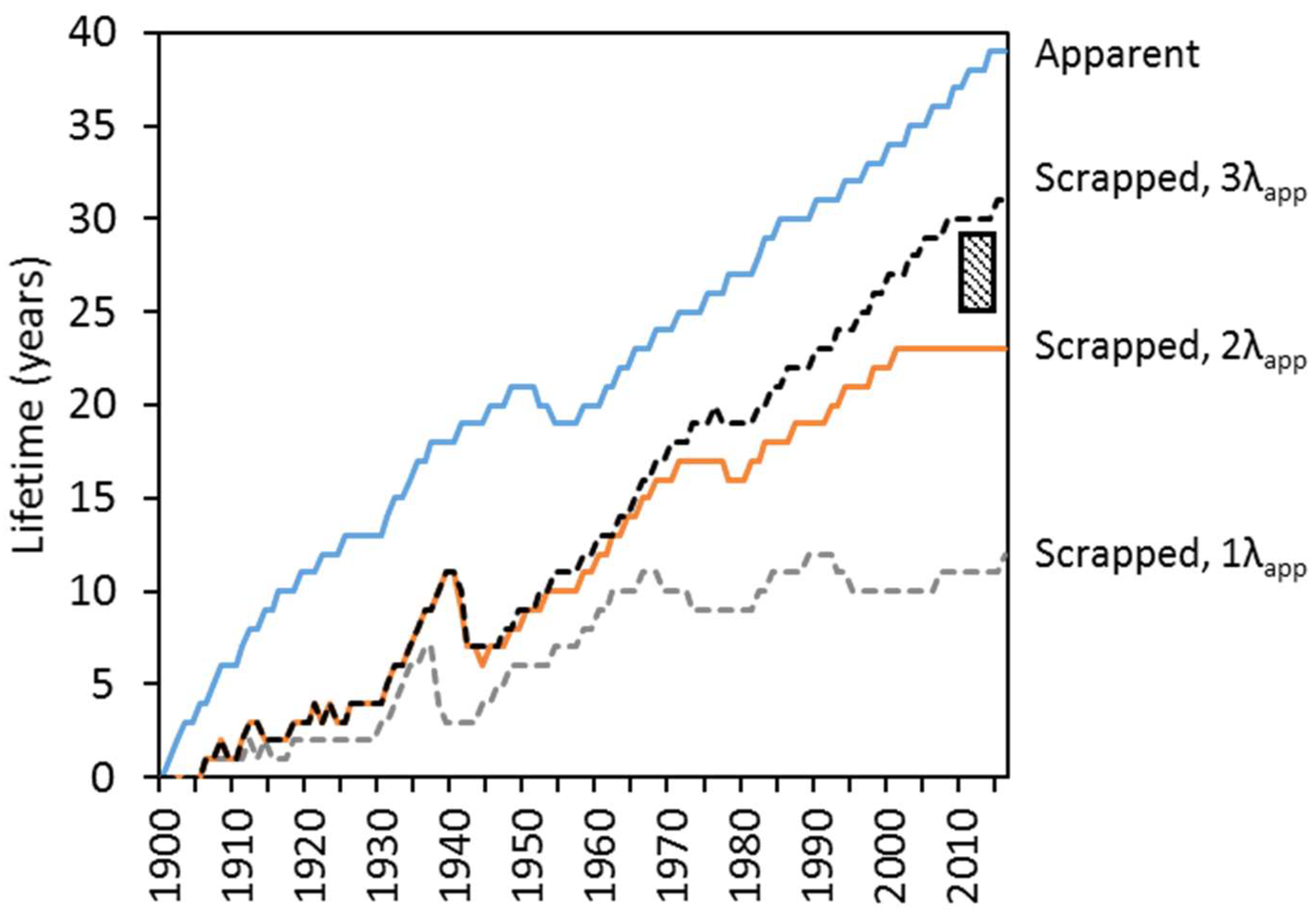
4.1. Calculated Lifetimes per Industry Sector in the U.S.
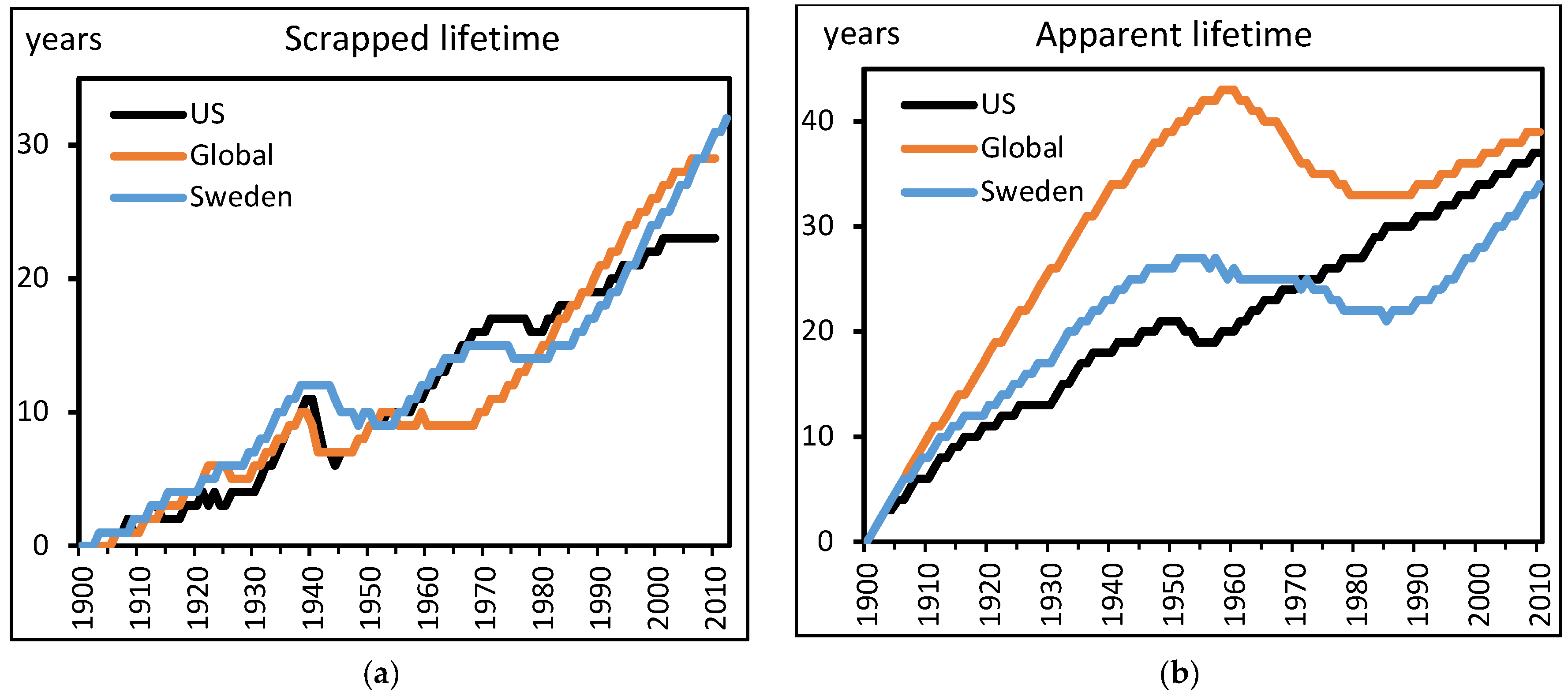
4.2. The Lifetimes of Steel in the U.S., Sweden, and the World
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Product groups | References | Method | Timeline | Average Lifetime |
|---|---|---|---|---|
| American Housing Survey, General Housing Data, all Housing Units. | U.S. Census Bureau, Current Housing Reports, Series H150/11, American Housing Survey for the United States: 2011, Table C-01-AH. [9] | Lifetime of buildings used in Unites States | 2015 2013–2014 2011 | 39 years 44 years 42 years |
| American Housing Survey, General Housing Data, all Housing Units. | U.S. Department of Commerce. Bureau of Economic Analysis. Table A-1. Characteristics of the housing inventory 1973, 1980 and 1970 page 6 or page 1. [9] | Lifetime of buildings used in Unites States | 1973 1980 | 24 years 28 years |
| Industrial buildings, mobile offices, office buildings, commercial warehouses, other commercial buildings, religious buildings, educational buildings, hospital and institutional buildings, hotels and motels, amusement and recreational buildings, all other nonfarm buildings. | U.S. Department of Commerce. Bureau of Economic Analysis. Fixed Assets and Consumer Durable Goods in the United States, 1925–1999. [9] | Lifetime estimates | 1925–1997 | 17–48 years |
| Bridges | National Bridge Inventory [10,11] | Lifetime of bridges in-use, maximum age distribution. Most bridges were built for a 50-year design life. | 2010 | 50 years |
| Product Groups | Reference | Method | Timeline | Average Lifetime |
|---|---|---|---|---|
| Construction machinery and equipment, metalworking machinery and equipment, general purpose machinery and equipment. | U.S. Department of Commerce. Bureau of Economic Analysis. Fixed Assets and Consumer Durable Goods in the United States, 1925–1999. [13] | Service lives and depreciation estimates. | 1925–1999 | 10–16 years |
| Agricultural and different machinery. | Division of Assessment Standards, Nevada Department of Taxation. [12] | Service lives. | 2010 | 7–30 years |
| Metalworking machinery, durable machinery, special industry machinery. | U.S. Department of Commerce. Bureau of Economic Analysis. Fixed Assets and Consumer Durable Goods in the United States, 1925–1997. [13] | Service lives. | 1925–1997 | 16–25 years |
| Product Groups | Reference | Method | Timeline | Average Lifetime |
|---|---|---|---|---|
| Boats and vessels—dry cargo, tanker, towboat, passenger, offshore support/crew-boats, dry barge, tank/liquid barge, (figures include vessels available for operation) | U.S. Army Corps of Engineers, Waterborne Transportation Lines of the United States, Volume 1, National Summaries, Table 4, available at http://www.navigationdatacenter.us/veslchar/pdf/ as of 21 June 2016. [15] | Age is based on the year the vessel was built or rebuilt. | 1990–2014 | 18–16 years |
| Locomotives, passenger and other train cars. | Amtrak Annual Report, Statistical Appendix. [17] | Fiscal year-end average (30 September of stated year). Active units less backshop units undergoing heavy maintenance, less back-ordered units undergoing progressive maintenance and running repairs. | 1972–2015 | 11–26 years |
| Commuter rail locomotives, commuter rail passenger coaches, commuter rail self-propelled passenger cars, heavy-rail passenger cars, light rail vehicles (streetcars), articulated full-small size trolley vans, ferry boats. | U.S. Department of Transportation, Federal Transit Administration, National Transit Database. National Transit Summaries and Trends, Table 25. [16] | Average Age of Urban Transit Vehicles. Locomotives used in Amtrak intercity passenger services are not included. | 1985–2014 | 11–16 years |
| Aircraft: Transportation by air, depository institutions and business services. | U.S. Department of Commerce. Bureau of Economic Analysis. Fixed Assets and Consumer Durable Goods in the United States, 1925–1999. [18] | Average age of aircraft. | 1960–1997 | 15–20 years |
| Product Groups | Reference | Method | Timeline | Average Lifetime |
|---|---|---|---|---|
| Mobile phones, cordless telephones, answering machines, fax machines, personal computers, laptops, printers, computer monitors, computer mice, keyboards (Metal content 8–69%). | Study of Life Expectancy of Home Components. Prepared by the Economics Group of NAHB. [14] | Current lifetime | 2011 | 5–11 years |
| Household appliances—air conditioners, dishwashers, dryers, freezers, microwave ovens, ranges, refrigerators, clothes washers, water heaters, trash compactors (metal content in all units between 46–96%). | National Association of Home Builders/Bank of America Home Equity. [14] | Life expectancy is based on first-owner use. | 2011 | 5–20 years |
| Video and audio products—projection TVs, plasma, LCD, and color TVs, TV/VCR combinations, videocassette players, VCR decks, DVD players, camcorders, home and portable audio products (Metal content 21–30%) | National Association of Home Builders/Bank of America Home Equity. [14] | Life expectancy is based on first-owner use. | 2011 | 9–15 years |
Appendix B
| Scrap Type | Percentage of Yearly Scrap (%) |
|---|---|
| Appliances | 11.37 |
| Vehicles | 19.78 |
| Tires | 0.02 |
| Packaging | 4.2 |
| Construction | 19.16 |
| Mechanical machinery | 4.57 |
| Electrical and Electronic products | 5.8 |
| Transport | 3.16 |
| Prompt scrap | 27.23 |
| Other | 4.71 |
| Total production of scrap | 19,095,547 ton |
Appendix C
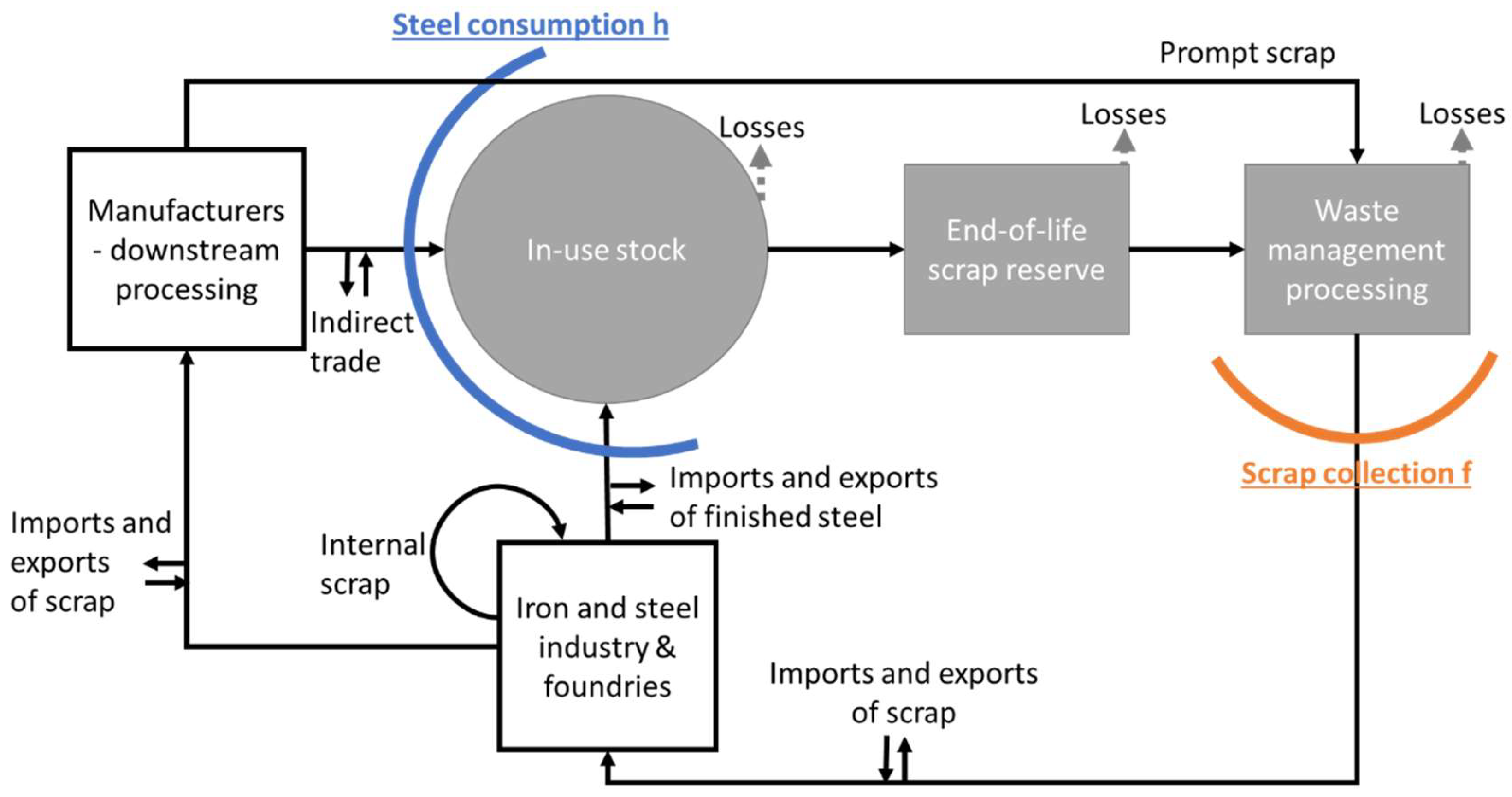
| Term | Definition |
|---|---|
| Steel consumption (h) | Net consumption of steel used for its application purpose plus prompt steel scrap. Marked with a thick blue curved line in Figure A1. |
| Scrap collection (f) | Net collection of obsolete and prompt steel scrap in the US. Domestic collected steel scrap which is commercially available. Marked with a thick orange curved line in Figure A1. |
| Purchased steel scrap | Net receipt of scrap in US iron and steel mills and foundries, including imports and excluding exports of scrap. |
| Internal scrap | Processing scrap generated at iron and steel mills and foundries. |
| Prompt scrap | Processing scrap generated at external manufacturers (during downstream processing); also termed “new scrap”. |
| Obsolete scrap | Old scrap which has been collected and processed from end-of-life products and applications. |
| Indirect trade | Imports and exports of steel in further manufactured goods; steel contained in products. |
References
- Grimes, S.; Donaldson, J.; Gomez, G.C. Report on the Environmental Benefits of Recycling; Bureau of International Recycling (BIR), Centre for Sustainable production & Resource Efficiency (CSPRE), Imperial College London: London, UK, 2008. [Google Scholar]
- Müller, E.; Hilty, L.M.; Widmer, R.; Schluep, M.; Faulstich, M. Modeling metal stocks and flows: A review of dynamic material flow analysis methods. Environ. Sci. Technol. 2014, 48, 2102–2113. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.B.; Cao, J.; Kongar, E.M.A.; Weiner, P.-H.; Graedel, T.E. Service Lifetimes of Mineral End Uses. Minerals Resources External Research Program. Available online: https://minerals.usgs.gov/mrerp/reports/Mueller-06HQGR0174.pdf (accessed on 7 May 2018).
- Müller, D.B.; Wang, T.; Duval, B. Patterns of iron use in societal evolution. Environ. Sci. Technol. 2001, 45, 182–188. [Google Scholar] [CrossRef] [PubMed]
- Pauliuk, S.; Milford, R.L.; Müller, D.B.; Allwood, J.M. The steel scrap age. Environ. Sci. Technol. 2013, 47, 3448–3454. [Google Scholar] [CrossRef] [PubMed]
- Cooper, D.R.; Skelton, A.C.H.; Moynihan, M.C.; Allwood, J.M. Component level strategies for exploiting the lifespan of steel in products. Resour. Conserv. Recycl. 2014, 84, 24–34. [Google Scholar] [CrossRef]
- Reck, B.K.; Chambon, M.; Hashimoto, S.; Graedel, T.E. Global stainless steel cycle exemplifies China’s rise to metal dominance. Environ. Sci. Technol. 2010, 44, 3940–3946. [Google Scholar] [CrossRef] [PubMed]
- Hatayama, H.; Daigo, I.; Matsuno, Y.; Adachi, Y. Outlook of the world steel cycle based on the stock and flow dynamics. Environ. Sci. Technol. 2010, 44, 6457–6463. [Google Scholar] [CrossRef] [PubMed]
- U.S. Census Bureau, Current Housing Reports. American Housing Survey for the United States: 2015–2013, 2011, 1997, 1980, 1973; U.S. Government Printing Office: Washington, DC, USA, 2016–2014, 2012, 1998, 1981, 1974.
- Emily, Yu. Analysis of National Bridge Inventory (NBI) Data for California Bridges. Master’s Thesis, California Polytechnic State University, Pomona, CA, USA, April 2015. [Google Scholar]
- NACE. Corrosion Control Plan for Bridges. A NACE International White Paper. Available online: https://www.nace.org/Newsroom/Press-Releases/NACE-International-White-Paper-Corrosion-Control-Plan-for-Bridges-Now-Available-Online/ (accessed on 3 May 2018).
- Personal Property Manual 2011–2012; Division of Assessment Standards, Department of Taxation: Carson City, NV, USA, 2010.
- U.S. Department of Commerce. Fixed Assets and Consumer Durable Goods in the United States, 1925–1997 and 1925–1999; U.S. Government Printing Office: Washington, DC, USA, 2003; pp. M-29–M-33.
- National Association of Home Builders/Bank of America Home Equity, Study of Life Expectancy of Home Components; NAHB: Washington, DC, USA, 2007.
- U.S. Army Corps of Engineers. Waterborne Transportation Lines of the United States, Volume 1, National Summaries; Table 4. Available online: http://www.navigationdatacenter.us/veslchar/pdf/wtlusvl1_04.pdf (accessed on 21 June 2016).
- U.S. Department of Transportation, Federal Transit Administration, National Transit Database (Washington, DC: Annual Reports). National Transit Summaries and Trends, Table 25. Available online: https://www.transit.dot.gov/ntd/annual-national-transit-summaries-and-trends (accessed on 3 May 2018).
- Amtrak Annual Report; Statistical Appendix and Personal Communications, Tables 1–33: Age and Availability of Amtrak Locomotive and Car Fleets; Amtrak: Washington, DC, USA, 1972–2015.
- Survey of current business, U.S. Department of Commerce. Fixed Assets and Consumer Durable Goods in the United States, 1925–99; U.S. Government Printing Office: Washington, DC, USA, 2000.
- Gauffin, A.; Andersson, N.Å.I.; Storm, P.; Tilliander, A.; Jönsson, P.G. Use of volume correlation model to calculate lifetime of end-of-life steel. Ironmak. Steelmak. 2015, 42, 88–96. [Google Scholar] [CrossRef]
- Gauffin, A.; Andersson, N.Å.I.; Storm, P.; Tilliander, A.; Jönsson, P.G. Time-varying losses in material flows of steel using dynamic material flow models. Resour. Conserv. Recycl. 2017, 116, 70–83. [Google Scholar] [CrossRef]
- Gauffin, A.; Andersson, N.; Storm, P.; Tilliander, A.; Jönsson, P. The Global Societal Steel Scrap Reserves and Amounts of Losses. Resources 2016, 5, 27. [Google Scholar] [CrossRef]
- Gauffin, A. Improved Mapping of Steel Recycling from an Industrial Perspective. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, November 2015. [Google Scholar]
- Gauffin, A.; Ekerot, S.; Tilliander, A.; Jönsson, P. KTH steel scrap model—Iron and Steel Flow in the Swedish Society 1889–2010. J. Manuf. Sci. Prod. 2013, 13, 47–54. [Google Scholar] [CrossRef]
- Fenton, M.D. 2015 Minerals Yearbook—Iron and Steel Scrap (Advanced Release); U.S. Geological Survey (USGS): Reston, VA, USA, 2014.
- Scrap Survey (Answers from Scrap Dealers Excluding Phone Interviews); World Steel Association: Brussels, Belgium, 2014.
- Ciftci, B. Statistical Data and Analysis on the World Steel Flow; World Steel Association: Brussels, Belgium, 2016. [Google Scholar]
- Minerals Yearbook (1932–2016) Iron and Steel Scrap Statistics; U.S. Geological Survey: Reston, VA, USA, 1933–2017.
- Pehrson, E.W. Minerals Yearbook Review of 1940, Iron and Steel Scrap Statistics; Figure 1; U.S. Geological Survey: Reston, VA, USA, 1941; p. 502.
- Damuth, R.J. Iron and Steel Scrap—Accumulation and Availability as of December 31, 2009; Institute of Scrap Recycling Industries: Washington, DC, USA, 2010. [Google Scholar]
- Zimring, C.A. The complex environmental legacy of the automobile shredder. Technol. Cult. 2011, 52, 523–547. [Google Scholar] [CrossRef]
- Bensel, R.F. The Political Economy of American Industrialization, 1877–1900; Cambridge University Press: Cambridge, UK, 2000; ISBN-13: 978-0521776042. [Google Scholar]
- Bever, M.B. The recycling of metals—I. Ferrous metals. Conserv. Recycl. 1976, 1, 55–69. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, R.; Wood, R.; Wang, C.; Hertwich, E.G. High sensitivity of metal footprint to national GDP in part explained by capital formation. Nat. Geosci. 2018, 11, 269–273. [Google Scholar] [CrossRef]
- Report on Indirect Trade in Steel (1970–2013); World Steel Association: Brussels, Belgium, 2015; p. 39.
- Steel Statistical Yearbook (2014–2017), Indirect Trade of Steel; Tables 55–57; World Steel Association: Brussels, Belgium, 2014–2017.
- Microsoft Office Excel Toolbox Release 2013 (Office15); Microsoft Redmond Campus: Redmond, WA, USA, 2013.
- MATLAB and Statistics Toolbox Release 2012a; The Math Works, Inc.: Natick, MA, USA, 2018.
- Graedel, T.E.; Buchert, M.; Reck, B.K.; Sonnemann, G. Assessing Mineral Resources in Society: Metal Stocks & Recycling Rates; United Nations Environment Programme: Nairobi, Kenya, 2011; ISBN 978-92-807-3182-0. [Google Scholar]
- Fenton, M.D. Iron and Steel Recycling in the United States in 1998; U.S. Geological Survey: Reston, VA, USA, 1998.
- Sawyer, J.W. Automotive Scrap Recycling: Processes, Prices and Prospects; Johns Hopkins University Press: Baltimore, MA, USA, 1974. [Google Scholar]
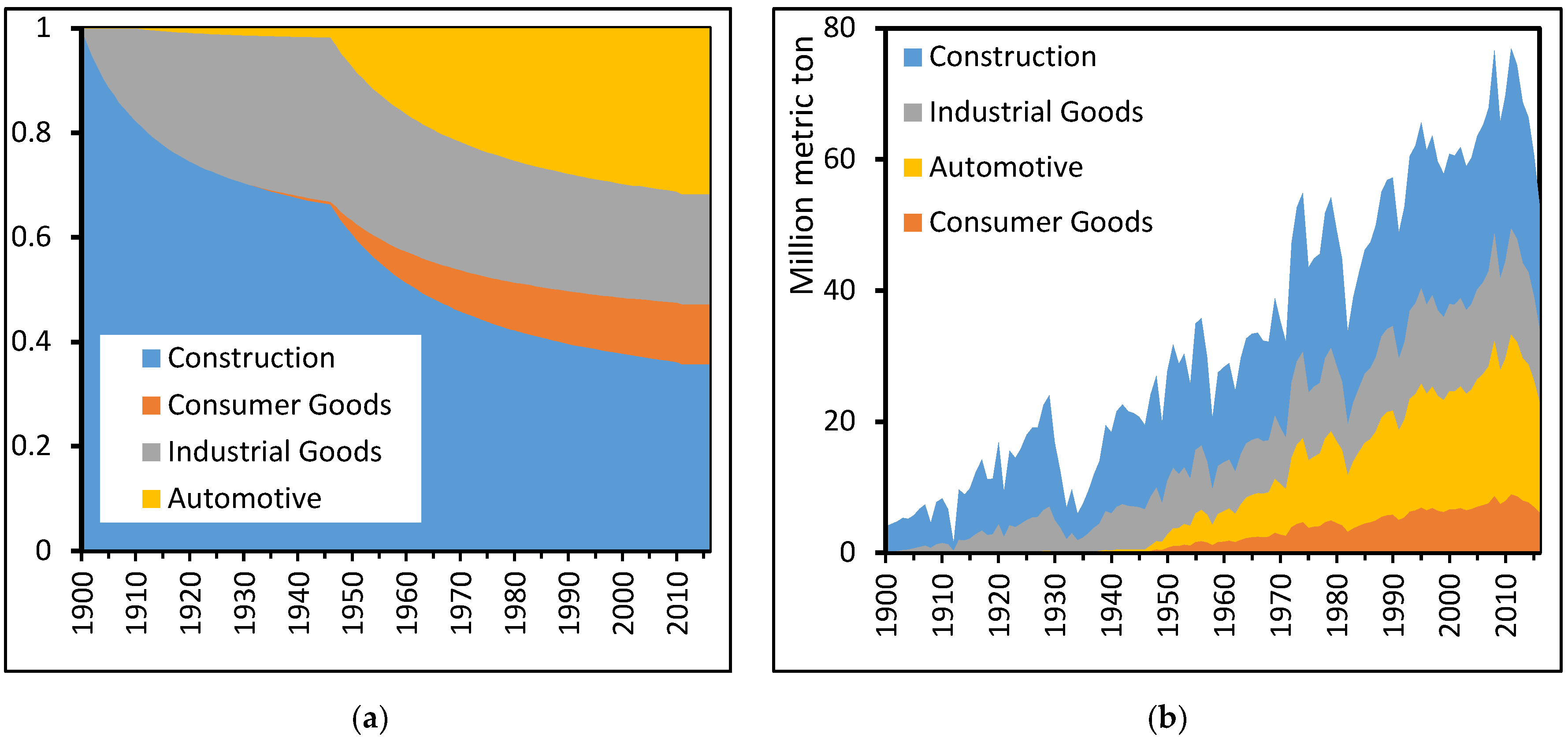
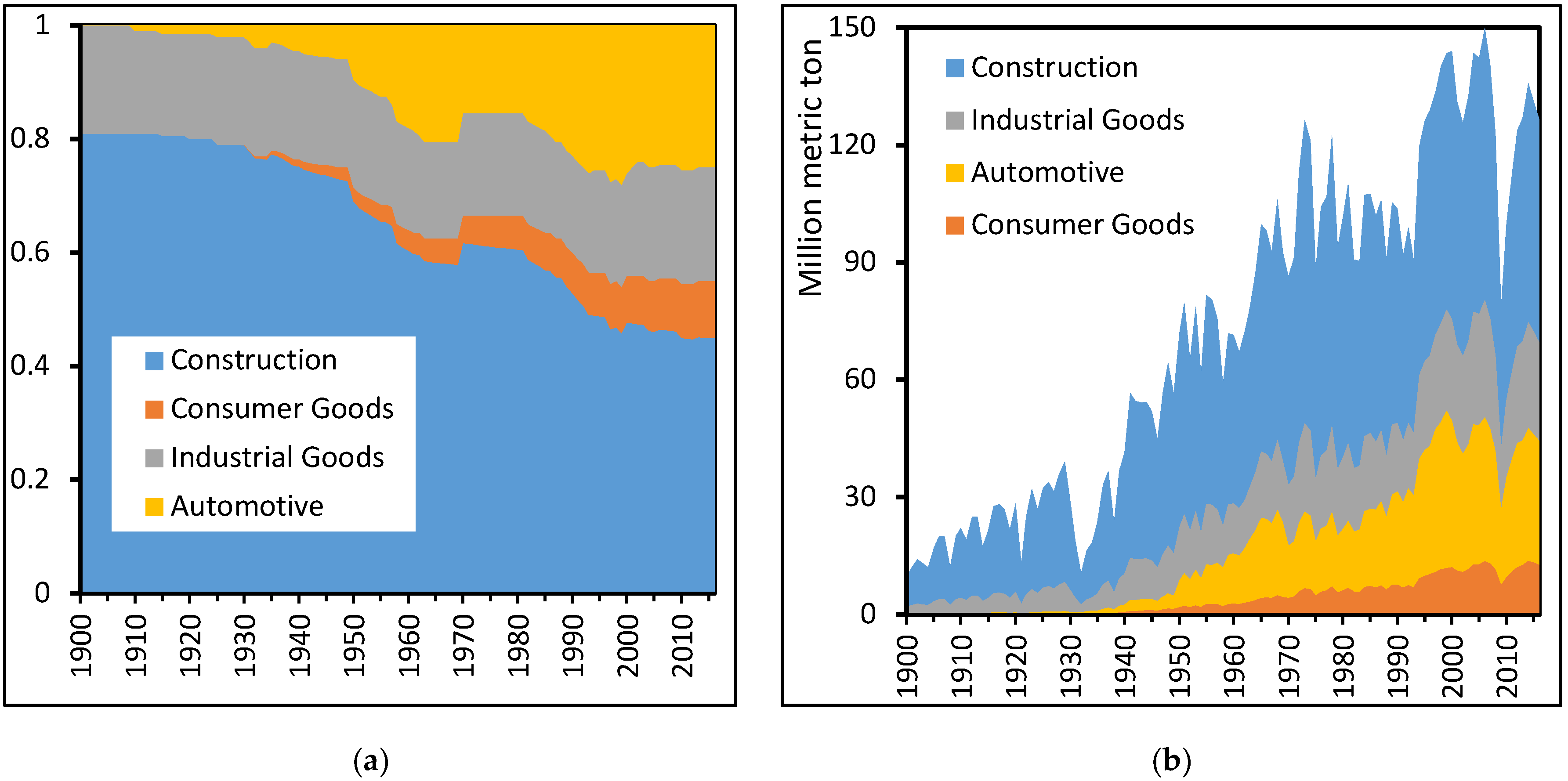
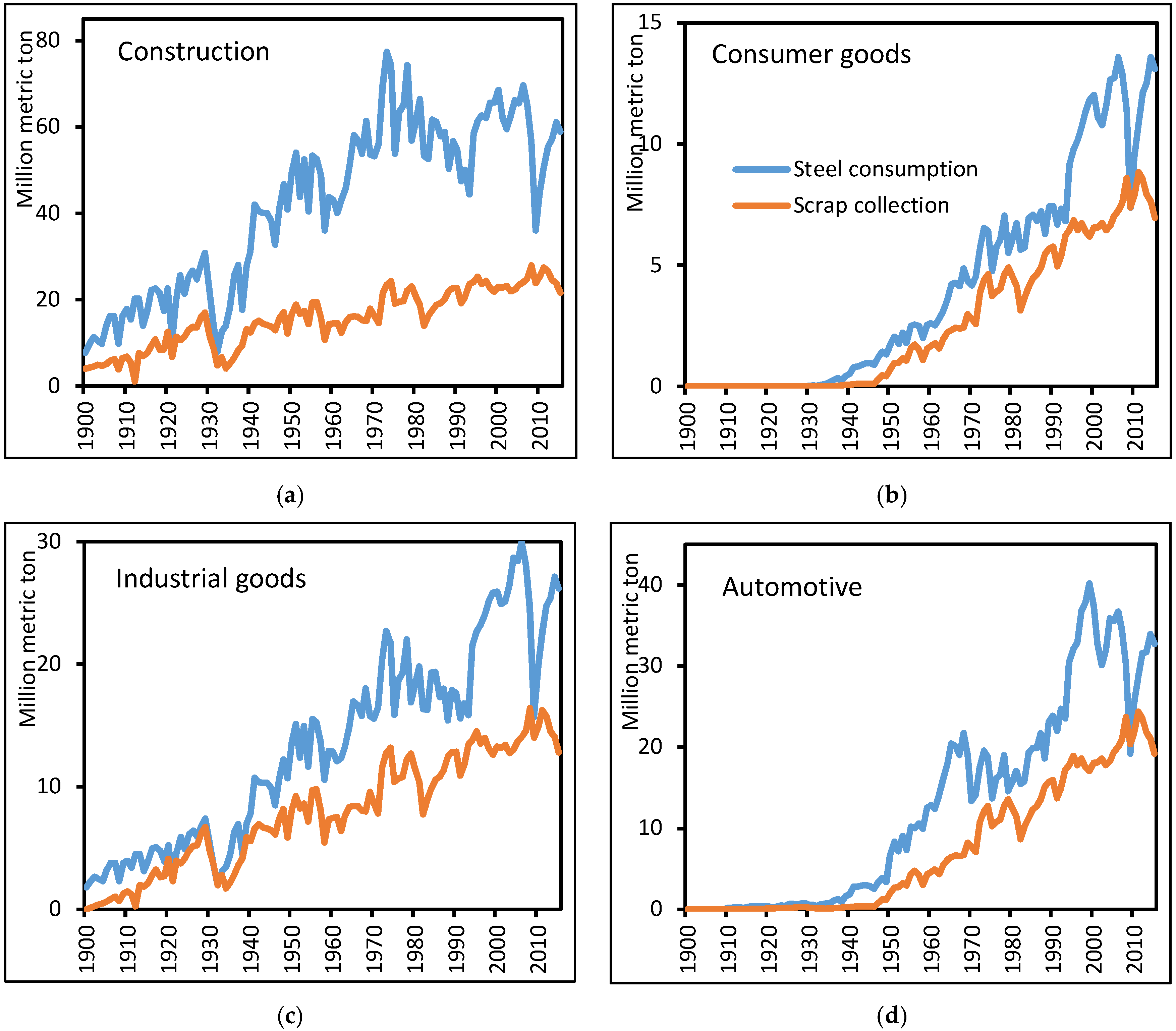
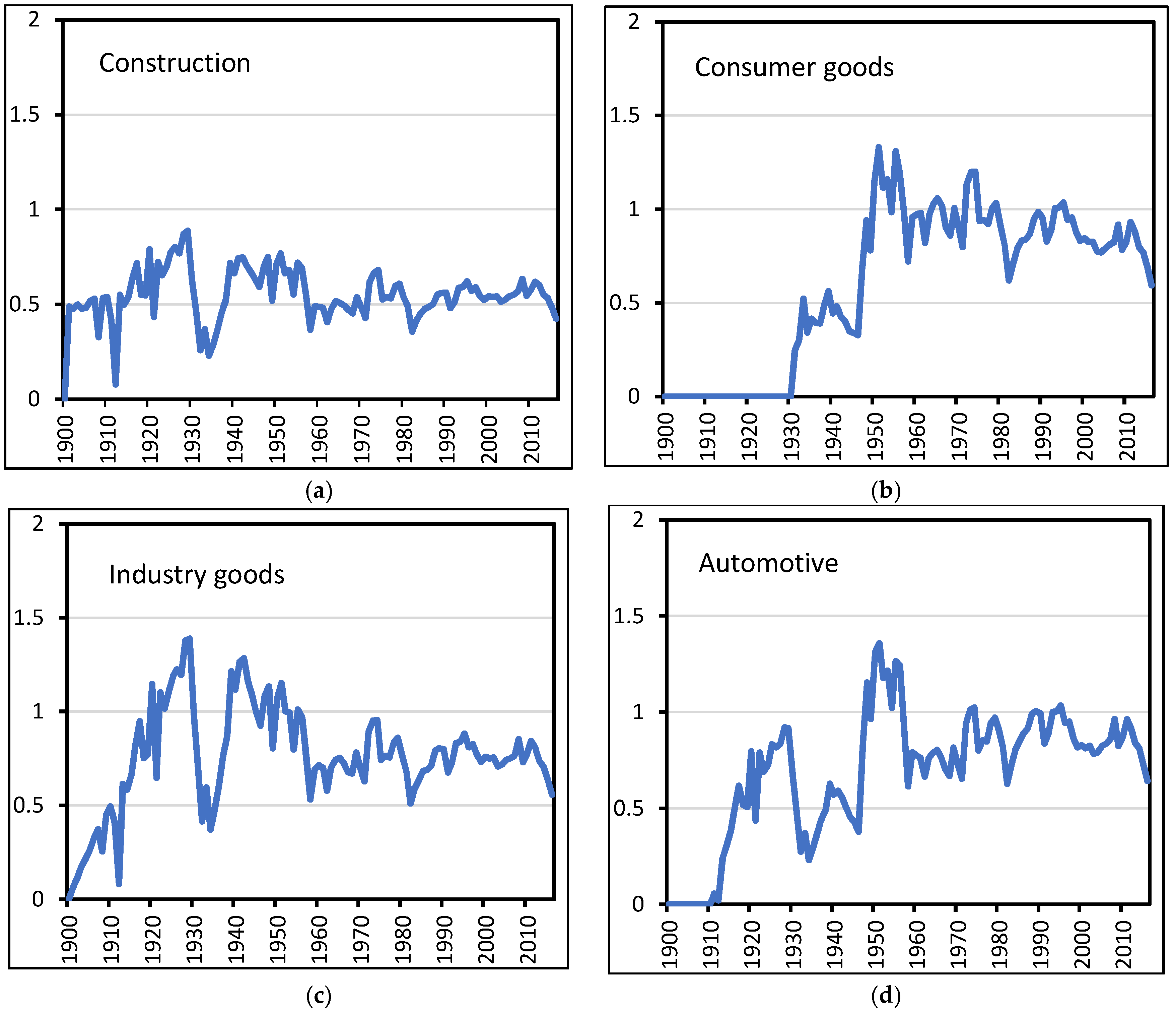
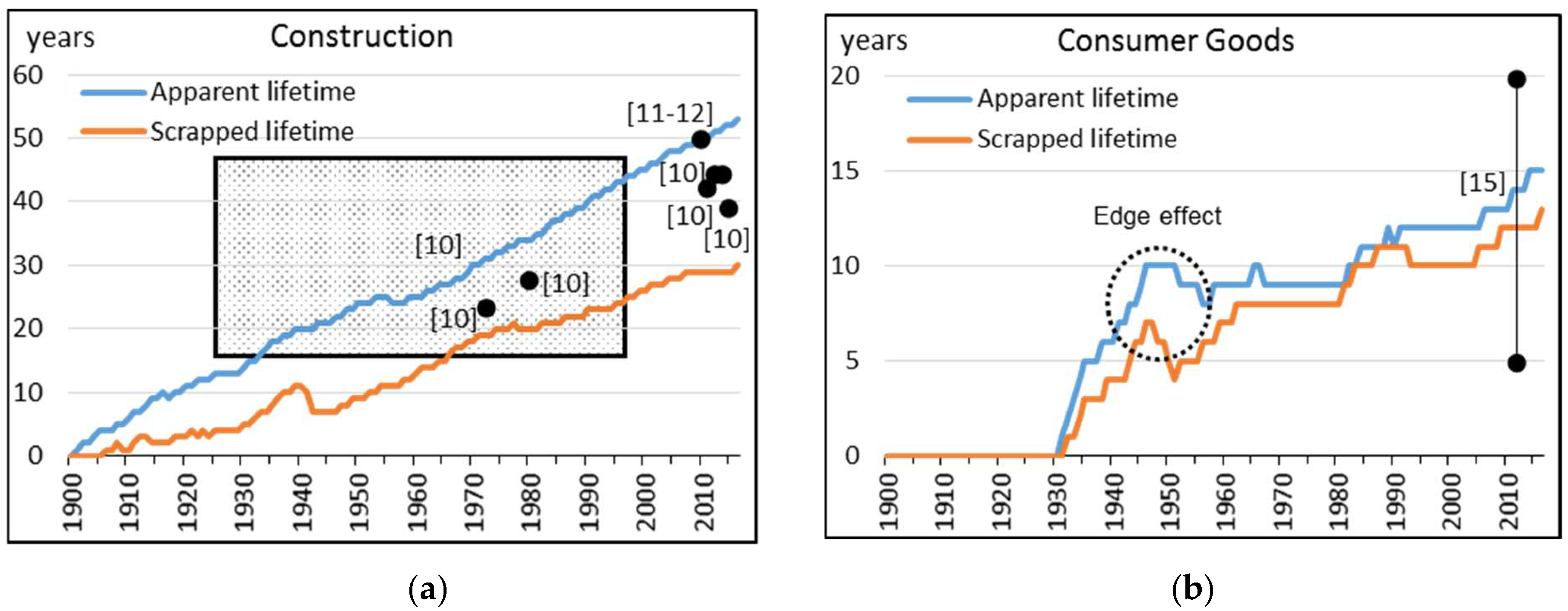
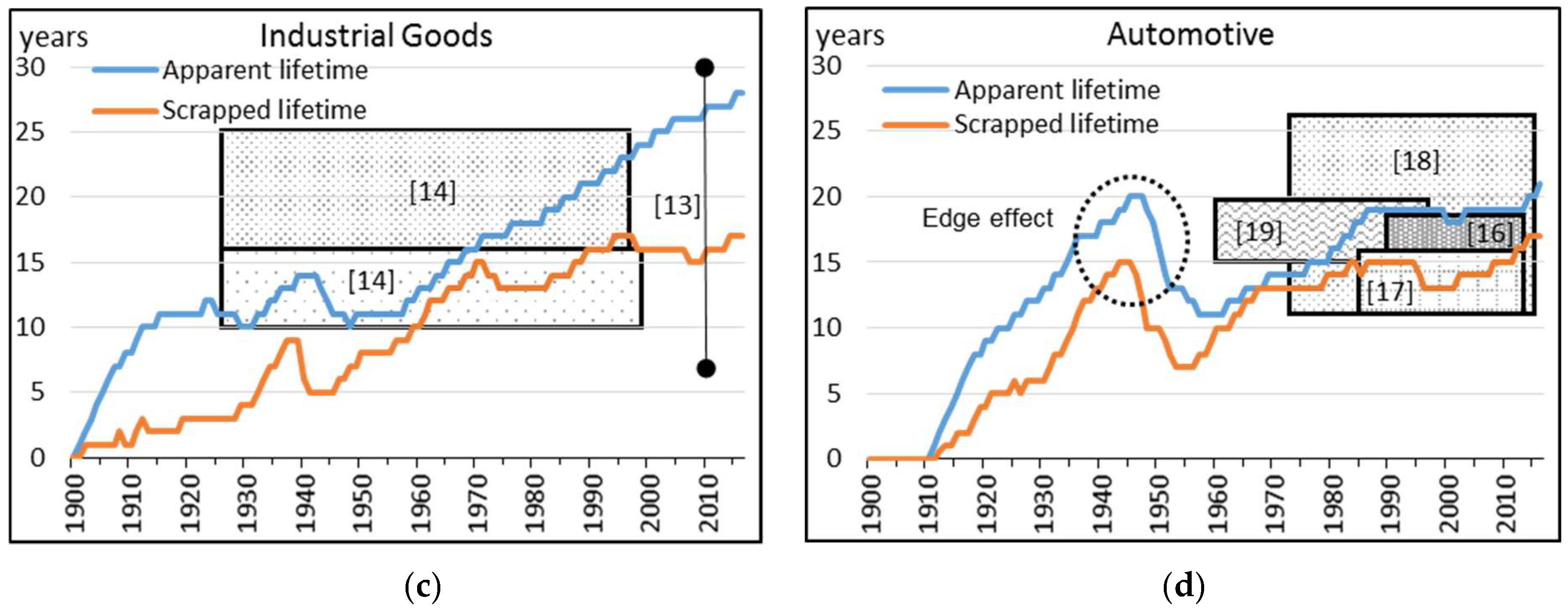
| Industry Sector | Methods | Typical Product Groups | Average Lifetime of Steel Products in Years 1 |
|---|---|---|---|
| Construction | Average age of buildings and bridges in-use in US | Housing, industrial buildings, mobile offices, office buildings, warehouses, bridges | 39 (2015) [9] 44 (2013 & 2014) [9] 42 (2011) [9] 50 (2010) [10,11] 17–48 (1925–1997) [9] 28 (1980) [9] 24 (1973) [9] |
| Industry goods | Service lives of machinery and depreciation estimates | Machinery for metalworking, construction, agriculture, and special industry | 7–30 (2010) [12] 10–16 (1925–1999) [13] 16–25 (1925–1997) [13] |
| Consumer goods | Average age of appliances in-use in US | Household appliances, video and audio products, computers | 5–20 (2011) [14] |
| Automotive | Average age of automobiles and trucks in operation in the United States | Transportation by air, automobiles, locomotives, ferry boats | 16–18 (1990–2014) [15] 11–16 (1985–2014) [16] 11–26 (1972–2015) [17] 15–20 (1960–1997) [18] |
| Industry Sector | Reported | Input Data |
|---|---|---|
| Construction | 32.4% | 35.7% |
| Consumer Goods | 15.6% | 11.5% |
| Industrial Goods | 20.4% | 21.1% |
| Automotive | 31.6% | 31.7% |
| Prompt scrap | 27.3% | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gauffin, A.; Pistorius, P.C. The Scrap Collection per Industry Sector and the Circulation Times of Steel in the U.S. between 1900 and 2016, Calculated Based on the Volume Correlation Model. Metals 2018, 8, 338. https://doi.org/10.3390/met8050338
Gauffin A, Pistorius PC. The Scrap Collection per Industry Sector and the Circulation Times of Steel in the U.S. between 1900 and 2016, Calculated Based on the Volume Correlation Model. Metals. 2018; 8(5):338. https://doi.org/10.3390/met8050338
Chicago/Turabian StyleGauffin, Alicia, and Petrus Christiaan Pistorius. 2018. "The Scrap Collection per Industry Sector and the Circulation Times of Steel in the U.S. between 1900 and 2016, Calculated Based on the Volume Correlation Model" Metals 8, no. 5: 338. https://doi.org/10.3390/met8050338
APA StyleGauffin, A., & Pistorius, P. C. (2018). The Scrap Collection per Industry Sector and the Circulation Times of Steel in the U.S. between 1900 and 2016, Calculated Based on the Volume Correlation Model. Metals, 8(5), 338. https://doi.org/10.3390/met8050338







