Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Assumptions
- treating the molten steel as an incompressible Newtonian fluid;
- the influence of the mold taper and oscillation are not considered;
- the mold flux and the level fluctuation of the molten steel are not neglected;
- the free surface of the mold is assumed to be adiabatic;
- the latent heat of the solid phase transformation is negligible, only the latent heat of solidification is considered;
- the inclusion is treated as spherical alumina inclusion, and its density is constantly 3500 kg·m−3;
- the aggregation and breakup of inclusions are not taken into account; and,
- the influence of inclusion motion on the flow and the heat transfer of the molten steel is ignored.
2.2. The Model Details
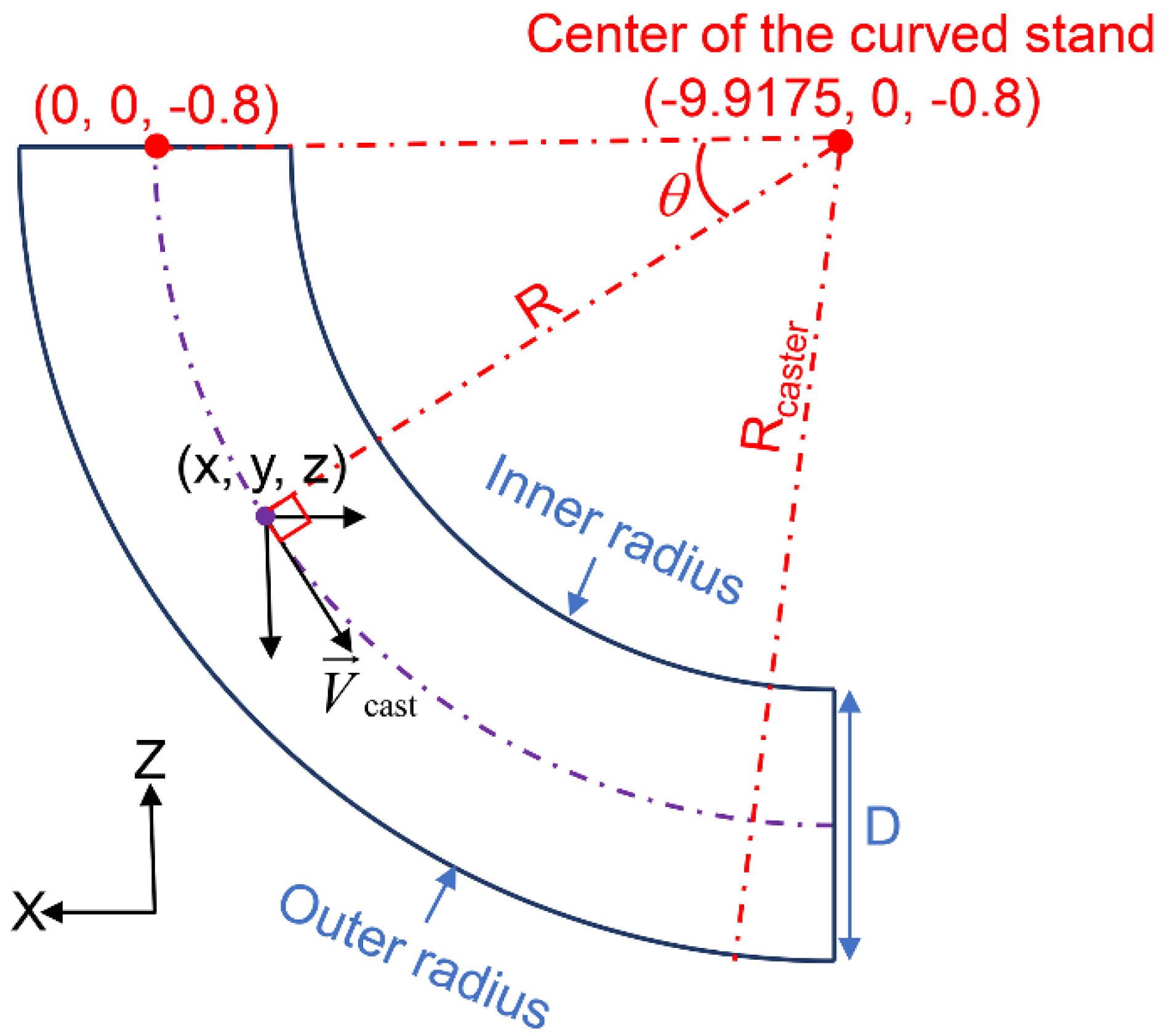
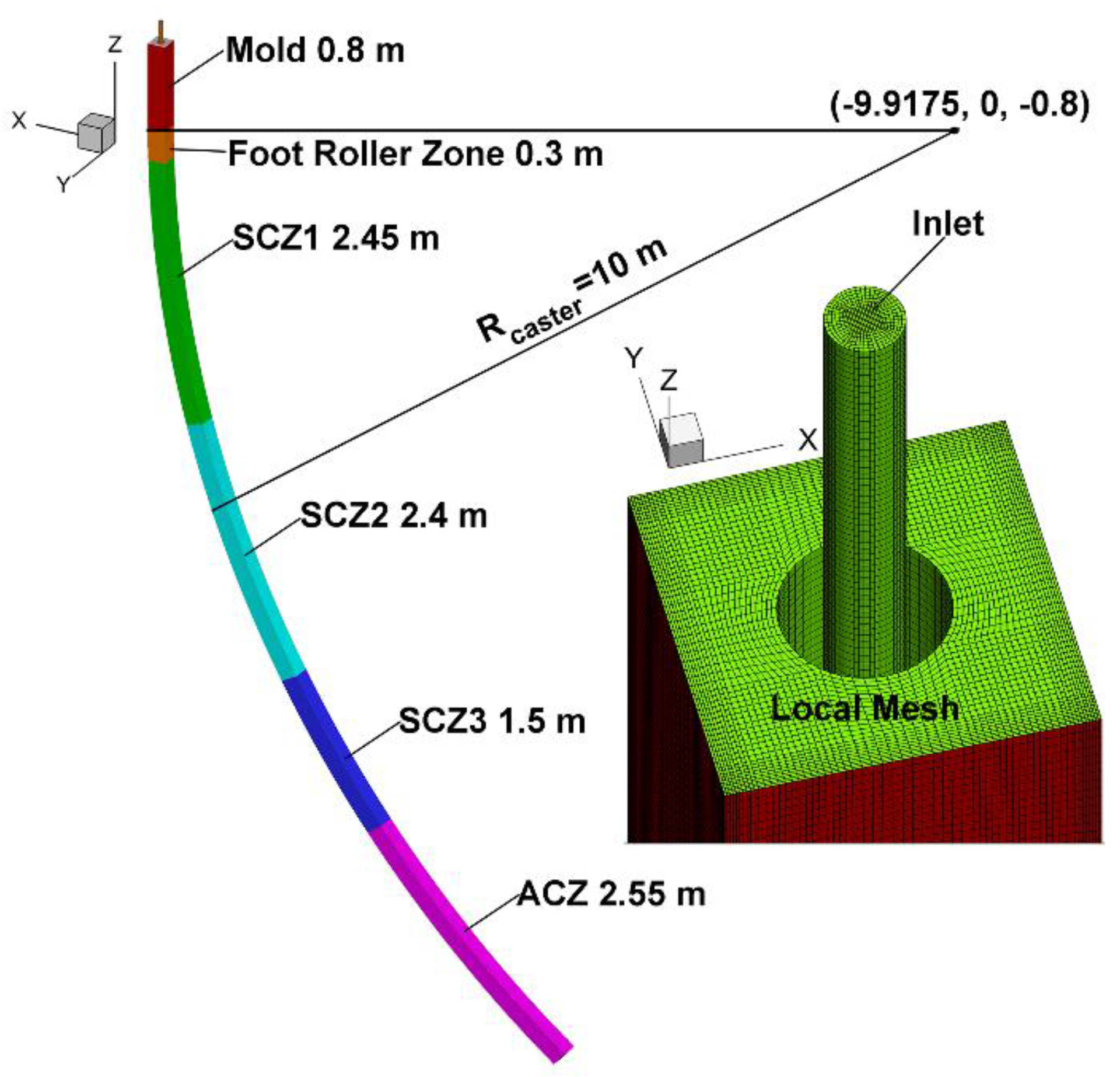
2.3. Geometry Model
2.4. Boundary Conditions
2.5. Numerical Procedure Details
3. Results and Discussion
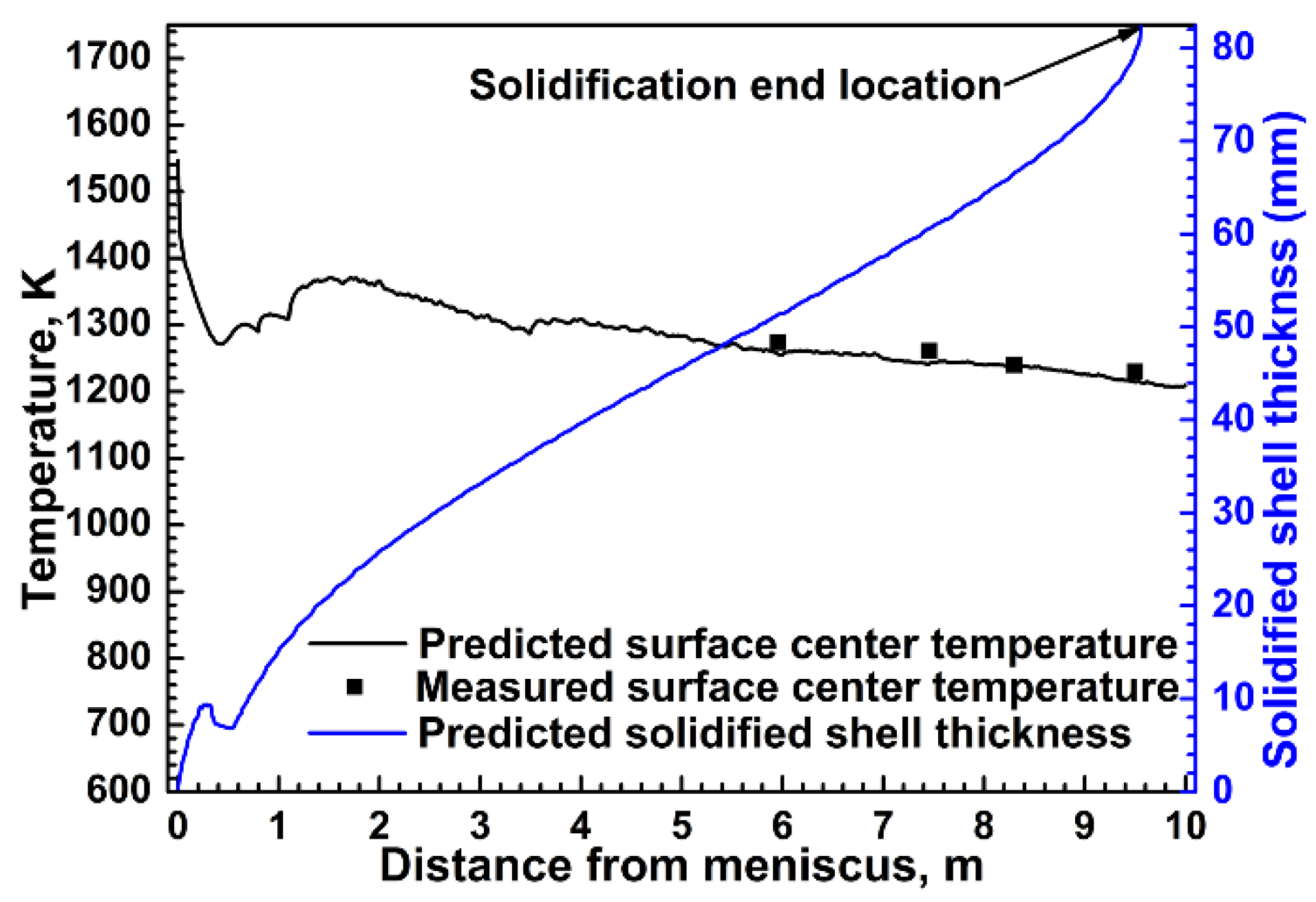
3.1. Solidification Model Validation
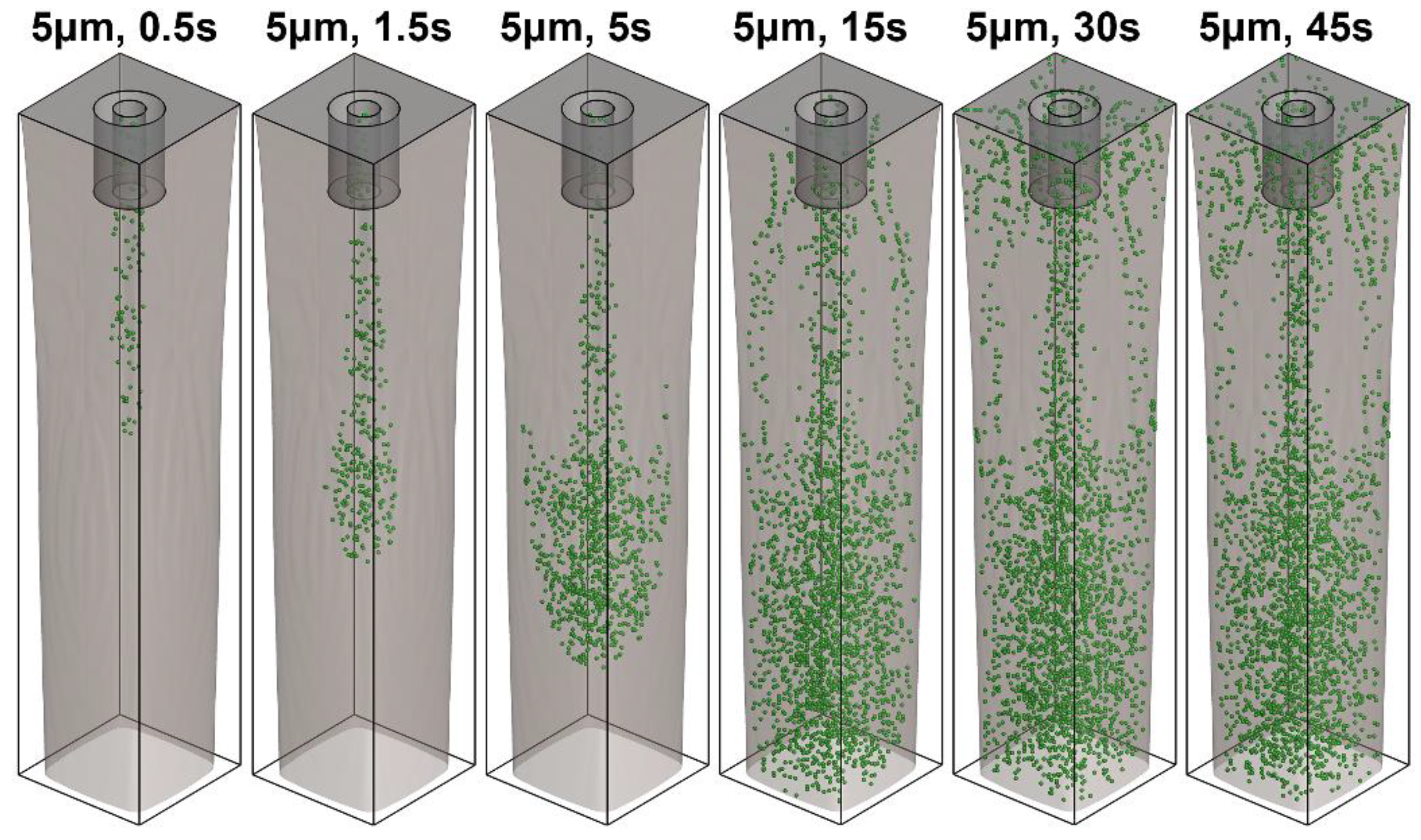
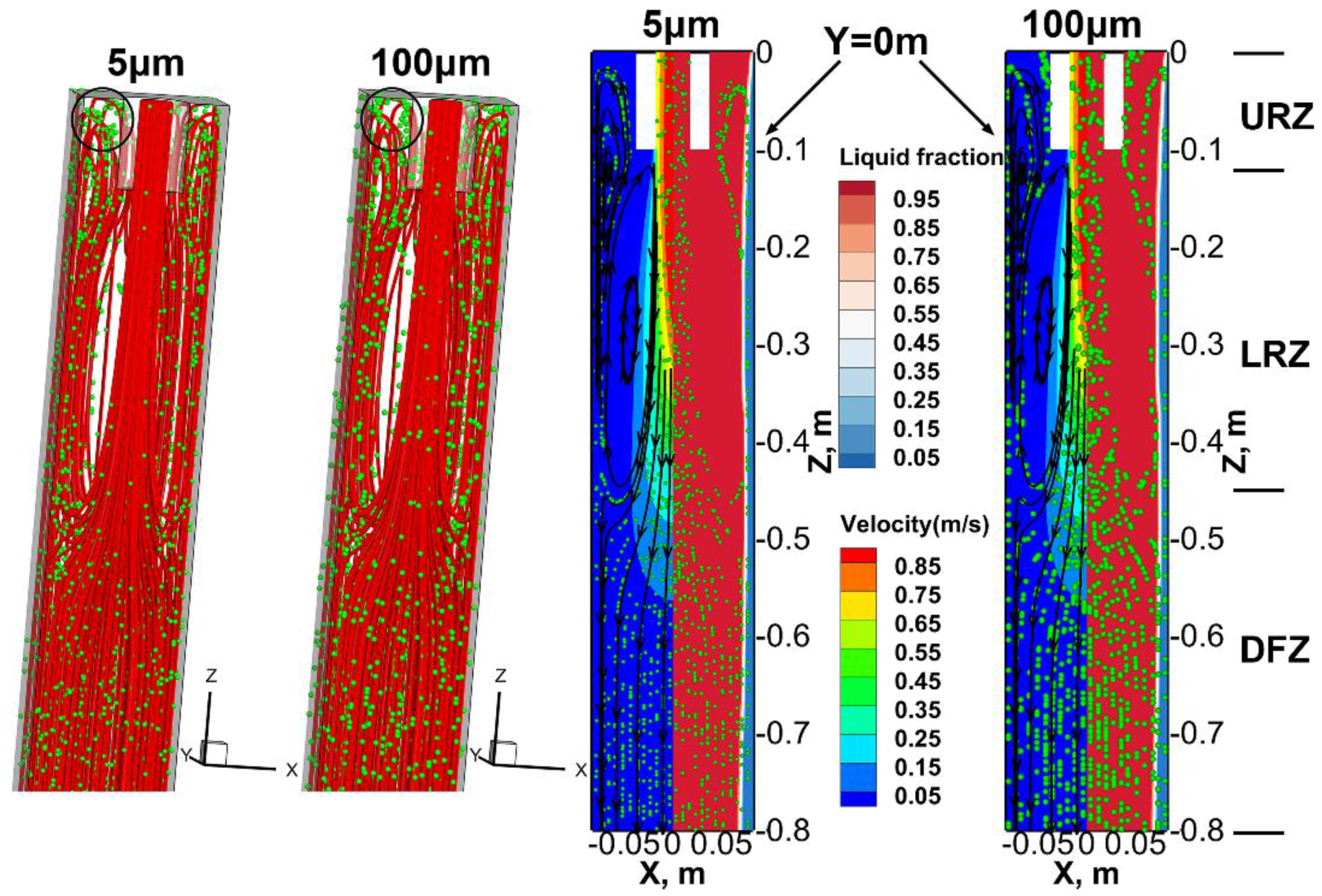
3.2. Inclusion Motion and Entrapment in Mold
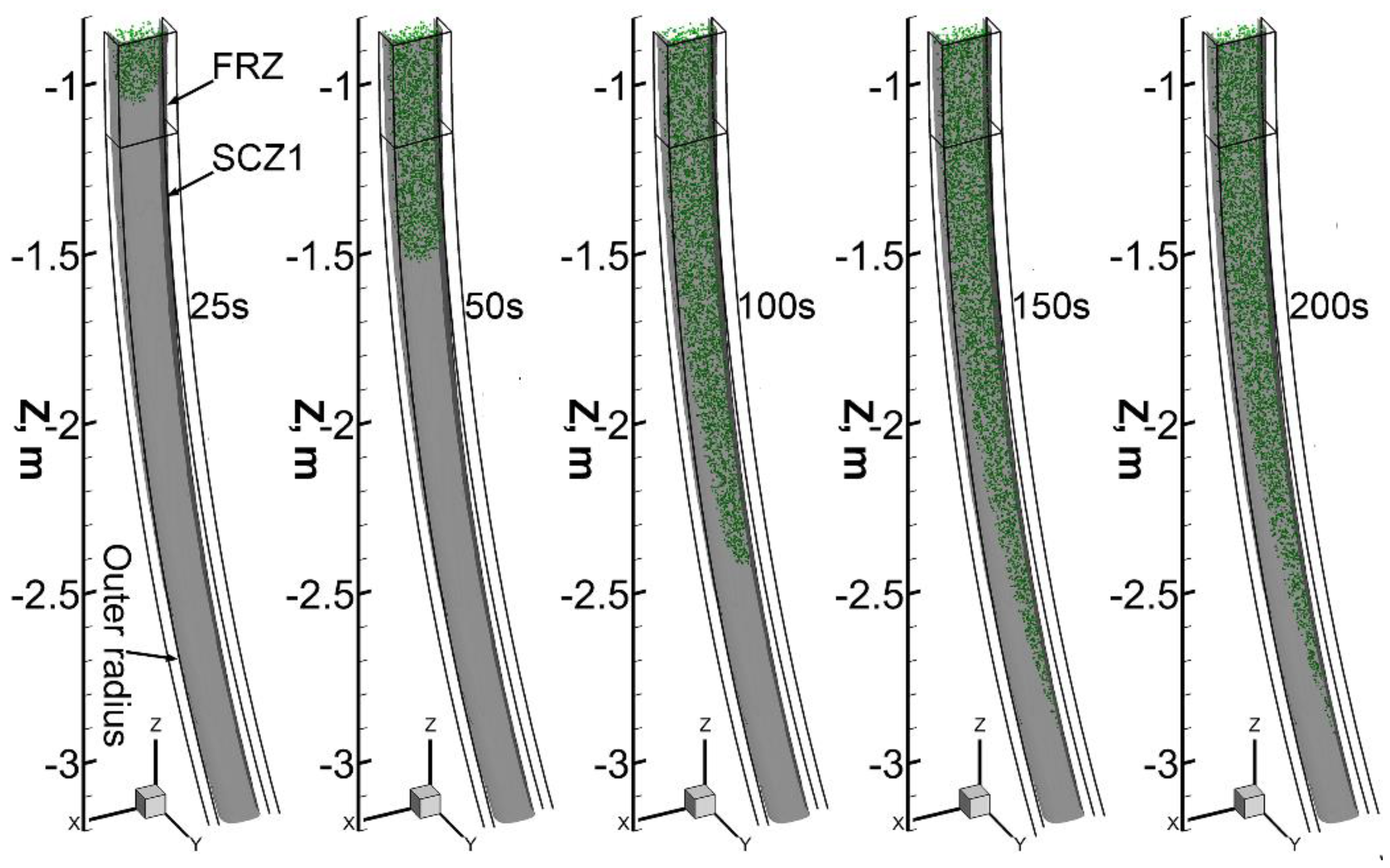
3.3. Inclusion Motion and Entrapment in the Curved Part of the Strand
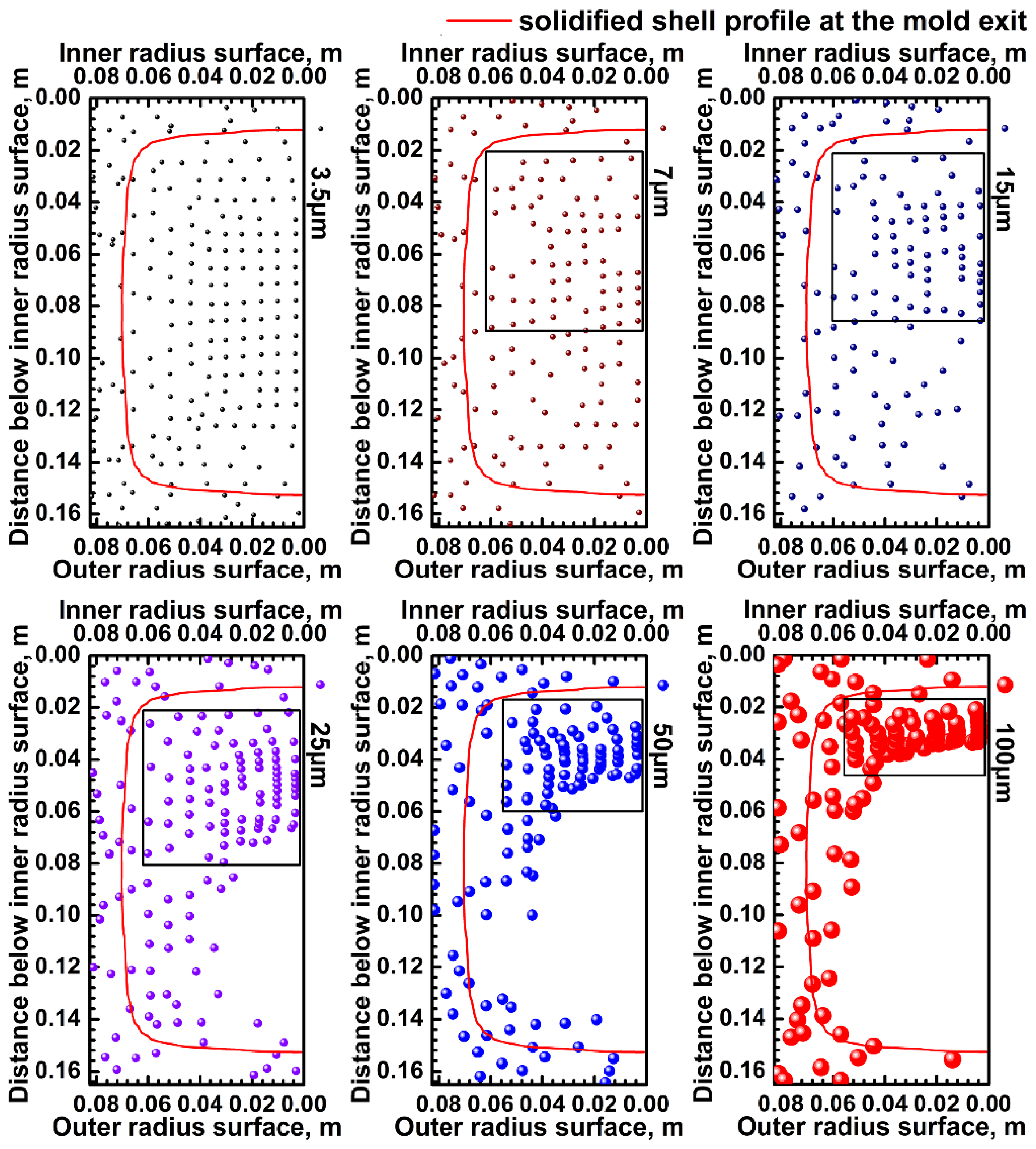
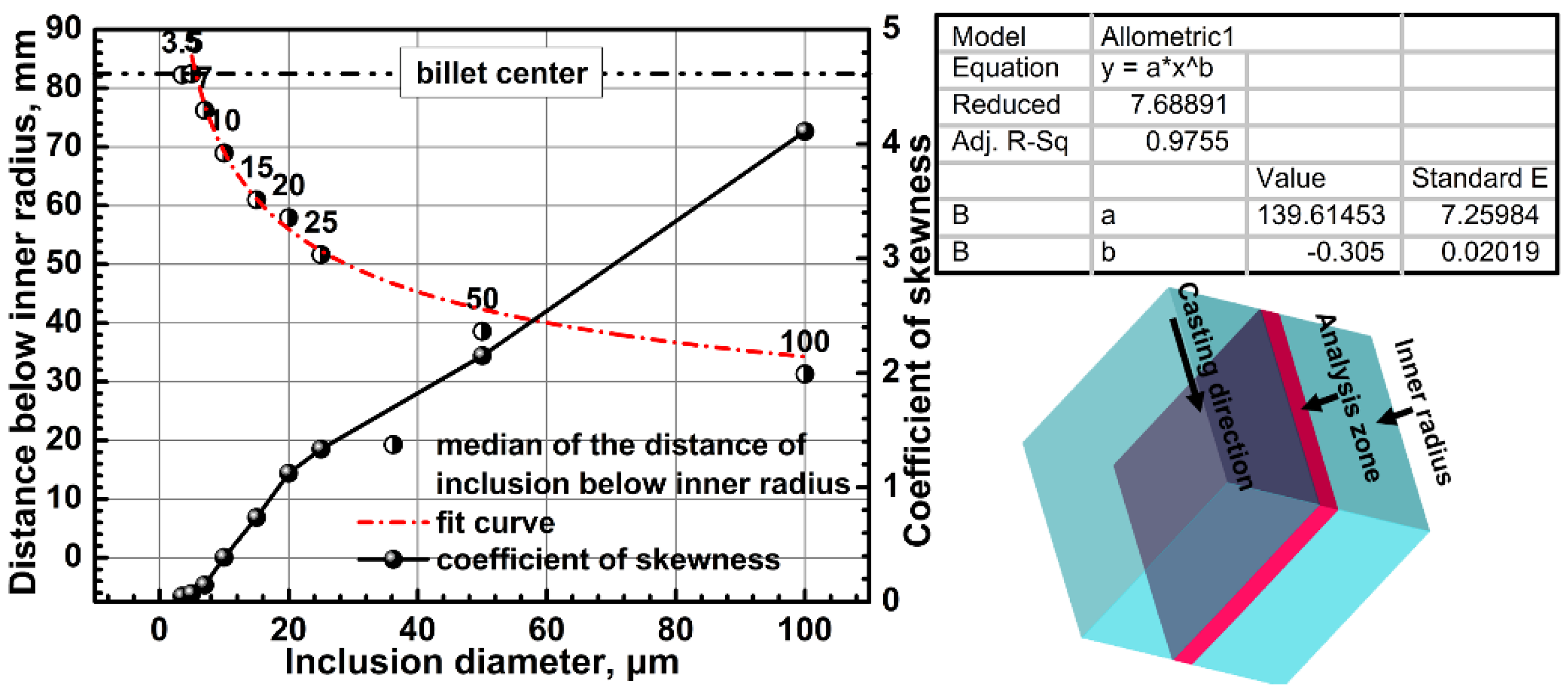
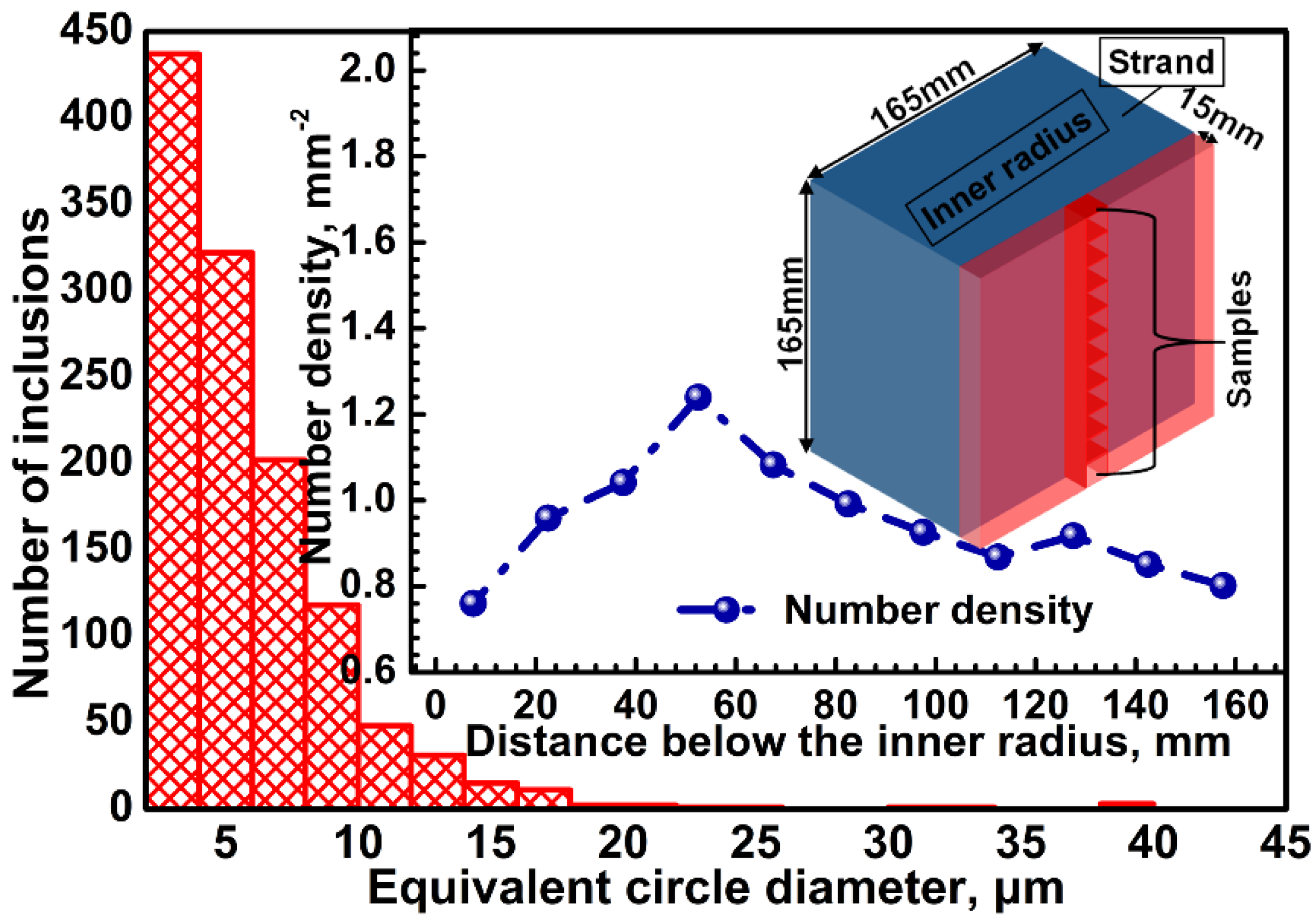
3.4. Inclusion Distribution in the Solidified Stand
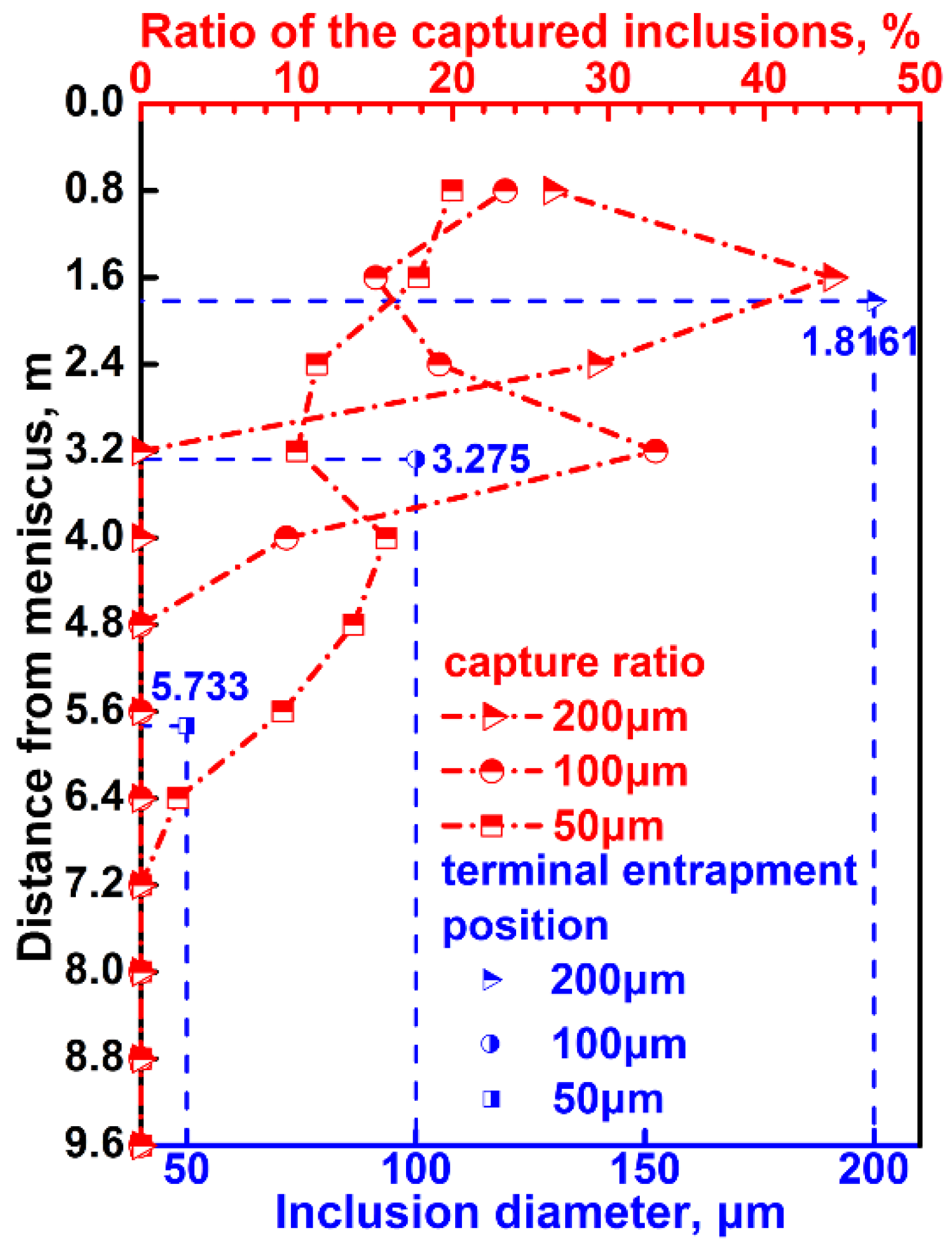
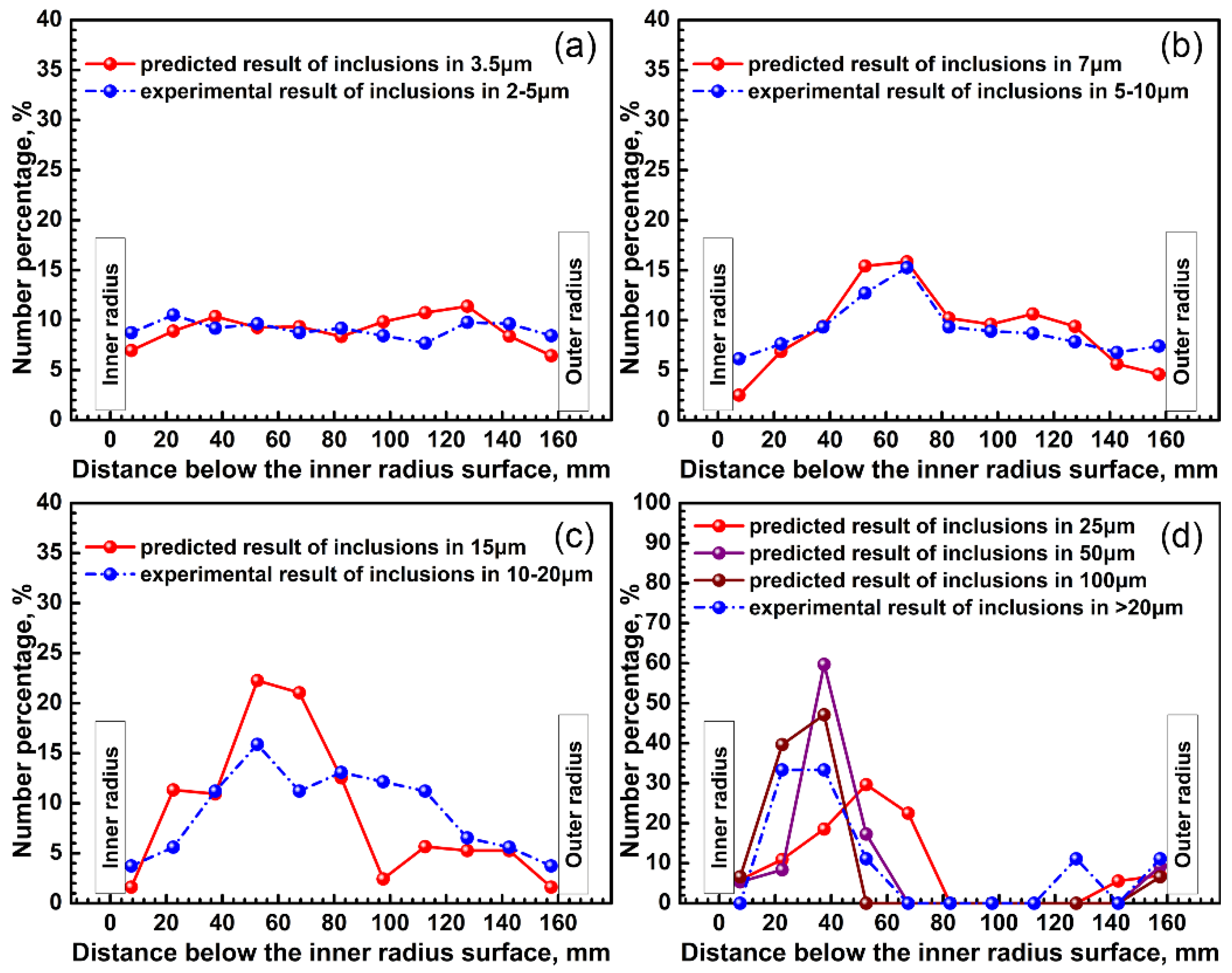
3.5. Comparison Between the Predicted and the Experimental Results
4. Conclusions
- the inclusion distribution inside the liquid pool of the mold is not perfectly symmetrical, resulting from the random injection of inclusions from the inlet and the effect of the molten steel turbulence;
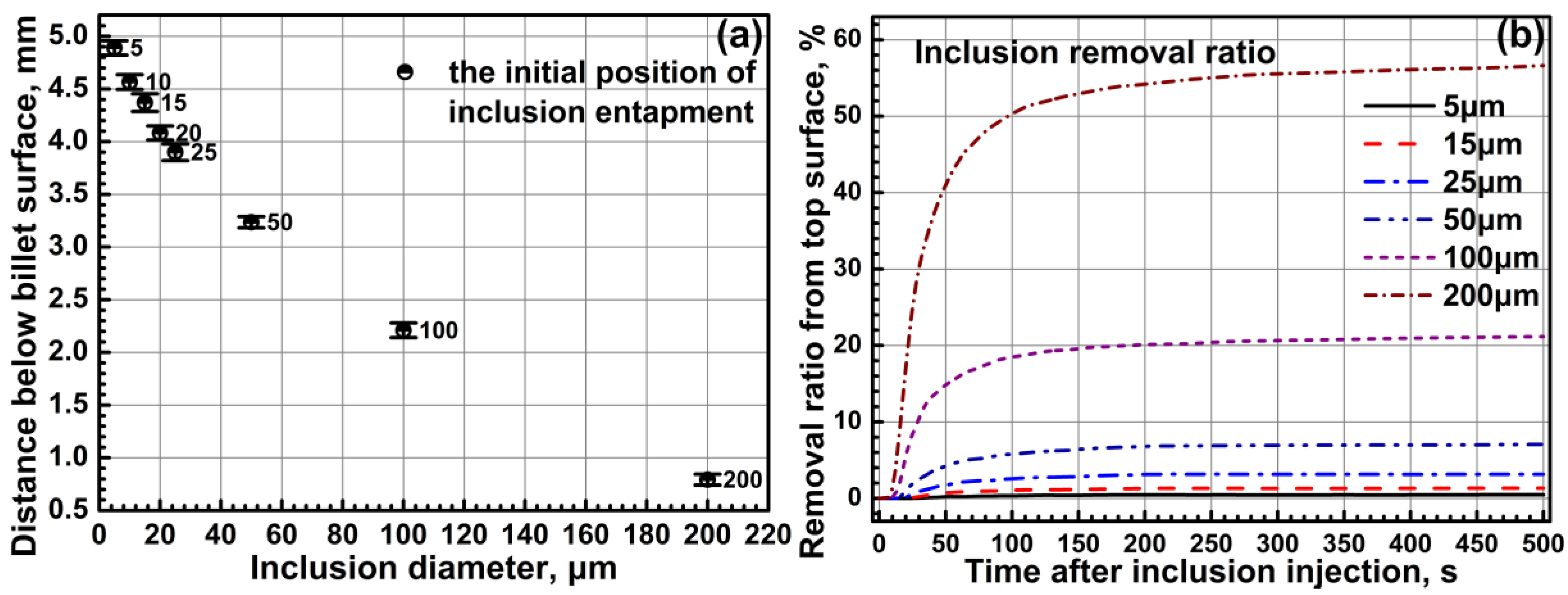
- the entrapping positions of larger inclusions are higher than those of smaller inclusions in the URZ with the effect of the buoyancy force. As a result, the initial entrapping positions of larger inclusions are more close to the billet surface;
- the motion and entrapment of micro inclusions in the mold are mainly affected by the molten steel flow pattern, since the buoyancy force of micro inclusions is negligible. However, the motion and entrapment of macro inclusions in the mold depend both on the molten steel flow pattern and the buoyancy force;
- owing to the effect of the buoyancy force, macro inclusions shift to the solidifying front of the inner radius in the curved part of the strand as time goes on, while the solidifying front of the outer radius cannot entrap the inclusions;
- the distributions of inclusions smaller than 5 μm in the solidified strand are even. However, for inclusions that are larger than 5 μm, their distributions become uneven. Furthermore, the inhomogeneity is enhanced with the increase of the inclusion diameter; and,
- good agreement is found between the predicted and experimental results. The comparison between the predicted and the experimental results indicates that the inclusion motion model is valid.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, L. Nucleation, growth, transport, and entrapment of inclusions during steel casting. JOM 2013, 65, 1138–1144. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, W.; Wan, C.; Wang, F.; Han, H. Effect of deoxidation process on inclusion and fatigue performance of spring steel for automobile suspension. Metall. Mater. Trans. B 2018, 49, 569–580. [Google Scholar] [CrossRef]
- Deng, X.; Ji, C.; Cui, Y.; Tian, Z.; Yin, X.; Shao, X.; Yang, Y.; McLean, A. Formation and evolution of macro inclusions in IF steels during continuous casting. Ironmak. Steelmak. 2017, 44, 739–749. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Li, Q.; Huang, F.; Li, H.; Yang, J. Control of stringer shaped non-metallic inclusions of Cao-Al2O3 system in API X80 linepipe steel plates. Steel Res. Int. 2014, 85, 155–163. [Google Scholar] [CrossRef]
- Lei, H.; Geng, D.; He, J. A continuum model of solidification and inclusion collision-growth in the slab continuous casting caster. ISIJ Int. 2009, 49, 1575–1582. [Google Scholar] [CrossRef]
- Lei, H.; Jiang, J.; Yang, B.; Zhao, Y.; Zhang, H.; Wang, W.; Dong, G. Mathematical model for collision-coalescence among inclusions in the bloom continuous caster with M-EMS. Metall. Mater. Trans. B 2018, 49, 666–676. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Large-eddy simulation of transient horizontal gas–liquid flow in continuous casting using dynamic subgrid-scale model. Metall. Mater. Trans. B 2017, 48, 1833–1849. [Google Scholar] [CrossRef]
- Liu, Z.; Qi, F.; Li, B.; Jiang, M. Multiple size group modeling of polydispersed bubbly flow in the mold: An analysis of turbulence and interfacial force models. Metall. Mater. Trans. B 2015, 46, 933–952. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Qi, F.; Cheung, S.C.P. Population balance modeling of polydispersed bubbly flow in continuous casting using average bubble number density approach. Powder Technol. 2017, 319, 139–147. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, M. Three-dimensional magnetohydrodynamic calculation for coupling multiphase flow in round billet continuous casting mold with electromagnetic stirring. IEEE Trans. Magn. 2010, 46, 82–86. [Google Scholar] [CrossRef]
- Ho, Y.; Hwang, W. Numerical simulation of inclusion removal in a billet continuous casting mold based on the partial-cell technique. ISIJ Int. 2003, 43, 1715–1723. [Google Scholar] [CrossRef]
- Li, B.; Tsukihashi, F. Numerical estimation of the effect of the magnetic field application on the motion of inclusion in continuous casting of steel. ISIJ Int. 2003, 43, 923–931. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Jiang, M.; Fumitaka, T. Euler-Euler-Lagrangian modeling for two-phase flow and particle transport in continuous casting mold. ISIJ Int. 2014, 54, 1314–1323. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B. Large eddy simulation of transient flow and inclusions transport in continuous casting mold under different electromagnetic brakes. JOM 2016, 68, 2180–2190. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Z.; Li, B. Modeling of quasi-four-phase flow in continuous casting mold using hybrid Eulerian and Lagrangian approach. Metall. Mater. Trans. B 2017, 48, 1248–1267. [Google Scholar] [CrossRef]
- Trindade, L.; Nadalon, J.; Vilela, A.; Vilhena, M.; Soares, R. Numerical modeling of inclusion removal in electromagnetic stirred steel billets. Steel Res. Int. 2007, 78, 708–713. [Google Scholar] [CrossRef]
- Wang, S.; De Toledo, G.; Välimaa, K.; Louhenkilpi, S. Magnetohydrodynamic phenomena, fluid control and computational modeling in the continuous casting of billet and bloom. ISIJ Int. 2014, 54, 2273–2282. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Fluid flow-related transport phenomena in steel slab continuous casting strands under electromagnetic brake. Metall. Mater. Trans. B 2011, 42, 1319–1351. [Google Scholar] [CrossRef]
- Yang, Y.; Jönsson, P.; Ersson, M.; Nakajima, K. Inclusion behavior under a swirl flow in a submerged entry nozzle and mold. Steel Res. Int. 2015, 86, 341–360. [Google Scholar] [CrossRef]
- Yang, Y.; Jönsson, P.; Ersson, M.; Su, Z.; He, J.; Nakajima, K. The influence of swirl flow on the flow field, temperature field and inclusion behavior when using a half type electromagnetic swirl flow generator in a submerged entry and mold. Steel Res. Int. 2015, 86, 1312–1327. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, M. Influence of electromagnetic stirring on transport phenomena in round billet continuous casting mould and macrostructure of high carbon steel billet. Ironmak. Steelmak. 2012, 39, 574–584. [Google Scholar] [CrossRef]
- Zhang, L.; Aoki, J.; Thomas, B. Inclusion removal by bubble flotation in a continuous casting mold. Metall. Mater. Trans. B 2006, 37, 361–379. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zuo, X. Flow transport and inclusion motion in steel continuous-casting mold under submerged entry nozzle clogging condition. Metall. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L. Determination for the entrapment criterion of non-metallic inclusions by the solidification front during steel centrifugal continuous casting. Metall. Mater. Trans. B 2016, 47, 1933–1949. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Effect of vertical length on asymmetric flow and inclusion transport in vertical-bending continuous caster. Powder Technol. 2018, 323, 403–415. [Google Scholar] [CrossRef]
- Pfeiler, C.; Wu, M.; Ludwig, A. Influence of argon gas bubbles and non-metallic inclusions on the flow behavior in steel continuous casting. Mater. Sci. Eng. A 2005, 413–414, 115–120. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B.; Jiang, M. Large eddy simulation of transient flow, solidification, and particle transport processes in continuous-casting mold. JOM 2014, 66, 1184–1196. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.; Thomas, B. Large eddy simulations of electromagnetic braking effects on argon bubble transport and capture in a steel continuous casting mold. Metall. Mater. Trans. B 2018. [Google Scholar] [CrossRef]
- Jin, K.; Thomas, B.; Ruan, X. Modeling and measurements of multiphase flow and bubble entrapment in steel continuous casting. Metall. Mater. Trans. B 2016, 47, 548–565. [Google Scholar] [CrossRef]
- Lei, S.; Zhang, J.; Zhao, X.; He, K. Numerical simulation of molten steel flow and inclusions motion behavior in the solidification processes for continuous casting slab. ISIJ Int. 2014, 54, 94–102. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Lei, S.; Dong, Q. Numerical study on the capture of large inclusion in slab continuous casting with the effect of in-mold electromagnetic stirring. ISIJ Int. 2017, 57, 2165–2174. [Google Scholar] [CrossRef]
- Jin, K.; Thomas, B.; Liu, R.; Vanka, S.; Ruan, X. Simulation and validation of two-phase turbulent flow and particle transport in continuous casting of steel slabs. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012095. [Google Scholar] [CrossRef]
- Pfeiler, C.; Thomas, B.; Wu, M.; Ludwig, A.; Kharicha, A. Solidification and particle entrapment during continuous casting of steel. Steel Res. Int. 2008, 79, 599–607. [Google Scholar] [CrossRef]
- Lei, S.; Zhang, J.; Zhao, X.; Dong, Q. Study of molten steel flow and inclusions motion behavior in the solidification processes for high speed continuous casting slab by numerical simulation. Trans. Indian Inst. Met. 2016, 69, 1193–1207. [Google Scholar] [CrossRef]
- Yuan, Q.; Thomas, B.; Vanka, S. Study of transient flow and particle transport in continuous steel caster molds: Part I. Fluid flow. Metall. Mater. Trans. B 2004, 35, 685–702. [Google Scholar] [CrossRef]
- Yuan, Q.; Thomas, B.; Vanka, S. Study of transient flow and particle transport in continuous steel caster molds: Part II. Particle transport. Metall. Mater. Trans. B 2004, 35, 703–714. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Transient motion of inclusion cluster in vertical-bending continuous casting caster considering heat transfer and solidification. Powder Technol. 2016, 287, 315–329. [Google Scholar] [CrossRef]
- Thomas, B.; Yuan, Q.; Mahmood, S.; Liu, R.; Chaudhary, R. Transport and entrapment of particles in steel continuous casting. Metall. Mater. Trans. B 2014, 45, 22–35. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Zhang, L.; Xu, G. Analysis of transient transport and entrapment of particle in continuous casting mold. ISIJ Int. 2014, 54, 2324–2333. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Wang, Q.; Yang, W.; Wang, Y.; Ren, L.; Cheng, L. Effect of electromagnetic parameters on the motion and entrapment of inclusions in FC-mold continuous casting strands. Metall. Res. Technol. 2016, 113, 205. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y. Modeling the entrapment of nonmetallic inclusions in steel continuous-casting billets. JOM 2012, 64, 1063–1074. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, J.; Liu, Q.; Yin, Y. Magnetohydrodynamic calculation for electromagnetic stirring coupling fluid flow and solidification in continuously cast billets. Steel Res. Int. 2017, 88, 1700067. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, J.; Yin, Y.; Wang, B. Three-dimensional numerical modeling of macrosegregation in continuously cast billets. Metals 2017, 7, 209. [Google Scholar] [CrossRef]
| Parameters | Values | Dimensions |
|---|---|---|
| cp, Specific heat | 650 | J·kg−1·K−1 |
| k', Thermal conductivity | 33.5 | W·m−1·K−1 |
| ρ, Steel density | 7340 | kg·m−3 |
| L, Steel latent heat | 231,637 | J·kg−1 |
| Tl, Liquid temperature | 1827 | K |
| Ts, Solid temperature | 1636 | K |
| µ, Molten steel molecular viscosity | 0.00461 | kg·s−1·m−1 |
| Ttun, Tundish temperature | 1758 | K |
| dp, Inclusion size | 3.5, 5, 7, 10, 15, 20, 25, 50, 100, 200 | μm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Zhang, J.; Dong, Q.; Li, Y. Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster. Metals 2018, 8, 320. https://doi.org/10.3390/met8050320
Yin Y, Zhang J, Dong Q, Li Y. Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster. Metals. 2018; 8(5):320. https://doi.org/10.3390/met8050320
Chicago/Turabian StyleYin, Yanbin, Jiongming Zhang, Qipeng Dong, and Yuanyuan Li. 2018. "Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster" Metals 8, no. 5: 320. https://doi.org/10.3390/met8050320
APA StyleYin, Y., Zhang, J., Dong, Q., & Li, Y. (2018). Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster. Metals, 8(5), 320. https://doi.org/10.3390/met8050320





