Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys
Abstract
:1. Introduction
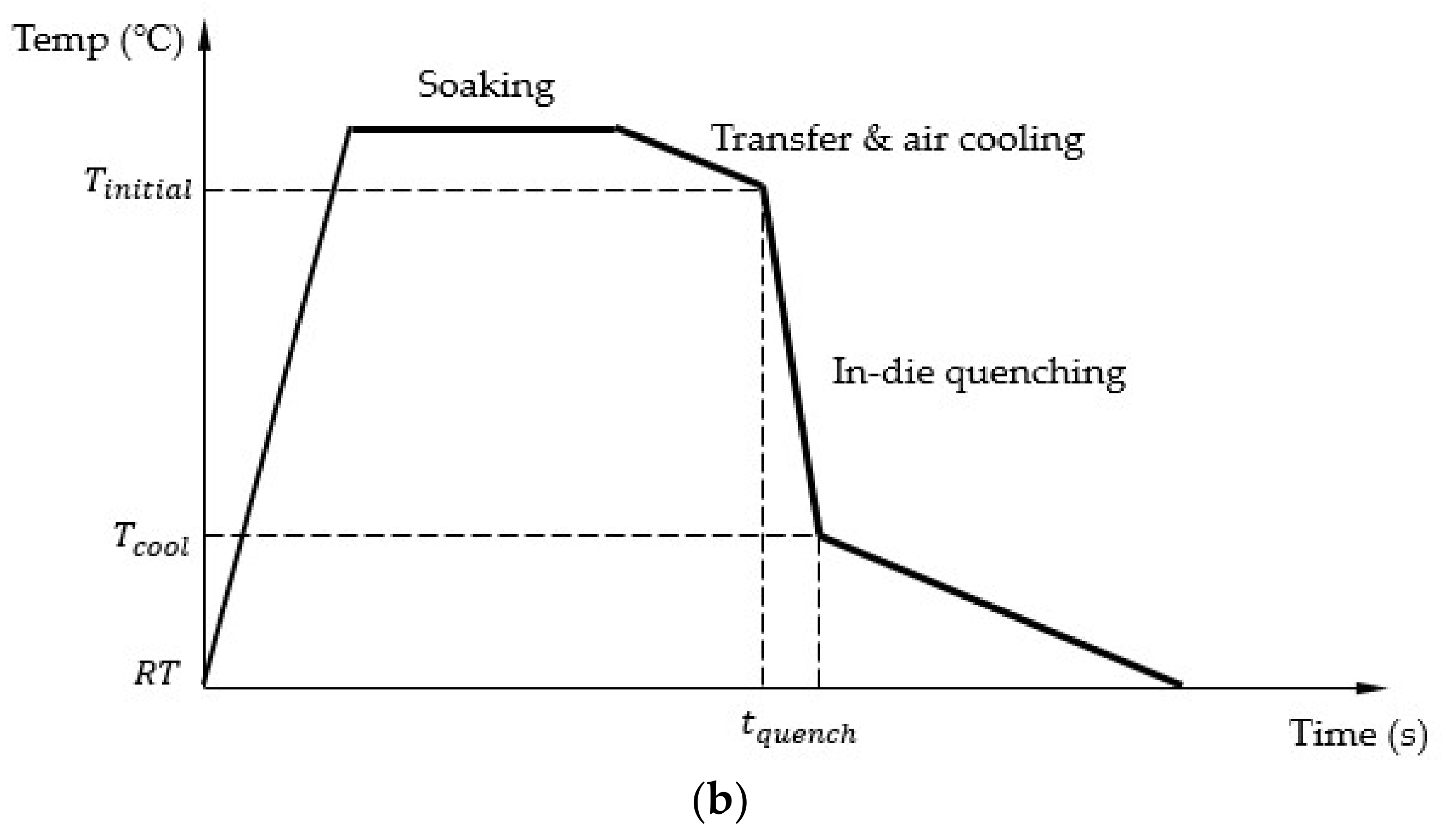
2. Experimentation
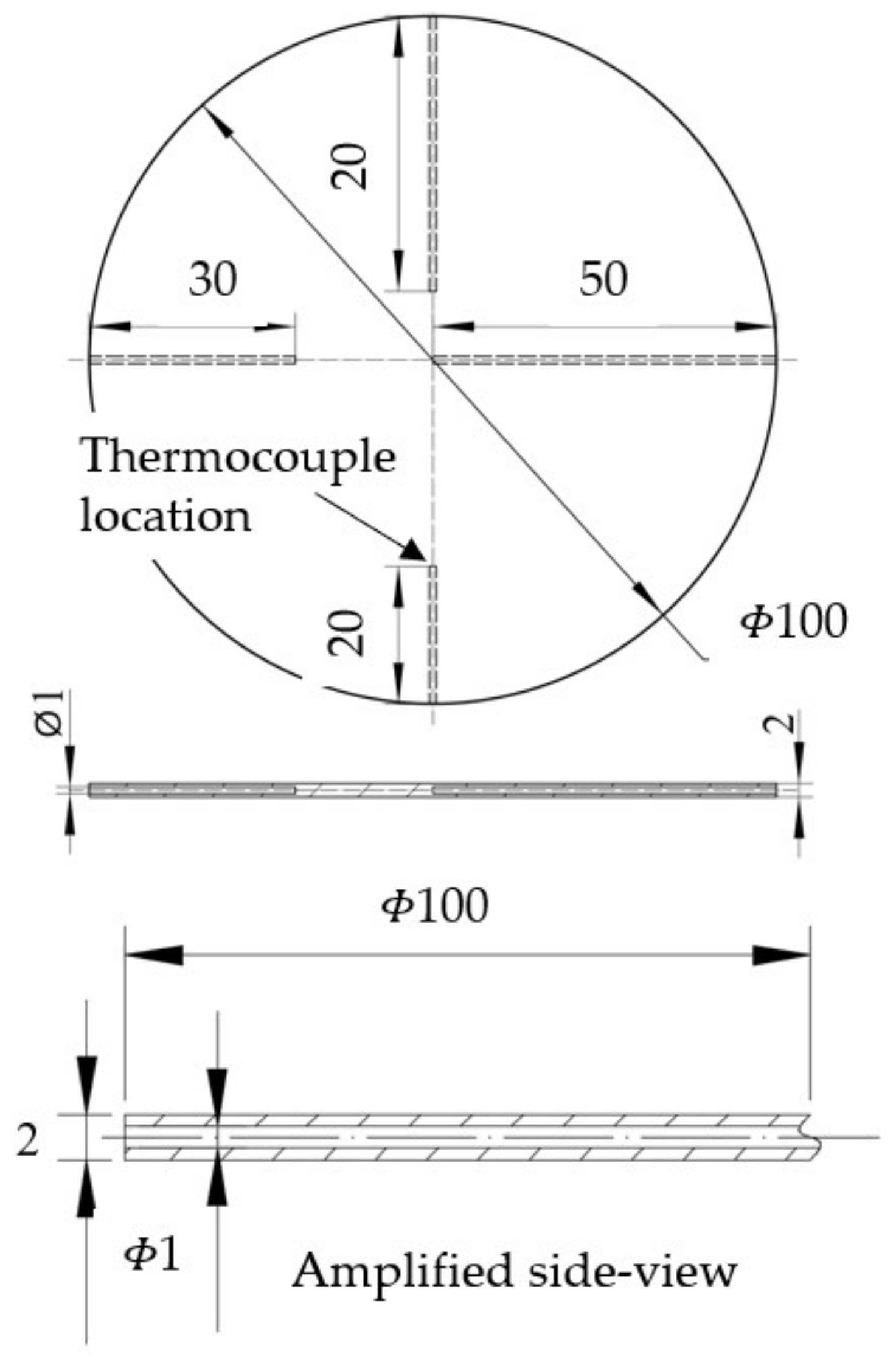
2.1. Material and Specimen Design
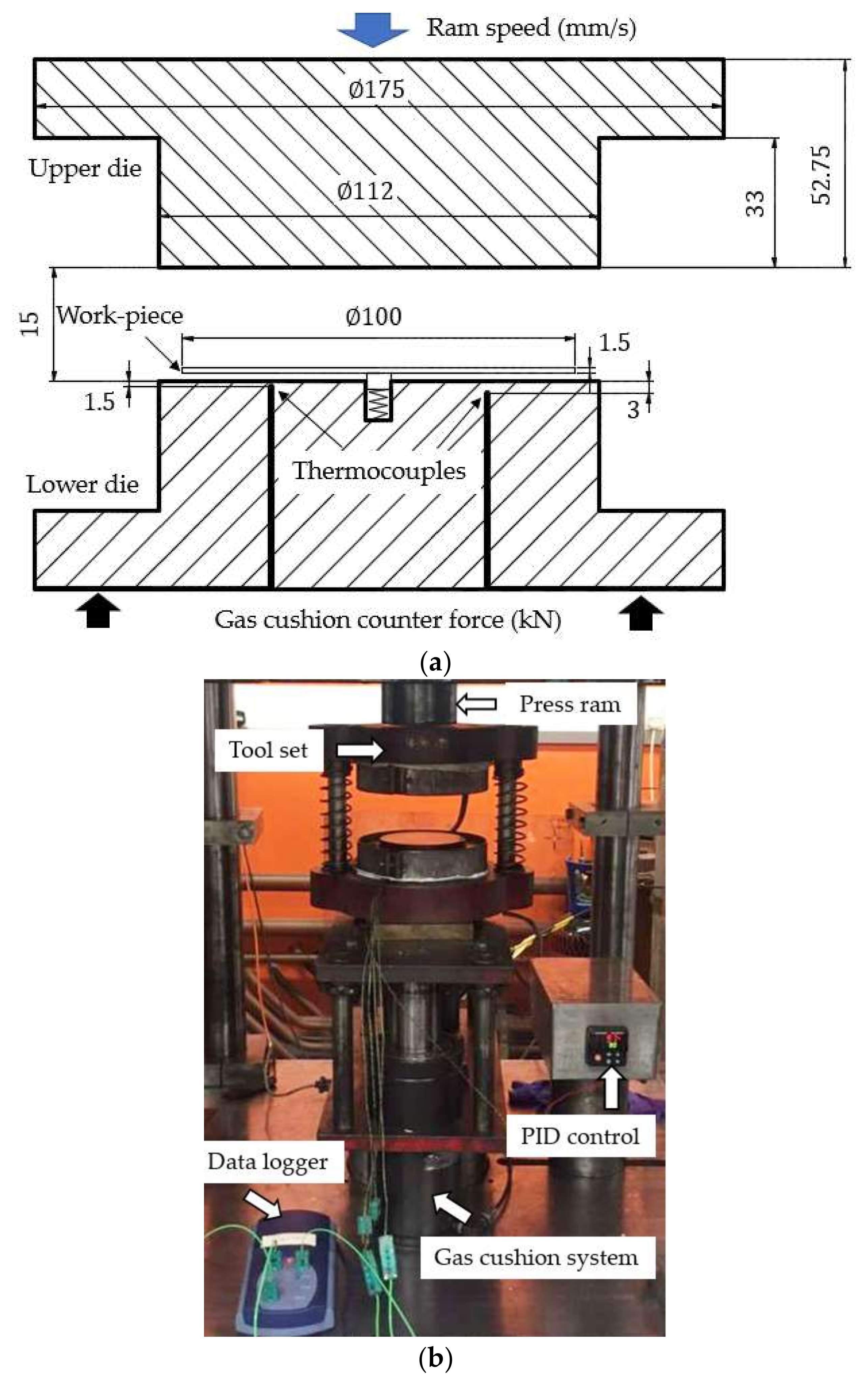
2.2. Experimental Setup
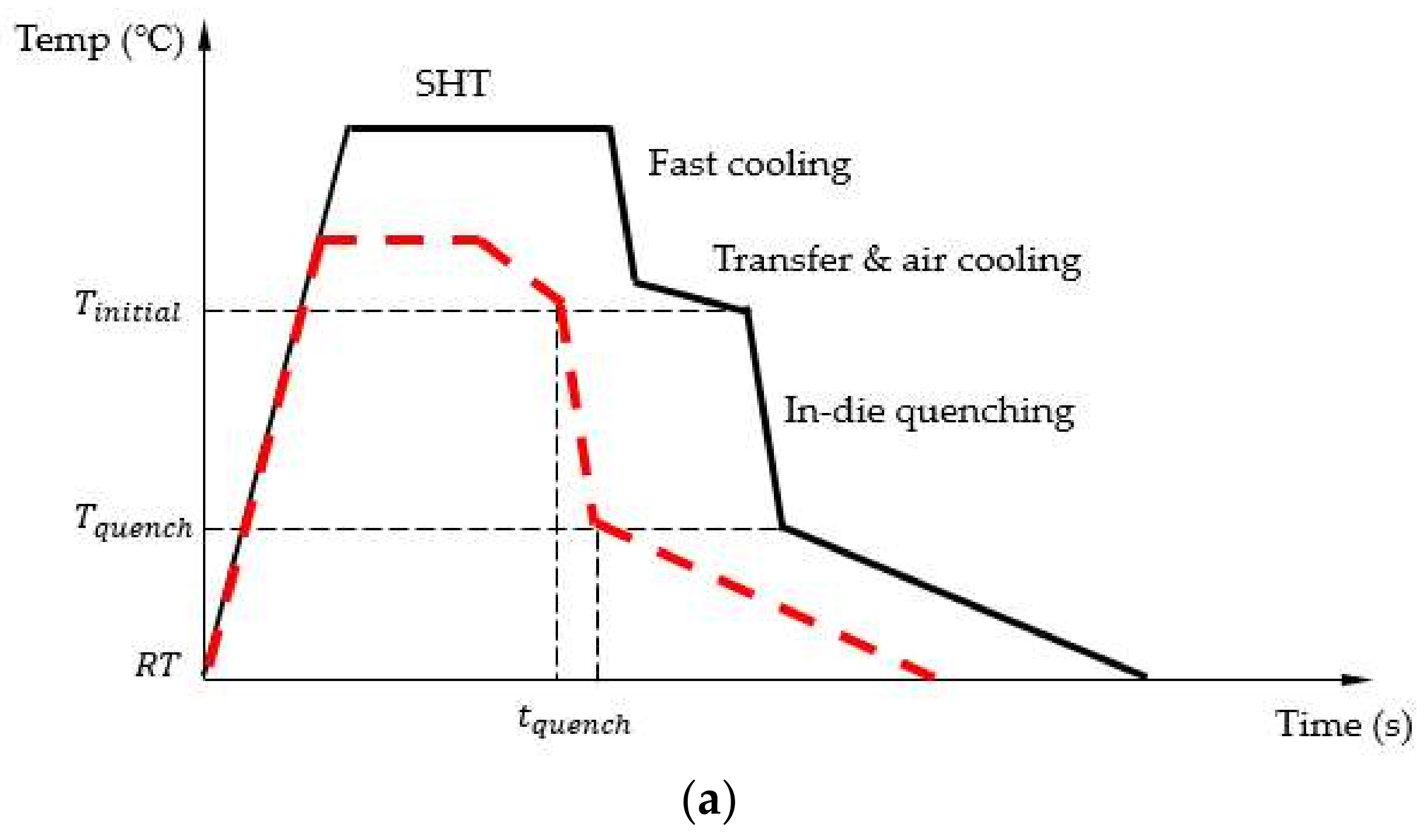
2.3. Test Programme
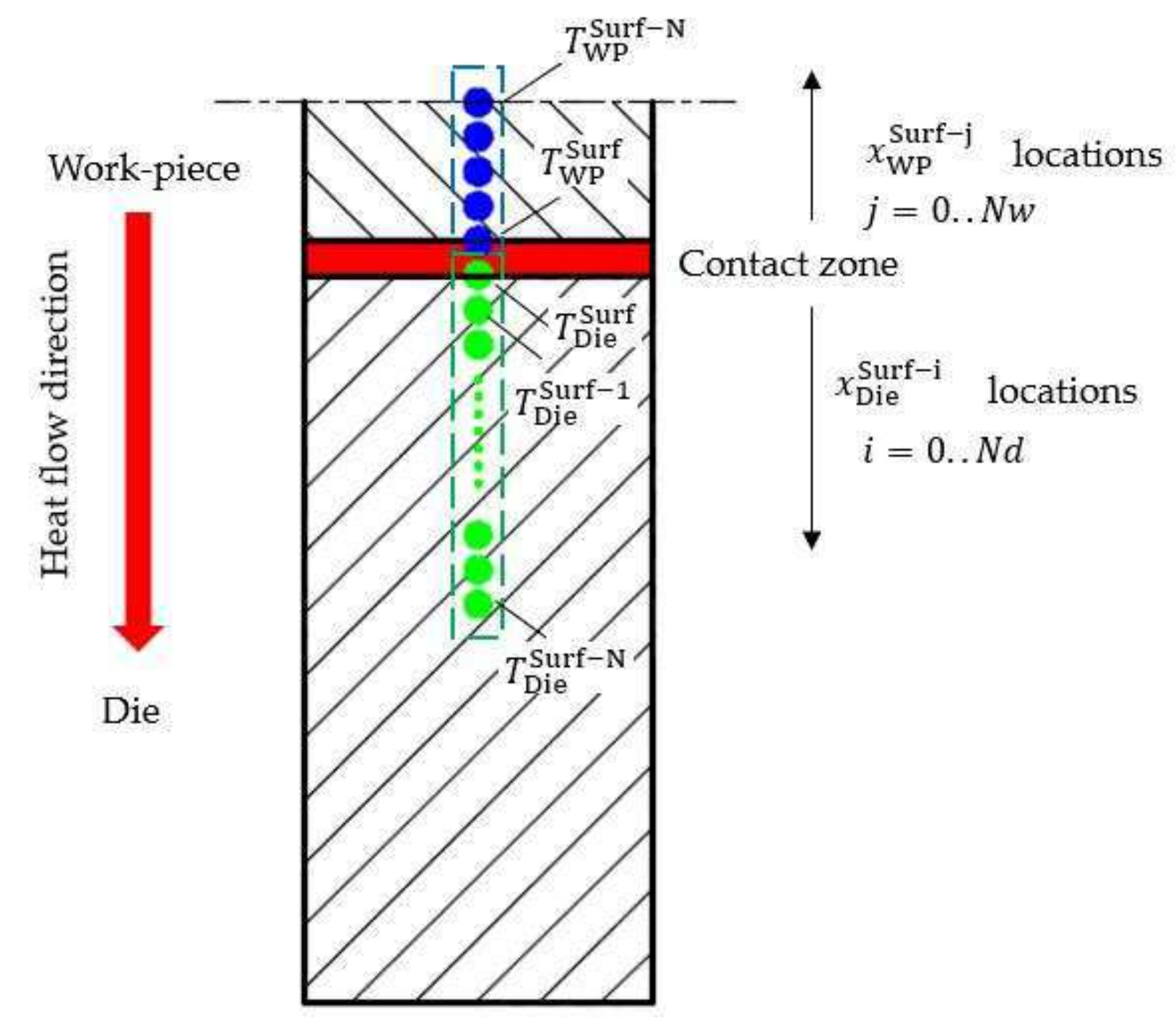
3. Die Surface Temperature Calculation
4. Results and Discussion
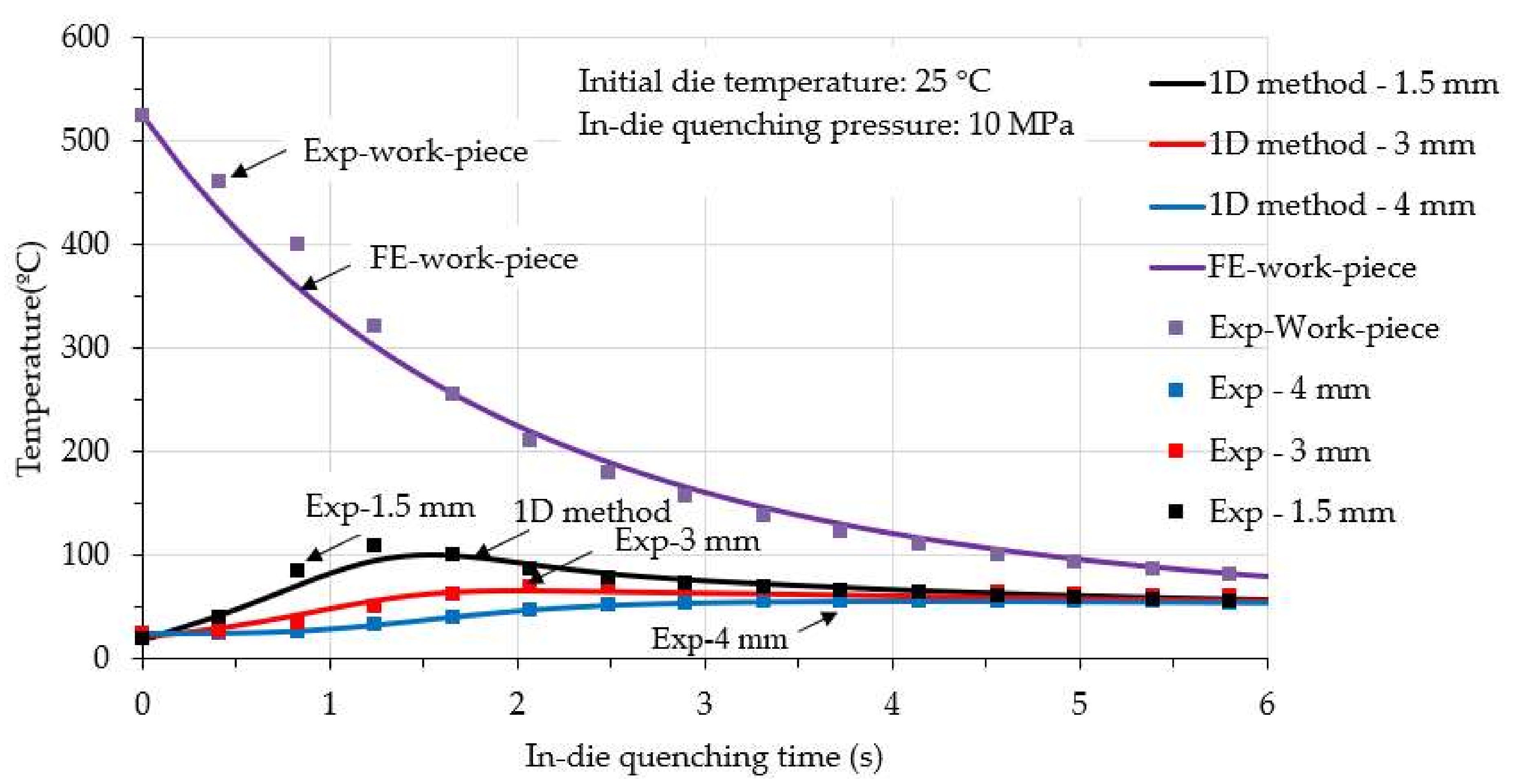
4.1. Validation of 1D Closed Form Calculation Method
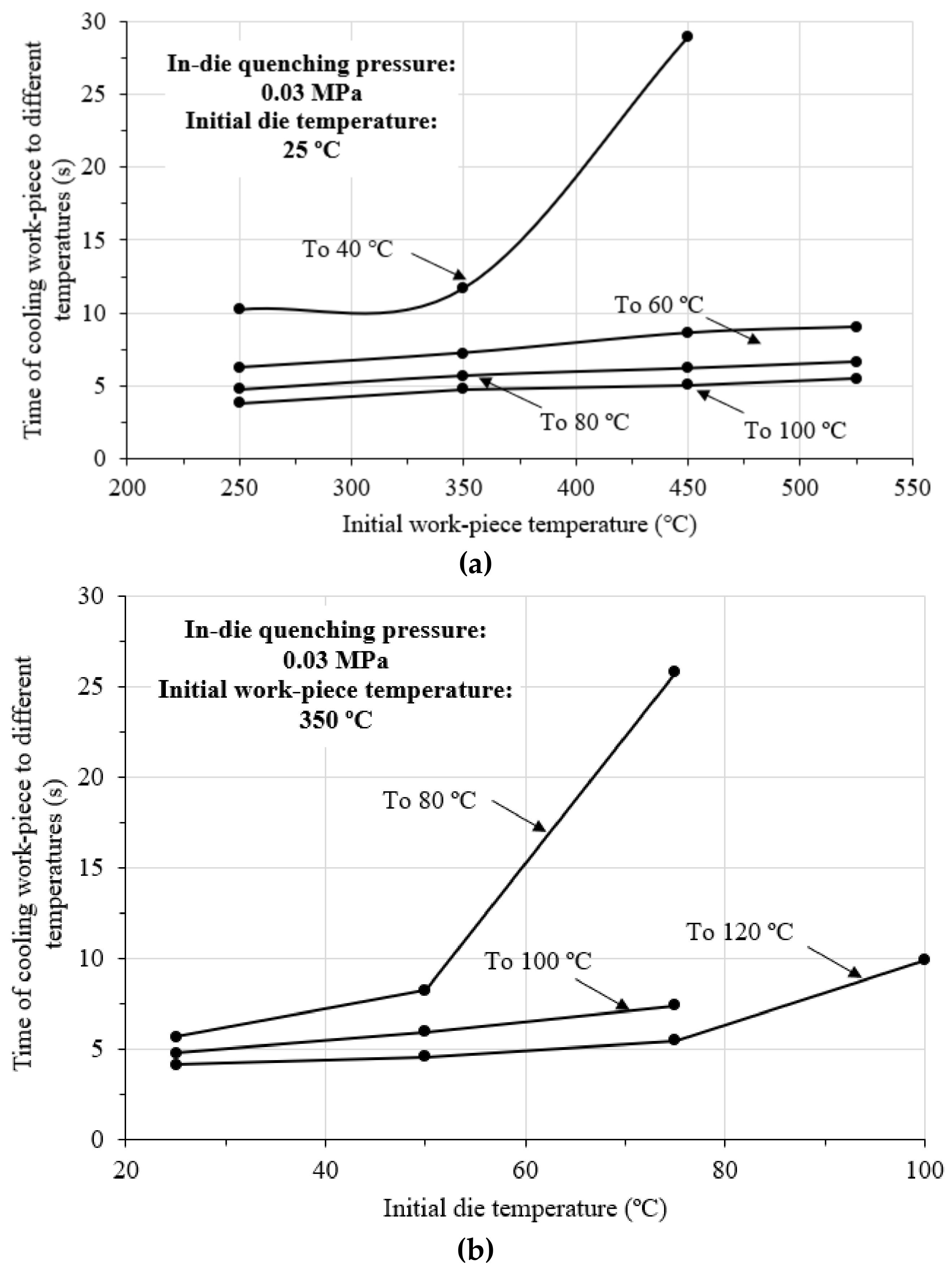
4.2. In-Die Quenching Efficiency
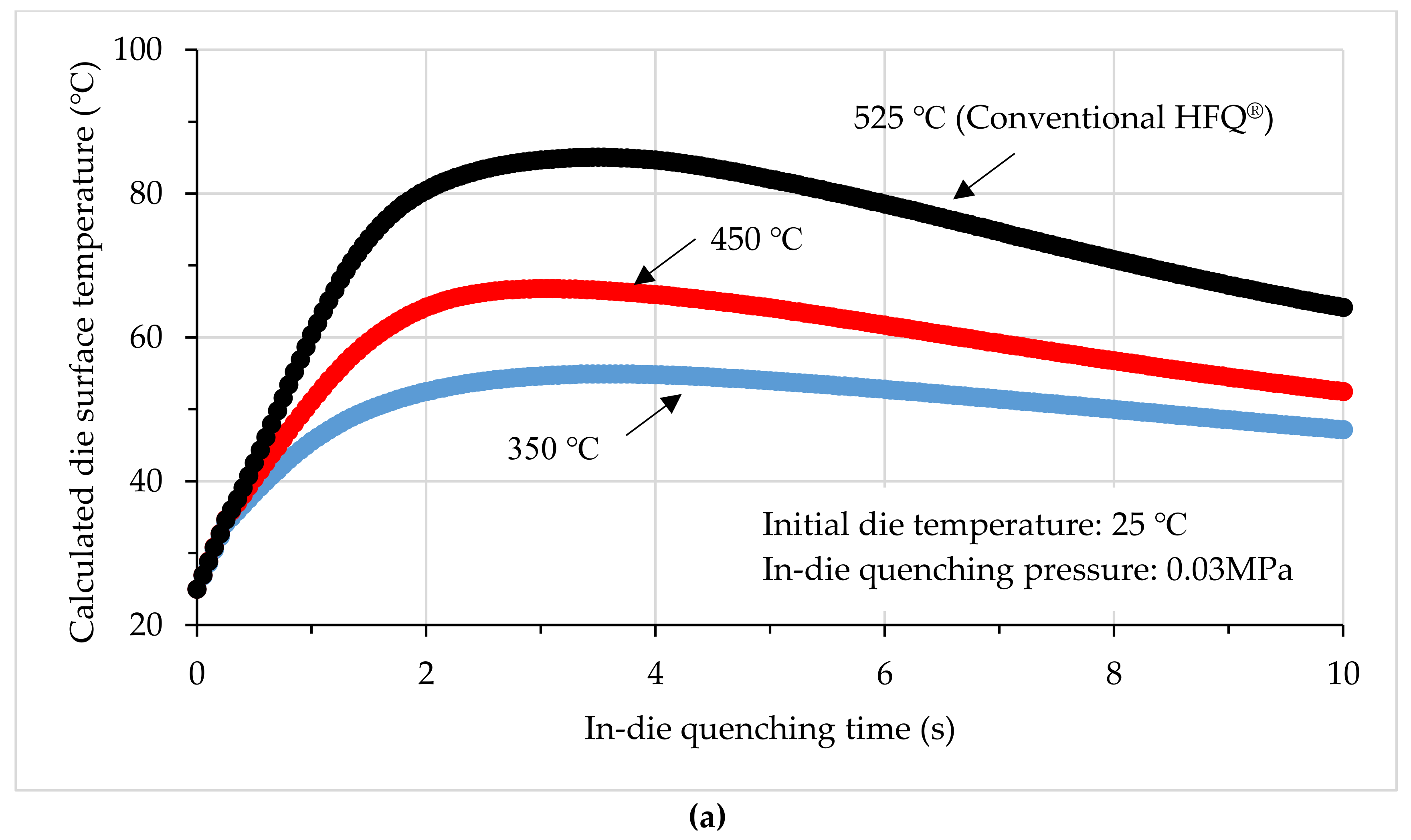
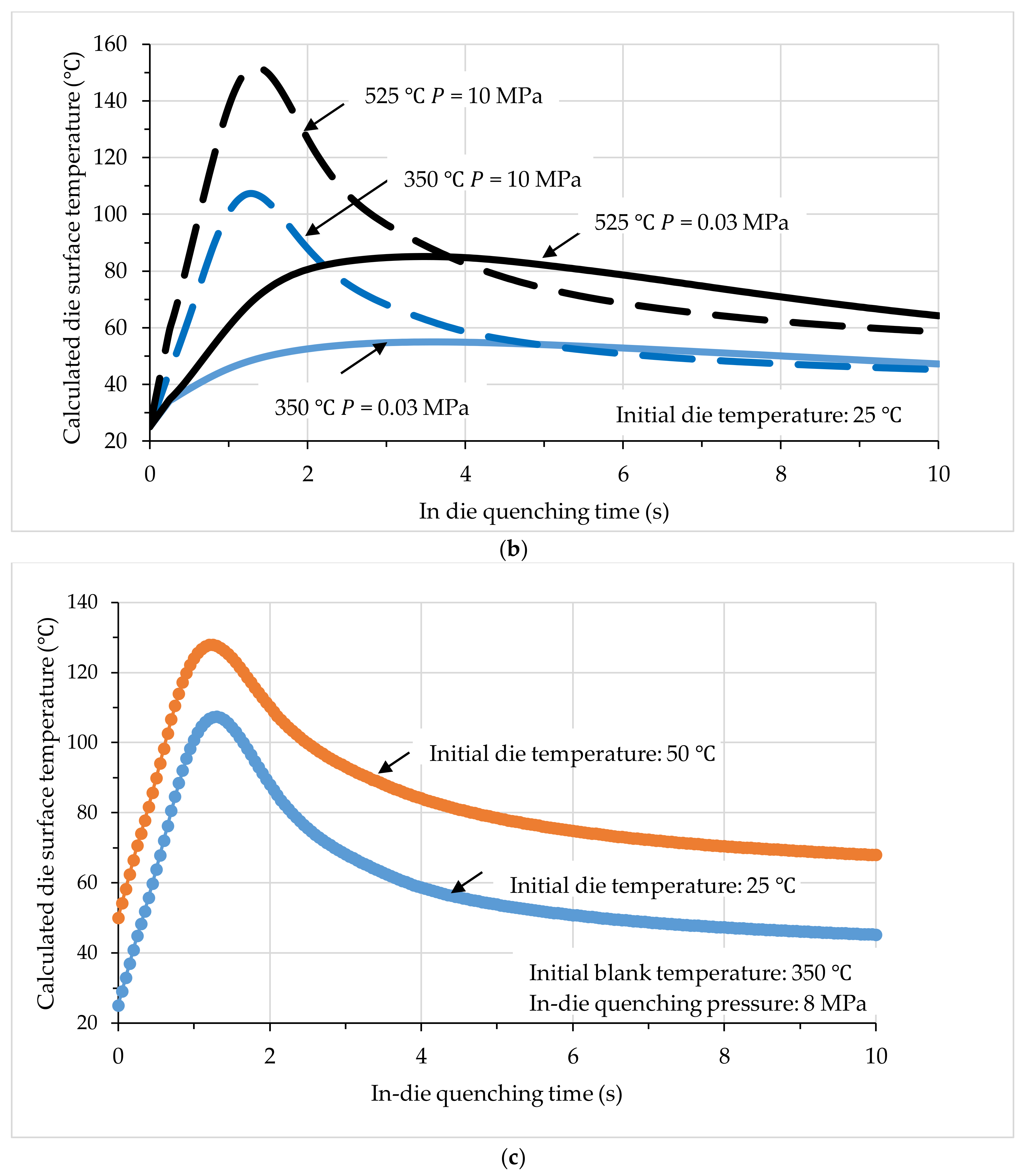
4.3. Evolutions of Die Surface Temperature
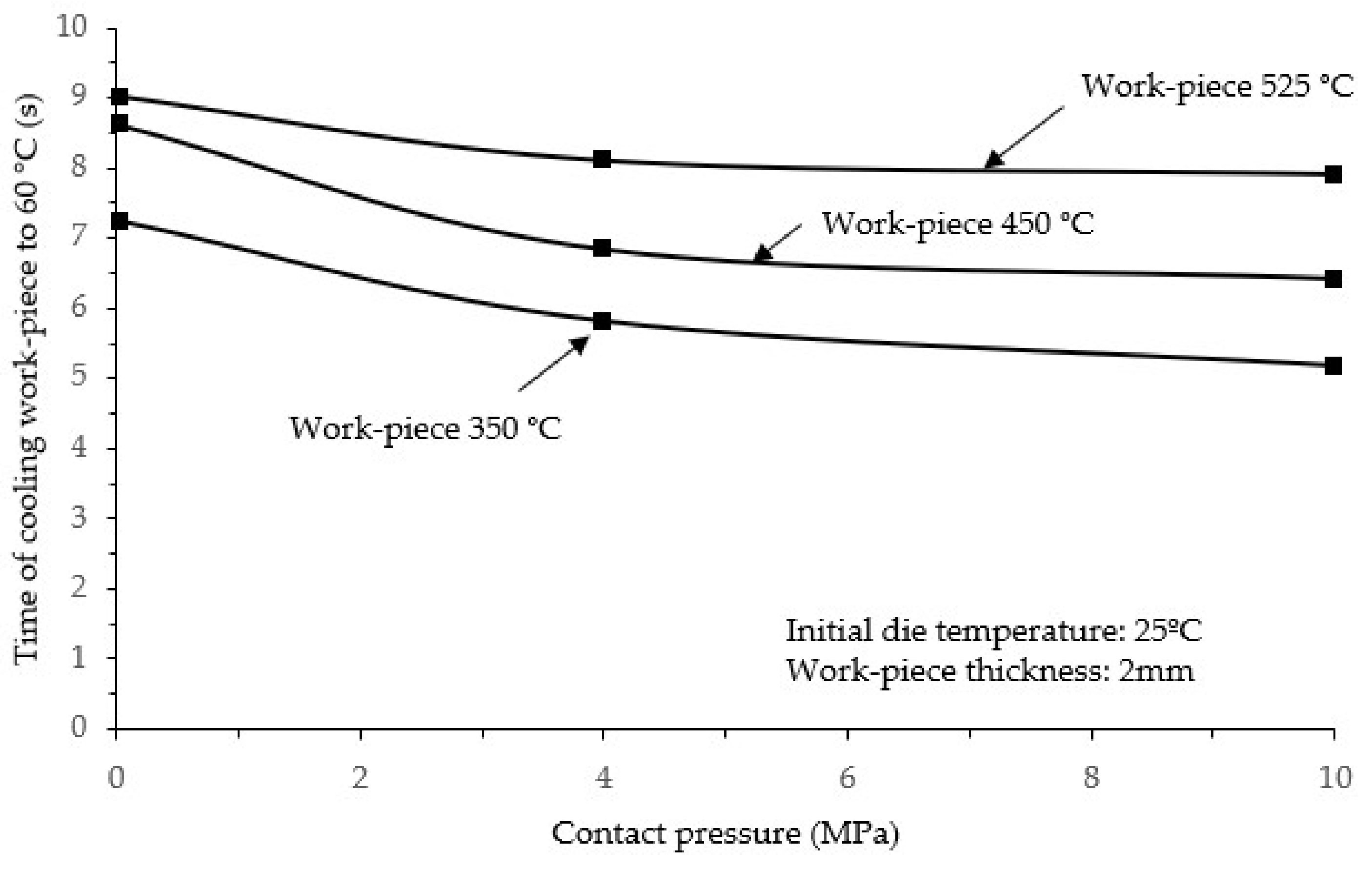
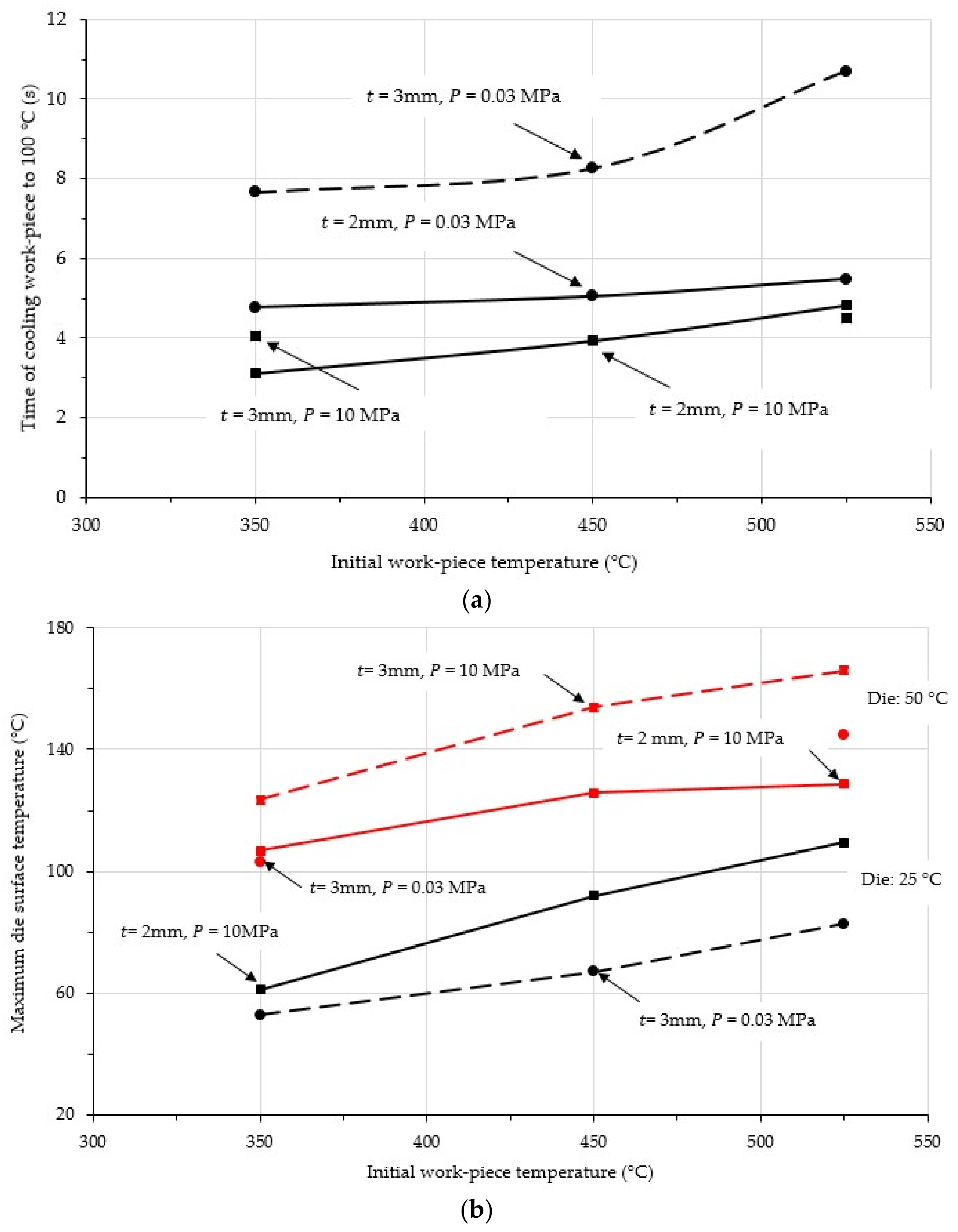
4.4. Effects of Contact Pressure
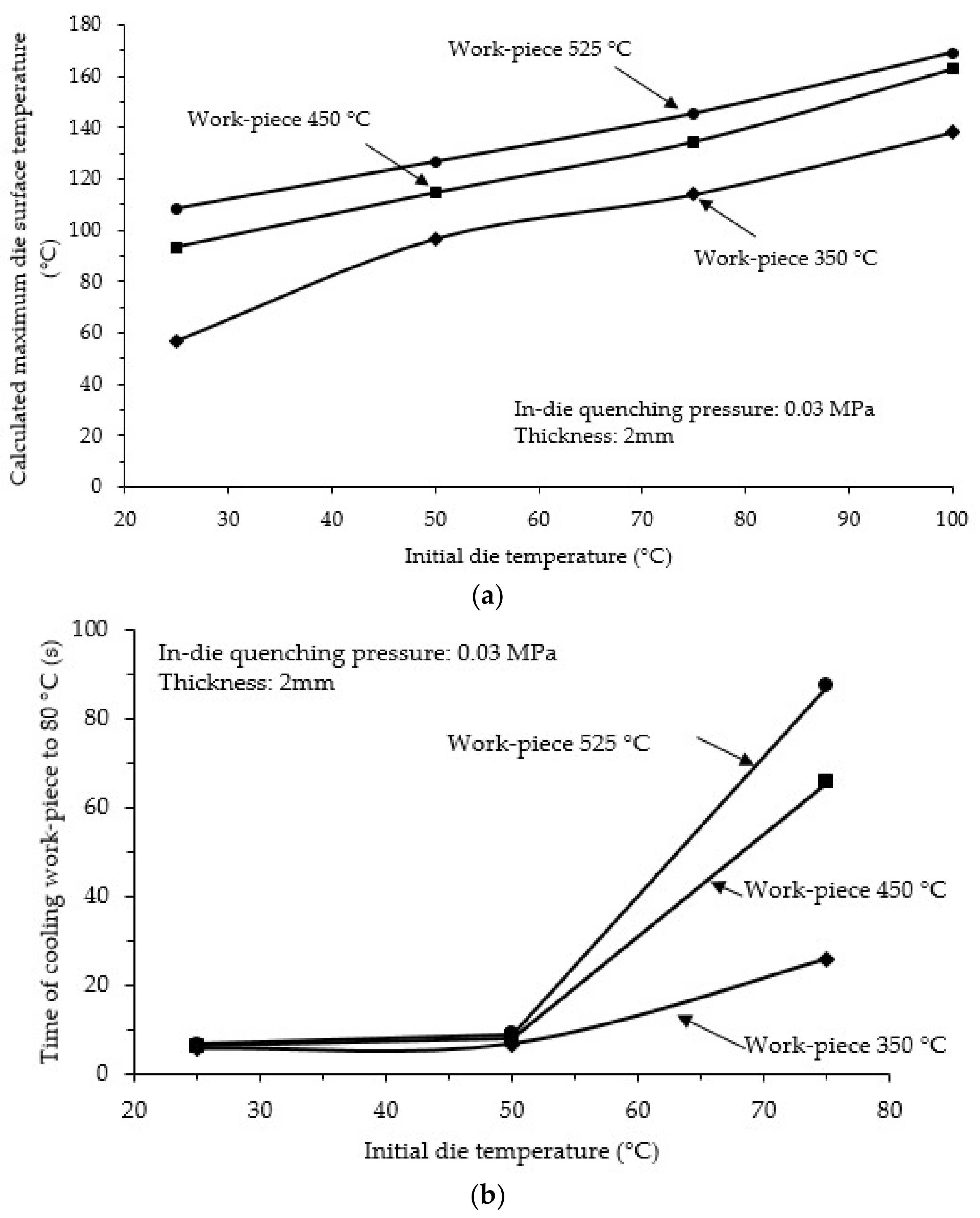
4.5. Effects of Die Temperature
4.6. Effect of Work-Piece Thickness
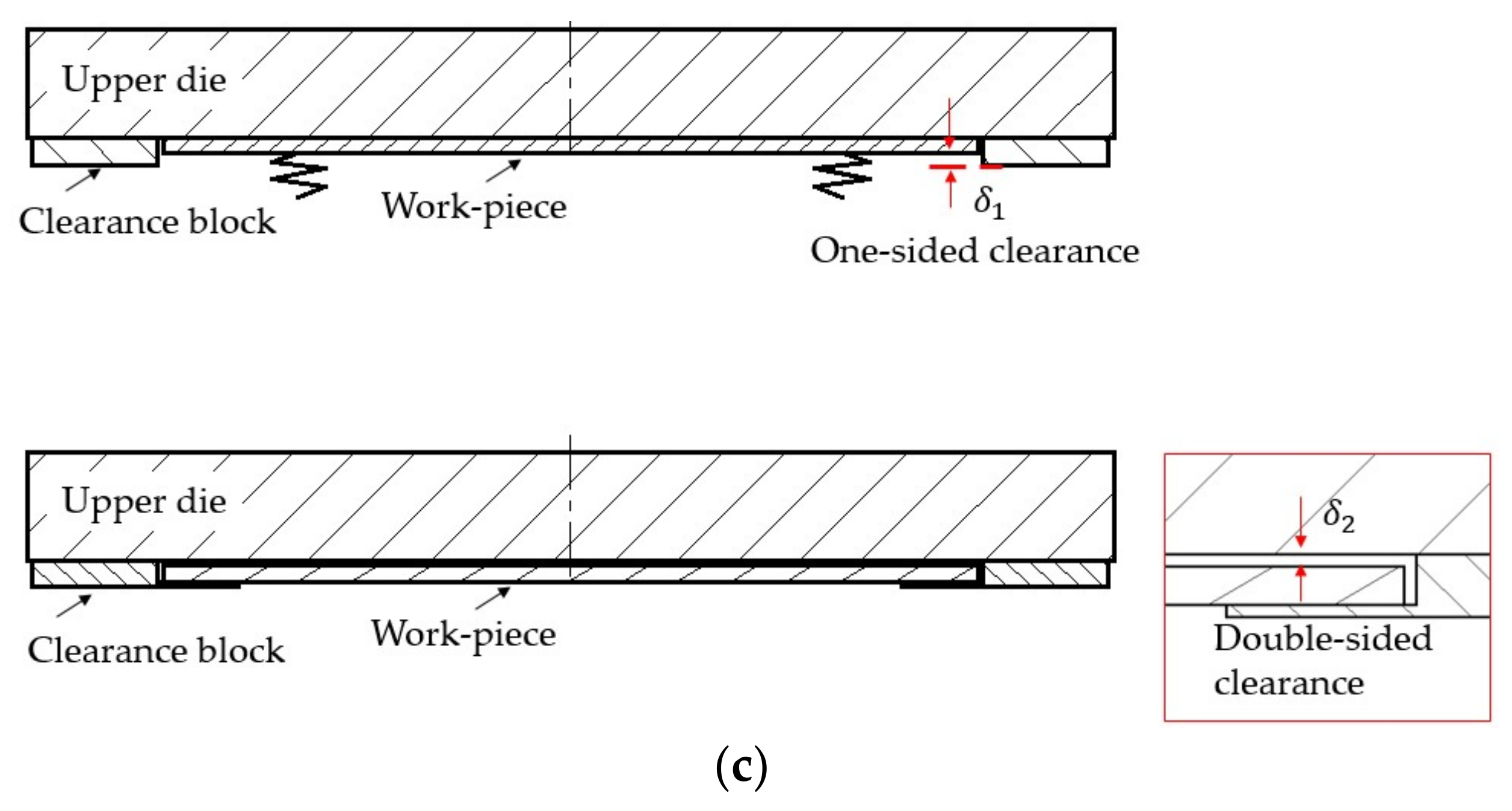
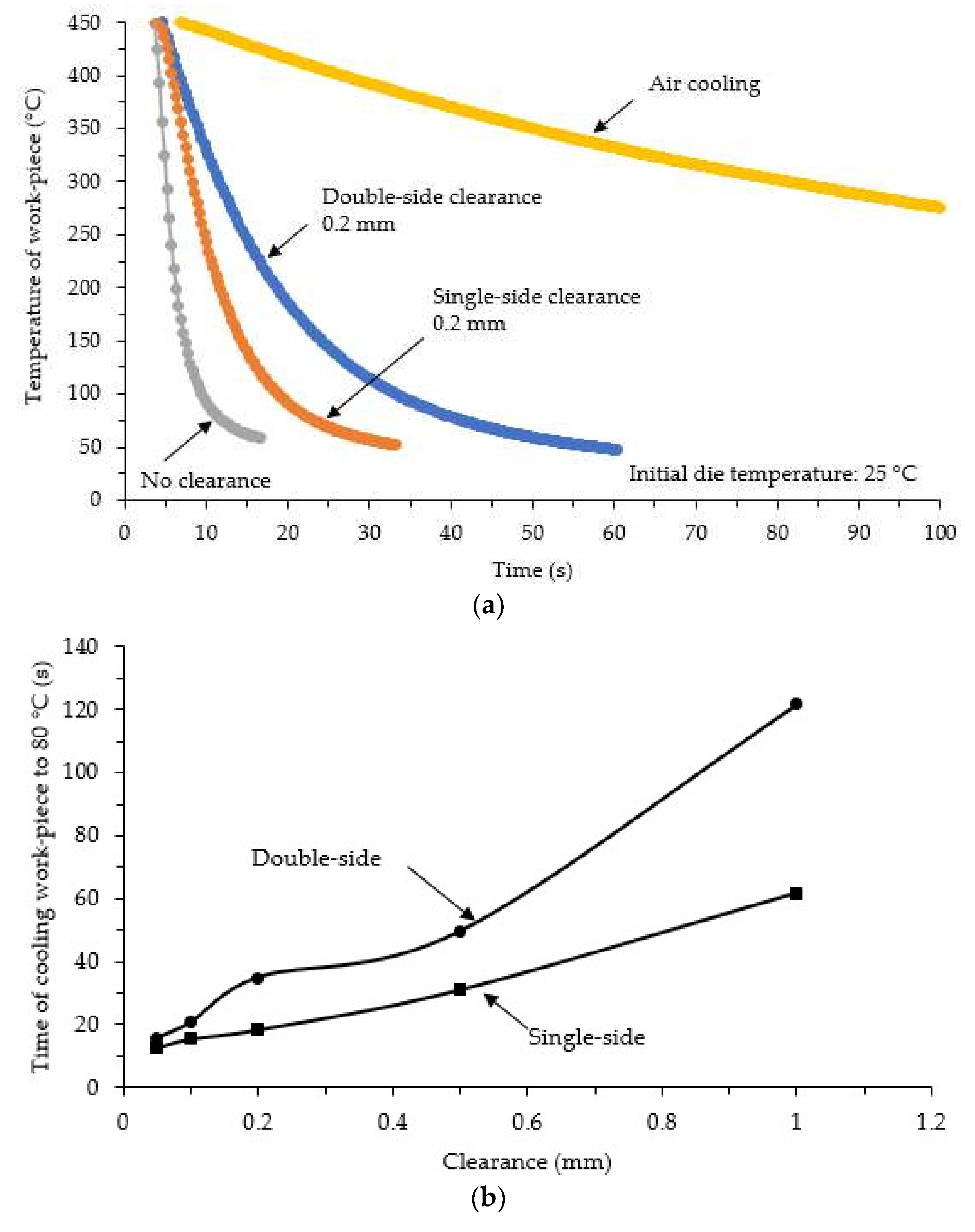
4.7. Effect of Die Clearance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- León, J.; Luis, J.C.; Fuertes, P.J.; Puertas, I.; Luri, R.; Salcedo, D. A proposal of a constitutive description for aluminium alloys in both cold and hot working. Metals 2016, 6, 244. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, T.; Zhou, J.; Xiu, D.; Li, T.; Cheng, K. Mechanical properties of thixoforged in situ Mg2Sip/AM60B composite at elevated temperatures. Metals 2018, 8, 106. [Google Scholar] [CrossRef]
- El Fakir, O.; Wang, L.; Balint, D.; Dear, J.P.; Lin, J.; Dean, T.A. Numerical study of the solution heat treatment, forming, and in-die quenching (HFQ) process on AA5754. Int. J. Mach. Tools Manuf. 2014, 87, 39–48. [Google Scholar] [CrossRef]
- Zheng, K.; Lee, J.; Lin, J.; Dean, T.A. A buckling model for flange wrinkling in hot deep drawing aluminium alloys with macro-textured tool surfaces. Int. J. Mach. Tools Manuf. 2017, 114, 21–34. [Google Scholar] [CrossRef]
- Nishibata, T.; Kojima, N. Effect of quenching rate on hardness and microstructure of hot-stamped steel. J. Alloys Compd. 2013, 577, S549–S554. [Google Scholar] [CrossRef]
- Sjöström, J.; Bergström, J. Thermal fatigue in hot-working tools. Scand. J. Metall. 2005, 34, 221–231. [Google Scholar] [CrossRef]
- Maeno, T.; Mori, K.I.; Fujimoto, M. Improvements in productivity and formability by water and die quenching in hot stamping of ultra-high strength steel parts. CIRP Ann. Manuf. Technol. 2015, 64, 281–284. [Google Scholar] [CrossRef]
- Cortina, M.; Arrizubieta, I.J.; Calleja, A.; Ukar, E.; Alberdi, A. Case study to illustrate the potential of conformal cooling channels for hot stamping dies manufactured using hybrid process of laser metal deposition (LMD) and milling. Metals 2018, 8, 102. [Google Scholar] [CrossRef]
- Abdollahpoor, A.; Chen, X.; Pereira, M.P.; Xiao, N.; Rolfe, B.F. Sensitivity of the final properties of tailored hot stamping components to the process and material parameters. J. Mater. Process. Technol. 2016, 228, 125–136. [Google Scholar] [CrossRef]
- Mendiguren, J.; Ortubay, R.; De Argandonã, E.S.; Galdos, L. Experimental characterization of the heat transfer coefficient under different close loop controlled pressures and die temperatures. Appl. Therm. Eng. 2016, 99, 813–824. [Google Scholar] [CrossRef]
- Li, H.; He, L.; Zhang, C.; Cui, H. Research on the effect of boundary pressure on the boundary heat transfer coefficients between hot stamping die and boron steel. Int. J. Heat Mass Transf. 2015, 91, 401–415. [Google Scholar] [CrossRef]
- Chang, Y.; Tang, X.; Zhao, K.; Hu, P.; Wu, Y. Investigation of the factors influencing the interfacial heat transfer coefficient in hot stamping. J. Mater. Process. Technol. 2016, 228, 25–33. [Google Scholar] [CrossRef]
- Liu, X.; Fakir, O.; El Meng, L.; Sun, X.; Li, X.; Wang, L. Effects of lubricant on the IHTC during the hot stamping of AA6082 aluminium alloy: Experimental and modelling studies. J. Mater. Process. Technol. 2018, 255, 175–183. [Google Scholar] [CrossRef]
- Hu, P.; Ying, L.; Li, Y.; Liao, Z. Effect of oxide scale on temperature-dependent interfacial heat transfer in hot stamping process. J. Mater. Process. Technol. 2013, 213, 1475–1483. [Google Scholar] [CrossRef]
- Merklein, M.; Lechler, J.; Stoehr, T. Investigations on the thermal behavior of ultra high strength boron manganese steels within hot stamping. Int. J. Mater. Form. 2009, 2, 259. [Google Scholar] [CrossRef]
- Ying, L.; Gao, T.; Dai, M.; Hu, P. Investigation of interfacial heat transfer mechanism for 7075-T6 aluminum alloy in HFQ hot forming process. Appl. Therm. Eng. 2017, 118, 266–282. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, B.; Zheng, K.; Zhou, J.; Lin, J. A study of interfacial heat transfer and its effect on quenching when hot stamping AA7075. Arch. Civ. Mech. Eng. 2018, 18, 723–730. [Google Scholar] [CrossRef]
- Liu, X.; Ji, K.; Fakir, O.; El Fang, H.; Gharbi, M.M.; Wang, L. Determination of the interfacial heat transfer coefficient for a hot aluminium stamping process. J. Mater. Process. Technol. 2017, 247, 158–170. [Google Scholar] [CrossRef]
- Bai, Q.; Lin, J.; Zhan, L.; Dean, T.A.; Balint, D.S.; Zhang, Z. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming. Int. J. Mach. Tools Manuf. 2012, 56, 102–110. [Google Scholar] [CrossRef]
| Element wt % | Mg | Si | Mn | Fe | Cu | Zn | Ti | Cr | Remainder |
|---|---|---|---|---|---|---|---|---|---|
| Min. | 0.6 | 0.7 | 0.4 | - | - | - | - | - | Al |
| Max. | 1.2 | 1.3 | 1 | 0.5 | 0.1 | 0.2 | 0.1 | 0.25 |
| Work-Piece Temperature (°C) | Work-Piece Thickness (mm) | Die Temperature (°C) | Contact Pressure (MPa) |
|---|---|---|---|
| 250, 350, 450, 525 | 2, 3 | 25, 50, 75, 100 | 0.03, 1, 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Lee, J.; Xiao, W.; Wang, B.; Lin, J. Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys. Metals 2018, 8, 231. https://doi.org/10.3390/met8040231
Zheng K, Lee J, Xiao W, Wang B, Lin J. Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys. Metals. 2018; 8(4):231. https://doi.org/10.3390/met8040231
Chicago/Turabian StyleZheng, Kailun, Junyi Lee, Wenchao Xiao, Baoyu Wang, and Jianguo Lin. 2018. "Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys" Metals 8, no. 4: 231. https://doi.org/10.3390/met8040231
APA StyleZheng, K., Lee, J., Xiao, W., Wang, B., & Lin, J. (2018). Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys. Metals, 8(4), 231. https://doi.org/10.3390/met8040231





