Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints
Abstract
1. Introduction
2. Determination of the Optimum Material Parameters for the Finite Element Method (FEM) by Genetic Algorithms (GA)
3. Genetic Algorithms with Multi-Objective Functions
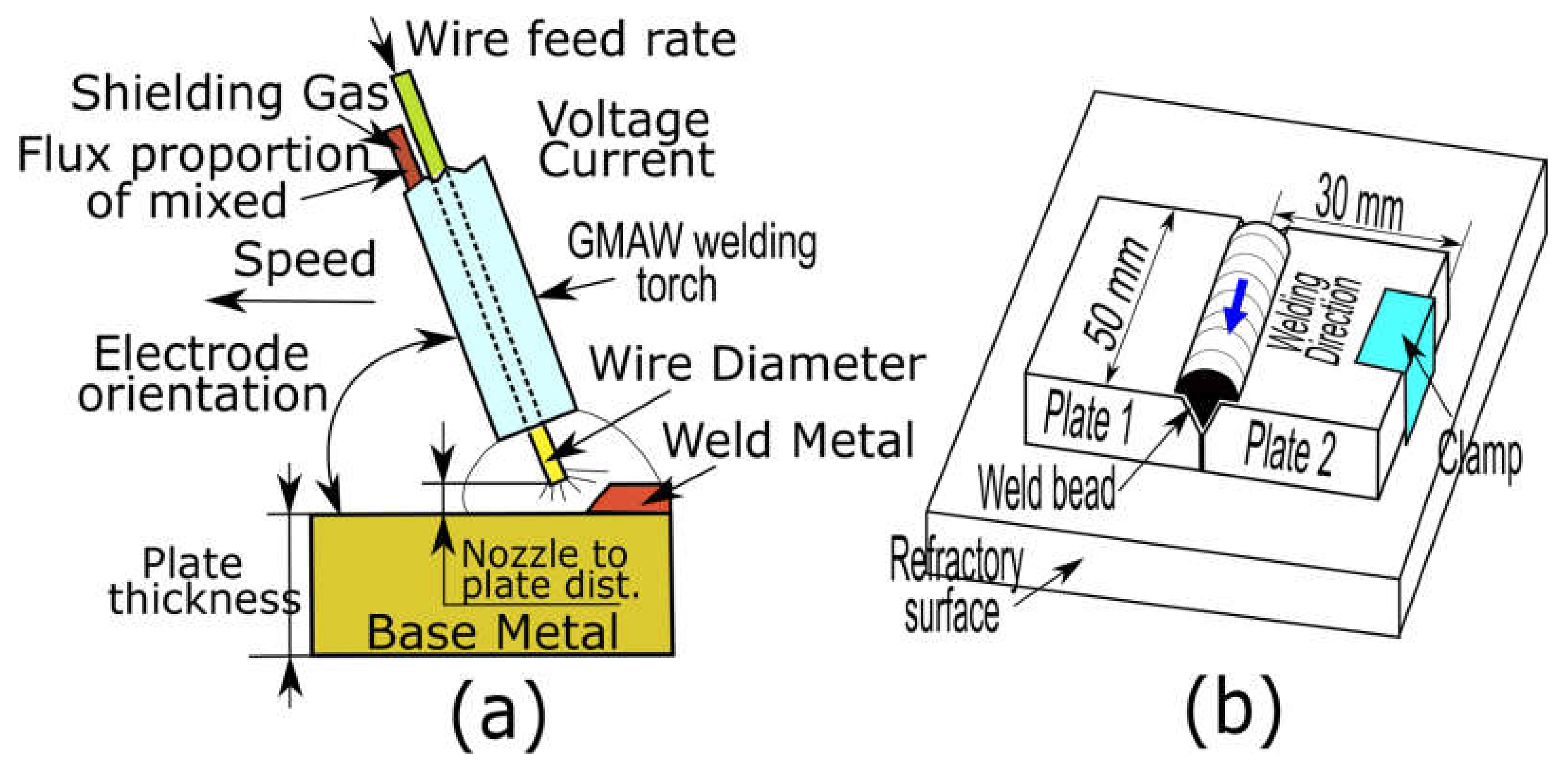
4. Experimental Procedure
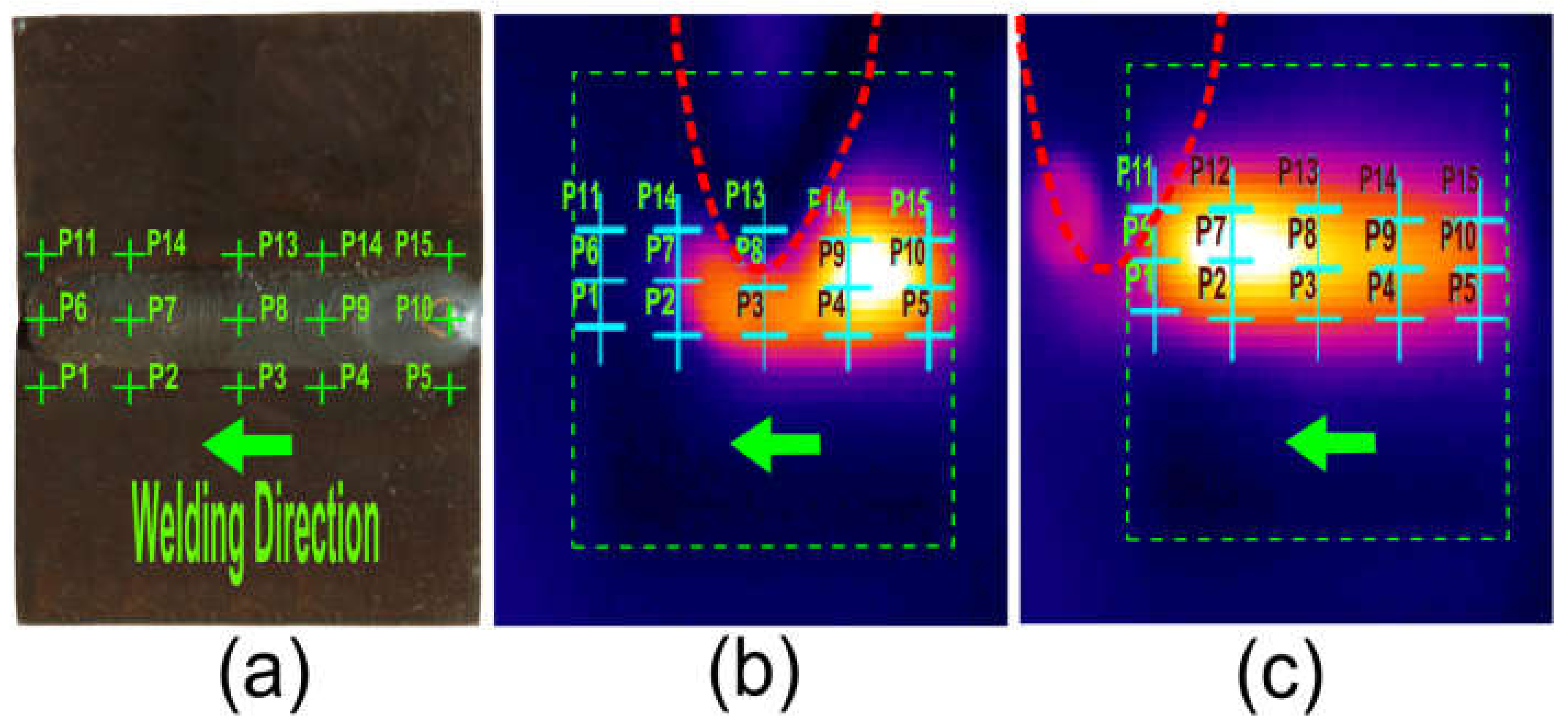
4.1. Measuring the Temperature Field
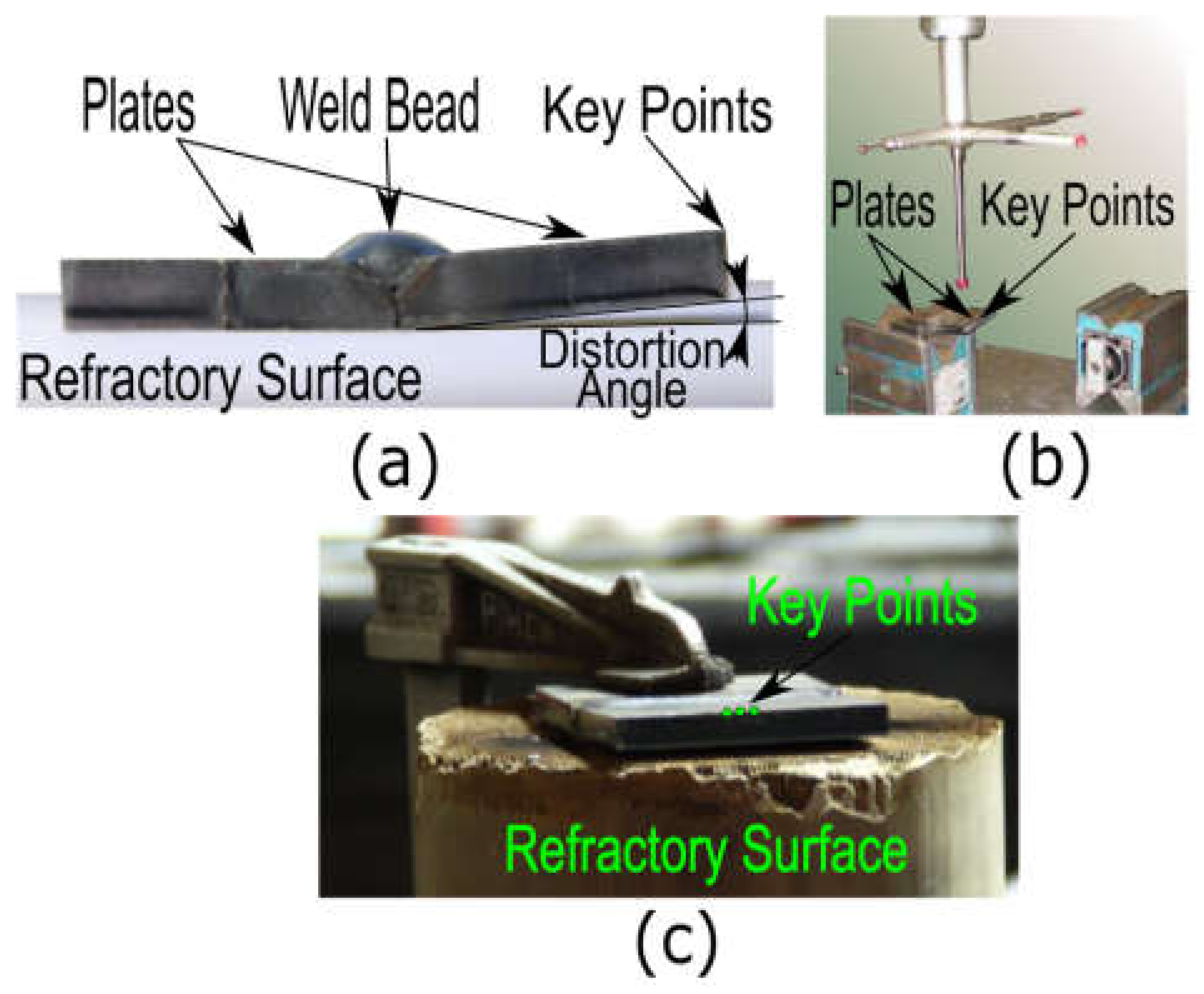
4.2. Measurement of Angular Distortion
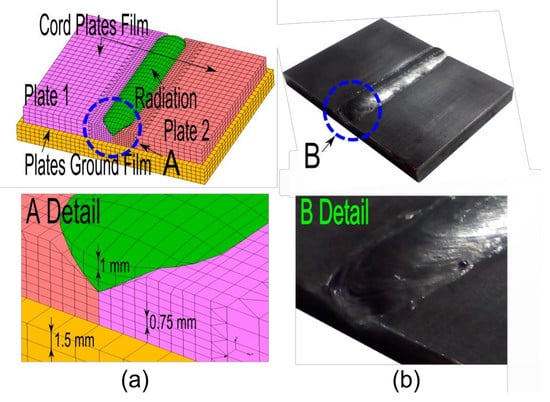
4.3. Characterization of the Welded Joint and Measurement of Weld Bead Geometry
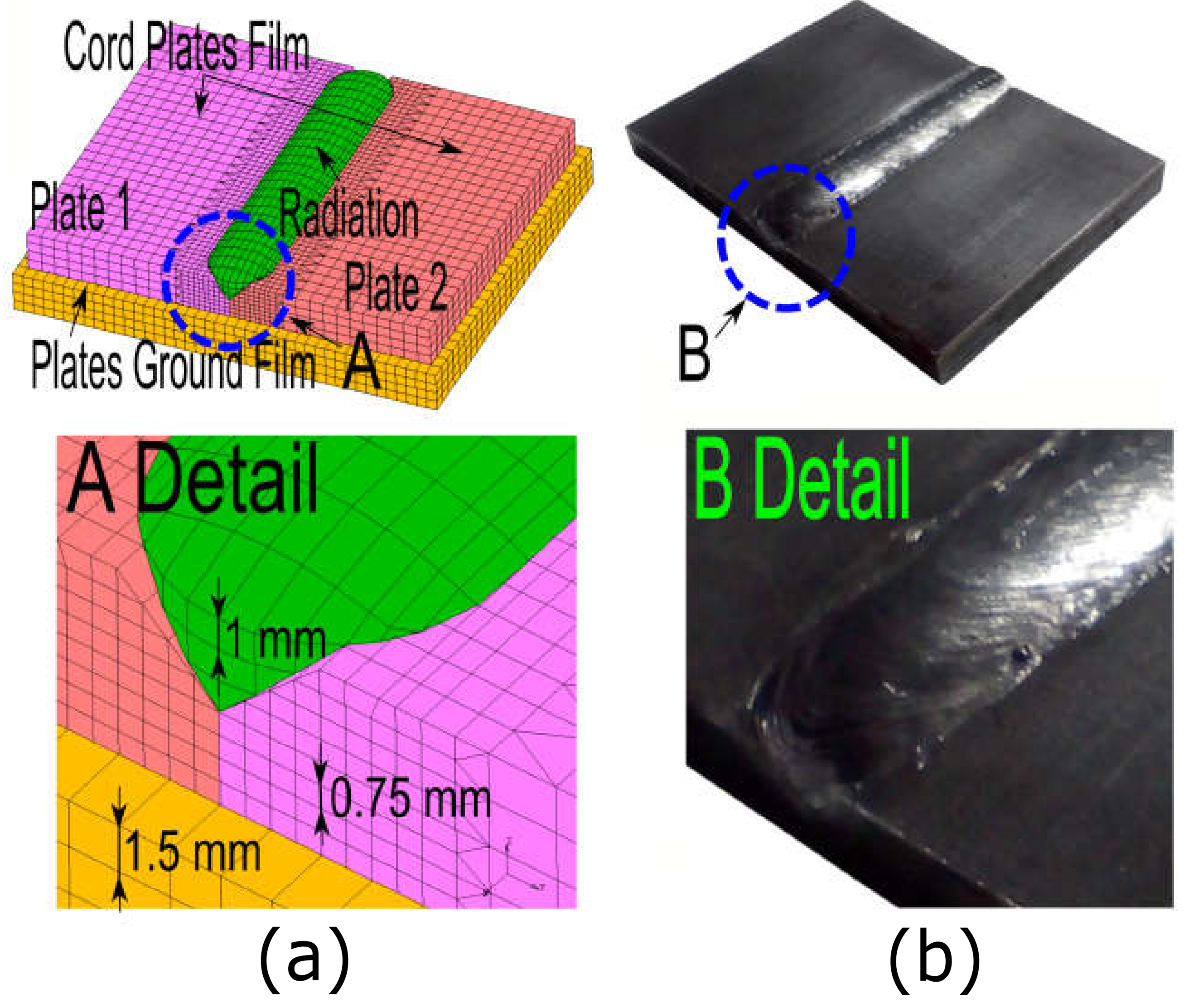
5. Finite Element Proposed for Modeling the Welded Joints
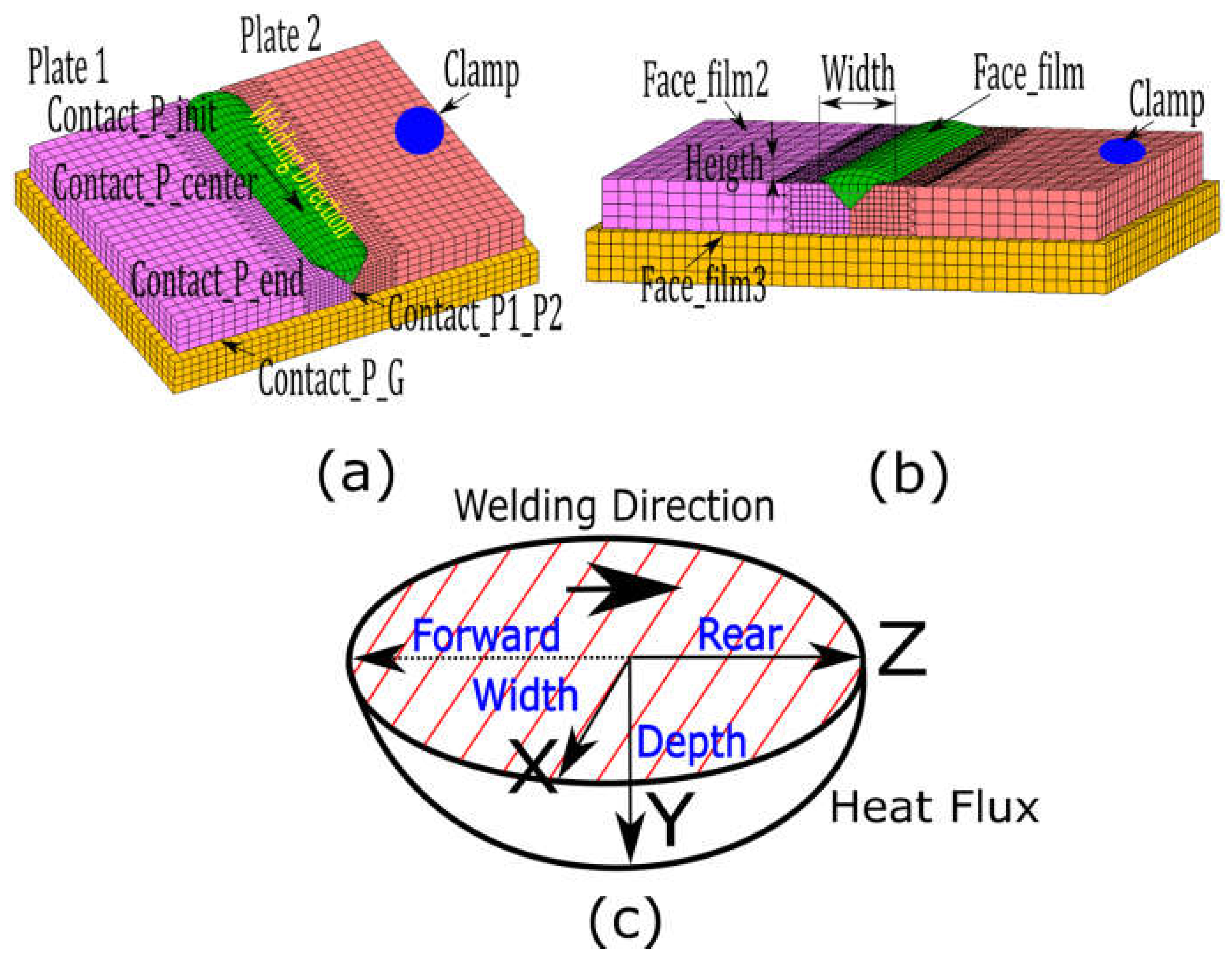
5.1. Parameterization of the Welded Joints FE Models
5.2. Adjusting the Welded Joints FE Models
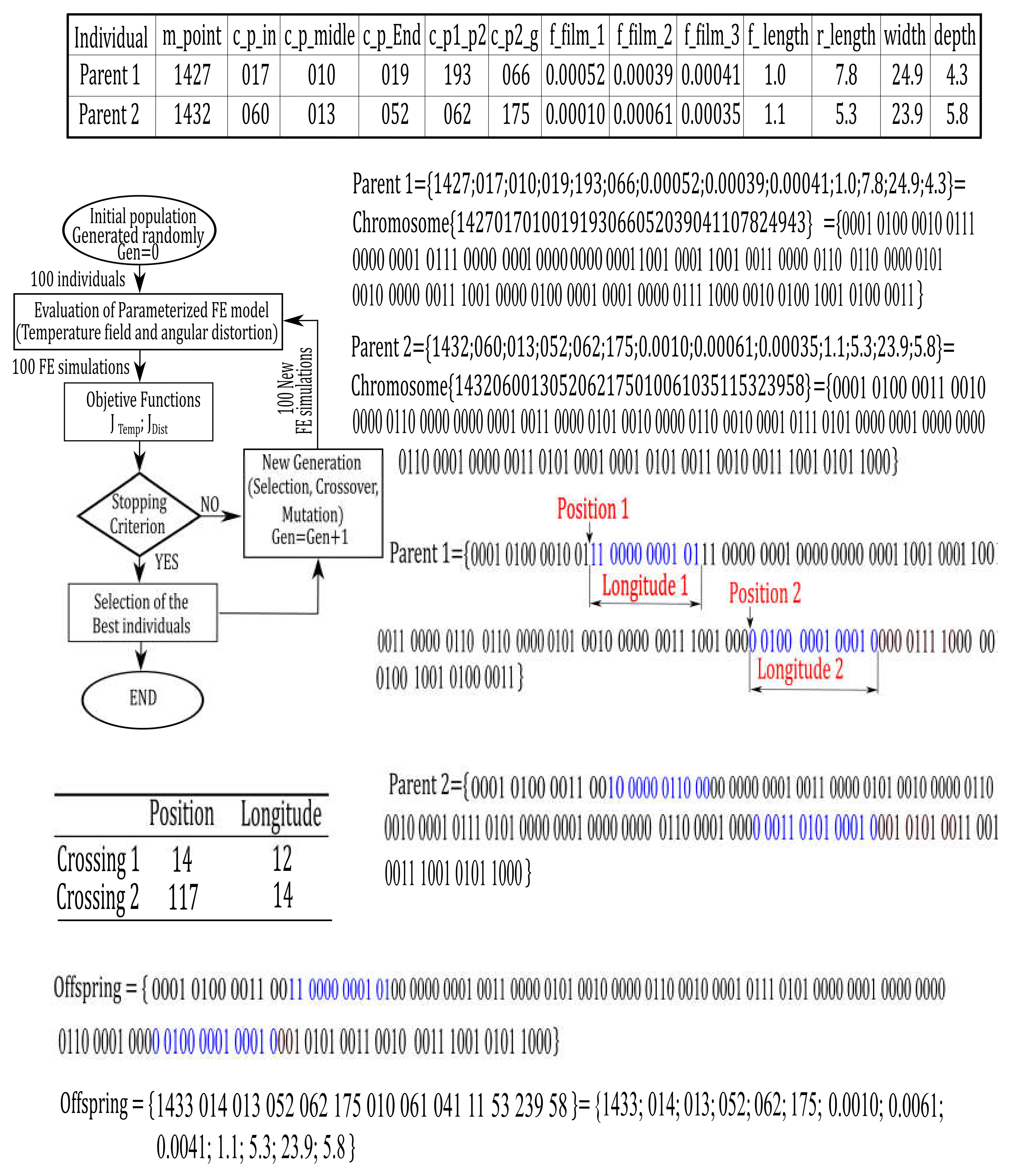
5.3. Crossovers and Mutations
- 30% of the individuals with the lowest objective function JTotalj values of the previous generation became parents of the new generation.
- 60% of individuals were created by crossing selected parents. The crossing was implemented by a script in “R” language [50]. It consists of a change in a random number of bits of chromosomes of two randomly selected best individuals. First, it was necessary to obtain two complete chromosomes from two selected parents. Then, each chromosome was coded to binary code to perform the process of crossing. Then, a random number of crossings (1, 2, 3, or 4) were selected. Also, for each crossing a position number that defined the position of the initial bit of each crossing was randomly selected too. In the same way, the longitude of the number of bits that form the crossing part of the chromosome was selected. With this information, some bits of the first parent were selected and the remaining bits were selected from the second parent to create a new chromosome for the next generation. Figure 7 shows the first and second positions 1 and 2, and the lengths (longitude 1) and (longitude 2) that were selected in this case for the crossing of two individuals from the generation “0”. In this case, position 1 was equal to “14” and position 2 was equal to “117”. Longitude 1 was equal to “12” and longitude was equal to “14” (all position and longitude values are in bits). Finally, the new chromosomes were decoded from their binary code to generate the new offspring that were formed by the parameters to be adjusted in order to model the thermo-mechanical behavior of the welded joints.
- The remaining 10% of individuals were obtained by mutation. A random number of bits (between one and the number that defines the longitude of the chromosome) are defined and random positions of the chromosome are selected and are commuted until reaching the number of the initial number of bits selected. Meanwhile, it was important to always check that the new randomly generated values were within the established ranges. The aim of generating individuals by mutation was to find new solutions in areas that had not been explored previously. This procedure was repeated separately for each of the welded joints that were studied for several generations until the objective function JTotalj no longer increased significantly.
5.4. Correlation-Based Feature Selection
6. Case Study
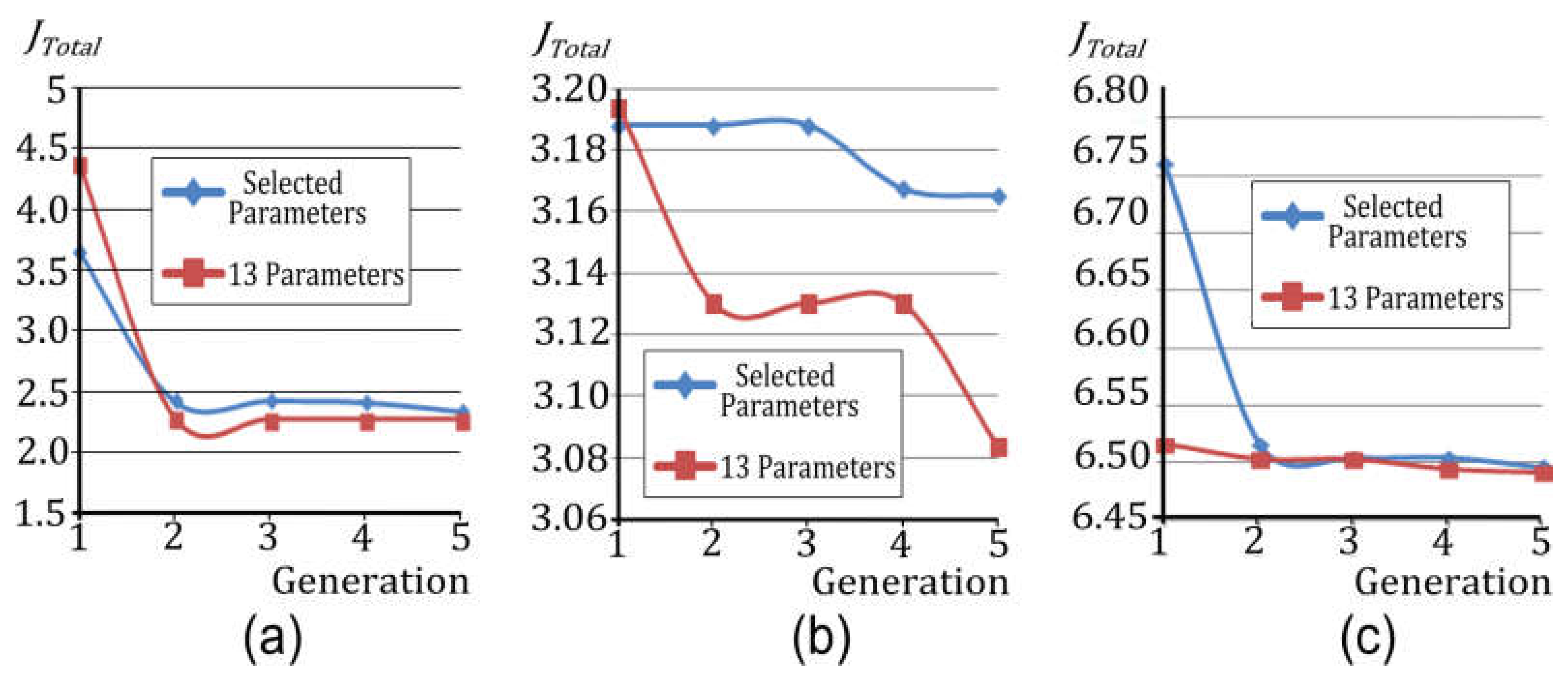
6.1. Results That are Based on CFS
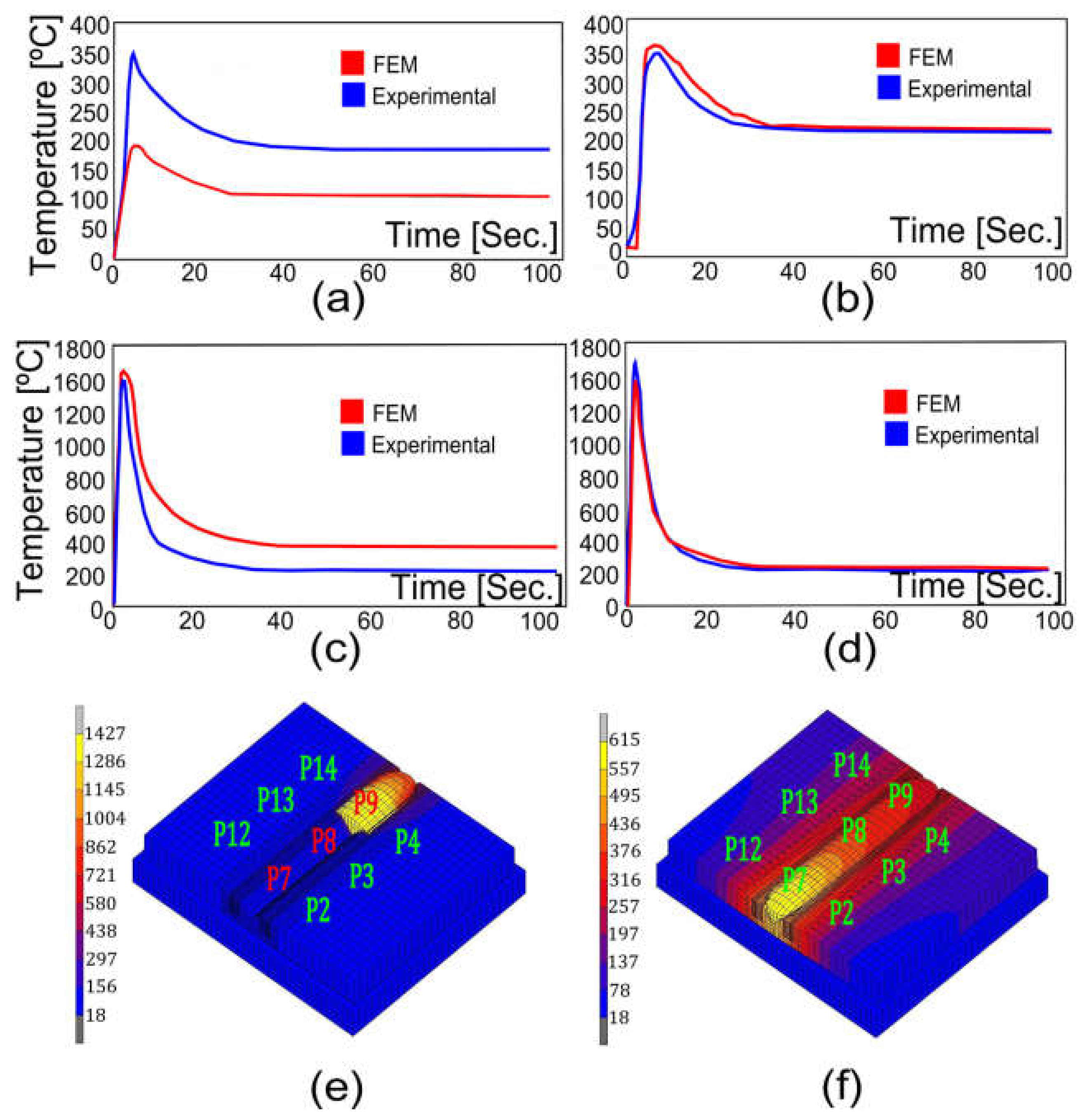
6.2. Results of FE Model Adjustment
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Macherauch, E.; Kloos, K.H. Origin, measurements and evaluation of residual stresses. In Residual Stress in Science and Technology, 1st ed.; DGM Verlag: Oberursel, Germany, 1987. [Google Scholar]
- Ozcelik, S.; Moore, K. Modeling, Sensing and Control of Gas Metal Arc Welding, 1st ed.; Elsevier Science Ltd.: Kidlington, Oxford, UK, 2003. [Google Scholar]
- Citarella, R.; Carlone, P.; Lepore, M.; Sepe, R. Hybrid technique to assess the fatigue performance of multiple cracked FSW joints. Eng. Fract. Mech. 2016, 132, 38–50. [Google Scholar] [CrossRef]
- Citarella, R.; Carlone, P.; Sepe, R.; Lepore, M. DBEM crack propagation in friction stir welded aluminum joints. Adv. Eng. Softw. 2016, 101, 50–59. [Google Scholar] [CrossRef]
- Lostado, R.; Martínez-de-Pisón, F.J.; Fernández, R.; Fernández, J. Using genetic algorithms to optimize the material behaviour model in finite element models of processes with cyclic loads. J. Strain Anal. Eng. 2011, 46, 143–159. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlaghi, M. Computational Welding Mechanics, 1st ed.; Springer Science & Business Media, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Brickstad, B.; Josefson, B.L. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes. Int. J. Press. Vessels Pip. 1998, 75, 11–25. [Google Scholar] [CrossRef]
- Ericsson, M.; Nylén, P. A look at the optimization of robot welding speed based on process modeling. Weld. J.-N. Y. 2007, 86, 238. [Google Scholar]
- Attarha, M.J.; Sattari-Far, I. Study on welding temperature distribution in thin welded plates through experimental measurements and finite element simulation. J. Mater. Process. Technol. 2011, 211, 688–694. [Google Scholar] [CrossRef]
- Lostado, R.; Corral, M.; Martínez, M.Á.; Villanueva Roldán, P.M. Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints. Metals 2017, 7, 136. [Google Scholar] [CrossRef]
- Bachorski, A.; Painter, M.J.; Smailes, A.J.; Wahab, M.A. Finite-element prediction of distortion during gas metal arc welding using the shrinkage volume approach. J. Mater. Process. Technol. 1999, 92, 405–409. [Google Scholar] [CrossRef]
- Pilipenko, A. Computer Simulation of Residual Stress and Distortion of Thick Plates in Multielectrode Submerged Arc Welding: Their Mitigation Techniques. Ph.D. Thesis, Department of Machine Design and Materials Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2001. [Google Scholar]
- Zhang, H.; Zhang, G.; Cai, C.; Gao, H.; Wu, L. Fundamental studies on in process controlling angular distortion in asymmetrical double-sided double arc welding. J. Mater. Process. Technol. 2008, 205, 214–223. [Google Scholar] [CrossRef]
- Aarbogh, H.M.; Hamide, M.; Fjaer, H.G.; Mo, A.; Bellet, M. Experimental validation of finite element codes for welding deformations. J. Mater. Process. Technol. 2010, 210, 1681–1689. [Google Scholar] [CrossRef]
- Chao, Y.J.; Zhu, X.; Qi, X. WELDSIM-A Welding simulation Code for the Determination of Transient and Residual Temperature, Stress, and Distortion. Adv. Comput. Eng. Sci. 2000, 2, 1207–1211. [Google Scholar]
- Tian, L.; Luo, Y.; Yang, W.; Wu, X. Prediction of transverse and angular distortions of gas tungsten arc bead-on plate welding using artificial neural network. Mater. Des. 2013, 54, 458–472. [Google Scholar] [CrossRef]
- Perić, M.; Tonković, Z.; Garašić, I.; Vuherer, T. An engineering approach for a T-joint fillet welding simulation using simplified material properties. Ocean Eng. 2016, 128, 13–21. [Google Scholar] [CrossRef]
- Lostado, R.; Escribano, R.; Martínez, M.Á.; Múgica, R. Improvement in the Design of Welded Joints of EN 235JR Low Carbon Steel by Multiple Response Surface Methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- Lostado, R.; Fernandez, R.; Mac Donald, B.J.; Villanueva, P.M. Combining soft computing techniques and the finite element method to design and optimize complex welded products. Integr. Comput.-Aid. Eng. 2015, 22, 153–170. [Google Scholar]
- Lostado, R.; Roldán, P.V.; Fernandez, R.; Mac Donald, B.J. Design and optimization of an electromagnetic servo braking system combining finite element analysis and weight-based multi-objective genetic algorithms. J. Mech. Sci. Technol. 2016, 30, 3591–3605. [Google Scholar] [CrossRef]
- Gentils, T.; Wang, L.; Kolios, A. Integrated structural optimisation of offshore wind turbine support structures based on finite element analysis and genetic algorithm. Appl. Energy 2017, 199, 187–204. [Google Scholar] [CrossRef]
- Duan, L.; Xiao, N.C.; Li, G.; Cheng, A.; Chen, T. Design optimization of tailor-rolled blank thin-walled structures based on-support vector regression technique and genetic algorithm. Eng. Optim. 2017, 49, 1148–1165. [Google Scholar] [CrossRef]
- Bag, S.; De, A. Development of a three-dimensional heat transfer model for the gas tungsten arc welding process using the finite element method coupled with a genetic algorithm based identification of uncertain input parameters. Metall. Mater. Trans. A 2008, 39, 2698–2710. [Google Scholar] [CrossRef]
- Voutchkov, I.; Keane, A.J.; Bhaskar, A.; Olsen, T.M. Weld sequence optimization: The use of surrogate models for solving sequential combinatorial problems. Comput. Method. Appl. Mech. Eng. 2005, 194, 3535–3551. [Google Scholar] [CrossRef]
- Xie, L.S.; Hsieh, C. Clamping and welding sequence optimisation for minimising cycle time and assembly deformation. Int. J. Mater. Prod. Technol. 2002, 17, 389–399. [Google Scholar] [CrossRef]
- Michalewicz, Z. GAs: What Are They? In Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin, Heidelberg, Germany, 1994. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. Genetic algorithms for multiobjective optimization: Formulation discussion and generalization. In Proceedings of the 5th International Conference on Genetic Algorithms (ICGA’ 93), Urbana-Champaign, IL, USA, 17–21 July 1993; pp. 416–423. [Google Scholar]
- Minnick, H.M. Gas Metal Arc Welding Handbook Textbook, 1st ed.; Goodheart–Willcox: Tinley Park, IL, USA, 2007. [Google Scholar]
- Murray, P.E. Selecting parameters for GMAW using dimensional analysis. Weld. J. 2002, 81, 125–131. [Google Scholar]
- Grong, O. Metallurgical Modelling of Welding. Institute of Materials, 1st ed.; Carlton House Terrace: London, UK, 1997. [Google Scholar]
- Bzymek, A.; Czuprýnski, A.; Fidali, M.; Jamrozik, W.; Timofiejczuk, A. Analysis of images recorded during welding processes. In Proceedings of the 9th International Conference on Quantitative InfraRed Thermography, Krakow, Poland, 2–5 July 2018. [Google Scholar]
- Tonkovic´, Z.; Peric´, M.; Surjak, M.; Garašic´, I.; Boras, I.; Rodic´, A.; Švaic´, S. Numerical and experimental modeling of a T-joint fillet welding process. In Proceedings of the 11th International Conference on Quantitative InfraRed Thermography, Naples, Italy, 11–14 June 2012. [Google Scholar]
- Perić, M.; Tonković, Z.; Rodić, A.; Surjak, M.; Garašić, I.; Boras, I.; Švaić, S. Numerical analysis and experimental investigation of welding residual stresses and distortions in a T-joint fillet weld. Mater. Des. 2014, 53, 1052–1063. [Google Scholar] [CrossRef]
- ISO 17636-1:2013 Non-Destructive Testing of Welds–Radiographic Testing—Part 1: X- and Gamma-Ray Techniques with Film. Available online: https://www.iso.org/standard/52981.html (accessed on 9 January 2018).
- ASTM E407-07. Standard Practice for Microetching Metals and Alloys. Available online: https://zh.scribd.com/document/259609551/ASTM-E407-07-StandardPractice-for-Microetching-Metals-and-Alloys (accessed on 9 January 2018).
- ASTM E92-16. Standard Test Methods for Vickers Hardness and Knoop Hardness of Metallic Materials. Available online: http://www.astm.org/Standards/E92 (accessed on 9 January 2018).
- Barsoum, Z. Residual stress prediction and relaxation in welded tubular joint. Weld. World 2007, 51, 23–30. [Google Scholar] [CrossRef]
- Friedman, E. Thermomechanical analysis of the welding process using the finite element method. J. Press. Vessel Technol. 1975, 97, 206–213. [Google Scholar] [CrossRef]
- Friedman, E. Numerical simulation of the gas tungsten-arc welding process. In Proceedings of the Numerical Modeling of Manufacturing Processes, ASME Winter Annual Meeting, Atlanta, GA, USA, 27 November–2 December 1977. [Google Scholar]
- Lindgren, L.E. Computational Welding Mechanics: Thermomechanical and Microstructural Simulations, 1st ed.; Woodhead Publishing: Cambridge, UK, 2007. [Google Scholar]
- Benzley, S.E.; Perry, E.; Merkley, K.; Clark, B.; Sjaardama, G. A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In Proceedings of the 4th International Meshing Roundtable, Sandia National Laboratories, Albuquerque, NM, USA, 16–17 October 1995. [Google Scholar]
- Cifuentes, A.O.; Kalbag, A. A performance study of tetrahedral and hexahedral elements in 3-D finite element structural analysis. Finite Elem. Anal. Des. 1992, 12, 313–318. [Google Scholar] [CrossRef]
- MSC Mentat Marc. MSC. MARC User Guide; Version 2010; MSC. Software Corporation: Santa Ana, CA, USA, 2010. [Google Scholar]
- Armentani, E.; Esposito, R.; Sepe, R. Finite element analysis of residual stresses on butt welded joints. In Proceedings of the 8th Biennial ASME Conference on Engineering Systems Design and Analysis, ESDA2006, Torino, Italy, 4–7 July 2006. [Google Scholar]
- Armentani, E.; Esposito, R.; Sepe, R. The influence of thermal properties and preheating on residual stresses in welding. Int. J. Comput. Mater. Sci. Surf. Eng. 2007, 1, 146–162. [Google Scholar] [CrossRef]
- Lostado, R.; García, R.E.; Martinez, R.F. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2016, 12, 353–373. [Google Scholar] [CrossRef]
- Hall, M.A.; Holmes, G. Benchmarking Attribute Selection Techniques for Discrete Class Data Mining. IEEE Trans. Knowl. Data Eng. 2003, 15, 1437–1447. [Google Scholar] [CrossRef]
- Hall, M. Correlation-Based Feature Selection for Discrete and Numeric Class Machine Learning; Working Paper 00/08; University of Waikato: Hamilton, New Zealand, 2000. [Google Scholar]
- R Development Core Team. R Language and Environment for Statistical Computing; R Foundation for Statistical Com-Putting; R Development Core Team: Vienna, Austria, 2011; ISBN 3-900051-07-0. Available online: https://www.r-project.org/ (accessed on 9 January 2018).

| Inputs | Specimen 1 | Specimen 2 | Specimen 3 |
|---|---|---|---|
| Current (amps) | 140.0 | 210.0 | 260.0 |
| Voltage (volts) | 26.0 | 28.0 | 35.0 |
| Speed (mm/s) | 6.0 | 6.0 | 6.0 |
| Heat Flux (KJ/mm) | 0.424 | 0.686 | 1.061 |
| Inputs | Specimen 1 | Specimen 2 | Specimen 3 |
|---|---|---|---|
| Height (mm) | 1.3 | 1.5 | 2.5 |
| Width (mm) | 9.5 | 8.7 | 12.0 |
| Angular Distortion (°) | 4.64 | 4.723 | 4.934 |
| Range of | Melt Point | Contact P_init | Contact P_center | Contact P_end | Contact P1_P2 | Contact P_G | Face_Film |
| Parameters | (°C) | (N/s·°K) | (N/s·°K) | (N/s·°K) | (N/s·°K) | (N/s·°K) | (N/s·°K·mm) |
| Min. | 1420 | 1 | 1 | 1 | 1 | 1 | 0.00001 |
| Max. | 1440 | 300 | 700 | 300 | 200 | 200 | 0.00100 |
| Step | 1 | 1 | 1 | 1 | 1 | 1 | 0.00001 |
| Range of | Face_film2 | Face_film3 | Forward Length | Rear Length | Width | Depth | - |
| Parameters | (N/s·°K·mm) | (N/s·°K·mm) | (mm) | (mm) | (mm) | (mm) | - |
| Min. | 0.00001 | 0.00001 | 1.0 | 5.0 | 23.0 | 4.0 | - |
| Max. | 0.00100 | 0.00100 | 2.0 | 10.0 | 26.0 | 6.0 | - |
| Step | 0.00001 | 0.00001 | 0.1 | 0.1 | 0.1 | 0.1 | - |
| Inputs | First FE Model | Second FE Model | Third FE Model |
|---|---|---|---|
| melt_point | - | - | - |
| contac_p_in. | - | - | - |
| contac_p_midle | X | - | - |
| contac_p_End | - | - | X |
| contact_p1_p2 | - | - | - |
| contact_p2_Ground | - | - | - |
| face_film | - | - | - |
| face_film2 | - | - | - |
| face_film3 | - | - | - |
| forward_lenght | - | - | X |
| rear_lenght | X | X | X |
| width | - | - | - |
| depth | - | - | - |
| Ways to Adjust | FE | Gen. | Melt | Contact | Contact | Contact | Contact | Contact | Face | Face | Face | Forward | Rear | Width | Depth | JTotal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weld | - | Point | P_init | P_center | P_end | P1_P2 | P_G | Film | Film_2 | Film_3 | Length | Length | - | - | - | |
| - | - | (°C) | (N/(s·K)) | (N/(s·K)) | (N/(s·K)) | (N/(s·K)) | (N/(s·K)) | (N/(s·°K·mm)) | (N/(s·°K·mm)) | (N/(s·°K·mm)) | (mm) | (mm) | (mm) | (mm) | - | |
| CFS algorithm | 1 | 01 | 1430 | 150.5 | 2 | 150.5 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.5 | 9.7 | 24.5 | 5.0 | 3.6652 |
| 05 | 1430 | 150.5 | 13 | 150.5 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.5 | 5.3 | 24.5 | 5.0 | 2.3416 | ||
| 2 | 01 | 1430 | 150.5 | 350.5 | 150.5 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.5 | 6.7 | 24.5 | 5.0 | 3.1879 | |
| 05 | 1430 | 150.5 | 350.5 | 150.5 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.5 | 6.5 | 24.5 | 5.0 | 3.1654 | ||
| 3 | 01 | 1430 | 150.5 | 350.5 | 163 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.3 | 6 | 24.5 | 5.0 | 6.7602 | |
| 05 | 1430 | 150.5 | 350.5 | 174 | 100.5 | 100.5 | 0.000505 | 0.000505 | 0.000505 | 1.7 | 5.2 | 24.5 | 5.0 | 6.4968 | ||
| 13 parameters | 1 | 01 | 1431 | 102 | 2 | 219 | 193.0 | 62.0 | 0.00051 | 0.00047 | 0.00051 | 1.4 | 7.8 | 24.8 | 4.3 | 4.3917 |
| 03 | 1427 | 17 | 10 | 19 | 193.0 | 66.0 | 0.00052 | 0.00039 | 0.00041 | 1.0 | 7.8 | 24.9 | 4.3 | 2.2680 | ||
| 2 | 01 | 1423 | 164 | 107 | 130 | 115.0 | 118.0 | 0.00055 | 0.00004 | 0.00011 | 1.4 | 7.5 | 26 | 5.1 | 3.1938 | |
| 03 | 1425 | 257 | 65 | 189 | 195.0 | 176.0 | 0.00071 | 0.00039 | 0.00033 | 1.8 | 7.4 | 23.8 | 4.3 | 3.0838 | ||
| 3 | 01 | 1429 | 162 | 582 | 198 | 127.0 | 83.0 | 0.00095 | 0.0008 | 0.0007 | 1.6 | 5.4 | 25.3 | 4.6 | 6.5161 | |
| 03 | 1429 | 203 | 662 | 247 | 159.0 | 182.0 | 0.00093 | 0.0008 | 0.00068 | 1.6 | 5.2 | 23.1 | 5.4 | 6.4918 |
| Specimen | FEM (°) | Experimental (°) | Error (%) |
|---|---|---|---|
| 1 | 4.73 | 4.64 | 4.11 |
| 2 | 4.92 | 4.723 | 4.17 |
| 3 | 5.21 | 4.934 | 5.59 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lostado Lorza, R.; Escribano García, R.; Fernandez Martinez, R.; Martínez Calvo, M.Á. Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints. Metals 2018, 8, 230. https://doi.org/10.3390/met8040230
Lostado Lorza R, Escribano García R, Fernandez Martinez R, Martínez Calvo MÁ. Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints. Metals. 2018; 8(4):230. https://doi.org/10.3390/met8040230
Chicago/Turabian StyleLostado Lorza, Rubén, Rubén Escribano García, Roberto Fernandez Martinez, and María Ángeles Martínez Calvo. 2018. "Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints" Metals 8, no. 4: 230. https://doi.org/10.3390/met8040230
APA StyleLostado Lorza, R., Escribano García, R., Fernandez Martinez, R., & Martínez Calvo, M. Á. (2018). Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints. Metals, 8(4), 230. https://doi.org/10.3390/met8040230