The Formation and Evolution of Shear Bands in Plane Strain Compressed Nickel-Base Superalloy
Abstract
1. Introduction
2. Experimental Procedures
3. Results and Discussion
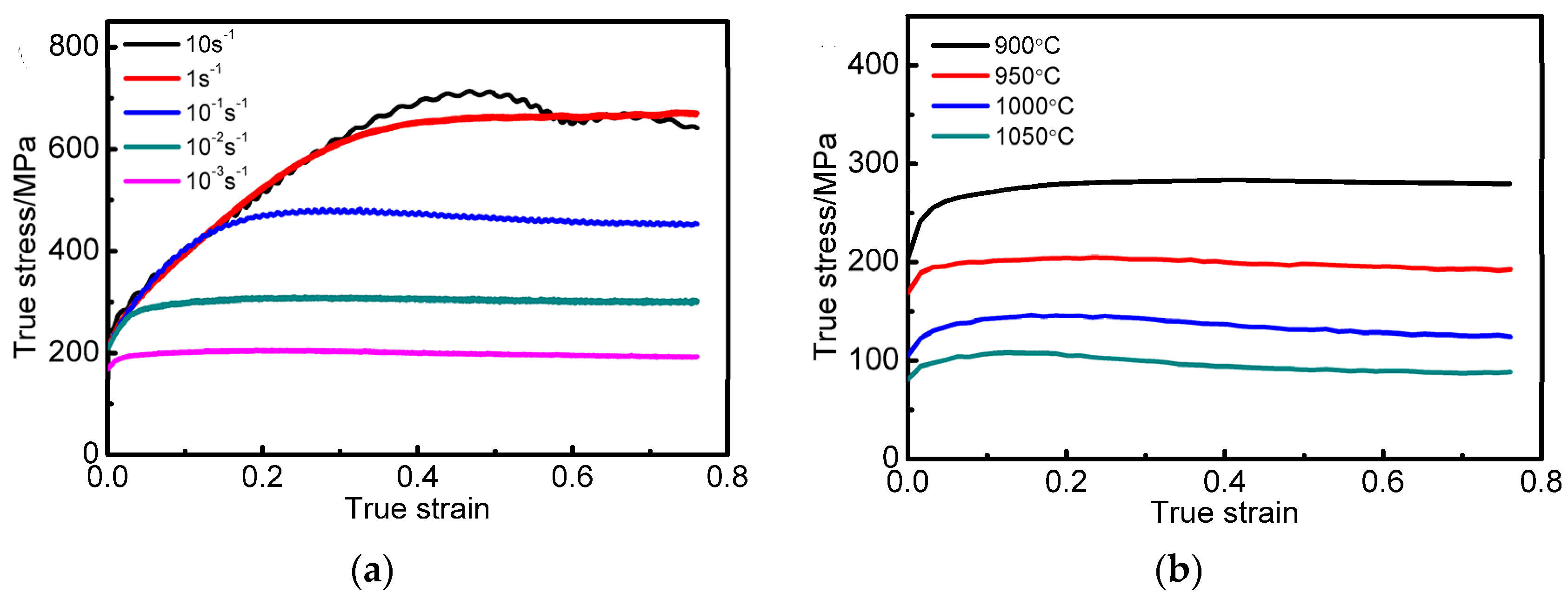
3.1. Flow Behavior
3.2. Characterization of Shear Bands
3.3. Initiation of Shear Bands
3.4. Evolution of Shear Bands
- (i)
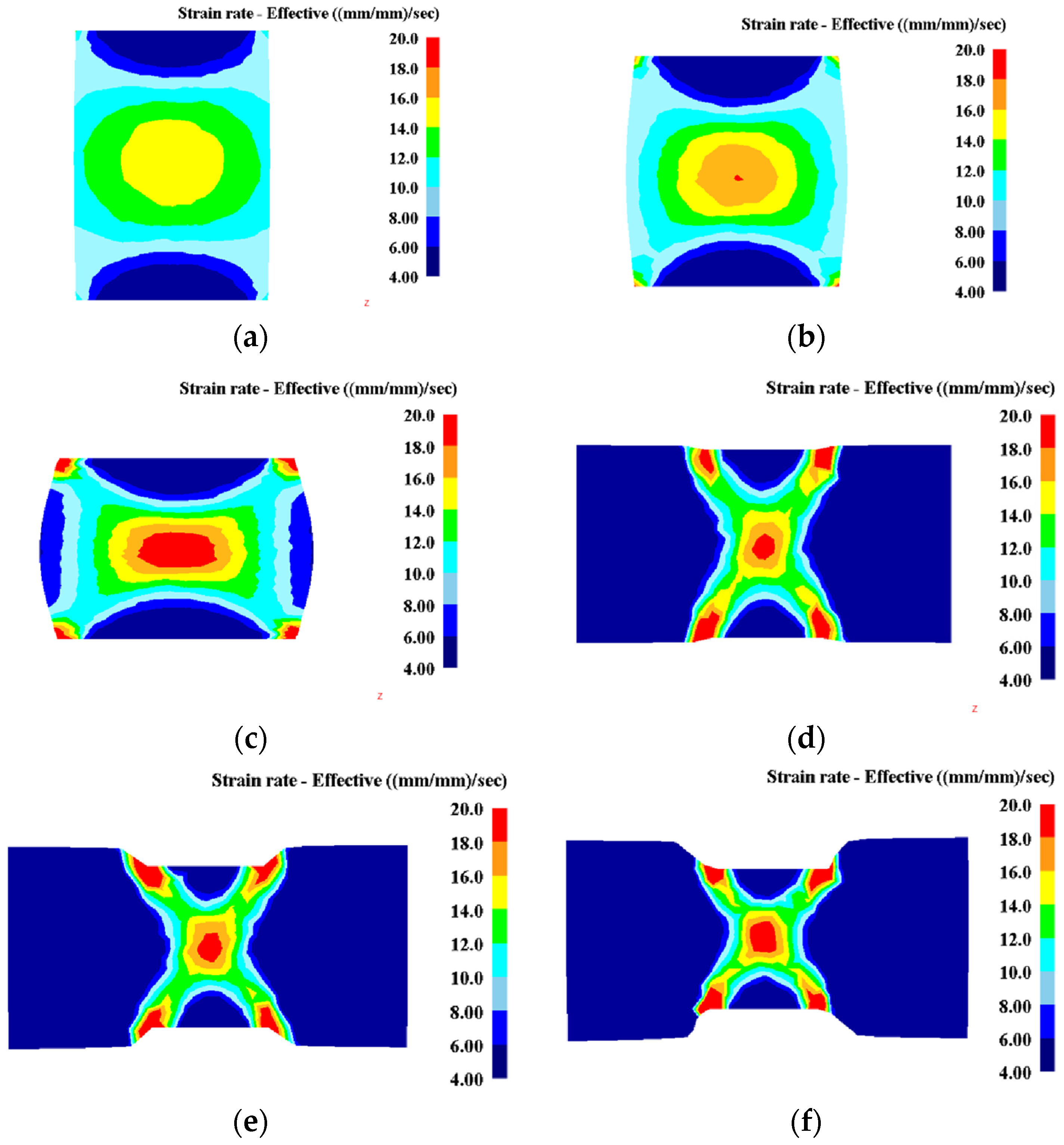
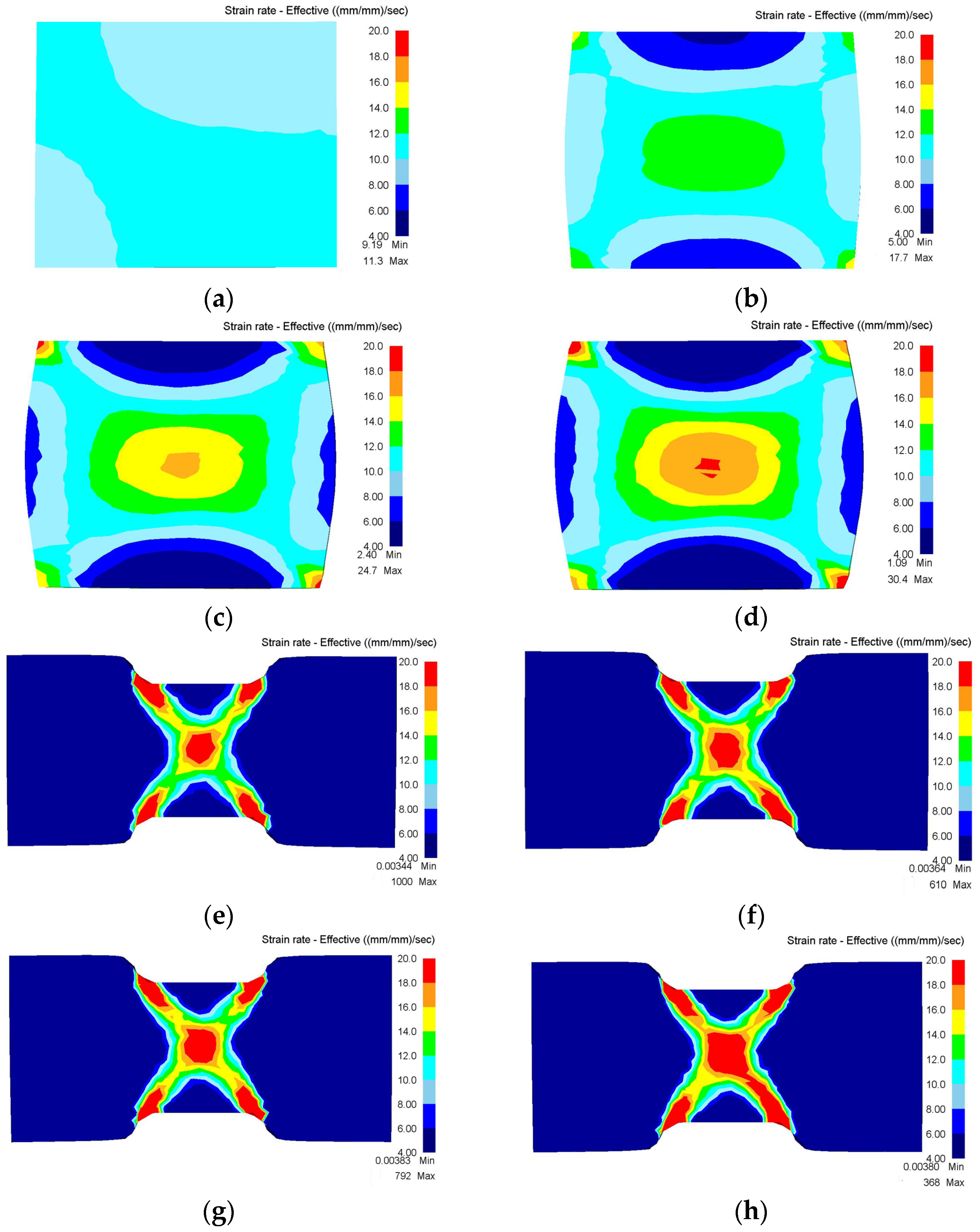
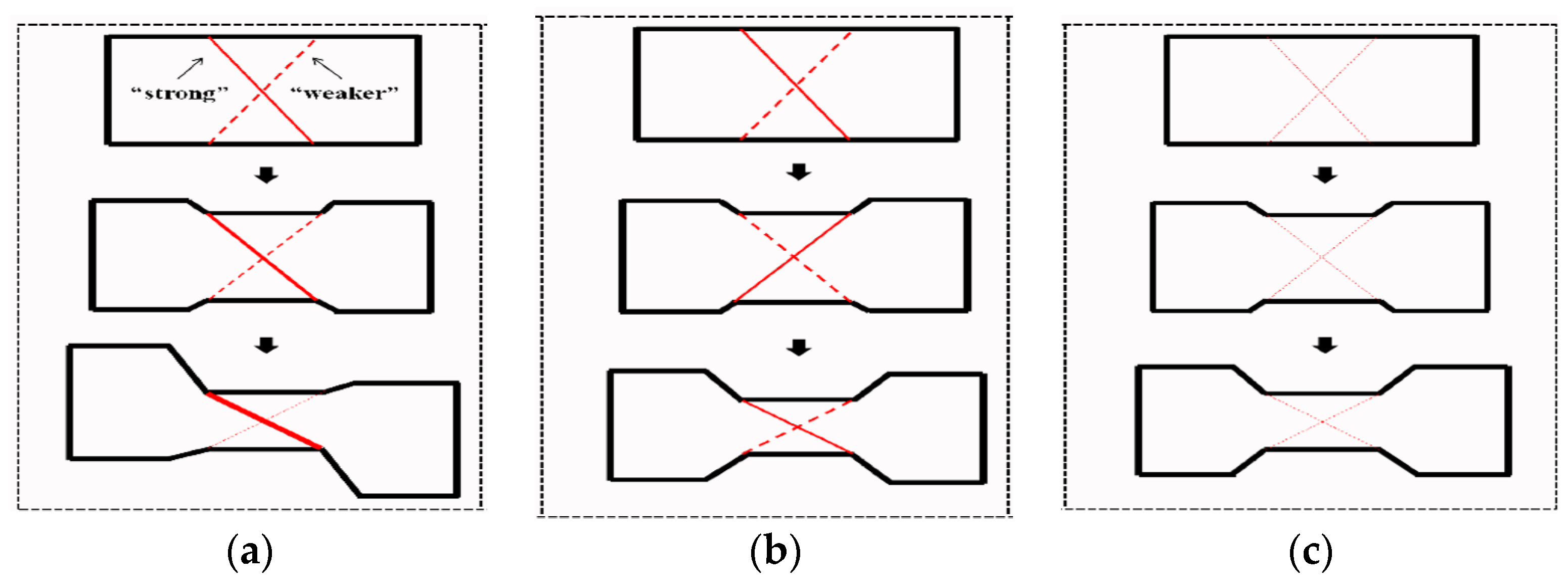
- In the case of high strain rate and low temperature, one of the two branches becomes stronger, weakening the second branch. It is due to the difference of deformation-induced heating (as shown in Figure 7a) and the nonuniform of instantaneous friction. With further compression, the interaction of adiabatic heating and strain, together with the increasing of interfacial friction, promotes the propagation of the stronger branch. Since the occurrence of shear bands are associated with material elements, their directions will rotate away from the compression axis once they initiated from the deformed region. Thus, the initial shear angle will increase, and leads to the formation of an asymmetrical specimen (Figure 3a and Figure 7a) finally.
- (ii)
- In the case of intermediate deformation, the deformation-induced heating can be neglected due to the much lower strain rates, and thus it is no longer the key factor to determine the evolution of shear bands. Therefore, the interfacial friction (f) and inherent material property, i.e., the positive strain rate sensitivity (m), are expected to control the formation of shear bands.
- (iii)
- In the case of high temperature and low strain rate, no shear bands can be found macroscopically. Even if unstable flow occurs, the “strengthening–relaxation” effect mentioned above can suppress the development of inhomogeneous deformation owing to the higher m values. Thus, homogenous microstructure can be obtained throughout the entire deformed region, as illustrated in Figure 7c.
4. Conclusions
- (1)
- The shape of shear bands under different deformation conditions can be divided into two categories: “S” shape for severe conditions, “X” shape for intermediate conditions.
- (2)
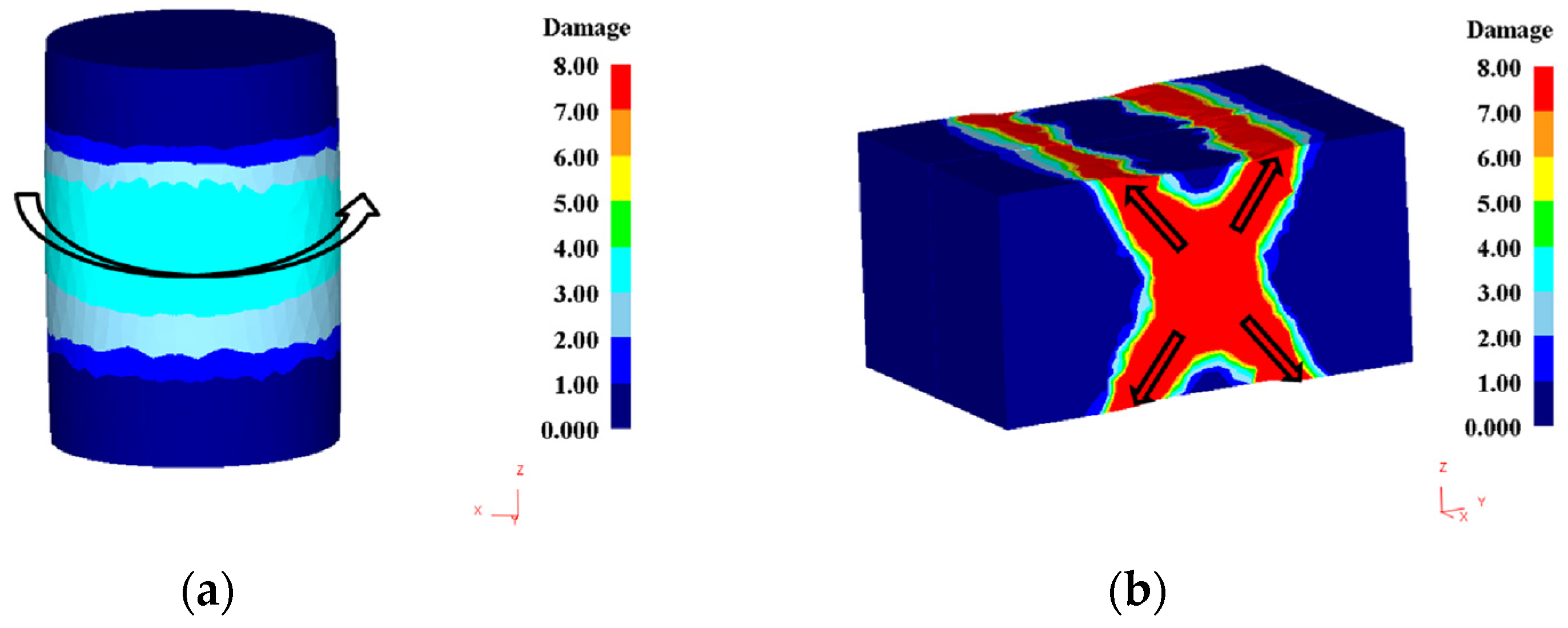
- The shear bands produced at plane strain compression propagates more rapidly than those under uniaxial compression tests. FEM simulation results of plane strain compression suggest that the shear bands are promoted by the secondary tensile stress located at the X-shape region in the specimen.
- (3)
- The morphology evolution of shear bands is determined by deformation conditions and interfacial friction. Compression at severe conditions yields “S” type shear bands due to the synergic effect of adiabatic heating, deforming and distributing of instantaneous friction. Because of the alternative “strengthening-relaxation” effect, intermediate conditions result in “X” type shear bands. A homogenous microstructure can be obtained throughout the entire deformed region if the metal flow is stable enough.
- (4)
- Due to the complex stress states and severe deformation conditions, shear bands are easy to appear during the plane strain compression process. Therefore, the influence of shear bands on strain–stress curves must be considered when the plane strain compression is applied for testing the high temperature compression properties.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qu, F.S.; Liu, X.G.; Xing, F.; Zhang, K.F. High temperature tensile properties of laser butt-welded plate of IN718 superalloy with ultra-fine grains. Trans. Nonferrous Met. Soc. China 2012, 22, 2379–2388. [Google Scholar] [CrossRef]
- Oblak, J.M.; Pauionis, D.F.; Duvall, D.S. Cohenency strengthening in Ni-base alloys hardened by DO22 precipitates. Metall. Trans. A 1974, 5, 143–153. [Google Scholar]
- Wang, M.J.; Wang, W.R.; Liu, Z.L.; Sun, C.Y.; Qian, L.Y. Hot workability integrating processing and activation energy maps of Inconel 740 superalloy. Mater. Today Commun. 2018, 14, 188–198. [Google Scholar] [CrossRef]
- Kar, S.K.; Sondhi, S.K. Microstructure based and temperature dependent model of flow behavior of a polycrystalline nickel based superalloy. Mater. Sci. Eng. A 2014, 601, 97–105. [Google Scholar] [CrossRef]
- Koeller, R.C.; Raj, R. Diffusional relaxation of stress concentration at second phase particles. Acta Metall. 1978, 26, 1551–1558. [Google Scholar] [CrossRef]
- Rogers, H.C. Adiabatic plastic deformation. Ann. Rev. Mater. Sci. 1979, 9, 283–311. [Google Scholar] [CrossRef]
- Etaati, A.; Dehghani, K. A study on hot deformation behavior of Ni-42.5Ti-7.5Cu alloy. Mater. Chem. Phys. 2013, 140, 208–215. [Google Scholar] [CrossRef]
- Poliakt, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Semiatin, S.L.; Lahoti, G.D. Deformation and unstable flow in hot forging of Ti-6Ai-2Sn-4Zr-2Mo-0.1Si. Metall. Trans. A 1981, 12, 1705–1717. [Google Scholar] [CrossRef]
- Cheng, L.; Chang, H.; Tang, B.; Kou, H.C.; Li, J.S. Deformation and dynamic recrystallization behavior of a high Nb containing TiAl alloy. J. Alloys Compd. 2013, 552, 363–369. [Google Scholar] [CrossRef]
- Dehghan, H.; Abbasi, S.M.; Momeni, A.; Taheri, A.K. On the constitutive modeling and microstructural evolution of hot compressed A286 iron-base superalloy. J. Alloys Compd. 2013, 564, 13–19. [Google Scholar] [CrossRef]
- Cheng, L.; Xue, X.Y.; Tang, B.; Kou, H.C.; Li, J.S. Flow characteristics and constitutive modeling for elevated temperature deformation of a high Nb containing TiAl alloy. Intermetallics 2014, 49, 23–28. [Google Scholar] [CrossRef]
- Cheng, L.; Chang, H.; Tang, B.; Kou, H.C.; Li, J.S. Characteristics of metadynamic recrystallization of a high Nb containing TiAl alloy. Mater. Lett. 2013, 92, 430–432. [Google Scholar] [CrossRef]
- Patil, S.P.; Prajapati, K.G.; Jenkouk, V.; Olivier, H.; Markert, B. Experimental and numerical studies of sheet metal forming with damage using gas detonation process. Metals 2017, 7, 556. [Google Scholar] [CrossRef]
- Na, Y.S.; Yeom, J.T.; Park, N.K.; Lee, J.Y. Simulation of microstructures for alloy 718 blade forging using 3D FEM simulator. J. Mater. Process. Technol. 2003, 141, 337–342. [Google Scholar] [CrossRef]
- Cheng, L.; Xue, X.Y.; Tang, B.; Liu, D.G.; Li, J.Z.; Kou, H.C.; Li, J.S. Deformation behavior of hot-rolled IN718 superalloy under plane strain compression at elevated temperature. Mater. Sci. Eng. A 2014, 606, 24–30. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, S.H.; Cheng, M.; Song, H.W. Dynamic recrystallization mechanism of Inconel 690 superalloy during hot deformation at high strain rate. J. Mater. Eng. Perform. 2013, 22, 2382–2388. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.Z.; Zhen, L.; Yang, L.; Zhang, X.M. Flow behavior and microstructures of superalloy 718 during high temperature deformation. Mater. Sci. Eng. A 2008, 497, 479–486. [Google Scholar] [CrossRef]
- Jia, N.; Eisenlohr, P.; Roters, F.; Raabe, D.; Zhao, X. Orientation dependence of shear banding in face-centered-cubic single crystals. Acta Mater. 2012, 60, 3415–3434. [Google Scholar] [CrossRef]
- Semiatin, S.L.; Lahoti, G.D. The occurrence of shear bands in isothermal, hot forging. Metall. Trans. A 1982, 13, 275–288. [Google Scholar] [CrossRef]
- Tang, X.F.; Wang, B.Y.; Huo, Y.M.; Ma, W.Y.; Zhou, J.; Ji, H.C.; Fu, X.B. Unified modeling of flow behavior and microstructure evolution in hot forming of a Ni-based superalloy. Mater. Sci. Eng. A 2016, 662, 54–64. [Google Scholar] [CrossRef]
- Domanti, A.T.J.; Horrobin, D.J.; Bridgwater, J. An investigation of fracture criteria for predicting surface fracture in paste extrusion. Int. J. Mech. Sci. 2002, 44, 1381–1410. [Google Scholar] [CrossRef]
- Cockroft, M.G.; Latham, D.J. Ductility and the Workability of Metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Shahriari, D.; Sadeghi, M.H.; Ebrahimi, G.R.; Kim, K.T. Effects of lubricant and temperature on friction coefficient during hot forging of Nimonic 115 superalloy. Kovove Mater. 2011, 49, 375–383. [Google Scholar] [CrossRef]
- Rudkins, N.T.; Hartley, P.; Pillinger, I.; Petty, D. Friction modelling and experimental observations in hot ring compression tests. J. Mater. Process. Technol. 1996, 60, 349–353. [Google Scholar] [CrossRef]
- Li, Y.P.; Onodera, E.; Chiba, A. Friction coefficient in hot compression of cylindrical sample. Mater. Trans. 2010, 51, 1210–1215. [Google Scholar] [CrossRef]


| Element | Ni | Cr | Nb | Mo | Ti | Al | Co. | Si | Mn | Ta | Cu | C | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wt. % | 53.02 | 18.50 | 5.34 | 3.26 | 1.04 | 0.52 | 0.12 | 0.08 | 0.054 | 0.050 | 0.048 | 0.029 | Bal. |
| 10 s−1 | 1 s−1 | 0.1 s−1 | 0.01 s−1 | 0.001 s−1 | |
|---|---|---|---|---|---|
| 900 °C | S | S | X | X | X |
| 950 °C | S | S | X | X | X |
| 1000 °C | S | X | X | X | X |
| 1050 °C | S | X | X | X | O |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Xiang, L.; Cheng, L.; Liu, D.; Kou, H.; Li, J. The Formation and Evolution of Shear Bands in Plane Strain Compressed Nickel-Base Superalloy. Metals 2018, 8, 141. https://doi.org/10.3390/met8020141
Tang B, Xiang L, Cheng L, Liu D, Kou H, Li J. The Formation and Evolution of Shear Bands in Plane Strain Compressed Nickel-Base Superalloy. Metals. 2018; 8(2):141. https://doi.org/10.3390/met8020141
Chicago/Turabian StyleTang, Bin, Lin Xiang, Liang Cheng, Degui Liu, Hongchao Kou, and Jinshan Li. 2018. "The Formation and Evolution of Shear Bands in Plane Strain Compressed Nickel-Base Superalloy" Metals 8, no. 2: 141. https://doi.org/10.3390/met8020141
APA StyleTang, B., Xiang, L., Cheng, L., Liu, D., Kou, H., & Li, J. (2018). The Formation and Evolution of Shear Bands in Plane Strain Compressed Nickel-Base Superalloy. Metals, 8(2), 141. https://doi.org/10.3390/met8020141






