Finite Element Simulation of the Presta Joining Process for Assembled Camshafts: Application to Aluminum Shafts
Abstract
:1. Introduction
2. Materials and Methods
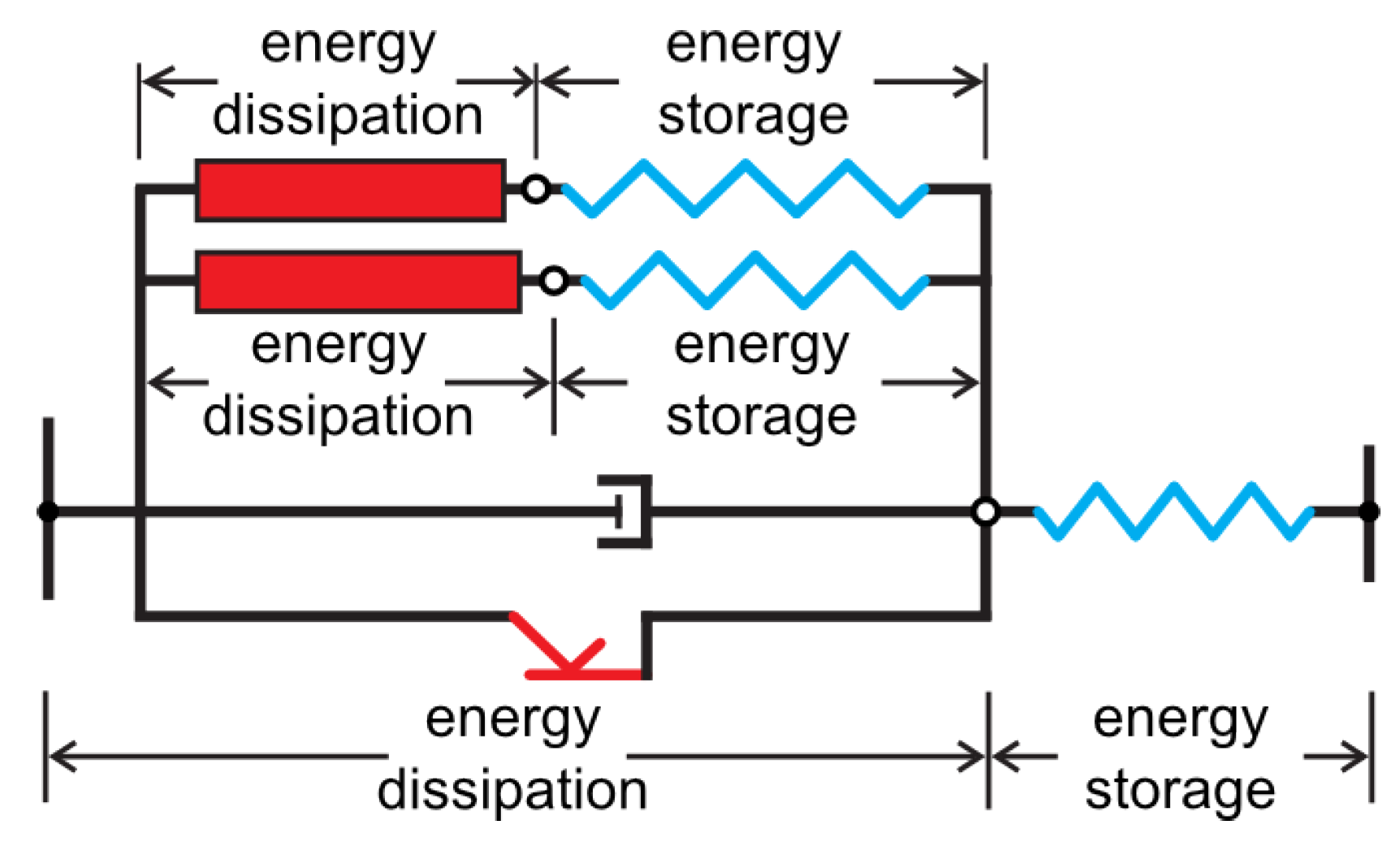
2.1. Material Modeling
2.2. Experimental Methods
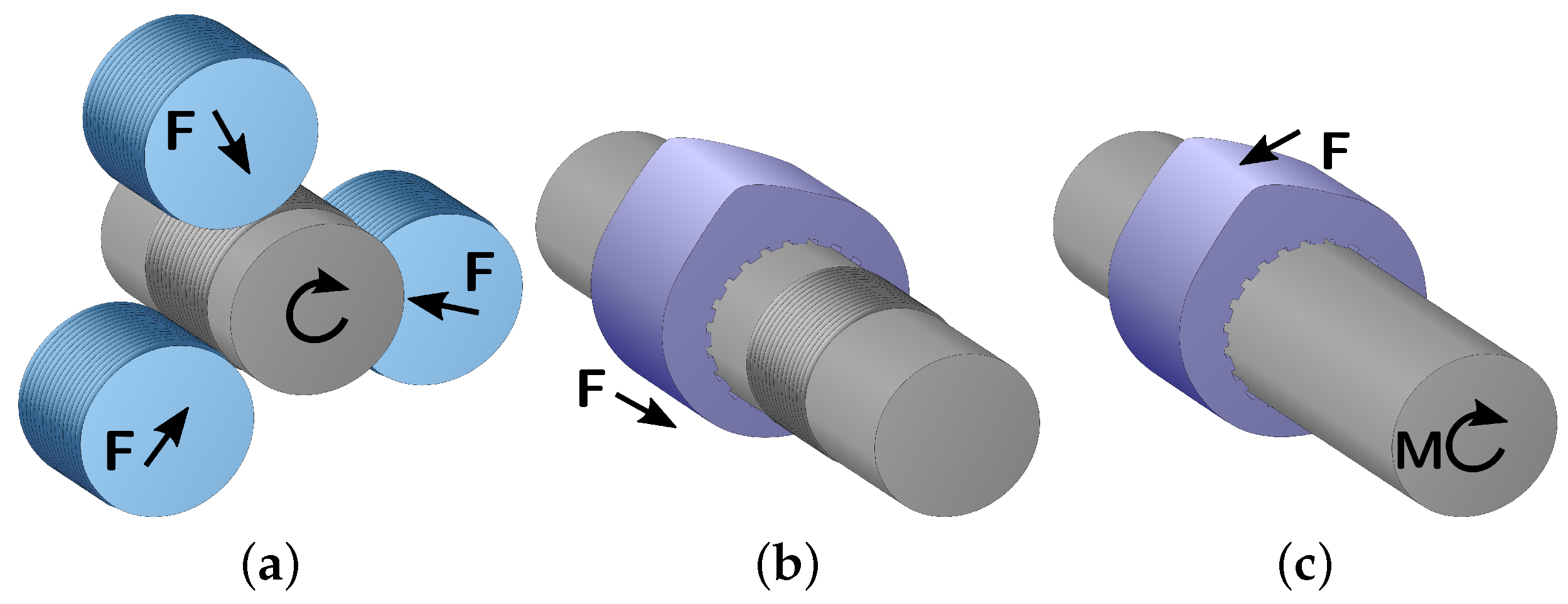
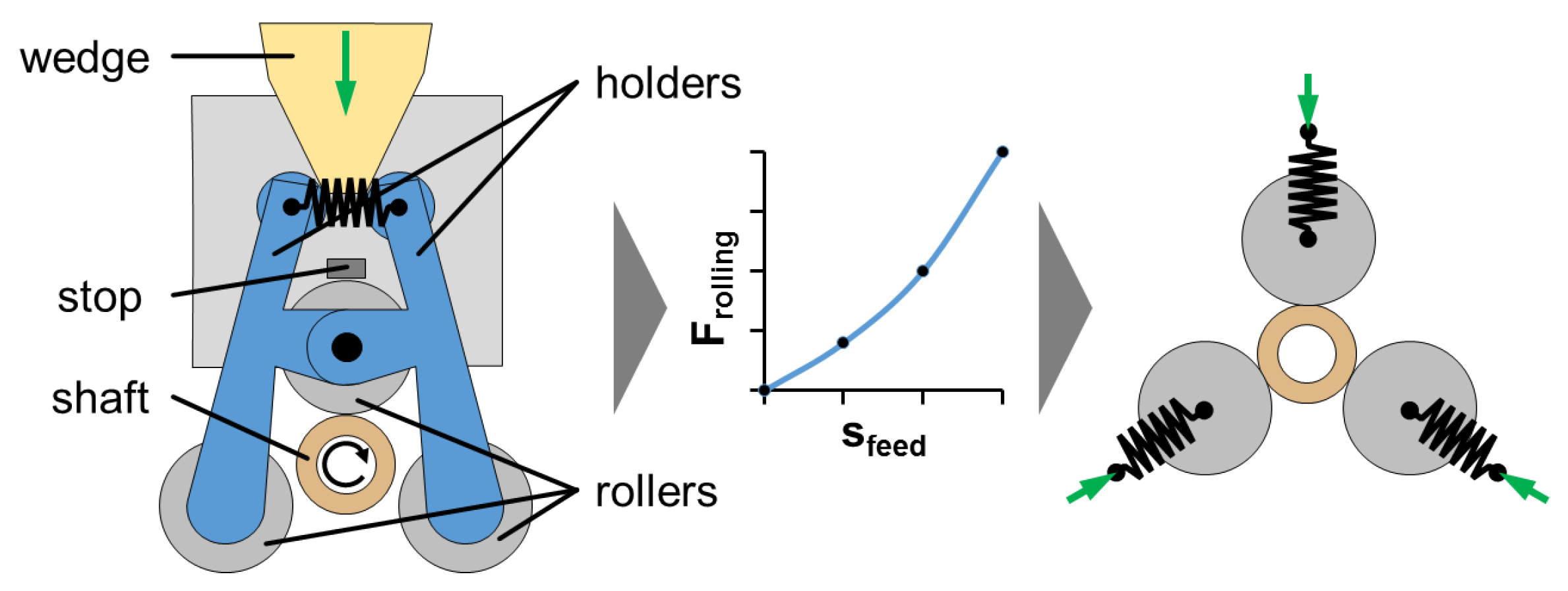
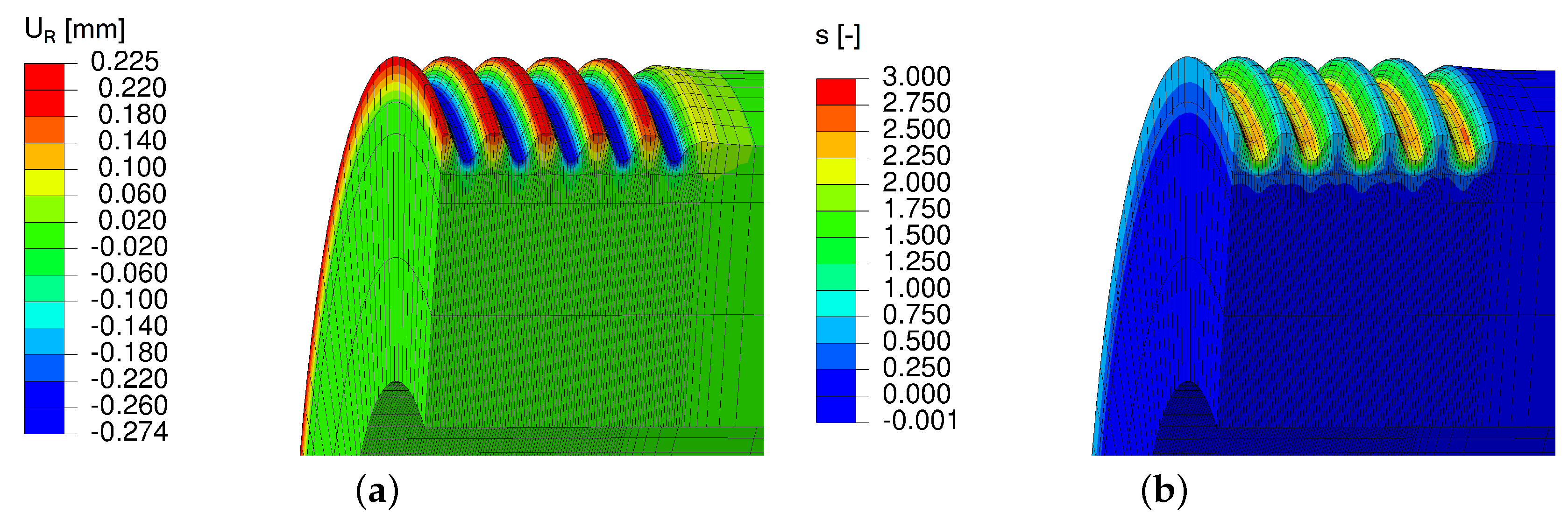
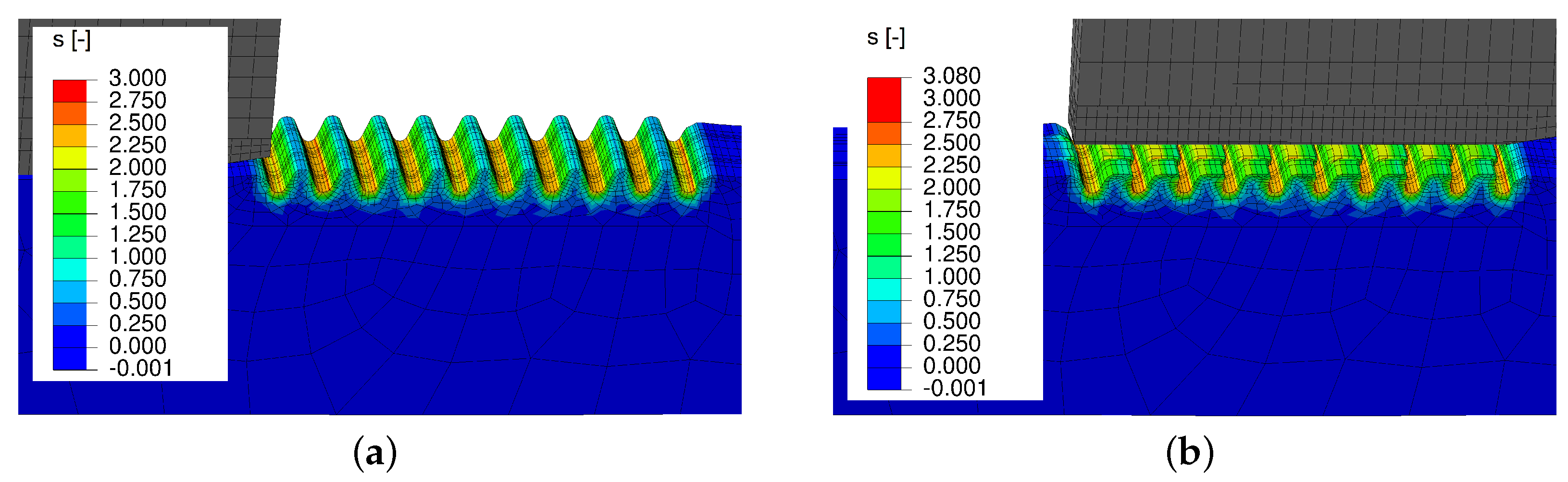
2.3. Rolling of the Shaft
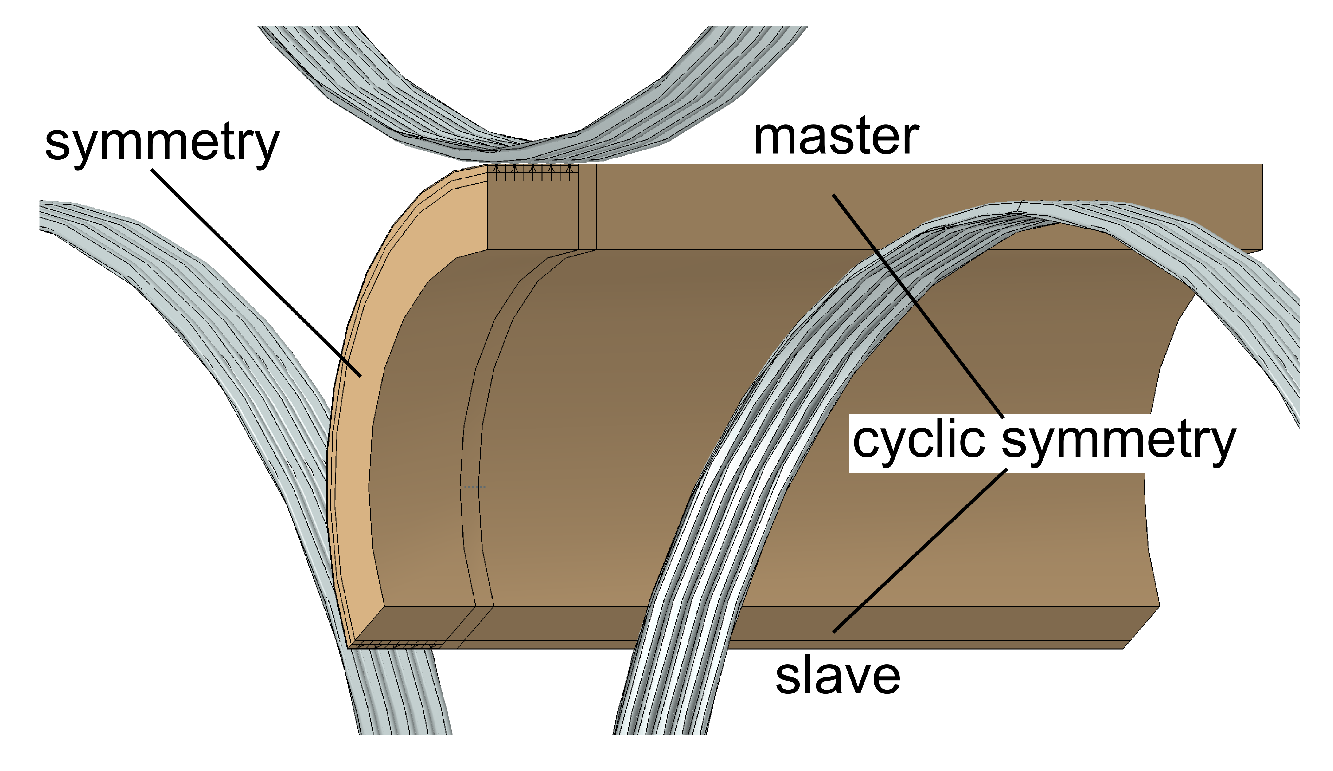
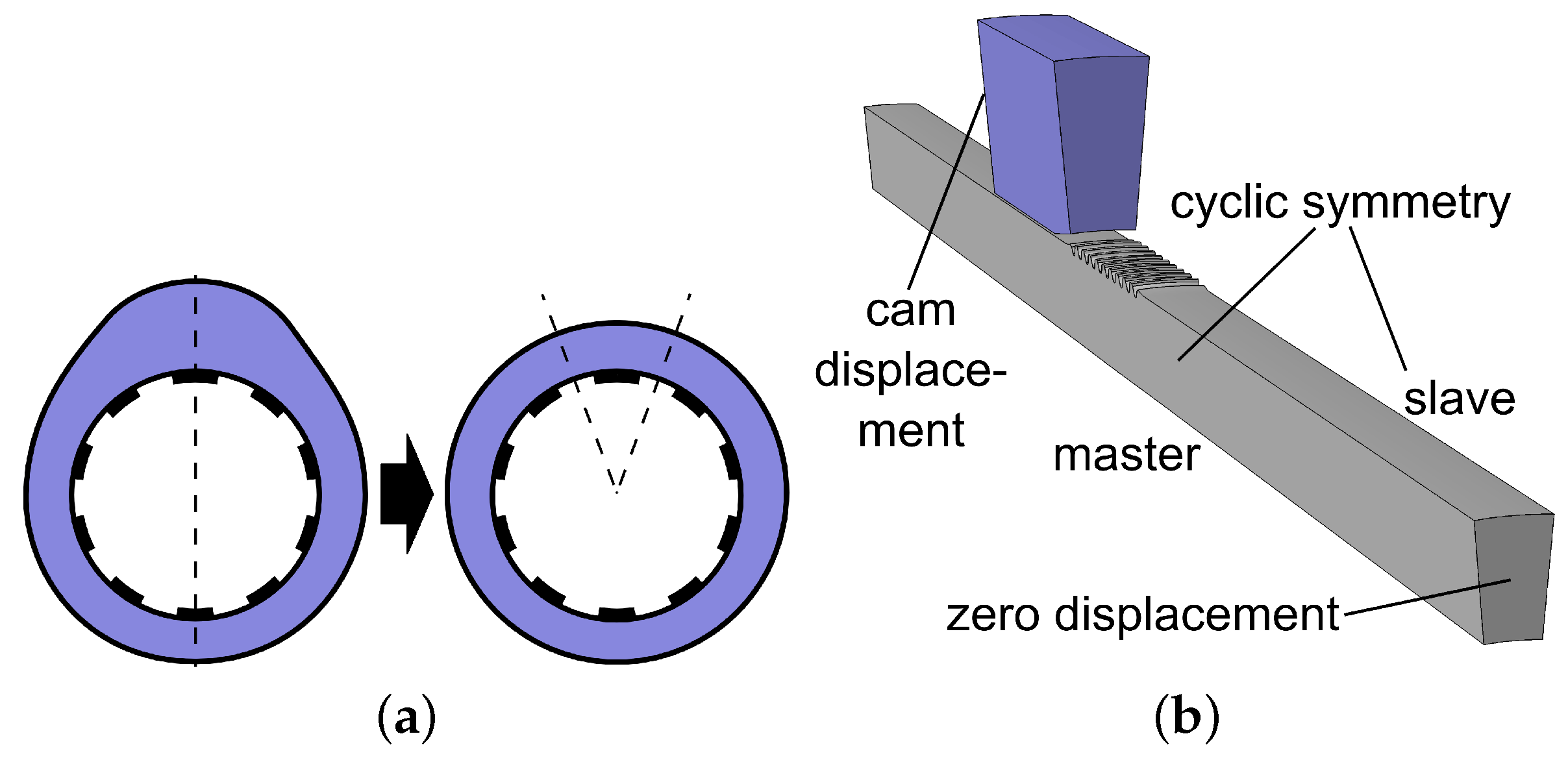
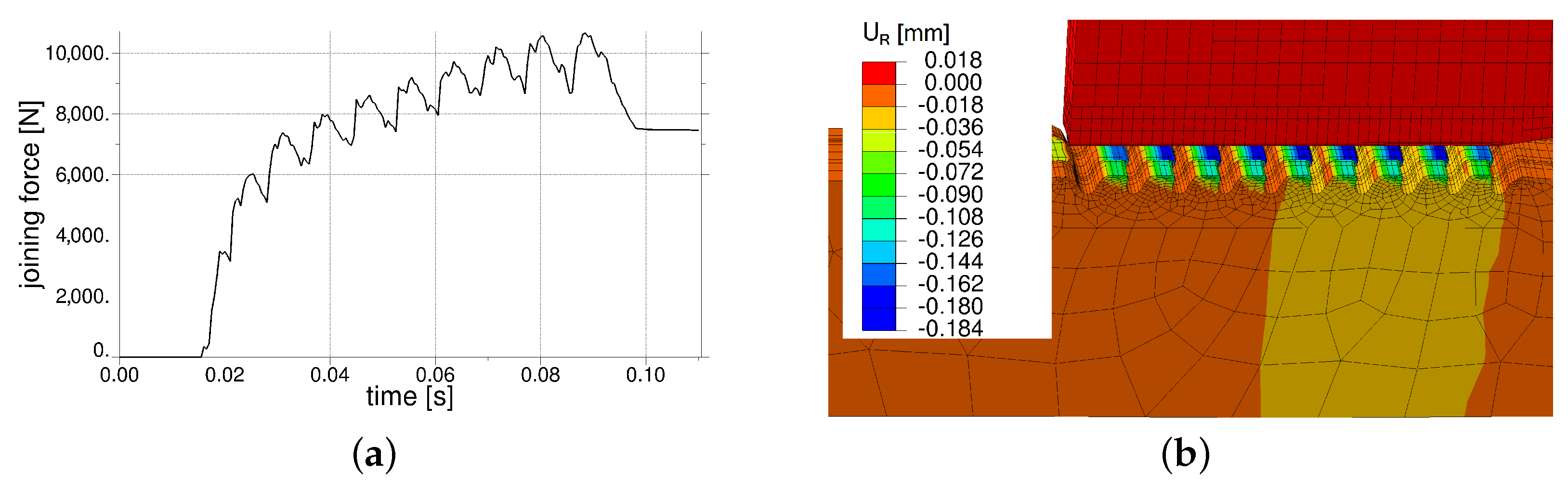
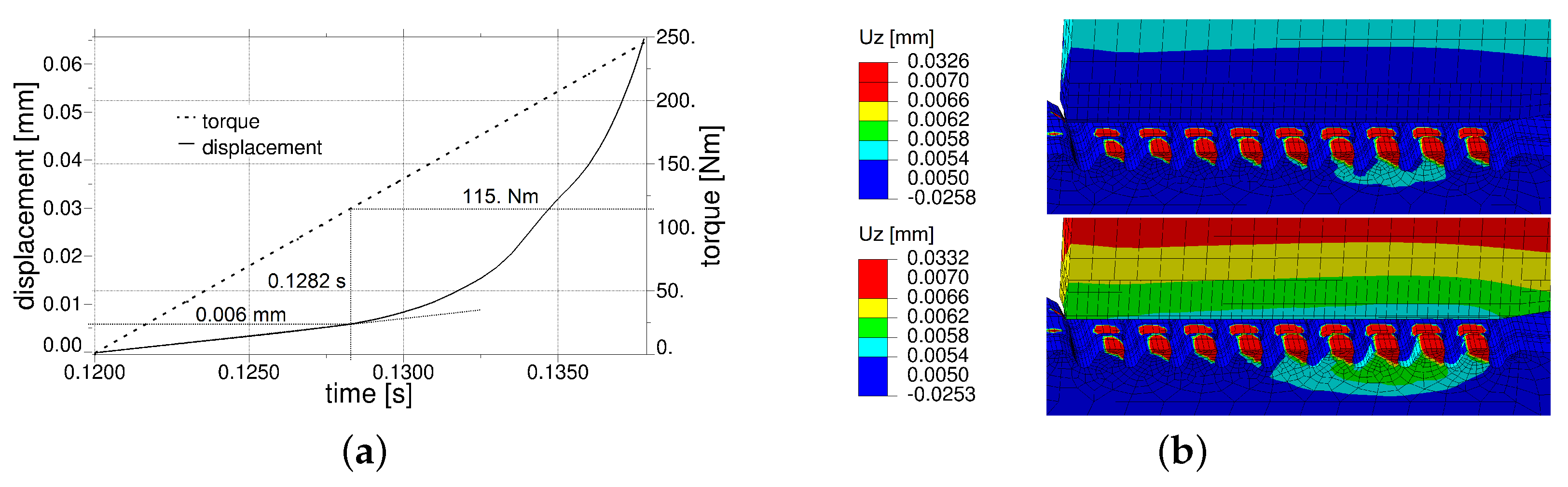
2.4. The Joining Process
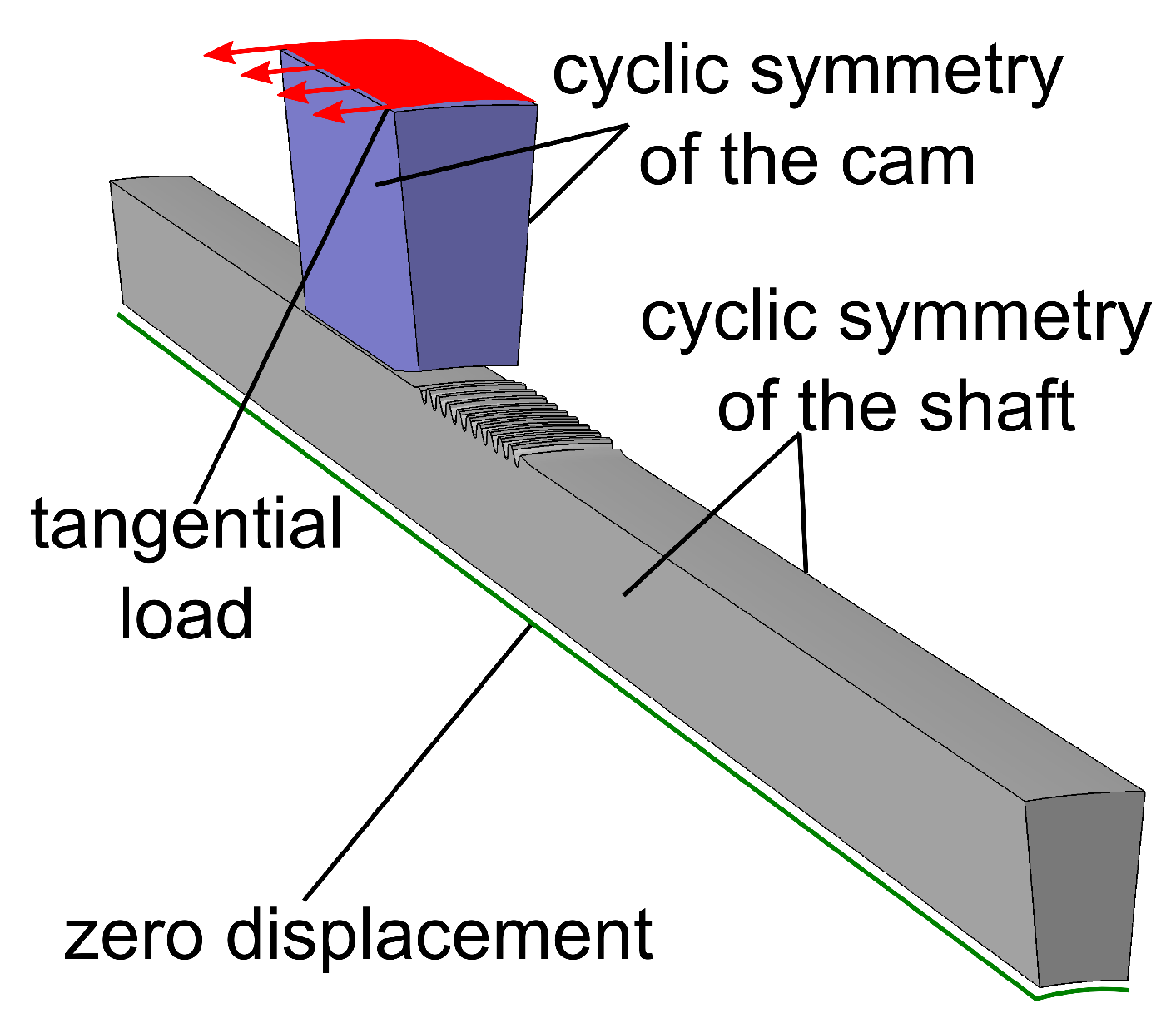
2.5. Loading of the Presta Connection
3. Results
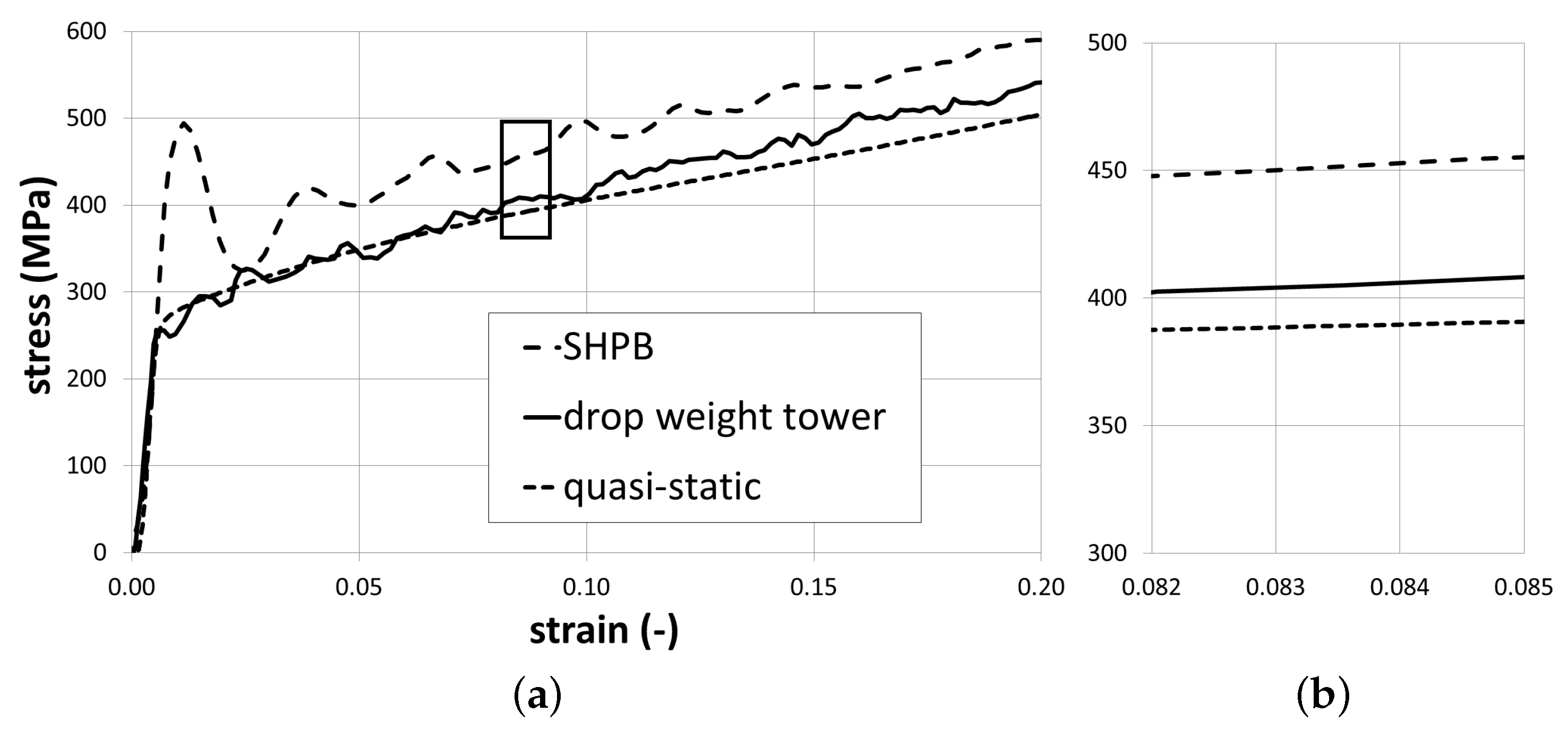
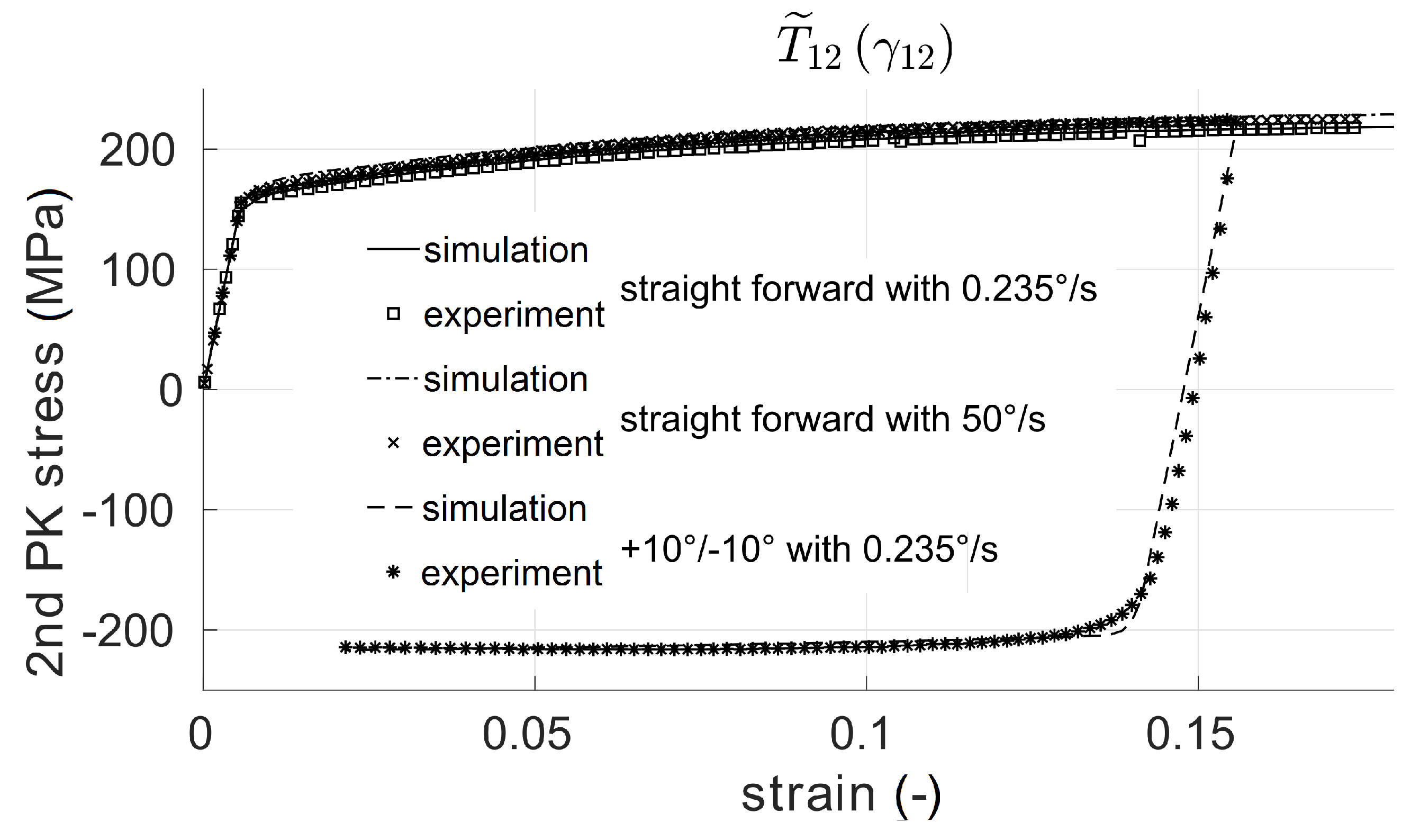
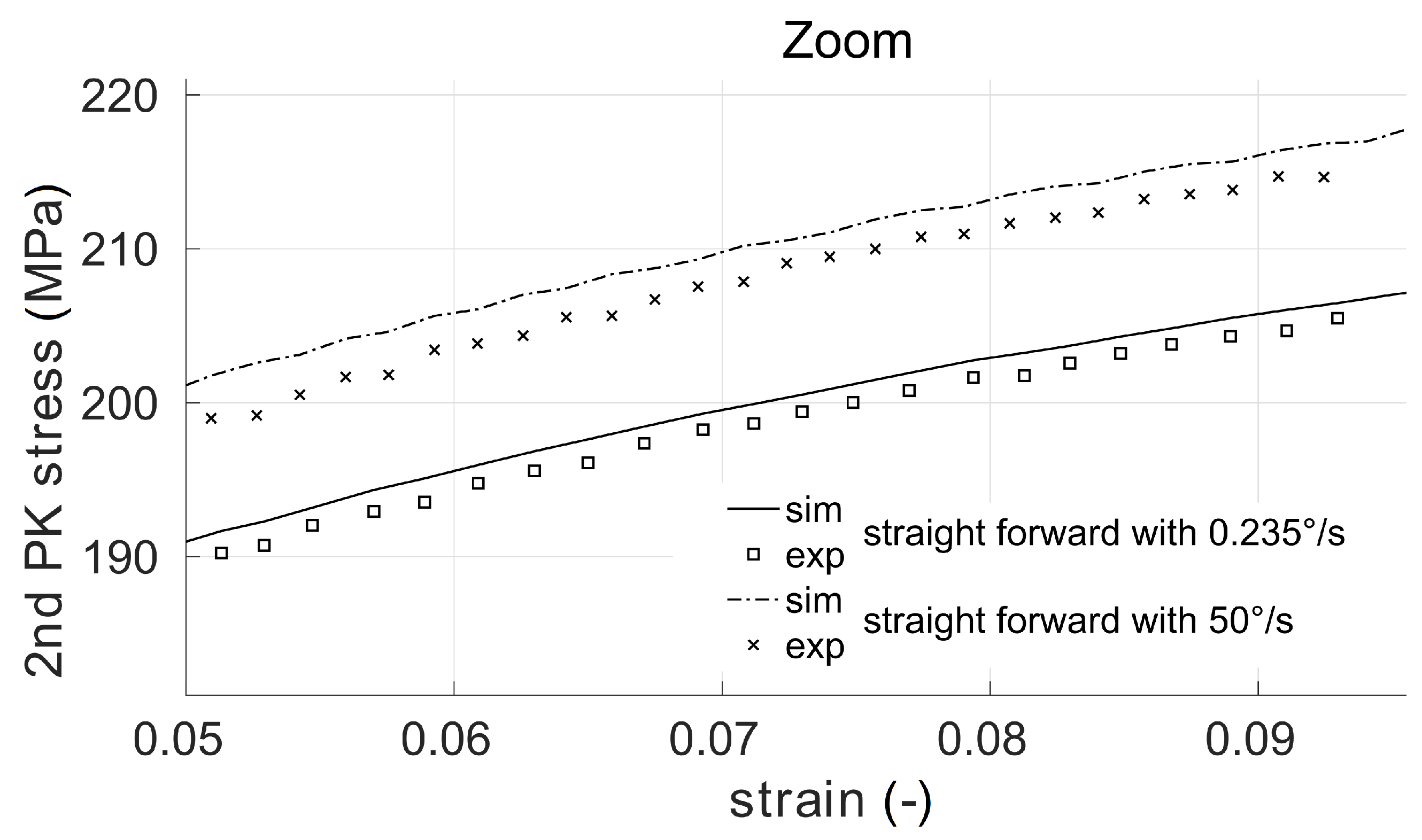
3.1. Material Tests and Parameter Identification for the Aluminum Alloy AA6082
3.2. Application of the Simulation Sequence on AA6082
4. Discussion
5. Summary
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DIC | Digital image correlation |
| FEM | Finite element method |
| PJP | Presta joining process |
| SFB | Sonderforschungsbereich (engl. collaborative research center) |
| SHPB | Split-Hopkinson pressure bar |
| UMAT | User subroutine to define a material’s mechanical behavior in ABAQUS |
References
- Shutov, A.V.; Kreißig, R. Finite strain viscoplasticity with nonlinear kinematic hardening: Phenomenological modeling and time integration. Comput. Methods Appl. Mech. Eng. 2008, 197, 2015–2029. [Google Scholar] [CrossRef]
- Meusburger, P. Lightweight design in engine construction by use of assembled camshafts. MTZ Worldw. 2006, 67, 10–12. [Google Scholar] [CrossRef]
- Lengwiler, A. Fehlerfortpflanzung, Simulation und Optimierung von Prozessketten Anhand der Gebauten Nockenwelle; Eidgenössische Technische Hochschule ETH Zürich: Zürich, Switzerland, 2011. [Google Scholar]
- Scherzer, R.; Silbermann, C.B.; Ihlemann, J. FE-simulation of the Presta joining process for assembled camshafts—Local widening of shafts through rolling. IOP Conf. Ser. Mater. Sci. Eng. 2016, 118, 12039. [Google Scholar] [CrossRef]
- Scherzer, R.; Silbermann, C.B.; Landgraf, R.; Ihlemann, J. FE-simulation of the Presta joining process for assembled camshafts—Modelling of the joining process. IOP Conf. Ser. Mater. Sci. Eng. 2017, 181, 12030. [Google Scholar] [CrossRef]
- Scherzer, R.; Ihlemann, J. Simulation of the Presta process—Transfer of deformation history. PAMM. (accepted 2017).
- Shutov, A.V.; Kuprin, C.; Ihlemann, J.; Wagner, M.X.; Silbermann, C. Experimentelle Untersuchung und numerische Simulation des inkrementellen Umformverhaltens von Stahl 42CrMo4. Materialwiss. Werkst. 2010, 41, 765–775. [Google Scholar] [CrossRef]
- Shutov, A.V.; Kreißig, R. Regularized strategies for material parameter identification in the context of finite strain plasticity. Tech. Mech. 2010, 30, 280–295. [Google Scholar]
- Kießling, R.; Landgraf, R.; Scherzer, R.; Ihlemann, J. Introducing the concept of directly connected rheological elements by reviewing rheological models at large strains. Int. J. Solids Struct. 2016, 97, 650–667. [Google Scholar] [CrossRef]
- Winter, S.; Schmitz, F.; Clausmeyer, T.; Tekkaya, A.E.; Wagner, M.F.-X. High temperature and dynamic testing of AHSS for an analytical description of the adiabatic cutting process. IOP Conf. Ser. Mater. Sci. Eng. 2017, 181, 12026. [Google Scholar] [CrossRef]
- Pouya, M.; Winter, S.; Fritsch, S.; Wagner, M.F.-X. A numerical and experimental study of temperature effects on deformation behavior of carbon steels at high strain rates. IOP Conf. Ser. Mater. Sci. Eng. 2017, 181, 12022. [Google Scholar] [CrossRef]
- Shutov, A.V. Efficient implicit integration for finite-strain viscoplasticity with a nested multiplicative split. Comput. Methods Appl. Mech. Eng. 2016, 306, 151–174. [Google Scholar] [CrossRef]
- Besdo, D.; Hohl, C.; Ihlemann, J. ABAQUS implementation and simulation results of the MORPH constitutive model. Const. Models Rubber IV 2005, 4, 223–228. [Google Scholar]
- Shutov, A.V.; Pfeiffer, S.; Ihlemann, J. On the simulation of multi-stage forming processes: Invariance under change of the reference configuration. Materialwiss. Werkst. 2012, 43, 617–625. [Google Scholar] [CrossRef]
| G (MPa) | K (MPa) | (MPa) | (s) | m (−) |
|---|---|---|---|---|
| 27, 300 | 76, 212.5 | 250 | 755.48 | 2.19 |
| (MPa) | (MPa) | (−) | (−) | (−) | (−) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|---|
| 136.109 | 51, 439.136 | 0.0717 | 0.0521 | −72.904 | 31.165 | 0.000304 | 2999.53 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scherzer, R.; Fritsch, S.; Landgraf, R.; Ihlemann, J.; Wagner, M.F.-X. Finite Element Simulation of the Presta Joining Process for Assembled Camshafts: Application to Aluminum Shafts. Metals 2018, 8, 128. https://doi.org/10.3390/met8020128
Scherzer R, Fritsch S, Landgraf R, Ihlemann J, Wagner MF-X. Finite Element Simulation of the Presta Joining Process for Assembled Camshafts: Application to Aluminum Shafts. Metals. 2018; 8(2):128. https://doi.org/10.3390/met8020128
Chicago/Turabian StyleScherzer, Robert, Sebastian Fritsch, Ralf Landgraf, Jörn Ihlemann, and Martin Franz-Xaver Wagner. 2018. "Finite Element Simulation of the Presta Joining Process for Assembled Camshafts: Application to Aluminum Shafts" Metals 8, no. 2: 128. https://doi.org/10.3390/met8020128
APA StyleScherzer, R., Fritsch, S., Landgraf, R., Ihlemann, J., & Wagner, M. F.-X. (2018). Finite Element Simulation of the Presta Joining Process for Assembled Camshafts: Application to Aluminum Shafts. Metals, 8(2), 128. https://doi.org/10.3390/met8020128






