Simulation of Sheet Metal Forming Processes Using a Fully Rheological-Damage Constitutive Model Coupling and a Specific 3D Remeshing Method

Abstract

Automatic process modeling has become an effective tool in reducing the lead-time and the cost for designing forming processes. The numerical modeling process is performed on a fully coupled damage constitutive equations and the advanced 3D adaptive remeshing procedure. Based on continuum damage mechanics, an isotropic damage model coupled with the Johnson–Cook flow law is proposed to satisfy the thermodynamic and damage requirements in metals. The Lemaitre damage potential was chosen to control the damage evolution process and the effective configuration. These fully coupled constitutive equations have been implemented into a Dynamic Explicit finite element code Abaqus using user subroutine. On the other hand, an adaptive remeshing scheme in three dimensions is established to constantly update the deformed mesh to enable tracking of the large plastic deformations. The quantitative effects of coupled ductile damage and adaptive remeshing on the sheet metal forming are studied, and qualitative comparison with some available experimental data are given. As illustrated in the presented examples this overall strategy ensures a robust and efficient remeshing scheme for finite element simulation of sheet metal-forming processes.

1. Introduction

The commercial finite element software has integrated various material models to describe the thermal-visco-plastic behaviors of sheet metal in different forming processes (deep-drawing, hydroforming, incremental forming, blanking). However, when materials are formed by these processes, they experience large plastic deformations leading to the onset of internal or surface micro-defects as voids and micro cracks. When micro-defects initiate and grow inside the plastically deformed metal, the thermo-mechanical fields are deeply modified, leading to significant modifications in the deformation process. On the other hand, the coalescence of micro-voids defects during the deformation can lead to the initiation of macro-cracks or damaged zones, inducing irreversible damage inside the formed part and consequently its loss. Taking into account the damage defect in sheet metal forming necessitates not only the development of a continuum damage theory, but also its coupling with the other mechanical fields. This is useful to avoid damage initiation to obtain a non-damaged work-piece (hot forging, stamping, deep-drawing and hydroforming) and develop the damage initiation and propagation to simulate the machining processes (orthogonal cutting, blanking, guillotining).

During the past decades, constitutive models of ductile damaged materials in the finite deformation range have received considerable attention. An important point in such phenomenological constitutive models is the appropriate choice of the physical nature of mechanical variables realistically describing the damage state of materials. Two main methods exist to predict the macro-defect in sheet metal forming:

(a)

The first uncoupled approach aims to calculate the damage (initiation and growth) distribution without taking into account its effect on the other mechanical fields (elastic, thermal, plastic, and hardening). This approach is used to predict zones where local failure has taken place inside the deformed work piece. Generally, this is achieved by post-processing the finite element analysis for a given time step to calculate the damage distribution using the stress and strain fields [1,2,3].

(b)

In the second fully coupled approach, the damage effect is directly introduced into the overall constitutive equations and affects all the mechanical fields. In this case, the damage field assumes that the degradation of structure is due to nucleation and growth of micro defects and their coalescence into macro-cracks. The fully coupled approach has shown their ability to optimize the process plane, not only to avoid the damage occurrence, but also to enhance the damage in order to simulate any metal cutting processes [4,5,6].

Damage mechanics in metal assumes that the degradation of material due to nucleation and growth of micro defects (voids and cracks), and their coalescence into macro-cracks [1,2,3]. McClintock [4] firstly develops the relationship between micro defects and ductile failure. After, three main approaches based on micro-defects [5] are extensively used to describe the damage mechanics: fracture mechanics [6], micro-based damage mechanics [7,8,9,10], and continuum damage mechanics (CDM). This somewhat fully coupled approach accounts for the direct interactions between the plastic flow, including different kinds of hardening, and the ductile damage initiation and growth. In CDM, the damage is assumed to be one of the internal state variables which relates to material behavior induced by the irreversible deterioration of microstructure. The function of damage variable works with effective stress. Kachanov [11] is the pioneer to characterized ductile damage by a scalar to define the effective stress. Without a clear physical meaning for damage, he introduced a scalar internal variable to model the creep failure of metal under uniaxial loads. A physical significance for the damage variable was given later by Rabotnov [12] who proposed the reduction of the cross sectional area due to micro-cracks as a suitable measure of the state of internal damage.

Lemaitre and Chaboche developed the continuum damage mechanic for ductile damage later [13]. The constitutive equations of damage variables are derived from specific damage potentials by using the effective state variables. These are defined from the classical state variables using one of the three following hypotheses: strain equivalence, stress equivalence or energy equivalence. The coupled constitutive equations of the damaged domain are generally deduced from the same state and dissipation potentials in which the state variable are replaced by the effective state variables [13,14,15,16].

In recent years, sets of constitutive equations for elasticity, plasticity and thermo-visco-plasticity coupled with ductile damage are given [15]. The works of Bouchard [17], Brünig [18], and Wang [19] summarized and compared various damage models.

The Johnson–Cook (JC) hardening model is the most attractive among well-known visco-plastic strain flow. This model takes into account both kinematic strengthening and adiabatic heating of the material undergoing strains and can describe the dynamic behavior of materials, which works in different thermal environments. For these advantages, the JC model has been modified in parameters and various forms to fit the different material behaviors. Peirs [20] used the advanced experiment method and finite element simulation tools to verify the material parameters in JC model, especially the strain rate hardening and thermal softening parameters. Through enhancing the thermal softening effects, the simulation results using corrected parameters agreed with the experiments and some strain localization phenomena happened. Calamaz [21] directly changed the JC model to the form of TANH model. A new term, which is controlled by temperature, was added to simulate the serrated chips formation in orthogonal cutting process. On the other hand, Zerilli and Armstrong proposed dislocation-mechanics-based constitutive relations for different crystalline structures, in which the effects of strain hardening, strain rate hardening, and thermal softening based on the thermal activation analysis were incorporated into constitutive relations [22,23,24]. Holmquist et al. [25] and Hor et al. and [26] propose a comparison of the models to be made independent of the material constants and procedure for which constants can be determined for different constitutive models using the same test data base.

In these models, the damage generates and evolves during tensile, shearing and cutting process had never introduced. This point is not identical to the practical situation. Actually, the stiffness of the material is deteriorating until to losing the abilities of loading which is following with the evolution of damage. Johnson and Cook [27] have given out a threshold, which is a function of stress state (stress triaxiality) for equivalent plastic strain. The damage generates when equivalent plastic strain reaches to this threshold. The limitation of this damage model is that, it can only predict the onset of the damage and the material stiffness will reduce to zero directly without any evolution process. Some phenomena (like strain localization) are hard to obtain and it will also lead the instability into the simulation system. Therefore, it is necessary to integrate a constitutive damage evolution into the JC model. Based on this aspect, a constitutive equation which couple fully the ductile damage into JC isotropic hardening model, is developed. These fully coupled constitutive equations have been implemented into a Dynamic Explicit finite element code (Abaqus/Explicit) using user subroutine. The local integration of the plastic-damage constitutive equations is performed using an asymptotic implicit scheme applied to solve the nonlinear local equations.

Numerical errors are intrinsic in Finite Element Analysis (FEA) of sheet metal forming processes and possess additional difficulties related to the large inelastic deformations with damage imply a severe distortion of the computational domain [28,29]. In fact, the deformed domain undergoes geometrical variation (large displacements and rotations) and are characterized by inhomogeneous spatial distribution of thermo-mechanical fields with evolving localized zones (stress, plastic strain, damage, temperature, etc.). In fact, the time and space discretization of the continuous differential equations governing the physical equilibrium events lead inevitably to numerical errors. In this case, frequent remeshing of the deformed domain during computation is necessary to obtain an accurate solution and complete the computation until the termination of the numerical simulation process. Accordingly, several remeshing have to be performed during the simulation in order to preserve the reliability of the obtained results by minimizing errors generated by either the geometrical transformations or the heterogeneous thermo-mechanical fields.

To decide when the remeshing is required during the analysis, some appropriate criteria are needed and should be automatically executed during the FEA. These are generally based on a priori and a posteriori error estimators. The main goal of any error estimator is the evaluation of the absolute global error as an addition of the estimated local error for each element. For metal forming, the error criteria is classified into three classes:

(1)

Geometrical: estimation of the element distortion due to the large transformation of the domain. Distortion criteria are based on the large variation of the geometry of finite elements with respect to their reference state.

(2)

Curvature: estimation of the element size needed to avoid inter-penetration between the deformed domain and complex tools. This geometric estimator is based on the curvature of the tools angles inside the contact zones.

(3)

Physical: adaptation of the element size to the local or global variation of some physical fields as temperature, displacement gradient, stress, plastic strain etc.

Accordingly, the damage growth induces a decrease in the stress-like variables generated by a decrease in physical properties of the material. When all Gauss points within a given finite element are fully damaged, the corresponding stiffness matrix is zero. Consequently, this element has no more contribution in the global tangent stiffness matrix and should be removed. Accordingly, there is problem for elements lying in boundaries of the deformed domain need special attention when this boundary is concerned with the contact zone between different domains (tools and deformable parts). The best way to treat the fully damaged elements consists in remeshing the domain after dropping the fully damaged elements and smoothing the newly created boundaries of the deformed part.

In this work the damage potential, introduced by Lemaitre [13], is used and coupled into an elasto-visco-plastic material model through defining the effective stress and plastic strain like a Johnson–Cook formulation [27]. 3D adaptive remeshing scheme using linear tetrahedral finite element is developed in order to simulate the large plastic deformations and crack propagation after damage occurring [28,29]. This scheme is established to simulate to predict when and where ductile damage zones may take place inside the deformed part during tensile, compressive, and shearing tests. The localization phenomenon of damage was illustrated clearly. The formation of the cracks and its propagation to the final fracture of the specimen are also illustrated. Four various sheet metal forming processes are proposed to prove that the numerical methodology is an advanced and a reliable tool to simulate various metal forming processes in order to avoid damage in incremental forming, deep drawing, and multi-point drawing or to enhance damage in order to simulate some sheet metal cutting operations.

2. Methods and Constitutive Model

2.1. Visco-Elastoplastic Model Fully Coupled to Isotropic Ductile Damage

This section provides a brief description of the major conception for coupling the ductile damage into the material elasto-visco-plastic behavior. The ductile damage is presented in the framework of irreversible processes with state variables. An isotropic ductile damage variable D (0 < D < 1) is measured in a macroscopic scale way through the surface density of intersection of micro-cracks and micro-cavities at a representative finite elementary volume. In order to perform the effect of this damage variable on the mechanical behavior, the effective state variables are introduced [11,12,13,14,15,16].

To another consideration, the damage caused by the micro-cracks and micro-cavities has a different evolution processes in tensile and compressive load conditions. In one aspect, the micro-cracks are opened in the tensile state and the module of elasticity reduces gradually until to zero. In another aspect, the micro-cracks are closed in compressive state and the module of elasticity could be able to restore to their initial values before the damage accumulates. This recovery effect of physical properties after closure of micro-cracks is called the quasi-unilateral effect [30,31,32,33,34,35,36,37]. It demands that the definition of effective state variable $\left(\underset{\_}{\overset{˜}{\mathsf{\sigma }}},\widetilde{\underset{\_}{\mathsf{\epsilon }}}\right)$ should be in the unilateral condition.

According to the theory of energy equivalence, we define the effective variables, which consider the isotropic ductile damage into state variables [38,39,40,41,42] as follows:

$$\underset{\_}{\tilde{\mathsf{\sigma }}}=\frac{\underset{\_}{\mathsf{\sigma }}}{\sqrt{1-D}},{\underset{\_}{\tilde{\mathsf{\epsilon }}}}^{\mathrm{e}}={\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}\sqrt{1-D},\underset{\_}{S}=\underset{\_}{\mathsf{\sigma }}-{\mathsf{\sigma }}_{\mathrm{H}}\underset{\_}{1}\mathrm{and}{\mathsf{\sigma }}_{\mathrm{H}}=\frac{1}{3}\mathrm{tr}\underset{\_}{\mathsf{\sigma }}$$

(1)

where ${\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}$ is the small elastic strain tensor representing the elastic flow associated with the Cauchy stress tensor $\underset{\_}{\mathsf{\sigma }}$, $\left(\underset{\_}{S},{\mathsf{\sigma }}_{\mathrm{H}}\right)$ are the deviatoric and hydrostatic Cauchy stresses respectively and D is the ductile damage associated with the potential Y.

The damaged elastoplastic behavior is described in the framework of the thermodynamics of irreversible processes with state variables. The Helmholtz free energy in which elasticity and plasticity are uncoupled gives the law of elasticity coupled with damage. Following the 2nd principle of thermodynamics, non-negativity of the mechanical dissipation, the stress like variables ($\underset{\_}{\mathsf{\sigma }},Y$) are derived from the state potential taken as the classical free energy $\mathsf{\Psi }\left({\underset{\_}{\mathsf{\epsilon }}}^{{}_{\mathrm{e}}},D\right)$ in deformation space [15,16], as follows:

$$\{\begin{array}{l}\underset{\_}{\mathsf{\sigma }}=\left(1-D\right)\left(2{\mathsf{\mu }}_{\mathrm{e}}\underset{\_}{\underset{\_}{I}}+{\lambda }_{\mathrm{e}}\underset{\_}{1}\otimes \underset{\_}{1}\right):{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}=\left(1-D\right)\underset{\_}{\underset{\_}{\mathrm{\Lambda }}}:{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}\\ Y=\frac{1}{2}{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}:\underset{\_}{\underset{\_}{\mathrm{\Lambda }}}:{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{e}}=\frac{J_2{\left(\underset{\_}{\mathsf{\sigma }}\right)}^2}{2E{(1-D)}^2}\left[\frac{2}{3}(1+\mathsf{\nu })+3(1-2\mathsf{\nu }){\left(\frac{{\mathsf{\sigma }}_{\mathrm{H}}}{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)}\right)}^2\right]\end{array}$$

(2)

where $\left({\lambda }_{\mathrm{e}},{\mathsf{\mu }}_{\mathrm{e}}\right)$ are the classical Lame’s constants which are a function of Young modulus E and Poison’s coefficient $\mathsf{\nu }$.

In order to couple the damage behavior, a single appropriate dissipation potential $F(\underset{\_}{\mathsf{\sigma }},Y,D)$ is defined to govern the evolution law for internal variables in the stress space [39,40,41,42]:

$$F\left(\underset{\_}{\mathsf{\sigma }},{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{p}},Y,D\right){=f}_{\mathrm{p}}+F_Y\le 0\{\begin{array}{l}{f}_{\mathrm{p}}\left(\underset{\_}{\mathsf{\sigma }},{\underset{\_}{\mathsf{\epsilon }}}^{\mathrm{p}},D\right)=\frac{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)}{\sqrt{1-D}}-R\left({\overline{\mathsf{\epsilon }}}^{\mathrm{p}}\right)\\ F_Y\left(Y,D\right)=\frac{\mathsf{\gamma }}{{\left(1-D\right)}^{\mathsf{\beta }}}\frac{1}{(\mathsf{\alpha }+1)}{\left(\frac{Y-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }+1}\end{array}$$

(3)

The parameters (α, β and γ and Y₀) are used to control the evolution of damage potential, $R\left({\overline{\mathsf{\epsilon }}}^{\mathrm{p}}\right)$ is the JC isotropic yield stress in various visco-plastic flow and $J_2(\underset{\_}{\mathsf{\sigma }})=\sqrt{\frac{3}{2}\underset{\_}{S}:\underset{\_}{S}}$ is the second invariant of the deviatoric Cauchy stress $\underset{\_}{S}$.

For the case of time independent plasticity, the plastic strain rate tensor ${\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}$ and the rate damage $\dot{\mathrm{D}}$ are obtained from the stationarity conditions as in which the plastic multiplier $\dot{\mathsf{\delta }}$ is deduced from the consistency condition [13]:

$$\{\begin{array}{l}{\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}=\dot{\lambda }\frac{\partial f_{\mathrm{p}}}{\partial \underset{\_}{\mathsf{\sigma }}}=\frac{3}{2}\frac{\dot{\lambda }}{\sqrt{1-D}}\frac{\underset{\_}{S}}{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)}\\ \dot{D}=\dot{\lambda }\frac{\partial F_Y}{\partial Y}=\dot{\lambda }{\left(\frac{Y-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }}\frac{1}{{(1-D)}^{\mathsf{\beta }}}\end{array}$$

(4)

where

$${\dot{\overline{\mathsf{\epsilon }}}}^{\mathrm{p}}=\sqrt{\frac{2}{3}{\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}:{\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}}$$

(5)

is the effective plastic strain rate.

Failure is assumed to initiate when the damage at a material point reaches the critical damage value D_c. When this happens, the stiffness of the failed element is significantly reduced and consequently incapable of carrying any load. The value of D_c for any material must be acquired through experimental tests. Assuming a fully isotropic material behavior, the plastic multiplier $\dot{\lambda }$ is obtained by the consistency condition $\left({\dot{f}}_{\mathrm{p}}=f_{\mathrm{p}}=0\right)$ associated with the loading–unloading condition [13,14,15]. It is a strictly positive scalar, which plays the role of Lagrange multiplier for dissipative phenomena:

$$\dot{\lambda }=\frac{1}{H_{\mathrm{p}}}\langle 3{\mathsf{\mu }}_{\mathrm{e}}\sqrt{1-D}\frac{1}{J_2(\underset{\_}{\mathsf{\sigma }})}\underset{\_}{S}:\underset{\_}{\dot{\mathsf{\epsilon }}}\rangle$$

(6)

The non-symmetric fourth order tangent elastoplastic operator ${\underset{\_}{\underset{\_}{L}}}_T$ defining the stress rate $\underset{\_}{\dot{\mathsf{\sigma }}}={\underset{\_}{\underset{\_}{L}}}_T:\underset{\_}{\dot{\mathsf{\epsilon }}}$ is defined as [28,29,36,40]:

$${\underset{\_}{\underset{\_}{L}}}_T=2{\mathsf{\mu }}_{\mathrm{e}}\left(1-D\right)-\frac{\left(1-D\right)}{H_{\mathrm{p}}}(3{\mathsf{\mu }}_{\mathrm{e}}\frac{\underset{\_}{S}}{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)}\mathrm{Ä}3{\mathsf{\mu }}_{\mathrm{e}}\frac{\underset{\_}{S}}{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)})-\frac{1}{H_{\mathrm{p}}{\left(1-D\right)}^{\mathsf{\beta }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\left(\frac{Y-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }}(3{\mathsf{\mu }}_{\mathrm{e}}\frac{\underset{\_}{S}}{J_2\left(\underset{\_}{\mathsf{\sigma }}\right)})\mathrm{Ä}\underset{\_}{S}$$

(7)

where $H_p$ is the tangent plastic hardening module given by:

$$H_p=3{\mathsf{\mu }}_{\mathrm{e}}-\frac{J_2(\underset{\_}{\mathsf{\sigma }})}{2{\left(1-D\right)}^{{}^{\mathsf{\beta }+\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}{\left(\frac{Y-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }}+\frac{1}{\sqrt{1-D}}\frac{\mathsf{\delta }R}{\mathsf{\delta }{\overline{\mathsf{\epsilon }}}^{\mathrm{p}}}$$

(8)

In this paper, the thermal effects are ignored [30,31,32,33,34,35,36,37,38,39,40] and the visco-plastic hardening yield stress is written as:

$$R\left({\overline{\mathsf{\epsilon }}}^{\mathrm{p}}\right)=\left[A+B{\left({\overline{\mathsf{\epsilon }}}^{\mathrm{p}}\right)}^n\right]\left[1+C\ln \frac{\dot{\overline{\mathsf{\epsilon }}}}{{\dot{\overline{\mathsf{\epsilon }}}}_0}\right]$$

(9)

where ${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}$ is the equivalent plastic strain, $\dot{\overline{\mathsf{\epsilon }}}$ is the equivalent plastic strain rate. The initial strain rate ${\dot{\overline{\mathsf{\epsilon }}}}_0$ is determined by experimental conditions. The parameters A, B and n represent the isotropic hardening evolution and C represent the material viscosity. The fully isotropic rate formulation assumes the small strain hypothesis in sheet forming processes where relative slow speeds and inertia effect can be neglected and dynamic phenomena not occur during the process.

For the constitutive equations, this hypothesis is justified by the fact that the applied load increments are still very small during remeshing procedure of sheet metal forming. Accordingly, the total strain rate tensor $\underset{\_}{\dot{\mathsf{\epsilon }}}$ is additively partitioned $\underset{\_}{\dot{\mathsf{\epsilon }}}={\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{e}}+{\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}$ with ${\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{e}}$ and ${\underset{\_}{\dot{\mathsf{\epsilon }}}}^{\mathrm{p}}$ are respectively the elastic and plastic strain rate components.

2.2. Local Time Integration of the Constitutive Equations

The fully coupled constitutive equations presented above together with an iterative implicit procedure for the time integration have been implemented using the user’s subroutine. By combining the Equations (2) and (4) and saving the damage evolution equation one may obtain the following system of two scalar equations [28,29]:

$$\{\begin{array}{cc}{f}_1\left(\Delta D_{n+1}^{},\Delta {\lambda }_{n+1}^{}\right)=\frac{J_2(\underset{\_}{\mathsf{\sigma }})}{\sqrt{1-D_{n+1}}}-\frac{3\mathrm{G}\Delta {\lambda }_{n+1}}{\sqrt{1-D_{n+1}}}-R_{n+1}=0\hfill & \hfill \left(\mathrm{a}\right)\\ f_2\left(\Delta D_{n+1}^{},\Delta {\lambda }_{n+1}^{}\right)=\Delta D_n^{n+1}{}_{n+1}-\frac{\Delta {\lambda }_{n+1}}{{\left(1-D_n\right)}^{\mathsf{\beta }}}{\left(\frac{Y_n-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }}=0\hfill & \hfill \left(\mathrm{b}\right)\end{array}$$

(10)

This simple system is iteratively solved thanks to Newton–Raphson scheme to determine the two unknowns at the time t_n+1. The knowledge of $\left(\Delta {\lambda }_{n+1},D_{n+1}\right)$ allows the updating of the hardening and damage variables at the end of the time step. The so-called elastic prediction-return mapping algorithm with an operator splitting methodology is used. For the calculation of stress and plastic strain tensors, accumulated plastic strain and ductile damage, we use the fully implicit Euler method since it contains the property of absolute stability and the possibility of appending further equations to the existing system of nonlinear equations [42,43].

The local numerical integration scheme is known to have important advantages for the constitutive models with a single yielding surface together with a fully implicit global resolution scheme. This approach within the coupled problem, consists in splitting it into two parts:

(1)

Damaged elastic prediction, where the problem is assumed to be purely elastic affected by the last damage value.

(2)

Damaged-plastic corrector, in which the system of equations includes the damaged elastic relation as well as the damaged-plastic consistency condition. Newton–Raphson iteration algorithm is then used to solve the discretized constitutive equations in the damaged plastic corrector stage around the current values of the state variables (plasticity, hardening, damage) [43].

Two procedures related to the damage coupling have been investigated. The first is the one discussed above and called the strong coupled procedure is implemented into Abaqus subroutines. The second one weak approach solves only the equation $f_1\left(\Delta D_{n+1}^{},\Delta {\lambda }_{n+1}^{}\right)=0$ without damage effect in order to obtain plastic multiplier $\Delta {\lambda }_{n+1}$. After the convergence the $\Delta {\lambda }_{n+1}$ is used to calculate the damage increment without any iteration procedure $\Delta D_{n+1}^{}=\frac{\Delta {\lambda }_{n+1}}{{\left(1-D_n\right)}^{\mathsf{\beta }}}{\left(\frac{Y_n-Y_0}{\mathsf{\gamma }}\right)}^{\mathsf{\alpha }}$.

If the ductile damage variable reaches its maximum value D $\ge$ D_max at a given integration point, the correspondent elastic modulus is set to zero giving zero stresses and no contribution to the elementary stiffness matrix. This fully damaged integration point is excluded from the integration domain of the element and has no more contribution in the elementary stiffness matrix. However, when a node is found to be connected with fully damaged elements, giving a singular global stiffness matrix, the calculation is terminated. In fact, this situation can be avoided by dropping the corresponding terms from the stiffness matrix. A new mesh is then generated after removing the fully damaged elements.

2.3. Global Resolution Strategy

The principal of virtual power written on the current damaged domain configuration with the volume V and boundary Γ can be written as:

$$\mathsf{\rho }{\displaystyle \underset{V}{\int }\ddot{u}}\cdot \mathsf{\delta }\dot{u}\mathrm{d}V=-{\displaystyle \underset{V}{\int }\underset{\_}{\mathsf{\sigma }}}:\mathsf{\delta }\dot{\underset{\_}{\mathsf{\epsilon }}}\mathrm{d}V+{\displaystyle \underset{V}{\int }f}\cdot \mathsf{\delta }\dot{u}\mathrm{d}V+{\displaystyle \underset{{\Gamma }_u}{\int }t}\cdot \mathsf{\delta }\dot{u}\mathrm{d}\Gamma +{\displaystyle \underset{{\Gamma }_{\mathrm{c}}}{\int }{t}_{\mathrm{c}}}\cdot \mathsf{\delta }{\dot{u}}_{\mathrm{c}}\mathrm{d}\Gamma$$

(11)

where $\mathsf{\delta }\dot{u}$ (kinematically admissible) and $\mathsf{\delta }\ddot{u}$ are the virtual velocity and acceleration fields respectively and $\mathsf{\delta }{\dot{u}}_{\mathrm{c}}$ is the virtual velocity vector of contact nodes.

The deformed domain at each time is supposed to be discretized on isoparametric finite elements (C⁰). By using the classical nodal approximation using displacement based Finite Element Analysis FEA, Equation (11) can be easily written, on the overall part, under the following nonlinear algebraic system:

$$I={\displaystyle \sum _{\mathrm{e}}{I}_{\mathrm{e}}}=\left[{\displaystyle \sum _{\mathrm{e}}\left(\left[M_e\right]\left\{{\ddot{u}}_{\mathrm{e}}^{\mathrm{N}}\right\}+\left\{F_{\mathrm{e}}^{\mathrm{int}}\right\}-\left\{F_{\mathrm{e}}^{\mathrm{ext}}\right\}\right)}\right]\left\{\mathsf{\delta }\dot{u}\right\}=0$$

(12)

where $\left[M_e\right]$ is the consistent mass matrix and $\left\{F_{\mathrm{e}}^{\mathrm{ext}}\right\}\mathrm{and}\left\{F_{\mathrm{e}}^{\mathrm{int}}\right\}$ are the vector of external and internal forces defined as:

$$\{\begin{array}{l}[M_e]=\underset{V_{\mathrm{e}}}{\int }\mathsf{\rho }{\left[N_N\right]}^T\cdot N_N\mathrm{d}{V}_{\mathrm{e}}\\ \{F_{\mathrm{e}}^{int}\}=\underset{V_{\mathrm{e}}}{\int }[{B_e^N]}^T:\underset{\_}{\mathsf{\sigma }}\mathrm{d}{V}_{\mathrm{e}}\\ \{F_{\mathrm{e}}^{ext}\}=\underset{V_{\mathrm{e}}}{\int }[N_N]\cdot \{\overrightarrow{f}\}\mathrm{d}{V}_{\mathrm{e}}+\underset{{\Gamma }_{\mathrm{u}}}{\int }[N_N]\cdot \{\overrightarrow{t}\}\mathrm{d}{\mathrm{\Gamma }}_{\mathrm{e}}+\underset{{\Gamma }_{\mathrm{c}}}{\int }[N_N]\cdot \{\overrightarrow{t_{\mathrm{c}}}\}\mathrm{d}{\mathrm{\Gamma }}_{\mathrm{e}}\end{array}$$

(13)

$\left[B_{\mathrm{e}}^N\right]$ is the geometric or strain-displacement matrix in the current configuration and $\left[N_N\right]$ is the matrix of the nodal interpolation functions. The index e refers to the e^th element.

The system (12) defines a highly nonlinear system expressing the mechanical equilibrium of the work-piece and the tool at each time step. It can be solved either by iterative static implicit methods or by explicit methods [44,45,46,47,48,49,50,51].

(1) The static implicit iterative procedure requires, at each time step, the calculation of the consistent stiffness matrix in order to preserve the quadratic convergence property of the Newton method. When the inertia effect is neglected, the system (Equation (12)) reduces to:

$$\left\{R_{n+1}\right\}={\left\{F_{\mathrm{e}}^{\mathrm{int}}\right\}}_{n+1}-{\left\{F_{\mathrm{e}}^{\mathrm{ext}}\right\}}_{n+1}=\left\{0\right\}$$

(14)

The nonlinear problem to be solved over the time increment as follows:

$$R_{n+1}^i+\frac{\partial R_{n+1}^i}{\partial U_{n+1}^h}{(\Delta U)}_{n+1}^{i+1}+\dots =0$$

(15)

where the global tangent stiffness matrix at the time t_n+1 and iteration (i) is defined by:

$${\left[K\right]}_{n+1}^i=\left[\frac{\partial R_{n+1}^i}{\partial U_{n+1}^i}\right]={\left[K_{\mathrm{Structural}}\left(U_{n+1}^i\right)\right]}_{n+1}^i+{\left[K_{\mathrm{Contact}}\left(U_{n+1}^i\right)\right]}_{n+1}^i+{\left[K_{\mathrm{Force}}\left(U_{n+1}^i\right)\right]}_{n+1}^i$$

(16)

represents the contribution of the elastoplastic behavior to the structural stiffness; the contact and friction stiffness and the external applied body forces.

Note that the tangent matrix are generally non-symmetric and nonlinear because the material Jacobian matrix are themselves non-symmetric. Due to its quadratic rates of asymptotic convergence, this method tends to produce relatively robust and efficient incremental nonlinear finite element schemes. However, the presence of the damage leads to a softening behavior and poses some difficulties for the calculation of the consistent matrix. This, together with the evolving contact conditions, induces some difficulties in the convergence of the iterative procedure. On the other hand, the Newton type implicit iterative resolution strategies are unconditionally stable and allow using large time or loading increments.

(2) The discretized dynamic explicit procedure is formulate as:

$${\left[M\right]}_{n+1}{\left\{\ddot{U}\right\}}_{n+1}+{\left\{F_{\mathrm{e}}^{\mathrm{int}}\right\}}_{n+1}-{\left\{F_{\mathrm{e}}^{\mathrm{ext}}\right\}}_{n+1}=\left\{0\right\}\Rightarrow {\left[M\right]}_{n+1}{\left\{\ddot{U}\right\}}_{n+1}=\left\{R_{n+1}\right\}$$

(17)

where the degrees of freedom $\left\{U_{n+1}\right\}$ are computed as:

$$\{\begin{array}{l}{\ddot{U}}_{n+1}={\left[M\right]}_{n+1}^{-1}{R}_{n+1}\\ {\dot{U}}_{n+1}={\dot{U}}_n+\frac{\Delta t_n}{2}\left({\ddot{U}}_n+{\ddot{U}}_{n+1}\right)\\ U_{n+1}=U_n+\Delta t_n{\dot{U}}_n+\frac{{\left(\Delta t_n\right)}^2}{2}{\ddot{U}}_n\end{array}$$

(18)

The dynamic explicit procedure avoids the iteration procedure by performing directly a solution of linearized algebraic system. It is extremely robust since there is no iterative procedure in solving the global equilibrium problem and there is no need to construct any consistent tangent matrix. This will reduce greatly the incremental size and generate a large number of increments to calculate the applied loading. The computing cost then will increase sharply for calculating the tangent matrices in each iteration. However, explicit procedure needs to control efficiently and automatically the time step size in order to satisfy the accuracy and stability requirements [43]. The central difference operator is conditionally stable according to the time increment $\Delta t$ and the stability limit for the operator (with no damping) [47]. Instead, it can be estimated by determining the maximum element dilatational mode of the mesh, and to estimate the time step by:

$$\Delta t\le \min \left(\frac{\hslash }{C_{\mathrm{d}}}\right),C_{\mathrm{d}}=\sqrt{\frac{E(1-\mathsf{\nu })}{\mathsf{\rho }(1+\mathsf{\nu })(1-2\mathsf{\nu })}}$$

(19)

where $\hslash$ is the mesh dependent stability factor and C_d is the current dilatational wave speed of the material function of material density $\mathsf{\rho }$, Young module E and Poisson ratio $\mathsf{\nu }$.

The unilateral contact with friction has a capital influence in metal forming processes in general and particularly in cutting operations. In fact, evolving contact with friction takes place between the formed metal sheet and the tools. The most widely used friction models implemented in FE codes are supposed isotropic and time independent (Tresca or Coulomb model) or time dependent (Norton–Hoff model). In this study, we limit ourselves to briefly describe the Coulomb isotropic model available in Abaqus where finite sliding contact with arbitrary rotation of the surfaces of two contacting bodies exist in sheet metal forming [22]. The Coulomb’s friction model is defined by:

$$\{\begin{array}{cc}{\mathsf{\tau }}_{\mathrm{eq}}<\mathsf{\eta }P\hspace{1em}\Rightarrow \hspace{1em}{\dot{u}}_t=0\hfill & \mathrm{Sticking}\hfill \\ {\mathsf{\tau }}_{\mathrm{e}\mathrm{q}}=\mathsf{\eta }P\hspace{1em}\Rightarrow \exists \mathsf{\chi }\ge 0/{\dot{u}}_t=-\mathsf{\chi }{\mathsf{\tau }}_{\mathrm{eq}}\hfill & \mathrm{Sliding}\hfill \end{array}$$

(20)

where $\mathsf{\eta }$ is the temperature dependent friction coefficient, ${\dot{u}}_t$ is the relative tangential velocity at the contact point lying on the contact boundary ${\Gamma }_{\mathrm{c}}$; $P$ is the normal contact pressure and ${\mathsf{\tau }}_{\mathrm{eq}}=\sqrt{{\mathsf{\tau }}_1^2+{\mathsf{\tau }}_2^2}$ is the equivalent tangential stress in tangential sheet plane. The so-called Signorini unilateral contact conditions where governs the contact between the master surface (representing the tool) and the slave surface (representing the metal sheet deforming plastically):

$$\begin{array}{cccc}{u}_n\le 0,& F_n\le 0& \mathrm{and}& u_n\cdot F_n=0\end{array}$$

(21)

where $u_n=\overrightarrow{u}\cdot {\overrightarrow{n}}_{\mathrm{c}}$ and $F_n=\left(\underset{\_}{\mathsf{\sigma }}\cdot {\overrightarrow{n}}_{\mathrm{c}}\right){\overrightarrow{n}}_{\mathrm{c}}$ are the normal components of the displacement and force vectors expressed in a local orthogonal triad and ${\overrightarrow{n}}_{\mathrm{c}}$ is the normal between the bodies at the contact node.

Note that conditions in Equation (21) are similar to the Kuhn–Tucker loading–unloading conditions in classical plasticity. The inequality $u_n\le 0$ expresses the non-penetration condition, $F_n\le 0$ expresses the fact that, at each contact point, the normal force is negative in the local triad. Finally $u_n\cdot F_n=0$ is valid for two cases:

• Case 1: There is contact $u_n\le 0$ but $F_n<0$
• Case 2: There no more contact $u_n<0$ but $F_n=0$

In the present work, the Dynamic Explicit resolution procedure is used within the general-purpose FE code ABAQUS/Explicit. The fully coupled constitutive equations presented above together with an iterative implicit procedure for the time integration were implemented using the user subroutine VUMAT.

2.4. 3D Adaptive Remeshing Procedure

In sheet forming, the blank shape, the tools geometry and the forming process parameters define the final product shape after metal forming. An incorrect design of the tools and blank shape or an incorrect choice of material and process parameters can yield a product with a deviating shape or with failures. A deviating shape is caused by spring-back after forming and retracting the tools. The most frequent types of failure are wrinkling (high compressive strains) and necking (high tensile strains). During the numerical simulation of sheet metal forming processes, the large plastic deformations imply a severe distortion of the computational mesh of the domain. In this case, frequent remeshing of the deformed domain during computation is necessary to obtain an accurate solution and complete the computation until the termination of the numerical simulation process. In this field, Borouchaki made great contributions in both 2D and 3D numerical simulations [48,49,50,51,52].

The advent of fast computers over the last few years has reduced the solution time once a mesh with an acceptable quality is provided as input. Hence, to obtain a cost and time effective solution to the forming problem is incremental remeshing of the work-piece at each step deformation. ‘When to remesh?’, and, ‘how to remesh?’ are the two high level issues that must be considered when automating process simulations. The criteria used to trigger an automatic remesh are collectively called the remeshing criteria. Four sources of errors that influence the remesh criteria are:

(i)

Geometric approximation errors;

(ii)

Element distortion errors;

(iii)

Mesh discretization errors;

(iv)

Mesh rezoning or physical errors.

The impact of the different types of errors encountered based on metrics to measure them will key a remeshing step. The process of remeshing focuses on controlling these errors so that the simulation can continue.

• Until recently, the remeshing process was performed manually and potentially took several days for each remeshing (several are typically needed to model the entire process) of 3D domain. In addition, manual remeshing can potentially smooth the geometry thus preventing boundary defects from being detected, or, introduce constraints that result in false prediction of surface defects from process modeling.
• Hence, a 3D modeling system, that would automatically generate a new mesh on the deformed domain and continue the analysis, can dramatically reduce the overall modeling time and result in this technology being widely used in the design of industrial forming processes.

This section presents 3D adaptive remeshing scheme based on the linear tetrahedral element. The application environment for this scheme was established by python script, which integrates the 3D adaptive mesher, the Abaqus/Explicit solver and the point-to-point field transfer algorithm to new mesh. In order to control the mesh size adaptively and optimize the element quality automatically, both the geometrical and physical error estimates criteria are developed in our scheme [47,48,49].

We consider computational deformable domain of R³, each domain Ω being defined from its boundary Γ which is expressed analytically by G₀(Γ). We assume that domains of tool Π_k are rigid. Let us denote by Ω_j,k the subset of deformable domains Ω which are in contact with a given rigid domain Π_k. To construct an initial mesh of each deformable domain Ω, at first each boundary of domain Γ is discretized and then the mesh of domain Ω is generated based on this boundary discretization. The discretization of boundary Γ is obtained from its analytical definition G₀(Γ). The method proposed in [25] is used to construct the initial “geometric” discretization T₀(Γ) of the boundary Γ.

Based on this discretization, an initial tetrahedral coarse mesh T₀(Ω) of deformable domain Ω is generated. This initial mesh can become invalid after a mechanical computation involving large deformations (zero or a negative Jacobian in one or more elements). The new mesh representation must preserve the original topology of the mesh and must form a “good” geometric approximation to the original mesh with respect the criterion related to the shape of the elements.

In the classical Euclidean space, a popular measure for the shape quality of a mesh element K in three dimensions is:

$$Q(K)=\underset{1\le i\le 4}{\min }\left[Q_i(K)\right],Q(K)=\mathsf{\xi }\frac{V(K)}{{\left[{\displaystyle \sum {}^2(e(K))}\right]}^{3/2}}$$

(22)

where V(K) denotes the volume of element K, i the vertex of K, e(K) the edges of K and $\mathsf{\xi }$ is the coefficient such that the quality of a regular element is valued by 1. From this definition, we deduce $0\le Q(K)\le 1$ and that a nicely shaped element has a quality close to 1 while an ill shaped element has a quality close to 0.

The final deformation after the whole simulation is assumed to be obtained iteratively by “small” deformations (which is the case in the framework of an explicit integration scheme to solve the problem). After such a small deformation, rigid domains are moved and deformable domains are slightly distorted (assuming that each mesh element is still valid).

The new geometry G_j(Γ) of boundary Γ can be defined in two ways, either by preserving a geometry close to the one before deformation, or by defining a new “smoother” geometry.

(1)

In the first case, the new geometry is simply defined by the current discretization T_j−1(Γ) of the boundary, and the new mesh nodes of T_j(Γ) are placed on the elements of this discretization.

(2)

In the second case, the new geometry is defined by a smooth curve interpolating the nodes and/or other geometric features of the current boundary discretization T_j−1(Γ). The new nodes are then placed on this curve. The advantage of this second approach (which seems more complicated) is that the geometry of domain Ω remains smooth during its deformation.

The new geometry G_j(Γ) of the domain includes two types of deformations:

(1)

Free node deformations: this type concerns the deformations due to mechanical constraints (for instance equilibrium conditions), freely in the space. In this case, the new geometry of the domain after deformation is only defined by the new position of the boundary nodes as well as their connections.

(2)

Bounded node deformations: these are the deformations limited by a contact with another domain (deformable or rigid tool domains for example). In this case, domain Ω locally takes the geometric shape of domains in contact Ω_k.

Based on the above classification of deformations, the free and bounded boundary nodes can be identified using the Hausdorff distance (δ). It consists in associating with each surface of part a region centered at this surface and in examining the possible intersection between the regions of the considered domain and those of the other domains. A node of the considered domain is classified as bounded if it belongs to one of the regions associated with the other domains or vice versa.

Formally, the region R_δ(e) associated with an edge e is defined by:

$$R_{\mathsf{\delta }}\left(e\right)=\{X\in R^3,\mathrm{d}\left(X,e\right)\le \mathsf{\delta }\}$$

(23)

where d(X,e) is the distance from point X to edge e, and δ is the maximum displacement step of domain Ω.

The above node identification allows us to define the new mesh size of boundary nodes.

• If the node is free, the size is proportional to the curvature radius of the new domain boundary or the new geometry G_j(Γ).
• If the node is bounded, the size is proportional to the curvature radius of the neighboring part of the related domain Ω_k in contact.

The following remeshing scheme is applied to each deformable domain Ω_i after each step increment load j:

(a)

Definition of the new geometry G_j(Γ) after computation of the field solution S associated to mesh T.

(b)

A posteriori geometrical error estimation from S including mesh gradation control to define a new discrete metric map: gap between the new geometry G_j(Γ) and the current boundary discretization T_k−1(Γ). Definition of a geometric size map h_g,j(Γ) necessary to rediscretize the boundary Γ of the domain Ω.

(c)

A posteriori physical error: gap between the physical solution S_j−1(Ω) obtained in Ω and an ideal “smooth” solution considered as the reference solution. Definition of a physical size map h_φ,j(Ω) necessary to govern the remeshing of domain Ω.

(d)

Calculation of size map h_j(Ω_j) = minimum (h_g,j(Γ) and h_φ,j(Ω)).

(e)

Definition of a unique size map with size gradation control parameter (fixed by the users between 1.2 and 2.15) resulting in a modified size map h_j(Ω_j).

(f)

Adaptive rediscretization T_j(Γ) of the domain boundary with respect to the size map h_j(Ω_j|Γ).

(g)

Adaptive remeshing T_j(Ω) of the domain with respect to the size map h_j(Ω).

(h)

Interpolation of mechanical fields F_j−1(Ω) of the old mesh on the new mesh T_j(Ω).

(i)

Loop if necessary.

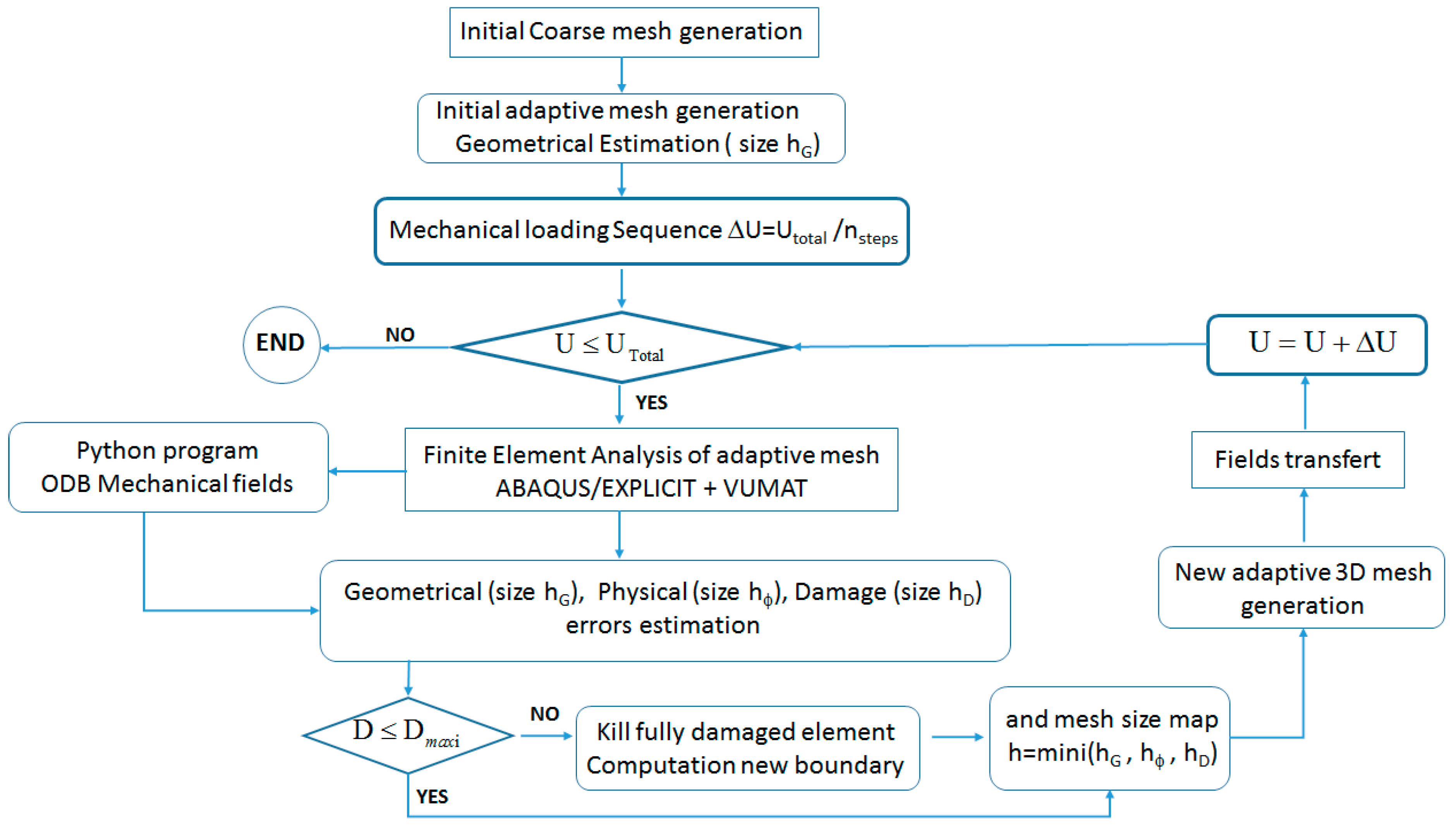
The overall adaptive methodology is implemented in the Optiform mesher package (see Figure 1). It includes the remeshing strategy, the interpolation error and the field transfer from the old mesh to the new one. For the simulations of sheet metal forming processes, a special procedure has been developed in order to execute Abaqus software [47] step by step. At each load increment, and after the convergence has been reached, the overall elements are tested in order to detect the fully damaged elements (elements where the damage variable has reach its critical value in all Gauss points). If so, the fully damaged element is removed from the structure and a new adaptive meshing of the part is worked out. The physical fields are interpolated from the old to the new mesh and the next loading step is worked out.

3. Results and Discussion

This section is dedicated to the validation of the proposed numerical methodology to simulate tensile, shearing, compression, and sheet metal forming processes using Abaqus/Explicit coupled with adaptive remeshing procedure. The characterization of the behavior of a given structure (titanium, copper, steel, and aluminum alloys), needs the knowledge of the material parameters. The difficult and not yet satisfactorily solved problem consists to compute automatically the material parameters under concern, by comparison with the available experimental database.

From a theoretical point of view, this defines a mathematical optimization problem using appropriated inverse analysis termed here as an identification procedure. Two different approaches (deterministic and statistical) exist to relate the problem of parameter identification to a least squares problem. In the deterministic approach, the inverse problem is expressed in a relaxed form and one just trying to minimize a distance between the data from a model and the experimental measurements. In the statistical approach, the inverse problem is seen as the search for the set of parameters which maximizes the probability of carrying out the experimental measurement.

In this study, the inverse constitutive parameter identification using Nelder–Mead Simplex algorithm is used [53,54]. The importance of this identification procedure is proportional to the increasing of the so-called advanced constitutive equations describing many coupled physical phenomena. The identification of the isotropic, isothermal elastoplastic constitutive equations accounting for isotropic hardening and ductile damage is based on the following steps [22,55]:

• The used database contains only uniaxial tensile tests conducted on a given specimen until the final fracture;
• The plastic parameters (A, B, C, n, ${\dot{\overline{\mathsf{\epsilon }}}}_0=1$) are determined on the hardening stage when damage effect is very small and can be neglected. The strain velocity is supposed fixed;
• The damage parameters $\left(Y_0,\mathsf{\alpha },\mathsf{\beta },\mathsf{\gamma },D_{\mathrm{c}}\right)$ are determined using the softening stage of the stress-strain curve;

The inverse identification procedure is performed by integrating the above constitutive equations on a single material point submitted to the tensile loading path using Matlab Software (Nelder–Mead Simplex algorithm) and the user’s subroutine. Using material parameters determined above, the real specimen in tensile, shear or compression test is simulated by FEA and the global force-displacement curve is compared to the experimental one. If needed, the material parameters are adjusted and new FEA simulations are performed until the experimental and numerical force-displacement curves compares well.

Some obvious phenomena, like strain localization and damage evolutions, were presented in order to test the capability of the proposed fully coupled model and adaptive remeshing scheme to simulate the sheet metal forming process like blanking, multi-point drawing, single incremental forming and deep-drawing. All the numerical simulation are performed on the Dell Precision T7600 Workstation, 2× Intel Xeon E5-2670 2.6 GHz 4 CPU Cores Processors; 128 GB Memory, Ubuntu Linux 64Mbit.

3.1. Uniaxial Tensile Test of XES Steel Sheet

The proposed constitutive equations are used to predict the stress-strain curve of XES steel which is used in the tensile experiment [20]. The fully coupled damage constitutive equations are implemented to predict the maximum stress ${\overline{\mathsf{\sigma }}}_{\max }=383\mathrm{MPa}$, the plastic strain at damage initiation ${\overline{\mathsf{\epsilon }}}_{\mathrm{c}}^{\mathrm{p}}=0.22$ and the plastic strain to fracture ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}=0.26$. The damage evolves from the damage initiation to the fracture D_max = 0.99 and the material stiffness degrades from maximum tensile force to zero. The best parameters found to fit the experiment stress-strain curve are shown in

Table 1. Material parameters of the used XES steel [55,56].

E (GPa)	$\mathsf{\nu }$	A (MPa)	B (MPa)	n	C	Y0 (MPa)	α	β	γ (MPa)	${\dot{\overline{\mathsf{\epsilon }}}}_0^{}$
210	0.29	150	448	0.406	0.025	0	2	1	0.37	1

. The validation focused on the tensile specimen with the dimension of 8.9 mm × 3.2 mm × 0.5 mm subject to displacement load of V = 5 mm/s (see Figure 2).

The tensile tests are simulated firstly without remeshing for both coupled and uncoupled damage with plasticity cases. The 3D hexahedral finite elements with reduced integration (C3D8R) are used and a fine mesh (size is h_min = 0.01 mm in the region of plastic strain localization) is applied. Secondly, the remeshing procedure is applied, with the parameters given in

Table 2. Adaptive remeshing parameters for the tensile test of the XES steel.

hmin (mm)	hmax (mm)	Physical Adaptive	Critical Value Dc	Dmax
0.05	2.0	Equivalent plastic strain	0.48	0.99

, to simulate the localization of the equivalent plastic strain and the ductile damage. The iso-values of the damage in the specimen with/without remeshing procedure using tetrahedral finite elements are shown in Figure 3:

(1)

In the coupled model without remeshing procedure (Figure 3b), the damage localization appears in the middle at a displacement of U = 0.5 mm. Then, two shear bands are formed quickly at a displacement of U = 1.24 mm. The damage variable reaches to the maximum value D_max = 0.99 in the cracked zones at a displacement of U = 1.5 mm.

(2)

In the uncoupled model (Figure 3a), no damage and shear bands localization exist.

(3)

In the coupled model with remeshing procedure the damage focused in the center of the specimen in Figure 3c and the shear band extended from center to the two sides along the direction of a 45°. Then, the crack generates in the center at a displacement of U = 1.0 mm and propagates along the shear band when the tensile displacement increased from U = 1.586 mm to U = 1.587 mm (see Figure 4).

Figure 3. Ductile damage localization in various cases.

Figure 3. Ductile damage localization in various cases.

Figure 4. Micro-crack initiation, growth and propagation in shear band localization [57].

Figure 4. Micro-crack initiation, growth and propagation in shear band localization [57].

The predicted force-displacement curves are compared with the experiment result in Figure 5. From these figures, one can observe the predicted results fit well the experiment values in the plastic stage and the effect of the damage-induced softening are clearly in the simulation using fully coupled damage constitutive equations.

The mesh size sensibility was also studied by comparing the tensile force-displacement curves for three minimum values h_min = 0.5, 0.1 and 0.05 mm as shown in Figure 6. It is clear that the damage evolution is sensitive to the element size, and the damage variable accumulates more quickly in the smaller mesh size.

Table 3. Remeshing time performance of tensile test.

	Element Number	CPU	Global Error Estimation
Coupled model with remeshing: hmin = 0.05	156,847	1 h 13 min	2.1%
Coupled model with remeshing: hmin = 0.1	88,168	55 min	8.5%
Coupled model with remeshing: hmin = 0.5	35,128	41 min	17%
Coupled model without remeshing	29,889	22 min	-
Uncoupled model without remeshing	15,289	15 min	-

presents the time performance (CPU time, number of elements) of numerical simulation with different mesh size h_min = 0.05, 0.1 and 0.5 mm). It is possible to confirm remeshing with small mesh (156,847 elements) advantage even for higher adaptive refinement compared with the coarse mesh (35,128 elements). A significant reduction in the overall error and CPU time (170%) in tensile stresses force is observed for fine meshes. These results prove that the proposed numerical methodology using elastoplastic fully coupled ductile damage model and adaptive remeshing procedure is reliable to predict the material behavior.

3.2. Pure Shear Test of Titanium Alloy Sheet

In the above tensile simulation, a short shear band was already observed after damage localization and propagation. With respect to the tensile test, there is no sectional reduction in the shear sample and pure shear stress conditions are imposed. The application to shearing test is compared with the Peirs’ work in literature [20]. The shear specimen of Peirs was recently studied and compared with other shear geometries proposed by Abedini [58] in which its capabilities for constitutive and fracture characterization of sheet metals was discussed. The low stress triaxiality in shear reduces the damage-accumulating rate, which can lead to a large strain than that in tensile test. The used shearing specimen dimension is shown in Figure 7.

The specific center shape of the specimen is adapted in order to concentrate shear stress in this zone. The titanium alloy was used, but the plastic hardening and damage parameters are estimated from the experimental shear curve (see

Table 4. Material parameters used for shear test of titanium alloy [55,56].

Plastic Hardening Parameters				Ductile Damage Parameters
A (MPa)	B (MPa)	C	n	Y0 (MPa)	α	γ (MPa)	β
951	892	0.027	0.37	0.15	2	9.3	1

). With these parameters, the maximum equivalent stress is about ${\overline{\mathsf{\sigma }}}_{\max }=1340\mathrm{MPa}$, and a ductility of ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}=0.297$ [55,56]. As shown in Figure 8, the coupled material model had fit the experiment value well when equivalent plastic strain less than ${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}=0.21$ and the material damage accumulate rapidly to D_max = 0.99 when equivalent plastic strain ${\overline{\mathsf{\epsilon }}}_{}^{\mathrm{p}}=0.297$. The parameters of remeshing procedure are given in

Table 5. Adaptive remeshing parameters for the pure shearing test.

hmin (mm)	hmax (mm)	Physical Adaptive	Critical Value Dc	Dmax
0.05	2.5	Equivalent plastic strain	0.3	0.999

and the initial coarse mesh for adaptive remeshing scheme with 3000 linear tetrahedral finite elements is illustrated in Figure 7.

The simulation of shear test is also under a load of constant velocity (V = 10 mm/s). Firstly, the predicted ductile damage generated not in the center of shearing specimen but on both sides where near to the shear band for U = 0.40 mm (Figure 9a). Afterwards, the damage is initiated in the center of the specimen for U = 0.60 mm (Figure 8b) and propagated fast until U = 0.72 mm (Figure 9c). Then, the micro-crack is localized along the shear band when the specimen is completely damaged for U = 0.74 mm. As seen in Figure 9d, the size of finite mesh was refined adaptively to the minimum value in the region where micro-crack propagated. Finally, the specimen fractured when the tensile displacement was between U = 0.74 mm and U = 0.75 mm. The damage variable and the 3D damage section were illustrated in Figure 9e.

This simulation process described a very clear phenomenon of the shear band formation and the crack propagation. The shear band and the crack propagation direction in pure shearing stress condition are in a straight line, which is obviously different comparing with the tensile test. Figure 10 shows the comparison of the predicted force versus displacement curves for this fully coupled model obtained with adaptive remeshing under a controlled displacement with the constant velocity. According to this figure, can note that the strong effect of the softening induced by the damage occurrence giving a final fracture of the specimen around U = 0.75 mm. The maximum force is F_max = 1504 N reached for U = 0.68 mm.

3.3. Compression of Thin Truncated Aluminum Sheet Cylinder

The third test concerns the study of truncated aluminum alloy 5086 sheet cylinder compression. The thick truncated cylinder sheet of thickness t = 5 mm and radius R = 22.5 mm is compressed between rigid flat tools that tend to flatten it a displacement of U = 10 mm (see Figure 11). Following with the move of the top tool, the localization phenomenon of damage, the formation of a crack and its propagation to the final fracture of the truncated cylinder was clearly simulated. The aluminum alloy 5086 is primarily alloyed with magnesium and is a high strength structural alloy. It is not strengthened by heat treatment, instead becoming stronger due to strain hardening, or cold mechanical working of the material. The chemical composition of the used alloy is: Al 95.4%, Mg 4%, Cr 0.15%, and Mn 0.4%. The elastic-plastic and damage parameters of the aluminum alloy (5086) are given in

Table 6. Material parameters of aluminum alloy 5086 [55,56].

Elastic Parameters	E (GPa)	$\mathsf{\nu }$
	85	0.38
Plastic Parameters	A (MPa)	B (MPa)	C	n
	150	460	0.025	0.41
Damage Parameters	Y0 (MPa)	α	γ (MPa)	β
	5	2	0.8	0

. The plastic parameters of the material are obtained, from the experimental curves, in which the maximum stress is about ${\overline{\mathsf{\sigma }}}_{\max }=366\mathrm{MPa}$ for equivalent plastic strain ${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}=0.17$ and then the material stiffness deteriorates to zero when equivalent plastic strain equal to ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}=0.27$ (Figure 12) [55,56]. The numerical meshing parameters of the compression test are presented in

Table 7. Adaptive remeshing parameters for the compressive test of aluminum alloy 5086.

hmin (mm)	hmax (mm)	Kill Element	Physical Adaptive	Critical Value
0.5	1.0	Dmax = 0.99	${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}$	0.27

. The proposed fully coupled methodology will be applied to improve compression test by avoiding the ductile damage occurrence in order to obtain a final part free from any defect.

Firstly, the damage generated at the four corners of the specimen, which contact with the compressive tools. After the accumulation of the plastic deformation, the damage in the center of the specimen was appearing as in Figure 13a when the top tool moved to U = 6.0 mm. Initially the damage is initiated at the four corners of the cylinder that come into contact with the top and bottom flat tools. After an accumulation of the plastic deformation is located in the center of the cylinder and the beginning of damage appeared for a displacement of the upper tool of U = 6.0 mm as shown in Figure 13a. The damage accumulated is propagated more rapidly from the center to the four corners of the cylinder at each compression stage. When the top tool move to U = 8.1 mm, the fully damaged element was generated and deleted firstly in the center as shown in Figure 13b. Two shear bands along the direction of 45° and 135° generated quickly after the center elements lost their stiffness. The crack propagated from center to the four corners along these two shear bands, and one main crack elongated faster than another as shown in Figure 13c. Finally, the specimen fractured when the top tool moved from U = 8.7 mm and U = 8.8 mm. The damage variable in the cross section of damaged specimen illustrated in Figure 13d. The final experiment fracture is presented in Figure 13f and two obviously cracks elongated from the center to the four corners. It is clear that the macro-crack initiation and propagation after damage localization were well simulated in the model using adaptive remeshing procedure for compressive test.

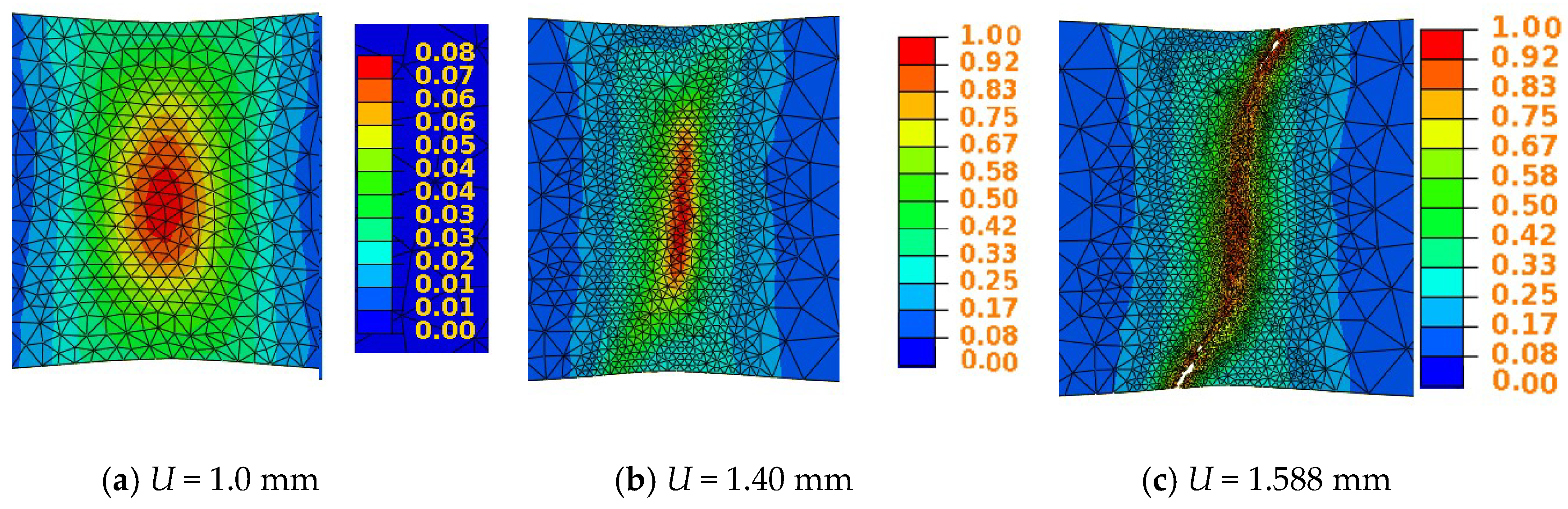
The predicted force-displacement curves using the fully coupled model and adaptive remeshing procedure under a controlled displacement was compared to the experiment values in Figure 14. From this figure, the effect of the softening induced by the damage occurrence giving a final fracture of the specimen around U = 8.7 mm which is a little earlier than that in experiment of U = 9.7mm. The predicted maximum force for coupled model is F_max = 105.7 kN which is also a slightly smaller than that of experiment value F_max = 106 kN. It is remarkable to see that the maximum force and the displacement corresponding to the final specimen cutting are predicted with a good precision (0.8% error) but over estimates the decrease of the compression-force in the softening stage.

However, for uncoupled approach, the total force increased monotonously and had non-degradation of the structure and the specimen is not completely damaged (see Figure 13e). Under the help of the adaptive remeshing procedure, only the coupled constitutive equation can predict the damage behavior clearly for compressive test.

3.4. Blanking of Oxygen-Free-High-Conductivity (OFHC) Copper Sheet Metal

The main purpose of the numerical simulation is to “virtually” predict a final sheared edge free from any defect (ratio of the burnished edge, burr height), to estimate the residual stress profile through the thickness and the maximum blanking force versus displacement. The punch force and penetration at fracture are important for tool and machine dimensioning. The shape of the cut edge and the burr height are crucial for the final product quality. The prediction of these parameters by numerical adaptive simulation may be very helpful in blanked or sheared part design.

This section focuses on simulating the sheet metal blanking process using the fully coupled model using the numerical methodology. The sheet metal is oxygen-free-high-conductivity (OFHC) copper.

The numerical model will be validated through comparing the blanking force and the profiles of sheared edges with the experimental values [59]. The geometrical model and the boundary conditions of cylindrical sheet metal blanking are described in Figure 15. For the friction of contact, the surface to surface contacts is defined between tools and piece; the self-contact is defined in the piece when some fully damage elements are removed. The friction coefficient between the blank and tools is taken as representing ‘dry’ friction without lubrication is used in both surface to surface contact (punch/die and work-piece) and self-contact (fractured surface).

The blanking parameters used to blank the sheet of OFHC copper sheet are presented in

Table 8. Geometrical parameters of sheet blanking.

t (mm)	RP = RD (mm)	J (mm)	DP (mm)	DD (mm)	Blanking Frequency	Friction Coefficient Tools/Sheet µ
0.58	0.01	0.0145	3.5	3.53	700 (stroke/min)	0.02

. The material parameters used in this model are listed in

Table 9. Elasto-plastic and damage parameters of the oxygen-free-high-conductivity copper [55,56].

E (GPa)	$\mathsf{\nu }$	A (MPa)	B (MPa)	n	C	Y0 (MPa)	α	β	γ (MPa)	${\dot{\overline{\mathsf{\epsilon }}}}_0^{}({\mathit{s}}^{-1})$
124	0.34	90	292	0.4	0.025	0.38	0.2	0.3	0.37	1

and it accurately predict the material behavior with a maximum stress of ${\overline{\mathsf{\sigma }}}_{\max }=350\mathrm{MPa}$, ${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}=0.77$ and ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}=0.9$. In order to save the computing cost, quarter of the round sheet is considered. The round sheet is initially discretized by a very coarse mesh (453 linear tetrahedral elements as shown in Figure 16a). Geometrical error estimation and the contact region with tools (punch and die) with respect the minimum size h_min then control the adaptive mesh (

Table 10. Adaptive remeshing parameters for the blanking of the OFHC sheet.

hmin (mm)	hmax (mm)	Dc	Dmax	δ (mm)
0.015	5	0.5	0.99	0.026

). In the following steps, the mesh regenerates adaptively according to the plastic strain and the damage variable. When the damage accumulates D_max > 0.99, the element will be removed and a new boundary will be generated. The macro-crack initiation and propagation during the sheet blanking were analyzed at each punch penetration in Figure 16b for U = 0.01 mm and in Figure 16c for U = 0.2 mm. The copper sheet was fully cut for U = 0.33 mm.

The predicted force versus displacement with/without adaptive remeshing is compared with the experiment results in Figure 17. Note that the predicted result without adaptive remeshing deviates to the experiment values more and more severely with the increasing of the punch displacement. These differences are due essentially to the qualities of finite elements, despite the used large number of elements (230,150) and to the convergence of the computational procedure. Also, note that the overall error is very large (19.0%) in the case without remeshing with significant time calculations (3 h 48 min). In the case of adaptive remeshing procedure, the predicted curve is in agreement with the experiment values with a maximum force of F_max = 3235 N (experimental value F_max = 3353 N) and displacement at fracture U_f = 0.34 mm (experimental value U_f = 0.36 mm). Also note that in this case using a number of elements not high (54,519), the overall error is small (1.23%) with relatively correct time calculation (2 h 17 min) (see

Table 11. Adaptive remeshing time performance of blanking process simulation.

	Element Number	CPU (hours)	Global Error Estimation
Without remeshing	230,150	3 h 48 min	19%
With remeshing	54,519	2 h 17 min	1%

).

The depth of Rollover (L_R), Burnish (L_B), Fracture (L_F) and Burr (L_Burr) define the morphology of the sheared edge of sheet. Compared to the experimental results given by Husson [60], the predicted sheared edges with L_R = 0.5 mm, L_B = 40 µm, L_F = 268 µm and L_Burr = 260 µm using both the models with and without adaptive remeshing scheme are shown in Figure 18. It is clear that the morphology of sheared edge predicted by adaptive remeshing scheme (middle) is similar to experiment one (right). The rollover depth L_r = 55 mm and burnish depths L_B = 271 mm are a little bigger than the experimental ones (L_r = 40 mm and L_B = 268 mm) and there is no burr generate in this blanking condition. The fracture angle α and rollover radius R are almost the same. Against in the case of a model without remeshing procedure the sheared edge profile obtained remains unrepresentative of the experimental result and is not in agreement with experimental profile. For these results, we can nothing that only the adaptive remeshing scheme is able to predict the sheared edge profile of sheet cutting (see

Table 12. Predicted blanking performance and sheet characterize with and without remeshing.

	Fmax (N)	Uf (mm)	α	R (mm)	LR (µm)	LB (µm)	LF (µm)	LBurr (µm)
Without remeshing	6640	0.53	-	0.65	56.5	270	248	55
With remeshing	3235	0.35	7°	0.53	55	271	242	0
Experiment	3353	0.36	5°	0.50	40	268	260	0

).

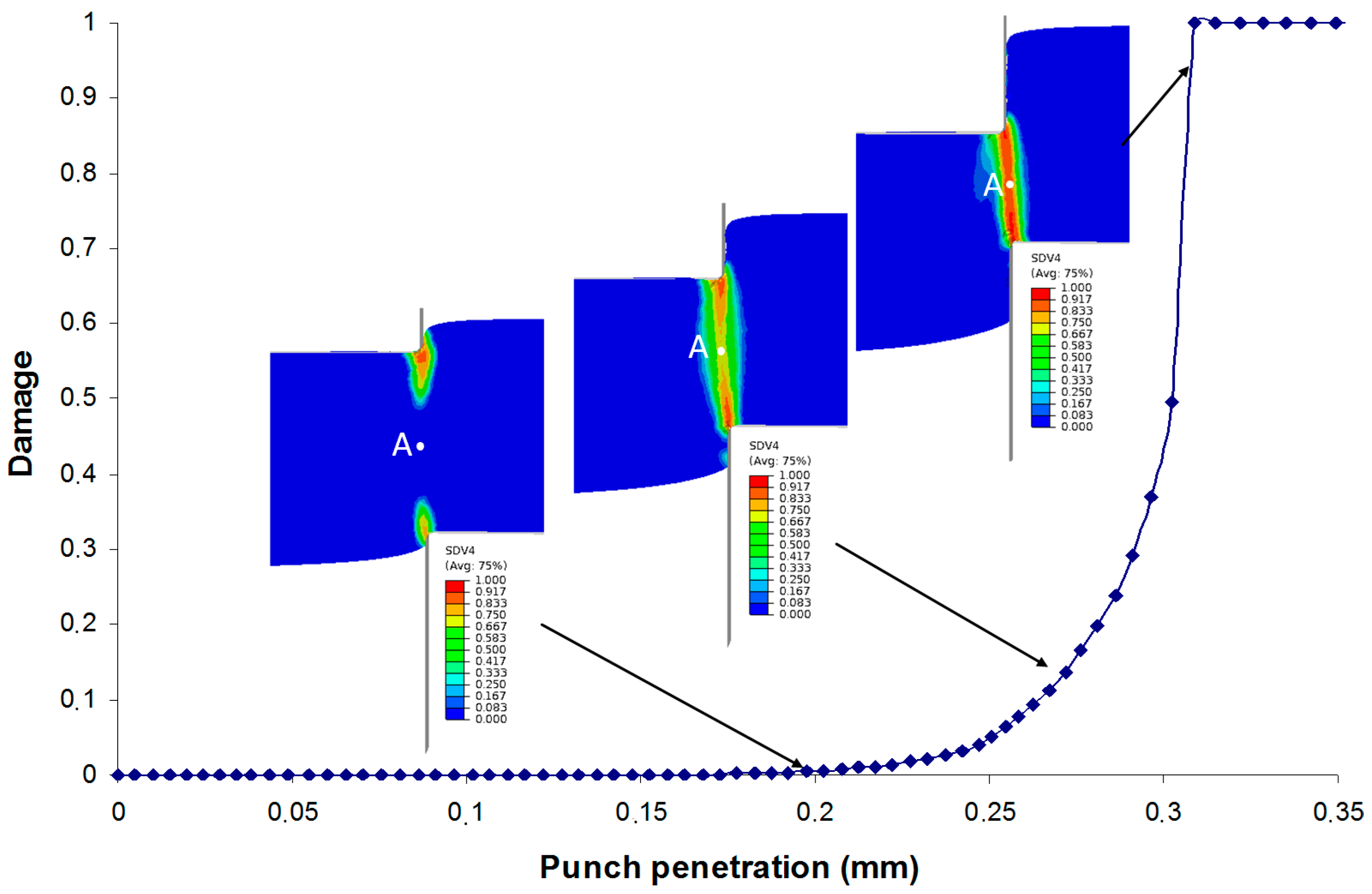
Figure 19 illustrates the damage evolution at the sheared edge during blanking process. We observe that the damage starts from two sides which contact with the tool tips (U = 0.10 mm) and extends to the center of sheared edge (U = 0.2 mm). When the punch achieves U = 0.31 mm, the elements fully damage at the sheared region are removed and a macro-crack is formed.

3.5. Multi-Point Forming of Thick Steel Sheet

Curved sheet metal parts are widely used in automotive and aerospace industries. Traditional deep-drawing or hydroforming process is difficult to deform plastically thick sheet. The fundamental component in the Multi-Point Forming (MPF) press is a pair of matrices of punches, which approximates to a continuous forming surface of dies [61]. MPF is a flexible forming technology, which is suitable to produce customized products. The factors influencing the shape accuracy of the final product are analyzed in order to minimize the spring-back.

The objective of the Multi-Point forming of thick steel sheet simulation is to highlight the abilities and capacities of numerical procedure to simulate complex shapes and its relative robustness of the quality of the final product obtained by discrete of the multipoint tool contact. According to the fact that the MPF operation is axisymmetric, only half of the billet section is modelled. Figure 20a shows the upper and lower matrices of square punches with curved ends in the MPF press, 100 punches for an effective forming surface of 1700 mm × 1700 mm. The initial thick sheet of steel material is 1500 × 1500 mm² and 40 mm of thickness is discretized with linear tetrahedral finite element. Tools (punch and die) are supposed as rigid surfaces. The output of the simulation is given in terms of the sheet profile, the strain history as well as the punch forming forces. Comparison between the simulation results and the experimental data is made.

The materials parameters of the used steel should be determined using the experimental results obtained from classical tensile tests conducted until the final fracture of the specimens. The damage parameters have been estimated in order to have a maximum stress ${\overline{\mathsf{\sigma }}}_{\max }=1200\mathrm{MPa}$, for ${\overline{\mathsf{\epsilon }}}^{\mathrm{p}}=12\%$ and a rupture of ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}=35\%$. A master–slave contact approach is used in the analysis where the tools are considered as the master surfaces, and the top and the bottom surfaces of the blank (surface facing the punch and the die) constitutes the slave surfaces. Friction (with coefficient $\mathsf{\eta }=0.12$) is introduced using Coulomb model and the interaction between the sheet and the billets is formulated using finite sliding approach, which allows for the possibility of separation between the two surfaces during sliding.

The adaptive remeshing simulation is performed under a load of constant velocity (V = 2 mm/s) and the small punch displacement U = 10 mm of the sheet were loaded by numerous small time steps. The simulation consists, in the present case, of 230 computational steps such an adaptive remeshing process ensures a maximum error in the whole computational domain to be limited by the threshold excepted in the zone where the element size h_min = 0.1 mm and h_max = 5 mm is achieved (see

Table 13. Adaptive remeshing parameters for Multi-Point Forming (MPF) process.

hmin (mm)	hmax (mm)	${\overline{\mathsf{\epsilon }}}_{\mathbf{c}}^{\mathbf{p}}$	${\overline{\mathsf{\epsilon }}}_{\mathbf{max}}^{\mathbf{p}}$	δ (mm)
0.1	5	0.1	0.35	2.5

).

Figure 20b–g illustrates the predicted deformed sheet ate each step with respect to the punch displacement. Noting that the mesh is only adapted when the punches are close to the sheet for $R_{\mathsf{\delta }}(e)\le 1\mathrm{mm}$. It can also be noted that the plastic strain and damage (D_max < 0.12) remains very low. Quantitative comparison with experimental result provides the performance of the proposed approach (Figure 20h).

The curves of forming force versus punch are presented in Figure 21 with and without remeshing. It can be seen clearly that the forming force depends on the contact state. During the initial forming step the punch force is small estimated at F_punch < 500 kN, and it increases very slowly since only a few punches contact with sheet (F_punch < 750 kN). After the displacement of punch reaches a value about the 3/4 of the total tool move more and more punches get into contact with sheet and the forming force increases sharply. At the end of MPF process the forming force reaches its maximum since all punches contact with sheet (F_punch = 3500 kN).

The formed work-piece profiles, before and after the spring-back, are shown in Figure 22. From these results, it is concluded that for thick sheet the spring-back during the MPF is very small.

Table 14. Adaptive remeshing time performance of MPF process simulation.

	CPU Time	Number of Steps/Increments	Initial n° of Elements	Final n° of Elements
Without remeshing	29 h 48 min	100 increments	700,143	700,143
With remeshing	4 h 17 min	230 remeshing steps	15,000	284,700

presents the time performance (CPU time, number of elements) of numerical simulation performed on Dell Precision T7600 Workstation, 2× Intel Xeon E5-2670 2.6 GHz 4 CPU Cores Processors; 128 GB Memory with and without remeshing. It is possible to confirm remeshing advantage even for higher adaptive refinement compared with the very fine mesh used here as reference (700,143 tetrahedral elements). A reduction of CPU time about approximately 75% has been obtained with the remeshing procedure (4 h 17 min) compared to the simulation without remeshing obtained with very fine mesh (700,143 elements).

3.6. Incremental Sheet Forming of Titanium Conical Shape

The study will be focused on Numisheet’2014 benchmark for the manufacturing of a truncated cone shape made by single point incremental forming process (SPIF). The incremental step-down size (∆z) is the amount of material deformed for each revolution of the forming tool (similar to depth of cut in machining) which does not require dies [62]. The advantages of this process are the flexibility of forming process for the manufacturing of complex shapes. Several applications of this process exist in the medical field for the manufacturing of personalized titanium prosthesis (cranial plate, knee prosthesis, etc.) due to the need of product customization to each patient. The CAD package CATIA is used to create solid models of parts and the tool path is generated according to the obtained profile. A 3-axis CNC machine is generally used to control the movement of the spherical tool. Tool trajectory is created and connected using a step or a spiral transition method [63,64,65,66,67,68].

The internal roughness of SPIF shaped component is influenced primarily by the tool (dp) and step (ΔZ) sizes, as other factors such as, sheet thickness, material properties, forming angle, feed rate and etc., may affect both the internal and external roughness [54,55,56,57,58]. The influence of forming speed, both rotational spindle speed N and feed rate V_f had an important effect on the heat generation due to the friction with the sheet. Too high friction generates an increase of temperature and sheet damage [47,48]. In this study, the forming conditions (see

Table 15. Single point incremental forming process (SPIF) process parameters.

ti	rc	h	dp	ΔZ	ØD	α	N	Vf
0.5 mm	5 mm	40 mm	5 mm	0.5 mm	130 mm	50°	40 RPM	600 mm/mm

) are adopted for the SPIF with rotational spindle speed N = 40 revolutions per minute (RPM) and feed rate V_f = 6000 mm/mm. Truncated cone that was formed using continuous spiral tool paths (Figure 22) also in order to achieve smaller surface roughness and to avoid tool entry and exit marks.

This section presents simulation results of the SPIF to produce a truncated conical height h = 40 mm titanium Ti-6Al-4V sheet. The effective working area of the initial circular specimen was ∅D = 130 mm and thickness t_i = 0.5 mm. The forming was made with semi hemispherical punch X160CrMoV12 steel in order to obtain prototypes according to the desired profiles. The plastic parameters of Ti-6Al-4V sheet presented in

Table 16. Elasto-plastic parameters of Ti-6Al-4V sheet [60,61].

A (MPa)	B (MPa)	C	n	${\dot{\overline{\mathsf{\epsilon }}}}_0^{}({\mathit{s}}^{-1})$
968	380	0.0197	0.421	1

was obtained following uniaxial tensile tests [59].

After incremental forming, visual control is performed first with goal to detect potential defects and estimate surface finish. On the both plates, the only problem identified was a slight increase in roughness of internal surface in the zone of the maximum deformation. The rest of internal surface was smooth and without tool marks. Dimensional control of the obtained parts was performed by coupling with the original one. For that purpose, both replicas were scanned applying the same measuring procedure. The obtained clouds of points are then transformed to CAD model and compared with the desired CAD profile.

The FEA simulation of conical forming design of single point incremental sheet forming SPIF presented in Figure 23 is performed on Dell Precision T7600 Workstation, 2× Intel Xeon E5-2670 2.6 GHz 4 CPU Cores Processors; 128 GB Memory, with same experimental working conditions. The friction of contact with coefficient $\mathsf{\eta }=0.14$ and the surface-to-surface contact formulation are defined to characterize the interaction between the punch and the sheet.

The main outputs results are the final shape of the sheet and the evolution of the thickness in a cross-section along the symmetric axis. The adaptive remeshing simulation is performed with fully coupled model under a load of constant velocity and the small punch displacement loaded by numerous incremental path (

Table 17. Adaptive remeshing parameters for SPIF.

hmin (mm)	hmax (mm)	${\overline{\mathsf{\epsilon }}}_{\mathbf{c}}^{\mathbf{p}}$	${\overline{\mathsf{\epsilon }}}_{\mathbf{max}}^{\mathbf{p}}$	δ (mm)
0.15	10	0.012	0.30	2.5

). During the SPIF simulation many elements are refined and coarsened, so as a result 1500 computational steps such an adaptive remeshing process ensures a maximum error in the whole computational domain to be limited by the threshold excepted in the zone where the element size h_min = 0.5 mm and h_max = 10 mm is achieved.

Table 18. Adaptive remeshing time performance of SPIF.

	CPU Time	N° Steps/Increments	Initial n° of Elements	Final n° of Elements
Without remeshing (coarse mesh)	06 days and 19 h	Stopped, convergence problem	100,000	100,000
Without remeshing (fine reference mesh)	09 days and 15 h	2460 increments	300,477	300,477
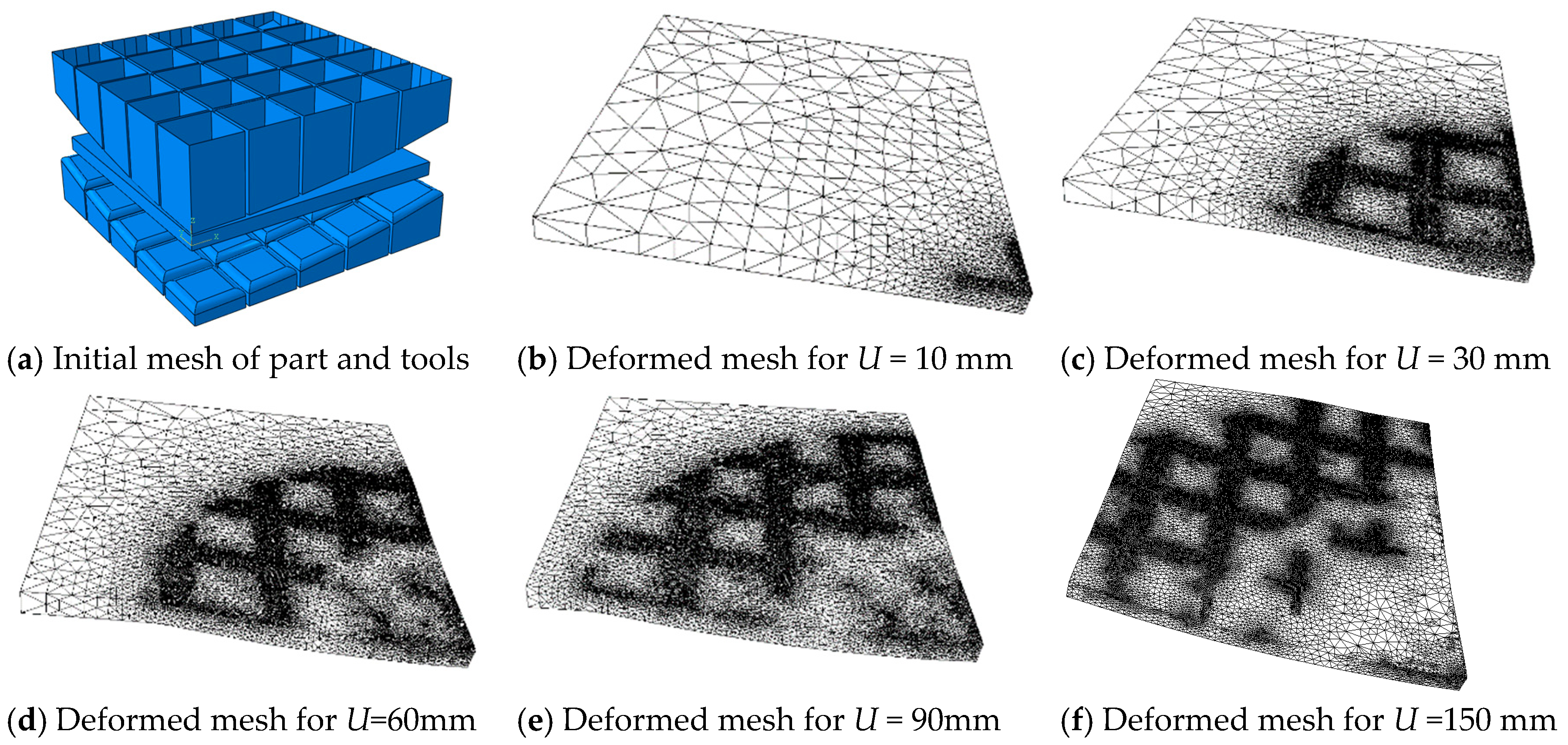
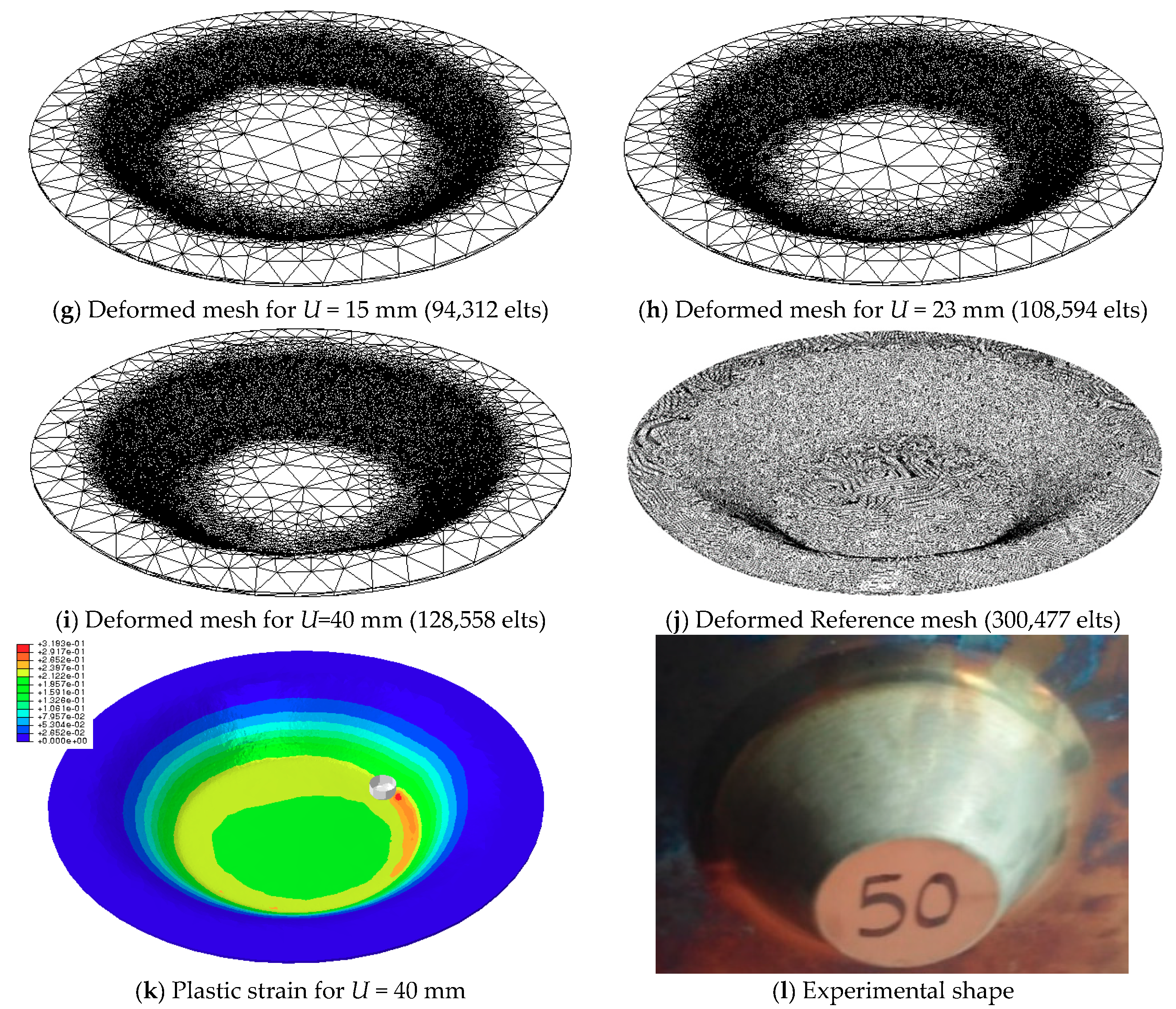
With remeshing	18 h and 20 min	1500 remeshing steps	2,853	128,558

presents the adaptive remeshing time performance for different level of refinement (CPU time, final sheet shape profile, convergence and strain thickness distribution). It is possible to confirm remeshing advantage even for higher adaptive refinement compared with the very fine mesh used here as reference (300,477 tetrahedral elements). The results are quite similar between the reference case and the remeshing process using high number nodes per edge.

They are higher with remeshing because the mesh used is coarser than the reference one. It is notable that the results (CPU time, convergence and sheet strain) are sensitive to the variation of the number of elements. A reduction of CPU time about approximately 85% has been obtained and at the same time good simulation results are achieved and compared to reference results. Figure 24b–j illustrates the deformed sheet at each step with respect to the spherical punch travel and the number of element used at the step forming. Noting that the mesh is only adapted when the punches are close to the sheet for $R_{\mathsf{\delta }}(e)\le 0.12\mathrm{mm}$. It can also be noted that, the plastic strain (${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}<0.3$) remains low and no damage occurs during forming process. Quantitative comparison with experimental result provides the performance of the proposed approach. Figure 25 and Figure 26 indicate a good prediction of the conical shape and the cross section thickness along central X-axis for compared with the experimental and the desired profiles. A lower thickness reduction is observed on the bottom surface of deformed sheet.

3.7. Deep Drawing Sheet Forming of a Front Door Panel

The last example concerns the numerical simulation of a front door panel proposed at Numisheet’2002 (Figure 27). The main goal is to illustrate the capability of the proposed fully coupled model and the numerical methodology to simulate complex shape part. The material properties used in the simulation curved mild steel with the initial thickness of t_i = 0.78 mm are shown in

Table 19. Elasto-plastic parameters of mild steel [60,61].

A (MPa)	B (MPa)	C	n	${\dot{\overline{\mathsf{\epsilon }}}}_0^{}({\mathit{s}}^{-1})$
203.39	645.24	0.010	0.25177	1

.

Solid linear tetrahedral finite elements (2628 elements) are used to discretize initially the curved blank (Figure 28a). The tools (lower punch, upper die, and blank-holder) whose geometry is presented on Figure 27 are discretized by rigid surfaces. A master–slave contact approach is used in the analysis where the tools are considered as the master surfaces, and the top and the bottom surfaces of the blank (surface facing the punch and the die) constitutes the slave surfaces. Friction (η = 0.15) is introduced using Coulomb model and the interaction between the blank and the tools is formulated using finite sliding approach, which allows for the possibility of separation between the two surfaces during sliding. The punch moves with the total displacement U = 130 mm, die and blank-holder tools are supposed fixed.

Meshes adapted to the lower punch curvature surface corresponding to different punch displacement (U = 30, 40, 50, 60, 80, 100, 120, and 130 mm) are given in Figure 28. The simulation is done using an initial coarse mesh (2628 elements), the deformed mesh is again refined uniformly at each punch displacement and the refinement is activated in regions of large curvature of tools using the remeshing parameters (

Table 20. Adaptive remeshing parameters for deep-drawing.

hmin (mm)	hmax (mm)	${\overline{\mathsf{\epsilon }}}_{\mathbf{c}}^{\mathbf{p}}$	${\overline{\mathsf{\epsilon }}}_{\mathbf{max}}^{\mathbf{p}}$	δ (mm)
1.0	15.0	10%	42%	2.5

). The final front door panel sheet is plastically deformed with small plastic strain ${\overline{\mathsf{\epsilon }}}_{\max }^{\mathrm{p}}<15\%$ (see Figure 28j) and no damage and wrinkling are occurred.

4. Conclusions

The paper is dedicated to the study of the multi-physical coupling in sheet metal forming. The standard framework of the thermodynamics of irreversible processes with state variables is used to derive a fully coupled elasto-visco-plastic equations accounting for nonlinear hardening and ductile damage. First, the proposed model had been validated by comparing predicted force-displacement curves in tensile, compressive and shearing tests. During the simulation of tensile, shearing and compression tests, the coupled damage constitutive equations were validated and the damage behavior in these various stress conditions were well simulated under the help of adaptive remeshing scheme. In practice, it is not easy to get the convergence of the problem without remeshing, and the elements that distort will lose their accuracies of reflecting the actual situation. In contrary, the adaptive remeshing scheme constantly optimized the element quality and refined the mesh size in the whole model. The finest finite elements (size and quality) were obtained in the front of crack, and the crack can propagate easily and accurately. The numerical analysis based on geometrical and physical criteria is integrated in a computational environment using the ABAQUS solver and OPTIFORM mesh. Applications are made to complex sheet metal forming.

It has been demonstrated that only the strong coupling between elasticity, plasticity and ductile damage effect at large plastic strain with contact/friction is able to predict the mechanical field in some dynamic metal forming or machining processes. In addition, the 3D solid finite element adaptive remeshing procedure of deformable sheet is capable to optimize the element quality and refined the mesh size in the whole model or in the crack zone.