A New Approach to Simulate HSLA Steel Multipass Welding through Distributed Point Heat Sources Model
Abstract
:1. Introduction
- Physical properties constant at room temperature (λ and α), independent of temperature;
- Point heat source moves in a straight line with constant speed ν;
- No energy generated or consumed within the plate, i.e., Q0 = 0;
- All the heat flow is transmitted by conduction. Radiation and convection through surfaces are neglected;
- The plate is semi-infinite, with a thickness d;
- The initial condition is defined by Equation (2).
- The boundary conditions are defined by Equation (3);
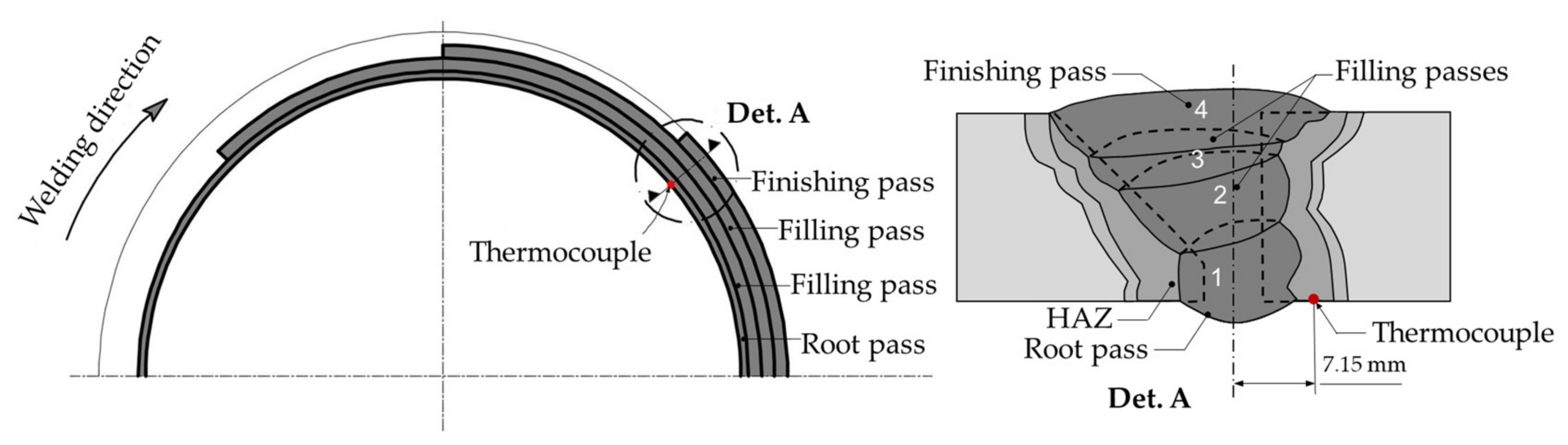
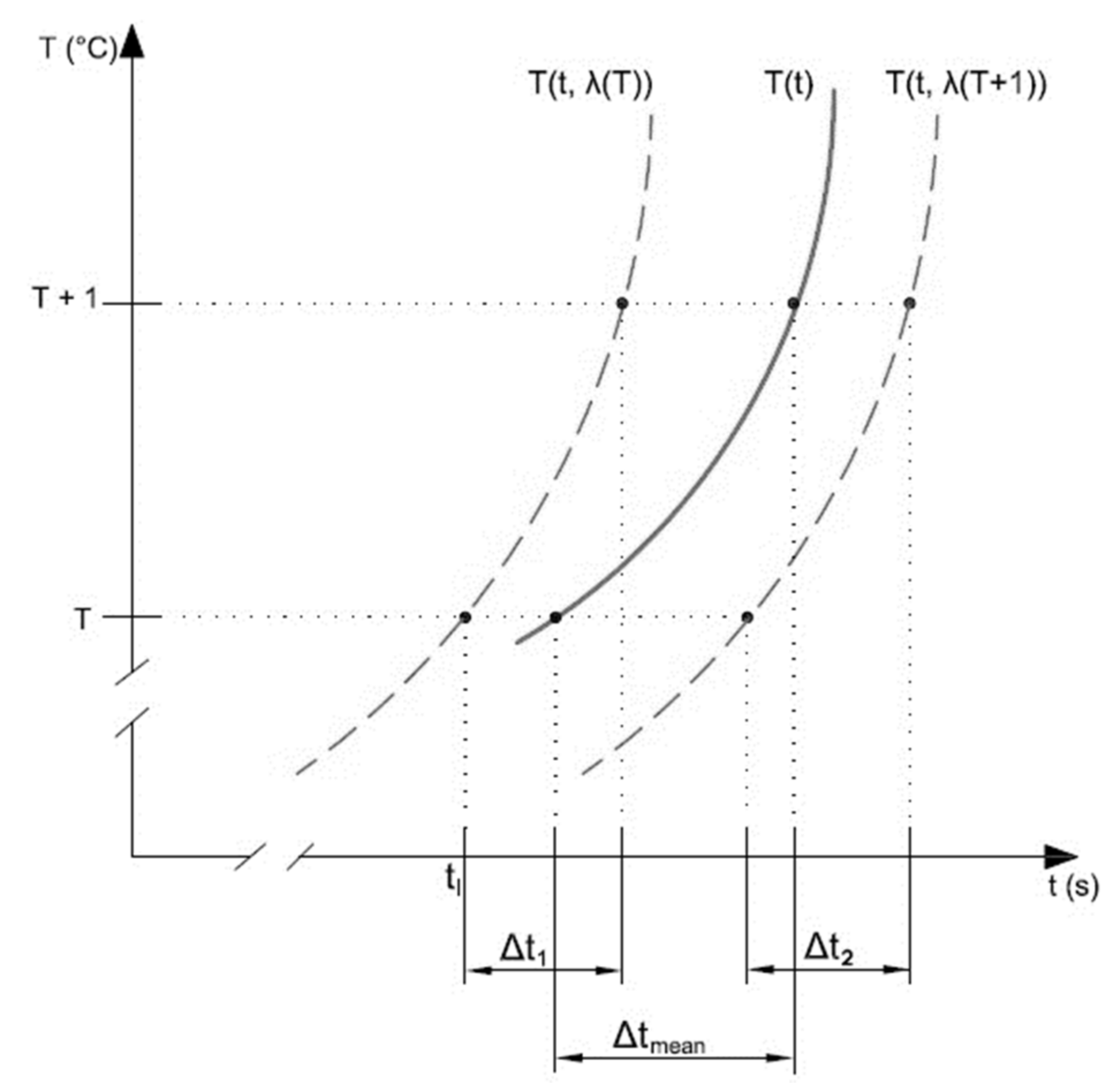
2. Materials and Methods
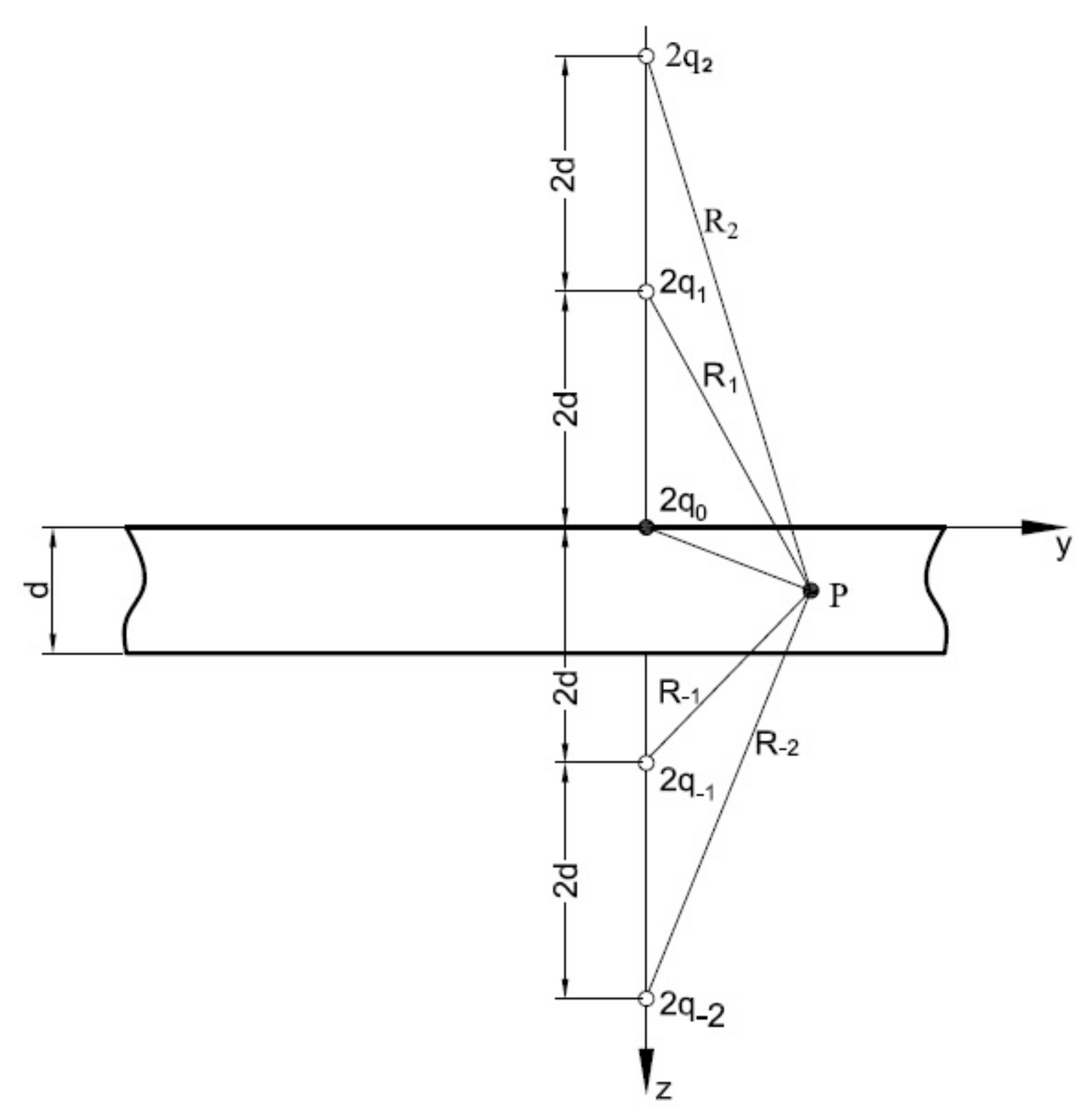
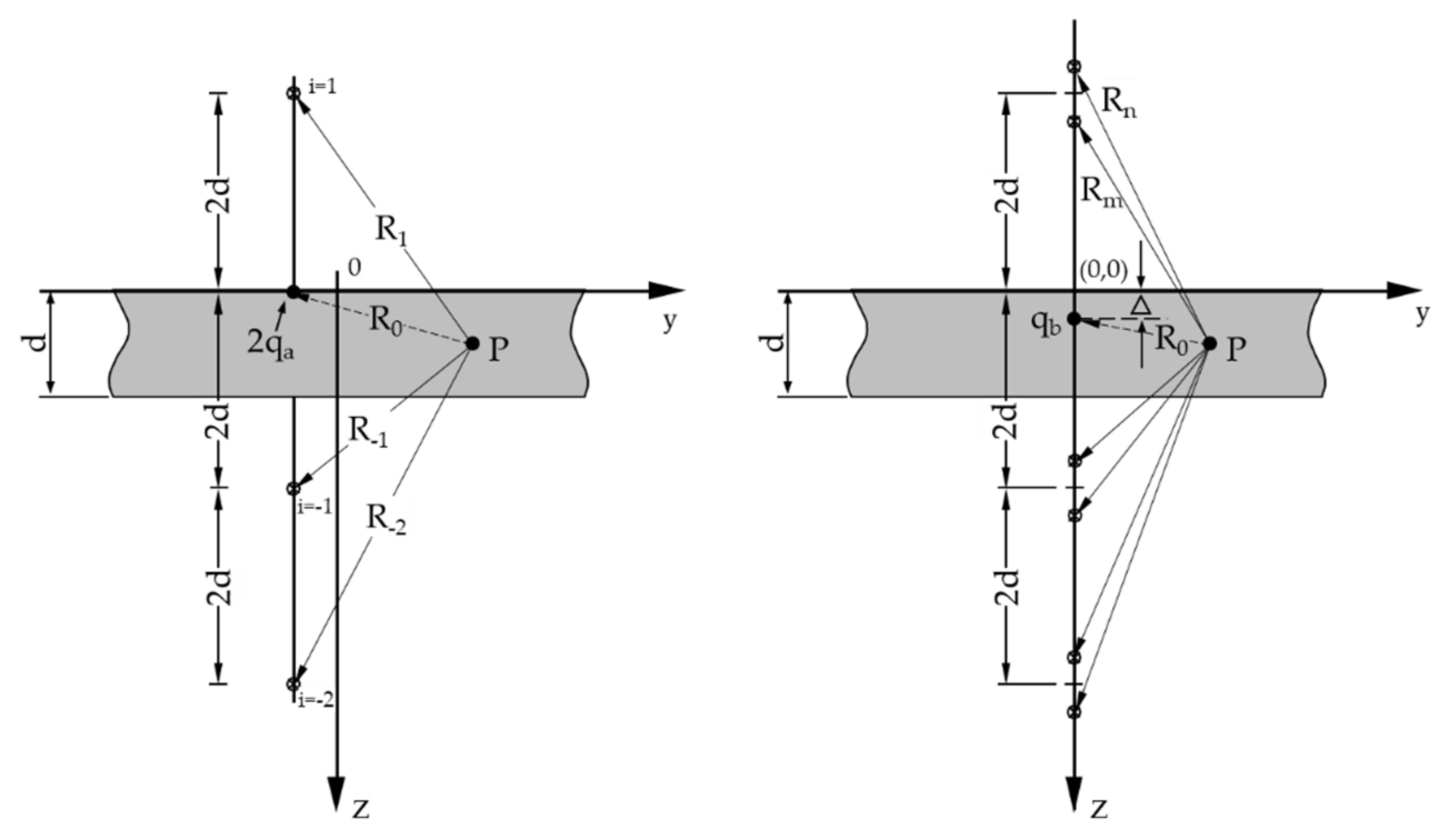
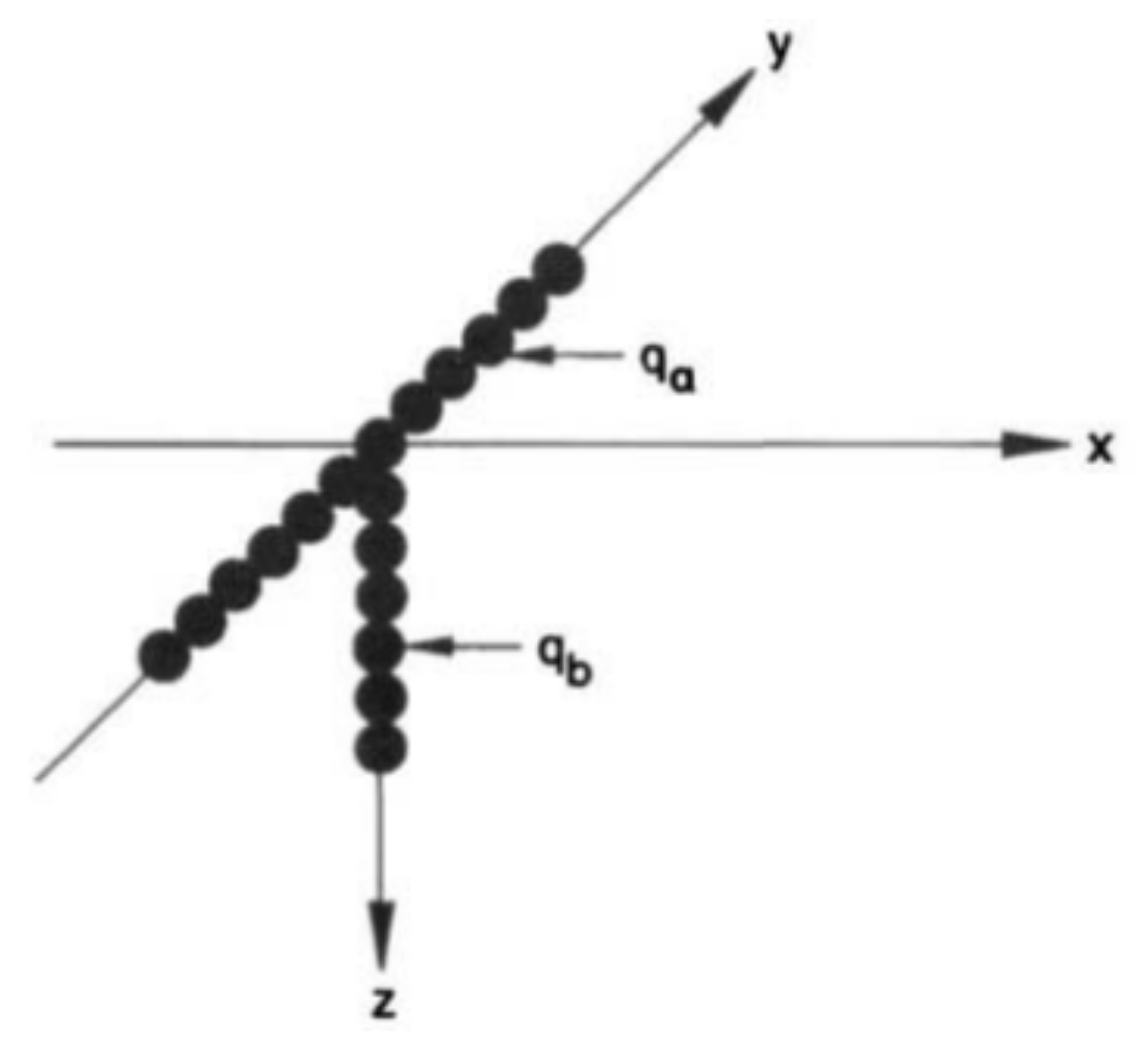
Extended Myhr and Grong′s Model
3. Results
3.1. Comparison between Different Analytical Models
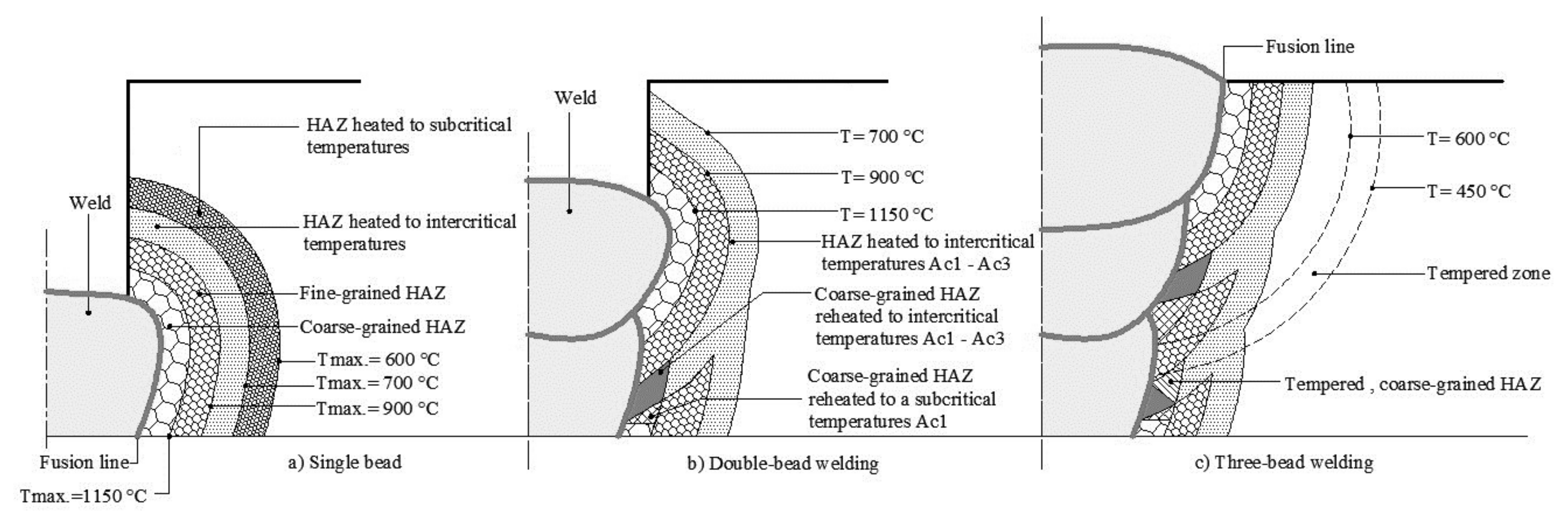
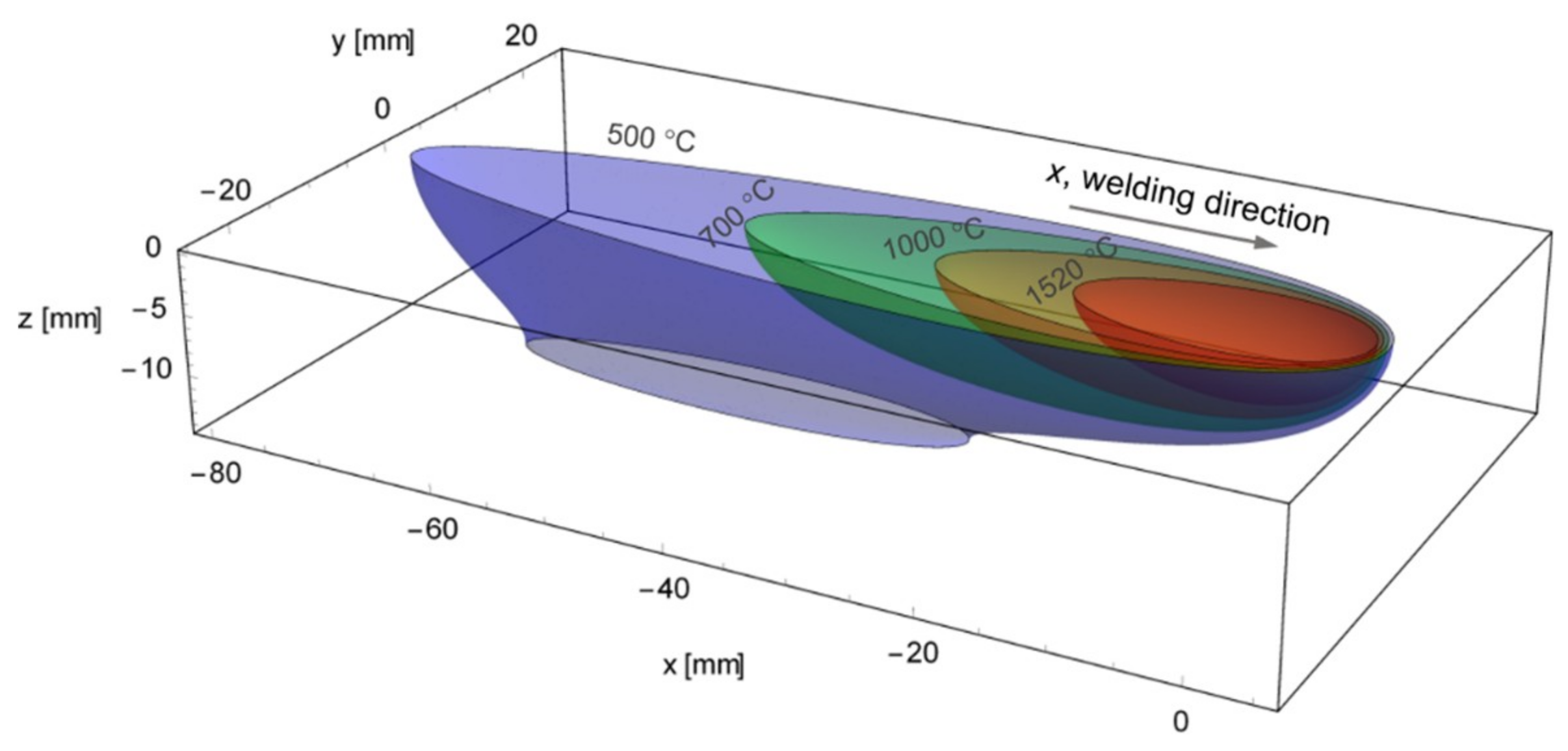
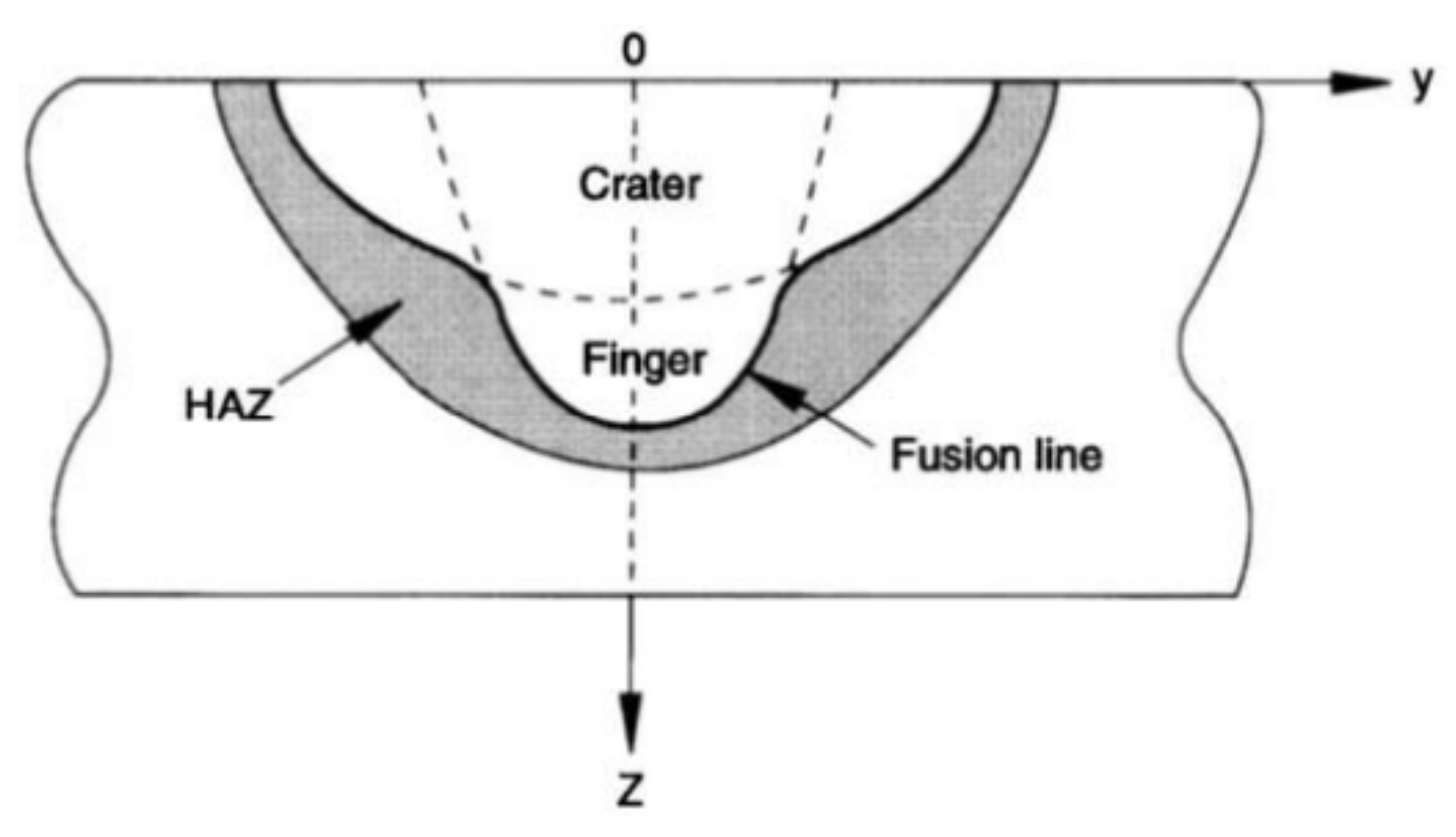
3.2. Multipass Welding Simulation through DHS Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Easterling, K.E. Introduction to the Physical Metallurgy of Welding, 2nd ed.; Butterworth-Heinemann: London, UK, 1992. [Google Scholar]
- Grong, O. Metallurgical Modelling of Welding, 2nd ed.; The Institute of Materials: London, UK, 1997. [Google Scholar]
- ASM HANDBOOK. Properties and Selection: Irons Steels and High Perfomance Alloys, 3rd ed.; ASM International: Cleveland, OH, USA, 1993. [Google Scholar]
- Adams, C.M., Jr. Cooling rates and peak temperatures in fusion welding. Weld. J. 1958, 37, 210s–215s. [Google Scholar]
- Lomozik, M. Effect of the welding thermal cycles on the structural changes in the heat affected zone and on its properfies in joints welded in low-alloy steels. Weld. Int. 2000, 14, 845–850. [Google Scholar] [CrossRef]
- Bang, K.S.; Kim, W.Y. Estimation and Prediction of HAZ Softening in Thermomechanically Controlled-Rolled and Accelerated-Cooled Steel. Weld. J. 2002, 8, 174–179. [Google Scholar]
- Yurioka, N.; Suzuki, H.; Okumura, M.; Ohshita, S.; Saito, S. Carbon Equivalents to Assess Cold Cracking Sensitivity and hardness of steel welds. Nippon Steel Tech. Rep. 1982, 20, 61–73. [Google Scholar]
- Fairchild, D.P.; Bangaru, N.V.; Koo, J.Y.; Harrison, P.L. A Study Concerning Intercritical HAZ Microstructure and Toughness in HSLA Steels. Weld. J. 1991, 70, 321s–330s. [Google Scholar]
- Di, X.J.; Cai, L.; Xing, X.-X.; Chen, C.-X.; Xue, Z.-K. Microstructure and mechanical properties of intercritical heat-affected zone of X80 pipeline steel in simulated in-service welding. Acta Met. Sin. 2015, 28, 883–891. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. About calculating the characteristics of the martensite-austenite constituent. In Proceedings of the International Seminar on Welding of High Strength Pipeline Steels, Araxa, Brazil, 28–30 November 2013; pp. 99–106. [Google Scholar]
- Chunyan, Y.; Cuiying, L.; Bo, Y. 3D modeling of the hydrogen distribution in X80 pipeline steel welded joints. Comput. Mater. Sci. 2014, 83, 158–163. [Google Scholar]
- Nóbrega, J.A.; Diniz, D.D.S.; Silva, A.A.; Maciel, T.M.; Albuquerque, V.H.C.; Tavares, J.M.R.S. Numerical evaluation of temperature field and residual stresses in an API 5L X80 steel welded joint using the finite element method. Metals 2016, 6, 28. [Google Scholar] [CrossRef]
- Cho, S.H.; Kim, J.W. Analysis of residual stress in carbon steel weldment incorporating phase transformations. Sci. Technol. Weld. Join. 2002, 7, 212–216. [Google Scholar] [CrossRef]
- Pasternak, H.; Launert, B.; Krausche, T. Welding of girders with thick plates—Fabrication, measurement and simulation. J. Constr. Steel Res. 2015, 115, 407–416. [Google Scholar] [CrossRef]
- Bate, S.K.; Charles, R.; Warren, A. Finite element analysis of a single bead-on-plate specimen using SYSWELD. Int. J. Press. Vessel. Pip. 2009, 86, 73–78. [Google Scholar] [CrossRef]
- Azar, A.S.; Ås, S.K.; Akselsen, O.M. Analytical modeling of weld bead shape in dry hyperbaric GMAW using Ar-He chamber gas mixtures. J. Mater. Eng. Perform. 2013, 22, 673–680. [Google Scholar] [CrossRef]
- Azar, A.S.; Ås, S.K.; Akselsen, O.M. Determination of welding heat source parameters from actual bead shape. Comput. Mater. Sci. 2012, 54, 176–182. [Google Scholar] [CrossRef]
- Lindgren, L.; Runnemalm, H.; Näsström, M.O. Simulation of multipass welding of a thick plate. Int. J. Numer. Methods Eng. 1999, 44, 1301–1316. [Google Scholar] [CrossRef]
- Börjesson, L.; Lindgren, L.E. Simulation of Multipass Welding with Simultaneous Computation of Material Properties. J. Eng. Mater. Technol. 2001, 123, 106. [Google Scholar] [CrossRef]
- Deng, D.; Kiyoshima, S. Numerical Investigation on Welding Residual Stress in 2.25Cr-1Mo Steel Pipes. Trans. JWRI 2007, 36, 73–90. [Google Scholar]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Maekawa, A.; Kawahara, A.; Serizawa, H.; Murakawa, H. Fast three-dimensional multipass welding simulation using an iterative substructure method. J. Mater. Process. Technol. 2015, 215, 30–41. [Google Scholar] [CrossRef]
- Duranton, P.; Devaux, J.; Robin, V.; Gilles, P.; Bergheau, J.M. 3D modelling of multipass welding of a 316L stainless steel pipe. In Proceedings of the International Conference on Advances in Materials and Processing Technologies—AMPT2003, Dublin, Ireland, 8–11 July 2003; pp. 974–977. [Google Scholar]
- Rosenthal, D. Mathematical Theory of Heat Distribution during Welding and Cutting. Weld. J. 1941, 20, 220s–234s. [Google Scholar]
- Rosenthal, D.; Schmerber, R. Thermal study of arc welding: experimental verification of theoretical formulas. Weld. J. Res. Suppl. 1938, 17, 2s–8s. [Google Scholar]
- Rosenthal, D. The theory of moving sources of heat and its application to metal treatments. Trans. ASME 1946, 43, 849–866. [Google Scholar]
- Jhaveri, P.; Moffatt, W.G.; Adams, C.M., Jr. The effect of plate thickness and radiation on the heat flow in welding and cutting. Weld. J. 1962, 41, 12s–16s. [Google Scholar]
- Ramirez, A.J.L.; Brandi, S.D. Application of discrete distribution point heat source model to simulate multipass weld thermal cycles in medium thick plates. Sci. Technol. Weld. Join. 2004, 9, 72–82. [Google Scholar] [CrossRef]
- Astm Committee E20 On Temperature Measur. Manual on the Use of Thermocouples in Temperature Measurement, 4th ed.; ASTM International: Philadelphia, PA, USA, 1993. [Google Scholar]
- Eagar, T.W.; Tsai, N.S. Temperature fields produced by traveling distributed heat sources. Weld. J. Res. Suppl. 1983, 62, 346s–355s. [Google Scholar]
- Pickering, F.B. High-Strength, Low-Alloy Steels—A Decade of Progress. In Microalloying 75, Proceedings of an International Symposium on High-Strength, Low-Alloy Steels; Union Carbide Corp.: New York, NY, USA, 1977. [Google Scholar]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new Finite Element Model for welding heat sources. Metall. Trans. B 1984, 15B, 299–305. [Google Scholar] [CrossRef]
- Pavelic, V.; Tanbakuchi, R.; Uyehara, O.A.; Myers, P.S. Experimental and Computed Temperature Histories in Gas Tungsten-Arc Welding of Thin Plate. Weld. J. Res. Suppl. 1969, 48, 295s–305s. [Google Scholar]
- Myhr, O.R.; Grong, Ø. Dimensionless maps for heat flow analyses in fusion welding. Acta Metall. Mater. 1990, 38, 449–460. [Google Scholar] [CrossRef]
- Poorhaydari, K.; Patchett, B.M.; Ivey, D.G. Estimation of cooling rate in the welding of plates with intermediate thickness. Weld. J. 2005, 84, 149s–155s. [Google Scholar]

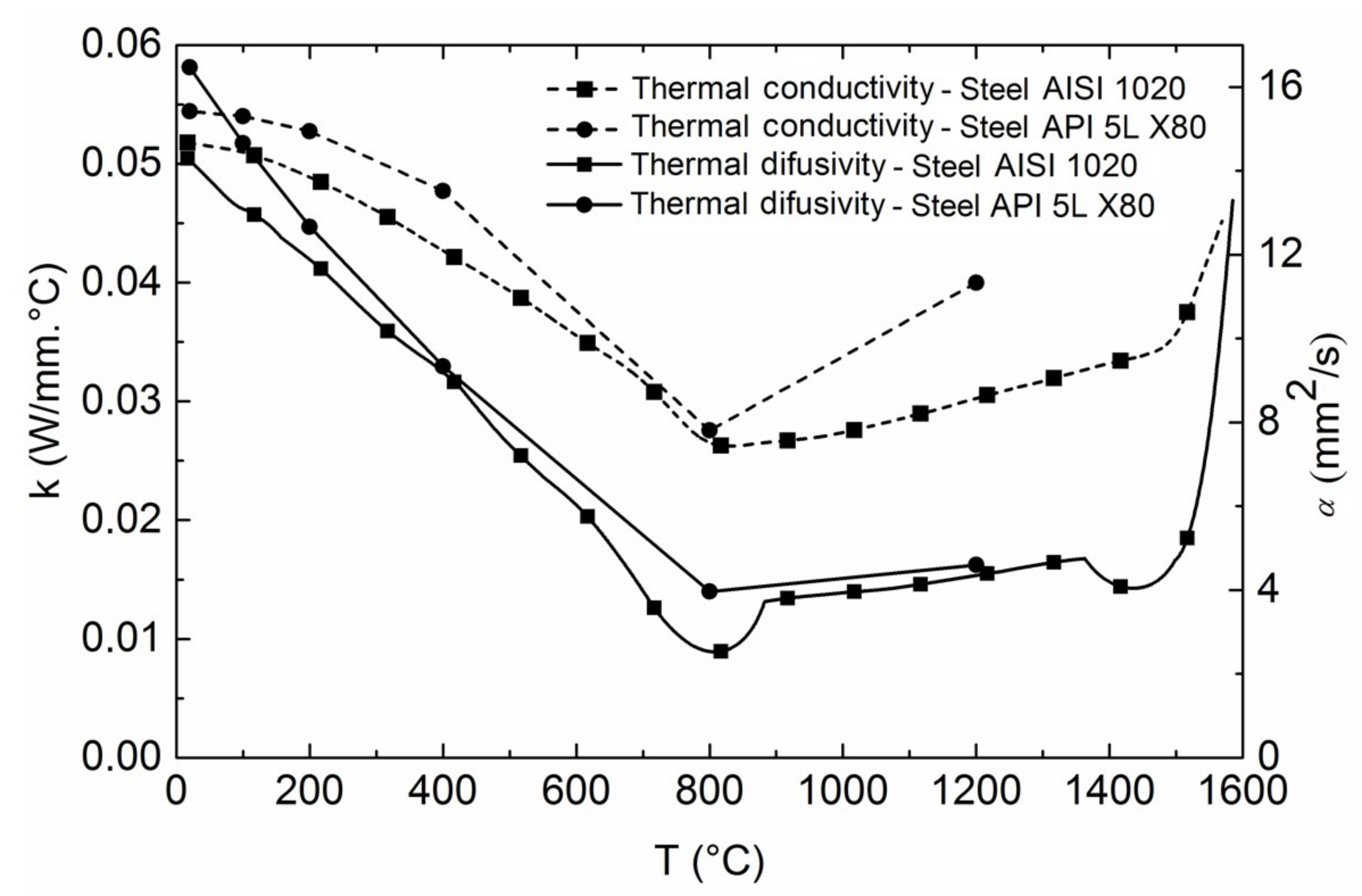
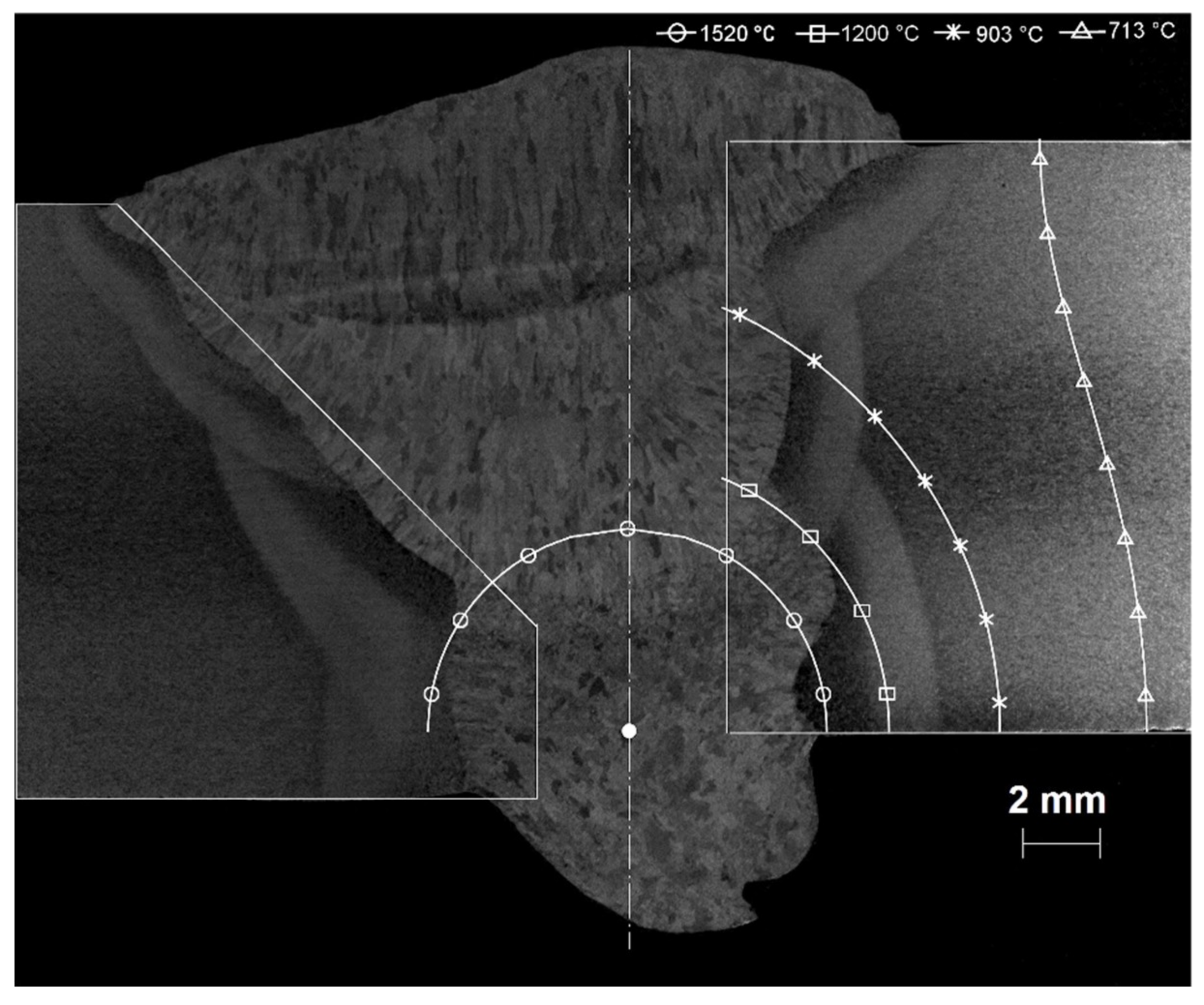
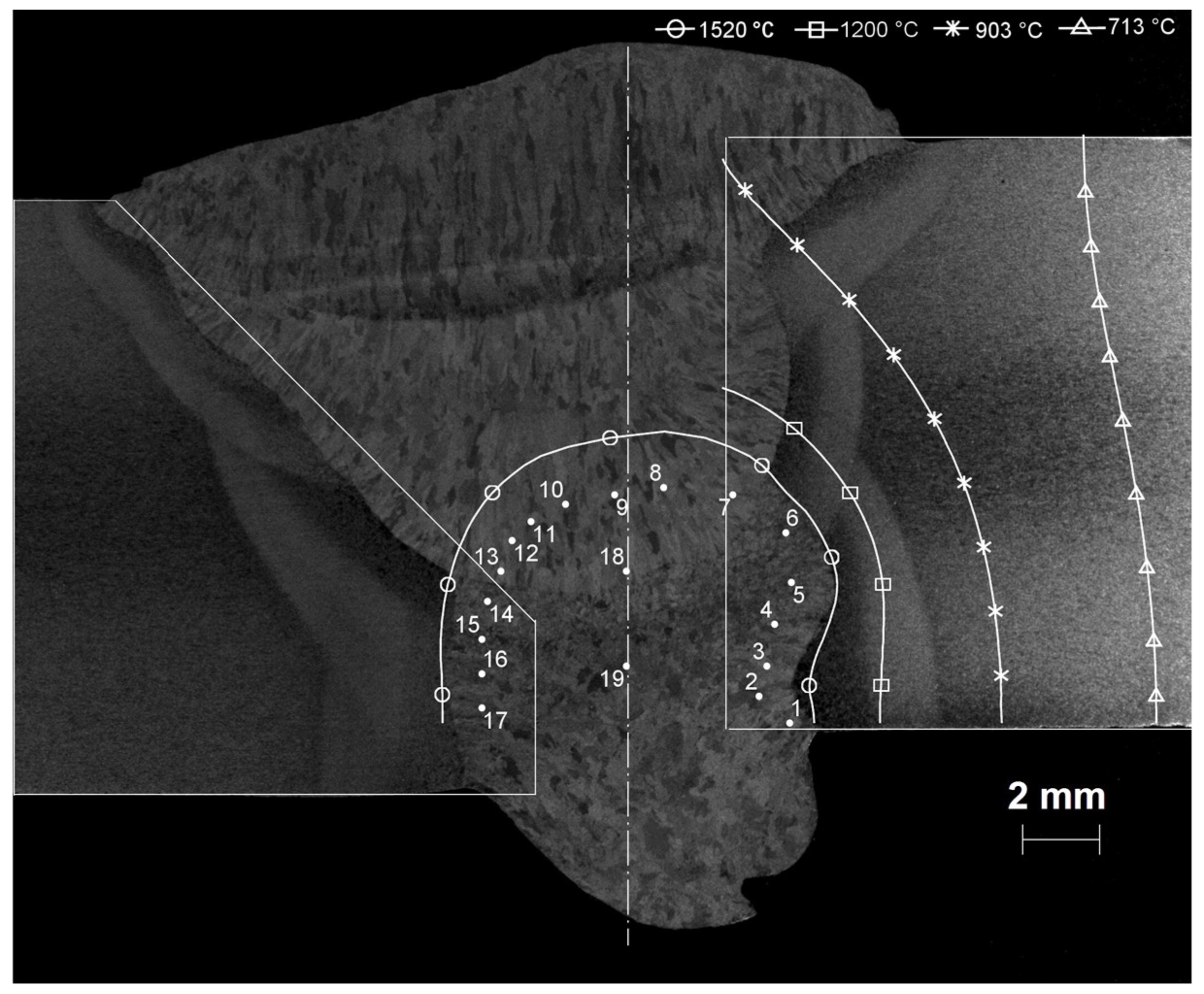


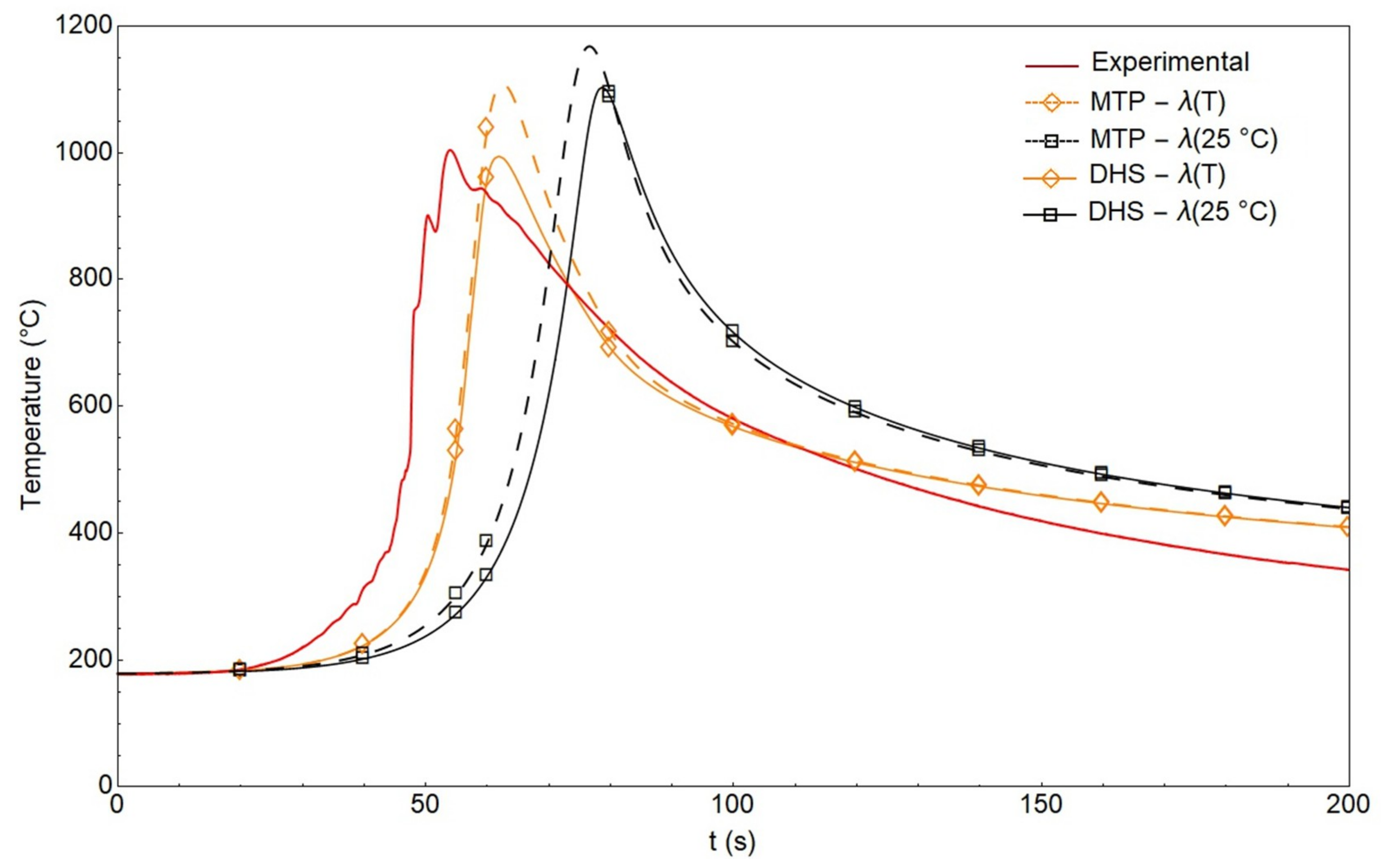
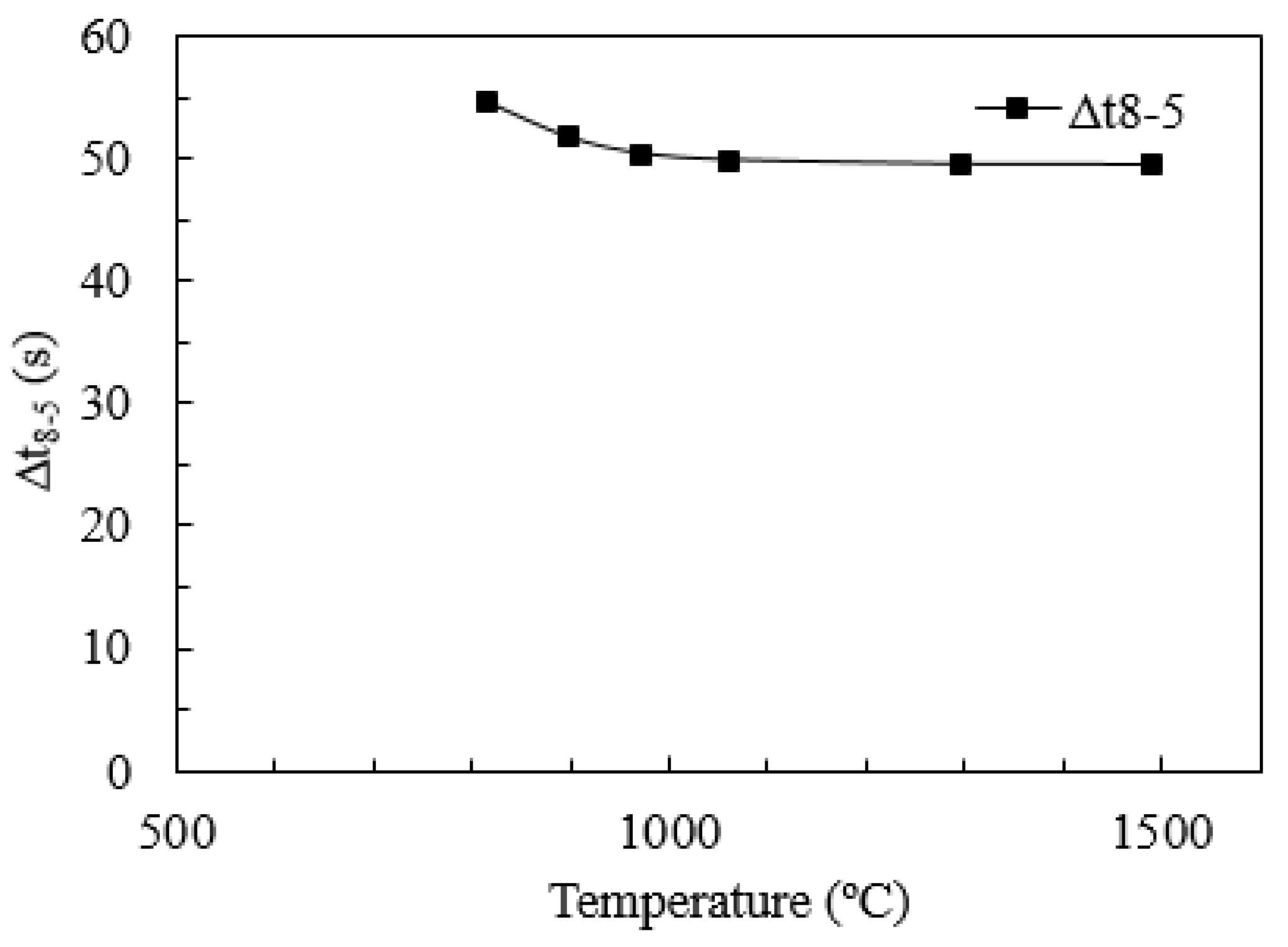
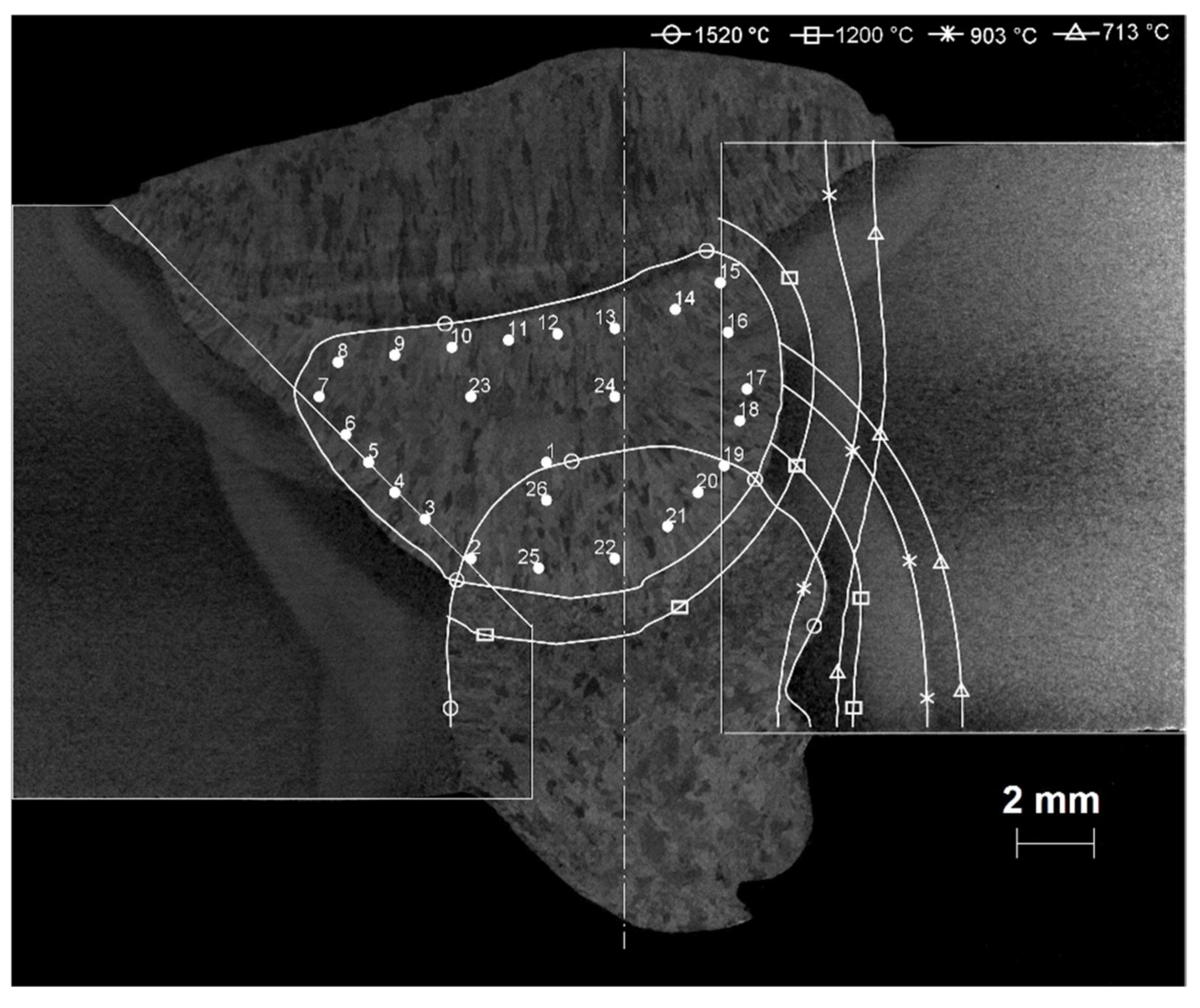
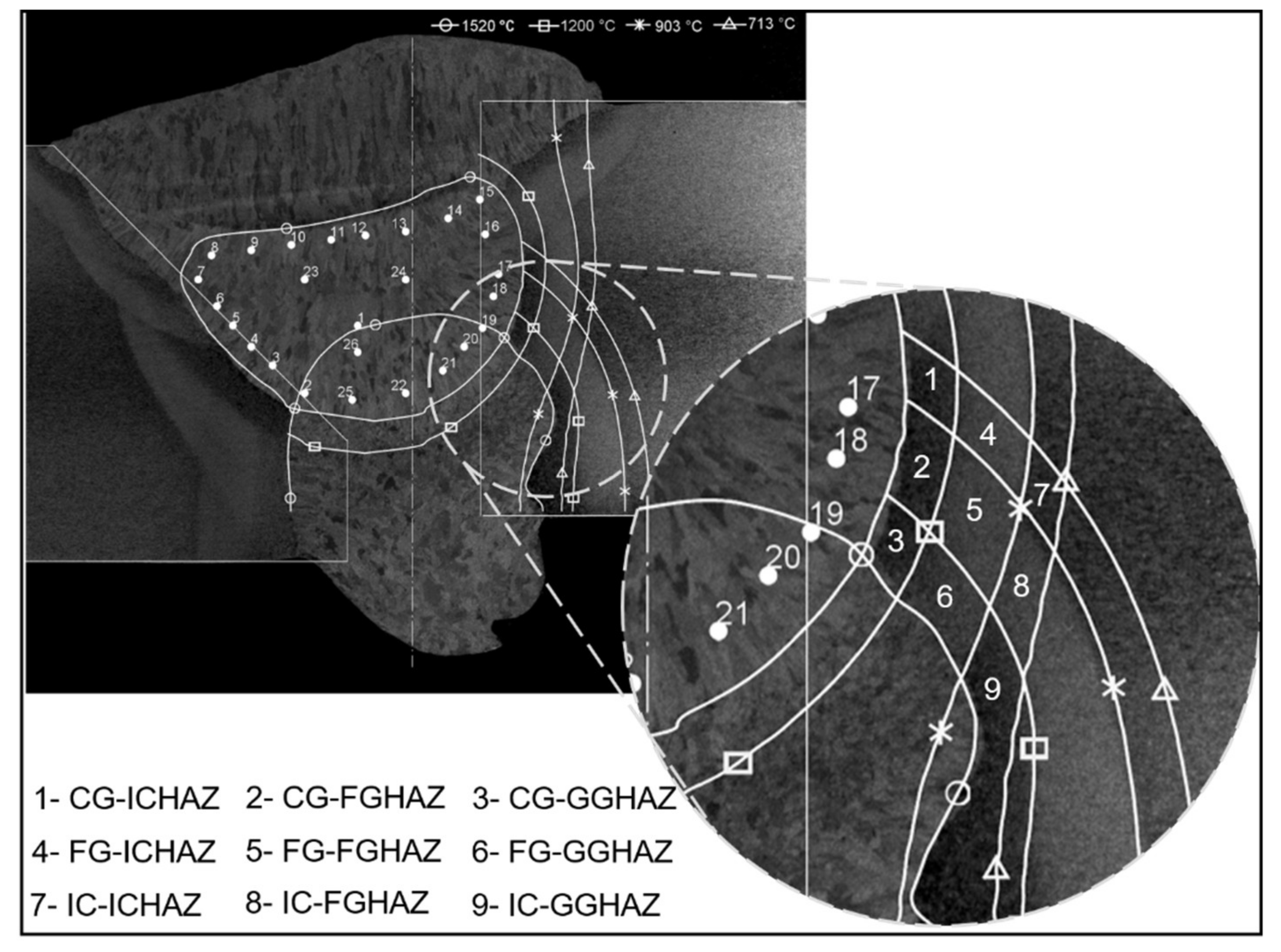
| Alloy | C | Mn | Si | Cr | Ni | Mo | Al | Cu | Ti | V | Nb | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wt% | 0.06 | 1.597 | 0.216 | 0.192 | 0.198 | 0.002 | 0.049 | 0.012 | 0.015 | 0.027 | 0.0649 | 0.0003 |
| Position | MTP | DHS | ||
|---|---|---|---|---|
| 1520 °C | 903 °C | 1520 °C | 903 °C | |
| 1 | 12.4% | 19.1% | 9.2% | 20.7% |
| 2 | −18.3% | 18.7% | 2.1% | 22.3% |
| 3 | −48.8% | 19.8% | 1.5% | 27.0% |
| Position | MTP | DHS | ||
|---|---|---|---|---|
| 1520 °C | 903 °C | 1520 °C | 903 °C | |
| 1 | 6.9% | 3.4% | −1.1% | −1.9% |
| 2 | −24.9% | 1.4% | −2.3% | −0.9% |
| 3 | −60.0% | −0.8% | −2.3% | 1.6% |
| Physical Property | MTP Simulation | DHS Simulation | ||||||
|---|---|---|---|---|---|---|---|---|
| Tmax (°C) | Tmax Error (%) | Tmax (°C) | Tmax Error (%) | |||||
| λ(T) | 1108.58 | 10.38 | 50.82 | 5.92 | 994.62 | −0.97 | 52.04 | 8.47 |
| λ(25 °C) | 1168.18 | 16.31 | 62.43 | 30.12 | 1103.53 | 9.88 | 63.18 | 31.68 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, D.M.B.; Alves, A.d.N.S.; Cruz Neto, R.M.d.A.; Martins, T.F.; Brandi, S.D. A New Approach to Simulate HSLA Steel Multipass Welding through Distributed Point Heat Sources Model. Metals 2018, 8, 951. https://doi.org/10.3390/met8110951
Ferreira DMB, Alves AdNS, Cruz Neto RMdA, Martins TF, Brandi SD. A New Approach to Simulate HSLA Steel Multipass Welding through Distributed Point Heat Sources Model. Metals. 2018; 8(11):951. https://doi.org/10.3390/met8110951
Chicago/Turabian StyleFerreira, Dario Magno Batista, Antonio do Nascimento Silva Alves, Rubelmar Maia de Azevedo Cruz Neto, Thiago Ferreira Martins, and Sérgio Duarte Brandi. 2018. "A New Approach to Simulate HSLA Steel Multipass Welding through Distributed Point Heat Sources Model" Metals 8, no. 11: 951. https://doi.org/10.3390/met8110951
APA StyleFerreira, D. M. B., Alves, A. d. N. S., Cruz Neto, R. M. d. A., Martins, T. F., & Brandi, S. D. (2018). A New Approach to Simulate HSLA Steel Multipass Welding through Distributed Point Heat Sources Model. Metals, 8(11), 951. https://doi.org/10.3390/met8110951






