Applied Mathematical Modelling of Continuous Casting Processes: A Review
Abstract
1. Introduction
2. Metallurgical Length
2.1. Pure Metals or Eutectic Alloys
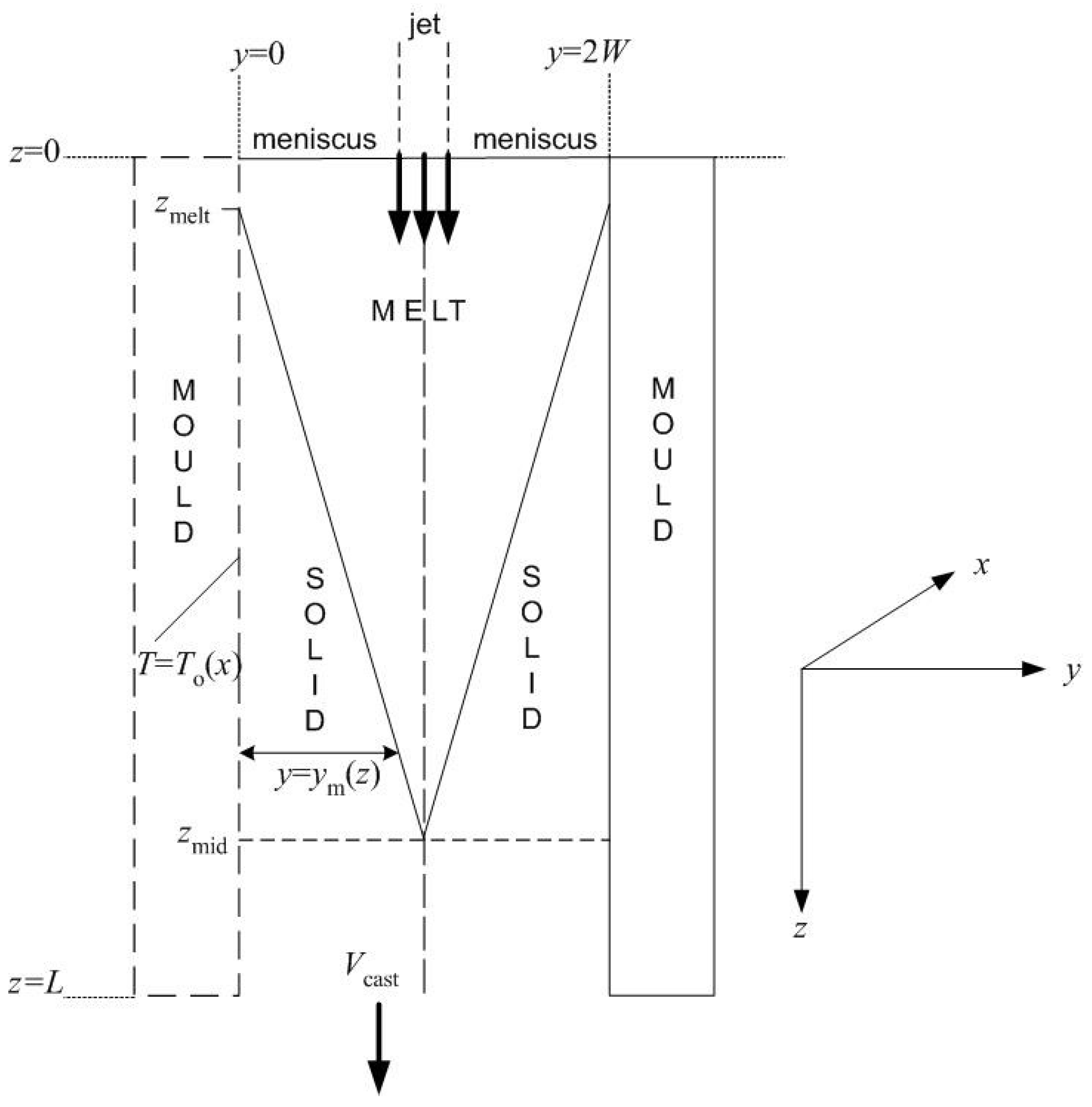
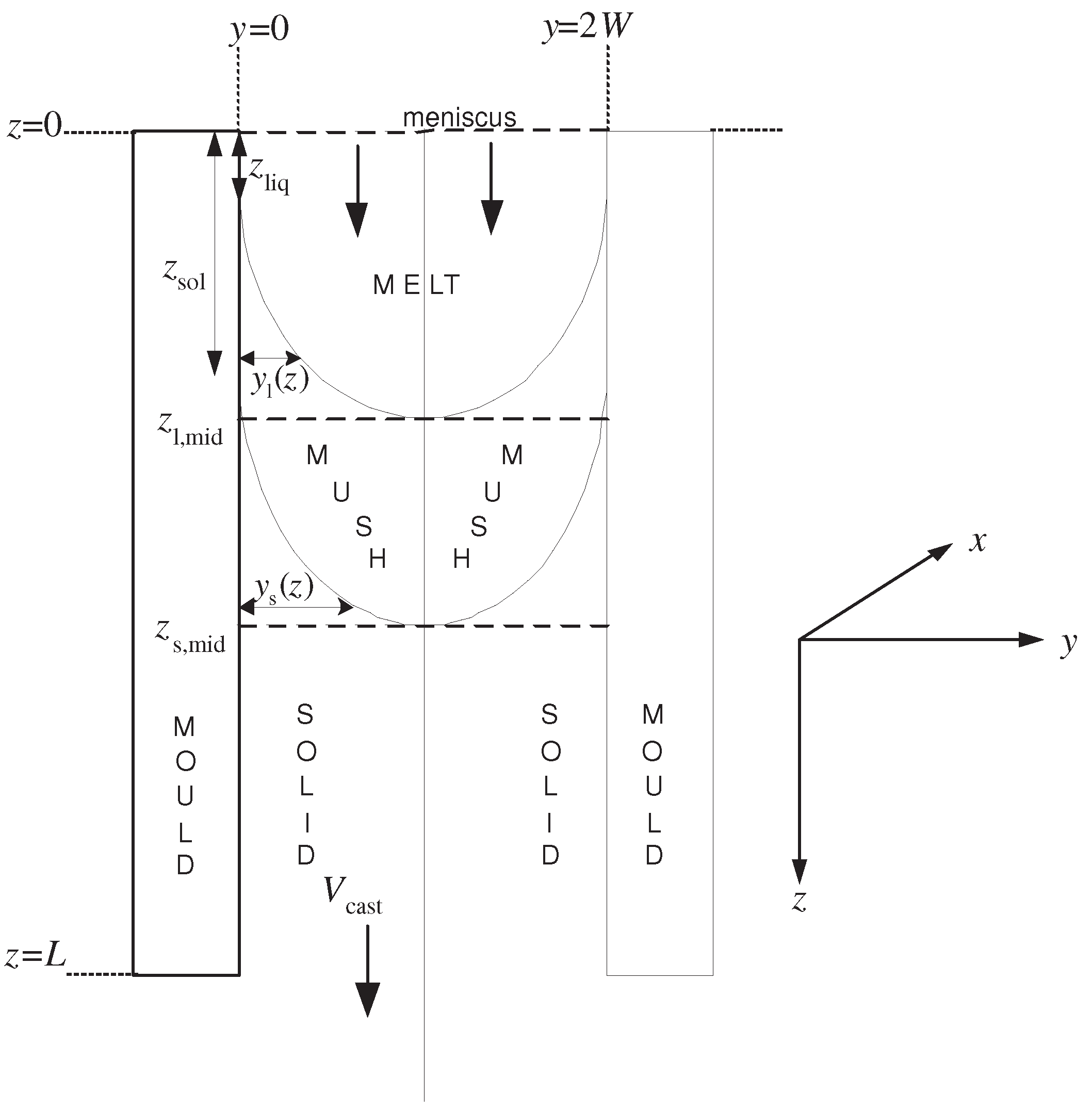
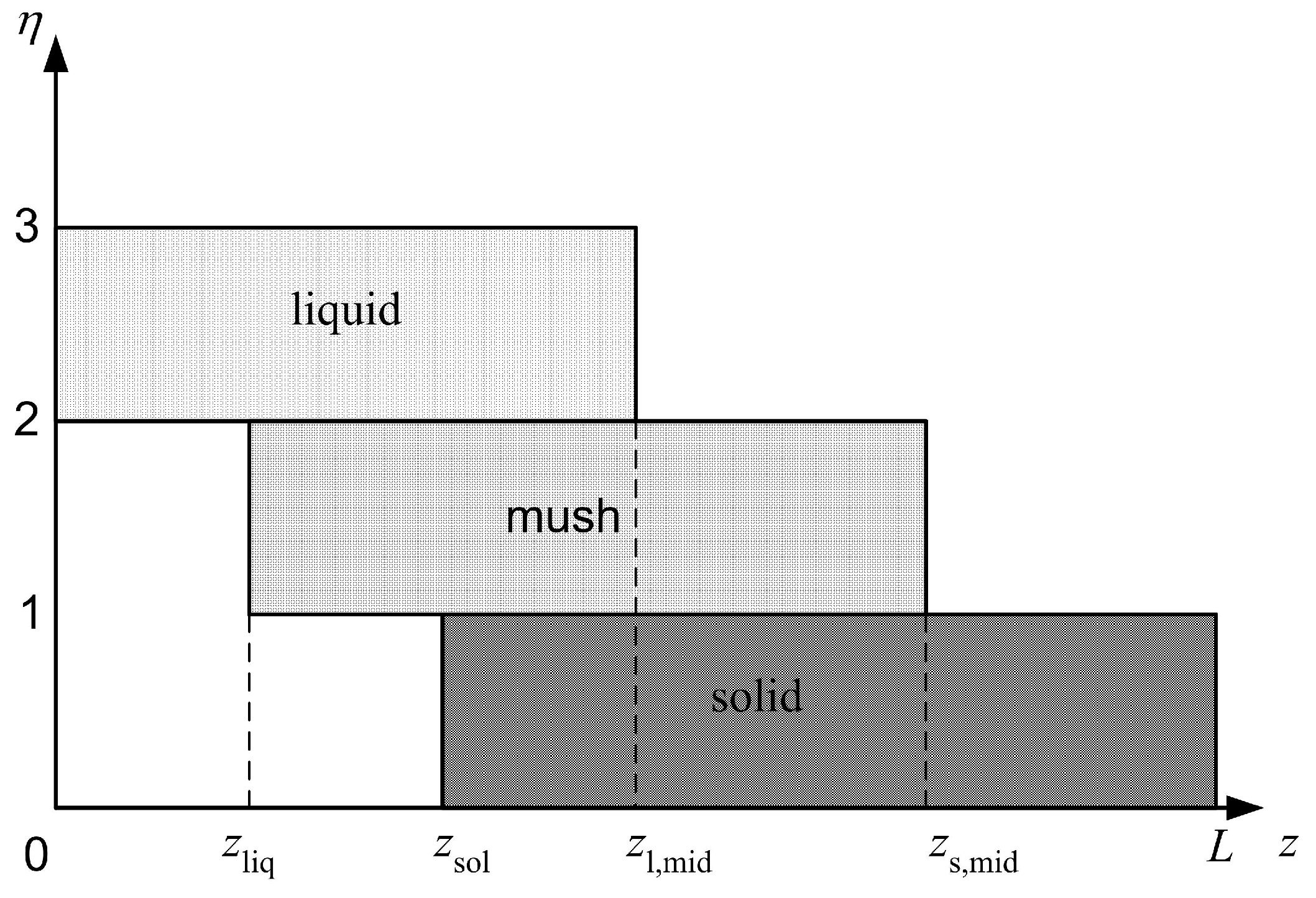
2.2. Alloys
- (A)
- an enthalpy-like formulation just mentioned using the full 2D time-independent equations;
- (B)
- an enthalpy-like formulation using a reduction of the full 2D time-independent equations to a 1D transient-like formulation of the type used in [21];
- (C)
- the proposed new formulation, which is also 1D transient-like but resolves the locations of the solidus and liquidus isotherms explicitly.
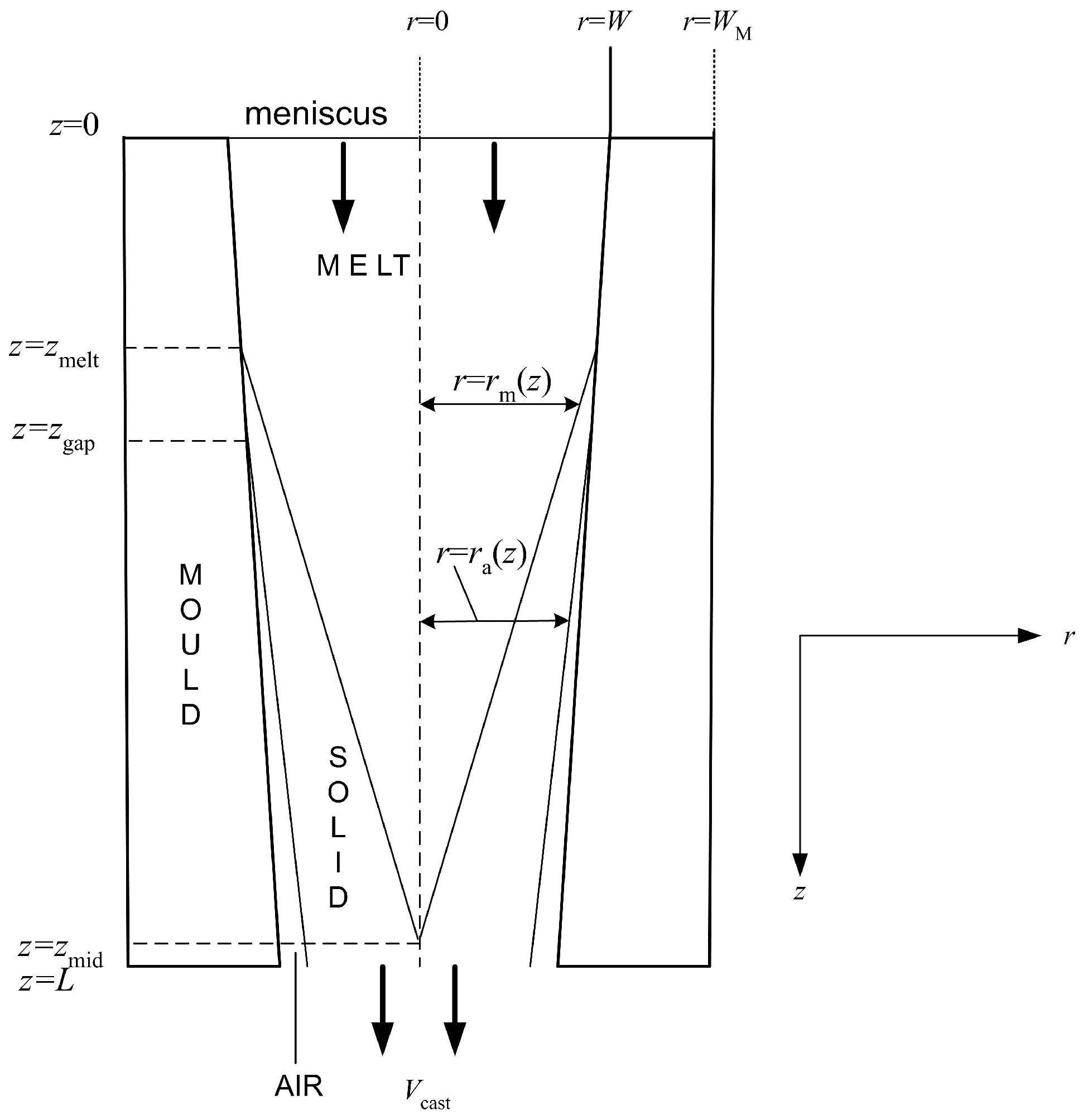
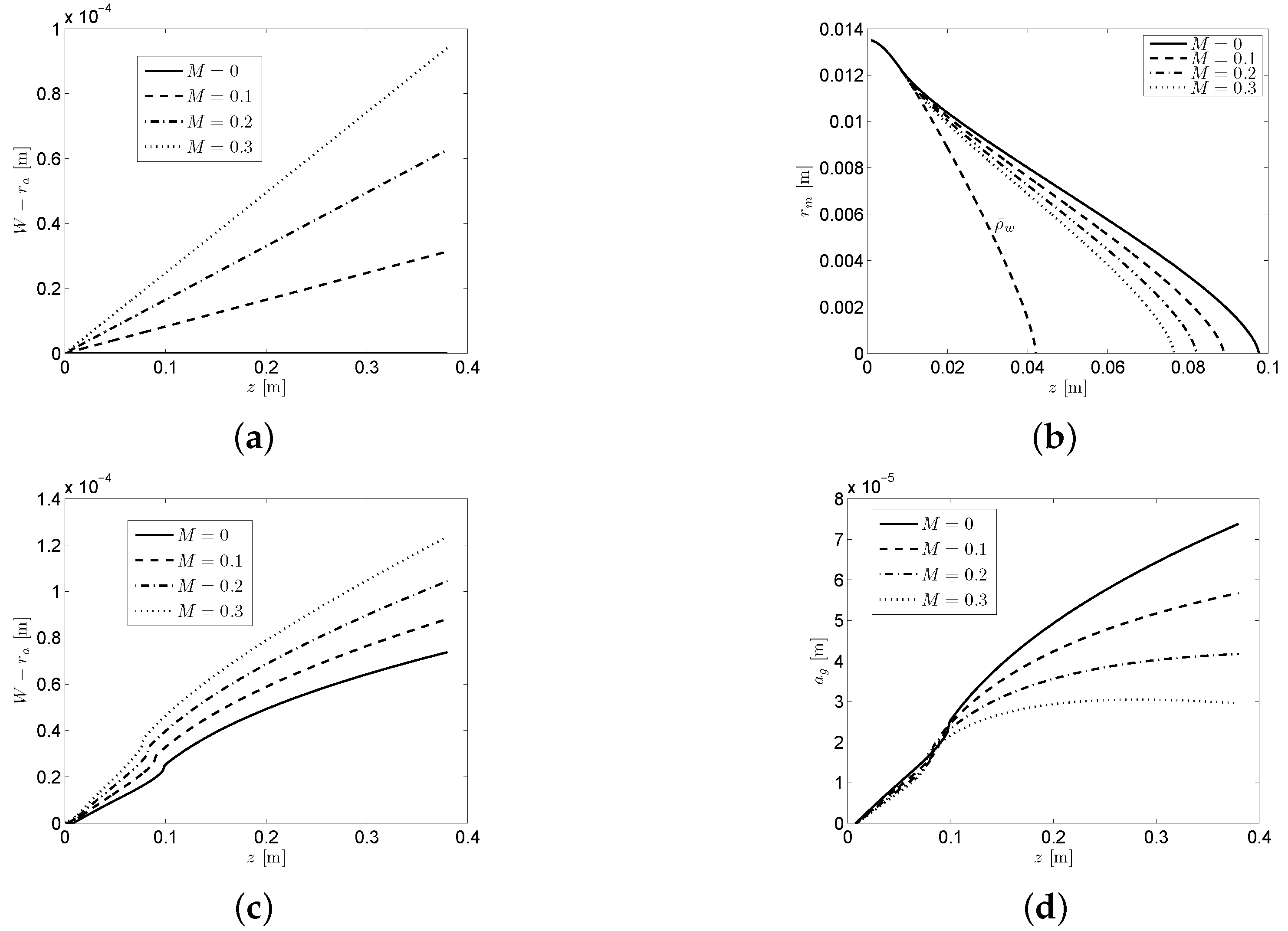
3. Air Gap and Mould Taper
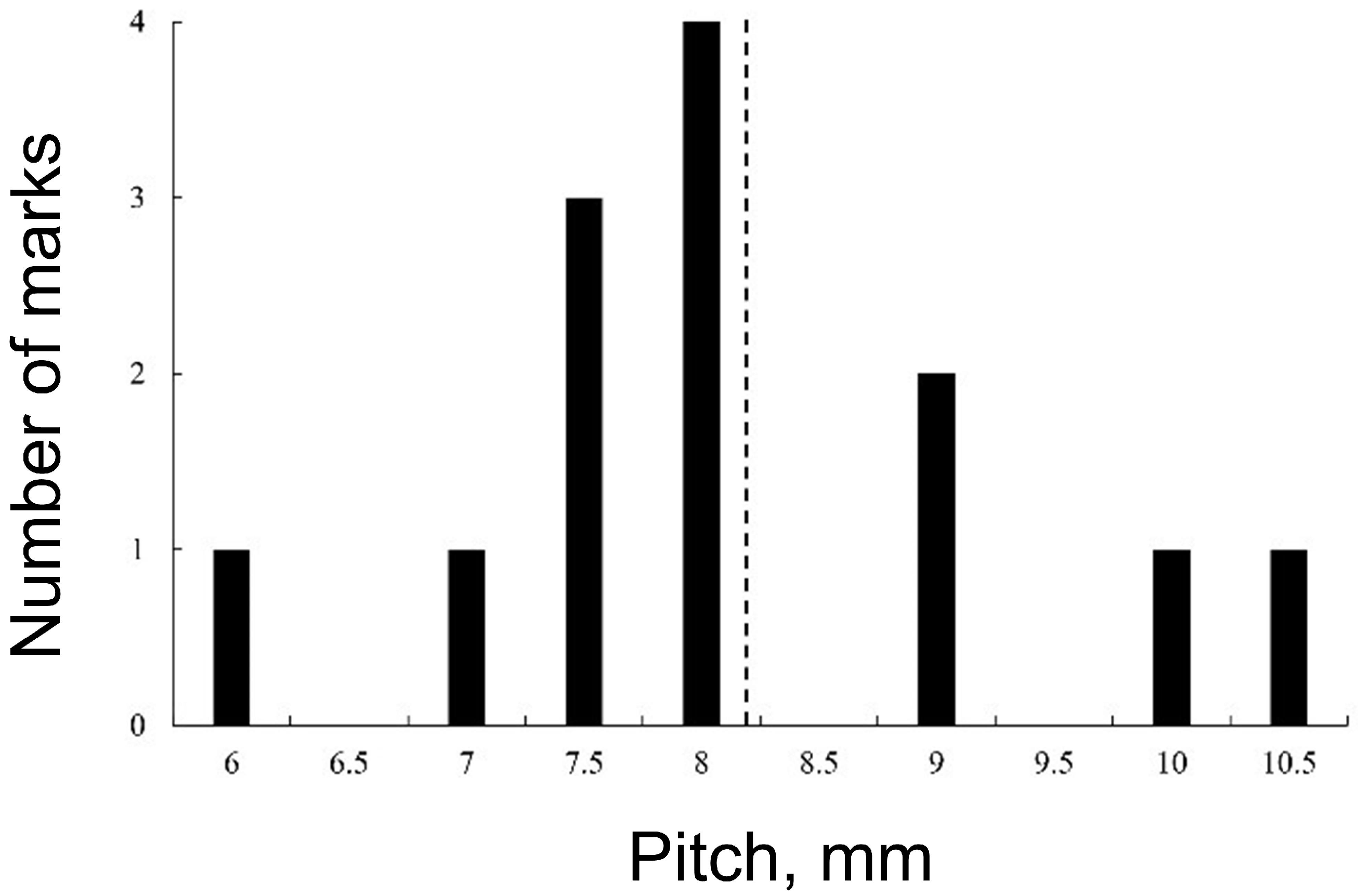
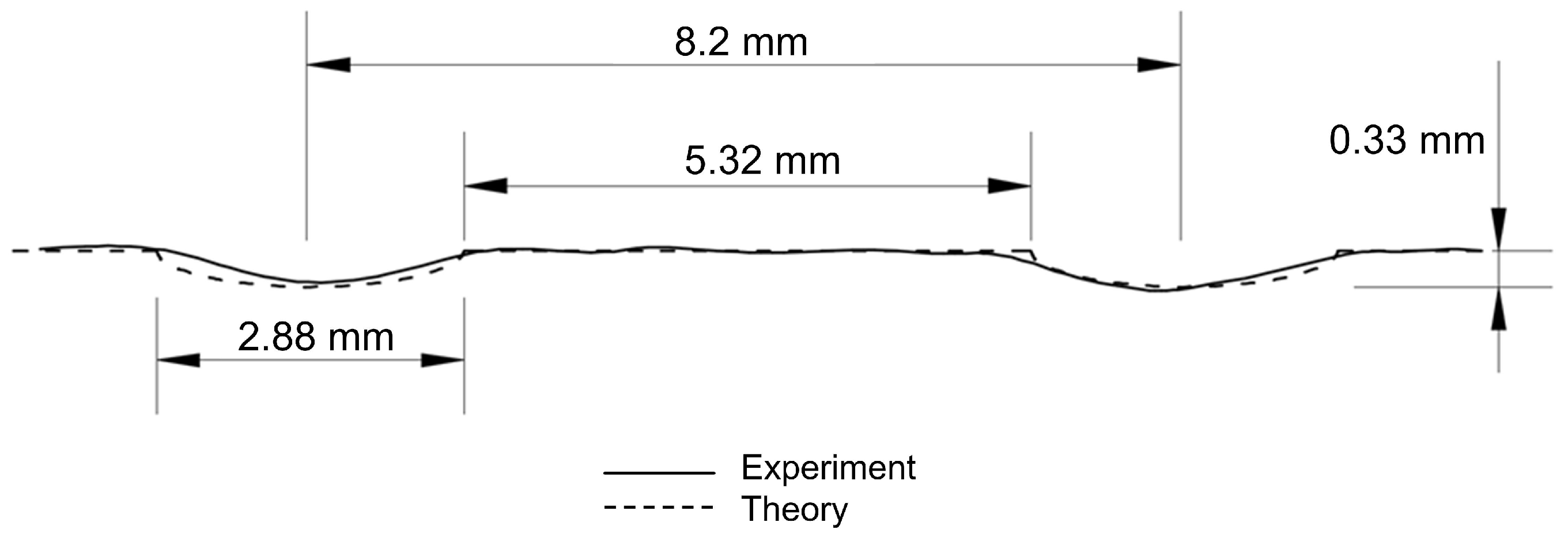
4. Oscillation-Mark Formation
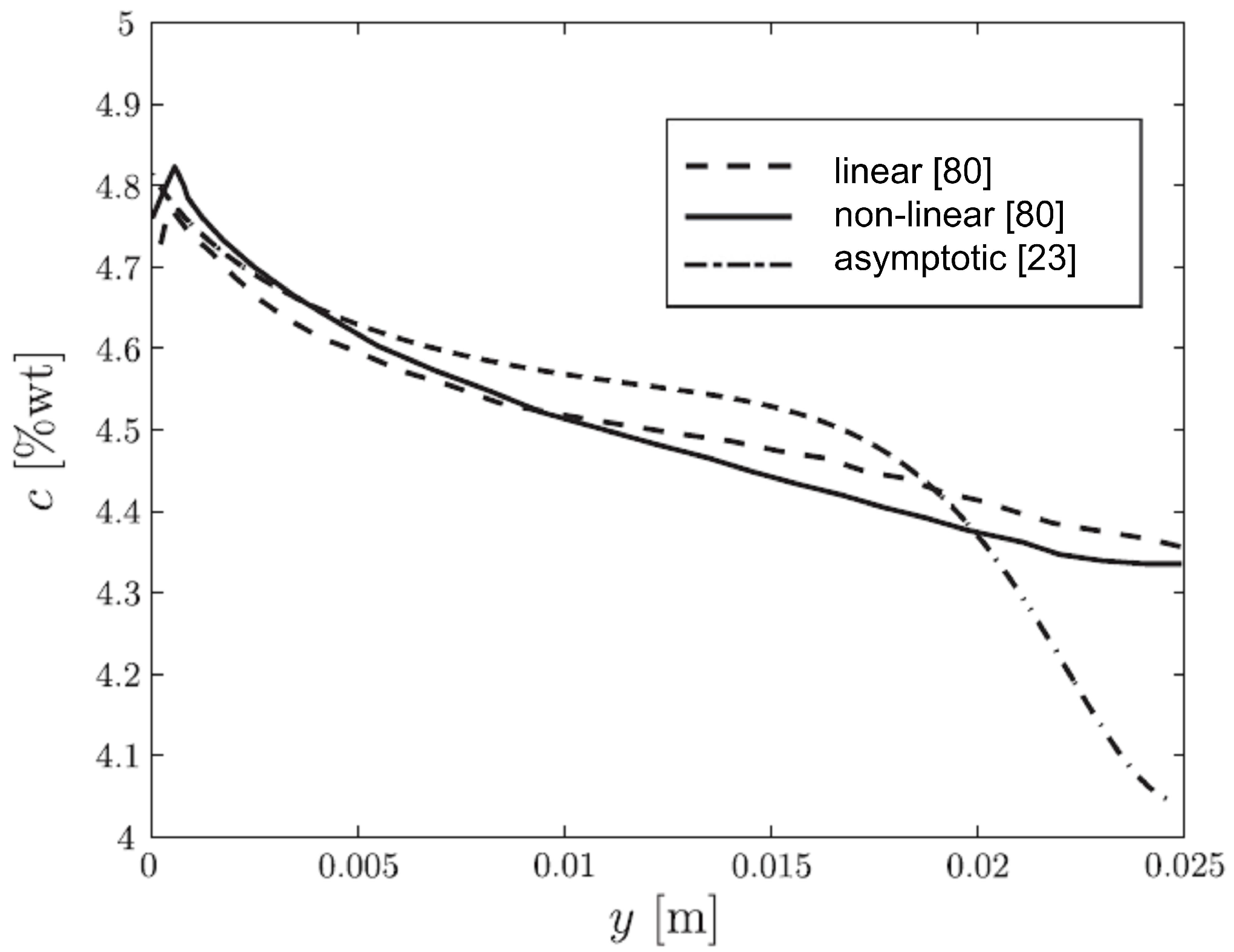
5. Macrosegregation
- in [80], numerical issues associated with the use of CFD, of the type mentioned earlier; and
- the fact that the geometry in question, which has an aspect ratio of six, is not slender enough for the asymptotic approach to be valid.
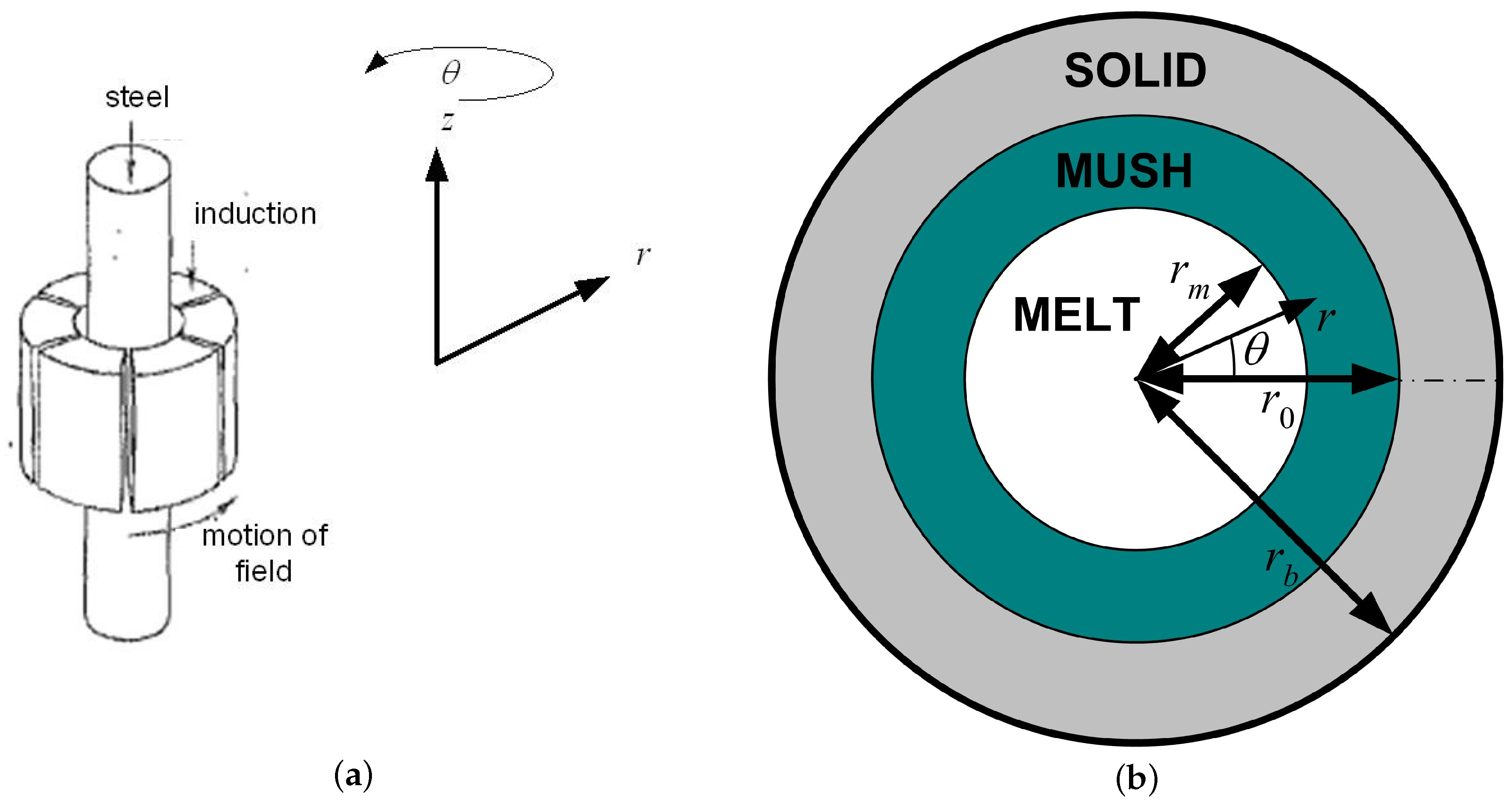
6. Electromagnetic Stirring
7. Conclusions
- For solidification shrinkage-induced macrosegregation in a binary alloy, reasonably good quantitative agreement was achieved for the cross-sectional macrosegregation profile, and even better agreement is to expected when the model has been developed to include superheat [23].
- For oscillation-mark formation, very good agreement was obtained with experimental results for fold-type marks [30].
Funding
Conflicts of Interest
Appendix A. Notes on Practical Asymptotics
- (a)
- Nondimensionalization of the original governing equations;
- (b)
- Analysis of the nondimensionalized governing equations, and identification of the key dimensionless parameters and asymptotic reduction;
- (c)
- Evidence that the computation of the reduced model is cheaper than the computation of the original model would have been (if the reduced model does not have an analytical solution); and
- (d)
- Evidence of agreement between the results of the original model and the asymptotically reduced model.
- Fewer partial differential equations (PDEs) rather than more;
- One-dimensional models rather than two-dimensional models, and two-dimensional models rather than three-dimensional models;
- Ordinary differential equations (ODEs) rather than PDEs; and
- Problems having fewer model parameters rather than more, with regard to the need for parameter studies to obtain a complete understanding of model behaviour.
- After nondimensionalization and asymptotic reduction, the model was one-dimensional and transient-like, consisted of two PDEs (or effectively different representations of the same PDE) and contained six model parameters [21].
- A direct comparison of CPU time and RAM was not carried out, but we note that one computation in [35] required 30 h of CPU time on a Cray J932 Supercomputer—with current computational architectures, this would no doubt take much less, but still would not be as short as the few seconds required for the formulation in [21].
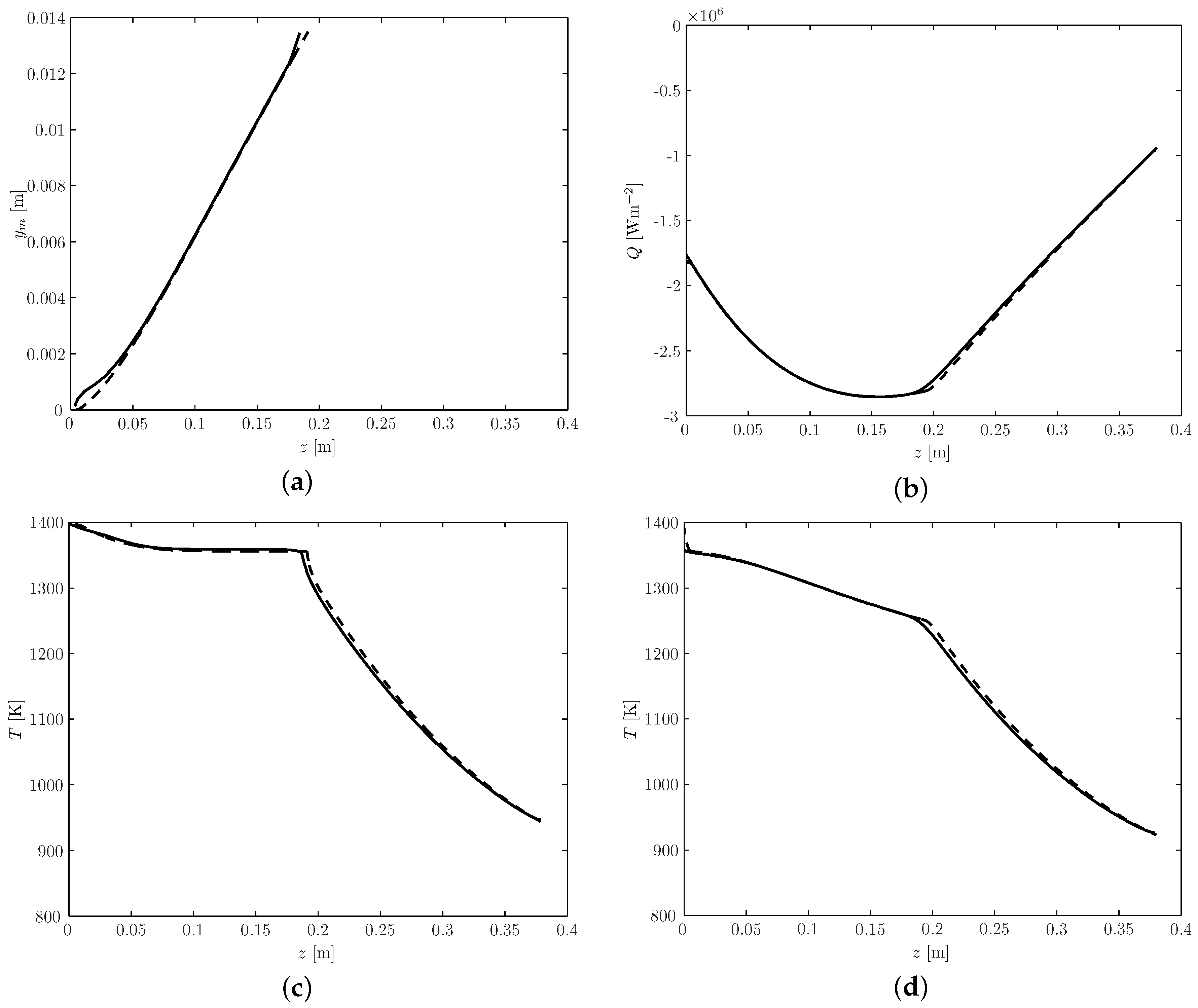
- The agreement between the model results was very good, as shown in Figure 3.
References
- Return to Introduction to Continuous Casting. Available online: http://ccc.illinois.edu/introduction/overview.html#fig1 (accessed on 6 November 2018).
- Thomas, B.G. Review on modeling and simulation of continuous casting. Steel Res. Int. 2018, 89, 1700312. [Google Scholar] [CrossRef]
- Kuiken, H.K. Practical Asymptotics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Holmes, M.H.; King, J.R. Practical Asymptotics II. J. Eng. Math. 2003, 45, 155–404. [Google Scholar] [CrossRef]
- Witelski, T.P.; Rienstra, S.W. Introduction to Practical Asymptotics III. J. Eng. Math. 2005, 53, 199. [Google Scholar] [CrossRef]
- McCue, S.W. Preface to the fourth special issue on practical asymptotics. J. Eng. Math. 2009, 63, 153–154. [Google Scholar] [CrossRef]
- Korobkin, A. Preface to the fifth special issue on practical asymptotics. J. Eng. Math. 2011, 69, 111–112. [Google Scholar] [CrossRef]
- Smith, W.R. Preface to the sixth special issue on “Practical Asymptotics”. J. Eng. Math. 2017, 102, 1–2. [Google Scholar] [CrossRef]
- Schilders, W.H.A.; van der Vorst, H.A.; Rommes, J. (Eds.) Model Order Reduction: Theory, Research Aspects and Applications, 1st ed.; Mathematics in Industry 13; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Voller, V.R.; Porte-Agel, F. Moore’s law and numerical modeling. J. Comput. Phys. 2002, 179, 698–703. [Google Scholar] [CrossRef]
- Pickering, E.J.; Chesman, C.; Al-Bermani, S.; Holland, M.; Davies, P.; Talamantes-Silva, J. A comprehensive case study of macrosegregation in a steel ingot. Metall. Mater. Trans. B 2015, 46, 1860–1874. [Google Scholar] [CrossRef]
- DiLellio, J.A.; Young, G.W. An asymptotic model of the mold region in a continuous steel caster. Metall. Mater. Trans. B 1995, 26B, 1225–1241. [Google Scholar] [CrossRef]
- Smelser, R.E.; Johnson, R.E. An asymptotic model of slab casting. Int. J. Mech. Sci. 1995, 37, 793–814. [Google Scholar] [CrossRef]
- Johnson, R.E.; Cherukuri, H.P. Vertical continuous casting of bars. Proc. R. Soc. A 1999, 455, 227–244. [Google Scholar] [CrossRef]
- Cherukuri, H.P.; Johnson, R.E. Modelling vertical continuous casting with temperature-dependent material properties. Int. J. Mech. Sci. 2001, 43, 1243–1257. [Google Scholar] [CrossRef]
- Bland, D.R. Flux and the continuous casting of steel. IMA J. Appl. Maths 1984, 32, 89–112. [Google Scholar] [CrossRef]
- Hill, J.M.; Wu, Y.H. On a nonlinear Stefan problem in the continuous casting of steel. Acta Mech. 1994, 107, 183–198. [Google Scholar] [CrossRef]
- Hill, J.M.; Wu, Y.H.; Wiwatanapataphee, B. Analysis of flux flow and the formation of oscillation marks in the continuous caster. J. Eng. Math. 1999, 36, 311–326. [Google Scholar] [CrossRef]
- King, J.R.; Lacey, A.A.; Please, C.P.; Wilmott, P.; Zoryk, A. The formation of oscillation marks on continuously cast steel. Math. Eng. Ind. 1993, 4, 91–106. [Google Scholar]
- Howison, S.D. Practical Applied Mathematics: Modelling, Analysis, Approximation; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Mitchell, S.L.; Vynnycky, M. Verified reduction of a model for a continuous casting process. Appl. Math. Mod. 2017, 48, 476–490. [Google Scholar] [CrossRef]
- Vynnycky, M.; Saleem, S. On the explicit resolution of the mushy zone in the modelling of the continuous casting of alloys. Appl. Math. Mod. 2017, 50, 544–568. [Google Scholar] [CrossRef]
- Vynnycky, M.; Saleem, S.; Fredriksson, H. An asymptotic approach to solidification shrinkage-induced macrosegregation in the continuous casting of binary alloys. Appl. Math. Mod. 2018, 54, 605–626. [Google Scholar] [CrossRef]
- Vynnycky, M. An asymptotic model for the formation and evolution of air gaps in vertical continuous casting. Proc. R. Soc. A 2009, 465, 1617–1644. [Google Scholar] [CrossRef]
- Vynnycky, M. Air gaps in vertical continuous casting in round moulds. J. Eng. Math. 2010, 68, 129–152. [Google Scholar] [CrossRef]
- Vynnycky, M. On the role of radiative heat transfer in air gaps in vertical continuous casting. Appl. Math. Mod. 2013, 37, 2178–2188. [Google Scholar] [CrossRef]
- Vynnycky, M. On the onset of air-gap formation in vertical continuous casting with superheat. Int. J. Mech. Sci. 2013, 73, 69–76. [Google Scholar] [CrossRef]
- Florio, B.J.; Vynnycky, M.; Mitchell, S.L.; O’Brien, S.B.G. Mould-taper asymptotics and air gap formation in continuous casting. Appl. Math. Comput. 2015, 268, 1122–1139. [Google Scholar] [CrossRef]
- Florio, B.J.; Vynnycky, M.; Mitchell, S.L.; O’Brien, S.B.G. On the interactive effects of mould taper and superheat on air gaps in continuous casting. Acta Mech. 2017, 228, 233–254. [Google Scholar] [CrossRef]
- Vynnycky, M.; Saleem, S.; Devine, K.M.; Florio, B.J.; Mitchell, S.L.; O’Brien, S.B.G. On the formation of fold-type oscillation marks in the continuous casting of steel. R. Soc. Open Sci. 2017, 4, 176002. [Google Scholar] [CrossRef] [PubMed]
- Vynnycky, M. On an anomaly in the modeling of electromagnetic stirring in continuous casting. Metall. Mater. Trans. B 2018, 49B, 399–410. [Google Scholar] [CrossRef]
- Vynnycky, M.; Zambrano, M. Towards a “moving-point” formulation for the modelling of oscillation-mark formation in the continuous casting of steel. Appl. Math. Mod. 2018, 63, 243–265. [Google Scholar] [CrossRef]
- Vynnycky, M. Porous-media braking of electromagnetic stirring in the continuous casting of steel. In Proceedings of the 24th ABCM International Congress of Mechanical Engineering, Curitiba, Brazil, 3–8 December 2017. [Google Scholar]
- Mahmoudi, J.; Vynnycky, M.; Fredriksson, H. Modelling of fluid flow, heat transfer and solidification in the strip casting of a copper base alloy: (III). Solidification—A theoretical study. Scand. J. Metall. 2001, 30, 136–145. [Google Scholar] [CrossRef]
- Mahmoudi, J.; Vynnycky, M.; Sivesson, P.; Fredriksson, H. An experimental and numerical study on the modelling of fluid flow, heat transfer and solidification in a copper continuous strip casting process. Mater. Trans. 2003, 44, 1741–1751. [Google Scholar] [CrossRef]
- AEA Technology. CFX 4.2 Flow Solver User Guide; AEA Technology: Harwell, UK, 1995. [Google Scholar]
- Swaminathan, C.R.; Voller, V.R. A general enthalpy method for modeling solidification processes. Met. Trans. B 1992, 23B, 651–664. [Google Scholar] [CrossRef]
- Voller, V.R.; Peng, S. An enthalpy formulation based on an arbitrarily deforming mesh for solution of the Stefan problem. Comput. Mech. 1994, 14, 492–502. [Google Scholar] [CrossRef]
- Aboutalebi, M.R.; Hasan, M.; Guthrie, R.I.L. Numerical study of coupled turbulent flow and solidification for steel slab casters. Numer. Heat Transf. 1995, 28, 279–297. [Google Scholar] [CrossRef]
- Aboutalebi, M.R.; Hasan, M.; Guthrie, R.I.L. Coupled turbulent flow, heat and solute transport in continuous casting processes. Metall. Mater. Trans. B 1995, 26, 731–744. [Google Scholar] [CrossRef]
- Thevik, H.J.; Mo, A.; Rusten, T. A mathematical model for surface segregation in aluminum direct chill casting. Metall. Mater. Trans. B 1999, 39, 135–142. [Google Scholar] [CrossRef]
- Savage, J. A theory of heat transfer and air gap formation in continuous casting molds. J. Iron Steel Inst. 1962, 198, 41–47. [Google Scholar]
- Richmond, O.; Tien, R.H. Theory of thermal stresses and air-gap formation during the early stages of solidification in a rectangular mold. J. Mech. Phys. Solids 1971, 19, 273–284. [Google Scholar] [CrossRef]
- Kristiansson, J.O. Thermal stresses in the early stage of the solidification of steel. J. Therm. Stresses 1982, 5, 315–330. [Google Scholar] [CrossRef]
- Tien, R.H.; Richmond, O. Theory of maximum tensile stresses in the solidifying shell of a constrained regular casting. J. Appl. Mech. 1982, 49, 481–486. [Google Scholar] [CrossRef]
- Kim, K.Y. Analysis of gap formation at mold-shell interface during solidification of aluminium alloy plate. ISIJ Int. 2003, 43, 647–652. [Google Scholar] [CrossRef]
- Kelly, J.E.; Michalek, K.P.; O’Connor, T.G.; Thomas, B.G.; Dantzig, J.A. Initial development of thermal and stress fields in continuously cast steel billets. Metall. Mater. Trans. A 1988, 19A, 2589–2602. [Google Scholar] [CrossRef]
- Grill, A.; Sorimachi, K.; Brimacombe, J.K. Heat flow, gap formation and break-outs in the continuous casting of steel slabs. Metall. Mater. Trans. B 1976, 7B, 177–189. [Google Scholar] [CrossRef]
- Bellet, M.; Decultieux, F.; Menai, M.; Bay, F.; Levaillant, C.; Chenot, J.L.; Schmidt, P.; Svensson, I.L. Thermomechanics of the cooling stage in casting processes: Three-dimensional finite element analysis and experimental validation. Metall. Mater. Trans. B 1996, 27, 81–99. [Google Scholar] [CrossRef]
- Huespe, A.E.; Cardona, A.; Fachinotti, V. Thermomechanical model of a continuous casting process. Comput. Methods Appl. Mech. Eng. 2000, 182, 439–455. [Google Scholar] [CrossRef]
- Li, C.; Thomas, B.G. Thermomechanical finite-element model of shell behavior in continuous casting of steel. Metall. Mater. Trans. B 2004, 35B, 1151–1172. [Google Scholar] [CrossRef]
- Sun, D.; Annapragada, S.R.; Garimella, S.V.; Singh, S.K. Analysis of gap formation in the casting of energetic materials. Numer. Heat Transf. 2007, 51, 415–444. [Google Scholar] [CrossRef]
- Saleem, S. On the Surface Quality of Continuously Cast Steels and Phosphor Bronzes. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2016. [Google Scholar]
- Saleem, S.; Vynnycky, M.; Fredriksson, H. A study of the oscillation marks’ characteristics of continuously cast Incoloy alloy 825 blooms. Metall. Mater. Trans. A 2016, 47, 4068–4079. [Google Scholar] [CrossRef]
- Takeuchi, E.; Brimacombe, J.K. The formation of oscillation marks in the continuous casting of steel slabs. Metall. Mater. Trans. B 1984, 15, 493–509. [Google Scholar] [CrossRef]
- Jonayat, A.S.M.; Thomas, B.G. Transient thermo-fluid model of meniscus behavior and slag consumption in steel continuous casting. Metall. Mater. Trans. A 2014, 45, 1842–1864. [Google Scholar] [CrossRef]
- Tomono, H. Elements of Oscillation Mark Formation and Their Effect on Transverse Fine Cracks in Continuous Casting of Steel. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 1979. [Google Scholar]
- Ramirez-Lopez, P.E.; Lee, P.D.; Mills, K.C. Explicit modelling of slag infiltration and shell formation during mould oscillation in continuous casting. ISIJ Int. 2010, 50, 425–434. [Google Scholar] [CrossRef]
- Ramirez-Lopez, P.E.; Lee, P.D.; Mills, K.C.; Santillana, B. A new approach for modelling slag infiltration and solidification in a continuous casting mould. ISIJ Int. 2010, 50, 1797–1804. [Google Scholar] [CrossRef]
- Lee, P.D.; Ramirez-Lopez, P.E.; Mills, K.C.; Santillana, B. Review: The “butterfly effect” in continuous casting. Ironmak. Steelmak. 2012, 39, 244–253. [Google Scholar] [CrossRef]
- Ramirez-Lopez, P.E.; Mills, K.C.; Lee, P.D.; Santillana, B. A unified mechanism for the formation of oscillation marks. Metall. Mater. Trans. B 2012, 43B, 109–122. [Google Scholar] [CrossRef]
- Bikerman, J.J. Physical Surfaces; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Flemings, M.C.; Nereo, G.E. Macrosegregation. I. AIME Met. Soc. Trans. 1967, 239, 1449–1461. [Google Scholar]
- Flemings, M.C.; Mehrabian, R.; Nereo, G.E. Macrosegregation. PT. 2. AIME Met. Soc. Trans. 1968, 242, 41–49. [Google Scholar]
- Reddy, A.V.; Beckermann, C. Modeling of macrosegregation due to thermosolutal convection and contraction-driven flow in direct chill continuous casting of an Al-Cu round ingot. Metall. Mater. Trans. B 1997, 28, 479–489. [Google Scholar] [CrossRef]
- Saleem, S.; Vynnycky, M.; Fredriksson, H. Formation of the tin rich layer and inverse segregation in phosphor bronzes during continuous casting. In Proceedings of the Minerals, Metals and Materials Society (TMS) 2015: 144th Annual Meeting and Exhibition, Orlando, FL, USA, 15–19 March 2015; pp. 15–22. [Google Scholar]
- Diao, Q.Z.; Tsai, H.L. Modelling of solute redistribution in the mushy zone during solidification of aluminium-copper alloys. Metall. Trans. 1993, 24A, 963–973. [Google Scholar] [CrossRef]
- Chen, J.H.; Tsai, H.L. Inverse segregation for a unidirectional solidification of aluminium-copper alloys. Int. J. Heat Mass Transf. 1993, 36, 3069–3075. [Google Scholar] [CrossRef]
- Diao, Q.Z.; Tsai, H.L. The formation of negative- and positive-segregated bands during solidification of aluminum-copper alloys. Int. J. Heat Mass Transf. 1993, 36, 4299–4305. [Google Scholar] [CrossRef]
- Mo, A. Mathematical modelling of surface segregation in aluminum DC casting caused by exudation. Int. J. Heat Mass Transf. 1993, 36, 4335–4340. [Google Scholar] [CrossRef]
- Voller, V.R.; Sundarraj, S. A model of inverse segregation: The role of microporosity. Int. J. Heat Mass Transf. 1995, 38, 1009–1018. [Google Scholar] [CrossRef]
- Minakawa, S.; Samarasekera, I.V.; Weinberg, F. Inverse segregation. Metall. Trans. 1985, 16, 595–604. [Google Scholar] [CrossRef]
- Du, Q.; Eskin, D.G.; Katgerman, L. Numerical issues in modelling macrosegregation during DC casting of a multi-component aluminium alloy. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 917–930. [Google Scholar] [CrossRef]
- Jalanti, T.; Swierkosz, M.; Gremaud, M.; Rappaz, M. Modelling of macrosegregation in continuous casting of aluminium. In Continuous Casting; Ehrke, K., Schneider, W., Eds.; WILEY-VCH Verlag GmbH: Weinheim, Germany, 2006; pp. 191–198. [Google Scholar]
- Založnik, M.; Xin, S.; Šarler, B. Verification of a numerical model of macrosegregation in direct chill casting. Int. J. Numer. Methods Heat Fluid Flow 2008, 18, 308–324. [Google Scholar] [CrossRef]
- Venneker, B.C.H.; Katgerman, L. Modelling issues in macrosegregation predictions in direct chill castings. J. Light Met. 2002, 2, 149–159. [Google Scholar] [CrossRef]
- Eskin, D.G.; Zuidema, J.; Savran, V.I.; Katgerman, L. Structure formation and macrosegregation under different process conditions during DC casting. Mater. Sci. Eng. A 2004, 384, 232–244. [Google Scholar] [CrossRef]
- Eskin, D.G.; Du, Q.; Katgerman, L. Relationship between shrinkage-induced macrosegregation and the sump profile upon direct-chill casting. Scr. Mater. 2006, 55, 715–718. [Google Scholar] [CrossRef]
- Du, Q.; Eskin, D.G.; Katgerman, L. Modeling macrosegregation during direct-chill casting of multicomponent aluminum alloys. Metall. Mater. Trans. A 2007, 38A, 180–189. [Google Scholar] [CrossRef]
- Jalanti, T. Etude et Modélisation de la Macroségrégation dans la Coulée Semi-Continue des Alliages d’Aluminium. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2000. [Google Scholar]
- Fredriksson, H.; Åkerlind, U. Materials Processing during Casting; Wiley: Chichester, UK, 2006. [Google Scholar]
- Tzavaras, A.A.; Brody, H.D. Electromagnetic stirring and continuous-casting—Achievements, problems, and goals. J. Met. 1984, 36, 31–37. [Google Scholar] [CrossRef]
- Spitzer, K.H.; Dubke, M.; Schwerdtfeger, K. Rotational electromagnetic stirring in continuous-casting of round strands. Metall. Mater. Trans. B 1986, 17, 119–131. [Google Scholar] [CrossRef]
- Dubke, M.; Tacke, K.H.; Spitzer, K.H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part I. Theory and experiments with cold models. Metall. Mater. Trans. B 1988, 19B, 581–593. [Google Scholar] [CrossRef]
- Dubke, M.; Tacke, K.H.; Spitzer, K.H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part II. Computation of flow fields in billets, blooms, and slabs of steel. Metall. Mater. Trans. B 1988, 19, 595–602. [Google Scholar] [CrossRef]
- Dubke, M.; Spitzer, K.H.; Schwerdtfeger, K. Spatial-distribution of magnetic-field of linear inductors used for electromagnetic stirring in continuous-casting of steel. Ironmak. Steelmak. 1991, 18, 347–353. [Google Scholar]
- Tacke, K.H.; Grill, A.; Miyazawa, K.; Schwerdtfeger, K. Macrosegregation in strand cast steel—Computation of concentration profiles with a diffusion-model. Arch. Eisenhüttenw. 1981, 52, 15–20. [Google Scholar] [CrossRef]
- Tacke, K.H.; Schwerdtfeger, K. Stirring velocities in continuously cast round billets as induced with rotating electromagnetic-fields. Stahl und Eisen 1979, 99, 7–12. [Google Scholar]
- Zhang, C.; Shatrov, V.; Priede, J.; Eckert, S.; Gerbeth, G. Intermittent behavior caused by surface oxidation in a liquid metal flow driven by a rotating magnetic field. Metall. Mater. Trans. B 2011, 42, 1188–1200. [Google Scholar] [CrossRef]
- Liu, H.; Xu, M.; Qiu, S.; Zhang, H. Numerical simulation of fluid flow in a round bloom mold with in-mold rotary electromagnetic stirring. Metall. Mater. Trans. B 2012, 43, 1657–1675. [Google Scholar] [CrossRef]
- Yang, J.; Xie, Z.; Ning, J.; Liu, W.; Ji, Z. A framework for soft sensing of liquid pool length of continuous casting round blooms. Metall. Mater. Trans. B 2014, 45, 1545–1556. [Google Scholar] [CrossRef]
- Poole, G.M.; Heyen, M.; Nastac, L.; El-Kaddah, N. Numerical modeling of macrosegregation in binary alloys solidifying in the presence of electromagnetic stirring. Metall. Mater. Trans. B 2014, 45, 1834–1841. [Google Scholar] [CrossRef]
- Ren, B.Z.; Chen, D.F.; Wang, H.D.; Long, M.J.; Han, Z.W. Numerical simulation of fluid flow and solidification in bloom continuous casting mould with electromagnetic stirring. Ironmak. Steelmak. 2015, 42, 401–408. [Google Scholar] [CrossRef]
- Fang, Q.; Ni, H.; Zhang, H.; Wang, B.; Lv, Z. The effects of a submerged entry nozzle on flow and initial solidification in a continuous casting bloom mold with electromagnetic stirring. Metals 2017, 7, 146. [Google Scholar] [CrossRef]
- Wang, X.; Fautrelle, Y.; Etay, J.; Moreau, R. A periodically reversed flow driven by a modulated traveling magnetic field: Part I. Experiments with GaInSn. Metall. Mater. Trans. B 2009, 40, 82–90. [Google Scholar] [CrossRef]
- Eckert, S.; Nikrityuk, P.A.; Raebiger, D.; Eckert, K.; Gerbeth, G. Efficient melt stirring using pulse sequences of a rotating magnetic field: Part I. Flow field in a liquid metal column. Metall. Mater. Trans. B 2007, 38, 977–988. [Google Scholar] [CrossRef]
- Beitelman, L.S.; Curran, C.P.; Lavers, J.D.; Tallback, G. Modulated Electromagnetic Stirring of Metals at Advanced Stage of Solidification. EP Patent EP080783247, 22 August 2011. [Google Scholar]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: Harlow, UK, 2007. [Google Scholar]
- Bridge, M.R.; Rogers, G.D. Structural effects and band segregate formation during the electromagnetic stirring of strand-cast steel. Met. Trans. B 1984, 15, 581–589. [Google Scholar] [CrossRef]
- Kor, G.J.W. Influence of circumferential electromagnetic stirring on macrosegregation in steel. Ironmak. Steelmak. 1982, 9, 244–251. [Google Scholar]
- M’Hamdi, M.; Håkonsen, A. Experimental and numerical study of surface macrosegregation in DC casting of aluminium sheet ingots. In Modeling of Casting, Welding and Advanced Solidification Processes-X, Proceedings of the 10th International Conference on Modeling of Casting, Welding and Advanced Solidification Processes, Destin, FL, USA, 25–30 May 2003; Stefanescu, D.M., Warren, J.A., Jolly, M.R., Krane, M.J.M., Eds.; Minerals, Metals & Materials Soc.: Warrendale, PA, USA, 2003; pp. 505–512. [Google Scholar]
- Haug, E.; Mo, A.; Thevik, H.J. Macrosegregation near a cast surface caused by exudation and solidification shrinkage. Int. J. Heat Mass Transf. 1995, 38, 1553–1563. [Google Scholar] [CrossRef]
- Luo, Y.Z.; Zhang, J.M.; Wei, X.D.; Xiao, C.; Hu, Z.F.; Yuan, Y.Y.; Chen, S.D. Numerical simulation of solidification structure of high carbon SWRH77B billet based on the CAFE method. Ironmak. Steelmak. 2012, 39, 26–30. [Google Scholar] [CrossRef]
- Luo, S.; Zhu, M.; Louhenkilpi, S. Numerical simulation of solidification structure of high carbon steel in continuous casting using cellular automaton method. ISIJ Int. 2012, 52, 823–830. [Google Scholar] [CrossRef]
- Wang, W.; Ji, C.; Luo, S.; Zhu, M. Modeling of dendritic evolution of continuously cast steel billet with cellular automaton. Metall. Mater. Trans. B 2018, 49, 200–212. [Google Scholar] [CrossRef]
- Guan, R.; Ji, C.; Zhu, M.; Deng, S. Numerical simulation of V-shaped segregation in continuous casting blooms based on a microsegregation model. Metall. Mater. Trans. B 2018, 49, 2571–2583. [Google Scholar] [CrossRef]
- Lee, P.; Chirazi, A.; See, D. Modeling microporosity in aluminum-silicon alloys: A review. J. Light Met. 2001, 1, 15–30. [Google Scholar] [CrossRef]
- Dantzig, J.A.; Rappaz, M. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Stefanescu, D.M. Computer simulation of shrinkage related defects in metal castings—A review. Int. J. Cast Met. Res. 2005, 18, 129–143. [Google Scholar] [CrossRef]
- Du, P. Numerical Modeling of Porosity and Macrosegregation in Continuous Casting of Steel. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2013. [Google Scholar]
- Rogberg, B.; Ek, L. Influence of soft reduction on the fluid flow, porosity and center segregation in CC high carbon- and stainless steel blooms. ISIJ Int. 2018, 58, 478–487. [Google Scholar] [CrossRef]
- Domitner, J.; Wu, M.; Kharicha, A.; Ludwig, A.; Kaufmann, B.; Reiter, J.; Schaden, T. Modeling the effects of strand surface bulging and mechanical softreduction on the macrosegregation formation in steel continuous casting. Metall. Mater. Trans. A 2014, 45, 1415–1434. [Google Scholar] [CrossRef]
- Mayer, F.; Wu, M.; Ludwig, A. On the formation of centreline segregation in continuous slab casting of steel due to bulging and/or feeding. Steel Res. Int. 2010, 81, 660–667. [Google Scholar] [CrossRef]
- Saleem, S.; Vynnycky, M.; Fredriksson, H. The influence of peritectic reaction/transformation on crack susceptibility in the continuous casting of steels. Metall. Mater. Trans. B 2017, 48, 1625–1635. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J. Study on the macrosegregation behavior for the bloom continuous casting: Model development and validation. Metall. Mater. Trans. B 2014, 45B, 1133–1149. [Google Scholar] [CrossRef]
- Hurtuk, D.J.; Tzavaras, A.A. Some effects of electromagnetically induced fluid-flow on macrosegregation in continuously cast steel. Metall. Trans. B Proc. Met. 1977, 8, 243–251. [Google Scholar] [CrossRef]
- Sasaki, K.; Sugitani, Y.; Kobayashi, S.; Ishimura, S. The effect of fluid flow on the formation of the negative segregation zone in steel ingots. Tetsu Hagane 1979, 65, 60–69. [Google Scholar] [CrossRef]
- Vynnycky, M.; Shugai, G.; Yakubenko, P.; Mellgren, N. Asymptotic reduction for numerical modeling of polymer electrolyte fuel cells. SIAM J. Appl. Math. 2009, 70, 455–487. [Google Scholar] [CrossRef]
- Ly, H.; Birgersson, E.; Vynnycky, M.; Sasmito, A.P. Validated reduction and accelerated numerical computation of a model for the proton exchange membrane fuel cell. J. Electrochem. Soc. 2009, 156, B1156–B1168. [Google Scholar] [CrossRef]
- Ly, H.; Birgersson, E.; Vynnycky, M. Asymptotically reduced model for a proton exchange membrane fuel cell stack: Automated model generation and verification. J. Electrochem. Soc. 2010, 157, B982–B992. [Google Scholar] [CrossRef]
- Ly, H.; Birgersson, E.; Vynnycky, M. Computationally efficient multi-phase models for a proton exchange membrane fuel cell: Asymptotic reduction and thermal decoupling. Int. J. Hydrog. Energy 2011, 36, 14573–14589. [Google Scholar] [CrossRef]
- Vynnycky, M.; Sharma, A.K.; Birgersson, E. A finite-element method for the weakly compressible parabolized steady 3D Navier-Stokes equations in a channel with a permeable wall. Comput. Fluids 2013, 81, 152–161. [Google Scholar] [CrossRef]
- Sharma, A.K.; Birgersson, E.; Vynnycky, M. Towards computationally-efficient modeling of transport phenomena in three-dimensional monolithic channels. Appl. Math. Comput. 2015, 254, 392–407. [Google Scholar] [CrossRef]

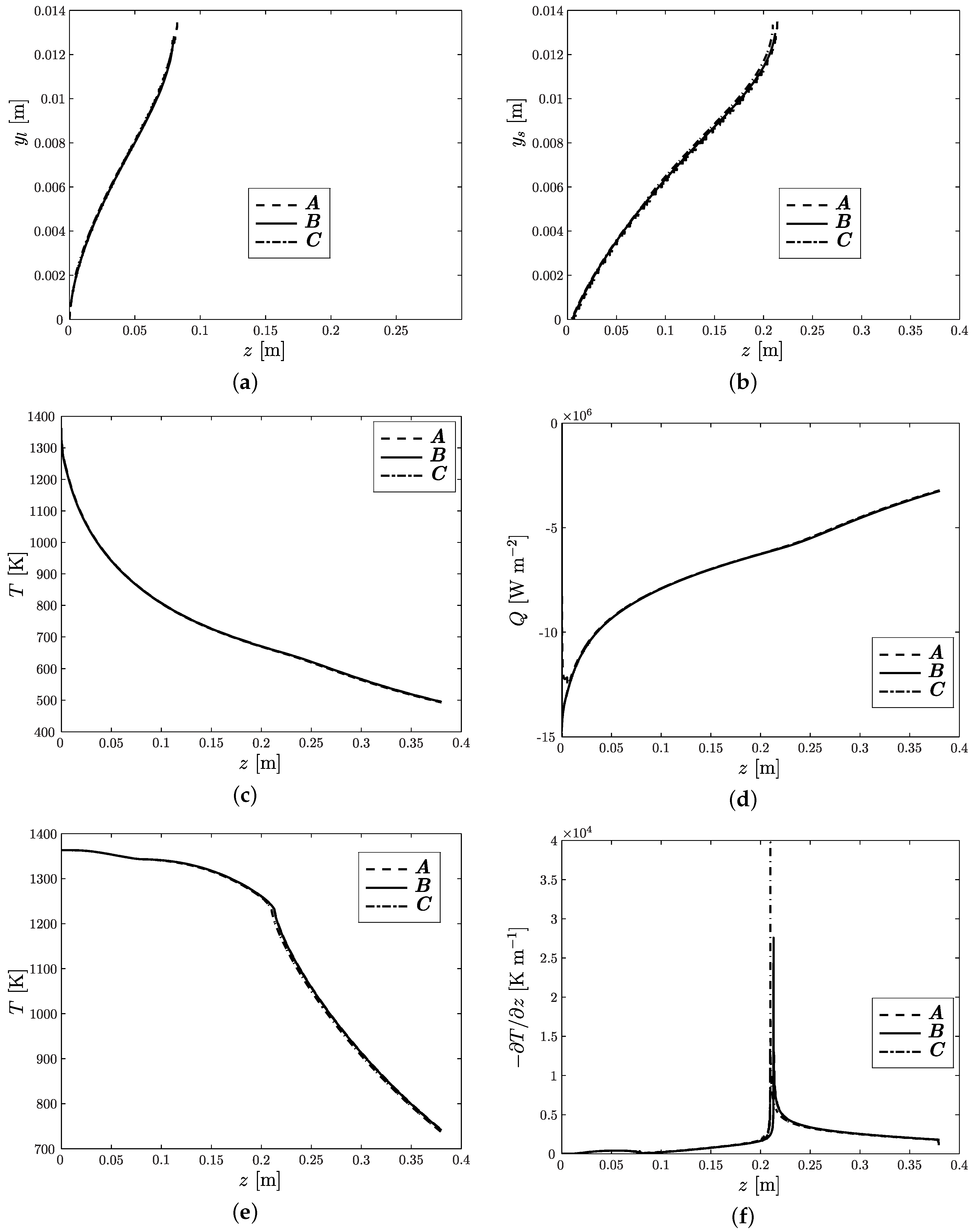
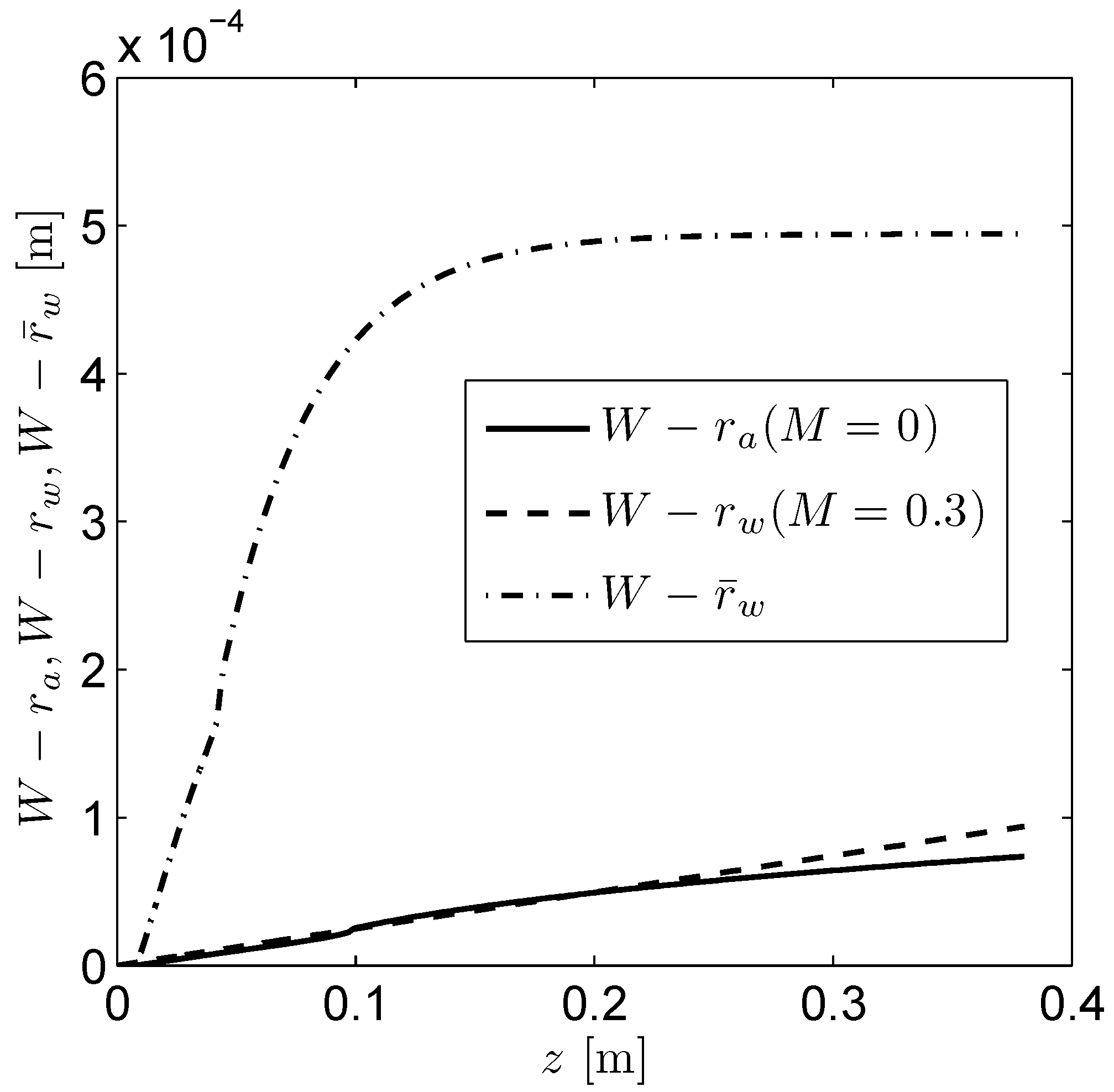

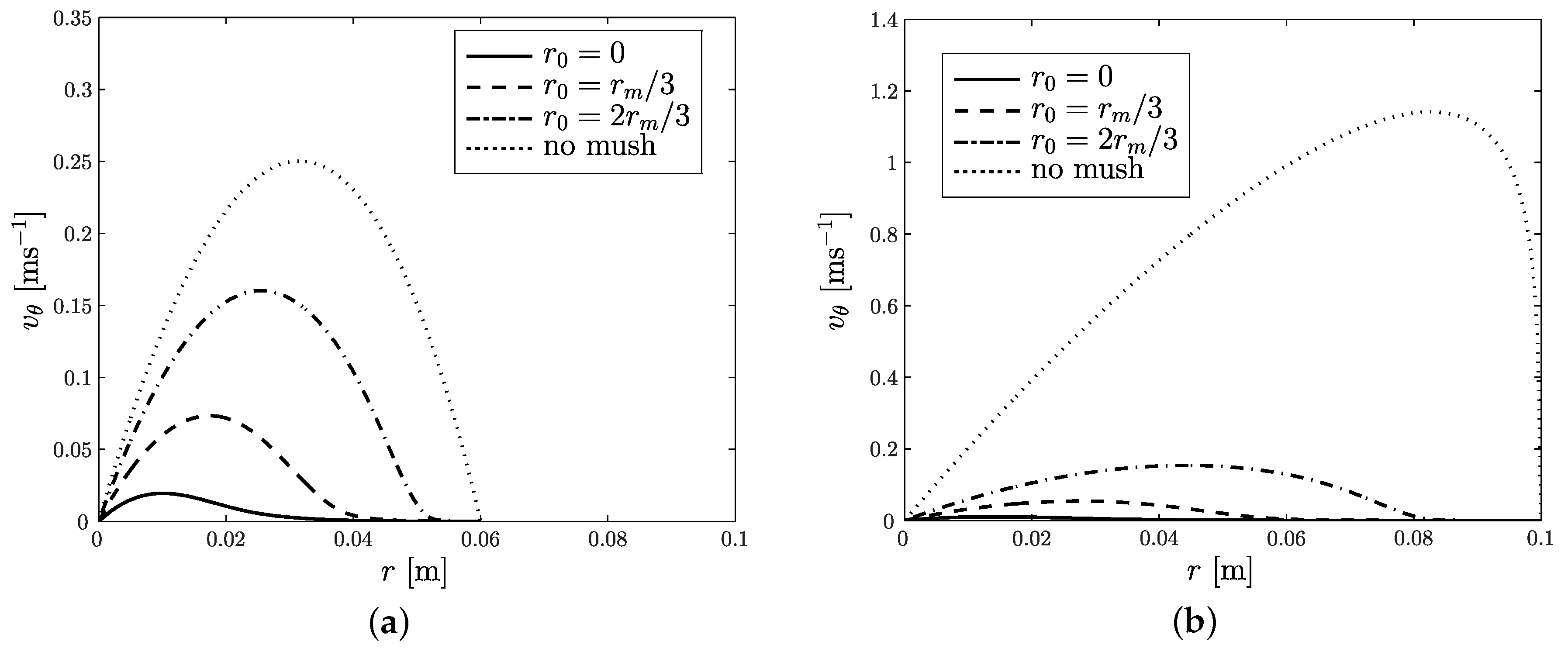
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vynnycky, M. Applied Mathematical Modelling of Continuous Casting Processes: A Review. Metals 2018, 8, 928. https://doi.org/10.3390/met8110928
Vynnycky M. Applied Mathematical Modelling of Continuous Casting Processes: A Review. Metals. 2018; 8(11):928. https://doi.org/10.3390/met8110928
Chicago/Turabian StyleVynnycky, Michael. 2018. "Applied Mathematical Modelling of Continuous Casting Processes: A Review" Metals 8, no. 11: 928. https://doi.org/10.3390/met8110928
APA StyleVynnycky, M. (2018). Applied Mathematical Modelling of Continuous Casting Processes: A Review. Metals, 8(11), 928. https://doi.org/10.3390/met8110928




