On the Critical Resolved Shear Stress and Its Importance in the Fatigue Performance of Steels and Other Metals with Different Crystallographic Structures
Abstract
1. Introduction
2. Materials and Methods
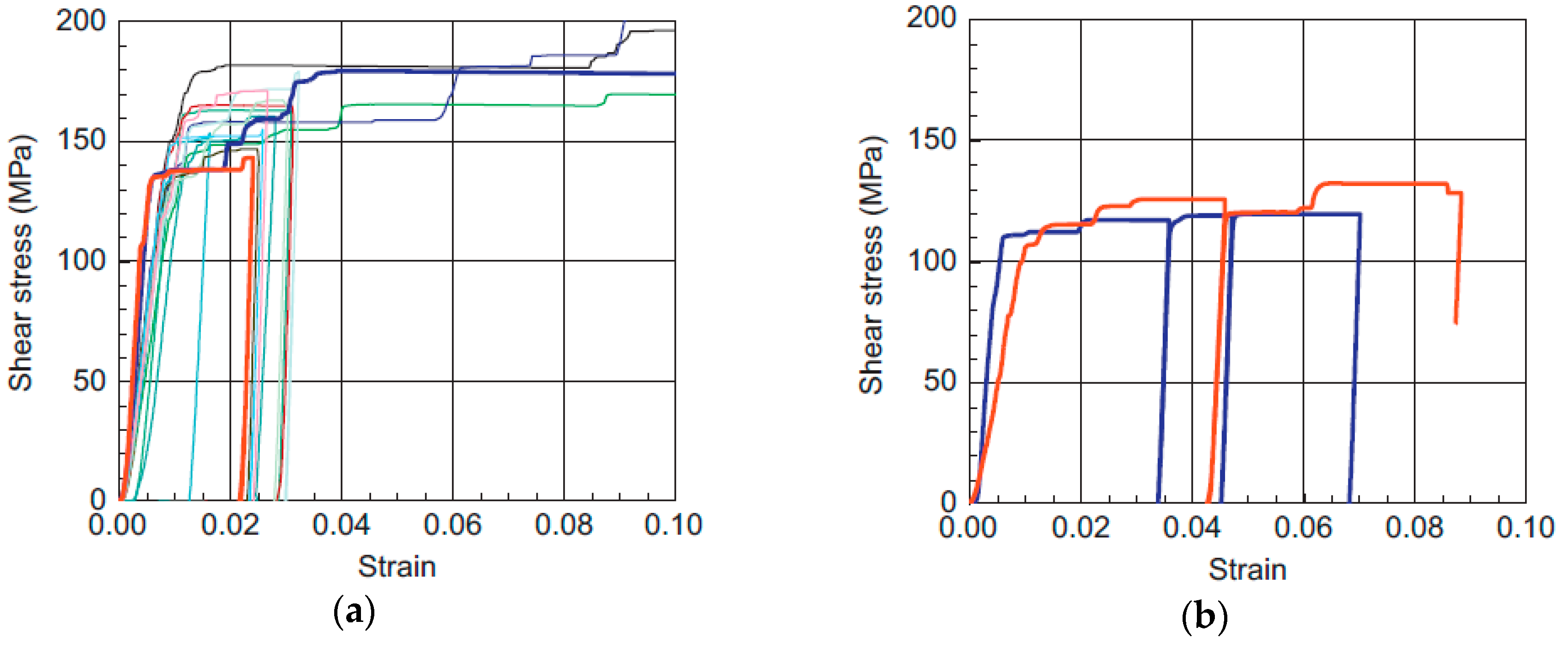
2.1. Compression Testing of Small Pillars
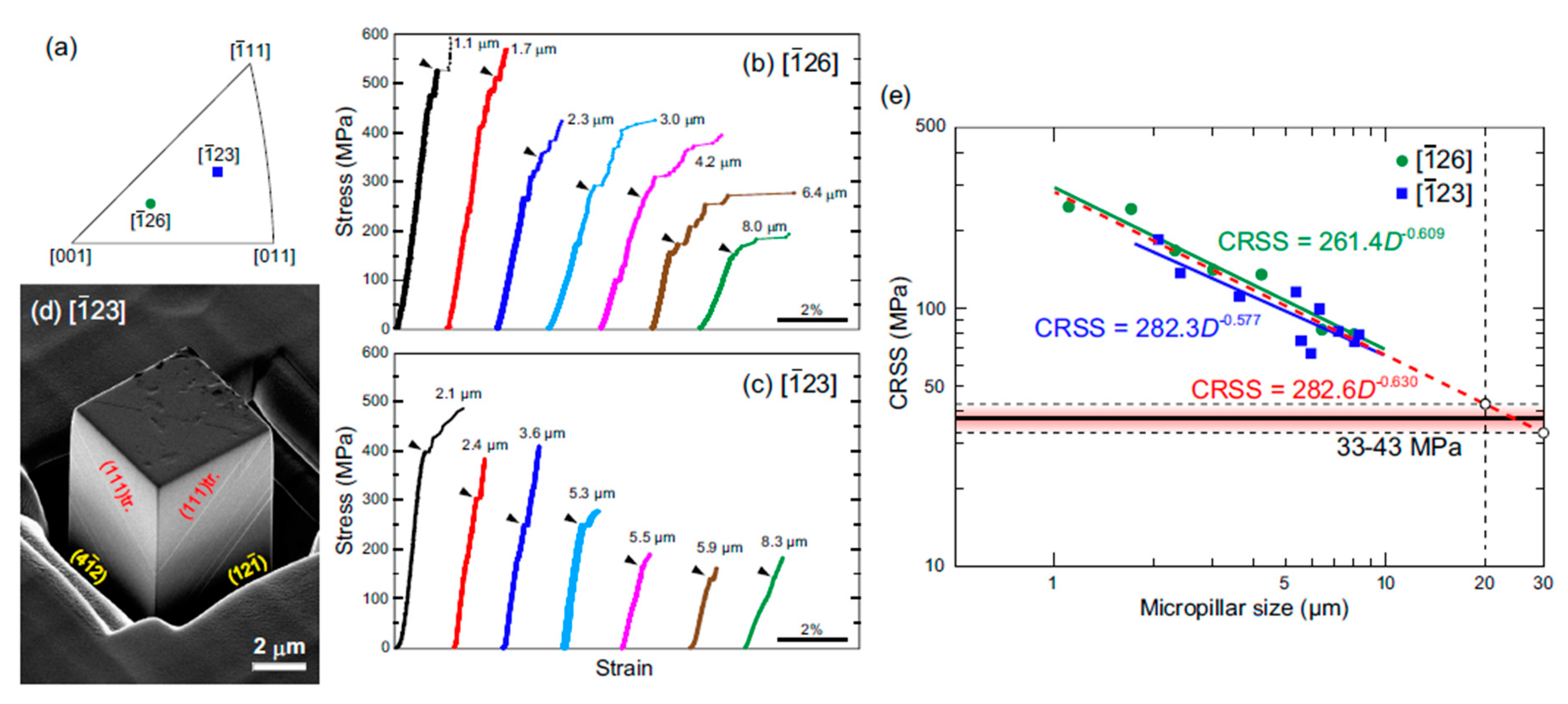
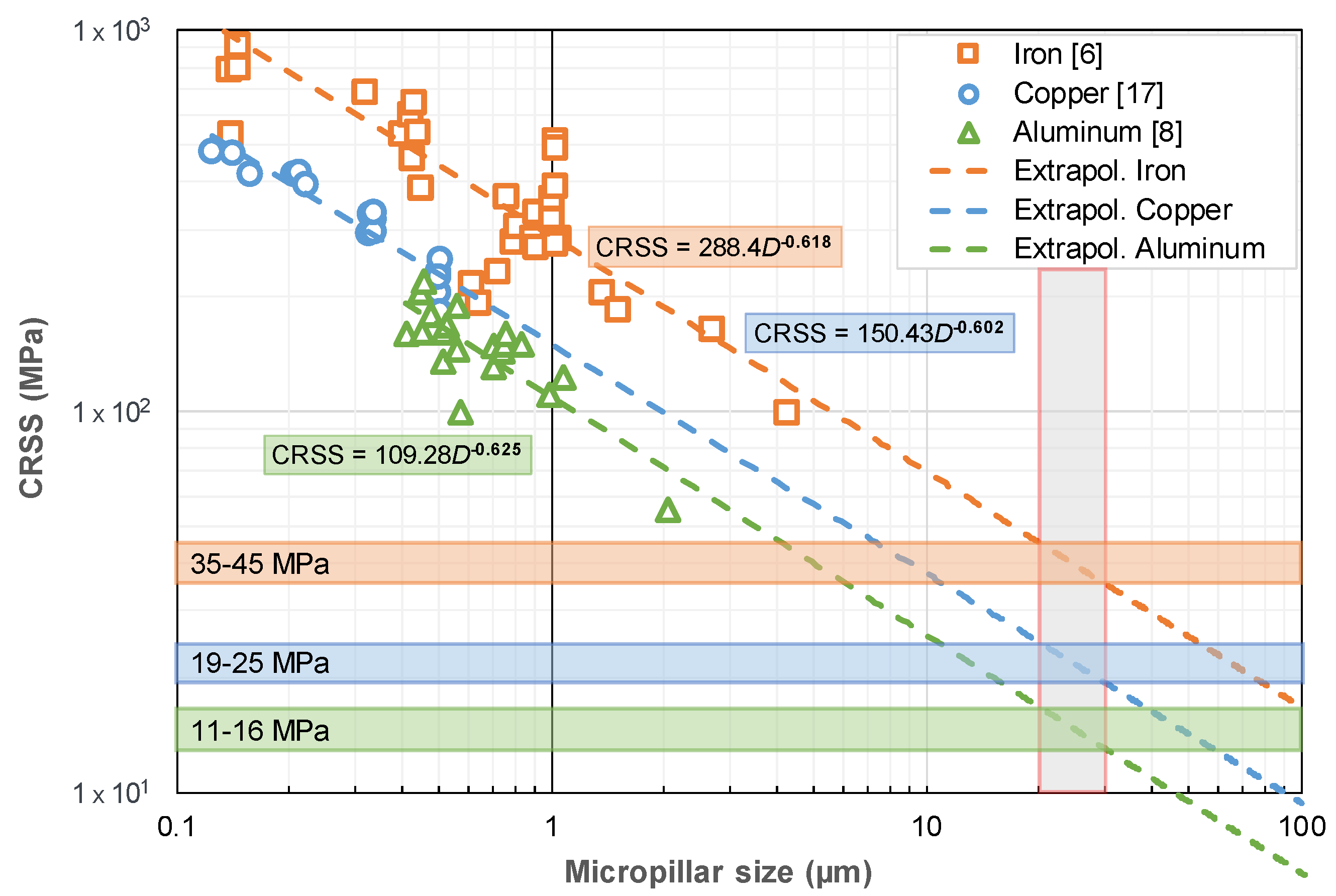
2.2. Size Effect or A Power-Law Relationship between CRSS and Pillar Diameter
2.3. Strengthening Mechanisms
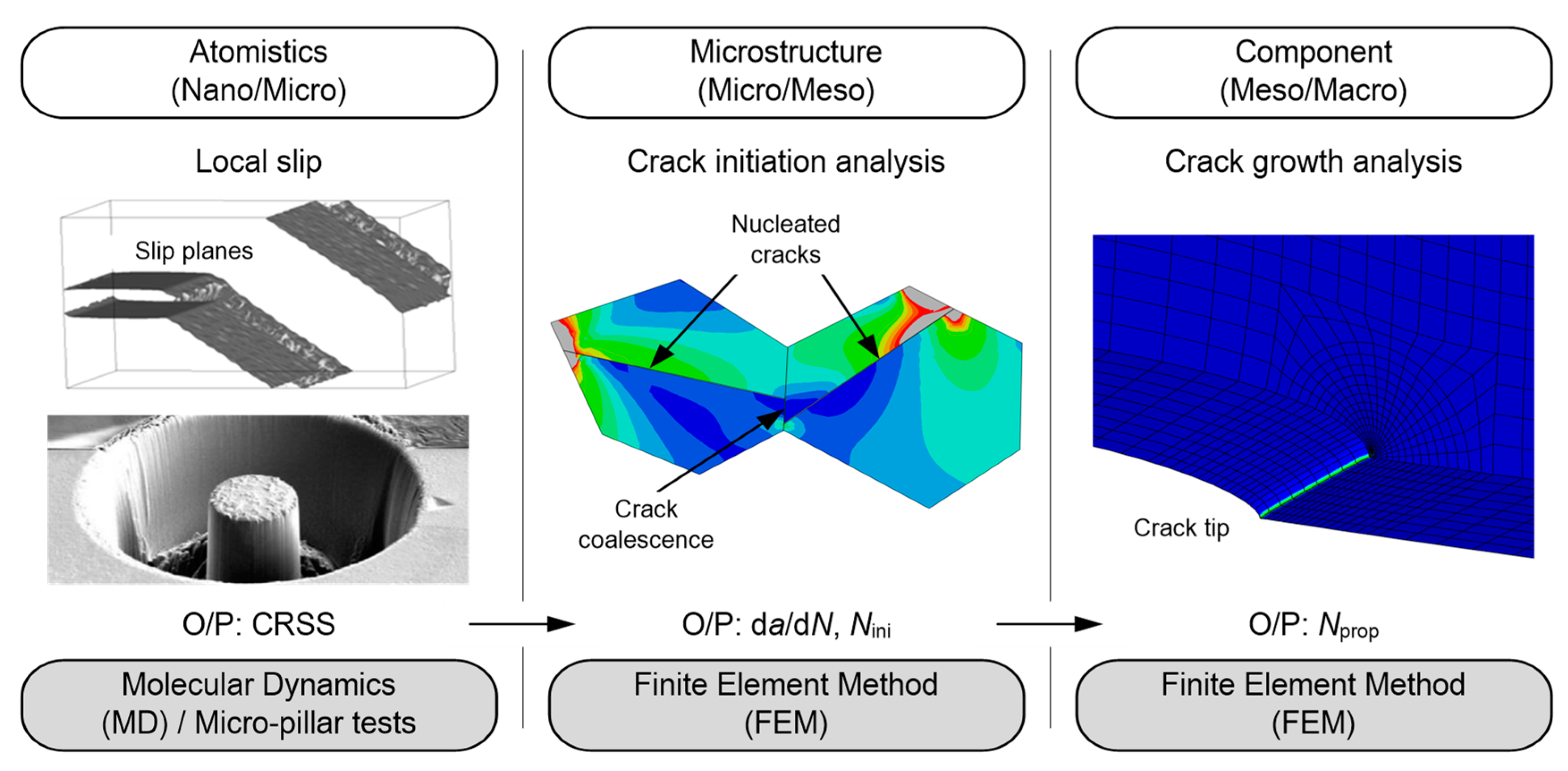
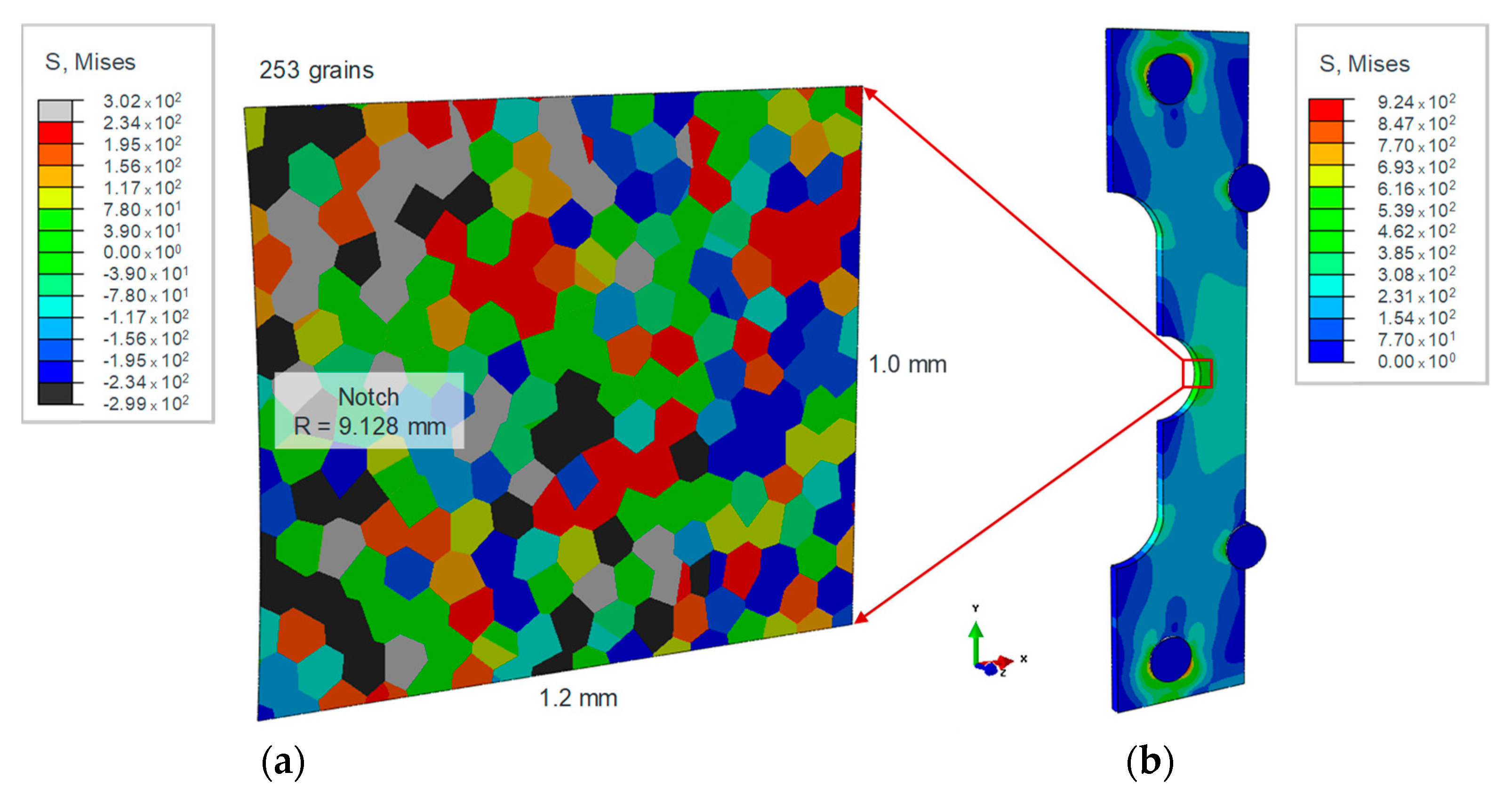
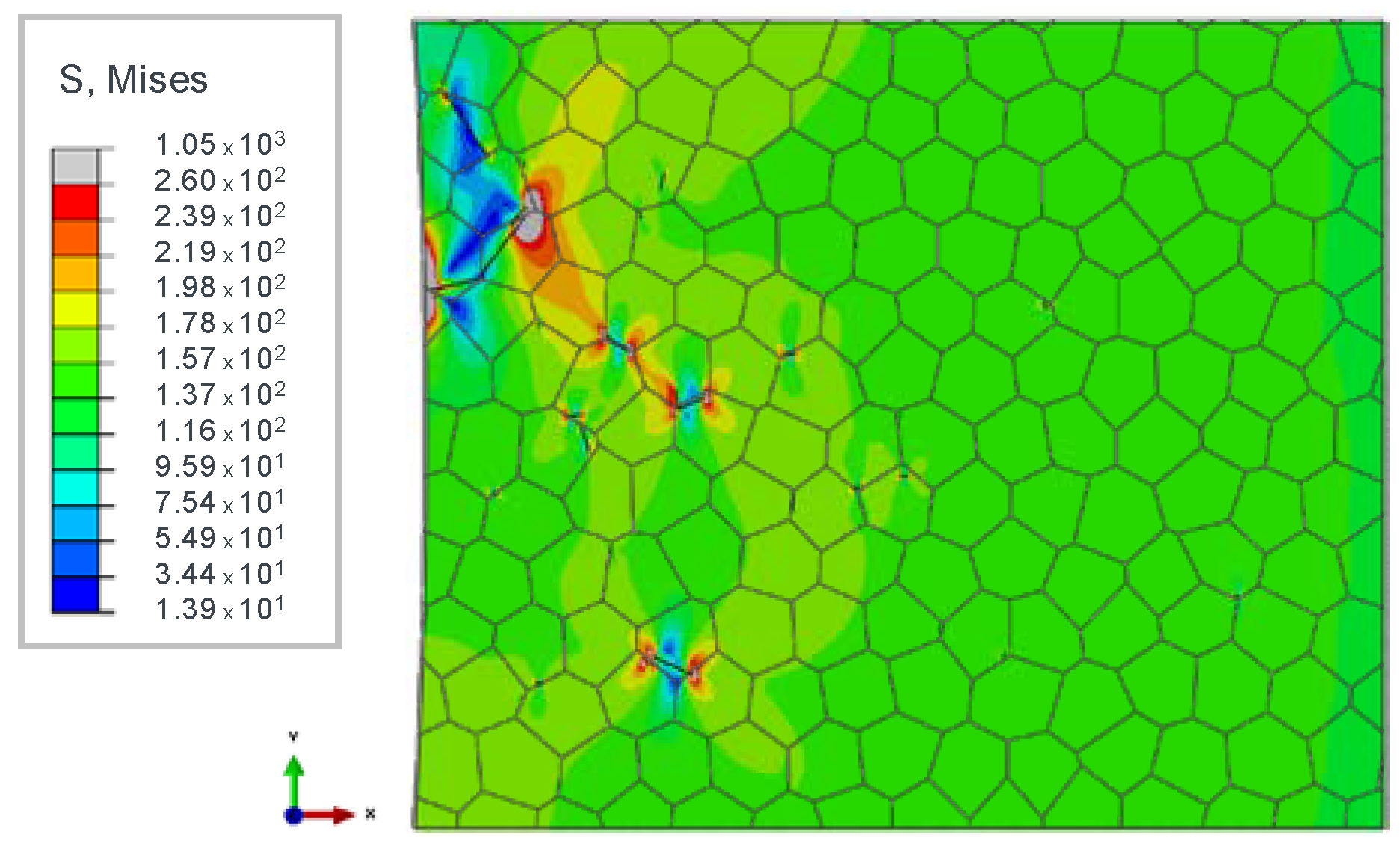
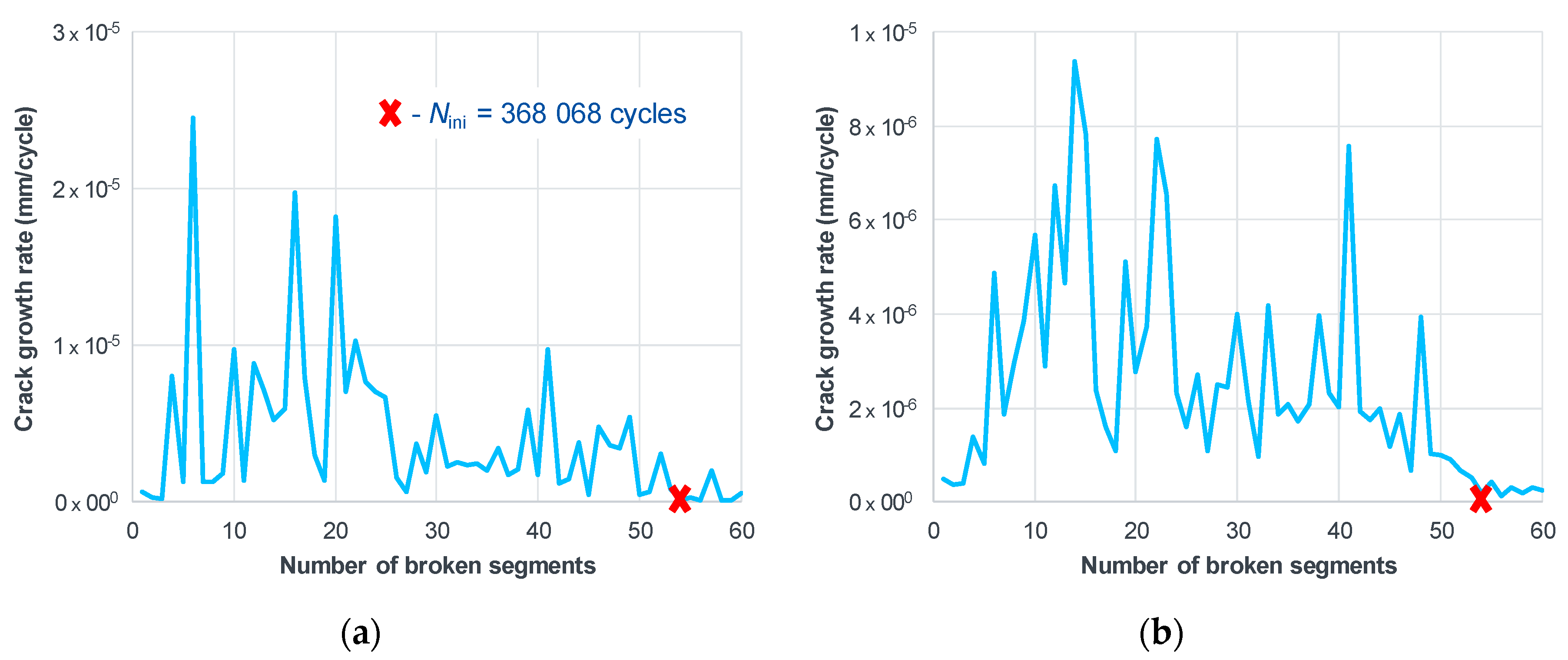
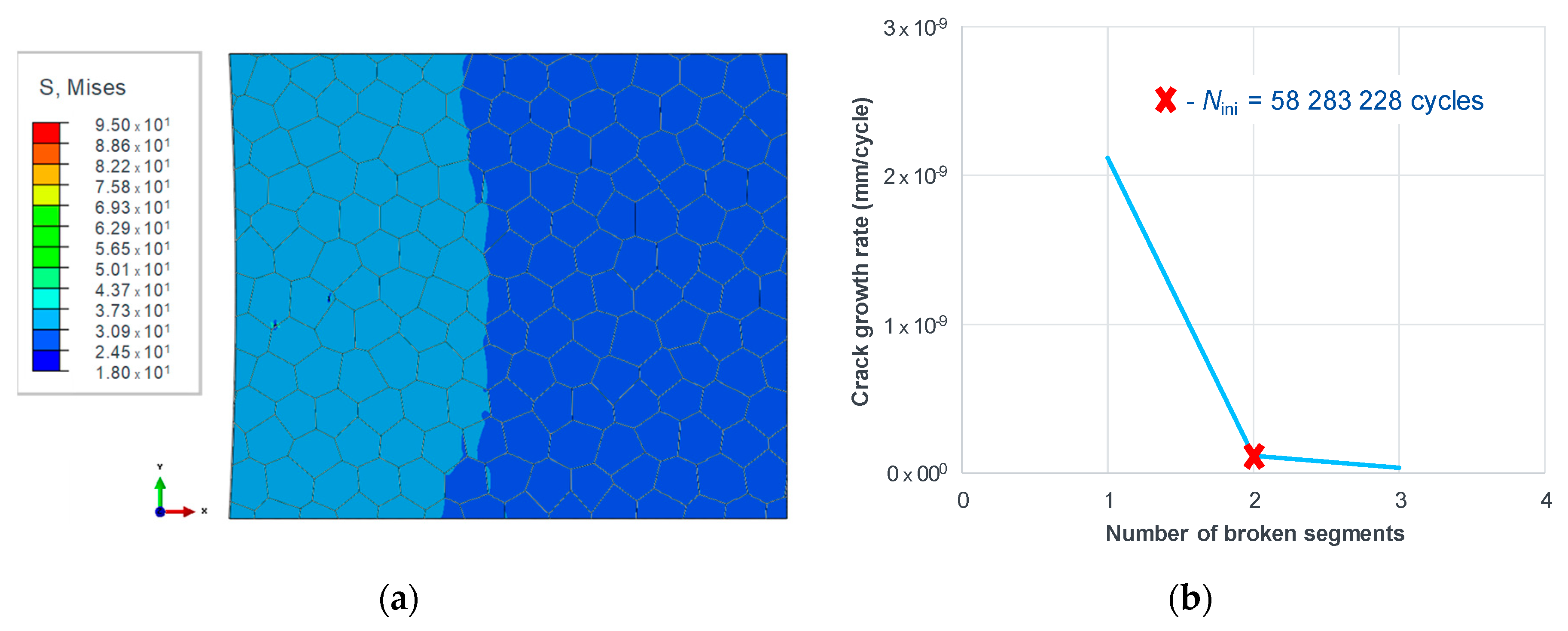
2.4. Numerical Estimation of Fatigue Behavior with the Help of CRSS
3. Results
4. Discussion and Conclusions
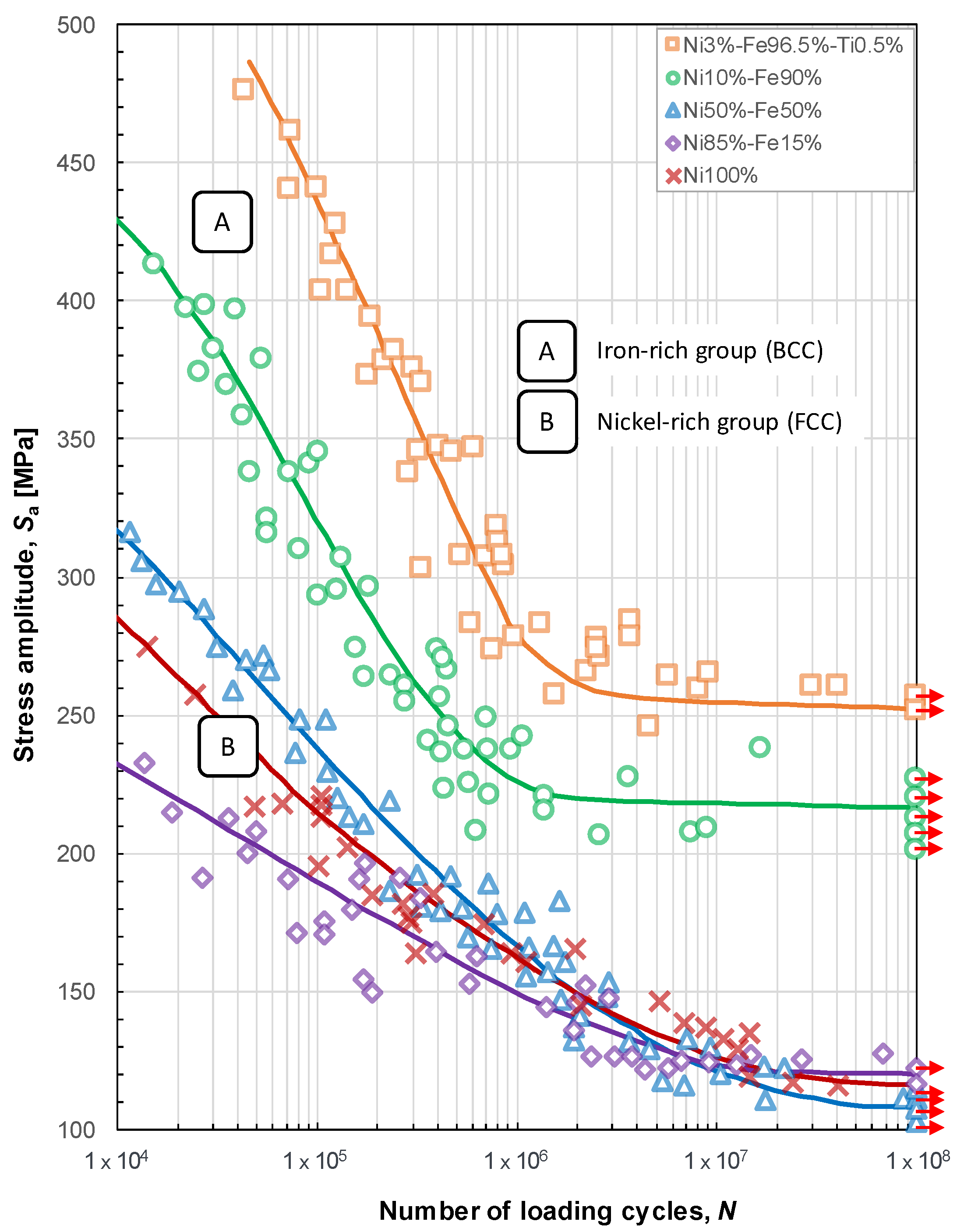
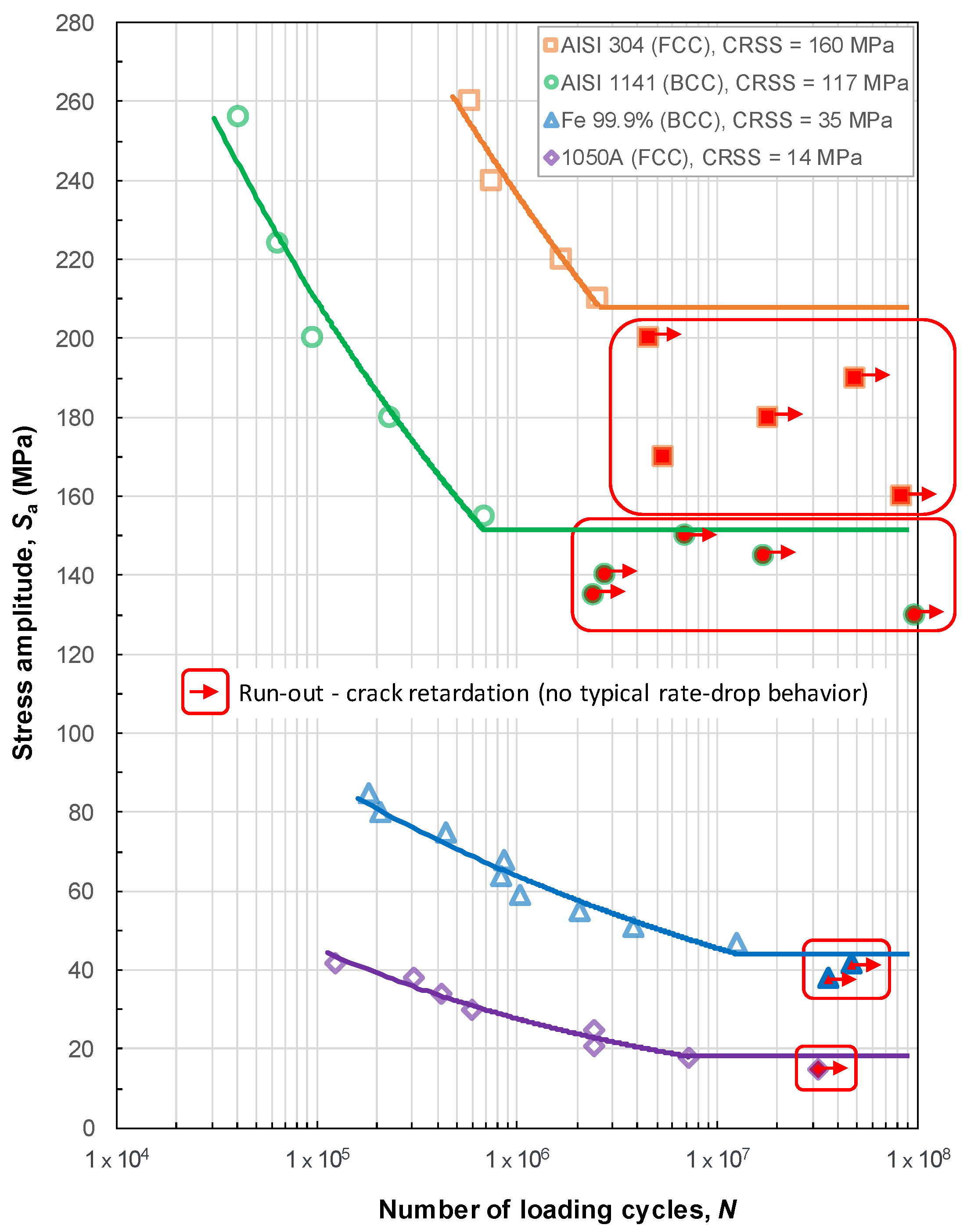
- The transition from infinite life (below the fatigue limit) to definite life (slope in the typical S-N curve) happens when a sufficient number of micro-cracks in the material microstructure (typically >10) have reached a condition for cracking. The cracking condition according to the TM equation says that the absolute magnitude of average shear stress on a grain slip band has to be higher than two times the CRSS.
- The higher the CRSS magnitude of the metal of interest, the higher the loading stress amplitude needed to accomplish the transition from the infinite to definite life, as shown in Figure 7. In other words, the higher the CRSS magnitude, the higher the accompanying fatigue endurance limit. Despite having different crystal structures, FCC austenitic stainless steel AISI 304 and BBC vanadium-based micro-alloyed forging steel AISI 1141 have relatively high CRSS values (160 MPa and 117 MPa, respectively) and as a result fatigue limits at considerably high positions in the S-N diagram, Figure 7.
- In the case of very high CRSS values, the stresses within the microstructural model are at a relatively high level at the moment of transition from infinite life to definite life, resulting in a high number of grains that are favorable for cracking. The higher the number of cracking favorable grains after the transition from infinite life to definite life, the steeper the slope of the finite life region in the S-N diagram.
- The study showed that the crystallographic structure is not the predominant factor that determines the shape and position of a fatigue life curve in the S-N diagram, but it is rather the CRSS magnitude. Namely, the higher the CRSS of a certain material, the higher the curve position is in the diagram, and the more pronounced the transition between the definite and the indefinite life region. Despite being an FCC material, the austenitic stainless steel AISI 304 showed an untypically high fatigue limit (208 MPa), which is higher than the fatigue limit of the BCC vanadium-based micro-alloyed forging steel AISI 1141 (152 MPa). The remaining two investigated FCC metals, the pure iron (Fe 99.9%) and the high purity aluminum (Al 99.5%) possess, according to this numerical study, relatively low fatigue limits, i.e., 44 and 19 MPa, respectively.
- The numerical study provided good agreement of the fatigue limits of the investigated materials with the experimentally determined fatigue limits. This observation refers firstly to AISI 1141 steel whose numerical fatigue limit of 152 MPa [52] is almost perfectly matching the experimental one, which is 155 MPa [60]. The value determined numerically for AISI 304 is fitting the span of experimental values that can be found in literature, too [63,64,65]. A relatively good agreement, however with a slight overestimation, has been achieved for aluminum 1050A (18 MPa vs. 10-14 MPa [66]). Reliable experimental data for Fe 99.9% could not be found. These results are summarized in Table 4 and depicted in Figure 7.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Budynas, R.G.; Nisbett, J.K. Fatigue failure resulting from variable loading. In Shigley’s Mechanical Engineering Design, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2015; pp. 273–349. ISBN 978-0-07-339820-4. [Google Scholar]
- Ferro, A.; Montalenti, G. On the effect of the crystalline structure on the form of fatigue curves. Philos. Mag. 1964, 10, 1043. [Google Scholar] [CrossRef]
- Ferro, A.; Mazzetti, P.; Montalenti, G. On the effect of the crystalline structure on fatigue: Comparison between body-centred metals (Ta, Nb, Mo and W) and face-centred and hexagonal metals. Philos. Mag. J. Theor. Exp. Appl. Phys. 1965, 12, 867–875. [Google Scholar] [CrossRef]
- Buck, A. Fatigue properties of pure metals. Int. J. Fract. Mech. 1967, 3, 145–152. [Google Scholar] [CrossRef]
- Grosskreutz, J.C. Fatigue mechanisms in the sub-creep range. ASTM 1971, 495, 5–60. [Google Scholar] [CrossRef]
- Rogne, B.; Thaulow, C. Strengthening mechanisms of iron micropillars. Philos. Mag. 2015, 95, 1814–1828. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Kunz, A.; Pathak, S.; Greer, J.R. Size effects in Al nanopillars: Single crystalline vs. bicrystalline. Acta Mater. 2011, 59, 4416–4424. [Google Scholar] [CrossRef]
- Greer, J.R.; Hosson, J.T.D. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Chen, Z.M.; Okamoto, N.L.; Demura, M.; Inui, H. Micropillar compression deformation of single crystals of Co3(Al,W) with the L12 structure. Scr. Mater. 2016, 121, 28–31. [Google Scholar] [CrossRef]
- Monnet, G.; Pouchon, M.A. Determination of the critical resolved shear stress and the friction stress in austenitic stainless steels by compression of pillars extracted from single grains. Mater. Lett. 2013, 98, 128–130. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Woodward, C.; LeSar, R.; Uchic, M.D. Scale-free intermittent flow in crystal plasticity. Science 2006, 312, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Csikor, F.F.; Motz, C.; Weygand, D.; Zaiser, M.; Zapperi, S. Dislocation Avalanches, Strain Bursts, and the Problem of Plastic Forming at the Micrometer Scale. Science 2007, 318, 251–254. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, N.L.; Kashioka, D.; Inomoto, M.; Inui, H.; Takebayashi, H.; Yamaguchi, S. Compression deformability of gamma- and zeta-Fe-Zn intermetallics to mitigate detachment of brittle intermetallic coating of galvannealed steels. Scr. Mater. 2013, 69, 307–310. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Fujimoto, S.; Kambara, Y.; Kawamura, M.; Chen, Z.M.T.; Matsunoshita, H.; Tanaka, K.; Inui, H.; George, E.P. Size effect, critical resolved shear stress, stacking fault energy, and solid solution strengthening in the CrMnFeCoNi high-entropy alloy. Sci. Rep. 2016, 6, 35863. [Google Scholar] [CrossRef] [PubMed]
- Kiener, D.; Motz, C.; Schöberl, T.; Jenko, M.; Dehm, G. Determination of mechanical properties of copper at the micron scale. Adv. Eng. Mater. 2006, 8, 1119–1125. [Google Scholar] [CrossRef]
- Jennings, A.T.; Burek, M.J.; Greer, J.R. Microstructure versus Size: Mechanical properties of electroplated single crystalline Cu nanopillars. Phys. Rev. Lett. 2010, 104, 135503. [Google Scholar] [CrossRef] [PubMed]
- Schneider, A.S.; Kaufmann, D.; Clark, B.G.; Frick, C.P.; Gruber, P.A.; Mönig, R.; Kraft, O.; Arzt, E. Correlation between critical temperature and strength of small-scale bcc pillars. Phys. Rev. Lett. 2009, 103, 105501. [Google Scholar] [CrossRef] [PubMed]
- Dimiduk, D.; Uchic, M.; Parthasarathy, T. Size-affected single-slip behavior of pure nickel microcrystals. Acta Mater. 2005, 53, 4065–4077. [Google Scholar] [CrossRef]
- Greer, J.R.; Oliver, W.C.; Nix, W.D. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Shade, P.; Uchic, M.; Dimiduk, D.; Viswanathan, G.; Wheeler, R.; Fraser, H. Size-affected single-slip behavior of Rene N5 microcrystals. Mater. Sci. Eng. A 2012, 535, 53–61. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Kashioka, D.; Hirato, T.; Inui, H. Specimen- and grain-size dependence of compression deformation behavior in nanocrystalline copper. Int. J. Plast. 2014, 56, 173–183. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Inomoto, M.; Adachi, H.; Takebayashi, H.; Inui, H. Micropillar compression deformation of single crystals of the intermetallic compound zeta-FeZn13. Acta Mater. 2014, 65, 229–239. [Google Scholar] [CrossRef]
- Zheng, H.; Cao, A.; Weinberger, C.R.; Huang, J.Y.; Du, K.; Wang, J.; Ma, Y.; Xia, Y.; Mao, S.X. Discrete plasticity in sub-10-nm-sized gold crystals. Nat. Commun. 2010, 1, 144. [Google Scholar] [CrossRef] [PubMed]
- Greer, J.R.; Weinberger, C.R.; Cai, W. Comparing the strength of f.c.c. and b.c.c. sub-micrometer pillars: Compression experiments and dislocation dynamics simulations. Mater. Sci. Eng. A 2008, 493, 21–25. [Google Scholar] [CrossRef]
- Schneider, A.; Clark, B.; Frick, C.; Gruber, P.; Arzt, E. Effect of orientation and loading rate on compression behavior of small-scale Mo pillars. Mater. Sci. Eng. A 2009, 508, 241–246. [Google Scholar] [CrossRef]
- Hagen, A.; Thaulow, C. Low temperature in-situ micro-compression testing of iron pillars. Mater. Sci. Eng. A 2016, 678, 355–364. [Google Scholar] [CrossRef]
- Bruesewitz, C.; Knorr, I.; Hofsaess, H.; Barsoum, M.W.; Volkert, C.A. Single crystal pillar microcompression tests of the MAX phases Ti2InC and Ti4AlN3. Scr. Mater. 2013, 69, 303–306. [Google Scholar] [CrossRef]
- Feller-Kniepmeier, M.; Hundt, M. Deformation properties of high purity alpha-Fe single crystals. Scr. Metall. 1983, 17, 905–908. [Google Scholar] [CrossRef]
- Stein, D.; Low, J.; Seybolt, A. The mechanical properties of iron single crystals containing less than 5 × 10−3 ppm carbon. Acta Metall. 1963, 11, 1253–1262. [Google Scholar] [CrossRef]
- Stein, D.F.; Low, J.R. Effects of orientation and carbon on the mechanical properties of iron single crystals. Acta Metall. 1966, 14, 1183–1194. [Google Scholar] [CrossRef]
- Guo, E.-Y.; Xie, H.-X.; Singh, S.S.; Kirubanandham, A.; Jing, T.; Chawla, N. Mechanical characterization of microconstituents in a cast duplex stainless steel by micropillar compression. Mater. Sci. Eng. A 2014, 598, 98–105. [Google Scholar] [CrossRef]
- Cruzado, A.; Gan, B.; Jimenez, M.; Barba, D.; Ostolaza, K.; Linaza, A.; Molina-Aldareguia, J.; Llorca, J.; Segurado, J. Multiscale modeling of the mechanical behavior of IN718 superalloy based on micropillar compression and computational homogenization. Acta Mater. 2015, 98, 242–253. [Google Scholar] [CrossRef]
- Jin, H.-H.; Ko, E.; Kwon, J.; Hwang, S.S.; Shin, C. Evaluation of critical resolved shear strength and deformation mode in proton-irradiated austenitic stainless steel using micro-compression tests. J. Nucl. Mater. 2016, 470, 155–163. [Google Scholar] [CrossRef]
- Wu, J.; Tsai, W.; Huang, J.; Hsieh, C.; Huang, G.-R. Sample size and orientation effects of single crystal aluminum. Mater. Sci. Eng. A 2016, 662, 296–302. [Google Scholar] [CrossRef]
- Palomares-Garcia, A.J.; Perez-Prado, M.T.; Molina-Aldareguia, J.M. Effect of lamellar orientation on the strength and operating deformation mechanisms of fully lamellar TiAl alloys determined by micropillar compression. Acta Mater. 2017, 123, 102–114. [Google Scholar] [CrossRef]
- Campos, M.; Bautista, A.; Caceres, D.; Abenojar, J.; Torralba, J. Study of the interfaces between austenite and ferrite grains in P/M duplex stainless steels. J. Eur. Ceram. Soc. 2003, 23, 2813–2819. [Google Scholar] [CrossRef]
- Ramazani, A.; Mukherjee, K.; Prahl, U.; Bleck, W. Modelling the effect of microstructural banding on the flow curve behaviour of dual-phase (DP) steels. Comput. Mater. Sci. 2012, 52, 46–54. [Google Scholar] [CrossRef]
- Hocker, S.; Schmauder, S.; Bakulin, A.V.; Kulkova, S.E. Ab initio investigation of tensile strengths of metal(1 1 1)/alpha-Al2O3(0 0 0 1) interfaces. Philos. Mag. 2014, 94, 265–284. [Google Scholar] [CrossRef]
- Kulkova, S.E.; Bakulin, A.V.; Kulkov, S.S.; Hocker, S.; Schmauder, S. Influence of interstitial impurities on the Griffith work in Ti-based alloys. Phys. Scr. 2015, 90, 094010. [Google Scholar] [CrossRef]
- Bakulin, A.V.; Spiridonova, T.; Kulkova, S.E.; Hocker, S.; Schmauder, S. Hydrogen diffusion in doped and undoped alpha-Ti: An ab-initio investigation. Int. J. Hydrogen Energy 2016, 41, 9108–9116. [Google Scholar] [CrossRef]
- Kohler, C.; Kizler, P.; Schmauder, S. Atomistic simulation of precipitation hardening in alpha-iron: Influence of precipitate shape and chemical composition. Modell. Simul. Mater. Sci. Eng. 2005, 13, 35–45. [Google Scholar] [CrossRef]
- Prskalo, A.-P.; Schmauder, S.; Ziebert, C.; Ye, J.; Ulrich, S. Molecular dynamics simulations of the sputtering of SiC and Si3N4. Surf. Coat. Technol. 2010, 204, 2081–2084. [Google Scholar] [CrossRef]
- Prskalo, A.-P.; Schmauder, S.; Ziebert, C.; Ye, J.; Ulrich, S. Molecular dynamics simulations of the sputtering process of silicon and the homoepitaxial growth of a Si coating on silicon. Comput. Mater. Sci. 2011, 50, 1320–1325. [Google Scholar] [CrossRef]
- Bozic, Z.; Schmauder, S.; Mlikota, M.; Hummel, M. Multiscale fatigue crack growth modelling for welded stiffened panels. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 1043–1054. [Google Scholar] [CrossRef]
- Bozic, Z.; Schmauder, S.; Mlikota, M.; Hummel, M. Multiscale fatigue crack growth modeling for welded stiffened panels. In Handbook of Mechanics of Materials; Schmauder, S., Chen, C.-S., Chawla, K.K., Chawla, N., Chen, W., Kagawa, Y., Eds.; Springer: Singapore, 2018; pp. 1–21. ISBN 978-981-10-6855-3. [Google Scholar]
- Tanaka, K.; Mura, T. A dislocation model for fatigue crack initiation. J. Appl. Mech. 1981, 48, 97–103. [Google Scholar] [CrossRef]
- Tanaka, K.; Mura, T. A theory of fatigue crack initiation at inclusions. Metall. Trans. A 1982, 13, 117–123. [Google Scholar] [CrossRef]
- Mlikota, M.; Staib, S.; Schmauder, S.; Bozic, Z. Numerical determination of Paris law constants for carbon steel using a two-scale model. J. Phys. Conf. Ser. 2017, 843, 012042. [Google Scholar] [CrossRef]
- Mlikota, M.; Schmauder, S.; Bozic, Z.; Hummel, M. Modelling of overload effects on fatigue crack initiation in case of carbon steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1182–1190. [Google Scholar] [CrossRef]
- Mlikota, M.; Schmauder, S. Numerical determination of component Woehler curve. DVM Bericht 2017, 1684, 111–124. [Google Scholar]
- Mlikota, M.; Schmauder, S.; Bozic, Z. Calculation of the Woehler (S-N) curve using a two-scale model. Int. J. Fatigue 2018, 114, 289–297. [Google Scholar] [CrossRef]
- ABAQUS, version 2018 ed; Abaqus Documentation; Simulia: Providence, RI, USA, 2018.
- Socie, D.F. Fatigue damage simulation models for multiaxial loading. In Proceedings of the Sixth International Fatigue Congress (Fatigue ’96), Berlin, Germany, 6–10 May 1996; pp. 967–976. [Google Scholar]
- Glodez, S.; Jezernik, N.; Kramberger, J.; Lassen, T. Numerical modelling of fatigue crack initiation of martensitic steel. Adv. Eng. Softw. 2010, 41, 823–829. [Google Scholar] [CrossRef]
- Jezernik, N.; Kramberger, J.; Lassen, T.; Glodez, S. Numerical modelling of fatigue crack initiation and growth of martensitic steels. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 714–723. [Google Scholar] [CrossRef]
- Huang, X.; Brueckner-Foit, A.; Besel, M.; Motoyashiki, Y. Simplified three-dimensional model for fatigue crack initiation. Eng. Fract. Mech. 2007, 74, 2981–2991. [Google Scholar] [CrossRef]
- Briffod, F.; Shiraiwa, T.; Enoki, M. Fatigue crack initiation simulation in pure iron polycrystalline aggregate. Mater. Trans. 2016, 57, 1741–1746. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Fatemi, A.; Zeng, Z.; Plaseied, A. Fatigue behavior and life predictions of notched specimens made of QT and forged microalloyed steels. Int. J. Fatigue 2004, 26, 663–672. [Google Scholar] [CrossRef]
- Newman, J.; Phillips, E.; Swain, M. Fatigue-life prediction methodology using small-crack theory. Int. J. Fatigue 1999, 21, 109–119. [Google Scholar] [CrossRef]
- Mughrabi, H. Microstructural mechanisms of Cyclic deformation, fatigue crack initiation and early crack growth. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373. [Google Scholar] [CrossRef] [PubMed]
- Boyer, H. Atlas of Fatigue Curves, 1st ed.; American Society for Metals: Materials Park, OH, USA, 1985; ISBN 0871702142. [Google Scholar]
- Atzori, B.; Meneghetti, G.; Ricotta, M. Analysis of the fatigue strength under two load levels of a stainless steel based on energy dissipation. Fract. Struct. Integrity 2011, 17, 15–22. [Google Scholar] [CrossRef]
- Ben Fredj, N.; Ben Nasr, M.; Ben Rhouma, A.; Sidhom, H.; Braham, C. Fatigue life improvements of the AISI 304 stainless steel ground surfaces by wire brushing. J. Mater. Eng. Perform. 2004, 13, 564–574. [Google Scholar] [CrossRef]
- Sakin, R. Investigation of bending fatigue-life of aluminum sheets based on rolling direction. Alex. Eng. J. 2018, 57, 35–47. [Google Scholar] [CrossRef]

| Lattice | Material | σu (MPa) | σe (MPa) | σe/σu |
|---|---|---|---|---|
| BCC | W | 1372 | 834 | 0.61 |
| Mo | 696 | 500 | 0.72 | |
| Ta | 308 | 265 | 0.86 | |
| Nb | 294 | 225 | 0.77 | |
| Fe (+0.2% Ti) | 265 | 182 | 0.69 | |
| Mild steel (0.13% C) | 421 | 224 | 0.53 | |
| 4340 steel | 1103 | 482 | 0.44 | |
| FCC | Ni | 303 | 108 | 0.36 |
| Cu | 301 | 110 | 0.37 | |
| Al | 90 | 34 | 0.38 | |
| 2024-T3 Al | 483 | 138 | 0.29 | |
| 7075-T6 Al | 572 | 159 | 0.28 | |
| HCP | Ti | 703 | 414 | 0.59 |
| Co (+0.5% Ti) | 521 | 165 | 0.32 | |
| Zn | 145 | 26 | 0.18 | |
| Mg | 182 | 30 | 0.16 |
| Material | CRSS (MPa) | Method | Source |
|---|---|---|---|
| AISI 304 (X5CrNi18-10) | 160 | MPT | Monnet and Pouchon [11] |
| AISI 1141 (40Mn2S12) | 117 | MD | Hummel et al. [45,46] |
| Fe 99.9% | 35 | MPT | Rogne and Thaulow [6] |
| 1050A (Al 99.5%) | 14 | MPT | Jennings et al. [17] |
| Material | E (GPa) | G1 (MPa) | υ1 - | C11 (MPa) | C12 (MPa) | C44 (MPa) | Wc1 (N/mm) | d1 (µm) |
|---|---|---|---|---|---|---|---|---|
| AISI 304 | 188 | 79,000 | 0.26 | 233,026 | 80,820 | 79,000 | 69 | ~30 |
| AISI 1141 | 200 | 78,125 | 0.28 | 255,682 | 99,432 | 78,125 | 19 | ~60 |
| Fe 99.9% | 205 | 81,000 | 0.28 | 262,073 | 101,918 | 81,000 | 19 | ~65 |
| 1050A | 72 | 26,000 | 0.33 | 106,678 | 52,543 | 26,000 | 11 | ~65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlikota, M.; Schmauder, S. On the Critical Resolved Shear Stress and Its Importance in the Fatigue Performance of Steels and Other Metals with Different Crystallographic Structures. Metals 2018, 8, 883. https://doi.org/10.3390/met8110883
Mlikota M, Schmauder S. On the Critical Resolved Shear Stress and Its Importance in the Fatigue Performance of Steels and Other Metals with Different Crystallographic Structures. Metals. 2018; 8(11):883. https://doi.org/10.3390/met8110883
Chicago/Turabian StyleMlikota, Marijo, and Siegfried Schmauder. 2018. "On the Critical Resolved Shear Stress and Its Importance in the Fatigue Performance of Steels and Other Metals with Different Crystallographic Structures" Metals 8, no. 11: 883. https://doi.org/10.3390/met8110883
APA StyleMlikota, M., & Schmauder, S. (2018). On the Critical Resolved Shear Stress and Its Importance in the Fatigue Performance of Steels and Other Metals with Different Crystallographic Structures. Metals, 8(11), 883. https://doi.org/10.3390/met8110883






