Fatigue Strength Analysis and Fatigue Damage Evaluation of Roller Chain
Abstract
1. Introduction
2. Materials and Methods
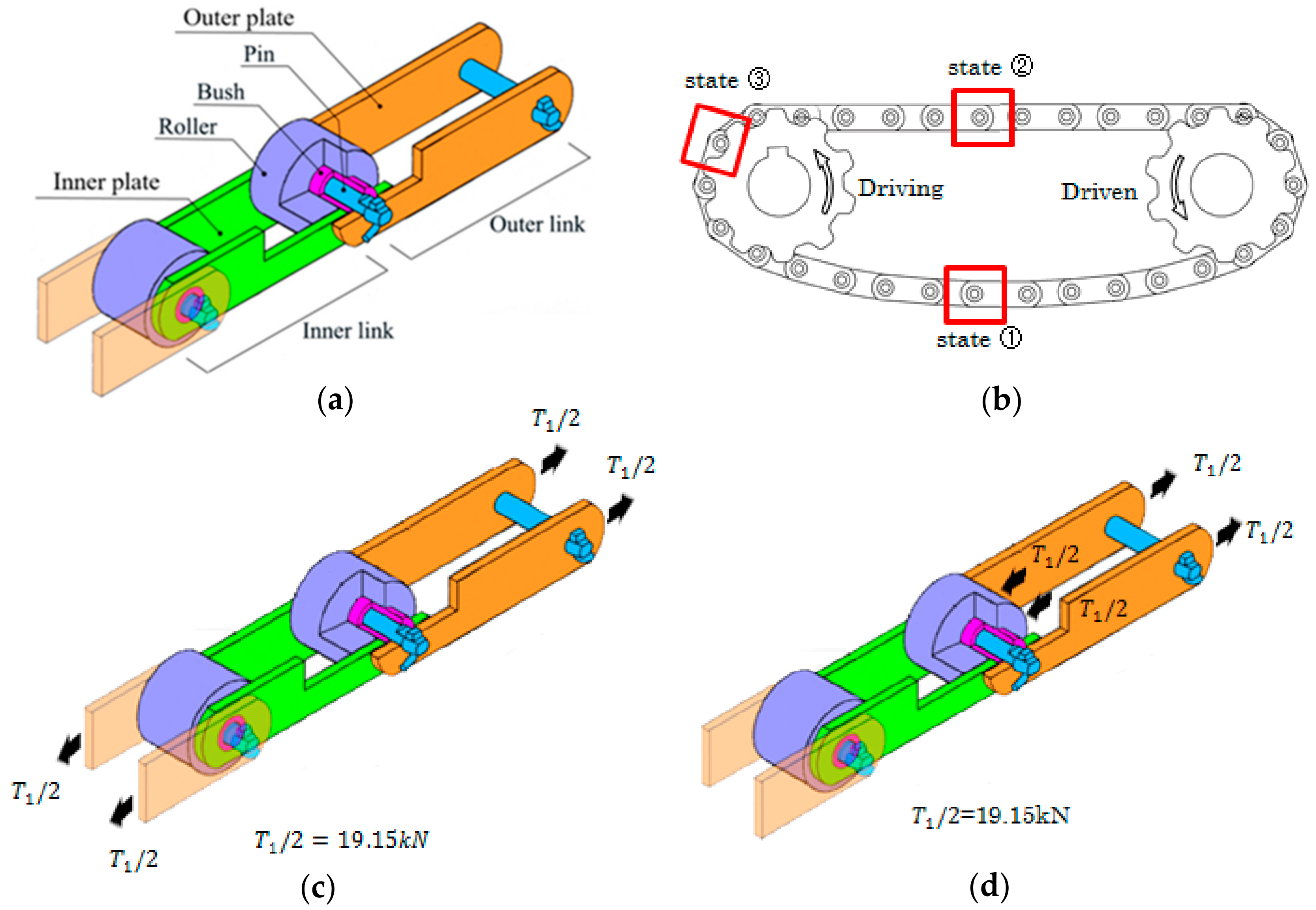
2.1. Structure of Roller Chain
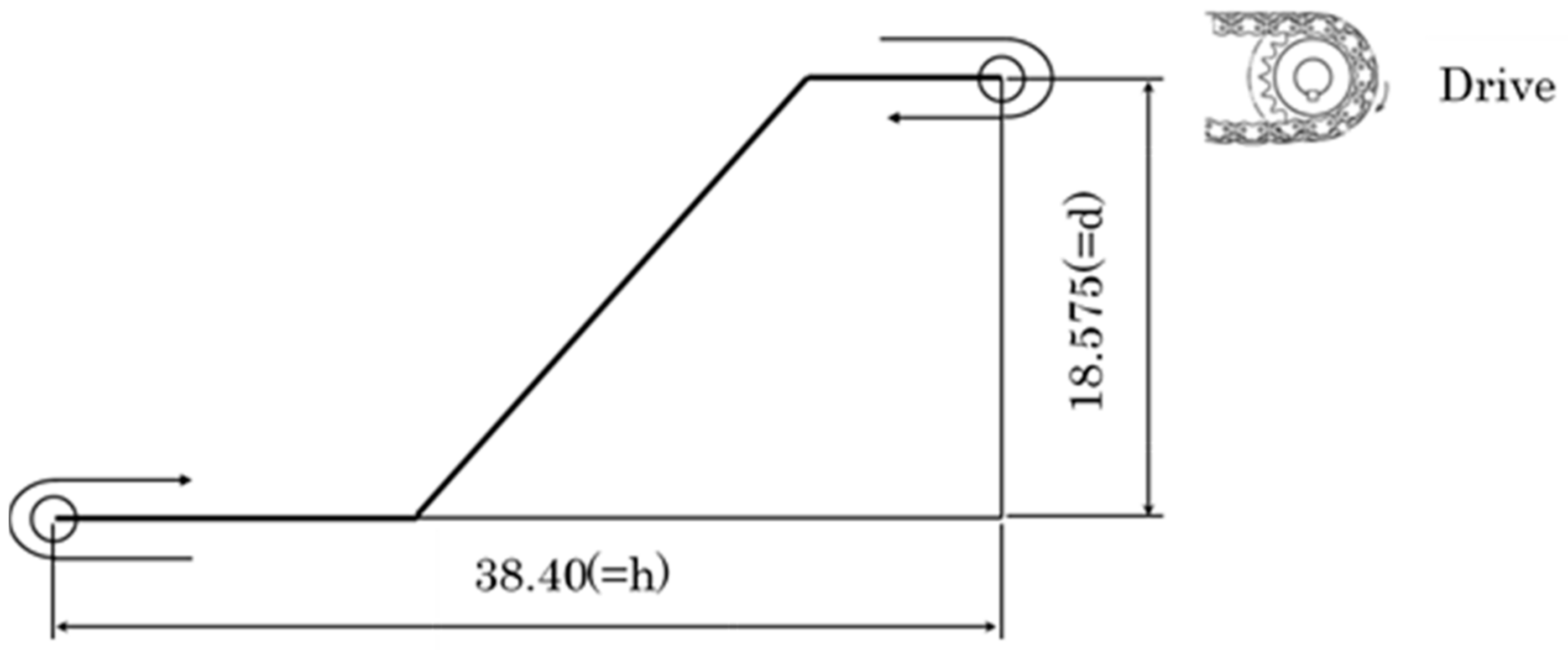
2.2. Calculation of Chain Tension
2.3. Dimensions and Mechanical Properties of Each Component
2.4. Analysis Model
3. Several Examples of Real Failure of Roller Chain
4. Results and Discussion
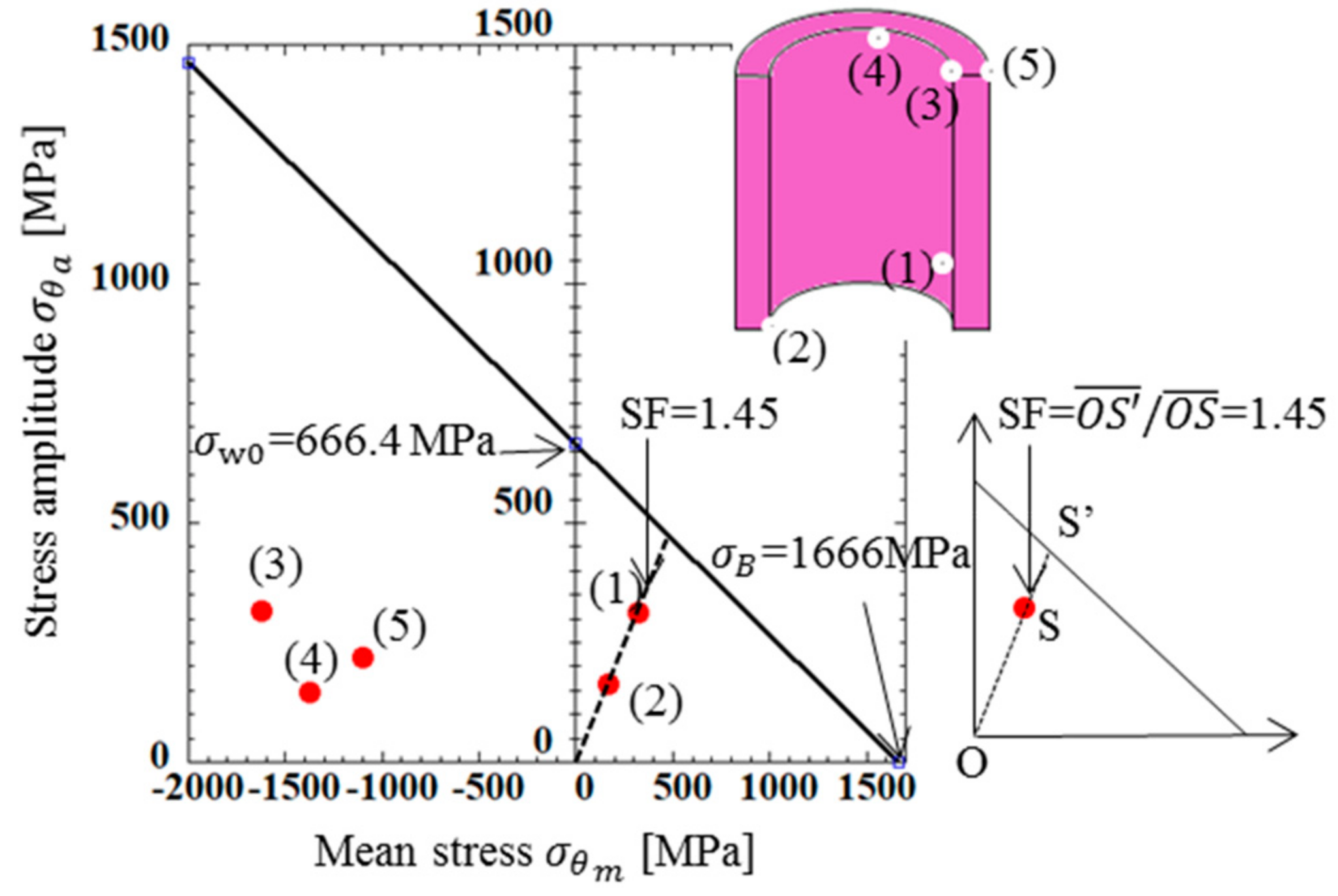
4.1. Stress Analysis Results for Bush
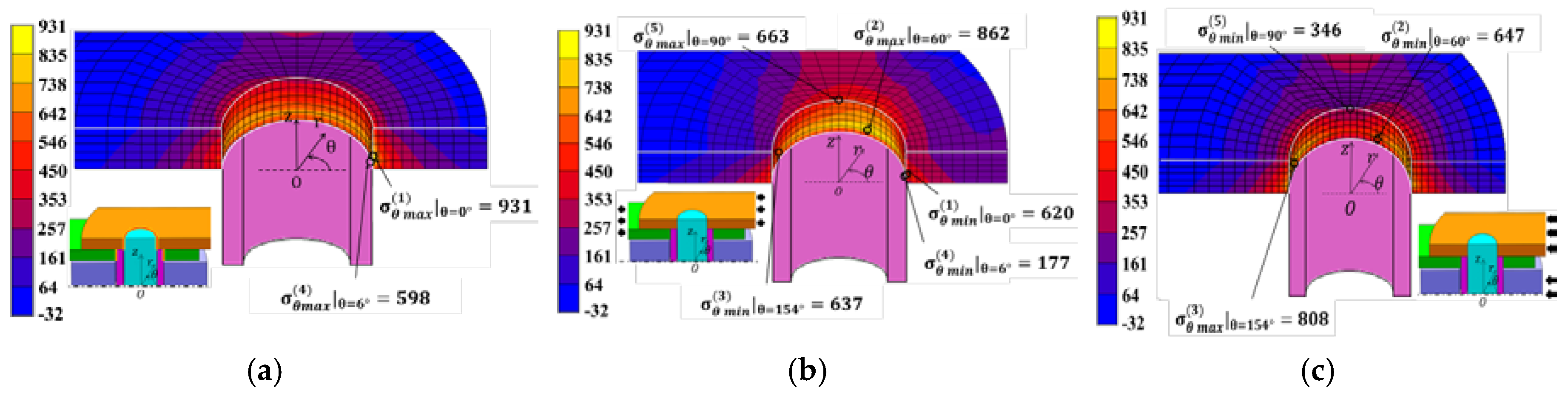
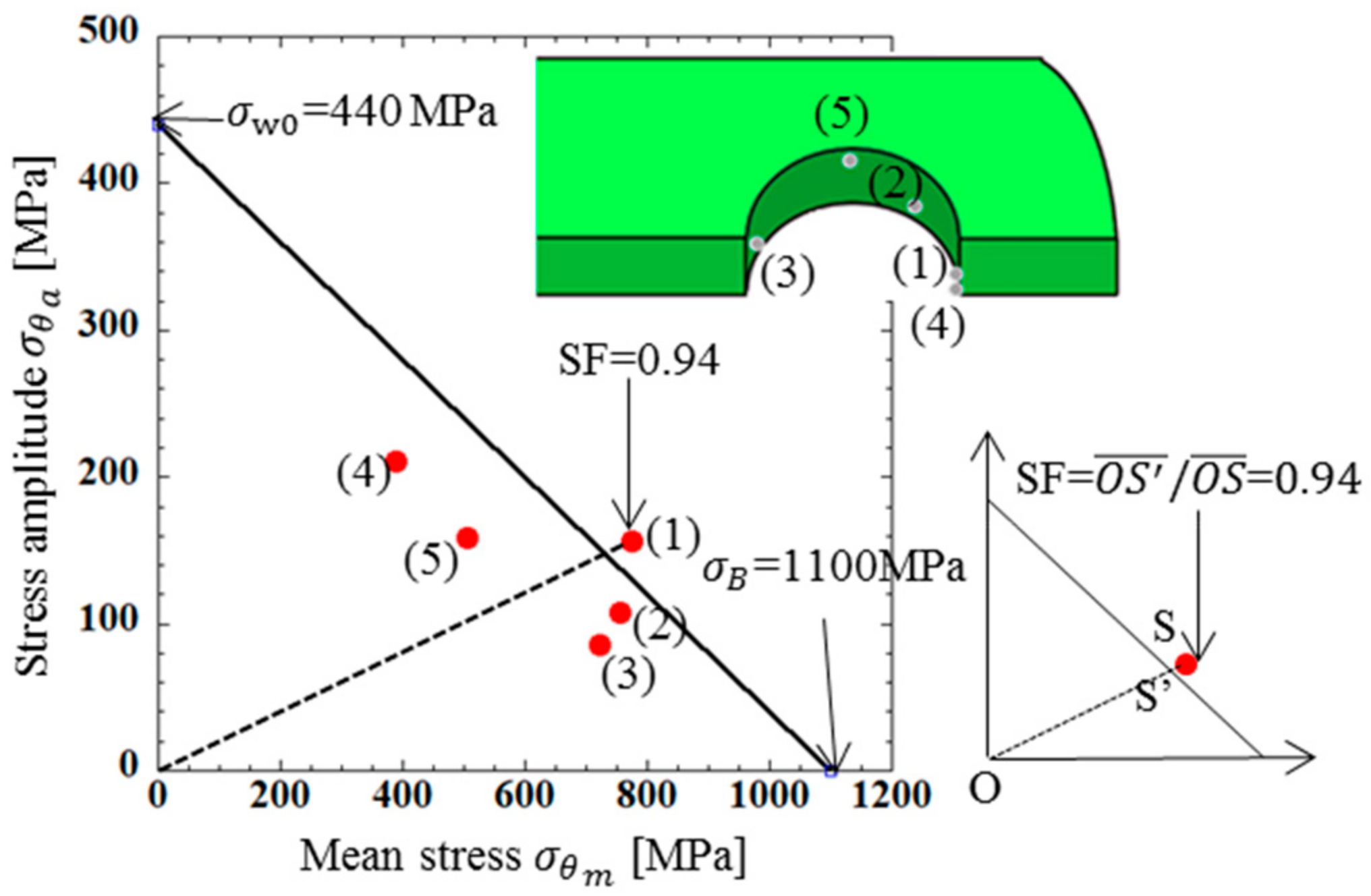
4.2. Stress Analysis Result for Inner Plate
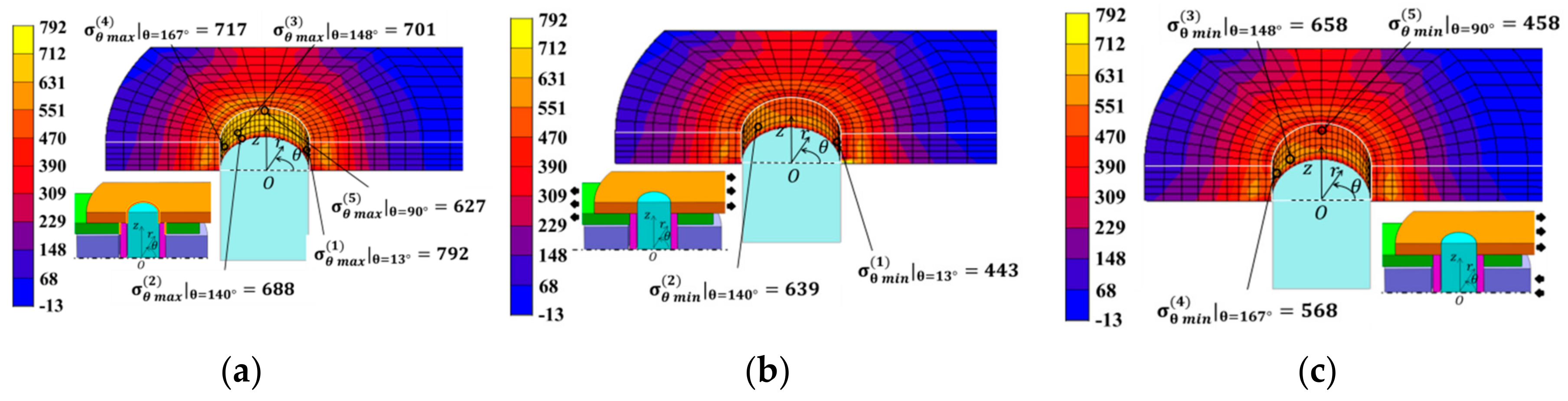
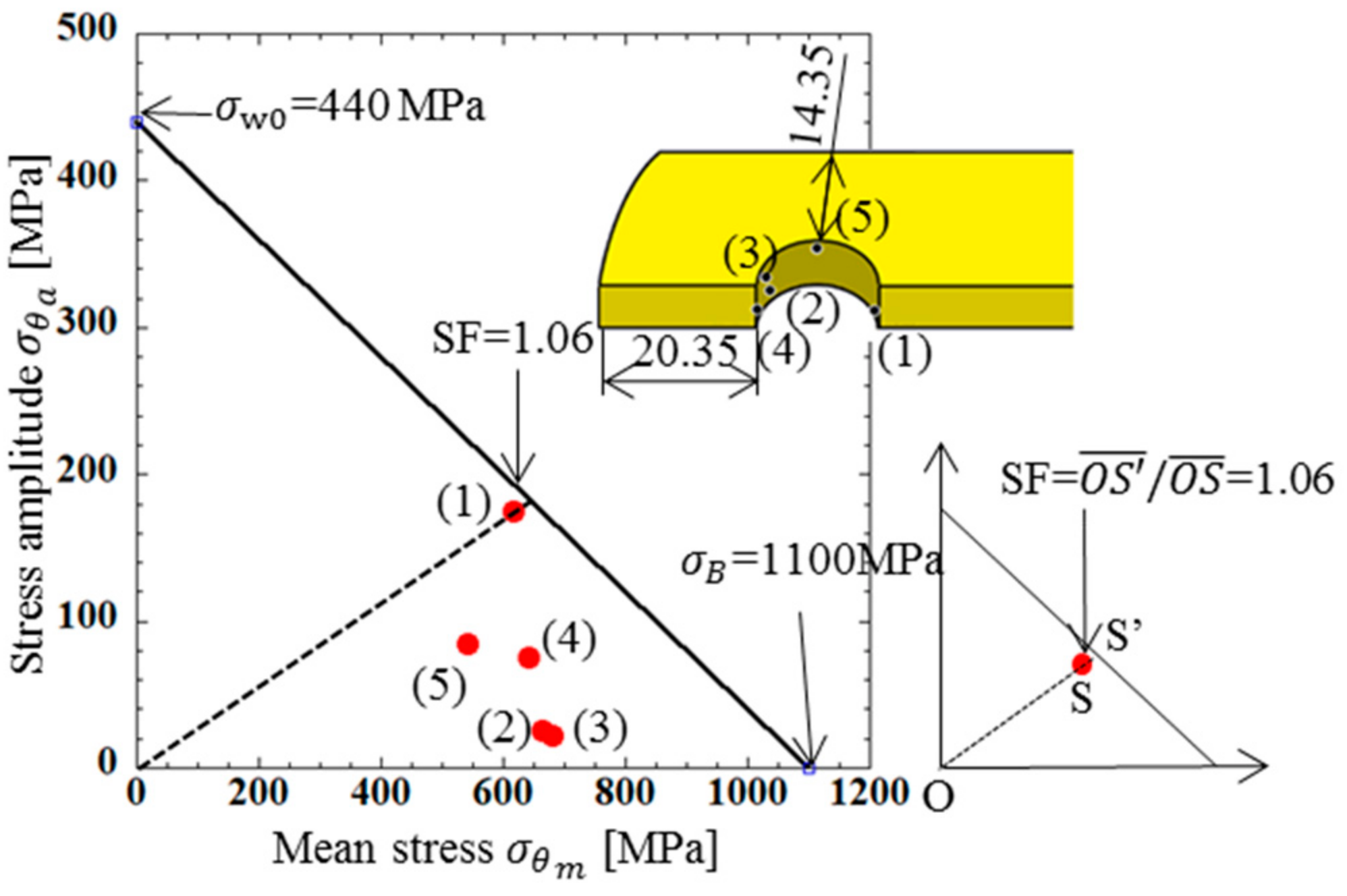
4.3. Stress Analysis Result for Outer Plate
5. Necessity of Three-Dimensional Modeling
- (1)
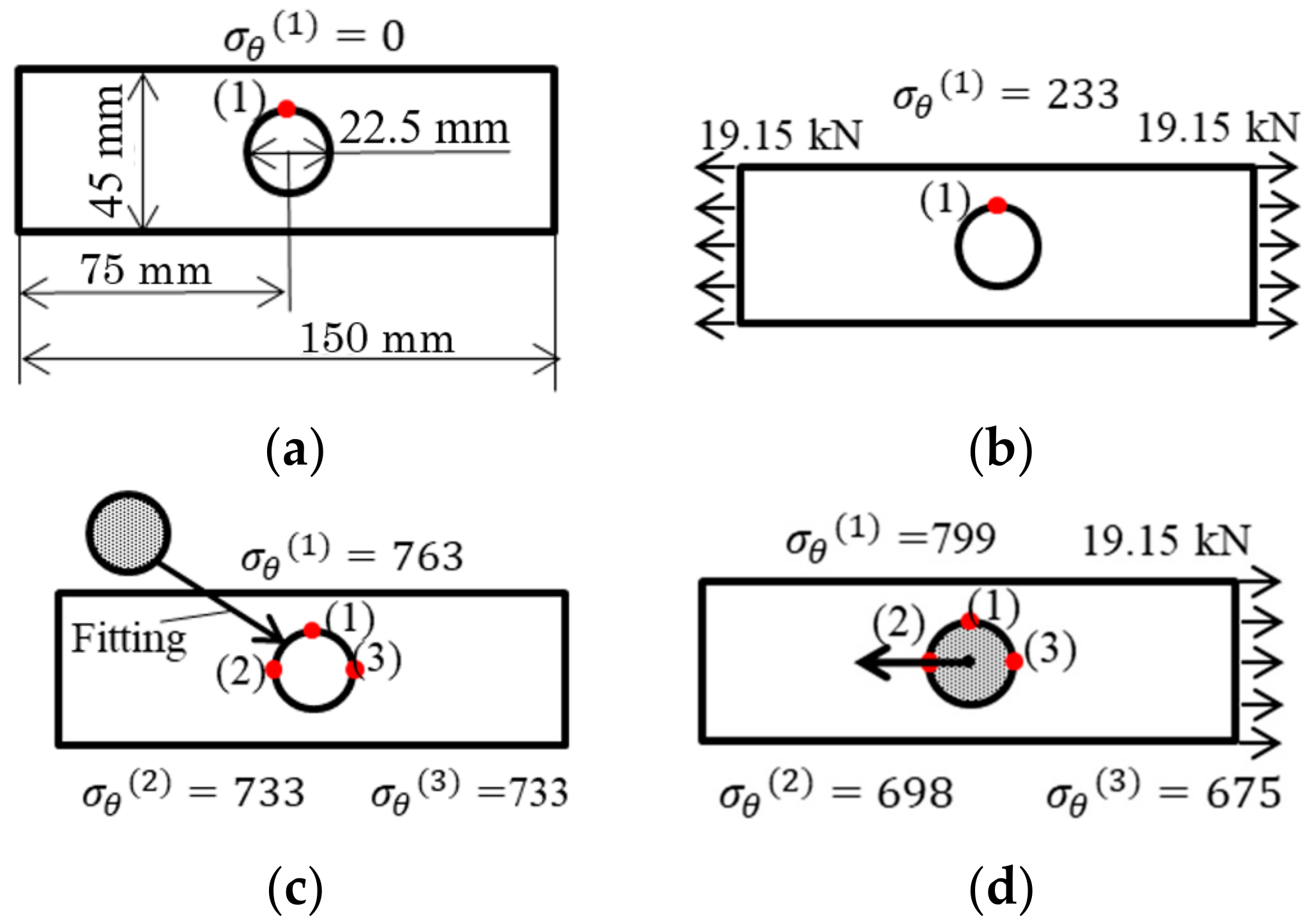
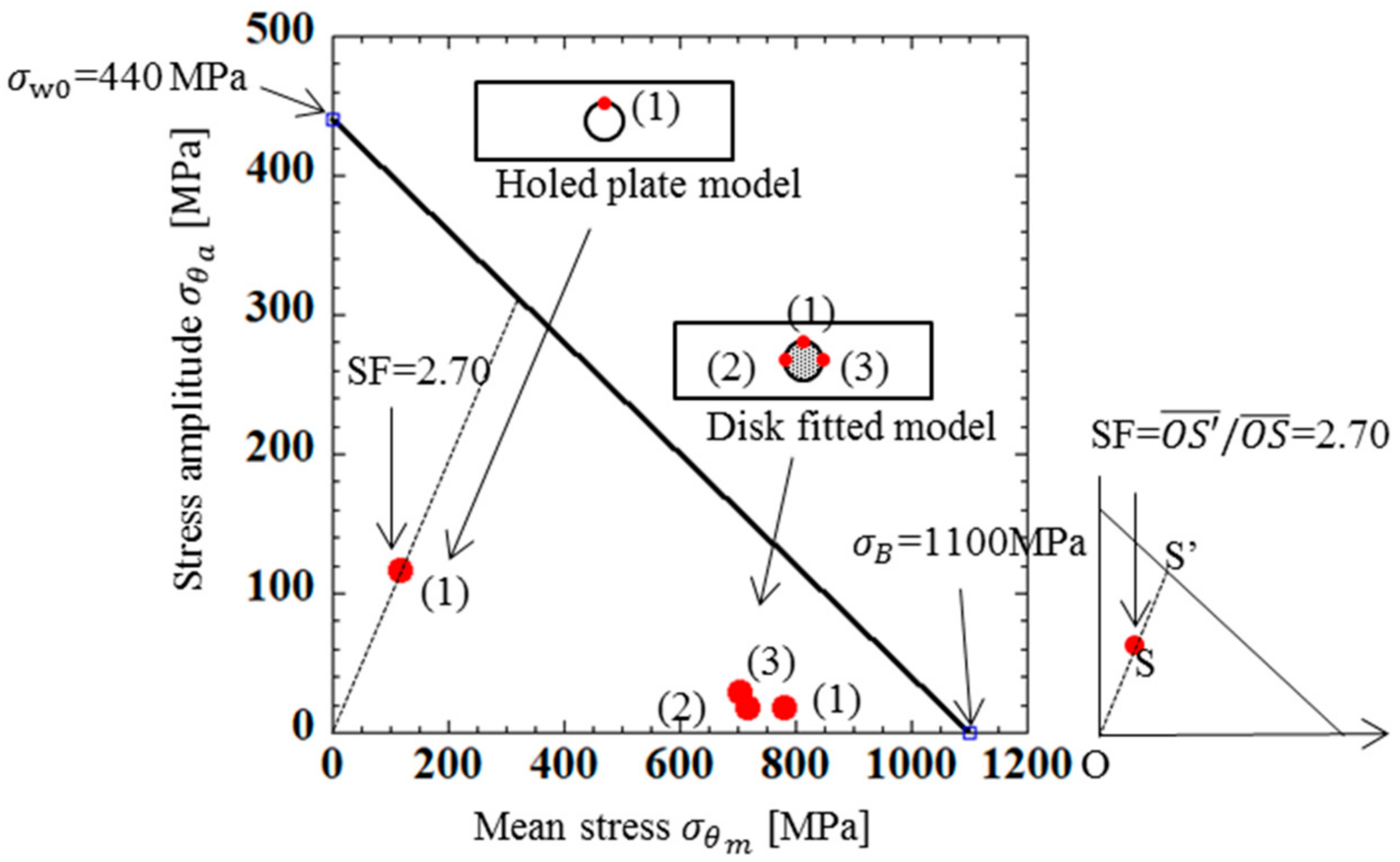
- From the comparison between the results of the holed plate model in Figure 12a,b, and the results of the disk-fitted model in Figure 12c,d, it can be found that the maximum stress, minimum stress, and average stress of the disk-fitted model in Figure 12c,d are 3 times larger than those of the holed plate model in Figure 12a,b.
- (2)
- (3)
- (4)
6. Effect of Plastic Region in Roller Chain on the Fatigue Strength
7. Conclusions
- (1)
- (2)
- (3)
- (4)
- The 2D hole model in Figure 12a,b is not suitable for the stress estimation since the pin is inserted in the hole. The results of the 2D pin-inserted model in Figure 12c,d are different from the 3D model. Therefore, 3D modeling is necessary. Since the discussion and approach in this paper are quite general, they can be applied to developing different and new types of roller chains.
- (5)
- The effect of the plastic region in roller chains on the fatigue strength was considered. It was found that present elastic analysis is sufficient because the plastic strain amplitude is not very large.
Author Contributions
Funding
Conflicts of Interest
References
- Shoji, N.; Hideaki, Y.; Satoshi, N.; Tohru, K. Evaluation of Wear between Pin and Bush in Roller Chain. J. Adv. Mech. Des. Syst. Manuf. 2009, 3, 355–365. [Google Scholar] [CrossRef]
- Jun, T.Z.; Shun, Z.W.; Zhen, X.W. The effects of the wear elongation on the load of a Long-distance transmission chain. Appl. Mech. Mater. Trans. Tech. Publ. 2014, 456, 60–64. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Meng, F. Study on the reliability evaluation method of the wear life of roller chains. J. Mech. Eng. Sci. 2006, 220, 1569–1574. [Google Scholar] [CrossRef]
- Perawat, T.; Patiparn, N.; Pruet, K. Wear resistance improvement of the roller chain parts at Thai Metro Industry (1973) Co., Ltd. Mater. Today 2018, 5, 9431–9439. [Google Scholar] [CrossRef]
- Metil’kov, S.A.; Berezhnoi, S.B.; Yunin, V.V. Wear of hinges in roller drive chain. Russ. Eng. Res. 2008, 28, 839–844. [Google Scholar] [CrossRef]
- Shoji, N.; Kohta, N.; Satoshi, N.; Tohru, K.; Toshiaki, N.; Takashi, O. Static Stress Analysis of Link Plate of Roller Chain using Finite Element Method and Some Design Proposals for Weight Saving. J. Adv. Mech. Des. Syst. Manuf. 2009, 3, 159–170. [Google Scholar] [CrossRef]
- Tushar, D.B.; Prashant, M.P.; Bhaskar, D.G. Fea Based Study of Effect of Radial Variation of Outer Link in A Typical Roller Chain Link Assembly. Int. J. Mech. Ind. Eng. 2012, 1, 65–70. [Google Scholar]
- Jagtap, M.D.; Gaikwad, B.D.; Pawar, P.M. Study of roller conveyor chain strip under tensile loading. IJMER 2014, 4, 2249–6645. [Google Scholar]
- Krishnakumar, K.; Arockia, S.A. A Review of failure analysis found in industrial roller chains. Int. J. Chem. Tech. Res. 2015, 8, 598–603. [Google Scholar]
- Masao, M. The effect of number of pitches of test pieces on the fatigue life of roller-chains. In Proceedings of the Fujihara Memorial Faculty of Engineering, Keio University; Keio University: Tokyo, Japan, 1961; pp. 146–153. [Google Scholar]
- Hiroshi, S.; Atuo, S. Nonlinear forced vibration of roller chain. Bull. JSME 1975, 18, 1090–1100. [Google Scholar] [CrossRef]
- Binder, R.C.; Cover, W.V. Impact between chain roller chain derives. Adv. Mater. Res. 2011, 291, 1551–1554. [Google Scholar]
- Liu, S.P.; Wang, K.W.; Hayek, S.I.; Trethewey, M.W.; Chen, F.H.K. A global–local integrated study of roller chain meshing dynamics. J. Sound Vib. 1997, 203, 41–62. [Google Scholar] [CrossRef]
- James, C.C.; Glen, E.J. Experimental investigation of link tension and roller-sprocket impact in roller chain drives. Mech. Mach. Theory 1996, 31, 533–544. [Google Scholar] [CrossRef]
- Wasan, S.; Chakrit, S. An Integrating Finite Element Method and Multi-body Simulation for Drive Systems Analysis. Eng. J. 2017, 21, 221–234. [Google Scholar] [CrossRef]
- Baolin, L.; Shuai, F.; Yan, Z. The modal analysis of roller chain drives. Adv. Mater. Res. 2011, 291, 1551–1554. [Google Scholar] [CrossRef]
- Jorge, A.; Candida, M.; Amilcar, R. Planar roller chain drive dynamics using a cylindrical contact force model. Mech. Based Des. Struct. Mach. 2016, 44, 109–122. [Google Scholar] [CrossRef]
- Xu, L.; Yang, Y.; Chang, Z.; Liu, J. Dynamic modeling of a roller chain drive system considering the flexibility of input shaft. Chin. J. Mech. Eng. 2010, 23, 367–374. [Google Scholar] [CrossRef]
- Sine, L.P.; Jone, M.H.; Jorge, A.C.A. A roller chain drive model including contact with guide-bars. Multibody Sys. Dyn. 2004, 12, 285–301. [Google Scholar]
- Chen, C.K.; Freudenstein, F. Toward a more exact kinematics of roller chain drives. J. Mech. Trans. Autom. Des. 1988, 110, 269–275. [Google Scholar] [CrossRef]
- Candida, M.P.; Jorge, A.A.; Amilcar, L.R. A methodology for the generation of planar models for multibody chain drives. Multibody Syst. Dyn. 2010, 24, 303–324. [Google Scholar] [CrossRef]
- Naji, M.R.; Marshek, K.M. The effects of the pitch difference on the load distribution of a roller chain drive. Mech. Mach. Theory 1989, 24, 351–362. [Google Scholar] [CrossRef]
- Suwannahong, W.; Suvanjumrat, C. Analysis of Roller Chain Drive System with Multi-Flexi Body Dynamics Methodology. EDP Sci. 2017, 95. [Google Scholar] [CrossRef]
- Fuglede, N.; Thomsem, J.J. Kinematic and dynamic modeling and approximate analysis of a roller chain drive. J. Sound Vib. 2016, 366, 447–470. [Google Scholar] [CrossRef]
- Wragge-Morley, R.; Yon, J.; Lock, R.; Alexander, B.; Burgess, S. A novel pendulum test for measuring roller chain efficiency. Meas. Sci. Technol. 2018, 29. [Google Scholar] [CrossRef]
- Ambrosio, J.; Malça, C.; Ramalho, A. Cylindrical Contact Force Models for the Dynamics of Roller Chain Drives. Multibody Mech. Syst. 2015, 25, 121–131. [Google Scholar] [CrossRef]
- Lu, P. Supplement of Several Problems in Roller Chain Drive Design. Adv. Mater. Res. 2013, 774, 176–179. [Google Scholar] [CrossRef]
- Xu, L.X.; Li, Y.G. Numerical Simulation on Dynamic Behavior of Intermittent Roller Chain Drives. Appl. Mech. Mater. 2012, 155, 535–539. [Google Scholar] [CrossRef]
- Pedesen, S.L. Model of contact between rollers and sprockets in chain-drive systems. Arch. Appl. Mech. 2005, 74, 489–508. [Google Scholar] [CrossRef]
- Oscar, D.C.; Arthur, A.S. Chain Feed Mechanism for an Induction Heating Furnace. United States Patent US4582972A, 15 April 1986. [Google Scholar]
- Shizuo, A. Chain Conveyor [Conveyor Series 2]; Yakumoshoten Co., Ltd.: Tokyo, Japan, 1961; p. 58. [Google Scholar]
- Senqcia Corporation. Selection of Roller Chain for Transmission; Senqcia Co.: Tokyo, Japan, 2016; p. 74. [Google Scholar]
- Msasakata, N.; Masao, M. Effects of Press-fit of Bushings and Number of Links on Fatigue Strength of Roller Chains. J. Jpn. Soc. Precis. Eng. 1984, 50, 665–671. [Google Scholar] [CrossRef]
- Tadashi, I. Strength of Metal; Yokendo Co., Ltd.: Tokyo, Japan, 1970; p. 127. [Google Scholar]
- Shigeru, H.; Yuu, S. Evaluation of fatigue limit characteristics of lamellar pearlitics steel in consideration of microstructure. Soc. Mater. Sci. 2011, 9, 790–795. [Google Scholar] [CrossRef]
- Teruyoshi, U.; Shigeru, N.; Iwao, K. Stress and Deformation of Thin Curved Tube. J. Jpn. High Press. Inst. 1968, 6, 1328–1336. [Google Scholar]
- Utaro, M. Chain Conveyor; Kogakutosho Co., Ltd.: Tokyo, Japan, 1982; p. 56. [Google Scholar]
- The Japan Society of Mechanical Engineers. JSME Data Book: Fatigue of Metals, IV Low Cycle Fatigue Strength; Japan Society of Mechanical Engineers: Tokyo, Japan, 1983; p. 12. [Google Scholar]
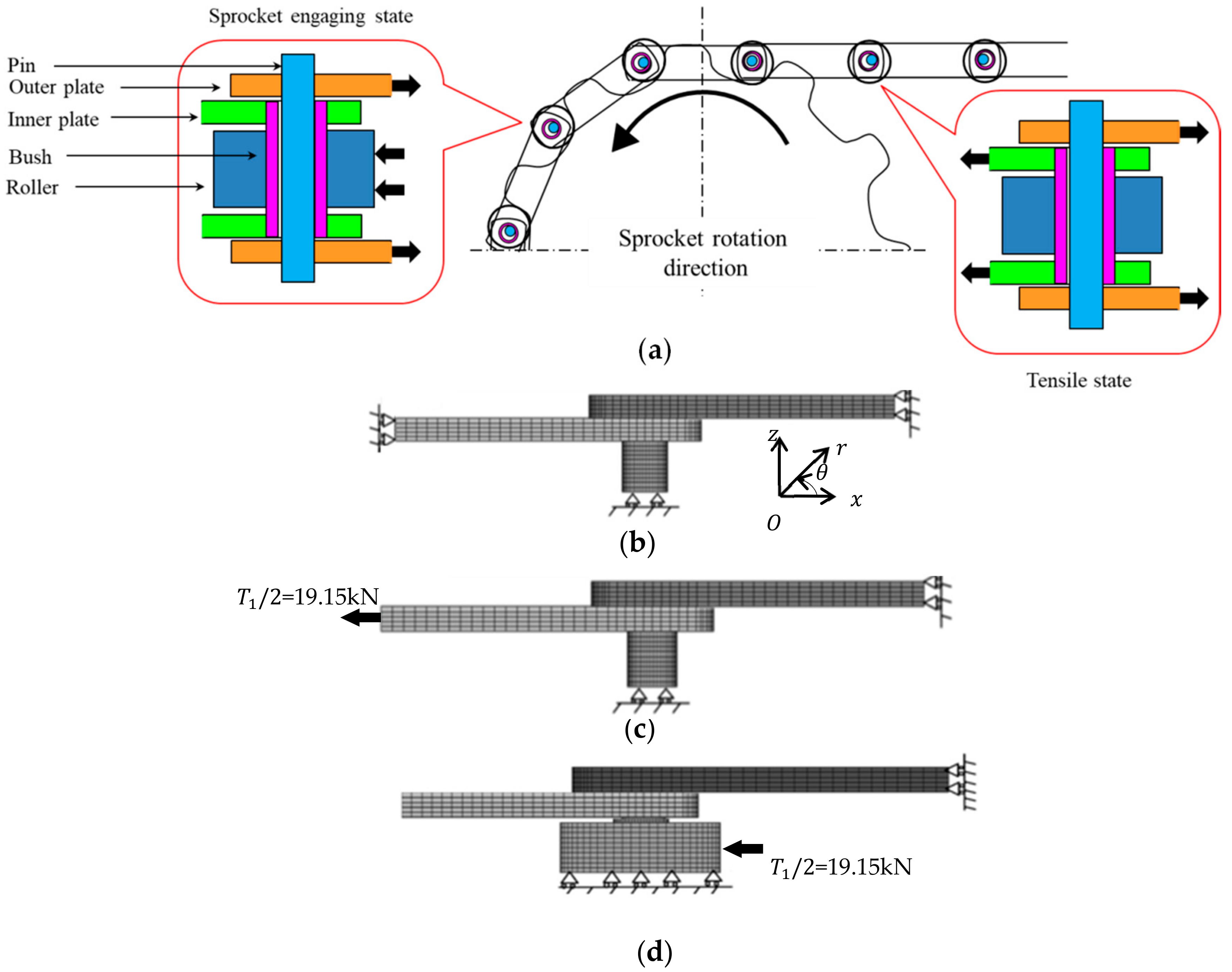


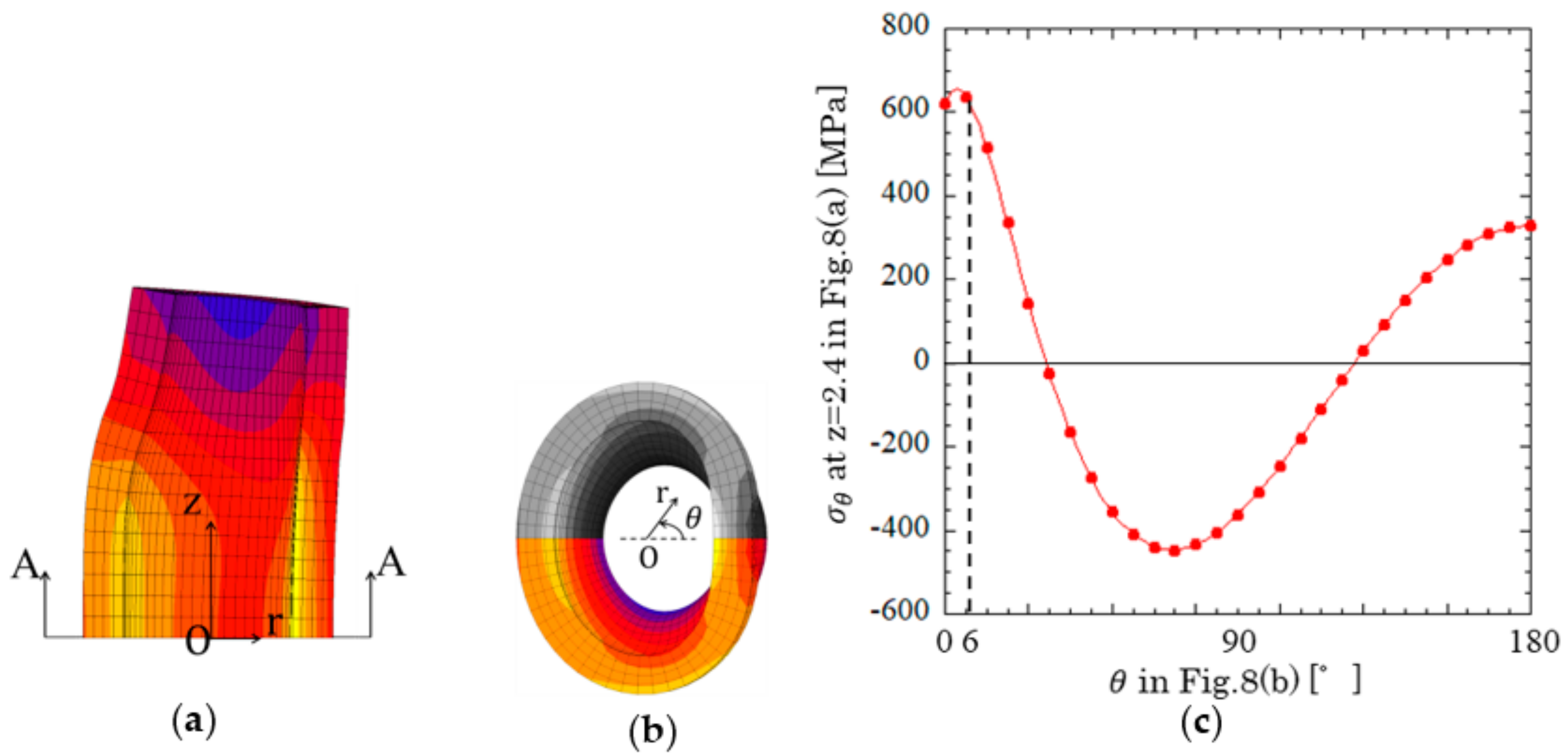
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.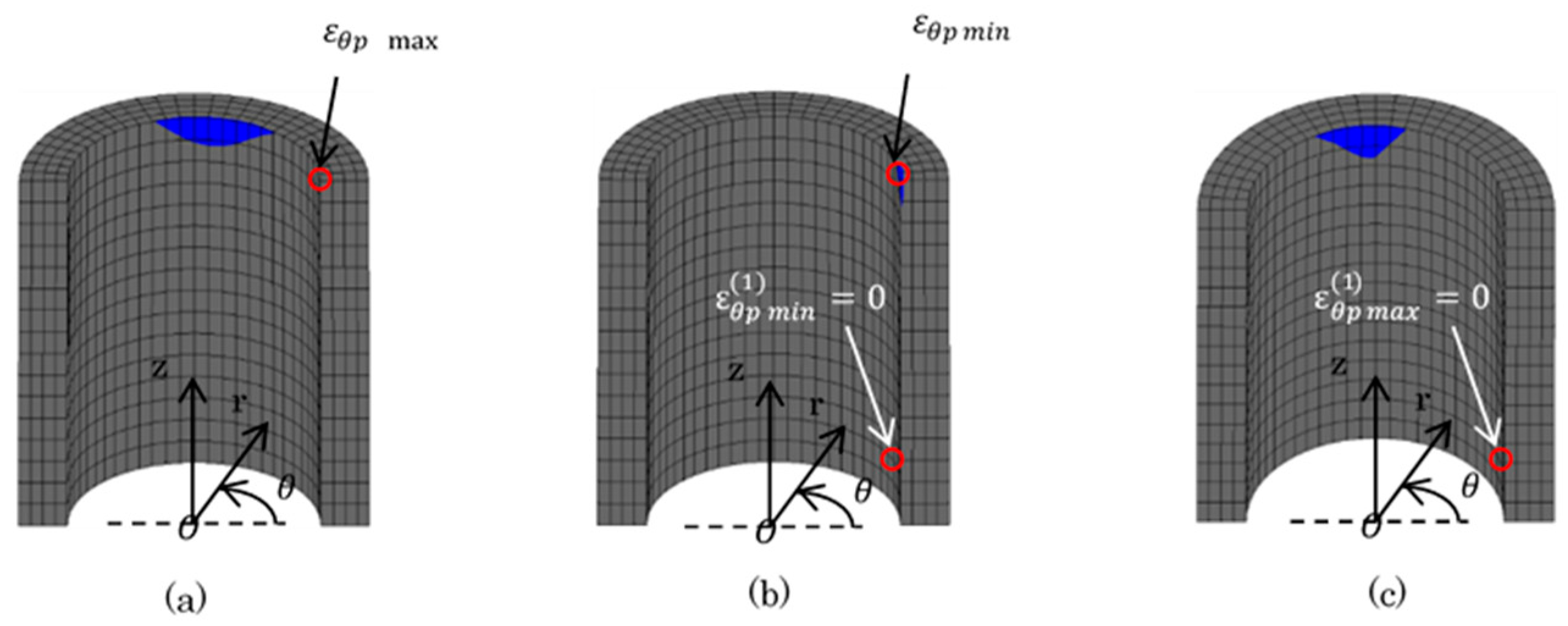
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
 : plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.
: plastic region): (a) press-fitting state; (b) tensile state; (c) sprocket-engaging state.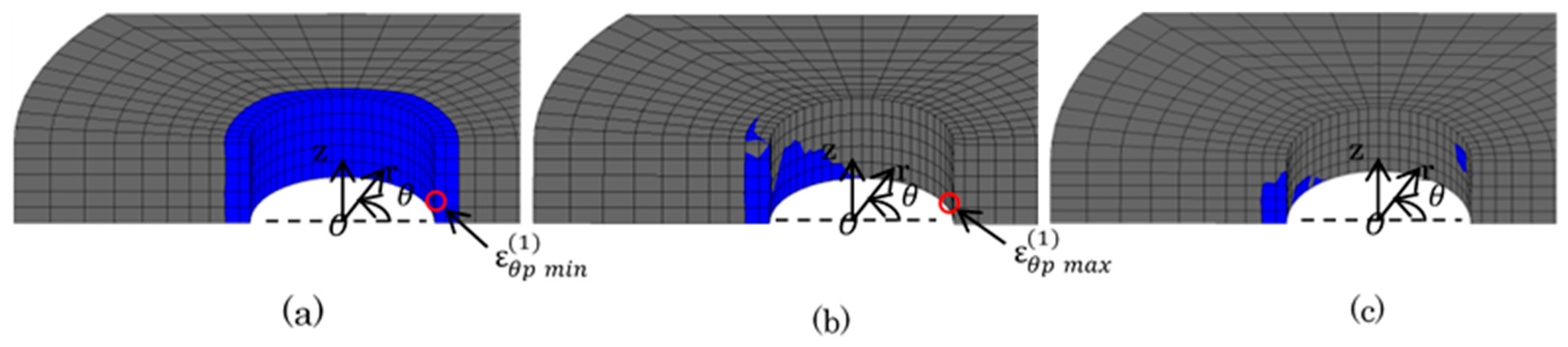
| Note | Definition | Value and Unit |
|---|---|---|
| P | Motor power (Base) */(Maximum) | 11 kW/18 kW |
| T | Chain tension (2 strands) | 63.8 kN |
| h | Horizontal distance of conveyor | 38.40 m |
| d | Vertical distance of conveyor | 18.58 m |
| V | Transfer speed | 10 m/min |
| η | Mechanical transmission efficiency | 0.8 |
| ― | Number of chain line | 2 |
| W1 | Per chain mass | 14 kg/m |
| W2 | Apron mass | 68 kg/m |
| W = 2W1 + W2 | Total mass | 0.94 kN/m |
| μ1 | Friction coefficient between the chain and the guide rail | 0.18 |
| Items | Outer plate | Inner plate | Pin | Bush | Roller |
|---|---|---|---|---|---|
| Diameter Inner | 15.8 | 22.55 | 15.8 | 16.30 | 23.35 |
| Diameter Outer | 15.8 | 22.55 | 15.8 | 22.55 | 65 |
| Length | 153 | 153 | 33.6 | 25.6 | 16 |
| Width | 44.5 | 44.5 | ― | ― | ― |
| Thickness | 8.0 | 8.0 | ― | ― | ― |
| Mesh size | 0.9~5.2 | 1.3~5.3 | 0.3~0.9 | 0.9~1.3 | 1.3~3.7 |
| Items | Plate | Pin | Bush | Roller |
|---|---|---|---|---|
| Material (JIS) | SS640 | SCM435 | SCM435 | S45C |
| Young’s modulus [GPa] E | 206 | 206 | 206 | 206 |
| Poisson’s ratio ν | 0.3 | 0.3 | 0.3 | 0.3 |
| Yield stress [MPa] | 970 | 1080 | 1390 | 780 |
| Tensile strength [MPa] | 1100 | 1180 | 1666 | 1012 |
| Friction coefficient μ | 0.3 | 0.3 | 0.3 | 0.3 |
| Position | σθ max | σθ min | σθ m | σθ a | SF |
|---|---|---|---|---|---|
| (1) | 638 | 15 | 327 | 312 | 1.45 |
| (2) | 343 | 14 | 179 | 165 | 2.73 |
| (3) | −1293 | −1923 | −1608 | 315 | - |
| (4) | −1207 | −1499 | −1353 | 146 | - |
| (5) | −830 | −1267 | −1049 | 219 | - |
| Position | σθ max | σθ min | σθ m | σθ a | SF |
|---|---|---|---|---|---|
| (1) | 931 | 620 | 776 | 156 | 0.94 |
| (2) | 862 | 647 | 755 | 108 | 1.10 |
| (3) | 808 | 637 | 723 | 86 | 1.16 |
| (4) | 598 | 177 | 388 | 211 | 1.23 |
| (5) | 663 | 346 | 505 | 159 | 1.19 |
| Position | σθ max | σθ min | σθ m | σθ a | SF |
|---|---|---|---|---|---|
| (1) | 792 | 443 | 617 | 175 | 1.06 |
| (2) | 688 | 639 | 664 | 25 | 1.52 |
| (3) | 701 | 658 | 680 | 22 | 1.50 |
| (4) | 717 | 568 | 643 | 75 | 1.28 |
| (5) | 627 | 458 | 543 | 85 | 1.44 |
| Model | Position | σθ max | σθ min | σθ m | σθ a | SF |
|---|---|---|---|---|---|---|
| 2D holed plate model | (1) | 233 | 0 | 117 | 117 | 2.70 |
| 2D disk fitting plate model | (1) | 799 | 763 | 781 | 18 | 1.31 |
| (2) | 733 | 698 | 716 | 18 | 1.44 | |
| (3) | 733 | 675 | 704 | 29 | 1.43 |
| Component | Plastic Strain [%] | Stress [MPa] | |||||
|---|---|---|---|---|---|---|---|
| /0.5 | σθ m | σθ a | SF | ||||
| Bush | 0 | −0.0313 | 0.031 | 0.062 | 327 | 312 | 1.45 |
| Inner plate | 0.0146 | 0.0002 | 0.014 | 0.028 | 776 | 156 | 0.94 |
| Outer plate | 0.567 | 0.559 | 0.008 | 0.016 | 617 | 175 | 1.06 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saito, R.; Noda, N.-A.; Sano, Y.; Song, J.; Minami, T.; Birou, Y.; Miyagi, A.; Huang, Y. Fatigue Strength Analysis and Fatigue Damage Evaluation of Roller Chain. Metals 2018, 8, 847. https://doi.org/10.3390/met8100847
Saito R, Noda N-A, Sano Y, Song J, Minami T, Birou Y, Miyagi A, Huang Y. Fatigue Strength Analysis and Fatigue Damage Evaluation of Roller Chain. Metals. 2018; 8(10):847. https://doi.org/10.3390/met8100847
Chicago/Turabian StyleSaito, Ryoichi, Nao-Aki Noda, Yoshikazu Sano, Jian Song, Takeru Minami, Yuuka Birou, Arata Miyagi, and Yinsa Huang. 2018. "Fatigue Strength Analysis and Fatigue Damage Evaluation of Roller Chain" Metals 8, no. 10: 847. https://doi.org/10.3390/met8100847
APA StyleSaito, R., Noda, N.-A., Sano, Y., Song, J., Minami, T., Birou, Y., Miyagi, A., & Huang, Y. (2018). Fatigue Strength Analysis and Fatigue Damage Evaluation of Roller Chain. Metals, 8(10), 847. https://doi.org/10.3390/met8100847




