Mathematical Model for Prediction and Optimization of Weld Bead Geometry in All-Position Automatic Welding of Pipes
Abstract
:1. Introduction
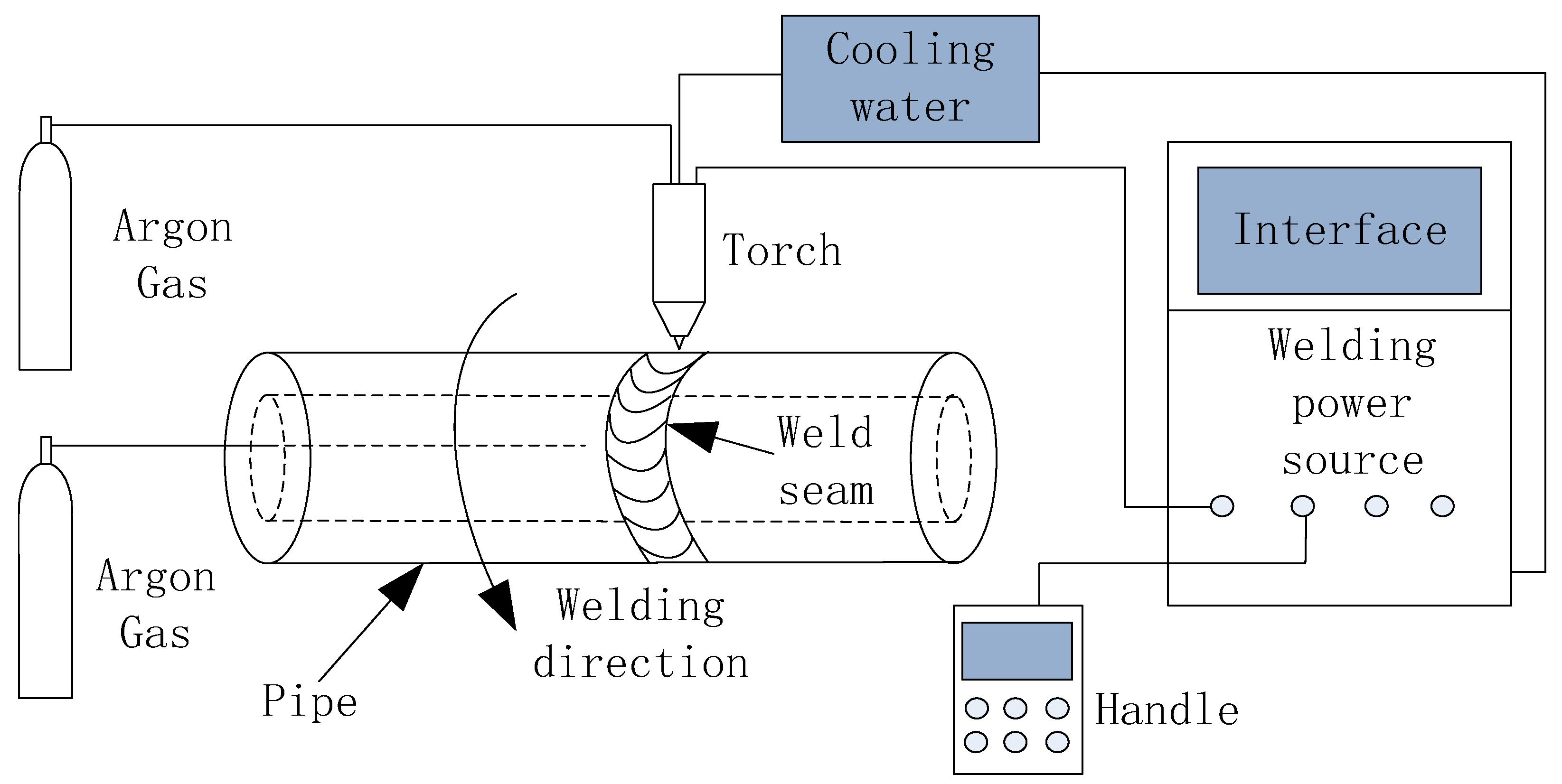
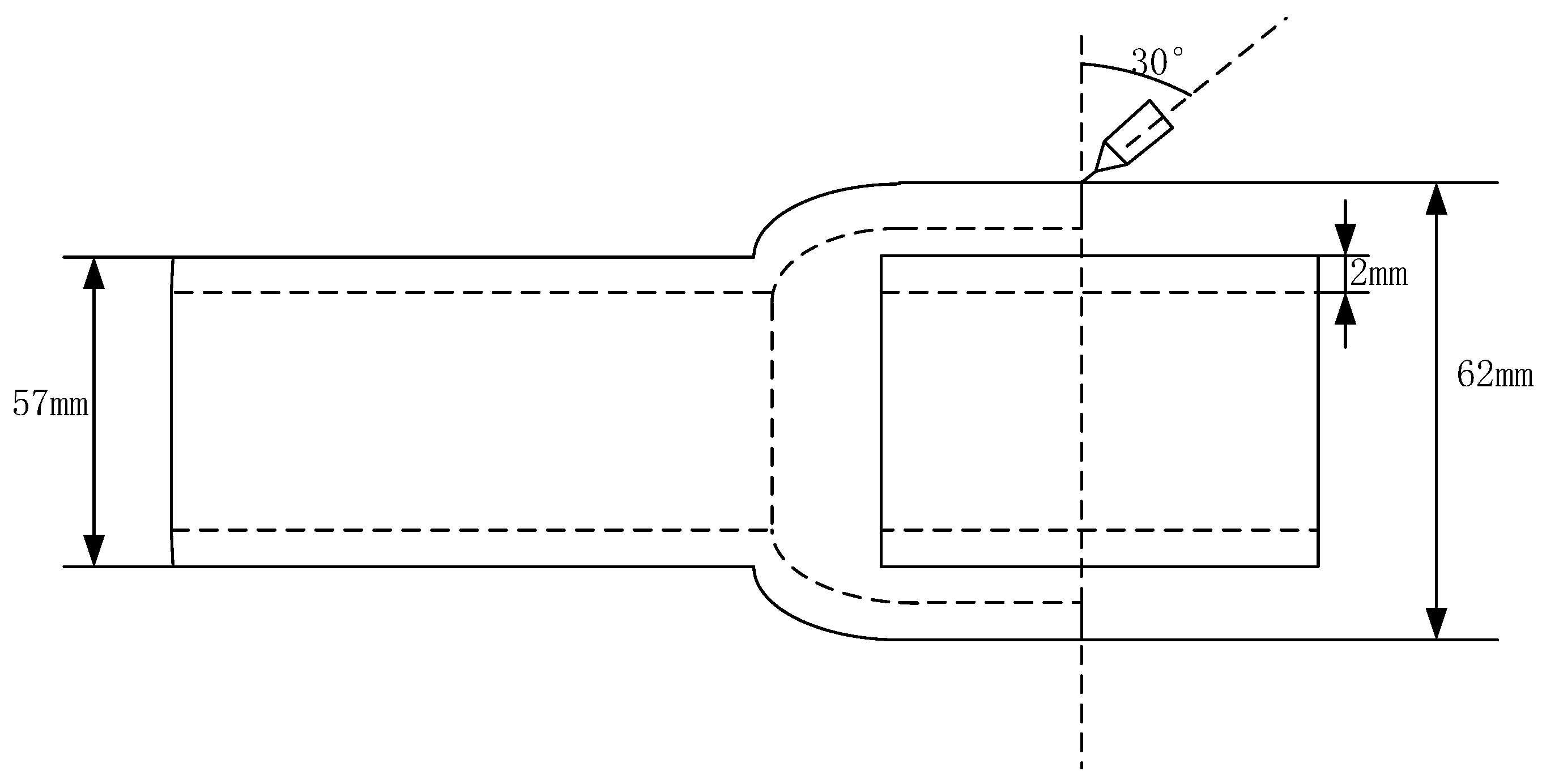
2. Materials and Methods
- (1)
- Fixing the pipes with a welding fixture.
- (2)
- Inputting the cool water and argon gas into the TOA77 welding torch.
- (3)
- The protective gas was inputted into the pipes.
- (4)
- The welding torch weld around the pipes.
- (a)
- Validation of the primary factors;
- (b)
- Confirming the working range of the control variables;
- (c)
- Establishing trial matrix by Design-Expert V10.0.7 software;
- (d)
- Conducting the experiments as per the design matrix;
- (e)
- Recording the response parameters;
- (f)
- Building statistical models;
- (g)
- Calculating regression coefficients of the multinomial;
- (h)
- Checking the adequacy of the statistical model;
- (i)
- Verification of models;
- (j)
- Receiving, finally, the statistical model;
- (k)
- Analysis of results;
- (l)
- Optimizing welding parameters.
3. Creating Mathematical Model
4. Verification of Models
5. Results and Discussion
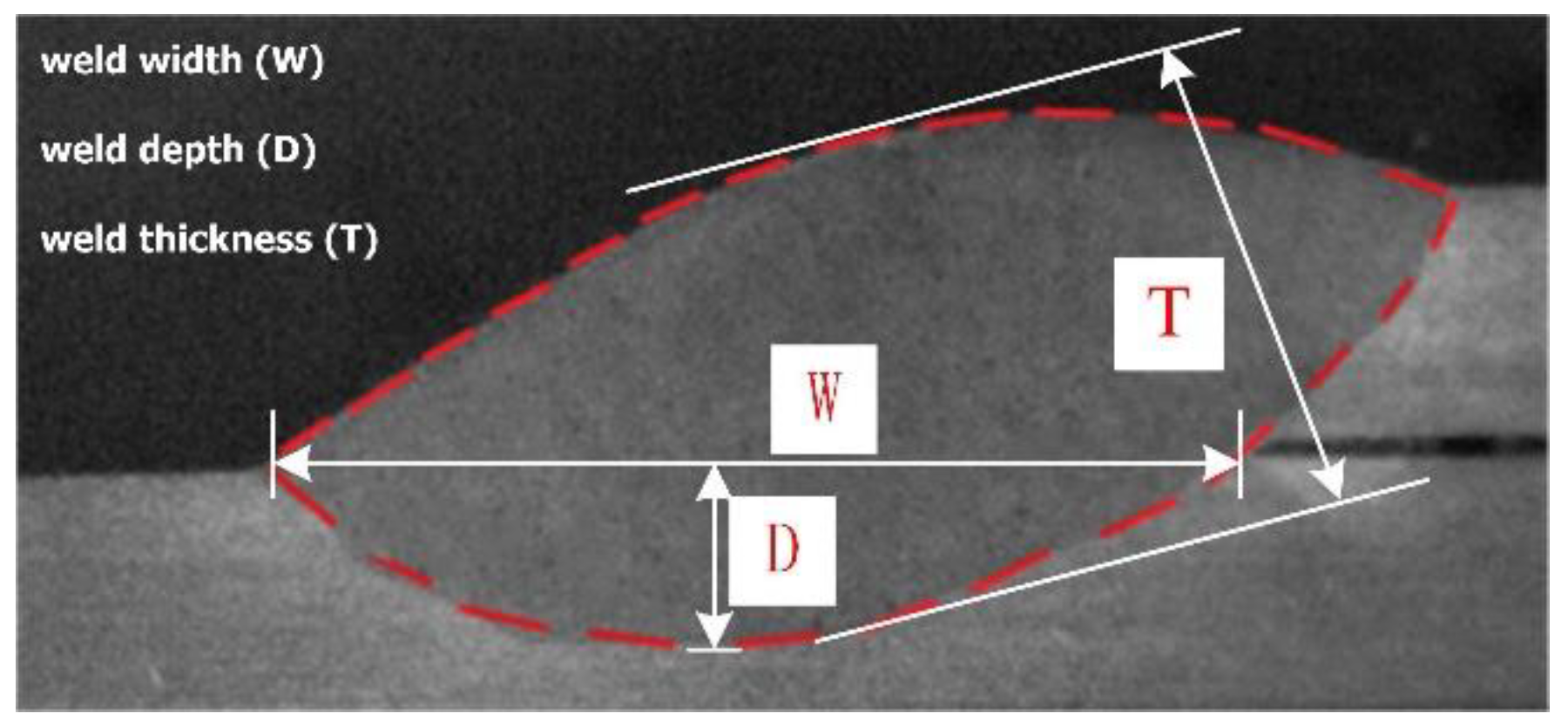
5.1. Influences of Welding Peak Current on Weld Width (W), Weld Depth (D), and Weld Thickness (T)
5.2. Influences of Weld Velocity on W, D and T
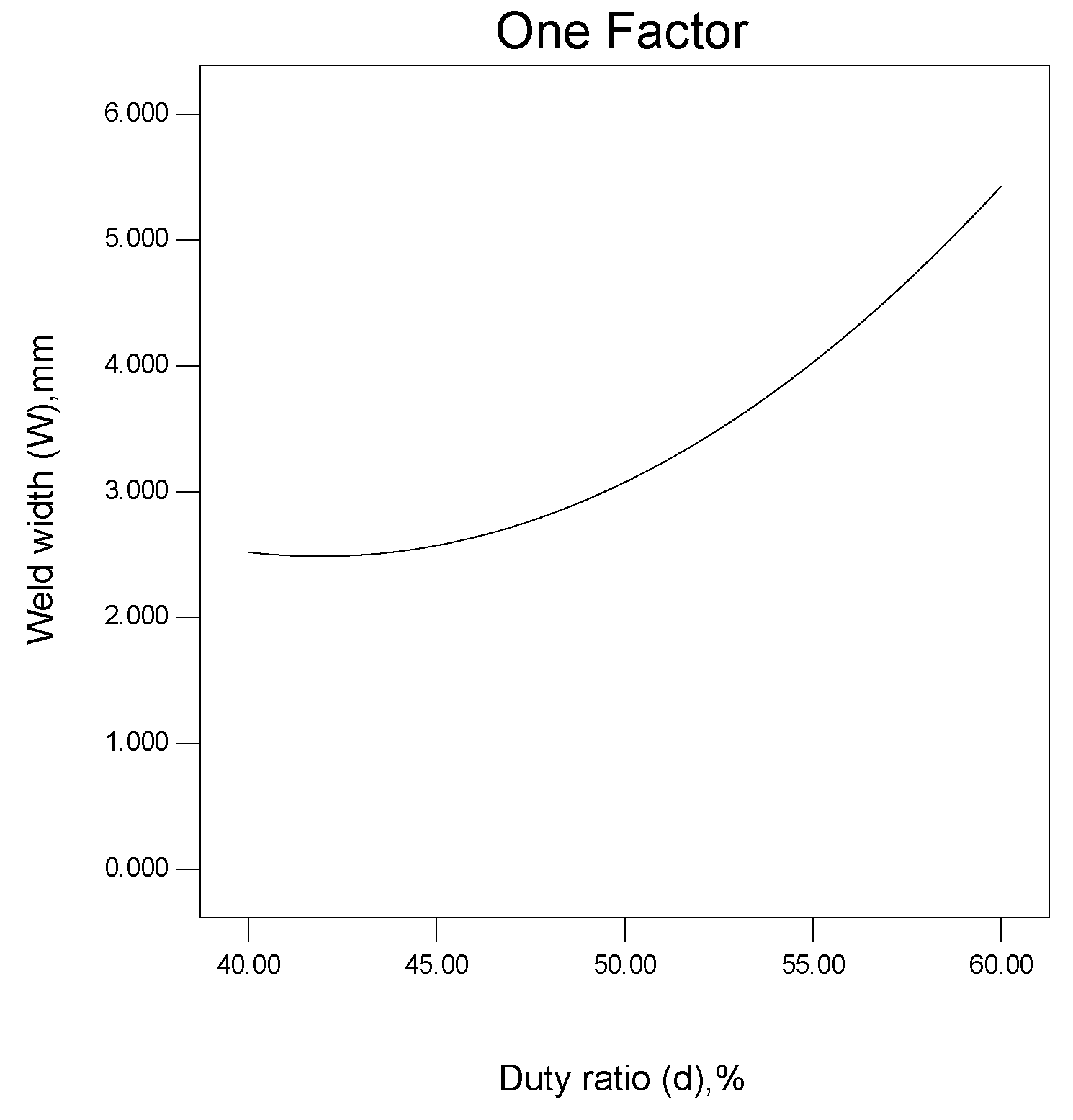
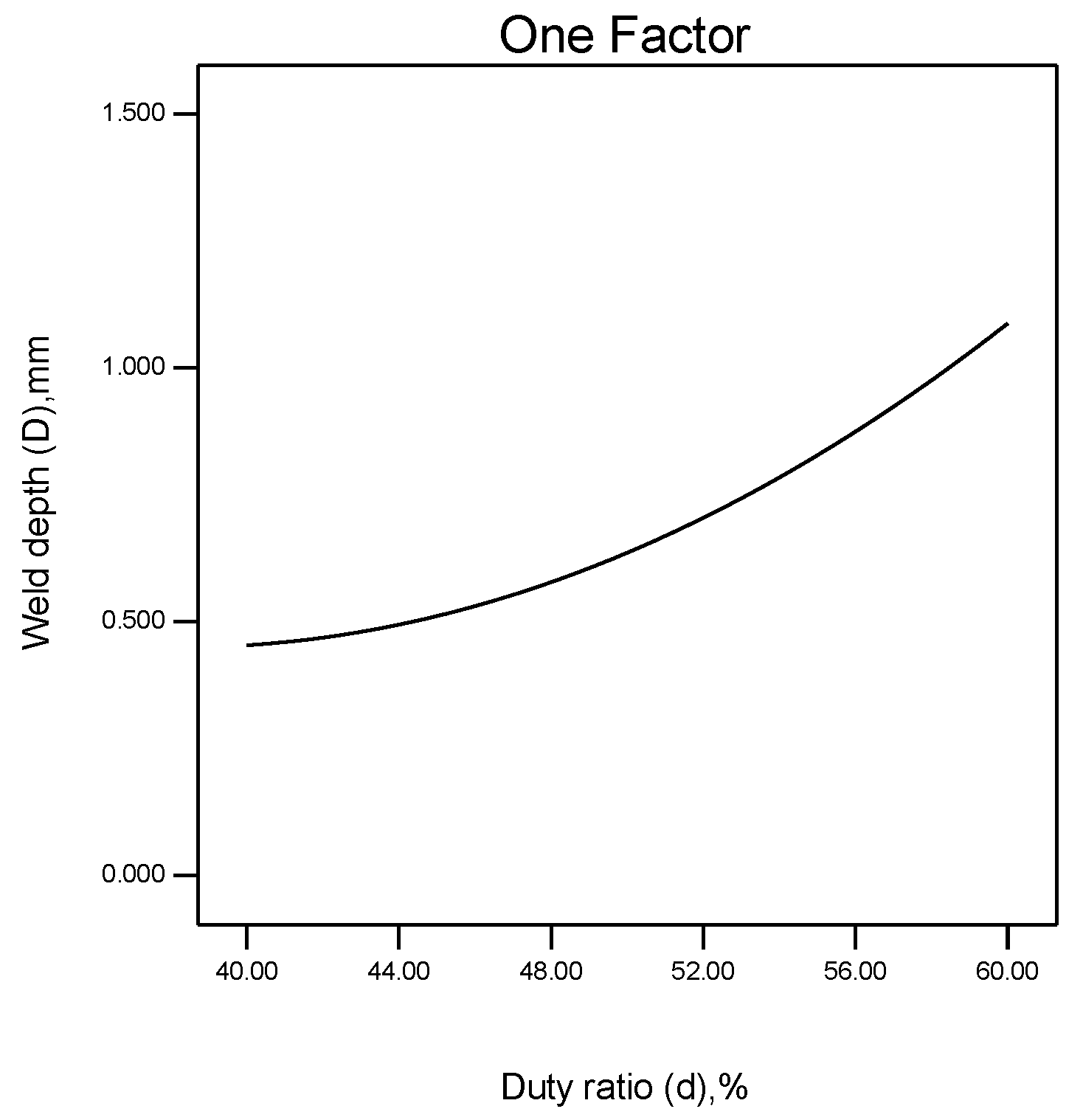
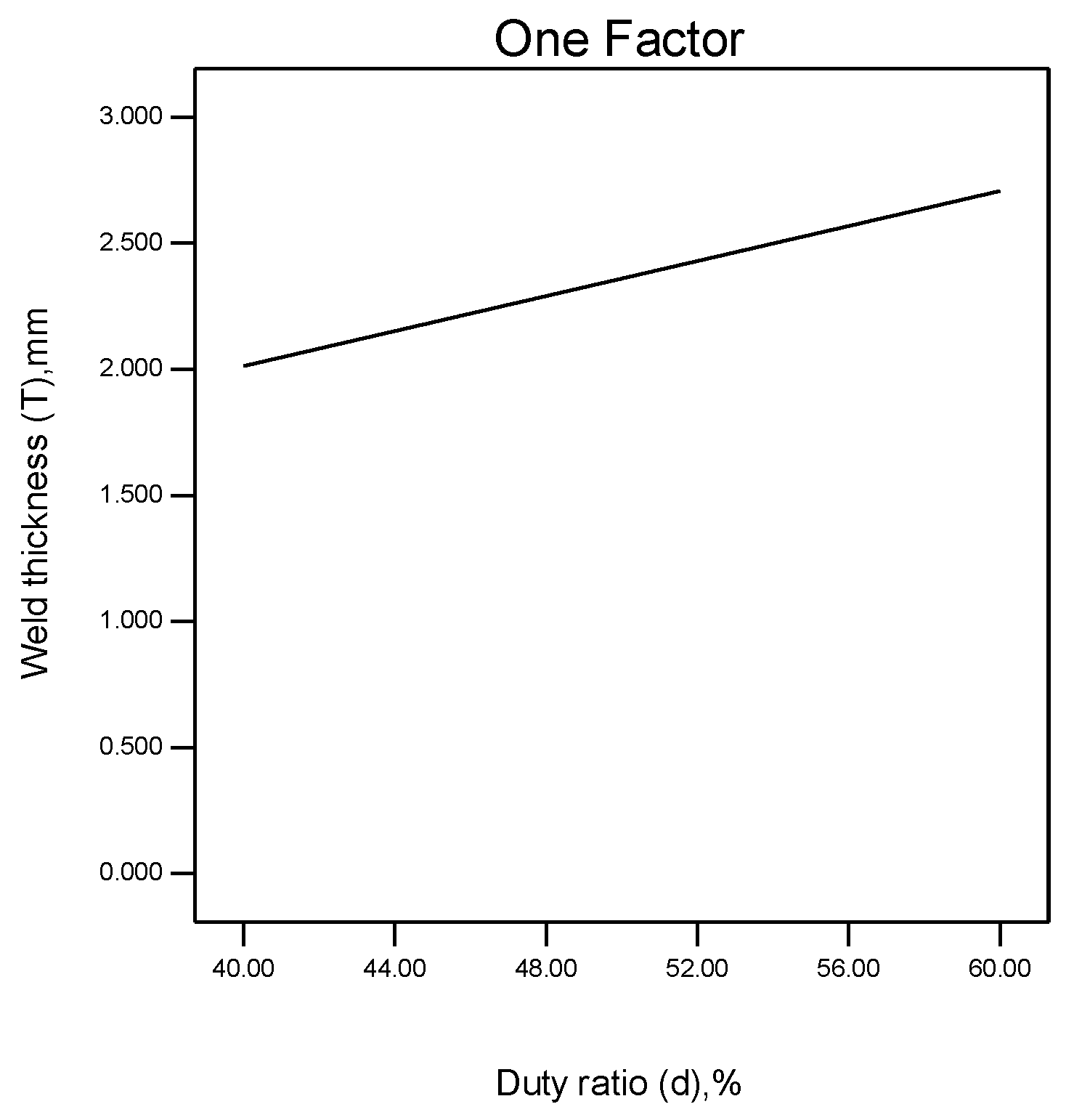
5.3. Effects of Duty Ratio on W, D and T
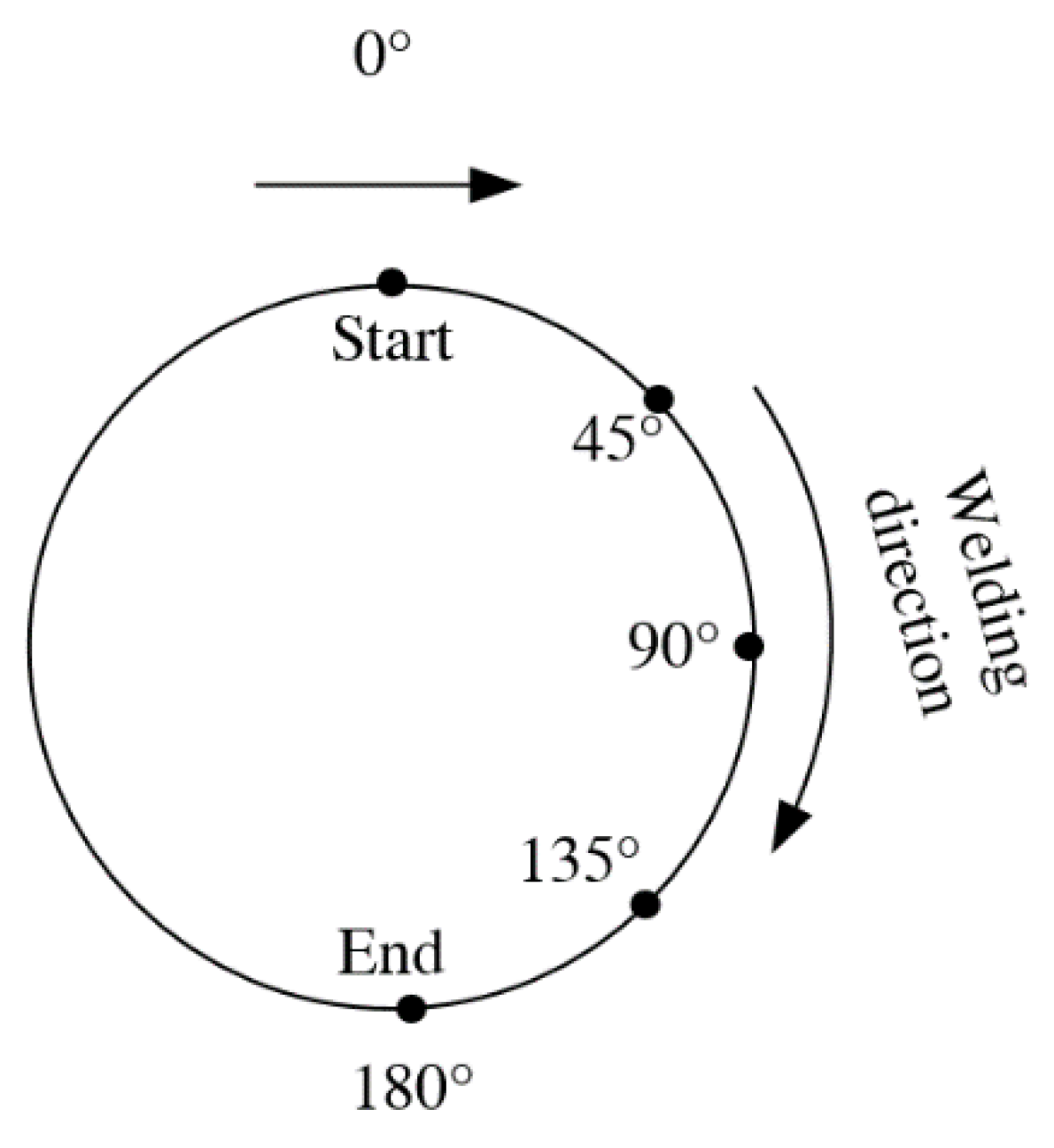
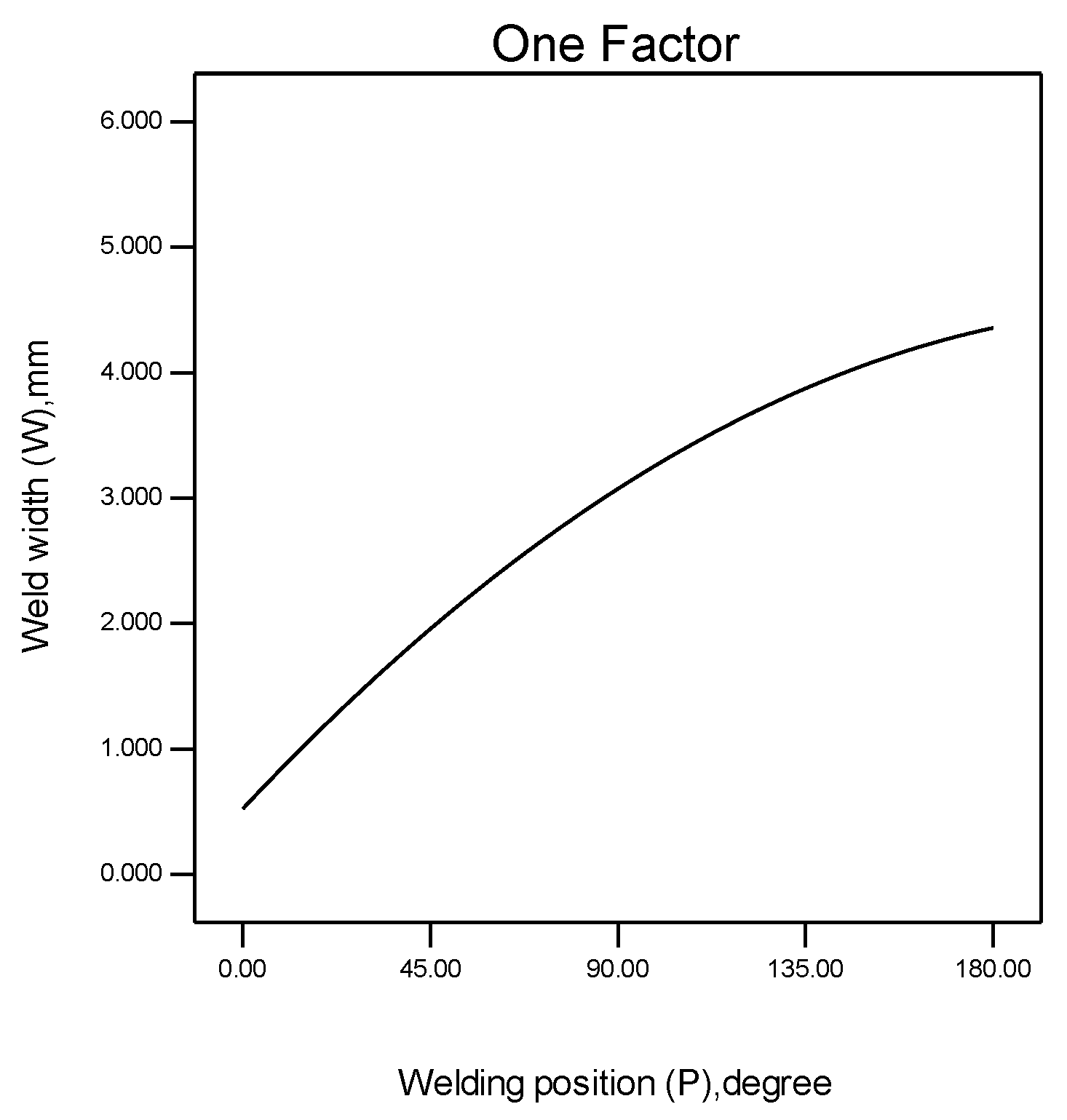
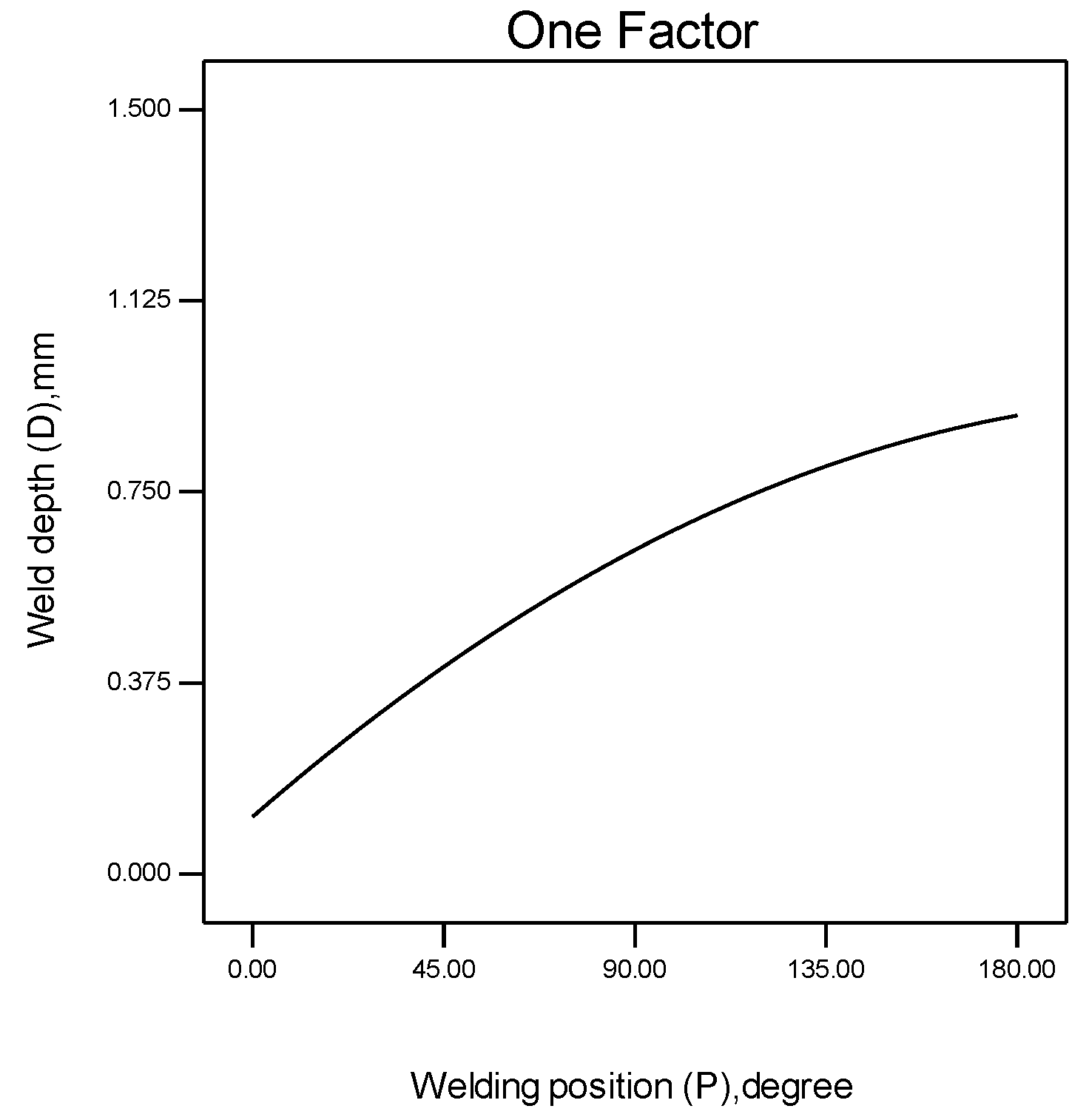
5.4. Effects of Welding Position on W, D and T
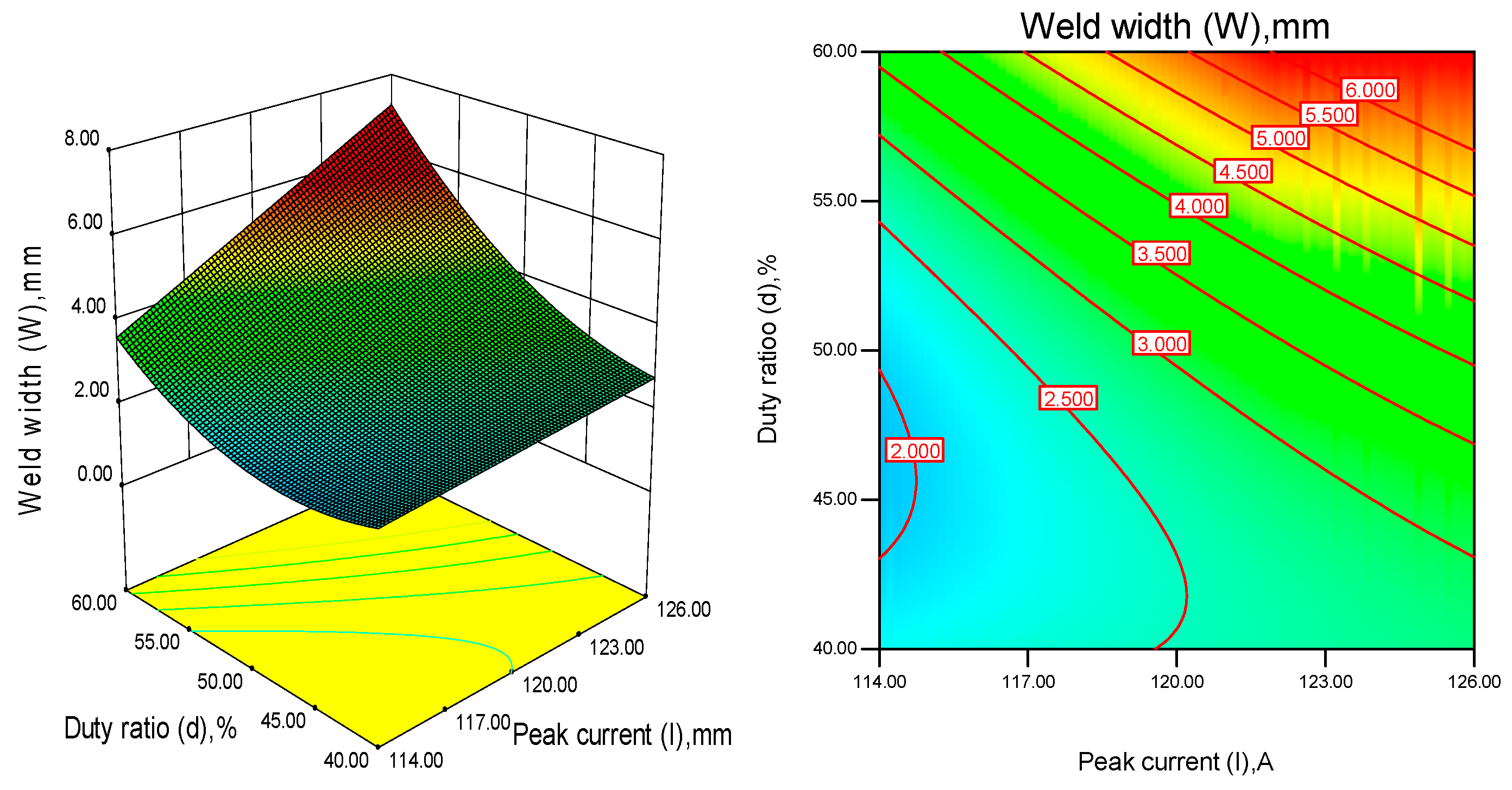
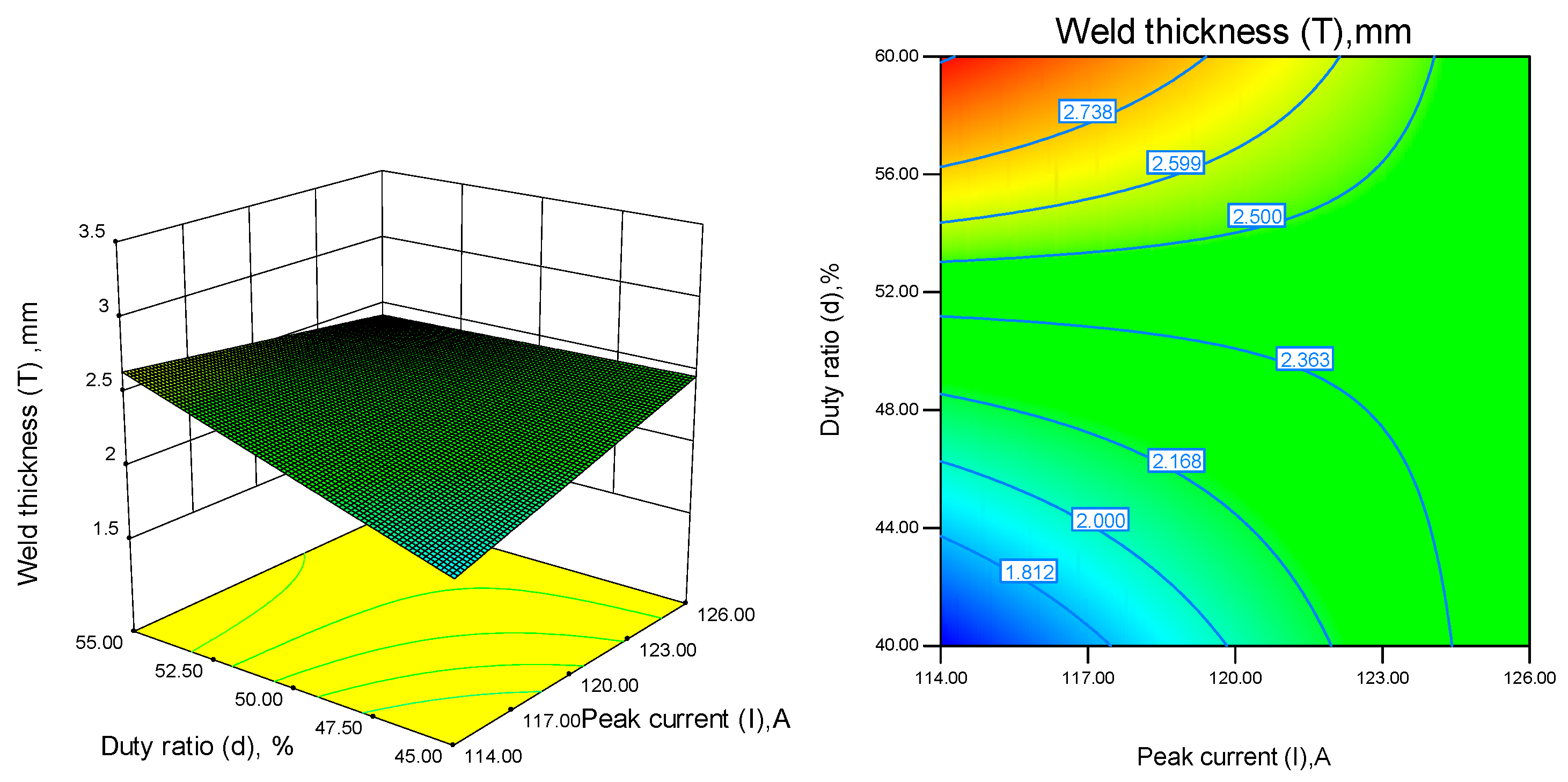
5.5. Effects of Two-Factor Interaction on W, D and T
5.6. Optimization of the Welding Parameters by Numerical Method
6. Conclusions
- (1)
- Response surface methodology (RSM) based on center composed design (CCD) can be used to establish a mathematical model, and it can predict weld bead shape in the all-position automatic welding of pipes.
- (2)
- Weld peak current had a prominent active influence on the important weld bead geometry parameters, while welding velocity had a negative influence on the important weld bead geometry parameters. The duty ratio exhibits a quadratic parabolic relationship with W and D, and the slope of the curve increases as the duty ratio increases, while T and the duty ratio increase linearly. The welding position has a quadratic parabolic relationship with the important weld bead geometry parameters, and the slope of the curve decreases as the degree of the welding position increases.
- (3)
- The ideal weld bead geometry can be obtained by choosing the optimal weld parameters with the established statistical models, and this model can be used for the all-position automatic welding of pipes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, W.H.; Lin, S.B.; Fan, C.L.; Zhuo, X.Q.; Yang, C.L. Statistical modelling of weld bead geometry in oscillating arc narrow gap all-position GMA welding. Int. J. Adv. Manuf. Technol. 2014, 72, 1705–1716. [Google Scholar] [CrossRef]
- Manonmani, K.; Murugan, N.; Buvanasekaran, G. Effects of process parameters on the bead geometry of laser beam butt welded stainless steel sheets. Int. J. Adv. Manuf. Technol. 2007, 32, 1125–1133. [Google Scholar] [CrossRef]
- Kim, D.I.S.; Basu, A.; Siores, E. Mathematical models for control of weld bead penetration in the GMAW process. Int. J. Adv. Manuf. Technol. 1996, 12, 393–401. [Google Scholar] [CrossRef]
- Xu, W.H.; Lin, S.B.; Fan, C.L.; Yang, C.L. Prediction and optimization of weld bead geometry in oscillating arc narrow gap all-position GMA welding. Int. J. Adv. Manuf. Technol. 2015, 79, 183–196. [Google Scholar] [CrossRef]
- Rao, P.S.; Gupta, O.P.; Murty, S.S.N.; Rao, A.B.K. Effect of process parameters and mathematical model for the prediction of bead geometry in pulsed GMA welding. Int. J. Adv. Manuf. Technol. 2009, 45, 496–505. [Google Scholar] [CrossRef]
- Koleva, E. Electron beam weld parameters and thermal efficiency improvement. Vacuum 2005, 77, 413–421. [Google Scholar] [CrossRef]
- Karthikeyan, R.; Balasubramanian, V. Predictions of the optimized friction stir spot welding process parameters for joining AA2024 aluminum alloy using RSM. Int. J. Adv. Manuf. Technol. 2010, 51, 173–183. [Google Scholar] [CrossRef]
- Ii, E.J.L.; Torres, G.C.F.; Felizardo, I.; Filho, F.A.R.; Bracarense, A.Q. Development of a robot for orbital welding. Ind. Robot 2005, 32, 321–325. [Google Scholar]
- Acherjee, B.; Kuar, A.S.; Mitra, S.; Misra, D. Modeling and analysis of simultaneous laser transmission welding of polycarbonates using an FEM and RSM combined approach. Opt. Laser Technol. 2012, 44, 995–1006. [Google Scholar] [CrossRef]
- Gunaraj, V.; Murugan, N. Application of response surface methodology for predicting weld bead quality in submerged arc welding of pipes. J. Mater. Process. Technol. 1999, 88, 266–275. [Google Scholar] [CrossRef]
- Acherjee, B.; Misra, D.; Bose, D.; Venkadeshwaran, K. Prediction of weld strength and seam width for laser transmission welding of thermoplastic using response surface methodology. Opt. Laser Technol. 2009, 41, 956–967. [Google Scholar] [CrossRef]
- Ruggiero, A.; Tricarico, L.; Olabi, A.G.; Benyounis, K.Y. Weld-bead profile and costs optimisation of the CO2 dissimilar laser welding process of low carbon steel and austenitic steel AISI316. Opt. Laser Technol. 2011, 43, 82–90. [Google Scholar] [CrossRef]
- Gunaraj, V.; Murugan, N. Prediction and comparison of the area of the heat-affected zone for the bead-on-plate and bead-on-joint in submerged arc welding of pipes. J. Mater. Process. Technol. 1999, 95, 246–261. [Google Scholar] [CrossRef]
- Murugan, N.; Gunaraj, V. Prediction and control of weld bead geometry and shape relationships in submerged arc welding of pipes. J. Mater. Process. Technol. 2005, 168, 478–487. [Google Scholar] [CrossRef]
- Rajakumar, S.; Balasubramanian, V. Diffusion bonding of titanium and AA7075 aluminum alloy dissimilar joints—Process modeling and optimization using desirability approach. Int. J. Adv. Manuf. Technol. 2016, 86, 1–18. [Google Scholar] [CrossRef]
- Colombini, E.; Sola, R.; Parigi, G.; Veronesi, P.; Poli, G. Laser quenching of ionic nitrided steel: Effect of process parameters on microstructure and optimization. Metall. Mater. Trans. A 2014, 45, 5562–5573. [Google Scholar] [CrossRef]
- Poli, G.; Sola, R.; Veronesi, P. Microwave-assisted combustion synthesis of NiAl intermetallics in a single mode applicator: Modeling and optimisation. Mater. Sci. Eng. A 2006, 441, 149–156. [Google Scholar] [CrossRef]










| Chemical Element | Ni | Fe | Mn | Pb | S | C | Zn | P | Cu |
|---|---|---|---|---|---|---|---|---|---|
| Measured Value | 10.66 | 1.60 | 0.79 | 0.01 | 0.0023 | 0.0065 | 0.019 | 0.01 | Bal |
| Factors | Unit | Coded Value | ||||
|---|---|---|---|---|---|---|
| −2 | −1 | 0 | 1 | 2 | ||
| I | A | 114 | 117 | 120 | 123 | 126 |
| V | mm/min | 57 | 60 | 63 | 66 | 69 |
| d | % | 40 | 45 | 50 | 55 | 60 |
| P | ° | 0 | 45 | 90 | 135 | 180 |
| Std | Run | Coded Variables | Response Parameters | |||||
|---|---|---|---|---|---|---|---|---|
| I (A) | V (mm/min) | D (%) | P (degree) | W (mm) | D (mm) | T (mm) | ||
| 1 | 7 | 117 | 60 | 45 | 45 | 1.416 | 0.29 | 1.978 |
| 2 | 10 | 123 | 60 | 45 | 45 | 1.615 | 0.363 | 2.142 |
| 3 | 6 | 117 | 66 | 45 | 45 | 1.016 | 0.199 | 1.797 |
| 4 | 19 | 123 | 66 | 45 | 45 | 1.325 | 0.272 | 1.89 |
| 5 | 11 | 117 | 60 | 55 | 45 | 2.877 | 0.577 | 2.541 |
| 6 | 24 | 123 | 60 | 55 | 45 | 4.2 | 0.851 | 2.751 |
| 7 | 22 | 117 | 66 | 55 | 45 | 1.575 | 0.315 | 1.995 |
| 8 | 26 | 123 | 66 | 55 | 45 | 2.373 | 0.462 | 2.232 |
| 9 | 29 | 117 | 60 | 45 | 135 | 3.255 | 0.637 | 2.185 |
| 10 | 30 | 123 | 60 | 45 | 135 | 4.956 | 1.02 | 2.314 |
| 11 | 14 | 117 | 66 | 45 | 135 | 2.583 | 0.525 | 1.932 |
| 12 | 8 | 123 | 66 | 45 | 135 | 3.591 | 0.706 | 2.73 |
| 13 | 5 | 117 | 60 | 55 | 135 | 4.074 | 0.835 | 3.024 |
| 14 | 23 | 123 | 60 | 55 | 135 | 5.796 | 1.298 | 2.541 |
| 15 | 16 | 117 | 66 | 55 | 135 | 3.297 | 0.606 | 2.379 |
| 16 | 15 | 123 | 66 | 55 | 135 | 5.754 | 1.179 | 2.034 |
| 17 | 12 | 114 | 63 | 50 | 90 | 2.268 | 0.441 | 2.331 |
| 18 | 28 | 126 | 63 | 50 | 90 | 3.717 | 0.762 | 2.436 |
| 19 | 20 | 120 | 57 | 50 | 90 | 3.402 | 0.697 | 2.667 |
| 20 | 9 | 120 | 69 | 50 | 90 | 2.856 | 0.462 | 1.827 |
| 21 | 27 | 120 | 63 | 40 | 90 | 2.226 | 0.356 | 1.659 |
| 22 | 4 | 120 | 63 | 60 | 90 | 5.859 | 1.201 | 2.478 |
| 23 | 13 | 120 | 63 | 50 | 0 | 0.987 | 0.202 | 1.533 |
| 24 | 17 | 120 | 63 | 50 | 180 | 4.032 | 0.826 | 2.184 |
| 25 | 3 | 120 | 63 | 50 | 90 | 3.412 | 0.699 | 2.331 |
| 26 | 2 | 120 | 63 | 50 | 90 | 3.533 | 0.724 | 2.826 |
| 27 | 25 | 120 | 63 | 50 | 90 | 3.641 | 0.528 | 2.461 |
| 28 | 21 | 120 | 63 | 50 | 90 | 2.755 | 0.597 | 2.098 |
| 29 | 1 | 120 | 63 | 50 | 90 | 2.562 | 0.74 | 2.356 |
| 30 | 18 | 120 | 63 | 50 | 90 | 2.878 | 0.742 | 2.501 |
| Source | Sum of Squares | df * | Mean Square | F Value | p Value (Prob > F) | Significance |
|---|---|---|---|---|---|---|
| Model | 47.8 | 8 | 5.98 | 30.86 | <0.0001 | Significant |
| I | 6.42 | 1 | 6.42 | 33.17 | <0.0001 | - |
| V | 2.51 | 1 | 2.51 | 12.98 | 0.0017 | - |
| d | 12.69 | 1 | 12.69 | 65.56 | <0.0001 | - |
| P | 22.04 | 1 | 22.04 | 113.82 | <0.0001 | - |
| I × d | 0.59 | 1 | 0.59 | 3.07 | 0.0945 | - |
| I × P | 1.13 | 1 | 1.13 | 5.85 | 0.0247 | - |
| d2 | 1.44 | 1 | 1.44 | 7.42 | 0.0127 | - |
| P2 | 0.72 | 1 | 0.72 | 3.69 | 0.0683 | - |
| Residual | 4.07 | 21 | 0.19 | - | - | - |
| Lack of Fit | 3.04 | 16 | 0.19 | 0.92 | 0.5944 | Not Significant |
| Pure Error | 1.03 | 5 | 0.21 | - | - | - |
| Cor total | 51.87 | 29 | - | - | - | - |
| Source | Sum of Squares | df | Mean Square | F Value | p Value (Prob > F) | Significance |
|---|---|---|---|---|---|---|
| Model | 2.21 | 8 | 0.28 | 31.63 | <0.0001 | Significant |
| I | 0.33 | 1 | 0.33 | 37.60 | <0.0001 | - |
| V | 0.18 | 1 | 0.18 | 20.56 | 0.0002 | - |
| d | 0.6 | 1 | 0.6 | 68.85 | <0.0001 | - |
| P | 0.93 | 1 | 0.93 | 106.39 | <0.0001 | - |
| I × d | 0.035 | 1 | 0.035 | 3.99 | 0.0589 | - |
| I × P | 0.067 | 1 | 0.067 | 7.63 | 0.0117 | - |
| d2 | 0.032 | 1 | 0.032 | 3.69 | 0.0685 | - |
| P2 | 0.030 | 1 | 0.030 | 3.43 | 0.0782 | - |
| Residual | 0.18 | 21 | 0.008744 | - | - | - |
| Lack of Fit | 0.14 | 16 | 0.009019 | 1.15 | 0.4786 | Not Significant |
| Pure Error | 0.039 | 5 | 0.007863 | - | - | - |
| Cor total | 2.40 | 29 | - | - | - | - |
| Source | Sum of Squares | df | Mean Square | F Value | p Value (Prob > F) | Significance |
|---|---|---|---|---|---|---|
| Model | 2.64 | 7 | 0.38 | 7.89 | <0.0001 | Significant |
| I | 0.043 | 1 | 0.043 | 0.9 | 0.3544 | - |
| V | 0.72 | 1 | 0.72 | 15.15 | 0.0008 | - |
| d | 0.72 | 1 | 0.72 | 15.15 | 0.0008 | - |
| P | 0.40 | 1 | 0.40 | 8.46 | 0.0081 | - |
| I × d | 0.15 | 1 | 0.15 | 3.20 | 0.0872 | - |
| V × d | 0.24 | 1 | 0.24 | 4.96 | 0.0365 | - |
| P2 | 0.35 | 1 | 0.35 | 7.39 | 0.0125 | - |
| Residual | 1.05 | 22 | 0.048 | - | - | - |
| Lack of Fit | 0.76 | 17 | 0.045 | 0.78 | 0.6845 | Not Significant |
| Pure Error | 0.29 | 5 | 0.058 | - | - | - |
| Cor total | 3.69 | 29 | - | - | - | - |
| Designation | Run | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Input Parameters | I (A) | 123 | 122 | 119 | 117 | 115 |
| V (mm/min) | 60 | 60 | 60 | 62 | 63 | |
| d (%) | 55 | 45 | 40 | 60 | 55 | |
| P (degree) | 0 | 45 | 90 | 135 | 180 | |
| Predicted Values | W (mm) | 1.977 | 1.818 | 2.788 | 3.958 | 4.067 |
| D (mm) | 0.426 | 0.372 | 0.574 | 0.783 | 0.799 | |
| T (mm) | 2.071 | 2.091 | 2.194 | 2.707 | 2.406 | |
| Actual Values | W (mm) | 1.839 | 1.978 | 2.581 | 3.615 | 4.256 |
| T (mm) | 0.346 | 0.346 | 0.596 | 0.759 | 0.954 | |
| W (mm) | 2.204 | 1.991 | 2.345 | 2.891 | 2.278 | |
| Percentage Error ** (%) | W | −6.98 | 8.8 | −7.43 | −8.67 | 4.65 |
| D | −7.04 | −6.99 | 3.38 | −4.29 | 6.88 | |
| T | 6.42 | −4.78 | 7.03 | 6.8 | −5.32 |
| Name | Goal | Lower | Upper | Importance |
|---|---|---|---|---|
| I | Is in range | 114 | 126 | 3 |
| V | Is in range | 57 | 69 | 3 |
| d | Is in range | 40 | 60 | 3 |
| P | Is equal to | 0 | 180 | 3 |
| W | maximize | 0.987 | 5.859 | 5 |
| D | Is in range | 0.8 | 1.5 | 5 |
| T | Is in range | 1.533 | 3.204 | 5 |
| I (A) | V (mm/min) | d (%) | P (Degree) |
|---|---|---|---|
| 126 | 57 | 60 | 0 |
| 125 | 58 | 59 | 45 |
| 124 | 60 | 58 | 90 |
| 122 | 60 | 54 | 135 |
| 119 | 61 | 54 | 180 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, B.; Shi, Y.; Cui, Y.; Cui, S.; Jiang, Z.; Yi, Y. Mathematical Model for Prediction and Optimization of Weld Bead Geometry in All-Position Automatic Welding of Pipes. Metals 2018, 8, 756. https://doi.org/10.3390/met8100756
Liao B, Shi Y, Cui Y, Cui S, Jiang Z, Yi Y. Mathematical Model for Prediction and Optimization of Weld Bead Geometry in All-Position Automatic Welding of Pipes. Metals. 2018; 8(10):756. https://doi.org/10.3390/met8100756
Chicago/Turabian StyleLiao, Baoyi, Yonghua Shi, Yanxin Cui, Shuwan Cui, Zexin Jiang, and Yaoyong Yi. 2018. "Mathematical Model for Prediction and Optimization of Weld Bead Geometry in All-Position Automatic Welding of Pipes" Metals 8, no. 10: 756. https://doi.org/10.3390/met8100756
APA StyleLiao, B., Shi, Y., Cui, Y., Cui, S., Jiang, Z., & Yi, Y. (2018). Mathematical Model for Prediction and Optimization of Weld Bead Geometry in All-Position Automatic Welding of Pipes. Metals, 8(10), 756. https://doi.org/10.3390/met8100756





