Development of Amplifier Circuit by Active-Dummy Method for Atmospheric Corrosion Monitoring in Steel Based on Strain Measurement
Abstract
:1. Introduction
2. Materials and Methods
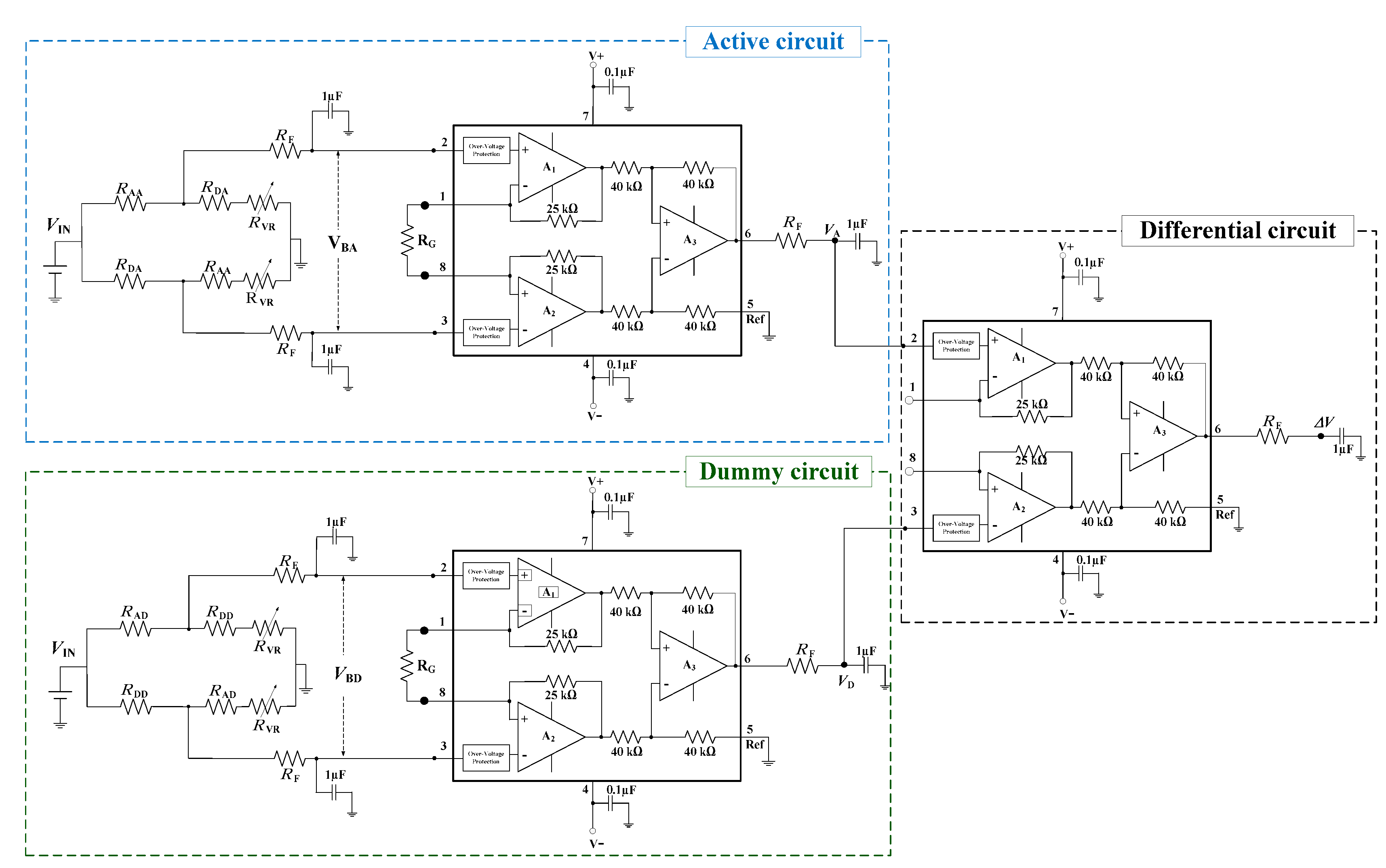
2.1. Design of Amplifier Circuit by Active-Dummy Method
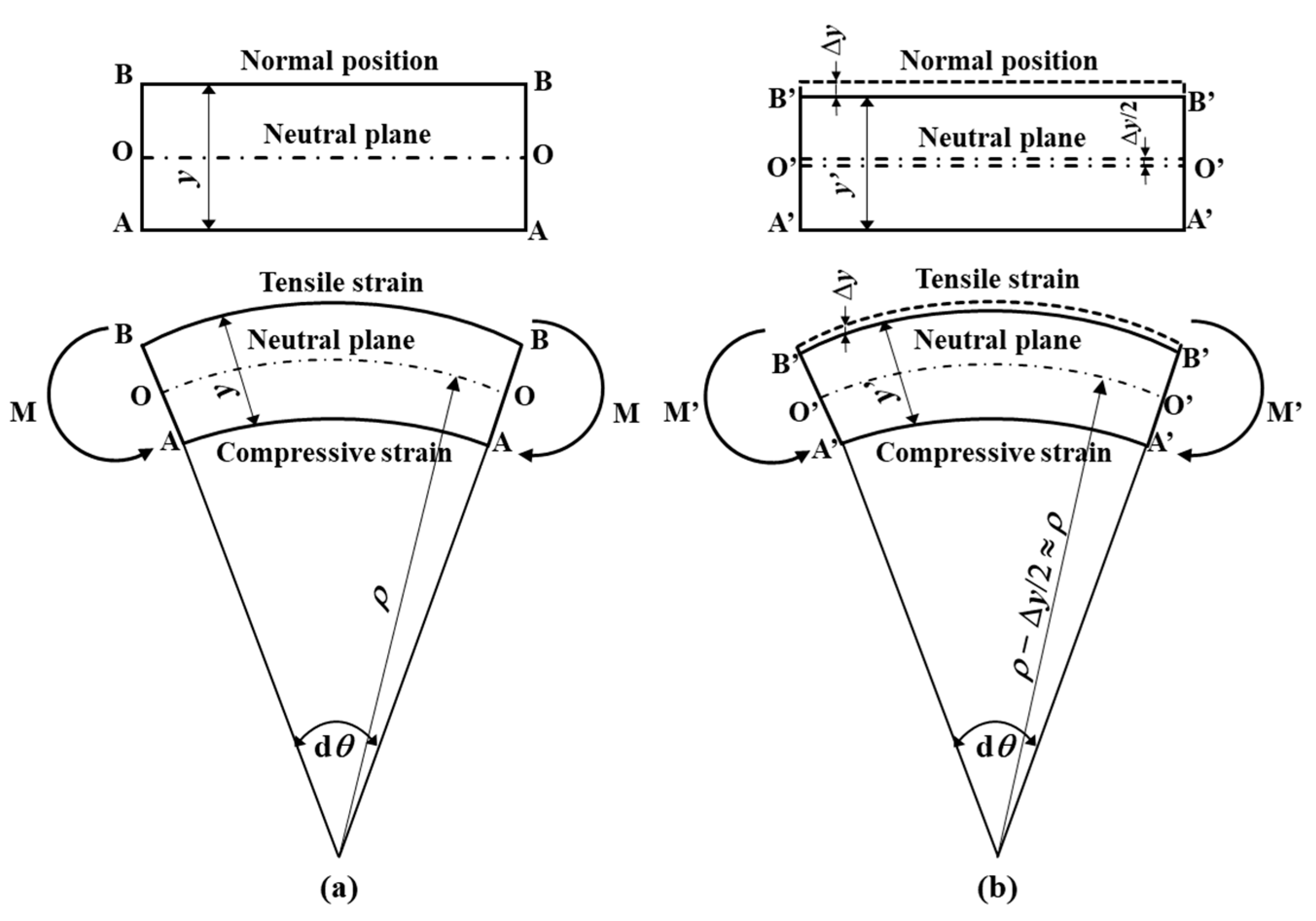
2.1.1. Principle of ACM (Atmospheric Corrosion Monitoring) Sensor Based on Strain Measurement
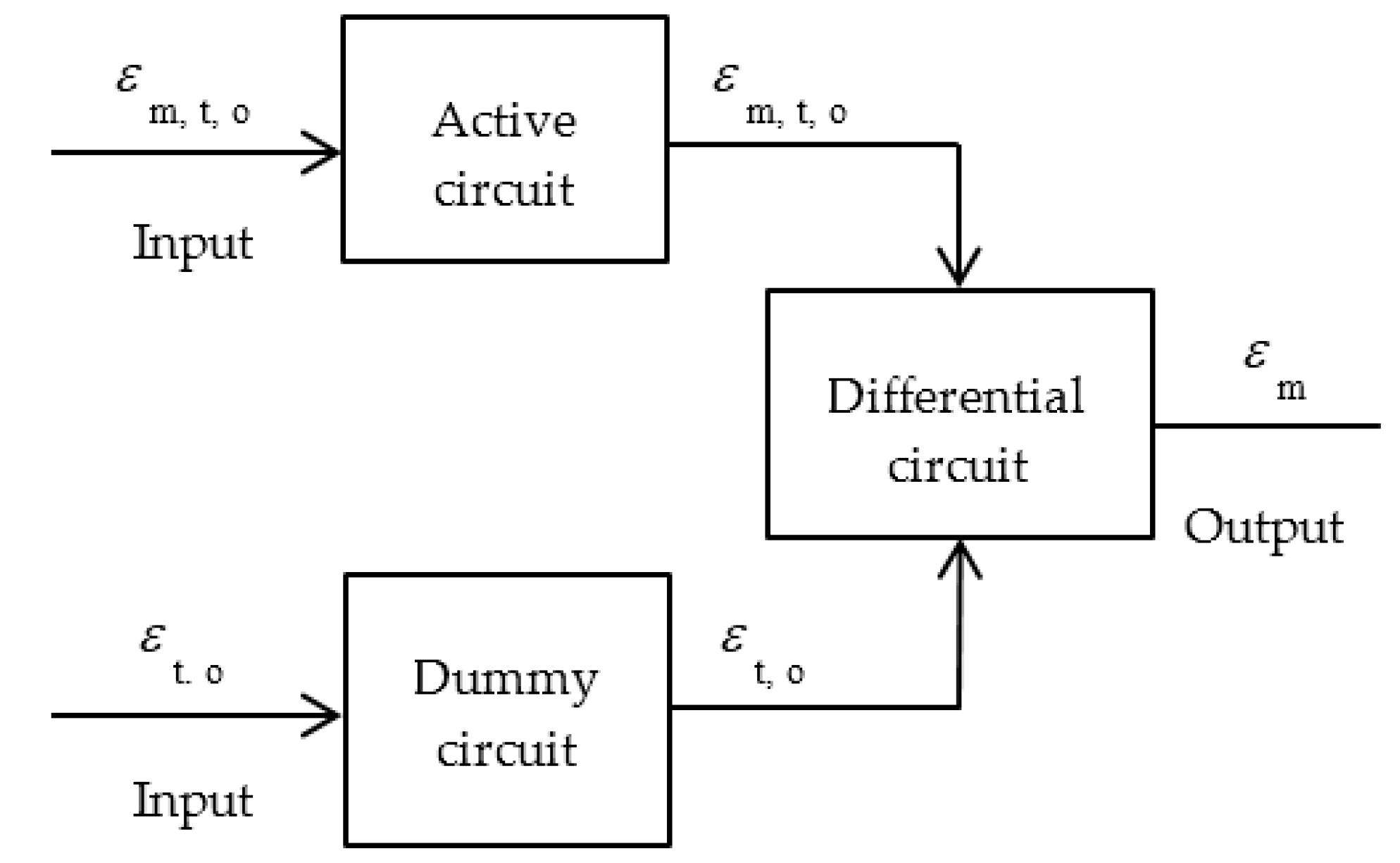
2.1.2. Concept of Amplifier Circuit by Active-Dummy Method
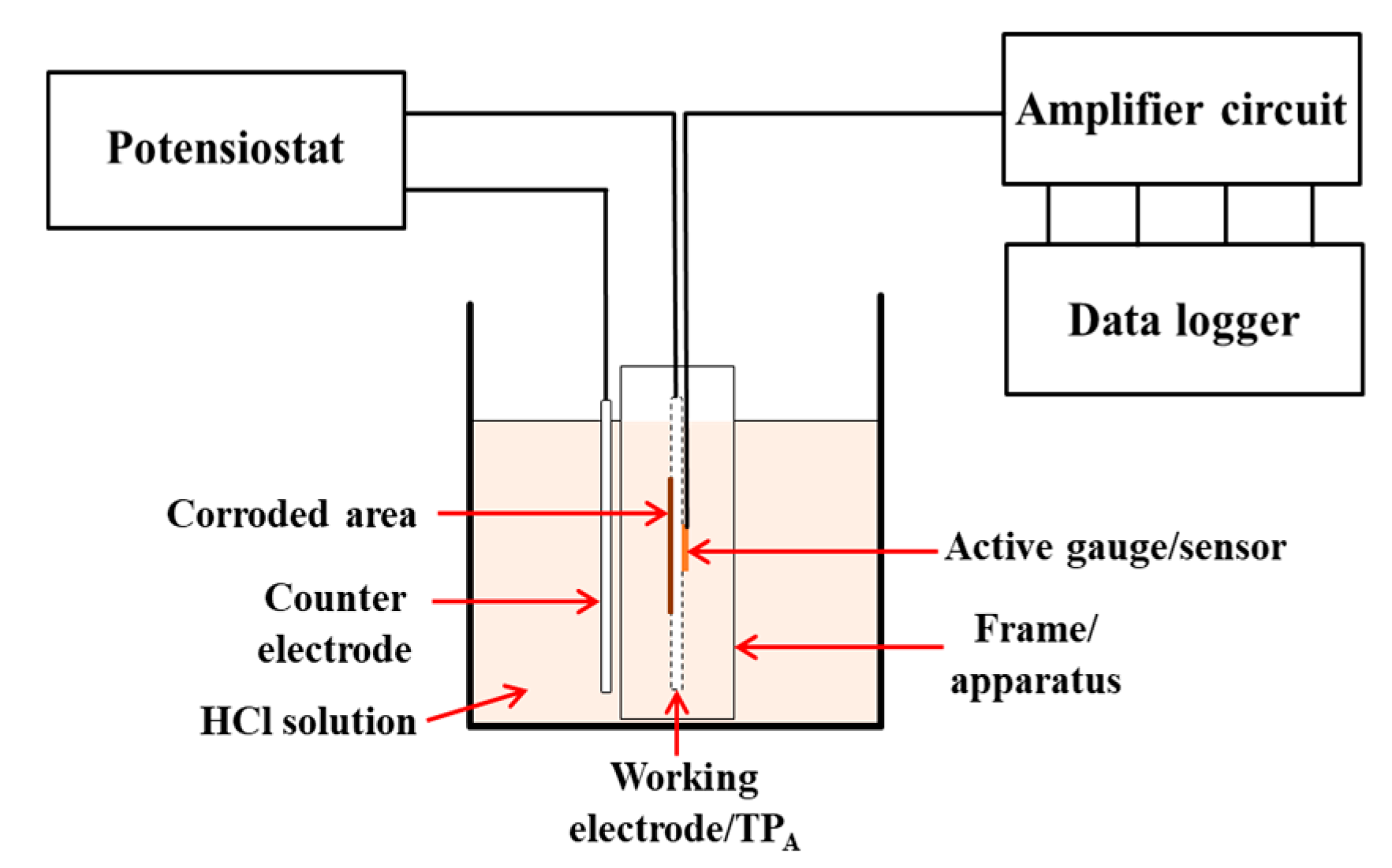
2.2. Experimental Setup
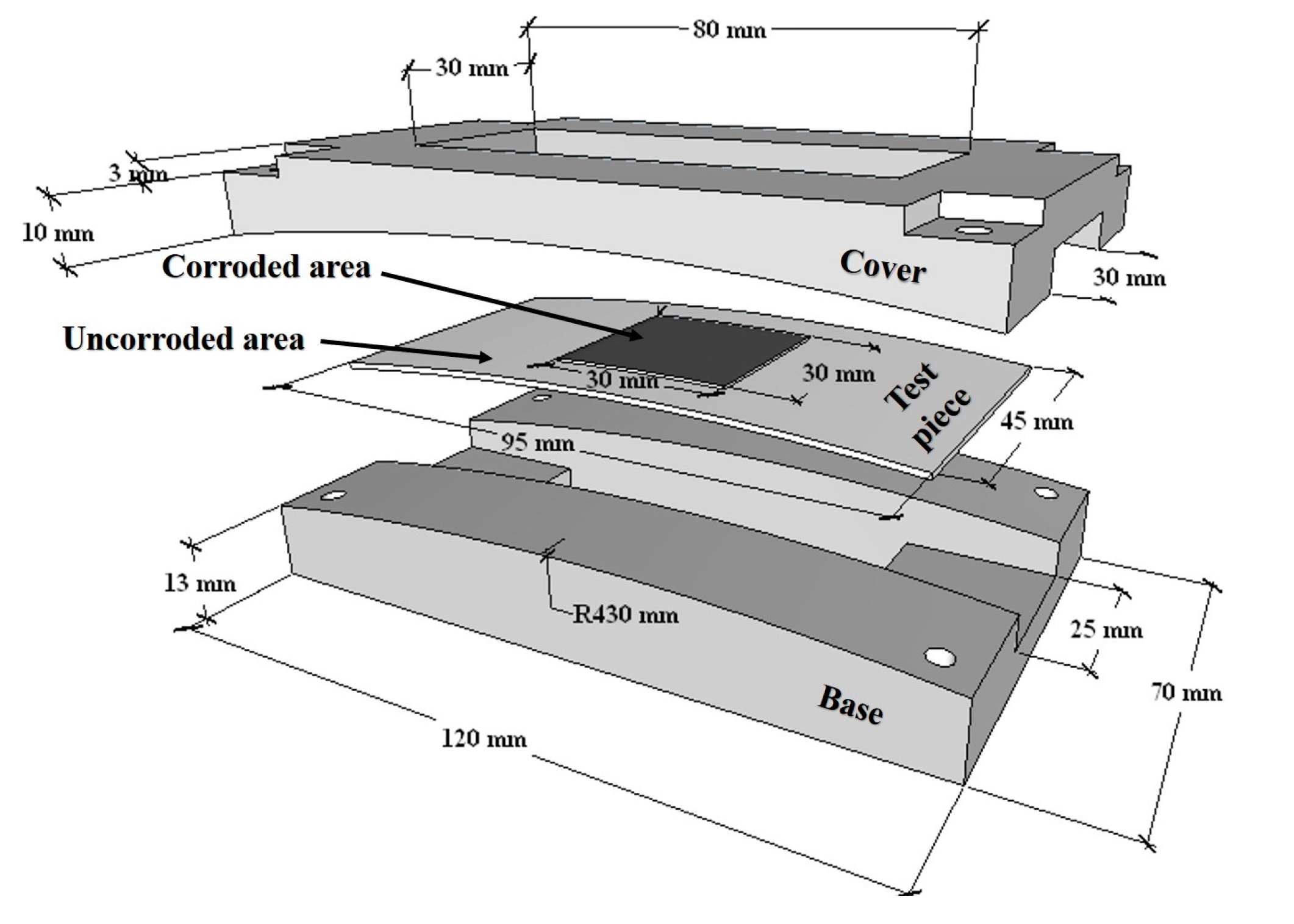
2.2.1. Design of ACM Sensor
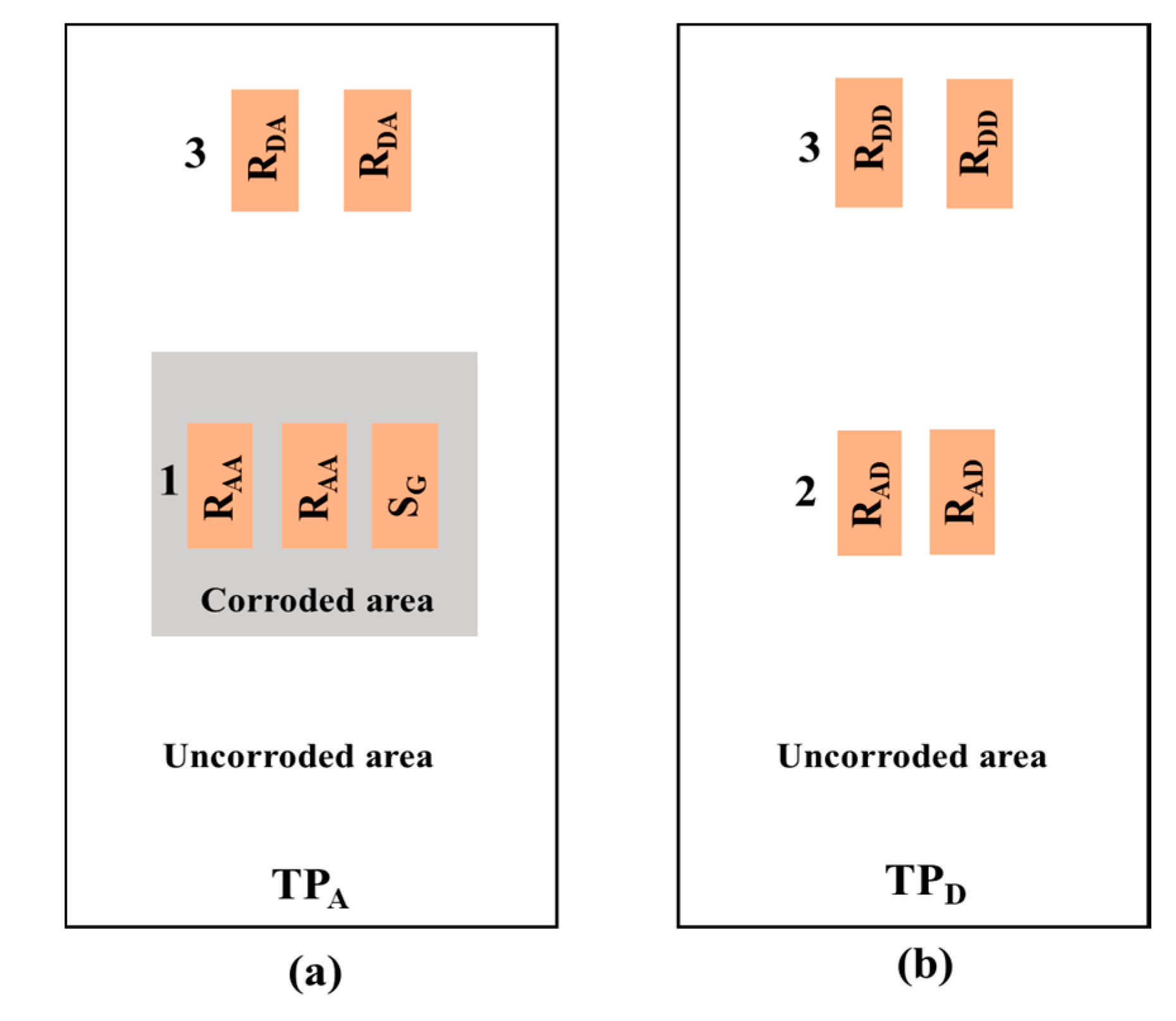
2.2.2. Strain Gauge Configuration of Test Piece for Active and Dummy Circuit
2.2.3. Design of the Amplifier Circuit with the Active-Dummy Method
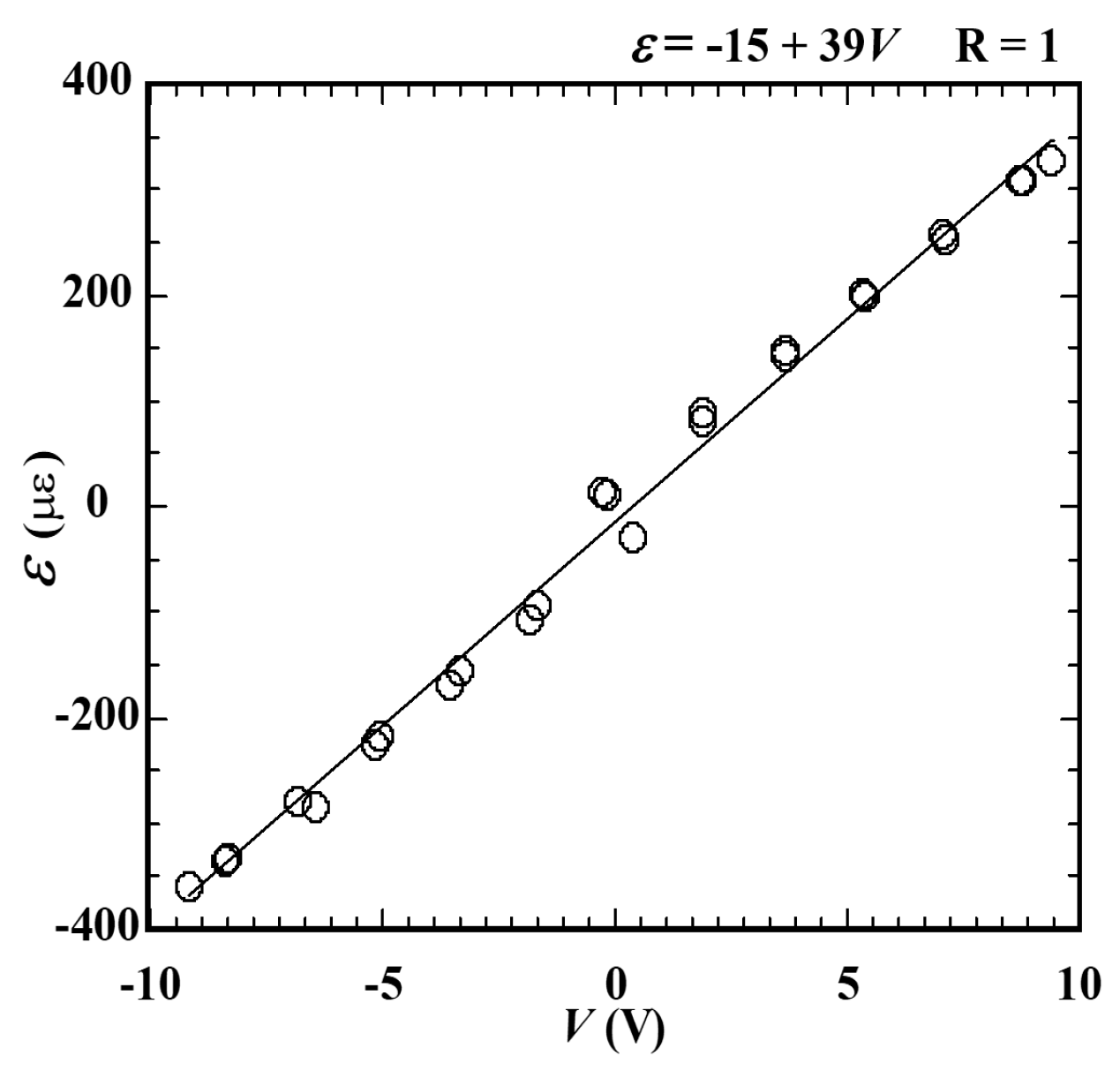
2.2.4. Master Curve of the Strain-Voltage Relationship
2.2.5. In Monitoring of Thinning of Test Piece by Galvanostatic Electrolysis
2.2.6. Strain Due to Temperature Change without Corrosion
3. Results and Discussion
3.1. Master Curve of the Strain-Voltage Relationship
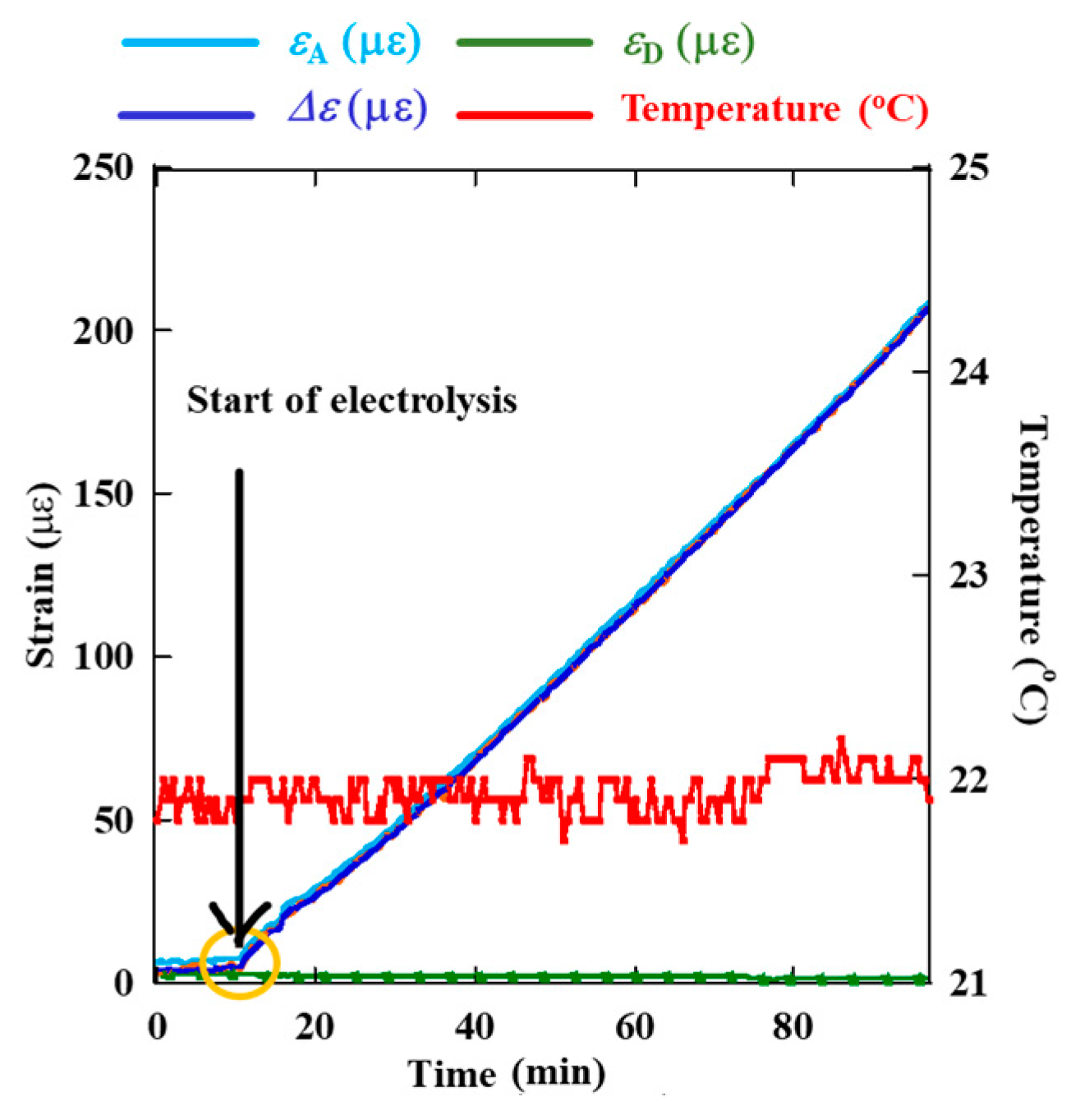
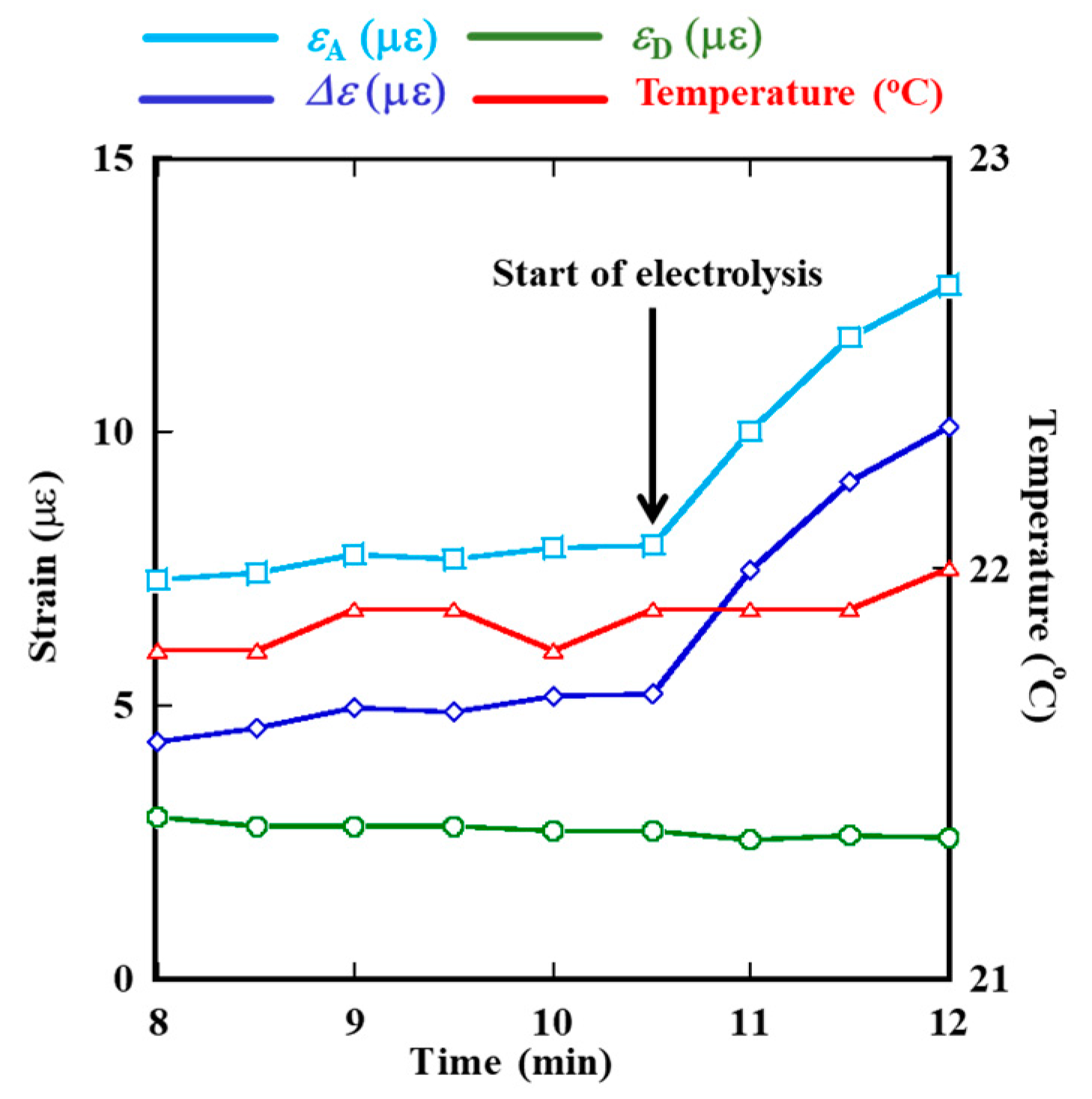
3.2. In Monitoring of Thinning of Test Piece by Galvano Static Electrolysis
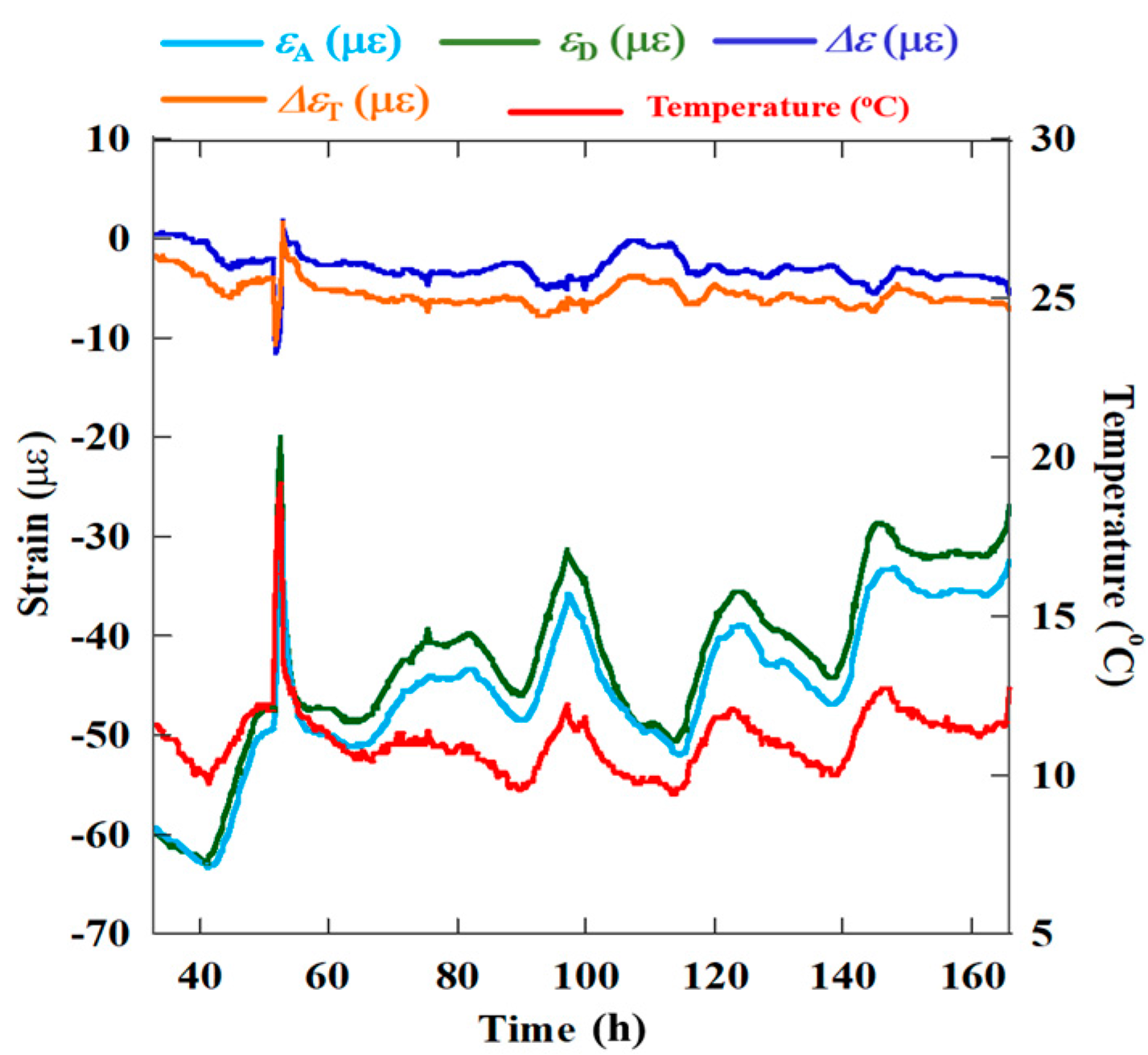
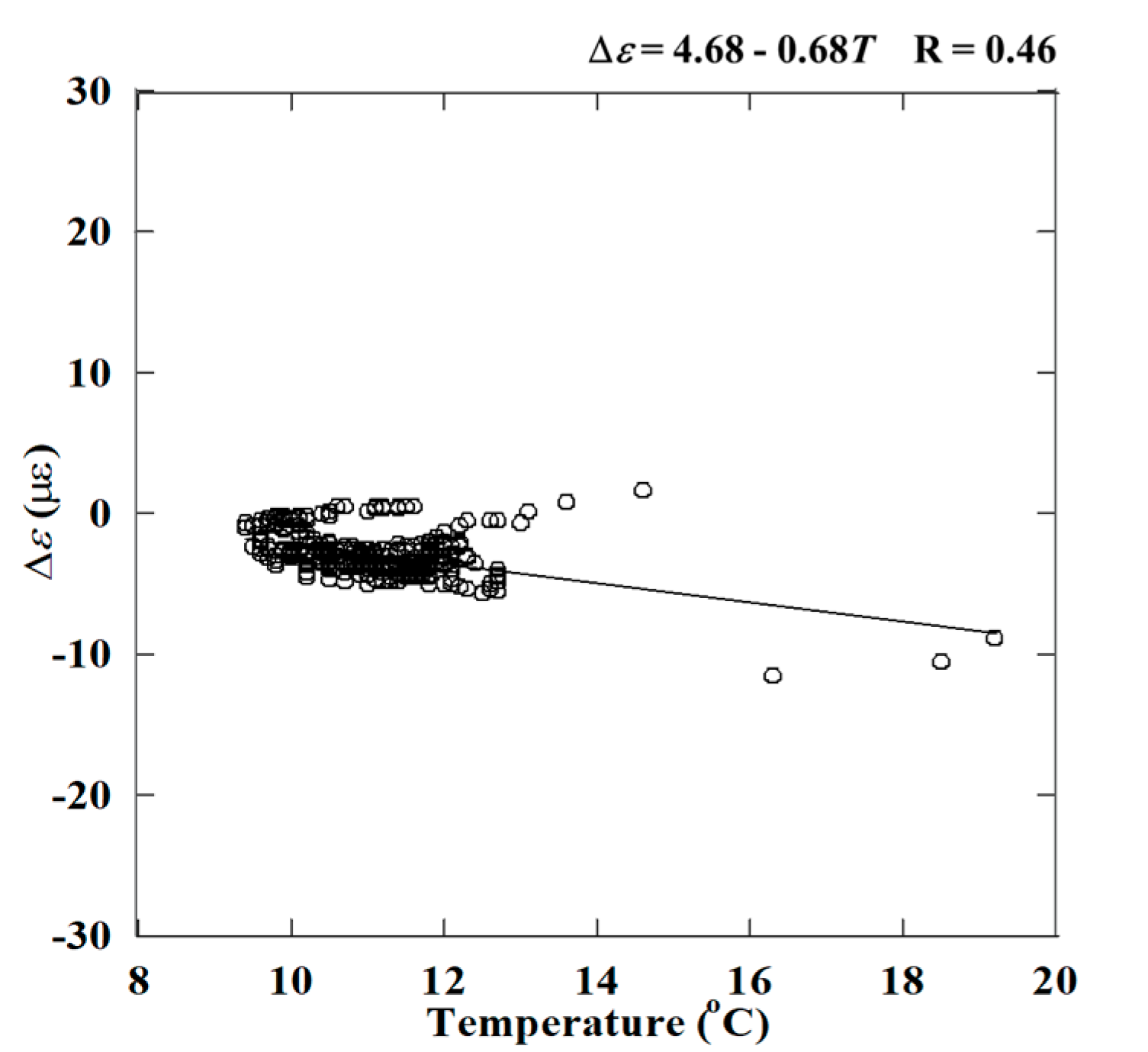
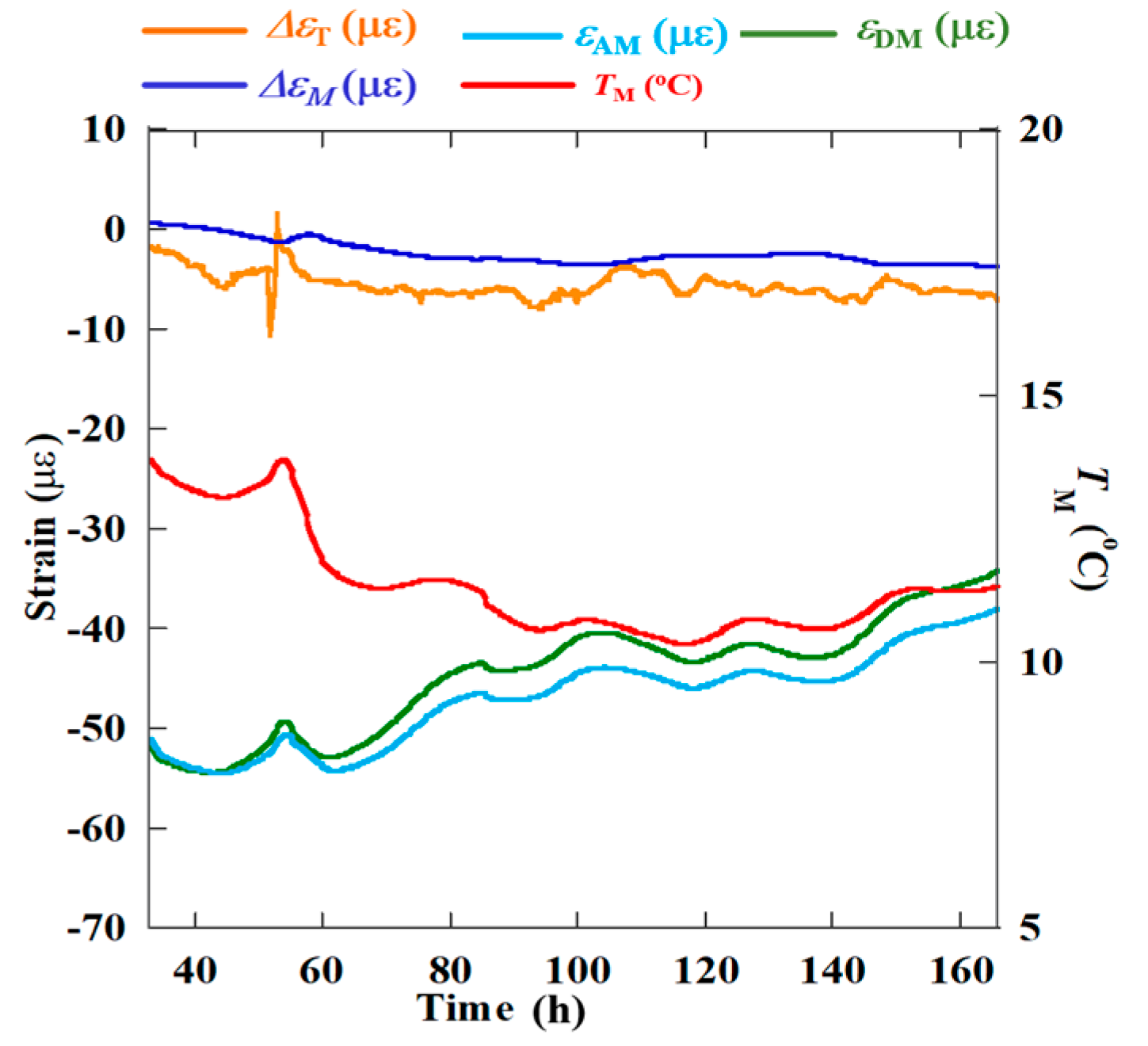
3.3. Strain Due to the Temperature Change of Measurement Environment
4. Conclusions
- An amplifier circuit using the active-dummy method for an ACM sensor based on strain measurement was developed. It successfully overcomes the noise from the environment by compensating from the dummy circuit to the active circuit.
- The master curve of strain versus voltage for the newly developed amplifier circuit indicated high sensitivity with a slope of 39 με/V.
- The experiment on the thickness reduction of the test piece by galvanostatic electrolysis revealed strong alignment between the calculated results and the strain measurements made with the amplifier circuit by using the active-dummy method. The error rate was approximately 12%.
- The strain due to temperature variation was obtained via Δε = 4.68 − 0.68T. The effect of temperature on Δε was around 0.68 με/°C.
- ΔεT remained slightly more constant than Δε with temperature variations in the measurement environment.
- ΔεM was significantly more constant than ΔεT, which indicated that the moving average should be used in experiments to obtain more accurate measurements.
- In the field measurement, the corrosion layers of the test piece of the ACM sensor might affect the signals, and its effect would benefit from further study. The relationship of corrosion progression and strain measurement need to be further verified in the future. After developing the ACM sensor system, including an amplifier circuit using the active-dummy method, and unveiling the effect of corrosion layers on the signal, atmospheric corrosion of steel structures can be estimated with an ACM sensor system. The ACM sensor can be installed on different surfaces of the structure.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| D | Density of test piece (g·cm−3) |
| dθ | Center angle of curvature of the test piece (°) |
| E | Young’s modulus of the test piece (Pa) |
| RAA | Resistance of active gauge for active circuit (Ω) |
| RAD | Resistance of active gauge for dummy circuit (Ω) |
| RDA | Resistance of dummy gauge for active circuit (Ω) |
| RDD | Resistance of dummy gauge for dummy circuit (Ω) |
| RVR | Resistance of variable resistor (Ω) |
| S | Corroded area of test piece (cm2) |
| SG | Strain gauge for measuring the strain by commercial strain (-) |
| T | Temperature (°C) |
| TM | Temperature with moving average analysis (°C) |
| VA | Output voltage of active circuit (V) |
| VBA | Output voltage of bridge circuit of active circuit (mV) |
| VBD | Output voltage of bridge circuit of dummy circuit (mV) |
| VCC | Positive input voltage for op-amp (V) |
| VD | Output voltage of dummy circuit (V) |
| VEE | Negative input voltage for op-amp (V) |
| VIN | Input voltage for bridge circuit (V) |
| Vp-p | Peak-to-peak voltage (V) |
| Y | Test piece thickness (m) |
| ΔV | Difference between the output voltages of the active and dummy circuits (V) |
| ΔW | Actual weight obtained by analysis (g) |
| Δy | Change in thickness of test piece (m) |
| ΔyA | Actual thickness obtained by analysis (μm) |
| ΔyW | Actual thickness obtained by electrochemical analysis (μm) |
| Δε | Differential strain (με) |
| ΔεM | Differen ce in strain between the active and dummy circuits, determined by moving average analysis (με) |
| ΔεT | Difference in strain, taking account of the temperature effect (με) |
| ε | Strain in test piece (-) |
| εA | Strain of the active circuit (με) |
| εAM | Strain of the active circuit obtained by moving average analysis (με) |
| εAT | Strain of active circuit, taking account of the temperature effect (με) |
| εD | Strain of dummy circuit (με) |
| εDM | Strain of dummy circuit obtained by moving average analysis (με) |
| εDT | Strain of dummy circuit, taking account of temperature effect (με) |
| εm | Strain with input only from signal (-) |
| εm,t,o | Strain with input from signal and environmental factors (-) |
| εt,o | Strain with input only from environmental factors (-) |
| ρ | Radius of curvature of test piece (m) |
| σy | Yield stress of test piece (Pa) |
References
- Alamin, M.; Tian, G.Y.; Andrews, A.; Jackson, P. Corrosion detection using low-frequency RFID technology. Insight-Non-Destr. Test. Cond. Monit. 2012, 54, 72–75. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, R.; He, Y.; Tian, G.Y.; Xu, L.; Wu, R. Identification and characterization of steel corrosion using passive high frequency RFID sensors. Measurement 2016, 92, 421–427. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, G.Y.; Marindra, A.M.J.; Sunny, A.I.; Zhao, A.B. A review of passive RFID tag antenna-based sensors and systems for structural health monitoring applications. Sensors 2017, 17, 265. [Google Scholar] [CrossRef] [PubMed]
- Gattan, S.K.T.; Taylor, S.E.; Sun, T.; Basheer, P.A.M.; Grattan, K.T.V. Monitoring of corrosion in structural reinforcing bars: Performance comparison using in situ fiber-optic and electric wire strain gauge systems. IEEE Sens. J. 2009, 9, 1494–1502. [Google Scholar] [CrossRef]
- Hu, W.; Cai, H.; Yang, M.; Tong, X.; Zhou, C.; Chen, W. Fe-C-coated fibre Bragg grating sensor for steel corrosion monitoring. Corros. Sci. 2011, 53, 1933–1938. [Google Scholar] [CrossRef]
- Zang, N.; Chen, W.; Zheng, X.; Hu, W.; Gao, M. Optical sensor for steel corrosion monitoring based on etched Fiber Bragg Grating sputtered with iron film. IEEE Sens. J. 2015, 15, 3511–3556. [Google Scholar]
- Al Handawi, K.; Vahdati, N.; Rostron, P.; Lawand, L.; Shiryayev, O. Strain based FBG sensor for real-time corrosion rate monitoring in pre-stressed structures. Sens. Actuator B 2016, 236, 276–285. [Google Scholar] [CrossRef]
- Almubaied, O.; Chai, H.K.; Islam, M.R.; Lim, K.; Tan, C.G. Monitoring corrosion process of reinforced concrete structure using FBG strain sensor. IEEE Trans. Instrum. Meas. 2017, 66, 2148–2155. [Google Scholar] [CrossRef]
- Mansfeld, F.; Kenkel, J.V. Electrochemical monitoring of atmospheric corrosion phenomena. Corros. Sci. 1976, 16, 111–112. [Google Scholar] [CrossRef]
- Mansfeld, F.; Tsai, S. Laboratory studies of atmospheric corrosion—I. Weight loss and electrochemical measurements. Corros. Sci. 1980, 20, 853–872. [Google Scholar] [CrossRef]
- Ridha, M.; Fonna, S.; Huzni, S.; Supardi, J.; Ariffin, A.K. Atmospheric corrosion of structural steels exposed in the 2004 tsunami-affected areas of Aceh. IJAME 2013, 7, 1014–1022. [Google Scholar] [CrossRef]
- Monsada, A.M.; Margarito, M.T.; Milo, L.C.; Casa, E.P.; Zabala, J.V.; Maglines, A.S.; Basilia, B.A.; Harada, S.; Shinohara, T. Atmospheric corrosion exposure study of The Philippine Historical all steel Basilica. Zairyo Kankyo 2016, C-107, 267–270. [Google Scholar]
- Dara, T.; Shinohara, T.; Umezawa, O. The Behavior of corrosion of low carbon steel affected by corrosion product and Na2SO4 concentration under artificial rainfall test. Zairyo Kankyo 2016, C-114, 298–302. [Google Scholar]
- Lien, L.T.H.; Hong, H.L.; San, P.T.; Hieu, N.T.; Nga, N.T.T. Atmospheric corrosion of carbon steel and weathering steel—Relation of corrosion and environmental factors. Zairyo Kankyo 2016, C-110, 280–284. [Google Scholar]
- Odara, T.; Tahara, A.; Dara, T. Atmospheric corrosion behaviors of steels in Japan. Zairyo Kankyo 2016, C-111, 285–288. [Google Scholar]
- Viyanit, E.; Pongsaksawad, W.; Sorachot, S.; Matsuyama, H.; Fukuda, N. Investigation of atmospheric corrosion behavior of austenitic and ferritic stain less steel welds under tropical climate of Thailand. Zairyo Kankyo 2016, C-109, 275–279. [Google Scholar]
- Mansfeld, F.; Jeanjaquet, S.L.; Kendig, M.W.; Roe, D.K. A new atmospheric corrosion rate monitor development and evaluation. Atmos. Environ. 1986, 20, 1179–1192. [Google Scholar] [CrossRef]
- Nishikata, A.; Yamashita, Y.; Katayama, H.; Tsuru, T.; Usami, A.; Tanabe, K.; Mabuchi, H. An electrochemical impedance study on atmospheric corrosion of steels in a cyclic wet–dry condition. Corros. Sci. 1995, 37, 2059–2069. [Google Scholar] [CrossRef]
- Nishikata, A.; Suzuki, F.; Tsuru, T. Corrosion monitoring of nickel-containing steels in marine atmospheric environment. Corros. Sci. 2005, 47, 2578–2588. [Google Scholar] [CrossRef]
- Cruz, R.P.V.; Nishikata, A.; Tsuru, T. AC impedance monitoring of pitting corrosion of stainless steel under a wet–dry cyclic condition in chloride-containing environment. Corros. Sci. 1996, 38, 1397–1406. [Google Scholar] [CrossRef]
- El-Mahdy, G.A.; Nishikata, A.; Tsuru, T. Electrochemical corrosion monitoring of galvanized steel under cyclic wet–dry conditions. Corros. Sci. 2000, 42, 183–194. [Google Scholar] [CrossRef]
- Yadav, A.P.; Nishikata, A.; Tsuru, T. Electrochemical impedance study on galvanized steel corrosion under cyclic wet–dry conditions-influence of time of wetness. Corros. Sci. 2004, 46, 169–181. [Google Scholar] [CrossRef]
- Yadav, A.P.; Suzuki, F.; Nishikata, A.; Tsuru, T. Investigation of atmospheric corrosion of Zn using ac impedance and differential pressure meter. Electrochim. Acta 2004, 49, 2725–2729. [Google Scholar] [CrossRef]
- El-Mahdy, G.A.; Nishikata, A.; Tsuru, T. AC impedance study on corrosion of 55% Al–Zn alloy-coated steel under thin electrolyte layers. Corros. Sci. 2000, 42, 1509–1521. [Google Scholar] [CrossRef]
- Dong, J.H.; Chen, W.; Ke, W. Corrosion evolution of steel simulated of SO2 polluted coastal atmospheres, Zairyo Kankyo 2016, C-112, 289–292. Zairyo Kankyo 2016, C-112, 289–292. [Google Scholar]
- Thee, C.; Dong, J.; Ke, W. Corrosion monitoring of weathering steel in a simulated coastal-industrial environment. Int. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2015, 9, 587–593. [Google Scholar]
- Parson, N.; Khamsuk, P.; Sorachot, S.; Khonraeng, W.; Wongpinkaew, K.; Kaewkumsai, S.; Pongsaksawad, W.; Viyanit, E.; Chianpairot, A. Atmospheric corrosion of structural steels in Thailand Tropical Climate. Zairyo Kankyo 2016, C-108, 271–274. [Google Scholar]
- Li, C.; Ma, Y.; Li, Y.; Wang, F. EIS monitoring study of atmospheric corrosion under variable relative. Corros. Sci. 2010, 52, 3677–3686. [Google Scholar] [CrossRef]
- Shitanda, I.; Okumura, A.; Itagaki, M.; Watanabe, K.; Asano, Y. Screen-printed atmospheric corrosion monitoring sensor based on electrochemical impedance spectroscopy. Sens. Actuators B 2009, 139, 292–297. [Google Scholar] [CrossRef]
- Cai, J.P.; Lyon, S.B. A mechanistic study of initial atmospheric corrosion kinetics using electrical resistance sensor. Corros. Sci. 2005, 47, 2956–2973. [Google Scholar] [CrossRef]
- Li, S.; Kim, Y.G.; Jung, S.; Song, H.S.; Lee, S.M. Application of steel thin film electrical resistance sensor for in situ corrosion monitoring. Sens. Actuators B 2007, 120, 368–377. [Google Scholar] [CrossRef]
- He, Y.; Tian, G.; Zhang, H.; Alamain, M.; Simm, A.; Jackson, P. Steel corrosion characterization using pulsed eddy current systems. IEEE Sens. J. 2012, 12, 2113–2120. [Google Scholar] [CrossRef]
- Yasri, M.; Gallee, F.; Lescop, B.; Diler, E.; Thierry, D.; Rioual, S. Passive wireless sensor for atmospheric corrosion monitoring. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP), The Hague, The Netherlands, 6–11 April 2014; pp. 2945–2949. [Google Scholar]
- Lin, A.N.; Saito, R.; Takaya, S.; Miyagawa, T. Determination of Young’s Modulus of Rush-Layer by Bending Experiment; Technical Paper; JCI: Tokyo, Japan, 2013; Volume 35, pp. 1117–1122. [Google Scholar]
- Kasai, N.; Hiroki, M.; Yamada, T.; Kihira, H.; Matsuoka, K.; Kuriyama, Y.; Okazaki, S. Atmospheric corrosion sensor based on strain measurement. Meas. Sci. Technol. 2017, 28, 15106. [Google Scholar] [CrossRef]
- Kasai, N.; Utatsu, K.; Park, S.; Kitsukawa, S.; Sekine, K. Correlation between corrosion rate and AE signal in an acidic environment for mild steel. Corros. Sci. 2009, 51, 1679–1684. [Google Scholar] [CrossRef]

| Positions of Strain Gauges | Active Circuit | Dummy Circuit |
|---|---|---|
| Active Strain Gauge | RAA: Corroded area with bending. Detects signals due to corrosion-induced thinning of test piece. | RAD: Uncorroded without bending. Detects signals without thinning of test piece. |
| Dummy Strain Gauge | RDA: Uncorroded area without bending. Compensates for effects of environmental conditions on RAA. | RDD: Uncorroded area without bending. Compensates for effects of environmental conditions on RAD. |
| Strain Gauge | SG: At the center of corroded area without bending. Measures the strain in the corroded area with commercial strain measurement device. | |
| Parameters of Thickness Reduction | Δy | ΔyA | ΔyW |
|---|---|---|---|
| Thickness (μm) | 177 | 200 | 202 |
| Error (%) | - | 11 | 12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purwasih, N.; Kasai, N.; Okazaki, S.; Kihira, H. Development of Amplifier Circuit by Active-Dummy Method for Atmospheric Corrosion Monitoring in Steel Based on Strain Measurement. Metals 2018, 8, 5. https://doi.org/10.3390/met8010005
Purwasih N, Kasai N, Okazaki S, Kihira H. Development of Amplifier Circuit by Active-Dummy Method for Atmospheric Corrosion Monitoring in Steel Based on Strain Measurement. Metals. 2018; 8(1):5. https://doi.org/10.3390/met8010005
Chicago/Turabian StylePurwasih, Nining, Naoya Kasai, Shinji Okazaki, and Hiroshi Kihira. 2018. "Development of Amplifier Circuit by Active-Dummy Method for Atmospheric Corrosion Monitoring in Steel Based on Strain Measurement" Metals 8, no. 1: 5. https://doi.org/10.3390/met8010005
APA StylePurwasih, N., Kasai, N., Okazaki, S., & Kihira, H. (2018). Development of Amplifier Circuit by Active-Dummy Method for Atmospheric Corrosion Monitoring in Steel Based on Strain Measurement. Metals, 8(1), 5. https://doi.org/10.3390/met8010005






