An Efficient Fluid-Dynamic Analysis to Improve Industrial Quenching Systems
Abstract
:1. Introduction
2. Materials and Methods
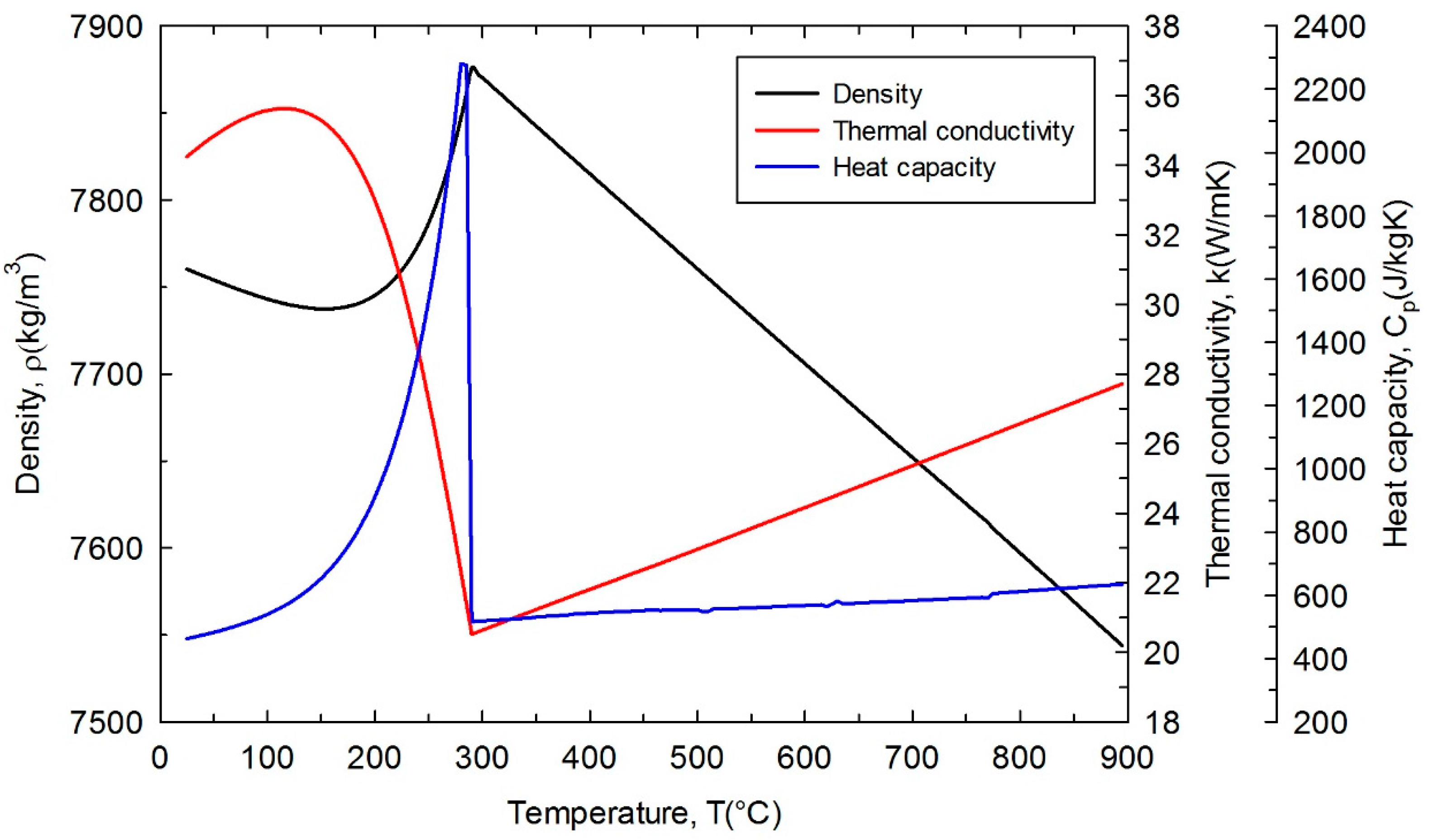
2.1. Materials Properties
2.2. Plant Temperature Measurements
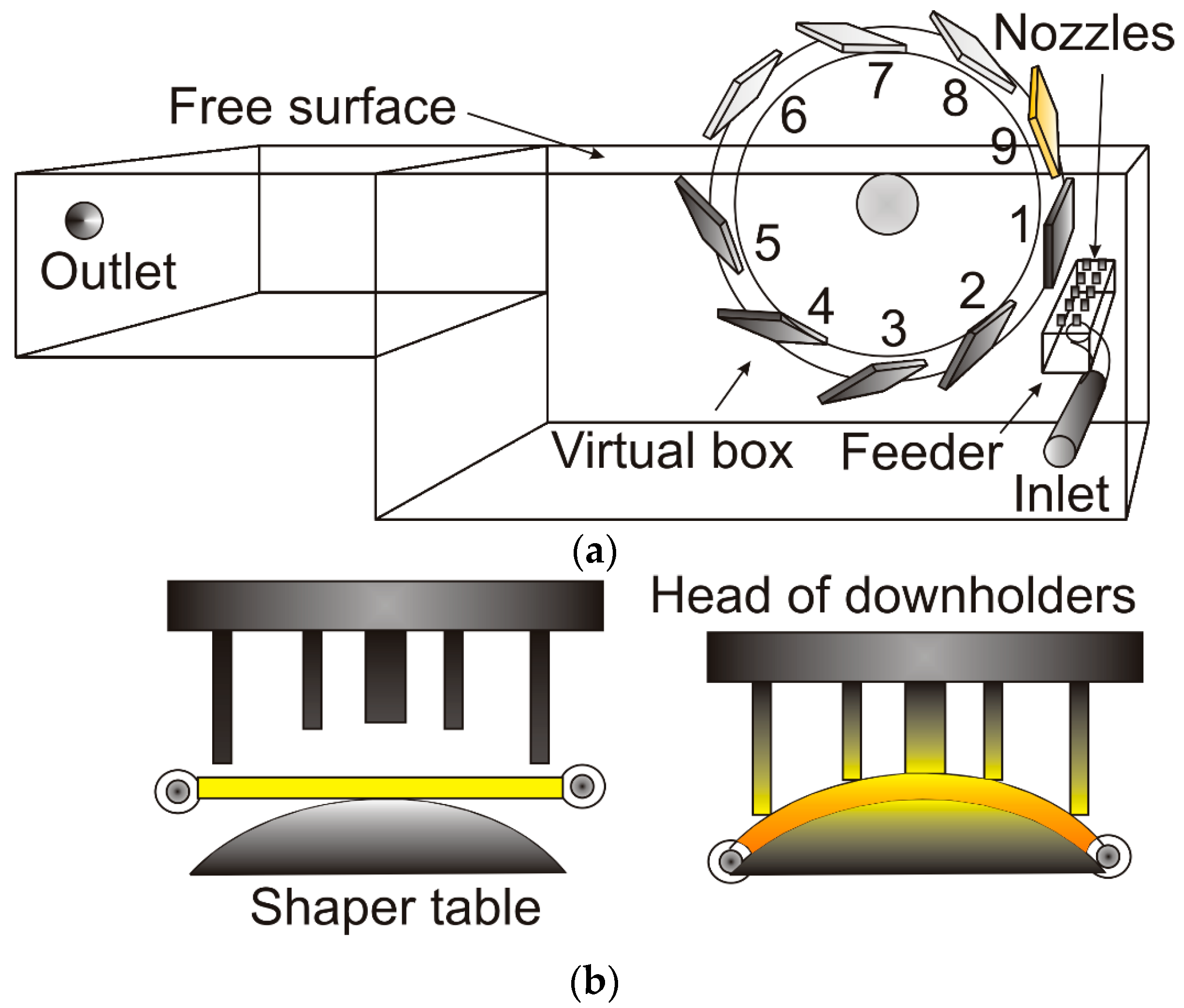
2.2.1. The Quenching System
2.2.2. Diagnostic Thermal Analysis
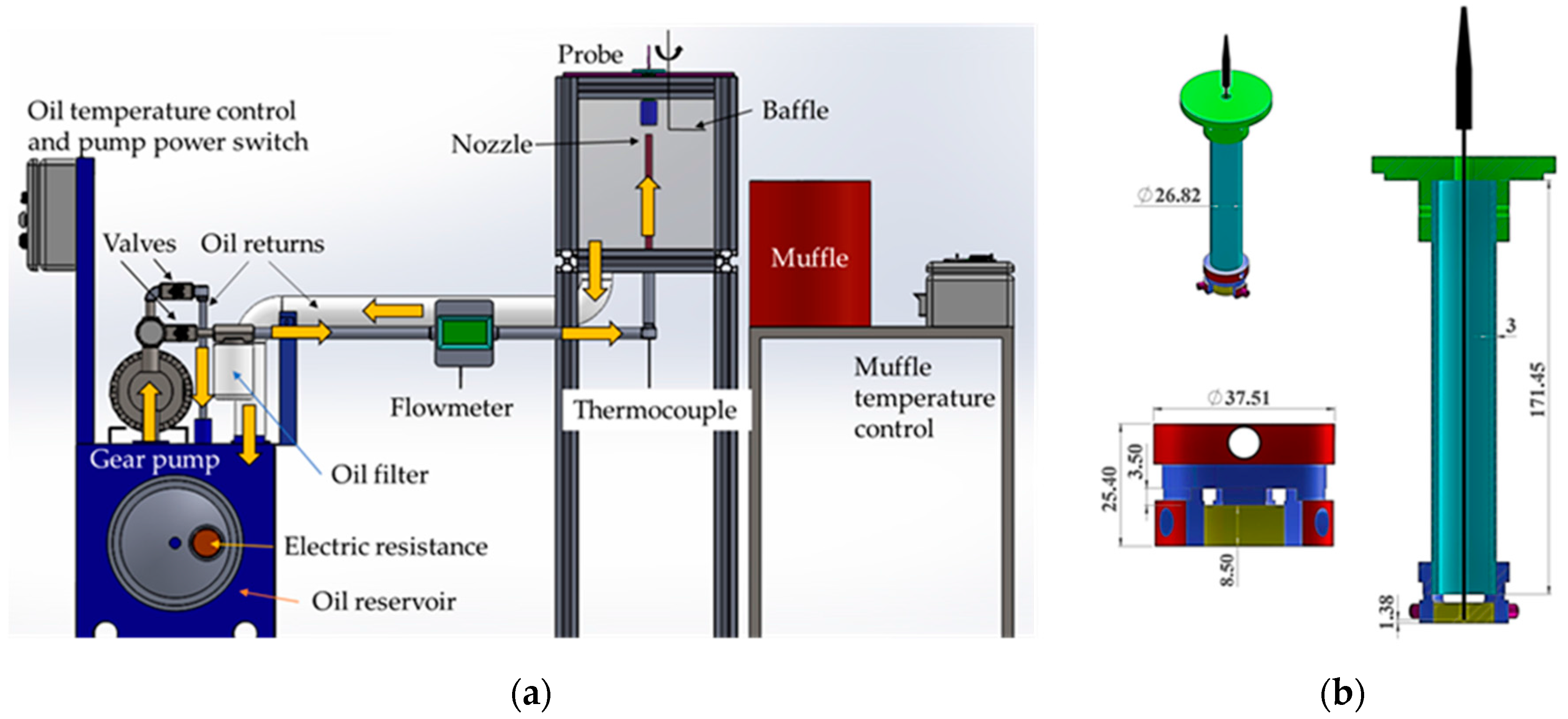
2.3. Laboratory Temperature Measurements
2.4. Connection between Fluid Flow and Heat Transfer
3. Formulation of the Model
3.1. Governing Differential Equations
3.2. Solution Method
4. Results and Discussion
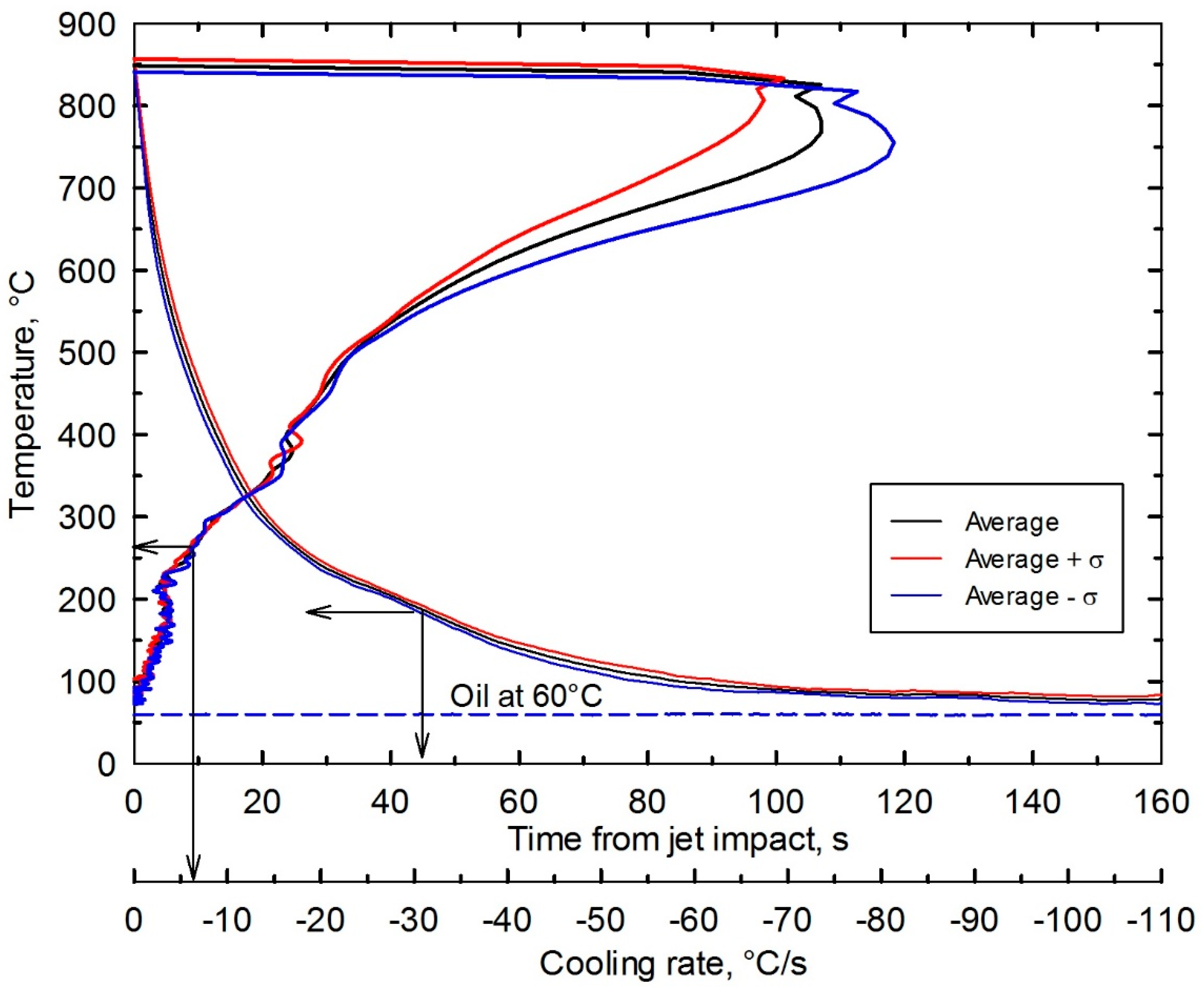
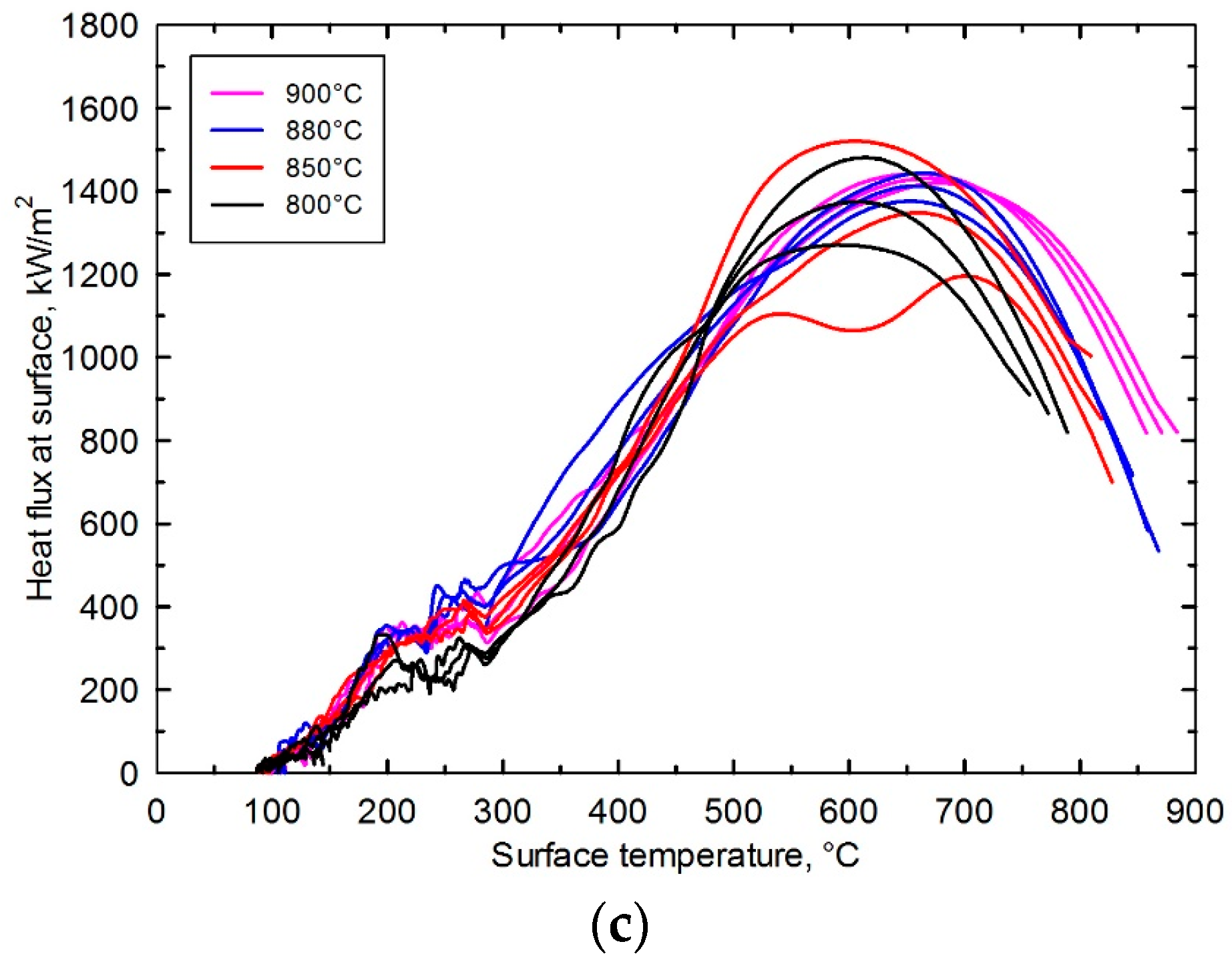
4.1. Laboratory Thermal Analysis
4.2. Plant versus Laboratory Thermal Analyses
4.3. Fluid Flow Analysis
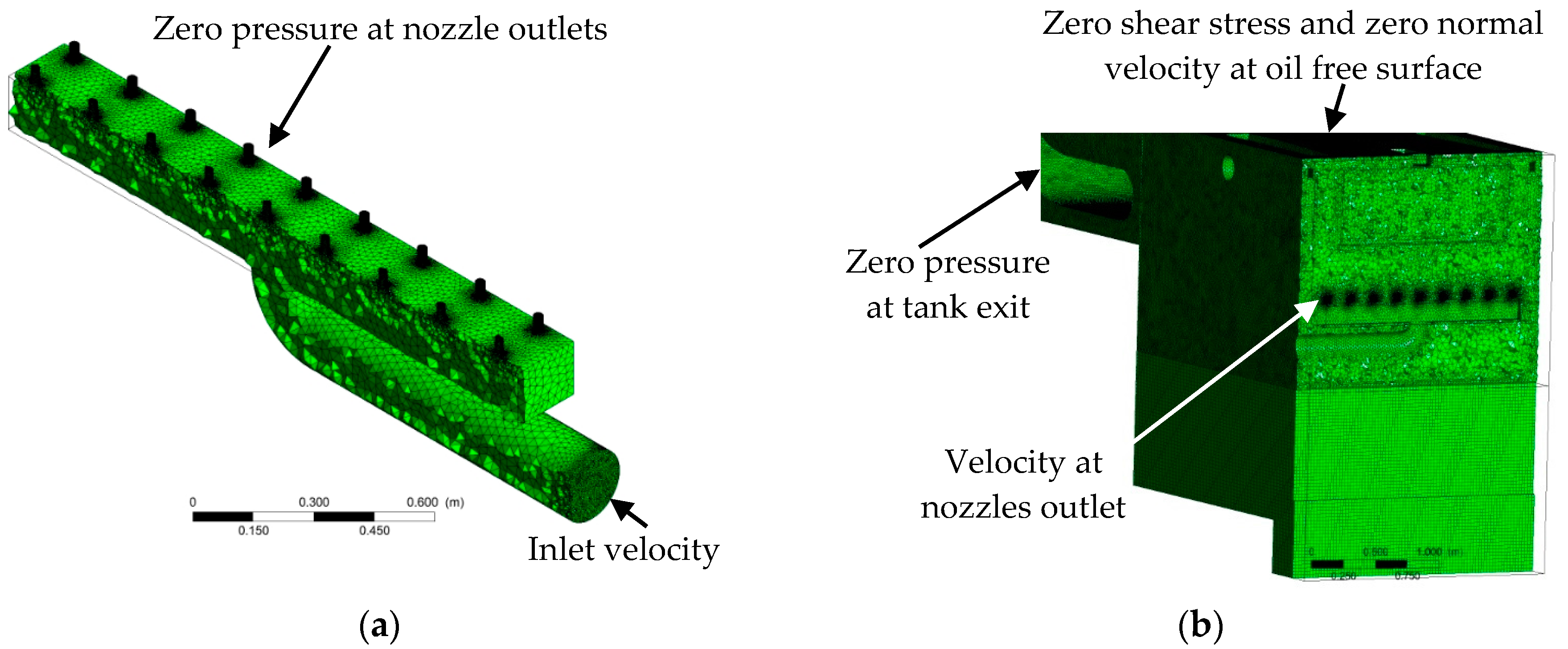
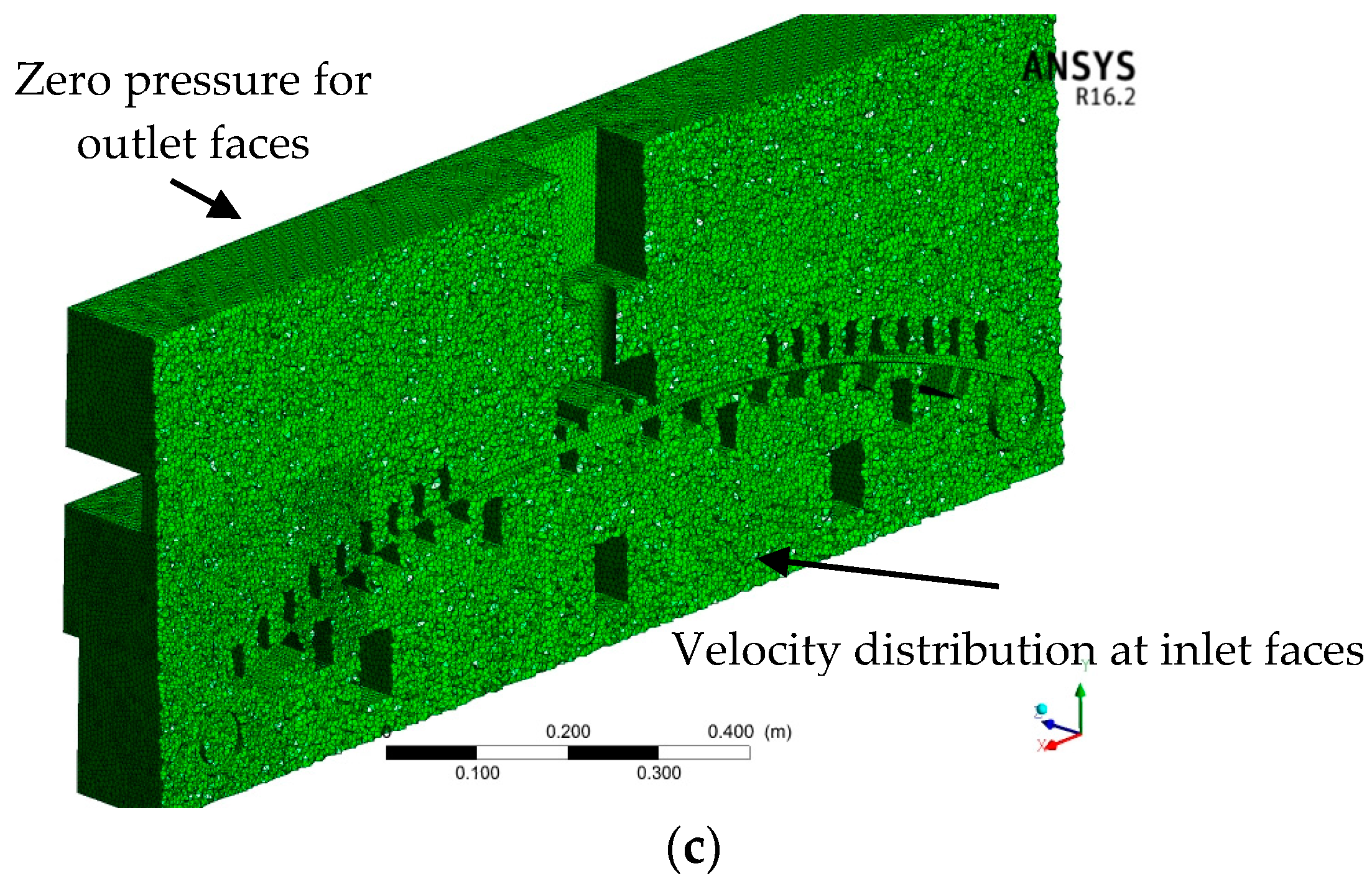
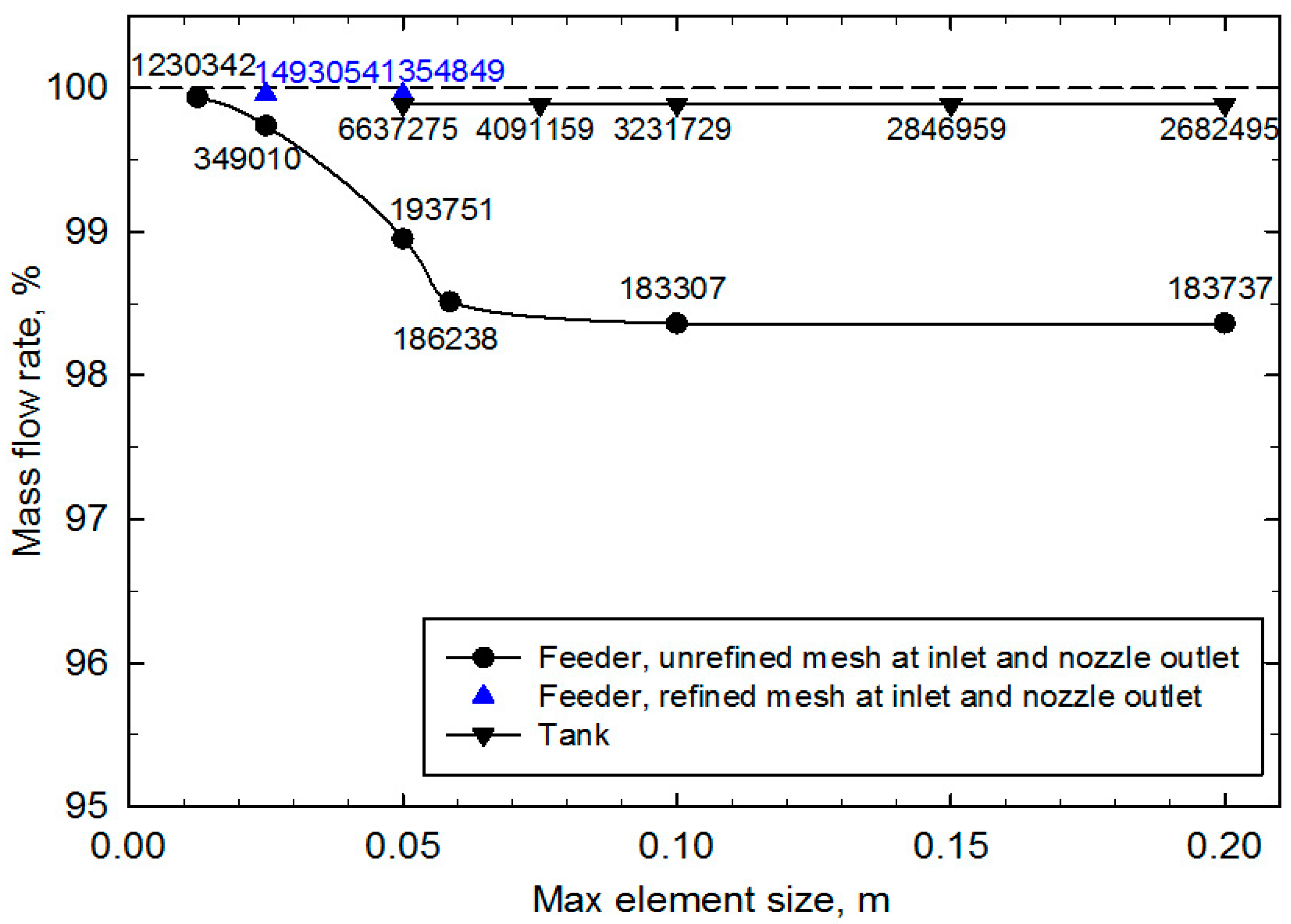
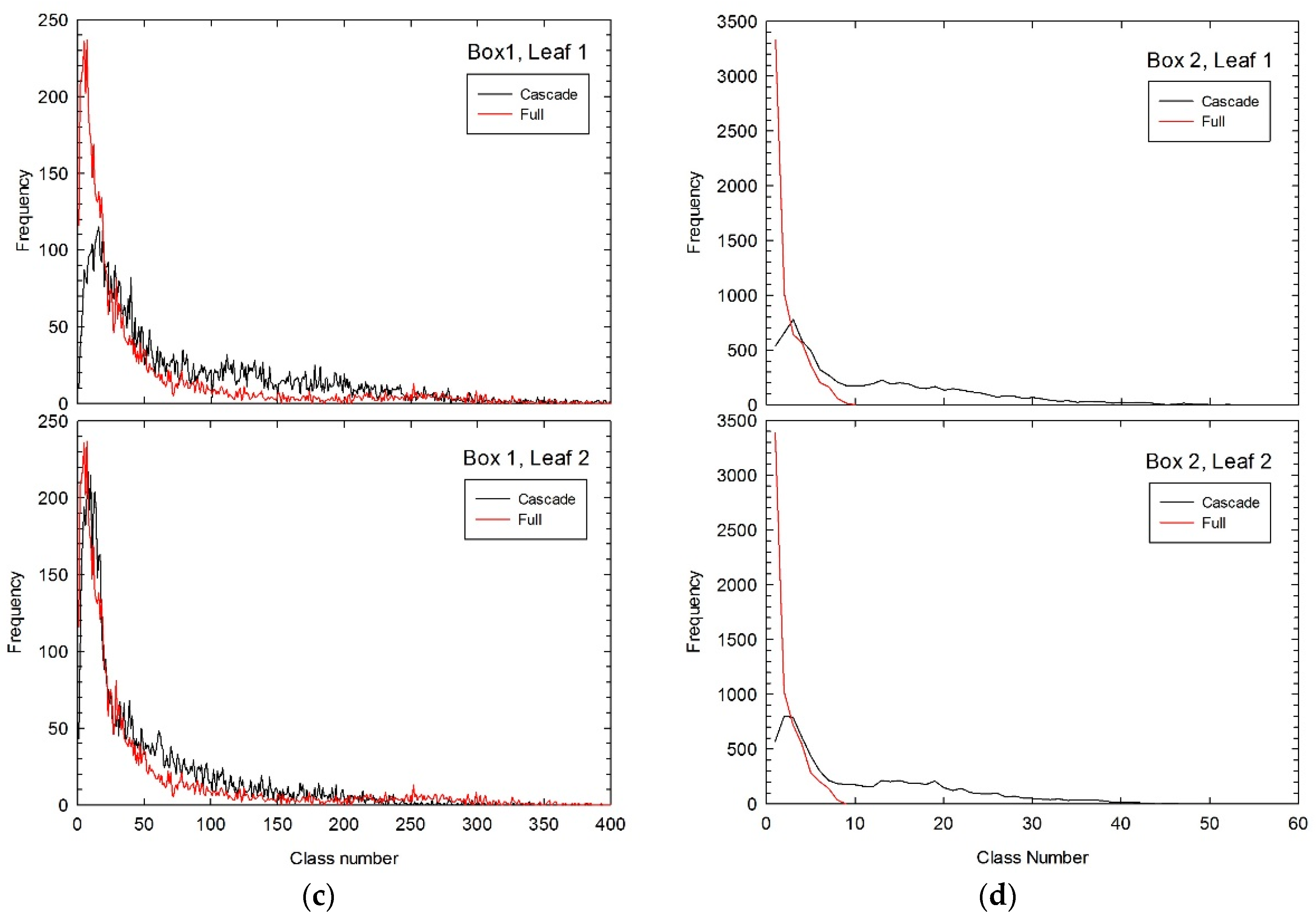
4.3.1. Mesh Quality
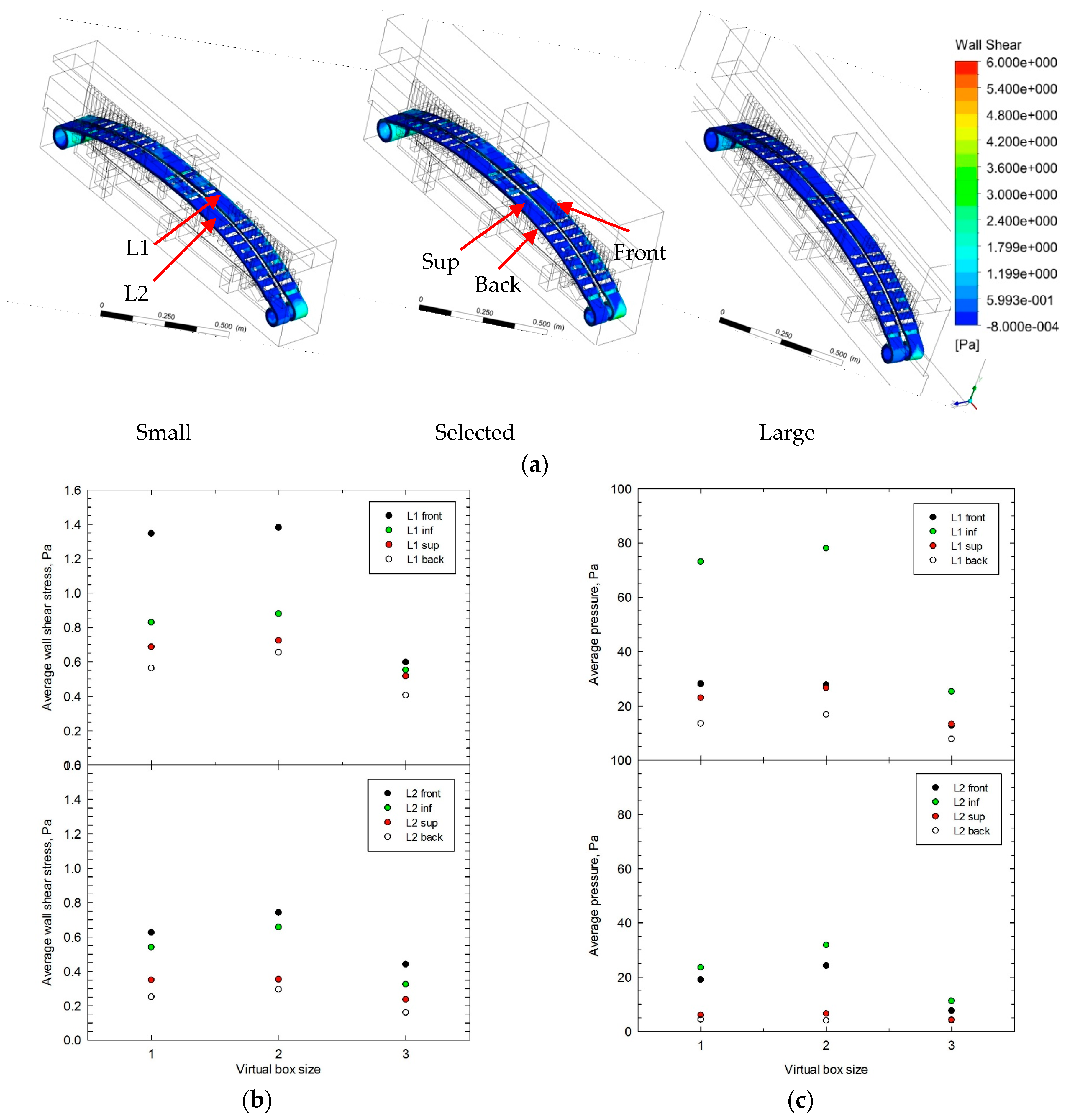
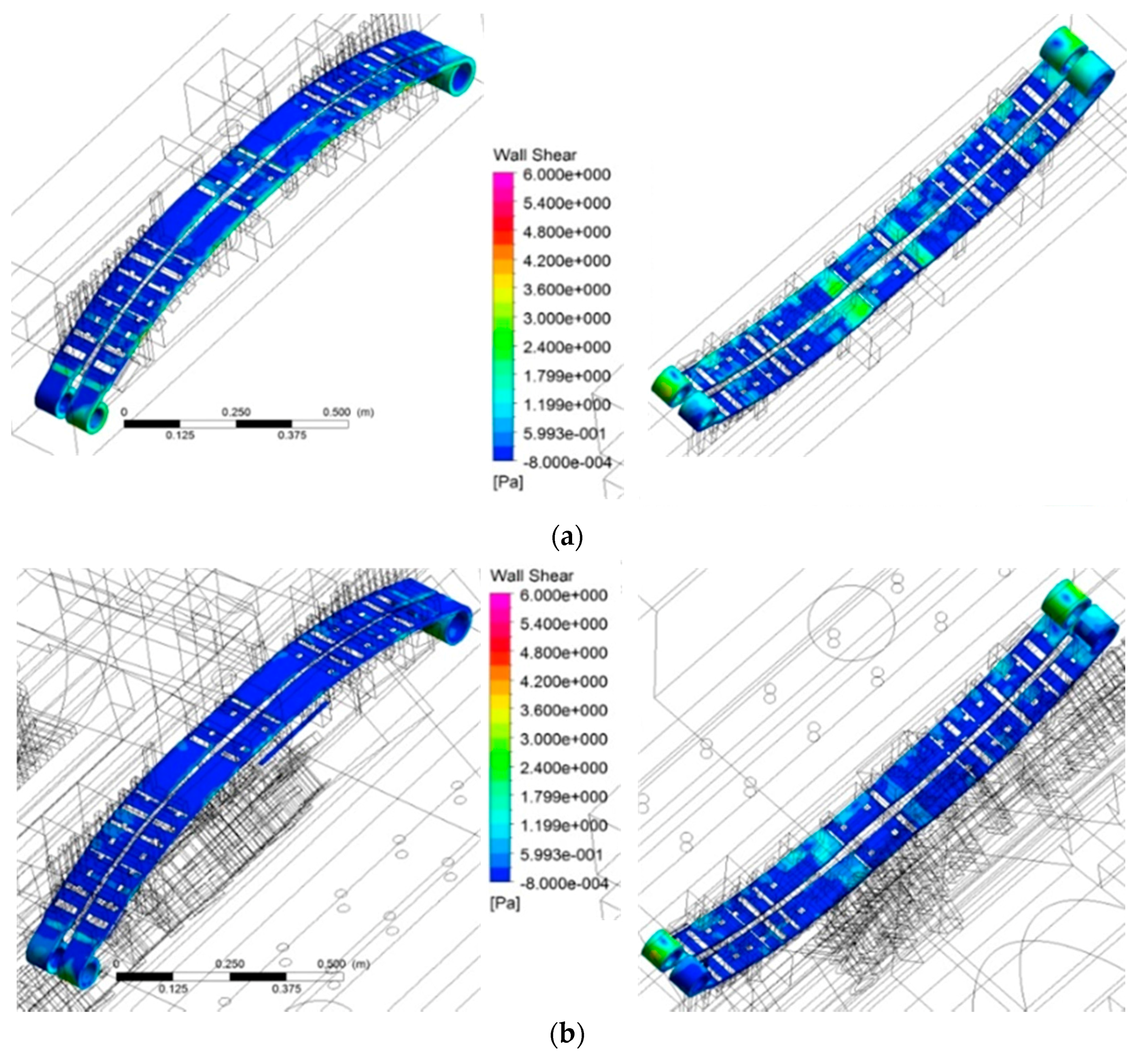
4.3.2. Choice of Virtual Box Size
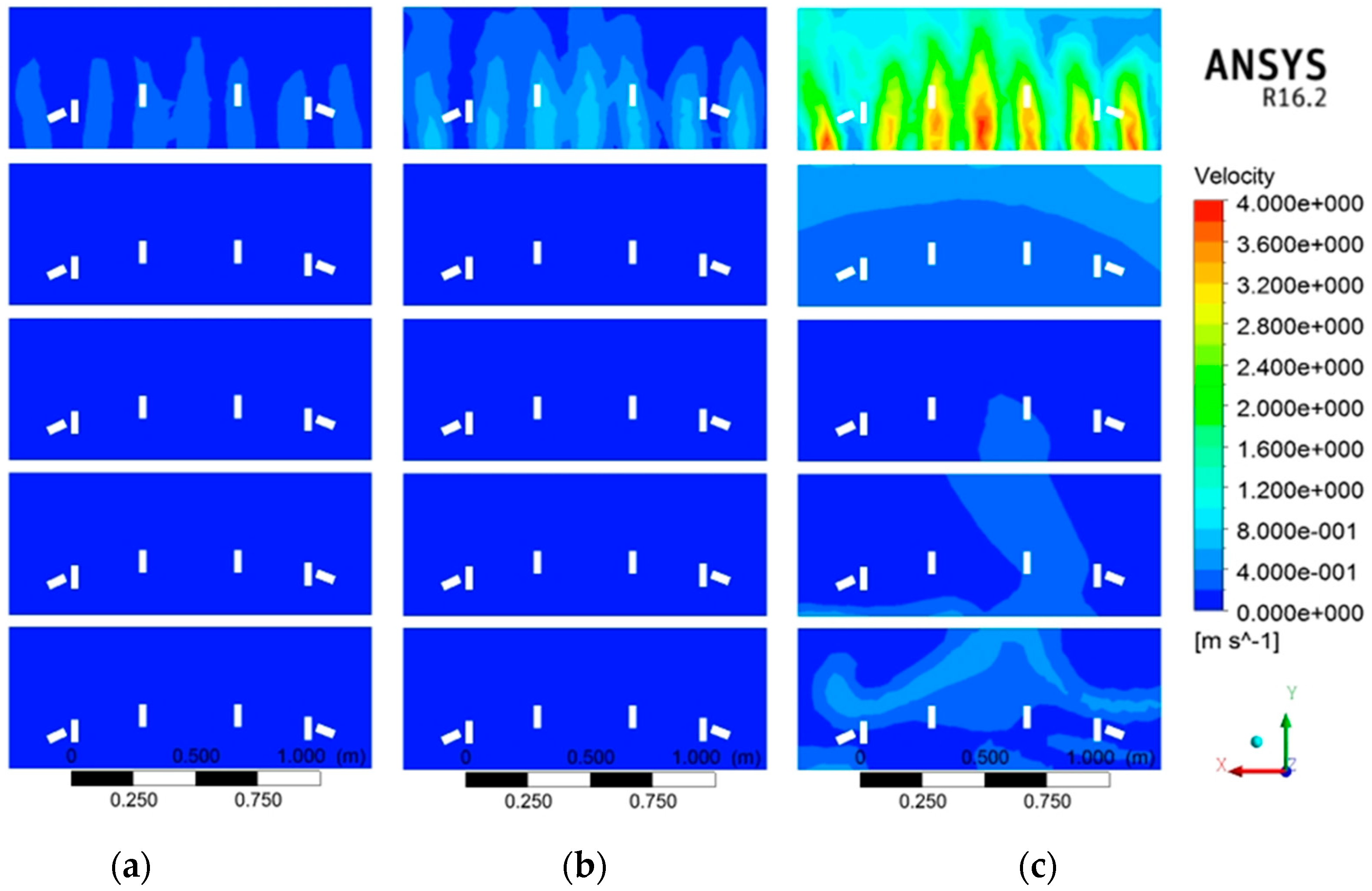
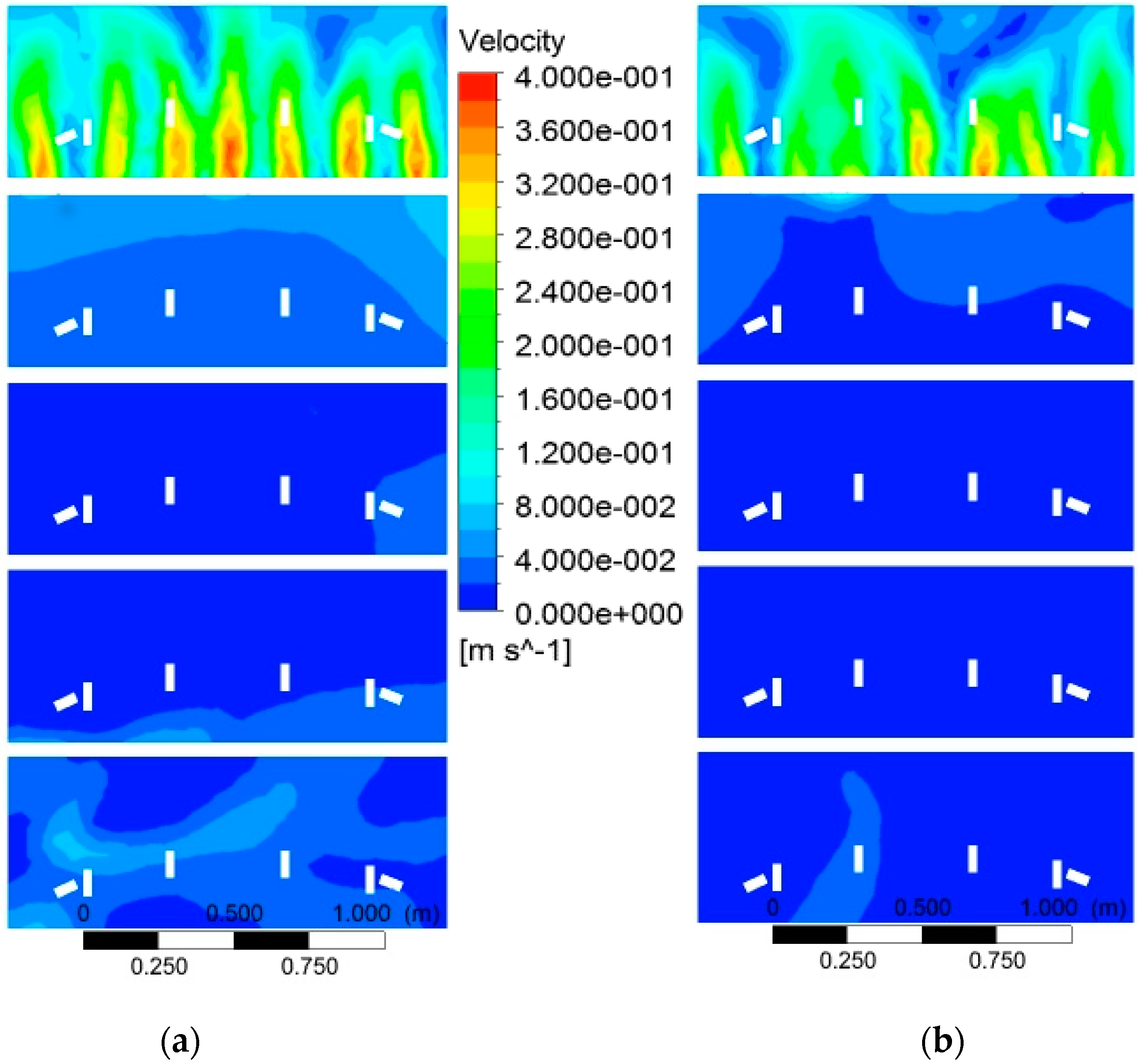
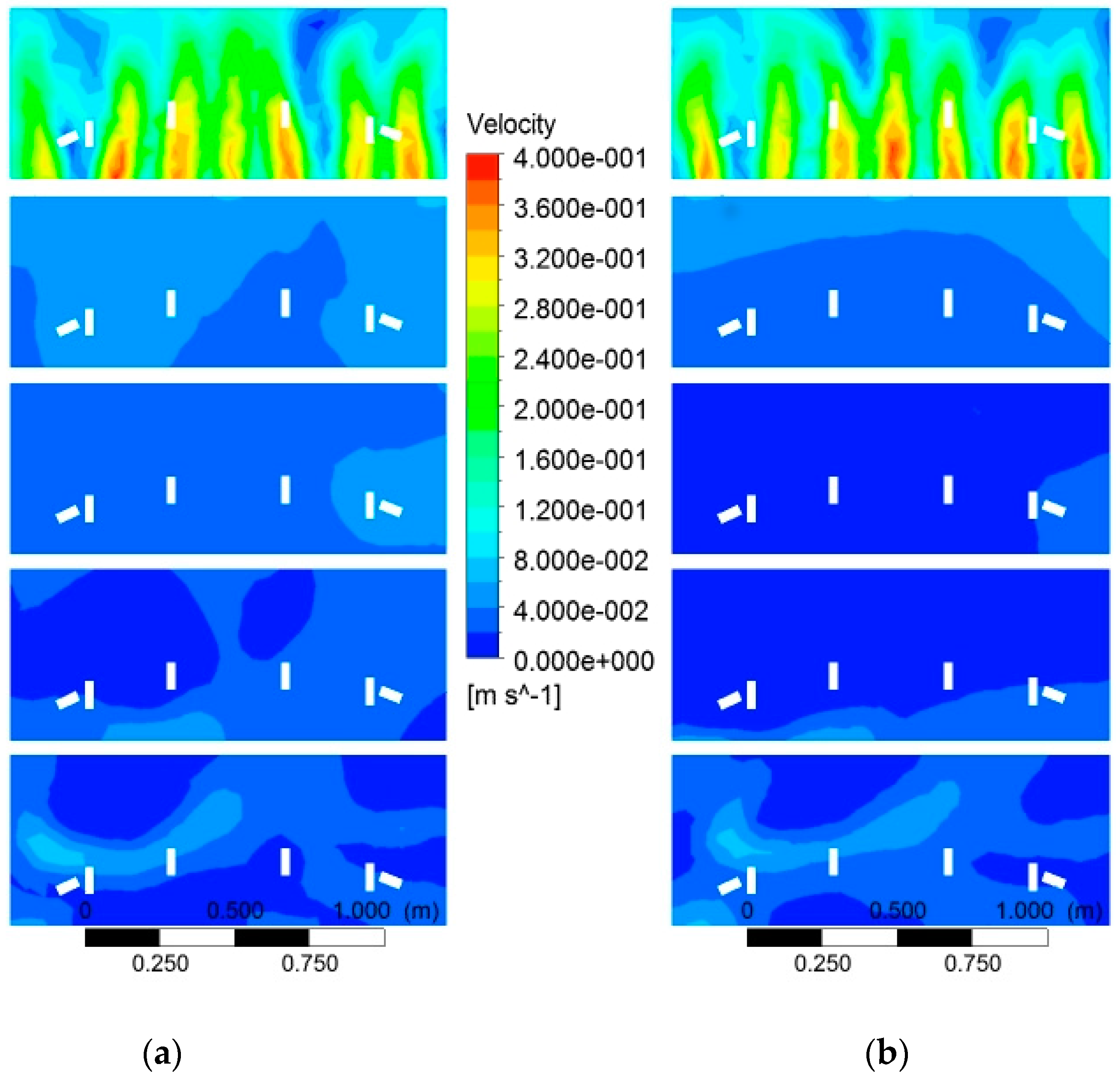
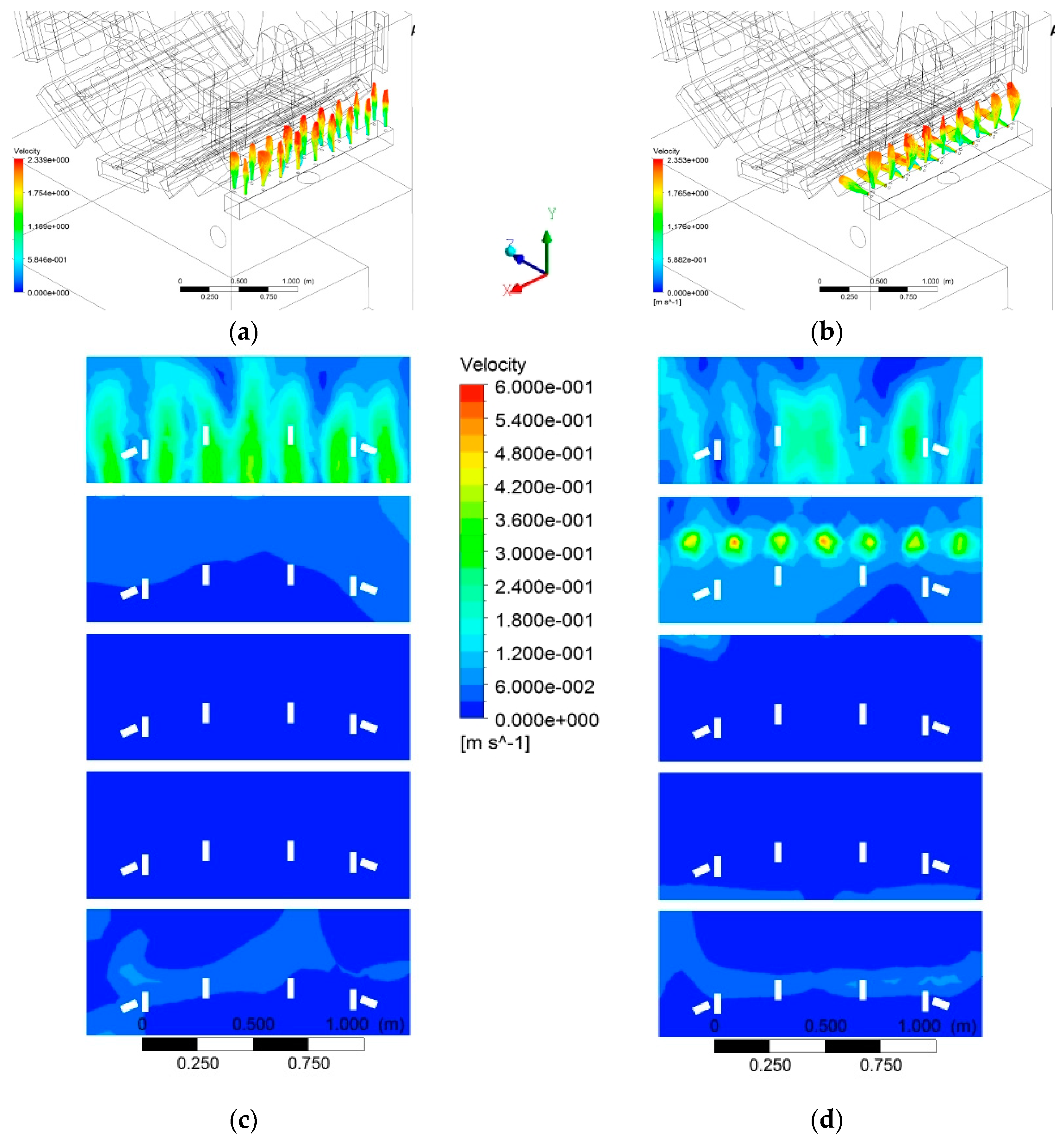
4.3.3. Fluid Flow Maps for Original Case
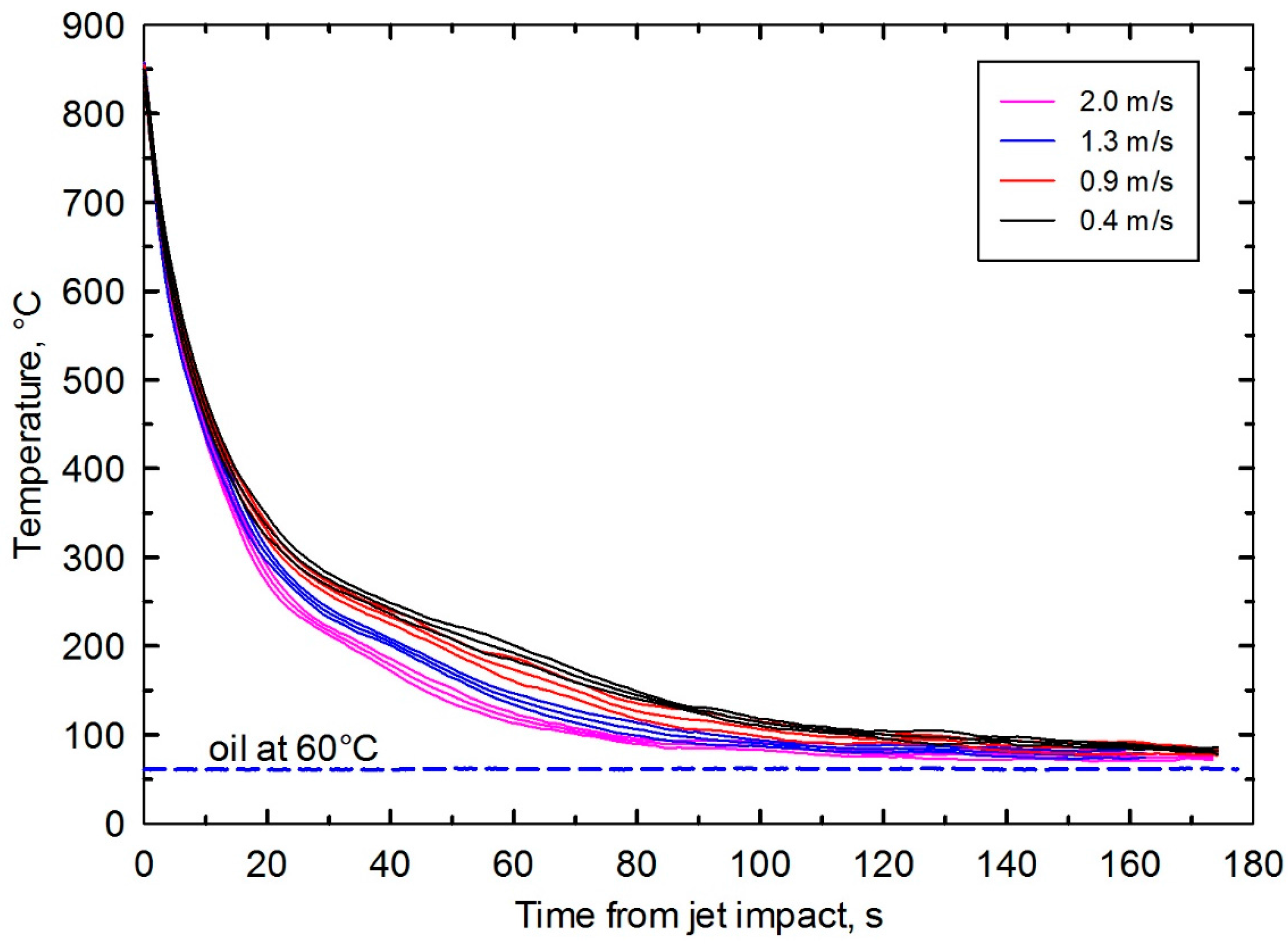
4.3.4. Effect of Oil Flowrate
4.3.5. Effect of Baffles at Carousel Periphery
4.3.6. Effect of Tank Depth
4.3.7. Effect of Nozzle Direction
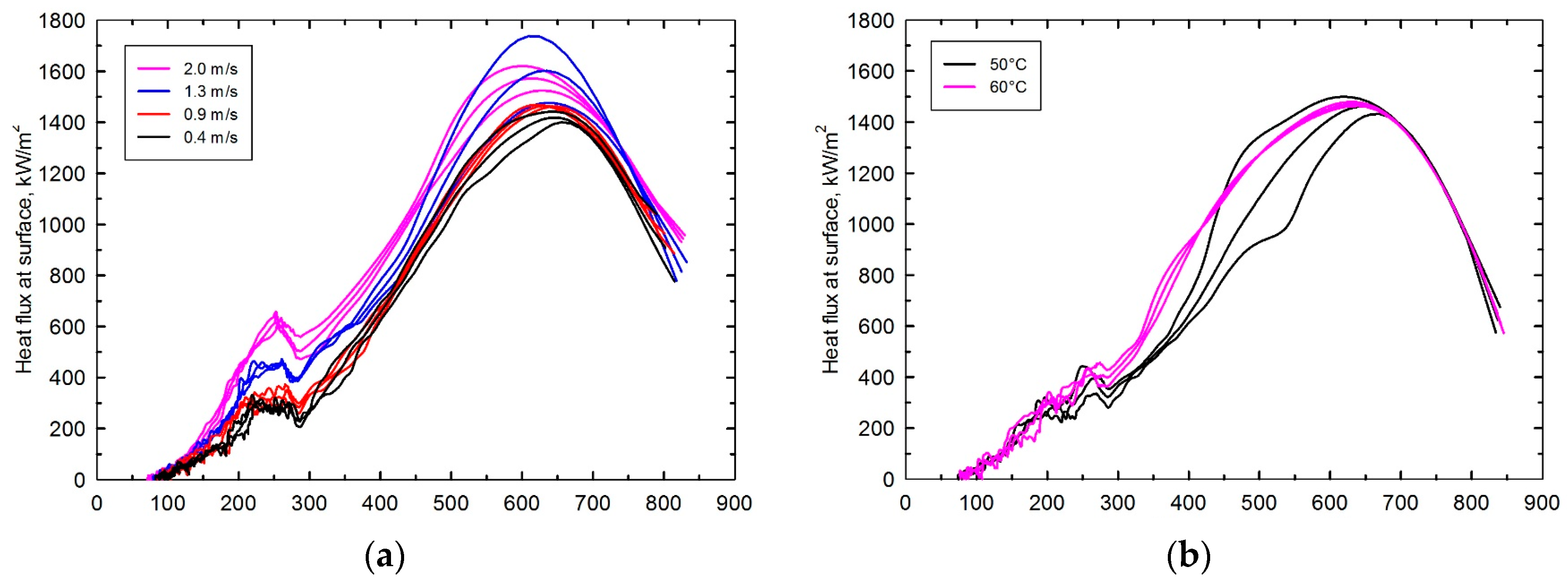
4.4. Isothermal Fluid Flow and Heat Flux
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Canale, L.D.C.F.; Totten, G.E. Quenching technology: A selected overview of the current state-of-the-art. Mater. Res. 2005, 8, 461–467. [Google Scholar] [CrossRef]
- Totten, G.E. Quench Process Sensors. In ASM Handbook; Dossett, J., Totten, G.E., Eds.; ASM International: Materials Park, OH, USA, 2013; pp. 192–197. [Google Scholar]
- Gür, C.H.; Şimşir, C. Simulation of quenching: A review. Mater. Perform. Charact. 2012, 1, 1–37. [Google Scholar] [CrossRef]
- Totten, G.E.; Bates, C.E.; Clinton, N.A. Handbook of Quenchants and Quenching Technology; ASM International: Materials Park, OH, USA, 1993; pp. 339–411. [Google Scholar]
- Garwood, D.R.; Lucas, J.D.; Wallis, R.A.; Ward, J. Modeling of the flow distribution in an oil quench tank. J. Mater. Eng. Perform. 1992, 1, 781–787. [Google Scholar] [CrossRef]
- Halva, J.; Volný, J. Modeling the flow in a quench bath. Hut. Listy 1993, 48, 30–34. [Google Scholar]
- Bogh, N. Quench Tank Agitation Design Using Flow Modeling. In Proceedings of the International Heat Treating Conference: Equipment and Processes, Schaumburg, IL, USA, 18–20 April 1994; Totten, G.E., Wallis, R.A., Eds.; ASM International: Materials Park, OH, USA, 1994; pp. 51–54. [Google Scholar]
- Kernazhitskiy, S.L. Numerical Modeling of a Flow in a Quench Tank. Master’s Thesis, Portland State University, Portland, OR, USA, 2003. [Google Scholar]
- Kumar, A.; Metwally, H.; Paingankar, S.; MacKenzie, D.S. Evaluation of Flow Uniformity around Automotive Pinion Gears during Quenching. In Proceedings of the 5th International Conference on Quenching and Control Distortion at 2007 European Conference on Heat Treatment, Berlin, Germany, 25–27 April 2007; International Federation for Heat Treatment and Surface Engineering: Berlin, Germany, 2007; pp. 1–8. [Google Scholar]
- Romão-Bineli, A.R.; Rocha-Barbosa, M.I.; Luiz-Jardini, A.; Maciel-Filho, R. Simulation to Analyze Two Models of Agitation System in Quench Process. In Proceedings of the 20th European Symposium on Computer Aided Process Engineering, Naples, Italy, 6–9 June 2010; Pierucci, S., Ferraris, G.B., Eds.; Elsevier B.V.: Naples, Italy, 2010; pp. 1–6. [Google Scholar]
- Krause, F.; Schüttenberg, S.; Fritsching, U. Modelling and simulation of flow boiling heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 312–331. [Google Scholar] [CrossRef]
- Srinivasan, V.; Moon, K.-M.; Greif, D.; Wang, D.; Kim, M.-H. Numerical simulation of immersion quench cooling process using an Eulerian multi-fluid approach. Appl. Therm. Eng. 2010, 30, 499–509. [Google Scholar] [CrossRef]
- Gao, W.-M.; Fabijanic, D.; Hilditch, T.; Kong, L.-X. Integrated fluid-thermal-structural numerical analysis for the quenching of metallic components. J. Shanghai Jiaotong Univ. Sci. 2011, 16, 137–140. [Google Scholar] [CrossRef]
- Ricci, M.G.; Santin, G.; Cascariglia, F.; Scimiterna, E.; Parrabbi, A.; Carpinelli, A. Numerical analysis applied to thermal and fluid-dynamic quenching simulation of large high quality forgings. La Metall. Italiana 2011, 9, 3–10. [Google Scholar]
- El Kosseifi, N. Numerical Simulation of Boiling for Industrial Quenching Processes. Ph.D. Thesis, Paris National School of Mines, Paris, France, 2012. [Google Scholar]
- Ko, D.-H.; Ko, D.-C.; Lim, H.-J.; Kim, B.-M. Application of QFA coupled with CFD analysis to predict the hardness of T6 heat treated A16061 cylinder. J. Mech. Sci. Technol. 2013, 27, 2839–2844. [Google Scholar] [CrossRef]
- Kopun, R.; Škerget, L.; Hriberšek, M.; Zhang, D.; Edelbauer, W. Numerical investigations of quenching cooling processes for different cast aluminum parts. J. Mech. Eng. 2014, 60, 571–580. [Google Scholar] [CrossRef]
- Passarella, D.N.; L-Cancelos, R.; Vieitez, I.; Varas, F.; Martín, E.B. Thermo-fluid-dynamics quenching model: Effect on material properties. Blutcher Mech. Eng. 2012, 1, 3625–3644. [Google Scholar]
- Yang, X.-W.; Zhu, J.-C.; He, D.; Lai, Z.-H.; Nong, Z.-S.; Liu, Y. Optimum design of flow distribution in quenching tank for heat treatment of A357 aluminum alloy large complicated thin-wall workpieces by CFD simulation and ANN approach. Trans. Nonferr. Met. Soc. China 2013, 23, 1442–1451. [Google Scholar] [CrossRef]
- Banka, A.L.; Ferguson, B.L.; MacKenzie, D.S. Evaluation of flow fields and orientation effects around ring geometries during quenching. J. Mater. Eng. Perform. 2013, 22, 1816–1825. [Google Scholar] [CrossRef]
- López-García, R.D.; García-Pastor, F.A.; Castro-Román, M.J.; Alfaro-López, E.; Acosta-González, F.A. Effect of immersion routes on the quenching distortion of a long steel component using a finite element model. Trans. Indian Inst. Met. 2016, 69, 1645–1656. [Google Scholar] [CrossRef]
- Standard Test Methods for Determining Hardenability of Steel; ASTM International: West Conshohocken, PA, USA, 2007; pp. 18–26.
- The Reynolds Analogy. Available online: http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node122.html (accessed on 20 March 2017).
- Ansys Fluent Theory Guide, Release 15.0; ANSYS, Inc.: Canonsburg, PA, USA, 2013; pp. 39–55.
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy-viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Kim, S.-E.; Choudhury, D.; Patel, B. Computations of Complex Turbulent Flows Using the Commercial Code ANSYS Fluent. In Proceedings of the ICASE/LaRC/AFOSR Symposium on Modeling Complex Turbulent Flows, Hampton, VA, USA, 11–13 August 1997. [Google Scholar]
- Ansys Fluent User’s Guide. Release 12.0; ANSYS, Inc.: Canonsburg, PA, USA, 2009; pp. 7-128–7-130.
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Beck, J.V. User’s Manual for CONTA: Program for Calculating Surface Heat Fluxes from Transient Temperatures Inside Solids; Michigan State University: East Lansing, MI, USA, 1983. [Google Scholar]
- Liscic, B.; Tensi, H.M.; Canale, L.C.F.; Totten, G.E. Quenching Theory and Technology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Lienhard IV, J.H.; Lienhard V, J.H. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2001; pp. 436–445. [Google Scholar]
- Bradshaw, P.; Love, E.M. The Normal Impingement of a Circular Air Jet on a Flat Surface; Her Majesty’s Stationary Office: London, UK, 1959; pp. 1–8. [Google Scholar]



| Author (s), Year | CFD | Heat Conduction | Solid-Phase Transformation | Residual Stress and Distortion |
|---|---|---|---|---|
| Totten et al., 1993 | Isothermal fluid flow | - | - | - |
| Garwood et al., 1992 | - | - | - | |
| Halva and Volny, 1993 | - | - | - | |
| Bogh, 1994 | - | - | - | |
| Kernazhitskiy, 2003 | - | - | - | |
| Kumar et al., 2007 | - | - | - | |
| R.-Bineli et al., 2010 | Non-isothermal but no-boiling flow | Non-isothermal solid | - | - |
| Krause et al., 2010 | Mixed fluids | Isothermal and non-isothermal solids | - | - |
| Srinivasan et al., 2010 | Non-isothermal solid | - | - | |
| Gao et al., 2011 | yes | yes | ||
| Ricci et al., 2011 | Computed interface, VOF | yes | - | |
| El-Kosseifi, 2012 | Computed interface, LS | Non-isothermal solid | - | - |
| Yang et al., 2013 | Isothermal flow | - | - | - |
| Banka et al., 2013 | Non-isothermal solid | yes | yes | |
| Ko et al., 2013 | Mixed fluids | Non-isothermal solid | - | Hardness prediction using Quenching Factor Analysis (QFA) |
| Kopun et al., 2014 | - | - | ||
| Passarella et al., 2014 | yes | yes |
| Chemical Composition | C | Si | Mn | P | S | Cr | V | Sum of Others 1 |
|---|---|---|---|---|---|---|---|---|
| Mass % | 0.50 | 0.24 | 0.97 | 0.04 | 0.008 | 1.04 | 0.14 | <0.281 |
| Material | kt (W/m·K) | ρ (kg/m3) | Cp (J/kg·K) | μ (mPa·s) | Tsat (°C) | Ms (°C) | M50 (°C) | M90 (°C) |
|---|---|---|---|---|---|---|---|---|
| Steel: 51CrV4 | k(T) | ρ(T) | Cp(T) | - | - | 288 | 251 | 166 |
| Oil: FTR (Equiquench 770) Houghto-Quench® | - | 827 at 60 °C | - | 7.3 at 60 °C | 290 | - | - | - |
| Tank Component | Length (m) | Width (m) | Height (m) | Diameter (m) |
|---|---|---|---|---|
| Feeder, tube | - | - | - | 0.197 |
| Feeder, hexahedron | 1.78 | 0.20 | 0.16 | - |
| Nozzle | 0.045 | - | - | 0.0254 |
| Tank (main body) | 2.96 | 2.11 | 2.74 | - |
| Virtual box | 0.22 (thickness) | 1.46 | 0.57 | - |
| Tank exit orifice | - | - | - | 0.250 |
| Initial Temperature TI (°C) | Impact Velocity VI (m/s) | Oil Temperature Tf (°C) |
|---|---|---|
| 800 | 0.9 | 60 |
| 850 | ||
| 880 | ||
| 900 | ||
| 850 | 0.4 | 60 |
| 0.9 | ||
| 1.3 | ||
| 2.0 | ||
| 850 | 0.9 | 50 |
| 60 |
| C1 | C2 | G | η | S | Sij | σk | σε |
|---|---|---|---|---|---|---|---|
| 1.9 | 1 | 1.2 |
| Case | Characteristics |
|---|---|
| Original | Feeder with two rows of nozzles pointing upward. Oil average velocity at feeder tube, 0.5 m/s. |
| Higher flowrate | Original feeder. Oil average velocity at feeder tube, 1 and 5 m/s. |
| Baffles installed around carousel | Original feeder and oil velocity at feeder tube, 0.5 m/s. |
| Shallow tank | Original feeder and oil velocity at feeder tube, 0.5 m/s. Depth of tank in carousel area, 1.73 m. |
| Nozzle rows at 90° | Feeder with nozzle rows at 90° from each other. Oil average velocity at feeder tube, 0.5 m/s. |
| Subdomain | Millions of Elements | Running Time—“Cascade” (h) | Millions of Elements | Running Time—Full System (h) |
|---|---|---|---|---|
| Feeder | 1.4 | 1.1 | 48.6 | 168 |
| Tank | 6.6 | 12.2 | ||
| Box 1 | 3.4 | 1.9 | ||
| Box 2 | 3.4 | 1.4 | ||
| Box 3 | 3.4 | 1.6 | ||
| Box 4 | 3.4 | 1.7 | ||
| Box 5 | 3.4 | 1.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrena-Rodríguez, M.D.J.; González-Melo, M.A.; Acosta-González, F.A.; Alfaro-López, E.; García-Pastor, F.A. An Efficient Fluid-Dynamic Analysis to Improve Industrial Quenching Systems. Metals 2017, 7, 190. https://doi.org/10.3390/met7060190
Barrena-Rodríguez MDJ, González-Melo MA, Acosta-González FA, Alfaro-López E, García-Pastor FA. An Efficient Fluid-Dynamic Analysis to Improve Industrial Quenching Systems. Metals. 2017; 7(6):190. https://doi.org/10.3390/met7060190
Chicago/Turabian StyleBarrena-Rodríguez, Manuel De J., Marco A. González-Melo, Francisco A. Acosta-González, Eddy Alfaro-López, and Francisco A. García-Pastor. 2017. "An Efficient Fluid-Dynamic Analysis to Improve Industrial Quenching Systems" Metals 7, no. 6: 190. https://doi.org/10.3390/met7060190
APA StyleBarrena-Rodríguez, M. D. J., González-Melo, M. A., Acosta-González, F. A., Alfaro-López, E., & García-Pastor, F. A. (2017). An Efficient Fluid-Dynamic Analysis to Improve Industrial Quenching Systems. Metals, 7(6), 190. https://doi.org/10.3390/met7060190






