A Phase Field Model for Rate-Dependent Ductile Fracture
Abstract
:1. Introduction
2. Formulation
2.1. Viscoplastic Model
2.2. Phase Field Approximation of a Crack
2.3. Phase Field Model for Brittle Fracture
2.4. Phase Field Model for Rate-Dependent Ductile Fracture
2.5. Integration Algorithm
- (1)
- Elastic predictor:
- (2)
- Check for viscoplastic flow:
- (3)
- Viscoplastic return mapping. Solve return mapping equation for in iterative form:
- (4)
- By at hand, update state variables:
- (5)
- Exit
2.6. Finite Element Implementation
3. Results and Discussion
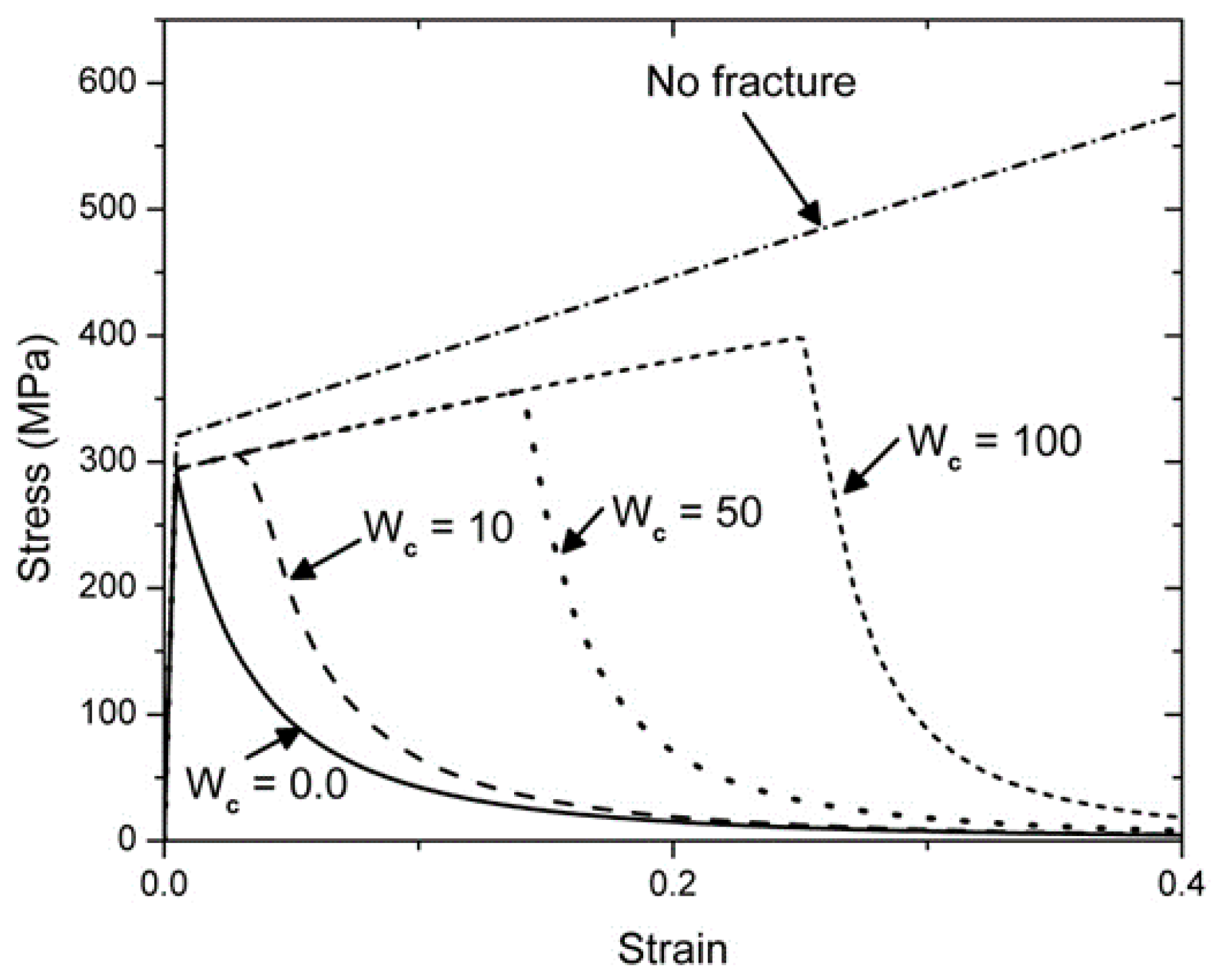
3.1. One-Dimensional Simulations
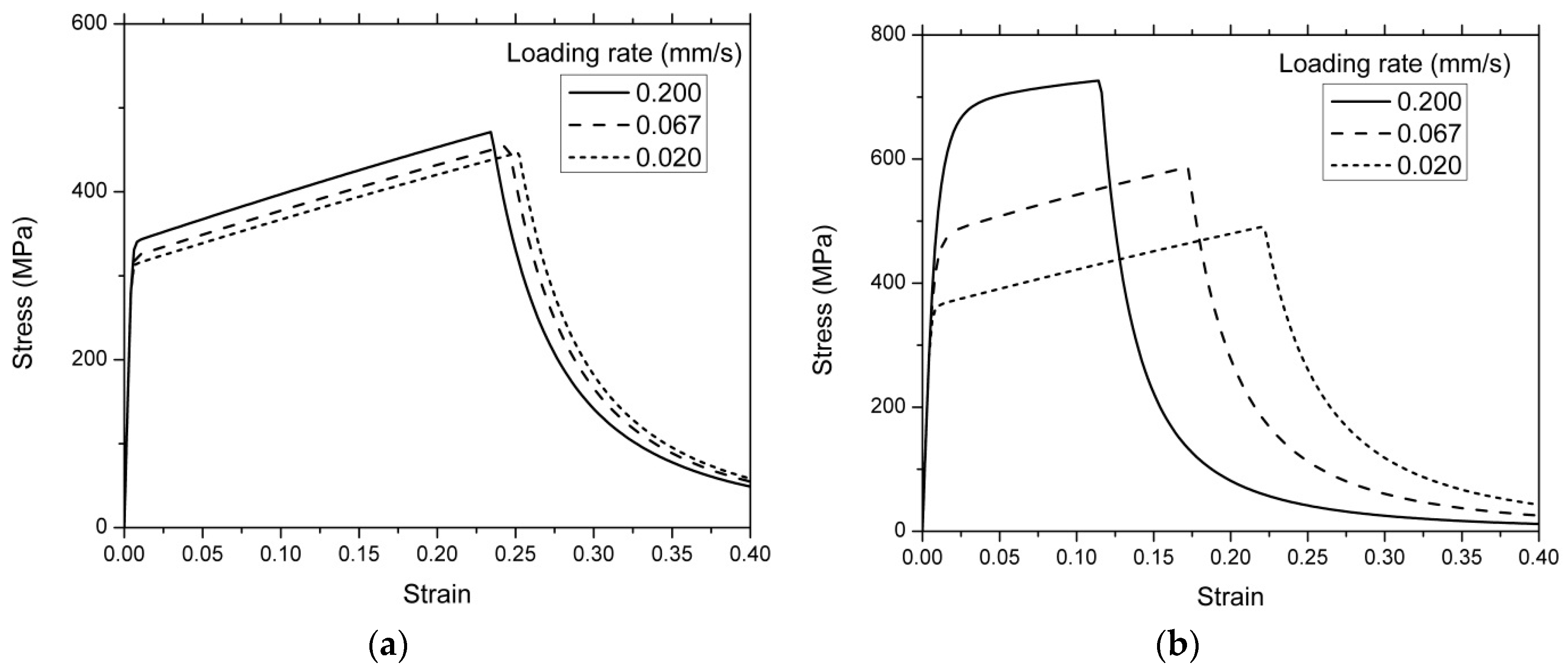
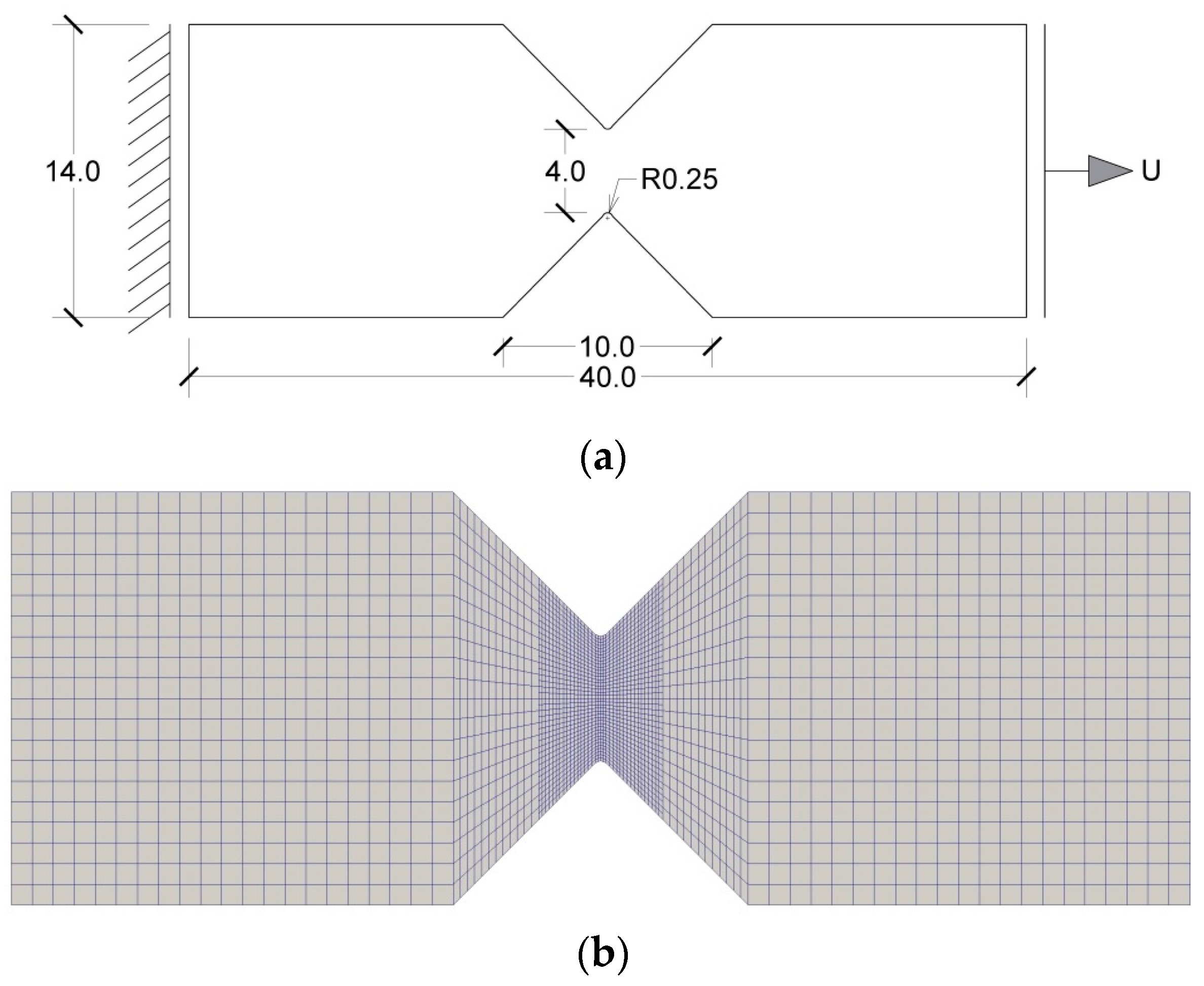
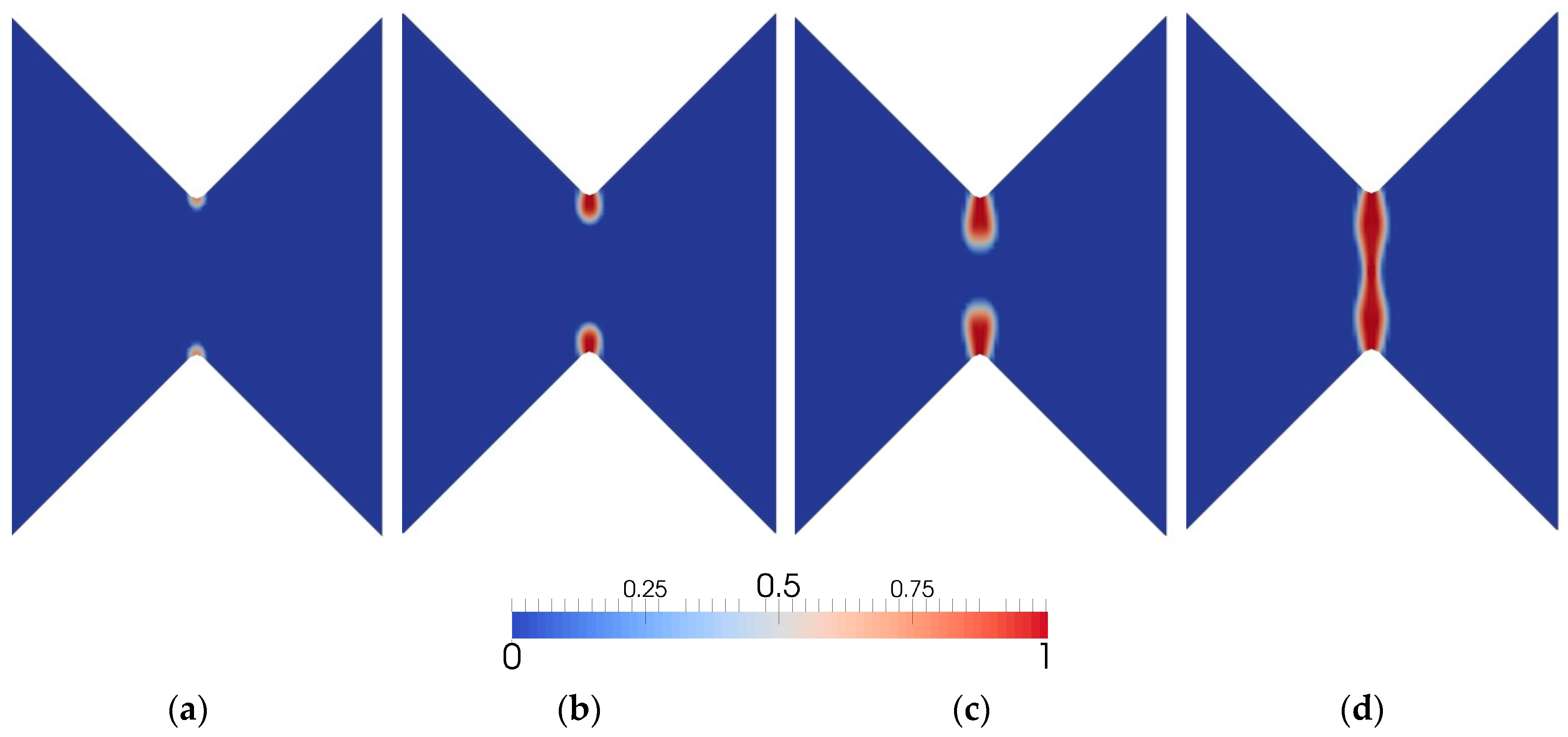
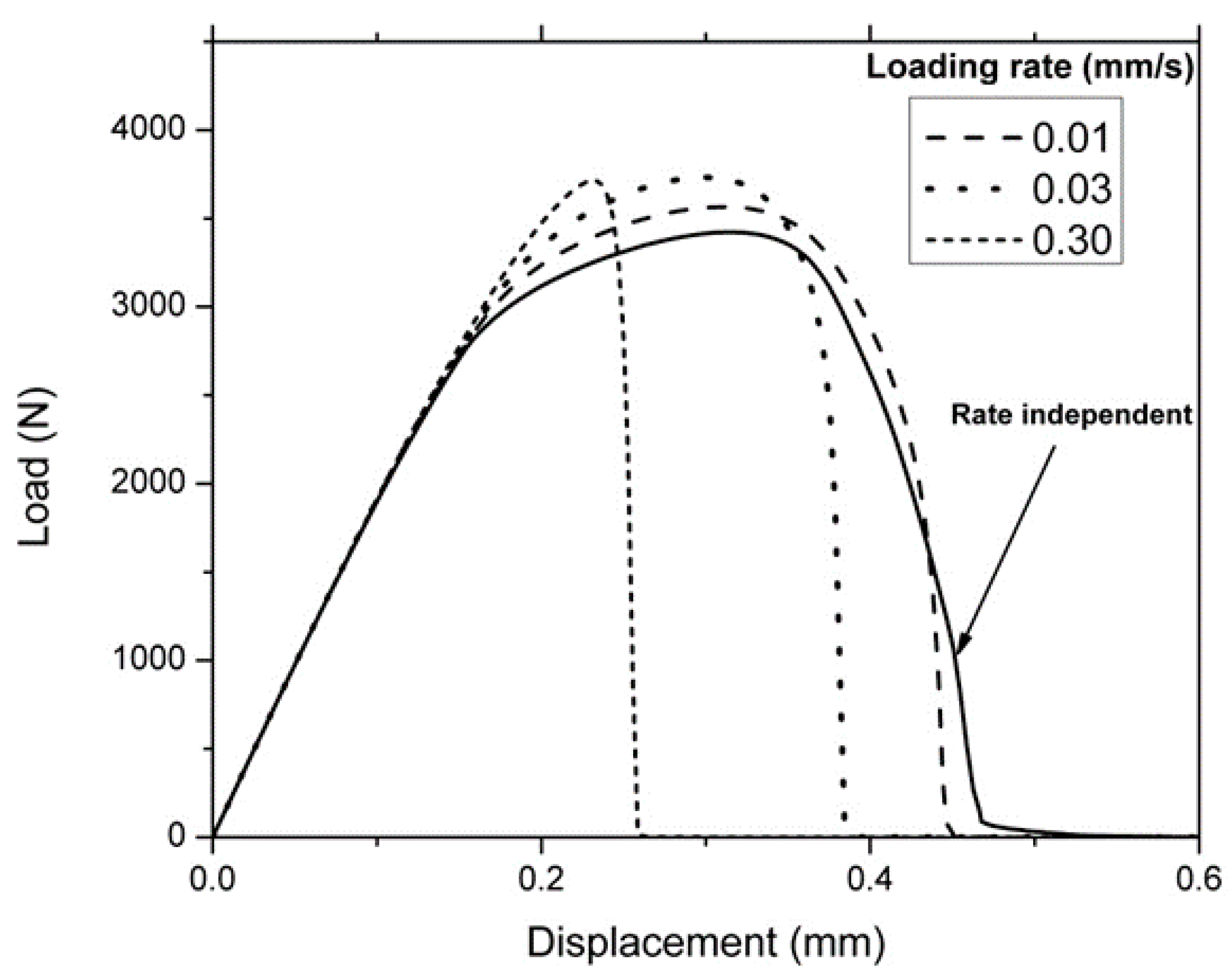
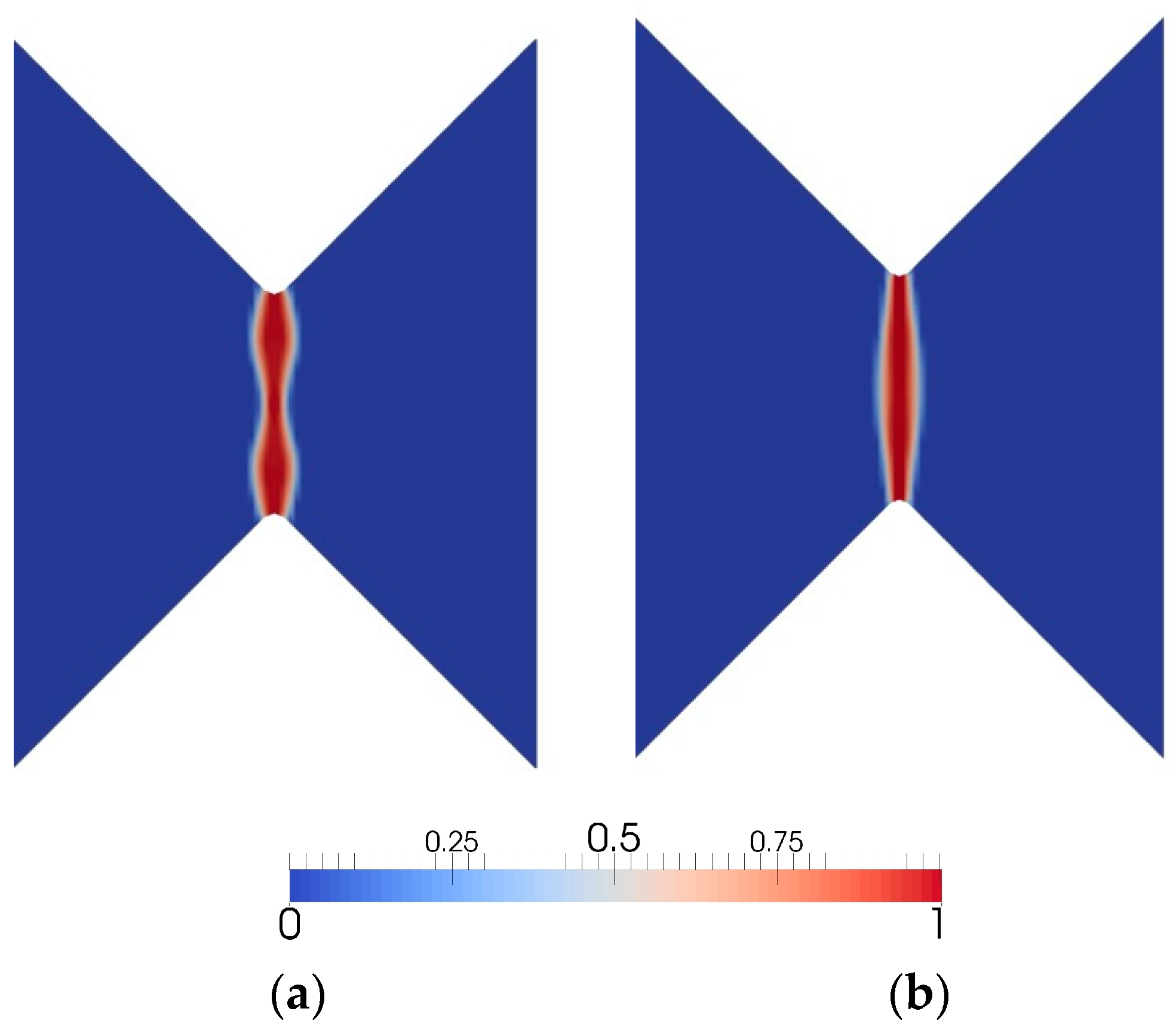
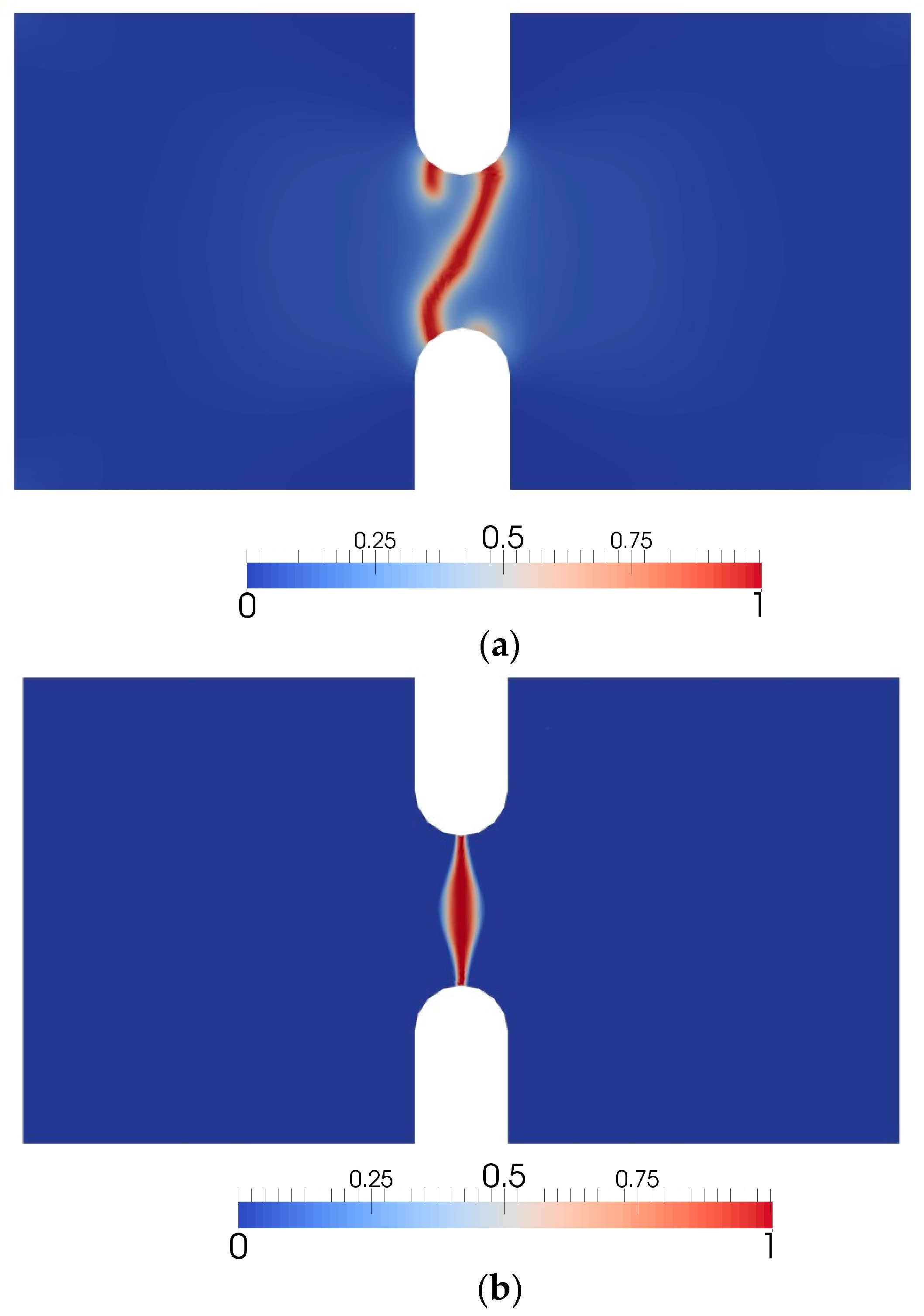
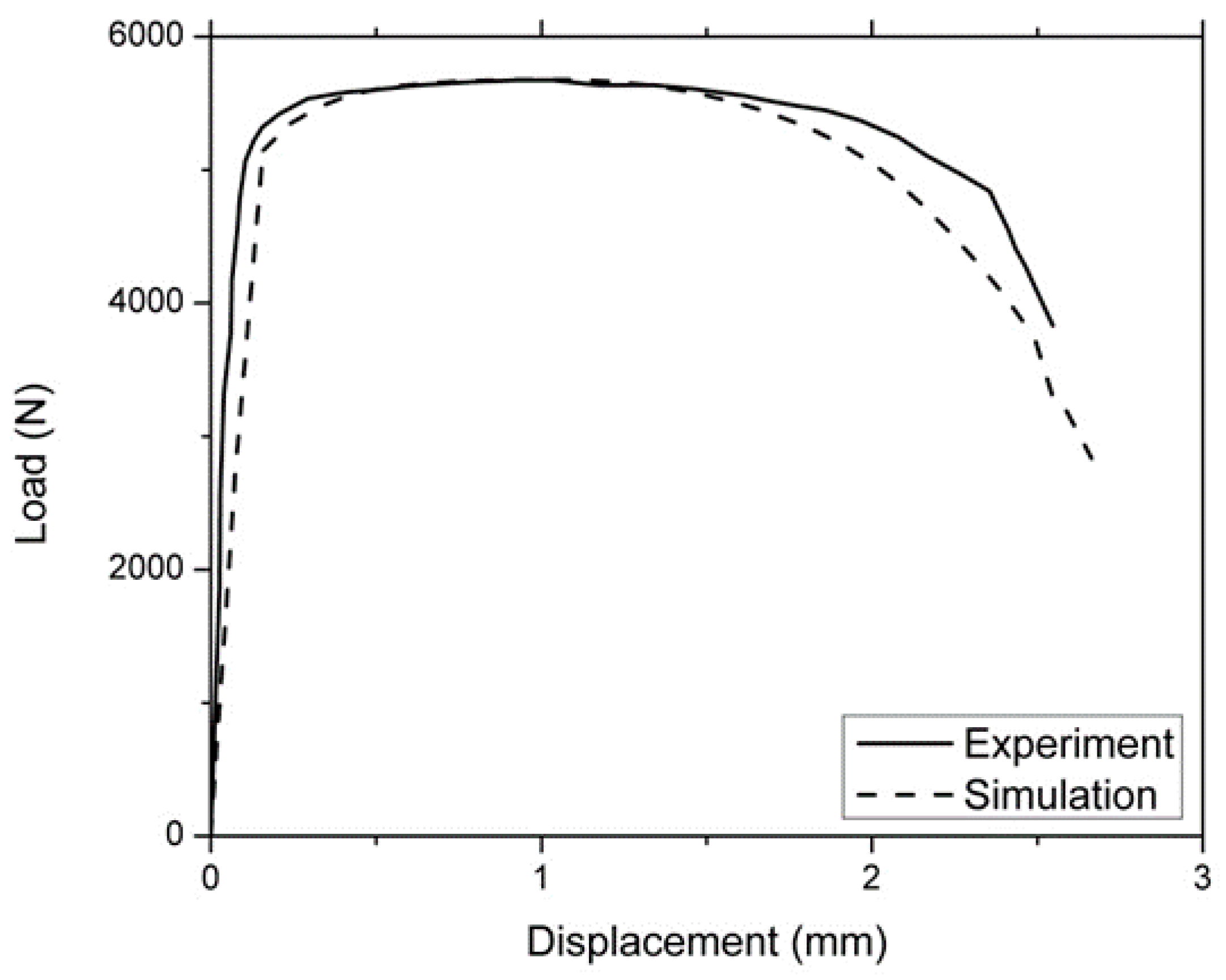
3.2. V-Notched Sample
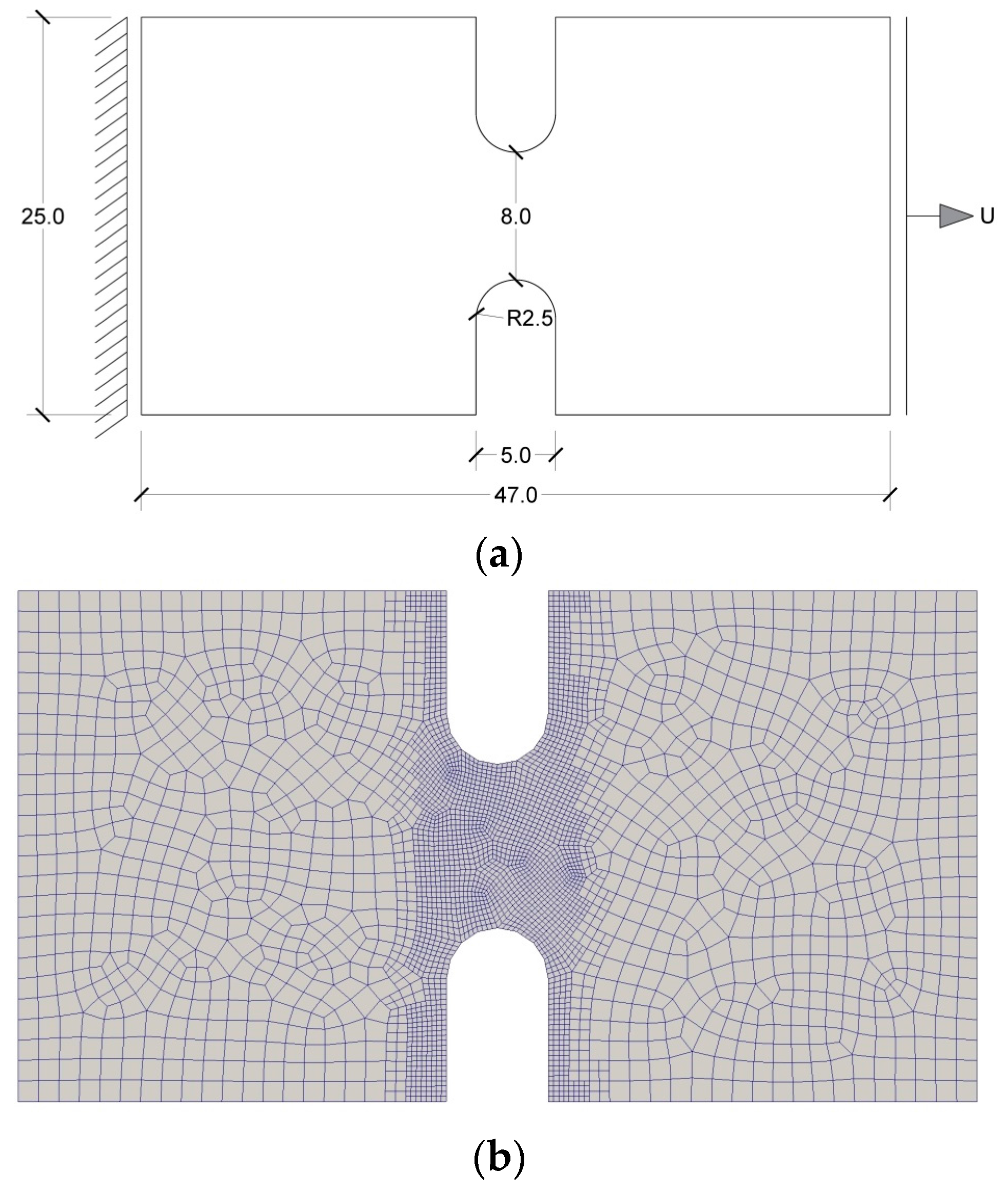
3.3. U-Notched Sample
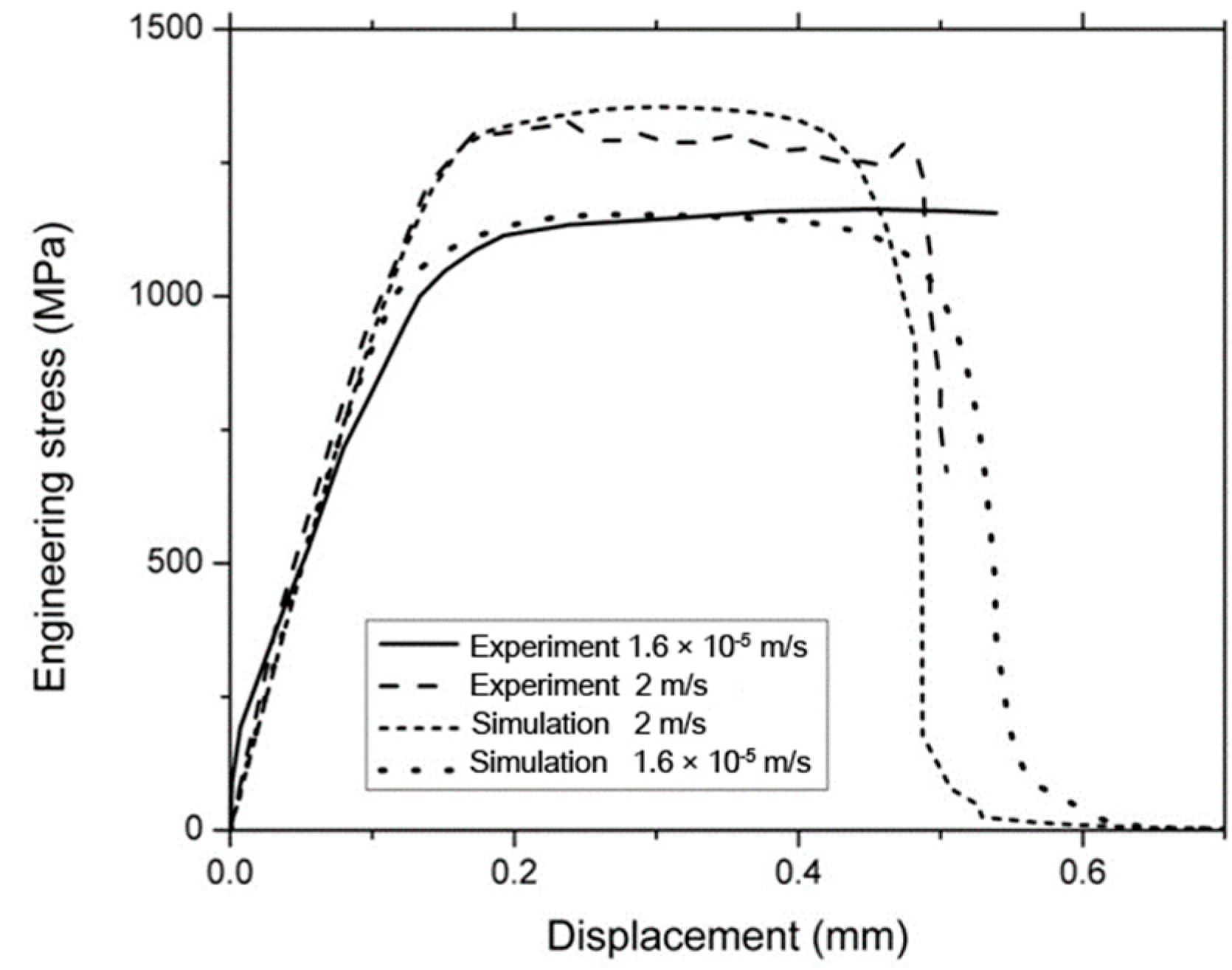
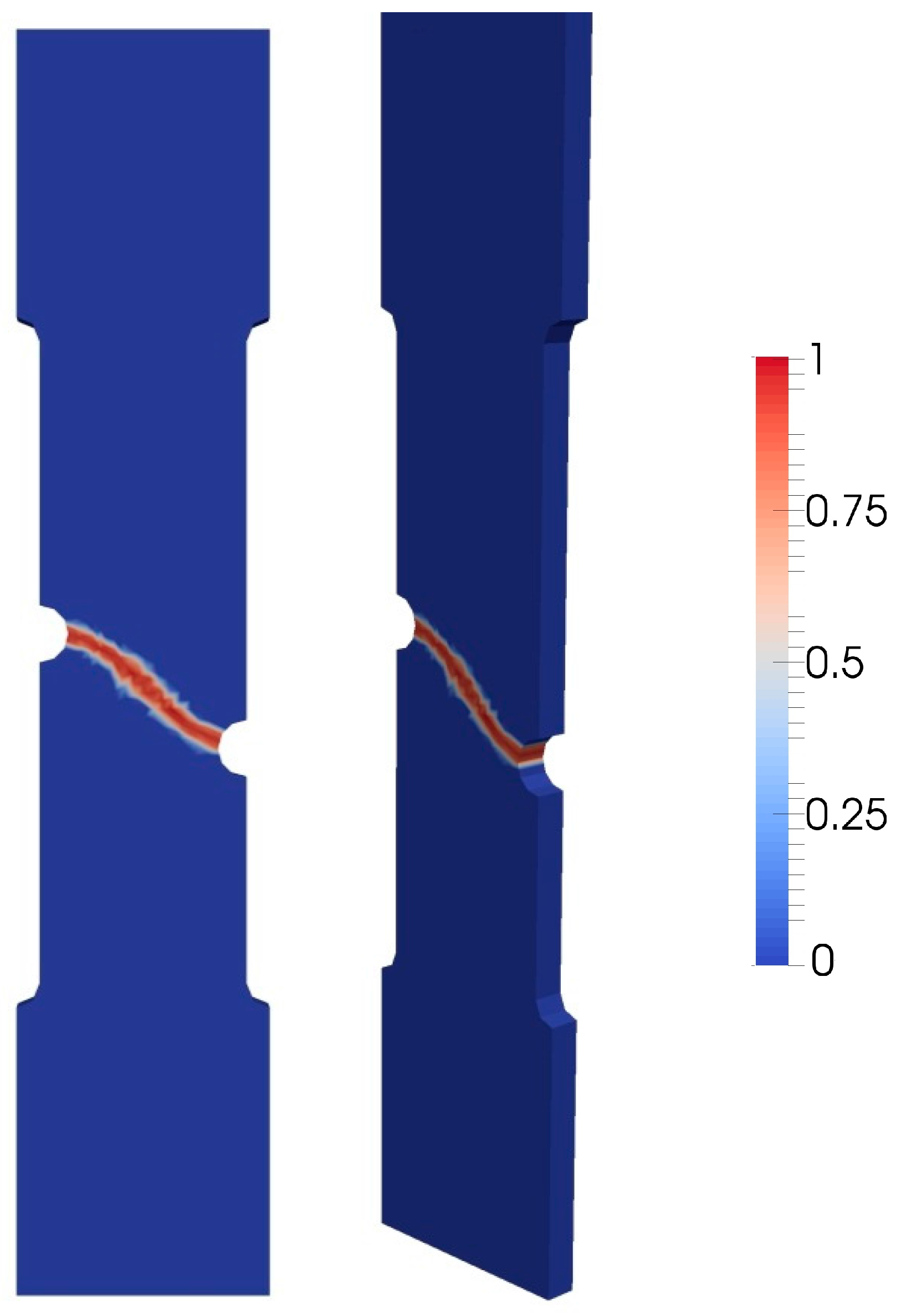
3.4. Three-Dimensional Asymmetric Notched Sample
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Schänzel, L.M. Phase field modeling of fracture in rubbery polymers. Part І: Finite elasticity coupled with brittle failure. J. Mech. Phys. Solids 2014, 65, 93–113. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. Continuum phase field modeling of dynamic fracture: Variational principles and staggered FE implementation. Int. J. Fract. 2012, 178, 113–129. [Google Scholar] [CrossRef]
- May, S.; Vignollet, J.; de Borst, R. A numerical assessment of phase-field models for brittle and cohesive fracture: Γ-convergence and stress oscillations. Eur. J. Mech. A Solids 2015, 52, 72–84. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Msekh, M.A.; Silani, M.; Jamshidian, M.; Areias, P.; Zhuang, X.; Zi, G.; He, P.; Rabczuk, T. Predictions of J integral and tensile strength of clay/epoxy nanocomposites material using phase field model. Compos. Part B Eng. 2016, 93, 97–114. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Msekh, M.A.; Zuo, Z. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model. Comput. Mater. Sci. 2016, 121, 35–47. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Ambati, M.; De Lorenzis, L. Phase-field modeling of brittle and ductile fracture in shells with isogeometric nurbs-based solid-shell elements. Comput. Methods Appl. Mech. Eng. 2016, 312, 351–373. [Google Scholar] [CrossRef]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Duda, F.P.; Ciarbonetti, A.; Sánchez, P.J.; Huespe, A.E. A phase-field/gradient damage model for brittle fracture in elastic–plastic solids. Int. J. Plast. 2015, 65, 269–296. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Miehe, C.; Kienle, D.; Aldakheel, F.; Teichtmeister, S. Phase field modeling of fracture in porous plasticity: A variational gradient-extended eulerian framework for the macroscopic analysis of ductile failure. Comput. Methods Appl. Mech. Eng. 2016, 312, 3–50. [Google Scholar] [CrossRef]
- Hernandez Padilla, C.A.; Markert, B. A coupled ductile fracture phase-field model for crystal plasticity. Contin. Mech. Thermodyn. 2015. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.R.; Landis, C.M.; Anvari, A.; Lee, I.J. A phase-field formulation for fracture in ductile materials: Finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput. Methods Appl. Mech. Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. Phase-field analysis of fracture-induced twinning in single crystals. Acta Mater. 2013, 61, 5341–5353. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. Phase field modeling of directional fracture in anisotropic polycrystals. Comput. Mater. Sci. 2015, 98, 158–169. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. Nonlinear phase field theory for fracture and twinning with analysis of simple shear. Philos. Mag. 2015, 95, 2661–2696. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. Phase field modeling and simulation of coupled fracture and twinning in single crystals and polycrystals. Comput. Methods Appl. Mech. Eng. 2016, 312, 447–467. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T.; Msekh, M. Phase-field analysis of finite-strain plates and shells including element subdivision. Comput. Methods Appl. Mech. Eng. 2016, 312, 322–350. [Google Scholar] [CrossRef]
- Areias, P.; Samaniego, E.; Rabczuk, T. A staggered approach for the coupling of Cahn–Hilliard type diffusion and finite strain elasticity. Comput. Mech. 2016, 57, 339–351. [Google Scholar] [CrossRef]
- Shanthraj, P.; Sharma, L.; Svendsen, B.; Roters, F.; Raabe, D. A phase field model for damage in elasto-viscoplastic materials. Comput. Methods Appl. Mech. Eng. 2016, 312, 167–185. [Google Scholar] [CrossRef]
- Shanthraj, P.; Svendsen, B.; Sharma, L.; Roters, F.; Raabe, D. Elasto-viscoplastic phase field modelling of anisotropic cleavage fracture. J. Mech. Phys. Solids 2017, 99, 19–34. [Google Scholar] [CrossRef]
- Perzyna, P. Fundamental problems in viscoplasticity. Adv. Appl. Mech. 1966, 9, 243–377. [Google Scholar]
- Perić, D. On a class of constitutive equations in viscoplasticity: Formulation and computational issues. Int. J. Numer. Methods Eng. 1993, 36, 1365–1393. [Google Scholar] [CrossRef]
- Neto, E.A.S.; Peric, D.; Owen, D.R.J. Computational Methods for Plasticity: Theory and Applications; Wiley: Chichester, UK, 2008. [Google Scholar]
- Badnava, H.; Mashayekhi, M.; Kadkhodaei, M. An anisotropic gradient damage model based on microplane theory. Int. J. Damage Mech. 2015, 3, 336–357. [Google Scholar] [CrossRef]
- Badnava, H.; Kadkhodaei, M.; Mashayekhi, M. A non-local implicit gradient-enhanced model for unstable behaviors of pseudoelastic shape memory alloys in tensile loading. Int. J. Solids Struct. 2014, 51, 4015–4025. [Google Scholar] [CrossRef]
- Badnava, H.; Kadkhodaei, M.; Mashayekhi, M. Modeling of unstable behaviors of shape memory alloys during localization and propagation of phase transformation using a gradient-enhanced model. J. Intell. Mater. Syst. Struct. 2015, 18, 2531–2546. [Google Scholar] [CrossRef]
- Areias, P.; Msekh, M.A.; Rabczuk, T. Damage and fracture algorithm using the screened poisson equation and local remeshing. Eng. Fract. Mech. 2016, 158, 116–143. [Google Scholar] [CrossRef]
- De Borst, R.; Verhoosel, C.V. Gradient damage vs phase-field approaches for fracture: Similarities and differences. Comput. Methods Appl. Mech. Eng. 2016, 312, 78–94. [Google Scholar] [CrossRef]
- Heister, T.; Wheeler, M.F.; Wick, T. A primal-dual active set method and predictor-corrector mesh adaptivity for computing fracture propagation using a phase-field approach. Comput. Methods Appl. Mech. Eng. 2015, 290, 466–495. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Bangerth, W.; Heister, T.; Heltai, L.; Kanschat, G.; Kronbichler, M.; Maier, M.; Turcksin, B.; Young, T.D. The deal.II Library, Version 8.1. Available online: http://arxiv.org/abs/1312.2266v4 (accessed on 7 April 2017).
- Bangerth, W.; Heister, T.; Kanschat, G. Deal.II Differential Equations Analysis Library, Technical Reference. Available online: http://www.dealii.org (accessed on 7 April 2017).
- Li, H.; Fu, M.W.; Lu, J.; Yang, H. Ductile fracture: Experiments and computations. Int. J. Plast. 2011, 27, 147–180. [Google Scholar] [CrossRef]
- Verleysen, P.; Peirs, J. Quasi-static and high strain rate fracture behaviour of Ti6Al4V. Int. J. Impact Eng. 2017. [Google Scholar] [CrossRef]


| Material Parameter | Values |
|---|---|
| Young’s modulus | 68.8 (GPa) |
| Poisson’s ratio | 0.33 |
| Yield stress () | 320 (MPa) |
| Hardening modulus | 655 (MPa) |
| Fracture energy () | 69 (N/mm) |
| Rate sensitivity () | 1.0 |
| and | 1.0 |
| Material Parameter | Values |
|---|---|
| Young’s modulus | 68.9 (GPa) |
| Poisson’s ratio | 0.33 |
| Yield stress () | 475 (MPa) |
| Hardening modulus | 561 (MPa) |
| Fracture energy () | 18 (N/mm) |
| Length scale (L) | 0.28 (mm) |
| Rate sensitivity () | 0.6 |
| Viscosity () | 10 (s) |
| Plastic work threshold () | 120.0 (MPa) |
| and | 1.0 |
| Material Parameter | Values |
|---|---|
| Shear modulus (G) | 80.8 (GPa) |
| Poisson’s ratio | 0.3 |
| Yield stress () | 780 (MPa) |
| Hardening modulus | 40 (MPa) |
| Fracture energy () | 23 (N/mm) |
| Length scale (L) | 0.50 (mm) |
| Rate sensitivity () | 0.06 |
| Viscosity () | 2 (s) |
| Plastic work threshold () | 139.0 (MPa) |
| and | 1.0 |
| Material Parameter | Values |
|---|---|
| Young’s modulus | 70.9 (GPa) |
| Poisson’s ratio | 0.34 |
| Yield stress () | 125 (MPa) |
| Hardening modulus | 28 (MPa) |
| Fracture energy () | 35 (N/mm) |
| Length scale (L) | 1.98 (mm) |
| Rate sensitivity () | 0.5 |
| Viscosity () | 5 (s) |
| Plastic work threshold () | 30.0 (MPa) |
| and | 1.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badnava, H.; Etemadi, E.; Msekh, M.A. A Phase Field Model for Rate-Dependent Ductile Fracture. Metals 2017, 7, 180. https://doi.org/10.3390/met7050180
Badnava H, Etemadi E, Msekh MA. A Phase Field Model for Rate-Dependent Ductile Fracture. Metals. 2017; 7(5):180. https://doi.org/10.3390/met7050180
Chicago/Turabian StyleBadnava, Hojjat, Elahe Etemadi, and Mohammed A. Msekh. 2017. "A Phase Field Model for Rate-Dependent Ductile Fracture" Metals 7, no. 5: 180. https://doi.org/10.3390/met7050180
APA StyleBadnava, H., Etemadi, E., & Msekh, M. A. (2017). A Phase Field Model for Rate-Dependent Ductile Fracture. Metals, 7(5), 180. https://doi.org/10.3390/met7050180






