Effect of Shot Blasting on Fatigue Strength of Q345B Steel Plate with a Central Hole
Abstract
:1. Introduction
2. Experimental Method
3. Experimental Results
3.1. Roughness Analysis
3.2. Fractographic Observation
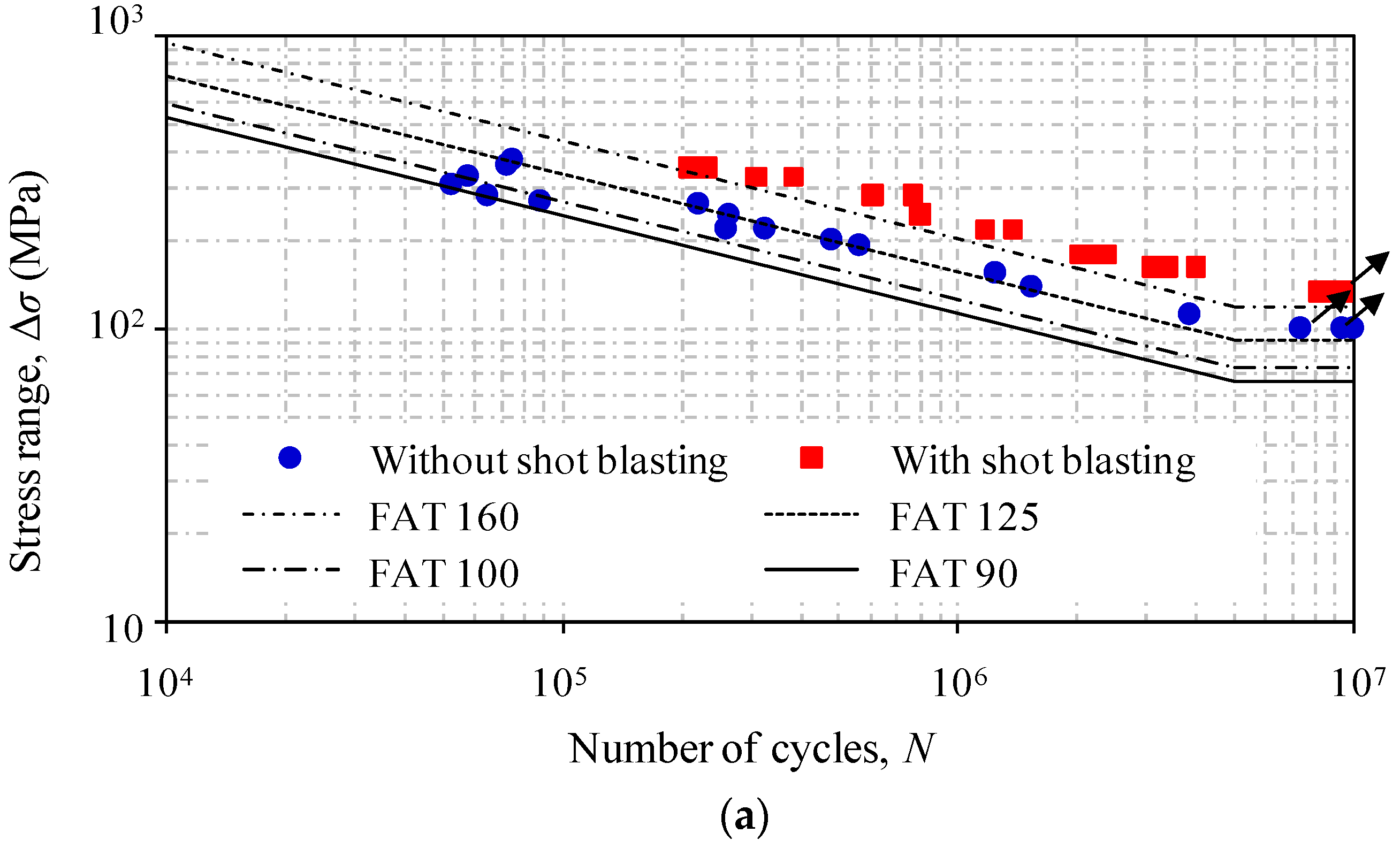
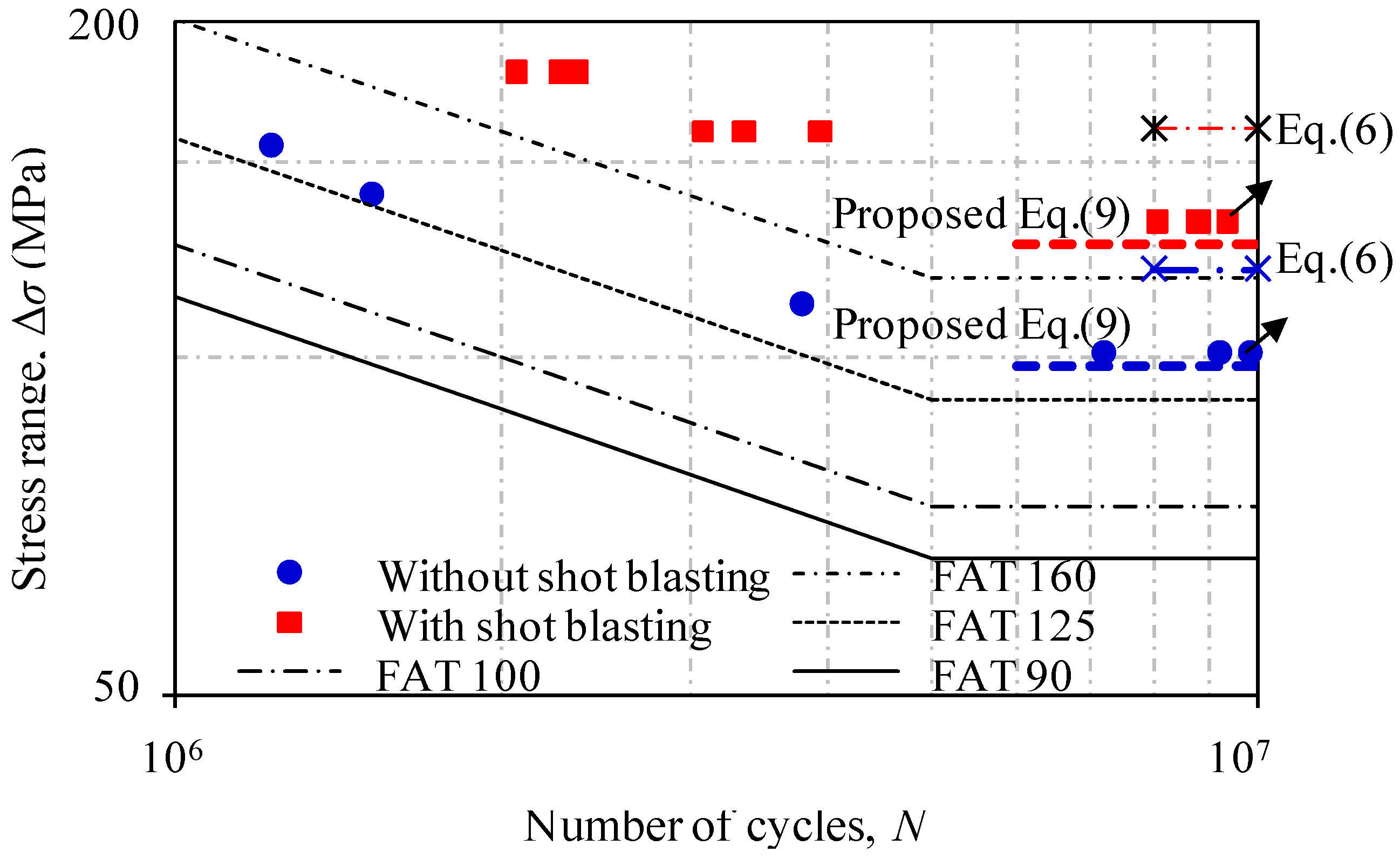
3.3. Stress Range versus Fatigue Life (S-N) Relation and Comparison
- (i)
- For specimens without shot blasting:
- (ii)
- For specimens with shot blasting:
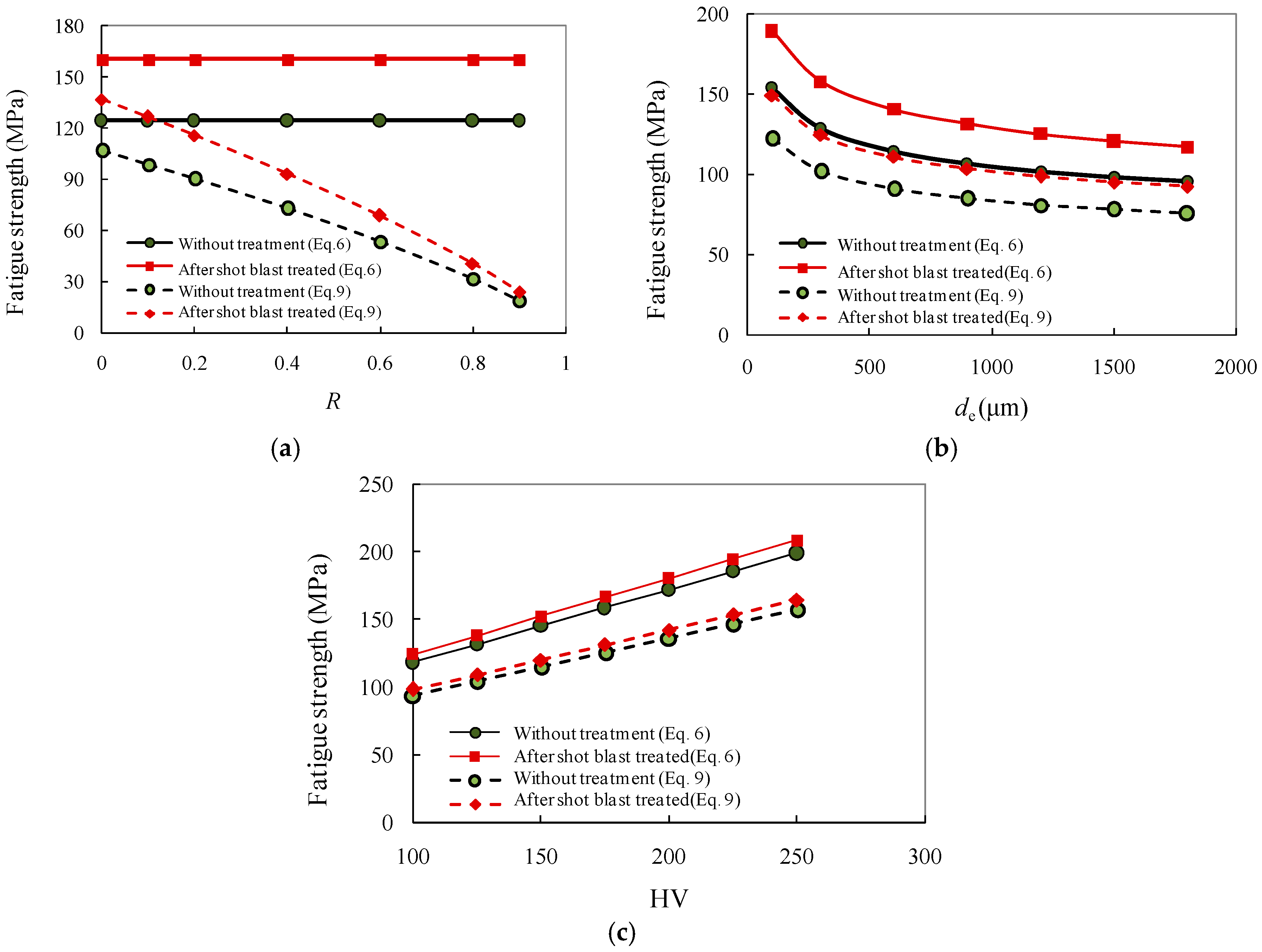
4. Discussion
5. Concluding Remarks
- For shot-blasted specimens, the fatigue failure is influenced by both the defect induced by the shot blasting process and stress concentration at the edge of the central hole. The fatigue cracks are found at the defect below the condensed surface induced by shot blasting. The defect can be regarded as critical since its further propagation can lead to first crack initiation. The shot blasting induces compressive pre-stress on the surface, which in turn condenses the size of the defect. On the other hand, the interaction of stress concentration is not negligible, since it may increase the crack propagation during fatigue loading.
- The codified category for the central holed specimens without shot blasting can be classified as FAT 90 in accordance with EN 1993-1-9. In contrast, shot blasting improves the fatigue category to FAT 160 for the test specimens. However, such an improvement is still lower than that reported by others for the specimens without clear geometric weakening or defects. In this regard, the local stress concentration should be taken into account in the evaluation of the beneficial effect induced by shot blasting.
- The modified Murakami model proposed in this study seems to give a better prediction of the fatigue strength of the central holed specimens with or without shot blasting. The difference between the proposed modification and original model lies in the proper allowance of the stress ratio and the size of the defect as well as the stress concentration induced by the presence of the hole details. These considerations are validated as compared against test results. Nevertheless, more experimental work is still needed to further the understanding of the crack initiation manner of the joint and provide further improvement to proposed method stated herein.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Z.Y.; Wang, Q.Y.; Li, H.; Zhang, N. Fatigue behaviour of CFRP strengthened open-hole steel plates. Thin-Walled Struct. 2017, 115, 176–187. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhang, N.; Wang, Q.Y. Tensile behaviour of open-hole and bolted steel plates reinforced by CFRP strips. Compos. Part B 2016, 100, 101–113. [Google Scholar] [CrossRef]
- Almen, J.O. Shot blasting to increase fatigue resistance. SAE J. 1943, 51, 7248–7268. [Google Scholar]
- Zimmerli, F.P. How shot blasting increases fatigue life. Mach. Des. 1940, 12, 62. [Google Scholar]
- Zimmerli, F.P. Shot blasting and its effect on fatigue life. ASM 1941, 1, 261–278. [Google Scholar]
- Naidu, N.K.R.; Raman, S.G.S. Effect of shot blasting on plain fatigue and fretting fatigue behaviour of Al-Mg-Si alloy AA6061. Int. J. Fatigue 2005, 27, 323–331. [Google Scholar] [CrossRef]
- Gil, F.J.; Planell, J.A.; Padrós, A.; Aparicio, C. The effect of shot blasting and heat treatment on the fatigue behavior of titanium for dental implant applications. Dent. Mater. 2007, 23, 486–491. [Google Scholar]
- Khan, S.A.; Bhuiyanb, M.S.; Miyashitab, Y.; Mutohc, Y.; Koiked, T. Corrosion fatigue behavior of die-cast and shot-blasted AM60 magnesium alloy. Mater. Sci. Eng. A 2011, 528, 1961–1966. [Google Scholar] [CrossRef]
- Fujimoto, H.; Ueda, H.; Ueji, R.; Fujii, H. Improvement of fatigue properties of resistance spot welded joints in high strength steel sheets by shot blast processing. ISIJ Int. 2016, 56, 1276–1284. [Google Scholar] [CrossRef]
- Gerin, B.; Pessarda, E.; Morel, F.; Verdub, C. Influence of surface integrity on the fatigue behaviour of a hot-forged and shot-peened C70 steel component. Mater. Sci. Eng. A 2017, 686, 121–133. [Google Scholar] [CrossRef]
- Yamabe, J.; Kobayashi, M. Effects of surface roughness and residual stress on fatigue strength of shot blasted ductile cast irons with casting surfaces. J. Soc. Mater. Sci. Jpn. 2006, 55, 301–308. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, NY, USA, 1998; Volume 21. [Google Scholar]
- European Committee for Standardization. Eurocode 3: Design of Steel Structural; Part 1–9; EN 1993-1-9; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Mayorga, L.G.; Sire, S.; Correia, J.A.; De Jesus, A.M.P.; Rebelo, C.; Fernández-Canteli, A.; Ragueneau, M.; Plu, B. Statistical evaluation of fatigue strength of double shear riveted connections and crack growth rates of materials from old bridges. Eng. Fract. Mech. 2017. [Google Scholar] [CrossRef]
- Garcia, T.; Cicero, S.; Alvarez, J.A.; Martín-Meizoso, A.; Bannister, A.; Klimpel, A.; Aldazabal, A. Fatigue performance of thermally cut bolt holes in structural steel S460M. Proc. Eng. 2015, 133, 590–602. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effects of hardness and crack geometries on ΔKth of small cracks emanating from small defects. In The Behaviour of Short Fatigue Cracks; Miller, K., De Los Rios, E., Eds.; MEP Publications: London, UK, 1986; pp. 275–293. [Google Scholar]
- Horger, O.J. Metals Engineering Design ASME Handbook, 2nd ed.; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
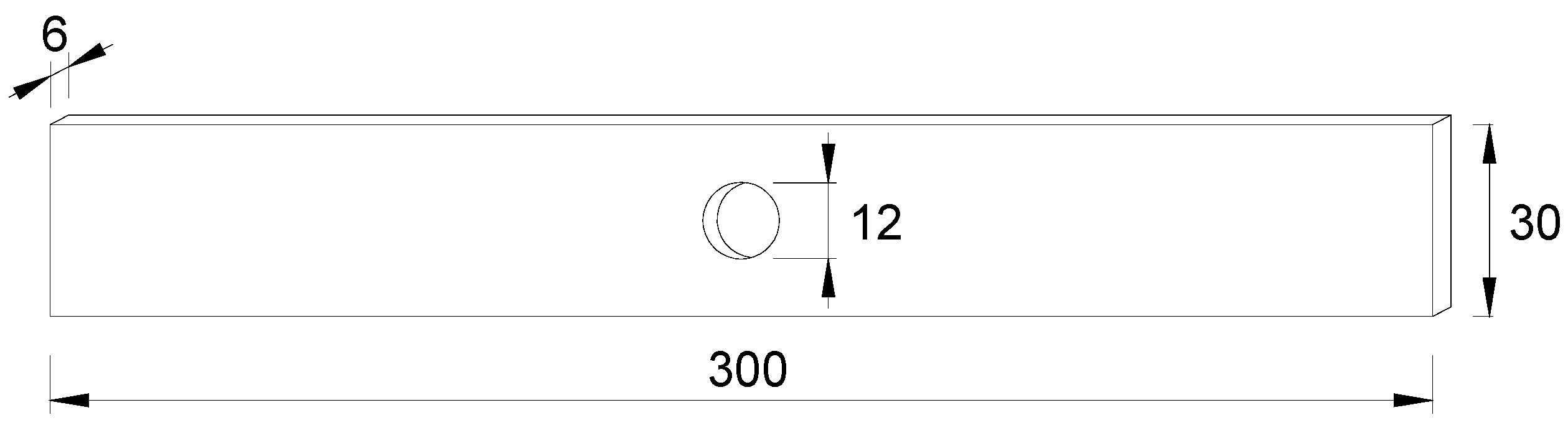
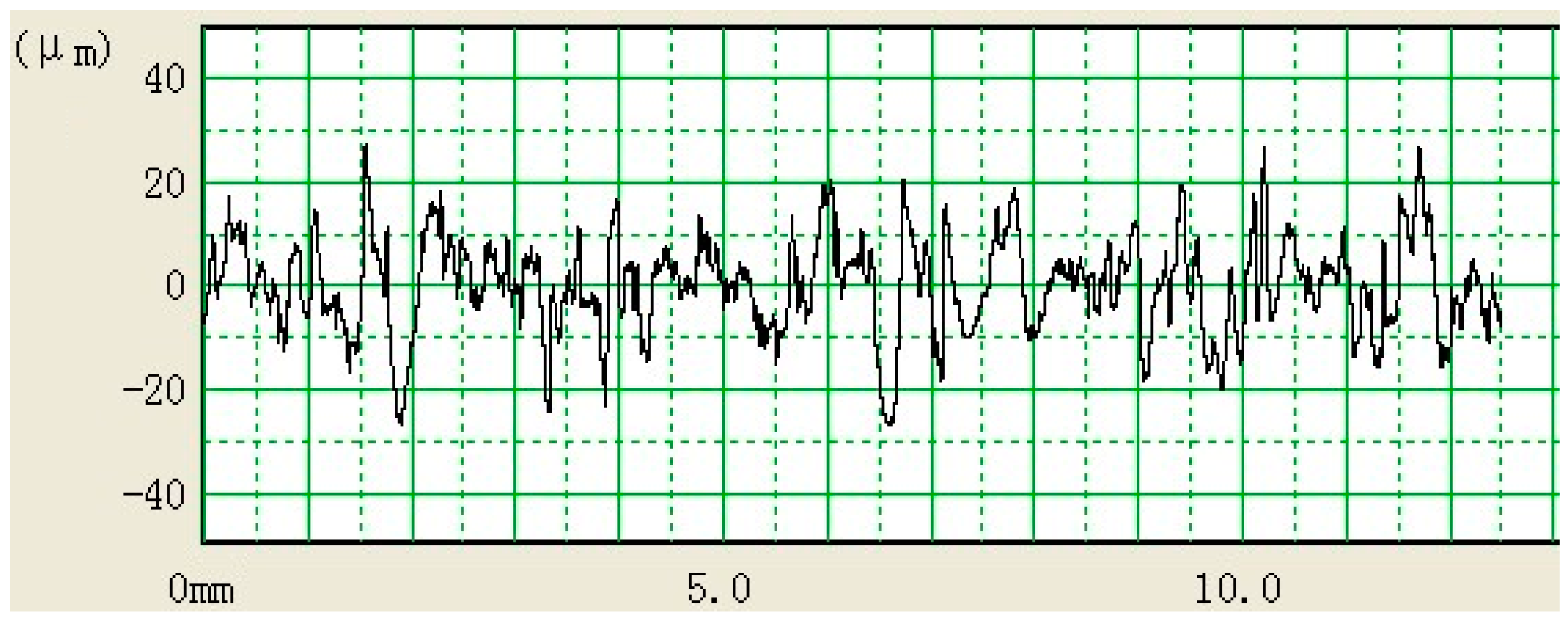



| Steel Grade | Chemical Composition (%) | Mechanical Properties | ||||||
|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Yield Strength (MPa) | Ultimate Strength (MPa) | Elongation (%) | |
| Q345B | 0.17 | 0.25 | 1.15 | 0.015 | 0.014 | 388 | 553 | 12 |
| Shot Ball | Projection Velocity | Shot Impact Angle | Arc Height | Output | ||
|---|---|---|---|---|---|---|
| Material | Hardness | Diameter | ||||
| Alloy steel | HRC 40–50 | 0.6–0.8 mm | 90 m/s | 45 | 0.35 mm A | 11 kW |
| Type | Roughness (μm) | Hardness (HV) |
|---|---|---|
| Without shot blasting | 1.07 | 109 |
| With shot blasting | 7.08 | 161 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X.; Wang, Z.; Wang, Q.; Cao, M.; Shen, M.; Huang, W. Effect of Shot Blasting on Fatigue Strength of Q345B Steel Plate with a Central Hole. Metals 2017, 7, 517. https://doi.org/10.3390/met7120517
You X, Wang Z, Wang Q, Cao M, Shen M, Huang W. Effect of Shot Blasting on Fatigue Strength of Q345B Steel Plate with a Central Hole. Metals. 2017; 7(12):517. https://doi.org/10.3390/met7120517
Chicago/Turabian StyleYou, Xiang, Zhiyu Wang, Qingyuan Wang, Mengqin Cao, Mengqin Shen, and Wanqiu Huang. 2017. "Effect of Shot Blasting on Fatigue Strength of Q345B Steel Plate with a Central Hole" Metals 7, no. 12: 517. https://doi.org/10.3390/met7120517
APA StyleYou, X., Wang, Z., Wang, Q., Cao, M., Shen, M., & Huang, W. (2017). Effect of Shot Blasting on Fatigue Strength of Q345B Steel Plate with a Central Hole. Metals, 7(12), 517. https://doi.org/10.3390/met7120517






