Virtual Testing of Composite Structures Made of High Entropy Alloys and Steel
Abstract
1. Introduction
- -
- Higher hardness, as a measure of resistance of solid materials to the penetration in surface of various types of penetrators, with permanent changes of shape when a static or dynamic force is applied to them; the macroscopic hardness is generally characterized by the nature and strength of inter-molecular links, the behavior of the solid material under the force action being complex;
- -
- High tenacity at low temperatures, because it represents the ability of the metallic material to absorb the breaking energy, to oppose the emergence and spread of various types of cracks, accumulating the energy necessary for the formation of surface rupture and for the fast local deformation under shock conditions;
- -
- High impact resistance, which is the relative susceptibility to damage by the action of forces applied at high speed.
2. Material Models for Virtual Ballistic Testing
3. Virtual Testing Campaign
- -
- Bullet caliber of 7.62 × 39 mm;
- -
- Shooting angle of 0°;
- -
- Incendiary perforating bullet weight of 7.67 g;
- -
- Steel core weight of 4 g.
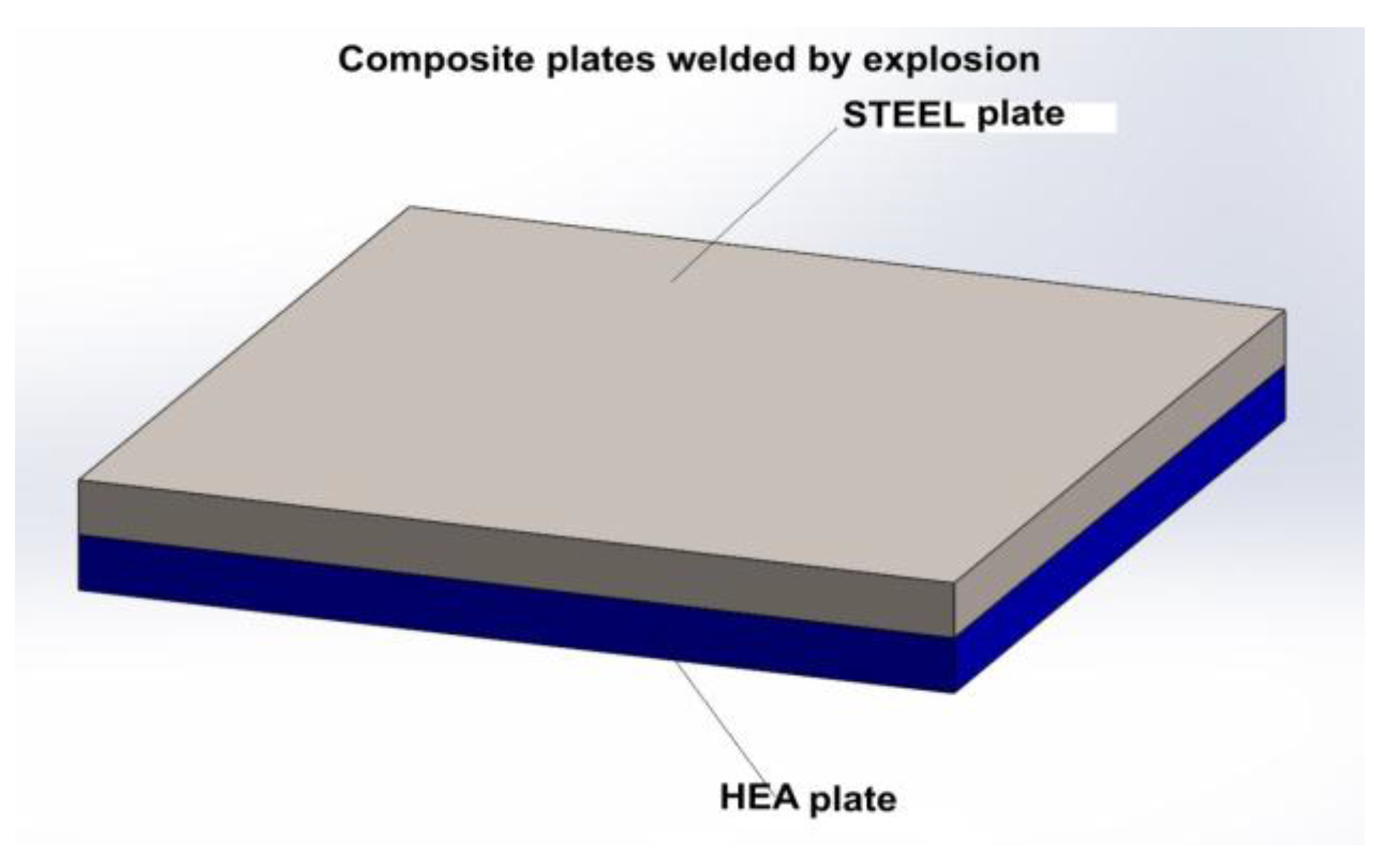
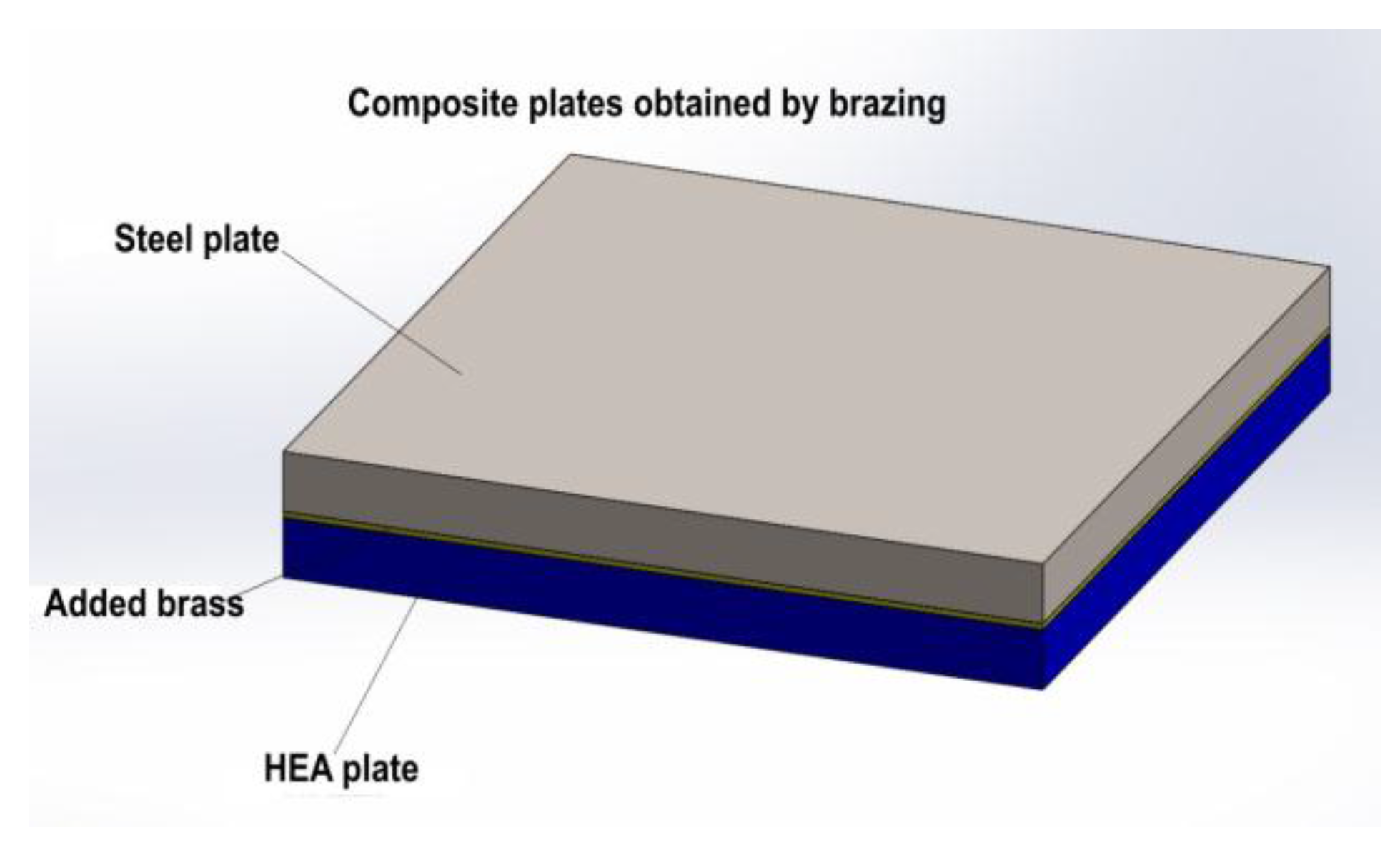
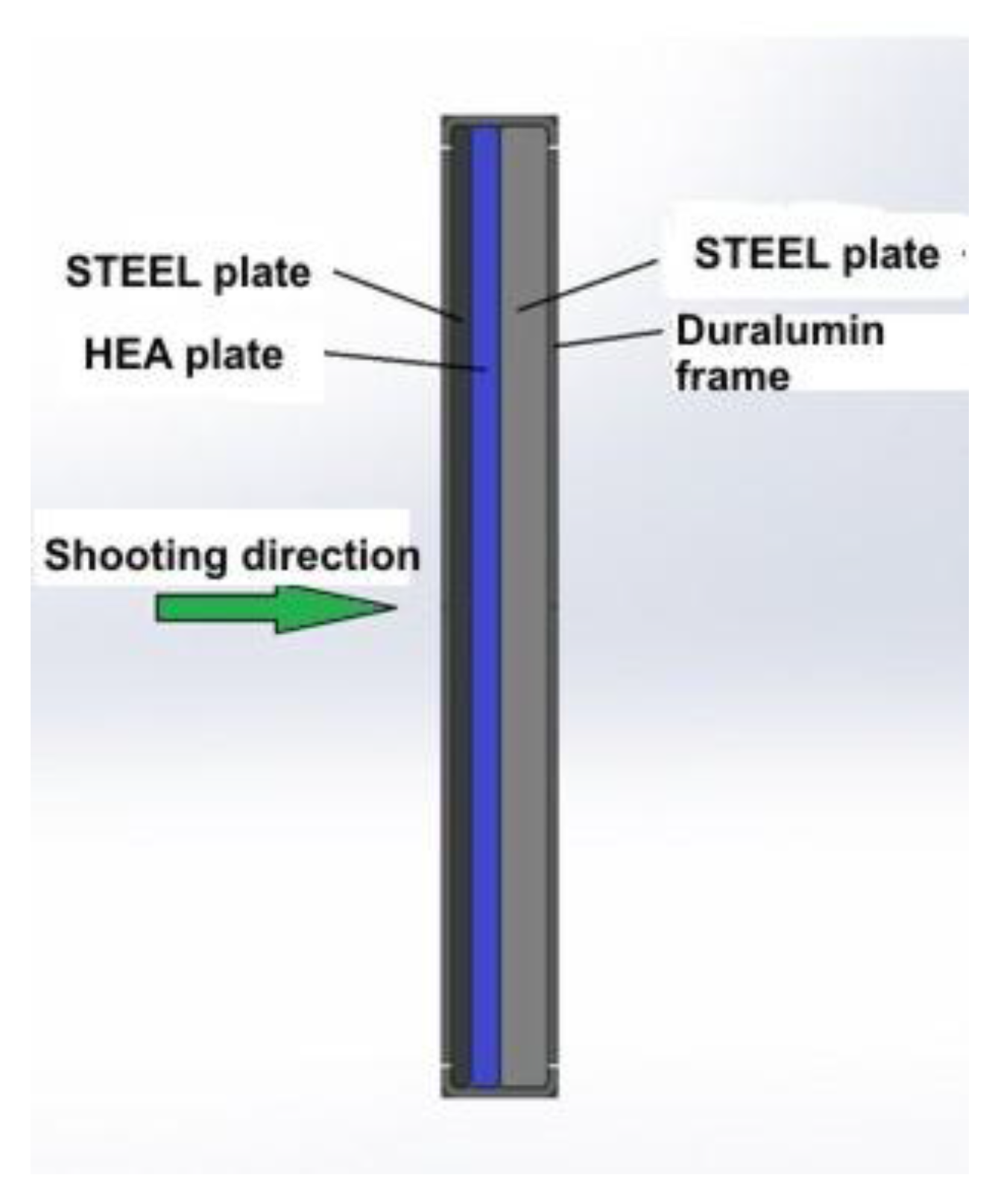
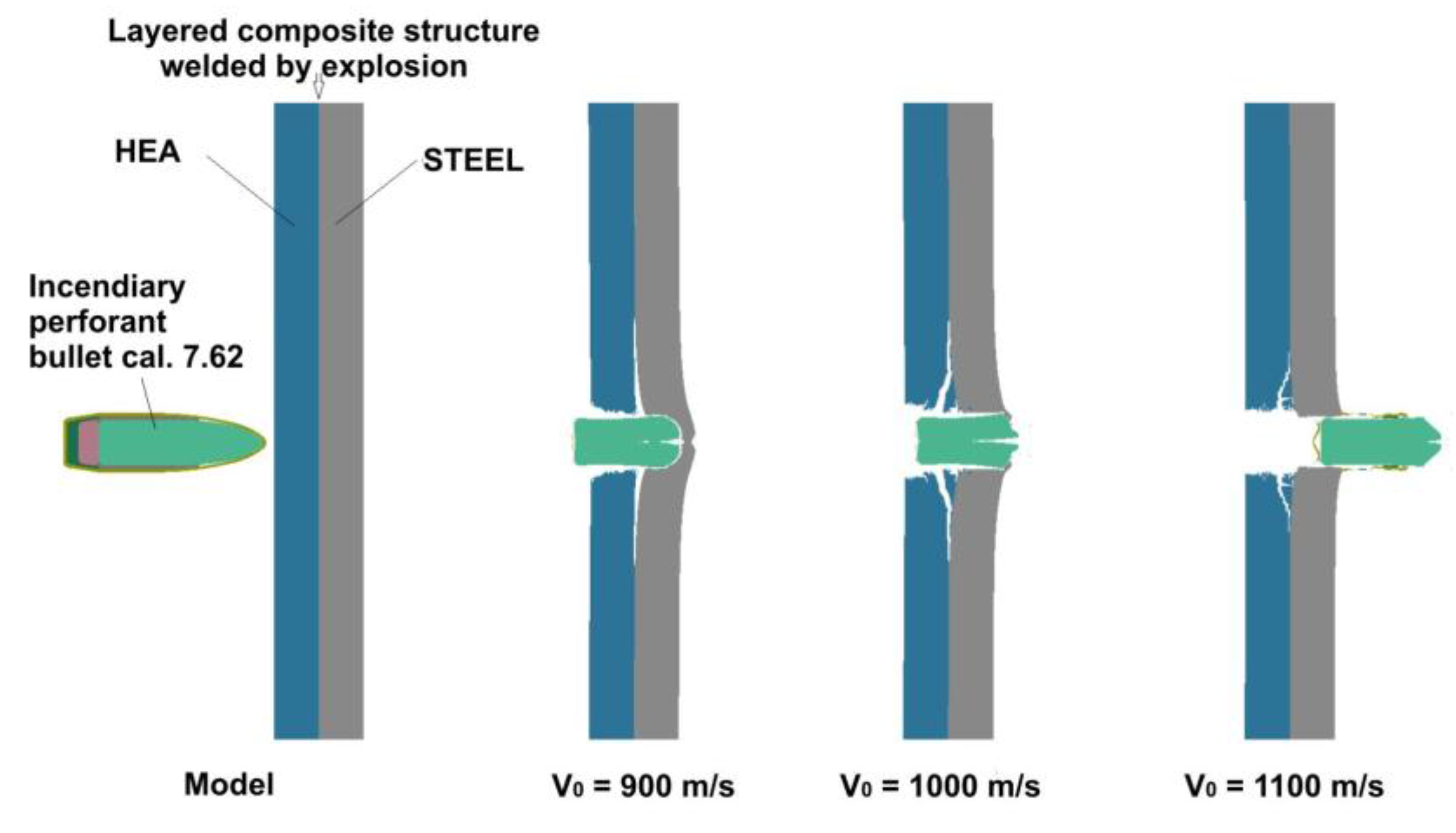
- Composite structure: HEA-STEEL welded by explosionTesting speeds: V01 = 900 m/s; V02 = 1000 m/s; V03 = 1100 m/s;
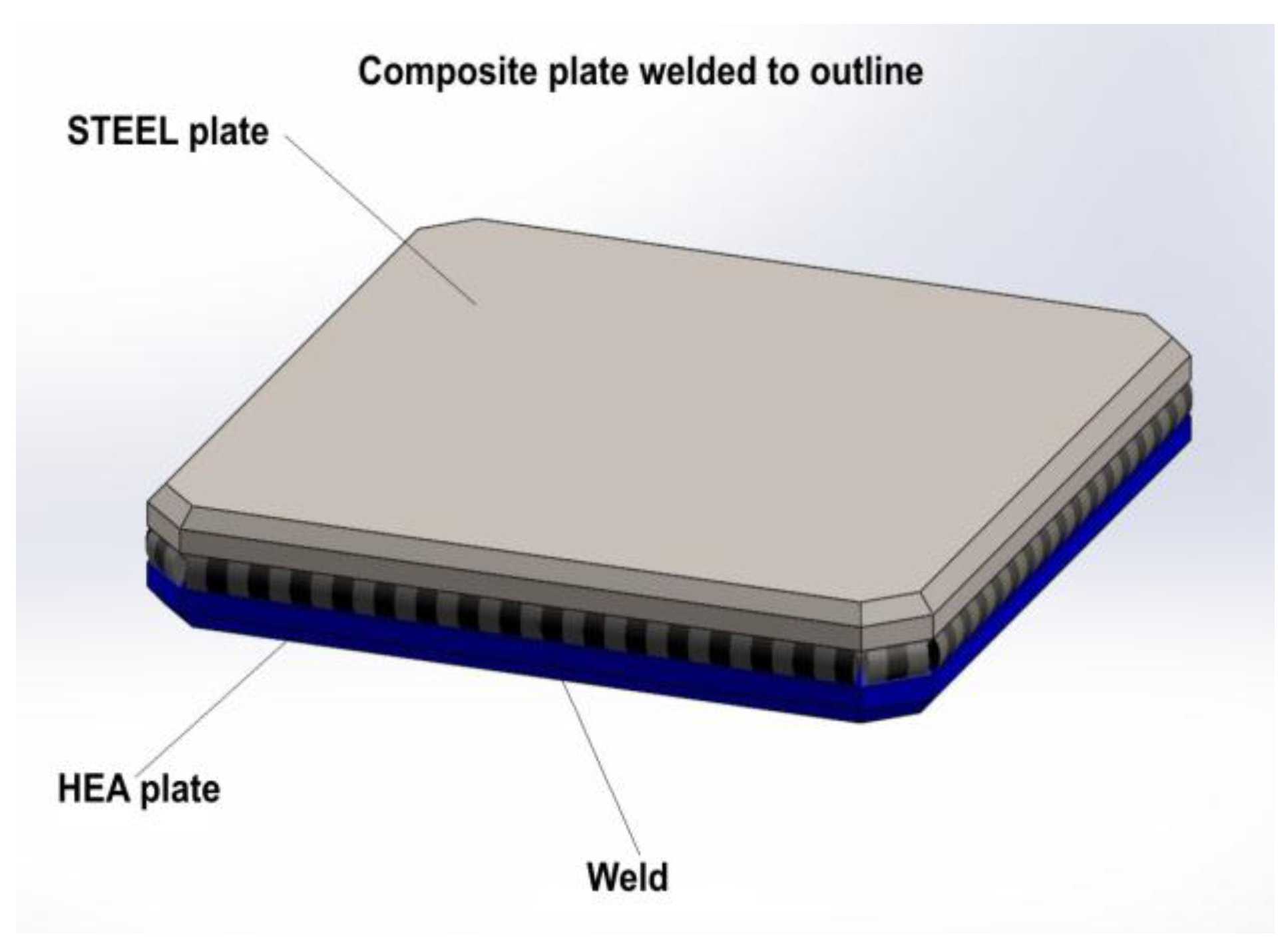
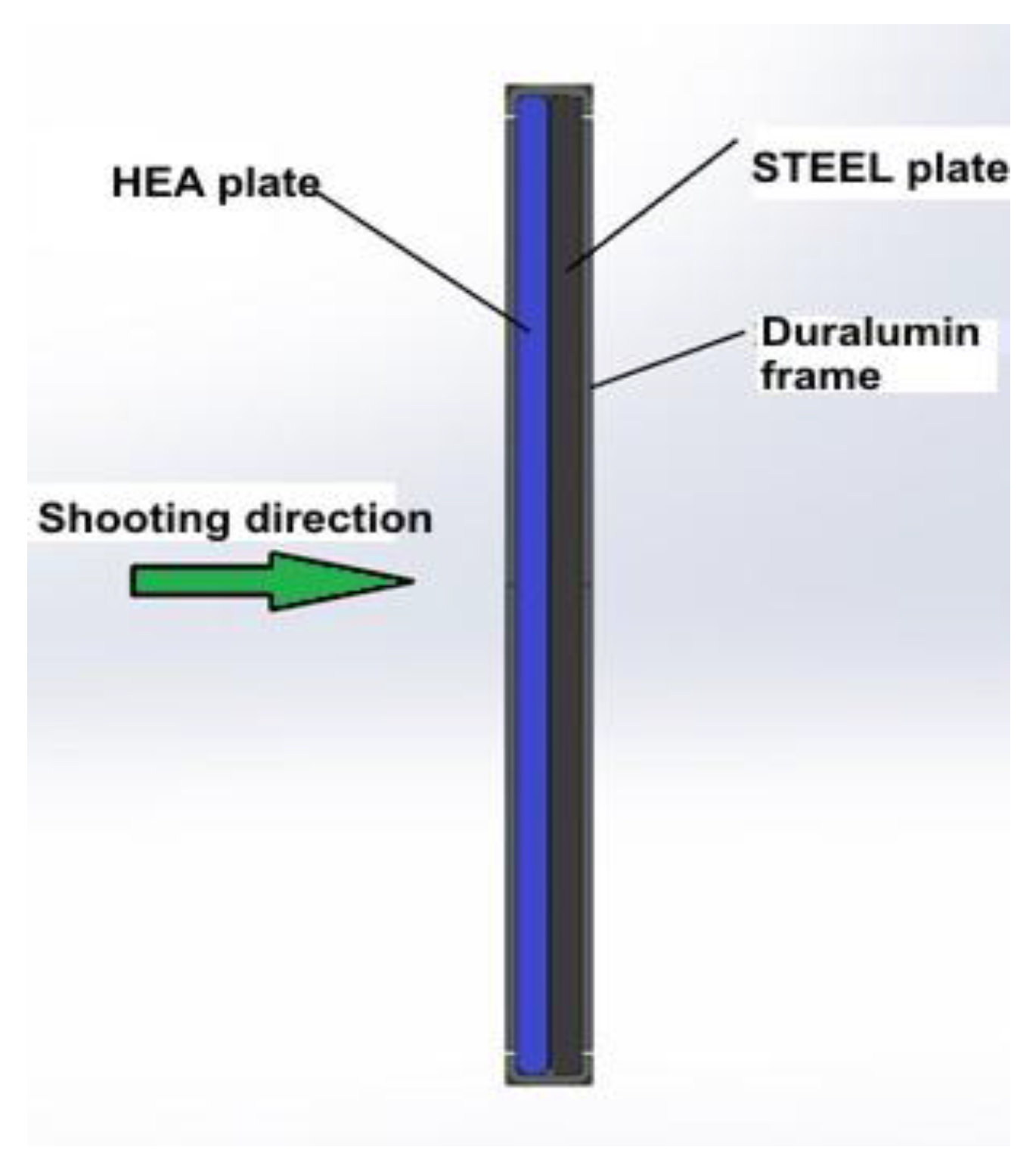
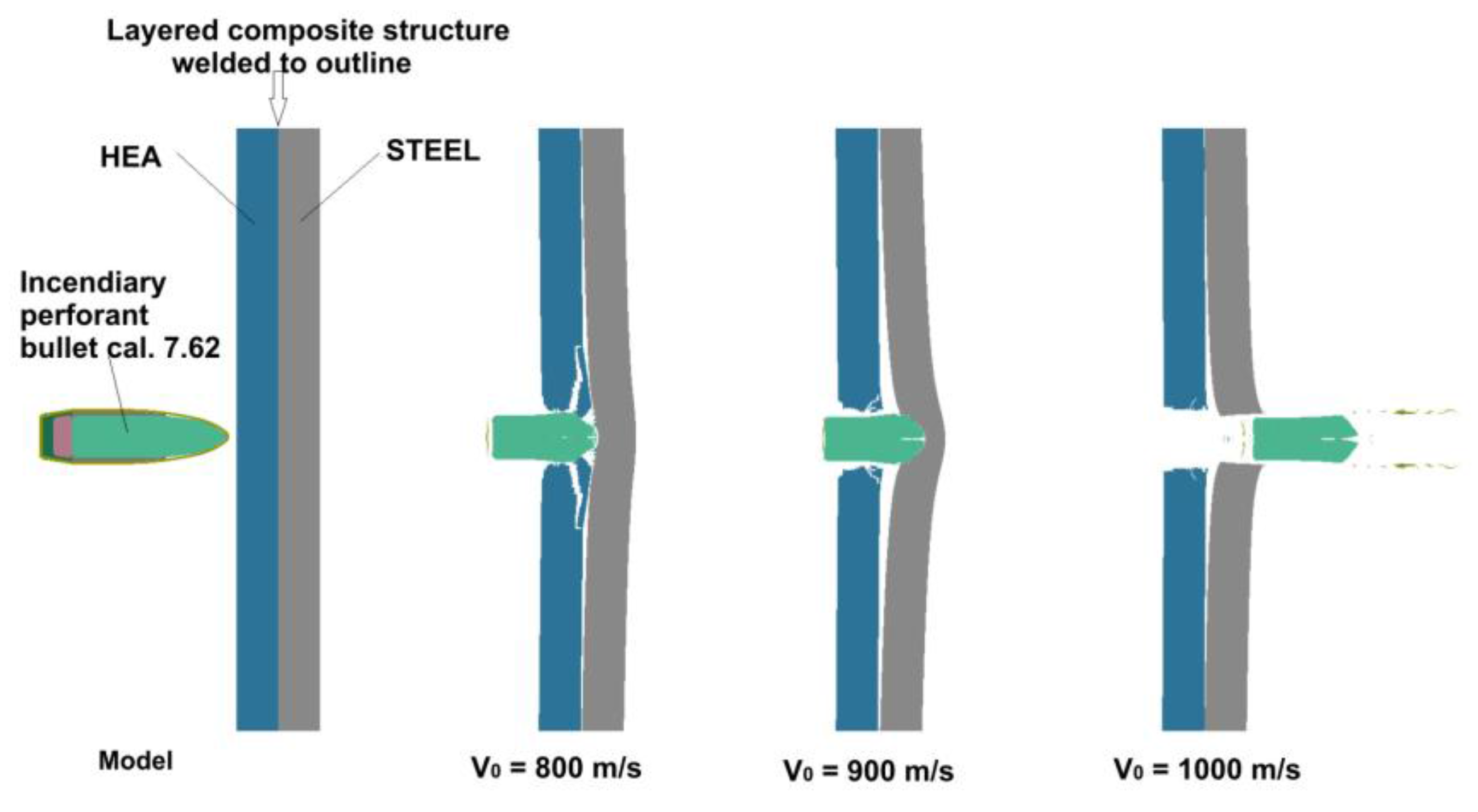
- Composite structure: HEA-STEEL contour weldedTesting speeds: V01 = 800 m/s; V02 = 900 m/s; V03 = 1000 m/s;
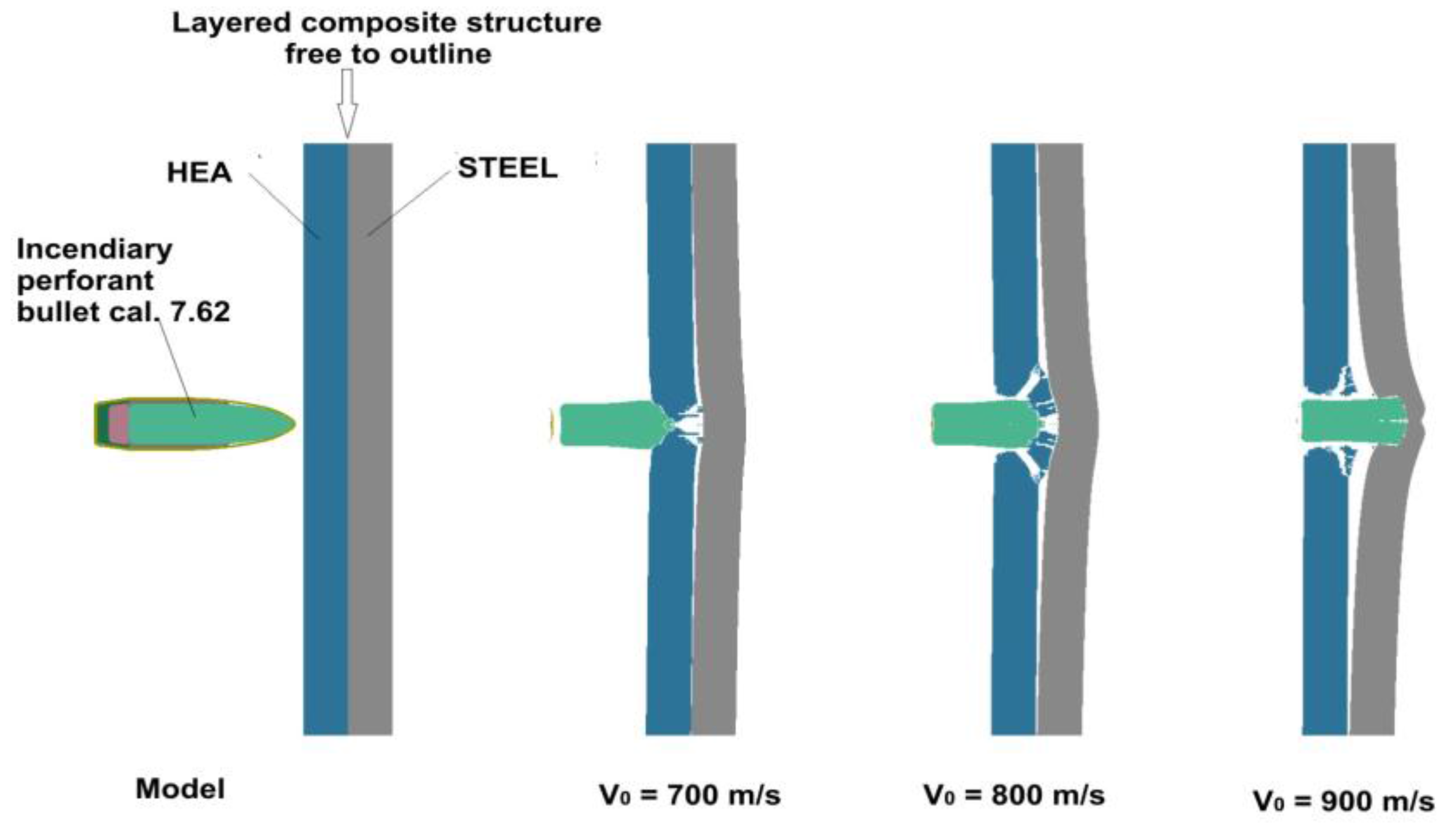
- Composite structure: HEA-STEEL free on contourTesting speeds: V01 = 700 m/s; V02 = 800 m/s; V03 = 900 m/s;
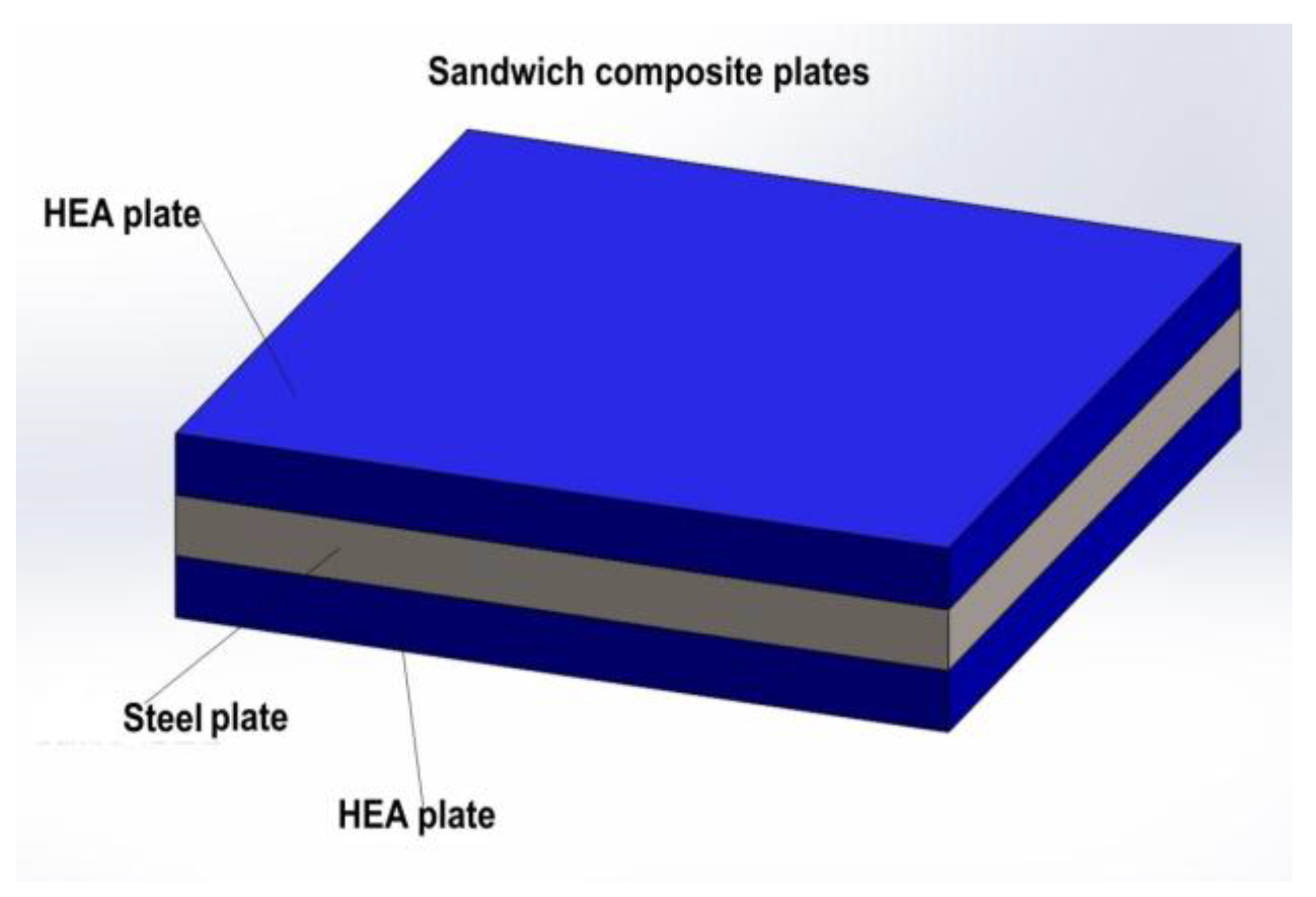
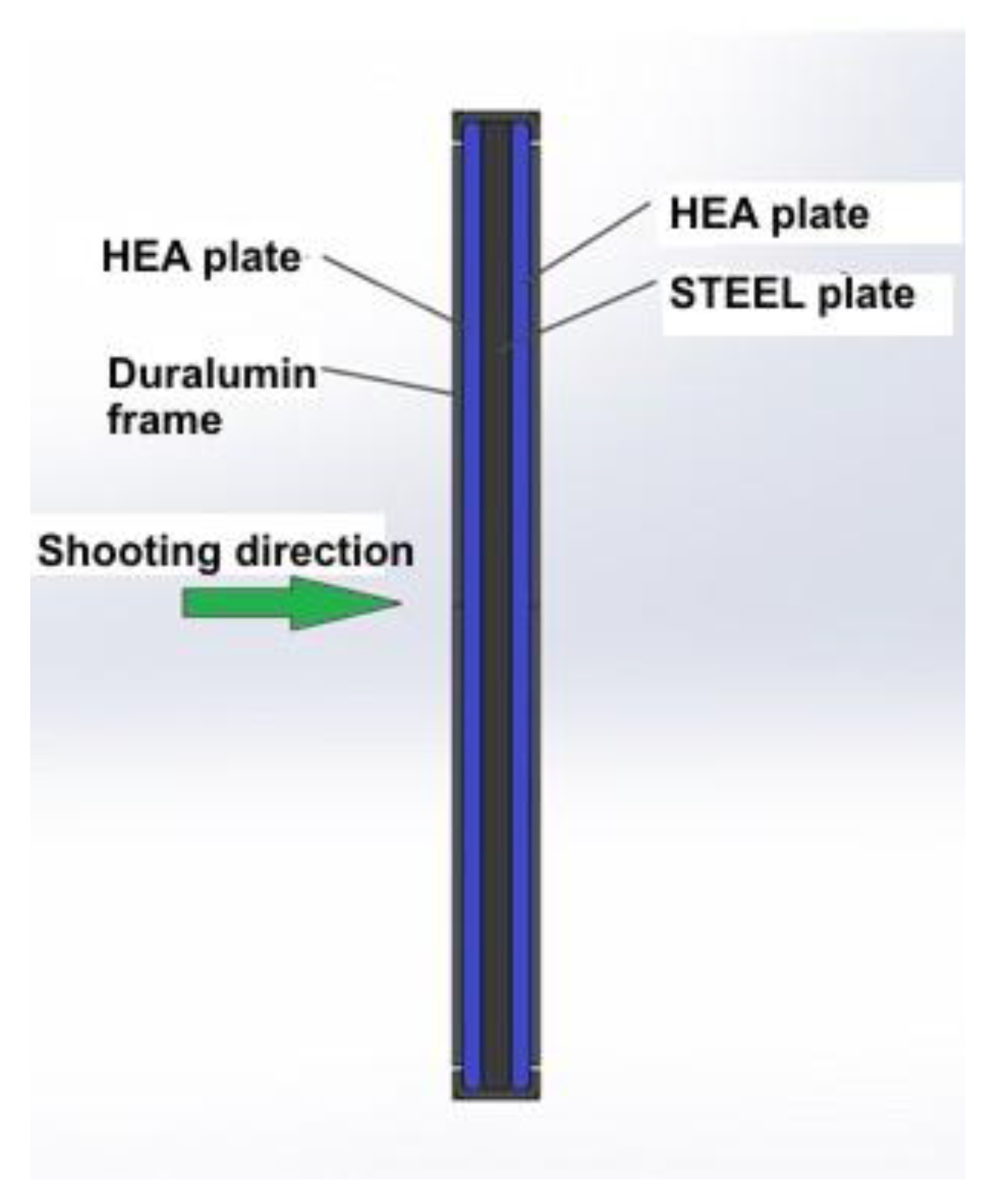
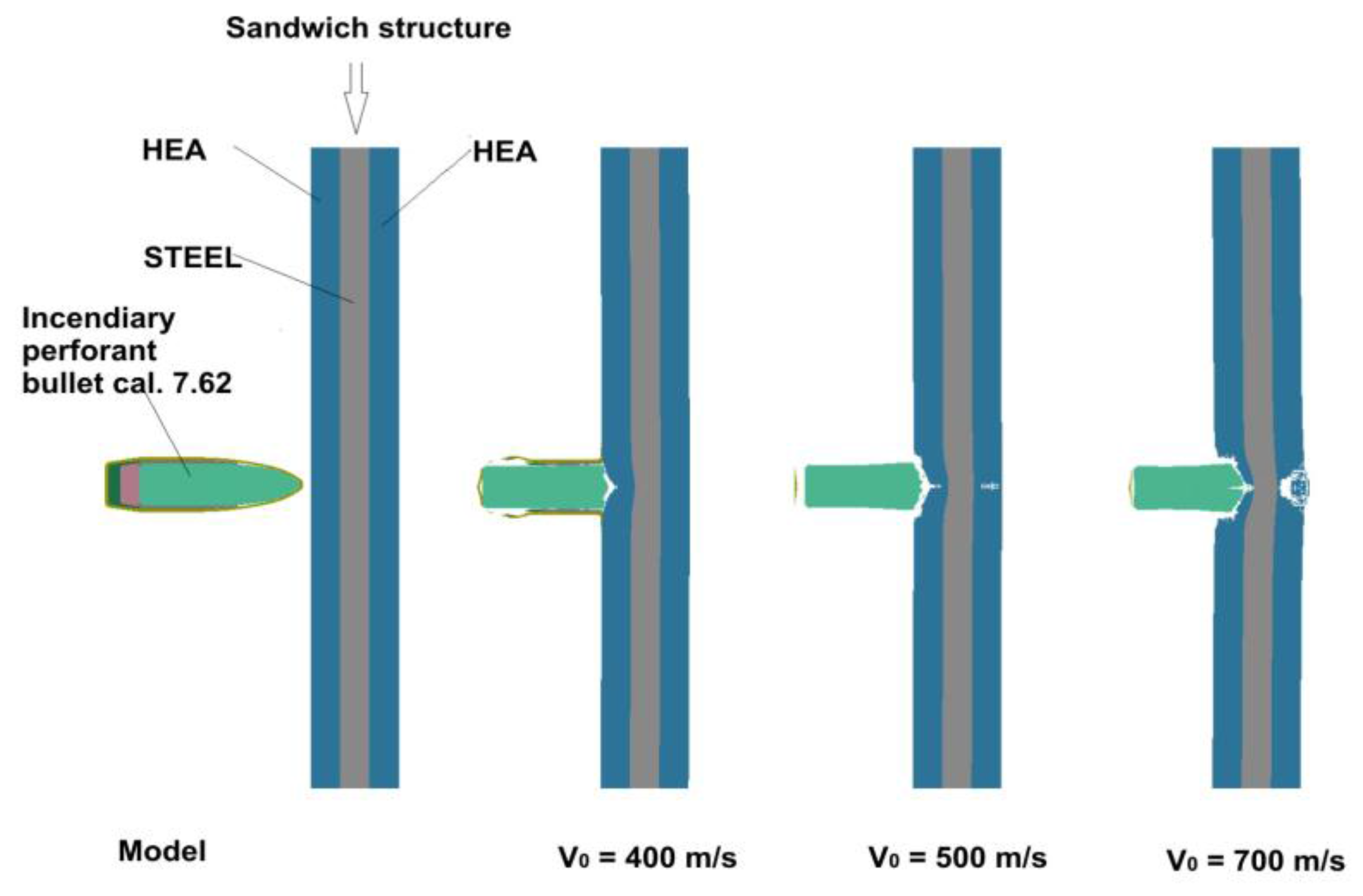
- Composite structure: HEA-STEEL-Duralumin sandwich typeTesting speeds: V01 = 400 m/s; V02 = 500 m/s; V03 = 700 m/s.
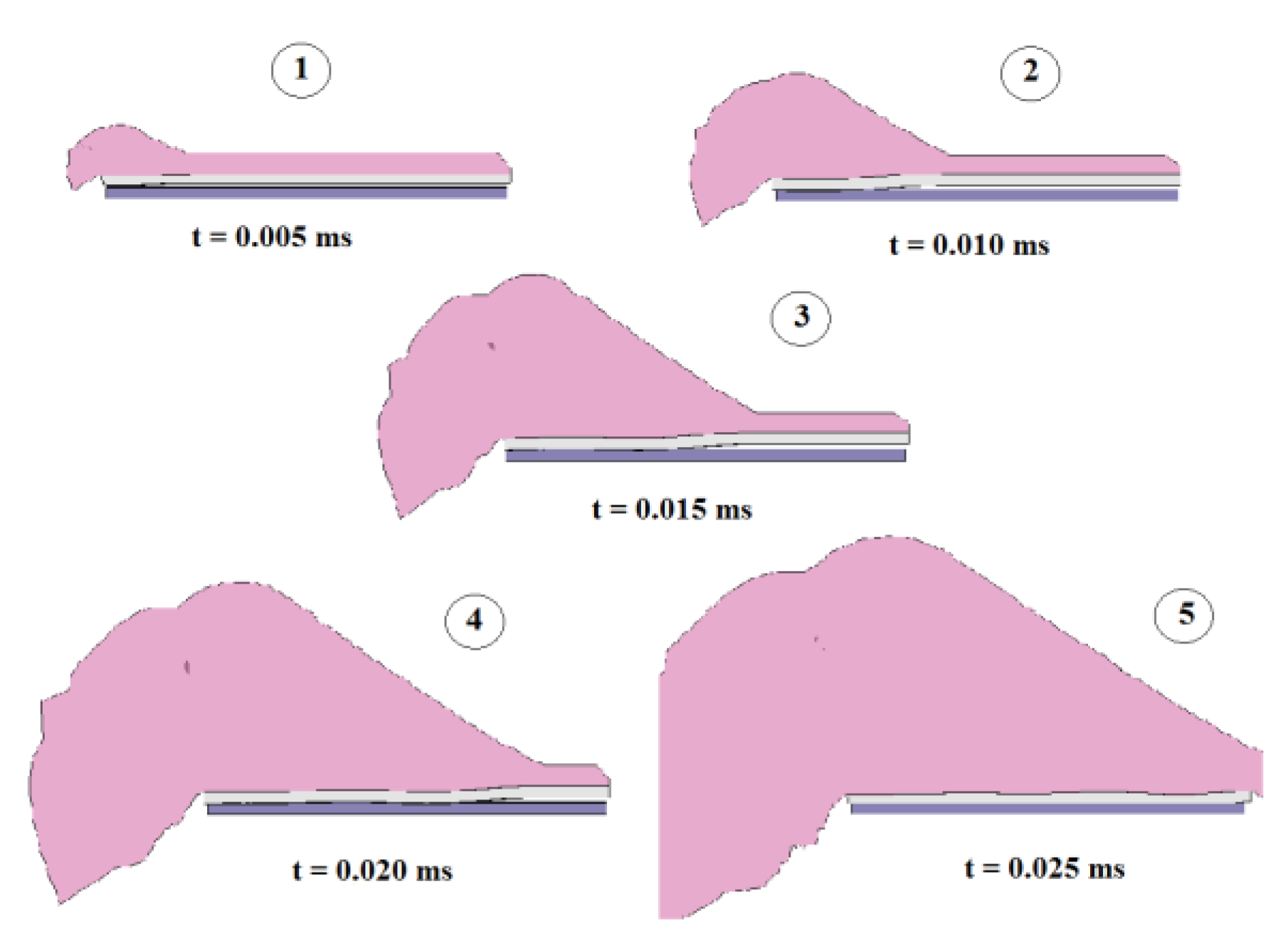
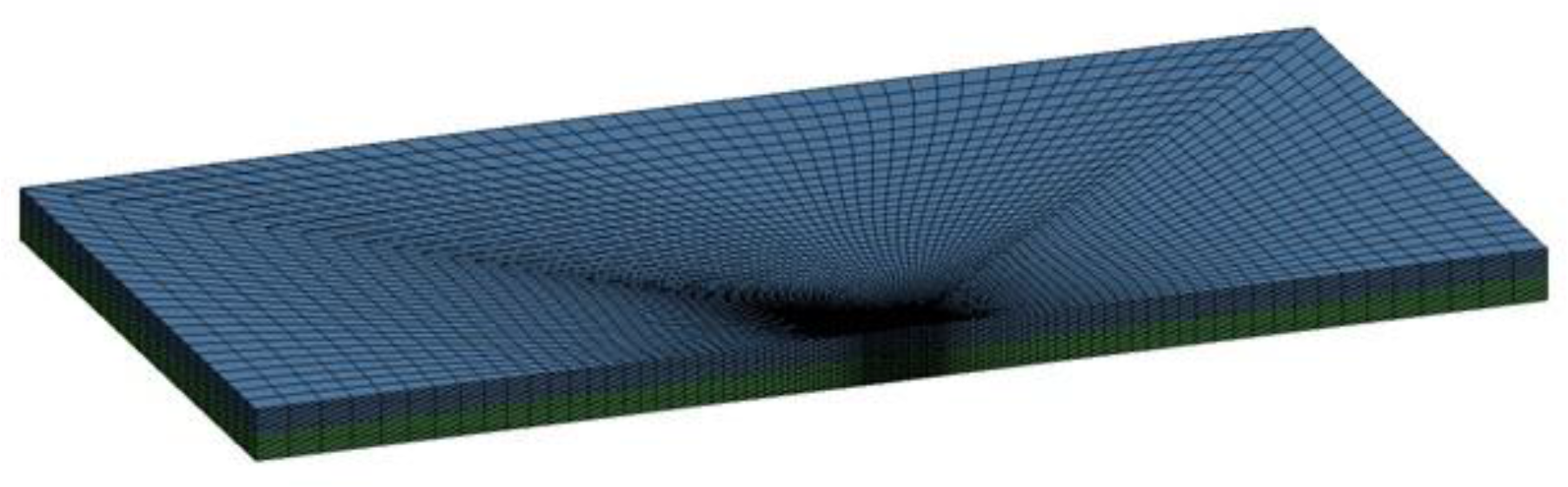
4. Results
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maweja, K.; Stumpf, W. The design of advanced performance high strength low-carbon martensitic armor steels, Microstructural considerations. Mater. Sci. Eng A 2008, 480, 160–166. [Google Scholar] [CrossRef]
- Maweja, K.; Strumpf, W.E. Fracture and ballistic-induced phase transformation in tempered martensitic low-carbon armor steels. Mater. Sci. Eng A 2006, 432, 158–169. [Google Scholar] [CrossRef]
- Hammond, R.I.; Proud, W.G. Does the pressure-induced a-e phase transition occur for all low-alloy steels? R. Soc. 2004, 460, 2959–2974. [Google Scholar] [CrossRef]
- Srivathsan, B.; Ramakrishnan, N. Ballistic performance maps for thick metallic armor. J. Mater. Process. Technol. 1999, 96, 81–91. [Google Scholar] [CrossRef]
- Srivathsan, B.; Ramakrishnan, N. A ballistic performance index for thick metallic armor. Comput. Simul. Model. Eng. 1998, 3, 33–40. [Google Scholar]
- Follensbee, P.S. Adiabatic shear localization in the dynamic punch test, part I: Experimental investigation. Int. J. Plast. 1999, 15, 241–262. [Google Scholar]
- Jena, P.K.; Kumar, K.S.; Krishna, V.R.; Singh, A.K.; Bhat, T.B. Studies on the role of microstructure on performance of high strength armor steel. Eng. Fail. Anal. 2008, 15, 1088–1096. [Google Scholar] [CrossRef]
- Verleysen, P.; Van Slycken, J.; Degriech, J.; De Cooman, B.C.; Samek, L. Impact—Dynamic Behaviour of AL-TRIP Steel. Available online: www.icf11.com/proceeding/EXTENDED/4108.pdf (accessed on 29 August 2017).
- Voiculescu, I.; Geantă, V.; Ștefănoiu, R.; Pătroi, D.; Binchiciu, H. Influence of the chemical composition on the microstructure and microhardness of AlCrFeCoNi high entropy alloy. Rev. Chim. Buchar. 2013, 64, 1441–1444. [Google Scholar]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Gao, M.C.; Yeh, J.W.; Liaw, P.K.; Zhang, Y. High-Entropy Alloys: Fundamentals and Applications, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Geanta, V.; Chereches, T.; Lixandru, P.; Voiculescu, I.; Stefanoiu, R.; Dragnea, D.; Zecheru, T.; Matache, L. Simulation of Impact Phenomena on the Composite Structures Containing Ceramic Plates and High Entropy Alloys. In IOP Conference Series: Materials Science and Engineering, Proceedings of the International Conference on Innovative Research (ICIR Euroinvent), Iasi, Romania, 25–26 May 2017; IOP Publishing: Bristol, UK, 2017; Volume 209. [Google Scholar] [CrossRef]
- Chung, D.D.L. Composite Materials, Science and Application, 2nd ed.; Springer: London, UK, 2010. [Google Scholar]
- Kaminski, M.M. Computational Mechanics of Composite Materials; Springer: London, UK, 2005. [Google Scholar]
- Wang, Y.P.; Li, B.S.; Ren, M.X.; Yang, C.; Fu, H.Z. Effects of creep on interfacial stresses of bonded structures. Mater. Sci. Eng. A Struct. 2008, 497, 471–478. [Google Scholar]
- Geantă, V.; Voiculescu, I.; Ştefănoiu, R.; Savastru, D.; Csaki, I.; Patroi, D.; Leonat, L. Processing and characterization of advanced multi-element high entropy materials from AlCrFeCoNi system. Optoelectron. Adv. Mater. 2013, 7, 874–880. [Google Scholar]
- Kao, Y.F.; Chen, T.J.; Chen, S.K.; Yeh, J.W. Microstructure and mechanical property of as-cast, -homogenized, and -deformed AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. J. Alloy. Compd. 2009, 488, 57–64. [Google Scholar] [CrossRef]
- Shun, T.T.; Du, Y.C. Microstructure and tensile behaviors of FCC Al0.3CoCrFeNi high entropy alloy. J. Alloy. Compd. 2009, 479, 157–160. [Google Scholar] [CrossRef]
- Ştefănoiu, R.; Geantă, V.; Voiculescu, I.; Csaki, I.; Ghiban, N. Researches regarding the influence of chemical composition on the properties of AlxCrFeCoNi alloys. Rev. Chim. Buchar. 2014, 65, 819–821. [Google Scholar]
- Herbrand, M.; Adam, V.; Classen, M.; Kueres, D.; Hegger, J. Strenghtening of existing bridge structures for shear and bending with carbon textile-reinforced mortar. Materials 2017, 10, 1099. [Google Scholar] [CrossRef] [PubMed]
- Wagner, C.; Bhatnagar, A. High Performance Woven and Non-woven Ballistic Materials for Flexible Vest. In Proceedings of the International Conference on Composite Materials (ICCM 14), San Diego, CA, USA, 14–18 July 2003. [Google Scholar]
- Abrate, S. The dynamics of impact on composite structures. Key Eng. Mater. 1998, 141, 671–694. [Google Scholar]
- Cantwell, W.J.; Morton, J. The impact resistance of composite materials—A review. Compos. Part B Eng. 1991, 22, 347–362. [Google Scholar] [CrossRef]
- Classen, M.; Herbrand, M.; Kueres, D.; Hegger, J. Derivation of design rules for innovative shear connections in steel-concrete composites through the systematic use of non-linear finite element analysis (FEA). Struct. Concr. 2016, 17, 646–655. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing elastic-plastic materials with a Split Hopkinson Pressure Bar. Exp. Mech. 2005, 45, 186–195. [Google Scholar] [CrossRef]
- Govender, R.A.; Cloete, T.J.; Nurick, G.N. A numerical investigation of dispersion in Hopkinson Pressure Bar experiments. J. Phys. IV 2006, 134, 521–526. [Google Scholar] [CrossRef]
- Rotariu, A.; Bugaru, M.; Chereches, T. Finite elements method in SHPB developing process. In Proceedings of the 6th WSEAS International Conference on System Science and Simulation in Engineering, Venice, Italy, 21–23 November 2007. [Google Scholar]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing brittle materials with a Split Hopkinson Pressure Bar. Exp. Mech. 2001, 42, 93–106. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Rotariu, A.; Chereches, T. Dedicated software application for split Hopkinson pressure bar and its critical assessment. In Proceedings of the 18th International DAAAM Symposium, Zadar, Croatia, 21–24 November 2007; DAAAM International: Vienna, Austria, 2007; pp. 651–653. [Google Scholar]
- Gorham, D.A. A numerical method for the correction of dispersion in pressure bar signals. J. Phys. E Sci. Instrum. 1983, 16, 477. [Google Scholar] [CrossRef]
- House, J.W.; Lewis, J.C.; Gillis, P.P.; Wilson, L.L. Estimation of flow stress under high rate plastic deformation. Int. J. Impact Eng. 1995, 2, 189–200. [Google Scholar] [CrossRef]
- Erlich, D.C.; Chartagnac, P. Determination of dynamic flow curve of metals at ambient and elevated temperatures by rod impact techniques. J. Phys. 1985, 46, C5-455–C5-462. [Google Scholar] [CrossRef][Green Version]
- Dong, Y.; Feng, S.; Huang, G.; Liu, C.; Xiao, L.; Song, Q. Ballistic impact characteristics of flat-nose projectile penetrating concrete and soil compound target. Int. J. Nonlinear Sci. Numer. 2012, 13, 255–260. [Google Scholar] [CrossRef]
- Huanran, W.; Canyuan, C.; Danian, C.; Chang, D.M. Dynamic constitutive behavior and fracture of lanthanum metal subjected to impact compression at different temperatures and impact tension. Int. J. Nonlinear Sci. Numer. 2013, 14, 21. [Google Scholar]
- Wu, H.J.; Huang, F.L.; Wang, Y.N.; Duan, Z.P.; Shan, Y. Mass loss and nose shape change on ogive-nose steel projectiles during concrete penetration. Int. J. Nonlinear Sci. Numer. 2012, 13, 273–280. [Google Scholar] [CrossRef]
- Structuri Compozite Rezistente la Solicitari Dinamice cu Viteze Mari de Deformare cu Aplicabilitate in Domeniul Protectiei Collective—Composite Structures Resistant at Dynamic Loadings Applied with High Deformation Speeds Used in the Field of Collective Protection—HEAMIL—PCCA 209/2012. Available online: www.uefiscdi.ro (accessed on 24 July 2017).
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading conditions. J. Appl. Phys. 2003, 93. [Google Scholar] [CrossRef]
- Optional Strain-Rate Forms for the Johnson Cook Constitutive Model and the Role of the Parameter Epsilon_01. Available online: http://www.dynalook.com/european-conf-2007/optional-strain-rate-forms-for-the-johnson-cook.pdf (accessed on 2 November 2017).


| Ensemble | Components | Elements | Nodes |
|---|---|---|---|
| Incendiary armor piercing bullet, 7.62 mm caliber | Core | 101,888 | 107,935 |
| Case | 46,080 | 54,719 | |
| Bullet | 20,160 | 24,375 | |
| Primer | 12,288 | 14,847 | |
| Propellant | 9216 | 10,735 | |
| Total | 189,632 | 212,611 | |
| HEA—steel composite structure | HEA | 92,160 | 99,977 |
| Steel | 92,160 | 99,977 | |
| Total | 184,320 | 199,954 | |
| TOTAL | 373,952 | 412,565 | |
| Material | Part | Mechanical Characteristics | ||||
|---|---|---|---|---|---|---|
| Density ρ | Young Modulus E | Poisson Coefficient | Yield Stress σy | Tangential Modulus Et | ||
| Kg/m3 | MPa | - | MPa | MPa | ||
| Hardened steel | Core | 7850 | 2.1 × 105 | 0.3 | 2800 | 15,000 |
| Brass | Case | 8100 | 1.5 × 105 | 0.33 | 320 | 10,000 |
| Lead | Bullet | 11,200 | 1 × 105 | 0.37 | 50 | 100 |
| Low carbon steel | Primer | 7850 | 2.05 × 105 | 0.3 | 210 | 5000 |
| Pyrotechnic material | Propellant | 1200 | 1.0 × 103 | 0.49 | 10 | 20 |
| HEA | Plate 1 | 7720 | 2.2 × 105 | 0.35 | 1550 | 5000 |
| Steel | Plate 2 | 7850 | 2.1 × 105 | 0.3 | 1250 | 3000 |
| Metallic Material | Mechanical Characteristics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Density, ρ | Transverse Modulus, G | Young Modulus, E | Poisson Coefficient, | Johnson–Cook Coefficients | |||||||
| A | B | n | C | m | Tmelt | T0 | |||||
| Kg/m−3 | MPa | MPa | - | MPa | MPa | - | - | - | K | K | |
| HEA | 7720 | 0.81 × 105 | 2.2 × 105 | 0.35 | 1550 | 1200 | 0.24 | 0.032 | 1.00 | 1850 | 300 |
| Armor steel | 7850 | 0.82 × 105 | 2.1 × 105 | 0.3 | 1250 | 3200 | 0.18 | 0.15 | 1.00 | 1763 | 300 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geantă, V.; Cherecheș, T.; Lixandru, P.; Voiculescu, I.; Ștefănoiu, R.; Dragnea, D.; Zecheru, T.; Matache, L. Virtual Testing of Composite Structures Made of High Entropy Alloys and Steel. Metals 2017, 7, 496. https://doi.org/10.3390/met7110496
Geantă V, Cherecheș T, Lixandru P, Voiculescu I, Ștefănoiu R, Dragnea D, Zecheru T, Matache L. Virtual Testing of Composite Structures Made of High Entropy Alloys and Steel. Metals. 2017; 7(11):496. https://doi.org/10.3390/met7110496
Chicago/Turabian StyleGeantă, Victor, Tudor Cherecheș, Paul Lixandru, Ionelia Voiculescu, Radu Ștefănoiu, Daniel Dragnea, Teodora Zecheru, and Liviu Matache. 2017. "Virtual Testing of Composite Structures Made of High Entropy Alloys and Steel" Metals 7, no. 11: 496. https://doi.org/10.3390/met7110496
APA StyleGeantă, V., Cherecheș, T., Lixandru, P., Voiculescu, I., Ștefănoiu, R., Dragnea, D., Zecheru, T., & Matache, L. (2017). Virtual Testing of Composite Structures Made of High Entropy Alloys and Steel. Metals, 7(11), 496. https://doi.org/10.3390/met7110496





