Abstract
To identify the optimal deformation parameters for 316LN austenitic stainless steel, it is necessary to study the macroscopic deformation and the microstructural evolution behavior simultaneously in order to ascertain the relationship between the two. Isothermal uniaxial compression tests of 316LN were conducted over the temperature range of 950–1150 °C and for the strain rate range of 0.001–10 s−1 using a Gleeble-1500 thermal-mechanical simulator. The microstructural evolution during deformation processes was investigated by studying the constitutive law and dynamic recrystallization behaviors. Dynamic recrystallization volume fraction was introduced to reveal the power dissipation during the microstructural evolution. Processing maps were developed based on the effects of various temperatures, strain rates, and strains, which suggests that power dissipation efficiency increases gradually with increasing temperature and decreasing stain rate. Optimum regimes for the hot deformation of 316LN stainless steel were revealed on conventional hot processing maps and verified effectively through the examination of the microstructure. In addition, the regimes for defects of the product were also interpreted on the conventional hot processing maps. The developed power dissipation efficiency maps allow optimized processing routes to be selected, thus enabling industry producers to effectively control forming variables to enhance practical production process efficiency.
1. Introduction
Stainless steels, and in particular 316LN austenitic stainless steel, have been widely used as the piping material for nuclear power plants (NPPs) due to their high resistance to corrosion and oxidation, whilst retaining high strength and excellent ductility over a wide range of temperatures [1]. As of present, the main methods for manufacturing the pipes for the AP1000 nuclear power plants are the use of forging and extrusion technologies to take advantage of the extraordinarily high ductility of the material.
The well-developed microstructures and desired properties are usually formed by the careful control of the strain, strain rate, and temperature [2,3,4,5]. Over the past decade, numerous scholars have attempted to investigate the microstructure of alloys through experimental and theoretical modeling work. A lot of researchers have placed attention on using different measures to analyze flow stress and dynamic recrystallization. Cram [6] extended and successfully applied a physically based description for nucleation in static recrystallization to nucleation during dynamic recrystallization (DRX), and comparisons between experiment and model calculations showed good agreement over a wide range of deformation temperature, initial grain size, and applied strain rate. Beltran [7] developed and validated a model describing recrystallization in metallic materials capable of handling DRX, post-dynamic recrystallization (PDRX), and grain growth against experimental test cases for multi-pass hot deformation of 304L austenitic stainless steel, predicting microstructural evolution due to different recrystallization regimes through a modified Kocks-Mecking equation. Madej [8] compared the mean and full field dynamic recrystallization models and concluded that full field approaches additionally extend predictive capabilities of DRX models by incorporating microstructure evolution in an explicit manner. Many studies have already focused on the investigation of microstructural evolution during the hot deformation in order to obtain eminent mechanical properties for 316LN products. Pan [9] established the constitutive equation for the material, revealing that the best condition for forming through the forging process is to maintain the temperature below 1150 °C and the strain rate below 0.01 s−1. However, the study neglected the effects of deformation processes on the processability of the material. Zhang [10] investigated the high temperature behavior of 316LN and simulated the microstructural evolution during deformation without an explanation of the microstructural evolution in locating the optimal regions for large plastic deformation processes. Bai [11] also constructed the constitutive equation for 316LN in a relatively narrow strain range, but did not explain the means in which microstructural evolution influences the macroscopic deformation. Zhang [12] studied the dynamic and post deformation recrystallization of 316LN stainless steel without clearly identifying the proper processing conditions for the material.
On the contrary to the research above, some researchers only studied the hot workability of the material. Processing maps, depicted by Prasad [13,14] firstly in 1984, can be employed to understand deformation mechanisms and determine the optimal deformation parameters for practical applications. Guo [15] constructed the power dissipation map of 316LN stainless steel without a clear description on its applications. He [16], Guo [17], and Liu [18] investigated the hot workability of 316LN and constructed the hot processing map, but the characteristics of different regions on the conventional processing map should be further detailed. Sun [19] also constructed the hot processing map with metallographic analysis.
In contrast to the large amount of research dedicated to separate investigations of microstructure or the macroscopic deformation of 316LN, the work conducted in this paper has attached importance to the application of the processing map and its characterization of the microstructure. In the interest of determining the optimal regimes for hot deformation of 316LN, it is important to discuss the deformation behavior of the material under different hot deformation conditions through the combined investigation on the macroscopic deformation and the microstructural evolution. Based on the experimental data, the kinetics of dynamic recrystallization for 316LN was illustrated by the use of the Avrami equation. Hot processing maps were established to locate the optimal regimes for the hot deformation of 316LN stainless steel, which were also verified effectively through the exploration of microstructure. To assist industry operators for practical production processes, the updated diagrams of the power dissipation efficiency and instability coefficient against the strain and the temperature were constructed, on which the optimized routes to obtain qualified products were presented.
2. Materials and Methods
The chemical composition of the 316LN specimen material used in the study is listed in Table 1. The present experiments were conducted on a Gleeble-1500 thermal-mechanical simulator (Dynamic Systems Inc., Poestenkill, NY, USA). To ensure the uniformity of the material, homogenizing annealing was employed before the preparation of the specimens. Carbon foils were placed on the top and the bottom of each specimen to reduce the friction between die and specimen during deformation. Cylindrical specimens (12 mm in height and 8 mm in diameter) were heated to 1200 °C at the rate of 10 °C/s and held for 300 s to obtain a homogenized microstructure, and then cooled to various testing temperatures at the rate of 10 °C/s and held for 30 s ahead of the isothermal compression at constant strain rate. The tests were then performed at temperatures between 950 °C and 1150 °C with intervals of 50 °C using uniaxial compression at the strain rates of 0.001 s−1, 0.01 s−1, 0.1 s−1, 1 s−1, and 10 s−1 up to the true (logarithmic) strain of 0.916 (the maximum compression ratio of all specimens was 60%), followed by water quenching. For microstructural investigations, the compressed specimens were then sectioned parallel to the deformation axis, mounted and then polished in aqua regia (HNO3 20 mL, HCl 60 mL).

Table 1.
Chemical composition of 316LN austenitic stainless steel.
3. Results and Discussion
3.1. Constitutive Analysis
The flow curves of experimental 316LN stainless steel at the temperature range of 950–1150 °C and strain rates of 0.001–10 s−1 are shown in Figure 1. As expected, the flow stress is dependent on both the deformation temperature and strain rate. Meanwhile, the flow stress increased with increase of the strain rate and decrease of the temperature. Furthermore, all the flow stress curves increased significantly at the initial stage of hot deformation, attributed to the work hardening, and then followed by a relatively steady state which indicates the occurrence of DRX [20,21].
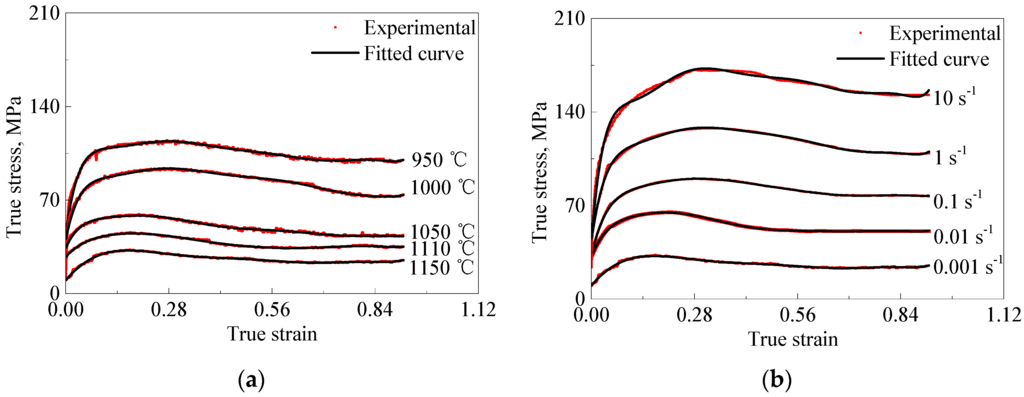
Figure 1.
Flow curves for the 316LN stainless steel at: (a) = 0.001 s−1; (b) T = 1150 °C.
The constitutive equation is an important mathematical model to predict and analyze the relationship among temperature, strain rate, and flow stress during hot deformation. Among all the equations, the Arrhenius-type equation proposed by Sellars [22] is the most widely used. Additionally, the well-known Zener-Hollomon parameter is also widely applied to describe the effects of temperature, strain rate, and apparent activation energy under different deformation conditions.
The Zener-Hollomon parameter can be described as follows:
where Qact is determined as the activation energy of deformation which is the threshold of the dynamic recrystallization; σp is the first peak stress of each curve; is the strain rate; R is the universal gas constant (8.314 J·mol−1·°C−1); T is the temperature; A1, A2, A3, n1, n, β, and α (≈β/n1) are material constants. Equation (2) is a transformation of Equation (1). So the variables can be defined as:
Hence, the parameters required for describing the material behavior are plotted in Figure 2 and the Zener-Hollomon parameter of the 316LN stainless steel can be depicted as:
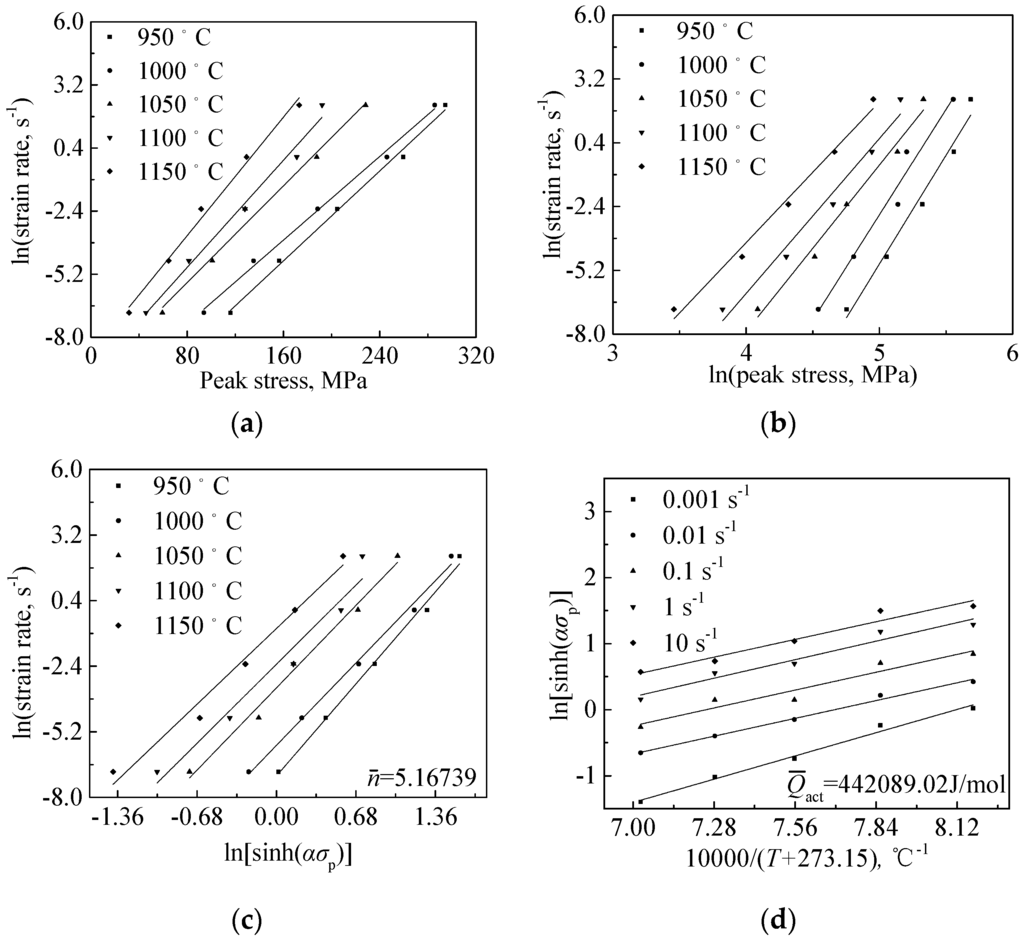
Figure 2.
Relationships between: (a) peak stress and ln(strain rate); (b) ln(peak stress)and ln(strain rate); (c) ln[sinh(ασp)] and ln(strain rate); (d) 10,000/(T + 273.15) and ln[sinh(ασp)].
Therefore, the constitutive equation for hot deformation behavior of the present 316LN stainless steel is given by:
3.2. Microstructure Evolution
Dynamic recovery (DRV) is the softening mechanism during single-stage hot deformation in which the grains are elongated yet the metal seems to exhibit higher ductility, lower stress and lower product strength than in cold working. At other times, equiaxed grains are observed at the end of the process, and if formed during deformation, that would be dynamic recrystallization [20]. Dynamic recrystallization, which is one of the main softening mechanisms at high temperatures, takes place after a critical strain εc has been attained. It is the core characteristic of the softening mechanism of the materials with low and medium stacking fault energy (SFE). When the softening process is governed by dynamic recrystallization, the flow stress passes through a peak σp and drops to a steady state regime, as shown in Figure 3. Generally, the critical strain εc symbolizing the start of DRX can be obtained either by a direct microstructure observation or through an analysis of the flow stress curve. However, microstructure observation is a more complicated and time-consuming method compared to the flow stress curve analysis, as it requires a large number of samples for examination. The flow stress curve analysis method, firstly proposed by Kocks and Mecking [23], and then further developed by McQueen and Ryan [24], can be used to emphasize the point where DRX occurs on the flow stress curve.
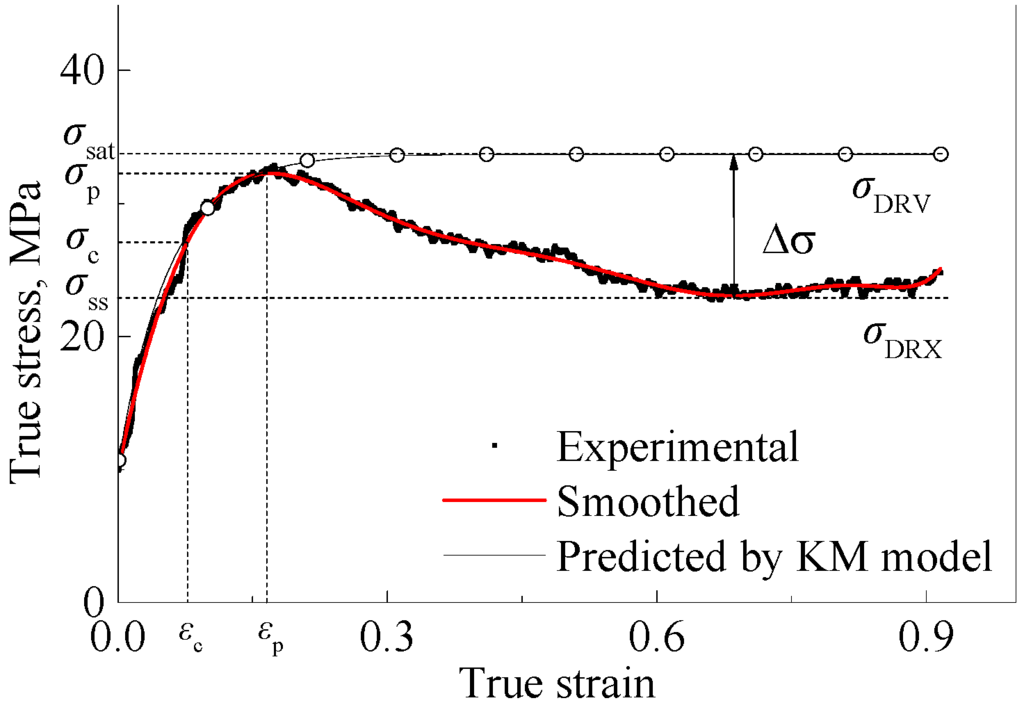
Figure 3.
Schematic description of the flow behavior of 316LN at high temperature T = 1150 °C/ = 0.001 s−1 (σsat is the saturation stress; σss is the steady state stress of the experimental data; σc is the critical stress; σp is the peak stress; εc is the critical strain; εp is the peak strain; Δσ = σsat − σss).
When the dislocation density ρ of the material reaches the dynamic balance, the flow stress tends towards the saturation stress σsat. During the entire process of deformation, work hardening occurs as a result of the refinement of the microstructure caused by the increased strain, and thus the flow stress can be described by:
where σ is the flow stress, ε is the true strain, α1 is dislocation interaction constant relating to dislocation spacing and stress component, G is the shear modulus, and b is the Burgers vector. Based on the Kocks-Mecking model, the apparent hardening depends on the dislocation density which is the result of interplay between storage and annihilation of dislocations as follows:
where k1 and k2 are constants related to microscopic parameters. Consequently, the Kocks-Mecking model assumes that hardening is caused by the increase of the average value of dislocation density, which is directly proportional to the square root of the dislocation density. Therefore, when combined with Equation (7), this can be written as:
and:
where σ0 is the initial real stress, C1 is the integration constant and ρ0 is the initial dislocation density. The equation can also be expressed as:
The research of Poliak and Jonas [25] states that the second derivative of the strain hardening rate θ = dσ/dε against flow stress σ vanishes when DRX begins:
where σc is the stress at critical strain εc. Figure 4a shows the relationship between εc and εp, and it is similar to the result studied by Ji [26]. Figure 4b shows the method to identify the saturation stress σsat and the steady flow stress σss due to the dynamic recrystallization: the intersection point where a tangent line at the critical strain point cuts the x-axis (θ = 0) is the σsat; the intersection point of the lower value where the σ-θ curve cuts the x-axis (θ = 0) is the σss [27,28].
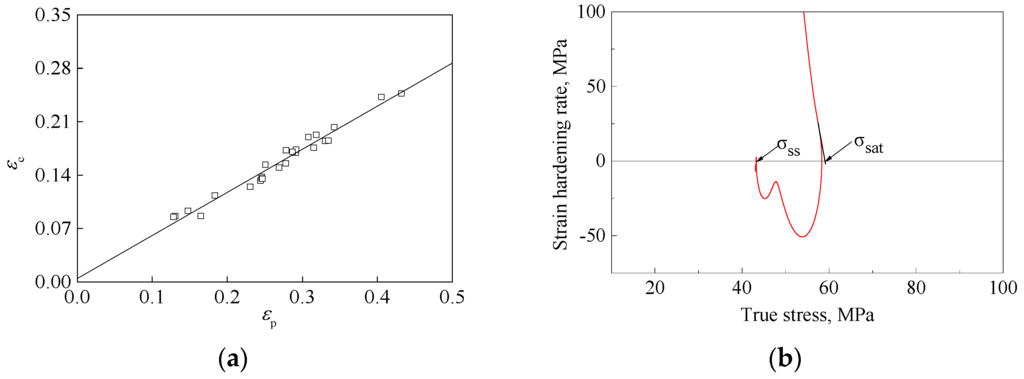
Figure 4.
(a) Relationship between εc and εp; (b) the true stress-strain hardening rate curve at T = 1050 °C/ = 0.001 s−1.
In flow stress models that include DRX, the flow stress is typically modeled as a piecewise function consisting of a strain hardening model, which is valid up to the critical point, and a rule of mixture, which is active when recrystallized and unrecrystallized grains coexist. It is worth mentioning that, for the computation of the flow stress, the Taylor factor has to be considered, but its influence is neglected here for the sake of compact notation [20,25]. If only the first recrystallization cycle is taken into account, the flow stress can be written as follows:
where h(ε) describes the evolution of flow stress due to strain hardening as well as softening by DRV in the absence of DRX, r(ε) describes the flow stress of recrystallized grains as a function of strain (in the first recrystallization cycle only), and X(ε) is the dynamically recrystallized volume fraction. For simplicity, it is assumed that both temperature and strain rate are constant, so that the flow stress is a function of strain only. Thus Equation (14) can also be expressed as:
where Δσ = σsat − σss. Therefore, the conditions in Equation (16) are only fulfilled if, so as to guarantee that κε is continuous which is defined as:
Many models for DRX are the modified forms of the original JMAK equation , due to Kolmogorov, Johnson, and Mehl and Avrami [29] who studied the kinetics of phase transformations. For modified JMAK kinetics to analyze the dynamic recrystallization, the recrystallized volume fraction is given as a function of strain via:
where εp is the first peak strain, q is the constant corresponding to nucleation mode, and α2 is the term associated with the nucleation and growth rates. These parameters can be used to represent the flow behavior of the material under consideration, although some rate equations must also be provided, as will be shown later in the paper. The reader must bear in mind that the latter approach neglects any possible hardening taking place concurrently with the deformation during the dynamic recrystallization regime. This approximation is valid when the deformation process is mainly governed by softening due to dynamic recrystallization, as is generally accepted once the peak stress has been attained. The experimental values of the Avrami exponents reported later also support the validity of this approach. Obviously, at the critical strain, X(εc) = 0.
The recrystallization fraction can also be described as the softening fraction of the deformation, which is given by:
where σDRX is the real stress derived from isothermal compression experimental data, σDRV is the predicted stress without the recrystallization when ε > εc. By plotting against , the material constant α2 and q can be calculated by the slope and the intercept of the linear regression line, as shown in Figure 5. The recrystallization fraction of the 316LN can be given by:
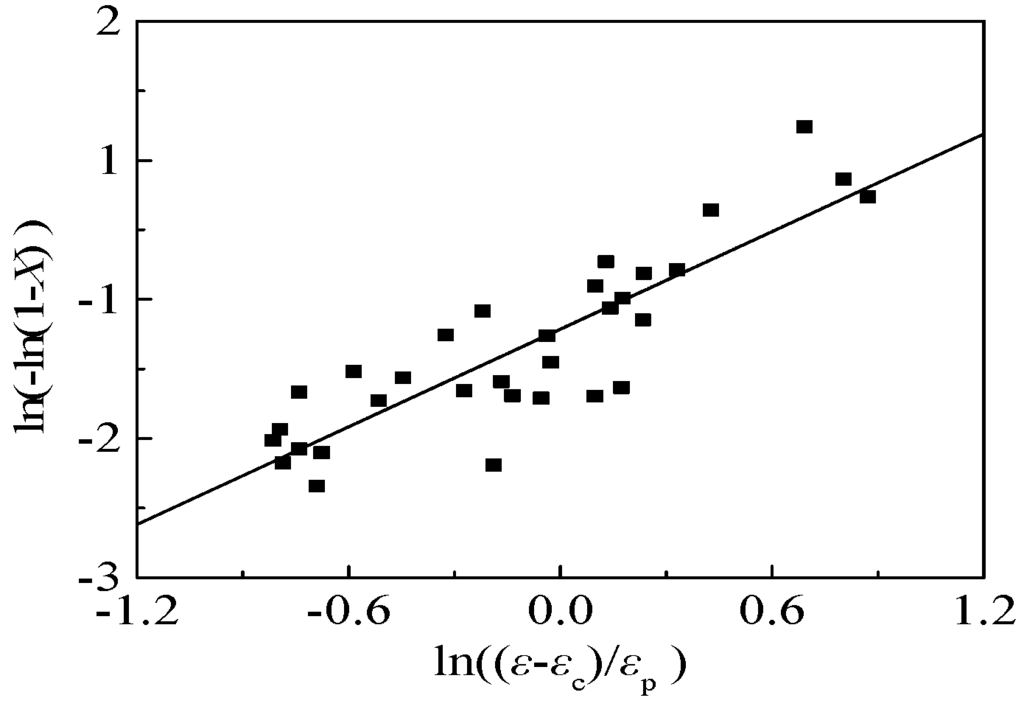
Figure 5.
Dependence of ln(–ln(1 – X(ε))) with ln(ε – εc)/εp.
Figure 6 displays some observed microstructures (taken by using DM4000M) at different strains during the isothermal compression experiments at 1150 °C and strain rate of 0.01 s−1. Figure 6a displays the initial microstructure of the material, in which the average size of the initial grains is measured to be about 75 μm. Figure 6b displays microstructure after deformation to a strain of 0.1, and because of the orientation difference between adjacent grains, smaller grains emerge at the grain boundaries. The mixed partially recrystallized structure observed in Figure 6c was attained after being compressed to a strain of 0.4, and the occurrence of dynamic recrystallization (finer equiaxed grains) during deformation can be clearly recognized, showing that the average size of the newly formed grains is measured to be about 45 μm. But there are still some unexpected grains (grain diameters above 45 μm at spot A). Figure 6d displays recrystallized grains obtained after being compressed to a strain of 0.9, in which grains are 75% (average size is measured to be about 20 μm) smaller than that of the initial microstructure state, corresponding to steady state of stresses.

Figure 6.
Microstructures of 316LN stainless steel at T = 1150 °C and = 0.01 s−1: (a) initial microstructure; (b) ε = 0.1; (c) ε = 0.4; (d) ε = 0.9.
3.3. Hot Deformation Behavior of 316LN Stainless Steel
Processing maps are constructed based on the dynamic materials model (DMM) in which the materials are considered as a dissipater of power [30,31]. The dynamic power dissipation at a certain deformation condition, i.e., at a constant temperature and strain rate, is partitioned by strain rate sensitivity (SRS) m. It is clear that the majority of dissipated power is transformed into heat resulting in a temperature rise, and only a small fraction of energy causes microstructure evolution. The total power dissipation (P) consisting of two complementary functions G and J is given by:
The quantity G which is given under the true stress-true strain rate curve, is designated as dissipater power content and its complementary component J as the dissipater power co-content. J in the model is assumed to be related to the microstructural changes occurring along with the deformation, as opposed to G which is related to continuum effects. As a rule of thumb, most of the dissipation is attributed to the temperature rise (G content), while a small amount is attributed to microstructural changes (J content). According to the dynamic constitutive equation for a certain condition of strain, temperature, and initial microstructure, the energy partitioning between G and J is determined by the strain rate sensitivity parameter (m) as follows:
In Equation (23), dynamic recrystallization volume fraction is introduced to reveal the power dissipation during the microstructural evolution which is indicated by the strain rate sensitivity value. The SRS value distribution map at strain of 0.4 is constructed depending on various temperatures and strain rates in Figure 7, revealing that the higher SRS values correspond to the regions in which the temperatures are higher than a threshold and the strain rates are relatively lower, which also shows that the dynamic recrystallization volume fraction is relatively higher in these regions. Due to the large strain and the lower strain rate during the deformation, the dislocations in the alloy have enough time to slip and climb, inducing sufficient annihilation and rearrangement of the dislocations, for the recrystallized grains to undergo nucleation growth. On the other hand, as a result of the large amount of heat generated in higher strain rate deformation processes, the microstructure is not uniform and internal flow is disordered [3,5,13,32,33].
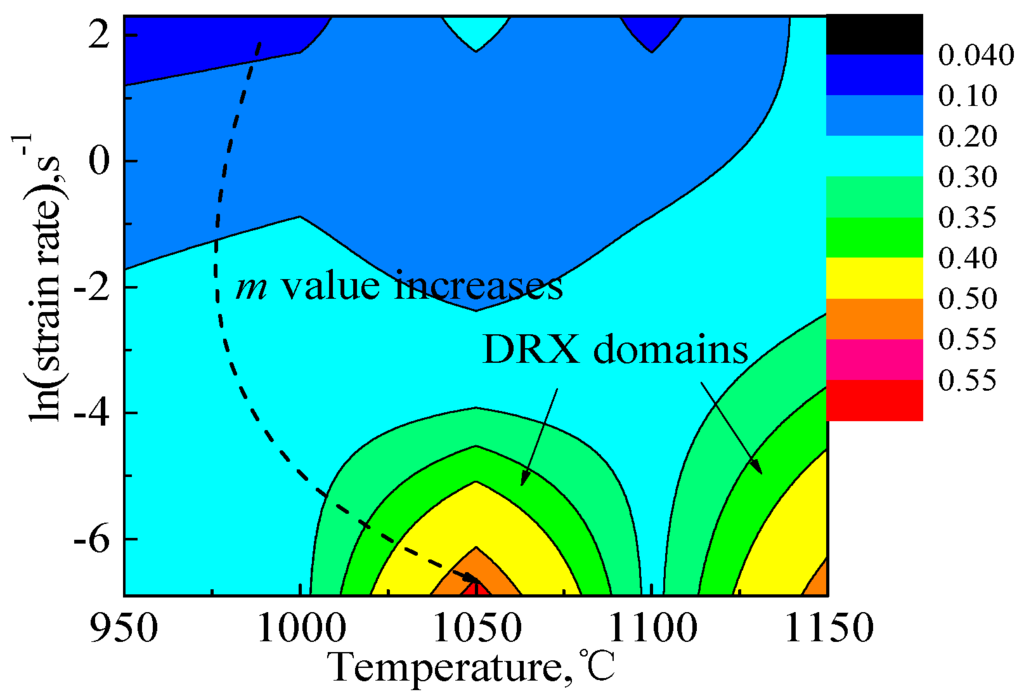
Figure 7.
SRS values at the strain of 0.4 for 316LN stainless steel.
The variation of the dimensionless parameter η, called the efficiency of power dissipation, constitutes a processing map in terms of strain ε, strain rate and temperature T, given by:
Furthermore, the principles of irreversible thermodynamics as applied to continuum mechanics of large plastic flow are explored to define a criterion for the onset of flow instability given by the equation for the instability parameter ζ which was first proposed by Ziegler [34] based on the DMM theory:
If Qact in the Equation (1) is replaced by the deformation energy Q and the σp is replaced by the real stress σ, the strain rate sensitivity m can be described as:
It is obvious that Q and A2 are the functions of strain ε, and it follows that m, η and ζ are also the functions against strain ε. Figure 8 demonstrates the hot processing map of 316LN stainless steel at ε = 0.4 and ε = 0.9. The number against each contour represents the power dissipation efficiency in the processing map, and the shaded area represents the flow instability (unstable) regime.
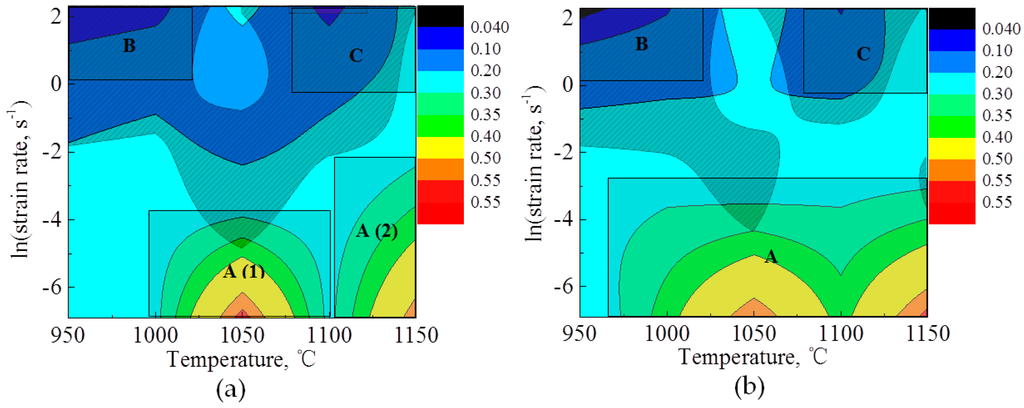
Figure 8.
Hot processing map of 316LN stainless steel at: (a) ε = 0.4; (b) ε = 0.9 (The legend scale represents the power dissipation efficiency).
The map at a strain of 0.4 exhibits four domains in the following temperature ranges and strain rate ranges: (A(1)) 1010–1085 °C and 0.001–0.01 s−1, with a peak efficiency of about 57% occurring at 1050 °C/0.001 s−1; (A(2)) 1110–1150 °C and 0.001–0.03 s−1, with a peak efficiency of about 53% occurring at 1150 °C/0.001 s−1; (B) 950–1010 °C and 3.25–10 s−1, with a peak efficiency of about 10%; as well as (C) 1100–1150 °C and 1–10 s−1, with a peak efficiency of about 31%.
The microstructures at ε = 0.4 obtained on a specimen deformed at 1150 °C/0.01 s−1 (Figure 6c) corresponds to the domain A(2) in Figure 8a, representing dynamically recrystallized microstructure with typical wavy grain boundaries and showing fine grains (average grain diameter is about 45 μm), while there are still some unexpected grains (grain diameters above 45 μm at spot A) due to the insufficient deformation. Domains A(1) and A(2) in Figure 8a transform into one domain in Figure 8b owing to the abundant dynamic recrystallization in the temperature range of 990–1150 °C and the strain rate range of 0.001–0.01 s−1 with the peak efficiency of 0.57 occurring at 1150 °C/0.001 s−1 (domain A in Figure 8b). The domain B in Figure 8a is the regime assumed to be inappropriate for hot deformation because its power dissipation efficiency is very low and its instability parameter ξ < 0. Along with the increase of strain, the power dissipation efficiency becomes smaller (shown as the domain B in Figure 8b), which means it may cause tearing, surface cracking, inter-crystalline cracks, or inhomogeneous microstructure. The microstructure of the specimen deformed at the temperature range of 1100–1150 °C and strain rate range of 1–10 s−1 (shown as the domain C in Figure 8a,b) corresponds to the flow instability regime exhibiting flow localization. In the localized regions, the material has undergone static recrystallization during cooling resulting in fine grains along the localized bands [3,5].
The conventional hot processing map sheds light on the relationships between the processability of the material and the strain rate. But in the practical hot deformation of the material, the strain rate does not change significantly during the process, especially in tube extrusion and bar extrusion processes. Therefore, it is necessary to construct an updated hot processing map according to Equation (26) which reveals the relationship of the variation of the power dissipation efficiency with the increase of the strain (shown in Figure 9). In Figure 9a, there are some shaded areas which are inappropriate for processing, so it is practical to avoid these regions to control the microstructure evolution through reining in the temperature during the process. In Figure 9b, the instability regime becomes even bigger, and the eligible region for obtaining the products with fine grain microstructures becomes smaller.
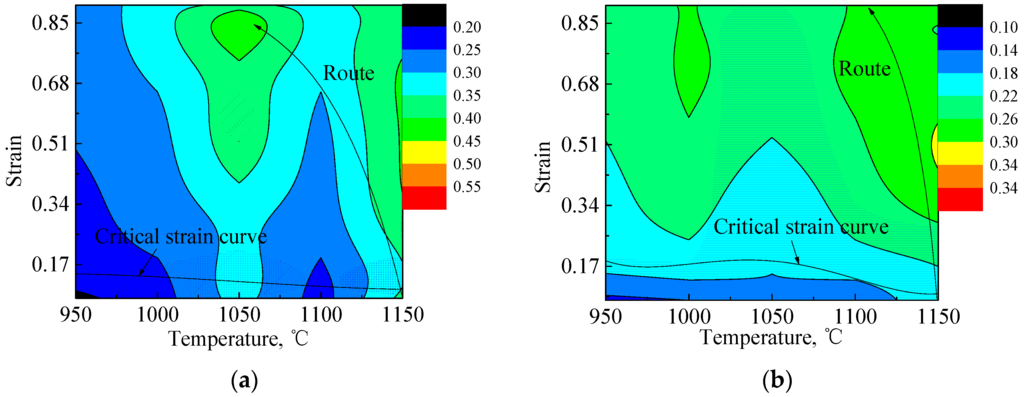
Figure 9.
Updated hot processing map of 316LN stainless steel at (a) = 0.01 s−1; and (b) = 0.1 s−1 (The legend scale represents the power dissipation efficiency. Critical strain curve is believed to be the start of the dynamic recrystallization).
4. Conclusions
The hot deformation behavior and dynamic recrystallization of 316LN stainless steel were studied by conducting isothermal compression tests over a wide range of temperatures and strain rates. The apparent activation energy was quantified, and a constitutive equation for hot deformation behavior was elaborated in the paper. The DRX of 316LN stainless steel was investigated and the parameters of JMAK equation were quantified. The following conclusions are drawn:
(1) Processing maps were produced that exhibit two domains for ε = 0.4 within the temperature and strain rate ranges: (a) 1010–1085 °C/0.001–0.01 s−1 and (b) 1110–1150 °C/0.001–0.03 s−1, in which dynamic recrystallization is apt to occur. The dynamic recrystallization domain at ε = 0.9 in the temperature range of 990–1150 °C and the strain rate range of 0.001–0.01 s−1 with the peak efficiency of 0.57 occurring at 1150 °C/0.001 s−1 is illustrated on the processing map.
(2) The updated processing maps have demonstrated that careful process design has to be followed to enable successful deformation process and microstructural control, and the instability regions can be avoided along with the decrease of the temperature during deformation.
Acknowledgments
The work presented in this paper has been supported by National Science and Technology Major Projects “High-end CNC Machine Tools and Basic Manufacturing Equipment” (No. 2014ZX04014-51), National Natural Science Foundation of China (No. 51105029, 51575039) and NSAF (No. U1330121).
Author Contributions
Chaoyang Sun and Yu Xiang designed and conducted the experiments; Chaoyang Sun, Mengqi Wang, Zhihui Sun, Yu Xiang, and Qingjun Zhou analyzed the data; Chaoyang Sun and Yu Xiang contributed to writing and editing of the manuscript; Denis J. Politis polished the English.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, S.; Yang, B.; Zhang, M.; Wu, H.; Peng, J.; Gao, Y. Numerical simulation and experimental verification of microstructure evolution in large forged pipe used for AP1000 nuclear power plants. Ann. Nucl. Energ. 2016, 87, 176–185. [Google Scholar] [CrossRef]
- Suresh, K.; Rao, K.P.; Prasad, Y.V.R.K.; Hort, N.; Kainer, K.U. Study of hot forging behavior of as-cast Mg-3Al-1Zn-2Ca alloy towards optimization of its hot workability. Mater. Des. 2014, 57, 697–704. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P. Processing maps and rate controlling mechanisms of hot deformation of electrolytic tough pitch copper in the temperature range 300–950 °C. Mater. Sci. Eng. A 2005, 391, 141–150. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.V.R.K.; Suresh, K. Materials modeling and simulation of isothermal forging of rolled AZ31B magnesium alloy: Anisotropy of flow. Mater. Des. 2011, 32, 2545–2553. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P. Materials modeling and finite element simulation of isothermal forging of electrolytic copper. Mater. Des. 2011, 32, 1851–1858. [Google Scholar] [CrossRef]
- Cram, D.G.; Zurob, H.S.; Brechet, Y.J.M.; Hutchinson, C.R. Modelling discontinuous dynamic recrystallization using a physically based model for nucleation. Acta Metall. 2009, 57, 5218–5228. [Google Scholar] [CrossRef]
- Beltran, O.; Huang, K.; Logé, R.E. A mean field model of dynamic and post-dynamic recrystallization predicting kinetics, grain size and flow stress. Comp. Mater. Sci. 2015, 102, 293–303. [Google Scholar] [CrossRef]
- Madej, L.; Sitko, M.; Pietrzyk, M. Perceptive comparison of mean and full field dynamic recrystallization models. Arch. Civ. Mech. Eng. 2016, 16, 569–589. [Google Scholar] [CrossRef]
- Pan, P.L.; Zhong, Y.X. Research on deformation property of 316LN nuclear main pipe steel at elevated temperature. China Mech. Eng. 2012, 11, 1354–1359. [Google Scholar]
- Zhang, P.P.; Sui, D.S. Modeling of flow stress and dynamic recrystallization for 316LN steel during hot deformation. J. Taiyuan Univ. Sci. Technol. 2014, 1, 44–51. [Google Scholar]
- Bai, Y.Q.; Chen, M.M. Hot deformation and dynamic recrystallization on behaviors of 316LN. J. Taiyuan Univ. Sci. Technol. 2009, 5, 424–427. [Google Scholar]
- Zhang, R.H.; Wang, Z.H.; Shi, Z.P.; Wang, B.; Fu, W.T. Dynamic and post deformation recrystallization of nuclear-grade 316LN stainless steel. Strength. Mater. 2015, 47, 94–99. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P.; Gupta, M. Hot workability and deformation mechanisms in Mg/nano-Al2O3 composite. Compos. Sci. Technol. 2009, 69, 1070–1076. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P. Effect of homogenization on the hot deformation behavior of cast AZ31 magnesium alloy. Mater. Des. 2009, 30, 3723–3730. [Google Scholar] [CrossRef]
- Guo, B.; Ji, H.; Liu, X.; Gao, L.; Dong, R.; Jin, M. Research on Flow Stress During Hot Deformation Process and Processing Map for 316LN Austenitic Stainless Steel. J. Mater. Eng. Perform. 2011, 21, 1455–1461. [Google Scholar] [CrossRef]
- He, A.; Yang, X.; Xie, G.; Wang, X. Processing map and character of hot working of 316LN pipe during hot working process. J. Iron Steel Res. 2015, 27, 34–37. [Google Scholar]
- Guo, M.W.; Wang, Z.H.; Zhou, Z.A.; Sun, S.H.; Fu, W.T. Effect of Nitrogen Content on Hot Deformation Behavior and Grain Growth in Nuclear Grade 316LN Stainless Steel. Adv. Mater. Sci. Eng. 2015. [Google Scholar] [CrossRef]
- Liu, X.G.; Ji, H.P.; Guo, H.; Jin, M.; Guo, B.F.; Gao, L. Study on hot deformation behavior of 316LN austenitic stainless steel based on hot processing map. Mater. Sci. Technol. 2013, 29, 24–29. [Google Scholar] [CrossRef]
- Sun, C.Y.; Li, Y.M.; Xiang, Y.; Yang, J. Hot deformation behavior and hot processing maps of 316LN stainless steel. Rare Met. Mater. Eng. 2016, 45, 688–695. [Google Scholar]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Yang, L.C.; Pan, Y.T.; Chen, I.G.; Lin, D.Y. Constitutive relationship modeling and characterization of flow behavior under hot working for Fe-Cr-Ni-W-Cu-Co super-austenitic stainless steel. Metals 2015, 5, 1717–1731. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Ryan, N.D.; McQueen, H.J. Flow stress, dynamic restoration, strain hardening and ductility in hot working of 316 steel. J. Mater. Process. Technol. 1990, 21, 177–199. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Metall. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Ji, H.P. Microstructure Prediction of 316LN Stainless Steel for Dynamic Recrystallization based on Cellular Automata Method. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, December 2013. [Google Scholar]
- Liu, X.; Zhang, L.; Qi, R.; Chen, L.; Jin, M.; Guo, B. Prediction of Critical conditions for dynamic recrystallization in 316LN austenitic steel. J. Iron. Steel. Res. Int. 2016, 23, 238–243. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P. Hot Working Guide: A Compendium of Processing Maps, 2nd ed.; ASM International: Cleveland, OH, USA, 2015; p. 261. [Google Scholar]
- Avrami, M. Kinetics of phase change. I general theory. J. Chem. Phys. 1939, 7, 1103. [Google Scholar] [CrossRef]
- Venugopal, S.; Mannan, S.L.; Prasad, Y.V.R.K. Optimization of cold and warm workability in stainless steel type AISI 316L using instability maps. J. Nucl. Mater. 1995, 227, 1–10. [Google Scholar] [CrossRef]
- Venugopal, S.; Mannan, S.L.; Prasad, Y.V.R.K. Processing map for mechanical working of stainless steel type AISI 316 L. Scr. Metall. Mater. 1993, 28, 715–720. [Google Scholar] [CrossRef]
- Venugopal, S.; Sivaprasad, P.V.; Prasad, Y.V.R.K. Validation of processing maps for 304L stainless steel using hot forging, rolling and extrusion. J. Mater. Process. Technol. 1995, 59, 343–350. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.V.R.K.; Dzwonczyk, J.; Hort, N.; Kainer, K.U. Hot Deformation mechanisms in AZ31 magnesium alloy extruded at different temperatures: Impact of texture. Metals 2012, 2, 292–312. [Google Scholar] [CrossRef]
- Ziegler, H. Some extremum principles in irreversible thermodynamics, with application to continuum mechanics. Swiss Fed. Inst. Technol. 1962. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).