Crack Detection Method Applied to 3D Computed Tomography Images of Baked Carbon Anodes
Abstract
:1. Introduction
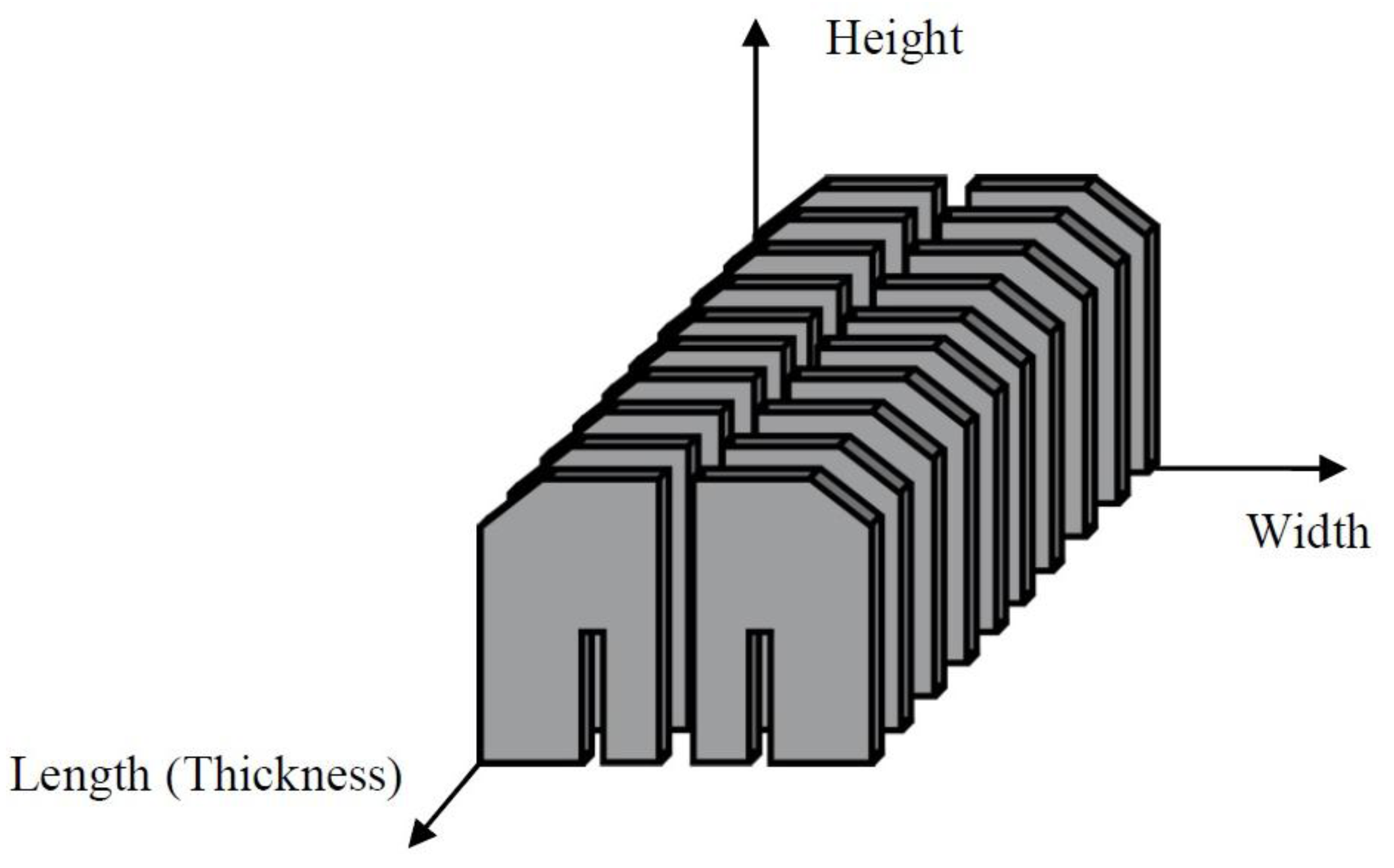
2. Materials and Methods
2.1. X-ray Computed Tomography
2.2. 2D Algorithm Overview
2.3. 3D Algorithm
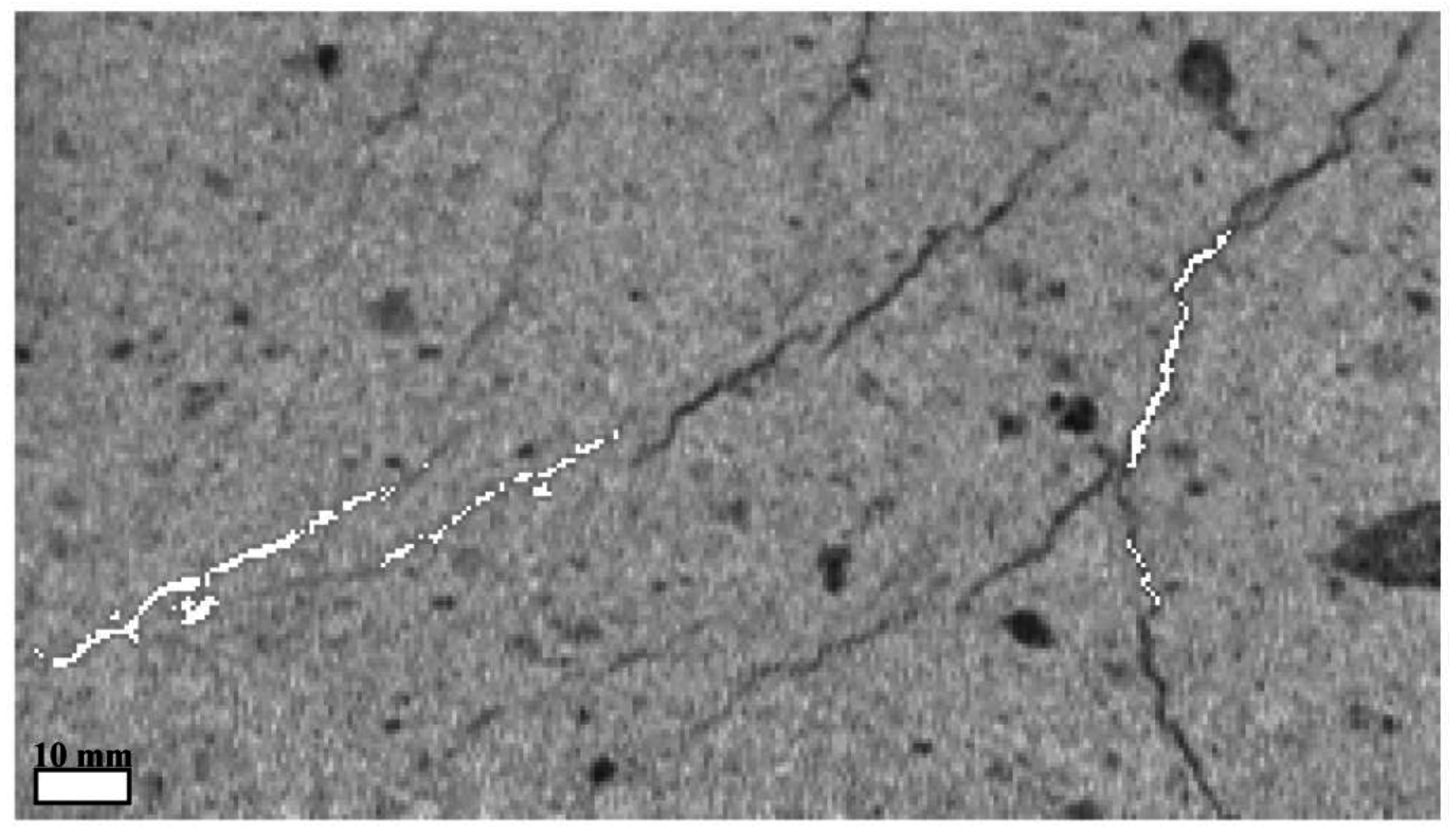
3. Results and Discussion
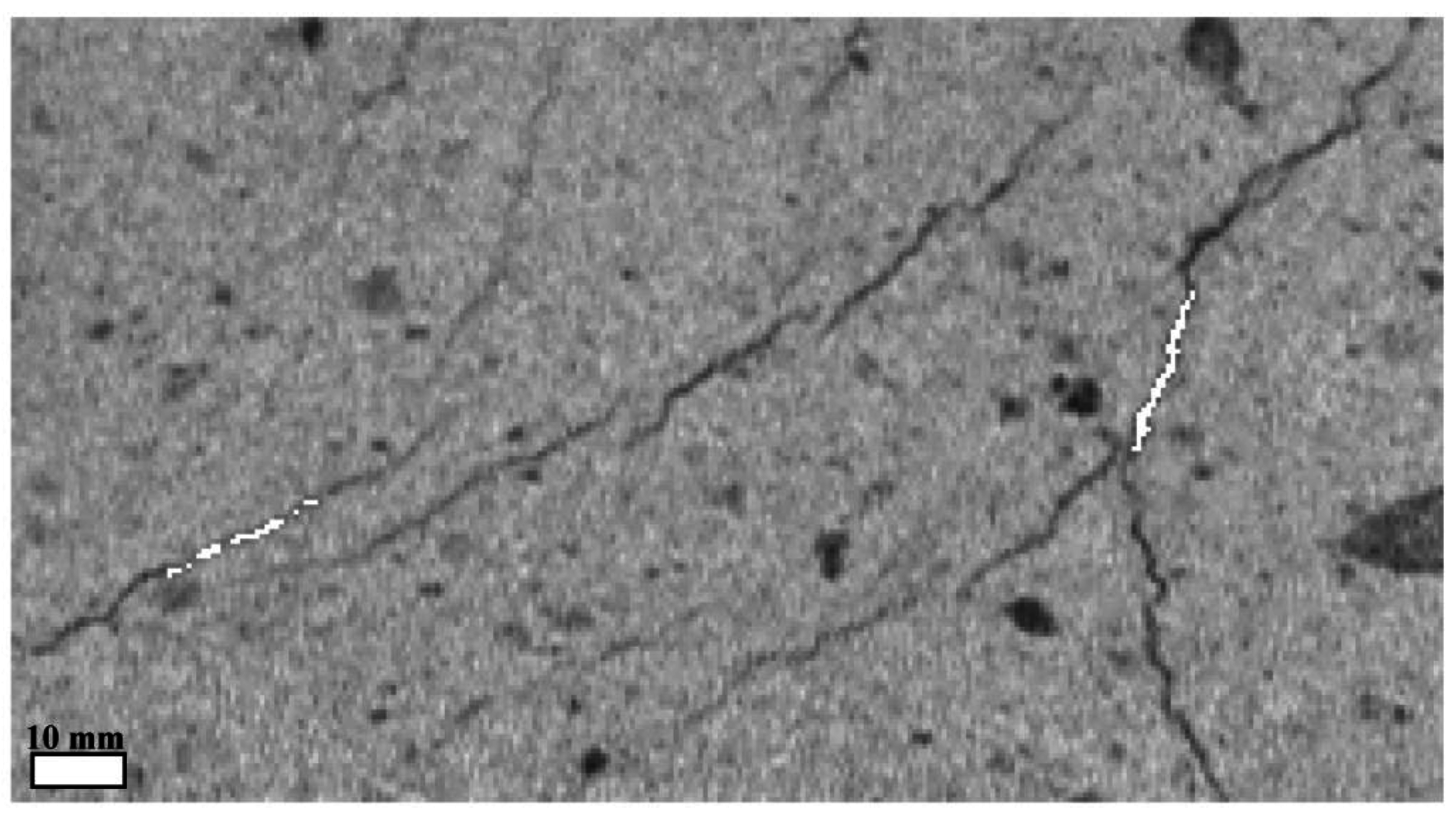
3.1. Pre-Processing
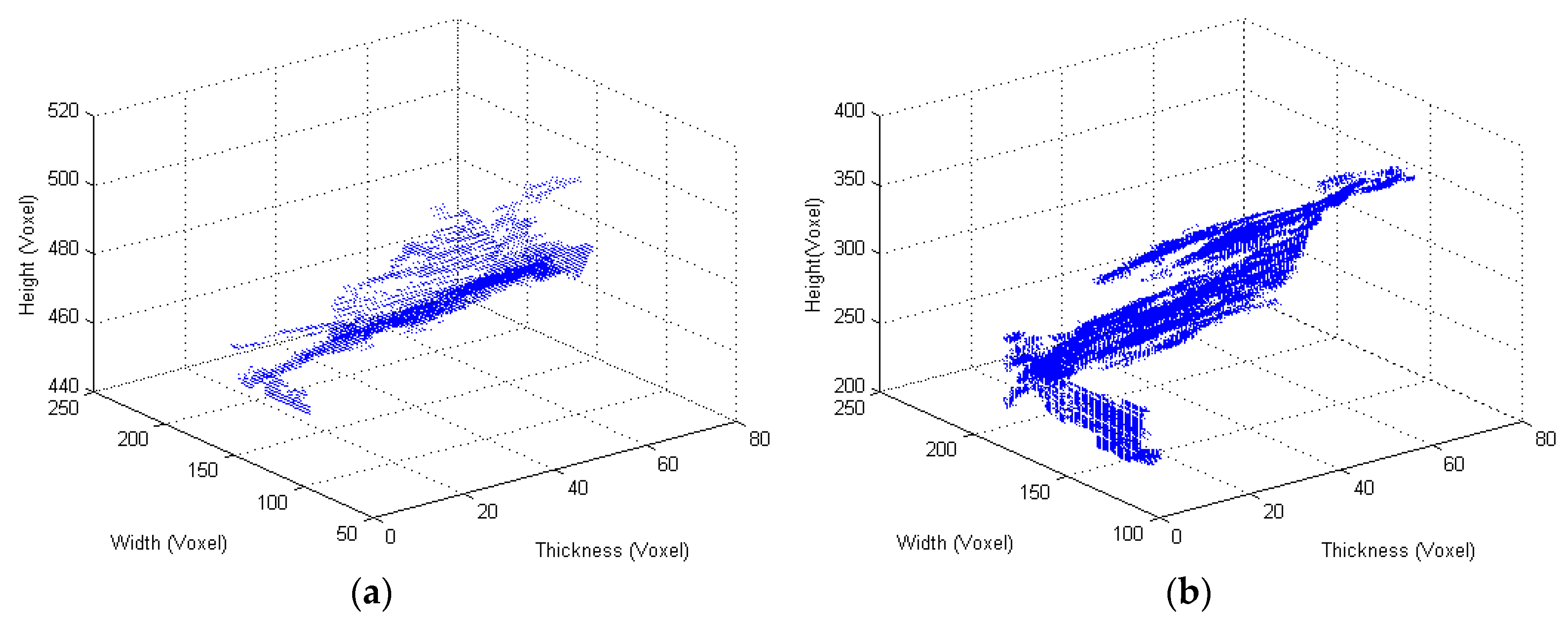
3.2. 3D Percolation—Anode Slice
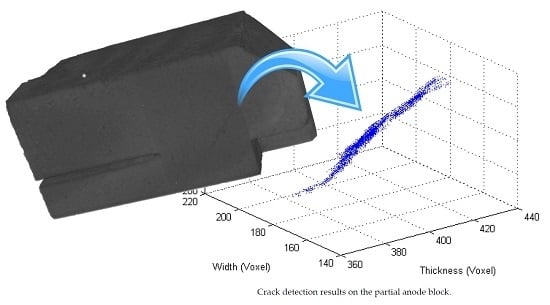
3.3. 3D Percolation—Partial Anode Block
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Edwards, L.; Backhouse, N.; Darmstadt, H.; Dion, M.-J. Evolution of Anode Grade Coke Quality, Proceedings of the Light Metals 2012—TMS 2012 Annual Meeting and Exhibition, Orlando, FL, USA, 11–15 March 2012; Minerals, Metals and Materials Society: Orlando, FL, USA, 2012; pp. 1207–1212.
- Andoh, M.-A.; Kocaefe, D.; Bhattacharyay, D.; Kocaefe, Y.; Marceau, D.; Morais, B. Measurement of the Electric Current Distribution in an Anode, Proceedings of the Light Metals 2016—TMS 2016: 145th Annual Meeting and Exhibition, Nashville, TN, USA, 14–18 February 2016; Minerals, Metals and Materials Society: Nashville, TN, USA, 2016; pp. 889–894.
- Kocaefe, Y.; Kocaefe, D.; Bhattacharyay, D. Quality Control via Electrical Resistivity Measurement of Industrial Anodes, Proceedings of the Light Metals 2015—TMS 2015 Annual Meeting and Exhibition, Orlando, FL, USA, 15–19 March 2015; Minerals, Metals and Materials Society: Orlando, FL, USA, 2015; pp. 1097–1102.
- Amrani, S.; Kocaefe, D.; Kocaefe, Y.; Bhattacharyay, D.; Bouazara, M.; Morais, B. Characterization of cracking mechanisms of carbon anodes used in aluminum industry by optical microscopy and tomography. J. Mater. Eng. Perform. 2016, 25, 4274–4282. [Google Scholar] [CrossRef]
- Chamam, Y.; Kocaefe, D.; Kocaefe, Y.; Bhattacharyay, D.; Morais, B. Effect of Heating Rate during Baking on the Properties of Carbon Anodes Used in Aluminum Industry, Proceedings of the Light Metals 2016—TMS 2016: 145th Annual Meeting and Exhibition, Nashville, TN, USA, 14–18 February 2016; Minerals, Metals and Materials Society: Nashville, TN, USA, 2016; pp. 947–951.
- Meier, M.W. Cracking Behaviour of Anodes; R & D Carbon Ltd.: Sierre, Switzerland, 1996. [Google Scholar]
- Yamaguchi, T.; Hashimoto, S. Fast crack detection method for large-size concrete surface images using percolation-based image processing. Mach. Vis. Appl. 2010, 21, 797–809. [Google Scholar] [CrossRef]
- Naebe, M.; Abolhasani, M.M.; Khayyam, H.; Amini, A.; Fox, B. Crack damage in polymers and composites: A review. Polym. Rev. 2016, 56, 31–69. [Google Scholar] [CrossRef]
- Torok, M.M.; Golparvar-Fard, M.; Kochersberger, K.B. Image-based automated 3D crack detection for post-disaster building assessment. J. Comput. Civ. Eng. 2014, 28, 13. [Google Scholar] [CrossRef]
- Ehrig, K.; Goebbels, J.; Meinel, D.; Paetsch, O.; Prohaska, S.; Zobel, V. Comparison of crack detection methods for analysing damage processes in concrete with computed tomography. In Proceedings of the International Symposium on Digital Industrial Radiology and Computed Tomography, Berlin, Germany, 20–22 June 2011.
- Paetsch, O.; Baum, D.; Ehrig, K.; Meinel, D.; Prohaska, S. Automated 3D Crack Detection for Analyzing Damage Processes in Concrete with Computed Tomography, Proceedings of the iCT2012—Conference on Industrial Computed Tomography University of Applied Sciences, Wels, Austria, 19–21 September 2012; University of Applied Sciences Upper Austria: Wels, Austria, 2012; pp. 321–330.
- Yamaguchi, T.; Hashimoto, S. Automated crack detection for concrete surface image using percolation model and edge information. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 3355–3360.
- Yamaguchi, T.; Hashimoto, S. Image processing based on percolation model. IEICE Trans. Inf. Syst. 2006, E89-D, 2044–2052. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nakamura, S.; Hashimoto, S. An efficient crack detection method using percolation-based image processing. In Proceedings of the ICIEA 2008—3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 1875–1880.
- Babaei, F.; Hong, T.L.C.; Yeung, K.; Cheng, S.H.; Lam, Y.W. Contrast-enhanced X-ray micro-computed tomography as a versatile method for anatomical studies of adult zebrafish. Zebrafish 2016, 13, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Cnudde, V.; Boone, M.N. High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications. Earth Sci. Rev. 2013, 123, 1–17. [Google Scholar] [CrossRef]
- Helliwell, J.R.; Sturrock, C.J.; Grayling, K.M.; Tracy, S.R.; Flavel, R.J.; Young, I.M.; Whalley, W.R.; Mooney, S.J. Applications of X-ray computed tomography for examining biophysical interactions and structural development in soil systems: A review. Eur. J. Soil Sci. 2013, 64, 279–297. [Google Scholar] [CrossRef]
- Mazonakis, M.; Damilakis, J. Computed tomography: What and how does it measure? Eur. J. Radiol. 2016, 85, 1499–1504. [Google Scholar] [CrossRef] [PubMed]
- Adams, A.N.; Karacan, O.; Grader, A.; Mathews, J.P.; Halleck, P.M.; Schobert, H.H. The non-destructive 3-D characterization of pre-baked carbon anodes using X-ray computerized tomography. Light Met. 2002, 2002, 535–539. [Google Scholar]
- Sommerseth, C.; Thorne, R.J.; Orvik, S.R.; Sandnes, E.; Ratvik, A.P.; Lossius, L.P.; Linga, H.; Svensson, A.M. Spatial Methods for Characterising Carbon Anodes for Aluminium Production, Proceedings of the Light Metals 2015—TMS 2015 Annual Meeting and Exhibition, Orlando, FL, USA, 15–19 March 2015; Minerals, Metals and Materials Society: Orlando, FL, USA, 2015; pp. 1141–1146.
- Picard, D.; Alamdari, H.; Ziegler, D.; Dumas, B.; Fafard, M. Characterization of Prebaked Carbon Anode Samples Using X-ray Computed Tomography and Porosity Estimation, Proceedings of the Light Metals 2012, Orlando, FL, USA, 11–15 March 2012; Minerals, Metals and Materials Society: Orlando, FL, USA, 2012; pp. 1283–1288.
- Azari, K.; Alamdari, H.; Aryanpour, G.; Picard, D.; Fafard, M.; Adams, A. Mixing variables for prebaked anodes used in aluminum production. Powder Technol. 2013, 235, 341–348. [Google Scholar] [CrossRef]
- Suriyapraphadilok, U.; Halleck, P.; Grader, A.; Andresen, J.M. Physical, chemical and X-ray computed tomography characterization of anode butt cores. In Light Metals 2005; Kvande, H., Ed.; Minerals, Metals and Materials Society: San Francisco, CA, USA, 2005; pp. 617–621. [Google Scholar]
- Picard, D.; Lauzon-Gauthier, J.; Duchesne, C.; Alamdari, H.; Fafard, M.; Ziegler, D. Automated Crack Detection Method Applied to ct Images of Baked Carbon Anode, Proceedings of the Light Metals 2014, San Diego, CA, USA, 16–20 February 2014; Minerals, Metals and Materials Society: San Diego, CA, USA, 2014; pp. 1275–1280.
- Heimann, T.; Meinzer, H.P. Statistical shape models for 3D medical image segmentation: A review. Med. Image Anal. 2009, 13, 543–563. [Google Scholar] [CrossRef] [PubMed]
- Roseman, A.M. Particle finding in electron micrographs using a fast local correlation algorithm. Ultramicroscopy 2003, 94, 225–236. [Google Scholar] [CrossRef]
- Legland, D.; Kieu, K.; Devaux, M.-F. Computation of minkowski measures on 2D and 3D binary images. Image Anal. Stereol. 2007, 26, 83–92. [Google Scholar] [CrossRef]
- Ben Boubaker, M.; Picard, D.; Duchesne, C.; Tessier, J.; Alamdari, H.; Fafard, M. The potential of acousto-ultrasonic techniques for inspection of baked carbon anodes. Metals 2016, 6, 151. [Google Scholar] [CrossRef]










© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picard, D.; Lauzon-Gauthier, J.; Duchesne, C.; Alamdari, H.; Fafard, M.; Ziegler, D.P. Crack Detection Method Applied to 3D Computed Tomography Images of Baked Carbon Anodes. Metals 2016, 6, 272. https://doi.org/10.3390/met6110272
Picard D, Lauzon-Gauthier J, Duchesne C, Alamdari H, Fafard M, Ziegler DP. Crack Detection Method Applied to 3D Computed Tomography Images of Baked Carbon Anodes. Metals. 2016; 6(11):272. https://doi.org/10.3390/met6110272
Chicago/Turabian StylePicard, Donald, Julien Lauzon-Gauthier, Carl Duchesne, Houshang Alamdari, Mario Fafard, and Donald P. Ziegler. 2016. "Crack Detection Method Applied to 3D Computed Tomography Images of Baked Carbon Anodes" Metals 6, no. 11: 272. https://doi.org/10.3390/met6110272
APA StylePicard, D., Lauzon-Gauthier, J., Duchesne, C., Alamdari, H., Fafard, M., & Ziegler, D. P. (2016). Crack Detection Method Applied to 3D Computed Tomography Images of Baked Carbon Anodes. Metals, 6(11), 272. https://doi.org/10.3390/met6110272