Mechanical Relaxation of Metallic Glasses: An Overview of Experimental Data and Theoretical Models
Abstract
:1. Introduction
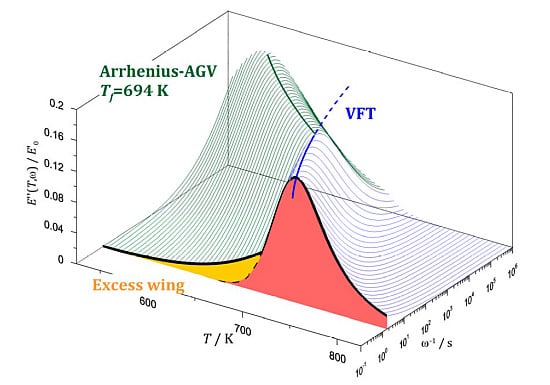
2. Basics of Glass Relaxation Dynamics
2.1. Relaxation in the Supercooled Liquid Region
2.2. Relaxation and Aging below Tg
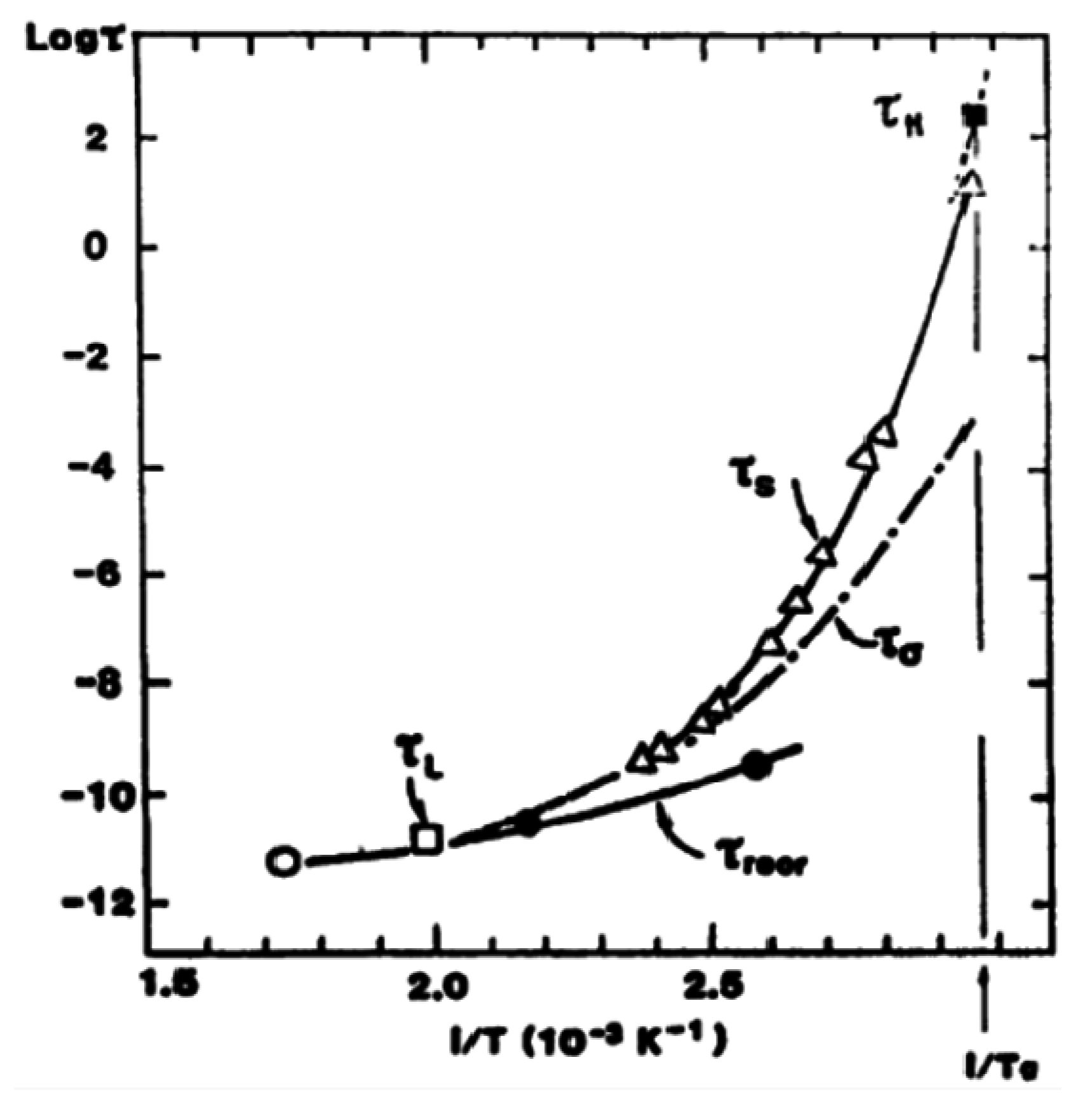
2.3. Theoretical Frameworks for Interpreting Glassy Dynamics
3. Mechanical Relaxation of Glasses
3.1. Introduction to Mechanical Relaxation
| Behavior | Complete Recoverability | Instantaneous | Linear |
|---|---|---|---|
| Ideal elasticity | Yes | Yes | Yes |
| Nonlinear elasticity | Yes | Yes | No |
| Instantaneous plasticity | No | Yes | No |
| Anelasticity | Yes | No | Not necessary |
| Viscoplasticity | No | No | Not necessary |
3.2. Time and Frequency Domain Response Functions
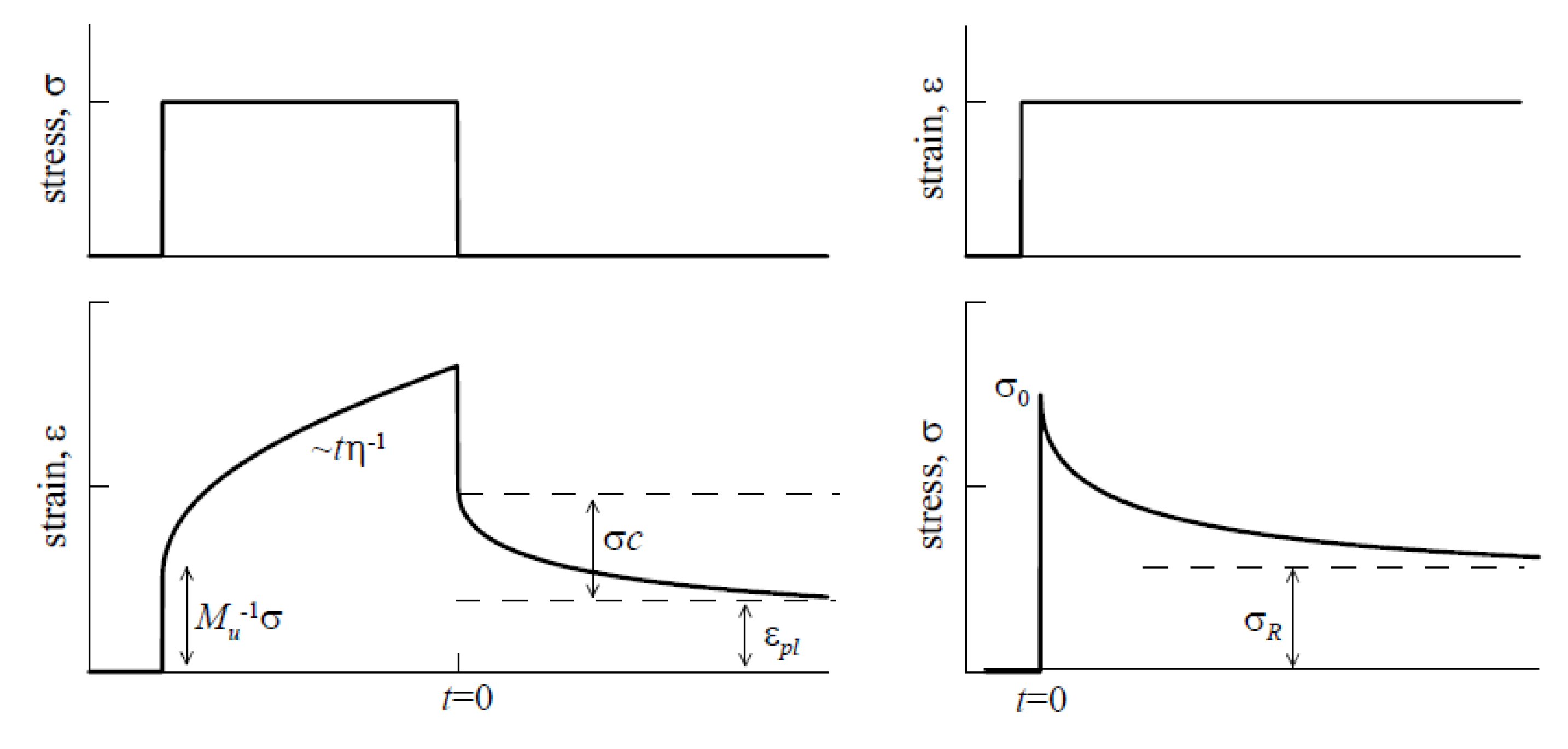
3.3. Thermally Activated Models
4. Mechanical Spectroscopy of Metallic Glasses
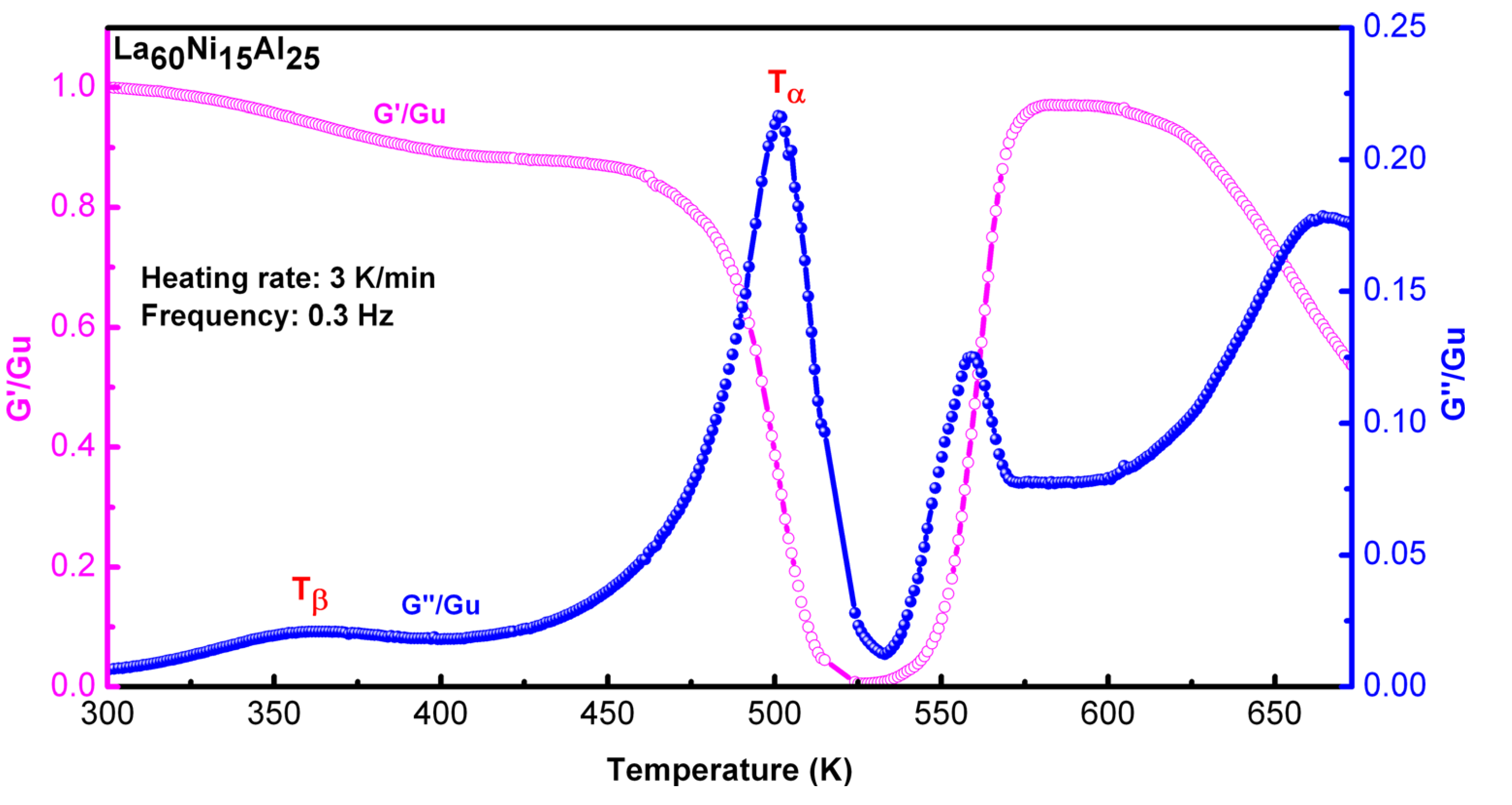
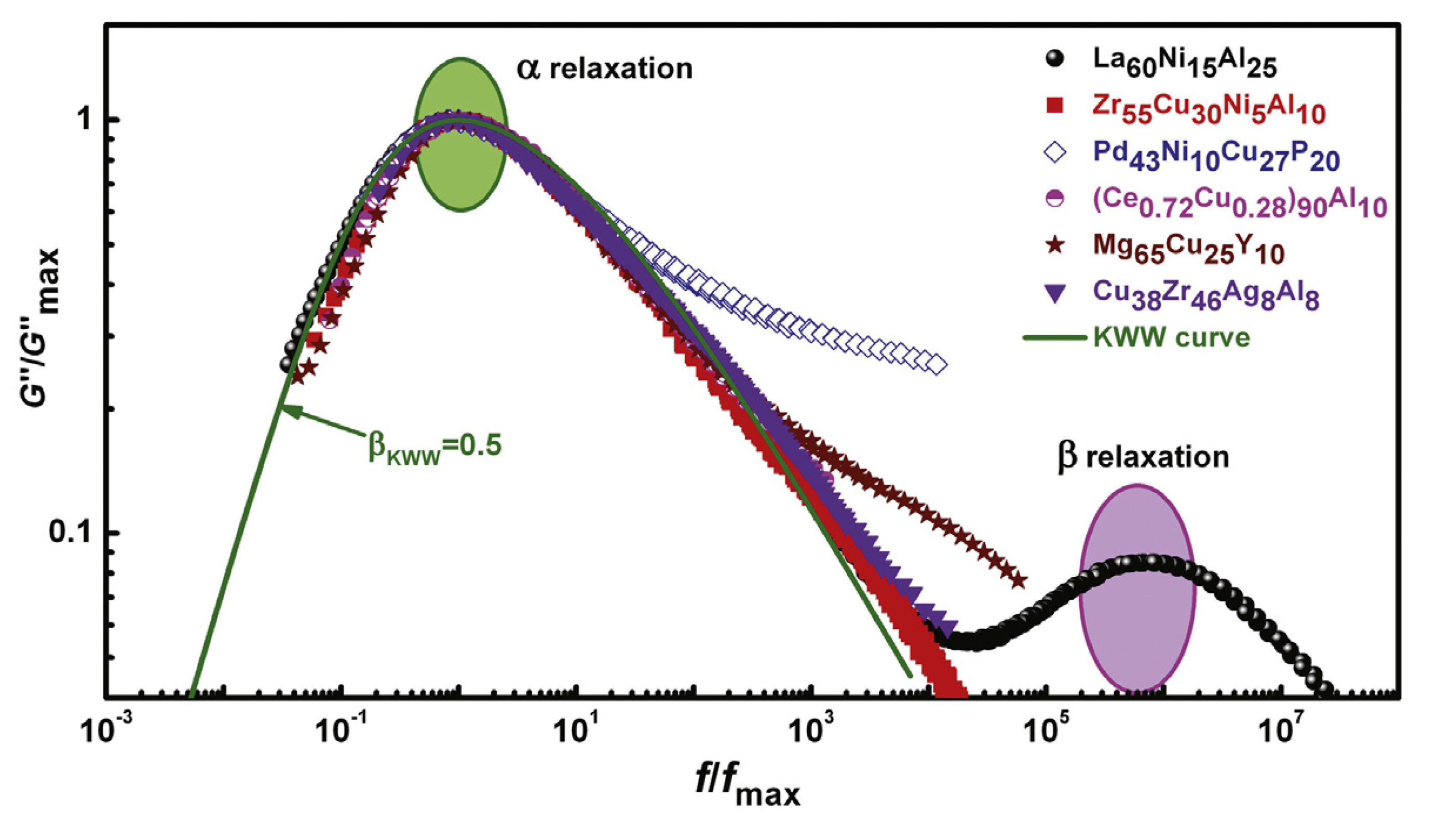
4.1. Secondary Relaxations
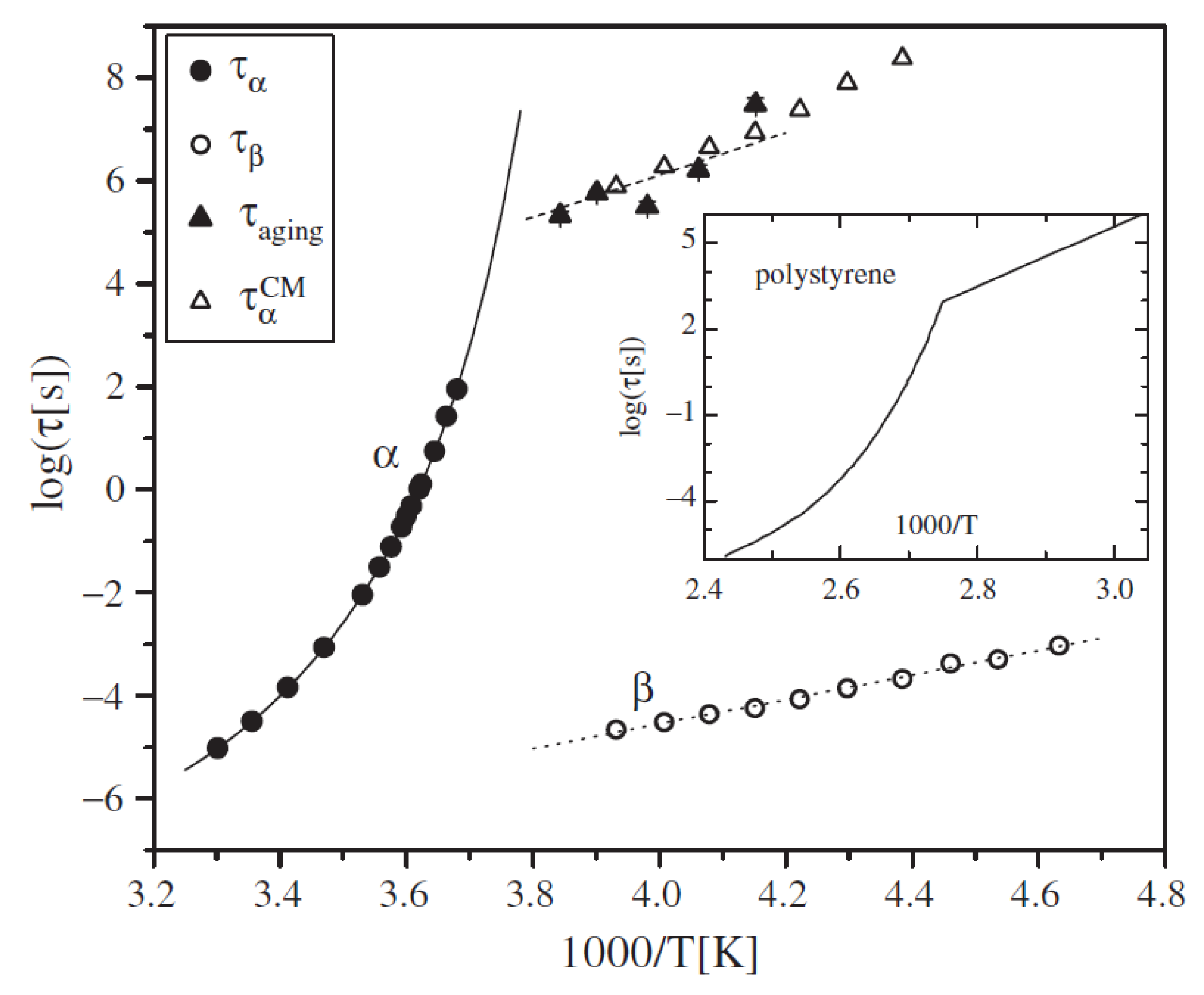

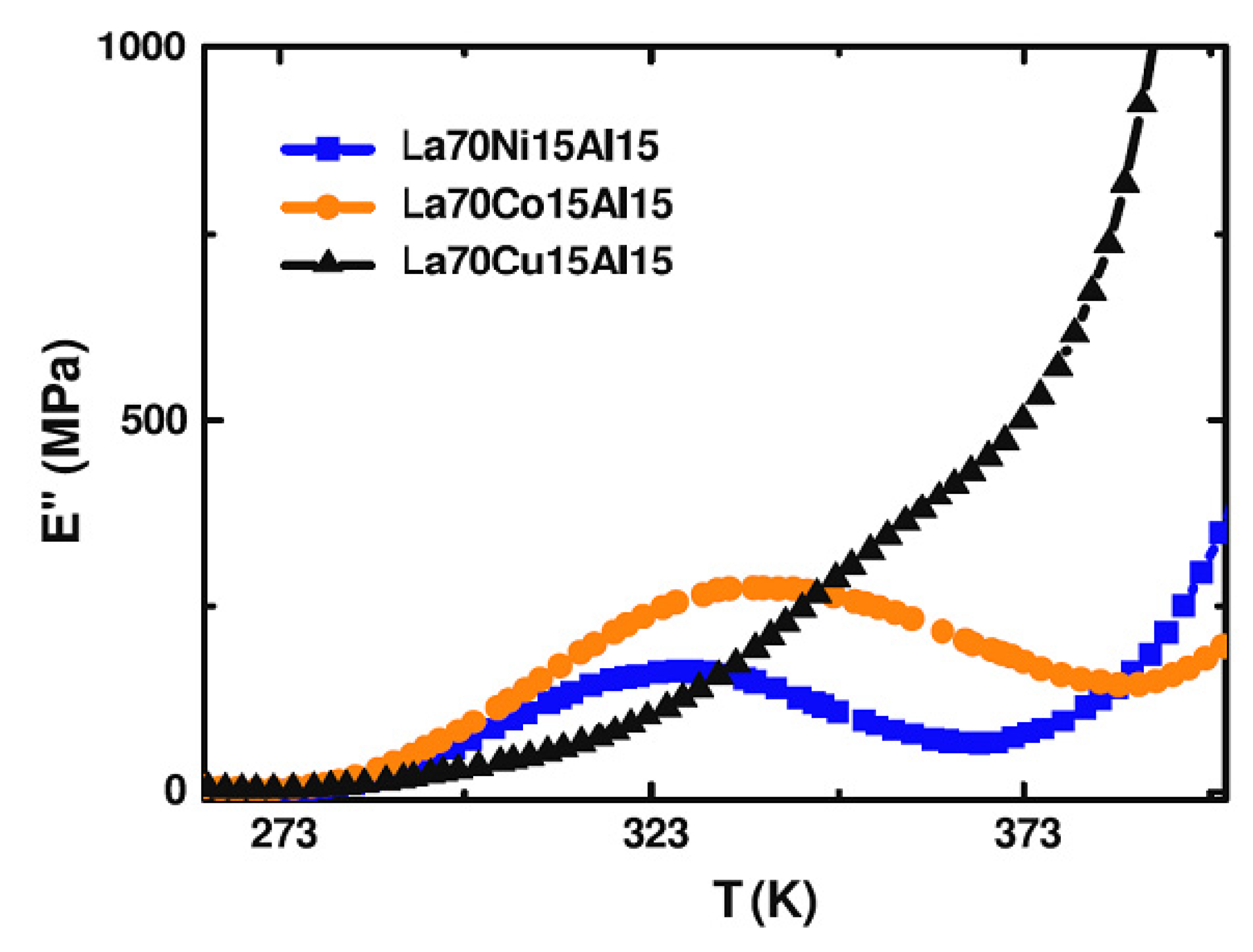
4.2. Influence of Aging
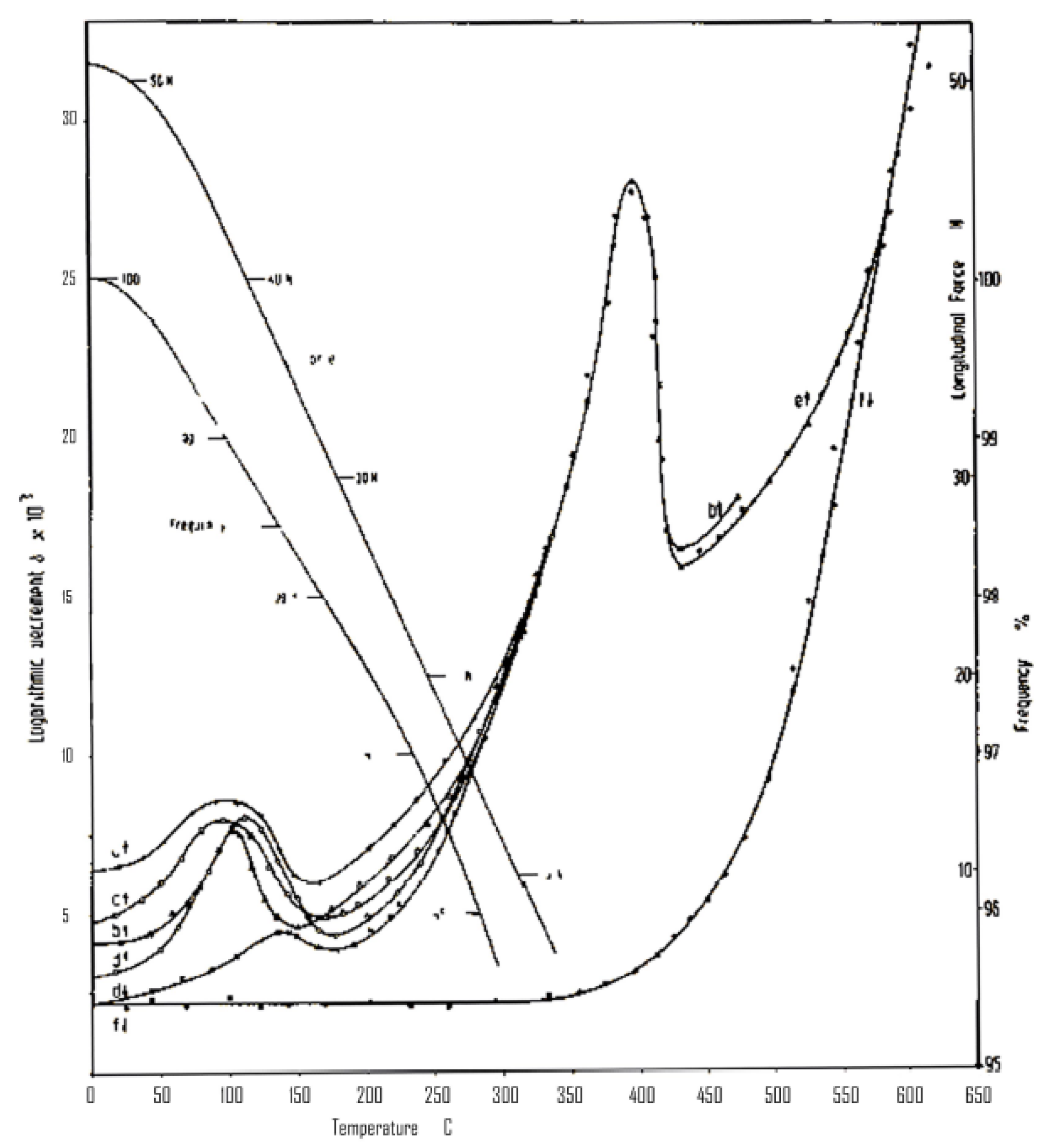
4.3. Modeling of the Mechanical Relaxation Spectrum
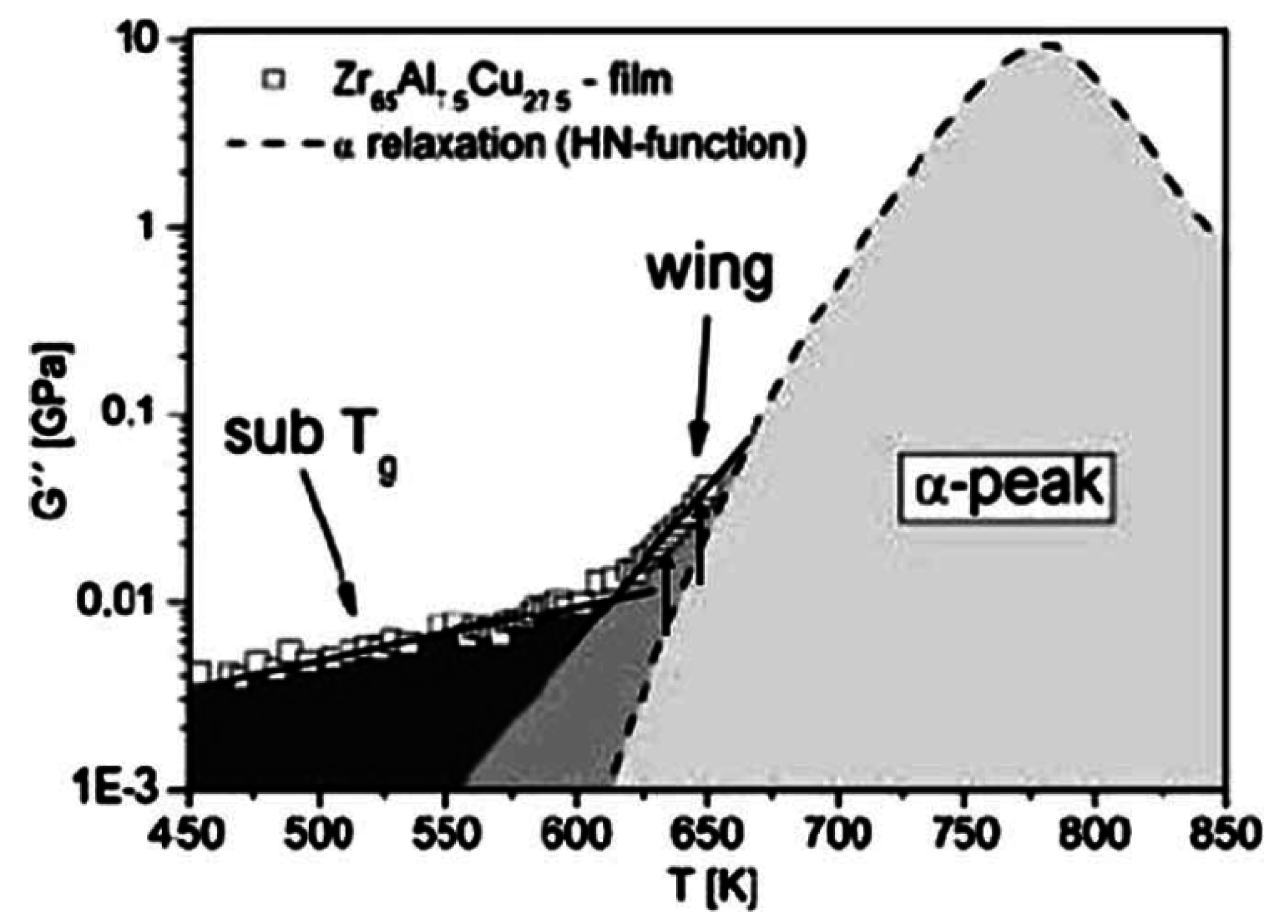
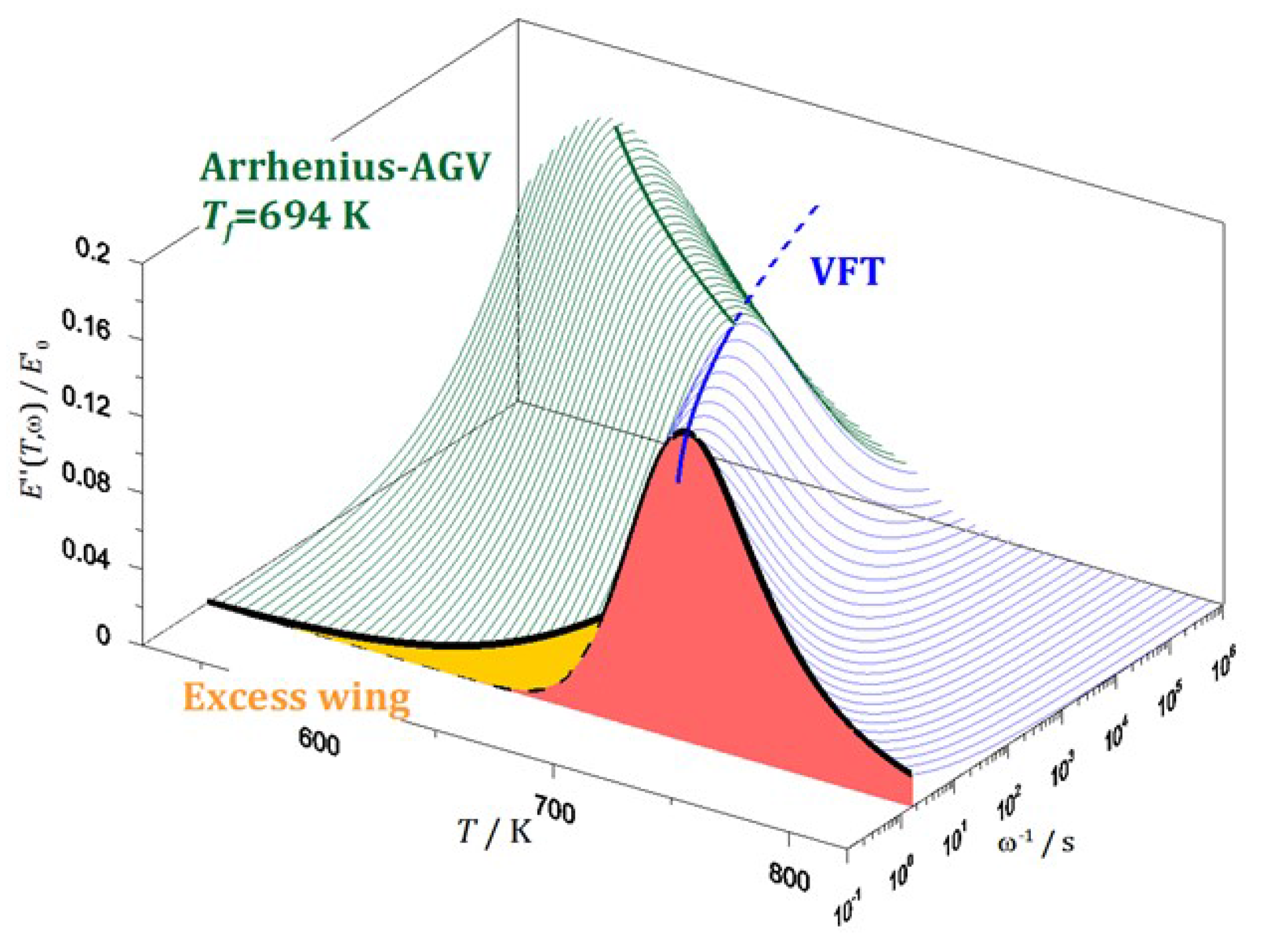
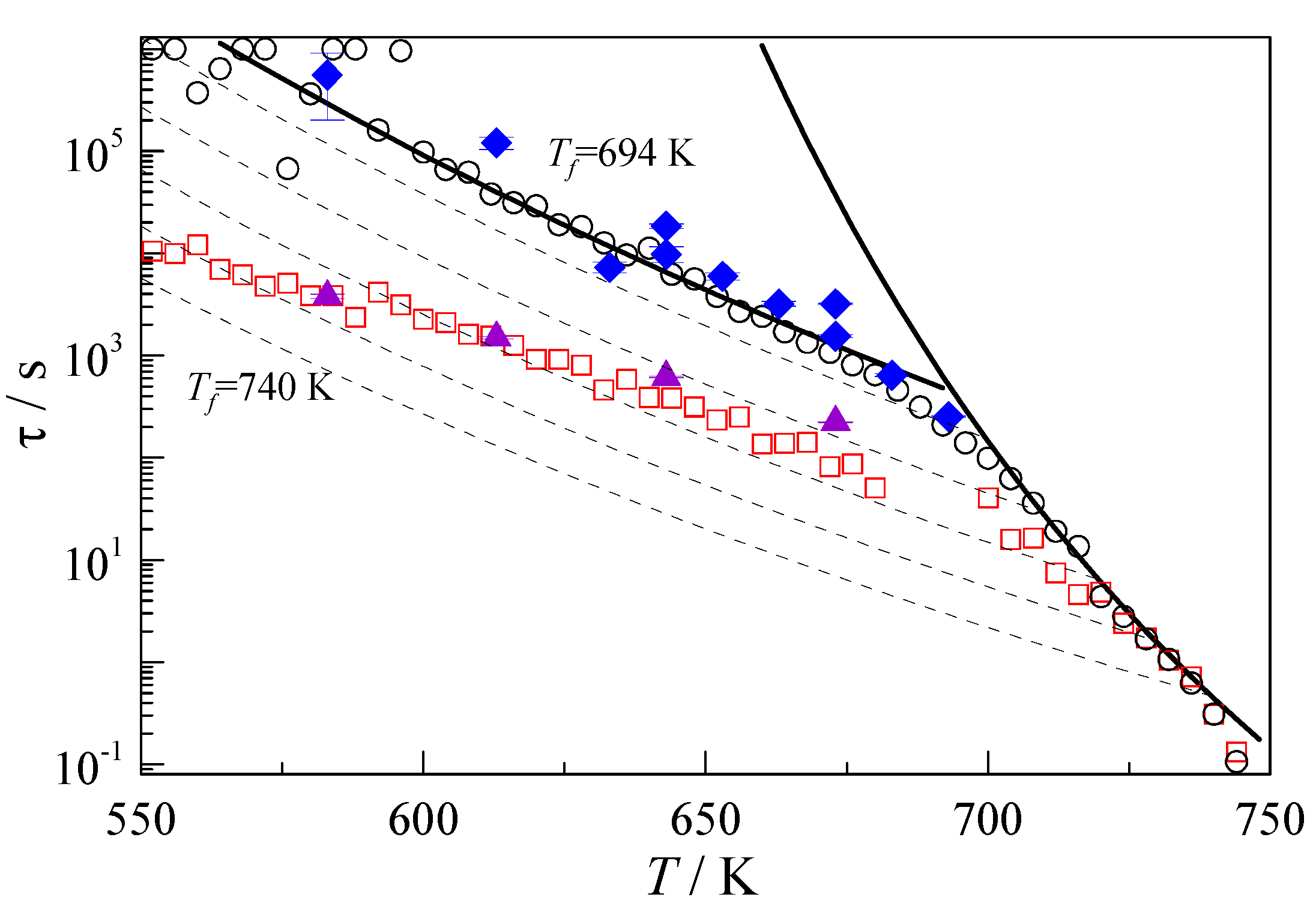
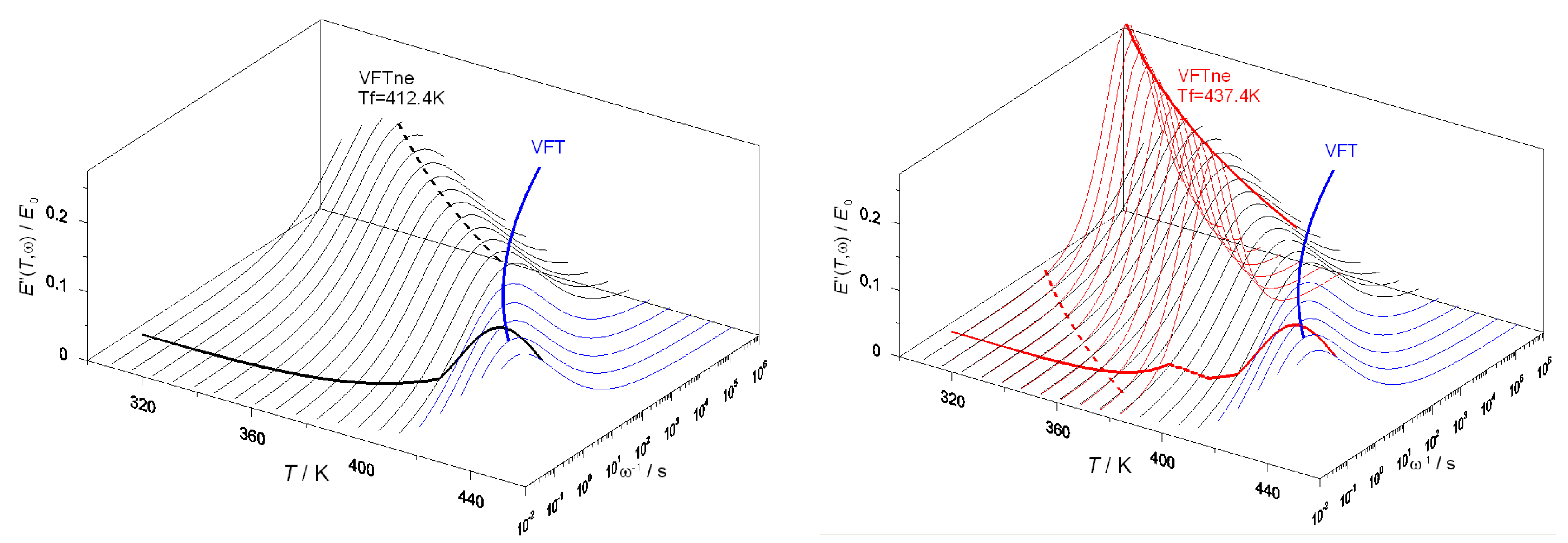
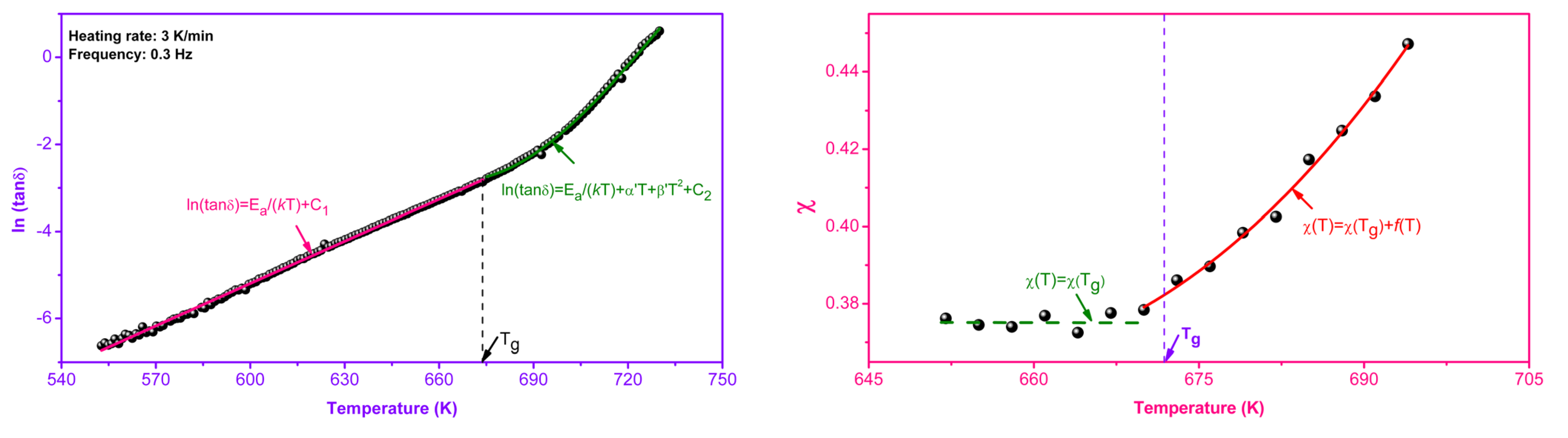
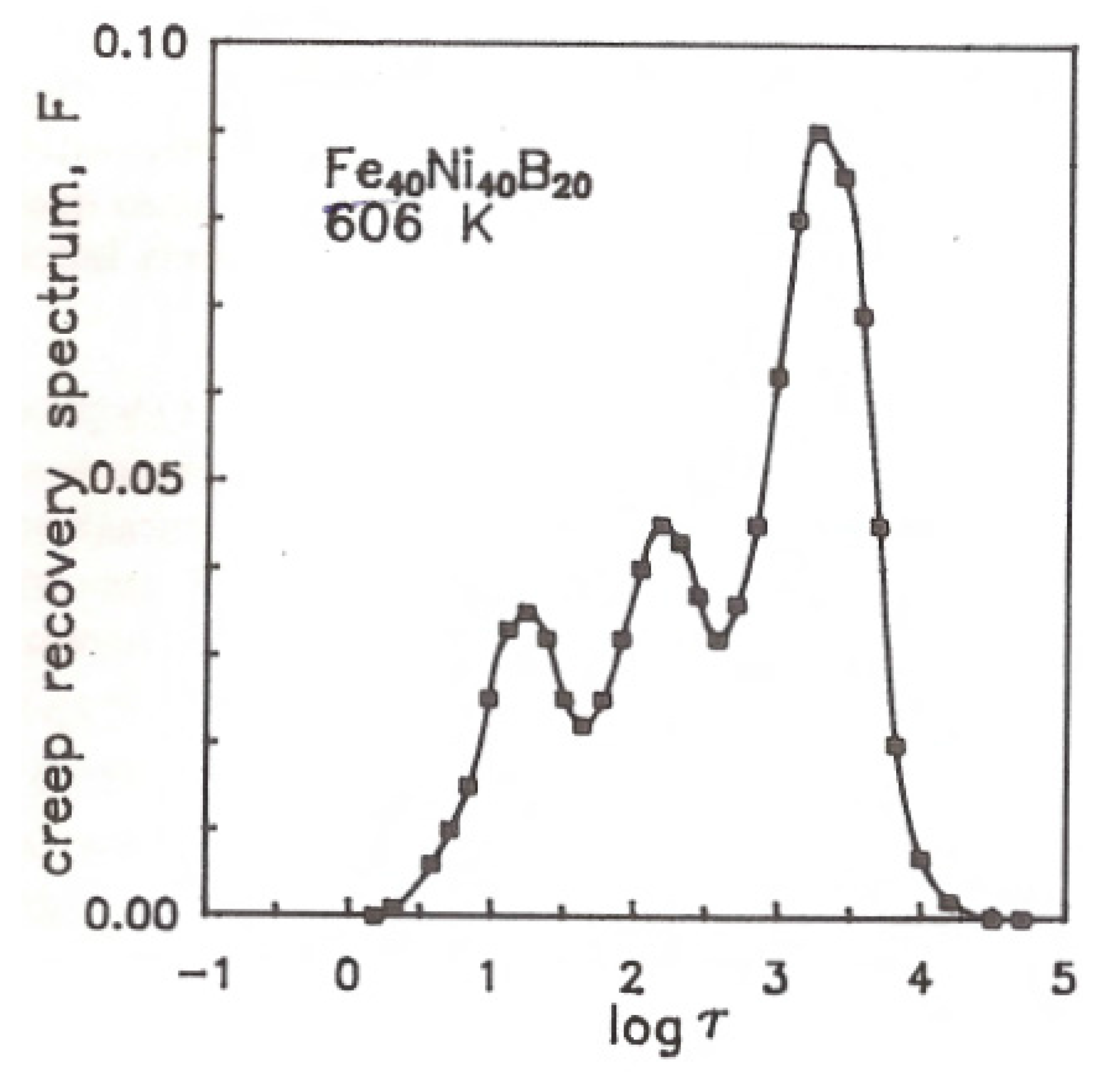
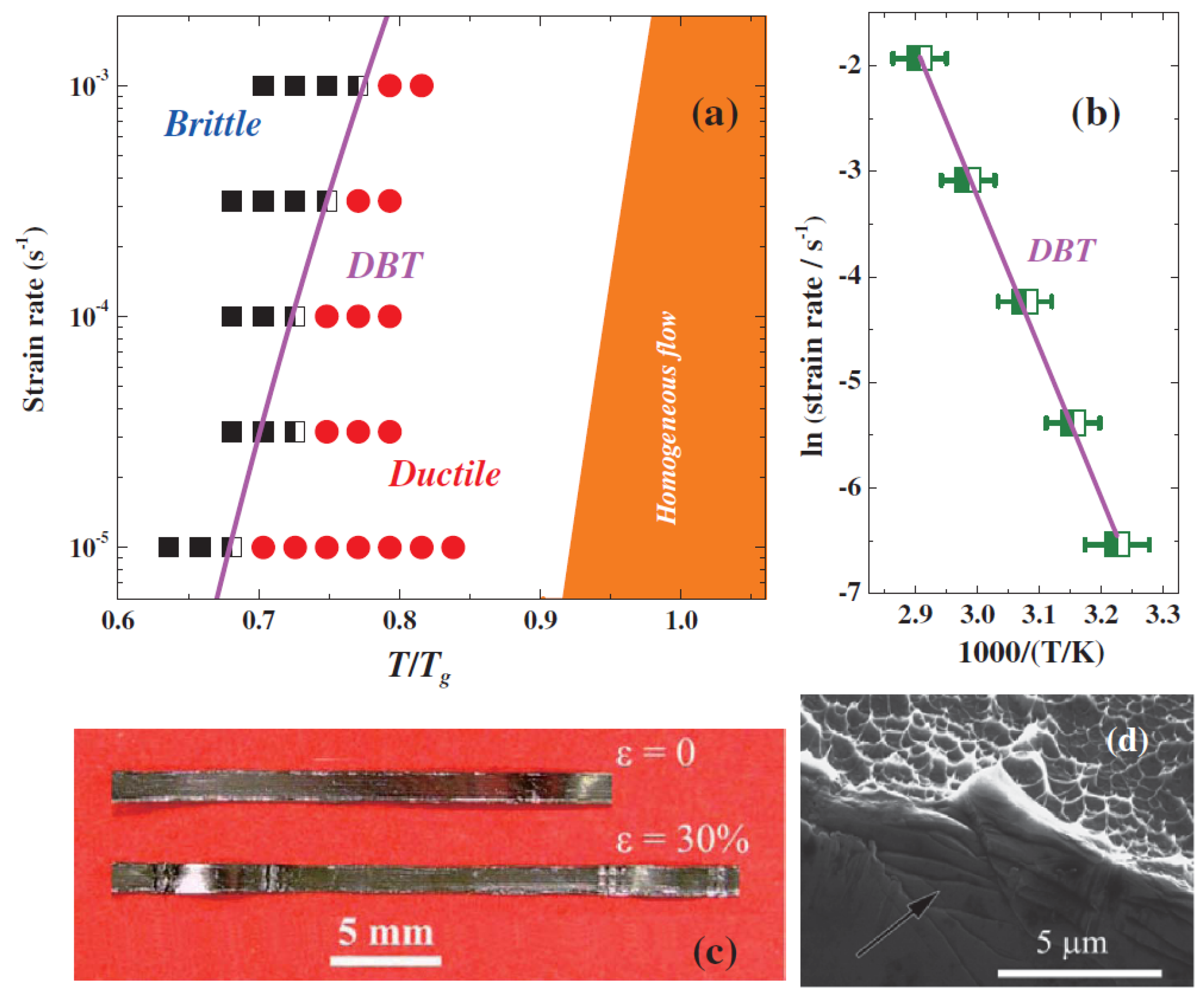
5. Relationship between the Relaxation Spectrum and the Mechanical Properties
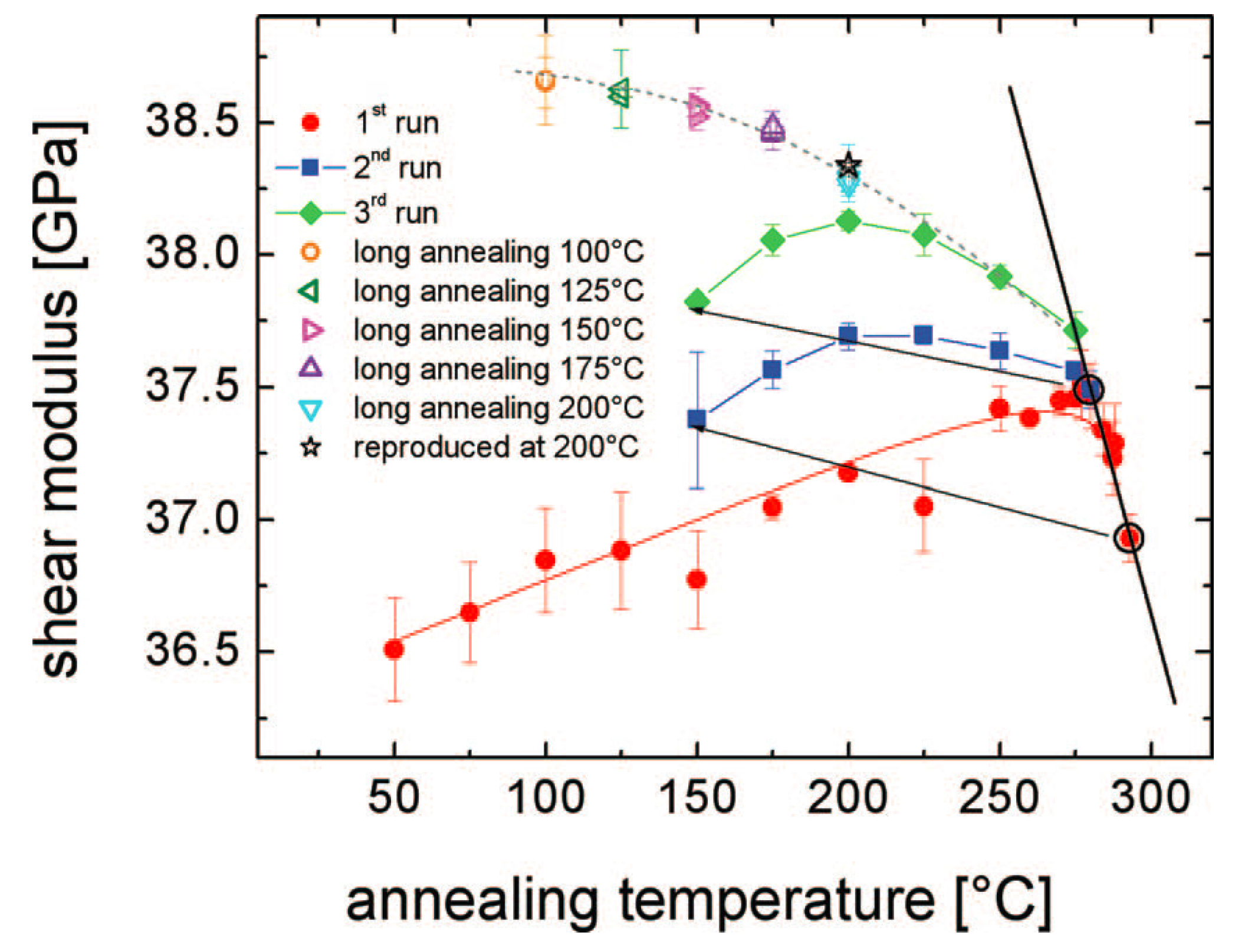
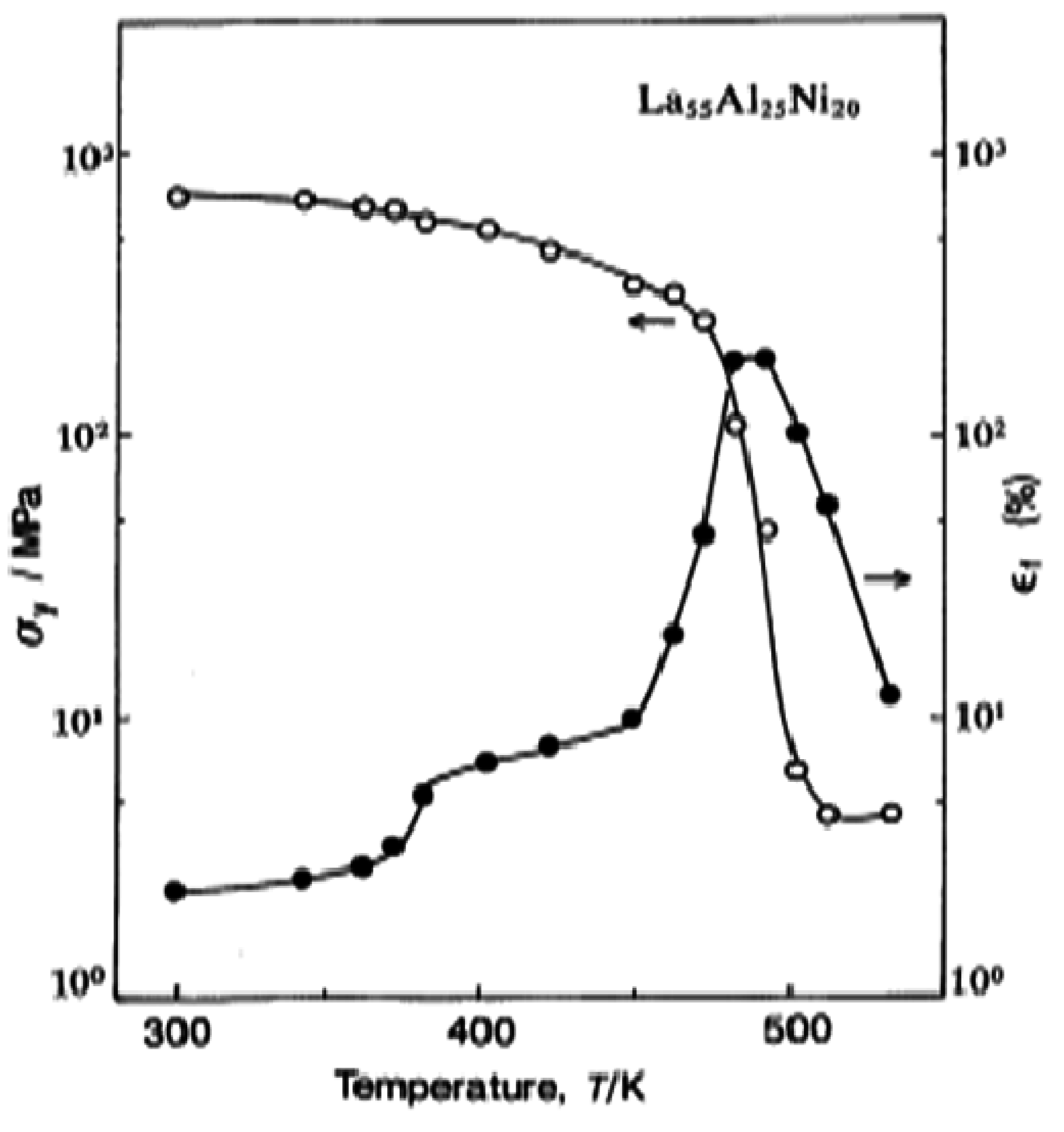
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Angell, C.A. Relaxation in liquids, polymers and plastic crystals strong/fragile patterns and problems. J. Non-Cryst. Solids 1991, 131–133, 13–31. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Debenedetti, P.G. Glass Transition Thermodynamics and Kinetics. Annu. Rev. Condens. Matter Phys. 2013, 4, 263–285. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Dyre, J.C. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; MaMillan, P.F.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef]
- Bohmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Johari, G.P.; Goldstein, M. Viscous liquids and the glass transition. II. Secondary relaxations in glasses of rigid molecules. J. Chem. Phys. 1970, 53, 2372–2388. [Google Scholar] [CrossRef]
- Borrego, J.M.; Conde, C.F.; Conde, A. Structural relaxation processes in FeSiB-Cu(Nb, X), X = Mo, V, Zr, Nb glassy alloys. Mater. Sci. Eng. A 2001, 304–306, 491–494. [Google Scholar] [CrossRef]
- Kumar, G.; Neibecker, P.; Liu, Y.H.; Schroers, J. Critical fictive temperature for plasticity in metallic glasses. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef]
- Hodge, I.M. Enthalpy relaxation and recovery in amorphous materials. J. Non-Cryst. Solids 1994, 169, 211–266. [Google Scholar] [CrossRef]
- Hodge, I.M. Effects of Annealing and Prior History on Enthalpy Relaxation in Glassy-Polymers 6. Adam-Gibbs Formulation of Nonlinearity. Macromolecules 1987, 20, 2897–2908. [Google Scholar] [CrossRef]
- Tool, A.Q. Relation Between Inelastic Deformability and Thermal Expansion of Glass in Its Annealing Range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Moynihan, C.T.; Macedo, P.B.; Montrose, C.J.; Gupta, P.K.; DeBolt, M.A.; Dill, J.F.; Dom, B.E.; Drake, P.W.; Easteal, A.J.; Elterman, P.B.; et al. Structural Relaxation in Vitreous Materials. Ann. N. Y. Acad. Sci. 1976, 279, 15–35. [Google Scholar] [CrossRef]
- Narayanaswamy, O.S. A Model of Structural Relaxation in Glass. J. Am. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Wehn, R.; Schneider, U.; Loidl, A. Glassy aging dynamics. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Chen, H.S.; Coleman, E. Structure relaxation spectrum of metallic glasses. Appl. Phys. Lett. 1976, 28, 245–247. [Google Scholar] [CrossRef]
- Tsyplakov, A.N.; Mitrofanov, Y.P.; Makarov, A.S.; Afonin, G.V.; Khonik, V.A. Determination of the activation energy spectrum of structural relaxation in metallic glasses using calorimetric and shear modulus relaxation data. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]
- Granato, A.V.; Khonik, V.A. An interstitialcy theory of structural relaxation and related viscous flow of glasses. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef]
- Khonik, S.V.; Granato, A.V.; Joncich, D.M.; Pompe, A.; Khonik, V.A. Evidence of distributed interstitialcy-like relaxation of the shear modulus due to structural relaxation of metallic glasses. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
- Nagel, C.; Rätzke, K.; Schmidtke, E.; Faupel, F.; Ulfert, W. Positron-annihilation studies of free-volume changes in the bulk metallic glass Zr65Al7.5Ni10Cu17.5 during structural relaxation and at the glass transition. Phys. Rev. B 1999, 60, 9212–9215. [Google Scholar] [CrossRef]
- Van den Beukel, A.; Radelaar, S. On the Kinetics of Structural Relaxation in Metallic Glasses. Acta Mater. 1983, 31, 419–427. [Google Scholar] [CrossRef]
- Van den Beukel, A.; van der Zwaag, S.; Mulder, A.L. A semi quantitative description of the kinetics of structural relaxataion in amorphous Fe40Ni40B20. Acta Metall. 1984, 32, 1895–1902. [Google Scholar] [CrossRef]
- Gibbs, M.R.J.; Sinning, H.R. A critique of the roles of TSRO and CSRO in metallic glasses by application of the activation energy spectrum model to dilatometric data. J. Mater. Sci. 1985, 20, 2517–2525. [Google Scholar] [CrossRef]
- Khonik, V.A.; Kosilov, A.T.; Mikhailov, V.A.; Sviridov, V.V. Isothermal creep of metallic glasses: A new approach and its experimental verification. Acta Mater. 1998, 46, 3399–3408. [Google Scholar] [CrossRef]
- Borrego, J.M.; Blázquez, J.S.; Lozano-Pérez, S.; Kim, J.S.; Conde, C.F.; Conde, A. Structural relaxation in Fe(Co)SiAlGaPCB amorphous alloys. J. Alloys Compd. 2014, 584, 607–610. [Google Scholar] [CrossRef]
- Khonik, V.A. The Kinetics of Irreversible Structural Relaxation and Homogeneous Plastic Flow of Metallic Glasses. Phys. Status Solidi A 2000, 177, 173–189. [Google Scholar] [CrossRef]
- Khonik, V.A. The kinetics of irreversible structural relaxation and rheological behavior of metallic glasses under quasi-static loading. J. Non-Cryst. Solids 2001, 296, 147–157. [Google Scholar] [CrossRef]
- Ruta, B.; Baldi, G.; Monaco, G.; Chushkin, Y. Compressed correlation functions and fast aging dynamics in metallic glasses. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef] [PubMed]
- Zhai, F.; Pineda, E.; Ruta, B.; Gonzalez-Silveira, M.; Crespo, D. Aging and structural relaxation of hyper-quenched Mg65Cu25Y10 metallic glass. J. Alloys Compd. 2014, 615, s9–s12. [Google Scholar] [CrossRef]
- Hu, L.; Zhou, C.; Zhang, C.; Yue, Y. Thermodynamic anomaly of the sub-Tg relaxation in hyperquenched metallic glasses. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef] [PubMed]
- Tsyplakov, A.N.; Mitrofanov, Y.P.; Khonik, V.A.; Kobelev, N.P.; Kaloyan, A.A. Relationship between the heat flow and relaxation of the shear modulus in bulk PdCuP metallic glass. J. Alloys Compd. 2015, 618, 449–454. [Google Scholar] [CrossRef]
- Chen, H.S. Glass transition and secondary relaxation in metal glasses. In Amorphous Metals and Semiconductors; Haasen, P., Jaffee, R.I., Eds.; Pergamon Press: Coronado, CA, USA, 1985; pp. 126–150. [Google Scholar]
- Maddin, R.; Masumoto, T. The deformation of amorphous palladium-20 at. % silicon. Mater. Sci. Eng. 1972, 9, 153–162. [Google Scholar] [CrossRef]
- Cohen, M.H.; Turnbull, D. Molecular Transport in Liquids and Glasses. J. Chem. Phys. 1959, 31, 1164–1169. [Google Scholar] [CrossRef]
- Turnbull, D.; Cohen, M.H. Free Volume Model of the Amorphous Phase: Glass Transition. J. Chem. Phys. 1961, 34, 120–125. [Google Scholar] [CrossRef]
- Turnbull, D.; Cohen, M.H. On the Free-Volume Model of the Liquid-Glass Transition. J. Chem. Phys. 1970, 52, 3038–3041. [Google Scholar] [CrossRef]
- Jackle, J. Models of the glass transition. Rep. Prog. Phys. 1986, 49, 171–231. [Google Scholar] [CrossRef]
- Goldstein, M. Viscous Liquids and the Glass Transition: A Potential Energy Barrier Picture. J. Chem. Phys. 1969, 51, 3728–3739. [Google Scholar] [CrossRef]
- Gotze, W.; Sjogren, L. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992, 55, 241–370. [Google Scholar] [CrossRef]
- Ngai, K.L.; Paluch, M. Classification of secondary relaxation in glass-formers based on dynamic properties. J. Chem. Phys. 2004, 120, 857–873. [Google Scholar] [CrossRef] [PubMed]
- Ngai, K.L. Johari-Goldstein relaxation as the origin of the excess wing observed in metallic glasses. J. Non-Cryst. Solids 2006, 352, 404–408. [Google Scholar] [CrossRef]
- Nowick, A.S.; Berry, B.S. Anelastic Relaxation in Crystalline Solids; Academic Press, Inc.: New York, NY, USA; London, UK, 1972. [Google Scholar]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Kuršumović, A.; Cantor, B. Anelastic crossover and creep recovery spectra in Fe40Ni40B20 metallic glass. Scr. Mater. 1996, 34, 1655–1660. [Google Scholar] [CrossRef]
- Jiao, W.; Wen, P.; Peng, H.L.; Bai, H.Y.; Sun, B.A.; Wang, W.H. Evolution of structural and dynamic heterogeneities and activation energy distribution of deformation units in metallic glass. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Hermida, É.B. Description of the Mechanical Properties of Viscoelastic Materials Using a Modified Anelastic Element. Phys. Status Solidi 1993, 178, 311–327. [Google Scholar]
- Alvarez, F.; Alegria, A.; Colmenero, J. Relationship between the time domain Kohlrausch Williams Watts and frequency domain Havriliak Negami relaxation functions. Phys. Rev. B 1991, 44, 7306–7312. [Google Scholar] [CrossRef]
- Svanberg, C. Correlation function for relaxations in disordered materials. J. Appl. Phys. 2003, 94, 4191–4197. [Google Scholar] [CrossRef]
- Qiao, J.; Casalini, R.; Pelletier, J.-M.M.; Kato, H. Characteristics of the structural and Johari-Goldstein relaxations in Pd-based metallic glass-forming liquids. J. Phys. Chem. B 2014, 118, 3720–3730. [Google Scholar] [CrossRef] [PubMed]
- Blanter, M.S.S.; Golovin, I.S.S.; Neuhauser, H.; Sinning, H.-R. Internal Friction in Metallic Materials; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Wen, P.; Zhao, D.Q.; Pan, M.X.; Wang, W.H.; Huang, Y.P.; Guo, M.L. Relaxation of metallic Zr46.75Ti8.25Cu7.5Ni10Be27.5 bulk glass-forming supercooled liquid. Appl. Phys. Lett. 2004, 84, 2790–2792. [Google Scholar] [CrossRef]
- Castellero, A.; Moser, B.; Uhlenhaut, D.I.; Dalla Torre, F.H.; Löffler, J.F. Room-Temperature creep and structural relaxation of Mg–Cu–Y metallic glasses. Acta Mater. 2008, 56, 3777–3785. [Google Scholar] [CrossRef]
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 2011, 57, 487–656. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Dynamic mechanical analysis in La-based bulk metallic glasses: Secondary (β) and main (α) relaxations. J. Appl. Phys. 2012, 112. [Google Scholar] [CrossRef]
- Ruta, B.; Chushkin, Y.; Monaco, G.; Cipelletti, L.; Pineda, E.; Bruna, P.; Giordano, V.M.; Gonzalez-Silveira, M. Atomic-Scale relaxation dynamics and aging in a metallic glass probed by X-ray photon correlation spectroscopy. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Wang, L.-M.; Liu, R.; Wang, W.H. Relaxation time dispersions in glass forming metallic liquids and glasses. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.; Busch, R.; Schober, H. Time-Temperature Superposition of Structural Relaxation in a Viscous Metallic Liquid. Phys. Rev. Lett. 1999, 83, 5027–5029. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Dynamic universal characteristic of the main (α) relaxation in bulk metallic glasses. J. Alloys Compd. 2014, 589, 263–270. [Google Scholar] [CrossRef]
- Casalini, R.; Roland, C.M. Aging of the secondary relaxation to probe structural relaxation in the glassy state. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Berry, B.S.; Pritchet, W.C.; Tsuei, C.C. Discovery of an internal-friction peak in the metallic glass Nb3Ge. Phys. Rev. Lett. 1978, 41, 410–413. [Google Scholar] [CrossRef]
- Berry, B.S.; Pritchet, W.C. Hydrogen related internal friction peaks in metallic glasses. Scr. Mater. 1981, 15, 637–642. [Google Scholar] [CrossRef]
- Yoon, H.N.; Eisenberg, A. Dynamic mechanical properties of metallic glasses. J. Non-Cryst. Solids 1978, 29, 357–364. [Google Scholar] [CrossRef]
- Fukuhara, M.; Wang, X.; Inoue, A.; Yin, F. Low temperature dependence of elastic parameters and internal frictions for glassy alloy Zr55Cu30Al10Ni5. Phys. Status Solidi 2007, 1, 220–222. [Google Scholar]
- Kunzi, H.U.U.; Agyeman, K.; Guntherodt, H.-J. Internal friction peaks in metallic glasses. Solid State Commun. 1979, 32, 711–714. [Google Scholar] [CrossRef]
- Zdaniewski, W.A.; Rindone, G.E.; Day, D.E. The internal friction of glasses. J. Mater. Sci. 1979, 14, 763–775. [Google Scholar]
- Khonik, V.A.; Spivak, L.V. On the nature of low temperature internal friction peaks in metallic glasses. Acta Mater. 1996, 44, 367–381. [Google Scholar] [CrossRef]
- Egami, T.; Maeda, K.; Vitek, V. Structural defects in amorphous solids A computer simulation study. Philos. Mag. A 1980, 41, 883–901. [Google Scholar] [CrossRef]
- Okumura, H.; Inoue, A.; Masumoto, T. Glass transition and viscoelastic behaviors of La55Al25Ni20 and La55Al25Cu20 amorphous alloys. Mater. Trans. 1991, 32, 593–598. [Google Scholar] [CrossRef]
- Okumura, H.; Chen, H.S.; Inoue, A.; Masumoto, T. Sub-Tg mechanical relaxation of a La55A125Ni20 amorphous alloy. J. Non-Cryst. Solids 1991, 130, 304–310. [Google Scholar] [CrossRef]
- Qiao, J.; Pelletier, J.-M.; Casalini, R. Relaxation of bulk metallic glasses studied by mechanical spectroscopy. J. Phys. Chem. B 2013, 117, 13658–13666. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yu, H.B.; Wen, P.; Bai, H.Y.; Wang, W.H. Pronounced slow beta-relaxation in La-based bulk metallic glasses. J. Phys. Condens. Matter 2011, 23. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.B.; Samwer, K.; Wang, W.H.; Bai, H.Y. Chemical influence on β-relaxations and the formation of molecule-like metallic glasses. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.S.; Morito, N. Sub-Tg α′ relaxation in a PdCuSi glass; internal friction measurements. J. Non-Cryst. Solids 1985, 72, 287–299. [Google Scholar] [CrossRef]
- Evenson, Z.; Naleway, S.E.; Wei, S.; Gross, O.; Kruzic, J.J.; Gallino, I.; Possart, W.; Stommel, M.; Busch, R. β relaxation and low-temperature aging in a Au-based bulk metallic glass: From elastic properties to atomic-scale structure. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Okumura, H.; Inoue, A.; Masumoto, T. Heating rate dependence of two glass transitions and phase separation for a La55Al25Ni20 amorphous alloy. Acta Metall. Mater. 1993, 41, 915–921. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Seki, I.; Yamamoto, T.; Kawaji, H.; Suryanarayana, C.; Inoue, A. Double-Stage glass transition in a metallic glass. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Cohen, Y.; Karmakar, S.; Procaccia, I.; Samwer, K. The nature of the β-peak in the loss modulus of amorphous solids. EPL 2012, 100. [Google Scholar] [CrossRef]
- Yu, H.B.; Samwer, K.; Wu, Y.; Wang, W.H. Correlation between belta relaxation and self-diffusion of the smallest constituting atoms in metallic glasses. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Liu, Y.H.; Fujita, T.; Aji, D.P.B.; Matsuura, M.; Chen, M.W. Structural origins of Johari-Goldstein relaxation in a metallic glass. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Morito, N.; Egami, T. Internal friction and reversible structural relaxation in the metallic glass Fe32Ni36Cr14P12B6. Acta Metall. 1984, 32, 603–613. [Google Scholar] [CrossRef]
- Bohonyey, A.; Kiss, L.F. A quantitative study on reversible structural relaxation of metallic glasses. J. Phys. Condens. Matter 1999, 3, 4523–4531. [Google Scholar] [CrossRef]
- Pineda, E.; Bruna, P.; Ruta, B.; Gonzalez-Silveira, M.; Crespo, D. Relaxation of rapidly quenched metallic glasses: Effect of the relaxation state on the slow low temperature dynamics. Acta Mater. 2013, 61, 3002–3011. [Google Scholar] [CrossRef]
- Kiss, S.; Posgay, G.; Harangozo, I.Z.; Kedves, F.J. Structural relaxation and crystallization of FeB and NiP metallic glasses followed by internal friction and modulus measurements. J. Phys. 1981, 42, C5:529–C5:534. [Google Scholar] [CrossRef]
- Hettwer, K.J.; Haessner, F. Influence of heat treatment on the internal friction of metglas Fe32Ni36Cr14P12B6. Mater. Sci. Eng. 1982, 52, 147–154. [Google Scholar] [CrossRef]
- Hausch, G. Internal Friction and Ultrasonic Attenuation in Solids; University of Tokyo Press: Tokyo, Japan, 1977; p. 265. [Google Scholar]
- Morito, N.; Egami, T. Internal friction of a glassy metal Fe32Ni36Cr14P12B6. IEEE Trans. Magn. 1983, 5, 1898–1900. [Google Scholar] [CrossRef]
- Morito, N. Internal friction study on structural relaxation of a glassy metal Fe32Ni36Cr14P12B6. Mater. Sci. Eng. 1983, 60, 261–268. [Google Scholar] [CrossRef]
- Deng, D.; Argon, A.S. Structural relaxation and embrittlement of Cu59Zr41 and Fe80B20 glasses. Acta Metall. 1986, 34, 2011–2023. [Google Scholar] [CrossRef]
- Deng, D.; Argon, A.S. Analysis of the effect of aging on distributed relaxations, hardness, and embrittlement in Cu59Zr41 and Fe80B20 glasses. Acta Metall. 1986, 34, 2025–2038. [Google Scholar] [CrossRef]
- Olsen, N.B.; Christensen, T.; Dyre, J.C. Time-Temperature superposition in viscous liquids. Phys. Rev. Lett. 2001, 86, 1271–1274. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, J.M.; van de Moortèle, B.; Lu, I.R. Viscoelasticity and viscosity of Pd–Ni–Cu–P bulk metallic glasses. Mater. Sci. Eng. A 2002, 336, 190–195. [Google Scholar] [CrossRef]
- Jeong, H.T.; Fleury, E.; Kim, W.T.; Kim, D.H.; Hono, K. Study on the Mechanical Relaxations of a Zr36Ti24Be40 Amorphous Alloy by Time-Temperature Superposition Principle. J. Phys. Soc. Jpn. 2004. [Google Scholar] [CrossRef]
- Jeong, H.T.; Kim, J.-H.; Kim, W.T.; Kim, D.H. The mechanical relaxations of a Mm55Al25Ni10Cu10 amorphous alloy studied by dynamic mechanical analysis. Mater. Sci. Eng. A 2004, 385, 182–186. [Google Scholar] [CrossRef]
- Guo, L.; Wu, X.; Zhu, Z. Mechanical relaxation studies of α and slow β processes in Nd65Fe15Co10Al10 bulk metallic glass. J. Appl. Phys. 2011, 109. [Google Scholar] [CrossRef]
- Ngai, K.L.; Capaccioli, S. Relation between the activation energy of the Johari-Goldstein belta relaxation and Tg of glass formers. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef]
- Wang, W.H. Correlation between relaxations and plastic deformation, and elastic model of flow in metallic glasses and glass-forming liquids. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
- Liu, X.F.; Zhang, B.; Wen, P.; Wang, W.H. The slow β-relaxation observed in Ce-based bulk metallic glass-forming supercooled liquid. J. Non-Cryst. Solids 2006, 352, 4013–4016. [Google Scholar] [CrossRef]
- Wang, W.H.; Wen, P.; Liu, X.F. The excess wing of bulk metallic glass forming liquids. J. Non-Cryst. Solids 2006, 352, 5103–5109. [Google Scholar] [CrossRef]
- Rosner, P.; Samwer, K.; Lunkenheimer, P. Indications for an excess wing in metallic glasses from the mechanical loss modulus in Zr65Al7.5Cu27.5. Europhys. Lett. 2004, 68, 226–232. [Google Scholar] [CrossRef]
- Hachenberg, J.; Bedorf, D.; Samwer, K.; Richert, R.; Kahl, A.; Demetriou, M.D.; Johnson, W.L. Merging of the alpha and beta relaxations and aging via the Johari-Goldstein modes in rapidly quenched metallic glasses. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Hachenberg, J.; Samwer, K. Indications for a slow β-relaxation in a fragile metallic glass. J. Non-Cryst. Solids 2006, 352, 5110–5113. [Google Scholar] [CrossRef]
- Liu, C.; Pineda, E.; Crespo, D. Characterization of mechanical relaxation in a Cu–Zr–Al metallic glass. J. Alloys Compd. 2014, in press. [Google Scholar]
- Ferrari, L.; Mott, N.F.; Russo, G. A defect theory of the viscosity in glass-forming liquids. Philos. Mag. A 1989, 59, 263–272. [Google Scholar] [CrossRef]
- Cavaille, J.Y.; Perez, J. Molecular theory for the rheology of glasses and polymers. Phys. Rev. B 1989, 39, 2411–2422. [Google Scholar] [CrossRef]
- Gauthier, C.; Pelletier, J.M.; David, L.; Vigier, G.; Perez, J. Relaxation of non-crystalline solids under mechanical stress. J. Non-Cryst. Solids 2000, 274, 181–187. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Mechanical relaxation in a Zr-based bulk metallic glass: Analysis based on physical models. J. Appl. Phys. 2012, 112. [Google Scholar] [CrossRef]
- Hecksher, T.; Nielsen, A.I.; Olsen, N.B.; Dyre, J.C. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nat. Phys. 2008, 4, 737–741. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drozd-Rzoska, A.; Martinez-Garcia, J. A universal description of ultraslow glass dynamics. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wen, P.; Huo, L.S.; Bai, H.Y.; Wang, W.H. Signature of viscous flow units in apparent elastic regime of metallic glasses. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Kuršumović, A.; Scott, M.G.; Cahn, R.W. Creep recovery spectra in Fe40Ni40B20 metallic glass. Scr. Mater. 1990, 24, 1307–1312. [Google Scholar] [CrossRef]
- Ocelík, V.; Csach, K.; Kasardová, A.; Bengus, V.Z. Anelastic deformation processes in metallic glasses and activation energy spectrum model. Mater. Sci. Eng. A 1997, 226–228, 851–855. [Google Scholar] [CrossRef]
- Ju, J.D.; Jang, D.; Nwankpa, A.; Atzmon, M. An atomically quantized hierarchy of shear transformation zones in a metallic glass. J. Appl. Phys. 2011, 109. [Google Scholar] [CrossRef]
- Ju, J.D.; Atzmon, M. A comprehensive atomistic analysis of the experimental dynamic-mechanical response of a metallic glass. Acta Mater. 2014, 74, 183–188. [Google Scholar] [CrossRef]
- Xi, X.K.; Zhao, D.Q.; Pan, M.X.; Wang, W.H.; Wu, Y.; Lewandowski, J.J. Fracture of brittle metallic glasses: Brittleness or plasticity. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Chen, M. Mechanical Behavior of Metallic Glasses: Microscopic Understanding of Strength and Ductility. Annu. Rev. Mater. Res. 2008, 38, 445–469. [Google Scholar] [CrossRef]
- Kahl, A.; Koeppe, T.; Bedorf, D.; Richert, R.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L.; Arnold, W.; Samwer, K. Dynamical and quasistatic structural relaxation paths in Pd40Ni40P20 glass. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Harmon, J.S.; Demetriou, M.D.; Johnson, W.L.; Samwer, K. Anelastic to plastic transition in metallic glass-forming liquids. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef]
- Spaepen, F. Homogeneous flow of metallic glasses: A free volume perspective. Scr. Mater. 2006, 54, 363–367. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Johnson, W.L.; Demetriou, M.D.; Harmon, J.S.; Lind, M.L.; Samwer, K. Rheology and Ultrasonic Properties of Metallic Glass-Forming Liquids: A Potential Energy Landscape Perspective. MRS Bull. 2007, 32, 644–650. [Google Scholar] [CrossRef]
- Zhao, Z.F.; Wen, P.; Shek, C.H.; Wang, W.H. Measurements of slow β-relaxations in metallic glasses and supercooled liquids. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Yu, H.B.; Wang, W.H.; Bai, H.Y.; Wu, Y.; Chen, M.W. Relating activation of shear transformation zones to β relaxations in metallic glasses. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Liu, S.T.; Wang, Z.; Peng, H.L.; Yu, H.B.; Wang, W.H. The activation energy and volume of flow units of metallic glasses. Scr. Mater. 2012, 67, 9–12. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl. Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef] [PubMed]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–838. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, J.J.; Wang, W.H.; Greer, A.L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 2005, 85, 77–87. [Google Scholar] [CrossRef]
- Yu, H.B.; Shen, X.; Wang, Z.; Gu, L.; Wang, W.H.; Bai, H.Y. Tensile plasticity in metallic glasses with pronounced β relaxations. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Lu, Z.; Jiao, W.; Wang, W.H.; Bai, H.Y. Flow unit perspective on room temperature homogeneous plastic deformation in metallic glasses. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Pineda, E.; Crespo, D. Mechanical Relaxation of Metallic Glasses: An Overview of Experimental Data and Theoretical Models. Metals 2015, 5, 1073-1111. https://doi.org/10.3390/met5021073
Liu C, Pineda E, Crespo D. Mechanical Relaxation of Metallic Glasses: An Overview of Experimental Data and Theoretical Models. Metals. 2015; 5(2):1073-1111. https://doi.org/10.3390/met5021073
Chicago/Turabian StyleLiu, Chaoren, Eloi Pineda, and Daniel Crespo. 2015. "Mechanical Relaxation of Metallic Glasses: An Overview of Experimental Data and Theoretical Models" Metals 5, no. 2: 1073-1111. https://doi.org/10.3390/met5021073
APA StyleLiu, C., Pineda, E., & Crespo, D. (2015). Mechanical Relaxation of Metallic Glasses: An Overview of Experimental Data and Theoretical Models. Metals, 5(2), 1073-1111. https://doi.org/10.3390/met5021073