A New Methodology for Determining the Friction Factor

Abstract

The friction law, which requires that the friction stress is a constant fraction of the local yield shear stress, is widely used for modeling bulk metal forming processes. Determining the friction factor involved in this friction law requires an experiment and its theoretical description. It is advantageous if the latter is not based on the finite element or similar methods, since the friction factor is unknown prior to the calculation. The present paper suggests using a plane strain compression test. The experimental setup is slightly more complicated than the standard ring compression test. However, its advantage lies in the availability of relatively simple and accurate theoretical solutions for a broad class of constitutive equations, which overcomes the experimental disadvantage. The present paper is limited to isotropic strain-hardening materials. The experimental research is conducted on aluminum alloy AA 6026 and steel C45. The friction factor is determined for three types of lubricant.

1. Introduction

Friction between the tool and the workpiece inevitably appears in nearly all metal forming processes. The accuracy of the friction law has a significant impact on the accuracy of theoretical solutions, including finite element solutions. One of the friction laws widely used for modeling cold bulk metal forming processes postulates that the friction stress is a fraction of the local shear yield stress. This law contains one constitutive parameter, the friction factor. A theoretical experimental method is required to determine this factor.

Until now, the ring compression test proposed in [1] has been one of the most widely used methods for determining the friction factor. In particular, paper [2] has emphasized adhesive friction. This paper has determined the strain-hardening behavior from the same test. The initial geometry of the ring may play a significant role, especially if the friction factor is sufficiently large. The standard geometry is classified by the ratios ‘outer diameter/inner diameter/height = 6:3:2.’ However, the friction law at sliding is invalid where the material sticks to the tool. In some cases, this sticking region occupies the entire friction surface, and the theoretical solution becomes insensitive to the increasing friction factor [3]. Generally, the sticking region enlarges with the friction factor but also depends on geometric parameters. Therefore, the standard ratios above are sometimes replaced with the ratios ‘outer diameter/inner diameter/height = 6:3:1’ in case of high friction [4]. The performance of several lubricants commonly used in metal forming processes has been evaluated using the ring compression test in [5]. It has been emphasized in [6] that the friction factor may change as the deformation proceeds. The hot ring compression test is also used for applications to metal forming processes at elevated temperatures [7]. The barrel compression test proposed in [8] can be regarded as a simplified version of the ring compression test.

A friction test, which essentially differs from the ring compression test, has been proposed in [9]. The test is based on a double backward extrusion process.

Independent of the experimental procedure, a theoretical solution is required to determine the friction factor. It is worth noting that this solution must be repeated multiple times because the friction factor is unknown and must be determined through this solution and experimental results. Therefore, it is desirable to employ a theoretical method that can quickly produce accurate solutions. Typically, the upper bound technique is adopted (for example, [8,10,11] among numerous publications). However, this technique provides reliable results only at the initial instant. One must use the sequential limit analysis to account for strain hardening and shape change [12]. The efficiency and simplicity of the classical limit analysis are lost in this case. Therefore, it is desirable to develop a method for determining the friction factor that is relatively simple experimentally and allows for a relatively simple and accurate theoretical solution to be found for a large class of material models.

The method proposed in this paper is plane strain compression between parallel platens, assuming that the specimen’s thickness is much smaller than its width and length. An approximate analytical solution for perfectly plastic materials is well-known [13] (p. 226). It is also known that this solution is very accurate [14]. Moreover, the solution for perfectly plastic materials has been generalized to many material models [15,16,17,18]. Particularly, continued compression of a strip of strain-hardening materials has been considered in [16], assuming linear hardening. This solution is extended to non-linear strain hardening in the present paper. Then, this solution, combined with the experimental results also obtained in the present paper, determines the friction factor for two materials (AA 6062 and C 45) and several frictional conditions.

2. Methodology

A schematic diagram of the experimental setup is shown in Figure 1, with the specimen in its initial position. The initial thickness, width, and length of the specimen are 2t₀, 2b₀, and 2a₀, respectively. The width remains constant throughout the deformation process. The ratio t₀/a₀ is supposed to be small enough so that the solutions in [16] are good approximations. The lateral contact surfaces between the specimen and the die must be treated to minimize friction. No special treatment is required for the other contact surfaces, where the friction factor is determined. It is convenient to choose the time-like parameter, which determines the stage of deformation, as

$$\eta ={\displaystyle \frac{t}{t_0}},$$

(1)

where 2t is the current thickness of the specimen. The compression force F is measured as a function of this parameter.

The material is supposed to be rigid-plastic, exhibiting strain-hardening behavior. The strain-hardening behavior is determined from the cylinder compression test by employing the Rastegaev method [19].

The theoretical dependence of the compression force on η is computed employing the solution in [16], the data of the standard tensile test, and several guessed friction factors. Comparison with the corresponding experimental curves allows for an estimation of the friction factor.

3. Plane Strain Compression for Determining the Friction Coefficient

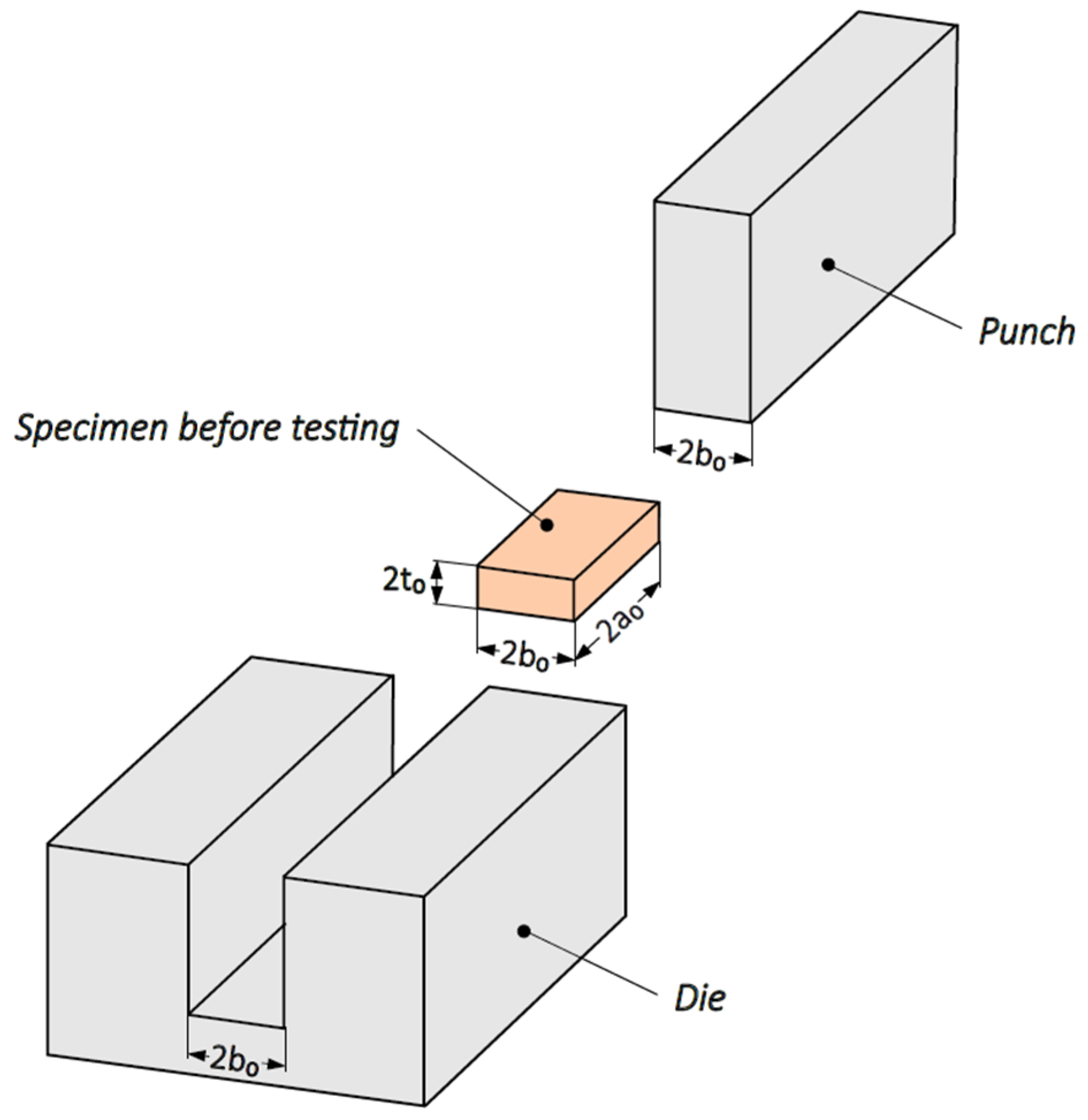
3.1. Theory

A solution for plane strain compression of a rigid-plastic, linear strain-hardening material has been provided in [16]. However, a significant part of this solution does not use a specific hardening law. Therefore, it is straightforward to generalize the final result to non-linear hardening. Owing to symmetry, it is sufficient to consider the domain $x\ge 0$ and $y\ge 0$ (Figure 2).

The current length of the strip is denoted as 2a. The speed of each die is V. The equivalent strain rate is defined as

$${\xi }_{eq}=\sqrt{{\displaystyle \frac{{\left({\xi }_{xx}-{\xi }_{yy}\right)}^2}{4}}+{\xi }_{xy}^2},$$

(2)

where ${\xi }_{xx}$, ${\xi }_{yy}$, and ${\xi }_{xy}$ are the strain rate components referred to a Cartesian coordinate system. The equivalent strain is calculated from the following equation:

$${\displaystyle \frac{d{\epsilon }_{eq}}{d\tau }}={\xi }_{eq},$$

(3)

where $d/d\tau$ is the material derivative. The plane strain yield criterion is

$$k=k_0\Phi \left({\epsilon }_{eq}\right),$$

(4)

where k is the shear yield stress, k₀ is its initial value, and $\Phi \left({\epsilon }_{eq}\right)$ is an arbitrary function of the equivalent strain satisfying the conditions $\Phi \left(0\right)=1$ and $d\Phi /d{\epsilon }_{eq}\ge 0$ for all ${\epsilon }_{eq}$. The friction law is

$${\tau }_f=m{k}_f,$$

(5)

where τ_f is the friction stress, k_f is the value of k at the friction surface, and m is the friction factor. Let ${\epsilon }_{eq}^f$ be the value of the equivalent strain at the friction surface. Then, Equations (4) and (5) combine to give

$${\tau }_f=m{k}_0\Phi \left({\epsilon }_{eq}^f\right).$$

(6)

The complete system of equations consists of (3), (4), the associated flow rule, and the stress equilibrium equations. It has been shown in [16] that the solution of this system is facilitated by introducing the following variable φ:

$$\cos 2\phi =-{\displaystyle \frac{{\tau }_f\mu }{k}},$$

(7)

where $\mu =y/t$. The equivalent strain rate defined in (2) is given by

$${\xi }_{eq}={\displaystyle \frac{V}{t\left|\sin 2\phi \right|}}.$$

(8)

It has also been shown in [16] that Equation (3) transforms to

$$V{\displaystyle \frac{\partial {\epsilon }_{eq}}{\partial t}}=-{\xi }_{eq}.$$

(9)

Eliminating here the equivalent strain rate employing (8), further eliminating φ employing (7), and replacing differentiation with respect to t with differentiation with respect to η using (1), one obtains

$${\displaystyle \frac{\partial {\epsilon }_{eq}}{\partial \eta }}=-{\displaystyle \frac{1}{\eta }}{\left[1-{\left({\displaystyle \frac{m{\Phi }_f\mu }{\Phi }}\right)}^2\right]}^{-1/2},$$

(10)

where ${\Phi }_f=\Phi \left({\epsilon }_{eq}^f\right)$. Since $\Phi ={\Phi }_f$ and $\mu =1$ at the friction surface, Equation (10) leads to

$${\displaystyle \frac{\partial {\epsilon }_{eq}^f}{\partial \eta }}=-{\displaystyle \frac{1}{\eta \sqrt{1-m^2}}}.$$

(11)

The solution of this equation satisfying the initial condition ${\epsilon }_{eq}^f=0$ at $\eta =1$ is

$${\epsilon }_{eq}^f=-{\displaystyle \frac{\ln \eta }{\sqrt{1-m^2}}}.$$

(12)

This equation allows one to represent ${\Phi }_f$ as a function of η. Therefore, Equation (10) can be solved numerically for any value of μ in the interval $0\le \mu \le 1$ employing the initial condition ${\epsilon }_{eq}=0$ at $\eta =1$. Having this solution for the equivalent strain, it is straightforward to calculate the through-thickness distribution of $\Phi \left({\epsilon }_{eq}\right)$.

The load on each die has been calculated in [16] as

$$F={\displaystyle \frac{2m{b}_0{k}_0\Phi \left({\epsilon }_{eq}^f\right)a^2}{t}}+{\displaystyle \frac{8a{b}_0{k}_0}{t}}{\displaystyle \underset{0}{\overset{t}{\int }}\sqrt{{\Phi }^2\left({\epsilon }_{eq}\right)-m^2{\Phi }^2\left({\epsilon }_{eq}^f\right){\frac{y}{t^2}}^2}dy}.$$

(13)

Replacing here the integration with respect to y with integration with respect to $\mu$ yields

$$F={\displaystyle \frac{2m{b}_0{k}_0\Phi \left({\epsilon }_{eq}^f\right)a^2}{t}}+8a{b}_0{k}_0{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{{\Phi }^2\left({\epsilon }_{eq}\right)-m^2{\Phi }^2\left({\epsilon }_{eq}^f\right){\mu }^2}d\mu }.$$

(14)

It follows from the equation of incompressibility and (1) that

$${\displaystyle \frac{a}{a_0}}={\displaystyle \frac{t_0}{t}}={\displaystyle \frac{1}{\eta }}.$$

(15)

Equations (14) and (15) combine to give

$$f={\displaystyle \frac{F}{4a_0{b}_0{k}_0}}={\displaystyle \frac{m\Phi \left({\epsilon }_{eq}^f\right)l_0}{2{\eta }^3}}+{\displaystyle \frac{2}{\eta }}{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{{\Phi }^2\left({\epsilon }_{eq}\right)-m^2{\Phi }^2\left({\epsilon }_{eq}^f\right){\mu }^2}d\mu },$$

(16)

where $l_0=a_0/t_0$.

3.2. Experiment

Two materials are used in the current study: aluminum alloy AA 6026 and steel C45. The specimens for plane strain compression were machined from 32 mm diameter rods. The initial dimensions of specimens were 2a₀ = 25 mm, 2b₀ = 14 mm, and 2t₀ = 6 mm (Figure 1). The frictional conditions varied using two types of lubricants and no lubricant. To conveniently describe the experimental conditions and results, the different frictional conditions are denoted by three types:

• MOLUB HK cold forging oil (ISO 6743/7 [20], L—MHE; ISO/TS 12927 [21]), manufactured by Oil Refinery Modriča, Bosnia and Herzegovina—type O,
• Mixture of MoS₂ grease and stearin—type GS,
• No lubricant—type D.

Three tests were conducted for each combination of the materials and the frictional conditions (a total of eighteen tests).

A computer-aided design (CAD) model of the experimental setup is shown in Figure 3. The tests were conducted on a Sack & Kieselbach hydraulic press, equipped with an ejector. The variation in the compression force F with the die stroke S was continuously recorded during the compression process using a Spider 8 Hottinger Baldwin Messtechnik electronic measuring system. The tests were carried out at room temperature with a punch speed of 0.015 mm/s. The specimen elongation direction coincides with the x-axis. The die elements in contact with the specimens were made of X210Cr12 steel and quenched to 58 + 2 HRC.

The specimens of the different types were treated differently for testing. The cleaned specimens of type O were immersed in a container with the oil. The die’s working surfaces were also covered with the same oil before each test. The cleaned specimens of type GS were first coated with MoS₂ grease and then sprinkled with stearin powder. The die’s working surfaces were coated with the same mixture. The specimens of type D were washed with benzene and then dried before testing. The die was disassembled, thoroughly cleaned, and washed of previous lubricants, and the die’s working surfaces were cleaned with benzene.

Figure 4 shows the representative specimens of types O, GS, and D, respectively, at the end of the compression test. Various geometrical and process parameters are presented in

Table 1. Final dimensions and process parameters of specimens made of AA 6026.

Specimen No.	2a [mm]	2b [mm]	2t [mm]	Stroke Smax [mm]	Fmax [kN]	Lubrication
O-1	40.50	14.42	3.66	2.40	827	Oil
O-2	40.60	14.37	3.71	2.39	1025	Oil
O-3	40.20	14.58	3.62	2.43	997	Oil
GS-1	55.10	14.42	2.88	3.35	1095	Grease + Stearin
GS-2	55.90	14.26	2.91	3.36	1098	Grease + Stearin
GS-3	55.82	14.25	2.62	3.36	1097	Grease + Stearin
D-1	36.90	14.41	3.79	2.05	1065	Without lubrication
D-2	37.10	14.40	3.83	2.07	1068	Without lubrication
D-3	36.90	14.41	3.78	2.05	1064	Without lubrication

and

Table 2. Final dimensions and process parameters of specimens made of C45.

Specimen No.	2a [mm]	2b [mm]	2t [mm]	Stroke Smax [mm]	Fmax [kN]	Lubrication
O-1	32.11	14.48	4.49	1.48	997	Oil
O-2	31.82	14.86	4.41	1.56	998	Oil
O-3	32.05	14.83	4.39	1.60	996	Oil
GS-1	35.40	15.21	3.85	2.10	995	Grease + Stearin
GS-2	35.87	14.88	3.87	2.05	997	Grease + Stearin
GS-3	35.65	14.84	3.92	2.02	1046	Grease + Stearin
D-1	30.80	15.15	4.39	1.50	1146	Without lubrication
D-2	31.40	14.91	4.36	1.52	1157	Without lubrication
D-3	31.81	14.87	4.36	1.55	1175	Without lubrication

. The variation in forming force (F) with plastic stroke (S) is depicted in Figure 5 for AA 6026 and Figure 6 for C45.

Based on the final compressed length of specimens made from the same material (AA6026 or C45) (Figure 4, Table 1 and Table 2), it can be observed that the shorter specimens (lubricated with mineral oil and dry lubrication) indicate higher values of contact friction compared to the GS-type specimens, which have the greatest length.

In addition, the C45 steel specimens, under the same lubrication conditions, are shorter compared to the corresponding aluminum specimens at approximately the same values of maximum strain, which is related to the mechanical properties of the materials (the flow curve of steel is significantly higher than that of aluminum), as shown in Table 1 and Table 2.

4. Cylinder Compression Test for Determining the Hardening Law

The strain hardening behavior of the materials was determined using the cylinder compression test by Rastegaev’s method [19]. The specimen’s geometry before testing is shown in Figure 7. The specific geometric parameters are H₀ = 20 mm, d₀ = 20 mm, u = 0.6 mm, and h₀ = 19.4 mm. Three nominally identical specimens of each material were tested. The variation in the compression force F with the die stroke S was continuously recorded during the compression process using a Spider 8 Hottinger Baldwin Messtechnik electronic measuring system. The corresponding curves are depicted in Figure 8. Assuming that the deformation is homogeneous and considering the plastic incompressibility of the materials, one can calculate the current area A and the flow stress ${\sigma }_f$ as

$$A={\displaystyle \frac{\pi d_0^2{h}_0}{4\left(h_0-S\right)}}\hspace{1em}\mathrm{and}\hspace{1em}{\sigma }_f={\displaystyle \frac{4\left(h_0-S\right)F}{\pi d_0^2{h}_0}}.$$

(17)

The equivalent Mises strain is

$${\phi }_e=\ln \left({\displaystyle \frac{h_0}{h_0-S}}\right).$$

(18)

The experimental data in Figure 8 and the equations in (17) and (18) enable the determination of the dependence of ${\sigma }_f$ on φ_e. The corresponding curves are depicted in Figure 9.

5. Determination of the Friction Factor

The yield stress required by the theoretical solution in Section 3.1 is replaced with the proof strength σ₀₂, as is commonly accepted. The value of σ₀₂ was determined using the experimental data in Figure 9. As a result, σ₀₂ = 302 MPa for AA 6062 and σ₀₂ = 575 MPa for C45. Assuming the von Mises yield criterion, one obtains $k_0={\sigma }_{02}/\sqrt{3}$.

The relationship between the equivalent strain ε_eq and the Mises equivalent strain φ_e is

$${\epsilon }_{eq}={\displaystyle \frac{\sqrt{3}}{2}}{\phi }_e.$$

(19)

The functions $\Phi \left({\epsilon }_{eq}\right)$ for the two materials were represented by interpolating functions of the first order using Equation (19) and the experimental data in Figure 9. Figure 10 and Figure 11 depict the variation in f with η for several m-factors computed by employing the theoretical solution in Section 3.1. The same figures display the experimental data obtained using Figure 5 and Figure 6, the definition of f in (16), the equation $S=2t_0\left(1-\eta \right)$, and the values of σ₀₂ mentioned above. The theoretical curves were computed within the range of the experimental data in the cylinder compression test (i.e., no extrapolation was used). The leftmost points of the theoretical curves correspond to the value of the equivalent strain at the friction surface equal to the maximum value of the equivalent strain in the cylinder compression test.

It is seen from Figure 10 and Figure 11 that the friction law in (5) does not represent the real frictional behavior, except for the steel specimens compressed with no lubricant. In the latter case, $m\simeq 0.7$ in the range of the equivalent strain covered by the experiment, except for a small range at the beginning of the process. It is not surprising because it is commonly accepted that the friction factor varies as the deformation of a subsurface layer proceeds [22]. There are several reasons for that, such as the change in surface roughness, the change in the lubricant’s properties, the rise in temperature, etc. Nevertheless, the study conducted allows for comparing the efficiency of the used lubricants and determining the initial friction factor. Particularly, Figure 10 and Figure 11 show that the lubricant denoted as type GS is more efficient than the lubricant denoted as type O under all the conditions investigated. Table 1 depicts the experimental values of f at the initial instant under the different conditions used. Note that the ideal frictionless compression requires f = 2 at the initial instant. Therefore, the lubricant denoted as type GS exhibits a frictional behavior that is relatively close to this ideal condition at the beginning of the process. On the other hand, it is expected that the stick-slip phenomenon occurs when the specimens made of AA 6062 are compressed with no lubricant. Particularly, the theoretical value of f computed at m = 0.97 is f = 3.63, which is still lower than the experimental value shown in Table 1. However, it follows from (12) that ${\epsilon }_{eq}^f\to \infty$ as $m\to 1$, which is a consequence of the general theory that requires the regime of sticking for strain-hardening materials if m = 1 [23]. A similar frictional behavior at the beginning of the process occurs when steel specimens are compressed without a lubricant. The initial values of m for all the cases not mentioned above were computed employing interpolating functions constructed using the calculated values of f for discrete values of m (Figure 10 and Figure 11). These values are summarized in

Table 3. Dependence of the initial value of the friction factor on the frictional conditions for the two materials.

	Type O, Al	Type GS, Al	Type D, Al	Type O, Steel	Type GS, Steel	Type D, Steel
f at η = 1	3.22	2.46	3.85	2.9	2.17	3.8
Initial value of m	0.67	0.22	Very close to unity	0.47	0.09	Very close to unity

.

6. Conclusions

From this work, the following conclusions can be drawn:

• The proposed method is efficient for evaluating the friction law (5), as the theoretical solution is relatively simple.
• The friction law (5) is not a good approximation of the friction stress, except for the steel specimens deformed with no lubricant.
• The lubricant denoted as type GS is more efficient than that denoted as type O.
• The overall structure of the theoretical solution suggests that it can be extended to a generalized friction law that accounts for the variation in the friction factor as deformation proceeds, providing a theoretical basis for further research.