Effect of Lanthanum-Cerium Rare Earth Elements on Steel at Atomic Scale: A Review
Abstract
1. Introduction
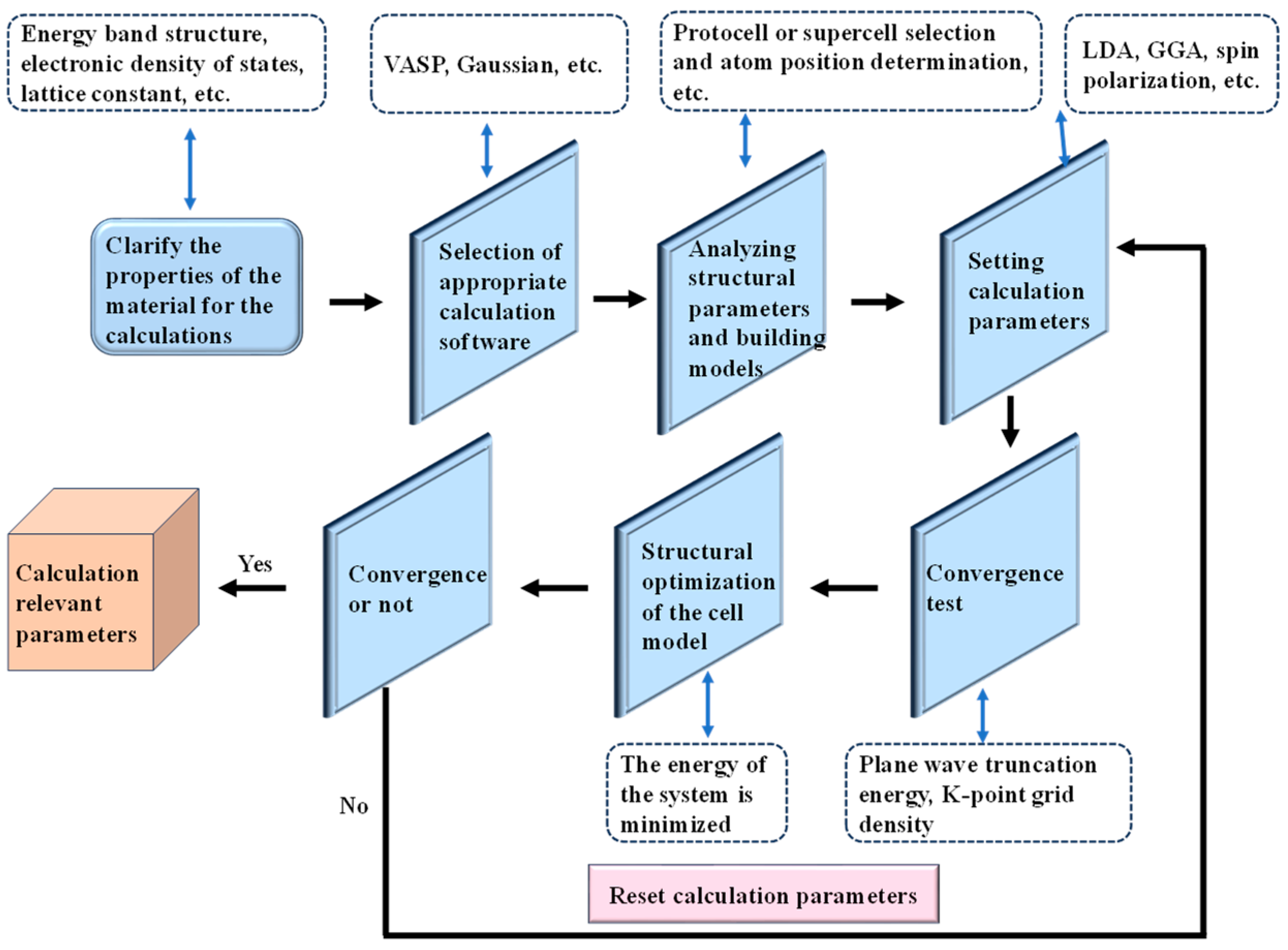
2. Overview of First Principles
3. Behavior of RE Inclusions in Steel
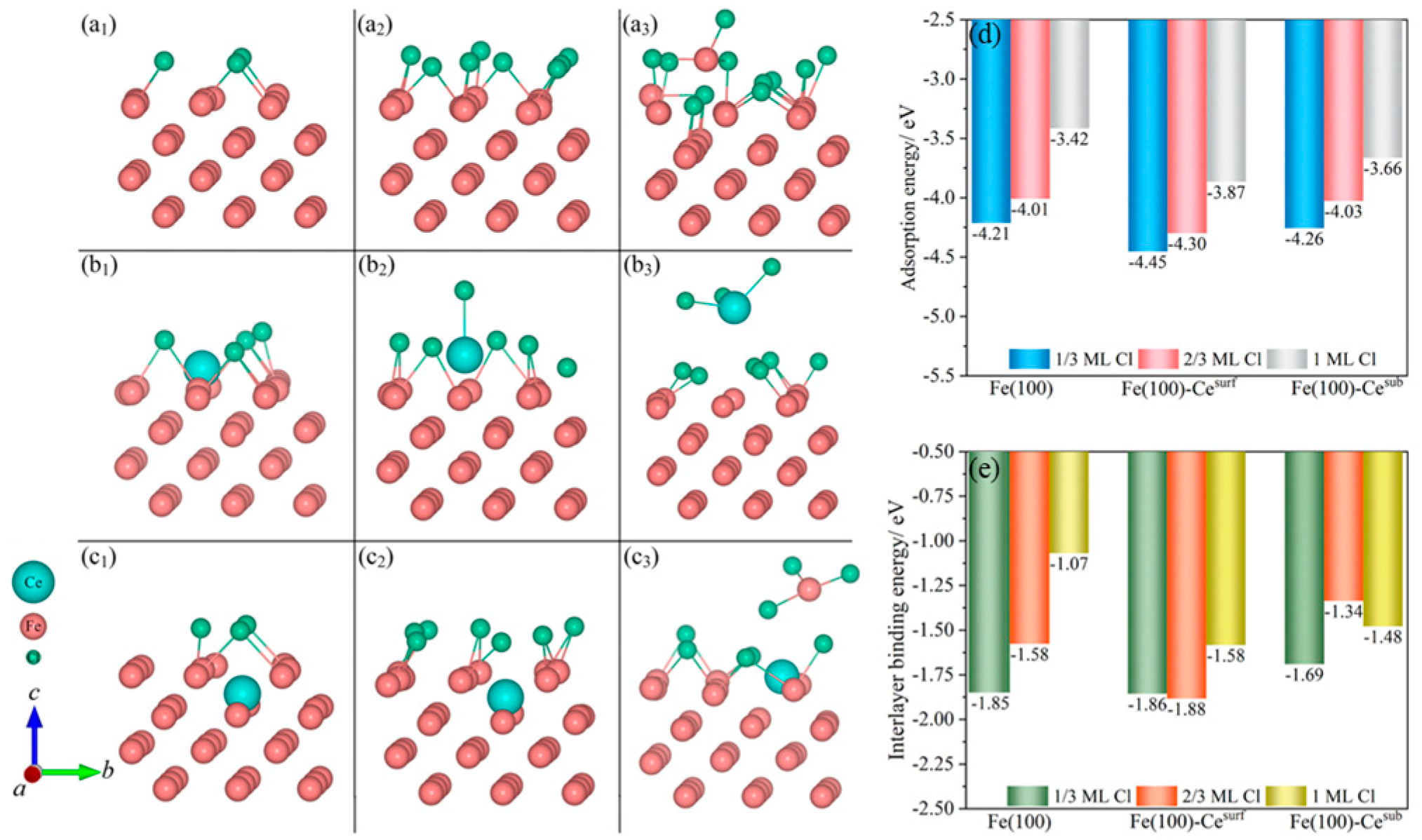
3.1. Nucleation of RE Inclusions
3.2. Properties of RE Inclusions
3.2.1. Formation Rule of RE Inclusions
3.2.2. Mechanical Properties of RE Inclusions
3.3. Effect of RE Inclusions on Steel Properties
3.3.1. Corrosion Behavior of RE Inclusions
3.3.2. Performance of RE Inclusions on Grain Refinement
4. Behavior of Solid Solution RE Atoms
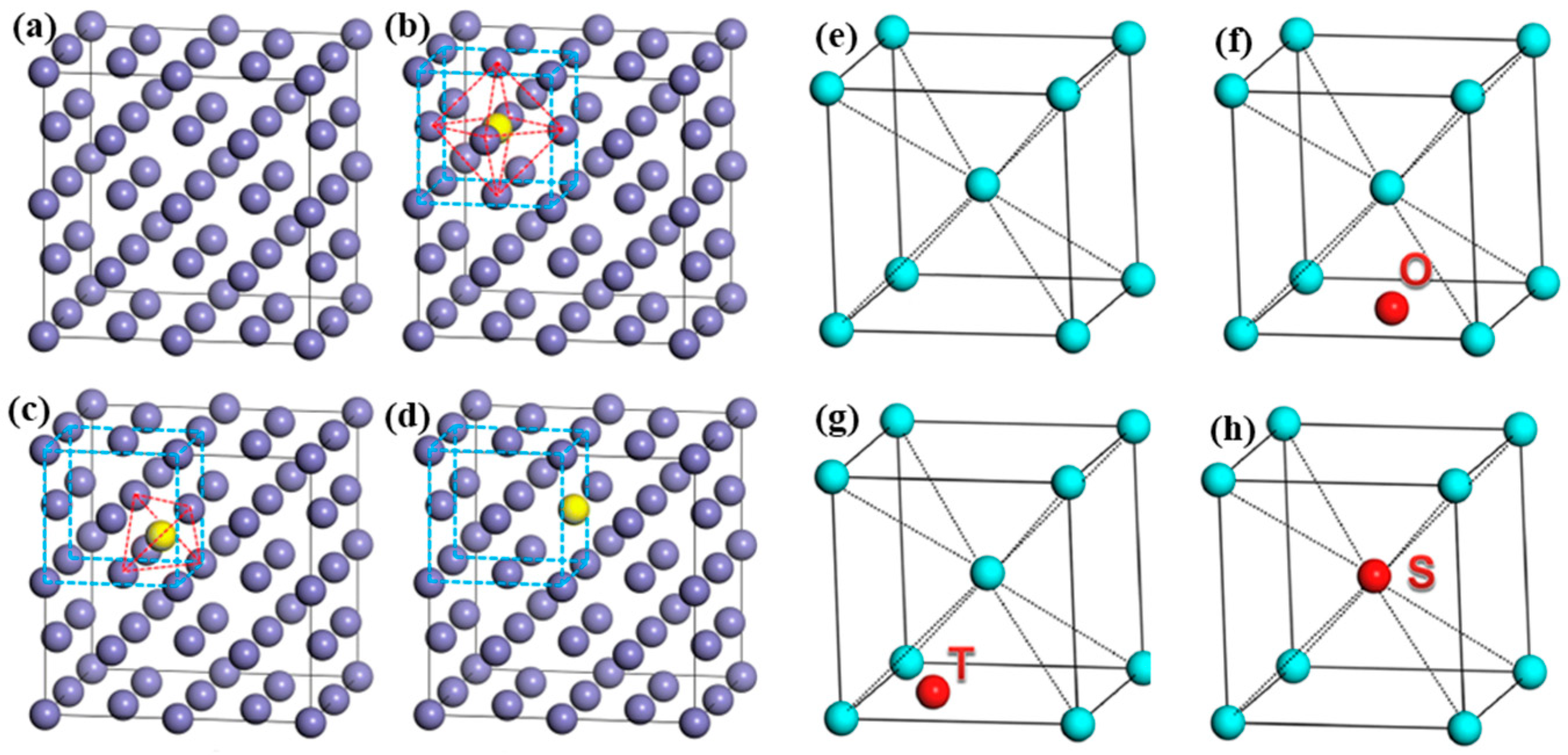
4.1. Solid Solution Positions of RE Atoms
4.2. Segregation of RE Atoms
4.3. Mechanism of Microalloying of RE Atoms
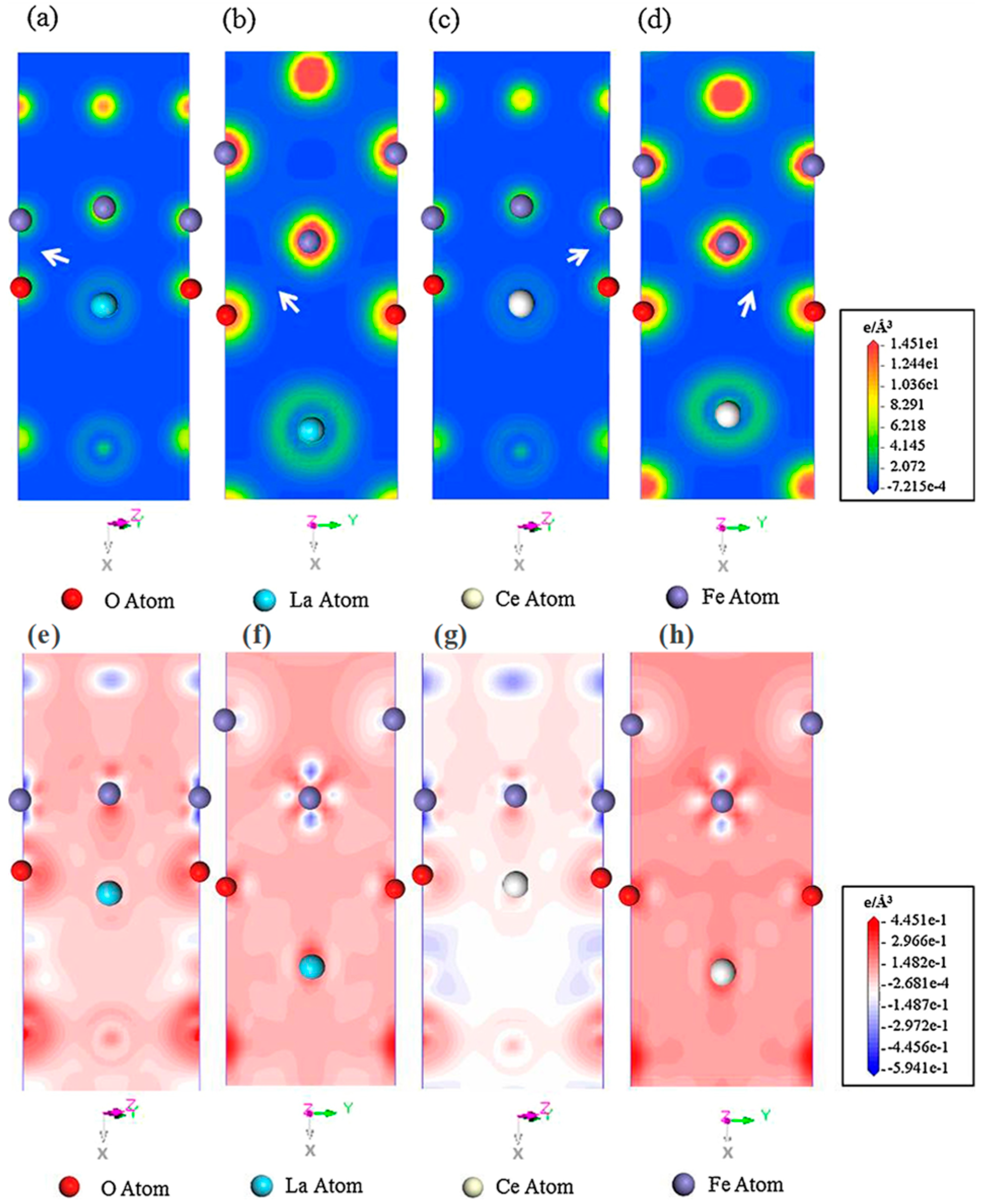
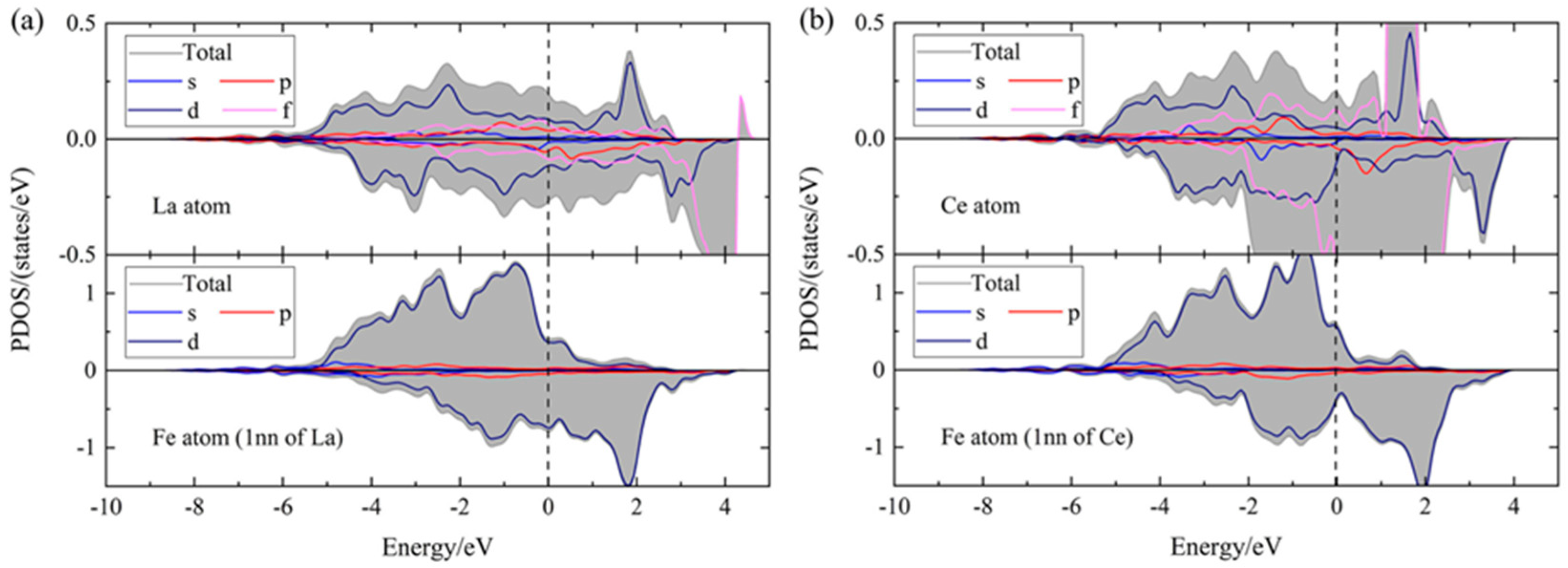
4.4. Interactions of RE Atoms with Other Atoms
5. Conclusions and Outlook
- The nucleation process of RE oxides involves the gradual evolution of RE elements combined with O to form crystals, nanoparticles and final phases. The formation of RE inclusions is prioritized as Re2O3 > ReAlO3 > Re2O2S > ReSx.
- The theoretical corrosion tendency of RE inclusions is associated with the system composition. Lanthanum-containing inclusions show the following order: LaS > La2O2S > LaAlO3 > Fe, and the theoretical corrosion tendency of cerium-containing inclusions is Ce2O3 > Ce2O2S > CeS > Fe > CeAlO3.
- Mechanical property analysis shows that ReAlO3 significantly enhances the deformation and fracture resistance of steel. Re2O3, Re2O2S and ReS behaved as ductile materials, while other RE inclusions behaved as brittle.
- Studies on the effect of RE inclusions on the heterogeneous nucleation of γ-Fe and α-Fe indicate that CeO2 and La2O3 can act as heterogeneous nucleation cores for γ-Fe, whereas La2O2S cannot, and ReAlO3 can act as a γ-Fe heterogeneous nucleation under the following conditions: the chemical potential of La ranges from −11.59 eV to −11.22 eV or −1.94 eV to −1.56 eV, and the chemical potential of Ce ranges from −6.27 eV to −5.97 eV. LaAlO3 can act as an α-Fe nucleation core at La chemical potentials of −2.447 eV and −1.009 eV.
- RE atoms tend to occupy S-point sites in the Fe matrix and segregate at GBs or vacancies, where up to 14 RE atoms can be stabilized at the vacancies. The interaction of RE atoms with other alloying elements in steel promotes or inhibits their solid solution behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T.; Wang, X.-L.; Song, S.-H.; Ma, Q. Effect of rare-earth Nd/Sm doping on the structural and multiferroic properties of BiFeO3 ceramics prepared by spark plasma sintering. Ceram. Int. 2020, 46, 15228–15235. [Google Scholar] [CrossRef]
- Balaram, V. Rare earth elements: A review of applications, occurrence, exploration, analysis, recycling, and environmental impact. Geosci. Front. 2019, 10, 1285–1303. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z.; Li, B.; Chen, W.; Zhang, J.; Mao, J. Inclusions modification by rare earth in steel and the resulting properties: A review. J. Rare Earths 2024, 42, 431–445. [Google Scholar] [CrossRef]
- Bai, Y.; Zheng, S.; Liu, N.; Liu, Y.; Wang, X.; Qiu, L.; Gong, A. The Role of Rare Earths on Steel and Rare Earth Steel Corrosion Mechanism of Research Progress. Coatings 2024, 14, 465. [Google Scholar] [CrossRef]
- Li, D.; Wang, P.; Chen, X.-Q.; Fu, P.; Luan, Y.; Hu, X.; Liu, H.; Sun, M.; Chen, Y.; Cao, Y. Low-oxygen rare earth steels. Nat. Mater. 2022, 21, 1137–1143. [Google Scholar] [CrossRef]
- Li, B.; Zhu, H.; Zhao, J.; Song, M.; Li, J.; Xue, Z. Effect of Rare-Earth La on Inclusion Evolution in High-Al Steel. Steel Res. Int. 2022, 93, 2100347. [Google Scholar] [CrossRef]
- Huang, F.; Li, J.; Geng, R.; Wang, C. Effect of rare earth on inclusion evolution and corrosion resistance of HRB400E steel. Mater. Corros. 2023, 74, 53–67. [Google Scholar] [CrossRef]
- Yang, C.; Luan, Y.; Li, D.; Li, Y. Effects of rare earth elements on inclusions and impact toughness of high-carbon chromium bearing steel. J. Mater. Sci. Technol. 2019, 35, 1298–1308. [Google Scholar] [CrossRef]
- Cao, Y.; Miao, Y.; Li, D.; Chen, Y.; Fu, P.; Liu, H.; Kang, X.; Liu, H.; Sun, C. On the Mechanism of Steel Homogenization via Rare Earth Addition: Experimental Characterization and Numerical Simulation. Metall. Mater. Trans. B 2022, 53, 1858–1874. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Y.; Zhang, S.; Zhang, L. Effect of rare earth element yttrium modified inclusion on corrosion properties of stainless steel. Mater. Today Commun. 2024, 39, 109185. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, Y.; Xu, X.; Fu, J. Modification of inclusion in high-strength steel treated with rare earth. J. Mater. Res. Technol. 2025, 36, 470–480. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, H.; Zhang, Y.; Tian, S.; Zhang, R.; Yang, Y.; Zhang, S.; Hong, Z.; Fang, X. First-principles study on the diffusion of interstitial hydrogen in rare earth doped α-Fe. Int. J. Hydrogen Energy 2025, 133, 363–376. [Google Scholar] [CrossRef]
- Wang, H.; Wang, A.; Li, C.; Yu, X.; Xie, J.; Liang, T.; Liu, C. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel. Rev. Adv. Mater. Sci. 2022, 61, 873–887. [Google Scholar] [CrossRef]
- Song, M.-M.; Song, B.; Zhang, S.-H.; Yang, Z.-B.; Xue, Z.-L.; Song, S.-Q.; Xu, R.-S.; Tong, Z.-B. Effect of heat input on microstructure and toughness of rare earth-contained C–Mn steel. J. Iron. Steel Res. Int. 2018, 25, 1033–1042. [Google Scholar] [CrossRef]
- Gao, J.; Fu, P.; Liu, H.; Li, D. Effects of rare earth on the microstructure and impact toughness of H13 steel. Metals 2015, 5, 383–394. [Google Scholar] [CrossRef]
- Shi, X.; Ren, H.; Li, X.; Liu, X.; Zhan, F.; Yang, C. Effect of Ce on Inclusions and Precipitates in 10Cr5MoV Steel and the Microscopic Behavior of Solid Solution Ce in Steel. Steel Res. Int. 2024, 95, 2300814. [Google Scholar] [CrossRef]
- Li, B.; Hou, D.; Liu, T.; Wang, D.; He, J.; Fan, L.; Wang, H.; Wang, Z. Evolutions of Microstructure by Cerium Treatment in As-Cast M2 High-Speed Steel. Steel Res. Int. 2025, 96, 2400601. [Google Scholar] [CrossRef]
- Lyu, Z.; Gu, C.; Wang, Z.; Bao, Y. In-depth analysis on the mechanism and reaction efficiency of hydrogen deoxidation in ultra-low carbon steel. Surf. Interfaces 2024, 55, 105284. [Google Scholar] [CrossRef]
- Zhang, J.; Su, C.; Chen, X.; Liu, H.; Zhang, L. First-principles study on pitting corrosion of Al deoxidation stainless steel with rare earth element (La) treatment. Mater. Today Commun. 2021, 27, 102204. [Google Scholar] [CrossRef]
- Fan, D.; Liu, C.; Yin, F.; Hou, Z.; Yang, J. Solid solution strengthening mechanism and interstitial diffusion behavior of rare earth element lanthanum in austenite using first-principles calculations. Theor. Chem. Acc. 2020, 139, 3. [Google Scholar] [CrossRef]
- Yang, H.; Ren, Y.; Wang, J.; Zhang, L. First-Principles Calculation and In Situ Observation on the Precipitation of Inclusions during Solidification of a High Sulfur Steel. Steel Res. Int. 2024, 95, 2400465. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Z.; Yang, C.; Li, X.; Yang, J.; Ren, H.; Ma, H. First-principles analysis of effects of cerium doping on electrochemical corrosion behaviors of steel. J. Rare Earths 2025, 43, 1758–1768. [Google Scholar] [CrossRef]
- Zhu, L.; Luo, J.; Zheng, S.; Yang, S.; Hu, J.; Chen, Z. Understanding hydrogen diffusion mechanisms in doped α-Fe through DFT calculations. Int. J. Hydrogen Energy 2023, 48, 17703–17710. [Google Scholar] [CrossRef]
- Liu, X.-J.; Yang, J.-C.; Ren, H.-P.; Jia, X.-B.; Zhang, M.-Y.; Yang, C.-Q. Effect of solute Ce, Mn, and Si on mechanical properties of silicon steel: Insights from DFT calculations. J. Iron. Steel Res. Int. 2024, 31, 700–709. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Milman, V.; Refson, K.; Clark, S.; Pickard, C.; Yates, J.; Gao, S.-P.; Hasnip, P.; Probert, M.; Perlov, A.; Segall, M. Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation. J. Mol. Struct. THEOCHEM 2010, 954, 22–35. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Liang, Y.; Chen, W.; Wang, F. Recent advances of stretched Gaussian distribution underlying Hausdorff fractal distance and its applications in fitting stretched Gaussian noise. Physica A 2020, 539, 122996. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-Nmaterials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Schwarz, K.; Blaha, P. Solid state calculations using WIEN2k. Comput. Mater. Sci 2003, 28, 259–273. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Zhang, F.; Fu, X.; Li, H.; Yang, C. Experimental and DFT study on cerium inclusions in clean steels. J. Rare Earths 2021, 39, 477–486. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Cai, C.; Li, A.; Lei, X.; Yang, C. Effect of Microalloyed Elements M (M = Ce, Ti, V, and Nb) on Mechanical Properties and Electronic Structures of γ-Fe: Insights from a First-Principles Study. Steel Res. Int. 2021, 92, 2100053. [Google Scholar] [CrossRef]
- Cao, Y.; Li, G.; Hou, Y.; Moelans, N.; Guo, M. DFT study on the mechanism of inclusion-induced initial pitting corrosion of Al-Ti-Ca complex deoxidized steel with Ce treatment. Phys. B 2019, 558, 10–19. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Wang, L.; Chen, C.; Yang, S.; Li, J.; Li, X. Cerium oxide inclusion nucleation mechanism based on classical nucleation theory and two-step nucleation. J. Rare Earths 2024, 42, 793–802. [Google Scholar] [CrossRef]
- You, Y.; Yan, J.; Yan, M. Atomistic diffusion mechanism of rare earth carburizing/nitriding on iron-based alloy. Appl. Surf. Sci. 2019, 484, 710–715. [Google Scholar] [CrossRef]
- Tang, M.; Wu, K.; Liu, J.; Cheng, L.; Zhang, X.; Chen, Y. Mechanism understanding of the role of rare earth inclusions in the initial marine corrosion process of microalloyed steels. Materials 2019, 12, 3359. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, W.; Cheng, L.; Liu, J.; Wu, K.; Liu, M. Effects of niobium and rare earth elements on microstructure and initial marine corrosion behavior of low-alloy steels. Appl. Surf. Sci. 2019, 475, 83–93. [Google Scholar] [CrossRef]
- Song, Y.; Li, C.; Qiao, Q.; Ren, L.; Yang, J. Impact of la on steel inclusions: A first-principles investigation into elastic properties and anisotropy. J. Phys. Conf. Ser. 2024, 3095, 012031. [Google Scholar] [CrossRef]
- Murad, M.; Ali, Z.; Idrees, M. Hybrid DFT study of structural, electronic, magnetic and elastic properties of laves phase binary intermetallics RFe2 (R = La, Ce, Pr and Nd). J. Rare Earths 2023, 41, 1367–1375. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, X.; Yang, X.; Zhang, S.; Li, D. First-principles analysis on the role of rare-earth doping in affecting nitrogen adsorption and diffusion at Fe surface towards clarified catalytic diffusion mechanism in nitriding. Acta Mater. 2020, 196, 347–354. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Fan, D.; Chen, S.; Zhao, X. Comparative investigation on RE (La, Ce) AlO3 (100)/γ-Fe (100) interfaces: A first-principles calculation. Appl. Surf. Sci. 2016, 384, 207–216. [Google Scholar] [CrossRef]
- Gao, X.; Ren, H.; Li, C.; Wang, H.; Ji, Y.; Tan, H. First-principles calculations of rare earth (Y, La and Ce) diffusivities in bcc Fe. J. Alloys Compd. 2016, 663, 316–320. [Google Scholar] [CrossRef]
- Luo, S.; Shen, Z.; Yu, Z.; Wang, W.; Zhu, M. Effect of Ce addition on inclusions and grain structure in gear steel 20CrNiMo. Steel Res. Int. 2021, 92, 2000394. [Google Scholar] [CrossRef]
- Ren, Q.; Hu, Z.; Cheng, L.; Kang, X.; Cheng, Y.; Zhang, L. Modification mechanism of lanthanum on alumina inclusions in a nonoriented electrical steel. Steel Res. Int. 2022, 93, 2200212. [Google Scholar] [CrossRef]
- Takamura, J.-i.; Mizoguchi, S. Roles of oxides in steels performance. In Proceedings of the sixth international iron and steel congress, Tokyo, Japan, 21–26 October 1990; pp. 591–597. [Google Scholar]
- Ren, Y.; Zhang, L. In-situ observation of nonmetallic inclusions in steel using confocal scanning laser microscopy: A review. Int. J. Miner. Metall. Mater. 2025, 32, 975–991. [Google Scholar] [CrossRef]
- Wang, Z.; Sohn, I. A review of in situ observations of crystallization and growth in high temperature oxide melts. JOM 2018, 70, 1210–1219. [Google Scholar] [CrossRef]
- You, D.; Michelic, S.K.; Presoly, P.; Liu, J.; Bernhard, C. Modeling inclusion formation during solidification of steel: A review. Metals 2017, 7, 460. [Google Scholar] [CrossRef]
- Park, J.H.; Zhang, L. Kinetic modeling of nonmetallic inclusions behavior in molten steel: A review. Metall. Mater. Trans. B 2020, 51, 2453–2482. [Google Scholar] [CrossRef]
- Jiang, X.; Luo, D.; Zhang, Z.; Liu, M.; Liu, Y.; Yu, Y.; Feng, X.; Lai, C. Multiscale nucleation growth model of yttrium oxide during the deoxidation of Fe–O–Y melt. J. Mater. Sci. 2022, 57, 6988–7000. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, C.; Zhang, H.; Li, J.; Liu, J. Solidification Characteristics and Eutectic Precipitates in 15Cr–22Ni–1Nb Austenitic Heat-Resistant Stainless Steel. Metall. Mater. Trans. B 2023, 54, 2302–2319. [Google Scholar] [CrossRef]
- Long, Q.; Wang, W.; Gao, X. Effect of Al–Ti Concentration on the Alumina Inclusions Agglomeration Behavior on the Surface of Molten Steel. Metall. Mater. Trans. B 2023, 54, 2552–2563. [Google Scholar] [CrossRef]
- Meng, Q.; Guo, X.; Li, T.; Shang, B.; Ju, L.; Zhang, F. First principles and experimental study on the atomic formation of MnS–Al2SiO5 inclusions in steel. ISIJ Int. 2022, 62, 1126–1135. [Google Scholar] [CrossRef]
- Mattsson, T.R.; Mattsson, A.E. Calculating the vacancy formation energy in metals: Pt, Pd, and Mo. Phys. Rev. B 2002, 66, 214110. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Zhang, L. First-principle study of the effect of cerium on the modification and corrosion of nonmetal inclusions in steel. Chin. J. Eng. 2022, 44, 1516–1528. [Google Scholar]
- Bai, G. Study on Behavior Characteristics and Industrial Application of Rare Earth. Ph.D. Thesis, Inner Mongolia University of Science & Technology, Baotou, China, 2023. [Google Scholar]
- Wang, T. Effect Rare Earth Element La on the Properties of Silicon Steel Insight from a First-Principles Study. Master’s Thesis, Inner Mongolia University of Science & Technology, Baotou, China, 2023. [Google Scholar]
- Voigt, W. Lehrbuch der Kristallphysik:(Mit Ausschluss der Kristalloptik); BG Teubner: Berlin, Germany, 1910; Volume 34. [Google Scholar]
- Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Chen, J.; Du, Y.; Yu, J.; Zhou, R. Stability, thermal and mechanical properties of PtxAly compounds. Mater. Des. 2011, 32, 3231–3239. [Google Scholar] [CrossRef]
- Zhang, J.; Su, C.; Liu, Y. First-principles study of bcc Fe-Cr-Si binary and ternary random alloys from special quasi-random structure. Phys. B 2020, 586, 412085. [Google Scholar] [CrossRef]
- Su, C.; Zhang, J. First-principles study on growth mechanism of TiN on MgO (1 0 0) and (1 1 0) surfaces. Comput. Mater. Sci 2021, 189, 110257. [Google Scholar] [CrossRef]
- Liu, H. First-Principles Calculation of Effect of Rare Earth Element Ce on Inclusion Modification and Corrosion Properties in Steel. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2023. [Google Scholar]
- Niu, Z.-W.; Cheng, Y.; Chen, X.-R.; Xu, K.; Ji, G.-F. Elastic and electronic properties of Ce2O3 from first principles. J. Alloys Compd. 2013, 551, 672–676. [Google Scholar] [CrossRef]
- Luo, X.; Wang, B.; Zheng, Y. First-principles study on energetics of intrinsic point defects in LaAlO3. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 104115. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, D.; Liu, Z. Structural and elastic DFT study of four structures for Cu2ZnSnS4 under high pressure. J. Alloys Compd. 2017, 696, 86–95. [Google Scholar] [CrossRef]
- Lebedeva, I.V.; Minkin, A.S.; Popov, A.M.; Knizhnik, A.A. Elastic constants of graphene: Comparison of empirical potentials and DFT calculations. Phys. E 2019, 108, 326–338. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Yang, S.; Li, J.; Chen, C.; Li, C.; Tuo, B. Study on localized corrosion induced by non-metallic inclusions in OCTG steel. Metall. Mater. Trans. B 2022, 53, 1212–1223. [Google Scholar] [CrossRef]
- Liu, C.; Revilla, R.I.; Li, X.; Jiang, Z.; Yang, S.; Cui, Z.; Zhang, D.; Terryn, H.; Li, X. New insights into the mechanism of localised corrosion induced by TiN-containing inclusions in high strength low alloy steel. J. Mater. Sci. Technol. 2022, 124, 141–149. [Google Scholar] [CrossRef]
- Luo, Y.; Tang, Y.; Chung, T.-F.; Tai, C.-L.; Chen, C.-Y.; Yang, J.-R.; Li, D. Electron work function: An indicative parameter towards a novel material design methodology. Sci. Rep. 2021, 11, 11565. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Chen, X.-Q.; Li, R.; Wang, S.; Dong, J.; Ke, W. First-principles modeling of anisotropic anodic dissolution of metals and alloys in corrosive environments. Acta Mater. 2017, 130, 137–146. [Google Scholar] [CrossRef]
- Wei, W.; Wu, K.; Zhang, X.; Liu, J.; Qiu, P.; Cheng, L. In-situ characterization of initial marine corrosion induced by rare-earth elements modified inclusions in Zr-Ti deoxidized low-alloy steels. J. Mater. Res. Technol. 2020, 9, 1412–1424. [Google Scholar] [CrossRef]
- Hou, Y.; Xiong, G.; Liu, L.; Li, G.; Moelans, N.; Guo, M. Effects of LaAlO3 and La2O2S inclusions on the initialization of localized corrosion of pipeline steels in NaCl solution. Scr. Mater. 2020, 177, 151–156. [Google Scholar] [CrossRef]
- Tuttle, R.; Lewandowski, J.; Tomazin, R. Effect of rare earth oxides on rolling performance on grain refined 1030. Proc. AISTech 2015, 2015, 3461–3471. [Google Scholar]
- Feifei, H.; Bo, L.; Da, L.; Ting, D.; Xuejun, R.; Qingxiang, Y.; Ligang, L. Effects of rare earth oxide on hardfacing metal microstructure of medium carbon steel and its refinement mechanism. J. Rare Earths 2011, 29, 609–613. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Sun, M.; Xu, B.; Yao, J.; Fan, Q.; Li, D. Cerium refinement of grains and primary carbides during solidification of Cr4Mo4V bearing steel. J. Rare Earths 2024, 42, 783–792. [Google Scholar] [CrossRef]
- Jian, Y.; Feifei, H.; Da, L.; Yefei, Z.; Xuejun, R.; Yulin, Y.; Qingxiang, Y. Effect of RE oxide on growth dynamics of primary austenite grain in hardfacing layer of medium-high carbon steel. J. Rare Earths 2012, 30, 814–819. [Google Scholar] [CrossRef]
- Tuttle, R.; Kapadia, H.A. Thermal analysis of rare earth grain refined 4130. Int. J. Metalcast. 2019, 13, 273–285. [Google Scholar] [CrossRef]
- Liu, P.; Hou, X.; Yang, C.; Luan, Y.; Zheng, C.; Li, D.; Ma, G. Tailoring microstructure evolution and austenite stability of TRIP steels by Rare-Earth micro-alloying. Mater. Charact. 2023, 203, 113035. [Google Scholar] [CrossRef]
- Jiao, X.; Fu, W.; Shi, Z.; Li, Z.; Zhou, Y.; Xing, X.; Wang, Z.; Yang, Q. First principles investigation on interface properties and formation mechanism of γ-Fe/CeO2 heterogeneous nucleation interface. J. Alloys Compd. 2020, 831, 154867. [Google Scholar] [CrossRef]
- Zhou, Y.; Ji, Y.; Li, Y.; Qi, J.; Xin, H.; Ren, H. Crystallographic Calculations and First-Principles Calculations of Heterogeneous Nucleation Potency of γ-Fe on La2O2S Particles. Materials 2022, 15, 1374. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Fan, D.; Chen, S.; Zhao, X. LaAlO3 as the heterogeneous nucleus of ferrite: Experimental investigation and theoretical calculation. J. Alloys Compd. 2016, 683, 357–369. [Google Scholar] [CrossRef]
- Jiao, X.; Fu, W.; Shao, W.; Zhu, X.; Zhou, Y.; Xing, X.; Wang, Z.; Yang, Q. First-principles calculation on γ-Fe/La2O3 interface properties and austenite refinement mechanism by La2O3. Mater. Chem. Phys. 2021, 259, 124194. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Shi, C.; Yang, S.; He, X.; Wang, M.; Shi, J. Influence of rare earth Ce on the characteristics and microstructure of sulfides in non-tempered steel. Chin. J. Met. 2022, 58, 365–374. [Google Scholar]
- Liu, Z.; Lian, X.; Liu, T.; Yang, Y.; Zhu, J.; Dong, H. Effects of rare earth elements on corrosion behaviors of low-carbon steels and weathering steels. Mater. Corros. 2020, 71, 258–266. [Google Scholar] [CrossRef]
- Fan, Z.; Zhu, J.; Lian, X.; Liu, T.; Xu, D.; Wei, X.; Dong, H. Microstructure, Inclusions, and Elemental Distribution of a Compacted Graphite Iron Alloyed by Ce and La Rare Earth (RE) Elements. Metals 2022, 12, 779. [Google Scholar] [CrossRef]
- Liu, H.; Ma, H.; Du, N.; Fu, P.; Liu, H.; Cao, Y.; Sun, C.; Guo, Q.; Chen, X.; Li, D. Probing rare earth segregation in steels. Scripta Materialia 2023, 230, 115407. [Google Scholar] [CrossRef]
- Alfe, D.; Gillan, M.; Price, G. Ab initio chemical potentials of solid and liquid solutions and the chemistry of the Earth’s core. J. Chem. Phys. 2002, 116, 7127–7136. [Google Scholar] [CrossRef]
- Olsson, P.; Klaver, T.; Domain, C. Ab initio study of solute transition-metal interactions with point defects in bcc Fe. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 054102. [Google Scholar] [CrossRef]
- You, Y.; Yan, J.; Yan, M.; Zhang, C.; Chen, H.; Wang, Y.; Zhang, Y.; Wang, C. La interactions with C and N in bcc Fe from first principles. J. Alloys Compd. 2016, 688, 261–269. [Google Scholar] [CrossRef]
- Liu, X. Study on the Occurrence State of Rare Earth Ce in Steel and Its Influence Mechanism of Mechanical Properties and Corrosion Properties of Steel. Ph.D. Thesis, Inner Mongolia University of Science & Technology, Baotou, China, 2021. [Google Scholar]
- Jiang, X.; Song, S.-H. Enhanced hot ductility of a Cr–Mo low alloy steel by rare earth cerium. Mater. Sci. Eng. A 2014, 613, 171–177. [Google Scholar] [CrossRef]
- Chen, L.; Ma, X.; Wang, L.; Ye, X. Effect of rare earth element yttrium addition on microstructures and properties of a 21Cr–11Ni austenitic heat-resistant stainless steel. Mater. Des. 2011, 32, 2206–2212. [Google Scholar] [CrossRef]
- Du, C.; Jin, S.; Fang, Y.; Li, J.; Hu, S.; Yang, T.; Zhang, Y.; Huang, J.; Sha, G.; Wang, Y. Ultrastrong nanocrystalline steel with exceptional thermal stability and radiation tolerance. Nat. Commun. 2018, 9, 5389. [Google Scholar] [CrossRef]
- Razmpoosh, M.; DiGiovanni, C.; Zhou, Y.; Biro, E. Pathway to understand liquid metal embrittlement (LME) in Fe-Zn couple: From fundamentals toward application. Prog. Mater Sci. 2021, 121, 100798. [Google Scholar] [CrossRef]
- Scheiber, D.; Romaner, L. Impact of the segregation energy spectrum on the enthalpy and entropy of segregation. Acta Mater. 2021, 221, 117393. [Google Scholar] [CrossRef]
- Wang, H.; Gao, X.; Ren, H.; Zhang, H.; Tan, H. A first-principles study of the occupancy tendency of rare earth La in α-Fe and its effect on grain boundaries. Chin. J. Phys. 2014, 63, 369–373. [Google Scholar]
- Jin, H.; Elfimov, I.; Militzer, M. Study of the interaction of solutes with Σ5 (013) tilt grain boundaries in iron using density-functional theory. J. Appl. Phys. 2014, 115, 093506. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, C.; Xu, W. A first-principles study on the effects of rare earth La and Ce segregation on α-Fe zinc-induced liquid metal embrittlement. Chin. J. Iron Steel Res. 2022, 34, 1433–1438. [Google Scholar]
- Wang, H.; Gao, X.; Xing, L.; Zhai, T.; Lv, M.; Ren, H.; Wei, H.; Zhi, J. Effects of RE (La, Ce) on fcc-bcc martensitic transformation of iron via Bain transformation path. J. Rare Earths 2022, 40, 1812–1818. [Google Scholar] [CrossRef]
- You, Y.; Yan, M. Behaviors and interactions of La atom with other foreign substitutional atoms (Al, Si, Ti, V, Cr, Mn, Co, Ni, Cu, Nb or Mo) in iron based solid solution from first principles. Comput. Mater. Sci 2013, 73, 120–127. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, X.; Pan, F.; Ma, Z.; Sa, R.; Zheng, J.; Wang, Q. Effect of rare-earth doping on adsorption of carbon atom on ferrum surface and in ferrum subsurface: A first-principles study. J. Rare Earths 2021, 39, 1144–1150. [Google Scholar] [CrossRef]
- Liu, Y.; Zhi, J.; Lyu, Z.; Gu, C.; Diao, W.; Qu, Z.; Bao, Y. Structure and transport behavior of the CaO-SiO2-Al2O3-La2O3 system: Insights from molecular dynamics simulations. Ceram. Int. 2025, 51, 38855–38863. [Google Scholar] [CrossRef]







| Element | Software | Research Content | Refs. |
|---|---|---|---|
| Ce | VASP | Calculation of surface energy, solvation energy, adsorption energy, electronic structure and work function of Fe-Ce surface model to study the effect of Ce on the corrosion of steel | [22] |
| Ce | VASP | Calculation of formation energies, elastic constants and coefficients of thermal expansion of Ce2O3, CeAlO3, Ce2O2S, and study of their basic physical properties | [32] |
| Ce | VASP | Calculation of the electronic structure and elastic constants of the Fe-Ce system and study of the effect of solid solution RE atoms on the mechanical properties of steels | [24,33] |
| Ce | VASP | Calculation of the solution enthalpies of Ce atoms in iron, segregation energy at grain boundaries (GBs), and interaction of REs with vacancies in iron to study the segregation behavior of RE atoms | [5] |
| Ce | VASP | Calculating the work function of La2O2S to study the mechanism of RE inclusion-induced corrosion | [34] |
| Ce | DMol3 | Study of the thermodynamic properties and nucleation mechanism of Ce2O3 | [35] |
| Ce | VASP | Calculation of the electronic structure of the Fe-Ce-Cr system and study of the interaction of solid solution RE atoms with Cr atoms | [16,17] |
| La | CASTEP | Calculated interaction energies of La atoms with C and N atoms to study the mechanism of RE nitriding and carburizing on iron-based alloys | [36] |
| La | CASTEP | Calculation of the elastic modulus, Poisson’s ratio and anisotropy of the system when La atoms are in different sites of γ-Fe, and study of the solid solution strengthening mechanism and diffusion behavior of RE atoms | [20] |
| La | VASP | Calculation of work functions of La2O3, LaAlO3, La2O2S and Fe to study the corrosion tendency of RE inclusions | [37,38] |
| La | CASTEP | Calculation of formation energies and elastic constants of La2O3, La2O2S and LaAlO3, and study of their basic physical properties | [39] |
| Ce, La | WIEN2k | Calculation of lattice constants, ground state energies, electromagnetism and resistivity of the La/CeFe2 system, and study of the structural, electronic, magnetic and elastic properties of the La/CeFe2 | [40] |
| Ce, La | VASP | Calculation of surface energies and adsorption energies of C and N atoms in the system before and after doping with RE Ce and La, and study of the effect of solid solution RE atoms on the diffusion of C and N atoms | [41] |
| Ce, La | CASTEP | Calculation of the electronic structures, interfacial ideal adhesion work and interfacial energies of ReAlO3(100)/γ-Fe(100) to study the conditions under which RE inclusions act as heterogeneous nucleation sites for γ-Fe | [42] |
| Ce, La, Y | VASP | Calculation of vacancy binding energies, migration energies, pre-factors, and activation energies for Y, La, and Ce to study the diffusivity of RE atoms in bcc-Fe | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhi, J.; Lyu, Z.; Gu, C.; Diao, W.; Qu, Z.; Bao, Y. Effect of Lanthanum-Cerium Rare Earth Elements on Steel at Atomic Scale: A Review. Metals 2025, 15, 993. https://doi.org/10.3390/met15090993
Liu Y, Zhi J, Lyu Z, Gu C, Diao W, Qu Z, Bao Y. Effect of Lanthanum-Cerium Rare Earth Elements on Steel at Atomic Scale: A Review. Metals. 2025; 15(9):993. https://doi.org/10.3390/met15090993
Chicago/Turabian StyleLiu, Yuhang, Jianguo Zhi, Ziyu Lyu, Chao Gu, Wangcai Diao, Zhibo Qu, and Yanping Bao. 2025. "Effect of Lanthanum-Cerium Rare Earth Elements on Steel at Atomic Scale: A Review" Metals 15, no. 9: 993. https://doi.org/10.3390/met15090993
APA StyleLiu, Y., Zhi, J., Lyu, Z., Gu, C., Diao, W., Qu, Z., & Bao, Y. (2025). Effect of Lanthanum-Cerium Rare Earth Elements on Steel at Atomic Scale: A Review. Metals, 15(9), 993. https://doi.org/10.3390/met15090993






