Experimental Study on Fatigue Performance of Q355D Notched Steel Under High-Low Frequency Superimposed Loading
Abstract
1. Introduction
2. Experimental Design and Results
2.1. Material and Specimen
2.2. Loading Conditions and Results
2.2.1. Generalization of HLSF Stress Waveform Patterns
2.2.2. Constant Amplitude Tests
2.2.3. Superimposed Loading Tests
2.3. Fracture Characteristics
3. Fatigue Life Analysis and Discussion
3.1. Existing Life Prediction Models
- Miner’s rule
- 2.
- T-K model
- 3.
- Yue model
3.2. Modeling of HLSF Block Nonlinear Damage Effects
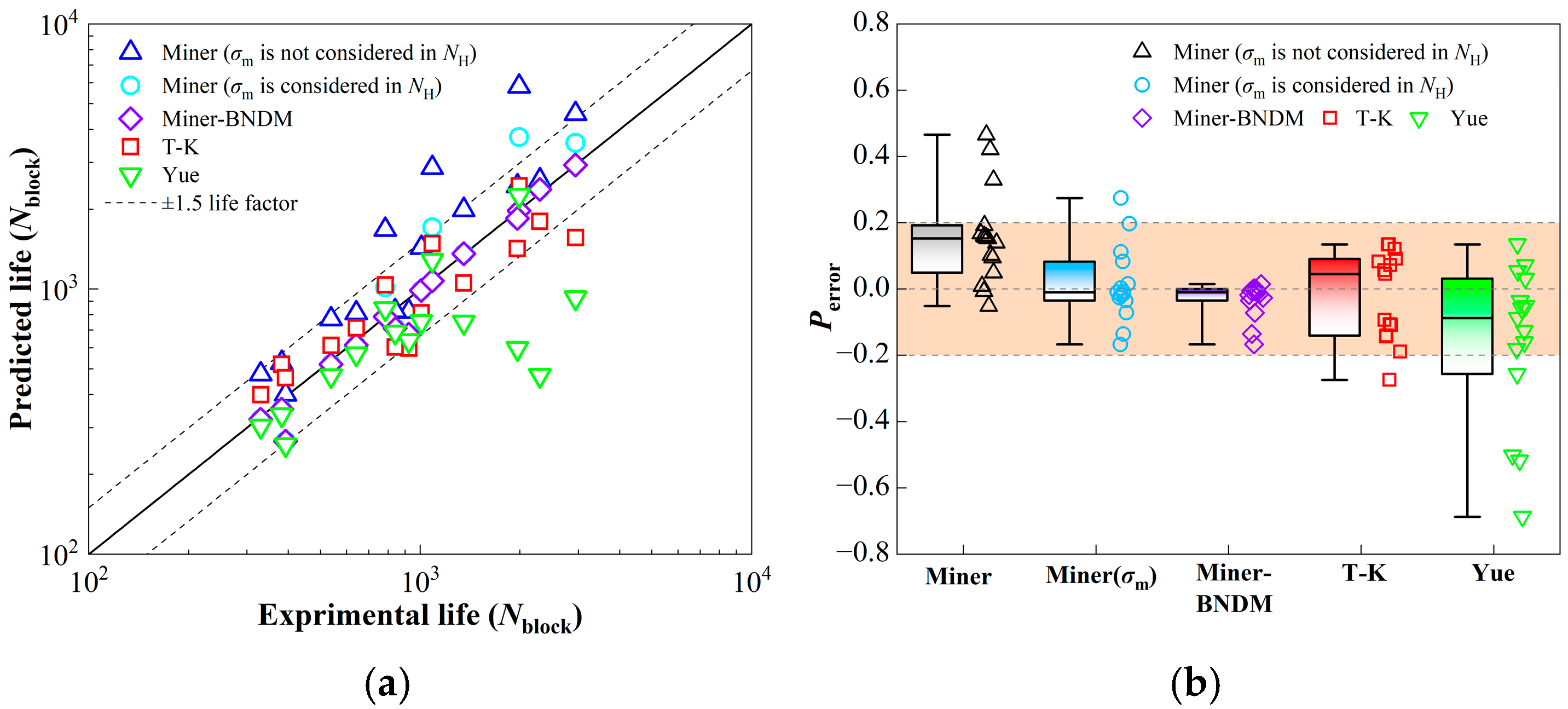
3.3. Life Analysis and Comparison
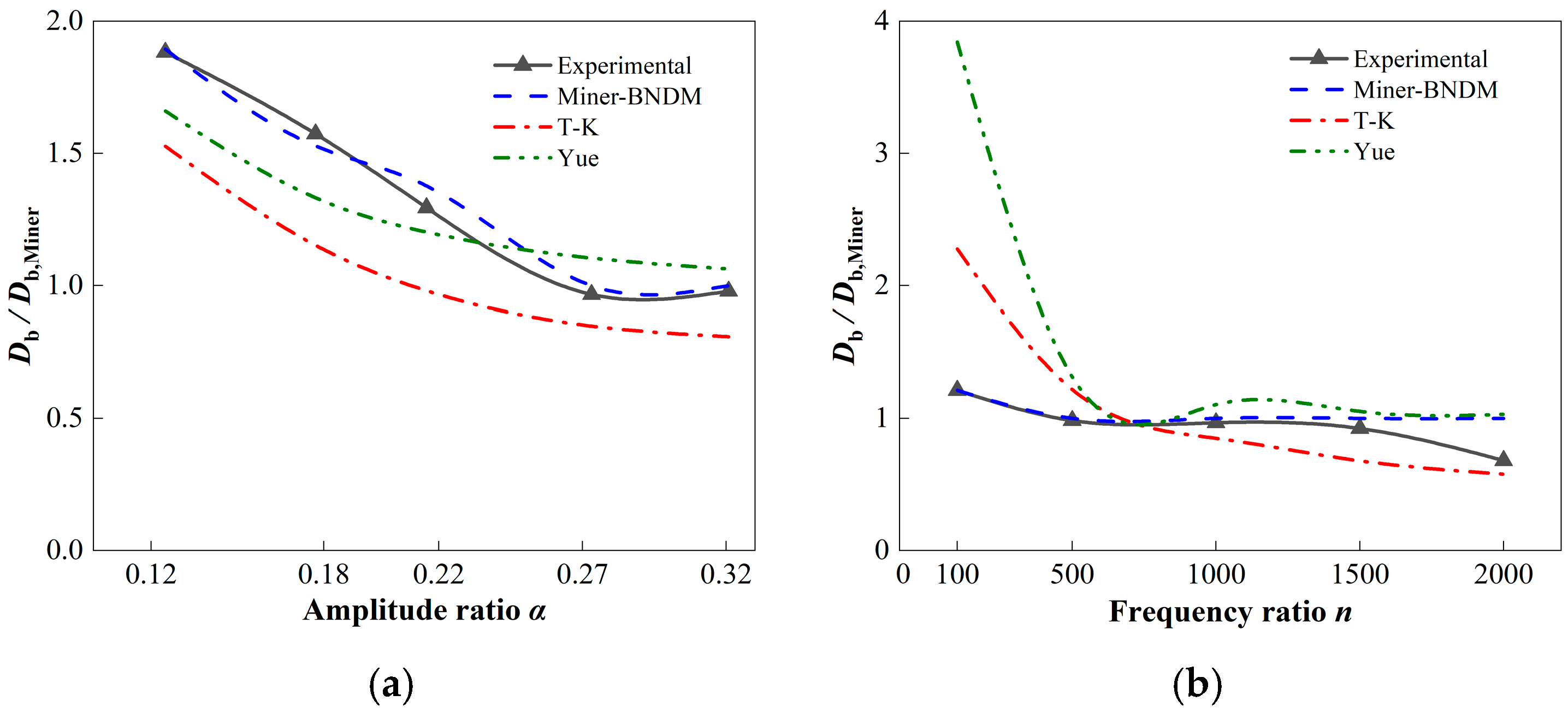
3.4. Discussion
4. Conclusions
- When other factors are held constant, the total number of high-frequency cycles is positively related to the amplitude ratio and the frequency ratio. Lower frequency ratios and lower amplitude ratios tend to accelerate fatigue damage, whereas higher frequency ratios and greater amplitude ratios contribute to the reduction of fatigue damage. When the amplitude ratio reaches 0.12 and the frequency ratio reaches 100, there is a reduction of at least 66% and 46% in HLSF high-frequency load cycles compared to constant amplitude loading.
- Under HLSF test conditions, the fracture surface exhibit striation band crack propagation characteristics in units of low-frequency block cycles. The higher the amplitude ratio and frequency ratio, the more pronounced the band width becomes. Additionally, the plastic protrusion observed on the crack propagation surface increases with rising mean stress.
- For fatigue life prediction of Q355D, the mean stress effect can be effectively accounted for by Walker’s formula without the other adverse effects on the number of high-frequency cycles. The T-K model underestimates the impact of low-amplitude ratios, while the Yue model overestimates the impact of low-frequency ratios and high mean stresses. The Miner’s rule tends to underestimate the impact of loading conditions with low-amplitude ratios and low-frequency ratios.
- A proposed model BNDM is developed to modify the block nonlinear damage by introducing an exponential acceleration damage factor referenced to low-frequency cyclic damage. The application of this model achieved a reduction in the average prediction error of Miner’s rule for fatigue life from 19.9% to 7.5%, thus enabling a more accurate prediction of HLSF fatigue life.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HLSF | high-low frequency superimposed loading fatigue |
| α | amplitude ratio |
| n | frequency ratio |
| σm | mean stress |
| σa | stress amplitude |
| Rm | master stress ratio |
| E | elastic modulus |
| ν | Poisson’s ratio |
| σy | yield strength |
| σu | ultimate tensile strength |
| σL | low-frequency stress amplitude |
| σH | high-frequency stress amplitude |
| fL | low-frequency stress amplitude frequency |
| fH | high-frequency stress amplitude frequency |
| σmax | maximum stress |
| σmin | minimum stress |
| Nb | fatigue life (the number of cycle blocks) |
| Db | damage caused by one block |
| NL | constant amplitude fatigue life (low frequency) |
| NH | constant amplitude fatigue life (high frequency) |
| γ | stress sensitivity coefficient in Walker′s formula |
| A | elongation after fracture |
| KRO | strength coefficient in Ramberg-Osgood model |
| nRO | strain hardening exponent in Ramberg-Osgood model |
References
- Hu, D.Y.; Meng, F.C.; Liu, H.W.; Song, J.; Wang, R.Q. Experimental investigation of fatigue crack growth behavior of GH2036 under combined high and low cycle fatigue. Int. J. Fatigue 2016, 85, 1–10. [Google Scholar] [CrossRef]
- Gan, J.; Liu, X.; Wang, Z.; Wu, W.G. Experimental study on the fatigue damage of designed T-type specimen with high-low frequency superimposed loading. Int. J. Fatigue 2021, 143, 105985. [Google Scholar] [CrossRef]
- Guo, T.; Li, A.Q.; Wang, H. Influence of ambient temperature on the fatigue damage of welded bridge decks. Int. J. Fatigue 2007, 30, 1092–1102. [Google Scholar] [CrossRef]
- Guo, T.; Li, A.Q.; Li, J.H. Fatigue Life Prediction of Welded Joints in Orthotropic Steel Decks Considering Temperature Effect and Increasing Traffic Flow. Struct. Health Monit. 2008, 7, 189–202. [Google Scholar]
- Liu, Y.; Zhang, H.P.; Liu, Y.M.; Deng, Y.; Jiang, N.; Lu, N.W. Fatigue reliability assessment for orthotropic steel deck details under traffic flow and temperature loading. Eng. Fail. Anal. 2017, 71, 179–194. [Google Scholar] [CrossRef]
- Di, J.; Ruan, X.Z.; Zhou, X.H.; Wang, J.; Peng, X. Fatigue assessment of orthotropic steel bridge decks based on strain monitoring data. Eng. Struct. 2021, 228, 111437. [Google Scholar] [CrossRef]
- Wang, C.S.; Zhang, P.J.; Wu, G.S.; Li, P.Y.; Wang, Y. Fatigue damage evaluation of steel bridges considering thermal effect. Struct. Infrastruct. Eng. 2022, 18, 1020–1033. [Google Scholar] [CrossRef]
- Huang, K.X.; Zhang, H.; Jiang, J.Q.; Zhang, Y.Y.; Zhou, Y.H.; Sun, L.F.; Zhang, Y.N. The optimal design of a piezoelectric energy harvester for smart pavements. Int. J. Mech. Sci. 2022, 232, 107609. [Google Scholar] [CrossRef]
- Xiang, T.; Huang, K.X.; Zhang, H.; Zhang, Y.Y.; Zhang, Y.N.; Zhou, Y.H. Detection of Moving Load on Pavement Using Piezoelectric Sensors. Sensors 2020, 20, 2366. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Shen, M.Z.; Zhang, Y.Y.; Chen, Y.S.; Lü, C.F. Identification of Static Loading Conditions Using Piezoelectric Sensor Arrays. J. Appl. Mech. 2018, 85, 011008. [Google Scholar] [CrossRef]
- CEN. Eurocode 3: Design of Steel Structures-Part 2: Steel Bridges; European Committee for Standardization: Brussels, Belgium, 2006. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials, Inc.: Washington, DC, USA, 2020. [Google Scholar]
- Tao, T.Y.; Wang, H.; Zhu, Q.X.; Zou, Z.Q.; Li, J.; Wang, L.B. Long-term temperature field of steel-box girder of a long-span bridge: Measurement and simulation. Eng. Struct. 2021, 236, 111924. [Google Scholar] [CrossRef]
- Fan, L.; Yang, W.P.; Zhou, D.; Li, Z.Y. Temperature Distribution and Mechanical Response of Orthotropic Steel Bridge Deck During Paving of Gussasphalt Pavement. Int. J. Steel Struct. 2021, 21, 315–328. [Google Scholar] [CrossRef]
- Guo, F.Q.; Zhang, S.H.; Duan, S.Y.; Shen, Z.L.; Yu, Z.W.; Jiang, L.Z.; He, C. Temperature gradient zoning of steel beams without paving layers in China. Case Stud. Constr. Mater. 2023, 18, e02054. [Google Scholar] [CrossRef]
- Li, Z.X.; Chan, T.; Ko, J. Fatigue damage model for bridge under traffic loading: Application made to Tsing Ma Bridge. Theor. Appl. Fract. Mech. 2001, 35, 81–91. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, B.; Zhou, X.Q.; Xu, Y.L. Field monitoring and numerical analysis of Tsing Ma Suspension Bridge temperature behavior. Struct. Control Health Monit. 2013, 20, 560–575. [Google Scholar] [CrossRef]
- Gou, H.Y.; Chen, Z.H. Thermal Field of Composite Girder-Ballastless Track System on Arch in Plateau and Regions with Large Diurnal Temperature Variation Based on Measured Data. J. China Railw. Soc. 2024, 46, 159–170. [Google Scholar]
- Ding, X.; Huang, D.W.; Guo, Z.X.; Yan, H.; Yan, X.J.; Wang, Y.Z.R.; Yin, F.; Luan, X. Experimental investigations on combined high and low cycle fatigue: Material-level specimen design and strain response characteristic. Chin. J. Aeronaut. 2025, 38, 103246. [Google Scholar] [CrossRef]
- Han, L.; Huang, D.W.; Yan, X.J.; Zhang, Y.S.; Gui, M.; Tao, M.; Zhang, X.Y.; Qi, M.J. Effects of aluminizing and combined strengthening on the fatigue property of K403 super alloy component under combined high and low cycle loading. Int. J. Fatigue 2019, 125, 491–504. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Sonsino, C.M. Course of SN-curves especially in the high-cycle fatigue regime with regard to component design and safety. J. Fatigue 2006, 29, 2246–2258. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue of structures and materials. Int. J. Fatigue 1994, 16, 21–32. [Google Scholar] [CrossRef]
- Gao, H.Y.; Huang, H.Z.; Zhu, S.P.; Li, Y.F.; Yuan, R. A Modified Nonlinear Damage Accumulation Model for Fatigue Life Prediction Considering Load Interaction Effects. Sci. World J. 2014, 100, 180–194. [Google Scholar] [CrossRef]
- Alcover, I.F.; Andersen, J.E.; Chryssanthopoulos, M.K. Performance Assessment and Prediction of Welded Joints in Orthotropic Decks Considering Hourly Monitoring Data. Struct. Eng. Int. 2013, 23, 436–442. [Google Scholar] [CrossRef]
- Trufyakov, V.I.; Koval’chuk, V.S. Determination of life under two-frequency loading (Report no.2. Proposed method). Strength Mater. 1982, 14, 1303–1308. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Lu, K.N.; Wang, L.F.; Liu, L.L.; Chen, W. Prediction of combined cycle fatigue life of TC11 alloy based on modified nonlinear cumulative damage model. Chin. J. Aeronaut. 2021, 34, 73–84. [Google Scholar] [CrossRef]
- Zhu, S.P.; Yue, P.; Yu, Z.Y.; Wang, Q.Y. A Combined High and Low Cycle Fatigue Model for Life Prediction of Turbine Blades. Materials 2017, 10, 698. [Google Scholar] [CrossRef]
- Wang, X.W.; Hou, J.; Guo, H.; Wang, Y.S.; Sun, Y.J.; Teng, B. A Miner’s rule based fatigue life prediction model for combined high and low cycle fatigue considering loading interaction effect. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 4525–4540. [Google Scholar] [CrossRef]
- Liu, P.S.; Wang, X.W.; Shen, Q.; Li, F.J.; Liu, M.; Sun, Y.J. On the consideration of loading interaction in combined high and low cycle fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2651–2661. [Google Scholar] [CrossRef]
- Ye, D.Y.; Wang, Z.L. A new approach to low-cycle fatigue damage based on exhaustion of static toughness and dissipation of cyclic plastic strain energy during fatigue. Int. J. Fatigue 2001, 23, 679–687. [Google Scholar] [CrossRef]
- Yue, P.; Ma, J.; Zhou, C.H.; Jiang, H.; Wriggers, P. A fatigue damage accumulation model for reliability analysis of engine components under combined cycle loadings. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1880–1892. [Google Scholar] [CrossRef]
- Hou, J.; Wang, X.W.; Guo, H.; Wang, Y.S.; Li, F.J.; Shen, Q. Combined high and low cycle fatigue life prediction model based on damage curve method considering loading interaction effect. Int. J. Damage Mech. 2023, 32, 185–203. [Google Scholar] [CrossRef]
- GB/T 1591-2018; High Strength Low Alloy Structural Steels. SAC: Beijing, China, 2018.
- GB/T 228.1-2021; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. SAC: Beijing, China, 2021.
- GB/T 714-2015; Structural Steel for Bridge. SAC: Beijing, China, 2015.
- Berto, F.; Ferro, P.; Salavati, H. Fatigue strength of sharp V-notched specimens made of ductile cast iron. Eng. Fail. Anal. 2017, 82, 308–314. [Google Scholar] [CrossRef]
- Fu, T.T.; Cebon, D. Predicting fatigue lives for bi-modal stress spectral densities. Int. J. Fatigue 2000, 22, 11–21. [Google Scholar] [CrossRef]
- Huang, W.B. The frequency domain estimate of fatigue damage of combined load effects based on the rain-flow counting. Mar. Struct. 2017, 52, 34–49. [Google Scholar] [CrossRef]
- Walker, E.K. The Effect of Stress Ratio During Crack Propagation and Fatigue for 2024-T3 and 7075-T6 Aluminum. In Effects of Environment and Complex Load History on Fatigue Life; ASTM Selected Technical Papers; ASTM International: West Conshohocken, PA, USA, 1970; Volume 462, pp. 1–14. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Polasek, M.; Krbaa, M.; Eckert, M.; Mikus, P. Contact Fatigue Resistance of Gun Barrel Steels. Procedia Struct. Integr. 2023, 43, 306–311. [Google Scholar] [CrossRef]
- Wang, R.Q.; Li, D.; Hu, D.Y.; Meng, F.C.; Liu, H.; Ma, Q.H. A combined critical distance and highly-stressed-volume model to evaluate the statistical size effect of the stress concentrator on low cycle fatigue of TA19 plate. Int. J. Fatigue 2017, 95, 8–17. [Google Scholar] [CrossRef]
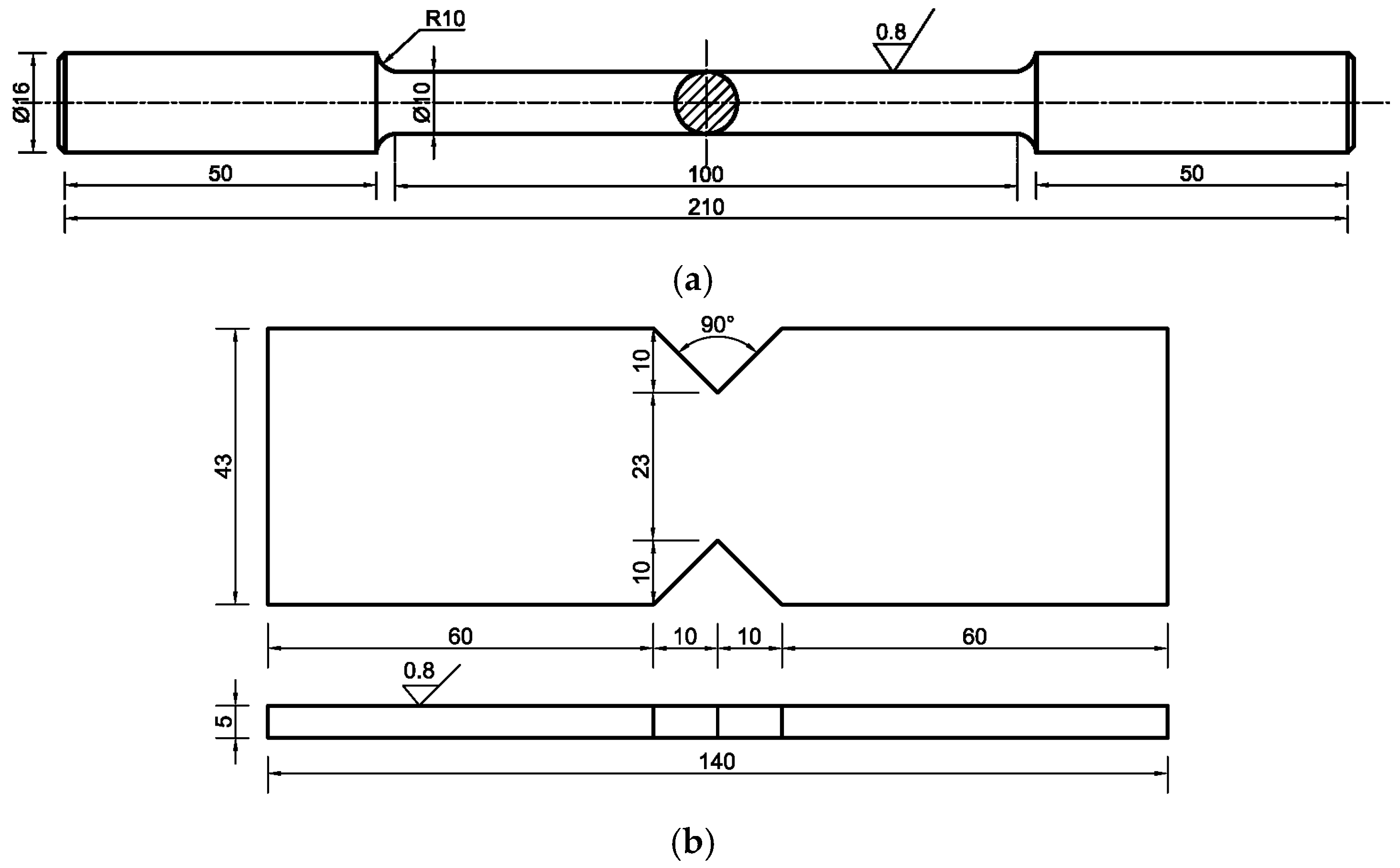
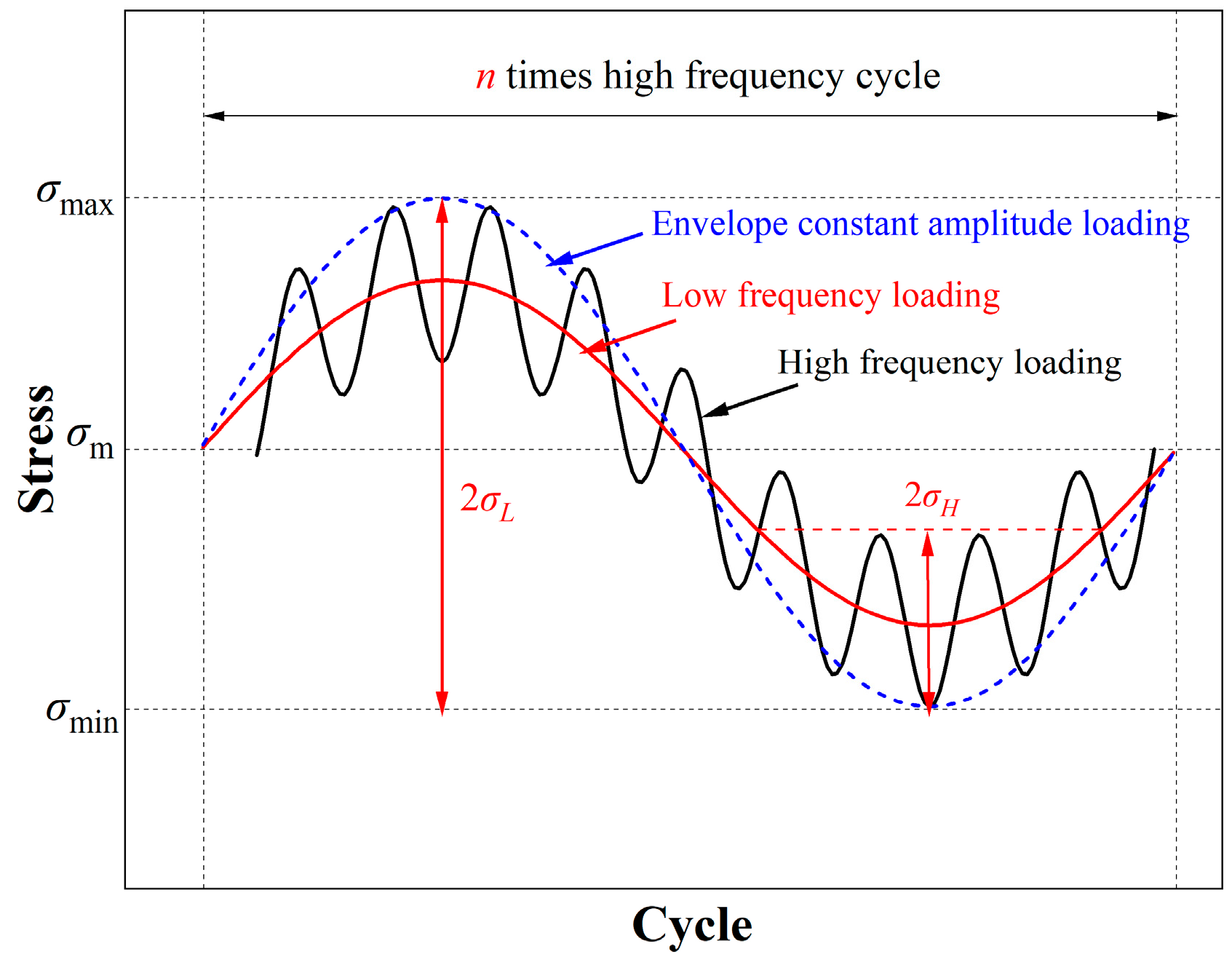

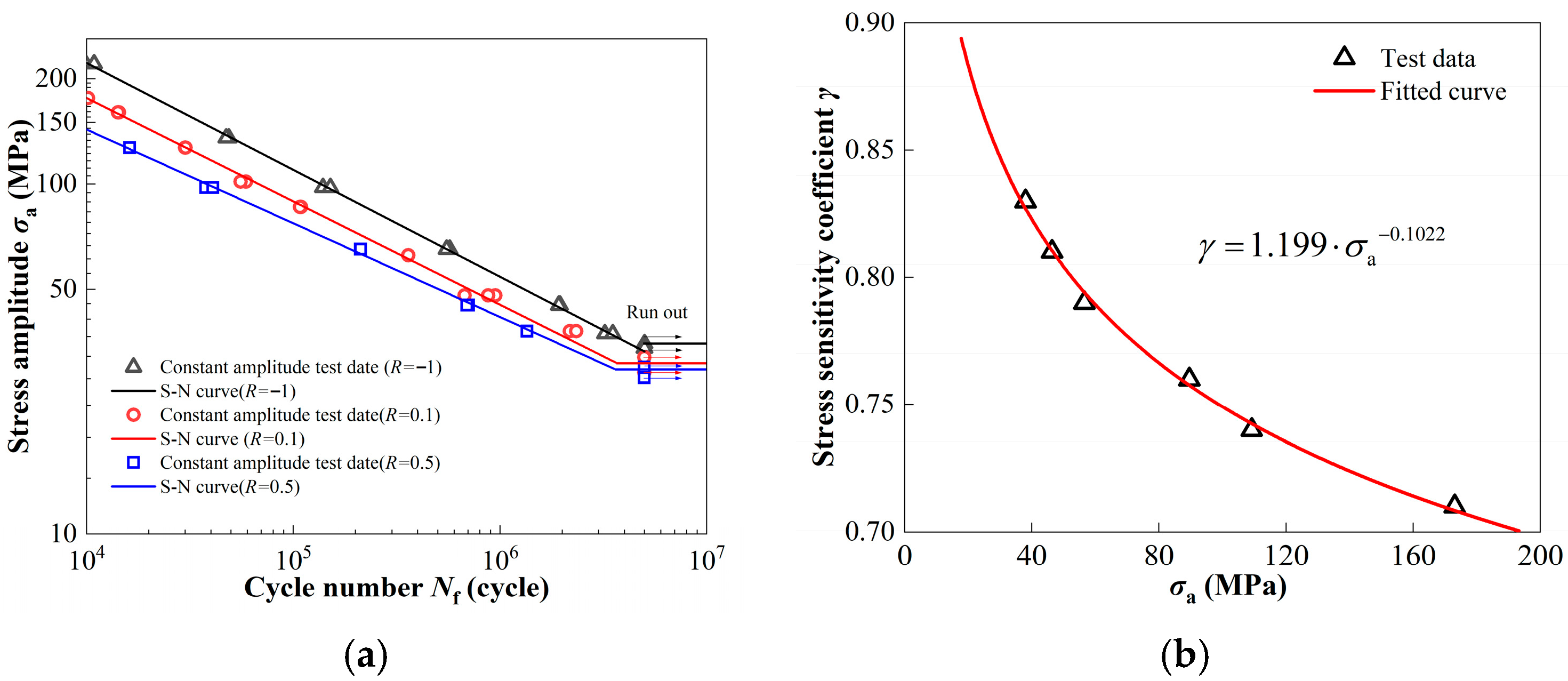
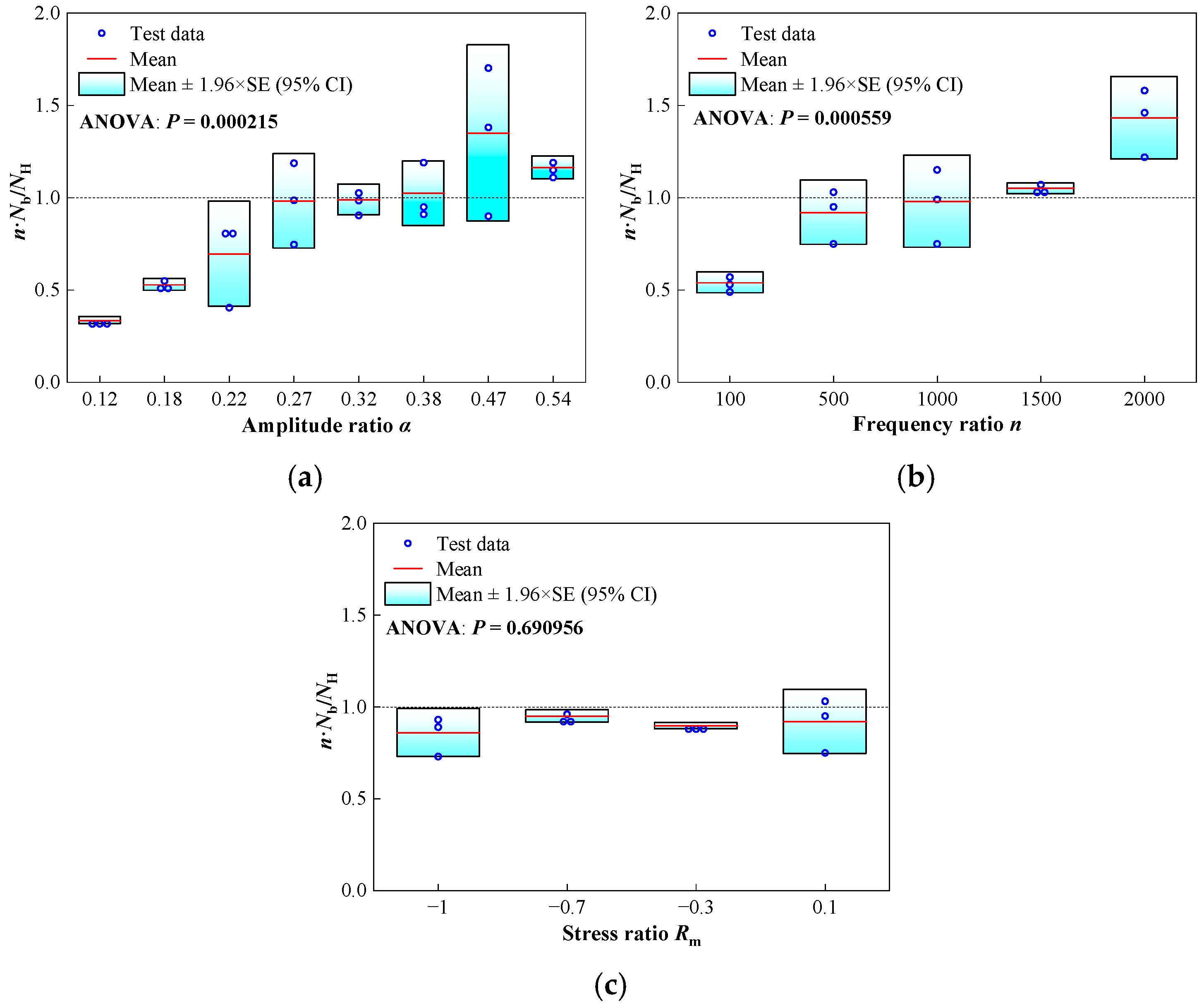



| Steel | C | Si | Mn | Cr | Ni | Nb | Cu | Als | Ti | P |
|---|---|---|---|---|---|---|---|---|---|---|
| Q355D | 0.09 | 1.24 | 1.57 | 0.20 | 0.04 | 0.04 | 0.12 | 0.03 | 0.02 | 0.02 |
| Mechanical Properties | E (GPa) | ν - | σy (MPa) | σu (MPa) | A (%) | KRO (MPa) | nRO - |
|---|---|---|---|---|---|---|---|
| Q355D | 216.71 | 0.30 | 440.33 | 587.39 | 32.33 | 428.89 | 0.15 |
| GB/T 714-2015 [36] | - | - | ≥345 | ≥490 | ≥20 | - | - |
| Test Conditions | σL (MPa) | σH (MPa) | n | α | σm (MPa) | Rm | Nb | Average |
|---|---|---|---|---|---|---|---|---|
| C-1 | 176.1 | 21.1 | 1000 | 0.12 | 215 | 0.1 | 1881, 2084, 1998 | 1988 |
| C-2 | 176.1 | 31.2 | 1000 | 0.18 | 215 | 0.1 | 1048, 1058, 1154 | 1087 |
| C-3 | 176.1 | 38 | 1000 | 0.22 | 215 | 0.1 | 953, 942, 457 | 784 |
| C-4 | 176.1 | 48.1 | 1000 | 0.27 | 215 | 0.1 | 549, 409, 656 | 538 |
| C-5 | 176.1 | 56.5 | 1000 | 0.32 | 215 | 0.1 | 341, 347, 302 | 330 |
| C-6 | 127.2 | 48.1 | 1000 | 0.38 | 155 | 0.1 | 569, 604, 751 | 641 |
| C-7 | 101.7 | 48.1 | 1000 | 0.47 | 124 | 0.1 | 962, 619, 1190 | 924 |
| C-8 | 89.6 | 48.1 | 1000 | 0.54 | 110 | 0.1 | 879, 808, 833 | 840 |
| C-9 | 176.1 | 48.1 | 100 | 0.27 | 215 | 0.1 | 3210, 2966, 2644 | 2940 |
| C-10 | 176.1 | 48.1 | 500 | 0.27 | 215 | 0.1 | 1056, 1146, 818 | 1007 |
| C-11 | 176.1 | 48.1 | 1500 | 0.27 | 215 | 0.1 | 394, 373, 380 | 382 |
| C-12 | 176.1 | 48.1 | 2000 | 0.27 | 215 | 0.1 | 441, 402, 334 | 392 |
| C-13 | 176.1 | 48.1 | 500 | 0.27 | 95 | −0.3 | 1356, 1372, 1328 | 1352 |
| C-14 | 176.1 | 48.1 | 500 | 0.27 | 31 | −0.7 | 1906, 1958, 2024 | 1963 |
| C-15 | 176.1 | 48.1 | 500 | 0.27 | 0 | −1 | 2534, 2398, 1954 | 2295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Zhou, J.; Zhang, H. Experimental Study on Fatigue Performance of Q355D Notched Steel Under High-Low Frequency Superimposed Loading. Metals 2025, 15, 975. https://doi.org/10.3390/met15090975
Zheng X, Zhou J, Zhang H. Experimental Study on Fatigue Performance of Q355D Notched Steel Under High-Low Frequency Superimposed Loading. Metals. 2025; 15(9):975. https://doi.org/10.3390/met15090975
Chicago/Turabian StyleZheng, Xianglong, Jiangyi Zhou, and He Zhang. 2025. "Experimental Study on Fatigue Performance of Q355D Notched Steel Under High-Low Frequency Superimposed Loading" Metals 15, no. 9: 975. https://doi.org/10.3390/met15090975
APA StyleZheng, X., Zhou, J., & Zhang, H. (2025). Experimental Study on Fatigue Performance of Q355D Notched Steel Under High-Low Frequency Superimposed Loading. Metals, 15(9), 975. https://doi.org/10.3390/met15090975







