Towards a Global Constitutive Formulation for Modeling the Hot Working Behavior of Low-Carbon Steels
Abstract
1. Introduction
2. Experimental Procedure
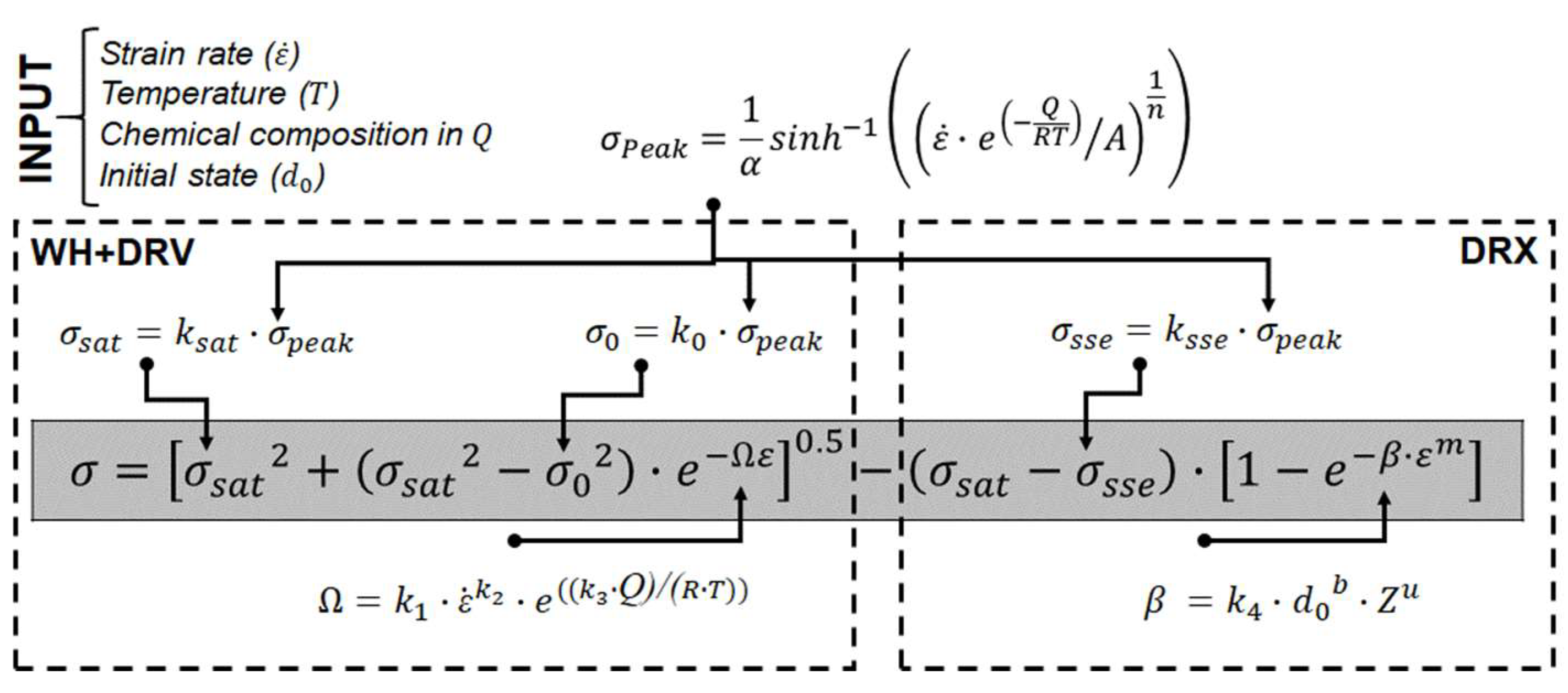
3. Description of the Model
3.1. Modeling up to the Peak Stress
3.2. Modeling of the Dynamic Recrystallization
3.3. Validation of the Hyperbolic Sine Equation
3.4. Parametrization of the Final Expression
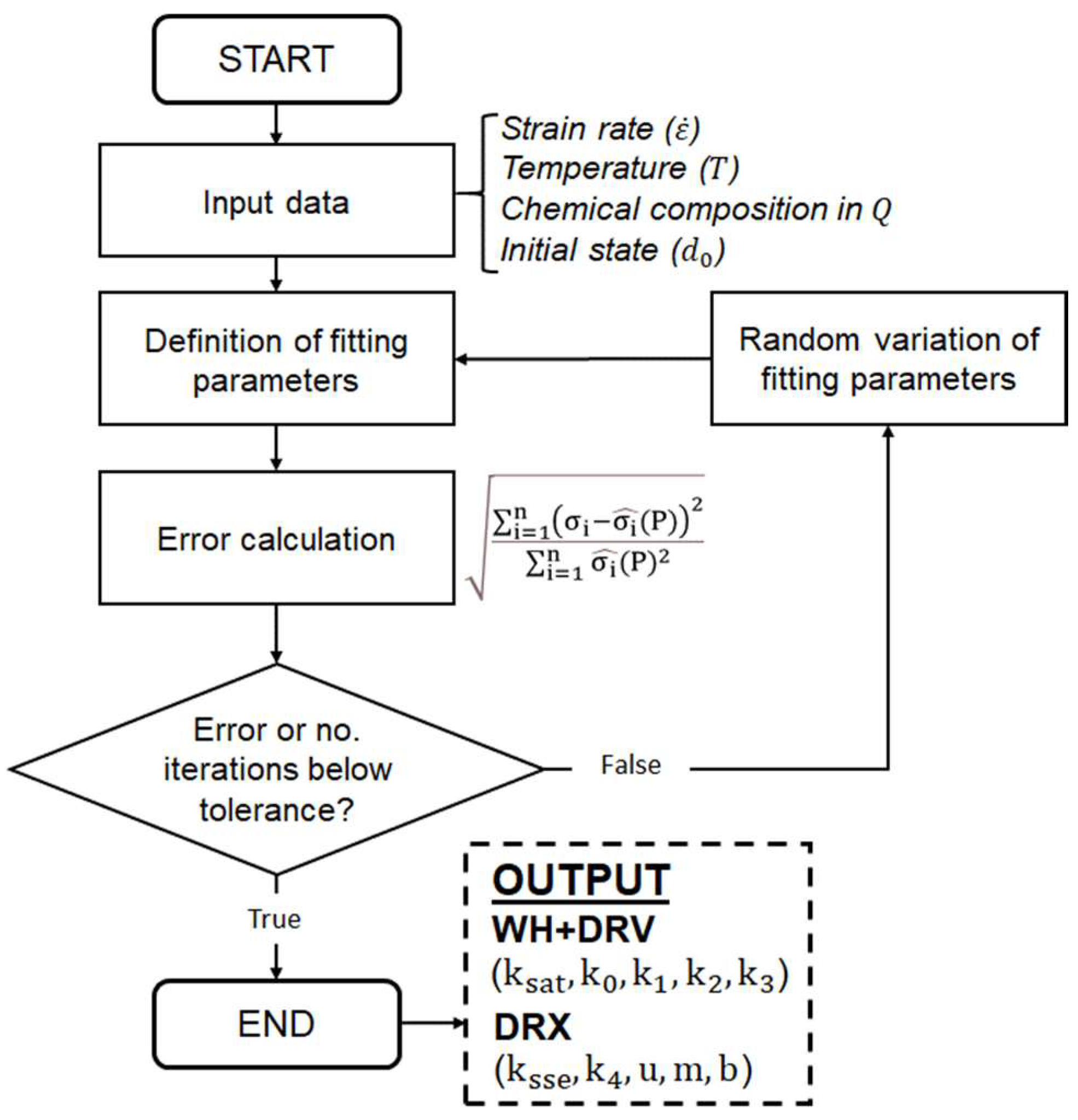
3.5. Optimization Method
4. Results and Discussion
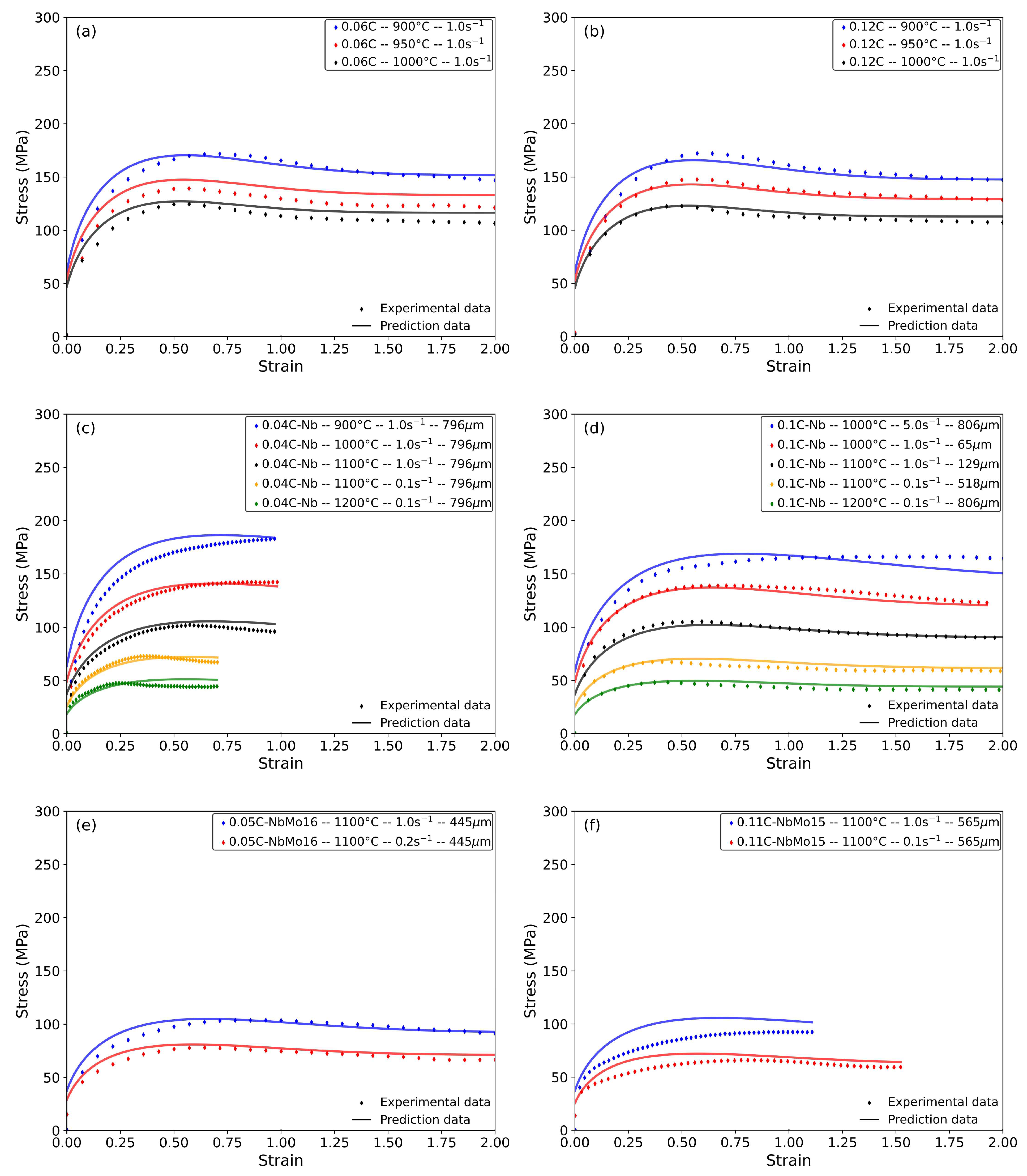
4.1. Modeling of the Complete Stress–Strain Curve
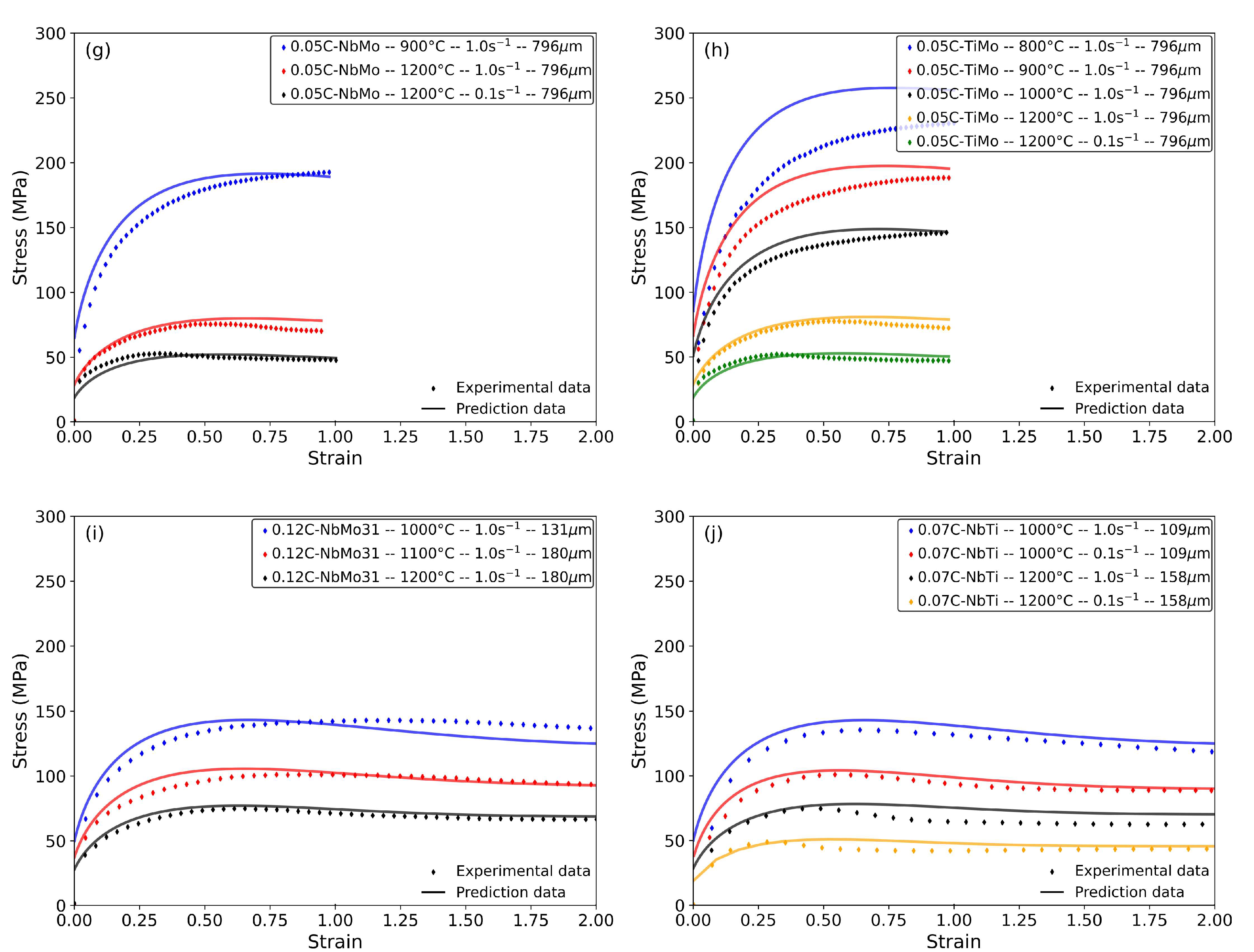
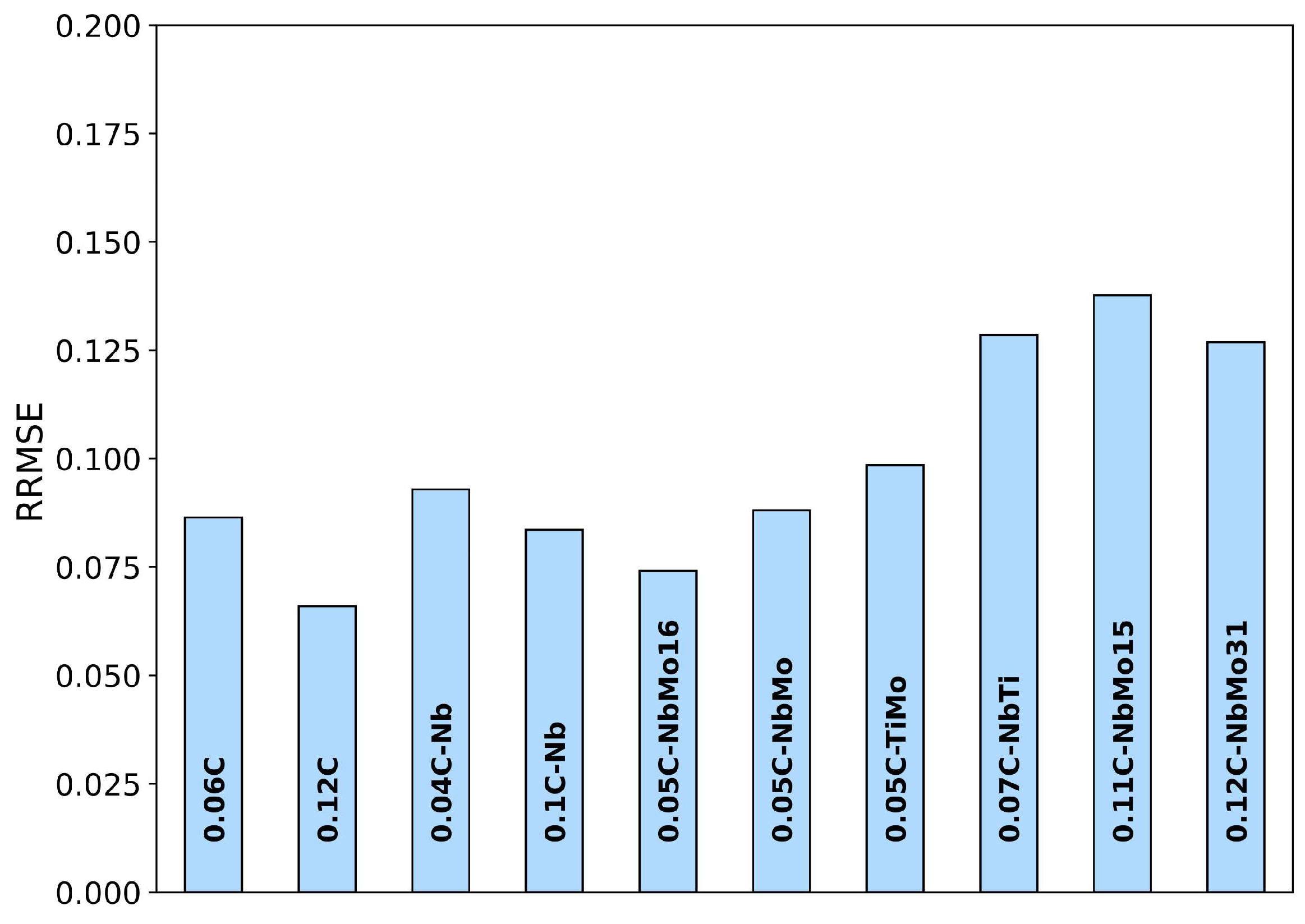
4.2. Effect of Microalloying Elements on Flow Behavior (Ti, Mo, Nb)
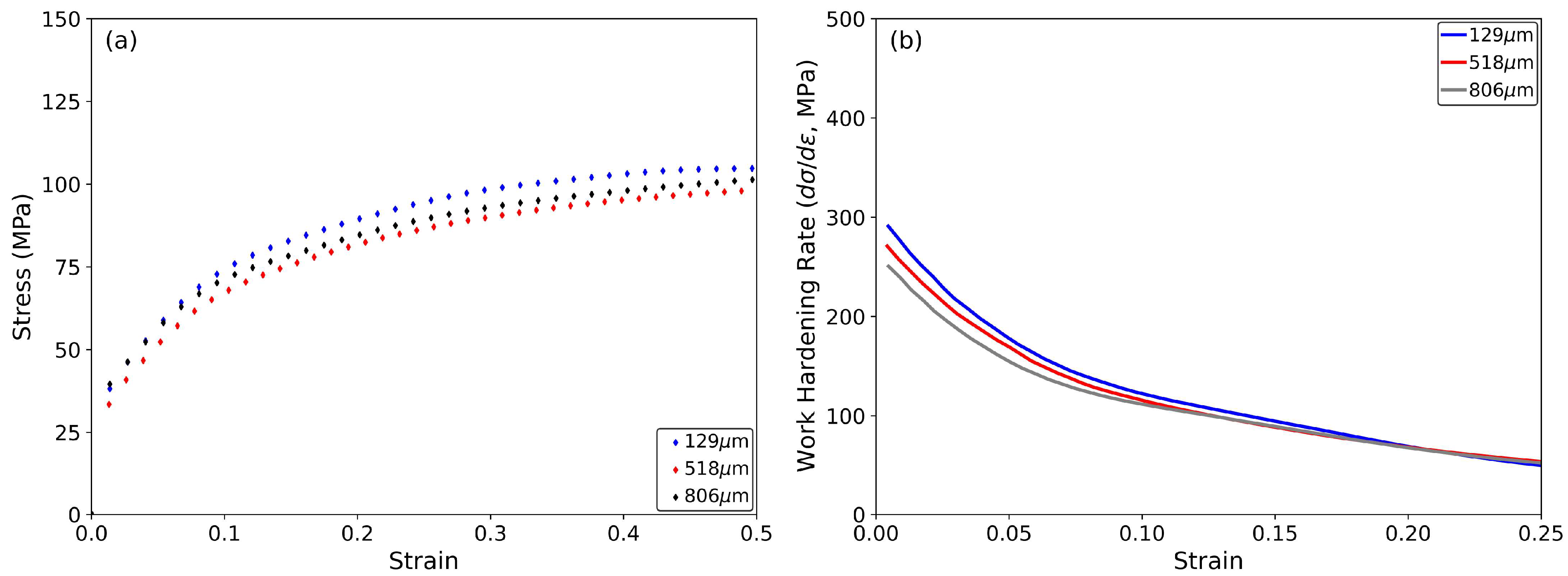
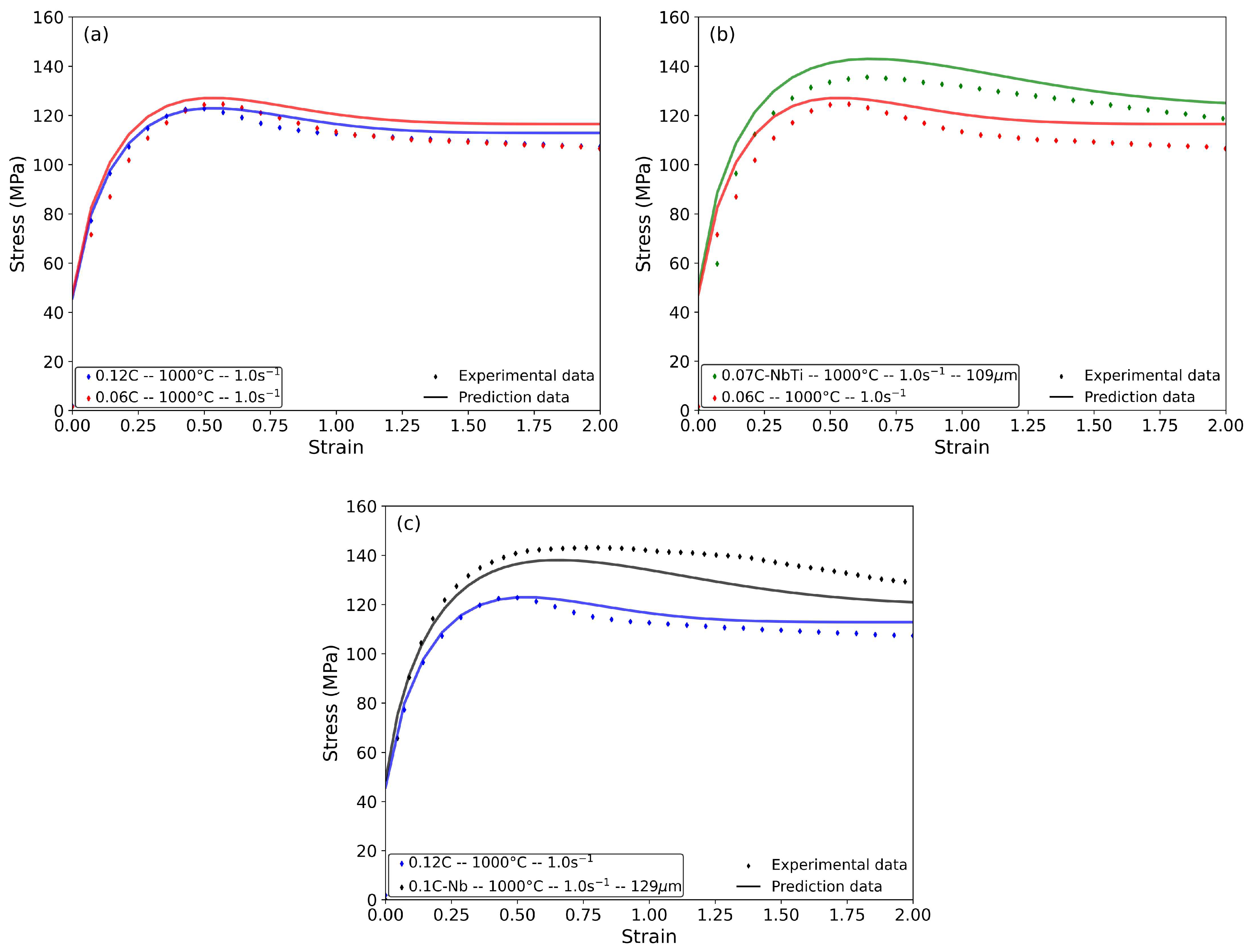
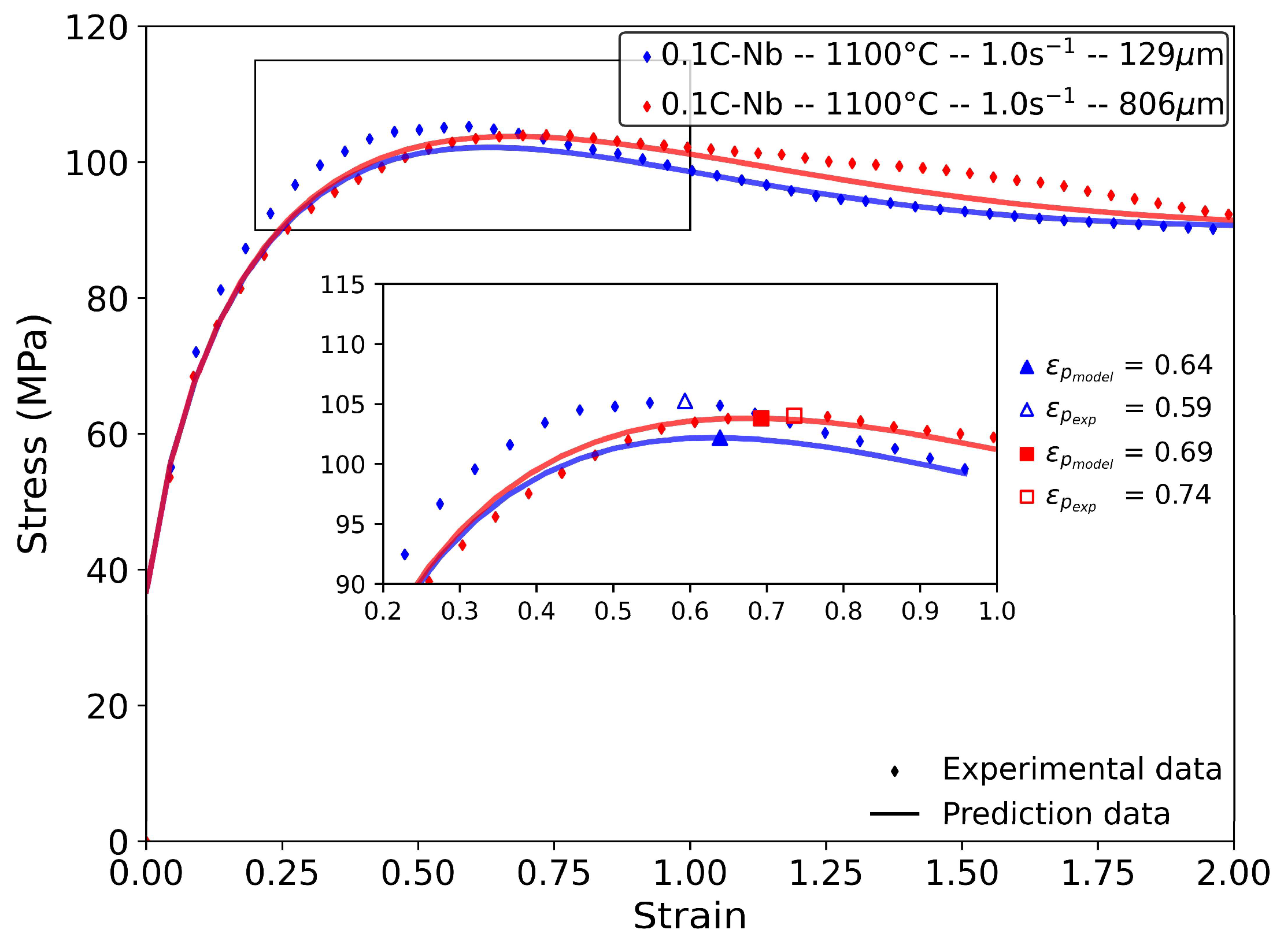
4.3. Effect of Austenite Grain Size
4.4. Robustness and Limitations of the Model
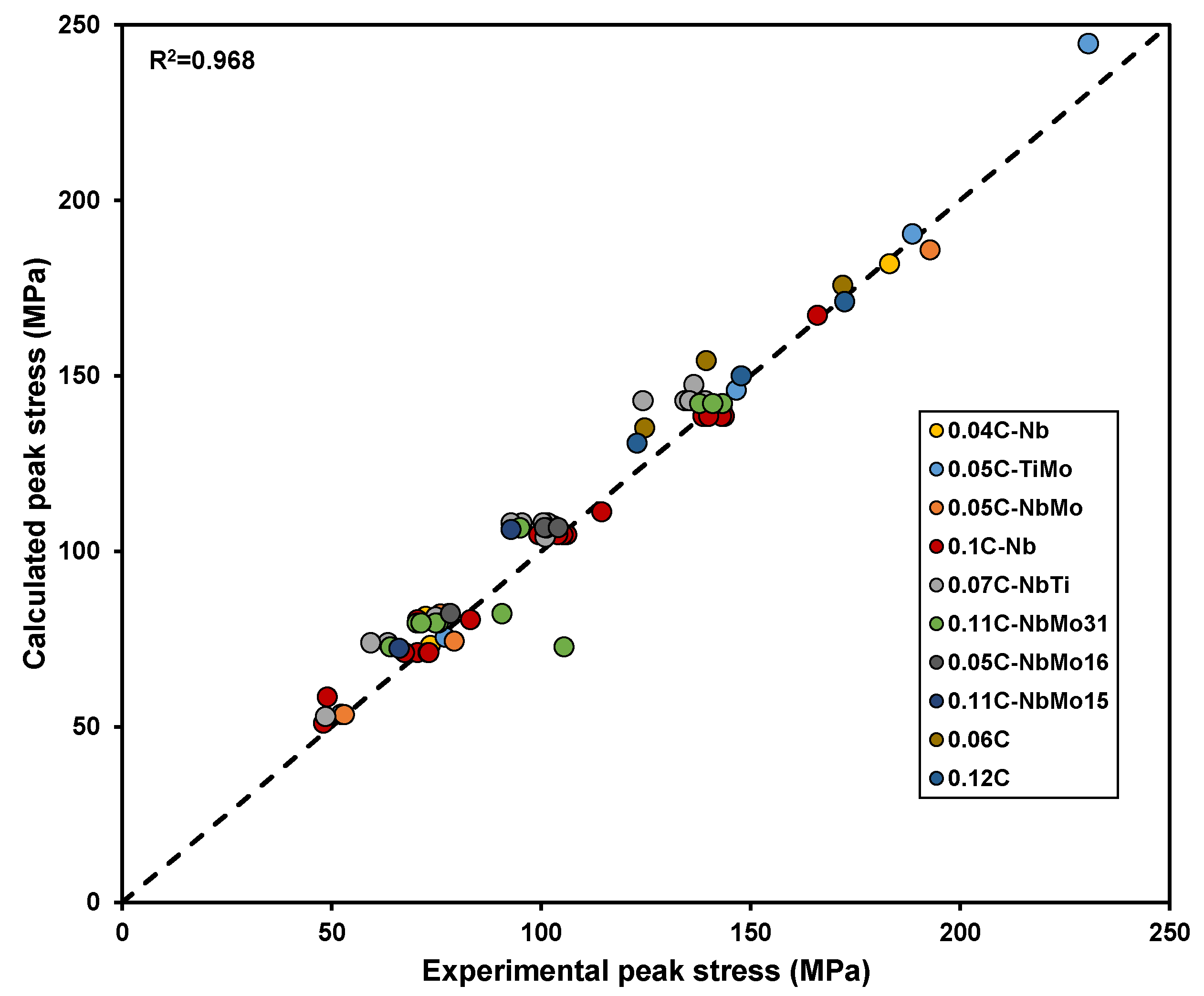
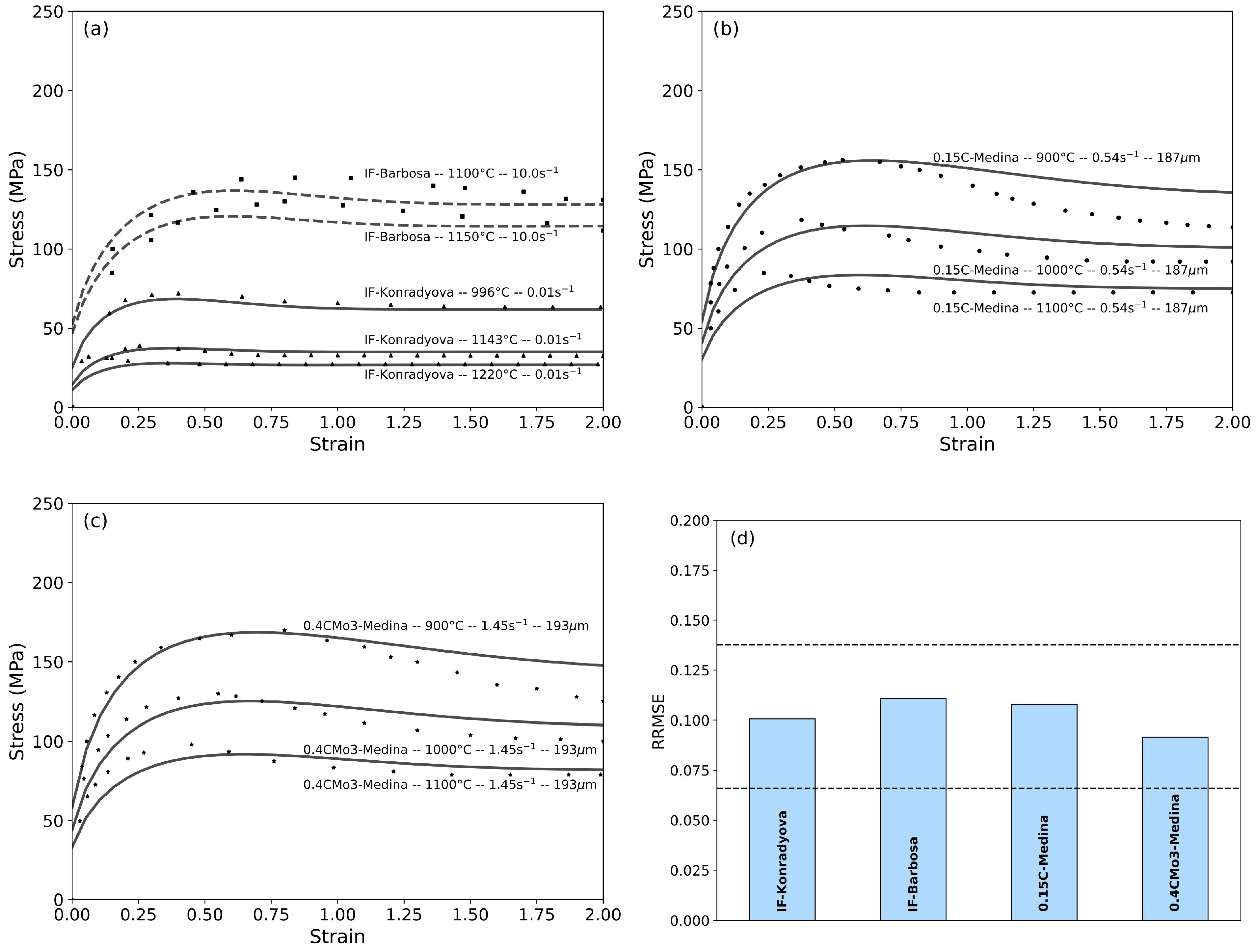
4.5. Validation
5. Conclusions
- (1)
- A hybrid model was devised that integrates the competition of various phenomena affecting the mechanical response of steel at high temperatures, such as strain-hardening, dynamic recovery and dynamic recrystallization. The first two mechanisms are modeled using a single dislocation-based formulation, while softening due to dynamic recrystallization is modeled using a phenomenological Avrami-type approach.
- (2)
- Applying the developed constitutive equation has significantly reduced the need for fitting parameters across different alloys. In particular, this formulation disregards the critical strain .
- (3)
- The model can describe the distinct metallurgical aspects of flow behavior for different alloy compositions or testing conditions:
- Alloys that are hot worked at higher temperatures or lower strain rates exhibit a characteristic dynamic recrystallization (DRX) behavior, characterized by a single peak stress, followed by a gradual decrease towards a steady-state stress. Conversely, the peak stress becomes less pronounced at higher strain rates or lower deformation temperatures. Clear correlations between stress and deformation temperature are observed under constant strain rate conditions, which further validates the predictive capability of the developed equation.
- The addition of carbon slightly decreases the peak stress value due to its hardening effect. Higher carbon content promotes a slight softening of the steel due to the increased dynamic recovery (DRV) rates and DRX. The model is consistent with experimental observations and predicts higher stresses for the steel with the lowest carbon content (0.06C).
- The influence of microalloying elements such as Ti, Mo and Nb on flow behavior is evident, with these elements contributing to an increased activation energy for deformation and higher saturation stresses. Despite the complexity introduced by the interactions between alloying elements and the precipitation kinetics, the model adequately describes the effects of these elements on the flow stress.
- Coarser grain sizes result in a delay of DRX, thereby resulting in larger strains at the onset of the steady-state regime. The model effectively captures the impact of coarser initial austenite grain sizes on flow curves.
- Although challenges remain in accurately predicting softening kinetics, particularly in highly alloyed steels and under high -value conditions ( > 1013 s−1), the developed equation is robust. The model exhibits low Relative Root Mean Square Error (RRMSE) values, consistently below 14%, across a broad range of compositions, initial austenite grain sizes, deformation temperatures and strain rates. Furthermore, the model has been validated using experimental torsion data from the literature, thereby expanding the range of chemical compositions to which the developed expression can be applied.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, C.; Qin, Y.; Liu, Y.; Xiao, G.; Zhou, J.; Zhang, J. New constitutive model and hot processing map for A100 steel based on high-temperature flow behavior. Heliyon 2024, 10, e40823. [Google Scholar] [CrossRef] [PubMed]
- Lei, M.; Huang, J.; Li, Y.; Zhang, L.; Yang, G.; Wen, B. High-strain-rate mechanical constitutive modeling with computational parameters. Int. J. Plast. 2025, 189, 104329. [Google Scholar]
- Pasco, J.; McCarthy, T.; Parlee, J.; Nazri, N.A.; Padmajan, S.; Rodrigues, S.; Aranas, C., Jr. Constitutive modeling of modified-H13 steel. MRS Commun. 2022, 12, 343–351. [Google Scholar] [CrossRef]
- Solhjoo, S. Revisiting the Common Practice of Sellars and Tegart’s Hyperbolic Sine Constitutive Model. Modelling 2022, 3, 359–373. [Google Scholar] [CrossRef]
- Quelennec, X.; Bozzolo, N.; Jonas, J.J.; Loge, R. A new approach to modeling the flow curve of hot deformed austenite. ISIJ Int. 2011, 51, 945–950. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Jiang, H.; Wei, X.; Song, J.; Chen, Y.; Liu, S. Constitutive behavior analysis of Al-Mg-Si-Sc alloy with a two-stage physical-based model. Mater. Today Commun. 2025, 47, 113099. [Google Scholar]
- Donati, L.; Segatori, A.; El Mehtedi, M.; Tomesani, L. Grain evolution analysis and experimental validation in the extrusion of 6XXX alloys by use of a lagrangian FE code. Int. J. Plast. 2013, 46, 70–81. [Google Scholar] [CrossRef]
- Vural, M.; Caro, J. Experimental analysis and constitutive modeling for the newly developed 2139-T8 alloy. Mater. Sci. Eng. A 2009, 520, 56–65. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M.; Liu, G. A modified Johnson–Cook model for tensile behaviour of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar]
- Rusinek, A.; Klepaczko, J.R. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Zerilli, P.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Almasri, A.H. A physically based constitutive model for fcc metals with applications to dynamic hardness. Mech. Mater. 2008, 40, 549–563. [Google Scholar] [CrossRef]
- Hensel, A.; Spittel, T. Kraft- und Arbeitsbedarf Bildsamer Formgeburgsverfahren; VEB Deutscher Verlag fur Grundstoffindustrie: Leipzig, Germany, 1978. [Google Scholar]
- Silva, M.L.N.; Pires, G.H.; Button, S.T. Damage evolution during cross wedge rolling of steel DIN 38MnSiVS5. Procedia Eng. 2011, 10, 752–757. [Google Scholar] [CrossRef]
- Chadha, K.; Shahriari, D.; Jahazi, M. An Approach to Develop Hansel–Spittel Constitutive Equation during Ingot Breakdown Operation of Low Alloy Steels. In Frontiers in Materials Processing, Applications, Research and Technology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 239–246. [Google Scholar]
- El Mehtedi, M.; Musharavati, F.; Spigarelli, S. Modelling of the flow behaviour of wrought aluminium alloys at elevated temperatures by a new constitutive equation. Mater. Des. 2014, 54, 869–873. [Google Scholar] [CrossRef]
- Chen, X.; Si, Y.; Bai, R.; Zhang, X.; Li, Z. Hot Formability Study of Cr5 Alloy Steel by Integration of FEM and 3D Processing Maps. Materials 2022, 15, 4801. [Google Scholar] [CrossRef]
- Spigarelli, S.; El Mehtedi, M. A New Constitutive Model for the Plastic Flow of Metals at Elevated Temperatures. J. Mater. Eng. Perform. 2014, 23, 658–665. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metal Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the Seventh Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Shokry, A.; Gowid, S.; Mulki, H.; Kharmanda, G. On the Prediction of the Flow Behavior of Metals and Alloys at a Wide Range of Temperatures and Strain Rates Using Johnson–Cook and Modified Johnson–Cook-Based Models: A Review. Materials 2023, 16, 1574. [Google Scholar] [CrossRef] [PubMed]
- Garofalo, F. An empirical relation defining the stress dependence of minimum creep rate in metals. Trans. Metall. Soc. AIME 1963, 227, 351–356. [Google Scholar]
- Sellars, C.M.; Tegart, W.J.M. Hot workability. Int. Metall. Rev. 1972, 17, 1–24. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Prado, J.M.; Najafizadeh, A. Hot deformation behavior of a medium carbon microalloyed steel. Mater. Sci. Eng. A 2011, 528, 3876–3882. [Google Scholar] [CrossRef]
- Rao, K.P.; Hawbolt, E.B. Development of constitutive relationships using compression testing of a medium carbon steel. J. Eng. Mater. Technol. 1992, 114, 116–123. [Google Scholar] [CrossRef]
- Ji, G.; Li, F.; Li, Q.; Li, H.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Nguyen-Minh, T.; Caruso, M.; Tolleneer, I.; Mayo, U.; Isasti, N.; Uranga, P.; Lorenz, U.; Duprez, L.; Akbary, F.H.; Petrov, R.; et al. Impact of Two-Phase Region Rolling on the Microstructure and Properties Distribution in Heavy Gauge Structural Steel Plate (INCROHSS)—Final Report; Publications Office of the European Union: Luxembourg, 2020; Available online: https://data.europa.eu/doi/10.2777/639791 (accessed on 18 September 2025).
- Pietrzyk, M.; Larzabal, G.; Uranga, P.; Isasti, N.; Jacolot, R.; Rauch, L.; Kuziak, R.; Diekmann, V.; Kitoeski, J.; Gutierrez, I.; et al. Virtual Strip Rolling Mill (VirtROLL)—Final Report; Publications Office of the European Union: Luxembourg, 2018; Available online: https://data.europa.eu/doi/10.2777/762189 (accessed on 18 September 2025).
- Fernandez, A. Estudio y Modelización del Conformado en Caliente de Aceros Microaleados. Aplicación a los Procesos de Laminación Directa de Formas Semiacabadas. Ph.D. Thesis, University of Navarra, Pamplona, Spain, 2001. [Google Scholar]
- Pereda, B. Study of the Effect of Mo Addition on the Austenite Microstructure Evolution During Hot Rolling of Nb Microalloyed steels. Application to Thin Slab Direct Rolling Technologies. Ph.D. Thesis, University of Navarra, Pamplona, Spain, 2009. [Google Scholar]
- Fields, D.S.; Backofen, W.A. Determination of Strain Hardening Characteristics by Torsion Testing. Proceeding Am. Soc. Test. Mater. 1957, 57, 1259–1272. [Google Scholar]
- Kocks, U.F. Laws for Work-Hardening and Low-Temperature Creep. ASME J. Eng. Mater. Tech. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Bergstrom, Y. A dislocation model for the stress-strain behaviour of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations. Mater. Sci. Eng. 1970, 5, 193–200. [Google Scholar] [CrossRef]
- Laasraoui, A.; Jonas, J. Prediction of steel flow stresses at high temperatures and strain rates. Metall. Trans. 1991, 22A, 1545–1558. [Google Scholar] [CrossRef]
- Yoshie, A.; Morikawa, H.; Onoe, Y. Formulation of Static Recrystallization of Austenite Hot Rolling Process of Steel Plate. Trans. Iron Steel Inst. Jpn. 1987, 27, 425. [Google Scholar] [CrossRef]
- Dunstan, D.J.; Bushby, A.J. Grain size dependence of the strength of metals: The Hall–Petch effect does not scale as the inverse square root of grain size. Int. J. Plast. 2014, 53, 56–65. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Ma, X.; Zhao, J.; Guo, F.; Fang, X.; Zhu, Y.; Wei, Y. The optimum grain size for strength-ductility combination in metals. Int. J. Plast. 2023, 164, 103574. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Kaneko, Y.; Uchida, M.; Vinogradov, A. The grain size effect on strain hardening and necking instability revisited from the dislocation density evolution approach. Mater. Sci. Eng. A 2022, 831, 142330. [Google Scholar] [CrossRef]
- Fernandez, A.I.; Uranga, P.; Lopez, B.; Rodriguez-Ibabe, J.M. Dynamic recrystallization behavior covering a wide austenite grain size range in Nb and Nb-Ti microalloyed steels. Mater. Sci. Eng. A 2003, 361, 367–376. [Google Scholar] [CrossRef]
- Shaban, M.; Eghbali, B. Determination of critical conditions for dynamic recrystallization of a microalloyed steel. Mater. Sci. Eng. A 2010, 527, 4320–4325. [Google Scholar] [CrossRef]
- Liu, C.; Barella, S.; Peng, Y.; Guo, S.; Liang, S.; Sun, J.; Gruttadauria, A.; Belfi, M.; Mapelli, C. Modeling and characterization of dynamic recrystallization under variable deformation states. Int. J. Mech. Sci. 2023, 238, 107838. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, E. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Li, X.; Duan, L.; Li, J.; Wu, X. Experimental study and numerical simulation of dynamic recrystallization behavior of a microalloyed plastic mold steel. Mater. Des. 2015, 66, 309–320. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Prediction of the critical conditions for initiation of dynamic recrystallization. Mater. Des. 2010, 31, 1174–1179. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change: I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change: II Transformation–time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- de Sousa Sulzbach, G.A.; Goncalves Rodrigues, M.V.; Rodrigues, S.F.; Macedo, G.M.E.; de Abreu, H.F.G.; Aranas, C., Jr.; Silva Reis, G.; Santos Silva, E. Constitutive analysis of stress–strain curves in dynamic softening of high Nb- and N-containing austenitic stainless-steel biomaterial. J. Mater. Res. Technol. 2022, 19, 4939–4956. [Google Scholar] [CrossRef]
- Medina, S.F.; Hernandez, C.A. General expression of the Zener Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Serajzadeh, S.; Taheri, A.K. An investigation into the effect of carbon on the kinetics of dynamic restoration and flow behavior of carbon steels. Mech. Mater. 2003, 35, 653–660. [Google Scholar] [CrossRef]
- Marques Ivaniski, T.; de Souza, T.F.; Épp, J.; da Silva Rocha, A. Constitutive Modelling of High Temperature Flow Behaviour for a Low Carbon High Silicon Bainitic Steel. Mater. Res. 2020, 23, e20200264. [Google Scholar] [CrossRef]
- Cao, R.; Wang, W.; Ma, S.; Yan, H.; Mu, Z.; Zhang, S. Arrhenius constitutive model and dynamic recrystallization behavior of 18CrNiMo7-6 steel. J. Mater. Res. Technol. 2023, 24, 6334–6347. [Google Scholar] [CrossRef]
- Peng, Y.; Guo, S.; Liu, C.; Barella, S.; Liang, S.; Gruttadauria, A.; Mapelli, C. Dynamic recrystallization behavior of low-carbon steel during hot rolling process: Modeling and simulation. J. Mater. Res. Technol. 2022, 20, 1266–1290. [Google Scholar] [CrossRef]
- Wang, L.; Ji, L.; Yang, K.; Gao, X.; Chen, H.; Chi, Q. The Flow Stress–Strain and Dynamic Recrystallization Kinetics Behavior of High-Grade Pipeline Steels. Materials 2022, 15, 7356. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Birnbaum, P.; Pilz, S.; Zhuang, X.; Zhao, Z.; Kräusel. Investigation of constitutive relationship and dynamic recrystallization behavior of 22MnB5 during hot deformation. Results Phys. 2019, 14, 102426. [Google Scholar] [CrossRef]
- Konrádyová, J.; Longauerová, M.; Jonšta, P.; Jonšta, Z.; Longauer, S.; Girman, V.; Vojtko, M.; Borûta, A.; Matvija, M.; Fujda, M.; et al. Hot ductility of TiNb IF steel slab after hot torsion testing. Metals 2019, 9, 752. [Google Scholar] [CrossRef]
- Viella, J.J.; Barbosa, R. Prediction of Stress–Strain Curves of Hot Deformed If Austenite. ISIJ Inter. 2002, 42, 319–321. [Google Scholar] [CrossRef]
- Hernandez, C.A.; Medina, S.F.; Ruiz, J. Modelling austenite flow curves in low alloy and microalloyed steels. Acta Mater. 1996, 44, 155–163. [Google Scholar] [CrossRef]
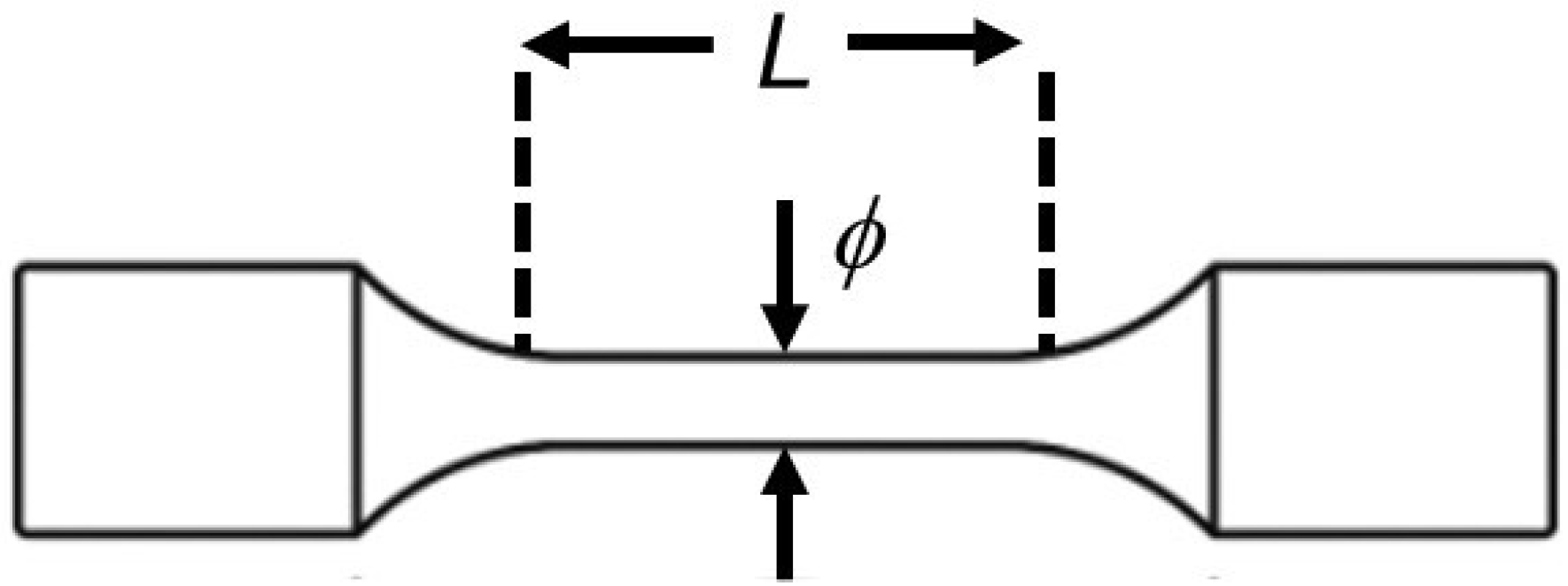
| Steel Reference | C | Mn | Si | Mo | Ti | Nb | Ref |
|---|---|---|---|---|---|---|---|
| 0.06C | 0.06 | 1.54 | 0.25 | 0.005 | 0.002 | 0.002 | [27] |
| 0.12C | 0.12 | 1.52 | 0.25 | 0.005 | 0.002 | 0.001 | [27] |
| 0.04C-Nb | 0.04 | 1.55 | 0.2 | 0.003 | 0.002 | 0.034 | [28] |
| 0.1C-Nb | 0.1 | 1.42 | 0.31 | 0.005 | 0.002 | 0.035 | [29] |
| 0.05C-NbMo16 | 0.05 | 1.58 | 0.04 | 0.16 | 0.002 | 0.03 | [30] |
| 0.11C-NbMo15 | 0.11 | 1.43 | 0.33 | 0.15 | 0.007 | 0.033 | [30] |
| 0.05C-TiMo | 0.05 | 1.61 | 0.2 | 0.2 | 0.09 | 0.003 | [28] |
| 0.05C-NbMo | 0.05 | 1.6 | 0.21 | 0.21 | 0.004 | 0.035 | [28] |
| 0.07C-NbTi | 0.07 | 0.62 | 0.01 | 0.005 | 0.067 | 0.034 | [29] |
| 0.12C-NbMo31 | 0.12 | 1.46 | 0.31 | 0.31 | 0.004 | 0.034 | [30] |
| Steel Reference | Initial Austenite Grain Size (µm) | Strain Rate (s−1) | Temperature (°C) |
|---|---|---|---|
| 0.04C-Nb | - | 0.1 | 1100 |
| 1200 | |||
| 1 | 900 | ||
| 1000 | |||
| 1100 | |||
| 1200 | |||
| 0.05C-TiMo | - | 0.1 | 1100 |
| 1200 | |||
| 1 | 800 | ||
| 900 | |||
| 1000 | |||
| 1200 | |||
| 0.05C-NbMo | - | 0.1 | 1100 |
| 1200 | |||
| 1 | 900 | ||
| 1200 | |||
| 0.1C-Nb | 22 | 0.1 | 1100 |
| 0.2 | 1100 | ||
| 1 | 1000 | ||
| 1100 | |||
| 65 | 0.1 | 1100 | |
| 1 | 1000 | ||
| 129 | 1 | 1000 | |
| 1100 | |||
| 518 | 0.1 | 1100 | |
| 1 | 1000 | ||
| 1100 | |||
| 806 | 0.1 | 1100 | |
| 1200 | |||
| 0.2 | 1000 | ||
| 1100 | |||
| 1200 | |||
| 1 | 1000 | ||
| 1100 | |||
| 5 | 1000 | ||
| 0.07C-NbTi | 60 | 1 | 1000 |
| 109 | 0.1 | 1000 | |
| 1100 | |||
| 1 | 1000 | ||
| 1100 | |||
| 10 | 1100 | ||
| 158 | 0.1 | 1100 | |
| 1200 | |||
| 1 | 1000 | ||
| 1100 | |||
| 1200 | |||
| 392 | 1 | 1000 | |
| 1100 | |||
| 796 | 1 | 1000 | |
| 1100 | |||
| 0.12C-NbMo31 | 131 | 0.1 | 1100 |
| 1 | 1000 | ||
| 1100 | |||
| 1200 | |||
| 180 | 1 | 1000 | |
| 1100 | |||
| 1200 | |||
| 550 | 0.1 | 1100 | |
| 650 | 0.2 | 1100 | |
| 1 | 1200 | ||
| 660 | 1 | 1000 | |
| 1200 | |||
| 0.05C-NbMo16 | 365 | 1 | 1100 |
| 445 | 0.2 | 1100 | |
| 1 | 1100 | ||
| 0.11C-NbMo15 | 565 | 0.1 | 1100 |
| 1 | 1100 | ||
| 0.06C | - | 1 | 900 |
| 950 | |||
| 1000 | |||
| 0.12C | - | 1 | 900 |
| 950 | |||
| 1000 |
| Parameter | |
|---|---|
| 4.458 | |
| 0.011875 |
| Test Condition | Strain | Strain Rate (s−1) | Temperature (°C) |
|---|---|---|---|
| Minimum | 0.75 | 0.1 | 800 |
| Maximum | 2 | 10 | 1200 |
| Fitting Parameters | |||||
| DRV | 1.09 | 0.35 | 1.7 | −0.07 | 0.03 |
| Fitting parameters | |||||
| DRX | 0.86 | 80 | −0.145 | 2.45 | −0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayo, U.; Fernandez-Sanchez, S.; Gutierrez, I.; Jorge-Badiola, D.; Iza-Mendia, A. Towards a Global Constitutive Formulation for Modeling the Hot Working Behavior of Low-Carbon Steels. Metals 2025, 15, 1044. https://doi.org/10.3390/met15091044
Mayo U, Fernandez-Sanchez S, Gutierrez I, Jorge-Badiola D, Iza-Mendia A. Towards a Global Constitutive Formulation for Modeling the Hot Working Behavior of Low-Carbon Steels. Metals. 2025; 15(9):1044. https://doi.org/10.3390/met15091044
Chicago/Turabian StyleMayo, Unai, Sergio Fernandez-Sanchez, Isabel Gutierrez, Denis Jorge-Badiola, and Amaia Iza-Mendia. 2025. "Towards a Global Constitutive Formulation for Modeling the Hot Working Behavior of Low-Carbon Steels" Metals 15, no. 9: 1044. https://doi.org/10.3390/met15091044
APA StyleMayo, U., Fernandez-Sanchez, S., Gutierrez, I., Jorge-Badiola, D., & Iza-Mendia, A. (2025). Towards a Global Constitutive Formulation for Modeling the Hot Working Behavior of Low-Carbon Steels. Metals, 15(9), 1044. https://doi.org/10.3390/met15091044








