Next Article in Journal
Recovery of Cu and Fe from a Sphalerite Concentrate by the MnO2–KI Leaching Oxidation System
Previous Article in Journal
Microstructural Evolution and Tensile Deformation Behavior of FeCoNiCrTi0.2 High-Entropy Alloys Regulated by Cold Rolling and Annealing
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 15
Issue 9
10.3390/met15091038
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

ISE of Precious Metals: Au, Ag, Pd, and Pt

by
Lenka Girmanová
,
Jozef Petrík
,
Marek Šolc
,
Peter Blaško
,
Alena Pribulová
* and
Peter Futáš
Institute of Metallurgical Technologies and Digital Transformation, Faculty of Materials Metallurgy and Recycling, Technical University of Kosice, 042 00 Košice, Slovakia
*
Author to whom correspondence should be addressed.
Metals 2025, 15(9), 1038; https://doi.org/10.3390/met15091038
Submission received: 6 August 2025 / Revised: 1 September 2025 / Accepted: 16 September 2025 / Published: 19 September 2025
Browse Figures
Versions Notes

Abstract

Precious metals play an important role in various fields, from industry to jewelry and finance. In the industrial field, it is often necessary to know their mechanical properties. Micro-hardness measurement is a suitable test. In this type of test, the results are usually influenced by the Indentation Size Effect (ISE). The paper addresses the problem of micro-hardness measurement and the subsequent interpretation of the measured values using Meyer’s index n, the PSR method, and the Hays–Kendall approach in order to determine the true, test-load-independent micro-hardness values of gold, silver, palladium, and platinum. The tester Hanemann (manufactured by Carl Zeiss, Jena, Germany) was used to measure micro-hardness. The loads applied during the micro-hardness test were between 0.09807 N and 0.9807 N. Investment precious metals with a declared purity of at least 99.95% were used for the measurements. Palladium and silver have a Meyer index close to the validity of Kick’s law, with neutral ISE. Gold and platinum show a slightly “normal” ISE. This may be the influence of the previous deformation of the sample.

Graphical Abstract

1. Introduction

Precious metals are widely used in several industries and in jewelry production. In industrial applications, it is often necessary to know the mechanical properties of both the semi-finished product and the final product. Because these are often small, high-priced items, they require testing in a minimally destructive manner. In addition to jewelry and components in electrical engineering, which also require a certain degree of strength, this requirement is highlighted in the case of implants, for which these metals are often used. One option is to measure micro-hardness. At low loads, indentations are practically invisible to the naked eye (for example, silver 0.04 mm at a load of 0.49035 N/50 gf).
The human eye’s limited resolution means there is a smallest visual angle at which two distinct points can be perceived as separate. Under ideal conditions, this angle is about 1 arc-minute (0.017 degrees or 0.0003 radians). This translates to the ability to distinguish objects about 0.07 mm apart at a distance of 25 cm [1].
The disadvantage of measuring micro-hardness, unlike the (macro)hardness, is its dependence on the applied load. There are two opposing tendencies here: the smaller the load we use, the smaller the indentations. On the other hand, as the load decreases, the difference between the measured and “true” micro-hardness increases. This influence is referred to as the Indentation Size Effect (ISE).
Westbrook and Conrad [2] state that “Hardness measurements are both the most infamous and the most magnificent of physical measurements” precisely because of the ISE phenomenon, which makes the interpretation of measured results difficult. Its omission can completely invalidate the data of such a measurement.
The ISE phenomenon has been observed in a wide range of materials. It was not only observed in glasses [3,4,5,6,7,8] but also in ceramics [9,10], metals [11,12,13], and crystalline materials [14]. It is defined as the influence of the applied load on the micro-hardness a tested material. Understanding ISE, especially knowing at what force hardness becomes independent of load, is very important. Ignoring ISE can lead to misleading interpretations of hardness. The nature of the ISE is a complex and a much-discussed topic [15,16,17,18,19].
Sangwal et al. [20], as well as other researchers, found that the Vickers method of micro-hardness test differs from the Vickers (macro) hardness test only by “a very low” applied test load. The form of the Vickers indentation is geometrically similar, and it is therefore to be expected that the value of the hardness is constant if we assume the homogeneity of the measured sample. The term “low load” or “a very low load” is controversial. As quoted in the standard ISO 6507-1 [21], the applied loads for the micro-hardness tests range between 0.009807 N (1 gf) and 0.9807 N (100 gf), and for the low-force hardness between 1.961 N (200 gf) and 29.42 N (3000 gf). Considering the recommendation of the standard ISO 14577-1 [22], the loads for the micro-hardness tests are less than 2 N (~200 gf), with the depth of indentation h > 0.2 μm.
ISE manifests itself in three ways when measuring micro-hardness. The first way is the area of Kick’s law validity with Meyer’s index n = 2. The micro-hardness is not influenced by the applied load and it’s “true value” is measured. In the second way the micro-hardness decreases with increasing load and Meyer’s index n < 2. In that case we are talking about a “normal” ISE. Meyer’s index n > 2 in the third way. It is “reverse” (RISE) type in which micro-hardness increases with increasing load. Due to the potential for surface degradation by large indentations, the tendency is to minimize the load with resulting small indentations. However, small indentations introduce greater relative variability in their measurement dimensions and ultimately greater error. Therefore, a reasonable compromise must be found [10,20].
The origin of ISE has been the subject of considerable controversy. Some scientists believe that it is a consequence of insufficient measurement capabilities or insufficiently characterized surfaces that are the object of measurement. For example, surface anomalies, such as surface layer disruption or contamination, can cause an apparent increase in micro-hardness at low loads [23].
As already mentioned, the nature of ISE has not yet been clarified and is the subject of the discussion. Its occurrence is often associated with the characteristics of the hardness tester used. Perhaps the greatest influence is the equipment on measuring indentation dimensions (measurement methodology, magnification used) and the characteristics of the indenter (for example, the influence of its geometry and wear) [10,20,24]. The physical and other internal properties of the measured sample also have a great influence, for example the load to initiate plastic deformation (parameter W), elastic recovery of the indentation, strain hardening during indentation, crystallographic orientation, grain size, and elastic resistance [25]. The grinding and polishing of the sample (residual stresses and roughness of the measured surface), the friction between the indenter and sample, lubrication, and corrosion are other important factors [26].
Given the experience with ISE analysis of metals, as well as the small number of works that deal with this phenomenon in precious metals, the authors of the article focused on solving this phenomenon in the case of gold, silver, palladium, and platinum.
The paper addresses the problem of micro-hardness measurement and subsequent interpretation of the measured values using Meyer’s index n, the PSR method, and the Hays–Kendall approach in order to determine the “true hardness”.

2. Materials and Methods

Precious metals represent a group of metals characterized by high resistance to corrosion and oxidation, as well as specific physical and chemical properties [27,28]. Gold (Au), silver (Ag), platinum (Pt), and palladium (Pd) are among the most important precious metals, with a wide range of applications in industry, medicine, and various technologies [29,30]. These metals are notable for their high density (ranging from 10.49 to 21.45 g/cm3) [28], exceptional electrical conductivity, and remarkable light reflectivity. Precious metals are technologically significant and often irreplaceable metallic materials.

2.1. Gold (Au)

2.1.1. Physical and Chemical Properties

Gold is a chemical element with atomic number 79 and an atomic weight of 196.97 [31,32]. It crystallizes in a face-centered cubic lattice with a lattice parameter a = 0.408 nm [33]. Its density is 19.32 g cm−3, melting point is 1064.18 °C, and boiling point is 2856 °C [31,32,34].
Gold is the most chemically inert of the precious metals, resistant to most acids, heat, moisture, and solvents [31,35]. It dissolves in aqua regia (a mixture of nitric and hydrochloric acids) and in alkaline cyanide solutions [35,36]. Its electron configuration provides exceptional stability and low reactivity [37].
Gold is the most malleable and ductile of all metals, capable of being drawn into extremely thin foils or wires [31,35]. Its outstanding electrical and thermal conductivity make it especially suitable for applications in the electronics industry [31,38].

2.1.2. Applications

Global use of gold is distributed as follows: jewelry (51%), gold coins and bars (25%), central bank reserves (15%), electronics and industry (7%), exchange-traded funds (1%), and dental and medical applications (1%) [35].
In electronics, gold is used for its exceptional conductive properties and resistance to corrosion, which is critical for the long-term functionality of connectors, switches, and circuit boards [31]. Gold nanoparticles find applications in biomedicine as contrast agents, in photothermal therapy, and as biosensors [39,40]. In catalysis, gold is used for its unique optical, electrical, and physicochemical properties [39,41].

2.2. Silver (Ag)

2.2.1. Physical and Chemical Properties

Silver has an atomic number of 47 and an atomic weight of 107.87 [32,38]. It features a face-centered cubic crystal lattice. Its density is 10.49 g cm−3 [28,38]. The melting point of silver is 961.78 °C, and the boiling point is 2162 °C [32,34,38].
Silver has the highest electrical and thermal conductivity of all metals [32,38,42]. It is highly ductile and malleable, making it suitable for various industrial applications [38,42]. Chemically, silver is relatively unreactive, but it reacts with sulfur compounds to form silver sulfide, which causes its passivation [38].

2.2.2. Antimicrobial Properties

Silver exhibits exceptional antimicrobial effects against a wide spectrum of microorganisms [42,43,44]. Silver ions (Ag+) are effective antimicrobial agents due to their interaction with thiol groups in important bacterial enzymes and proteins [42,43]. The antimicrobial effect of silver is observed even at minimal concentrations, known as the “oligodynamic” effect [43]. The mechanism of antimicrobial action involves damage to the cell wall and cytoplasmic membrane, leading to inhibition of cellular respiration [42,43]. Silver ions bind to DNA and RNA molecules, causing their condensation and inhibiting protein synthesis [43].

2.2.3. Applications

Silver has broad application in electronics due to its highest electrical conductivity [38,42]. It is used in fibers, energy production, and as a conductive dye [42]. In medicine, silver is utilized in disinfectants, odor-resistant clothing, detergents, and cosmetics [44,45]. Silver nanoparticles are used in food packaging, sporting goods, and medical devices for their antimicrobial properties [42,45]. In dentistry, silver is traditionally used in amalgam fillings, and its antimicrobial properties are exploited in preventive and therapeutic applications [44].

2.3. Platinum (Pt)

2.3.1. Physical and Chemical Properties

Platinum has an atomic number of 78 and an atomic weight of 195.08 [32,46]. Its density is 2.45 g cm−3, melting point is 1768.3 °C, and boiling point is 3825 °C [32,34,46]. Platinum crystallizes in a face-centered cubic system [33,47].
Platinum is exceptionally resistant to corrosion and oxidation, making it ideal for applications in aggressive environments [27,46]. It is characterized by high thermal stability and the ability to withstand strong acids [46]. Platinum is one of the most malleable precious metals, yet highly resistant to wear and corrosion [32,46].

2.3.2. Catalytic Properties

Platinum is considered one of the most effective catalysts [48,49]. Its catalytic properties include the ability to accelerate chemical reactions without self-degradation and high tolerance to catalytic products [48].
Platinum catalysts exhibit superior efficiency in specific reactions compared to other metals, enabling the formation of desired products with minimal side reactions. Platinum has a broader range of reactions compared to iridium catalysts and remains stable even at higher temperatures [48].

2.3.3. Applications

Platinum is primarily used as a catalyst in the automotive industry, petroleum refining, environmental protection, and the production of industrial chemicals [30,50]. In the automotive industry, it is used in catalytic converters to reduce harmful emissions [30,46].
In the chemical industry, platinum–rhodium catalysts are used in the production of nitric acid, a key component of fertilizers. Platinum is also used in the production of paraxylene and in fuel cells [50].
In medicine, platinum is used in medical devices due to its biocompatibility and resistance [46]. Platinum alloys are used in dentistry for the manufacture of crowns, bridges, and other dental prostheses [51].

2.4. Palladium (Pd)

2.4.1. Physical and Chemical Properties

Palladium belongs to the platinum group of metals with an atomic number of 46 [52]. It has a lustrous, silvery-white appearance, a high melting point of 1554.9 °C, and a density of 12.023 g cm−3 [32,34,52].
Palladium is resistant to corrosion and passivation, making it suitable for jewelry and dental applications [52]. It has exceptional catalytic properties and the ability to absorb large amounts of hydrogen [52,53].

2.4.2. Catalytic Properties and Hydrogen Applications

Palladium exhibits outstanding catalytic properties, especially in organic synthesis and pharmaceutical production [52,54]. Palladium catalysts are widely used for their efficiency [54].
Palladium has a unique ability to absorb hydrogen, which is utilized in hydrogen refining using palladium membranes [52]. This property enables the production of highly pure hydrogen for various applications. Photo-induced hydrogen release from formic acid using palladium catalysts represents a new area of research in hydrogen storage and transport [23].

2.4.3. Applications

In the automotive industry, palladium is used in catalysts to reduce harmful pollutants, particularly nitrogen oxides (NOx) gases. In fuel cells, it plays a key role in converting hydrogen and oxygen into electrical energy [52].
In electronics, palladium is used due to its exceptional electrical conductivity in various components, including capacitors, connectors, and switches. It is also used in plating circuit boards to improve conductivity and prevent oxidation [52].
In jewelry and fashion, palladium is becoming popular due to its silvery-white appearance and hypoallergenic properties. In dentistry, palladium alloys are commonly used for the manufacture of crowns, bridges, and other dental prostheses due to their biocompatibility and durability [51,52].
Gold, silver, platinum, and palladium are key materials in modern technologies and industry due to their exceptional physicochemical properties [27,28].
Their unique characteristics, such as high electrical conductivity, catalytic activity, chemical stability, and biocompatibility, make them suitable for a wide range of applications, from electronics to medicine [30,55].
Future research focuses on optimizing the use of these precious metals, developing new catalytic systems, and expanding their applications in areas such as renewable energy, nanomedicine, and environmental technologies [55,56]. Ongoing research on nanostructured forms of these metals opens new possibilities for their more efficient use while preserving their unique properties [57,58].
The final products often have a modified surface that does not require metallographic treatment and can be directly used for micro-hardness measurement. Investment processing of precious metals in the form of prisms with a chemical composition declared by the manufacturer was used as samples. The purity of gold (2 g) and silver (31.103 g) is 99.99%wt, palladium, and platinum (both 1 g) 99.95%wt. The final shape of the samples was achieved by forming them without further details. The hardness was measured on the back side (without text) of the prisms. A place without mechanical damage (scratches) was chosen, outside the protrusions (depressions) (Figure 1).
All measurements were performed by an operator using a Hanemann handheld tester (type Mod D32, part of the optical microscope Neophot-32, manufacturer Carl Zeiss, Jena, Germany) with a magnification of 480×. Test loads of 10/0.09807, 25/0.245175, 50/0.49035, and 100/0.9807 gf/N with a load duration of 15 s. Five indentations (trials) at each load. The same operator measured all samples on the metallographic surface according to the standard ISO 6507-1 [21]. The result was the “cluster” of 20 indentations for each sample. The average hardness from five measurements at each load is shown in Figure 2.
Due to the manual control of the hardness tester, the speed of penetration of the indenter into the metal should be approximately the same, as it has a certain influence on the resulting micro-hardness value. According to Table 1, these speeds fluctuated around 1 µm s−1.
The value of the smallest division of the device measuring the diagonals of the indentation (discrimination) of the tester is 0.000313 mm. CRM (certified reference material, reference block) with a specified hardness of Hc (195 HV0.05) and a standard uncertainty of uCRM (4 HV0.05) was used for the calibration of the tester. The results are expressed as the repeatability rrel = 2.64%, the error of tester Erel = −0.91, and the relative expanded uncertainty of calibration Urel = 5.82%. Based on the calibration results, it can be concluded that the hardness tester meets the requirements of the standard ISO 6507-2 [59].
The mean of micro-hardness of individual “clusters” HV, its standard deviation HV SD, and p-value of Anderson–Darling normality test are in Table 1, as well as micro-hardness at selected loads and environmental conditions (temperature and relative humidity) of measurement. The “clusters” with p > 0.05 can be considered to have a normal distribution.
p-ANOVA in Table 2 represents the p-value of one-way ANOVA (analysis of variance), which expresses the influence of the test load on the micro-hardness value. Even if its value is greater than the significance level of a = 0.05, the load does not have a statistically significant effect, as in the case of palladium. The value in the last column of the table expresses the percentage of variability in the measured hardness, which is a consequence of the test load (others may be, for example, the influence of the environment, loading speed, uneven operator performance, etc.).

3. Results

The purpose of this article is to measure the micro-hardness of precious metals: Au, Ag, Pd, and Pt under different loads and subsequently to determine the type and size of the ISE, if any.
The calculation of the basic parameters characterizing the size and nature of the ISE was carried out according to the procedure mentioned in articles [60,61], whereby works [8,10,20,62,63] were also used. As demonstrated by Ren et al. [24], Meyer’s Power Law or Proportional Specimen Resistance model (PSR) describes ISE quantitatively. Also, the Hays-Kendall approach has been most commonly used to determine the ISE characteristics.
The parameter n, the Meyer index, is determined by an exponential curve fit to the gear diagonal d (mm) as a function of the applied load P (N). If the value of Meyer’s index n is 2 (±0.05), the test load does not influence the measured micro-hardness value, and Kick’s law applies. If the value is lower, it is a “normal” ISE, which is typical for brittle materials, such as ceramics, semiconductors, and sintered materials. Higher values, on the other hand, are typical of a “reverse” ISE (RISE), which is normally associated with plastic materials, such as pure metals. With increasing deformation, metallic materials undergo a hardening that exhausts the possibilities of plastic deformation, and in extreme cases, the metal behaves like a brittle material with a “normal” ISE.
The other parameters of the ISE are c1 (N mm−1), which characterizes the elastic properties, and c2 (N mm−2), which characterizes the plastic properties of the tested material, and c0 (N), the measure of the residual surface stress. The parameter c1 characterizes the load dependence of the micro-hardness and describes the ISE in the PSR model. The ratio c1/c2 (mm) is the measure of the residual stresses remaining after metallographic surface preparation (for example, grinding and polishing).
Parameter A1 (other parameters can also be used, e.g., c2) can be used to calculate the “true hardness”, which is not influenced by the applied load. The harder material with a higher modulus of elasticity has a higher value of A1 [63,64]. The parameter A1 (N mm−2) is not dependent on the load, and, therefore, the “true hardness” HPSRA1, calculated by Equation (1), is not dependent on the applied load.
HPSRA1 = 0.1891 ∗ A1
Similarly, “true hardness” can be determined from other indices, such as a2, c2, or Amoc.
The research showed a controversy over the parameter W (gf), which according to the professional literature (for example [20]) characterizes deformation resistance of tested material. In practice, it is the smallest load that leads to a visible indentation. In fact, visible indentations were observed even at lower loads than the W values reported in Table 3. This phenomenon was observed in not deformed [65], as well as in deformed metals [60,61]. The investigation and explanation of the above anomalies will be the subject of further research.
The values of Meyer’s index n and other ISE parameters are listed in Table 3.
In Figure 3, the average micro-hardness of the “cluster” HV, HV0.05, and “true hardness” HPSR A1 and HPSR c2 are shown for individual metals.

4. Discussion

In the professional literature, contributions related to ISE of precious metals are rare. This was the impetus for the authors to focus their research on this area. To some extent, it builds upon their previous research, which focused on the ISE of metals.
The authors have previously published two papers in which they partially dealt with the ISE of precious metals, specifically silver. In the first [65], they evaluated the ISE of 99.95% in the rolled state with n = 2.169, which is probably a consequence of strain hardening. In the second paper, they dealt with the ISE of Ag–Cu alloy coins [66], an investment silver “ounce” with a content of 99.99% Ag (n = 2.1312) was measured. A cast piece of silver with a purity of 99.95% had n = 1.9907.
To make coins are used circular blanks of pure silver (Ag 999) and silver-copper alloys (Ag 925 and Ag 333). The analysis of their uneven micro-hardness as a result of forming was carried out by Greil et al. [67]. The micro-hardness mapping (micro-hardness HV 0.05 protocol) quantified localized strengthening effects, revealing peripheral hardness enhancement approaching 30% relative to bulk values. Hardness distribution analysis confirmed radial gradients extending from specimen edges toward central regions. Analogous heterogeneity patterns emerge in the current specimen set, where forming operations generate comparable surface topology variations, in formed blanks with deeper relief.
Pure (99.995%) platinum was tested by Maughan et al. [68] with Berkovich nanoindenter and loads up to 3500 μN to various depths. The indent pattern was created on the as-polished specimen before heat treatment, after heat treatment at 500 °C for 30 min, and again after further heat treatment at 1000 °C for 30 min. The variability in the measured hardness decreased as the indentation depth increased from 50 to 300 nm.
In order to avoid problems associated with oxide on the surface, Ma and Clarke [23] have chosen to work on silver and gold, using thick, epitaxial single-crystal films formed by vapor phase growth. The vapor phase growth also avoids the introduction of any surface artifacts associated with polishing and cleaning. The indentation experiments were performed using a nanoindenter (Nano Instruments, Inc., Knoxville, TN, USA) fitted with a Berkovich indenter.
Nanoporous gold (np-Au) has received significant attention for potential applications as sensors, actuators, and catalysts due to its high specific surface area and chemical stability. Studies on the mechanical properties of np-Au have been numerous because its fragility is critical in applications.
Four nanoporous-Au samples of ligament sizes 26 (±4.0), 73 (±8.8), 127 (±12.8), 630 (±61.4) nm were prepared using the alloy of Au 30 at.% and Ag 70 at.%, both 99.99% pure. Nitric acid was used for the dealloying. The nano-hardness indentations were measured using Berkovich indenter. Lingament sizes 26, 73, and 126 nm showed almost identical ISE, while size 630 nm showed relatively enhanced ISE [69].

5. Conclusions

The research results are the basic parameters that characterize the influence of ISE in measuring the micro-hardness of selected precious metals: silver, gold, palladium, and platinum. Silver and palladium have a Meyer index close to the validity of Kick’s law, while gold and platinum show a slightly “normal” ISE. This may be the influence of the previous deformation of the sample.
The paper presents the use of multiple approaches to determine the ISE parameters of these precious metals in the micro-hardness range. Given the lack of professional publications devoted to this phenomenon in precious metals, the article presents a new perspective on this issue. At the same time, it is a challenge for research focused on other precious metals.

Author Contributions

Conceptualization, L.G.; data curation, P.B. and J.P.; methodology, M.Š.; software, M.Š. and P.F.; validation, L.G. and A.P.; formal analysis, J.P.; investigation, M.Š.; resources, P.B.; data curation, P.B.; writing—original draft preparation, J.P.; writing—review and editing, L.G. and M.Š.; visualization, L.G.; supervision, A.P.; project administration, L.G. and A.P.; funding acquisition, M.Š. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Scientific grant agency of the Ministry of Education, Re-search, Development and Youth of the Slovak Republic and the Slovak Academy of Sciences (VEGA) grants number: VEGA 1/0359/25, VEGA 1/0001/25, VEGA 1/0267/25 and SLOVAK RESERCH AND DEVELOPMENT AGENCY grant number APVV-22-0580.

Data Availability Statement

The original contributions presented in this study are included in the article material. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Verhoeven, G. Resolving some spatial resolution issues—Part 1: Between line pairs and sampling distance. AARGnews 2018, 57, 25–35. [Google Scholar] [CrossRef]
  2. Westbrook, H.; Conrad, H. The Science of Hardness Testing and Its Research Application; American Society for Metals: Metals Park, Novelty, OH, USA, 1973. [Google Scholar]
  3. Smedskjaer, M.M. Indentation size effect and the plastic compressibility of glass. Appl. Phys. Lett. 2014, 104, 251906. [Google Scholar] [CrossRef]
  4. Kazembeyki, M.; Bauchy, M.; Hoover, C.G. New insights into the indentation size effect in silicate glasses. J. Non-Cryst. Solids 2019, 521, 119494. [Google Scholar] [CrossRef]
  5. Kazembeyki, M.; Yang, K.; Mauro, J.C.; Smedskjaer, M.M.; Bauchy, M.; Hoover, C.G. Decoupling of indentation modulus and hardness in silicate glasses: Evidence of ashear- to densification-dominated transition. J. Non-Cryst. Solids 2021, 553, 120518. [Google Scholar] [CrossRef]
  6. Quinn, G.D.; Green, P.; Xu, K. Cracking and the indentation size effect for knoop hardness of glasses. J. Am. Ceram. Soc. 2003, 86, 441–448. [Google Scholar] [CrossRef]
  7. Jang, J.; Yoo, B.-G.; Kim, Y.-J.; Oh, J.-H.; Choi, I.-C.; Bei, H. Indentation size effect in bulk metallic glass. Scr. Mater. 2011, 64, 753–756. [Google Scholar] [CrossRef]
  8. Li, H.; Bradt, R.C. The indentation load/size effect and the measurement of the hardness of vitreous silica. J. Non-Cryst. Solids 1992, 146, 197–212. [Google Scholar] [CrossRef]
  9. Bull, S.J.; Page, T.F.; Yoffe, E.H. An explanation of the indentation size effect in ceramics. Philos. Mag. Lett. 1989, 59, 281–288. [Google Scholar] [CrossRef]
  10. Gong, J.; Wu, J.; Guan, Z. Examination of the Indentation Size Effect in Low-Load Vickers Hardness Testing of Ceramics. J. Eur. Ceram. Soc. 1999, 19, 2625–2631. [Google Scholar] [CrossRef]
  11. Elmustafa, A.A.; Stone, D.S. Indentation size effect in polycrystalline F.C.C. metals. Acta Mater. 2002, 50, 3641–3650. [Google Scholar] [CrossRef]
  12. Zong, Z.; Lou, J.; Adewoye, O.O.; Elmustafa, H.F.; Soboyejo, W.O. Indentation size effects in the nano- and micro-hardness of fcc single crystal metals. Mater. Sci. Eng. 2006, 434, 178–187. [Google Scholar] [CrossRef]
  13. Durst, K.; Backes, B.; Franke, O.; Göoken, M. Indentation size effect in metallic materials: Modeling strength from pop-in to macroscopic hardness using geometrically necessary dislocations. Acta Mater. 2006, 54, 2547–2555. [Google Scholar] [CrossRef]
  14. Nix, W.D.; Gao, H. Indentation size effects in crystalline: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
  15. Bernhardt, E.O. Über die Mikrohärte der Feststoffe im Grenzbereich des Kick’schen Ahnlichkeitssatzes. Int. J. Mater. Res. 1941, 33, 135–144. [Google Scholar] [CrossRef]
  16. Shi, Y.; Deng, B.; Neuefeind, J.; Zhou, Q.; Smedskjaer, M.M.; Elliott, S.R.; Bauchy, M. Revealing the effect of medium-range structure on silicate glass hardness. Phys. Rev. Mater. 2023, 7, 013602. [Google Scholar] [CrossRef]
  17. Li, H.; Ghosh, A.; Han, Y.H.; Bradt, R.C. The frictional component of the indentation size effect in low load microhardness testing. J. Mater. Res. 1993, 8, 1028–1032. [Google Scholar] [CrossRef]
  18. Swain, M.V.; Wittling, M. Indentation Size Effects for Ceramics: Is There a Fracture Mechanics Explanation? Fracture Mechanics of Ceramics; Plenum: New York, NY, USA, 1996; Volume 11, pp. 379–387. [Google Scholar]
  19. Shrestha, P.; Smedskjaer, M.M.; Bauchy, M.; Hoover, G. Impact of strain rate on the Indentation Size Effect: Evidence of an intimate link between Size effect, Strain Rate and Ductility in Soda-lime Silica glass. J. Non-Cryst. Solids 2024, 637, 123031. [Google Scholar] [CrossRef]
  20. Sangwal, K.; Surowska, B.; Błaziak, P. Analysis of the Indentation Size Effect in the Microhardness Measurement of Some Cobalt-Based Alloys. Mater. Chem. Phys. 2003, 77, 511–520. [Google Scholar] [CrossRef]
  21. ISO 6507-1; Metallic materials—Vickers hardness test Part 1—Test method. International Organization for Standardization ISO: Geneva, Switzerland, 2018.
  22. ISO 14577-1; Metallic materials—Instrumented indentation test for hardness and materials parameters Part 1—Test method. International Organization for Standardization ISO: Geneva, Switzerland, 2015.
  23. Ma, Q.; Clarke, D.R. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
  24. Ren, X.J.; Hooper, R.M.; Griffiths, C.; Henshall, J.L. Indentation Size Effect in Ceramics: Correlation with H/E. J. Mater. Sci. Lett. 2003, 22, 1105–1106. [Google Scholar] [CrossRef]
  25. Sangwal, K. On the Reverse Indentation Size Effect and Microhardness Measurement of Solids. Mater. Chem. Phys. 2000, 63, 145–152. [Google Scholar] [CrossRef]
  26. Navrátil, V.; Novotná, J. Some Problems Of Microhardness Of Metals. J. Appl. Math. 2009, 2, 241–244. Available online: https://www.researchgate.net/publication/268268064_SOME_PROBLEMS_OF_MICRO-HARDNESS_OF_METALS (accessed on 29 June 2025).
  27. Gold Nanoparticules and Uses in Cancer. Acta Pharmaceutica Turcica. 2021. Available online: https://dergipark.org.tr/tr/doi/10.33483/jfpau.773430 (accessed on 12 March 2023).
  28. Faricha, A.; Chakraborty, P.; Chang, T.-F.M.; Sone, M.; Nakamoto, T. New Trend of Amperometric Gas Sensors Using Atomic Gold-Decorated Platinum/Polyaniline Composites. Chemosensors 2024, 12, 27. [Google Scholar] [CrossRef]
  29. Akh, P.A. Vernonia amygdalina Del (Bitter leaf) a traditional anti-diabetic gold mine—Mini Review. MDPI. J. Ayurveda Integr. Med. Sci. 2024, 10, 170–175. [Google Scholar] [CrossRef]
  30. Ray, S.K.; Ghosh, N.; Vitkin, A. Diattenuation and retardance signature of plasmonic gold nanorods in turbid media revealed by Mueller matrix polarimetry. Sci. Rep. 2021, 11, 20376. [Google Scholar] [CrossRef]
  31. Lee, C.H.; Chae, J.; Yang, H.R. Scientific Characterization of Coloration Pigments and Deterioration Diagnosis on the Surface for the Gilt-bronze Seated Bodhisattva at Cheongyang Unjangam Hermitage. J. Conserv. Sci. 2023, 39, 137–151. [Google Scholar] [CrossRef]
  32. Haueis, P. A generalized patchwork approach to scientific concepts. Philos. Sci. 2021, 88, 716179. [Google Scholar] [CrossRef]
  33. Daggumati, P.; Kurtulus, O.; Chapman, C.A.R.; Dimlioglu, D.; Seker, E. Microfabrication of nanoporous gold patterns for cell-material interaction studies. J. Vis. Exp. 2013, 78, 50678. [Google Scholar] [CrossRef]
  34. Benesova, E.; Vidova, V.; Spacil, Z. A comparative study of synthetic winged peptides for absolute protein quantification. Sci. Rep. 2021, 11, 90087. [Google Scholar] [CrossRef]
  35. Gold Properties and Uses. Energy & Mining. 2019. Available online: https://www.energymining.sa.gov.au/home/events/discover_gold/gold_properties_and_uses (accessed on 12 August 2023).
  36. Gold: Element Properties and Uses. Stanford Advanced Materials. 2025. Available online: https://www.samaterials.com/blog/gold-element-properties-and-uses.html (accessed on 29 June 2025).
  37. Oldenburg, S.J. Silver Nanomaterials: Properties & Applications. Sigma-Aldrich. 2025. Available online: https://www.sigmaaldrich.com/SK/en/technical-documents/technical-article/materials-science-and-engineering/biosensors-and-imaging/silver-nanomaterials-properties (accessed on 29 June 2025).
  38. Platinum: Element Properties and Uses. Stanford Advanced Materials. 2025. Available online: https://www.samaterials.com/blog/platinum-element-properties-and-uses.html (accessed on 29 June 2025).
  39. Shults, R. Palladium: Properties and Uses. 2024. Available online: https://borro.com/the-basics-of-palladium-a-comprehensive-guide-to-its-properties-and-uses/ (accessed on 21 May 2025).
  40. Study.com. Gold|Definition, Properties & Uses—Lesson. Available online: https://study.com/learn/lesson/what-is-gold-properties-uses.html (accessed on 29 June 2025).
  41. Stanford Advanced Materials. Silver: Element Properties and Uses. 2025. Available online: https://www.samaterials.com/blog/silver-element-properties-and-uses.html (accessed on 29 June 2025).
  42. Gopalakrishnan, U. Frontiers in Bioengineering and Biotechnology. Assessing the Potential Association Between Microbes and Corrosion of Intra-Oral Metallic Alloy-Based Dental Appliances Through a Systematic Review of the Literature. Front. Bioeng. Biotechnol. 2021, 9, 631103. [Google Scholar] [CrossRef]
  43. Michael, B.; Mooiman, M.B.; Kathryn, C.; Sole, K.C.; Dinham, N. The Precious Metals Industry. Wiley Online Library. 2016. Available online: https://onlinelibrary.wiley.com/doi/10.1002/9781119009115.ch16 (accessed on 29 June 2025).
  44. Precious Metals, vs. Base Metals: Nature and Experiment. Minerals. 2023. Available online: https://www.mdpi.com/journal/minerals/special_issues/PMBMNE (accessed on 29 June 2025).
  45. Scientific Properties of Precious Metals. APMEX. 2024. Available online: https://learn.apmex.com/learning-guide/science/scientific-properties-of-precious-metals/ (accessed on 20 January 2024).
  46. Mohamed, D.S.; Abd El-Baky, R.M.; Sandle, T.; Mandour, S.A.; Ahmed, E.F. Antimicrobial Activity of Silver-Treated Bacteria against Other Multi-Drug Resistant Pathogens in Their Environment. Antibiotics 2020, 9, 181. [Google Scholar] [CrossRef]
  47. Precious Metals. Total Materia. 2011. Available online: https://www.totalmateria.com/en-us/articles/precious-metals/ (accessed on 20 January 2024).
  48. Huang, X.; Li, Z.; Yu, Z.; Deng, X.; Xin, Y. Recent Advances in the Synthesis, Properties, and Biological Applications of Platinum Nanoclusters. J. Nanomater. 2019, 2019, 6248725. [Google Scholar] [CrossRef]
  49. Volostnykh, M.V. Water-soluble platinum and palladium porphyrins with peripheral ethyl phosphonic acid substituents: Synthesis, aggregation in solution, and photocatalytic properties. R. Soc. Chem. 2025, 54, 6. [Google Scholar] [CrossRef]
  50. Loza, K.; Heggen, M.; Epple, M. Synthesis, Structure, Properties, and Applications of Bimetallic Nanoparticles of Noble Metals. Adv. Funct. Mater. 2020, 30, 1909260. [Google Scholar] [CrossRef]
  51. Key Advantages of Platinum-Based Catalysts Over Iridium. 2023. Available online: https://www.nikalyte.com/key-advantages-of-platinum-based-catalysts-over-iridium/ (accessed on 21 January 2024).
  52. Hughes, A.E.; Haque, N.; Northey, S.A.; Giddey, S. Platinum Group Metals: A Review of Resources, Production and Usage with a Focus on Catalysts. Resources 2021, 10, 93. [Google Scholar] [CrossRef]
  53. Crystal Structures of Metals. Chemistry LibreTexts. 2021. Available online: https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Introduction_to_Inorganic_Chemistry_(Wikibook)/06:_Metals_and_Alloys-_Structure_Bonding_Electronic_and_Magnetic_Properties/6.04:_Crystal_Structures_of_Metals (accessed on 30 June 2022).
  54. C&CS. Palladium-Platinum Catalysts. 2024. Available online: https://www.candcs.de/en/product-category/palladium-platinum-catalysts/ (accessed on 29 June 2025).
  55. Takano, S.; Tsukuda, T. Chemically Modified Gold/Silver Superatoms as Artificial Elements at Nanoscale: Design Principles and Synthesis Challenges. J. Am. Chem. Soc. 2021, 143, 11465. [Google Scholar] [CrossRef]
  56. Wikipedia. Gold. 2001. Available online: https://en.wikipedia.org/wiki/Gold (accessed on 29 June 2025).
  57. Schmidbaur, H.; Cronje, S.; Djordjevic, B.; Schuster, O. Understanding gold chemistry through relativity. Chem. Phys. 2005, 311, 151–161. [Google Scholar] [CrossRef]
  58. Sim, W.; Barnard, R.T.; Blaskovich, M.A.T.; Ziora, Z.M. Antimicrobial Silver in Medicinal and Consumer Applications. 2018. Available online: https://pmc.ncbi.nlm.nih.gov/articles/PMC6315945/ (accessed on 29 April 2020).
  59. ISO 6507-2; Metallic materials—Vickers hardness test Part 2—Verification and calibration of testing machines. International Organization for Standardization ISO: Geneva, Switzerland, 2005.
  60. Petrík, J.; Blaško, P.; Petryshynets, I.; Mihaliková, M.; Pribulová, A.; Futáš, P. The Influence of the Degree of Tension and Compression of Aluminum on the Indentation Size Effect (ISE). Metals 2022, 12, 2063. [Google Scholar] [CrossRef]
  61. Petrík, J.; Blaško, P.; Mihaliková, M.; Vasilňáková, A.; Mikloš, V. The Relationship between the Deformation and the Indentation Size Effect (ISE). Metall. Res. Technol. 2019, 116, 622. [Google Scholar] [CrossRef]
  62. Liu, N.; Yang, X.; Yu, Z.; Zhao, L. Indentation Size Effect of Germanium Single Crystal with Different Crystal Orientations. Trans. Nonferrous Met. Soc. China 2020, 30, 181–190. [Google Scholar] [CrossRef]
  63. Kim, H.; Kim, T. Measurement of Hardness on Traditional Ceramics. J. Eur. Ceram. Soc. 2002, 22, 1437–1445. [Google Scholar] [CrossRef]
  64. Machaka, R.; Derry, T.E.; Sigalas, I.; Herrmann, M. Analysis of the Indentation Size Effect in the Microhardness Measurements in B6O. Adv. Mater. Sci. Eng. 2011, 2011, 539252. [Google Scholar] [CrossRef]
  65. Petrík, J.; Blaško, P.; Markulík, Š.; Šolc, M.; Palfy, P. The Indentation Size Effect (ISE) of Metals. Crystals 2022, 12, 795. [Google Scholar] [CrossRef]
  66. Šolc, M.; Blaško, P.; Petrík, J.; Palfy, P.; Girmanová, L. The Indentation Size Effect (ISE) of Ag–Cu Alloys. Crystals 2023, 13, 91. [Google Scholar] [CrossRef]
  67. Greil, S.; Edtmaier, C.; Haubner, R.; Lauter, L. Metallographic investigations of silver alloys used for minting. Mater. Sci. Forum. 2017, 891, 89–94. [Google Scholar] [CrossRef]
  68. Maughan, M.R.; Zbib, H.M.; Bahr, D.F. Variation in the nanoindentation hardness of platinum. J. Mater. Res. 2013, 28, 2819–2828. [Google Scholar] [CrossRef]
  69. Kim, Y.C.; Gwak, E.J.; Ahn, S.M.; Jang, J.I.; Han, H.N.; Kim, J.Y. Indentation size effect in nanoporous gold. Acta Mater. 2017, 138, 52–60. [Google Scholar] [CrossRef]
Metals 15 01038 g001
Figure 1. Used samples and measurement locations.
Figure 1. Used samples and measurement locations.
Metals 15 01038 g001
Metals 15 01038 g002
Figure 2. The average hardness from five measurements at each load.
Figure 2. The average hardness from five measurements at each load.
Metals 15 01038 g002
Metals 15 01038 g003
Figure 3. The average micro-hardness of “cluster” HV, HV0.05, and “true hardness” HPSR A1 and HPSR c2.
Figure 3. The average micro-hardness of “cluster” HV, HV0.05, and “true hardness” HPSR A1 and HPSR c2.
Metals 15 01038 g003
Table 1. The average speed of penetration of the indenter into the metal.
Table 1. The average speed of penetration of the indenter into the metal.
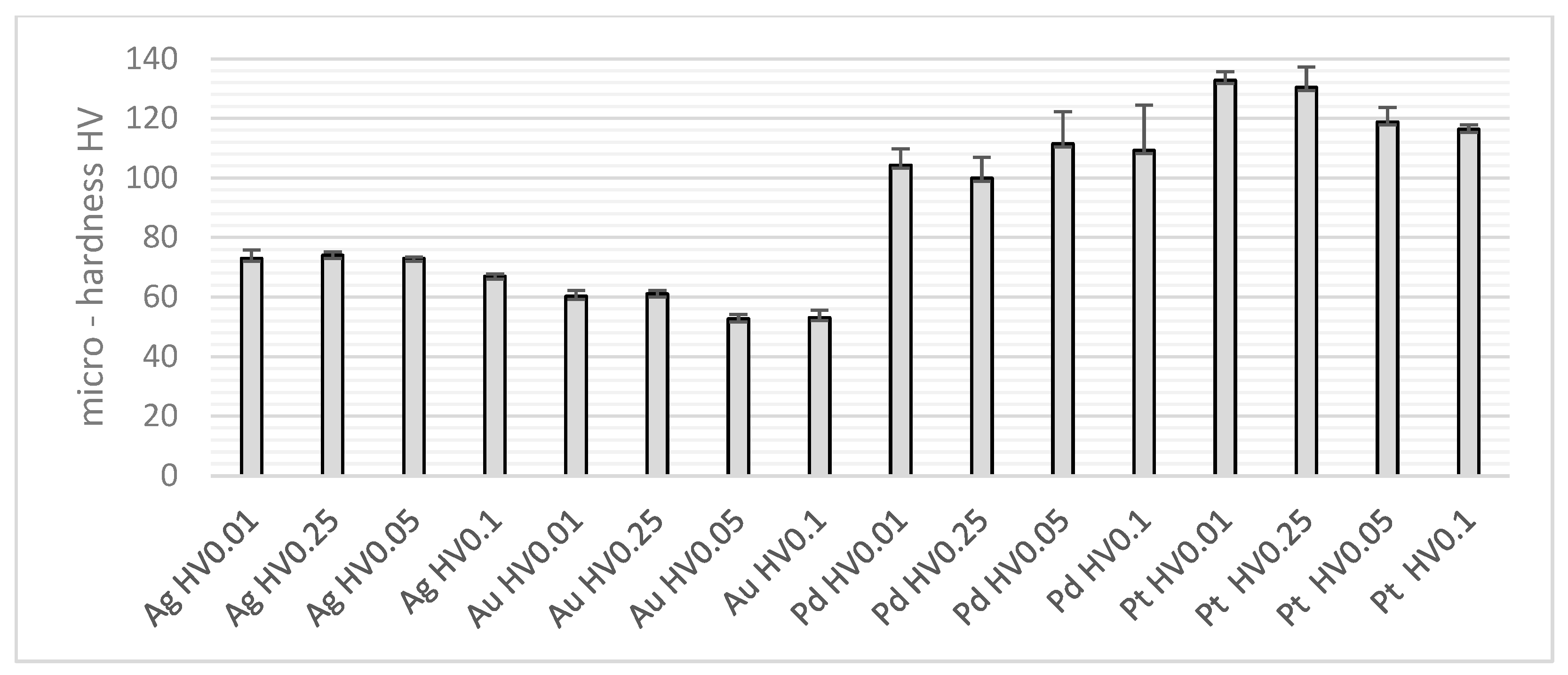
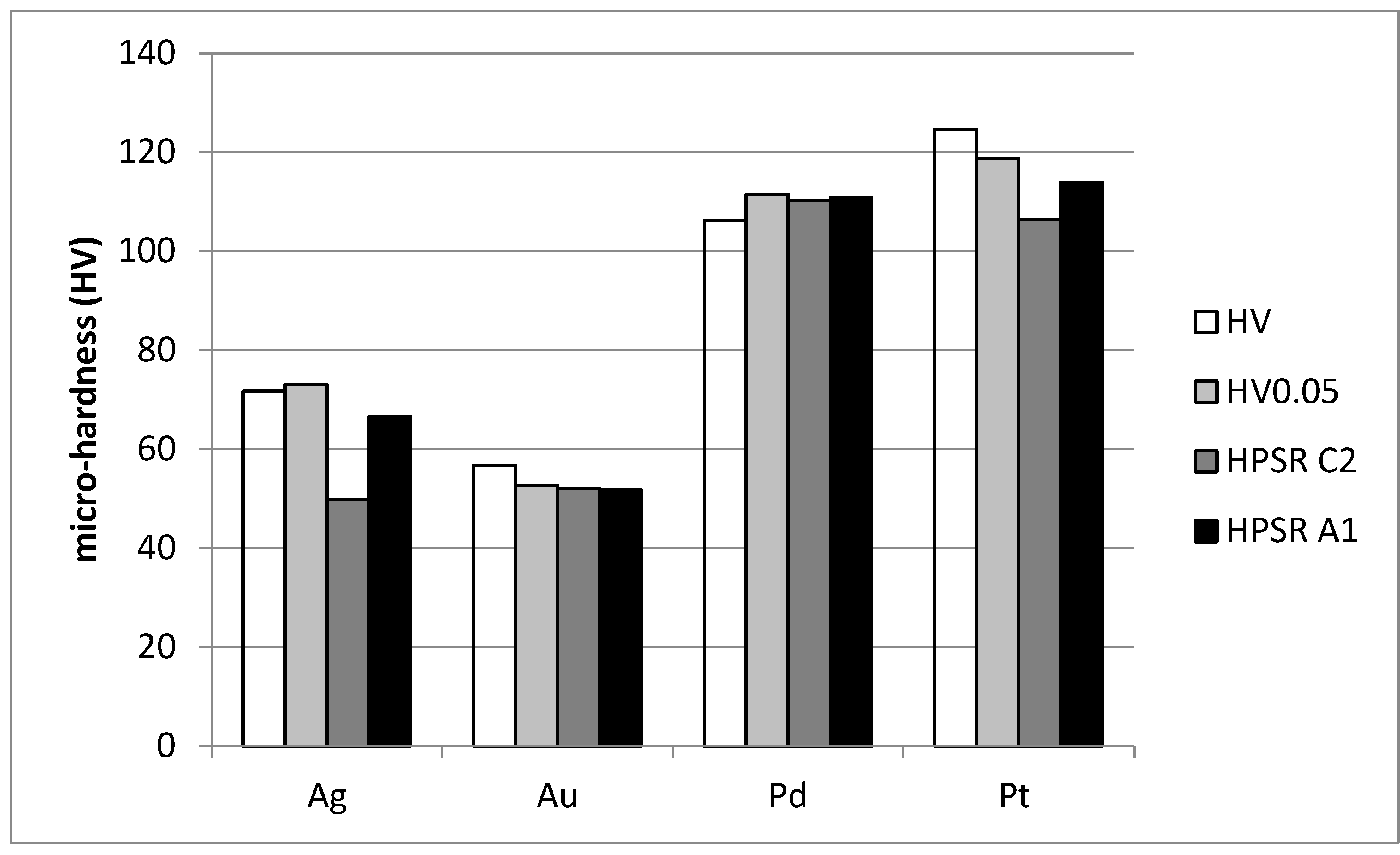
HV0.01HV0.025HV0.05HV0.1
Ag1.4271.2391.3851.286
Au1.2201.3411.2041.392
Pd1.0800.9311.0110.869
Pt0.7510.8380.9890.991
Table 2. The mean of micro-hardness of individual “clusters” HV, its standard deviation HV SD, p-value of Anderson–Darling normality test, temperature, and relative humidity of measurement.
Table 2. The mean of micro-hardness of individual “clusters” HV, its standard deviation HV SD, p-value of Anderson–Darling normality test, temperature, and relative humidity of measurement.
HVSD (HV)p-Normality TestT (°C)RH (%)p-ANOVAα
Ag71.733.120.005619.233.51.97∙10−577.5
Au56.784.360.0548718.633.87.57∙10−785.1
Pd106.2310.550.8297720.936.70.331318.7
Pt124.588.450.0898420.439.53.54∙10−575.7
Table 3. Meyer’s index n and other ISE parameters.
Table 3. Meyer’s index n and other ISE parameters.
nAmoc (N mm−2)c0 (N)c1 (N mm−1)c2 (N mm−2)W (g)A1 (N mm−2)c1/c2 (mm)
Ag1.9447312.30−0.07306.351263.032.28352.470.02415
Au1.8696192.040.0226−0.095275.012.22273.80−0.00035
Pd2.0606703.29−0.01340.193582.55−1.12585.960.00033
Pt 1.8795415.86−0.00252.136562.252.19602.140.00380
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Girmanová, L.; Petrík, J.; Šolc, M.; Blaško, P.; Pribulová, A.; Futáš, P. ISE of Precious Metals: Au, Ag, Pd, and Pt. Metals 2025, 15, 1038. https://doi.org/10.3390/met15091038

AMA Style

Girmanová L, Petrík J, Šolc M, Blaško P, Pribulová A, Futáš P. ISE of Precious Metals: Au, Ag, Pd, and Pt. Metals. 2025; 15(9):1038. https://doi.org/10.3390/met15091038

Chicago/Turabian Style

Girmanová, Lenka, Jozef Petrík, Marek Šolc, Peter Blaško, Alena Pribulová, and Peter Futáš. 2025. "ISE of Precious Metals: Au, Ag, Pd, and Pt" Metals 15, no. 9: 1038. https://doi.org/10.3390/met15091038

APA Style

Girmanová, L., Petrík, J., Šolc, M., Blaško, P., Pribulová, A., & Futáš, P. (2025). ISE of Precious Metals: Au, Ag, Pd, and Pt. Metals, 15(9), 1038. https://doi.org/10.3390/met15091038

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop