Abstract
Novel structural materials, high-entropy alloys (HEAs), have attracted considerable interest owing to their tunable microstructural designs and adjustable mechanical properties. In the present work, the microstructural evolution and tensile deformation behavior of FeCoNiCrTi0.2 HEA are comprehensively examined through cold rolling (with 80% thickness reduction) followed by annealing, combined with multiscale characterization techniques (EBSD/TEM) and mechanical tests. The results reveal that the as-rolled microstructure was characterized by the presence of strong Brass, Goss/Brass, and S textures, along with the formation of high-density dislocation walls (DDWs) and dislocation cells (DCs). As the annealing temperature increased, recrystallized grains preferentially nucleated at grain boundaries with higher stress concentrations and dislocation densities. The grain size decreased from 120.33 μm in the as-rolled state to 10.26 μm after annealing at 1000 °C. Low-angle grain boundaries (LAGBs) progressively transformed into high-angle grain boundaries (HAGBs), while the fraction of Σ3 twin boundaries initially decreased and subsequently increased, reaching a maximum of 43.7% after annealing at 1000 °C. At annealing temperatures exceeding 800 °C, deformed grains became equiaxed, with partial retention of primary texture components observed. After annealing at 1000 °C, the yield strength and tensile strength decreased compared to the as-rolled state, while the elongation significantly increased from 17.2% to 69.8% Simultaneously, the yield ratio decreased by 53%, and the strain-hardening capacity was enhanced. Ultimately, a constitutive model integrating the influences of dislocation mean free path and twin boundary obstruction was developed, providing microscopic explanations for the inverse relationship between strength and recrystallization fraction.
1. Introduction
High-entropy alloys (HEAs), distinguished by their unique multi-principal-element solid-solution structures, have become a pivotal research area in materials science. Their capacity to inhibit the formation of intermediate phases and intermetallic compounds simplifies alloy phase structures, endowing them with excellent mechanical properties, corrosion resistance, and thermal stability [1,2,3]. However, many scholars question whether high-entropy alloys can exhibit superior mechanical properties if most of them exist in simple solid solution forms [4]. The superior characteristics exhibited by HEAs are attributed to synergistic effects intrinsic to these materials, including the high-entropy effect, lattice distortion effect, sluggish diffusion effect, and cocktail effect [5,6]. Among these, FeCoNiCr-based HEAs have garnered significant attention due to their face-centered cubic (FCC) structure, which imparts remarkable toughness and processability [7,8].
However, FCC-structured alloys generally demonstrate inherently low strength, thereby limiting their applications in engineering [9,10]. To overcome this limitation, thermomechanical processing (TMP) is employed to tailor microstructures for enhanced strengthening and toughening [11,12]. Li [13] utilized powder metallurgy to incorporate AlCoCrFeNi high-entropy alloy as reinforcing particles, which form well-bonded interfaces with the matrix. The addition of the high-entropy alloy also enhanced the ductility, thereby broadening the application prospects of HEAs. Studies indicate that the mechanical properties of HEAs can be customized through optimized combinations of deformation processes and annealing conditions. Post-annealing mechanical behavior is significantly influenced by microstructural features, including dislocations [14,15]. Haase et al. [16] demonstrated that non-recrystallized regions contribute minimally to plasticity during tensile deformation in cold-rolled and annealed CoCrFeMnNi HEAs. Saha et al. [17] reported that warm-rolled HEAs after annealing exhibit larger grain sizes compared to their cold-rolled counterparts, achieving an optimal balance between strength and ductility via rolling and annealing [18,19]. Bhattacharjee [20] identified that cold-rolled CoCrFeMnNi HEAs predominantly develop a Brass-type texture ({110}<112>), exhibiting similarities to low-stacking fault energy (SFE) TWIP steels. Liang et al. [21,22] attributed mechanical anisotropy to contributions from Goss ({110}<001>) and G/B textures in cold-rolled sheets. As annealing temperatures increase, texture intensity diminishes, reducing property anisotropy. Chen et al. [23] further demonstrated that annealing cold-rolled FeCoNiCr sheets at elevated temperatures drastically reduces the density of dislocation cells and walls generated during cold rolling [24]. Sousa et al. [25] revealed that interactions between dislocations and mechanical twin boundaries enhance mechanical strength. Guo [26] proposed that high-density dislocations in cold-rolled samples transform into subgrain boundaries (i.e., high-angle grain boundaries, HAGBs) during annealing, reducing dislocation interactions and significantly improving elongation while lowering strength. Lin [27] found that cold rolling accelerates the phase transformation during subsequent annealing, resulting in a finer quenched microstructure and thereby increasing the yield strength of the material.
In comparison to FeCoNiCr HEAs, the incorporation of Ti enhances strength and hardness in FeCoNiCr-based alloys through solid-solution strengthening and secondary-phase precipitation, albeit with some sacrifice in ductility [28,29]. This study focuses on FeCoNiCrTi0.2 HEA, employing a coupled cold rolling-annealing process to systematically investigate its microstructural evolution, including grain size, texture orientation, grain boundary misorientation, and dislocation density, using electron backscatter diffraction (EBSD) and transmission electron microscopy (TEM). Despite the generally good ductility of FeCoNiCr-based FCC HEAs, their intrinsic strength is still limited for many engineering applications. Microalloying with Ti (0.2 at.%) can increase strength via solid solution and potential precipitation, but may also alter recrystallization and twinning behavior, affecting the strength–ductility balance [27,28,29,30]. Therefore, this work focuses on the coupling between large cold deformation (80% thickness reduction) and subsequent stepped annealing (700–1000 °C) to systematically investigate its microstructural evolution, including grain size, texture orientation, grain boundary misorientation, and dislocation density. This study proposes a microstructure-informed constitutive description to guide process optimization toward strong synergy with high levels of toughness, thereby providing robust theoretical support for the design of processing routes and the advancement of practical engineering applications of this alloy.
2. Materials and Methods
2.1. Preparation of Specimens
The FeCoNiCrTi0.2 high-entropy alloy was fabricated via vacuum arc melting, using Fe, Co, Ni, Cr, and Ti with purities exceeding 99.9 wt.%. To achieve a homogeneous composition, the alloy was remelted three times and subsequently cast into rectangular ingots measuring 15 mm × 40 mm in cross-section and 90 mm in length. The surface of the ingot was cleaned and then annealed at 1150–1200 °C for homogenization. The samples were subsequently hot-rolled in multiple passes to produce 1-mm-thick plates. The plates underwent cold rolling in multiple passes, with uniform annealing at 1200 °C in an argon atmosphere for 4 h before each pass, ultimately yielding 0.2 mm-thick FeCoNiCrTi0.2 high-entropy alloy plates. After cold rolling, the samples were annealed in an argon atmosphere for 0.5 h. The annealing temperature ranged from 700 °C to 1000 °C, followed by water quenching for cooling.
2.2. Microscopic Observation
X-ray diffraction (XRD) analysis was performed using a Rigaku D/max-2500 diffractometer (Rigaku, Tokyo, Japan) with Cu Kα radiation (λ = 0.154 nm) operated at 50 kV and 50 mA. The scanning range was 2θ = 40–100°, with a step size of 0.03° and a scanning speed of 4°·min−1. Prior to measurement, the specimen surfaces were ground using fine-grit SiC papers and cleaned with ethanol to ensure reliable surface conditions. These settings ensured accurate phase identification and minimized surface contamination effects. The microstructures of both rolled and annealed specimens were analyzed with a Talos F200S G2 transmission electron microscope (TEM, Thermo Fisher Scientific, Waltham, MA, USA) and a Nordlys Max3 electron backscatter diffraction (EBSD) detector (Oxford Instruments, Abingdon, UK). For TEM analysis, samples underwent sequential preparation: mechanical grinding (SiC papers; 800–4000 grit) to ~60 μm thickness, disc punching (3-mm diameter), and final thinning via controlled ion polishing (3–5 keV) to minimize artifacts. For the purpose of EBSD analysis, the samples were subjected to mechanical polishing and subsequently to argon ion beam polishing using an Ilion + II 697 system (Gatan, Pleasanton, CA, USA) at 5 kV for 30 min. EBSD scans on the RD-TD plane employed a 20 kV accelerating voltage, 15 mm working distance, and 0.5 μm step size.
2.3. Hardness Test and Uniaxial Tensile Test
Vickers hardness (HV0.5) measurements of the specimens were conducted with an HV-1000DT microhardness tester (Siomn, Shanghai, China). The indenter was then pressed against the material under test with a load of 500 g force, with a holding time of 15 s, and then the load was removed. A total of seven points were selected for testing on different specimen surfaces to obtain representative measurements. From the rolled plates, dog-bone-shaped tensile specimens were machined from the rolled plates via electric discharge machining (EDM) along the rolling direction (RD), with a gauge length of 10 mm, gauge width of 3 mm, and thickness of 0.2 mm. Uniaxial tensile tests at room temperature were conducted at a constant strain rate of 0.01 s per minute using an Instron 5967 universal testing machine (Instron, Norwood, MA, USA).
3. Results and Discussion
3.1. Microstructures
Figure 1 presents the X-ray diffraction (XRD) patterns of the FeCoNiCrTi0.2 high-entropy alloy in the as-rolled condition and after annealing at various temperatures. The results indicate that all specimens retain a single-phase face-centered cubic (FCC) structure, confirming the alloy’s excellent phase stability across the temperature range from 25 °C to 1000 °C. The primary diffraction peaks clearly correspond to the (111), (200), (220), (311), and (222) crystallographic planes of the FCC phase. Notably, a weak diffraction signal is observed near the (200) peak in the specimen annealed at 700 °C, which may be attributed to the minor precipitation of the σ phase [31]. The diffraction peak positions remain largely unchanged across the entire temperature range, suggesting that the small addition of Ti does not lead to significant phase decomposition or appreciable lattice parameter variations, thereby further supporting the thermal stability of the alloy.
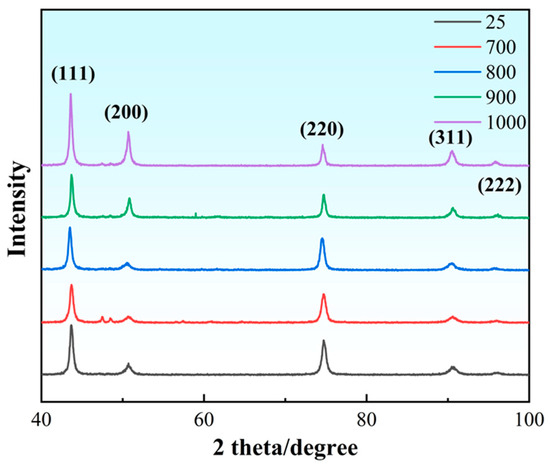
Figure 1.
XRD patterns of specimens after annealing at different temperatures.
Figure 2 presents inverse pole figure (IPF) maps of the FeCoNiCrTi0.2 alloy under as-rolled and annealed conditions at different temperatures. The as-rolled microstructure (Figure 2a) exhibits pronounced deformation features, characterized by grains substantially elongated parallel to the rolling direction, forming a coarse fibrous structure. As illustrated in Figure 2b, annealing at 700 °C initiates the nucleation of fine recrystallized grains at grain boundaries. However, deformation-induced microstructural features persist as the predominant feature in most regions. As the annealing temperature is increased, equiaxed subgrains undergo a process of nucleation and coarsening at grain boundaries [32]. This gradual replacement of deformed grains with strain-free equiaxed grains occurs as the annealing process progresses. Deformation bands in the as-rolled sample have been identified as preferential sites for recrystallization nucleation [33]. When the annealing temperature is increased to 1000 °C (Figure 2e), a refined microstructure consisting of abundant equiaxed grains and annealing twins is observed. The grain boundaries are distinctly defined, and the crystallographic orientations exhibit a high degree of randomness, indicating the complete eradication of the initial rolled microstructure.

Figure 2.
IPF maps of different temperatures annealed samples. (a) Cold-rolled sheet; (b) 700 °C; (c) 800 °C; (d) 900 °C; (e) 1000 °C.
Figure 3 illustrates the grain size distributions of the FeCoNiCrTi0.2 alloy after cold rolling and annealing at various temperatures. As shown in Figure 3a, the inhomogeneous deformation induced by cold rolling leads to a distinct bimodal grain size distribution in the metal, where coarse deformed grains (>150 μm), accounting for 34% of the population, dominate in the as-rolled condition. Recrystallization is a process that has been shown to progressively homogenize the grain size distribution. At a temperature of 1000 °C (Figure 3d), grains measuring less than 20 μm constitute 91% of the microstructure. The area-weighted average grain size is reduced to 10.26 μm, indicating substantial grain refinement that occurs during the annealing process.
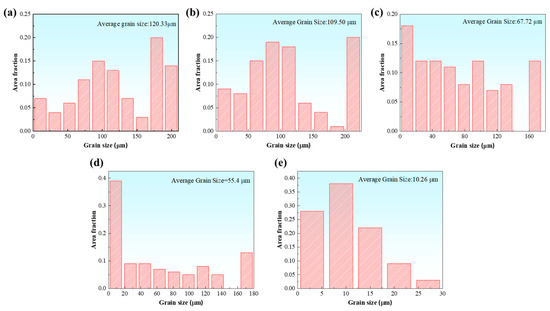
Figure 3.
Grain size distribution histograms of samples after annealing at different temperatures. (a) Cold rolled sheet; (b) 700 °C; (c) 800 °C; (d) 900 °C; (e) 1000 °C.
Figure 4 displays the Grain Boundary map (GB) of the cold-rolled FeCoNiCrTi0.2 alloy before and after being annealed at different temperatures. Grain boundary analysis (Figure 4a) indicates that low-angle grain boundaries (LAGBs, 2° < θ < 5°) are the most prevalent type in the as-rolled state, comprising 68% of all boundaries. The gradual replacement of low-angle grain boundaries (LAGBs) by high-angle grain boundaries (HAGBs) in annealed samples is widely recognized as a key characteristic of the recrystallization process [23]. Following annealing at 700 °C, the grain boundary composition remained highly similar to that of the as-rolled samples, suggesting that no substantial recrystallization had occurred at this temperature [34,35]. Upon increasing the annealing temperature to 900 °C, the proportion of high-angle grain boundaries rose to 77.9%, indicating a significant degree of recrystallization (Figure 4c–e). When the annealing temperature reached 1000 °C, HAGBs accounted for 72.1% of the total grain boundaries. Nevertheless, as shown in Figure 4e, a certain amount of low-angle grain boundaries remained, displaying a banded distribution aligned with the rolling direction. This phenomenon suggests that the recrystallization process was not yet fully completed at this stage.
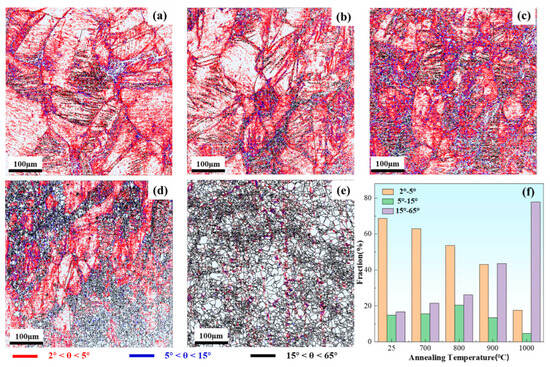
Figure 4.
Grain boundary diagrams of specimens after annealing at different temperatures. (a) Cold rolled sheet; (b) 700 °C; (c) 800 °C; (d) 900 °C; (e) 1000 °C; (f) The fraction of boundaries.
As illustrated in Figure 5, a comparison of the orientation distribution function (ODF) maps for cold-rolled samples before and after annealing is presented. The primary texture components include Brass ({110}<112>), Goss/Brass ({110}<001>), and S ({123}<634>). As shown in Figure 5a, the primary intensity peaks of the cold-rolled samples are situated in the vicinity of Goss/Brass, and the associated ODF section also reveals an enhancement of the S weave. The associated ODF section further demonstrates an augmentation of the S weave, which is congruent with the rolled weave of conventional low-layer dislocation-energy FCC metals such as TWIP steels [36,37]. As the annealing temperature increases from 700 °C to 1000 °C, major weaving components such as Brass- and Copper-type textures are partially retained after annealing. However, there is a concomitant decrease in their strength with increasing annealing temperature, and the orientation of the weave becomes more random. This evolution indicates that the recrystallized weave can be described as a weakly retained rolled weave [38]. As is the case with the majority of FCC metals, the samples present α-fiber textures (ND//<110>) that extend from Goss to Brass orientations [36], with annealing twins playing a crucial role in the stabilization of these components [39].
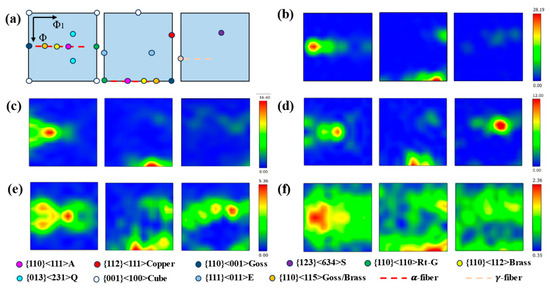
Figure 5.
ODF sections (with φ2 = 0°, 45°, 65°). (a) The main ideal orientations present in rolled fcc material; (b) cold rolled sheet; (c) 700 °C; (d) 800 °C; (e) 900 °C; (f) 1000 °C.
The kernel average misorientation (KAM) and twin boundary distribution maps are presented in Figure 6. A cross-reference of Figure 4 and Figure 6 indicates that regions characterized by a high density of low-angle grain boundaries (LAGBs) correspond to elevated KAM values, while lower KAM values suggest that recrystallization has occurred in these regions. These values reflect increased dislocation densities and localized microstrains at the grain boundaries. This observation lends further credence to the hypothesis that recrystallization occurs through dislocation cell nucleation, thereby providing the driving force for subsequent recrystallization [34,40]. As illustrated in Figure 6b, static recrystallization is observed to initiate preferentially at grain boundaries, where stress concentrations are known to be more pronounced. As annealing temperatures increase (Figure 6c–e), intra-grain misorientation significantly decreases, indicating strain relaxation [41]. Annealing has been shown to effectively facilitate recrystallization and strain relief (Figure 6e). However, residual banded high-strain zones along the rolling direction persist, thereby underscoring incomplete recrystallization.
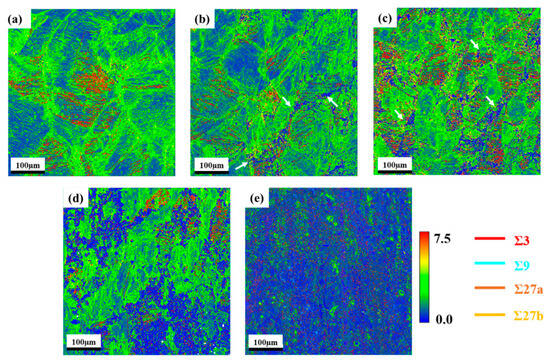
Figure 6.
Twin boundaries and KAM plots of specimens after annealing at different temperatures. (a) Cold rolled sheet; (b) 700 °C; (c) 800 °C; (d) 900 °C; (e) 1000 °C.
The dynamic evolution of twin boundaries during annealing plays a critical role in regulating recrystallization. Overall, the number of twin boundaries tends to increase with rising annealing temperature. As shown in Figure 6a, deformation twin regions are observed in the as-rolled sample, with Σ3 twin boundaries constituting 54.4% of the total boundaries (Table 1). This observation is commonly reported in metals with low stacking fault energy (SFE) [16]. Owing to their robust interfacial stability, Σ3 twin boundaries function as efficient obstacles to dislocation movement, rendering them key focuses for enhancing the strength–toughness balance in materials [42]. Figure 6b reveals that annealing at 700 °C results in a twin distribution similar to the as-rolled state, albeit with a reduced Σ3 fraction of 31.3%. Wang et al. [43,44] demonstrated that low-angle grain boundaries (LAGBs) undergo a progressive transformation into stable twin boundaries and low-energy grain boundaries at elevated annealing temperatures. For the sample annealed at 800 °C, annealing twins were observed to form within the recrystallized regions, while most deformation twins were retained as a result of incomplete recrystallization. As shown in Table 1, further increases in temperature led to a non-monotonic variation in the Σ3 boundary content—initially decreasing and subsequently increasing with the progression of recrystallization. In contrast, the fractions of Σ9 and Σ27a twins consistently increased [37]. The migration of grain boundaries promotes the nucleation of annealing twins (Σ3), while interactions between pre-existing and newly formed Σ3 boundaries result in the formation of Σ9 and Σ27 boundaries [45].

Table 1.
Type and number of twins in the specimen at different annealing temperatures.
Figure 7 shows the microstructure of the FeCoNiCrTi0.2 samples. As illustrated in Figure 7a,b, the presence of dense dislocation walls (DDWs) and dislocation cells (DCs) has been observed in both the cold-rolled state and the annealed samples at 700 °C [46]. These observations are in alignment with the characteristic sub-structural features typically associated with cold-deformed materials. For the samples that underwent annealing at 900 °C, a substantial decrease in dislocation density was observed. However, the presence of prominent dislocation walls (DDWs) remains evident in the images, and the dislocation entanglement networks and nano-twins persist in a localized manner (Figure 7d). As illustrated in Figure 7f, the grains exhibit annealed twins, which are indicative of the characteristic substructure associated with recrystallization [31,47]. As annealing temperature rises, dislocation density diminishes, whereas dislocation rearrangement leads to the gradual vanishing of dislocation cell boundaries.

Figure 7.
TEM images of samples annealed at different temperatures. (a) Cold-rolled sheet; (b) 700 °C; (c,d) 900 °C; (e,f) 1000 °C.
3.2. Mechanical Property
As shown in Figure 8, the hardness test results reveal a slight increase in hardness at temperatures below 700 °C compared to the as-rolled condition. This enhancement in hardness is likely attributed to the presence of residual dislocation tangles, substructures, and potential precipitation strengthening mechanisms [48,49]. As illustrated in Figure 1 and Figure 4, the sample annealed at 700 °C exhibited limited recrystallization along with the presence of precipitates, which collectively contribute to the observed increase in hardness. At this stage, the absence of significant recrystallization explains the lack of hardness reduction in the specimens. We use the content of high-angle grain boundaries as the criterion for determining whether recrystallization occurs and analyze it in conjunction with Figure 4. When the temperature exceeds 800 °C, a marked decrease in hardness is observed, with a clear linear inverse correlation between hardness and the degree of recrystallization. Despite the concurrent grain refinement resulting from recrystallization with increasing annealing temperature, the analysis indicates that the reduction in dislocation density plays a more dominant role in determining hardness evolution. This phenomenon can be attributed to the elimination of lattice distortions and internal stresses through the formation of recrystallized grains, which leads to substantial microstructural refinement [50]. It is noteworthy that even at a temperature of 1000 °C, the cold-rolled FeCoNiCrTi0.2 alloy exhibits incomplete recrystallization, a phenomenon that has been frequently observed in high-entropy alloys (HEAs) and is often associated with their sluggish diffusion kinetics [26].
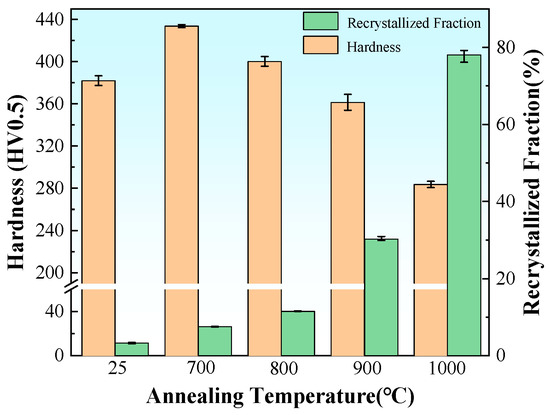
Figure 8.
Recrystallization fraction and hardness as a function of annealing temperature.
Figure 9 shows the tensile curves of FeCoNiCrTi0.2 under various annealing temperatures. As the annealing temperature rises, both yield strength (YS) and ultimate tensile strength (UTS) exhibit a declining trend. Following the annealing process at 1000 °C, a significant decline in YS and UTS was observed, reaching 513.57 MPa and 924.41 MPa, respectively. These values represent a substantial reduction of 55% and 20.6%, respectively, when compared to the initial as-rolled state. Concurrently, the elongation undergoes a substantial increase from 17.2% (as-rolled) to 69.8% (annealed at 1000 °C). As illustrated in Figure 9b, the yield ratio (YS/UTS) exhibits a decline from 0.994 (as-rolled) to 0.714 (950 °C) and further to 0.556 (1000 °C). The reduction can be attributed to the decrease in dislocation density and the subsequent microstructure homogenization induced by high-temperature annealing [51]. The inverse relationship between the yield ratio and elongation indicates that achieving optimal strength–ductility synergy can be accomplished by manipulating the post-rolling annealing conditions [52,53].
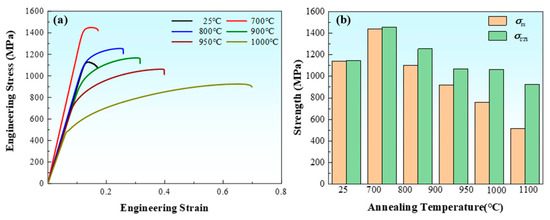
Figure 9.
(a) Engineering stress–strain curves of specimens annealed at different temperatures; (b) histograms of σ YS and σ UTS.
Figure 10 shows the strain-hardening curves of cold-rolled FeCoNiCrTi0.2 after annealing at various temperatures. For samples annealed at temperatures lower than 700 °C, the strain-hardening rate decreases rapidly with increasing strain. This behavior can be attributed to the high initial dislocation density resulting from the cold rolling process, which leads to rapid dislocation entanglement and saturation of their storage capacity. Conversely, for samples that have been subjected to annealing at temperatures above 800 °C, lower initial dislocation densities can facilitate the sustained multiplication of dislocations. The strain-hardening behavior exhibited by these materials can be categorized into three distinct stages: The first stage is characterized by a substantial decrease in the strain-hardening rate as true strain increases. The second stage is characterized by the attainment of a steady-state regime, wherein the processes of dislocation multiplication and annihilation attain dynamic equilibrium. This equilibrium is facilitated by substructures such as deformation twins, which enhance dislocation storage and mitigate the reduction in hardening rate. The third stage features a sharp decrease in hardening rate due to localized necking until reaching the tensile strength limit. For example, for the sample annealed at 1000 °C, the strain-hardening rate diminishes from approximately 7500 MPa at a strain of 0.058 to around 580 MPa at a strain of 0.51. Thus, an increase in annealing temperature correlates with a decrease in the strain-hardening rate for any given level of strain while simultaneously leading to an increased proportion within the second stage of strain hardening. This observation indicates an augmented hardening capacity of the material.
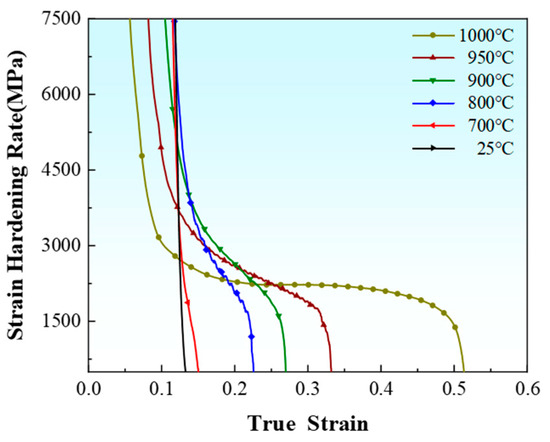
Figure 10.
Strain-hardening behavior of specimens annealed at different temperatures.
3.3. Flow Stress Size Effect Model
It has been demonstrated through microstructural and tensile analyses that the hindrance of dislocation motion is a pivotal factor in determining the flow stress of cold-rolled and annealed samples [54]. The relationship between flow stress (σf) and dislocation density (ρ) is articulated by the Taylor hardening model [55,56].
where M represents the Taylor factor, α is a material constant, G denotes the shear modulus, and b signifies the Burgers vector of dislocations. Studies have demonstrated that the dislocation mean free path (L) is significantly influenced by obstacles such as dislocation tangles and twins [23,57,58]. It can be described as the physical stopping of dislocations after a slip distance L. It can be shown that ρ0.5 is inversely proportional to L [35,59,60], and the relationship can be expressed as Equation (2).
In the present study, k1 is the scaling factor. This factor is related to the dislocation structure itself as well as the nano twinning of the HEA. Therefore, it can be posited that L can be expressed in equation form as indicated in Equation (3).
In the formula, Ld is the dislocation mean free path governed by the grain size; Ltw represents the characteristic spacing of average deformation twins and stacking faults, and its reduction will lead to a decrease in the dislocation mean free path L. iL is a constant that scales the contribution of average twin spacing to the effective boundary distance (taken as 0.14 by reference to the TWIP steel) [59]. In accordance with the geometric twin evolution theory [61], the characteristic size and volume fraction of twins can be expressed by Equation (4).
The formula presents the twin fraction (F) and average twin thickness (e) versus Ltw, with the parameter e set to 10 nm [23,62,63]. As shown in Equation (5), Olson and Cohen [23,63] developed a quantitative relationship between F and strain through the application of the shape-nucleus statistical model.
Here, ϕ represents the material constant, which is set to 0.155 [23,64]. The symbol εt denotes the initial twin strain, which is determined by the critical twinning stress. Steinmetz et al. developed a model of critical twinning stress based on the Mahajan-Chin three-layer twinning mechanism [65]. In this study, the critical twinning stress was set to 820 MPa, referencing the FeCoNiCr high-entropy alloy [66,67]. Tensile test results indicated that the true strains of the samples annealed at 950 °C and 1000 °C were 0.01 and 0.096, respectively. For samples that underwent annealing at temperatures below 950 °C, the yield stress exceeds 820 MPa, suggesting that εt can be considered negligible. According to the principles of dislocation dynamics theory, Kubin et al. [68] advanced a model for the evolution of the mean dislocation-free path. This model is predicated on the assumption that deformation twinning does not exert an effect on the deformation process, as delineated in Equation (6).
where Ly and Ls represent the characteristic lengths corresponding to the yield initiation and dynamic recovery saturation phases, respectively. The kinetic coefficient KL is a quantitative descriptor of the rearrangement rate of stored dislocations, which is positively correlated with lamination energy [69]. Therefore, the σf can be calculated by combining Equations (2)–(6):
Analysis of microstructure evolution reveals a strong positive correlation between the recrystallization volume fraction (Fa) of rolled plates and the annealing temperature (Figure 3). The unrecrystallized region is predominantly characterized by low-angle grain boundaries (LAGBs), where the stored energy level approaches the dynamic recovery threshold. Additionally, textural features indicate saturation of deformation energy storage. The limited ability of LAGBs to coordinate lattice distortion impedes the effective initiation and propagation of twin nucleation during subsequent plastic deformation [16]. Consequently, the recrystallization fraction (Fa) can be incorporated into the formula, thereby refining the synergistic strengthening mechanism of the recrystallization-deformation two-phase microstructure. In summary, the final constitutive model for FeCoNiCrTi0.2 cold-rolled sheet is expressed in equation form as follows:
The physically significant parameters in Equation (8) are listed in Table 2. The utilization of these parameters enables the calculation of additional parameters, thereby facilitating the determination of flow stress profiles for various annealed samples. The values of Fa can be obtained from Figure 7. The remaining parameters in the equation are closely tied to specific microstructures and plastic deformations. These parameters are determined iteratively via the quasi-Newton method (BFGS) and the generalized global optimization method.

Table 2.
Values of partial parameters.
Figure 11 presents a comparison between experimental and calculated flow stress values, with a high degree of consistency. Therefore, the model that incorporates the free range of motion of dislocations can provide a relatively accurate characterization of the tensile flow stresses in FeCoNiCrTi0.2 high-entropy alloys.
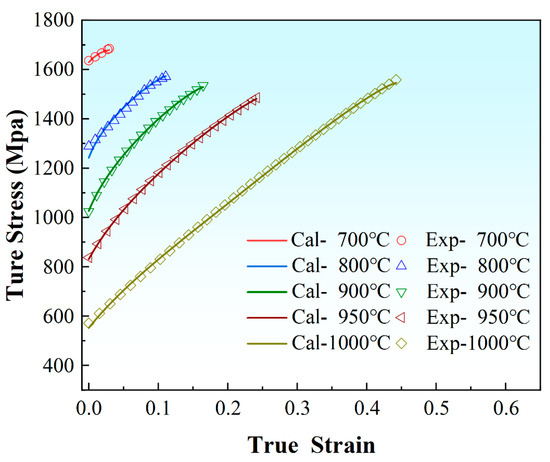
Figure 11.
Experimental and calculated true stress-true strain curves.
As illustrated in Figure 12a, with the increase in strain, the number of deformation twinning groups progressively rises, while the Lt value diminishes. For samples subjected to cold rolling and annealing at various temperatures, the trends observed for Lt and the number of deformation twinning groups are consistent; however, the initial strains of the curves for samples annealed at different temperatures vary. According to Equations (3) and (7), when plastic strain exceeds the εt value, L is found to be lower than Ld. This indicates that deformation twins contribute to a reduction in average free path due to obstructed dislocations. Figure 12b demonstrates that Ld decreases as strain increases, with samples annealed at lower temperatures being more susceptible to reaching Ls due to blocked dislocation effects, thereby exhibiting inferior plasticity.
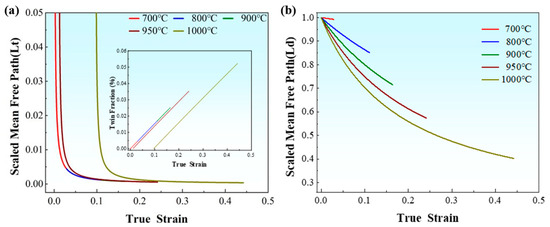
Figure 12.
Evolution of mean free path normalized to max value: (a) Lt; (b) Ld.
4. Conclusions
In this study, the microstructure, weave analysis, and evolution of mechanical properties of cold-rolled FeCoNiCrTi0.2 high-entropy alloys under varying annealing temperatures are systematically investigated. The key findings are summarized as follows:
- (1)
- Annealing above 800 °C induces significant recrystallization in FeCoNiCrTi0.2 HEAs. The degree of recrystallization increases with temperature, homogenizing grain size distribution and reducing the average grain size from 120.33 μm (as-rolled) to 10.26 μm (1000 °C).
- (2)
- The as-rolled texture is dominated by S, Brass, and Goss/Brass components. Annealing reduces texture intensity and enhances random orientations, although a weak residual texture persists. Recrystallization replaces LAGBs with HAGBs, while Σ3 and Σ9 annealing twins form in recrystallized regions.
- (3)
- Hardness and yield ratio decrease markedly with recrystallization, whereas ductility and strain-hardening capacity improve significantly. Optimal strength–ductility combinations can be achieved by tailoring annealing conditions.
- (4)
- A dislocation mean free path-based model, integrating twin boundary hindrance and recrystallization effects, accurately predicts tensile flow stress behavior. This model provides a theoretical framework for optimizing the processing routes and engineering applications of FeCoNiCrTi0.2 HEA.
Author Contributions
Conceptualization, G.C. and Q.Z.; Methodology, P.Z. and D.L.; Software, J.Z. and Y.S.; Validation, L.Z. and K.L.; Formal analysis, L.Z. and K.L.; Data curation, J.Z. and Y.S.; Writing—original draft, P.Z. and D.L.; Writing—review & editing, G.C. and Q.Z.; Visualization, J.Z. and Y.S.; Funding acquisition, P.Z. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China (Grant No. 52205347, 52175306), the Shandong Province Key Research and Development Plan, China (Grant No. 2024CXGC010803, 2024TSGC0673), and the Science and Technology Support Plan for Youth Innovation of Colleges and Universities of Shandong Province of China (Grant No. 2024KJH022).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Author Qiang Zhu was employed by Weihai Tianhang Information Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloy. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Tsai, K.Y.; Tsai, M.H.; Yeh, J.W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater. 2013, 61, 4887. [Google Scholar] [CrossRef]
- Lu, Y.P.; Dong, Y.; Jiang, H.; Wang, Z.J.; Cao, Z.Q.; Guo, S.; Wang, T.M.; Li, T.G.; Liaw, P.K. Promising properties and future trend of eutectic high entropy alloys. Scr. Mater. 2020, 187, 202–209. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Akhlaghi, P.; Amirjan, M.; Parvin, N. The effect of processing parameters and heat-treatment on the microstructure and mechanical properties of PM CoCrFeMnNiTi0.1 high-entropy alloy. Mater. Chem. Phys. 2021, 257, 123722. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhou, J.H.; Liu, Y.F.; Lu, C.Y.; Shi, L.; Zheng, W.J.; Jin, W.Y.; Gao, Z.L.; Yang, J.G.; He, Y.M. Microstructural evolution and mechanical characterization for the AlCoCrFeNi2.1 eutectic high-entropy alloy under different temperatures. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1881–1892. [Google Scholar] [CrossRef]
- Stepanov, N.; Tikhonovsky, M.; Yurchenko, N.; Zyabkin, D.; Klimova, M.; Zherebtsov, S.; Efimov, A.; Salishchev, G. Effect of cryo-deformation on structure and properties of CoCrFeNiMn high-entropy alloy. Intermetallics 2015, 59, 8. [Google Scholar] [CrossRef]
- Gao, N.; Lu, D.H.; Zhao, Y.Y.; Liu, X.W.; Liu, G.H.; Wu, Y.; Liu, G.; Fan, Z.T.; Lu, Z.P.; George, E.P. Strengthening of a CrMnFeCoNi High-Entropy Alloy by Carbide Precipitation. J. Alloys Compd. 2019, 792, 1028–1035. [Google Scholar] [CrossRef]
- Wang, Z.W.; Baker, I.; Cai, Z.H.; Chen, S.; Poplawsky, J.D.; Guo, W. The Effect of Interstitial Carbon on the Mechanical Properties and Dislocation Substructure Evolution in Fe40.4Ni11.3Mn34.8Al7.5Cr6 High Entropy Alloys. Acta Mater. 2016, 120, 228–239. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhý, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61, 5743. [Google Scholar] [CrossRef]
- Shabani, A.; Toroghinejad, M.R.; Aminaei, M. Effect of prior cold deformation on recrystallization behavior of a multi-phase FeCrCuMnNi high entropy alloy. Mater. Chem. Phys. 2021, 272, 124991. [Google Scholar] [CrossRef]
- Li, R.; Song, X.L.; Duan, Z.X.; Hao, Z.K.; Yang, Y.; Han, Y.; Ran, X.; Liu, Y. Improving the high-temperature ductility of γ-TiAl matrix composites by incorporation of AlCoCrFeNi high entropy alloy particles. J. Alloys Compd. 2025, 1012, 178515. [Google Scholar] [CrossRef]
- Schmidt, S.; Sathiaraj, G.D.; Kumar, S.S.; Sulkowski, B.; Suwas, S.; Jaschinski, J.; Gu, A.B.; Skrotzki, W. Effect of rolling and annealing temperature on the mechanical properties of CrMnFeCoNi high-entropy alloy. Mater. Chem. Phys. 2021, 270, 124830. [Google Scholar] [CrossRef]
- Pérez, P.; Medina, J.; Vega, M.F.; Garcés, G.; Adeva, P. Control of the microstructure in a Al5Co15Cr30Fe25Ni25 high entropy alloy through thermo-mechanical and thermal treatments. Metals 2023, 13, 180. [Google Scholar] [CrossRef]
- Haase, C.; Barrales-Mora, L.A. Influence of deformation and annealing twinning on the microstructure and texture evolution of face-centered cubic high-entropy alloys. Acta Mater. 2018, 150, 88–103. [Google Scholar] [CrossRef]
- Saha, J.; Ummethala, G.; Malladi, S.R.K.; Bhattacharjee, P.P. Severe warm-rolling mediated microstructure and texture of equiatomic CoCrFeMnNi high entropy alloy: A comparison with cold-rolling. Intermetallics 2021, 129, 107029. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, Z.C.; Zhao, H.W.; Ren, L.Q. Refinement strengthening, second phase strengthening and spinodal microstructure-induced strength-ductility trade-off in a high-entropy alloy. Mater. Sci. Eng. A 2022, 847, 143343. [Google Scholar] [CrossRef]
- Hou, J.X.; Qiao, J.W.; Lian, J.H.; Liaw, P.K. Revealing the relationship between microstructures, textures, and mechanical behaviors of cold-rolled Al0.1CoCrFeNi high-entropy alloys. Mater. Sci. Eng. A 2021, 804, 140752. [Google Scholar] [CrossRef]
- Bhattacharjee, P.P.; Sathiaraj, G.D.; Zaid, M.; Gatti, J.R.; Lee, C.; Tsai, C.W.; Yeh, J.W. Microstructure and texture evolution during annealing of equiatomic CoCrFeMnNi high-entropy alloy. J. Alloys Compd. 2014, 587, 544–552. [Google Scholar] [CrossRef]
- Tsai, C.W.; Tsai, M.H.; Tsai, K.Y.; Chang, S.Y.; Yeh, J.W.; Yeh, A.C. Microstructure and tensile properties of Al0.5CoCrCuFeNi alloys produced by simple rolling and annealing. Mater. Sci. Technol. 2015, 31, 1178–1183. [Google Scholar] [CrossRef]
- Liang, X.P.; Kang, L.; Li, H.Z.; Wang, R.X.; Wu, Q.B.; Liu, B. Effect of annealing temperature on anisotropy of mechanical properties in powder metallurgy FeCoCrNiN0.07 high-entropy alloy sheets. Mater. Sci. Eng. A 2021, 823, 141585. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, Q.; Chen, S.R.; Yao, S.J.; Wang, H.; Zhao, L.; Zhang, P.; Wang, C.J. Influence of heat treatment on the texture, microstructure and tensile deformation behaviours of cold rolled FeCoNiCr sheets. Mater. Sci. Eng. A 2022, 848, 143412. [Google Scholar] [CrossRef]
- Lozinko, A.; Gholizadeh, R.; Zhang, Y.; Klement, U.; Tsuji, N.; Mishin, O.V.; Guo, S. Evolution of microstructure and mechanical properties during annealing of heavily rolled AlCoCrFeNi2.1 eutectic high-entropy alloy. Mater. Sci. Eng. A 2022, 833, 142558. [Google Scholar] [CrossRef]
- Sousa, G.H.; Zepon, G.; Mazzer, E.M. Microstructure evolution and strengthening by cold rolling of CrMnFeCoNi high-entropy alloy processed by spray forming. Mater. Sci. Eng. A 2020, 793, 139814. [Google Scholar] [CrossRef]
- Guo, T.; Li, J.S.; Wang, J.; Wang, W.Y.; Liu, Y.; Luo, X.M.; Kou, H.C.; Beaugnon, E. Microstructure and properties of bulk Al0.5CoCrFeNi high-entropy alloy by cold rolling and subsequent annealing. Mater. Sci. Eng. A 2018, 729, 141–148. [Google Scholar] [CrossRef]
- Hua, L.; Du, Y.C.; Qian, D.S.; Sun, M.L.; Wang, F. Influence of Prior Cold Rolling on Bainite Transformation of High Carbon Bearing Steel. Metall. Mater. Trans. A 2025, 56, 640–654. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, D.; Han, B.; Wang, J.; Feng, R.; Yang, T.; Zhao, C.; Zhao, Y.L.; Guo, W.; Shimizu, Y.; et al. Outstanding tensile properties of a precipitation-strengthened FeCoNiCrTi0.2 high-entropy alloy at room and cryogenic temperatures. Acta Mater. 2019, 165, 228–240. [Google Scholar] [CrossRef]
- Cui, P.; Ma, Y.M.; Zhang, L.J.; Zhang, M.D.; Fan, J.T.; Dong, W.Q.; Yu, P.F.; Li, G.; Liu, R.P. Effect of Ti on microstructures and mechanical properties of high entropy alloys based on CoFeMnNi system. Mater. Sci. Eng. A 2018, 737, 198–204. [Google Scholar] [CrossRef]
- Lv, Y.; Song, P.; Wang, Y.; Zhao, X.; Gao, W.; Zhang, J.; Lei, Y.; Chen, J. Improving Mechanical Properties of Fe-Mn-Co-Cr High-Entropy Alloy via Annealing After Cold Rolling. Materials 2024, 17, 676. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.Y.; Sun, Y.G.; Yu, H.P.; Huang, Y.J.; Su, S.; Ning, Z.L.; Cheng, Z.J.; Fu, W.J.; Sun, J.F.; Liaw, P.K. Microstructure evolution and mechanical behavior of a CoCrFeNiMn0.75Cu0.25 high-entropy alloy by thermo-mechanical treatment. Mater. Sci. Eng. A 2022, 860, 144274. [Google Scholar] [CrossRef]
- Reddy, S.R.; Ahmed, M.Z.; Sathiaraj, G.D.; Bhattacharjee, P.P. Effect of strain path on microstructure and texture formation in cold-rolled and annealed FCC equiatomic CoCrFeMnNi high entropy alloy. Intermetallics 2017, 87, 94–103. [Google Scholar] [CrossRef]
- Yin, F.X.; Sakurai, A.; Son, X.Y. Determination of spatial grain size with the area-weighted grain area distribution of the planar sections in polycrystalline materials. Metall. Mater. Trans. A 2006, 37, 3707–3714. [Google Scholar] [CrossRef]
- Elkatatny, S.; Gepreel, M.A.H.; Hamada, A.; Nakamura, K.; Yamanaka, K.; Chiba, A. Effect of Al content and cold rolling on the microstructure and mechanical properties of Al5Cr12Fe35Mn28Ni20 high-entropy alloy. Mater. Sci. Eng. A 2019, 759, 380–390. [Google Scholar] [CrossRef]
- Guo, B.Q.; Ray, R.K.; Yoshida, S.; Bai, Y.; Tsuji, N. In-situ observations of static recrystallization and texture formation in a cold-rolled CoCrFeMnNi high entropy alloy. Scr. Mater. 2022, 215, 114706. [Google Scholar] [CrossRef]
- Sathiaraj, G.D.; Bhattacharjee, P.P. Effect of cold-rolling strain on the evolution of annealing texture of equiatomic CoCrFeMnNi high entropy alloy. Mater. Charact. 2015, 109, 189–197. [Google Scholar] [CrossRef]
- Bracke, L.; Verbeken, K.; Kestens, L.; Penning, J. Microstructure and texture evolution during cold rolling and annealing of a high Mn TWIP steel. Acta Mater. 2009, 57, 1512–1524. [Google Scholar] [CrossRef]
- Liu, H.X.; He, Y.X.; Li, M.Y.; Wu, Y.H.; Li, S.L.; Liu, X.D.; Zhi, H.H.; Wang, H.F. Promoting strength-ductility synergy through sequential martensitic transformation in a hierarchical heterostructured eutectic high-entropy alloy. Int. J. Plast. 2025, 190, 104374. [Google Scholar] [CrossRef]
- Klimova, M.; Zherebtsov, S.; Stepanov, N.; Salishchev, G.; Haase, C.; Molodov, D.A. Microstructure and texture evolution of a high manganese TWIP steel during cryo-rolling. Mater. Charact. 2017, 132, 20–30. [Google Scholar] [CrossRef]
- Zhou, P.; Liang, Z.Y.; Liu, R.D.; Huang, M.X. Evolution of dislocations and twins in a strong and ductile nanotwinned steel. Acta Mater. 2016, 111, 96–107. [Google Scholar] [CrossRef]
- Jones, A.R.; Ralph, B.; Hansen, N. Subgrain coalescence and the nucleation of recrystallization at grain boundaries in aluminium. Proc. R. Soc. A Math. Phys. Sci. 1997, 368, 345–357. [Google Scholar]
- Zhang, X.X.; Lv, Y.; Hashimoto, T.; Nilsson, J.O.; Zhou, X.R. Intergranular corrosion of AA6082 Al–Mg–Si alloy extrusion: The influence of trace Cu and grain boundary misorientation. J. Alloys Compd. 2020, 853, 157288. [Google Scholar] [CrossRef]
- Wang, H.; Chen, X.H.; Zhou, H.L.; Jiang, Y.; Liu, P. Static recrystallized annealing treatment-induced strength-ductility trade-off in cold-rolled Co36Fe36Cr18Ni10 multi-principal alloy. Mater. Charact. 2021, 179, 111254. [Google Scholar] [CrossRef]
- Bay, B.; Hansen, N.; Hughes, D.A.; Wilsdorf, D.K. Overview No-96—Evolution of fcc deformation structures in polyslip. Acta Mater. 1992, 40, 205–219. [Google Scholar] [CrossRef]
- Li, C.Y.; Lu, Y.; Li, X.L.; Zhao, Z.X.; Kou, S.Z. Microstructures and properties of Fe1.25CoNi1.25CrxAl0.25 high-entropy alloys after cold-rolling and annealing. J. Non-Cryst. Solids 2021, 570, 121023. [Google Scholar] [CrossRef]
- Mehranpour, M.S.; Shahmir, H.; Nili-ahmadabadi, M. Microstructure and excess free volume of severely cold shape rolled CoCrFeNiMn high entropy alloy. J. Alloys Compd. 2020, 840, 155672. [Google Scholar] [CrossRef]
- Fullman, R.L.; Fisher, J.C. Formation of annealing twins during grain growth. Trans. AIME 1951, 22, 1350–1355. [Google Scholar] [CrossRef]
- Gu, J.; Ni, S.; Liu, Y.; Song, M. Regulating the strength and ductility of a cold rolled FeCrCoMnNi high-entropy alloy via annealing treatment. Mater. Sci. Eng. A 2019, 755, 289–294. [Google Scholar] [CrossRef]
- Gu, J.; Song, M.; Ni, S.; Guo, S.F.; He, Y.H. Effects of annealing on the hardness and elastic modulus of a Cu36Zr48Al8Ag8 bulk metallic glass. Mater. Des. 2013, 47, 706–710. [Google Scholar] [CrossRef]
- Zhou, J.; Liao, H.C.; Chen, H.; Huang, A.J. Effects Of Hot-Forging and Subsequent Annealing on Microstructure and Mechanical Behaviors of Fe35Ni35Cr20Mn10 High-Entropy Alloy. Mater. Charact. 2021, 178, 111251. [Google Scholar] [CrossRef]
- Joo, S.H.; Kato, H.; Jang, M.J.; Moon, J.; Tsai, C.W.; Yeh, J.W.; Kim, H.S. Tensile deformation behavior and deformation twinning of an equimolar CoCrFeMnNi high-entropy alloy. Mater. Sci. Eng. A 2017, 689, 122–133. [Google Scholar] [CrossRef]
- Slone, C.E.; Miao, J.; George, E.P.; Mills, M.J. Achieving ultra-high strength and ductility in equiatomic CrCoNi with partially recrystallized microstructures. Acta Mater. 2019, 165, 496–507. [Google Scholar] [CrossRef]
- Sunkari, U.; Reddy, S.R.; Rathod, B.D.S.; Satheesh Kumar, S.S.; Saha, R.; Chatterjee, S.; Bhattacharjee, P.P. Heterogeneous precipitation mediated heterogeneous nanostructure enhances strength-ductility synergy in severely cryo-rolled and annealed CoCrFeNi2.1Nb0.2 high entropy alloy. Sci. Rep. 2020, 10, 6056. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.H.; Xu, X.; Dye, D.; Rivera-Díaz-del-Castillo, P.E.J. Microstructural evolution and strain-hardening in TWIP Ti alloys. Acta Mater. 2020, 183, 155–164. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- Barlat, F.; Glazov, M.V.; Brema, J.C.; Lege, D.J. A simple model for dislocation behavior, strain and strain rate hardening evolution in deforming aluminum alloys. Int. J. Plast. 2002, 18, 919–939. [Google Scholar] [CrossRef]
- Staker, M.R.; Holt, D.L. The dislocation cell size and dislocation density in copper deformed at temperatures between 25 and 700 °C. Acta Metall. Sin. 1972, 20, 569–579. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Liang, Z.Y.; Wang, X.; Huang, W.; Huang, M.X. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel. Acta Mater. 2015, 88, 170–179. [Google Scholar] [CrossRef]
- He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef]
- Bouaziz, O.; Guelton, N. Modelling of TWIP effect on work-hardening. Mater. Sci. Eng. A 2001, 319–321, 246–249. [Google Scholar] [CrossRef]
- Kang, J.H.; Ingendahl, T.; Bleck, W. A constitutive model for the tensile behaviour of TWIP steels: Composition and temperature dependencies. Mater. Des. 2016, 90, 340–349. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. Kinetics of strain-induced martensitic nucleation. Metall. Mater. Trans. A 1975, 6, 791–795. [Google Scholar] [CrossRef]
- Zhang, T.W.; Ma, S.G.; Zhao, D.; Wu, Y.C.; Zhang, Y.; Wang, Z.H.; Qiao, J.W. Simultaneous enhancement of strength and ductility in a NiCoCrFe high-entropy alloy upon dynamic tension: Micromechanism and constitutive modeling. Int. J. Plast. 2020, 124, 226–246. [Google Scholar] [CrossRef]
- Steinmetz, D.R.; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed–Akbari, A.; Hickel, T.; Roters, F.; Raabe, D. Revealing the strain-hardening behavior of twinning-induced plasticity steels: Theory, simulations, experiments. Acta Mater. 2013, 61, 494–510. [Google Scholar] [CrossRef]
- Huang, H.; Li, X.Q.; Dong, Z.H.; Li, W.; Huang, S.; Meng, D.Q.; Lai, X.C.; Liu, T.W. Critical stress for twinning nucleation in CrCoNi-based medium and high entropy alloys. Acta Mater. 2018, 149, 388–396. [Google Scholar] [CrossRef]
- Meyers, M.A.; Vöhringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025. [Google Scholar] [CrossRef]
- Kubin, L.P.; Estrin, Y. Evolution of dislocation densities and the critical conditions for the Portevin-Le Châtelier effect. Acta Metall. Mater. 1990, 38, 697–708. [Google Scholar] [CrossRef]
- Wang, C.J.; Xue, S.X.; Chen, G.; Zhang, P. Constitutive model based on dislocation density and ductile fracture of Monel 400 thin sheet under tension. Met. Mater. Int. 2017, 23, 264–271. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).