AI Design for High Entropy Alloys: Progress, Challenges and Future Prospects
Abstract
1. Introduction
1.1. High Entropy Alloys
1.2. The Thermodynamic-Dynamic Controversy
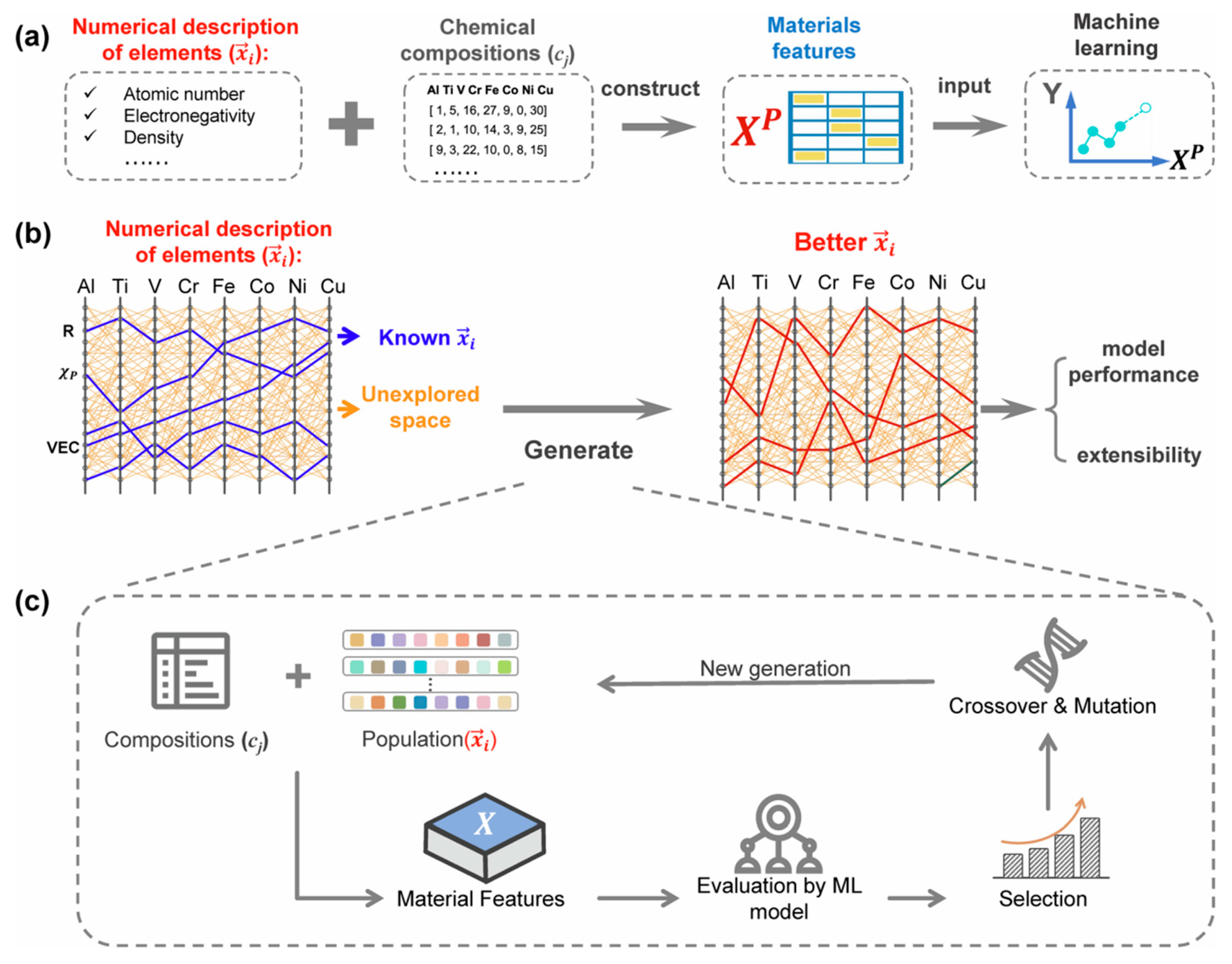
1.3. Material Design
2. AI Technology in HEA Design
2.1. Algorithm Principle and Applicability Analysis
2.1.1. Random Forest and Gradient Boosting—Algorithmic “Multi-Burn-In”
2.1.2. Deep Neural Network—“Diffusion Channel” Perspective
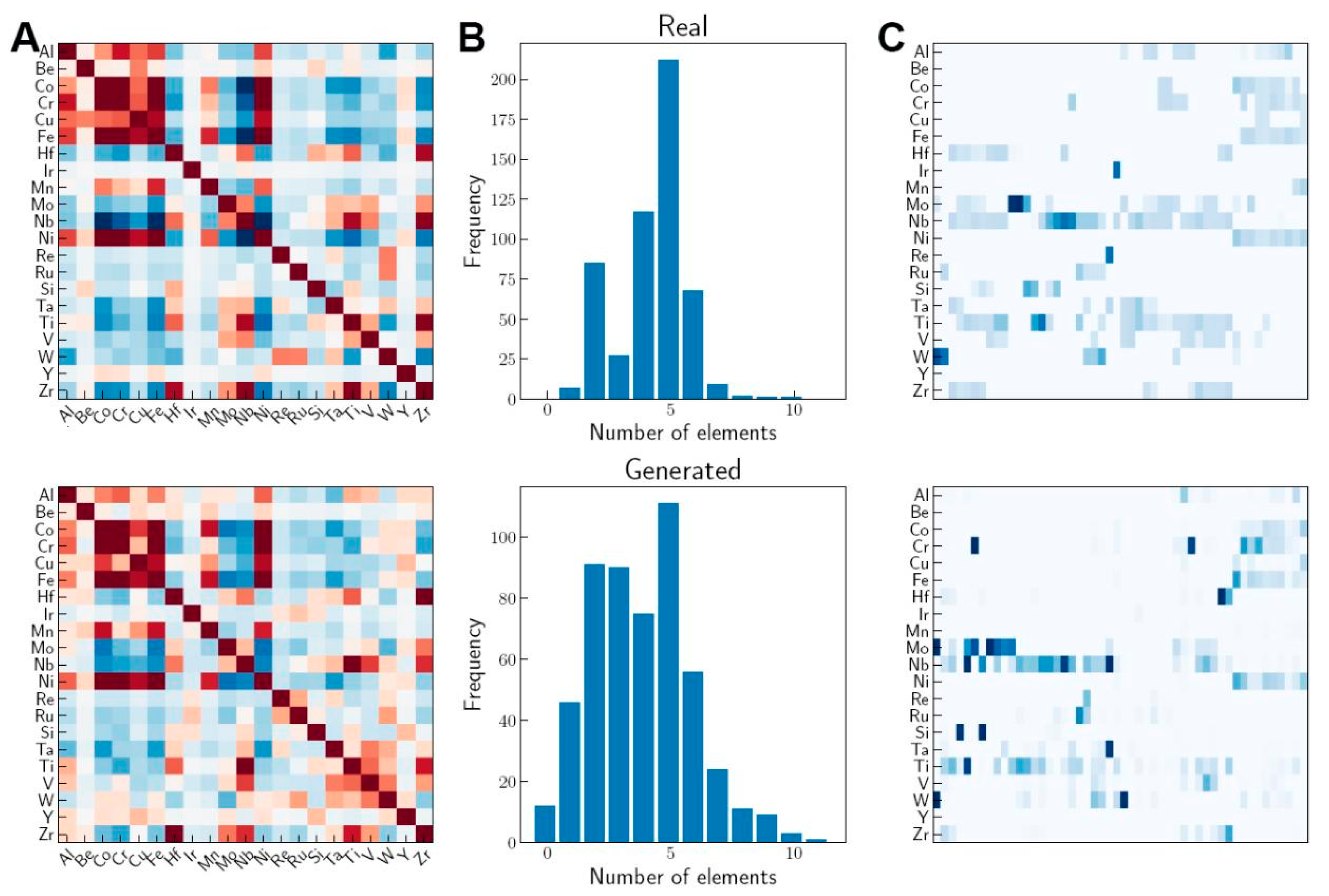
2.1.3. Conditions Generate Adversarial Networks—“Reverse Design Casting”
2.1.4. Active Learning—“Sampling Strategy”
2.1.5. Transfer Learning—“Experience Transfer”
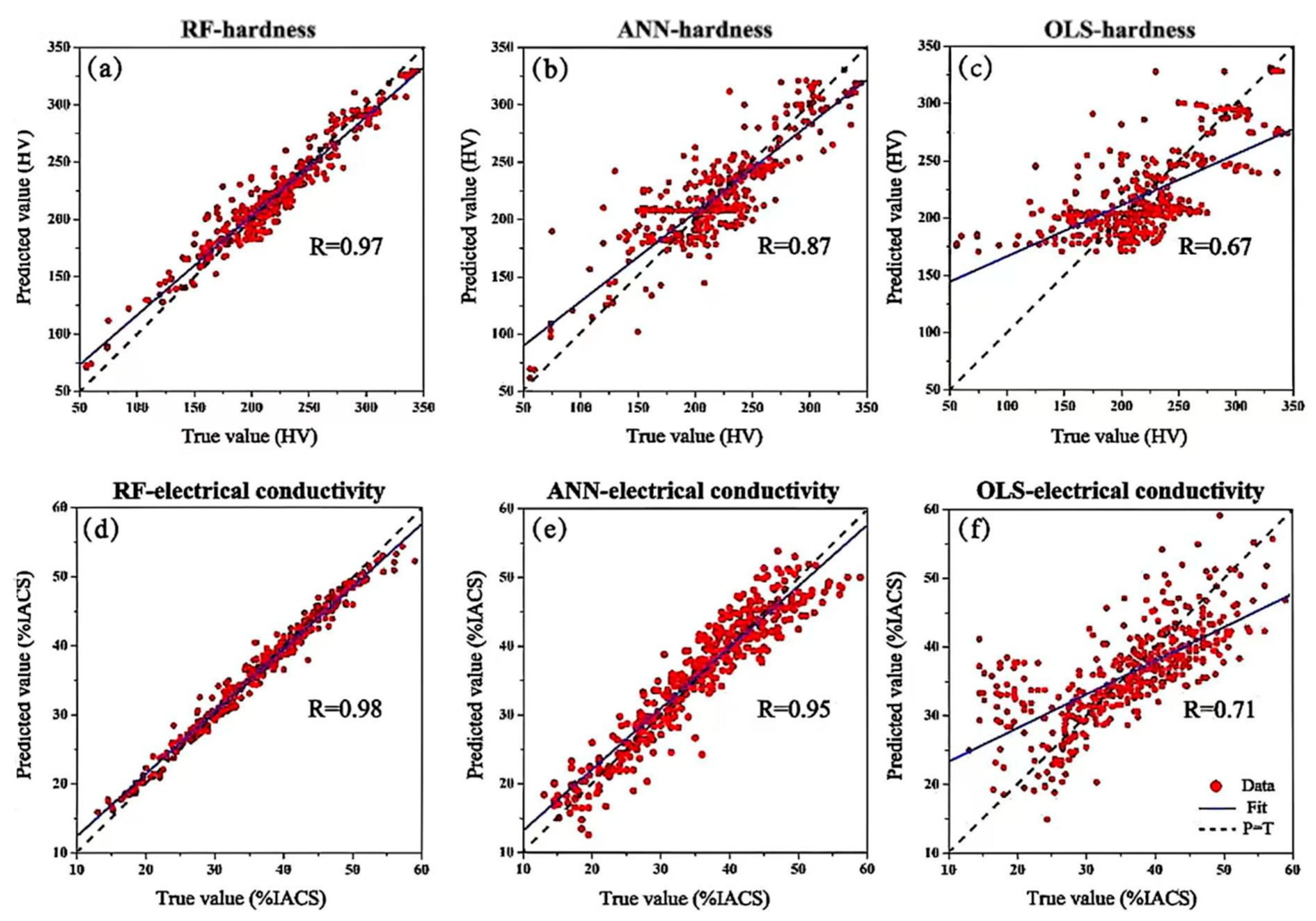
2.2. Machine Learning Model
2.3. Data Processing and Analysis
2.4. Performance Prediction
2.5. Limitations of DFT and MD in HEA Modeling
2.5.1. Calculate the Expansion Law of Cost with the Number of Master Elements
2.5.2. The Accuracy of Phase Stability Prediction
3. Application Cases of AI in HEA Design
3.1. Component Design
3.1.1. Application of the Generation Model in Refractory HEA Design
3.1.2. Design of Multi-Objective Optimization Framework for Refractory HEAs
3.1.3. Comparison and Discussion
3.2. Phase Structure Prediction
3.2.1. Classification and Prediction of HEA Phase Composition by Deep Learning Algorithm
3.2.2. Combination of Conditional Generation Adversarial Network and Active Learning
3.2.3. Element Feature Transfer Adversarial Network
3.2.4. Comparison and Discussion
3.2.5. The Gap Between Machine Learning Predictions and Real Synthetic Dynamics
3.3. Performance Optimization
3.3.1. Synergistic Optimization of High Temperature Strength and Room Temperature Toughness of HEAs
3.3.2. Hardness Optimization of Al-Co-Cr-Cu-Fe-Ni HEAs
3.3.3. Comparison and Discussion
3.4. Material Screening and Discovery
3.4.1. Cu-Ni-Co-Si HEA System
3.4.2. Low Thermal Expansion Coefficient HEA
3.4.3. Nb-Ta-Zr-Hf-Mo Refractory HEA System
3.4.4. Single-Phase Refractory HEA
3.4.5. Comparison and Discussion
3.4.6. Limitations and Mitigation Strategies of Combinatorial Synthesis
4. Challenges of AI Technology in HEA Design
4.1. Data Related Issues
4.1.1. Scarcity of High-Quality Data
4.1.2. Data Skew and Lack of Representativeness
4.1.3. Negative-Sample Deficit
4.2. Insufficient Model Interpretation
4.3. Cross-Domain Transferability
4.4. Extrapolation Risk When Far from the Training Distribution
4.5. Interdisciplinary Integration Issues
4.6. Typical Case: “Predictive-Synthetic” Bias
4.6.1. Problem Causes
4.6.2. Solutions
- (1)
- Introduction of Dynamic Descriptors
- (2)
- Negative Sample Augmentation and Active Learning Closed-loop
- (3)
- Cross-scale verification—Digital twin
5. Future Development Direction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yeh, J.-W. Overview of high-entropy alloys. In High-Entropy Alloys: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–19. [Google Scholar]
- Wang, X.; Liu, Q.; Wang, X. High-Entropy Materials: From Bulk to Sub-nano. Adv. Funct. Mater. 2025, 35, 2504275. [Google Scholar] [CrossRef]
- Schweidler, S.; Botros, M.; Strauss, F.; Wang, Q.; Ma, Y.; Velasco, L.; Cadilha Marques, G.; Sarkar, A.; Kübel, C.; Hahn, H. High-entropy materials for energy and electronic applications. Nat. Rev. Mater. 2024, 9, 266–281. [Google Scholar] [CrossRef]
- Sun, J.; Liu, W.; Liang, F.; Liu, R.; Yao, Y.; Zou, Q.; Dong, P.; Wang, S. Insight Into High Entropy Compounds: Advances, Challenges and Energy Applications. Adv. Funct. Mater. 2025, e10855. [Google Scholar] [CrossRef]
- Ren, J.-T.; Chen, L.; Wang, H.-Y.; Yuan, Z.-Y. High-entropy alloys in electrocatalysis: From fundamentals to applications. Chem. Soc. Rev. 2023, 52, 8319–8373. [Google Scholar] [CrossRef]
- Ren, J.; Kumkale, V.Y.; Hou, H.; Kadam, V.S.; Jagtap, C.V.; Lokhande, P.E.; Pathan, H.M.; Pereira, A.; Lei, H.; Liu, T.X. A review of high-entropy materials with their unique applications. Adv. Compos. Hybrid Mater. 2025, 8, 195. [Google Scholar] [CrossRef] [PubMed]
- Li, L.Y.; Zhang, M.; Jiang, M.; Gao, L.H.; Ma, Z.; Cao, M.S. High entropy ceramics for electromagnetic functional materials. Adv. Funct. Mater. 2025, 35, 2416673. [Google Scholar] [CrossRef]
- Gu, X.; Guo, X.-B.; Li, W.-H.; Jiang, Y.-P.; Liu, Q.-X.; Tang, X.-G. High-entropy materials for application: Electricity, magnetism, and optics. ACS Appl. Mater. Interfaces 2024, 16, 53372–53392. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.; Pu, G.; Xue, Y.; Zhang, K.; Huang, Y. High-entropy materials: Controllable synthesis, deep characterization, electrochemical energy application, and outlook. Energy Fuels 2022, 37, 36–57. [Google Scholar] [CrossRef]
- Odetola, P.I.; Babalola, B.J.; Afolabi, A.E.; Anamu, U.S.; Olorundaisi, E.; Umba, M.C.; Phahlane, T.; Ayodele, O.O.; Olubambi, P.A. Exploring high entropy alloys: A review on thermodynamic design and computational modeling strategies for advanced materials applications. Heliyon 2024, 10, e39660. [Google Scholar] [CrossRef]
- Miao, L.; Sivak, J.T.; Kotsonis, G.; Ciston, J.; Ophus, C.L.; Dabo, I.; Maria, J.P.; Sinnott, S.B.; Alem, N. Chemical Environment and Structural Variations in High Entropy Oxide Thin Film Probed with Electron Microscopy. ACS Nano 2024, 18, 14968–14977. [Google Scholar] [CrossRef]
- Sharma, P.; Gandhi, P.M.; Chintersingh, K.L.; Schoenitz, M.; Dreizin, E.L.; Liou, S.C.; Balasubramanian, G. Accelerated intermetallic phase amorphization in a Mg-based high-entropy alloy powder. J. Magnes. Alloys 2024, 12, 1792–1798. [Google Scholar] [CrossRef]
- Wang, H.; He, Q.-F.; Yang, Y. High-entropy intermetallics: From alloy design to structural and functional properties. Rare Met. 2022, 41, 1989–2001. [Google Scholar] [CrossRef]
- Marques, F.; Balcerzak, M.; Winkelmann, F.; Zepon, G.; Felderhoff, M. Review and outlook on high-entropy alloys for hydrogen storage. Energy Environ. Sci. 2021, 14, 5191–5227. [Google Scholar] [CrossRef]
- Karpov, S. Application of high-entropy alloys in hydrogen storage technology. Probl. At. Sci. Technol. 2024, 2, 48–61. [Google Scholar] [CrossRef]
- Davies, D.W.; Butler, K.T.; Jackson, A.J.; Morris, A.; Frost, J.M.; Skelton, J.M.; Walsh, A. Computational screening of all stoichiometric inorganic materials. Chem 2016, 1, 617–627. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Li, J.; Yang, L.; Mo, P.; Wu, Y. Preparation of high-entropy nitride ceramics (TiVCrNbZr1-x) Ny by introducing nitrogen vacancies. J. Asian Ceram. Soc. 2024, 12, 249–256. [Google Scholar] [CrossRef]
- Aruchamy, K.; Balasankar, A.; Ramasundaram, S.; Oh, T.H. Recent design and synthesis strategies for high-performance supercapacitors utilizing ZnCo2O4-based electrode materials. Energies 2023, 16, 5604. [Google Scholar] [CrossRef]
- Kuehmann, C.; Olson, G. Computational materials design and engineering. Mater. Sci. Technol. 2009, 25, 472–478. [Google Scholar] [CrossRef]
- Pyzer-Knapp, E.O.; Pitera, J.W.; Staar, P.W.; Takeda, S.; Laino, T.; Sanders, D.P.; Sexton, J.; Smith, J.R.; Curioni, A. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. npj Comput. Mater. 2022, 8, 84. [Google Scholar] [CrossRef]
- Panchal, J.H.; Kalidindi, S.R.; McDowell, D.L. Key computational modeling issues in integrated computational materials engineering. Comput.-Aided Des. 2013, 45, 4–25. [Google Scholar] [CrossRef]
- Chen, H.-L.; Mao, H.; Chen, Q. Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 2018, 210, 279–290. [Google Scholar] [CrossRef]
- Schmid-Fetzer, R.; Andersson, D.; Chevalier, P.-Y.; Eleno, L.; Fabrichnaya, O.; Kattner, U.; Sundman, B.; Wang, C.; Watson, A.; Zabdyr, L. Assessment techniques, database design and software facilities for thermodynamics and diffusion. Calphad 2007, 31, 38–52. [Google Scholar] [CrossRef]
- Chang, Y.A.; Chen, S.; Zhang, F.; Yan, X.; Xie, F.; Schmid-Fetzer, R.; Oates, W.A. Phase diagram calculation: Past, present and future. Prog. Mater. Sci. 2004, 49, 313–345. [Google Scholar] [CrossRef]
- Greenaway, R.L.; Jelfs, K.E. Integrating computational and experimental workflows for accelerated organic materials discovery. Adv. Mater. 2021, 33, 2004831. [Google Scholar] [CrossRef]
- Talapatra, A.; Boluki, S.; Honarmandi, P.; Solomou, A.; Zhao, G.; Ghoreishi, S.F.; Molkeri, A.; Allaire, D.; Srivastava, A.; Qian, X. Experiment design frameworks for accelerated discovery of targeted materials across scales. Front. Mater. 2019, 6, 82. [Google Scholar] [CrossRef]
- Gao, L.; Lin, J.; Wang, L.; Du, L. Machine learning-assisted design of advanced polymeric materials. Acc. Mater. Res. 2024, 5, 571–584. [Google Scholar] [CrossRef]
- Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mater. 2020, 5, 706–723. [Google Scholar] [CrossRef]
- Gu, D.; Shi, X.; Poprawe, R.; Bourell, D.L.; Setchi, R.; Zhu, J. Material-structure-performance integrated laser-metal additive manufacturing. Science 2021, 372, eabg1487. [Google Scholar] [CrossRef]
- Pragya, A.; Ghosh, T.K. Soft functionally gradient materials and structures–natural and manmade: A review. Adv. Mater. 2023, 35, 2300912. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.; Li, Z.; Yu, W.; Wang, A.; Ke, X.; Guo, H.; Su, J.; Li, L.; Gui, Q.; Zhao, S. Machine learning paves the way for high entropy compounds exploration: Challenges, progress, and outlook. Adv. Mater. 2023, 37, 2305192. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Xiang, X.; Yang, J.; Zhao, Z.-Y. High-entropy oxides as energy materials: From complexity to rational design. Mater. Futures 2024, 3, 042103. [Google Scholar] [CrossRef]
- Katiyar, N.K.; Goel, G.; Goel, S. Emergence of machine learning in the development of high entropy alloy and their prospects in advanced engineering applications. Emergent Mater. 2021, 4, 1635–1648. [Google Scholar] [CrossRef]
- Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; Chandak, P.; Liu, S.; Van Katwyk, P.; Deac, A. Scientific discovery in the age of artificial intelligence. Nature 2023, 620, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Batra, R.; Song, L.; Ramprasad, R. Emerging materials intelligence ecosystems propelled by machine learning. Nat. Rev. Mater. 2021, 6, 655–678. [Google Scholar] [CrossRef]
- Xu, L.; Lux, T.; Chang, T.; Li, B.; Hong, Y.; Watson, L.; Butt, A.; Yao, D.; Cameron, K. Prediction of high-performance computing input/output variability and its application to optimization for system configurations. Qual. Eng. 2021, 33, 318–334. [Google Scholar] [CrossRef]
- Ansari, T.S.; Taqvi, S.A.A. State-of-the-art review on the applications of nonlinear and artificial intelligence-based controllers in petrochemical processes. ChemBioEng Rev. 2023, 10, 884–906. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. Artificial intelligence in high-entropy materials. Next Mater. 2025, 9, 100993. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef] [PubMed]
- Badini, S.; Regondi, S.; Pugliese, R. Unleashing the Power of Artificial Intelligence in Materials Design. Materials 2023, 16, 5927. [Google Scholar] [CrossRef]
- Huang, J.; Liew, J.; Ademiloye, A.; Liew, K.M. Artificial intelligence in materials modeling and design. Arch. Comput. Methods Eng. 2021, 28, 3399–3413. [Google Scholar] [CrossRef]
- Correa-Baena, J.-P.; Hippalgaonkar, K.; van Duren, J.; Jaffer, S.; Chandrasekhar, V.R.; Stevanovic, V.; Wadia, C.; Guha, S.; Buonassisi, T. Accelerating materials development via automation, machine learning, and high-performance computing. Joule 2018, 2, 1410–1420. [Google Scholar] [CrossRef]
- Xie, J.; Su, Y.; Xue, D.; Jiang, X.; Fu, H.; Huang, H. Machine learning for materials research and development. Acta Metall. Sin. 2021, 57, 1343–1361. [Google Scholar]
- Xu, D.; Zhang, Q.; Huo, X.; Wang, Y.; Yang, M. Advances in data-assisted high-throughput computations for material design. Mater. Genome Eng. Adv. 2023, 1, e11. [Google Scholar] [CrossRef]
- Montoya, J.H.; Aykol, M.; Anapolsky, A.; Gopal, C.B.; Herring, P.K.; Hummelshøj, J.S.; Hung, L.; Kwon, H.-K.; Schweigert, D.; Sun, S. Toward autonomous materials research: Recent progress and future challenges. Appl. Phys. Rev. 2022, 9, e11. [Google Scholar] [CrossRef]
- Morgan, D.; Jacobs, R. Opportunities and challenges for machine learning in materials science. Annu. Rev. Mater. Res. 2020, 50, 71–103. [Google Scholar] [CrossRef]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Ten, J.S.J.; Yeong, W.Y. Progress and opportunities for machine learning in materials and processes of additive manufacturing. Adv. Mater. 2024, 36, 2310006. [Google Scholar] [CrossRef]
- Xie, T.; Li, W.; Velisa, G.; Chen, S.; Meng, F.; Liaw, P.K.; Tong, Y. An overview of high-throughput synthesis for advanced high-entropy alloys. Mater. Genome Eng. Adv. 2025, 3, e87. [Google Scholar] [CrossRef]
- Wang, Q.; Velasco, L.; Breitung, B.; Presser, V. High-entropy energy materials in the age of big data: A critical guide to next-generation synthesis and applications. Adv. Energy Mater. 2021, 11, 2102355. [Google Scholar] [CrossRef]
- Shang, Y.; Xiong, Z.; An, K.; Hauch, J.A.; Brabec, C.J.; Li, N. Materials genome engineering accelerates the research and development of organic and perovskite photovoltaics. Mater. Genome Eng. Adv. 2024, 2, e28. [Google Scholar] [CrossRef]
- Stier, S.P.; Kreisbeck, C.; Ihssen, H.; Popp, M.A.; Hauch, J.; Malek, K.; Reynaud, M.; Goumans, T.; Carlsson, J.; Todorov, I. Materials acceleration platforms (MAPs): Accelerating materials research and development to meet urgent societal challenges. Adv. Mater. 2024, 36, 2407791. [Google Scholar] [CrossRef]
- Zeni, C.; Pinsler, R.; Zügner, D.; Fowler, A.; Horton, M.; Fu, X.; Wang, Z.; Shysheya, A.; Crabbé, J.; Ueda, S.; et al. A generative model for inorganic materials design. Nature 2025, 639, 624–632. [Google Scholar] [CrossRef]
- Han, N.; Su, B.-L. AI-driven material discovery for energy, catalysis and sustainability. Natl. Sci. Rev. 2025, 12, nwaf110. [Google Scholar] [CrossRef]
- Park, H.; Li, Z.; Walsh, A. Has generative artificial intelligence solved inverse materials design? Matter 2024, 7, 2355–2367. [Google Scholar] [CrossRef]
- Zeni, C.; Pinsler, R.; Zügner, D.; Fowler, A.; Horton, M.; Fu, X.; Shysheya, S.; Crabbé, J.; Sun, L.; Smith, J. Mattergen: A generative model for inorganic materials design. arXiv 2023, arXiv:2312.03687. [Google Scholar]
- Zhang, Y.; Wen, C.; Wang, C.; Antonov, S.; Xue, D.; Bai, Y.; Su, Y. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 2020, 185, 528–539. [Google Scholar] [CrossRef]
- Liu, S.; Yang, C. Machine learning design for high-entropy alloys: Models and algorithms. Metals 2024, 14, 235. [Google Scholar] [CrossRef]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.-Y.; Li, Z.; Gupta, B.B.; Chen, X.; Wang, X. A survey of deep active learning. ACM Comput. Surv. (CSUR) 2021, 54, 1–40. [Google Scholar] [CrossRef]
- Sun, Y.; Ni, J. Machine learning advances in high-entropy alloys: A mini-review. Entropy 2024, 26, 1119. [Google Scholar] [CrossRef]
- Wu, S.; Song, Z.; Wang, J.; Niu, X.; Chen, H. Enhanced phase prediction of high-entropy alloys through machine learning and data augmentation. Phys. Chem. Chem. Phys. 2025, 27, 717–729. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, C.; Tran, N.-D.; Lu, Y.; Li, Z.; Chen, Y.; Ni, J. EFTGAN: Elemental features and transferring corrected data augmentation for the study of high-entropy alloys. npj Comput. Mater. 2025, 11, 54. [Google Scholar] [CrossRef]
- Sulley, G.A.; Raush, J.; Montemore, M.M.; Hamm, J. Accelerating high-entropy alloy discovery: Efficient exploration via active learning. Scr. Mater. 2024, 249, 116180. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Yu, Z.; Liu, Z.; Liu, D.; Lin, H.; Li, M.; Ma, S.; Avdeev, M.; Shi, S. Generative artificial intelligence and its applications in materials science: Current situation and future perspectives. J. Mater. 2023, 9, 798–816. [Google Scholar] [CrossRef]
- Fuhr, A.S.; Sumpter, B.G. Deep generative models for materials discovery and machine learning-accelerated innovation. Front. Mater. 2022, 9, 865270. [Google Scholar] [CrossRef]
- Madika, B.; Saha, A.; Kang, C.; Buyantogtokh, B.; Agar, J.; Wolverton, C.M.; Voorhees, P.; Littlewood, P.; Kalinin, S.; Hong, S. Artificial Intelligence for Materials Discovery, Development, and Optimization. ACS Nano 2025, 19, 27116–27158. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J. Recent advances and applications of deep learning methods in materials science. npj Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M.; Furht, B. Text data augmentation for deep learning. J. Big Data 2021, 8, 101. [Google Scholar] [CrossRef]
- Kumar, T.; Brennan, R.; Mileo, A.; Bendechache, M. Image data augmentation approaches: A comprehensive survey and future directions. IEEE Access 2024, 12, 187536–187571. [Google Scholar] [CrossRef]
- Kininis, P. Robustness and Domain Generalization in Computer Vision by Using Adversarial Data Augmentation. 2025. Available online: https://dspace.lib.ntua.gr/xmlui/bitstream/handle/123456789/60642/Thesis%20(1).pdf?sequence=1 (accessed on 9 July 2024).
- Zhou, C.; Zhang, Y.; Xin, H.; Li, X.; Chen, X. Complex multiphase predicting of additive manufactured high entropy alloys based on data augmentation deep learning. J. Mater. Res. Technol. 2024, 28, 2388–2401. [Google Scholar] [CrossRef]
- Yang, Z.; Li, S.; Li, S.; Yang, J.; Liu, D. A two-step data augmentation method based on generative adversarial network for hardness prediction of high entropy alloy. Comput. Mater. Sci. 2023, 220, 112064. [Google Scholar] [CrossRef]
- Peivaste, I.; Jossou, E.; Tiamiyu, A.A. Data-driven analysis and prediction of stable phases for high-entropy alloy design. Sci. Rep. 2023, 13, 22556. [Google Scholar] [CrossRef] [PubMed]
- Callister Jr, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Feng, S.; Zhou, H.; Dong, H. Application of deep transfer learning to predicting crystal structures of inorganic substances. Comput. Mater. Sci. 2021, 195, 110476. [Google Scholar] [CrossRef]
- Golbabaei, M.H.; Zohrevand, M.; Zhang, N. Applications of Machine Learning in High-Entropy Alloys: A Review of Recent Advances in Design, Discovery, and Characterization. Nanoscale 2025. Online ahead of print. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, C.-L.; Li, X.-D.; Pan, L.; Liang, C.-J.; Liu, W.-J. Machine Learning-Based High Entropy Alloys-Algorithms and Workflow: A Review. Acta Metall. Sin. (Engl. Lett.) 2025, 38, 1453–1480. [Google Scholar] [CrossRef]
- Kaufmann, K.; Maryanovsky, D.; Mellor, W.M.; Zhu, C.; Rosengarten, A.S.; Harrington, T.J.; Oses, C.; Toher, C.; Curtarolo, S.; Vecchio, K.S. Discovery of high-entropy ceramics via machine learning. npj Comput. Mater. 2020, 6, 42. [Google Scholar] [CrossRef]
- Li, R.; Xie, L.; Wang, W.Y.; Liaw, P.K.; Zhang, Y. High-throughput calculations for high-entropy alloys: A brief review. Front. Mater. 2020, 7, 290. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; Fang, Q.; Liu, B.; Liu, Y.; Liaw, P.K. High-throughput simulation combined machine learning search for optimum elemental composition in medium entropy alloy. J. Mater. Sci. Technol. 2021, 68, 70–75. [Google Scholar] [CrossRef]
- Rittiruam, M.; Noppakhun, J.; Setasuban, S.; Aumnongpho, N.; Sriwattana, A.; Boonchuay, S.; Saelee, T.; Wangphon, C.; Ektarawong, A.; Chammingkwan, P. High-throughput materials screening algorithm based on first-principles density functional theory and artificial neural network for high-entropy alloys. Sci. Rep. 2022, 12, 16653. [Google Scholar] [CrossRef]
- Conway, P.L.; Klaver, T.; Steggo, J.; Ghassemali, E. High entropy alloys towards industrial applications: High-throughput screening and experimental investigation. Mater. Sci. Eng. A 2022, 830, 142297. [Google Scholar] [CrossRef]
- Mooraj, S.; Chen, W. A review on high-throughput development of high-entropy alloys by combinatorial methods. J. Mater. Inform. 2023, 3, 4. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Xiao, B.; Shu, J. Accelerated development of hard high-entropy alloys with data-driven high-throughput experiments. J. Mater. Inform. 2022, 2, 3. [Google Scholar] [CrossRef]
- Ong, S.P. Accelerating materials science with high-throughput computations and machine learning. Comput. Mater. Sci. 2019, 161, 143–150. [Google Scholar] [CrossRef]
- Chen, C.; Nguyen, D.T.; Lee, S.J.; Baker, N.A.; Karakoti, A.S.; Lauw, L.; Owen, C.; Mueller, K.T.; Bilodeau, B.A.; Murugesan, V. Accelerating computational materials discovery with machine learning and cloud high-performance computing: From large-scale screening to experimental validation. J. Am. Chem. Soc. 2024, 146, 20009–20018. [Google Scholar] [CrossRef]
- Shahzad, K.; Mardare, A.I.; Hassel, A.W. Accelerating materials discovery: Combinatorial synthesis, high-throughput characterization, and computational advances. Sci. Technol. Adv. Mater. Methods 2024, 4, 2292486. [Google Scholar] [CrossRef]
- Naghdi, A.H.; Massa, D.; Karimi, K.; Papanikolaou, S. High Entropy Alloy Composition Design for Mechanical Properties. 2024. Available online: https://www.intechopen.com/online-first/1172734 (accessed on 8 September 2025).
- Huo, W.; Wang, S.; Dominguez-Gutierrez, F.J.; Ren, K.; Kurpaska, Ł.; Fang, F.; Papanikolaou, S.; Kim, H.S.; Jiang, J. High-entropy materials for electrocatalytic applications: A review of first principles modeling and simulations. Mater. Res. Lett. 2023, 11, 713–732. [Google Scholar] [CrossRef]
- Sun, Y.; Dai, S. High-entropy materials for catalysis: A new frontier. Sci. Adv. 2021, 7, eabg1600. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, G.; Lu, Y.; Pang, H. Applications of machine learning in electrochemistry. Renewables 2023, 1, 668–693. [Google Scholar] [CrossRef]
- Feng, R.; Zhang, C.; Gao, M.C.; Pei, Z.; Zhang, F.; Chen, Y.; Ma, D.; An, K.; Poplawsky, J.D.; Ouyang, L. High-throughput design of high-performance lightweight high-entropy alloys. Nat. Commun. 2021, 12, 4329. [Google Scholar] [CrossRef] [PubMed]
- Miracle, D.B.; Li, M.; Zhang, Z.; Mishra, R.; Flores, K.M. Emerging capabilities for the high-throughput characterization of structural materials. Annu. Rev. Mater. Res. 2021, 51, 131–164. [Google Scholar] [CrossRef]
- Liu, X.; Liu, B.; Ding, J.; Deng, Y.; Han, X.; Zhong, C.; Hu, W. Building a library for catalysts research using high-throughput approaches. Adv. Funct. Mater. 2022, 32, 2107862. [Google Scholar] [CrossRef]
- Green, M.L.; Choi, C.; Hattrick-Simpers, J.; Joshi, A.; Takeuchi, I.; Barron, S.; Campo, E.; Chiang, T.; Empedocles, S.; Gregoire, J. Fulfilling the promise of the materials genome initiative with high-throughput experimental methodologies. Appl. Phys. Rev. 2017, 4, 011105. [Google Scholar] [CrossRef]
- Wang, D.; Jiang, W.; Li, S.; Yan, X.; Wu, S.; Qiu, H.; Guo, S.; Zhu, B. A comprehensive review on combinatorial film via high-throughput techniques. Materials 2023, 16, 6696. [Google Scholar] [CrossRef]
- Jain, S.; Jain, R.; Kumar, V.; Samal, S. Data-driven design of high bulk modulus high entropy alloys using machine learning. J. Alloys Metall. Syst. 2024, 8, 100128. [Google Scholar] [CrossRef]
- Eldabah, N.M.; Pratap, A.; Pandey, A.; Sardana, N.; Sidhu, S.S.; Gepreel, M.A.H. Design Approaches of High-Entropy Alloys Using Artificial Intelligence: A Review. Adv. Eng. Mater. 2025, 27, 2402504. [Google Scholar] [CrossRef]
- Shenai, P.M.; Xu, Z.; Zhao, Y. Applications of principal component analysis (PCA) in materials science. Princ. Compon. Anal. Appl. 2012, 25–40. [Google Scholar]
- Rajan, K. Materials informatics. Mater. Today 2005, 8, 38–45. [Google Scholar] [CrossRef]
- Vazquez, G.; Sauceda, D.; Arróyave, R. Deciphering chemical ordering in High Entropy Materials: A machine learning-accelerated high-throughput cluster expansion approach. Acta Mater. 2024, 276, 120137. [Google Scholar] [CrossRef]
- Lee, K.; Ayyasamy, M.V.; Delsa, P.; Hartnett, T.Q.; Balachandran, P.V. Phase classification of multi-principal element alloys via interpretable machine learning. npj Comput. Mater. 2022, 8, 25. [Google Scholar] [CrossRef]
- Chanda, B.; Jana, P.P.; Das, J. A tool to predict the evolution of phase and Young’s modulus in high entropy alloys using artificial neural network. Comput. Mater. Sci. 2021, 197, 110619. [Google Scholar] [CrossRef]
- Yao, Y.; Dong, Q.; Brozena, A.; Luo, J.; Miao, J.; Chi, M.; Wang, C.; Kevrekidis, I.G.; Ren, Z.J.; Greeley, J. High-entropy nanoparticles: Synthesis-structure-property relationships and data-driven discovery. Science 2022, 376, eabn3103. [Google Scholar] [CrossRef]
- Anand, A.; Liu, S.-J.; Singh, C.V. Recent advances in computational design of structural multi-principal element alloys. Iscience 2023, 26, 107751. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.; Hossain, M.S.; Siddique, A.-B. Review: Machine learning approaches for diverse alloy systems. J. Mater. Sci. 2025, 60, 12189–12221. [Google Scholar] [CrossRef]
- Risal, S.; Zhu, W.; Guillen, P.; Sun, L. Improving phase prediction accuracy for high entropy alloys with machine learning. Comput. Mater. Sci. 2021, 192, 110389. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big data creates new opportunities for materials research: A review on methods and applications of machine learning for materials design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Dixit, S.; Rodriguez, S.; Jones, M.R.; Buzby, P.; Dixit, R.; Argibay, N.; DelRio, F.W.; Lim, H.H.; Fleming, D. Refractory High-Entropy Alloy Coatings for High-Temperature Aerospace and Energy Applications. J. Therm. Spray Technol. 2022, 31, 1021–1031. [Google Scholar] [CrossRef]
- Ubaidy, S.K.A.; Bouraoui, C. High-Entropy Alloys: Advantages and Applications in Challenging Environments. Ann. Chim.—Sci. Des Matériaux 2024, 48, 125–136. [Google Scholar] [CrossRef]
- Li, J.; Xiong, W.; Zhang, T.; Cheng, H.; Shen, K.; He, M.; Zhang, Y.; Song, J.; Deng, Y.; Chen, Q. Machine Learning and Explainable AI-Guided Design and Optimization of High-Entropy Alloys as Binder Phases for WC-Based Cemented Carbides. Comput. Mater. Contin. 2025, 84, 2189–2216. [Google Scholar] [CrossRef]
- Yuan, J.; Li, Z.; Yang, Y.; Yin, A.; Li, W.; Sun, D.; Wang, Q. Applications of machine learning method in high-performance materials design: A review. J. Mater. Inform. 2024, 4, 14. [Google Scholar] [CrossRef]
- Thike, P.H.; Zhao, Z.; Shi, P.; Jin, Y. Significance of artificial neural network analytical models in materials’ performance prediction. Bull. Mater. Sci. 2020, 43, 211. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, W.; Huang, C.; Mei, T. A Review of Performance Prediction Based on Machine Learning in Materials Science. Nanomaterials 2022, 12, 2957. [Google Scholar] [CrossRef] [PubMed]
- Debnath, A.; Krajewski, A.M.; Sun, H.; Lin, S.; Ahn, M.; Li, W.; Priya, S.; Singh, J.; Shang, S.; Beese, A.M.; et al. Generative deep learning as a tool for inverse design of high entropy refractory alloys. J. Mater. Inform. 2021, 1, 3. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, Y.; Wang, C.; Huang, H.; Wu, Y.; Lookman, T.; Su, Y. Machine-Learning-Assisted Compositional Design of Refractory High-Entropy Alloys with Optimal Strength and Ductility. Engineering 2025, 46, 214–223. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Dang, P.; Jiang, X.; Xue, D.; Su, Y. Elemental numerical descriptions to enhance classification and regression model performance for high-entropy alloys. npj Comput. Mater. 2025, 11, 75. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, H.; Long, W.; Wang, G.; Ren, J. Phase prediction for high-entropy alloys using generative adversarial network and active learning based on small datasets. Sci. China Technol. Sci. 2023, 66, 3615–3627. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Y.; Yu, J.; Yang, M.; Zhang, Y.; Wei, H.; Chen, Y.; Wu, J.; Han, J.; Wang, C.; et al. Accelerated discovery of high-performance Cu-Ni-Co-Si alloys through machine learning. Mater. Des. 2021, 209, 109929. [Google Scholar] [CrossRef]
- Rao, Z.; Tung, P.-Y.; Xie, R.; Wei, Y.; Zhang, H.; Ferrari, A.; Klaver, T.; Körmann, F.; Sukumar, P.T.; da Silva, A.K.; et al. Machine learning-enabled high-entropy alloy discovery. Science 2022, 378, 78–85. [Google Scholar] [CrossRef]
- Wen, C.; Shen, H.; Tian, Y.; Lou, G.; Wang, N.; Su, Y. Accelerated discovery of refractory high-entropy alloys for strength-ductility co-optimization: An exploration in NbTaZrHfMo system by machine learning. Scr. Mater. 2024, 252, 116240. [Google Scholar] [CrossRef]
- Yonggang, Y.; Dan, L.; Kun, W. Accelerated discovery of single-phase refractory high entropy alloys assisted by machine learning. Comput. Mater. Sci. 2021, 199, 110723. [Google Scholar] [CrossRef]
- Yu, F.; Wang, Y.; Zhang, K.; Shen, H.; Zhang, Y.; Yang, Z.; Zeng, G.; Cui, D.; Xia, J.; Liu, J. High entropy MXenes in energy storage: Structural design, characterization, and applications. J. Mater. Chem. A 2025. [Google Scholar] [CrossRef]
- Hauser, D.J.; Moss, A.J.; Rosenzweig, C.; Jaffe, S.N.; Robinson, J.; Litman, L. Evaluating CloudResearch’s Approved Group as a solution for problematic data quality on MTurk. Behav. Res. Methods 2023, 55, 3953–3964. [Google Scholar] [CrossRef]
- Wuest, T.; Tinscher, R.; Porzel, R.; Thoben, K.-D. Experimental research data quality in materials science. arXiv 2015, arXiv:1501.01149. [Google Scholar] [CrossRef]
- Abdalla, H.B.; Kumar, Y.; Marchena, J.; Guzman, S.; Awlla, A.; Gheisari, M.; Cheraghy, M. The Future of Artificial Intelligence in the Face of Data Scarcity. Comput. Mater. Contin. 2025, 84, 1073–1099. [Google Scholar] [CrossRef]
- Han, L.; Zhu, S.; Rao, Z.; Scheu, C.; Ponge, D.; Ludwig, A.; Zhang, H.; Gutfleisch, O.; Hahn, H.; Li, Z. Multifunctional high-entropy materials. Nat. Rev. Mater. 2024, 9, 846–865. [Google Scholar] [CrossRef]
- Oses, C.; Toher, C.; Curtarolo, S. High-entropy ceramics. Nat. Rev. Mater. 2020, 5, 295–309. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, X. Artificial intelligence-powered materials science. Nano-Micro Lett. 2025, 17, 135. [Google Scholar] [CrossRef]
- Kibrete, F.; Trzepieciński, T.; Gebremedhen, H.S.; Woldemichael, D.E. Artificial intelligence in predicting mechanical properties of composite materials. J. Compos. Sci. 2023, 7, 364. [Google Scholar] [CrossRef]
- Su, Y.; Wang, X.; Ye, Y.; Xie, Y.; Xu, Y.; Jiang, Y.; Wang, C. Automation and machine learning augmented by large language models in a catalysis study. Chem. Sci. 2024, 15, 12200–12233. [Google Scholar] [CrossRef]
- DeCost, B.L.; Hattrick-Simpers, J.R.; Trautt, Z.; Kusne, A.G.; Campo, E.; Green, M. Scientific AI in materials science: A path to a sustainable and scalable paradigm. Mach. Learn. Sci. Technol. 2020, 1, 033001. [Google Scholar] [CrossRef]
- Sha, W.; Guo, Y.; Yuan, Q.; Tang, S.; Zhang, X.; Lu, S.; Guo, X.; Cao, Y.-C.; Cheng, S. Artificial intelligence to power the future of materials science and engineering. Adv. Intell. Syst. 2020, 2, 1900143. [Google Scholar] [CrossRef]
- Lowe, P.; Phillipson, J. Barriers to research collaboration across disciplines: Scientific paradigms and institutional practices. Environ. Plan. A 2009, 41, 1171–1184. [Google Scholar] [CrossRef]
- Dalieva, M. Interoperation of Language, Scientific Terminology, and Interdisciplinary Collaboration. West. Eur. J. Linguist. Educ. 2024, 2, 1–4. [Google Scholar]
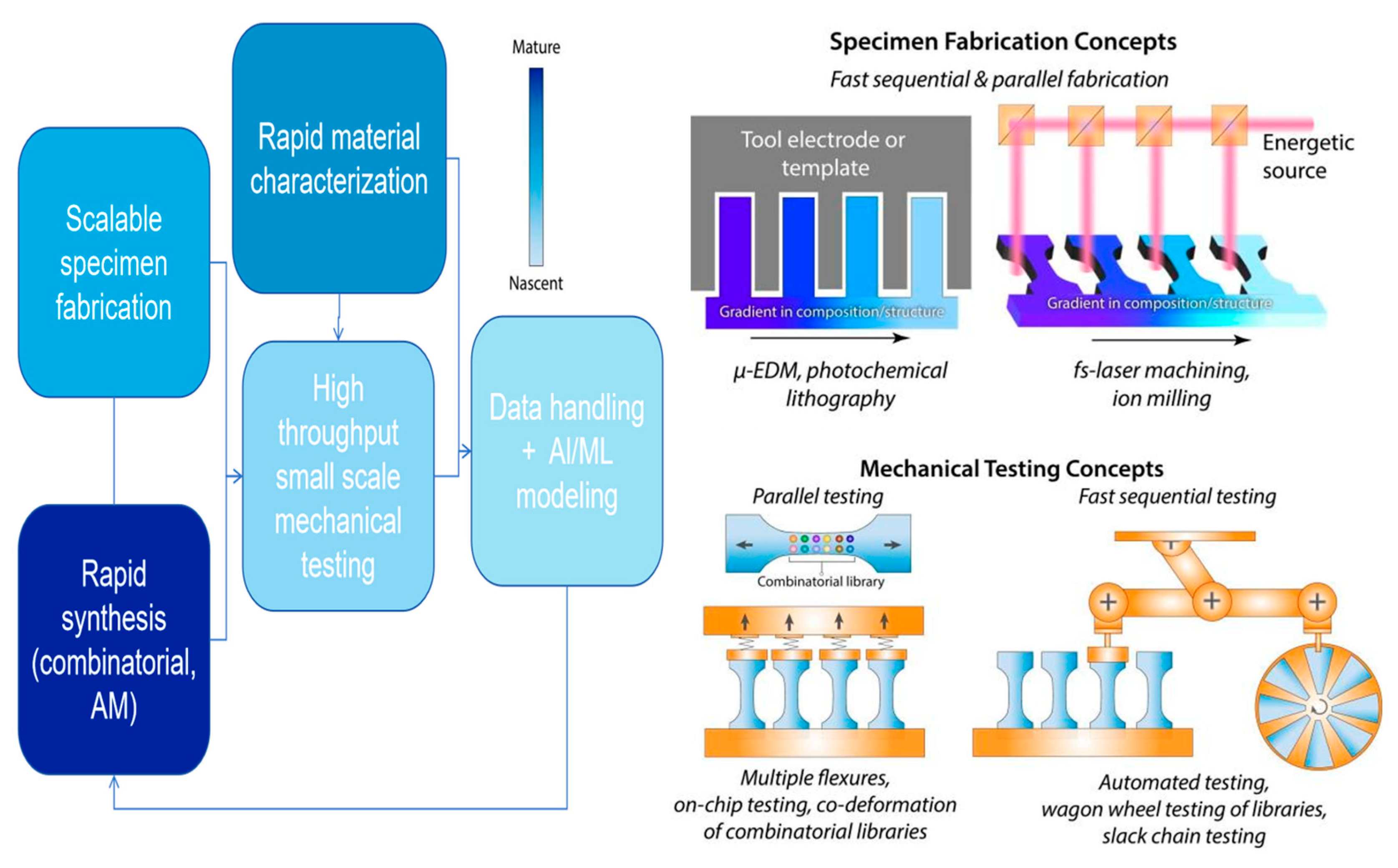
- Gianola, D.S.; della Ventura, N.M.; Balbus, G.H.; Ziemke, P.; Echlin, M.P.; Begley, M.R. Advances and opportunities in high-throughput small-scale mechanical testing. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101090. [Google Scholar] [CrossRef]








| Category of Algorithm | Metallurgical Analogy | The Role in the Study |
|---|---|---|
| Random Forest (RF) | The median is taken after tensile tests with multiple furnace cycles and sampling points | Robust regression or classification baseline |
| Gradient Boosting (GB) | Continuous refining: each round of remelting for residual error | Single phase/multi-phase classification, F1 highest |
| Deep neural network(DNN) | High temperature diffusion: inter-layer weights, such as diffusion channels | Mechanical performance end-to-end mapping |
| Conditions generate adversarial networks(CGAN) | Oriented solidification: Generator = mold, discriminator = quality control | Generate alloy composition on demand |
| Active learning(AL) | Additional sampling at key experimental points | Pick the alloy with the most information for the experiment under a small sample |
| Transfer learning(TL) | The strengthening mechanism of low-carbon steel is transferred to high-entropy steel | Accelerate the modeling of new systems using known alloy knowledge |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, E.; Yang, C. AI Design for High Entropy Alloys: Progress, Challenges and Future Prospects. Metals 2025, 15, 1012. https://doi.org/10.3390/met15091012
Xie E, Yang C. AI Design for High Entropy Alloys: Progress, Challenges and Future Prospects. Metals. 2025; 15(9):1012. https://doi.org/10.3390/met15091012
Chicago/Turabian StyleXie, Enzhi, and Chao Yang. 2025. "AI Design for High Entropy Alloys: Progress, Challenges and Future Prospects" Metals 15, no. 9: 1012. https://doi.org/10.3390/met15091012
APA StyleXie, E., & Yang, C. (2025). AI Design for High Entropy Alloys: Progress, Challenges and Future Prospects. Metals, 15(9), 1012. https://doi.org/10.3390/met15091012







