Self-Organization in Metal Plasticity: An ILG Update †
Abstract
1. Introduction
2. The Deterministic ILG Mechanics Framework
3. Effect of Stochasticity: Combined Gradient-Stochastic Models
4. Serrated Stress–Strain Curves and Metallic Micropillar Compression
5. Propagating Lüders Bands (LBs) and Portevin-Le Chatelier (PLC) Bands in Metals and Alloys
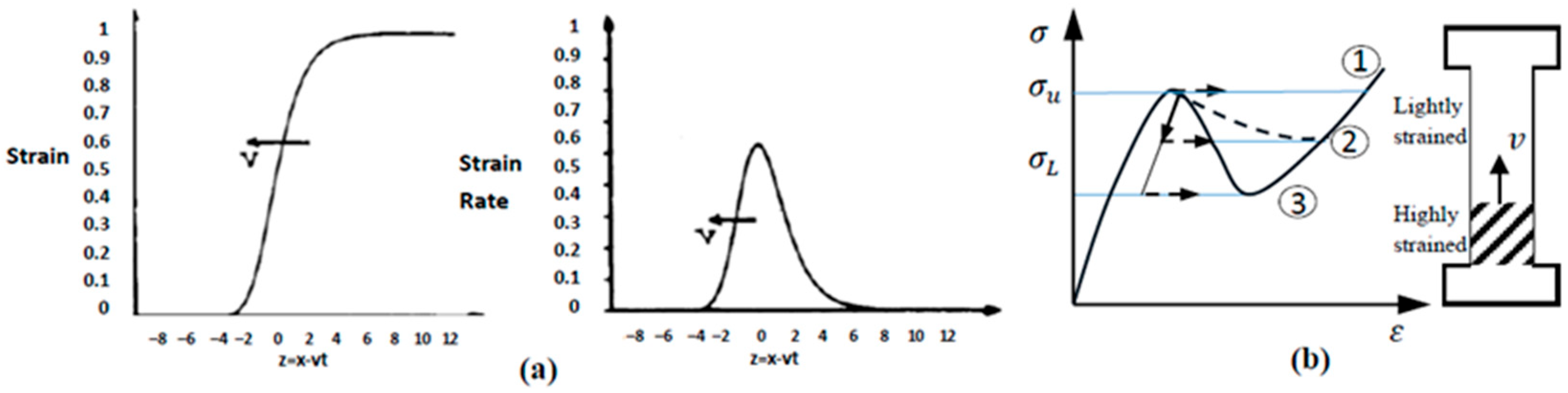
5.1. Propagating Lüders Bands in Steel
5.2. Traveling Portevin-Le Chatelier Bands in Al-Mg Alloys
6. Stationary PSBs in Cu Crystals and Extension of the Walgraef–Aifantis (W-A) Model: Finite Domains/Bifurcation Diagrams, the EFM Method, and DDD Simulations/Diffusion Maps
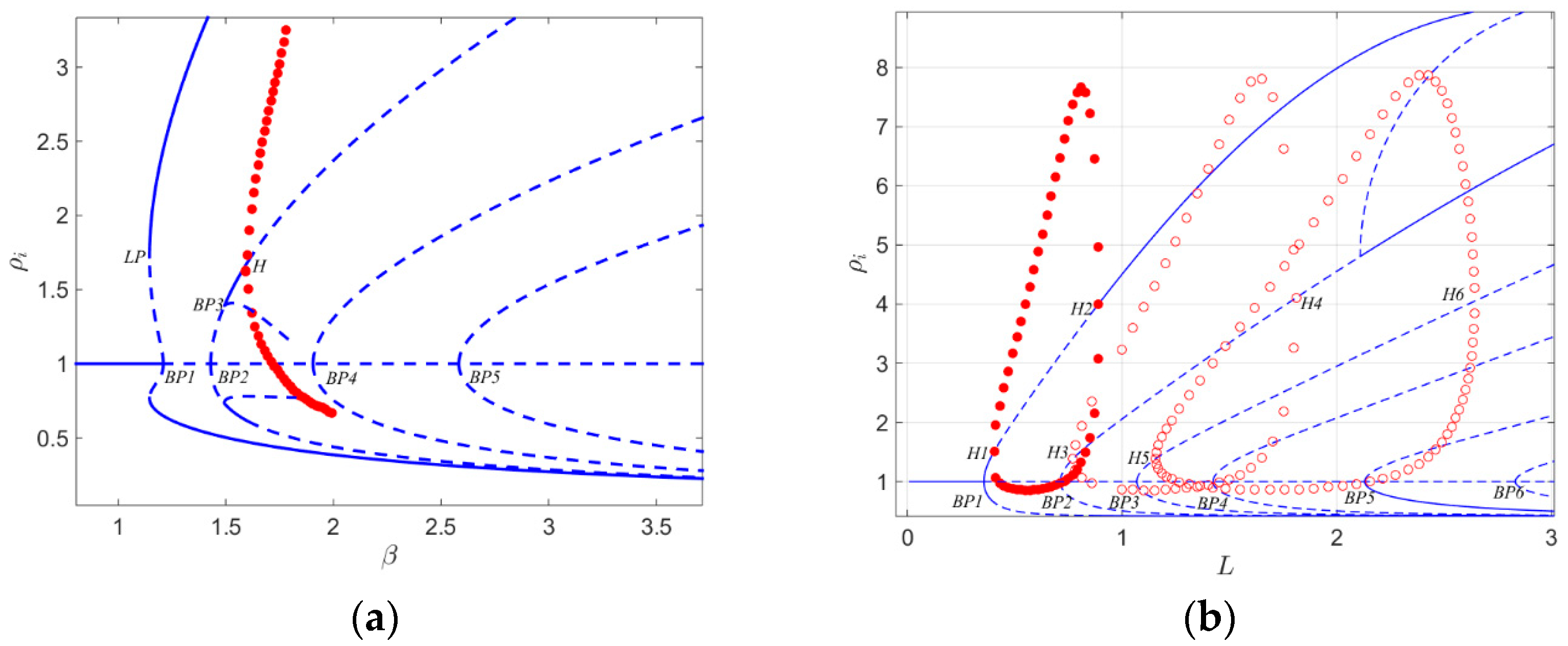
6.1. Finite Domains and Bifurcation Diagrams
6.2. The EFM Method
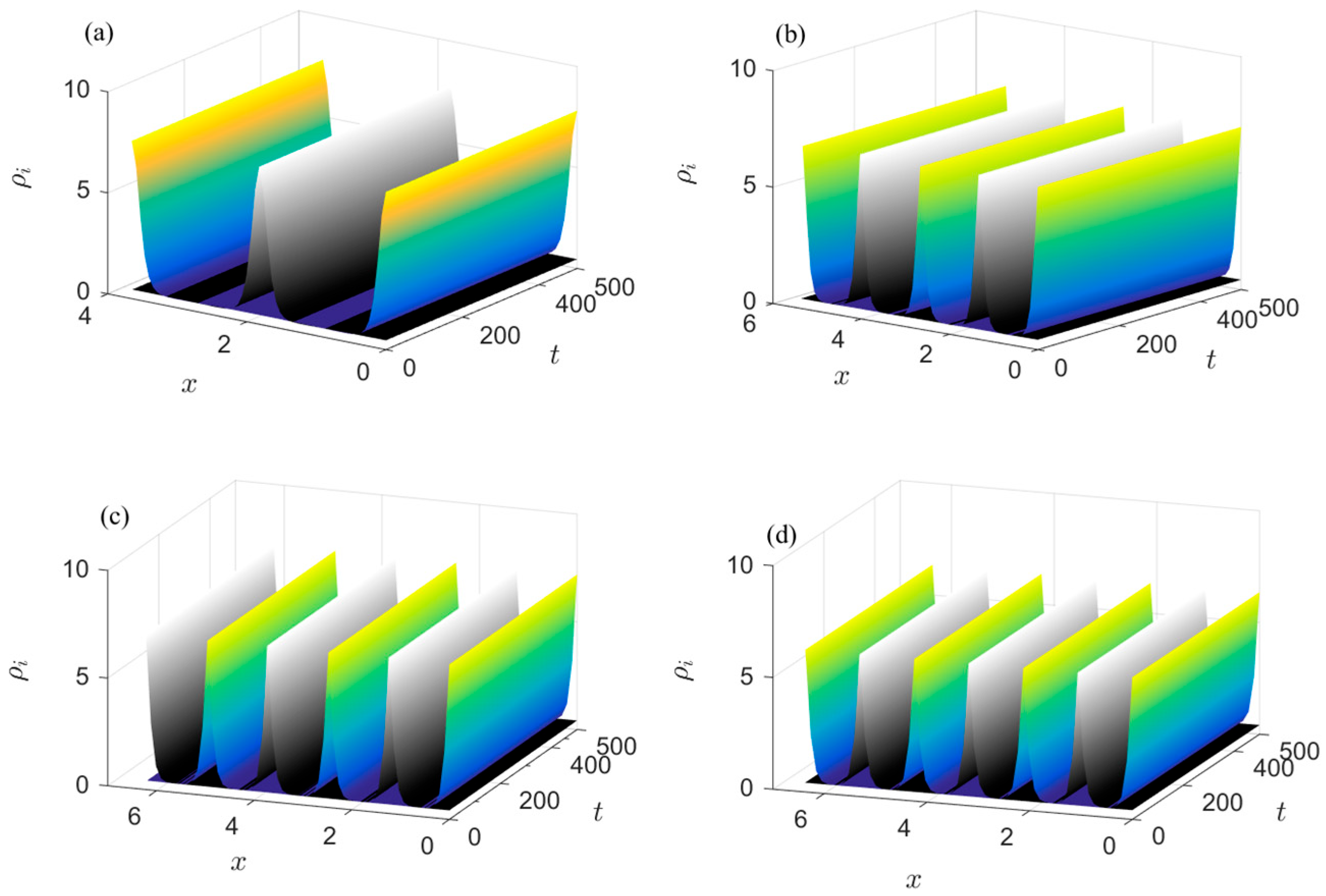
6.3. DDD Simulations and Diffusion Maps
7. No Equations—Tsallis Statistics
7.1. Methodology
7.2. Serrated Stress–Strain Graphs in Ultrafine Grain (UFG) Materials
7.3. Fractal Microstructures
7.4. Multiple Shear Bands
8. Guidelines for Future Work: Gradient-Stochastic Dislocation Evolution Models and Current Experimental Literature on Self-Organization in Metal Plasticity
8.1. Deterministic Gradient Dislocation Evolution
8.2. Combined Gradient-Stochastic Dislocation Evolution
8.3. Stochastic Differential Equations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aifantis, E.C. The physics of plastic deformation. Int. J. Plast. 1987, 3, 211–247. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [Google Scholar] [CrossRef]
- Aifantis, E.C. Pattern formation in plasticity. Int. J. Eng. Sci. 1995, 33, 2161–2178. [Google Scholar] [CrossRef]
- Aifantis, E.C. Gradient deformation models and nano, micro, and macro scales. J. Eng. Mater. Technol. 1999, 121, 189–202. [Google Scholar] [CrossRef]
- Aifantis, E.C. Update on a class of gradient theories. Mech. Mater. 2003, 35, 259–280. [Google Scholar] [CrossRef]
- Avlonitis, M.; Ioannidou, T.; Frantziskonis, G.; Aifantis, E.C. Statistical aspects of gradient theory. J. Mech. Behav. Mater. 2001, 12, 77–84. [Google Scholar] [CrossRef]
- Aifantis, E.C. Deformation and failure of bulk nanograined and ultrafine-grained materials. Mater. Sci. Eng. A 2009, 503, 190–197. [Google Scholar] [CrossRef]
- Aifantis, E.C. Internal length gradient (ILG) material mechanics across scales and disciplines. In Advances in Applied Mechanics; ScienceDirect: Amsterdam, The Netherlands, 2016; Volume 49, pp. 1–110. [Google Scholar]
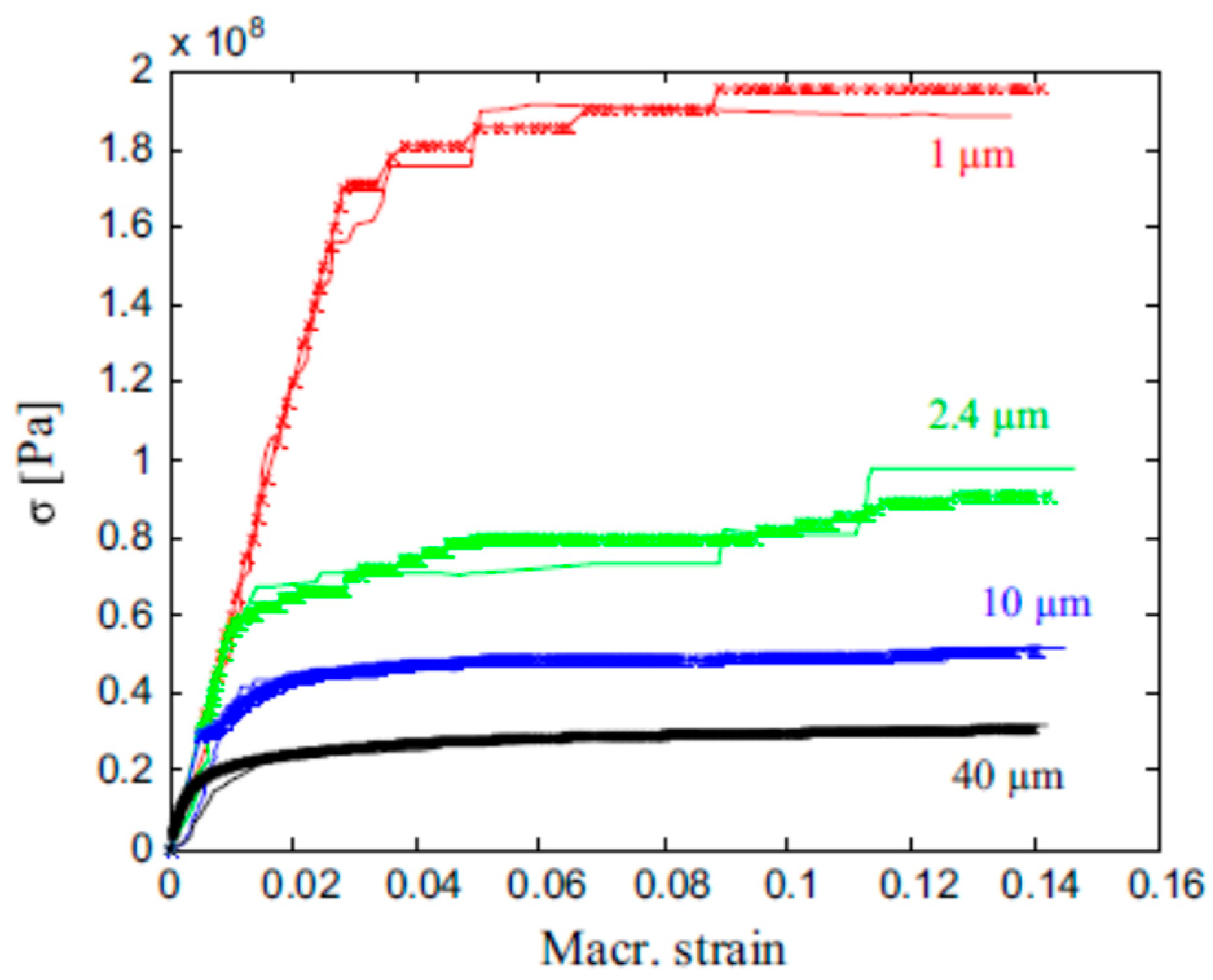
- Konstantinidis, A.A.; Aifantis, K.E.; De Hosson, J.T.M. Capturing the stochastic mechanical behavior of micro and nanopillars. Mater. Sci. Eng. A 2014, 597, 89–94. [Google Scholar] [CrossRef]
- Zhang, X.; Aifantis, K.E. Interpreting strain bursts and size effects in micropillars using gradient plasticity. Mater. Sci. Eng. A 2011, 528, 5036–5043. [Google Scholar] [CrossRef]
- Konstantinidis, A.A.; Zhang, X.; Aifantis, E.C. On the combined gradient-stochastic plasticity model: Application to Mo-micropillar compression. AIP Conf. Proc. 2015, 1646, 3–9. [Google Scholar]
- Dimiduk, D.M.; Uchic, M.D.; Parthasarathy, T.A. Size-affected single-slip behavior of pure nickel microcrystals. Acta Mater. 2005, 53, 4065–4077. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Zaiser, M.; Schwerdtfeger, J.; Schneider, A.S.; Frick, C.P.; Clark, B.G.; Gruber, P.A.; Arzt, E. Strain bursts in plastically deforming molybdenum micro- and nanopillars. Phil. Mag. 2008, 28, 3861–3874. [Google Scholar] [CrossRef]
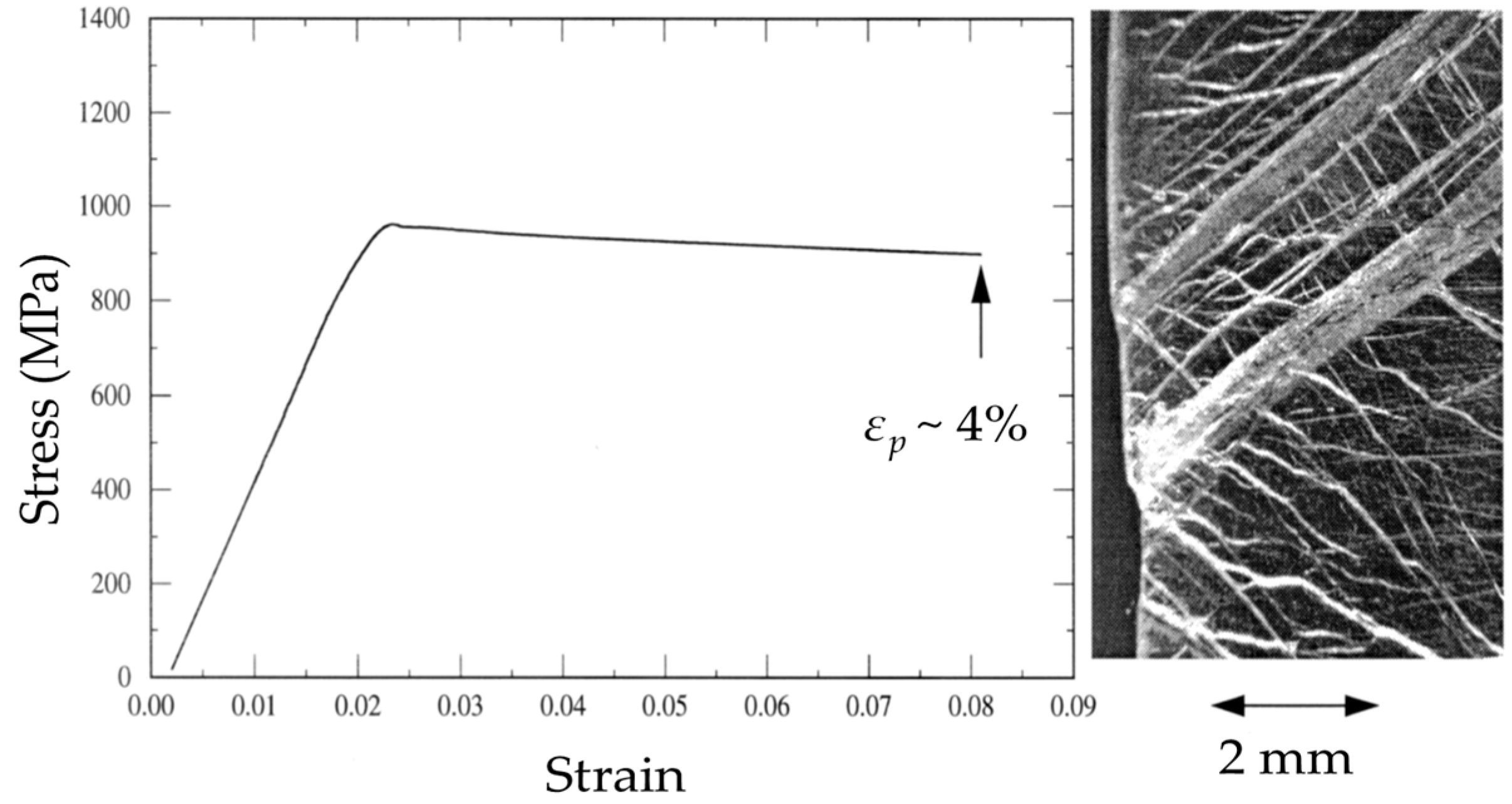
- Rizzardi, Q.; Sparks, G.; Maass, R. Fast slip velocity in a high-entropy alloy. JOM 2018, 70, 1088–1093. [Google Scholar] [CrossRef]
- McClintock, F.A.; Argon, A.S. Mechanical Behavior of Materials; Addison-Wesley Publishing Company: Boston, MA, USA, 1966. [Google Scholar]
- Aifantis, E.C. Gradient Extension of Classical Material Models: From Nuclear & Condensed Matter Scales to Earth & Cosmological Scales. In Size-Dependent Continuum Mechanics Approaches; Springer Tracts in Mechanical Engineering; Ghavanloo, E., Fazelzadeh, S.A., Marotti de Sciarra, F., Eds.; Springer: Cham, Switzerland, 2021; pp. 417–452. [Google Scholar]
- Gurevich, A.V.; Pitaevskii, L.P. Averaged description of waves in the Korteweg-de Vries-Burgers equation. Sov. Phys. JETP 1987, 66, 490–495. [Google Scholar]
- Walgraef, D.; Aifantis, E.C. Dislocation patterning in fatigued metals as a result of dynamical instabilities. J. Appl. Phys. 1985, 58, 688–691. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, G.P. Effects of grain size and initial immobile dislocation density on fatigue behavior of polycrystalline metals. Mater. Sci. Eng. A 2014, 590, 194–198. [Google Scholar] [CrossRef]
- Ord, A.; Hobbs, B. Patterns in our planet: Defining new concepts for the application of multi-scale non-equilibrium thermodynamics to Earth-system science. Philos. Trans. R. Soc. A 2010, 368, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Kubin, L.P.; Lepinoux, J. The dynamic organization of dislocation structures. In Proceedings of the 8th International Conference on the Strength of Metals and Alloys, Tampere, Finland, 22–26 August 1988; Kettunen, P.O., Lepistö, T.K., Lehtonen, M.E., Eds.; Pergamon Press: Elmsford, NY, USA, 1988; Volume 1, pp. 35–59. [Google Scholar]
- Rhee, M.; Zbib, H.M.; Hirth, J.P.; Huang, H.; de la Rubia, T.D. Models for long/short range interactions in 3D dislocation simulation. Model. Simul. Mater. Sci. Eng. 1998, 6, 467–492. [Google Scholar] [CrossRef]
- Groma, I.; Csikor, F.F.; Zaiser, M. Spatial correlations and higher-order gradient terms in a continuum description of dislocation dynamics. Acta Mater. 2003, 51, 1271–1281. [Google Scholar] [CrossRef]
- Sandfeld, S.; Hochrainer, T.; Zaiser, M.; Gumbsch, P. Continuum modeling of dislocation plasticity: Theory, numerical implementation, and validation by discrete dislocation simulations. J. Mater. Res. 2011, 26, 623–632. [Google Scholar] [CrossRef]
- Glazov, M.; Llanes, L.M.; Laird, C. Self-organized dislocation structures (SODS) in fatigued metals. Phys. Status Solidi A 1995, 149, 297–321. [Google Scholar] [CrossRef]
- Spiliotis, K.G.; Russo, L.; Siettos, C.; Aifantis, E.C. Analytical and numerical bifurcation analysis of dislocation pattern formation of the Walgraef–Aifantis model. Int. J. Non-Linear Mech. 2018, 102, 41–52. [Google Scholar] [CrossRef]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Seydel, R. Practical Bifurcation and Stability Analysis; Springer: New York, NY, USA, 2010. [Google Scholar]
- Theodoropoulos, C.; Qian, Y.; Kevrekidis, I.G. “Coarse” stability and bifurcation analysis using time-steppers: A reaction-diffusion example. Proc. Natl. Acad. Sci. USA 2000, 97, 9840–9843. [Google Scholar] [CrossRef]
- Van Leemput, P.; Lust, K.W.; Kevrekidis, I.G. Coarse-grained numerical bifurcation analysis of lattice Boltzmann models. Phys. D 2005, 210, 58–76. [Google Scholar] [CrossRef][Green Version]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Gardiner, G.W. Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences; Springer: New York, NY, USA, 1983. [Google Scholar]
- Gulluoglu, A.N.; Srolovitz, D.J.; LeSar, R.; Lomdahl, P.S. Dislocation distributions in two dimensions. Scr. Metall. 1989, 23, 1347–1352. [Google Scholar] [CrossRef]
- LeSar, R. Introduction to Computational Materials Science: Fundamentals to Applications; Cambridge Univ. Press: Cambridge, UK, 2013. [Google Scholar]
- Coifman, R.; Kevrekidis, I.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion Maps, Reduction Coordinates, and Low Dimensional Representation of Stochastic Systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching A Complex World; Springer: Berlin, Germany, 2009. [Google Scholar]
- Iliopoulos, A.C.; Aifantis, E.C. Tsallis q-triplet, intermittent turbulence and Portevin–Le Chatelier effect. Phys. A 2018, 498, 17–32. [Google Scholar] [CrossRef]
- Morton, G.M. A computer Oriented Geodetic Data Base; and a New Technique in File Sequencing; Technical Report; IBM Ltd.: Ottawa, ON, Canada, 1966. [Google Scholar]
- Eddahbi, M.; Monge, M.A.; Muñoz, A.; Pareja, R. Serrated flow in powder metallurgy Al–5%Mg–1.2%Cr alloy processed by equal channel angular pressing. Mater. Charact. 2012, 73, 16–30. [Google Scholar] [CrossRef]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Ahouri, R. Travelling Wave Solutions. Master’s Thesis, University of Manchester, Manchester, UK, 2016. [Google Scholar]
- Chattopadhyay, A.K.; Aifantis, E.C. Stochastically forced dislocation density distribution in plastic deformation. Phys. Rev. E 2016, 94, 022139. [Google Scholar] [CrossRef]
- Jaber, H.; Beausir, B.; Entemeyer, D.; Lebedkina, T.; Novelli, M.; Lebyodkin, M. Influence of surface pre-deformation on the Portevin-Le Chatelier effect and the related multiscale complexity of plastic flow in an Al-Mg alloy. Acta Mater. 2024, 279, 120330. [Google Scholar] [CrossRef]
- Brechtl, J.; Feng, R.; Liaw, P.K.; Beausir, B.; Jaber, H.; Lebedkina, T.; Lebyodkin, M. Mesoscopic-scale complexity in macroscopically-uniform plastic flow of an Al0.3CoCrFeNi high-entropy alloy. Acta Mater. 2023, 242, 118445. [Google Scholar] [CrossRef]
- Beygelzimer, Y.E.; Spuskanyuk, A.V. The thick yield surface: Idea and approach for investigating its structure. Philos. Mag. A 1999, 79, 2437–2459. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Kulagin, R.; Toth, L.S.; Ivanisenko, Y. The self-similarity theory of high pressure torsion. Beilstein J. Nanotechnol. 2016, 7, 1267–1277. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Filippov, A.; Estrin, Y. ‘Turbulent’ shear flow of solids under high-pressure torsion. Philos. Mag. 2023, 103, 1017–1028. [Google Scholar] [CrossRef]
- Fried, E.; Gurtin, M.E. A continuum mechanical theory for turbulence: A generalized Navier–Stokes-α equation with boundary conditions. Theor. Comput. Fluid Dyn. 2008, 22, 433–470. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. Dislocation inhomogeneity in cyclic deformation. In Micromechanics and Inhomogeneity—The Toshio Mura Anniversary Volume; Weng, G.J., Taya, M., Abe, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 511–533. [Google Scholar]
- Beygelzimer, Y. Grain refinement versus voids accumulation during severe plastic deformations of polycrystals: Mathematical simulation. Mech. Mater. 2005, 37, 753–767. [Google Scholar] [CrossRef]
- An, X.H.; Lin, Q.Y.; Wu, S.D.; Zhang, Z.F.; Figueiredo, R.B.; Gao, N.; Langdon, T.G. The influence of stacking fault energy on the mechanical properties of nanostructured Cu and Cu–Al alloys processed by high-pressure torsion. Scr. Mater. 2011, 64, 954–957. [Google Scholar] [CrossRef]
- Olugbade, T.O.; Lu, J. Literature review on the mechanical properties of materials after surface mechanical attrition treatment (SMAT). Nano Mater. Sci. 2020, 2, 3–31. [Google Scholar] [CrossRef]
- Lebyodkin, M.A.; Lebedkina, T.A.; Brechtl, J.; Liaw, P.K. Serrated flow in alloy systems. In High-Entropy Materials: Theory, Experiments, and Applications; Brechtl, J., Liaw, P.K., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 523–644. [Google Scholar]
- Shibkov, A.A.; Zheltov, M.A.; Gasanov, M.F.; Zolotov, A.E.; Denisov, A.A.; Lebyodkin, M.A. Dynamics of deformation band formation investigated by high-speed techniques during creep in an AlMg alloy. Mater. Sci. Eng. A 2020, 772, 138777. [Google Scholar] [CrossRef]
- Hassanpour, H.; Jamaati, R.; Hosseinipour, S.J. Effect of gradient microstructure on the mechanical properties of aluminum alloy. Mater. Charact. 2021, 174, 111023. [Google Scholar] [CrossRef]
- Lebyodkin, M.; Bougherira, Y.; Lebedkina, T.; Entemeyer, D. Scaling in the local strain-rate field during jerky flow in an Al-3%Mg alloy. Metals 2020, 10, 134. [Google Scholar] [CrossRef]
- Brechtl, J.; Chen, S.; Lee, C.; Shi, Y.; Feng, R.; Xie, X.; Hamblin, D.; Coleman, A.M.; Straka, B.; Shortt, H.; et al. A review of the serrated-flow phenomenon and its role in the deformation behavior of high-entropy alloys. Metals 2020, 10, 1101. [Google Scholar] [CrossRef]
- Pan, Q.; Zhang, L.; Feng, R.; Lu, Q.; An, K.; Chuang, A.C.; Poplawsky, J.D.; Liaw, P.K.; Lu, L. Gradient cell–structured high-entropy alloy with exceptional strengthand ductility. Science 2021, 374, 984–989. [Google Scholar] [CrossRef]
- Kubin, L.P.; Fressengeas, C.; Ananthakrishna, G. Chapter 57 Collective behaviour of dislocations in plasticity. In Dislocations in Solids; Nabarro, F.R.N., Duesbery, M.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; pp. 101–192. [Google Scholar]
- Weiss, J.; Richeton, T.; Louchet, F.; Chmelik, F.; Dobron, P.; Entemeyer, D.; Lebyodkin, M.; Lebedkina, T.; Fressengeas, C.; McDonald, R.J. Evidence for universal intermittent crystal plasticity from acoustic emission and high-resolution extensometry experiments. Phys. Rev. B 2007, 76, 224110. [Google Scholar] [CrossRef]
- Shibkov, A.A.; Lebyodkin, M.A.; Lebedkina, T.A.; Gasanov, M.F.; Zolotov, A.E.; Denisov, A.A. Millisecond dynamics of deformation bands during discontinuous creep in an AlMg polycrystal. Phys. Rev. E 2020, 102, 043003. [Google Scholar] [CrossRef] [PubMed]
- Shashkov, I.V.; Lebyodkin, M.A.; Lebedkina, T.A. Multiscale study of acoustic emission during smooth and jerky flow in an AlMg alloy. Acta Mater. 2020, 60, 6842–6850. [Google Scholar] [CrossRef]


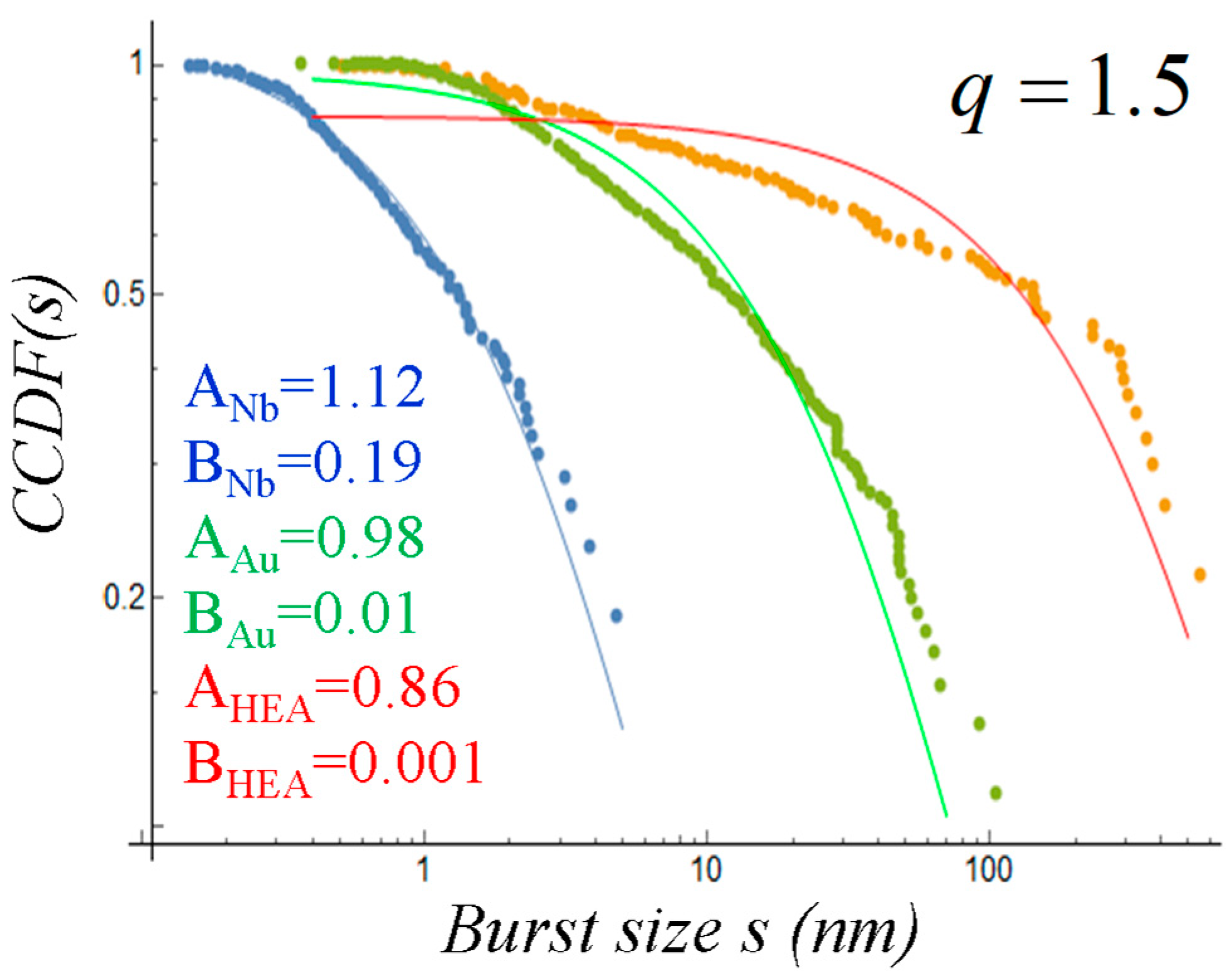

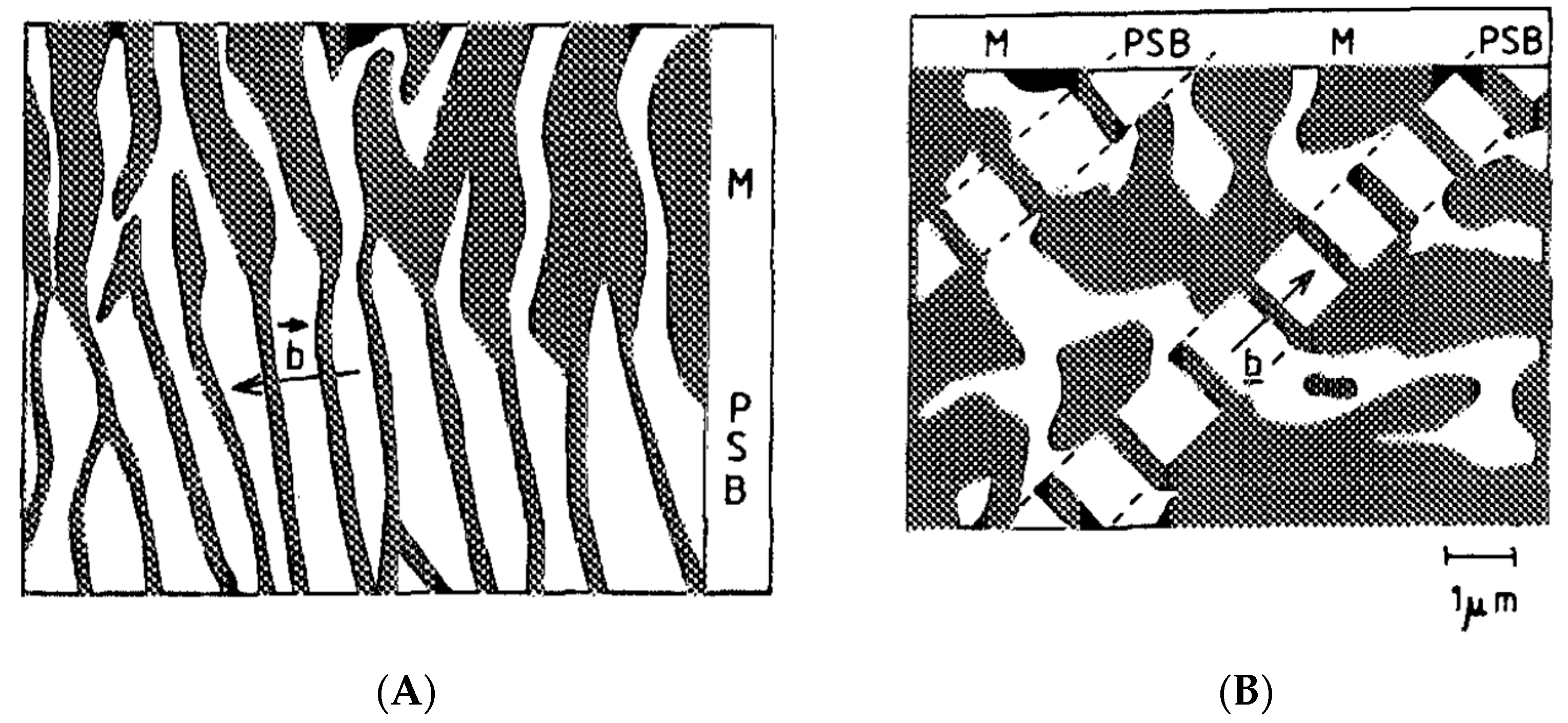
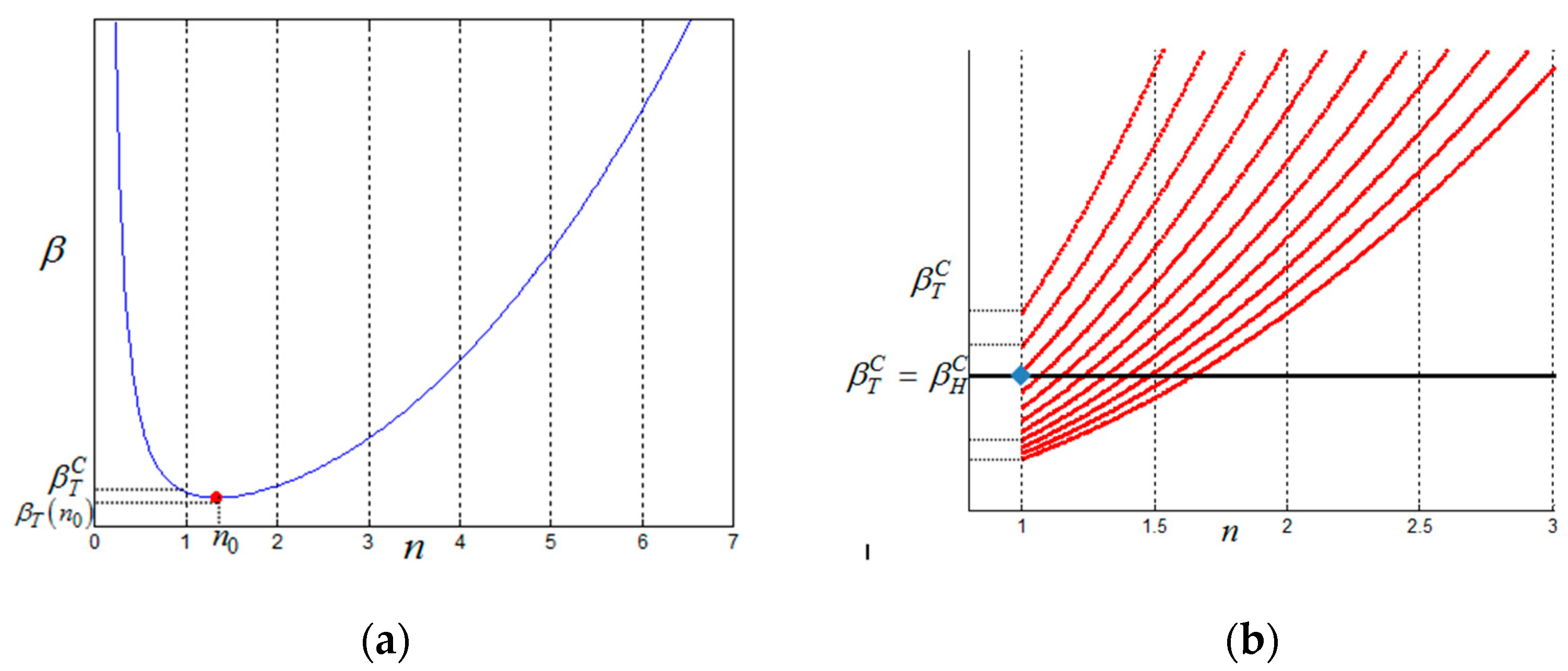
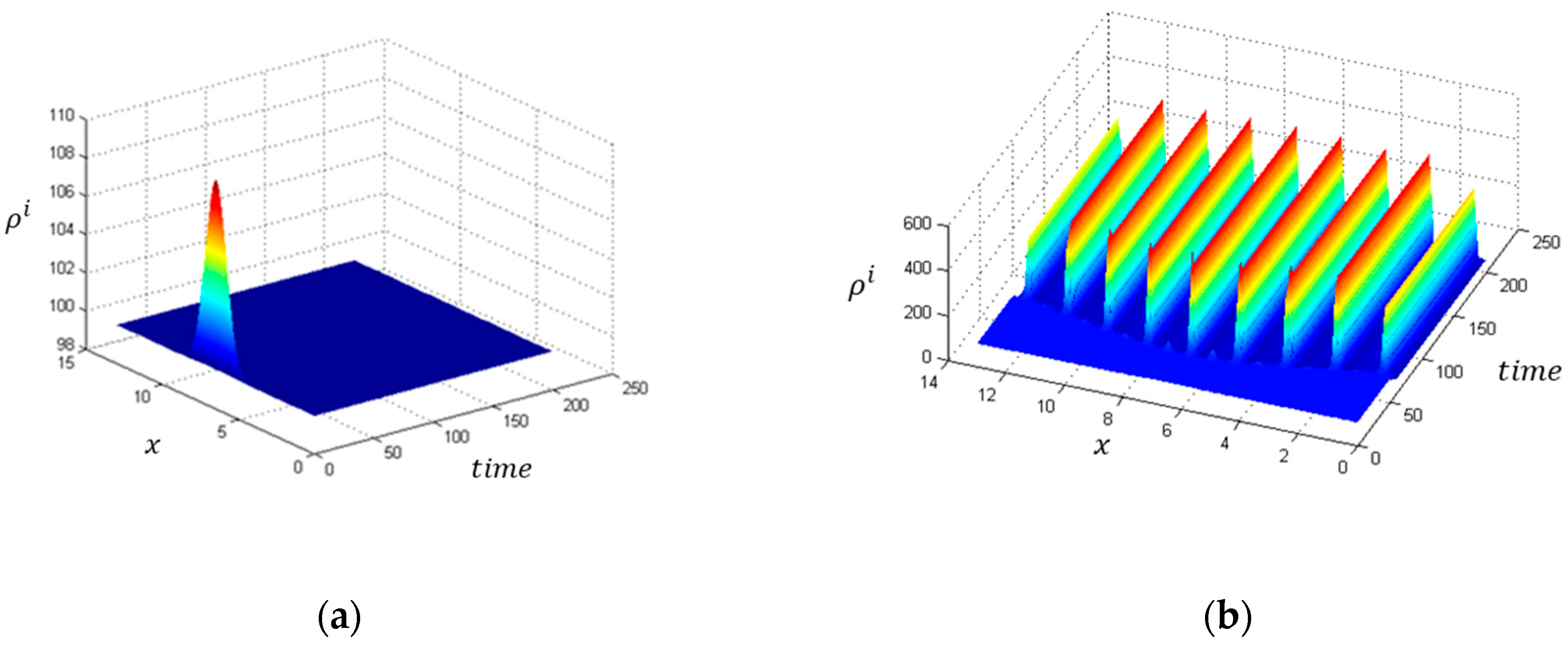
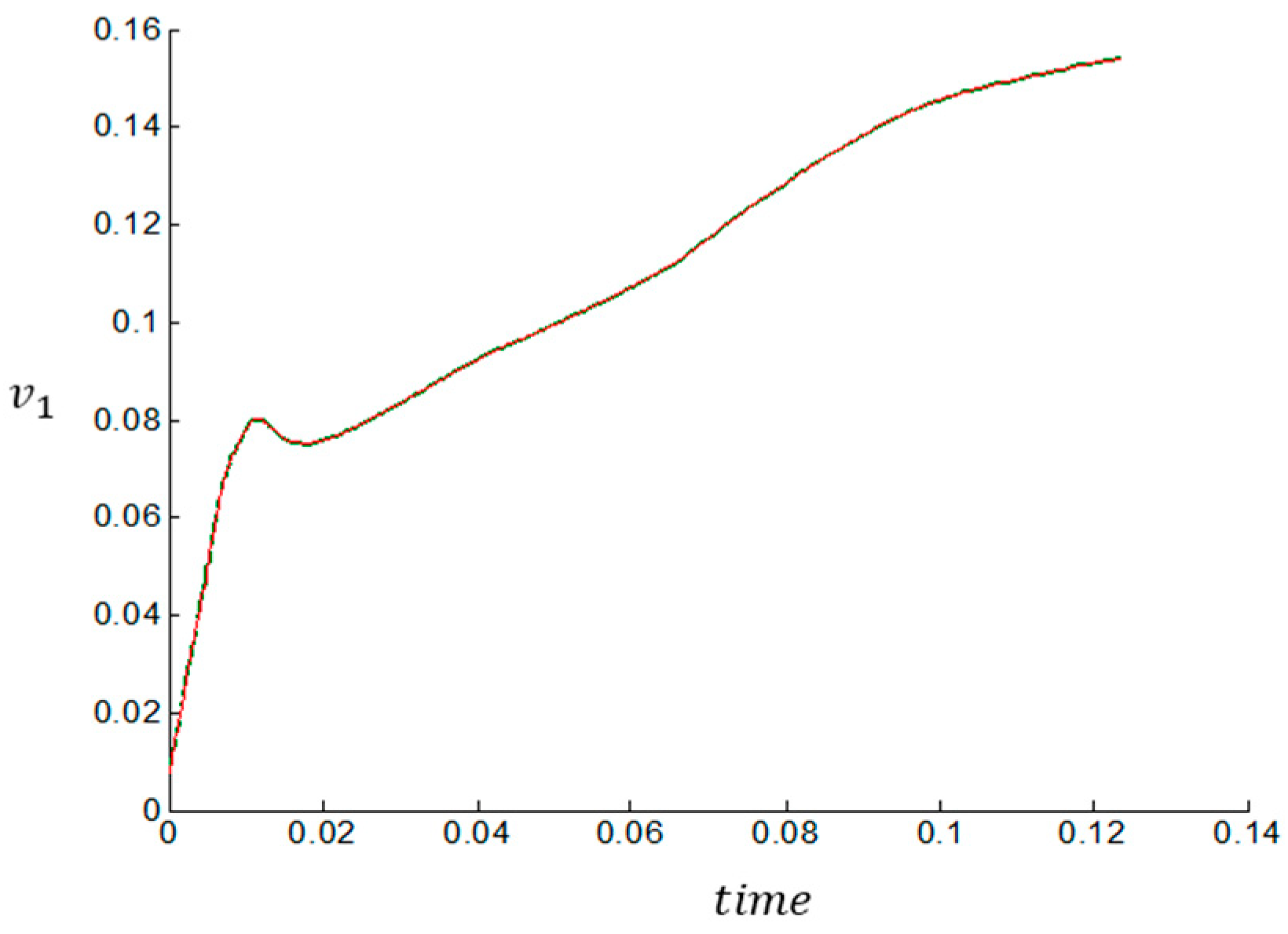
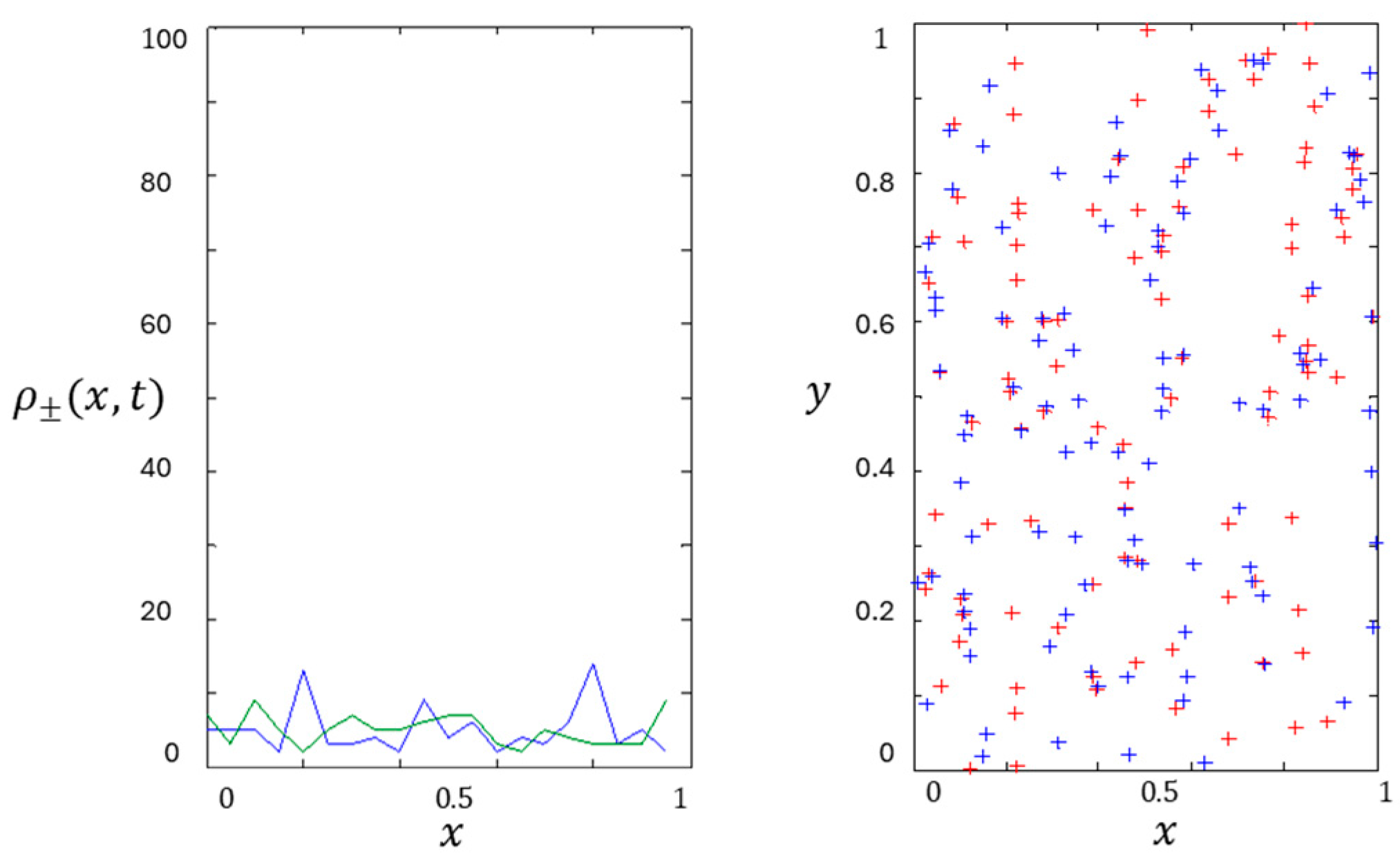


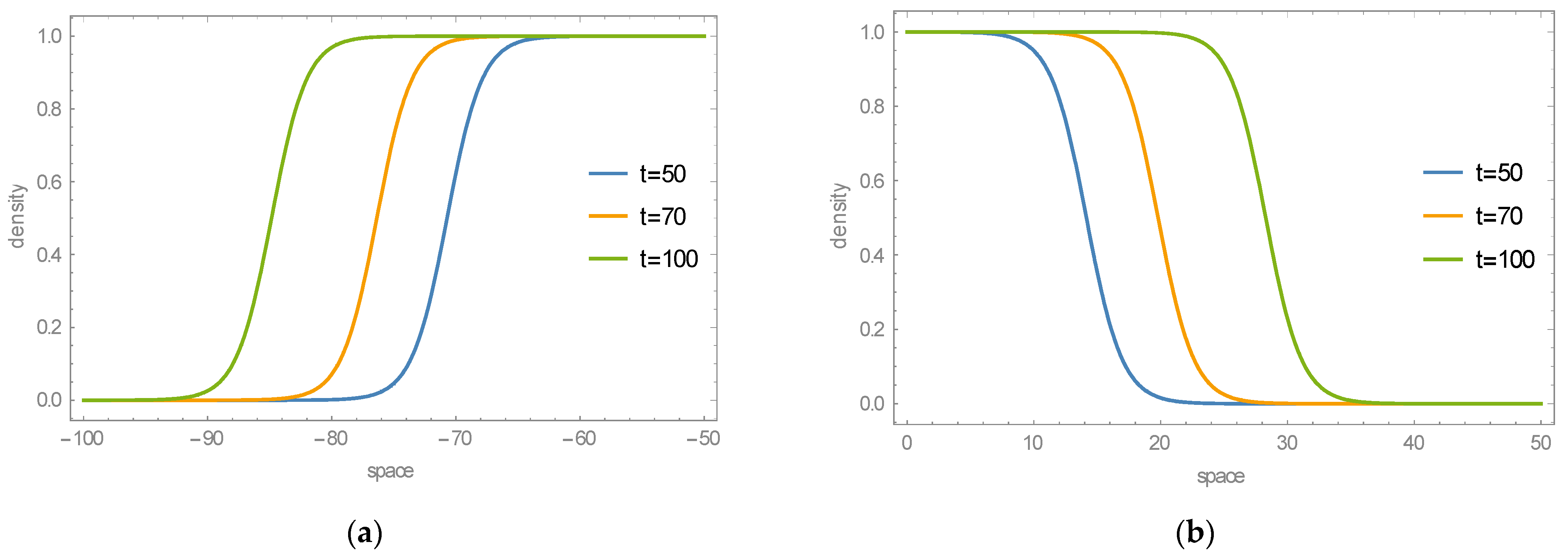
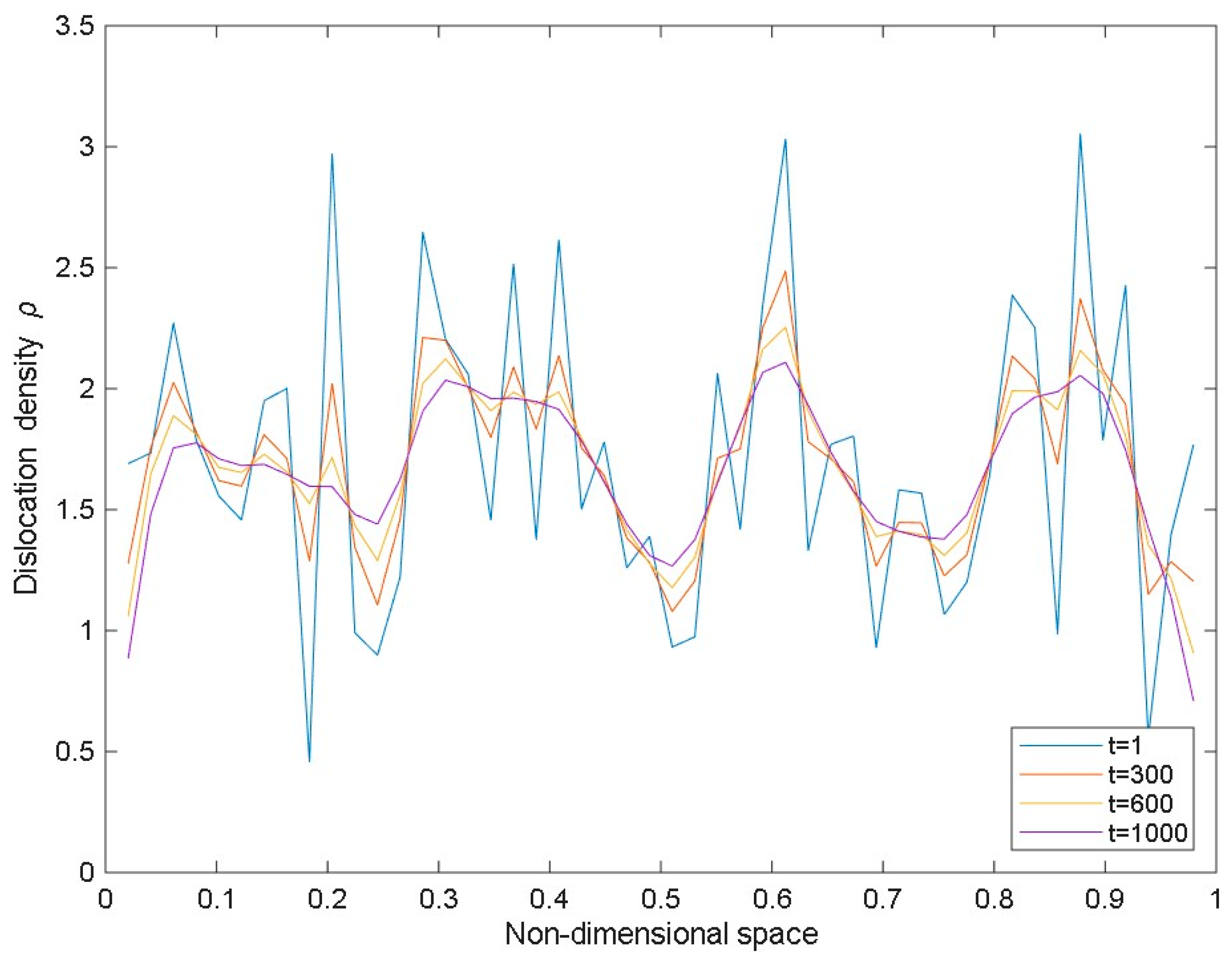
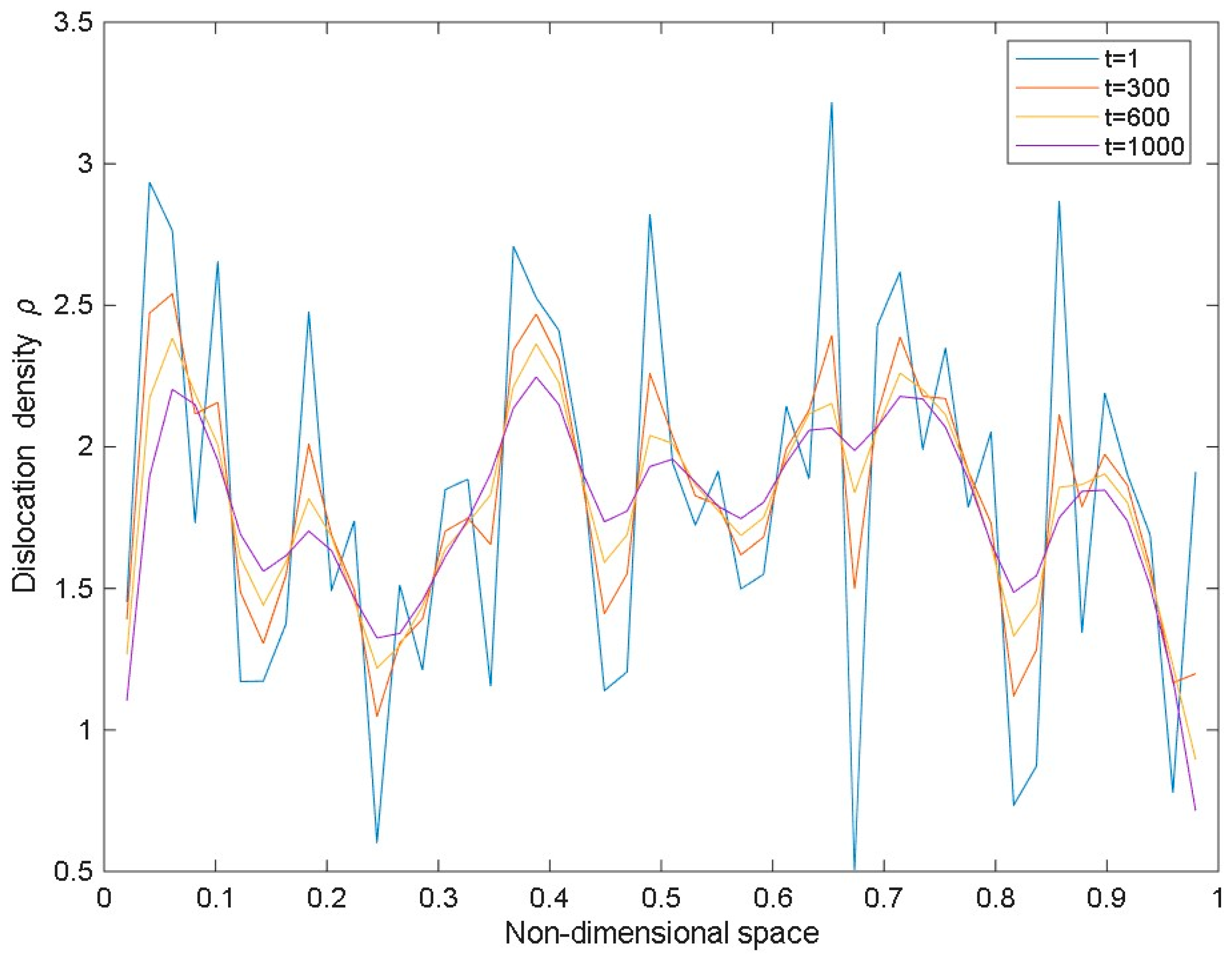
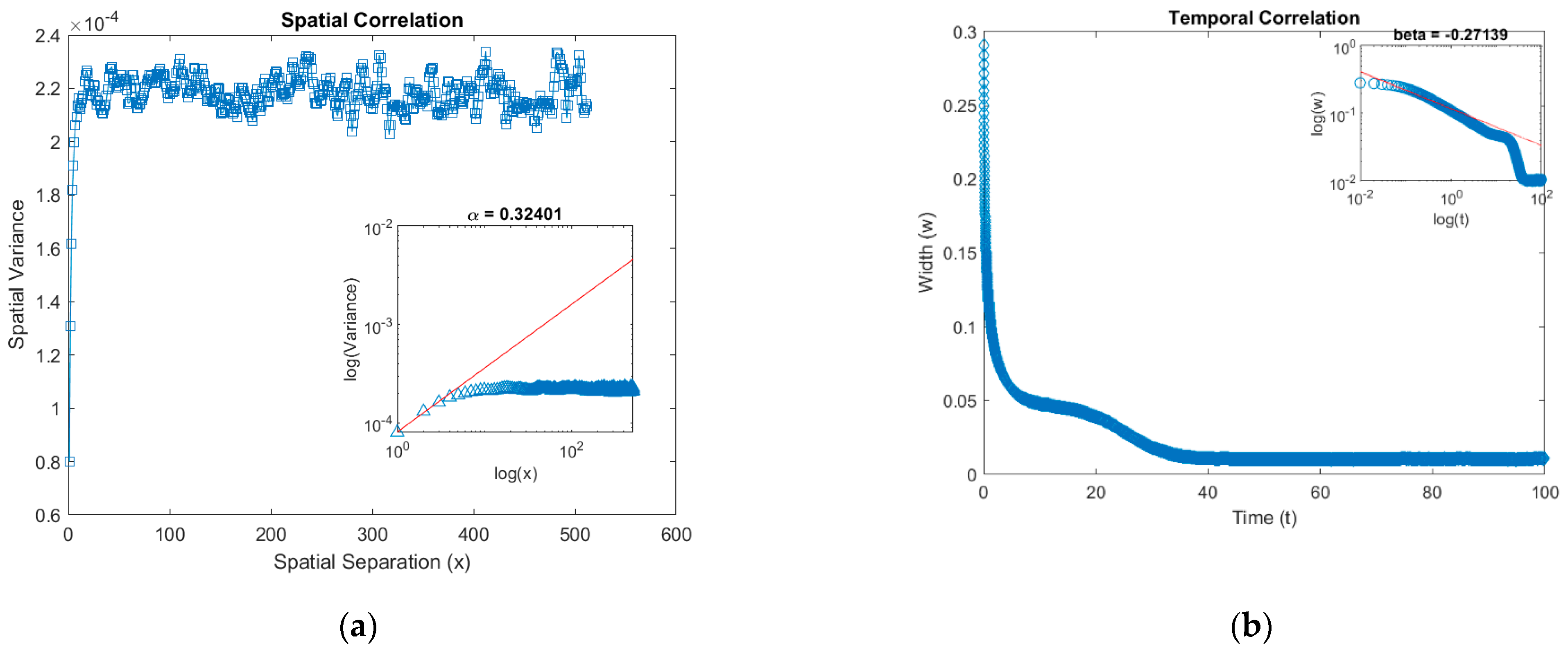
| Images of Microstructures and Multiple Shear Bands [40] | |||||
|---|---|---|---|---|---|
| 1.103 | 1.0034 | 1.5477 | 1.315 | 1.393 | |
| FD | 2.5645 | 2.9409 | 2.2642 | 2.1758 | 2.2187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinidis, A.; Spiliotis, K.; Chattopadhyay, A.; Aifantis, E.C. Self-Organization in Metal Plasticity: An ILG Update. Metals 2025, 15, 1006. https://doi.org/10.3390/met15091006
Konstantinidis A, Spiliotis K, Chattopadhyay A, Aifantis EC. Self-Organization in Metal Plasticity: An ILG Update. Metals. 2025; 15(9):1006. https://doi.org/10.3390/met15091006
Chicago/Turabian StyleKonstantinidis, Avraam, Konstantinos Spiliotis, Amit Chattopadhyay, and Elias C. Aifantis. 2025. "Self-Organization in Metal Plasticity: An ILG Update" Metals 15, no. 9: 1006. https://doi.org/10.3390/met15091006
APA StyleKonstantinidis, A., Spiliotis, K., Chattopadhyay, A., & Aifantis, E. C. (2025). Self-Organization in Metal Plasticity: An ILG Update. Metals, 15(9), 1006. https://doi.org/10.3390/met15091006








