Influence of Casting Texture on Local Material Flow During ECAP of Commercially Pure Aluminum
Abstract
1. Introduction
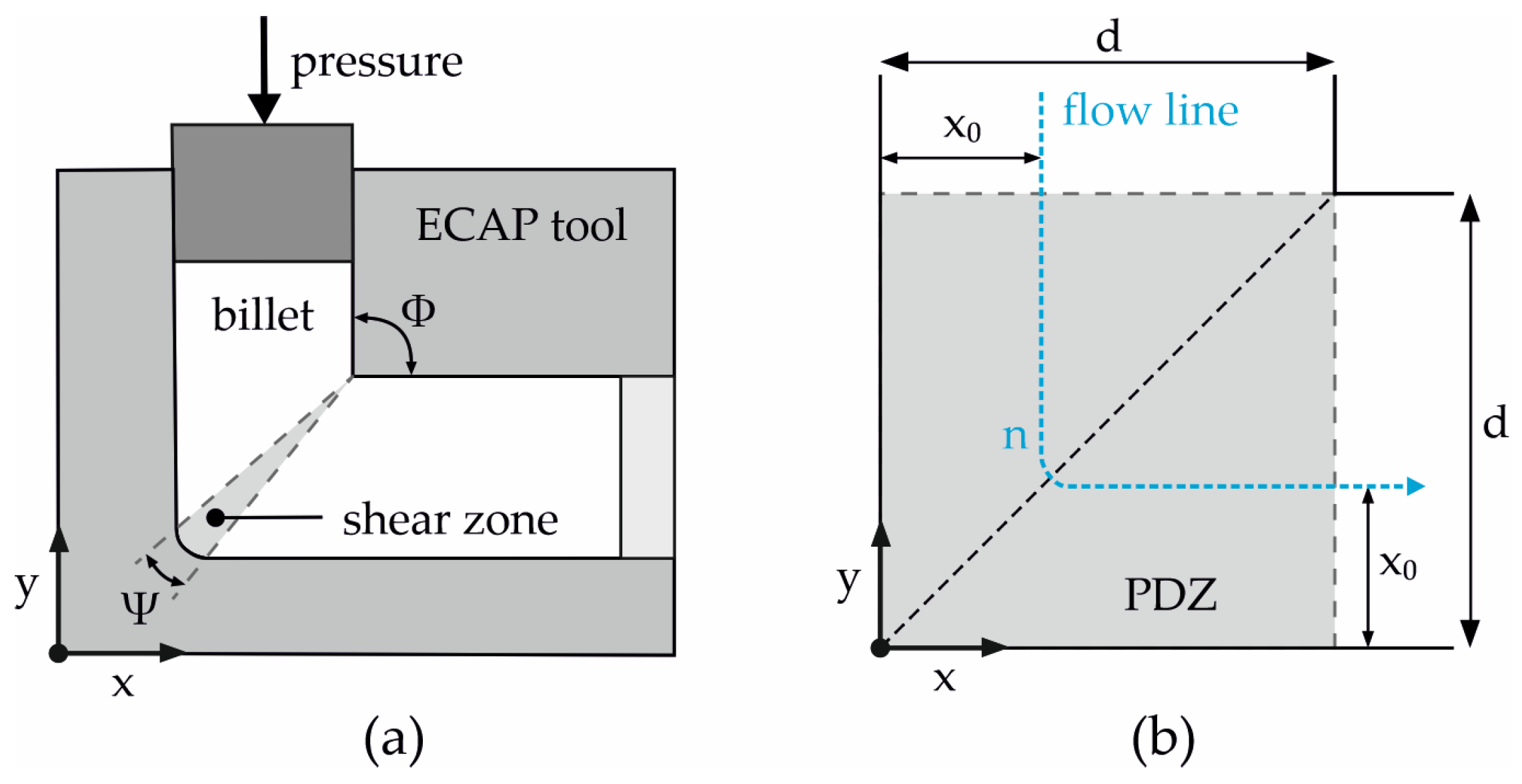
2. Materials and Methods
3. Results and Discussion
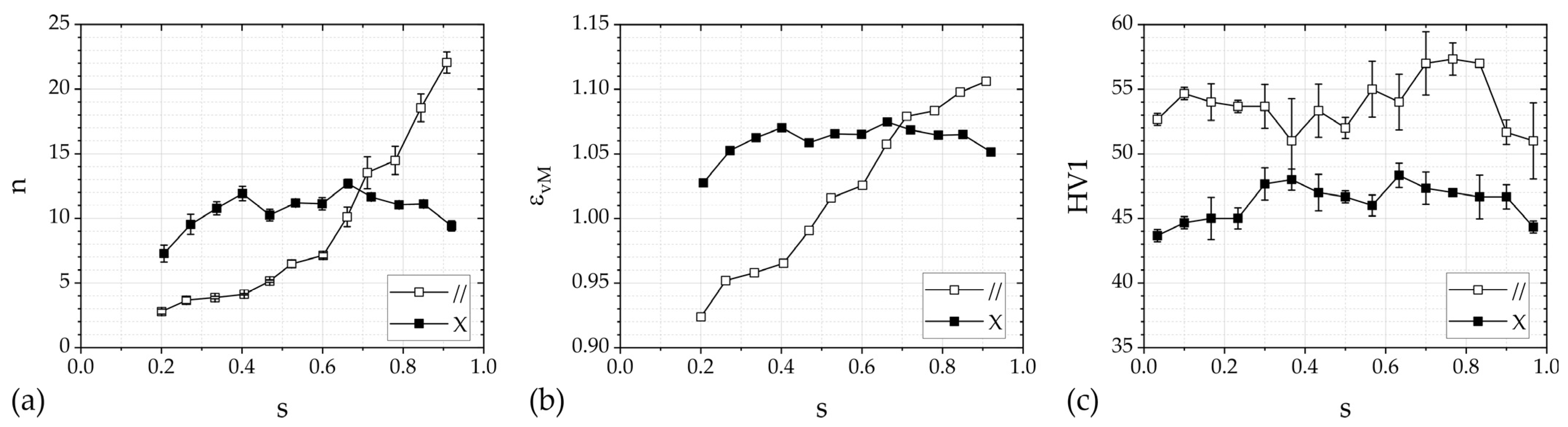
3.1. Flow Line Analysis and Mechanical Properties
3.2. Microstructural Evolution in the Plastic Deformation Zone
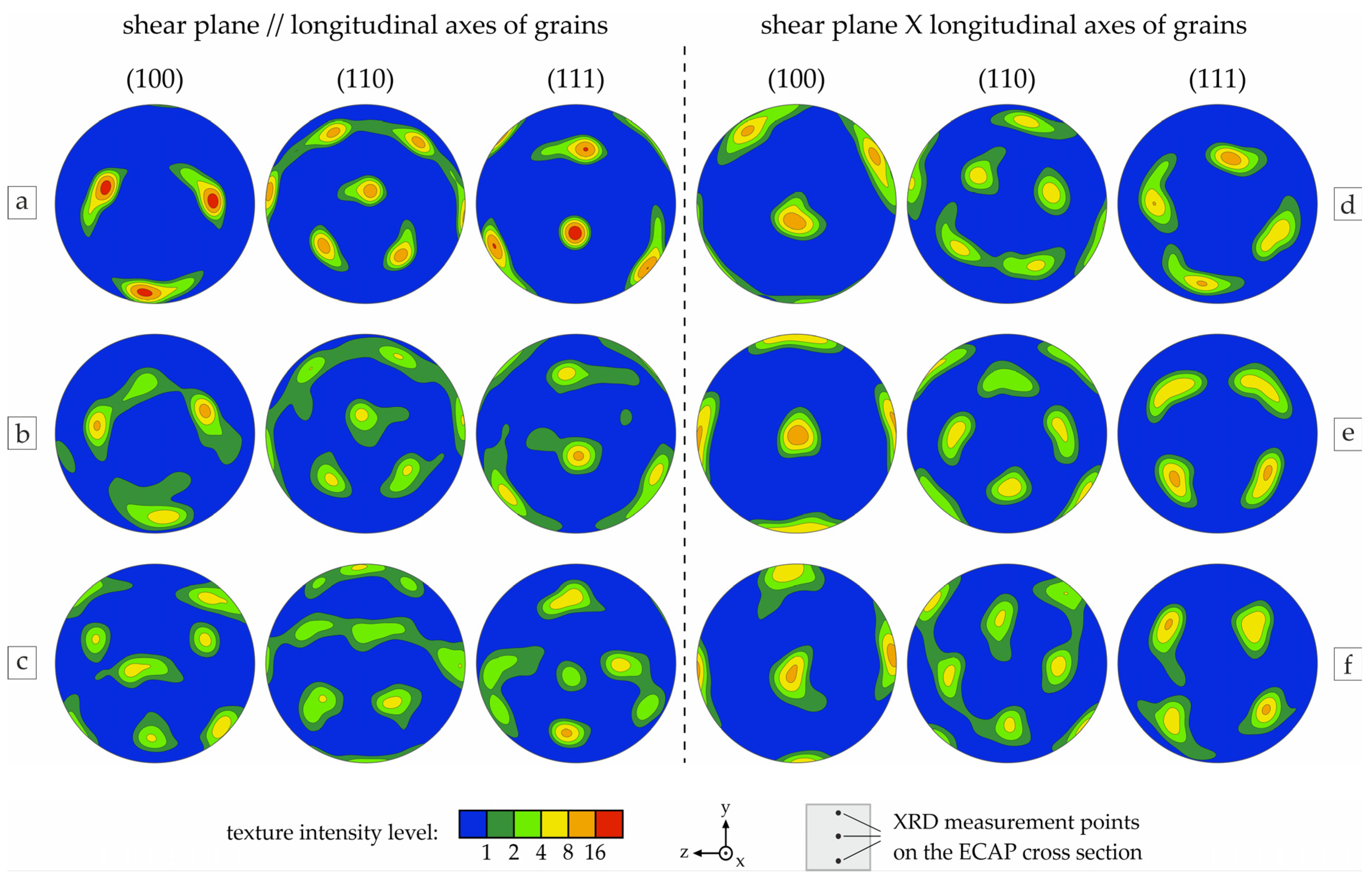
3.3. Microstructure and Texture in the Fully Deformed Material
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CD | Casting Direction |
| EBSD | Electron-Backscatter Diffraction |
| ECAP | Equal-Channel Angular Pressing |
| PDZ | Plastic Deformation Zone |
| RD | Radial Direction |
| XRD | X-ray Diffraction |
References
- Srinivasan, R.; Cherukuri, B.; Chaudhury, P.K. Scaling up of Equal Channel Angular Pressing (ECAP) for the Production of Forging Stock. In Proceedings of the 3rd International Conference on Nanomaterials by Severe Plastics Deformation, NanoSPD3, Fukuoka, Japan, 22–26 September 2005; Trans Tech Publications Ltd.: Fukuoda, Japan, 2006; pp. 371–378. [Google Scholar]
- Sun, J.; Xu, B.; Yang, Z.; Zhuo, X.; Han, J.; Wu, Y.; Song, D.; Liu, H.; Jiang, J.; Ma, A. Developing an Industrial-Scale ECAP Mg-Al-Zn Alloy with Multi-Heterostructure for Synchronously High Strength and Good Ductility. Mater. Charact. 2020, 164, 110341. [Google Scholar] [CrossRef]
- Awasthi, A.; Gupta, A.; Saxena, K.K.; Diwedi, R.K. Equal Channel Angular Processing on Aluminium and Its Alloys—A Review. Mater. Today Proc. 2022, 56, 2388–2391. [Google Scholar] [CrossRef]
- Varone, A.; Fabrizi, A.; Ferro, P.; Montanari, R.; Berto, F.; Bonollo, F. AZ31 Alloy Produced by ECAP: Metallurgical and Mechanical Investigation. J. Mater. Sci. 2024, 60, 495–518. [Google Scholar] [CrossRef]
- Chinna Maddaiah, K.; Naresh, K.; Veeresh Kumar, G.B.; Pramod, R.; Baburao, T.; Rama Sreekanth, P.S. Influence of Equal Channel Angular Extrusion on Mechanical Characteristics and Associated Microstructural Changes of Aluminum, Copper, Titanium and Magnesium Alloys and Their Metal Matrix Composites—A Review. J. Test. Eval. 2023, 51, 1219–1252. [Google Scholar] [CrossRef]
- Bian, Y.L.; Feng, Z.D.; Zhang, N.B.; Li, Y.X.; Wang, X.F.; Zhang, B.B.; Cai, Y.; Lu, L.; Chen, S.; Yao, X.H.; et al. Ultrafast Severe Plastic Deformation in High-Entropy Alloy Al0.1CoCrFeNi via Dynamic Equal Channel Angular Pressing. Mater. Sci. Eng. A 2022, 847, 143221. [Google Scholar] [CrossRef]
- Naseri, M.; Moghadam, A.O.; Anandkumar, M.; Sudarsan, S.; Bodrov, E.; Samodurova, M.; Trofimov, E. Enhancing the Mechanical Properties of High-Entropy Alloys through Severe Plastic Deformation: A Review. J. Alloys Metall. Syst. 2024, 5, 100054. [Google Scholar] [CrossRef]
- Hendriok, L.; Nienaber, M.; Kurz, G.; Ben Khalifa, N. Die Geometry Influence on the Texture and Microstructure Development during Extrusion of AZ31 and ZK60 Magnesium Alloy Chips. Mater. Des. 2025, 249, 113545. [Google Scholar] [CrossRef]
- Krolo, J.; Gudić, S.; Vrsalović, L.; Lela, B.; Dadić, Z. Fatigue and Corrosion Behavior of Solid-State Recycled Aluminum Alloy EN AW 6082. J. Mater. Eng. Perform. 2020, 29, 4310–4321. [Google Scholar] [CrossRef]
- Iwahashi, Y.; Wang, J.; Horita, Z.; Nemoto, M.; Langdon, T.G. Principle of Equal-Channel Angular Pressing for the Processing of Ultra-Fine Grained Materials. Scr. Mater. 1996, 35, 143–146. [Google Scholar] [CrossRef]
- Skrotzki, W. Deformation Heterogeneities in Equal Channel Angular Pressing. Mater. Trans. 2019, 60, 1331–1343. [Google Scholar] [CrossRef]
- da Silva Lima, M.N.; Rodrigues, S.F.; Al-Maharbi, M.; Muñoz, J.C.; Cabrera Marrero, J.M.; Gomes de Abreu, H.F. Effect of ECAP Processing Temperature on an Austenitic TWIP Steel’s Microstructure, Texture and Mechanical Properties. J. Mater. Res. Technol. 2023, 24, 1757–1775. [Google Scholar] [CrossRef]
- Gupta, A.; Saxena, K.K.; Bharti, A.; Lade, J.; Chadha, K.; Paresi, P.R. Influence of ECAP Processing Temperature and Number of Passes on Hardness and Microstructure of Al-6063. Adv. Mater. Process. Technol. 2022, 8, 1635–1646. [Google Scholar] [CrossRef]
- Li, S.; Bourke, M.A.M.; Beyerlein, I.J.; Alexander, D.J.; Clausen, B. Finite Element Analysis of the Plastic Deformation Zone and Working Load in Equal Channel Angular Extrusion. Mater. Sci. Eng. A 2004, 382, 217–236. [Google Scholar] [CrossRef]
- Suo, T.; Li, Y.; Guo, Y.; Liu, Y. The Simulation of Deformation Distribution during ECAP Using 3D Finite Element Method. Mater. Sci. Eng. A 2006, 432, 269–274. [Google Scholar] [CrossRef]
- Panigrahi, A.; Scheerbaum, N.; Chekhonin, P.; Scharnweber, J.; Beausir, B.; Hockauf, M.; Sankaran, S.; Skrotzki, W. Effect of Back Pressure on Material Flow and Texture in ECAP of Aluminum. IOP Conf. Ser. Mater. Sci. Eng. 2014, 63, 012153. [Google Scholar] [CrossRef]
- Mckenzie, P.W.J.; Lapovok, R.; Estrin, Y. The Influence of Back Pressure on ECAP Processed AA 6016: Modeling and Experiment. Acta Mater. 2007, 55, 2985–2993. [Google Scholar] [CrossRef]
- Daghigh, M.; Mohri, M.; Nili-ahmadabadi, M. Tailoring Deformation Homogeneity of WE43 Alloy through Strain Rate Sensitivity and Back Pressure during Equal Channel Angular Pressing. J. Mater. Eng. Perform. 2024, 33, 12604–12619. [Google Scholar] [CrossRef]
- An, X.H.; Wu, S.D.; Zhang, Z.F. Influence of Stacking Fault Energy on the Microstructures and Grain Refinement in the Cu-Al Alloys during Equal-Channel Angular Pressing. Mater. Sci. Forum 2011, 667–669, 379–384. [Google Scholar] [CrossRef]
- Asano, M.; Yuasa, M.; Miyamoto, H. Effects of Stacking Fault Energy and Solute Atoms on Microstructural Evolution of Cu, Ag and Cu–Al Alloys Processed by Equal Channel Angular Pressing. Mater. Sci. Eng. A 2021, 803, 140716. [Google Scholar] [CrossRef]
- Fukuda, Y.; Oh-Ishi, K.; Furukawa, M.; Horita, Z.; Langdon, T.G. Influence of Crystal Orientation on the Processing of Copper Single Crystals by ECAP. J. Mater. Sci. 2007, 42, 1501–1511. [Google Scholar] [CrossRef]
- Meng, Q.; Yang, X.; Liu, X.; Luo, L. Effects of Initial Grain Size on Microstructure and Properties of Pure Ti Processed by ECAP. Rare Met. Mater. Eng. 2022, 51, 1949–1956. [Google Scholar] [CrossRef]
- Bian, L.; Liu, X.; Wang, T.; Liang, W.; Zheng, Y. Influence of Various Initial Microstructures on Microstructure and Mechanical Property of ECAP Processed Mg-8.4Li-3.58Al-0.36Si-0.05Ti-0.01B Alloys. Mater. Sci. Eng. A 2023, 872, 144022. [Google Scholar] [CrossRef]
- Frint, P.; Wagner, M.F.-X. Strain Partitioning by Recurrent Shear Localization during Equal-Channel Angular Pressing of an AA6060 Aluminum Alloy. Acta Mater. 2019, 176, 306–317. [Google Scholar] [CrossRef]
- Fukuda, Y.; Oh-ishi, K.; Furukawa, M.; Horita, Z.; Langdon, T.G. The Application of Equal-Channel Angular Pressing to an Aluminum Single Crystal. Acta Mater. 2004, 52, 1387–1395. [Google Scholar] [CrossRef]
- Fukuda, Y.; Oh-ishi, K.; Furukawa, M.; Horita, Z.; Langdon, T.G. Influence of Crystal Orientation on ECAP of Aluminum Single Crystals. Mater. Sci. Eng. A 2006, 420, 79–86. [Google Scholar] [CrossRef]
- Furukawa, M.; Kawasaki, Y.; Miyahara, Y.; Horita, Z.; Langdon, T.G. An Investigation of the Deformation Process during Equal-Channel Angular Pressing of an Aluminum Single Crystal. Mater. Sci. Eng. A 2005, 410–411, 194–200. [Google Scholar] [CrossRef]
- Miyamoto, H.; Ikeda, T.; Uenoya, T.; Vinogradov, A.; Hashimoto, S. Reversible Nature of Shear Bands in Copper Single Crystals Subjected to Iterative Shear of ECAP in Forward and Reverse Directions. Mater. Sci. Eng. A 2011, 528, 2602–2609. [Google Scholar] [CrossRef]
- Guo, T.; Wei, S.; Wang, C.; Li, Q.; Jia, Z. Texture Evolution and Strengthening Mechanism of Single Crystal Copper During ECAP. Mater. Sci. Eng. A 2019, 759, 97–104. [Google Scholar] [CrossRef]
- Grosdidier, T.; Fundenberger, J.J.; Goran, D.; Bouzy, E.; Suwas, S.; Skrotzki, W.; Tóth, L.S. On Microstructure and Texture Heterogeneities in Single Crystals Deformed by Equal Channel Angular Extrusion. Scr. Mater. 2008, 59, 1087–1090. [Google Scholar] [CrossRef]
- Syarif, J.; Altoyuri, A.; Mohamed, I.F. Equal Channel Angular Pressing of Single Crystal Aluminum: A Molecular Dynamics Simulation. J. Mater. Res. Technol. 2022, 17, 888–897. [Google Scholar] [CrossRef]
- Altoyuri, A.H.; Syarif, J.; Sajuri, Z. Deformation Behavior of Single-Crystal Magnesium during Nano-ECAP Simulation. Heliyon 2022, 8, e11837. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, H.; Luan, T.; Jin, Y. Molecular Dynamics Analysis of Microstructural Deformation Mechanisms in Single Crystal Copper Undergoing Equal Channel Angular Pressing. AIP Adv. 2025, 15, 015110. [Google Scholar] [CrossRef]
- Lee, C.S.; Duggan, B.J.; Smallman, R.E. A Theory of Deformation Banding in Cold Rolling. Acta Metall. Mater. 1993, 41, 2265–2270. [Google Scholar] [CrossRef]
- Zhu, L.; Seefeldt, M.; Verlinden, B. Deformation Banding in a Nb Polycrystal Deformed by Successive Compression Tests. Acta Mater. 2012, 60, 4349–4358. [Google Scholar] [CrossRef]
- Tóth, L.S. Texture Evolution in Severe Plastic Deformation by Equal Channel Angular Extrusion. Adv. Eng. Mater. 2003, 5, 308–316. [Google Scholar] [CrossRef]
- Tóth, L.S.; Massion, R.A.; Germain, L.; Baik, S.C.; Suwas, S. Analysis of Texture Evolution in Equal Channel Angular Extrusion of Copper Using a New Flow Field. Acta Mater. 2004, 52, 1885–1898. [Google Scholar] [CrossRef]
- Berndt, N.; Böhme, M.; Wagner, M.F.-X. Multi-Gradient Structures by Cold Extrusion of Strongly Textured Continuously Cast Commercially Pure Aluminum. J. Mater. Res. Technol. 2024, 31, 1355–1366. [Google Scholar] [CrossRef]
- Wagner, M.F.-X.; Nostitz, N.; Frint, S.; Frint, P.; Ihlemann, J. Plastic Flow During Equal-Channel Angular Pressing with Arbitrary Tool Angles. Int. J. Plast. 2020, 134, 102755. [Google Scholar] [CrossRef]
- Berndt, N.; Reiser, N.A.; Wagner, M.F.-X. Evolution of Plastic Deformation during Multi-Pass ECAP of an AA6060 Aluminum Alloy—An Experimental Flow Line Analysis. J. Mater. Res. Technol. 2025, 34, 359–371. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX- Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef]
- Niemann, R.; Hahn, S.; Diestel, A.; Backen, A.; Schultz, L.; Nielsch, K.; Wagner, M.F.-X.; Fähler, S. Reducing the Nucleation Barrier in Magnetocaloric Heusler Alloys by Nanoindentation. APL Mater. 2016, 4, 064101. [Google Scholar] [CrossRef]
- Schleifenbaum, S.; Prietzel, T.; Aust, G.; Boldt, A.; Fritsch, S.; Keil, I.; Koch, H.; Möbius, R.; Scheidt, H.A.; Wagner, M.F.X.; et al. Acellularization-Induced Changes in Tensile Properties Are Organ Specific—An In-Vitro Mechanical and Structural Analysis of Porcine Soft Tissues. PLoS ONE 2016, 11, e0151223. [Google Scholar] [CrossRef] [PubMed]
- Rade, L.; Westergren, B. Mathematics Handbook for Science and Engineering, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Beyerlein, I.J.; Tomé, C.N. Analytical modeling of material flow in equal channel angular extrusion (ECAE). Mater. Sci. Eng. A 2004, 380, 171–190. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berndt, N.; Wagner, M.F.-X. Influence of Casting Texture on Local Material Flow During ECAP of Commercially Pure Aluminum. Metals 2025, 15, 904. https://doi.org/10.3390/met15080904
Berndt N, Wagner MF-X. Influence of Casting Texture on Local Material Flow During ECAP of Commercially Pure Aluminum. Metals. 2025; 15(8):904. https://doi.org/10.3390/met15080904
Chicago/Turabian StyleBerndt, Nadja, and Martin Franz-Xaver Wagner. 2025. "Influence of Casting Texture on Local Material Flow During ECAP of Commercially Pure Aluminum" Metals 15, no. 8: 904. https://doi.org/10.3390/met15080904
APA StyleBerndt, N., & Wagner, M. F.-X. (2025). Influence of Casting Texture on Local Material Flow During ECAP of Commercially Pure Aluminum. Metals, 15(8), 904. https://doi.org/10.3390/met15080904







