Experimental Study on the Microscale Milling Process of DD5 Nickel-Based Single-Crystal Superalloy
Abstract
1. Introduction
2. Micro-Scale Milling Finite Element Analysis
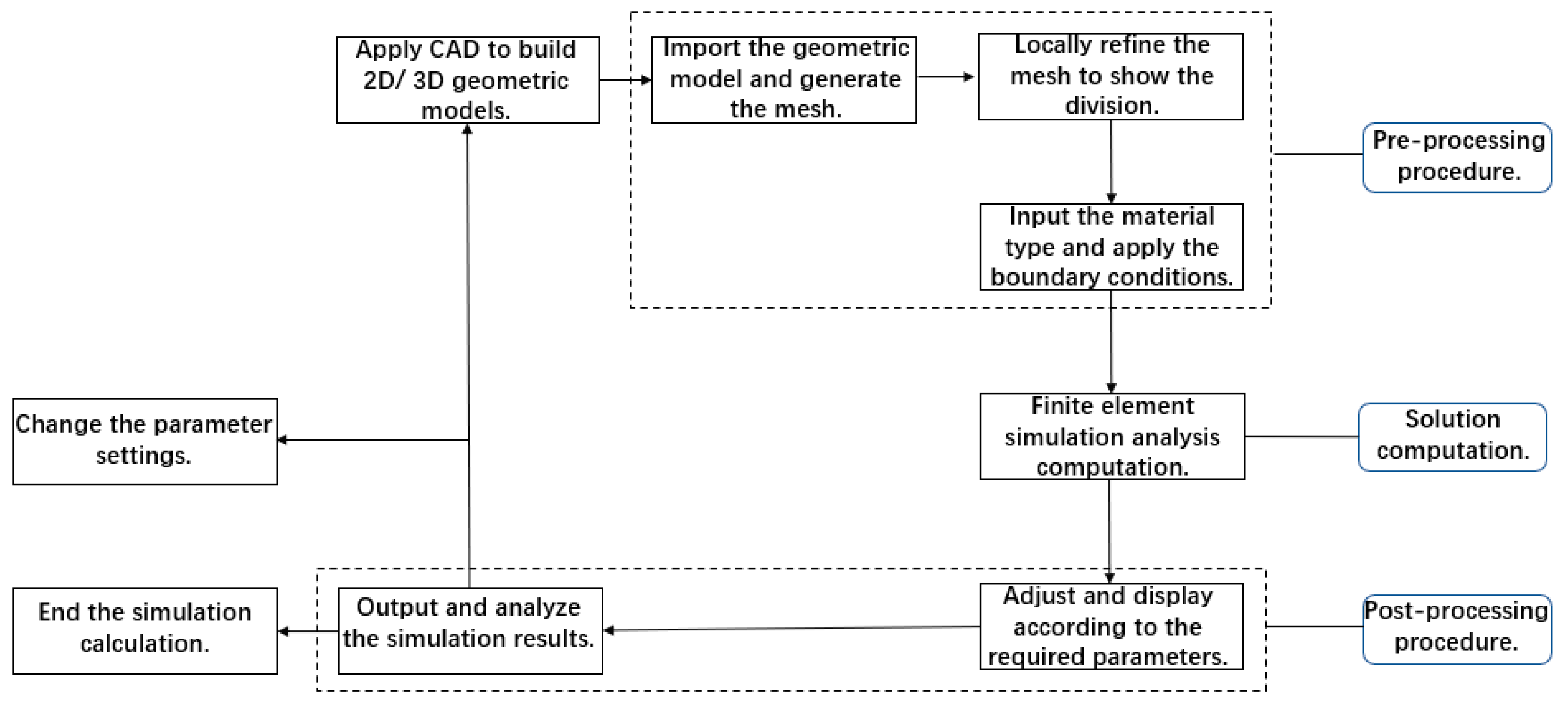
2.1. ABAQUS Analysis Steps
2.2. Micro-Milling Model Establishment
2.2.1. Determination of Constitutive Model and Material Constants
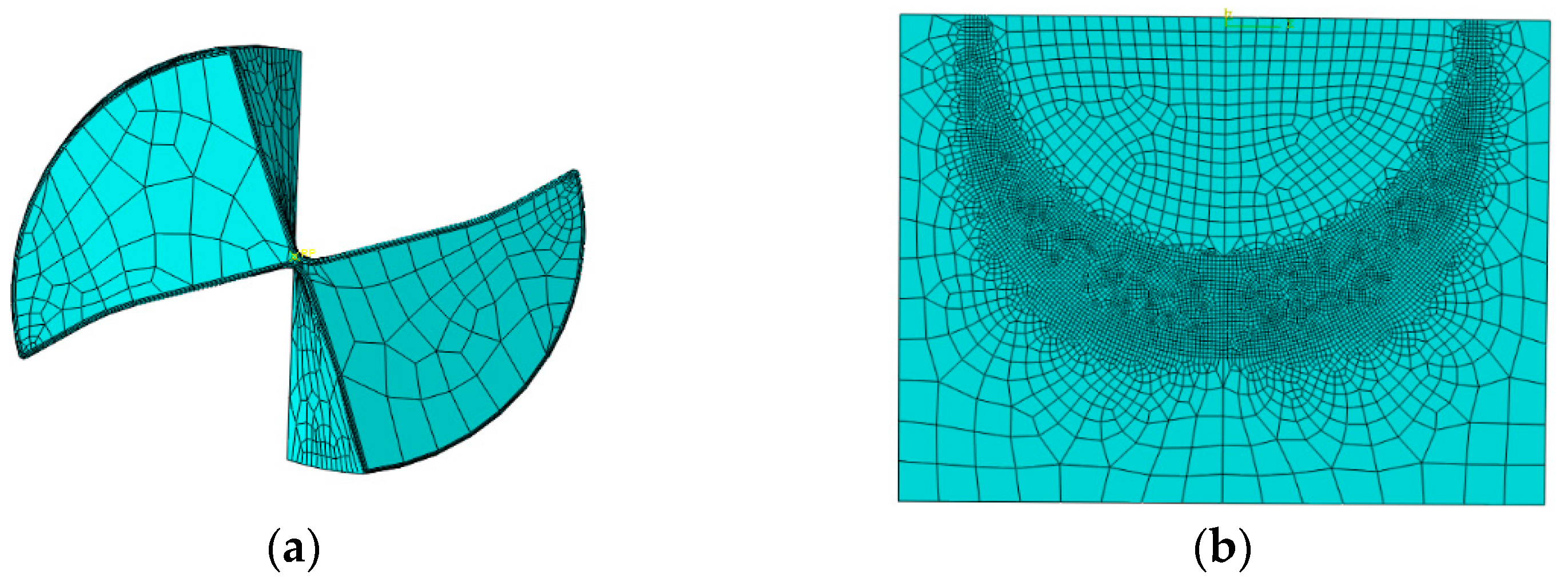
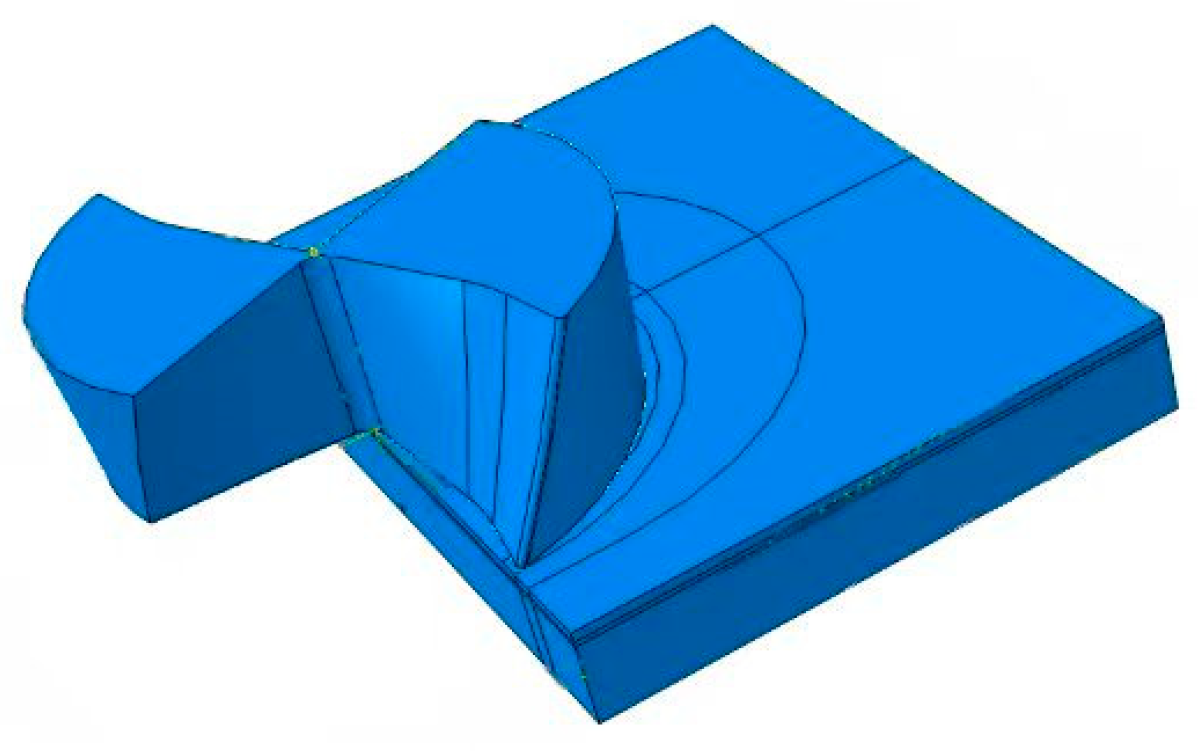
2.2.2. Model Establishment, Assembly, and Meshing
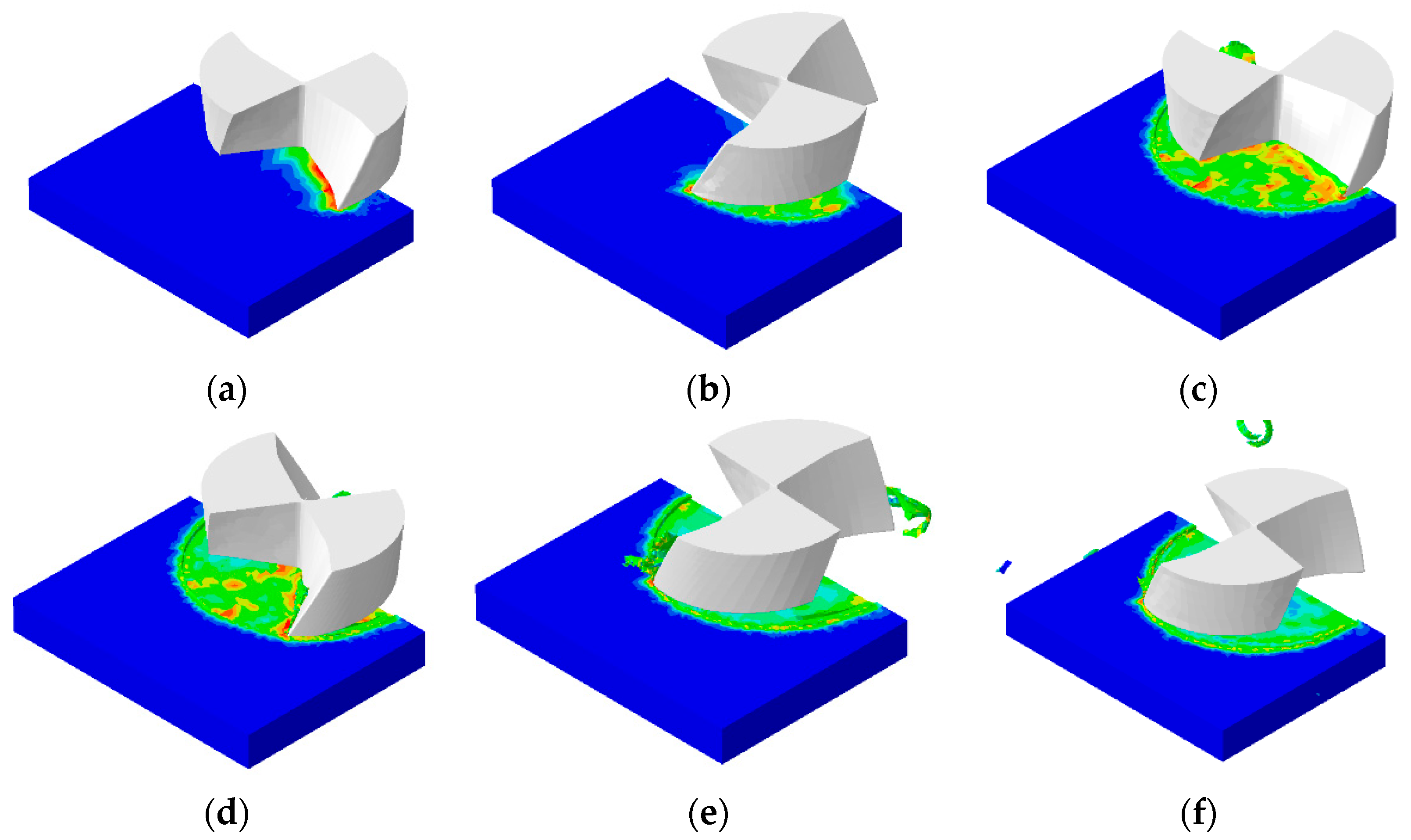
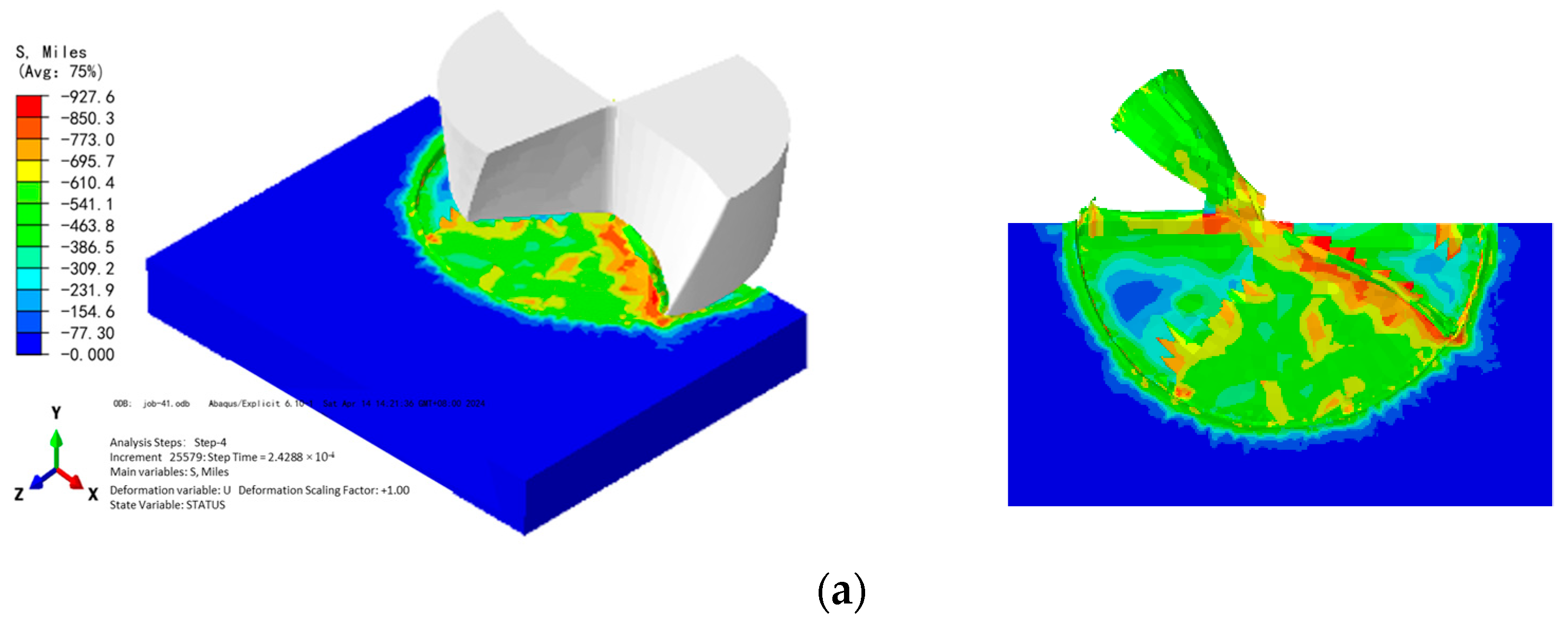
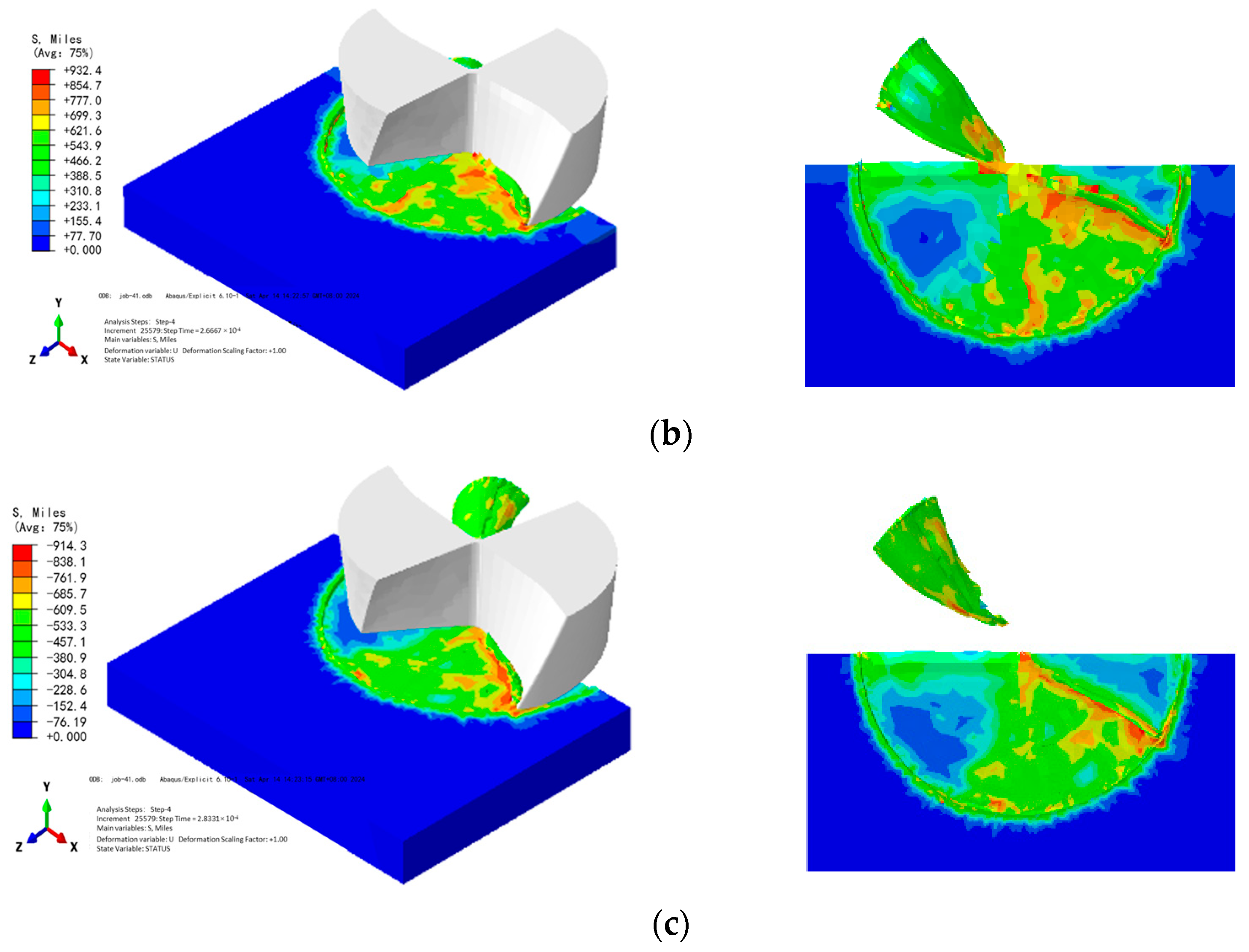
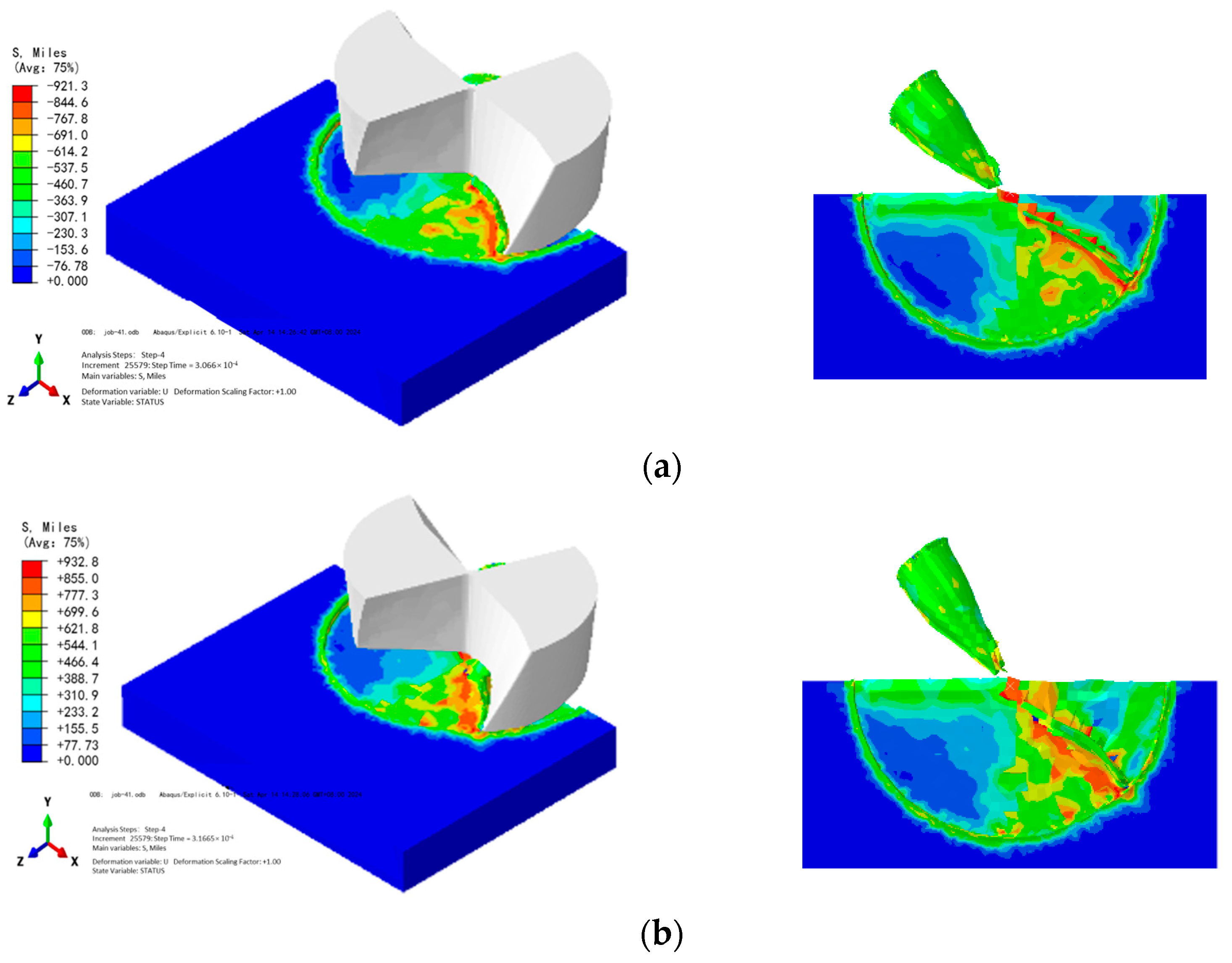
2.3. Analysis of Simulation Results
3. Experimental Design Methods and Instruments and Equipment
3.1. Experimental Equipment and Testing Instruments
3.1.1. Processing Equipment
3.1.2. Testing Equipment
3.2. Experimental Design Scheme
4. Experimental Plan and Results
4.1. Experimental Plan and Data
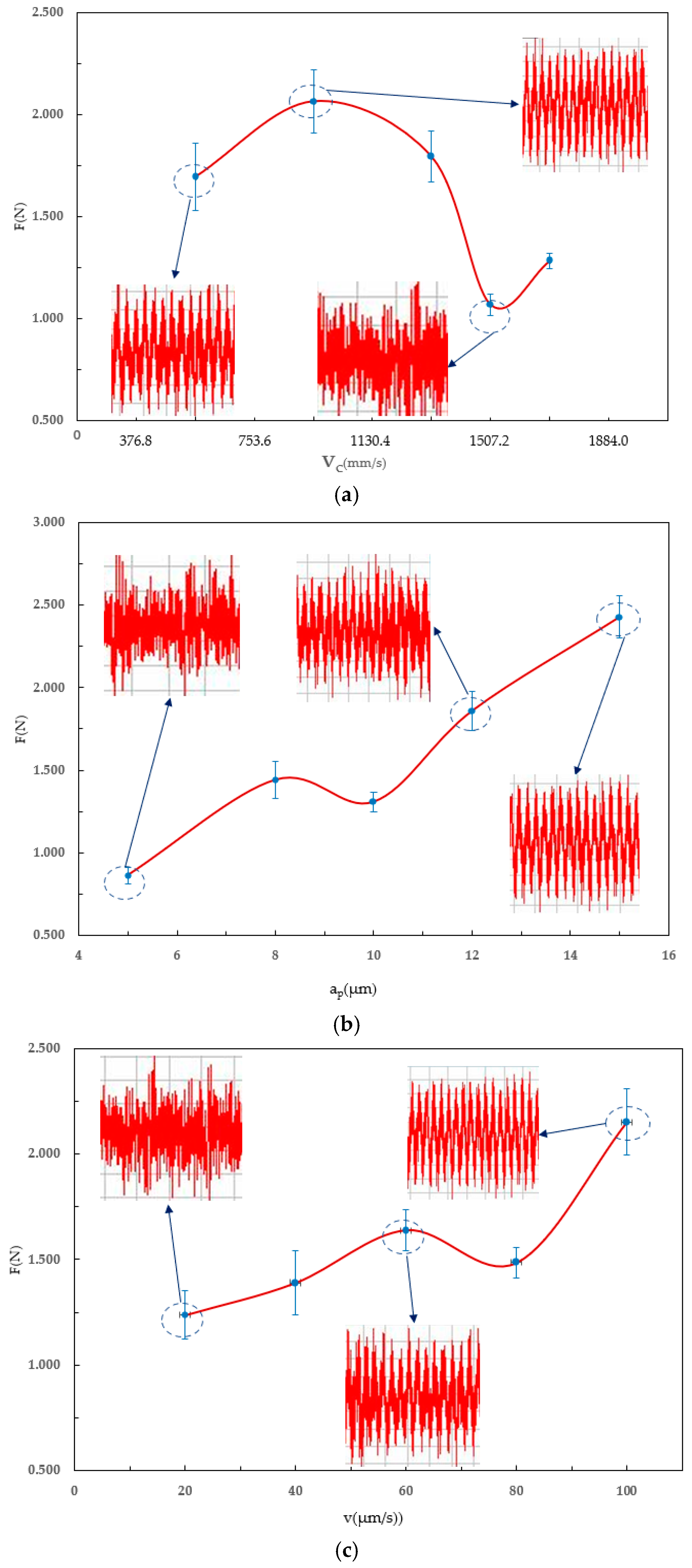
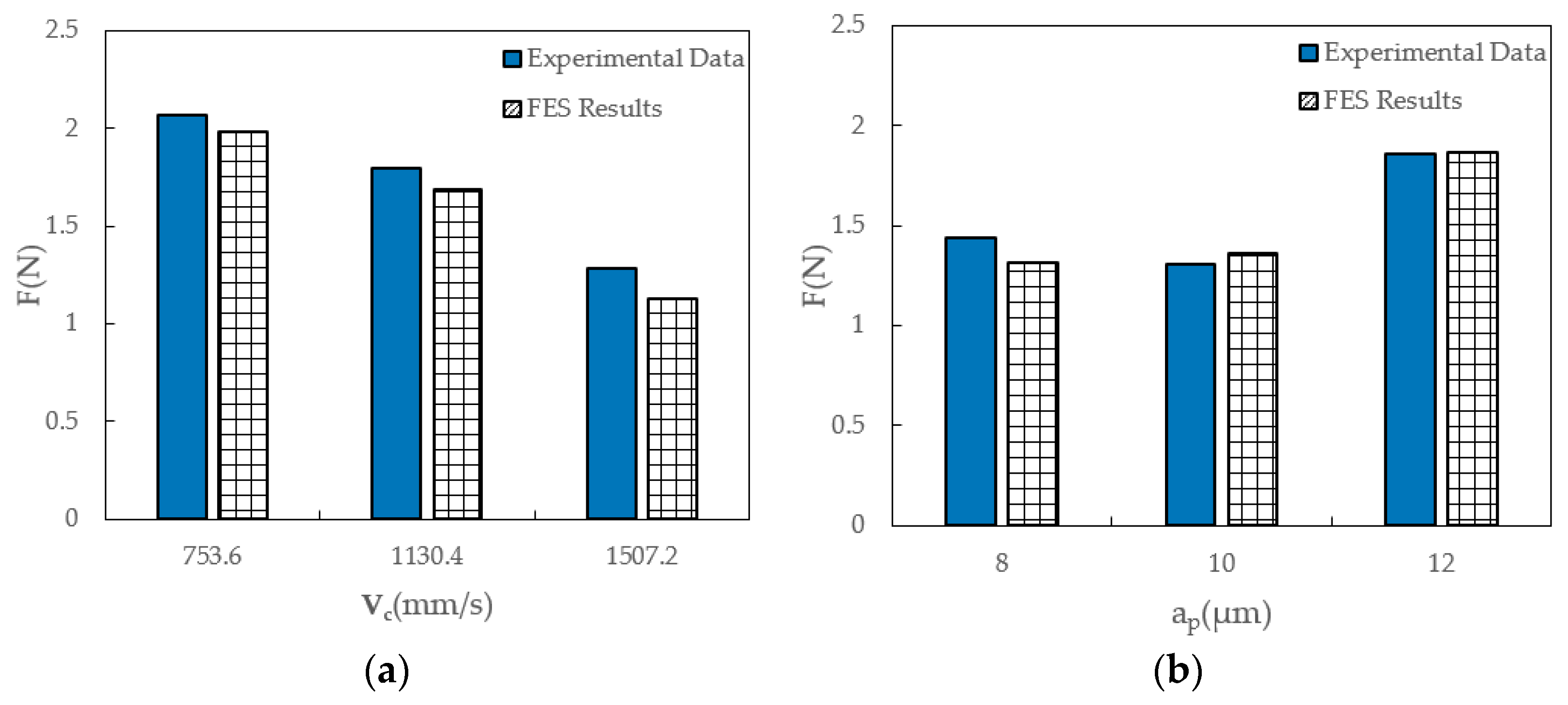
4.2. Effect of Cutting Parameters on Milling Force
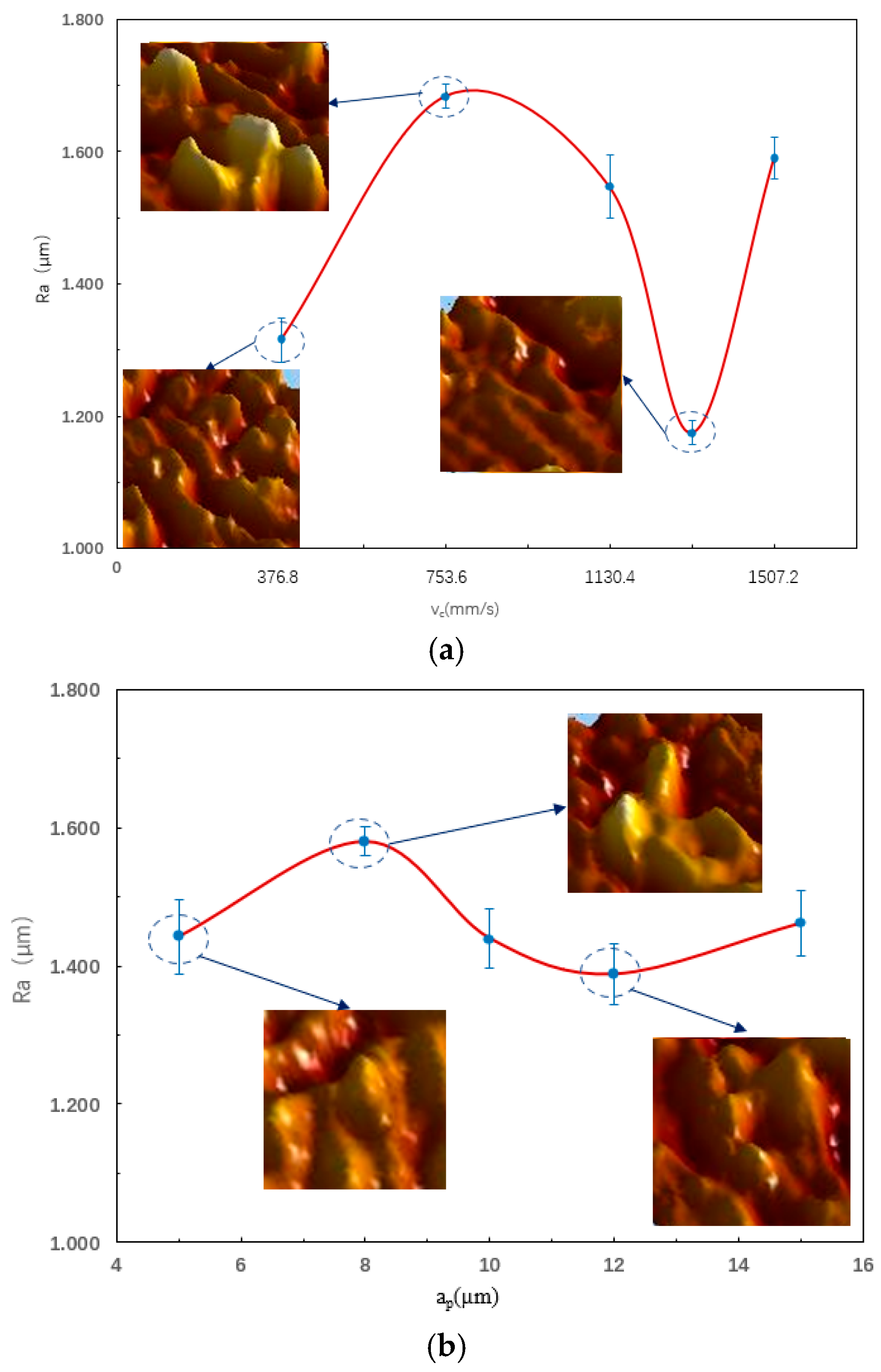
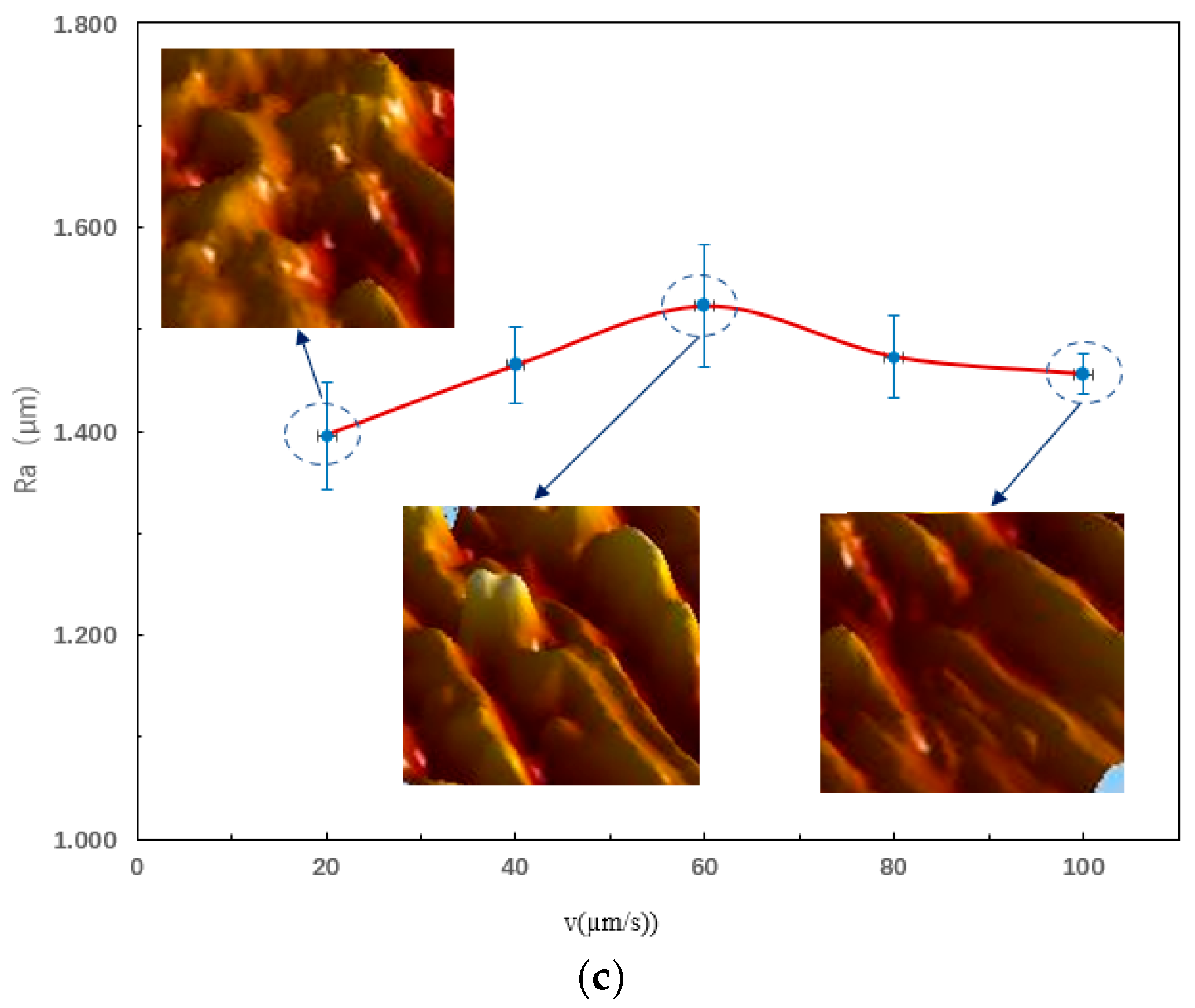
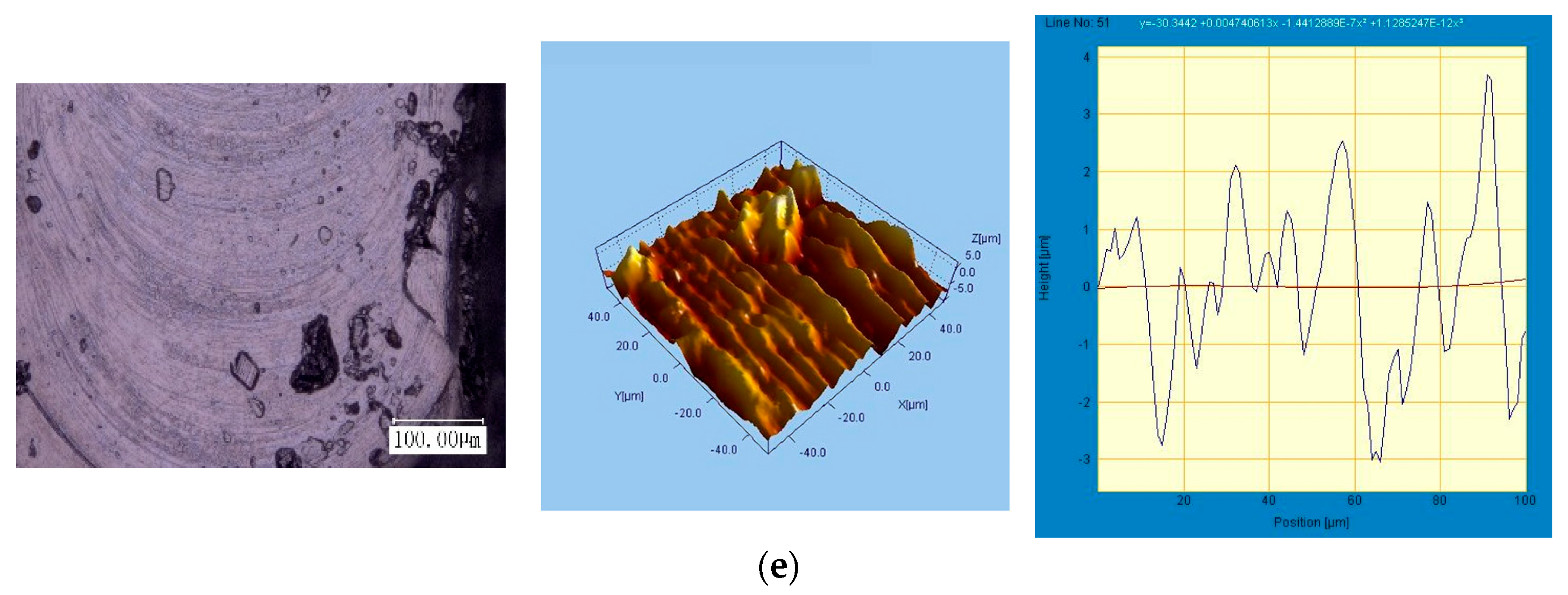
4.3. Effect of Cutting Parameters on Surface Quality
5. Conclusions
- (1)
- This study employed finite element analysis and orthogonal experimental methods to investigate the micro-milling process of nickel-based single-crystal superalloy DD5 components. The influences of cutting speed, cutting depth, and feed rate on the milling forces and surface quality were systematically analyzed and characterized.
- (2)
- In practical machining, the surface quality of parts is usually used as the measurement standard. From the perspective of surface quality, when the milling speed is 1318.8 mm/s, the milling depth is 12 µm, and the feed rate is 20 µm/s, the surface roughness value is at its minimum, indicating the best surface quality. Naturally, this set of data is solely based on the experimental methods and parameters employed in this study. Its application to actual production would require further research and investigation.
- (3)
- In this study, the surface roughness of DD5 micro-milled parts was most significantly affected by spindle speed, followed by milling depth, with feed rate having the least impact. However, while high-speed cutting improved efficiency, it also intensified tool wear. Therefore, the optimized processing parameter combination obtained in this study holds great significance for practical machining production.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rehan, M.; He, T.; Khalil, A.K.; Tahir, D.; Yip, W.S.; To, S.S. Experimental Investigation of the Micro-Milling of Additively Manufactured Titanium Alloys: Selective Laser Melting and Wrought Ti6Al4V. Chin. J. Mech. Eng. 2024, 37, 115–127. [Google Scholar] [CrossRef]
- Liu, J.; Chen, N.; Jia, Y.; Zhao, J.; Wu, L.; Xiao, H.; He, N.; Yu, N.; Li, L. Machinability improvement in micro milling AlN after laser chemical milling. Chin. J. Aeronaut. 2024, 37, 588–602. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, Y.R.; Huang, Y.M.; Gong, S.; Sun, M.S.; Liu, M. Study on developing predicted system model of cutting-edge trajectory for micro-milling process based on tool runout error, chip thickness and force signal. Mech. Syst. Signal Process. 2025, 228, 112410. [Google Scholar] [CrossRef]
- Li, C.; Wang, K.; Zakharov, O.; Cui, H.; Wu, M.; Zhao, T.; Yan, Y.; Geng, Y. Damage evolution mechanism and low-damage grinding technology of silicon carbide ceramics. Int. J. Extrem. Manuf. 2025, 7, 022015. [Google Scholar] [CrossRef]
- Xiang, D.; Liu, Y.; Yu, T.; Wang, D.; Leng, X.; Wang, K.; Liu, L.; Pan, J.; Yao, S.; Chen, Z. Review on wear resistance of laser cladding high-entropy alloy coatings. J. Mater. Res. Technol. 2024, 28, 911–934. [Google Scholar] [CrossRef]
- Hu, Y.; Jin, X.; Jiang, X.; Zheng, Z. Inverse kinematics model and trajectory generation of a dual-stage micro milling machine. J. Manuf. Process. 2024, 132, 425–450. [Google Scholar] [CrossRef]
- Hojati, F.; Baraheni, M.; Azarhoushang, B. Research on Ploughing to Shearing Transition in Micro Milling of Titanium Alloy Using Gramian Angular Field and Machine Learning Methods. Arab. J. Sci. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Bai, Q.; Wang, P.; Cheng, K.; Zhao, L.; Zhang, Y. Machining dynamics and chatters in micro-milling: A critical review on the state-of-the-art and future perspectives. Chin. J. Aeronaut. 2024, 37, 59–80. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, M.A.; Aziz, S.; Faraz, M.I.; Tahir, A.M.; Jaffery, S.H.I.; Jung, D.W. Experimental Evaluation of Surface Roughness, Burr Formation, and Tool Wear during Micro-Milling of Titanium Grade 9 (Ti-3Al-2.5V) Using Statistical Evaluation Methods. Appl. Sci. 2023, 13, 12875. [Google Scholar] [CrossRef]
- Ding, P.; Huang, X.; Miao, X.; Li, S.; Liu, H. Dynamic stability simulation of micro-milling under the condition of multi-parameter uncertainty. Probabilistic Eng. Mech. 2023, 74, 103499. [Google Scholar] [CrossRef]
- Ding, P.; Huang, X. Sustainable optimization of micro-milling machining parameters considering reliability assessment. Mech. Based Des. Struct. Mach. 2025, 53, 864–901. [Google Scholar] [CrossRef]
- Ding, P.; Huang, X.; Rong, Z.; Li, S.; Gao, W. Modeling and reliability analysis of the micro-milling process considering stochastic tool wear with surrogate models. Mech. Based Des. Struct. Mach. 2025, 53, 611–640. [Google Scholar] [CrossRef]
- Mahmat, A.; Agar, S.; Tosun, N. Ultrasonic-assisted high-speed micro-milling of Ti6Al4V. J. Braz. Soc. Mech. Sci. Eng. 2024, 47, 46. [Google Scholar] [CrossRef]
- Yang, K.; Cao, Z.; Zhao, X.; Mei, W.; Wu, Q. Experimental Study of Micro-Milling Carbon Fibre Reinforced Composites Under Variable Cooling and Lubrication Strategies. Int. J. Precis. Eng. Manuf.-Green Technol. 2024, 12, 1247–1260. [Google Scholar] [CrossRef]
- Karkantonis, T.; Penchev, P.; Nasrollahi, V.; Le, H.; See, T.L.; Bruneel, D.; de Ramos Campos, J.A.; Dimov, S. Laser micro-machining of freeform surfaces: Accuracy, repeatability and reproducibility achievable with multi-axis processing strategies. Precis. Eng. 2022, 78, 233–247. [Google Scholar] [CrossRef]
- Yu, H.; He, Z.; Li, J.; Li, B.; Xin, J.; Yao, L.; Yan, F. Finite element modeling on micro-machining of graphene-reinforced aluminum matrix composites. Int. J. Adv. Manuf. Technol. 2022, 124, 97–110. [Google Scholar] [CrossRef]
- Kundiya, R.R.; Kadam, M.; Jadhav, P.; Pawade, R. A review on high speed micro-milling of shape memory alloy (NiTinol): Process and post perspective. Int. J. Interact. Des. Manuf. 2024, 19, 2337–2353. [Google Scholar] [CrossRef]
- Oymak, A.M.; Bahçe, E.; Gezer, İ. Experimental and numerical study on micro-milling of CoCrW alloy produced by selective laser melting and casting. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2024, 238, 1924–1939. [Google Scholar] [CrossRef]
- Ji, H.; Song, Q.; Du, Y.; Zhao, Y.; Liu, Z. Grain-scale material removal mechanisms of crystalline material micro-cutting. Int. J. Mech. Sci. 2022, 233, 107671. [Google Scholar] [CrossRef]
- Liu, C.; Wu, C.; Li, X.; Hou, B.; Wang, G.; Wu, J.; Sun, R.; Chen, M. Modeling and analysis of radial throw of micro-milling tool based on tool-attachment errors in high-speed rotating. J. Manuf. Process. 2023, 108, 779–790. [Google Scholar] [CrossRef]
- Wen, X.; Wen, M.; Ye, C.; Yu, S.; Yue, S.; Lu, T.M.; Zhao, Q. Highly Thermal-Conductive Cubic Boron Arsenide: Single-Crystal Growth, Properties, and Future Thin-Film Epitaxy. J. Phys. Chem. Lett. 2025, 16, 682–695. [Google Scholar] [CrossRef]
- Wang, J.; Yu, W.; Xu, S. Simultaneous regulation of grain size and interface of single-crystal ultrahigh-nickel LiNi0.9Co0.055Mn0.045O2 via one-step Li2ZrO3 coating. J. Colloid Interface Sci. 2025, 685, 427–436. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Liu, J.; Yan, Z.; Chen, J. Syntheses, challenges and modifications of single-crystal cathodes for lithium-ion battery. J. Energy Chem. 2021, 63, 217–229. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, B.; Xue, J.P.; Xie, J.; Yao, Z.S.; Tao, J. Giant single-crystal-to-single-crystal transformations associated with chiral interconversion induced by elimination of chelating ligands. Nat. Commun. 2021, 12, 6908. [Google Scholar] [CrossRef] [PubMed]
- Bahnmüller, U.J.; Kuper, H.; Seewald, T.; Yalҫinkaya, Y.; Becker, J.A.; Schmidt-Mende, L.; Weber, S.A.L.; Polarz, S. On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties. Nanomaterials 2021, 11, 3057. [Google Scholar] [CrossRef] [PubMed]
- Durham, D.B.; Ophus, C.; Siddiqui, K.M.; Minor, A.M.; Filippetto, D. Accurate quantification of lattice temperature dynamics from ultrafast electron diffraction of single-crystal films using dynamical scattering simulations. Struct. Dyn. 2022, 9, 064302. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zeng, T.; Li, G.; Wan, T.; Li, M.; Zhang, X.; Li, M.; Su, M.; Dou, A.; Zeng, W. The surface double-coupling on single-crystal LiNi0.8Co0.1Mn0.1O2 for inhibiting the formation of intragranular cracks and oxygen vacancies. Energy Storage Mater. 2022, 52, 534–546. [Google Scholar] [CrossRef]
- Yan, T.; Shi, W.; Zhu, L.; Dong, L.; Wang, L.; Xie, C.; Yang, Y. Simulation analysis and experimental study on aramid fiber reinforced polymer micro-milling mechanism. J. Manuf. Process. 2023, 105, 431–443. [Google Scholar] [CrossRef]
- Pang, S.; Zhao, W.; Qiu, T.; Liu, W.; Jiao, L.; Wang, X. Study on surface quality and mechanical properties of micro-milling WE43 magnesium alloy cardiovascular stent. J. Manuf. Process. 2023, 101, 1080–1090. [Google Scholar] [CrossRef]
- Hellen, T.K. A frontal solution program for finite element analysis. Int. J. Numer. Methods Eng. 2010, 3, 149. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, P.; Yan, R.; Tian, G.; Yang, M.; Shi, Y. Quantitative finite element analysis of microscopic surface formation for TC4 aeroengine blade polishing using single-grain method. Int. J. Adv. Manuf. Technol. 2024, 132, 2941–2955. [Google Scholar] [CrossRef]
- Lee, M.Y.; Park, J.H.; Park, S.J.; Chang, N.Y.; Chae, J.M. A finite element analysis of stress distribution with various directions of intermaxillary fixation using orthodontic mini-implants and elastics following mandibular advancement with a bilateral sagittal split ramus osteotomy. Orthod. Craniofacial Res. 2024, 27, 8. [Google Scholar] [CrossRef]
- Xu, S.; Yang, X.; Hu, X.; Ma, H.; Li, J.; Ren, G. Preparation of Negative Poisson’s Ratio 316L Stainless Steel Porous Bone Scaffolds Based on Finite Element Analysis and 3D Printing Technology. Mater. Res. 2025, 28, e20240479. [Google Scholar] [CrossRef]





| Density (kg/m3) | Shear Modulus (MPa) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| 8200 | 23,400 | 13,000 | 0.313 |
| Unit System | Length | Force | Mass | Time | Stress | Energy | Density | Acceleration |
|---|---|---|---|---|---|---|---|---|
| SI (mm) | mm | N | ton | s | MPa | mJ | ton/mm3 | mm/s2 |
| Performance Indicator | Technical Parameter |
|---|---|
| X-axis Working Travel | 490 mm |
| Y-axis Working Travel. | 460 mm |
| Z-axis Working Travel | 120 mm |
| Worktable Working Range | 560 mm × 500 mm |
| Maximum Cutting Feed Rate | 9 m/min |
| Milling speed | 3000 r/min~6000 r/min |
| Positioning Precision | 0.006 mm |
| Tool Setting Precision | 0.002 mm |
| Control System | GUC-400-ESV |
| Dimension | 1300 mm × 1500 mm × 2050 mm |
| Level | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Factor | ||||||
| Milling Speed vc (mm/s) | 376.8 | 753.6 | 1130.4 | 1318.8 | 1507.2 | |
| Milling Depth ap (µm) | 5 | 8 | 10 | 12 | 15 | |
| Feed Rate v (µm/s) | 20 | 40 | 60 | 80 | 100 | |
| Experiment Number | Milling Speed vc (mm/s) | Milling Depth ap (µm) | Feed Rate v (µm/s) | Milling Force F (N) | Surface Roughness Ra (µm) |
|---|---|---|---|---|---|
| 1 | 376.8 | 5 | 20 | 0.561 | 1.102 |
| 2 | 376.8 | 8 | 40 | 0.986 | 1.540 |
| 3 | 376.8 | 10 | 60 | 1.365 | 1.172 |
| 4 | 376.8 | 12 | 80 | 2.176 | 1.184 |
| 5 | 376.8 | 15 | 100 | 3.381 | 1.580 |
| 6 | 753.60 | 5 | 40 | 0.605 | 1.630 |
| 7 | 753.60 | 8 | 60 | 2.715 | 1.600 |
| 8 | 753.60 | 10 | 80 | 1.388 | 1.710 |
| 9 | 753.60 | 12 | 100 | 3.108 | 1.590 |
| 10 | 753.60 | 15 | 20 | 2.510 | 1.890 |
| 11 | 1130.40 | 5 | 60 | 0.923 | 1.988 |
| 12 | 1130.40 | 8 | 80 | 1.597 | 1.760 |
| 13 | 1130.40 | 10 | 100 | 1.886 | 1.460 |
| 14 | 1130.40 | 12 | 20 | 1.399 | 1.240 |
| 15 | 1130.40 | 15 | 40 | 3.160 | 1.286 |
| 16 | 1318.80 | 5 | 80 | 0.830 | 1.210 |
| 17 | 1318.80 | 8 | 100 | 0.982 | 1.370 |
| 18 | 1318.80 | 10 | 20 | 0.786 | 1.115 |
| 19 | 1318.80 | 12 | 40 | 1.080 | 1.126 |
| 20 | 1318.80 | 15 | 60 | 1.658 | 1.055 |
| 21 | 1507.20 | 5 | 100 | 1.399 | 1.280 |
| 22 | 1507.20 | 8 | 20 | 0.929 | 1.630 |
| 23 | 1507.20 | 10 | 40 | 1.119 | 1.740 |
| 24 | 1507.20 | 12 | 60 | 1.535 | 1.800 |
| 25 | 1507.20 | 15 | 80 | 1.434 | 1.500 |
| Processing Number | Vc | ap | v | |||
|---|---|---|---|---|---|---|
| K1j | 8.469 | 1.694 | 4.318 | 0.864 | 6.184 | 1.237 |
| K2j | 10.326 | 2.065 | 7.209 | 1.442 | 6.950 | 1.390 |
| K3j | 8.965 | 1.793 | 6.544 | 1.309 | 8.196 | 1.639 |
| K4j | 5.336 | 1.067 | 9.298 | 1.860 | 7.425 | 1.485 |
| K5j | 6.416 | 1.283 | 12.143 | 2.429 | 10.756 | 2.151 |
| K1j2 | 71.720 | 18.646 | 38.248 | |||
| K2j2 | 106.626 | 51.963 | 48.300 | |||
| K3j2 | 80.376 | 42.819 | 67.174 | |||
| K4j2 | 28.468 | 86.461 | 55.129 | |||
| K5j2 | 41.162 | 147.446 | 115.695 | |||
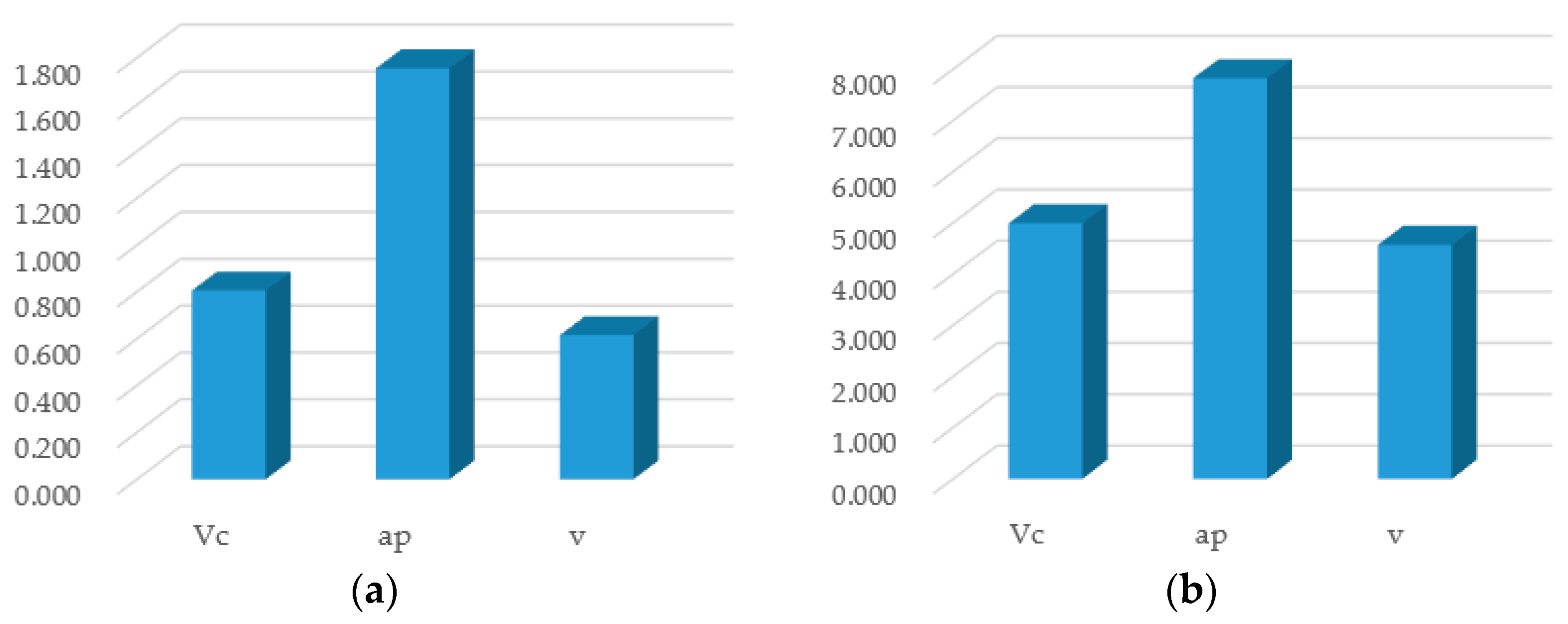
| R | 4.990 | 7.825 | 4.572 | |||
| T | 39.511 | |||||
| CT | 62.446 | |||||
| SS | 3.225 | 7.021 | 2.463 | |||
| V | 0.806 | 1.755 | 0.616 |
| Processing Number | Vc | ap | v | |||
|---|---|---|---|---|---|---|
| K1j | 6.578 | 1.316 | 7.210 | 1.442 | 6.977 | 1.395 |
| K2j | 8.420 | 1.684 | 7.900 | 1.580 | 7.322 | 1.464 |
| K3j | 7.734 | 1.547 | 7.197 | 1.439 | 7.615 | 1.523 |
| K4j | 5.876 | 1.175 | 6.940 | 1.388 | 7.364 | 1.473 |
| K5j | 7.950 | 1.590 | 7.311 | 1.462 | 7.280 | 1.456 |
| K1j2 | 43.270 | 51.984 | 48.679 | |||
| K2j2 | 70.896 | 62.410 | 53.612 | |||
| K3j2 | 59.815 | 51.797 | 57.988 | |||
| K4j2 | 34.527 | 48.164 | 52.228 | |||
| K5j2 | 63.203 | 53.451 | 52.998 | |||
| R | 2.544 | 0.960 | 0.638 | |||
| T | 36.558 | |||||
| CT | 53.459 | 53.459 | ||||
| SS | 0.883 | 0.102 | 0.042 | |||
| V | 0.221 | 0.025 | 0.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Gong, Y.; Liu, Y.; Wang, Z.; Zhao, J.; Wang, Z.; Xu, Z. Experimental Study on the Microscale Milling Process of DD5 Nickel-Based Single-Crystal Superalloy. Metals 2025, 15, 898. https://doi.org/10.3390/met15080898
Li Y, Gong Y, Liu Y, Wang Z, Zhao J, Wang Z, Xu Z. Experimental Study on the Microscale Milling Process of DD5 Nickel-Based Single-Crystal Superalloy. Metals. 2025; 15(8):898. https://doi.org/10.3390/met15080898
Chicago/Turabian StyleLi, Ying, Yadong Gong, Yang Liu, Zhiheng Wang, Junhe Zhao, Zhike Wang, and Zelin Xu. 2025. "Experimental Study on the Microscale Milling Process of DD5 Nickel-Based Single-Crystal Superalloy" Metals 15, no. 8: 898. https://doi.org/10.3390/met15080898
APA StyleLi, Y., Gong, Y., Liu, Y., Wang, Z., Zhao, J., Wang, Z., & Xu, Z. (2025). Experimental Study on the Microscale Milling Process of DD5 Nickel-Based Single-Crystal Superalloy. Metals, 15(8), 898. https://doi.org/10.3390/met15080898





