1. Introduction
The emergence of new data science techniques for material processes has pushed the process modelling and simulation concepts beyond the state of the art, triggering fast and reliable design loops and efficient process controlling. This paper presents an overview of the generation of data solvers and interpolators, their rigorous validation concepts, and their performances for real-world process applications. The mathematical and computational features of these data models were briefly elaborated herein, and their limitations, performances, and challenges are highlighted. The applications of these real-time models for popular material processes such as casting, extrusion, and AM have also been shown using real-world case studies. The goal here is to show the predictive power of these models along with their limitations and shortcomings for material process simulations.
With the emergence of numerical simulations in the last century, process modeling and optimization have undergone revolutionary changes, moving towards reducing design and optimization loops that were previously based on experimental trial and error. By incorporating more complexities into these simulations, multi-physical and multi-scale phenomena can be modeled, albeit at the expense of greater computational efforts and costs. Powerful computing facilities, including cluster and cloud computing, along with advanced algorithms, have been developed to meet the substantial computational demands of these sophisticated numerical models. Most manufacturing processes are inherently thermal events involving cooling and heating, and the characteristics of the final products are highly dependent on the evolutions of lower-scale phenomena, such as microstructure formations. Consequently, many numerical techniques developed for these processes are inherently capable of handling phase changes, bridging scales, managing thermal evolutions, and calculating mechanical properties [
1].
Further challenges of these numerical models include the transient nature of these processes, which require consideration of startup and shutdown conditions, as well as changing conditions during the processes [
2]. Additionally, some manufacturing processes are generative in nature, where parts are built up over time (e.g., casting, AM). Typically, numerical simulations for these processes are set up using a predefined fixed domain size with a fixed discretization grid, where initial boundary and external conditions can be enforced [
3]. This can be particularly challenging, as generative processes may require dynamic domain sizes, meshes, and boundaries to accurately model the transient process. Consequently, some numerical modeling schemes tend to use steady-state, pseudo-steady-state, or even superposition of steady-state snapshots to construct a transient replica of the actual process.
The most critical issue with today’s state-of-the-art numerical simulation schemes for transient processes is generating reliable and accurate results within a reasonable computational time while maintaining adequate detail and capturing the relevant physics and phases during the processes. Although powerful numerical techniques, such as finite element (FE) and computational fluid dynamics (CFD), have been repeatedly used to address the multi-physical, multi-phase, and multi-scale nature of material processes, achieving reasonable results still requires significant computational effort. Furthermore, for processes with multi-scale aspects (e.g., microstructure evolution modeling) and phase changes, capturing phenomena at lower scales and phase transitions, along with their associated thermal and stress histories, necessitates solver interactions and interfacing. This requirement limits the time efficiency and increases the computational cost of these interactive simulations, often necessitating fine discretization resolutions.
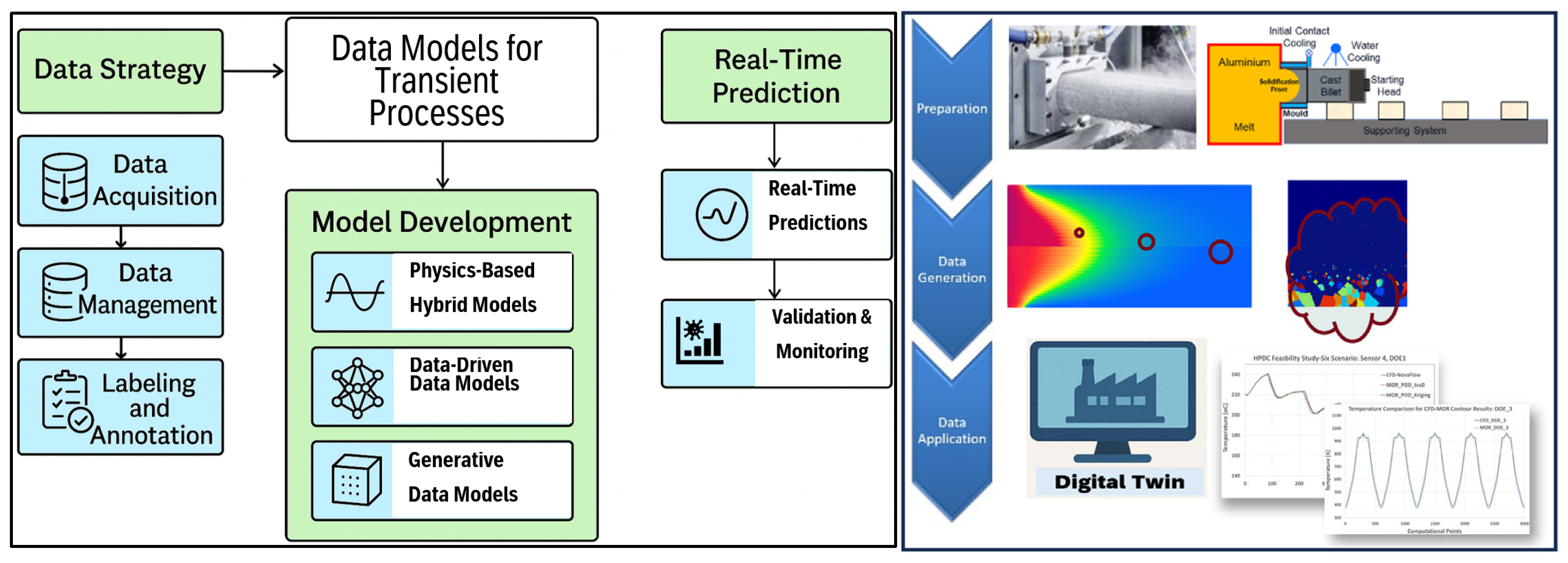
This study explores the application of data science methodologies to the modeling of material processing operations under both transient and steady-state conditions. It systematically addresses key challenges such as data availability and quality, the selection of appropriate data solvers and interpolation methods, snapshot generation, validation strategies, and the construction of generative data models and databases. The innovation lies in the seamless integration of machine learning (ML) techniques, data solvers, and advanced interpolation methods into a unified framework capable of handling both steady-state and transient manufacturing scenarios. By employing reduced-order modeling and iterative data training, this research delivers a solution that not only significantly lowers computational costs but also improves predictive accuracy—particularly in complex; multi-physical; multi-phase; and multi-scale environments. Real-world case studies are presented to demonstrate these concepts in practice. Furthermore, the research highlights ongoing efforts in process data acquisition and synthetic data generation, offering insights into best practices for selecting suitable solvers and interpolators, along with practical implementation considerations.
2. Methodology—Data Models for Processes
The use of data science techniques in engineering process applications has grown rapidly in recent years, driven by the need to quickly predict process trends and understand complex process parameters more accurately and efficiently. Traditionally, analytical and empirical methods, along with physical testing, were employed for material process modeling. These methods later evolved into sophisticated numerical approaches. As computational power increased over the decades, the field of numerical process simulation began to incorporate more detailed mathematical models to represent various physical states, phases, and phenomena at different length scales. The implementation of data science techniques in material processes has started to revolutionize process modeling by addressing several critical functions. Firstly, they provide fast and real-time predictions under various process conditions, which can be used to develop real-time control and optimization schemes for digital twinning. Secondly, they help in understanding the evolution of fundamental properties of materials during processes, resulting in better quality control for products. Thirdly, these models can be combined with physics-based, analytical, and numerical approaches to rely more on fundamental material science principles, utilizing ML and data training to analyze large and complex process databases.
Over the past two decades, the rapid advancement of data science has led to the emergence of powerful data-driven and hybrid physical–data-driven modeling techniques in manufacturing. Several frameworks have been proposed to integrate these methods into process engineering, including Data-Driven Engineering Design (DDED), Data-Driven Process Systems Engineering (PSE), and Model-Based Systems Engineering (MBSE) [
4,
5,
6,
7,
8]. In addition, hybrid approaches such as Data–Model Fusion (DMF) for smart manufacturing have been introduced by Tao et al. [
9], while Dogan et al. [
10] provide a comprehensive review of ML and data mining (DM) applications in manufacturing, covering both supervised and unsupervised learning techniques. Wang et al. [
11] discuss the role of big data analytics in manufacturing, including frameworks, technologies, applications, and challenges. Ghahramani et al. [
12] explore AI-based process modeling and optimization, proposing evaluation strategies for intelligent manufacturing systems. Furthermore, Sofianidis et al. [
13] highlight the use of explainable AI (XAI) to enhance transparency and trust in AI-driven production environments. The application of reduced-order data models for real-time process prediction has also been explored by Horr et al. [
14,
15,
16,
17], focusing on the integration of data-driven techniques for process optimization and control.
Traditional modeling approaches for metal manufacturing processes can be categorized into several classes, including steady-state and transient modeling, multi-physical and multi-phase modeling, multi-scale and interactive modeling, and hybrid analytical–numerical modeling. The integration of data science is transforming how these models are developed and applied. The evolution of data modeling techniques can be summarized as follows:
Data Models for Steady-State and Pseudo-Static Processes— For processes that can be approximated as steady-state or pseudo-static, spatial variations in process parameters can be used to construct 1D, 2D, or 3D data models. These models may incorporate multi-physical, multi-phase, and multi-scale phenomena (e.g., microstructure evolution), with transient effects approximated using statistical or averaging techniques.
Time-Series Data Models for Transient and Temporal Processes—These models capture the evolution of materials; boundary conditions; and process parameters over time. When multi-scale effects are included, appropriate length and time scales must be defined. The data modeling techniques must be agile enough to handle both gradual and abrupt changes in material properties (e.g., melting, solidification), thermal inputs/outputs, and control parameters.
Hybrid Analytical—Data and Generative Models— These models combine physical understanding of the process with trained data-driven components. They are particularly effective for systems where the underlying physics is known, but complex interactions are better captured through data science. Hybrid models may use single or split databases, integrating analytical and learned data to enhance prediction accuracy and computational efficiency.
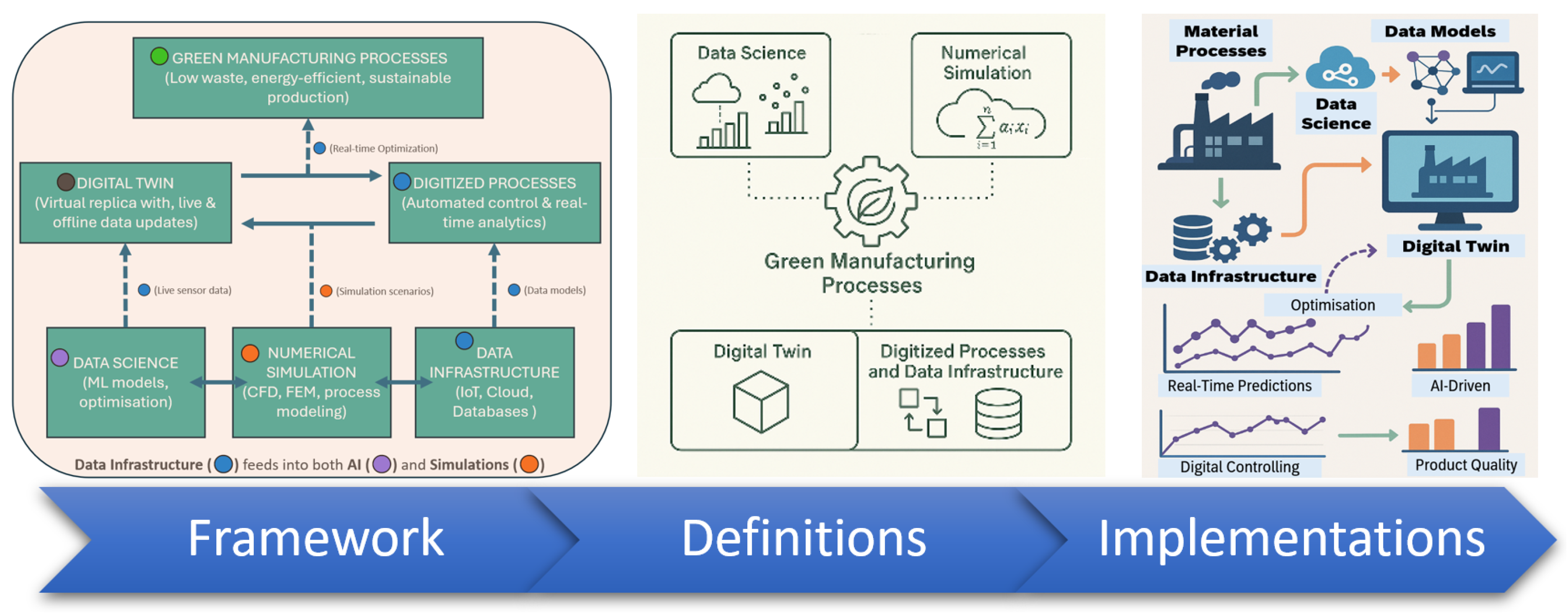
Figure 1 shows the framework for the data strategy for process modeling and its role in digitalization of manufacturing industries. The framework offers a structured approach for managing and leveraging process data as a strategic asset for optimization and control of manufacturing processes throughout the production chain. It shapes how industrial data are collected, stored, processed, accessed, and used to support active controlling and optimization. This data strategy helps the implementation of process digital twins, enhances predictive power through AI-based techniques, facilitates operational efficiency, and drives innovation in smart manufacturing environments.
3. Steady State Processes—Data Strategy
Most manufacturing processes exhibit some degree of transient behavior, with process parameters and conditions often changing over time. Factors such as startup conditions, shifts in boundary conditions, abrupt disturbances, and planned ramp-up or ramp-down phases naturally introduce transient effects that can significantly influence the quality of the final product. However, in many widely adopted manufacturing processes, these transient phases are typically short-lived. Once stabilized, the process can operate under consistent conditions, making it suitable for steady-state modeling to support real-world predictive applications. Developing such models involves a structured methodology encompassing spatial data acquisition, strategic planning, data storage, model development, validation, and deployment [
17,
18]. For processes such as continuous casting, long wire extrusion, and the production of large-scale additively manufactured components with uniform geometry and process parameters, steady-state modeling approaches can be effectively applied. These approaches help streamline model development, reducing both time and effort while maintaining predictive accuracy.
3.2. Process Case Studies
To explore the application of real-time data models in manufacturing processes, two real-world case studies—casting and extrusion—are briefly discussed to illustrate the practical implementation of data modeling techniques. These studies focus on steady-state conditions, excluding the transient behaviors typically observed during process start-up. The evolution of thermal fields in both processes is analyzed, and spatial temperature variations at selected points are predicted.
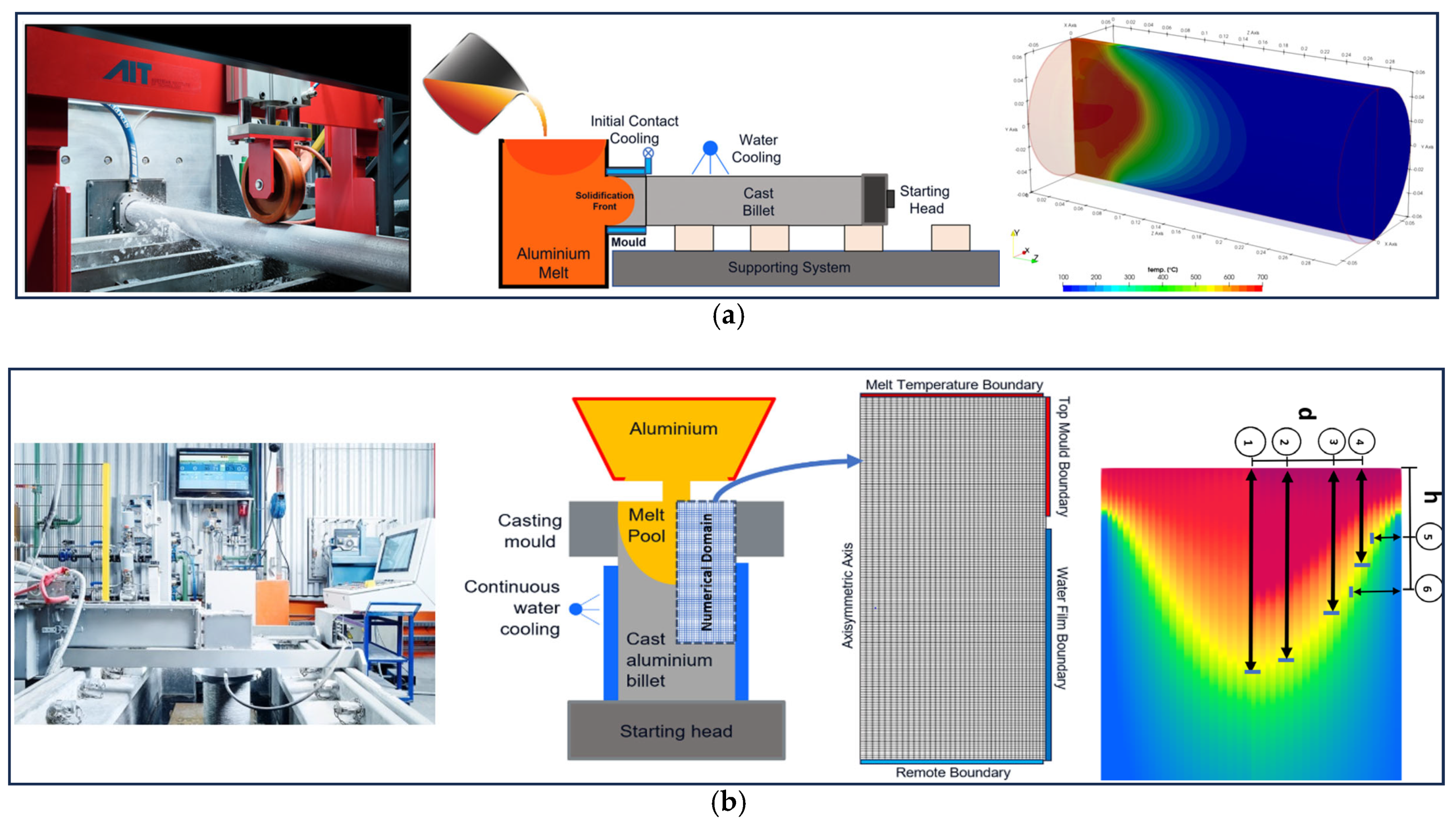
Casting Process: Developing a digital twin or shadow of the casting process enables the evaluation of various process scenarios under different sets of parameters and boundary conditions. Casting is inherently a multi-physical, multi-phase, and multi-scale process, where macro-scale thermal fields significantly influence solidification behavior and microstructural evolution at smaller scales. Creating real-time data models for casting presents several challenges, particularly in data generation, handling, training, and interpretation across different length scales. To build the casting data model, appropriate solver technologies and data interpolation routines were employed. The following steps outline the methodology used in this case study:
Simulation Model Calibration and Validation: The CFD simulation model was calibrated and validated using experimental measurements.
Definition of Prediction Objectives: Key prediction goals—such as thermal and microstructural events—were defined and implemented for a laboratory-scale semi-continuous casting process.
Scenario Development: Variations in process parameters were considered to define realistic operational scenarios, forming a snapshot matrix.
Simulation and Data Generation: Using the calibrated CFD model, snapshot scenarios were simulated with open-source software to generate a small database for model training. Additional DOE scenarios were simulated for validation purposes.
Data Model Construction: Real-time data models were iteratively developed using a suitable combination of solvers and interpolators. Machine learning techniques were also applied to enhance model performance.
Performance Evaluation: The accuracy and reliability of the data models were assessed using DOE-based validation scenarios.
Integration into Advisory Framework: Finally, the data models were customized for integration into an existing web-based casting process advisory system.
For the numerical simulations of the snapshot matrix scenarios, fixed-domain fluid-thermal CFD simulations were employed to analyze thermal evolution and solidification behavior during the casting processes. The open-source solver directChillFoam [
21], built on top of the OpenFOAM simulation framework [
22,
23,
24], was used for melt flow modeling. The initial CFD validation setup was based on a previous project utilizing directChillFoam, where simulation results were benchmarked against experimental data from Vreeman et al. [
25]. The casting material was defined as a binary alloy, Al–6 wt% Cu. Solidification modeling incorporated temperature-dependent melt fraction data (e.g., from CALPHAD routines), while solute redistribution followed the Lever rule [
26]. For thermal modeling, heat transfer coefficients (HTCs) at the mold–melt interface (primary cooling) were locally averaged based on the solid fraction. Secondary cooling at the billet–water interface was modeled using tabulated HTC values derived from the correlation proposed in [
27]. All snapshot scenarios were simulated with a runtime of 2000 s—more than twice the time required to reach quasi-steady-state conditions. Time-averaged values of temperature and melt fraction over the final 1000 s were recorded at all cell centers, along with their spatial coordinates (X and Z).
Figure 3 presents the experimental setup, simulation domain, and melt pool size calculations for both horizontal and vertical die chill casting studies.
Extrusion Process: Using data science technologies, advanced data models can be developed to optimize and control metal extrusion processes. Extrusion is characterized by distinct features such as large material deformation, plastic material flow, microstructural recrystallization, and grain restructuring. Therefore, any digital twin or digital shadow of the extrusion process must account for thermal evolution, large-scale deformation, and microstructure development to ensure accurate real-time predictions. In this research, a steady-state data modeling framework has been established using a multi-scale simulation and data integration approach. This framework incorporates geometric, material, boundary, and operational data. A specialized data structure was developed to manage information across different length scales, and a sequence of numerical solvers was employed to simulate phenomena at both macro and micro levels. The data modeling workflow, similar to the casting case study, followed these steps:
Definition of Prediction Objectives: Macro- and micro-scale prediction targets were established across different length scales.
Parameter Variation Analysis: Critical process parameters were identified, and their effects were analyzed through a range of process scenarios.
Balanced Sampling Strategy: Techniques such as Latin Hypercube Sampling and Sobol sequences were used to evenly distribute parameter variations within the multi-dimensional design space, forming the final snapshot matrix.
Simulation and Data Generation: A calibrated FE model was used to simulate the snapshot scenarios, and the resulting data were processed.
Multi-Scale Database Construction: A split structured database was created to store macro- and micro-scale responses, organized using semantic rules.
Data Model Development: Predictive models were generated for macro-scale thermal fields and micro-scale microstructural evolution.
Machine Learning Enhancement: Additional training using machine learning techniques was conducted to improve model accuracy and robustness.
Model Validation: Extensive validation studies were performed under normal, near-boundary, and extreme conditions using DOE scenarios.
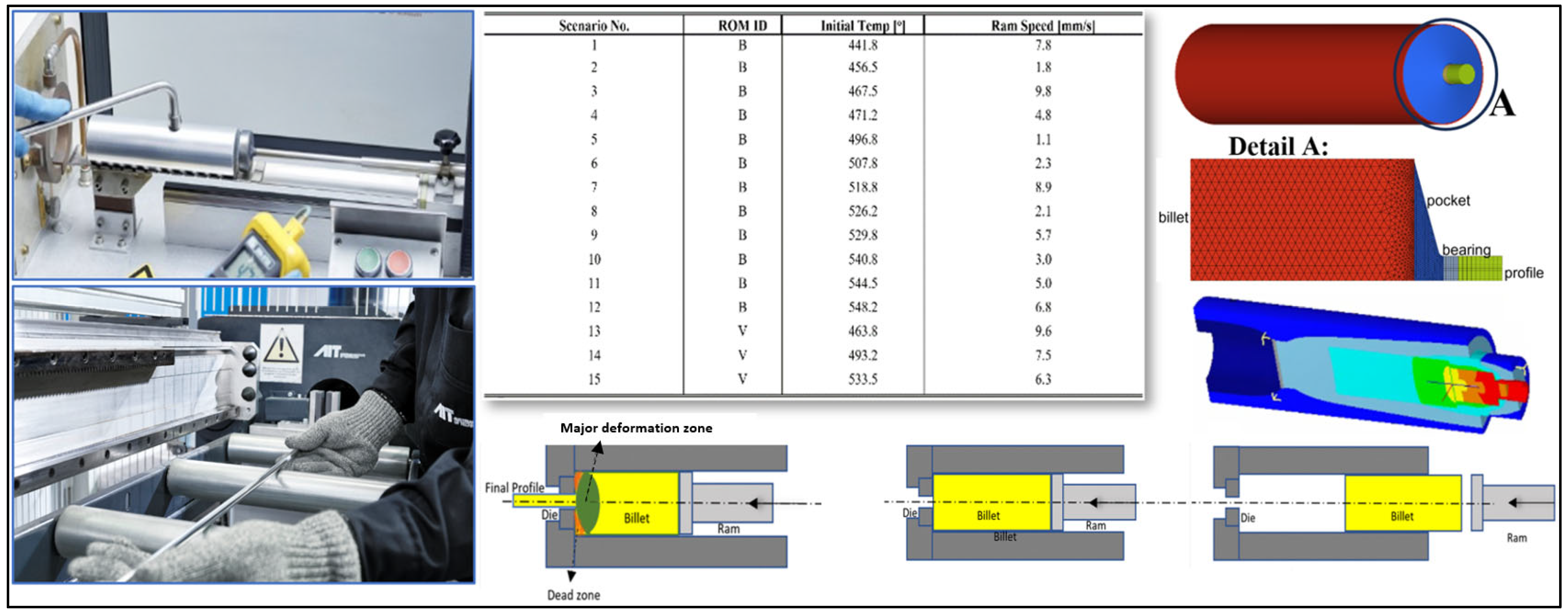
To execute the scenarios defined in the snapshot matrix, numerical simulations of the extrusion process were performed using the thermo-mechanical solver HyperXtrude (HX). This solver utilizes an Arbitrary Lagrangian-Eulerian (ALE) hybrid technique to accurately capture large material deformations [
28]. The primary process parameters—ram speed and initial billet temperature—were systematically varied; with aluminum 6060 selected as the billet material. The parameter ranges were set between 440 °C and 550 °C for the initial billet temperature and 1 to 10 mm/s for the ram speed, based on a cylindrical billet with a 50 mm diameter. The computational domain was discretized using approximately 172,000 volumetric elements, modeled as a quarter section due to double symmetry conditions.
Figure 4 presents the experimental setup, the snapshot matrix, and the FE simulation of the extrusion process.
3.3. Analyses and Performance—Steady State Processes
The comparative analyses and performance studies for real-time data models can be performed to assess their performances for steady-state process modelling. However, there are challenges and difficulties related to multi-physical and multi-phase casting processes, which highly depend on thermal field evolution during these processes. Likewise, for the extrusion process modeling, the simulation of thermal field development during the start of the process and within the large deformation zone is necessary to have accurate predictions. Hence, the data model needs to be adequately trained to properly reflect the thermal field, including heat transfer, cooling, and temperature-dependent material properties. Data from properly designed experimental work and verified numerical simulations can be employed to adjust the models for an accurate prediction of the thermal field.
Casting Processes: Casting processes can significantly benefit from the integration of data-driven models, particularly by analyzing variations in key process parameters such as initial melt temperature, water-cooling configurations, and casting speed. Leveraging such models can help mitigate the risks of hot tearing, cold cracking, and the formation of voids and other defects. Additionally, it is important to account for buoyancy effects induced by gravity in both numerical CFD simulations and data-driven models. This consideration necessitates extending the computational domain vertically—from the top to the bottom of the billet—to accurately capture thermal and flow dynamics. However, for vertical casting processes, geometric simplifications are possible. The domain can often be reduced to a quarter section or even a quasi-2D symmetric wedge, particularly when modeling round billet geometries, thereby reducing computational cost without compromising accuracy.
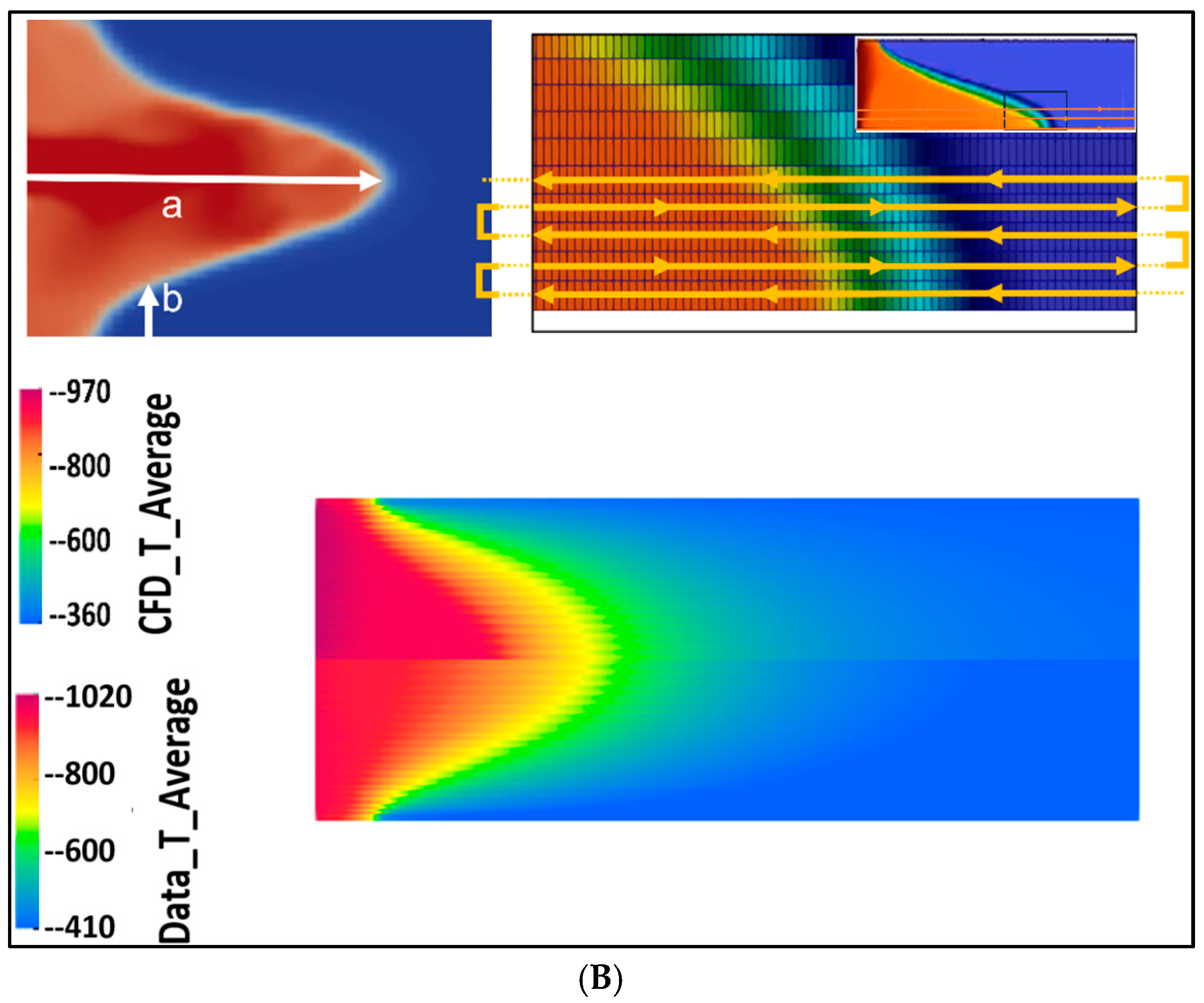
When calculating melt pool depth and temperature contours using data-driven models, a key challenge arises from the structure of the data produced by the CFD solver. The solver is optimized for minimal matrix sizes, which results in a computational node ordering that may not be suitable for data model training. Specifically, reading nodal temperatures in computational order—from the bottom of the billet to the top of the melt pool—can produce abrupt temperature gradients and discontinuities. These high-gradient data sequences are difficult for data models to interpret and generalize from effectively. To address this, additional post-processing was performed to transform the raw CFD output into a format more suitable for data modeling. A snake-shaped nodal reordering scheme was applied to smooth the data gradients and reduce sharp transitions. This reordering improves the continuity and consistency of the input data, enhancing the performance and reliability of the data models.
Figure 5 illustrates the nodal reordering strategy for both vertical and horizontal casting processes, while
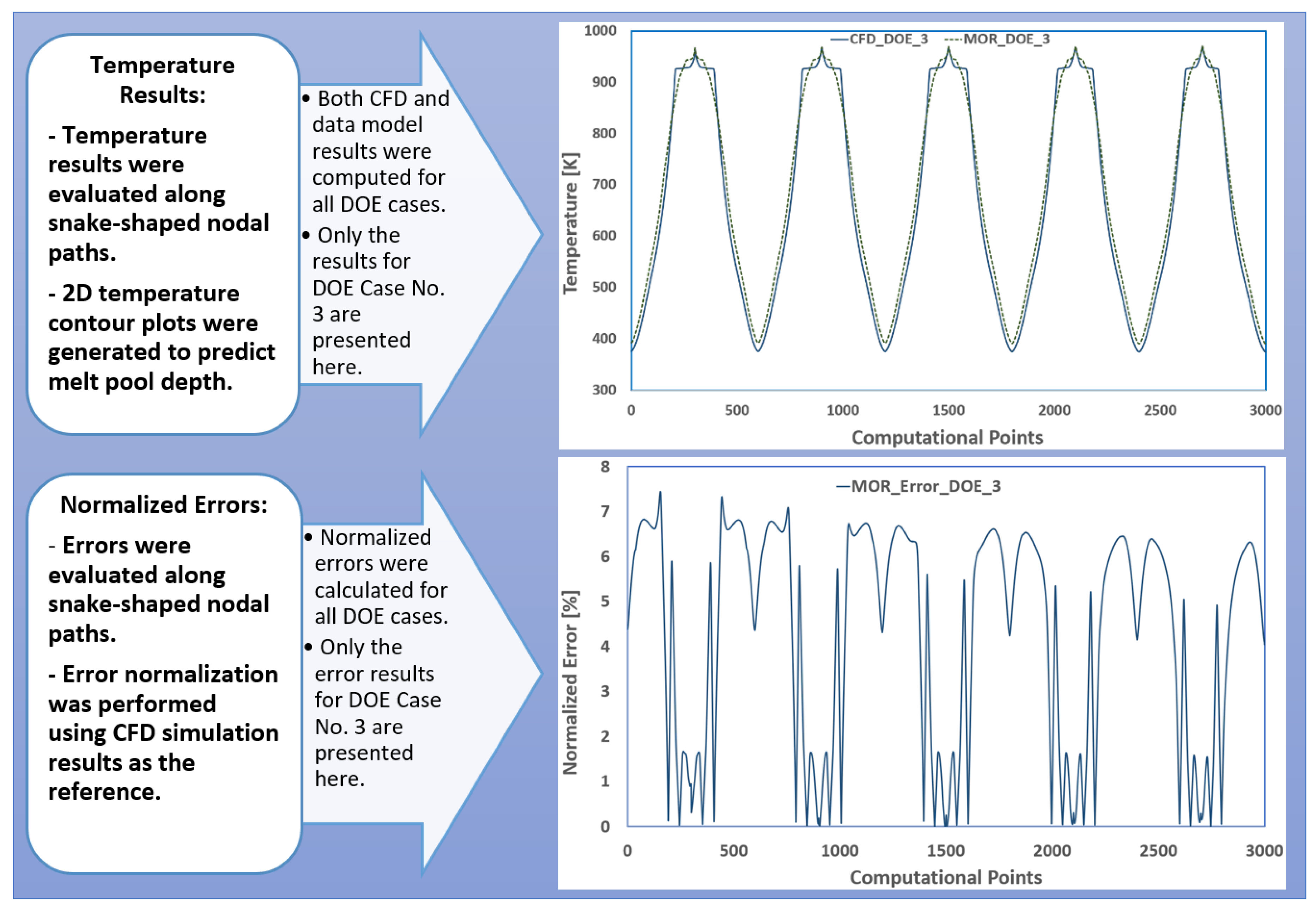
Figure 6 presents a comparison between CFD-calculated and data model-estimated temperature values, along with the normalized error graph for the first 3000 nodes in DOE scenario no. 3.
For comparison, the computational wall-clock time for each CFD simulation ranges from approximately 720 to 1200 s using eight parallel computing cores. In contrast, the real-time data-driven solver requires only about 1.3 s on a single core to estimate the thermal responses. Upon examining the comparison graphs, it becomes evident that the highest normalized errors—ranging from approximately 6% to 8%—occur at locations with steep temperature gradients; particularly near the bottom of the melt pool. As the snake-like estimation path traverses from the solidified billet toward the melt pool base, the temperature variations become more pronounced. Consequently, even with the most optimized combination of data solver and interpolator, the real-time data model struggles to fully capture the rapid thermal transitions in this region.
Extrusion Process: Extrusion processes are highly adaptable manufacturing methods used to produce components with a wide range of shapes, sizes, and complex cross-sections through the use of pre-designed dies. Numerical simulations, along with fast real-time predictive models, play a crucial role in optimizing these processes by providing insights into the large thermo-mechanical deformations that occur during material flow. To develop effective data-driven models for extrusion, it is essential to construct a well-structured initial database that offers sufficient data points with balanced density across the multi-dimensional parameter space. As outlined in previous sections, a snapshot matrix was generated using advanced sampling techniques to capture the variability of key process parameters within the operational limits of the extrusion machine.
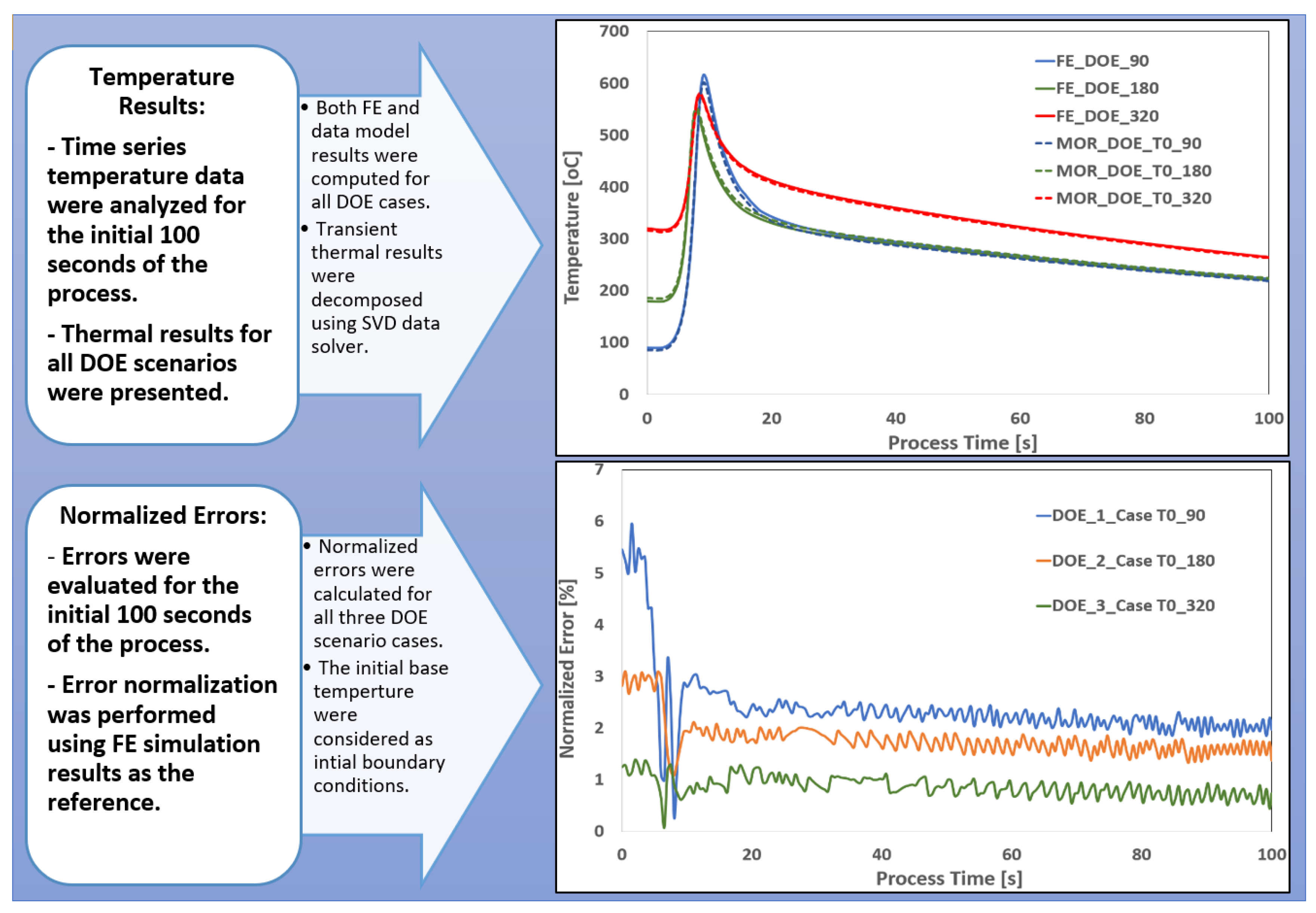
Similar to the casting case, validation and comparative analyses were conducted to evaluate the performance of data-driven models for extrusion processes. The objective was to assess the reliability and accuracy of real-time predictive models using data derived from the process scenarios defined in the snapshot matrix. For model development, widely adopted eigenvalue-based techniques—specifically Singular Value Decomposition (SVD)—were employed alongside regression analysis methods.
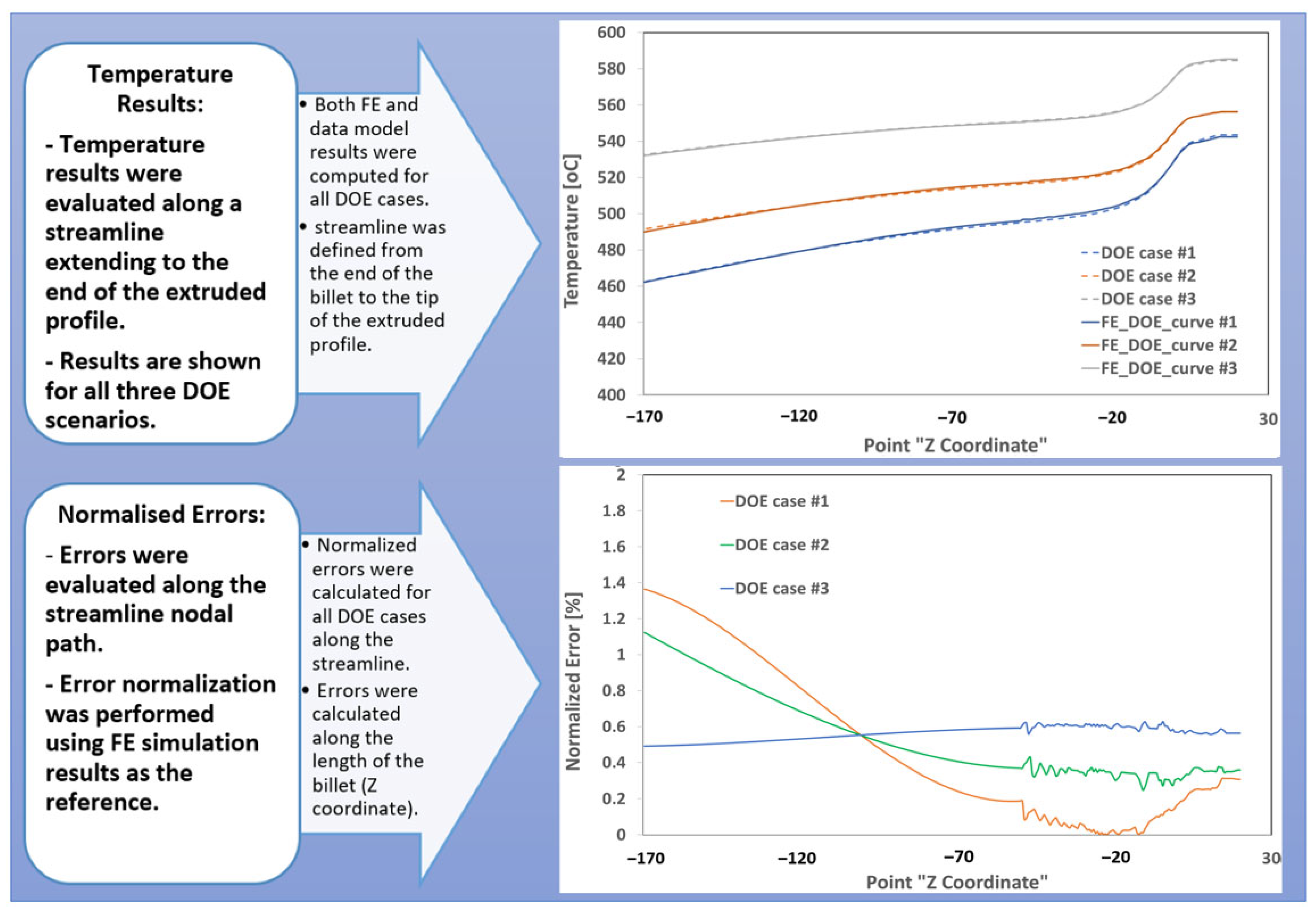
Figure 7 presents a comparison of temperature graphs generated using both SVD and regression-based models, benchmarked against DOE results. To interpolate process data for validation cases, the inverse distance weighting (InvD) technique was applied, enabling localized estimation based on proximity within the parameter space.
Steady-state FE thermal results for three validation scenarios were compared with predictions from the real-time data-driven models along the entire length of the billet and the final extruded profile. Normalized error percentages were calculated by comparing the data model predictions at each node along the billet with the corresponding FE simulation results. The analysis revealed that the highest normalized errors occurred at the billet boundaries—specifically at the initial billet entry and near the die exit—where significant material deformation takes place. These regions are characterized by complex thermo-mechanical interactions and rapid temperature fluctuations as the material undergoes large deformation while passing through the die. Such conditions present challenges for the data model, limiting its ability to accurately capture the thermal behavior in these zones.
6. Results and Discussion
The performance, accuracy, reliability, and validation of real-time data models for manufacturing processes—including steady-state; transient; and generative types—must be rigorously evaluated to ensure their applicability to real-world industrial challenges. For such models to gain acceptance in practical settings, they must demonstrate robustness under varying process conditions and align with industry-specific requirements. In this research, a combination of data solvers, interpolation techniques, and ML routines was employed to develop efficient and accurate real-time data models. ML-based training and learning were conducted in one or two iterative rounds, both prior to and following the initial model generation, to optimize performance and enhance predictive capability.
7. Concluding Remarks
In conclusion, the development of comprehensive databases and data-driven models for manufacturing processes holds substantial promise for advancing process sustainability, understanding, control, and optimization. However, the successful integration of these models into process advisory systems and digital twin frameworks requires careful consideration of several interdependent factors. This study emphasizes that the selection of appropriate data solvers, interpolators, and machine learning techniques must be closely aligned with the specific characteristics of the manufacturing process—whether it is steady-state; transient; or generative in nature. Eigenvalue-based solvers such as SVD, when combined with advanced interpolators like Kriging or RBF, have demonstrated strong capabilities in capturing complex temporal and spatial dynamics, particularly in transient and high-gradient scenarios. Conversely, regression-based approaches continue to offer effective and interpretable solutions for steady-state modeling and spatial data decomposition. These insights underscore the importance of methodological alignment and data strategy in realizing the full potential of data-driven modeling in modern manufacturing environments. The proposed frameworks and case studies provide a foundation for future integration into digital manufacturing ecosystems, supporting real-time control, optimization, and sustainability.
The availability, distribution, and quality of process data are foundational to the success of data-driven modeling in manufacturing. High-resolution, well-balanced datasets that comprehensively span the full spectrum of process conditions—including normal; boundary; and extreme scenarios—are essential for building robust and generalizable models. Addressing data fitting challenges, particularly in the presence of sparse, noisy, or high-gradient data, requires the implementation of advanced data preprocessing techniques, including filtering, translation, and mapping strategies. Moreover, the inherent multi-physical, multi-phase, and multi-scale complexity of many manufacturing processes adds further layers of difficulty. Accurately capturing the interactions across different physical domains and scales—from microstructural evolution at the microscale to macroscopic process dynamics—demands the development of scalable; adaptive modeling frameworks. These frameworks must be capable of integrating heterogeneous data sources and supporting real-time updates, ensuring that models remain accurate and relevant in dynamic production environments.
Ultimately, the future of data modeling in manufacturing—and its integration into online advisory systems; digital twin platforms; and digital shadow frameworks—depends on the development of adaptive; self-updating; and interpretable models that can evolve in parallel with advancing manufacturing technologies. These models must not only deliver high predictive accuracy but also support seamless integration into broader digitalization ecosystems, including real-time control architectures and intelligent process advisory systems. By addressing the challenges outlined in this work and implementing the recommended strategies, the procedures for developing data models will become more robust, leading to the creation of more powerful, accurate, and resilient solutions. It is important to highlight the role of these models in supporting digital twin and digital shadow frameworks by enabling real-time monitoring, control, and optimization of manufacturing processes. This approach establishes a foundational framework for managing data as a strategic asset and facilitates the transition from traditional experimental and simulation-based modeling to AI-enhanced, real-time digital optimization and control systems. For instance, in the casting and extrusion case studies, the data models were explicitly designed to be embedded within web-based advisory systems, demonstrating their practical applicability in industrial settings. These advancements will play a critical role in enabling efficient, intelligent, and sustainable manufacturing processes—and will form the foundation of our next manuscript contribution.
Author Contributions
A.M.H.: conceptualization, methodology, writing-original draft preparation, software (data models), validation, data curation, writing-review, editing, visualization. M.H.: conceptualization, methodology, supervision, project administration, funding acquisition, proofreading. F.H.: Software (FE simulations), investigation, data curation, validation, proofreading. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financially supported by the Austrian Institute of Technology (AIT) under the UF2024 funding program, by the Austrian Research Promotion Agency (FFG) through the opt1mus project (FFG No. 899054), and by the European Commission under the Horizon Europe program for the metaFacturing project (HORIZON-CL4-2022-RESILIENCE-01, Project ID: 101091635).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the technical and financial support provided by the Austrian Federal Ministry for Innovation, Mobility, and Infrastructure, the Federal State of Upper Austria, and the Austrian Institute of Technology (AIT). Special thanks are extended to Hugo Drexler, Sindre Hovden, Rodrigo Gómez Vázquez, David Blacher, Siamak Rafiezadeh, and Johannes Kronsteiner for their valuable contributions to this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Horr, A.M. Notes on New Physical & Hybrid Modelling Trends for Material Process Simulations. J. Phy. Conf. Ser. 2020, 1603, 12008. [Google Scholar] [CrossRef]
- Liu, C.; Gao, H.; Li, L. A review on metal additive manufacturing: Modeling and application of numerical simulation for heat and mass transfer and microstructure evolution. China Foundry 2021, 18, 317–334. [Google Scholar] [CrossRef]
- Bordas, A.; Le Masson, P.; Weil, B. Model design in data science: Engineering design to uncover design processes and anomalies. Res. Eng. Des. 2025, 36, 1. [Google Scholar] [CrossRef]
- Vlah, D.; Kastrin, A.; Povh, J.; Vukašinović, N. Data-driven engineering design: A systematic review using scientometric approach. Adv. Eng. Inform. 2020, 54, 101774. [Google Scholar] [CrossRef]
- Bishnu, S.K.; Alnouri, S.Y.; Al-Mohannadi, D.M. Computational applications using data driven modeling in process Systems: A review. Digit. Chem. Eng. 2023, 8, 100111. [Google Scholar] [CrossRef]
- Van de Berg, D.; Savage, T.; Petsagkourakis, P.; Zhang, D.; Shah, N.; Del Rio-Chanona, E.A. Data-driven optimization for process systems engineering applications. Chem. Eng. Sci. 2022, 248, 117135. [Google Scholar] [CrossRef]
- Wilking, F.; Horber, D.; Goetz, S.; Wartzack, S. Utilization of system models in model-based systems engineering: Definition, classes and research directions based on a systematic literature review. Des. Sci. 2024, 10, e6. [Google Scholar] [CrossRef]
- Tao, F.; Li, Y.; Wei, Y.; Zhang, C.; Zuo, Y. Data–Model Fusion Methods and Applications Toward Smart Manufacturing and Digital Engineering. J. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Dogan, A.; Birant, D. Machine learning and data mining in manufacturing. Expert Syst. Appl. 2021, 166, 114060. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C.; Zhang, J.; Zhong, R. Big data analytics for intelligent manufacturing systems: A review. J. Manuf. Syst. 2022, 62, 2022. [Google Scholar] [CrossRef]
- Ghahramani, M.H.; Qiao, Y.; Zhou, M.; O’Hagan, A.; Sweeney, J. AI-Based Modeling and Data-Driven Evaluation for Smart Manufacturing Processes. IEEE/CAA J. Autom. Sin. 2020, 7, 1026–1037. [Google Scholar] [CrossRef]
- Sofianidis, G.; Rožanec, J.M.; Mladenić, D.; Kyriazis, D. A Review of Explainable Artificial Intelligence in Manufacturing. arXiv 2021. [Google Scholar] [CrossRef]
- Horr, A.; Gómez Vázquez, R.; Blacher, D. Data Models for Casting Processes–Performances, Validations and Challenges. IOP Conf. Ser. Mater. Sci. Eng. 2024, 1315, 12001. [Google Scholar] [CrossRef]
- Horr, A.M.; Blacher, D.; Gómez Vázquez, R. On Performance of Data Models and Machine Learning Routines for Simulations of Casting Processes. BHM Berg-Und Hüttenmännische Monatshefte 2025, 170, 28–36. [Google Scholar] [CrossRef]
- Horr, A.M. Real-Time Modeling for Design and Control of Material Additive Manufacturing Processes. Metals 2024, 14, 1273. [Google Scholar] [CrossRef]
- Horr, A.M.; Drexler, H. Real-Time Models for Manufacturing Processes: How to Build Predictive Reduced Models. Processes 2025, 13, 252. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Gao, R.X.; Zhang, F. Hybrid physics-based and data-driven models for smart manufacturing: Modelling, simulation, and explainability. J. Manuf. Syst. 2022, 63, 381–391. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data Driven Science & Engineering-Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Qin, J.; Hu, F.; Liu, Y.; Witherell, P.; Wang, C.L.; Rosen, D.W.; Simpson, T.W.; Lu, Y.; Tang, Q. Research and application of machine learning for additive manufacturing. Addit. Manuf. 2022, 52, 102691. [Google Scholar] [CrossRef]
- Lebon, B. directChillFoam: An OpenFOAM application for direct-chill casting. J. Open Source Softw. 2023, 8, 4871. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. Available online: https://openfoam.org (accessed on 30 July 2025).
- Bennon, W.D.; Incropera, F.P. A continuum model for momentum, heat and species transport in binary solid-liquid phase change systems—I. Model formulation. Int. J. Heat Mass Transf. 1987, 30, 2161–2170. [Google Scholar] [CrossRef]
- Greenshields, C.; Weller, H. Notes on Computational Fluid Dynamics: General Principles; CFD Direct Ltd.: London, UK, 2022; 291p, ISBN 978-1-3999-2078-0; Available online: https://doc.cfd.direct/notes/cfd-general-principles/ (accessed on 30 July 2025).
- Vreeman, C.J.; Schloz, J.D.; Krane, M.J.M. Direct Chill Casting of Aluminium Alloys: Modelling and Experiments on Industrial Scale Ingots. J. Heat Transf. 2002, 124, 947–953. [Google Scholar] [CrossRef]
- directChillFoam Documentation. Available online: https://blebon.com/directChillFoam/ (accessed on 30 July 2025).
- Weckman, D.C.; Niessen, P. A numerical simulation of the D.C. continuous casting process including nucleate boiling heat transfer. Met. Trans. B 1982, 13, 593–602. [Google Scholar] [CrossRef]
- Hoque, S.E.; Hovden, S.; Culic, S.; Nietsch, J.A.; Kronsteiner, J.; Horwatitsch, D. Modeling friction in hyperxtrude for hot forward extrusion simulation of EN AW 6060 and EN AW 6082 alloys. Key Eng. Mater. 2022, 926, 416–425. [Google Scholar] [CrossRef]
- Rizkya, I.; Syahputri, K.; Sari, R.M.; Siregar, I.; Utaminingrum, J. Autoregressive Integrated Moving Average (ARIMA) Model of Forecast Demand in Distribution Centre. IOP Conf. Ser. Mater. Sci. Eng. 2019, 598, 12071. [Google Scholar] [CrossRef]
- Brötz, S.; Horr, A.M. Framework for progressive adaption of FE mesh to simulate generative manufacturing processes. Manuf. Lett. 2020, 24, 25–55. [Google Scholar] [CrossRef]
- Antoulas, A.C.; Ionutiu, R.; Martins, N.; Ter Maten, E.J.W.; Mohaghegh, K.; Pulch, R.; Rommes, J.; Saadvandi, M.; Striebel, M. Model Order Reduction: Methods, Concepts and Properties. In Coupled Multiscale Simulation and Optimization in Nanoelectronics; Mathematics in Industry; Günther, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 21. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Trans. 1984, 15B, 299–305. [Google Scholar] [CrossRef]
- NovaFlow&Solid NovaCast Systems AB. Available online: https://www.novacast.se/product/novaflowsolid/ (accessed on 30 July 2025).
- Olleak, A.; Xi, Z. Part-Scale Finite Element Modeling of the Selective Laser Melting Process with Layer-Wise Adaptive Remeshing for Thermal History and Porosity Prediction. ASME J. Manuf. Sci. Eng. 2020, 142, 121006. [Google Scholar] [CrossRef]
- Fucheng, T.; Xiaoliang, T.; Tingyu, X.; Junsheng, Y.; Liangbin, L. A hybrid adaptive finite element phase-field method for quasi-static and dynamic brittle fracture. Int. J. Numer. Methods Eng. 2019, 12, 1108–1125. [Google Scholar] [CrossRef]
- Stefano, M.; Umberto, P. Extended finite element method for quasi-brittle fracture. Int. J. Numer. Methods Eng. 2003, 58, 103–126. [Google Scholar] [CrossRef]
- Sukumar, N.; Moës, N.; Moran, B.; Belytschko, T. Extended finite element method for three-dimensional crack modelling. Int. J. Numer. Methods Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]
- Modesar, S. Chapter Three—Numerical modeling of highly nonlinear phenomena in heterogeneous materials and domains. In Advances in Applied Mechanics; Stéphane, P.A.B., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, pp. 111–239. [Google Scholar] [CrossRef]
- Cunyi, L.; Jianguang, F.; Na, Q.; Chi, W.; Grant, S.; Qing, L. Phase field fracture in elasto-plastic solids: Considering complex loading history for crushing simulations. Int. J. Mech. Sci. 2024, 268, 108994. [Google Scholar] [CrossRef]
- Jayanath, S.; Achuthan, A. A Computationally Efficient Finite Element Framework to Simulate Additive Manufacturing Processes. J. Manuf. Sci. Eng. 2018, 140, 41009. [Google Scholar] [CrossRef]
- Jeehwan, L.; Giseok, Y.; Do-Nyun, K. An adaptive procedure for the analysis of transient wave propagation using interpolation covers. Comput. Methods Appl. Mech. Eng. 2025, 445, 118167. [Google Scholar] [CrossRef]
- Ramani, R.; Shkoller, S. A fast dynamic smooth adaptive meshing scheme with applications to compressible flow. J. Comput. Phys. 2023, 490, 112280. [Google Scholar] [CrossRef]
- Radovitzky, R.; Ortiz, M. Error estimation and adaptive meshing in strongly nonlinear dynamic problems. Comput. Methods Appl. Mech. Eng. 1999, 172, 203–240. [Google Scholar] [CrossRef]
- Barros, G.F.; Grave, M.; Viguerie, A.; Reali, A.; Coutinho, A.L.G.A. Dynamic mode decomposition in adaptive mesh refinement and coarsening simulations. Eng. Comput. 2022, 38, 4241–4268. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. A Robust Adaptive Mesh Generation Algorithm: A Solution for Simulating 2D Crack Growth Problems. Materials 2023, 16, 6481. [Google Scholar] [CrossRef] [PubMed]
- Horr, A.M. Computational Evolving Technique for Casting Process of Alloys. Math. Probl. Eng. 2019, 2019, 6164092. [Google Scholar] [CrossRef]
- Baiges, J.; Chiumenti, M.; Moreira, C.A.; Cervera, M.; Codina, R. An adaptive Finite Element strategy for the numerical simulation of additive manufacturing processes. Addit. Manuf. 2021, 37, 101605. [Google Scholar] [CrossRef]
- Ash, T. Dynamic Node Creation in Backpropagation Networks. Connect. Sci. 1989, 1, 365–375. [Google Scholar] [CrossRef]
- Patil, N.; Pal, D.; Stucker, B. A New Finite Element Solver Using Numerical Eigen Modes for Fast Simulation of Additive Manufacturing Processes. In Proceedings of the International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–13 August 2013. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, P.; Cheng, L.; Min, Z.; Chyu, M.; To, A.C. Finite element modeling and validation of thermomechanical behavior of Ti-6Al-4V in directed energy deposition additive manufacturing. Addit. Manuf. 2016, 12, 169–177. [Google Scholar] [CrossRef]
- Horr, A.M. Real-Ttime Modelling and ML Data Training for Digital Twinning of Additive Manufacturing Processes. BHM Berg-Und Hüttenmännische Monatshefte 2024, 169, 48–56. [Google Scholar] [CrossRef]
Figure 1.
Framework for data strategy in manufacturing processes: foundational concepts and workflow implementation for developing process digital twins.
Figure 2.
Basic foundational development plan for modeling steady-state manufacturing processes within broader digitalization framework.
Figure 3.
(a) Experimental and simulation setup for horizontal and (b) vertical casting processes, including melt pool size estimation.
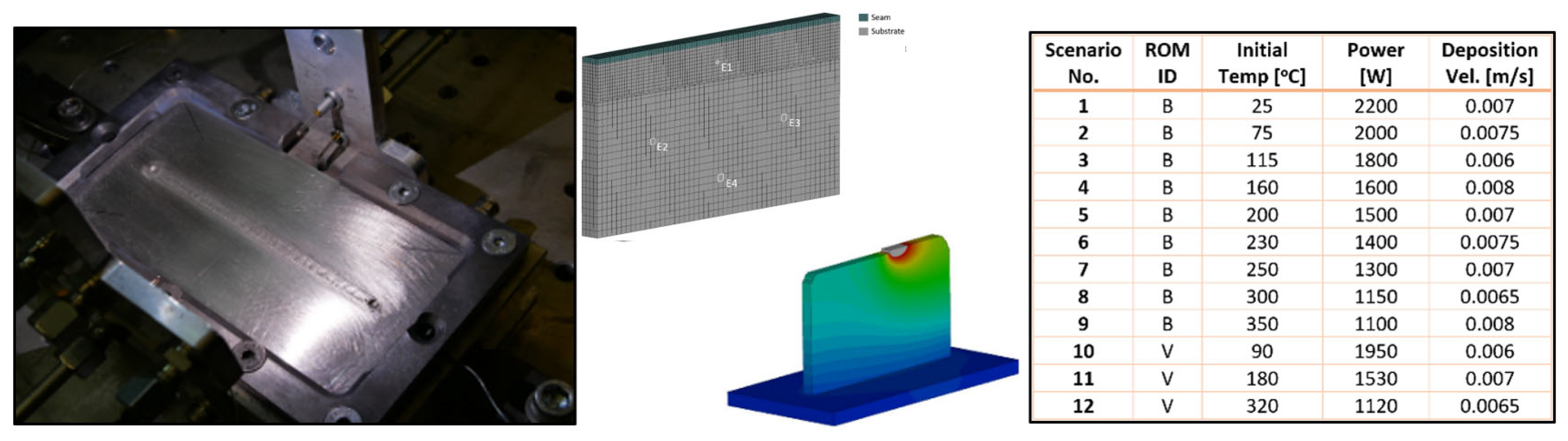
Figure 4.
Experimental, simulation, and snapshot scenario matrix including basic and DOE scenarios for extrusion case study Adapted from Ref. [
17]. The letter “A” indicates a detailed view within the same figure, and a corresponding side view of this detail is also presented.
Figure 5.
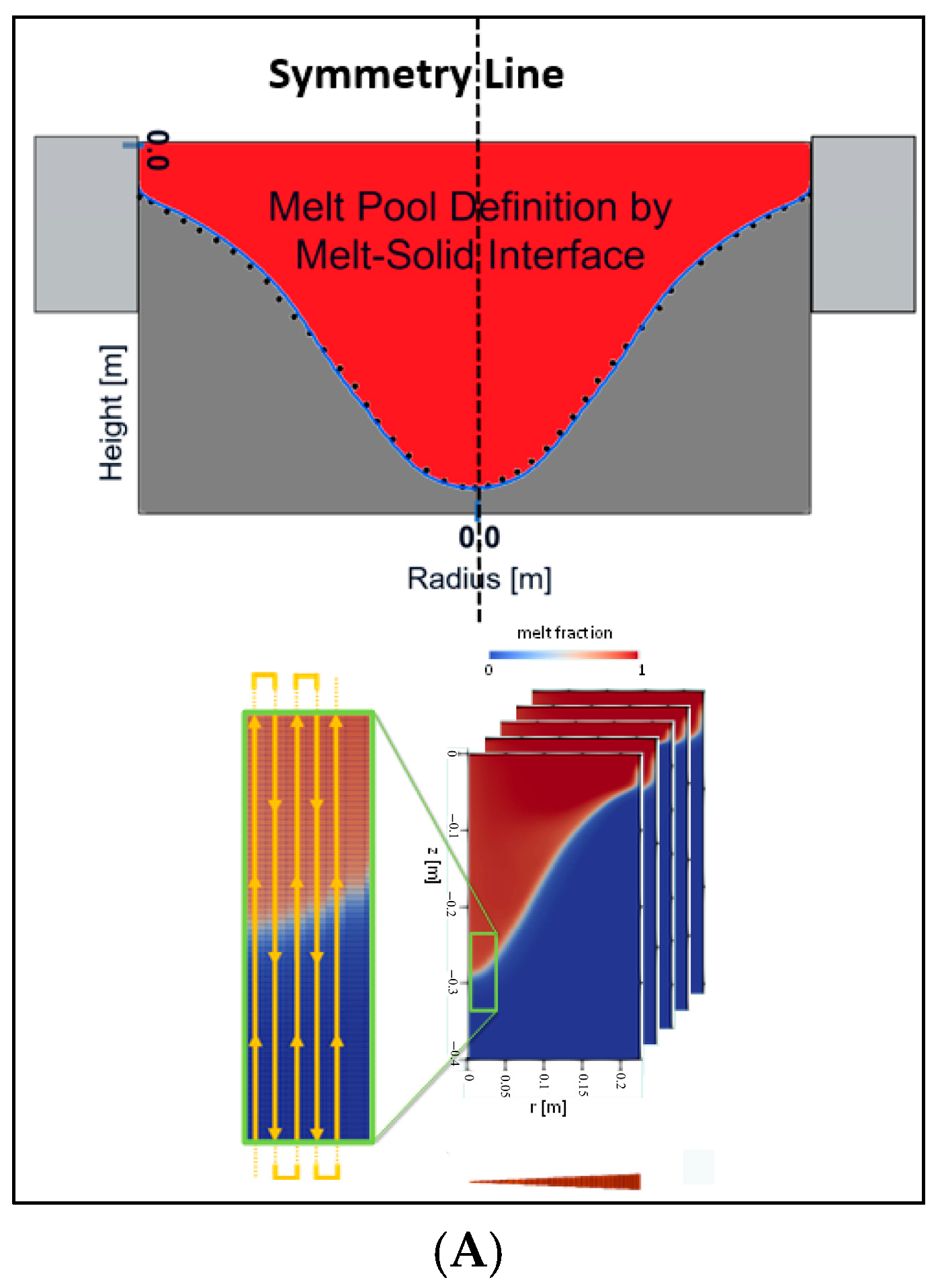
Model setup and nodal reordering strategy for both (
A) vertical casting—illustrating a snake-path reordering scheme at the melt pool—and (
B) horizontal casting processes, showing depth of melt pool “a” and solidify shell thickness “b” with similar snake-path reordering scheme. Adapted from Ref. [
14].
Figure 6.
Comparison between CFD-calculated and data model-estimated temperature values and normalized error graph for first 3000 nodes in DOE scenario no. 3.
Figure 7.
Comparative analysis of FE-calculated and data model-estimated temperature values, along with a normalized error graph along the streamline points for all DOE scenarios.
Figure 8.
Experimental, simulation, and snapshot scenario matrix including basic and DOE scenarios for AM case study Adapted from Ref. [
16].
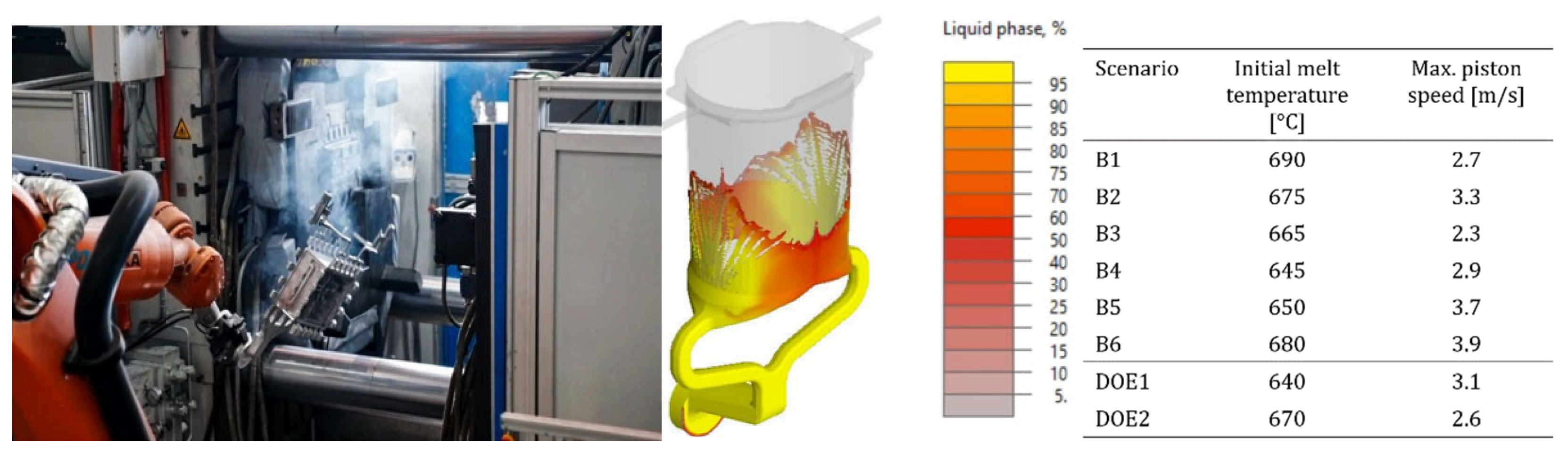
Figure 9.
Experimental setup and numerical CFD domain for multi-cycle transient HPDC process, encompassing all six fundamental filling cycles and two DOE snapshot scenario matrices Adapted from Ref. [
14].
Figure 10.
Comparative analysis of FE-calculated and data model-estimated temperature values, along with a normalized error history along the streamline for all DOE scenarios.
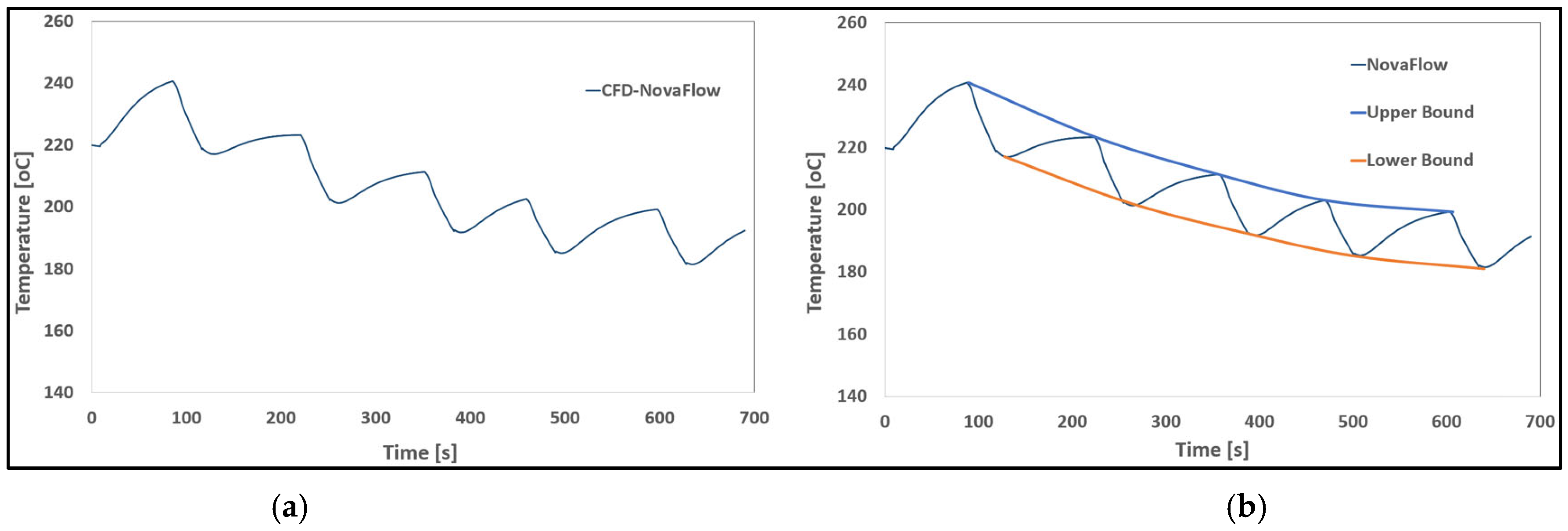
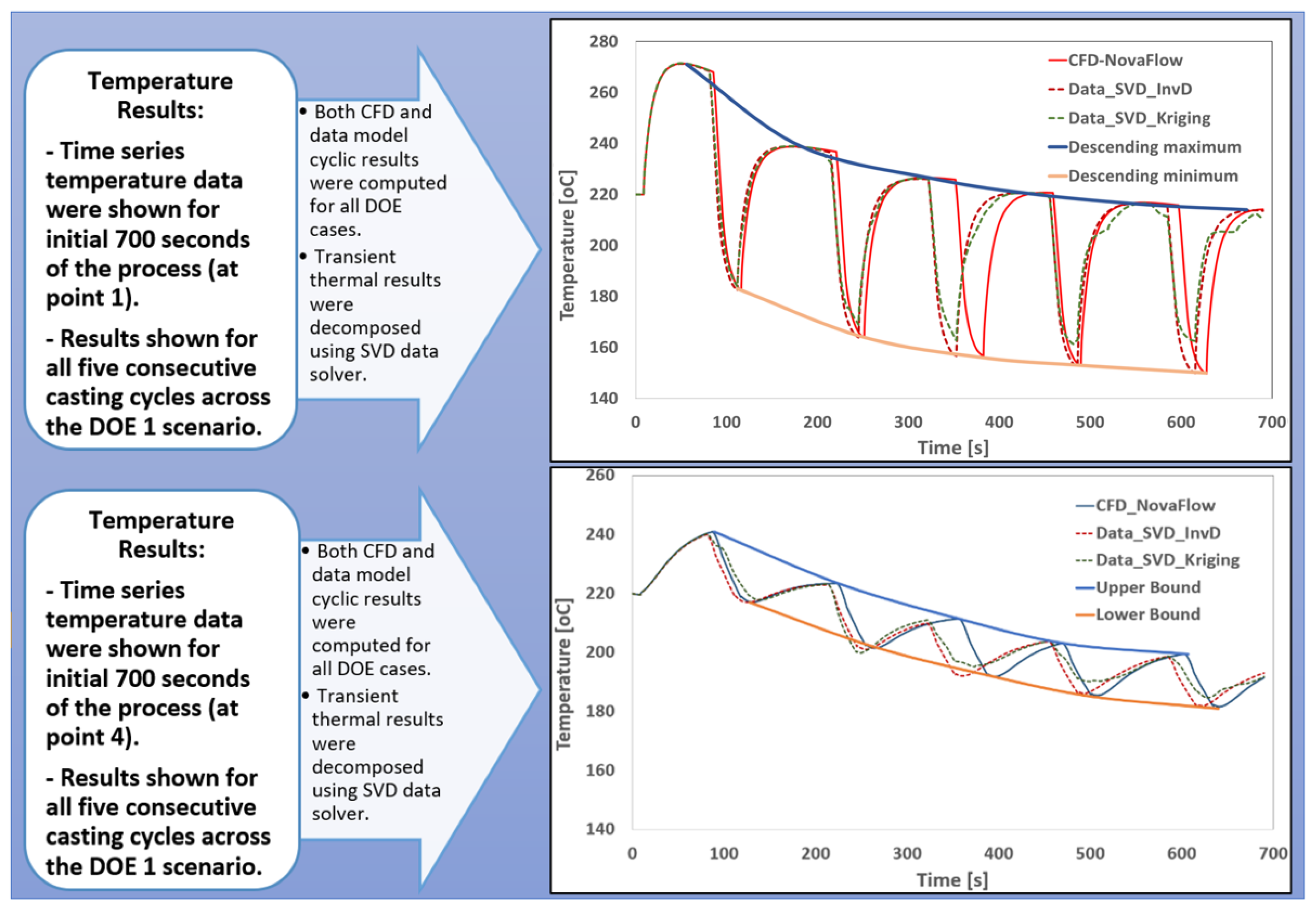
Figure 11.
(a) Thermal cycle results from a typical CFD numerical simulation, and (b) with descending maximum and minimum temperature curves across six filling cycles.
Figure 12.
Time-history temperature curves at two sensor locations, comparing the predictions from SVD-InvD and SVD-Kriging data models against CFD simulation results.
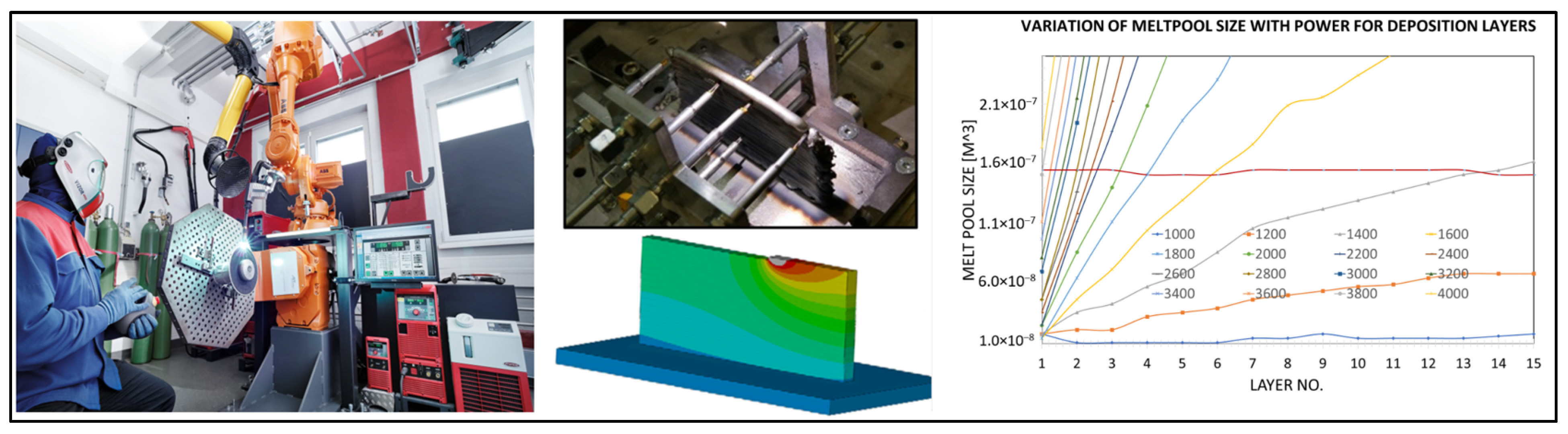
Figure 13.
Schematic overview of generative data modeling framework, including key definitions and the iterative model generation loop.
Figure 14.
Experimental setup, simulation, and initial power calculation results using initial snapshot matrix and constant welding power for all deposition layers Adapted from Ref. [
52].
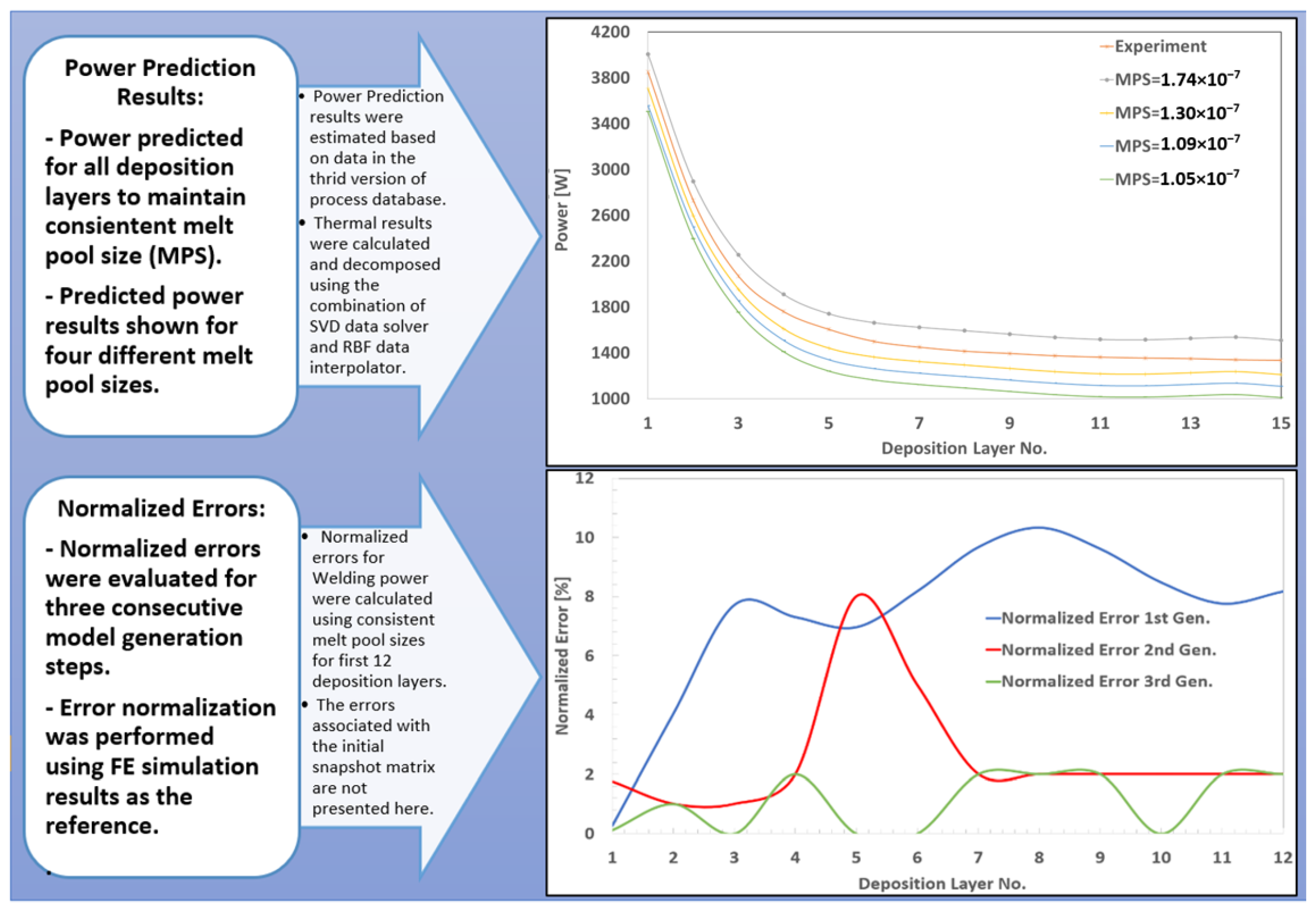
Figure 15.
(a) Initial variation of welding power in relation to the resulting melt pool size, and (b) the corresponding data correlation matrix.
Figure 16.
Predicted welding power across different deposition layers aimed at maintaining consistent melt pool size using third-generation data model and the normalized error percentages for three consecutive stages of data model development.
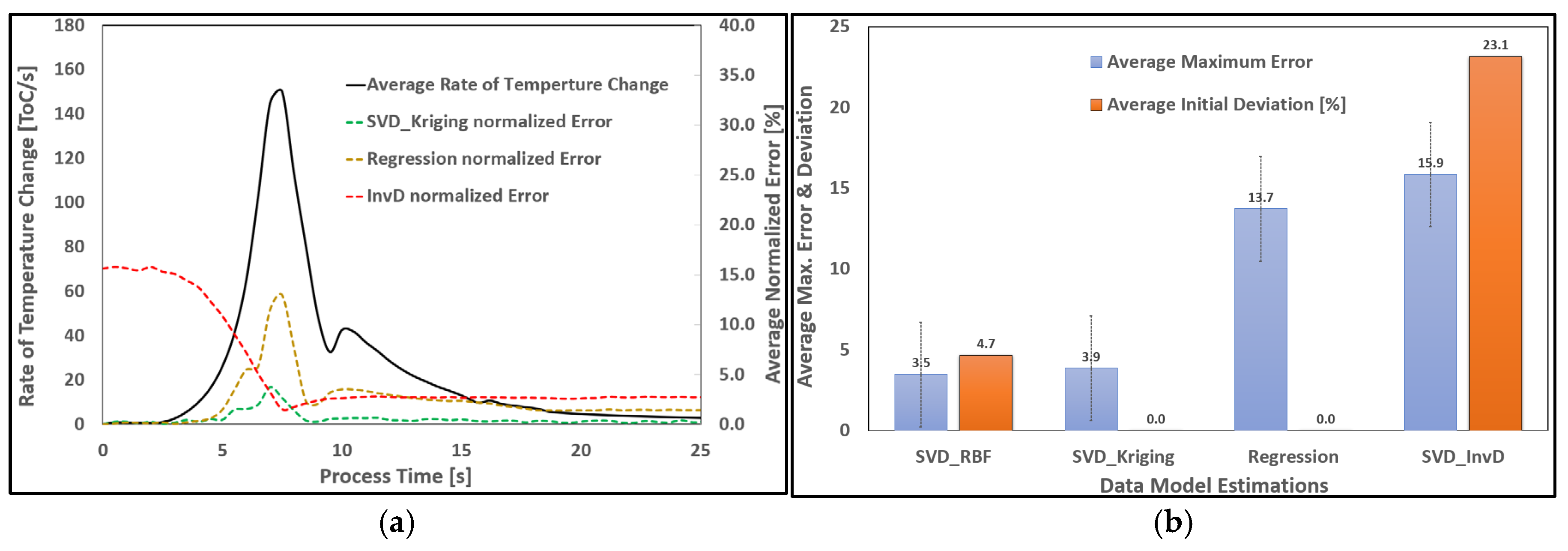
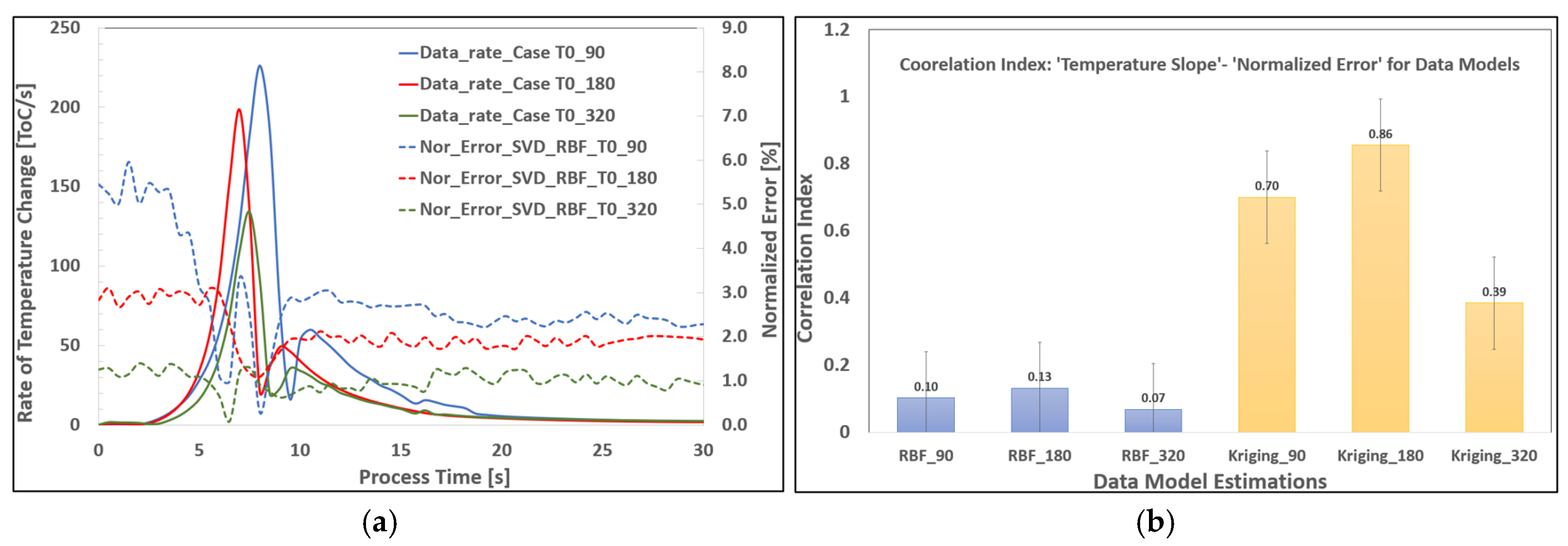
Figure 17.
(a) Comparative performance of various solver–interpolator combinations, including correlation study for rate dependency and average maximum errors (over all DOEs), and (b) initial boundary data fitting and average maximum errors for real-time models.
Figure 18.
(a) Correlation study for rate dependency and average maximum errors (over all DOEs) for different solver-interpolator combinations, and (b) initial boundary data fitting and average maximum errors data real-time models.
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).