Dispersion of TiB2 Particles in Al–Ni–Sc–Zr System Under Rapid Solidification
Abstract
1. Introduction
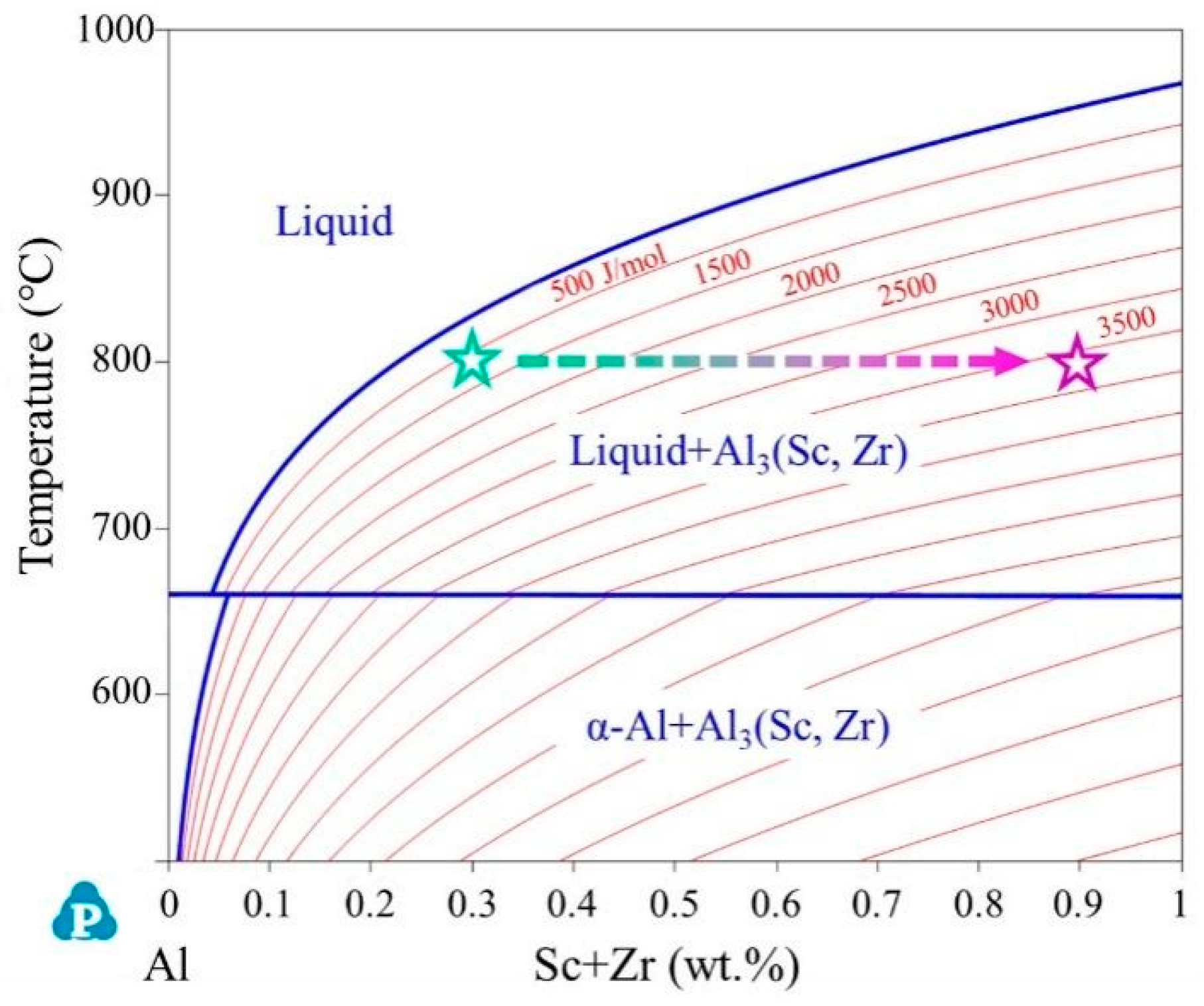
2. Materials Design
3. Materials and Methods
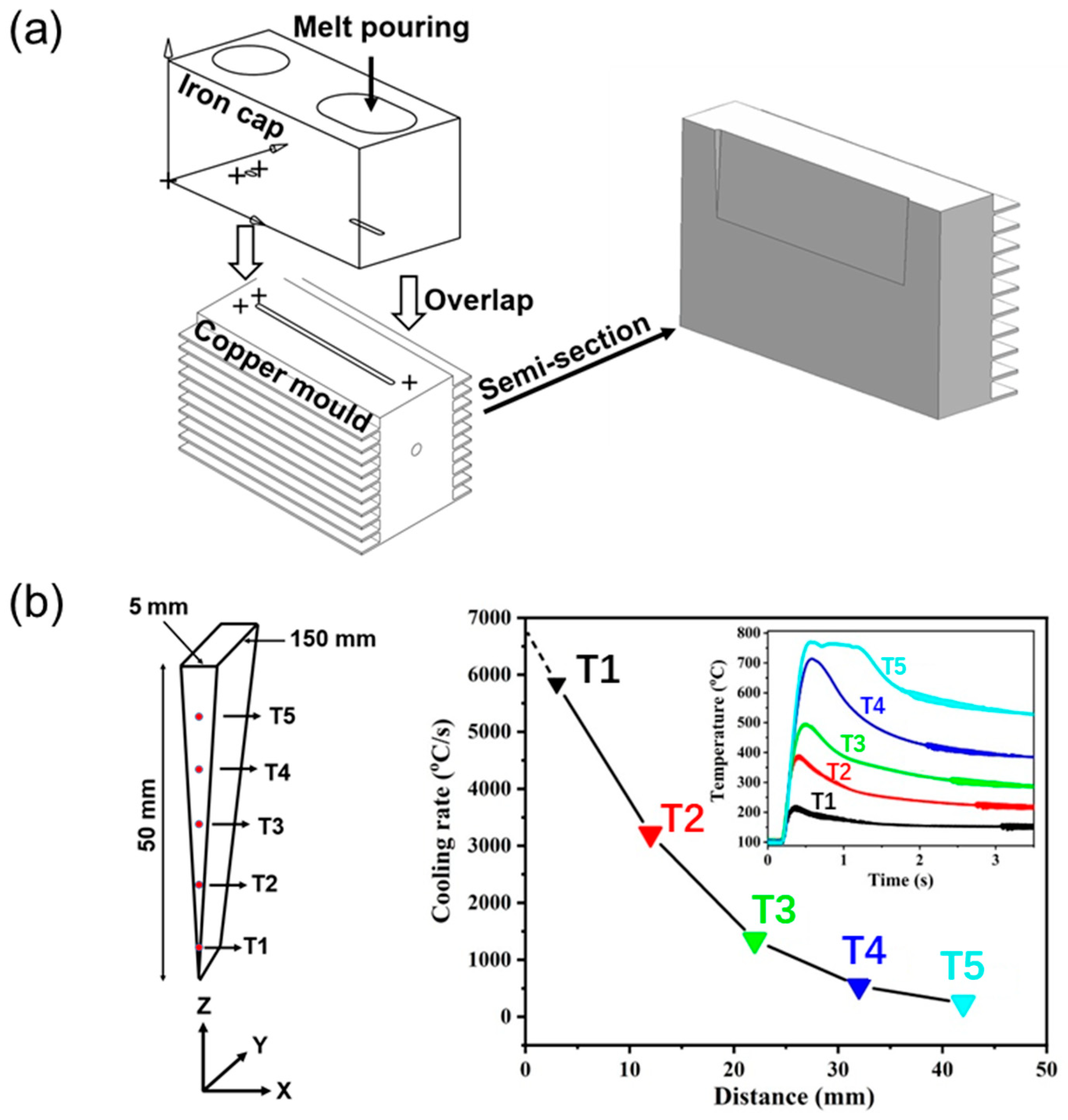
3.1. Materials Fabrication
3.2. Characterization Methods
3.3. Thermodynamic Calculation
4. Results
4.1. Microstructure of Wedge-Cast Samples
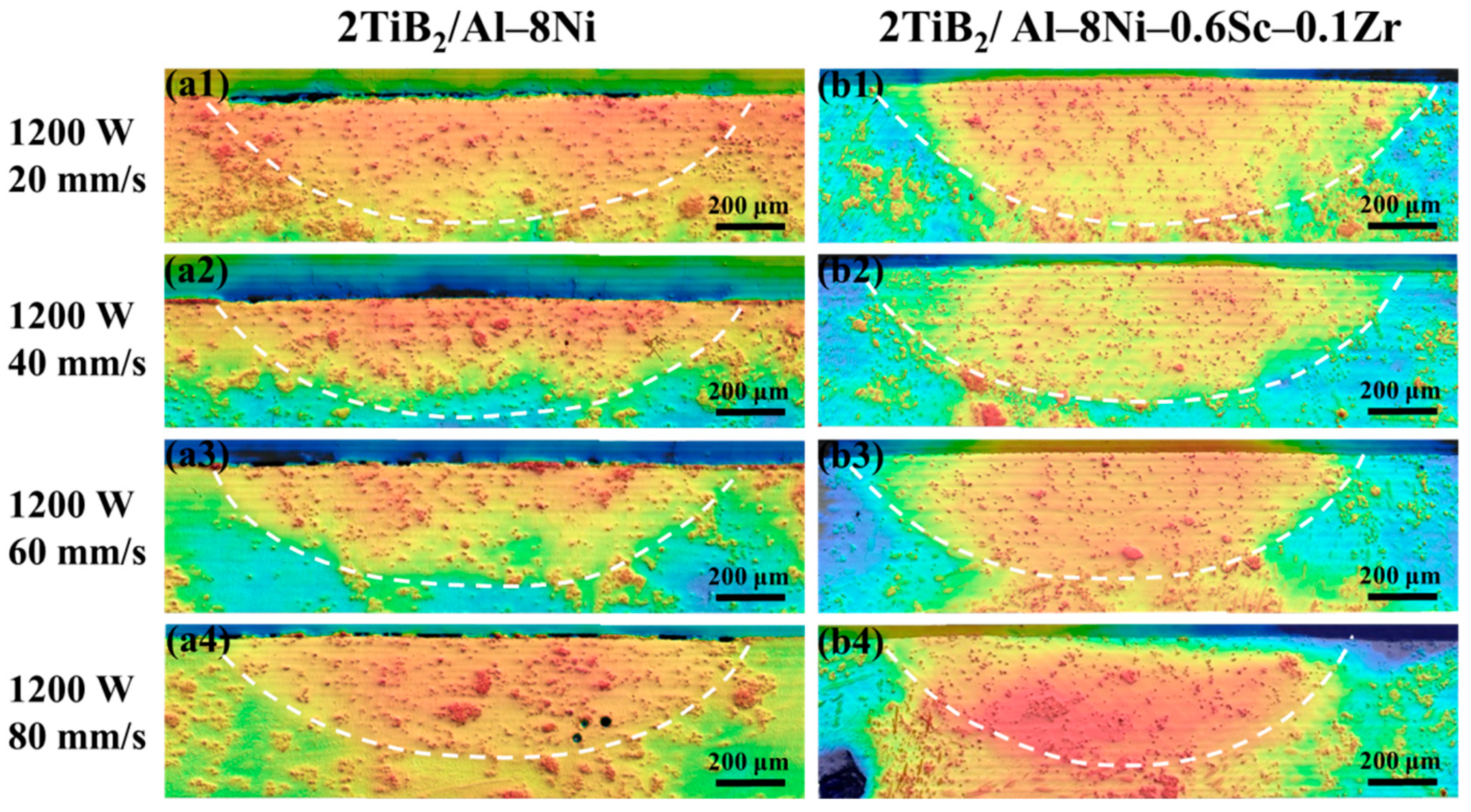
4.2. Microstructure of Laser-Remelted Samples
4.3. Orientation Relationship Between TiB2 and α-Al
5. Discussion
5.1. Nucleation and Growth of Al3(Sc,Zr) on TiB2 Surfaces
- -
- Interfacial energy between Al3(Sc,Zr) and liquid Al (γ)
- -
- Volumetric Gibbs free energy change (ΔGᵥ)
- -
- Wetting angle (θ)
- -
- Nucleation site density (N)
- -
- Diffusion coefficient (D)
- -
- Interfacial concentration (
- -
- Incubation time
- -
- Stage I (805–923 °C, low undercooling): Al3(Sc,Zr) nucleation is negligible; Sc/Zr atoms segregate onto the (0001) TiB2 surface and construct a two-dimensional cluster (2DC) whose lattice must expand to achieve edge-to-edge matching with TiB2. The resulting elastic strain suppresses subsequent α-Al nucleation.
- -
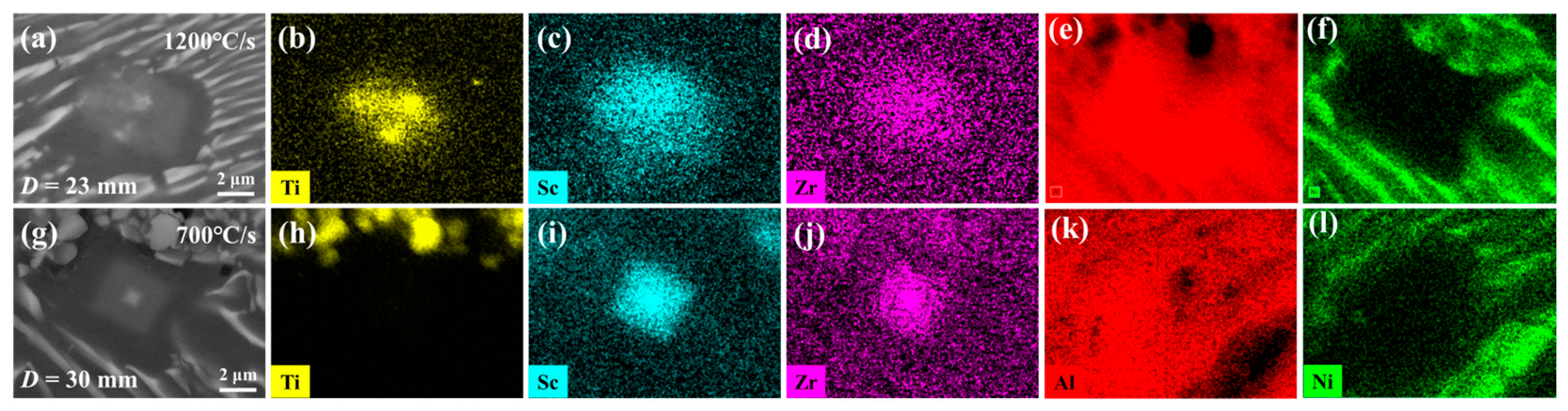
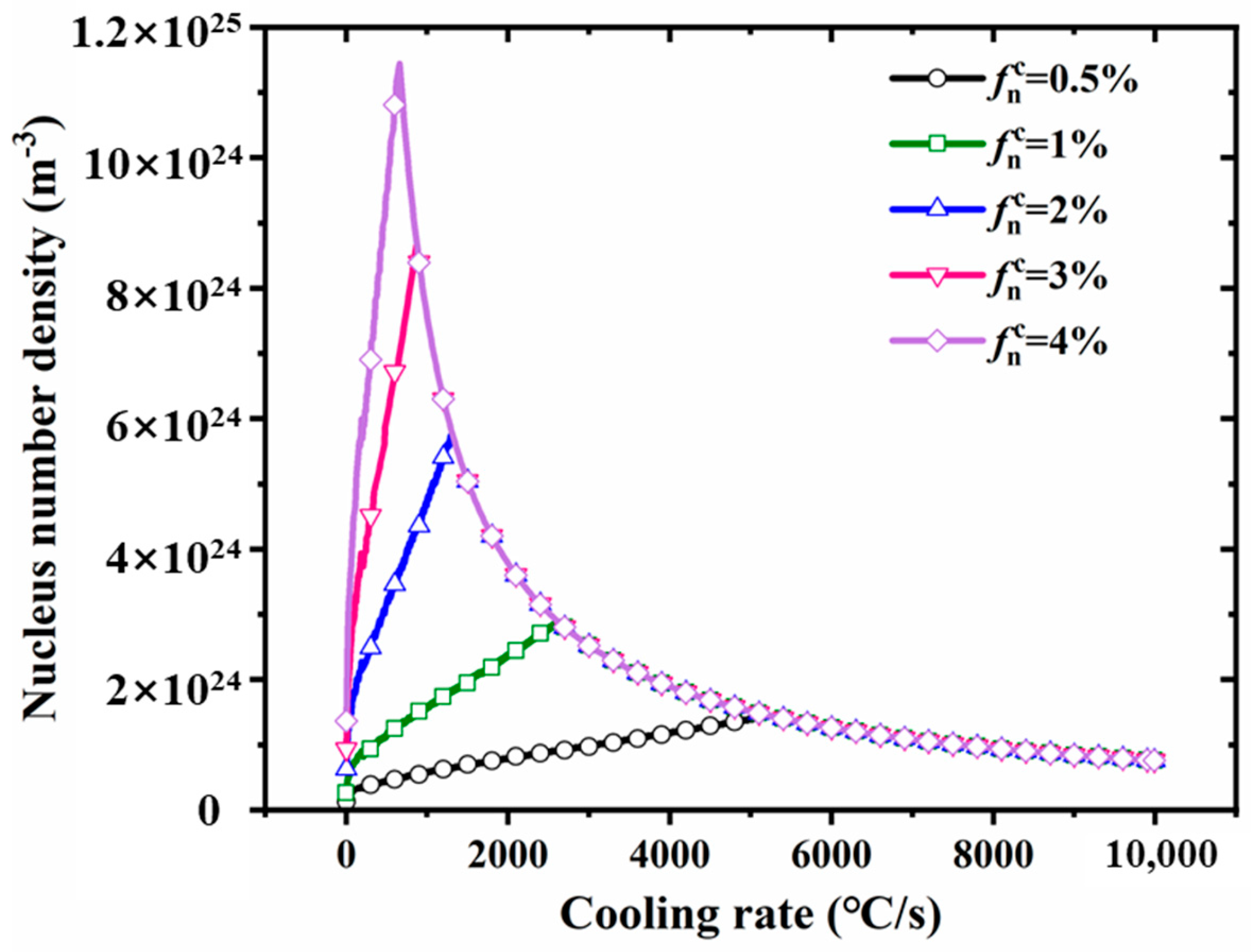
- Stage II (765–805 °C): the 2DC transforms into three-dimensional cap-shaped embryos (3DC) whose formation rate rises explosively (Figure 7b). These 3DC embryos spread over the TiB2 surface to form a continuous shell; the process is most complete near 1200 °C/s (Figure 4b). Once the shell exceeds a critical thickness, lattice mismatch at the Al3(Sc,Zr)/TiB2 interface is fully relaxed, enabling coherent matching with α-Al.
- -
- Stage III (≤765 °C): nucleation of new 3DC embryos ceases because their critical height falls below one atomic layer, and growth of the existing Al3(Sc,Zr) shell dominates. For cooling rates ≤850 °C/s, the planar shell becomes morphologically unstable and evolves into seaweed/dendritic Al3(Sc,Zr) (Figure 5a).
5.2. Effect of Composite Interface on TiB2 Dispersion
- (1)
- Interfacial tension (FI): Dominates when the particle–interface gap is <0.2–0.4 nm [43]:where Rp is the particle radius; Δγ denotes the change in interfacial energy upon particle engulfment by the interface; ao is the atomic spacing; dp/s is the distance between the particle and the solidification front; and α is the interface shape factor. Given that the interfacial tension decays rapidly with increasing dp/s, n is assigned a value of 7.
- (2)
- (3)
- Viscous drag (FD): The viscous force originates from the relative motion between the liquid phase and the particles displaced by the advancing solidification front. According to Stokes’ law, the viscous force is proportional to both the solidification rate and the viscosity of the liquid, and can be expressed as [43]:where η is melt viscosity and V is particle velocity.
6. Conclusions
- (1)
- The volumetric driving force for Al3(Sc,Zr) precipitation, governed by the Sc and Zr contents in the melt, plays a critical role in determining the heterogeneous nucleation rate. Based on thermodynamic analysis, the Sc and Zr contents were set to 0.6 wt.% and 0.1 wt.%, respectively, balancing sufficient nucleation driving force, melt temperature control, and model simplicity.
- (2)
- The formation of the Al3(Sc,Zr)/TiB2 composite interface depends on the cooling rate and strongly influences TiB2 dispersion. In wedge-cast samples, TiB2 agglomeration occurred at 700 °C/s, with primary Al3(Sc,Zr) forming around clusters. At 1200 °C/s, Al3(Sc,Zr) precipitated on TiB2 surfaces, forming core–shell structures and improving particle dispersion. At 1750 °C/s, these structures disappeared, and agglomeration reappeared.
- (3)
- In laser surface–remelted 2TiB2/Al–8Ni samples, TiB2 particles showed severe agglomeration and lacked a consistent orientation with the α-Al matrix. In contrast, the addition of Sc and Zr in the 2TiB2/Al–8Ni–0.6Sc–0.1Zr alloy significantly improved dispersion. Dispersion first increased and then decreased with rising scanning speed. A reproducible orientation relationship of (111) α-Al//(0001) TiB2 was observed.
- (4)
- The formation of the Al3(Sc,Zr)/TiB2 interface is closely linked to Al3(Sc,Zr) nucleation under rapid solidification. Classical nucleation theory indicates that the highest nucleation density occurs near 1200 °C/s, at which the composite interface forms most effectively, thereby promoting uniform TiB2 dispersion.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Murty, B.S.; Kori, S.A.; Chakraborty, M. Grain refinement of aluminium and its alloys by heterogeneous nucleation and alloying. Int. Mater. Rev. 2002, 47, 3–29. [Google Scholar] [CrossRef]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.A.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Wang, Y.; Zhang, Y.; Qin, T.; Zhou, X.R.; Thompson, G.E.; Pennycook, T.; Hashimoto, T. Grain refining mechanism in the Al/Al–Ti–B system. Acta Mater. 2015, 84, 292–304. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.C.; Zhang, X.Y.; Huang, Y.C. Understanding grain refinement of Sc addition in a Zr containing Al-Zn-Mg-Cu aluminum alloy from experiments and first-principles. Intermetallics 2020, 123, 106823. [Google Scholar] [CrossRef]
- Opprecht, M.; Garandet, J.P.; Roux, G.; Flament, C. An understanding of duplex microstructures encountered during high strength aluminium alloy laser beam melting processing. Acta Mater. 2021, 215, 117204. [Google Scholar] [CrossRef]
- Jiang, A.; Wang, X. Dendritic and seaweed growth of proeutectic scandium tri-aluminide in hypereutectic Al-Sc undercooled melt. Acta Mater. 2020, 200, 56–65. [Google Scholar] [CrossRef]
- Dai, J.; Wang, Q.; Yang, C.; Chen, H.; Luo, G.; Li, H.; Sun, G.; Wang, H.; Chen, Z. Effects of sintering temperature on microstructure and mechanical properties of Al–Ni–Sc–Zr alloy fabricated by powder metallurgy. Mater. Charact. 2025, 221, 114772. [Google Scholar] [CrossRef]
- Belov, N.A.; Alabin, A.N.; Eskin, D.G. Improving the properties of cold-rolled Al–6%Ni sheets by alloying and heat treatment. Scr. Mater. 2004, 50, 89–94. [Google Scholar] [CrossRef]
- Boussinot, G.; Döring, M.; Hemes, S.; Stryzhyboroda, O.; Apel, M.; Schmidt, M. Laser powder bed fusion of eutectic Al–Ni alloys: Experimental and phase-field studies. Mater. Des. 2021, 198, 109299. [Google Scholar] [CrossRef]
- Deng, J.; Chen, C.; Liu, X.; Li, Y.; Zhou, K.; Guo, S. A high-strength heat-resistant Al−5.7Ni eutectic alloy with spherical Al3Ni nano-particles by selective laser melting. Scr. Mater. 2021, 203, 114031. [Google Scholar] [CrossRef]
- Dhal, A.; Thapliyal, S.; Agrawal, P.; Rpy, A.; Sharma, A.; Mishra, R.S.; Faierson, E. Multimodal and multiscale strengthening mechanisms in Al-Ni-Zr-Ti-Mn alloy processed by laser powder bed fusion additive manufacturing. Mater. Des. 2024, 237, 112602. [Google Scholar] [CrossRef]
- Ding, R.; Deng, J.; Liu, X.; Wu, Y.; Geng, Z.; Li, D.; Zhang, T.; Chen, C.; Zhou, K. Enhanced mechanical properties and thermal stability in additively manufactured Al-Ni alloy by Sc addition. J. Alloys Compd. 2023, 934, 167894. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, C.; Cheng, Y.; Zhu, X.; Wei, T.; Wang, C.; Jia, Q. Manipulating the fine grain nucleation in Sc/Zr-modified Al alloys through a novel process strategy of laser powder bed fusion. Scr. Mater. 2025, 261, 116606. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Hu, L.; Chen, T.; Ji, G.; Chen, H.; Wang, H.; Wang, H.; Chen, Z. Nanoscale engineering of low-misfit TiB2/Al3(Sc,Zr)/α-Al multi-interface to improve strength-ductility synergy for direct energy deposited aluminum alloy. Addit. Manuf. 2024, 79, 103913. [Google Scholar] [CrossRef]
- Lohar, A.K.; Mondal, B.N.; Panigrahi, S.C. Influence of cooling rate on the microstructure and ageing behavior of as-cast Al–Sc–Zr alloy. J. Mater. Process. Technol. 2010, 210, 2135–2141. [Google Scholar] [CrossRef]
- Taendl, J.; Orthacker, A.; Amenitsch, H.; Kothleitner, G.; Poletti, C. Influence of the degree of scandium supersaturation on the precipitation kinetics of rapidly solidified Al-Mg-Sc-Zr alloys. Acta Mater. 2016, 117, 43–50. [Google Scholar] [CrossRef]
- Li, X.P.; Ji, G.; Chen, Z.; Addad, A.; Wu, Y.; Wang, H.W.; Vleugels, J.; Van Humbeeck, J.; Kruth, J.P. Selective laser melting of nano-TiB2 decorated AlSi10Mg alloy with high fracture strength and ductility. Acta Mater. 2017, 129, 183–193. [Google Scholar] [CrossRef]
- Chen, M.; Li, X.; Ji, G.; Wu, Y.; Chen, Z.; Baekelant, W.; Vanmeensel, K.; Wang, H.; Kruth, J.-P. Novel composite powders with uniform TiB2 nano-particle distribution for 3D printing. Appl. Sci.-Basel 2017, 7, 250. [Google Scholar] [CrossRef]
- Cao, W.; Chen, S.L.; Zhang, F.; Wu, K.; Yang, Y.; Chang, Y.A.; Schmid-Fetzer, R.; Oates, W.A. PANDAT software with PanEngine, PanOptimizer and PanPrecipitation for multi-component phase diagram calculation and materials property simulation. Calphad 2009, 33, 328–342. [Google Scholar] [CrossRef]
- Zhao, Y.-Z.; Zhao, Y.-H.; Li, Q.; Chen, S.-L.; Zhang, J.-Y.; Chou, K.-C. Effects of step size and cut-off limit of residual liquid amount on solidification simulation of Al-Mg-Zn system with Scheil model. Intermetallics 2009, 17, 491–495. [Google Scholar] [CrossRef]
- Yang, W.; Wang, P.; Huang, X.; Zhang, S. Thermodynamic analysis of the Al–Ni system. Intermetallics 2022, 149, 107647. [Google Scholar] [CrossRef]
- Bo, H.; Liu, L.B.; Jin, Z.P. Thermodynamic analysis of Al–Sc, Cu–Sc and Al–Cu–Sc system. J. Alloys Compd. 2010, 490, 318–325. [Google Scholar] [CrossRef]
- Shevchenko, M.A.; Ivanov, M.I.; Berezutskii, V.V.; Kudin, V.G.; Sudavtsova, V.S. Thermodynamic properties of alloys of the Ni–Sc and Ni–Y systems. Russ. J. Phys. Chem. A 2014, 88, 897–902. [Google Scholar]
- Kardellass, S.; Servant, C.; Selhaoui, N.; Iddaoudi, A.; Ait Amar, M.; Bouirden, L. Thermodynamic description of the Ni–Sc system. Calphad 2013, 42, 59–65. [Google Scholar] [CrossRef]
- Wang, T.; Jin, Z.P.; Zhao, J.C. Thermodynamic assessment of the Al-Zr binary system. J. Phase Equilib. Diff. 2001, 22, 544–551. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Du, Z.; Wang, F. Experimental study and thermodynamic re-assessment of the Ni–Zr system. Calphad 2007, 31, 413–421. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, S.L.; Wang, C.P. Thermodynamic assessments of the Sc–M (M: Ag, B and Th) systems. J. Alloys Compd. 2009, 469, 186–192. [Google Scholar] [CrossRef]
- Campbell, C.E.; Kattner, U.R. A thermodynamic assessment of the Ni-Al-B system. J. Phase Equilib. Diff. 1999, 20, 485–496. [Google Scholar] [CrossRef]
- Bo, H.; Liu, L.B.; Hu, J.L.; Jin, Z.P. Experimental study and thermodynamic modeling of the Al-Sc-Zr system. Comput. Mater. Sci. 2017, 133, 82–92. [Google Scholar] [CrossRef]
- He, J.Q.; Fan, L.; Liu, H.S.; Peng, H.L.; Jin, Z.P. Experimental investigation of phase equilibria in the Al–Ni–Sc system. J. Mater. Sci. 2019, 54, 10516–10528. [Google Scholar] [CrossRef]
- Miao, H.; Zhang, L.; Liu, L.; Deng, Z.; Wang, H.; Masset, P.J. Experimental investigation and thermodynamic optimization of the Al–Ni–Sc ternary system. Calphad 2022, 76, 102397. [Google Scholar] [CrossRef]
- Witusiewicz, V.T.; Sommer, F. Thermodynamics of liquid Al–Ni–Zr and Al–Cu–Ni–Zr alloys. J. Alloys Compd. 1999, 289, 152–167. [Google Scholar] [CrossRef]
- Witusiewicz, V.T.; Bondar, A.A.; Hecht, U.; Zollinger, J.; Artyukh, L.V.; Velikanova, T.Y. The Al–B–Nb–Ti system V. Thermodynamic description of the ternary system Al–B–Ti. J. Alloys Compd. 2009, 474, 86–104. [Google Scholar] [CrossRef]
- Hu, L.; Li, Y.; Luo, G.; Shi, Q.; Wang, Y.; Ma, S.; Cui, Y.; Wang, H.; Chen, Z. Understanding cellular structure formation in rapidly solidified Al–Ni alloys by constructing solidification microstructure selection maps. Addit. Manuf. 2023, 73, 103671. [Google Scholar] [CrossRef]
- Luo, G.; Chen, H.; Li, Y.; Yang, C.; Hu, L.; Ma, S.; Wang, H.; Chen, Z.; Wu, Y.; Wang, M.; et al. Improved elevated-temperature strength and thermal stability of additive manufactured Al–Ni–Sc–Zr alloys reinforced by cellular structures. Addit. Manuf. 2024, 90, 104313. [Google Scholar]
- Shao, G.; Tsakiropoulos, P. Prediction of phase selection in rapid solidification using time dependent nucleation theory. Acta Metall. Mater. 1994, 42, 2937–2942. [Google Scholar] [CrossRef]
- Turnbull, D.; Fisher, J.C. Rate of nucleation in condensed systems. J. Chem. Phys. 1949, 17, 71–73. [Google Scholar] [CrossRef]
- Turnbull, D. Formation of crystal nuclei in liquid metals. J. Appl. Phys. 1950, 21, 1022–1028. [Google Scholar] [CrossRef]
- Eustathopoulos, N.; Coudurier, L.; Joud, J.C.; Desré, P. Tension interfaciale solide-liquide des systémes Al-Sn, Al-In et Al-Sn-In. J. Cryst. Growth 1976, 33, 105–115. [Google Scholar] [CrossRef]
- Wearing, D.; Horsfield, A.P.; Xu, W.; Lee, P.D. Which wets TiB2 inoculant particles: Al or Al3Ti? J. Alloys Compd. 2016, 664, 460–468. [Google Scholar] [CrossRef]
- Lu, Z.; Tang, Y.; Zhang, L. Atomic mobility in liquid and fcc Al–Si–Mg–RE (RE = Ce, Sc) alloys and its application to the simulation of solidification processes in RE-containing A357 alloys. Int. J. Mater. Res. 2017, 108, 465–476. [Google Scholar] [CrossRef]
- Klein, S.; Herlach, D.M. Crystal nucleation in undercooled melts of PdZr2. J. Appl. Phys. 2013, 114, 183510. [Google Scholar] [CrossRef]
- Shangguan, D.; Ahuja, S.; Stefanescu, D.M. An analytical model for the interaction between an insoluble particle and an advancing solid/liquid interface. Metall. Trans. A 1992, 23, 669–680. [Google Scholar] [CrossRef]
- Shi, R.; Meier, J.M.; Luo, A.A. Controlling particle/metal interactions in metal matrix composites during solidification: The role of melt viscosity and cooling rate. Metall. Mater. Trans. A 2019, 50, 3736–3747. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Q. Interaction between nucleant particles and a solid-liquid interface in Al-4.5Cu alloy. Acta Mater. 2021, 213, 116956. [Google Scholar] [CrossRef]
- Youssef, Y.M.; Dashwood, R.J.; Lee, P.D. Effect of clustering on particle pushing and solidification behaviour in TiB2 reinforced aluminium PMMCs. Compos. Part A Appl. S. 2005, 36, 747–763. [Google Scholar] [CrossRef]
- Xu, J.Q.; Chen, L.Y.; Choi, H.; Li, X.C. Theoretical study and pathways for nanoparticle capture during solidification of metal melt. J. Phys. Condens. Matter 2012, 24, 255304. [Google Scholar] [CrossRef]
- Pötschke, J.; Rogge, V. On the behaviour of foreign particles at an advancing solid-liquid interface. J. Cryst. Growth 1989, 94, 726–738. [Google Scholar] [CrossRef]
- Li, Y.; Hu, B.; Liu, B.; Nie, A.; Gu, Q.; Wang, J.; Li, Q. Insight into Si poisoning on grain refinement of Al-Si/Al-5Ti-B system. Acta Mater. 2020, 187, 51–65. [Google Scholar] [CrossRef]



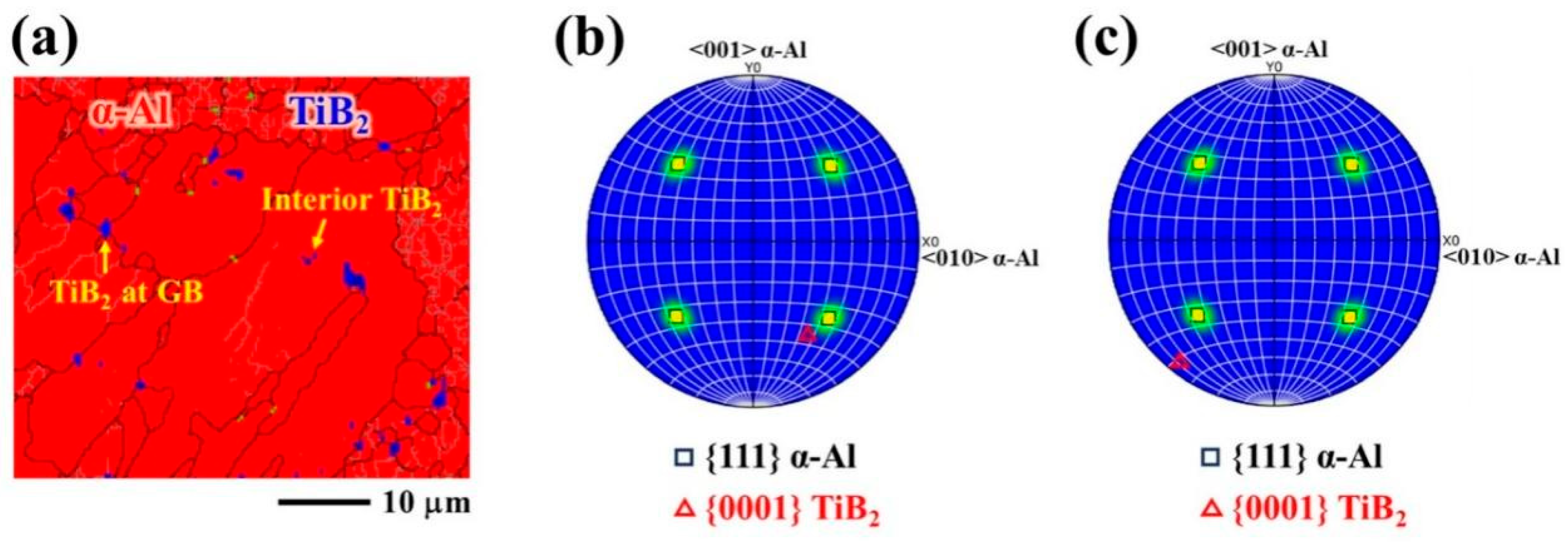
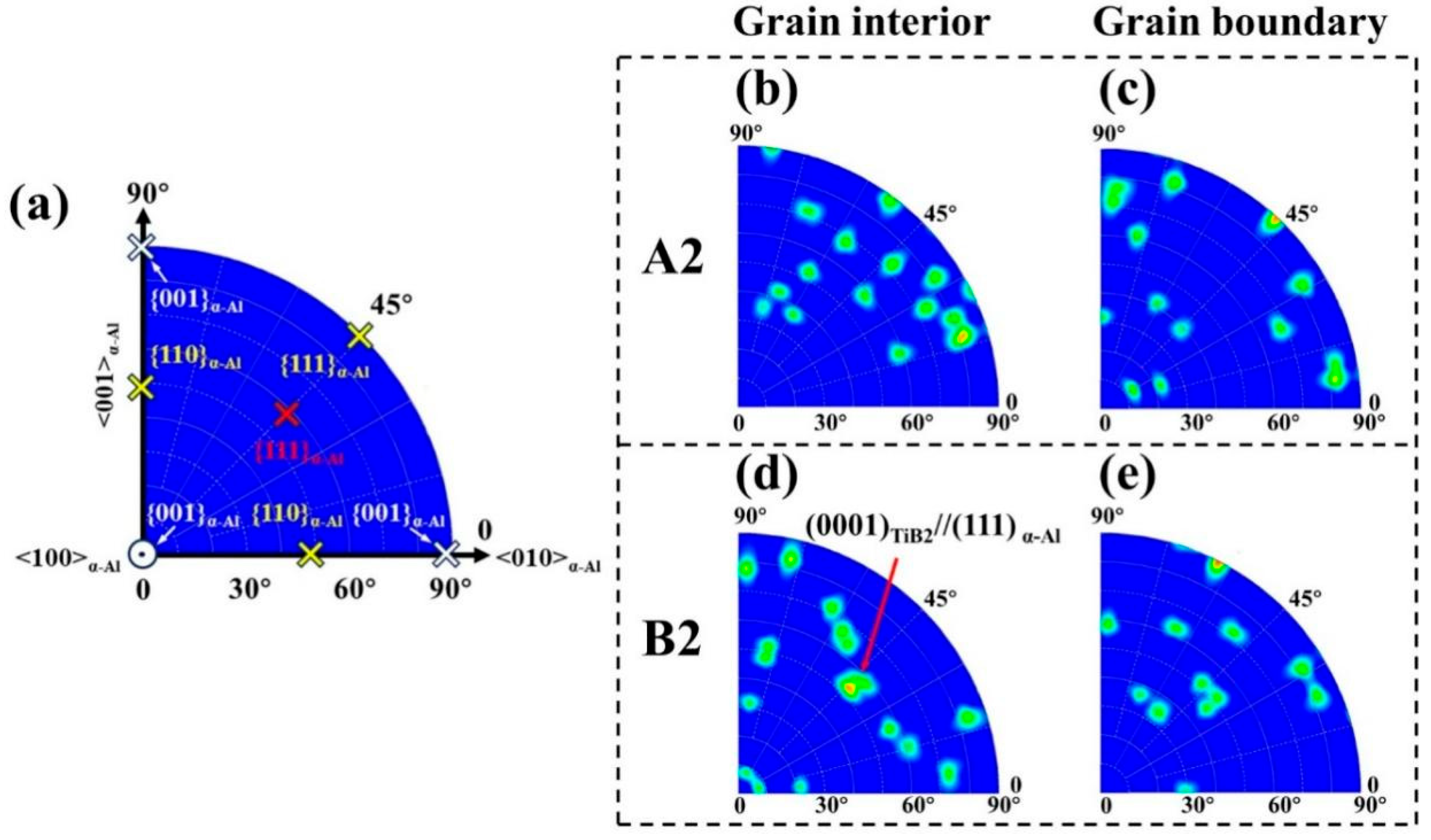

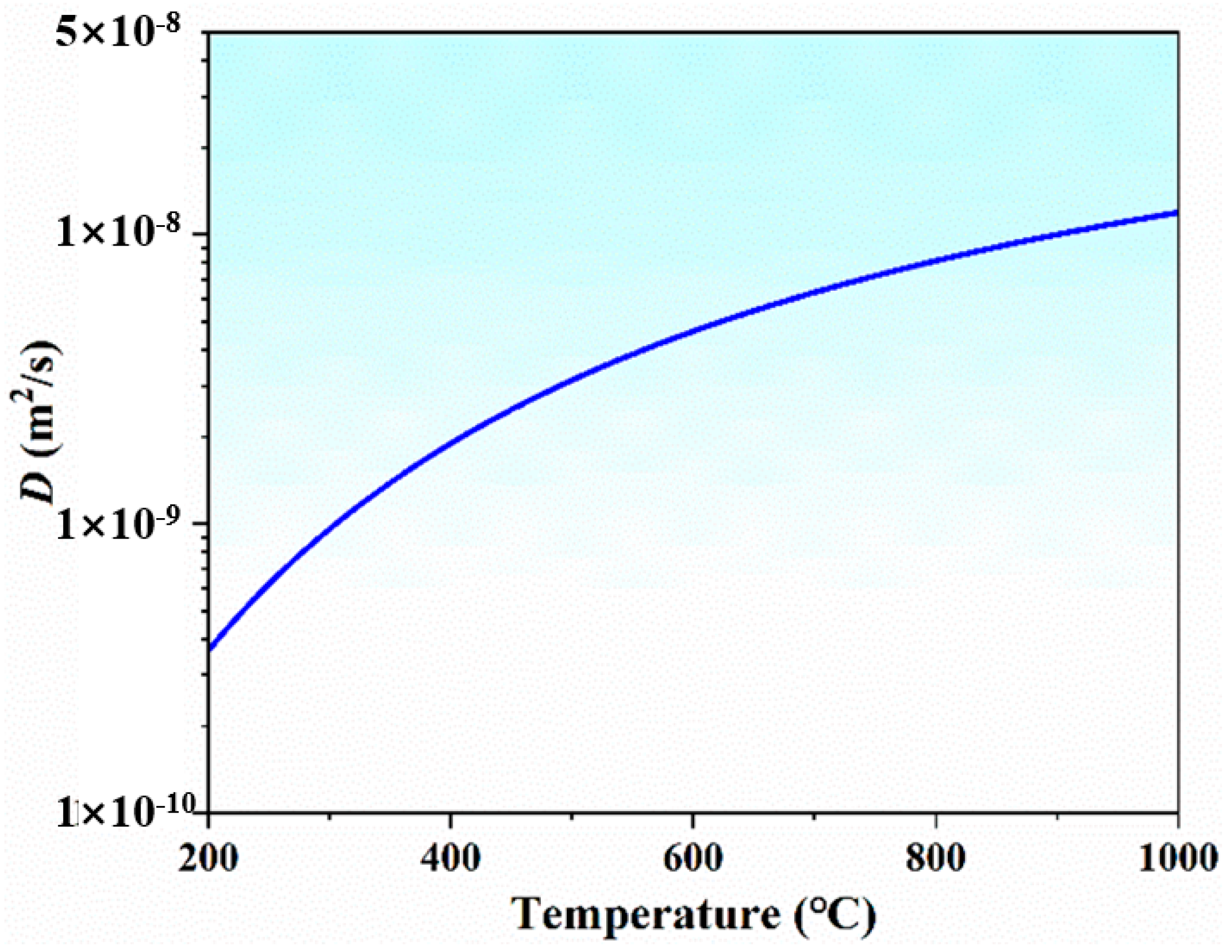
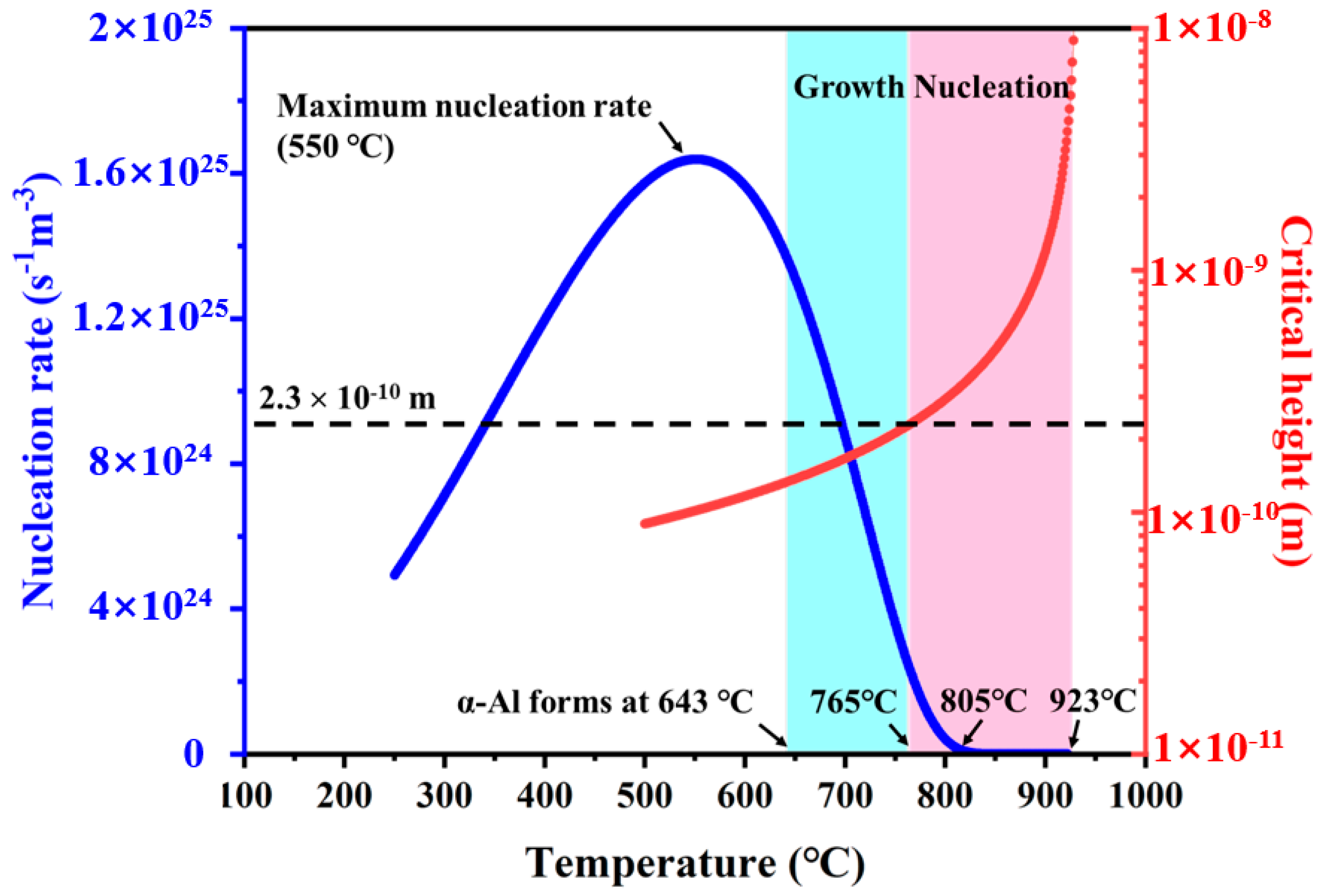
| Alloy | Ni | Sc | Zr | Ti | B | Al |
|---|---|---|---|---|---|---|
| 2TiB2/Al–8Ni–0.6Sc–0.1Zr | 8.40 ± 0.32 | 0.57 ± 0.06 | 0.13 ± 0.02 | 1.55 ± 0.09 | 0.69 ± 0.06 | Bal. |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| TL | 932 | °C | 0.017 | ||
| γS/L | 0.43 | J⸱m−3 | 31.5 | g/mol | |
| θ | 30 | ° | 2.61 × 103 | kg⸱m−3 | |
| N | 5.0 × 1017 | 3.02 × 103 | kg⸱m−3 | ||
| a | 2.6 × 10−10 | m | 4.49 × 103 | kg⸱m−3 |
| Interface | Symbol | Energy (J/m2) |
|---|---|---|
| α-Al/L-Al | 0.158 | |
| TiB2/α-Al | 2.72 | |
| TiB2/L-Al | 2.39 | |
| Al3(Sc,Zr)/L-Al | 4.3 | |
| Al3(Sc,Zr)/α-Al | 0.14 | |
| Al3(Sc,Zr)/TiB2 | 2.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Hu, L.; Rong, P.; Li, Y. Dispersion of TiB2 Particles in Al–Ni–Sc–Zr System Under Rapid Solidification. Metals 2025, 15, 872. https://doi.org/10.3390/met15080872
Fang X, Hu L, Rong P, Li Y. Dispersion of TiB2 Particles in Al–Ni–Sc–Zr System Under Rapid Solidification. Metals. 2025; 15(8):872. https://doi.org/10.3390/met15080872
Chicago/Turabian StyleFang, Xin, Lei Hu, Peng Rong, and Yang Li. 2025. "Dispersion of TiB2 Particles in Al–Ni–Sc–Zr System Under Rapid Solidification" Metals 15, no. 8: 872. https://doi.org/10.3390/met15080872
APA StyleFang, X., Hu, L., Rong, P., & Li, Y. (2025). Dispersion of TiB2 Particles in Al–Ni–Sc–Zr System Under Rapid Solidification. Metals, 15(8), 872. https://doi.org/10.3390/met15080872






