Abstract
A novel approach to estimating the absorbed energy (toughness) in a uniaxial tensile test with only knowledge of the microstructure is presented. The flow behavior of each Dual-Phase (DP) steel grade is predicted using idealized Representative Volume Elements (RVEs) up to uniform elongation. To estimate the flow behavior beyond uniform elongation, the stress-modified fracture strain in a non-local damage model was implemented in Abaqus. Damage parameters were calibrated using Finite Element (FE) simulations of purely ferritic tensile specimens. The damage parameters remained unchanged, except for the coefficient of triaxiality. This coefficient was adjusted based on the average triaxiality of ferrite elements at the instability point of the uniaxially loaded RVEs for each DP steel grade. The proposed approach comprises two steps: micron-sized RVEs to predict the flow behavior up to the point of uniform elongation and the average triaxiality and full-scale tensile-test simulations to predict the rest of the curves. The results show that the damage parameters calibrated for high-strain ferrite effectively estimate the absorbed energy during failure in tension tests. This approach is also geometry-independent; varying the geometry of the tensile specimen, including miniature or notched specimens, still yields predicted absorbed energies that are in good agreement with the experimental results.
1. Introduction
Owing to their strength-to-weight ratio and capacity to absorb crash energy and reduce intrusion into the passenger compartment, advanced high-strength steels (AHSS) are used in auto body structures. These steels encompass several well-known steel types, including TRansformation-Induced Plasticity (TRIP), Complex Phases (CP) steels, TWinning-Induced Plasticity (TWIP) steels, and a significant group known as Dual-Phase (DP) steels [1]. The main advantage of DP steels is their high Ultimate Tensile Strength (UTS) due to the presence of the martensite phase, combined with a low initial yield stress attributed to the ferrite phase. This combination results in high early-stage strain-hardening and homogenous plastic deformation [2]. Several key criteria are typically considered in research on DP steels, including yield strength, strain-hardening rate, strengthening coefficient, uniform elongation, ultimate tensile strength (UTS), and elongation to failure [2]. Another critical factor evaluated is the area under the stress–strain curve, which represents energy absorption or toughness. It is important to note that while the energy absorption measured from a uniaxial tension test can provide insights into toughness, it is not the primary method for assessing energy absorption during crash. In the automotive industry, more specialized tests have been developed for this purpose, as detailed in [1].
Nevertheless, the uniaxial tension test still offers a reasonable basis to asses a material’s capacity for energy absorption on account of failure and fracture.
The simulation of mechanical behavior, particularly uniaxial tension, through incorporating the microstructural features of DP steels remains a crucial research area due to the significant aid it provides in the design of novel DP steel grades. In the uniaxial tension stress–strain curve, uniform elongation represents the material’s flow behavior up to the maximum stress, or its ultimate tensile strength (UTS), which marks the beginning of necking. Non-uniform elongation begins with the initiation of necking and extends to the fracture point of the specimen. Two types of models have been used to assess the stress–strain behavior of DP steels up to the point of uniform elongation. The phenomenological models described in [3,4] rely on empirical equations to determine material properties and ordinary differential equations for the plastic strain and dislocation densities described by the Mecking–Kocks relationship.
The second approach uses Representative Volume Elements (RVE) that are developed using realistic morphologies obtained through electron miscroscopy [5,6,7] or synthetic microstructures obtained from material design software [8,9]. Representative Volume Elements comprising the constitutent phases and morphological details of the microstructure are meshed and loaded uniaxially in a finite element software. The flow behavior of the constituent phases is described by phenomenological models, which are ideally ferrite and martensite in the case of DP steels. Many phenomenological descriptions used to model the flow behavior of ferrite and martensite have been developed; in the case of dual-phase steels, [3] presented a modification to ferrite and martensite. In Allain et al. [3]’s relationship for ferrite, the density of geometrically necessary dislocations (GNDs) was added to the well-known Mecking–Kocks, equation which only considers the alteration in the dislocation density with respect to the deformation increment [10]. Allain et al. [3] also implemented a Continuum Composite Approach (CCA) for martensite. Based on their studies [3,11], the strength of martensite depends on its carbon content, which can vary from one island to another. Therefore, martensite should not be treated as a single-phase material, but rather as a heterogeneous composite consisting of soft and hard regions. In this model, the soft martensite contributes to the plasticization of the material, while the delayed yielding of hard martensite is responsible for its initially high hardening [3,4]. Using Allain et al. [3]’s models for ferrite and martensite, Sardar et al. [4] and Espinosa et al. [6] could predict the flow curves, up to uniform elongation, of a number of dual-phase steels using their microstructural data in the literature, including the exact DP steel grades used in the current paper. It should be emphasized that both the phenomenological models and the RVE-based methods restrict description of the steel behavior up to the point of necking.
In order to model the stress–strain curve beyond necking and to the point of failure, an appropriate damage model is needed. In practice, the modeling of the tensile test (or multi-axial loading) to the point of fracture is underpinned by the flow behavior measured in tension tests. Typically, these stress–strain curves are derived by fitting experimental stress–strain curves [12,13]. However, the predicted curves from phenomenological models or representative volume elements (RVE), which were explained previously, serve as an alternative to experimental curves, particularly for materials whose tensile stress–strain response is unknown. Beyond the onset of necking, the damage model that is used to model damage evolution and eventual fracture play a crucial role. For instance, a damage model calibrated with tensile stress–strain curves was used by Simha et al. [14] to model the static loading of a pipeline steel Drop Weight Tear Test specimen. The latter is then used to assess the energy-absorption capacity of the steel.
Research on the modeling of failure can be broadly divided into two main methodologies. The first method involves micro-mechanical models for ductile fracture, which account for void nucleation, growth, and coalescence; one example of these models is the Gurson–Tvergaard–Needleman (GTN) model [15,16,17,18]. The second methodology uses phenomenological models, where cohesive zone elements are implemented to simulate ductile fracture behavior, such as that presented in [19,20]. Defining the parameters of these damage models is often a challenge. For instance, the GTN model involves eight damage parameters, which can lead to significant effort and potential unreliability for authors and readers. Another phenomenological damage model is based on stress-modified fracture strain, which has fewer damage parameters and relies on the variation in stress triaxiality at each increment of plastic deformation. In this model, the fracture strain depends on stress triaxiality, which is the ratio of hydrostatic stress to von-Mises stress [12,21,22,23].
As it stands, methods to estimate the stress–strain response of DP steels up to the point of necking using only knowledge of the microstructural details exist. However, to model the post-necking and eventual fracture behavior, experimental stress–strain curves are required. In other words, when only knowledge of the microstructure is provided, we do not have methods to estimate the entire stress–strain curve, including failure and fracture. However, when using cuboid RVEs whose sides are on the order of tens of microns, can we estimate the entire stress–strain curve?
In this work, a novel approach to estimating the uniaxial tensile response up to the point of necking, as well as subsequent fracture, is presented. Initially, the flow behavior of each of the DP steel grades is predicted using idealized Representative Volume Elements (RVEs) up to uniform elongation. It should be noted that the flow behavior of the constituent phases, ferrite and martensite, was obtained using the phenomenological models described by our group in [6]. To estimate the flow behavior beyond uniform elongation, the stress-modified fracture strain non-local damage model was implemented in ABAQUS. Damage parameters were calibrated for purely ferritic uniaxial tensile specimens. For DP steels, damage parameters obtained from the latter simulations were used directly, with a significant adjustment based on the average triaxiality of ferrite elements at the point of instability in uniaxially loaded RVE for DP-grade steel. The proposed approach is a two-step approach that uses the RVE to model the flow behavior up to the point of uniform elongation and the average triaxiality of the soft phase. Then, the average triaxiality from the RVE is used to modify the damage parameters for the pure ferrite, and to model the failure and fracture of the DP tensile specimen.
Three different uniaxial tension specimen geometries were used to demonstrate that the calibrated damage parameters are independent of geometry and the estimated absorbed energy falls within an acceptable range. Section 4 contains important details about the damage model and its implementation. We also use the model to estimate the energy required for plastic deformation and fracture in notched and un-notched specimens, and compare these with the experimental results.
2. Materials and Test Methods
Three dual-phase steels, with chemical compositions presented in Table 1 and a thickness of 1 mm, were investigated in this study. The studied samples were extracted from heat-treated hot-rolled strips. The phase volume fractions and grain sizes, previously characterized by our research group [6], are summarized in Table 2. Sample preparation for optical and scanning electron microscopy involved polishing with a 9 μm diamond suspension, followed by sequential polishing with 3 μm and 1 μm suspensions, and finally etching with 1% Nital [6]. After etching, the microstructure was examined using optical microscopy (OM). The contrast between ferrite and martensite was clearly distinguishable, with ferrite appearing light and martensite appearing as dark regions. Each phase, ferrite and martensite, was then isolated and analysed separately using the ImageJ 1.53d software to determine its volume fraction and average grain size. Three different geometries of the tensile specimens were tested under uniaxial loading. The samples were aligned along the rolling direction and a total of three repeat tests were conducted for each material. One of the geometries was a rectangular tension test, conforming to the ASTM E8 [24] sub-size specimen specifications, with a gage length of 25 mm and a width of 6 mm, while the other two were miniature geometries, smooth and notched, based on the drawing presented in Figure 1. The miniature specimen geometry was shown to reproduce the same uniform elongation stress–strain response as the standard ASTM E8 dog-bone specimen in the work of Bardelcik et al. [25]. The miniature dog-bone specimens were CNC-machined from a flat sheet and flushed with coolant to prevent heating, which could lead to unintended heat treatment. All the miniature tensile tests were performed using a MTI miniature tensile stage (SEMTester 1000) (Albany, NY, USA) with a 4 kN load cell, as shown in Figure 1c. This Figure presents an image of the tester in the SEM, but for these tests, we used the tester on the benchtop and used an SLR camera for Digital Image Correlation (DIC). The cross-head displacement increments were 100 μm throughout the test, resulting in a very low strain rate in the order of 0.001 . It should be noted that results for the uniaxial miniature dog-bone specimen are not available for DP980GA.

Table 1.
Chemical composition of the studied grades (wt.%).

Table 2.
Microstructural characteristics of the studied grades. Reprinted with permission from Ref. [6]. Copyright 2025 Elsevier.
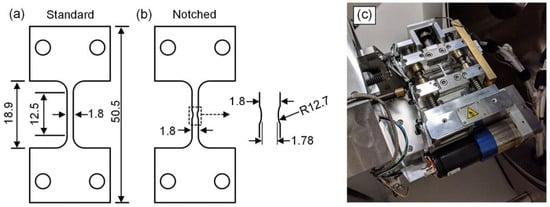
Figure 1.
The (a) standard (smooth) and (b) notched miniature dog-bone specimen drawings; dimensions are in mm. (c) MTI tensile stage (Reprinted with permission from Ref. [26]. Copyright 2025 Elsevier).
3. Rve Modeling for True Stress–Strain Prediction
To build the idealized RVE using data extracted from the microstructure (Table 2), Digimat software was used. There are several options for creating an RVE for dual-phase materials. The first option, called ‘Generic’ in Digimat, involves a matrix with a high-volume fraction and a second phase with a low-volume fraction. Various geometries, such as spheres, ellipsoids, and prisms, can be used for the precipitates. However, this method is not accurate for materials with a high fraction in the second phase, like DP980GA, which contained 47% martensite in this study. Therefore, the ‘Metal’ option in the software was used instead. This approach constructs the RVE to resemble a metal microstructure with individual grains. The input data included the volume fraction of phases, average grain size, grain size distribution (assumed to be normal), and the number of grains. Determining the number of grains can be tricky, as it dictates the minimum 3D RVE size and must be established through trial and error to achieve the desired RVE dimensions. Each grain corresponds to one of the phases, as shown in Figure 2, which illustrates ferrite and martensite grains separately and together. After building, meshing, and applying the Periodic Boundary Conditions (PBC) to the RVE in Digimat, the ABAQUS input file was generated and imported into ABAQUS for solving. Uniaxial displacement was applied along the X-axis. On CentOS Linux 7, typical run times range between 1 and 2 h when using eight cores (Intel® Xeon® CPU E5-2697 v2 @ 2.70 GHz × 48).
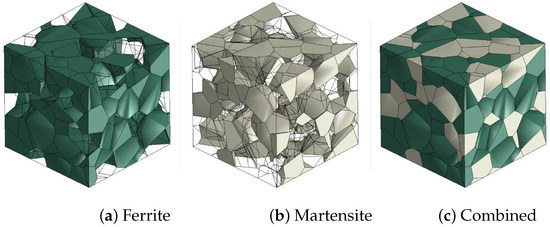
Figure 2.
DP800 RVE, (a) Ferrite grains, (b) Martensite grains, (c) Combined.
Cubic RVEs with dimensions of μm were selected for this study, which is large enough when considering the average grain sizes of ferrite and martensite [6,9,27]. The number of elements for DP800, DP980GI, and DP980GA was identical, totaling 125,000 elements The RVEs were meshed using linear brick elements of type C3D8R. The final meshed volume elements are displayed in Figure 3, where the ferrite region is shown in green and the remaining region is martensite.
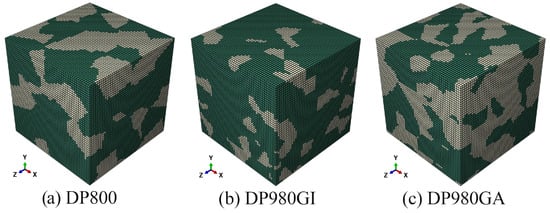
Figure 3.
Final meshed RVEs for (a) DP800, (b) DP980GI, and (c) DP980GA.
3.1. True Flow Behavior of the Individual Phases
The material properties of the ferrite and martensite phases vary across the three DP grades—DP800, DP980GI, and DP980GA—due to differences in chemical composition and grain size, as shown in Table 1 and Table 2. The flow behavior of the individual phases was obtained by using the equations presented in Espinosa et al. [6], which report the true stress–strain curves for ferrite and martensite, corresponding to the exact same materials.
3.2. Predicting the True Flow Behavior of DP Steels
As mentioned, idealized RVEs were created using the data from Table 2 on the microstructure of DP800, DP980GI, and DP980GA, and were then subjected to uniaxial displacement in ABAQUS 2019. The true stress–strain curve obtained from the RVE model is a fundamental step in predicting the absorbed energy, which is the main purpose. This curve is essential as it serves as the material property input for subsequent tensile models. Figure 4 shows the equivalent plastic strain and von-Mises stress contours of the DP800 RVE under uniaxial displacement along the X-axis, and Figure 4c represents the true stress–strain curve and the instability point, determined using the Considère criterion. The von-Mises stress and equivalent plastic strain distributions indicate that martensite contributes to the strengthening of the steel, while martensite islands typically experience either elastic deformation or minimal plastic deformation, unlike the ferrite phase. As it stands, we are able to predict the flow behavior of the steel up to the point of uniform elongation.
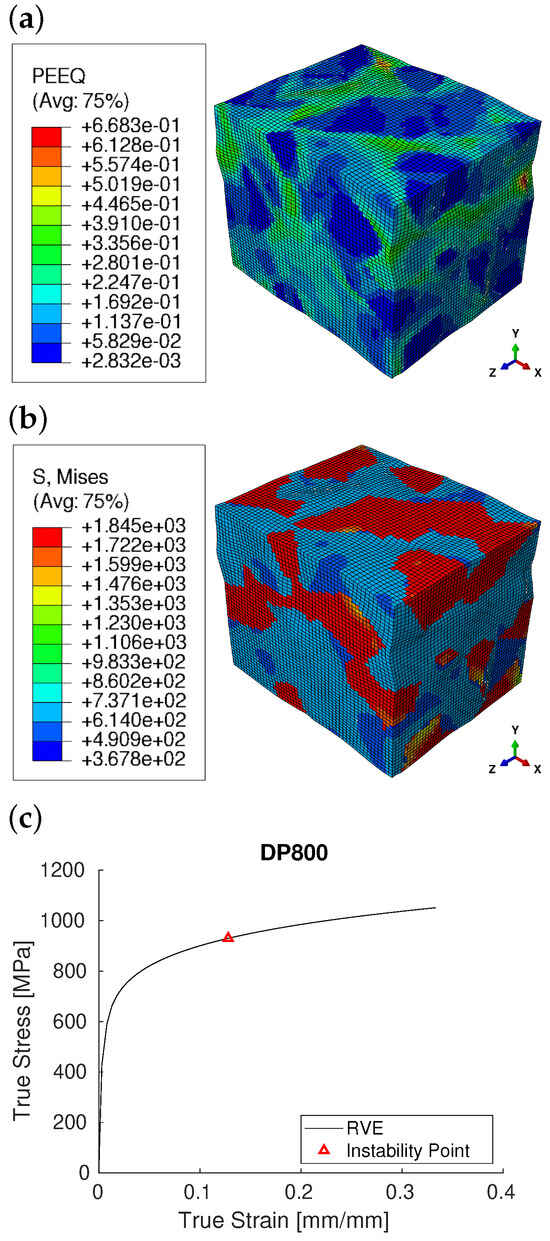
Figure 4.
DP800 RVE under uniaxial displacement along the X-direction; (a) equivalent plastic strain contour; (b) Von-Mises stress contour; (c) resultant true stress–strain curve and the instability point.
4. Damage Model and Failure Simulation
In this section, we outline an approach to estimate the stress–strain curve beyond the onset of localization and up to the point of fracture. Accordingly, we assumed that the damage to the ferrite, mediated by the initiation, growth, and coalescence of voids, is the dominant mechanism.
We further assumed that triaxiality (ratio of mean stress to the von-Mises stress) is the governing parameter and used the stress-modified fracture strain damage approach, which was implemented using the Abaqus finite element software. In this model, the fracture strain depends on stress triaxiality, which is the ratio of hydrostatic stress to von-Mises stress as
where A, B, and C are damage constants. Using Equation (1), fracture strain is available as a function of stress triaxiality at each increment of deformation. Thus, the damage increment caused by plastic deformation is defined as follows:
where represents the increment in the equivalent plastic strain. Hence, accumulated damage is provided by . When the accumulated damage variable reaches the critical value , ductile failure is assumed, and incremental crack growth is simulated by sharply reducing all stress components to a small plateau value, as shown schematically in Figure 5. Reducing stresses to zero can cause numerical issues; therefore, stresses are maintained at a finite (cut-off) value [22]. The cut-off value and decreasing slope in this work were chosen to be 10% of the yield strength [22] and 1/2000, respectively. Equation (1) includes three parameters—A, B, and To estimate these parameters experimentally, multiple tensile tests at various levels of triaxiality are required; Nam et al. [28]. However, when such test data is unavailable, C is set to 1.5 based on the result from Rice and Tracey [23].
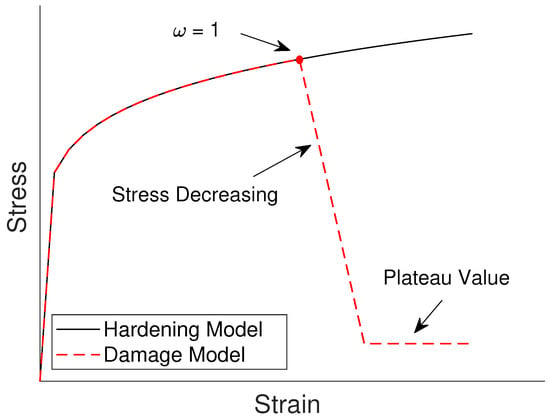
Figure 5.
Illustration of damage model.
Another simplification involves setting A to a constant positive value. In this paper, A was set to 0.1 for all grades, as per Oh et al. [22]. Consequently, the simplified version of is as follows:
In summary, the damage model includes one parameter, B, which requires calibration.
When a damage model is incorporated into the FE simulation, the element size becomes a crucial factor. It is well-known that damage models dependent on stress and strain states lead to mesh dependency in the results. A non-local approach was used to mitigate the mesh dependency. A non-local model, similar to the one used by Simha et al. [14], was utilized in this study. The described damage model was implemented using USFLD and UHARD subroutines in the Abaqus/Implicit solver. The non-local implementation proceeded as follows. At the beginning of the computation, the .inp job file was processed to identify the nodes and elements associated with the user material. Based on the centroids of these elements, an element neighbor table was created. For each element, all neighboring elements within a specified radius, R, were identified and recorded. The neighbor tables were updated at each time step. Then, the non-local plastic strain was defined through a volume integral as follows:
where r is the non-local scale, is a weighting function, and is a normalizing function. Volume denotes the region enclosed by a sphere with a radius R around an arbitrary material point (Figure 6); the weighting and normalizing functions applied are the same as those used by Simha et al. [14].
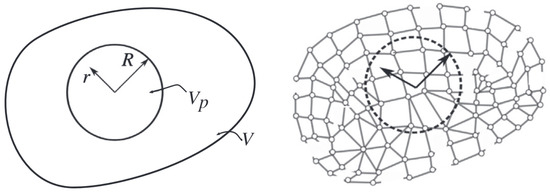
Figure 6.
Schematic of non-local model, and finite element idealization. Reprinted with permission from Ref. [14]. Copyright 2025 Elsevier.
Failure Strain in Pure Ferrite Specimens
Since our goal is to predict the energy absorbed in a tension test with only knowledge of the DP microstructure, and we assume that the damage is dominant in the softer phase, this section discusses the failure strain observed in ferrite specimens. The latter observations, obtained from pure ferrite specimens, will be used when modeling damage in DP steels, which in turn allows us to estimate response in a stress–strain test.
Using in situ tensile tests carried out using an electron microscope, Espinosa et al. [6], Bardelcik and Butler [26] demonstrated that the maximum local strain occurs in the ferrite phase, which is 2.5 to 3 times higher than the global strain in DP800. This behavior can be attributed to the material’s heterogeneity, which arises from the significant difference in strength between the ferrite and martensite phases, which in turn causes higher triaxiailty (ratio of mean stress to von-Mises stress) [29]. These conditions reduce ductility and promote the nucleation and growth of voids. Based on this, an assumption is made—damage calibration is first performed on a pure ferritic tension specimen using Equation (3). The calibrated damage parameters obtained are then used in the subsequent step, with a critical adjustment to the triaxiality coefficient, as detailed in Section 5.3.
The sub-size ASTM E8 specimen, which is the most commonly used geometry in the literature for DP steels, was selected for modeling the pure ferrite case. This geometry (illustrated later in Figure 10a) was modeled and loaded uniaxially in ABAQUS using the non-local damage UHARD subroutine. The minimum element size that totally covers the gauge length was 0.125 mm, with a non-local radius of 0.625 mm. The model was meshed with 33,408 linear hexahedral elements of type C3D8R. However, a criterion is still needed for calibrating the damage parameter. The uniaxial tensile failure strain of pure ferrite material is assumed to be a reasonable criterion because it significantly affects the measurement of absorbed energy, represented by the area under the stress–strain curve.
Data from the literature on failure in DP steels, including studies by Liu [30], Chen [31], Dulucheanu et al. [32], Wang [33], Bergstrom et al. [34], Son et al. [35], Ahmad et al. [36] and Kim et al. [37], are shown in Figure 7, where the relationship between the volume fraction of martensite and total elongation for various DP steels is plotted. Trendlines are shown in the figure and, for zero percent martensite, the failure strain is well bounded between 30 and 35%.
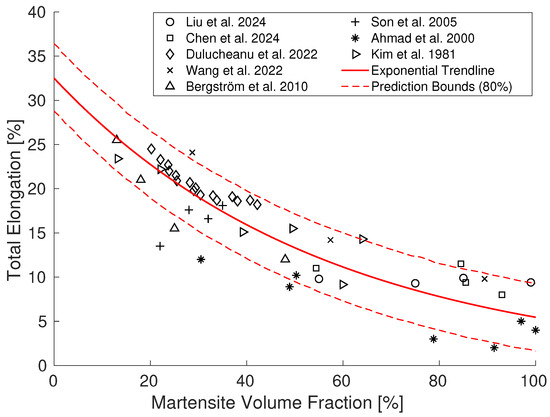
Figure 7.
Relationship between the volume fraction of martensite and uniaxial elongation to failure strain in various DP steels. Data are from Liu [30], Chen [31], Dulucheanu et al. [32], Wang [33], Bergstrom et al. [34], Son et al. [35], Ahmad et al. [36] and Kim et al. [37].
In this study, ferrite material with a 30% failure strain is referred to as “Low-Strain Ferrite”, and ferrite material with a 35% failure strain is referred to as “High-Strain Ferrite”. For pure ferrite, parameter B requires calibration.
5. Estimating the Entire Engineering Stress–Strain Curve
Using the microstructure for DP steel, an estimation of the engineering stress–strain curve including failure is described in this section.
5.1. Step 1
Using the RVE simulation, the true stress–strain curve is obtained, which in turn provides the engineering stress–strain response up to the point of uniform elongation; see Figure 4c. This provides part of the stress–strain curve for the DP grades.
5.2. Step 2
Based on the assumption that damage dominates in the ferrite phase, we carried out simulations of a tensile test specimen of pure ferrite with flow behavior governed by the phenomenological equations for ferrite, as described in [6]. It should be emphasized that the obtained flow behavior depends on chemistry as well as the grain size and incorporates hardening effects (Mecking–Kocks) owing to the geometrically and statistically necessary dislocation. Again, this provides the flow behavior of ferrite up to the point of uniform elongation.
Accordingly, the sole damage variable, B, in Equation (3) was calibrated through conducting finite element simulations for each ferrite curve corresponding to DP800, DP980GI, and DP980GA for both low-strain and high-strain ferrite. For instance, Figure 8 illustrates the effect of varying the B parameter on the engineering stress–strain curve for pure ferrite, corresponding to the DP800 grade. It shows that B values of 1.25 and 7 are appropriate for achieving failure strains of 30% and 35%, respectively. Similarly, the B values for pure ferrite of DP980GI and DP980GA were calibrated through a trial-and-error approach, as described. The obtained damage parameters for pure ferrite are reported in Table 3.
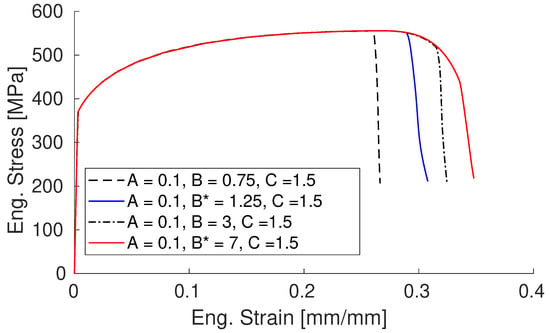
Figure 8.
Effect of varying the damage parameter B on the stress–strain curve for pure ferrite (for DP800). The values correspond to low-strain and high-strain ferrite.

Table 3.
Obtained damage parameters for pure ferrite uniaxial tension model using Finite Element Simulations.
5.3. Step-3
Here, we take into account the increased triaxiality in DP grades owing to the presence of the harder phases.
As described in Step 2, the sole damage parameter, B, was calibrated for a purely ferritic tensile specimen to achieve 30% and 35% failure strains. As shown in Table 3, the triaxiality coefficient, C, was set to 1.5 based on Rice and Tracey [23] model. However, in DP steels, unlike single-phase materials, the variation in triaxiality during the uniaxial tension test arises not only from geometry but also, significantly, from material heterogeneity. Therefore, to directly apply the damage parameters calibrated for pure ferrite to DP steels, this factor must be accounted for.
To adjust the damage parameters for DP grades, the RVEs were analyzed at the point of instability. Figure 9 shows the triaxiality contour at the point of instability point in the DP800 RVE under uniaxial displacement along the X-direction. As indicated, the maximum triaxiality occurs in the ferrite phase, with a value of 2.191, which is approximately 2.6 times higher than the maximum triaxiality in the martensite region. This highlights the greater vulnerability of ferrite to failure. It is noteworthy that for a single-phase RVE under PBC and uniaxial displacement, the triaxiality remains constant at 0.33. To address this disparity in triaxiality, the parameter D is introduced as follows:
Note that this reduces to unity for pure ferrite. This parameter is incorporated into Equation (3) as a new coefficient, multiplying the triaxiality term , and resulting in Equation (6).
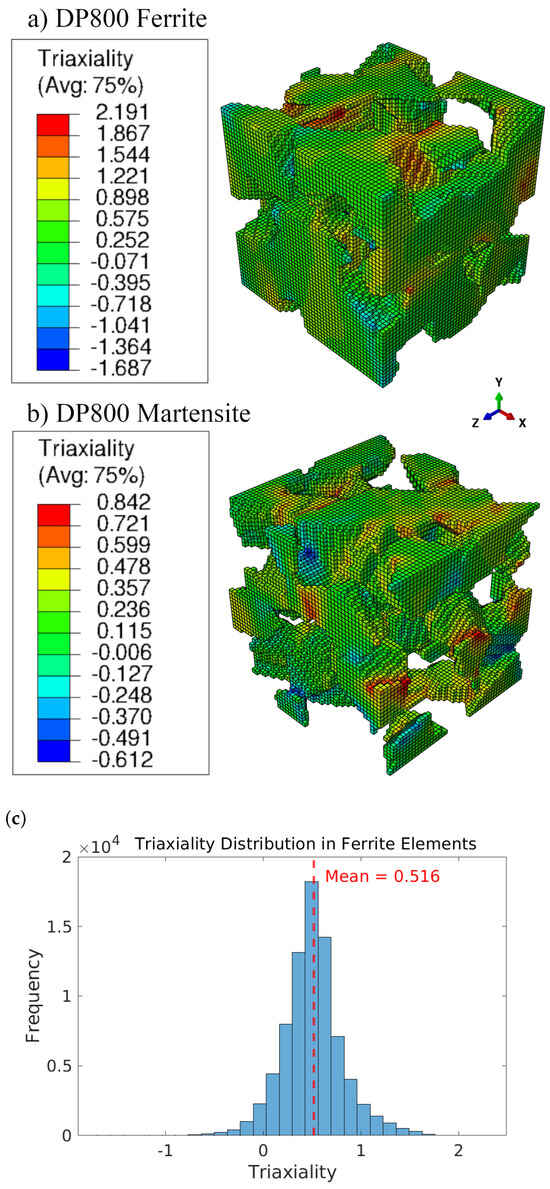
Figure 9.
Triaxiality distribution in the RVE at the instability point for DP800, (a) Ferrite region, (b) Martensite region, and (c) Triaxiality histogram of ferrite elements.
To define the D parameter, the ferrite triaxiality at the instability point must be extracted. While one approach is to take the maximum triaxiality, this method significantly underpredicts the DP stress–strain curves. This underprediction likely stems from the fact that maximum triaxiality occurs only in localized regions at the microstructure, rather than uniformly everywhere at the macro-scale. Therefore, using the average triaxiality of all ferrite elements in the RVE at the instability point, as presented in Figure 9c, provides a more accurate representation of the triaxiliaty that can be used to model damage in the tensile specimen. This value is extracted and presented in Table 4 for the three DP grades.

Table 4.
Damage parameter D extracted from the average ferrite triaxiality at the point of instability for the RVEs.
Multiple RVEs of varying sizes were created to examine the sensitivity of the damage parameter D. Although the results are not shown here, it was concluded that as long as the volume fractions, grain sizes, and phase stress–strain curves remain consistent, the triaxiality in the ferrite phase remains largely unaffected. This implies that if the grain size and input-hardening curves for ferrite and martensite are held constant, variations in volume fraction can influence the average ferrite triaxiality at instability and, consequently, the calibrated D parameter. For instance, in hypothetical extreme cases with 98% ferrite and 1.5% martensite, and the reverse, with 98% martensite and 1.5% ferrite, the corresponding D values were found to be 1.03 and 10.9, respectively. A D value of 10.9 promotes early failure, as an increase in D leads to a decrease in the failure strain , as described by Equation (6), consistent with the expectations for a nearly fully martensitic microstructure.
5.4. Step 4: Applying the Adjusted Damage Parameters to Tensile Specimens Using the Material Properties Predicted in the Second Step
The obtained damage parameters, B and D, were then applied to the corresponding DP grades for all three geometries shown in Figure 10 to obtain the full engineering stress–strain curve. It should be noted that A and C were set as constants for all cases, with values of 0.1 and 1.5, respectively. Regarding the details of the miniature dog-bone FE models, it should be noted that the smooth miniature model had a minimum element size of 0.125 mm, with a non-local radius of 0.625 mm (see Figure 10b), as well as the ASTM E8 subsize model. The notched mini dog-bone model had a finer minimum element size of 0.05 mm around the notch and through the thickness, with a non-local radius of 0.25 mm (see Figure 10c). Both models employed C3D8R elements, with 6392 and 72,580 elements for the smooth and notched miniature dog-bone specimens, respectively. All models employed double symmetry along the length and thickness of the specimens. One end was fixed, while the other was subjected to uniaxial displacement to mimic the experimental uniaxial tensile test.
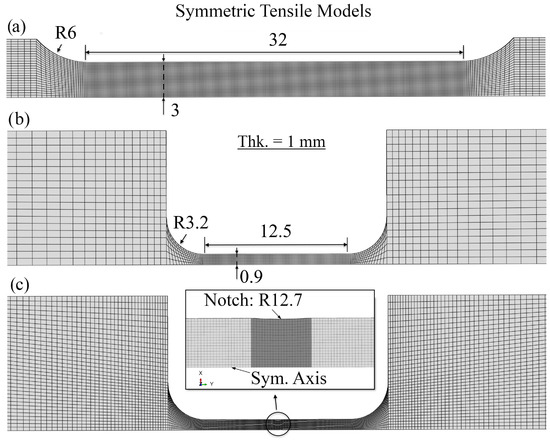
Figure 10.
Symmetric models of tensile specimens: (a) subsize ASTM E8; (b) smooth/standard miniature dog-bone; (c) notched miniature dog-bone.
5.5. Step 5: Validation Based on Experimental and Predicted Absorbed Energies
Figure 11 shows a comparison of the the full FE stress–strain curve for DP800 using subsize ASTM E8 geometry and the experimental curve. For this result, the damage parameters A, B, C, and D were set to 0.1, 7, 1.5, and 1.56, respectively, as shown in Table 3 and Table 4. The peak load signifies the onset of necking in the tensile specimen, and the von-Mises stress gradually concentrated in the necking region. Once an element reached the critical damage value of unity, the stress relaxed to a plateau value. For example, the blue elements in the necking area in Figure 11 relaxed.
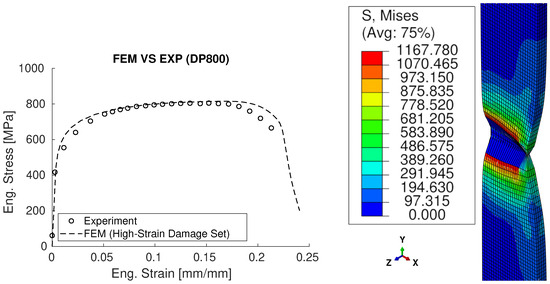
Figure 11.
FE full stress–strain curve for DP800 using subsize ASTM E8 geometry versus the experimental curve, along with the von-Mises stress distribution at fracture, showing the relaxed elements.
6. Results
The results from the uniaxial tensile loading of the idealized RVEs for DP grades are compared with the experimental true stress–strain curves in Figure 12. For DP800, except for the initial stage, the prediction aligns very well with the experimental data up to the maximum stress. For the other two grades, the idealized RVE slightly underpredicts the actual curves, but the difference is less than 10 percent, which is still a reliable estimation. It can be concluded that synthetic RVEs constructed from 2D microstructural data can effectively predict the true stress–strain curves of DP steels. Red markers indicate the point of instability, as determined by the Considère criterion.
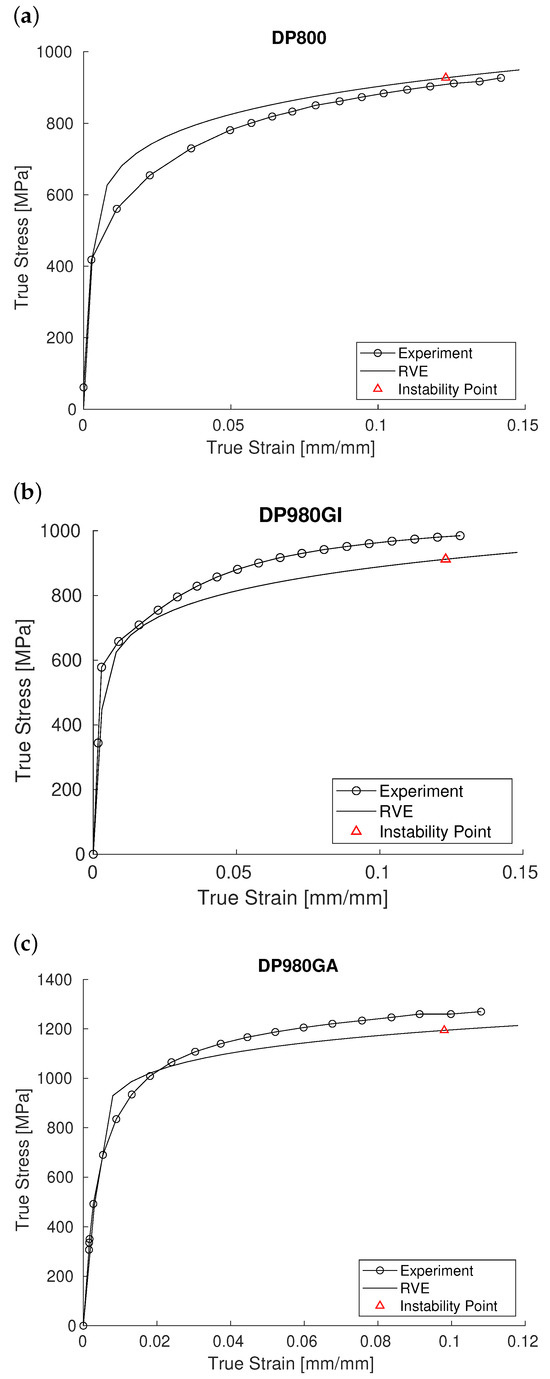
Figure 12.
Comparison of the the results generated from idealized RVEs for the DP grades with experimental true stress–strain curves, (a) DP800, (b) DP980GI, and (c) DP980GA; red markers indicate the point of instability based on the Considère criterion.
In the following finite element simulations and the results obtained using the UHARD damage subroutine, all hardening behaviors were modeled using the Swift power law, expressed as , where is the yield stress, is the plastic strain, and a and n are the hardening coefficient and exponent, respectively. The Swift parameters for DP800, DP980GI, and DP980GA are reported in Table 5.

Table 5.
Swift power law, , parameters predicted from RVE simulations of DP materials.
Figure 13 presents the engineering stress–strain curves from the FE simulation of uniaxial tensile specimens for pure ferrite corresponding to each DP grade, using the calibrated damage parameters listed in Table 3. As illustrated in the figure, the damage parameters, particularly parameter B, achieve the assumed failure strain for low-strain ferrite at 30% and the failure for high-strain ferrite at around 35%.
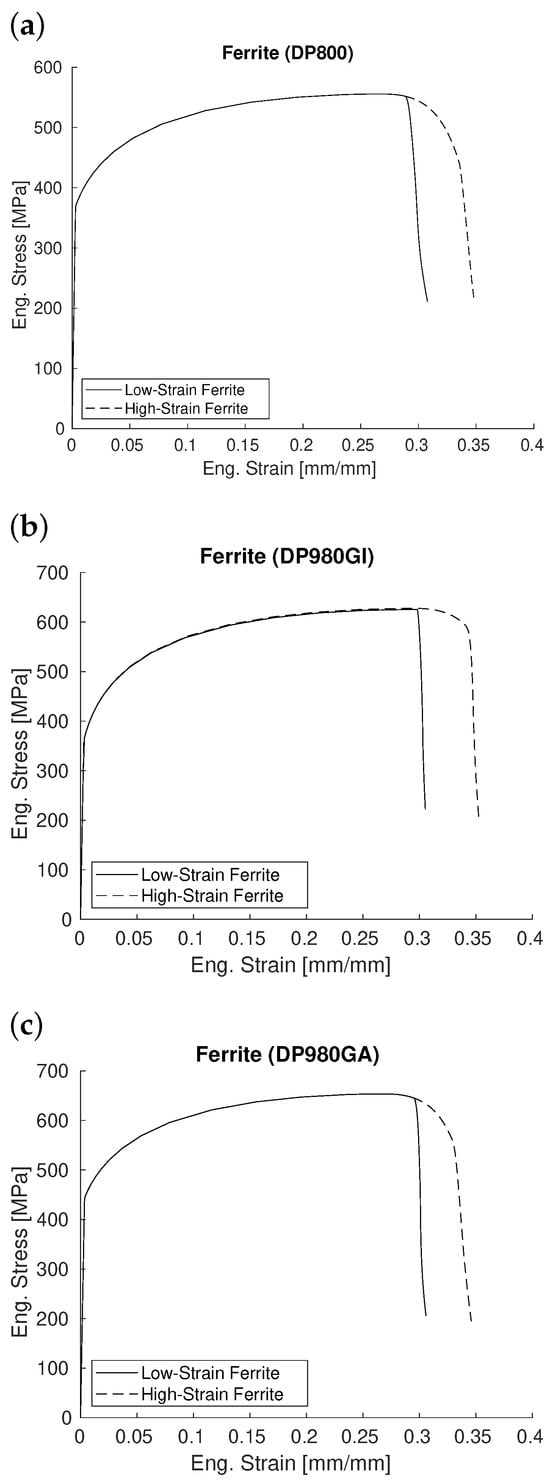
Figure 13.
Engineering stress–strain curves for pure ferrite, obtained from an FE simulation of uniaxial tensile specimen using the UHARD damage subroutine: (a) DP800, (b) DP980GI, and (c) DP980GA.
After deriving the true stress–strain curves from the idealized RVEs and determining the appropriate damage parameters for low-strain and high-strain ferrite, finite element simulations were conducted for each assumed tensile specimen, including sub-size ASTM E8, miniature smooth, and notched dog-bone specimens. As previously mentioned, the damage parameters used in these simulations were consistent with those in Table 3 and Table 4.
The FE stress–strain curves for a sub-size ASTM E8 geometry generated for DP800, DP980GI, and DP980GA were compared with the experimental results of the uniaxial tensile test in Figure 14. The corresponding area under the curve (AUC), representing the absorbed energy for each of the FE results and experiments, was calculated and recorded in the figure legend. A general review of Figure 14 and its legend indicates that, for the three DP grades—DP800, DP980GI, and DP980GA—both the low-strain and high-strain damage parameters from Table 3 predicted the absorbed energy reliably, within an error range of 10%. The lowest error was observed for the DP800 low-strain damage set, which obtained a negative error of 2.3% compared to the experiment, while the highest error was found for the DP800 high-strain damage set, with a positive error of 10.4%, which is still considered an acceptable estimation.
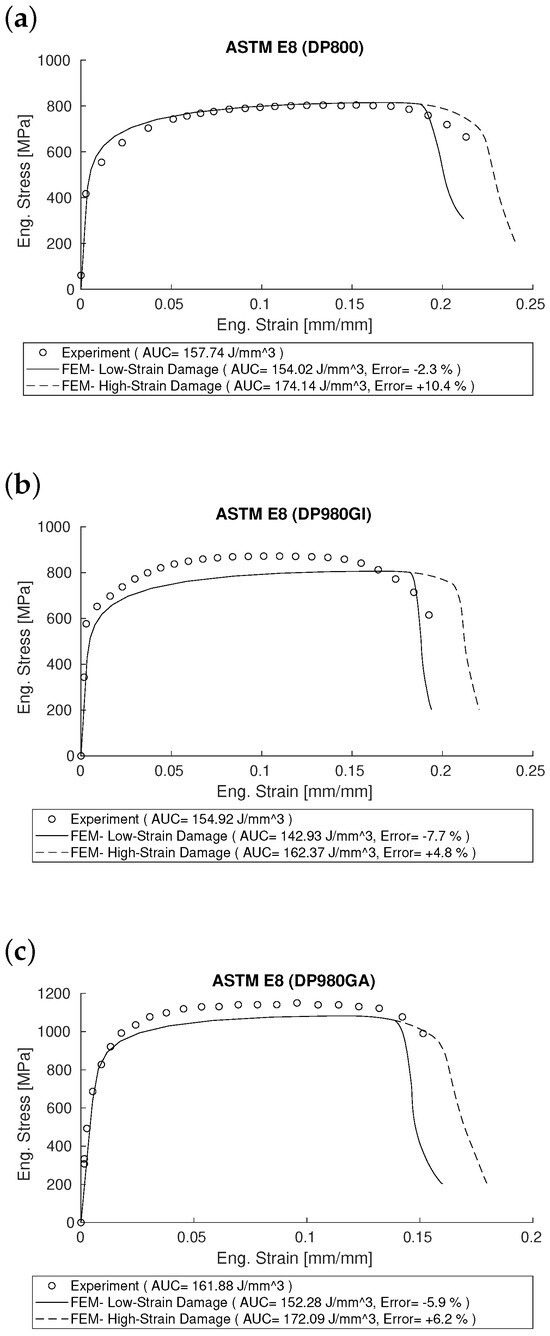
Figure 14.
Engineering stress–strain curves for DP grades, obtained from FE simulation and experiment using an ASTM E8 subsize specimen: (a) DP800, (b) DP980GI, and (c) DP980GA.
The goal of the following simulations and results is to determine whether changing the geometry affected the prediction of the stress–strain curve and the absorbed energy. To isolate the impact of geometry, every detail of the finite element and damage model was kept intact except for the tensile specimen’s geometry. Due to the use of non-standard and notched specimens from this point onward, force-displacement curves were considered the primary criteria to avoid the influence of post-processing on the data. This is especially important for notched specimens, where stress and strain calculations are highly subjective and depend on how gauge length and cross-sectional area are accounted for. Figure 15 shows the force–displacement curves for the miniature smooth dog-bone geometry for DP800 and DP980GI, comparing both the experimental and FE results. The absorbed energy values for this geometry are also provided in the figure legend. As shown, the low-strain damage set underpredicts the absorbed energy by 18%; however, the high-strain damage set obtained a much more accurate prediction of both failure strain and absorbed energy, with errors of less than 1% for DP800 and approximately 5% for DP980GI.
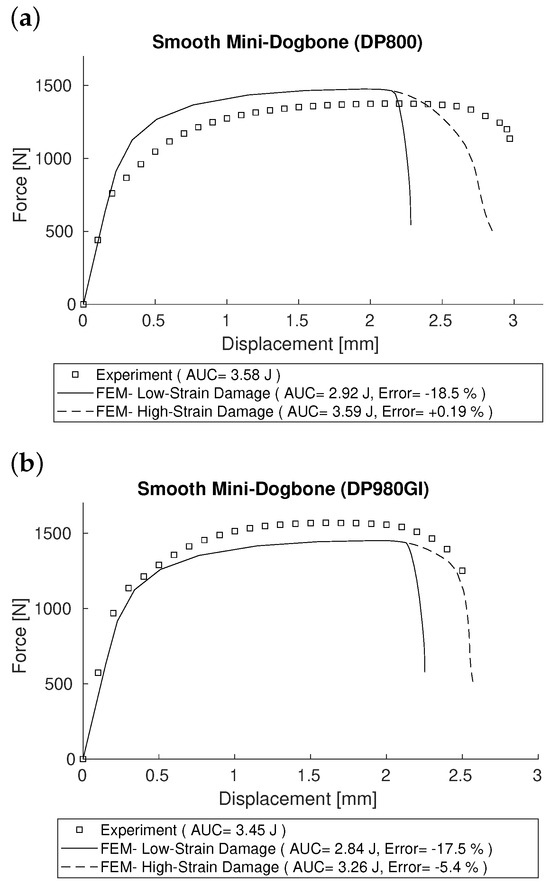
Figure 15.
Force–displacement curves for DP grades, derived from FE simulation and tested on miniature smooth specimens: (a) DP800 and (b) DP980GI.
The final set of results pertains to the miniature notched specimen. The force–displacement curves and absorbed energy for both DP800 and DP980GI grades are presented in Figure 16 and the Figure legend, respectively. As demonstrated, both the low-strain and high-strain damage sets proved to be more effective for estimating absorbed energy in the notched geometry. For both materials, the low-strain damage parameters provide better estimations, with errors of only 7.8% for DP800 and around 3% for DP980GI. Even the high-strain damage parameters predict the energies with errors of less than 12%, which is still considered reliable. However, the curves for DP800 deserve additional commentary. In Figure 16a, solid and dashed lines correspond to simulations carried out based on flow behaviors that were estimated using a volume fraction of ferrite and martensite in Table 2. Though the AUC was estimated to within approximately 11% of the experimental value, the slope of the curves indicate that hardening was overpredicted in the simulation. We reexamined the volume fraction of martensite in the DP800, which was found to be 22%; (see Figure 13 of Bardelcik and Butler [26]). The specimen was machined from a region of the sheet where the volume fraction of martensite was lower than 37%. Accordingly, we created an RVE with the lower volume fraction of martensite, and carried out the steps outlined in Section 5 to obtain the stress–strain curve, which was used to estimate the response of the notched specimen. The recomputed curves are shown using lines with triangles and circles in Figure 16, and it can be seen that there is better agreement with the experimental load–displacement curve and the corresponding AUC for the high-strain damage was within 7.7% of the experimental curve.
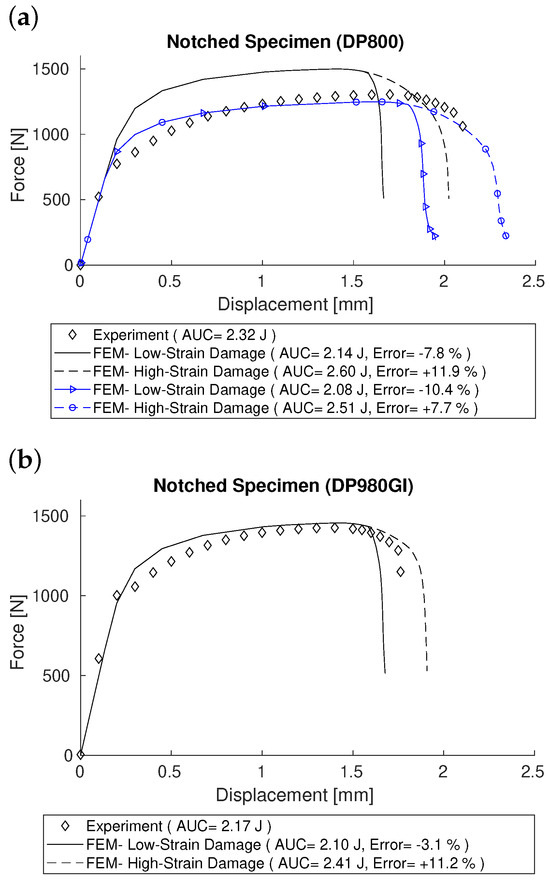
Figure 16.
Force–displacement curves for DP grades, based on finite element simulations and tests on a miniature notched specimen: (a) DP800 and (b) DP980GI.
7. Discussion
In the study by Espinosa et al. [6], it was demonstrated that phenomenological models and realistic RVEs are effective methods for predicting the flow behavior of ferrite, martensite, and their combination in dual-phase steels. In this study, it was shown that idealized RVEs, built from microstructure data, are just as effective as realistic ones in predicting the true stress–strain curves of DP steels up to the peak load (see Figure 12). This is because the flow behavior of DP steel results from the interaction of the ferrite–martensite composite, which is influenced by the differential strength between phases, the size of the individual phases, and the physics of their interaction [3,38,39]. Most of these influential parameters affecting the flow behavior can be taken into account in the creation of idealized RVEs. Beyond estimating the flow behavior of DP steels up to the peak load, the primary goal of this study was to predict the complete uniaxial tensile stress–strain curve, with a particular focus on obtaining reasonable estimates of the absorbed energy to failure (toughness) using only microstructure features.
To achieve this, a simple damage model with minimal parameters is required. The simplified Rice and Tracey [23] model, Equation (3), is an excellent choice because it requires only a couple of parameters for calibration. After calibrating the damage parameter for each unique ferrite phase corresponding to DP800, DP980GI, and DP980GA based on low-strain (30% failure strain) and high-strain (35% failure strain) behaviors, this damage set was applied to the respective DP grade with an adjustment to the triaxiality coefficient. Bardelcik and Butler [26] and Espinosa et al. [6] demonstrated that the maximum local strain in DP800 occurs within the ferrite phase, and is 2.5 to 3 times higher than the global strain. This behavior can be explained by the material’s heterogeneity, which stems from the significant difference in strength between the ferrite and martensite phases. This causes the ferrite phase to experience higher hydrostatic stress and triaxiality, which reduces ductility and promotes the formation and growth of voids [29]. Similarly, intense dislocation within ferrite grains under high-stress triaxiality conditions may lead to separation at the ferrite–martensite (F/M) interface in conventional dual-phase steels [30]. As a result, adjusting the triaxiality coefficient became necessary. This was accomplished by analysing the triaxiality within ferrite regions in the RVEs at the point of instability. Accordingly, parameter D was introduced into the damage model to account for the effect of high-triaxiality regions, which are primarily located within the ferrite at the ferrite–martensite interfaces. From a physical perspective, these regions could potentially correspond to areas of high dislocation density that are susceptible to void formation and growth or even decohesion [29,30]. Another objective of this study was to demonstrate that this approach is geometry-independent. This means that even when the geometry of the tensile specimen is altered, the estimated absorbed energy remains accurate and aligns well with the experimental results. To test this, two miniature dog-bone geometries were used, one with a smooth gauge area and the other with a notched gouge area. Figure 14, Figure 15 and Figure 16 confirm that this assumption is valid, as the high-strain damage set in FE simulations of uniaxial tensile specimens consistently provided a reasonable prediction of the absorbed energy to failure (with less than 12% error), regardless of the specimen’s geometry. This damage application approach is geometry-independent because the damage model’s fracture strain depends on stress triaxiality, which is the ratio of hydrostatic stress to von-Mises stress , and the damage increment determined by the ratio of plastic strain increment to fracture strain (). Throughout all FE simulations for a specific DP grade carried out in this study, including ASTM E8 and both smooth and notched miniature geometries, all variables were kept unchanged, with only the geometry varying. This setup was intended to isolate and assess the impact of geometry alone. After reaching the peak load, which signifies the onset of necking, triaxiality begins to increase from 0.33 to higher values. This variation in triaxiality is influenced by the stress distribution, which in turn depends on the geometry. Therefore, triaxiality, an important parameter in the fracture strain formula (Equation (1)), is automatically adjusted according to the geometry. On the other hand, the increment of plastic strain, which is the numerator in the incremental damage equation, also depends on stress distribution and hardening values. These parameters are automatically adjusted with changes in geometry. Thus, any changes in the geometry of the specimen are automatically reflected in the damage model due to the natural variations in stress triaxiality and increment of plastic strain.
8. Conclusions
We introduced a novel method for estimating the fracture-absorbed energy in the uniaxial tension testing of DP steels. The primary results indicate the following:
- Idealized RVEs, built from microstructure data, are sufficiently reliable to predict the true stress–strain response of DP steels.
- Calibrated damage parameters for high-strain ferrite (with a failure strain of 35%) can be directly used to predict the full stress–strain curve and the corresponding failure in absorbed energy.
- Incorporating the triaxiality adjustment parameter, D, into the damage model—which is based on the average triaxiality of the ferrite regions in the RVE—enables the calibrated damage parameters for pure ferrite to be effectively applied to DP grades to predict fracture-absorbed energy.
- This approach to predicting failure-absorbed energy in a uniaxial tensile test is effective for all geometries due to the natural adjustments to triaxiality and plastic strain with changes in geometry.
Author Contributions
Conceptualization, A.L.V. and H.M.S.; methodology, A.L.V. and A.B.; software; writing—original draft preparation, A.L.V.; writing—review and editing, H.M.S. and A.B.; supervision, H.M.S.; project administration, H.M.S. and A.B.; funding acquisition, H.M.S. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Sciences and Engineering Research Council of Canada through the Discovery Grant and Alliance Grant.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Chad Cathcart and Shane D. Semeniuk-Pasek of STELCO are gratefully acknowledged for providing the material and helpful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bouaziz, O.; Zurob, H.; Huang, M. Driving Force and Logic of Development of Advanced High Strength Steels for Automotive Applications. Steel Res. Int. 2013, 84, 937–947. [Google Scholar] [CrossRef]
- Tasan, C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An Overview of Dual-Phase Steels: Advances in Microstructure-Oriented Processing and Micromechanically Guided Design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- Allain, S.; Bouaziz, O.; Pushkareva, I.; Scott, C. Towards the microstructure design of DP steels: A generic size-sensitive mean-field mechanical model. Mater. Sci. Eng. A 2015, 637, 222–234. [Google Scholar] [CrossRef]
- Sardar, A.; Simha, C.; Bardelcik, A. Phenomenological model for yield, flow, and failure behavior of dual-phase steels. Mater. Sci. Eng. A 2020, 798, 140136. [Google Scholar] [CrossRef]
- Öztürk, E.; Arıkan, H. Investigation of mechanical properties of laser welded dual-phase steels at macro and micro levels. Opt. Laser Technol. 2023, 157, 108713. [Google Scholar] [CrossRef]
- Espinosa, E.; Sardar, A.; Simha, C.H.M.; Bardelcik, A. Realistic Morphology-Based Representative Volume Elements for Dual-Phase Steels. Mech. Mater. 2021, 160, 24. [Google Scholar] [CrossRef]
- Ha, J.; Lee, J.; Kim, J.H.; Lee, M.G.; Barlat, F. Investigation of plastic strain rate under strain path changes in dual-phase steel using microstructure-based modeling. Int. J. Plast. 2017, 93, 89–111. [Google Scholar] [CrossRef]
- Cavusoglu, O.; Toros, S. Three-Dimensional Micromechanical Modeling of Martensite Particle Size Effects on the Deformation Behavior of Dual-Phase Steels. Materials 2024, 17, 5004. [Google Scholar] [CrossRef]
- Amirmaleki, M.; Samei, J.; Green, D.E.; Van Riemsdijk, I.; Stewart, L. 3D micromechanical modeling of dual phase steels using the representative volume element method. Mech. Mater. 2016, 101, 27–39. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Allain, S.; Bouaziz, O.; Takahashi, M. Toward a New Interpretation of the Mechanical Behaviour of As-quenched Low Alloyed Martensitic Steels. ISIJ Int. 2012, 52, 717–722. [Google Scholar] [CrossRef]
- Park, E.K.; Hwang, J.H.; Kim, Y.J.; Kumagai, T. Strain-Based damage model for ductile tearing simulation under combined tensile and shear modes. Eng. Fract. Mech. 2024, 303, 110122. [Google Scholar] [CrossRef]
- Nahrmann, M.; Matzenmiller, A. Modelling of nonlocal damage and failure in ductile steel sheets under multiaxial loading. Int. J. Solids Struct. 2021, 232, 111166. [Google Scholar] [CrossRef]
- Simha, C.H.M.; Xu, S.; Tyson, W. Computational modeling of the drop-weight tear test: A comparison of two failure modeling approaches. Eng. Fract. Mech. 2015, 148, 304–323. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Dotta, F.; Ruggieri, C. Structural integrity assessments of high pressure pipelines with axial flaws using a micromechanics model. Int. J. Press. Vessel. Pip. 2004, 81, 761–770. [Google Scholar] [CrossRef]
- Espeseth, V.; Morin, D.; Børvik, T.; Hopperstad, O.S. A gradient-based non-local GTN model: Explicit finite element simulation of ductile damage and fracture. Eng. Fract. Mech. 2023, 289, 109442. [Google Scholar] [CrossRef]
- Pericoli, V.; Lao, X.; Ziccarelli, A.; Kanvinde, A.; Deierlein, G. Integration of an adaptive cohesive zone and continuum ductile fracture model to simulate crack propagation in steel structures. Eng. Fract. Mech. 2021, 258, 108041. [Google Scholar] [CrossRef]
- Cornec, A.; Scheider, I.; Schwalbe, K.H. On the practical application of the cohesive model. Eng. Fract. Mech. 2003, 70, 1963–1987. [Google Scholar] [CrossRef]
- Nam, H.S.; Lee, J.M.; Kim, Y.J.; Kim, J.W. Numerical ductile fracture prediction of circumferential through-wall cracked pipes under very low cycle fatigue loading condition. Eng. Fract. Mech. 2018, 194, 175–189. [Google Scholar] [CrossRef]
- Oh, C.S.; Kim, N.H.; Kim, Y.J.; Baek, J.H.; Kim, Y.P.; Kim, W.S. A finite element ductile failure simulation method using stress-modified fracture strain model. Eng. Fract. Mech. 2011, 78, 124–137. [Google Scholar] [CrossRef]
- Rice, J.; Tracey, D. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2022. Available online: https://www.astm.org/e0008_e0008m-22.html (accessed on 4 July 2025).
- Bardelcik, A.; Worswick, M.; Winkler, S.; Wells, M. A strain rate sensitive constitutive model for quenched boron steel with tailored properties. Int. J. Impact Eng. 2012, 50, 49–62. [Google Scholar] [CrossRef]
- Bardelcik, A.; Butler, Q. Strain partitioning characterization of advanced high strength steels using in-situ tensile tests with Micro digital image correlation—Methodology and analysis. Mater. Charact. 2024, 218, 114451. [Google Scholar] [CrossRef]
- Lertkiatpeeti, K.; Janya-Anurak, C.; Uthaisangsuk, V. Effects of spatial microstructure characteristics on mechanical properties of dual phase steel by inverse analysis and machine learning approach. Comput. Mater. Sci. 2024, 245, 113311. [Google Scholar] [CrossRef]
- Nam, H.S.; Oh, Y.R.; Kim, Y.J.; Kim, J.S.; Miura, N. Application of engineering ductile tearing simulation method to CRIEPI pipe test. Eng. Fract. Mech. 2016, 153, 128–142. [Google Scholar] [CrossRef]
- Anderson, D.; Winkler, S.; Bardelcik, A.; Worswick, M. Influence of stress triaxiality and strain rate on the failure behavior of a dual-phase DP780 steel. Mater. Des. 2014, 60, 198–207. [Google Scholar] [CrossRef]
- Liu, L. The unexpected low fracture toughness of dual-phase steels caused by ferrite/martensite interface decohesion. Scr. Mater. 2024, 244, 116030. [Google Scholar] [CrossRef]
- Chen, H. Microstructure, mechanical properties and strengthening mechanism of high strength hot-rolled ferrite-martensite dual phase steel. Mater. Charact. 2024, 207, 113545. [Google Scholar] [CrossRef]
- Dulucheanu, C.; Severin, T.L.; Cerlinca, D.A.; Irimescu, L. Structures and Mechanical Properties of Some Dual-Phase Steels with Low Manganese Content. Metals 2022, 12, 189. [Google Scholar] [CrossRef]
- Wang, J. Effect of martensite morphology and volume fraction on the low-temperature impact toughness of dual-phase steels. Mater. Sci. 2022, 832, 142424. [Google Scholar] [CrossRef]
- Bergstrom, Y.; Granbom, Y.; Sterkenburg, D. A Dislocation-Based Theory for the Deformation Hardening Behavior of DP Steels: Impact of Martensite Content and Ferrite Grain Size. J. Metall. 2010, 2010, 647198. [Google Scholar] [CrossRef]
- Son, Y.I.; Lee, Y.K.; Park, K.T.; Lee, C.S.; Shin, D.H. Ultrafine grained ferrite–martensite dual phase steels fabricated via equal channel angular pressing: Microstructure and tensile properties. Acta Materialia 2005, 53, 3125–3134. [Google Scholar] [CrossRef]
- Ahmad, E.; Manzoor, T.; Ali, K.L.; Akhter, J.I. Effect of microvoid formation on the tensile properties of dual-phase steel. J. Mater. Eng. Perform. 2000, 9, 306–310. [Google Scholar] [CrossRef]
- Kim, N.J.; Thomas, G. Effects of morphology on the mechanical behavior of a dual phase Fe/2Si/0.1C steel. Metall. Mater. Trans. A 1981, 12, 483–489. [Google Scholar] [CrossRef]
- Han, Q.; Kang, Y.; Hodgson, P.D.; Stanford, N. Quantitative measurement of strain partitioning and slip systems in a dual-phase steel. Scr. Mater. 2013, 69, 13–16. [Google Scholar] [CrossRef]
- Kang, J.; Ososkov, Y.; Embury, J.; Wilkinson, D. Digital image correlation studies for microscopic strain distribution and damage in dual phase steels. Scr. Mater. 2007, 56, 999–1002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).