Rotational Bending Fatigue Crack Initiation and Early Extension Behavior of Runner Blade Steels in Air and Water Environments
Abstract
1. Introduction
2. Materials and Methods
2.1. Material of 04Cr13Ni5Mo
2.2. Hardness and Tensile Properties
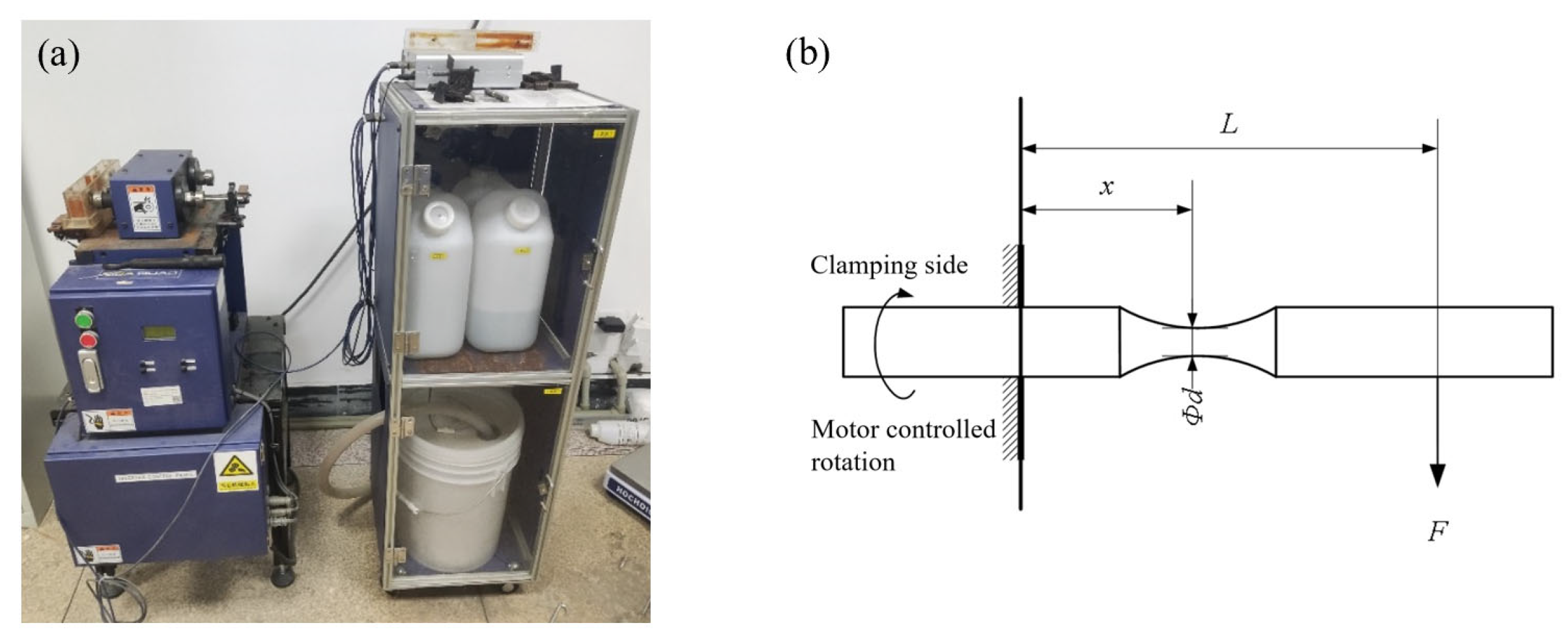
2.3. Fatigue Test
2.4. Fatigue Analysis
2.5. Crack Evolution Test
3. Results
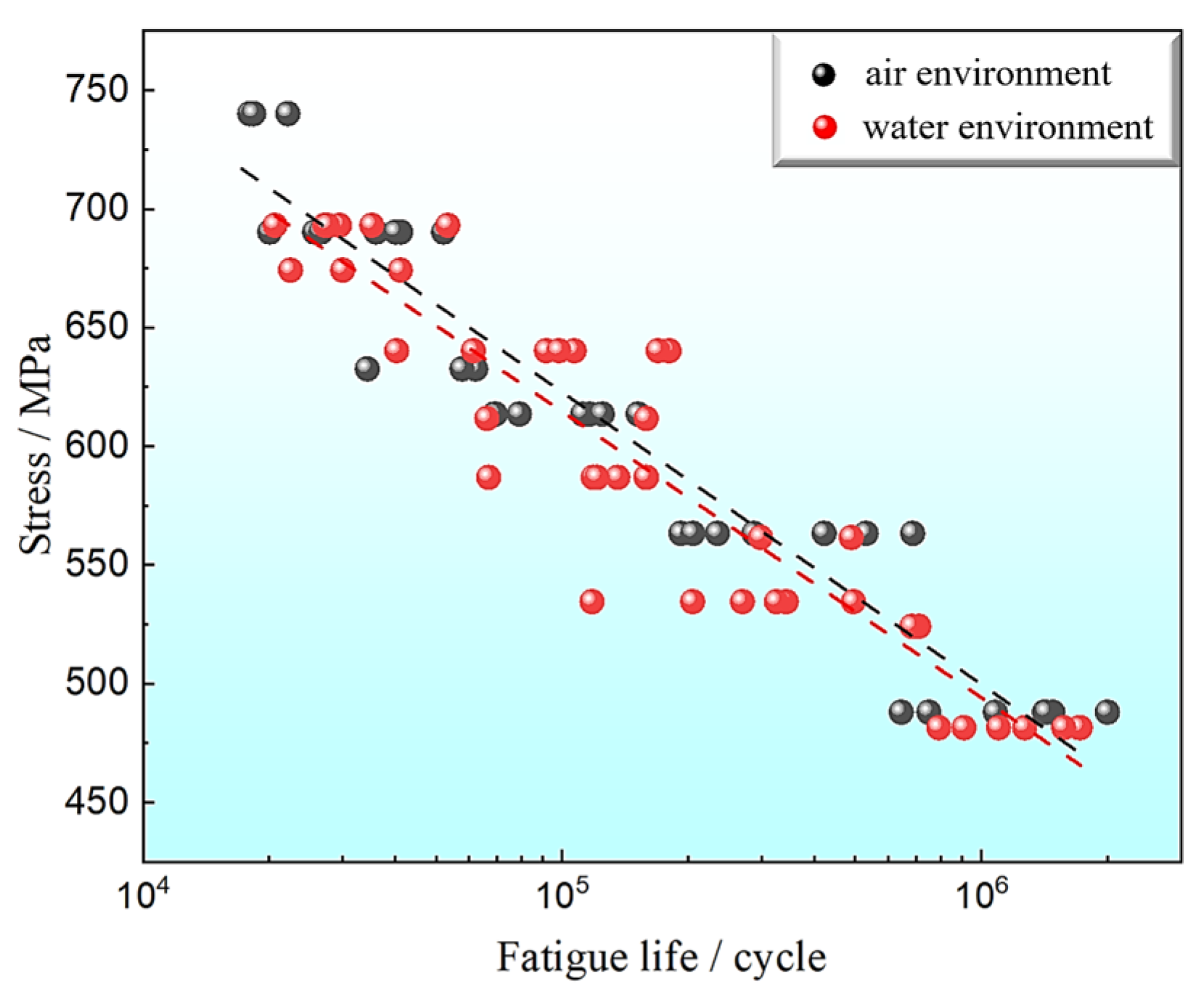
3.1. Rotational Bending Fatigue Results
3.2. Fatigue Fracture Analysis
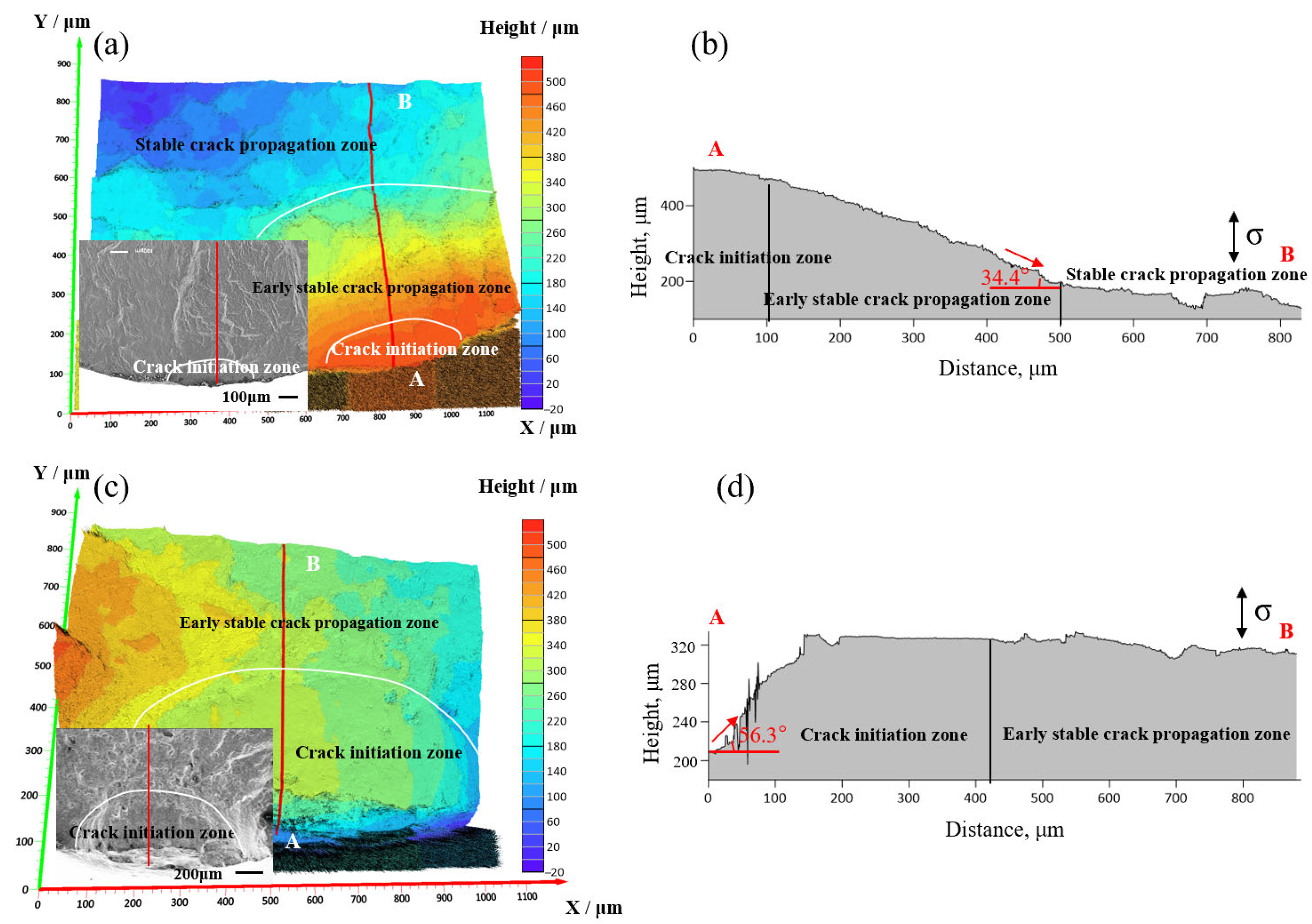
3.3. Morphological 3D Analysis
4. Discussion
4.1. Fatigue Life Prediction
- (1)
- For the normal distribution model (ND model):
- (2)
- For the normal logarithmic distribution model (LND mode):
- (3)
- For the Weibull two-parameter distribution model (Weibull-2 model):
- (4)
- For the Weibull three-parameter distribution model (Weibull-3 model):
4.2. Crack Initiation Mechanism
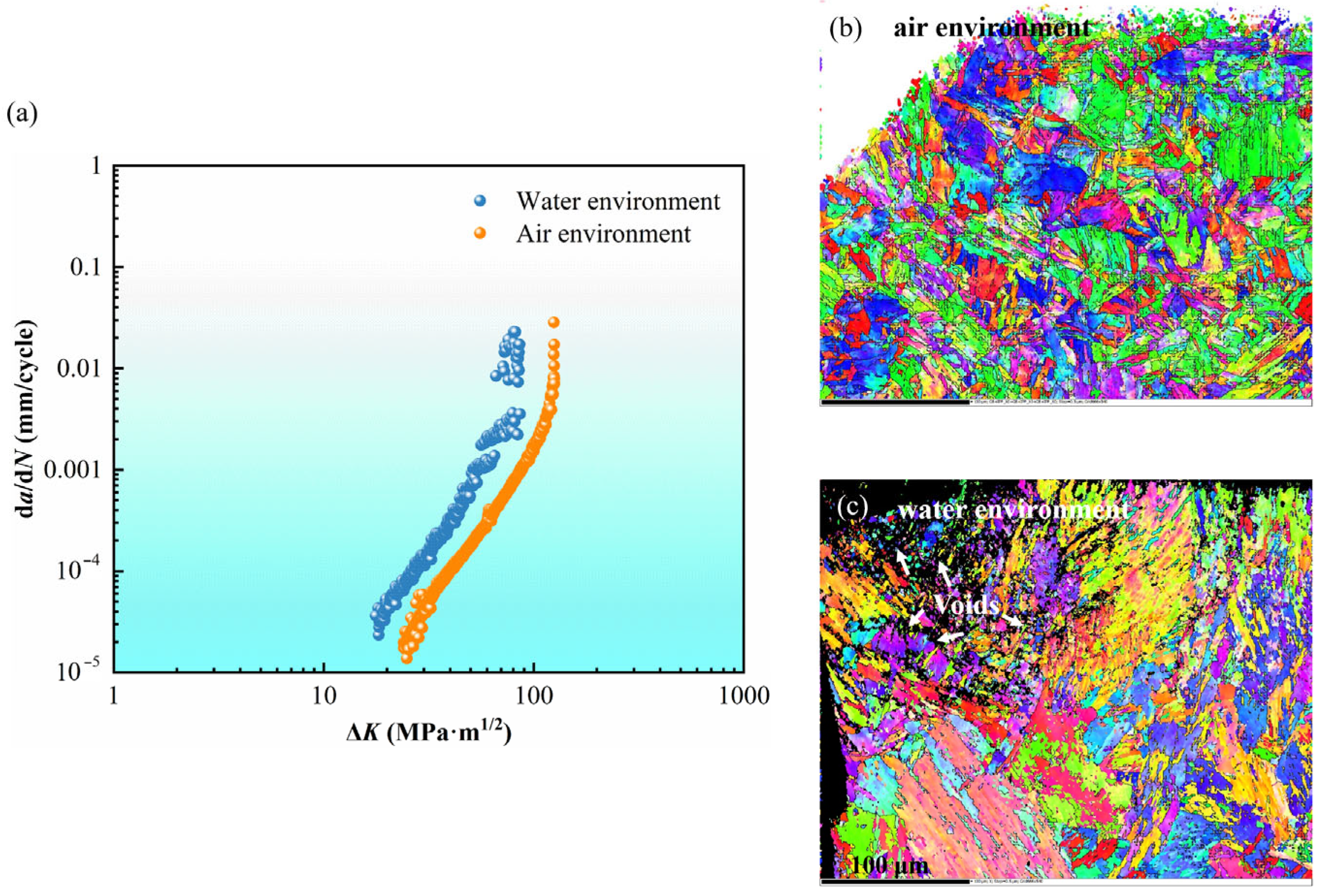
4.3. Crack Propagation
5. Conclusions
- 1.
- Through a comprehensive evaluation of various related models, the Weibull three-parameter model was found to best describe the fatigue life data of super martensitic stainless steels of 04Cr13Ni5Mo. Also, such a model is effective for analyzing fatigue test data in both air and water environments.
- 2.
- In air, cracks primarily propagate along the densest crystallographic planes, driven by the maximum shear stress. In contrast, in water, corrosion significantly exacerbates fatigue damage, with cracks more likely to initiate from corrosion-induced weak points, leading to more tortuous crack paths.
- 3.
- In addition, the ingress of corrosive media in water could significantly accelerate the crack propagation rate and lead to the formation of microvoids at the crack tip, thereby depicting a reduction of the material’s fatigue resistance. These findings highlight the critical need to consider the impact of corrosion on fatigue performance in engineering applications involving aqueous environments to ensure structural safety.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haijun, L.; Lei, Z. Effect of oxyacetylene flame cutting method on the micro-structure and properties of ZG04Cr13Ni4Mo material. China Foundry Mach. Technol. 2015, 58, 89–91. (In Chinese) [Google Scholar]
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Georgievskaia, E. Justification of the hydraulic turbines lifetime from the standpoint of the fracture mechanics. Procardia Struct. Integr. 2018, 13, 971–975. [Google Scholar] [CrossRef]
- Flores, M.; Urquiza, G.; Rodríguez, J.M. A Fatigue Analysis of a Hydraulic Francis Turbine Runner. World J. Mech. 2012, 2, 28–34. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, H.; Deng, Y.; Cao, Y.; He, Y.; Liu, Y.; Deng, Y. Fatigue behavior of high-strength steel wires considering coupled effect of multiple corrosion-pitting. Corros. Sci. 2025, 244, 112633. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, J.; Yuan, S.; Li, K.; Hu, X.; Wang, Q. Variable fatigue loading effects on corrugated steel box girders with recycled concrete. J. Constr. Steel Res. 2024, 215, 108526. [Google Scholar] [CrossRef]
- Seidel, U.; Mende, C.; Hübner, B.; Weber, W.; Otto, A. Dynamic loads in Francis runners and their impact on fatigue life. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032054. [Google Scholar] [CrossRef]
- Georgievskaia, E. Hydraulic turbines lifetime in terms of fracture mechanics. Eng. Fail. Anal. 2019, 105, 1296–1305. [Google Scholar] [CrossRef]
- Gagnon, M.; Tahan, A.; Bocher, P.; Thibault, D. A probabilistic model for the onset of High Cycle Fatigue (HCF) crack propagation: Application to hydroelectric turbine runner. Int. J. Fatigue 2013, 47, 300–307. [Google Scholar] [CrossRef]
- Romano, S.; Brandão, A.; Gumpinger, J.; Gschweitl, M.; Beretta, S. Qualification of AM parts: Extreme value statistics applied to tomographic measurements. Mater. Des. 2017, 131, 32–48. [Google Scholar] [CrossRef]
- D’Andrea, A.; Gagnon, M.; Beretta, S.; Bocher, P. Measurements and prediction of extreme defect distributions for fatigue assessment in multi-pass weld of 13%Cr–4%Ni alloy for hydraulic turbines. Int. J. Fatigue 2024, 188, 108501. [Google Scholar] [CrossRef]
- Atik, B.; Bozkurt, Y.B.; Kavasoğlu, Y.S.; Kocaci, H.; Celik, A. Pitting corrosion performance of plasma oxidized Cp-Ti and effects of fabrication methods. Surf. Coat. Technol. 2024, 478, 130384. [Google Scholar] [CrossRef]
- Ebara, R. Corrosion fatigue crack initiation behavior of stainless steels. Procedia Eng. 2010, 2, 1297–1306. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Wang, X.; Dai, Y.; Zhan, M.; Liu, Y.; Yang, K.; He, C.; Wang, Q. Effect of microstructure on small fatigue crack initiation and early propagation behavior in super austenitic stainless steel 654SMO. Int. J. Fatigue 2024, 179, 108022. [Google Scholar] [CrossRef]
- Chai, G. The formation of subsurface non-defect fatigue crack origins. Int. J. Fatigue 2006, 28, 533–1539. [Google Scholar] [CrossRef]
- Chai, G.; Forsman, T.; Gustavsson, F.; Wang, C. Formation of fine grained area in martensitic steel during very high cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1315–1323. [Google Scholar] [CrossRef]
- Gao, G.; Liu, R.; Fan, Y.; Qian, G.; Gui, X.; Misra, R.D.K.; Bai, B. Mechanism of subsurface microstructural fatigue crack initiation during high and very-high cycle fatigue of advanced bainitic steels. J. Mater. Sci. Technol. 2022, 108, 142–157. [Google Scholar] [CrossRef]
- Li, X.; Dai, Y.; Wang, X.; Liu, Y.; Chen, Y.; Wang, C.; Zhang, H.; Li, L.; Liu, H.; He, C.; et al. Effects of local microstructure on crack initiation in super martensitic stainless steel under very-high-cycle fatigue. Int. J. Fatigue 2022, 163, 107019. [Google Scholar] [CrossRef]
- Vasudevan, A.K.; Sadananda, K. Classification of environmentally assisted fatigue crack growth behavior. Int. J. Fatigue 2009, 31, 1696–1708. [Google Scholar] [CrossRef]
- Schönbauer, B.M.; Stanzl-Tschegg, S.E. Influence of environment on the fatigue crack growth behaviour of 12% Cr steel. Ultrasonics 2013, 53, 1399–1405. [Google Scholar] [CrossRef]
- ASTM E8/E8M-24; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2024.
- ASTM E647-23; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2023.
- Dai, Y.; Wang, S.; He, Q.; Liu, C.; Wang, X.; Li, X.; Li, L.; Liu, Y.; He, C.; Wang, Q. Effect of microstructure on slip-induced crack initiation and early propagation of martensitic steel during high cycle fatigue. Int. J. Fatigue 2023, 167, 107275. [Google Scholar] [CrossRef]
- Zhan, M.; Liu, C.; Dai, Y.; Wang, X.; Chen, Y.; Liu, Y.; Wang, C.; Li, L.; Wang, Q.; He, C. Effect of microstructure and local stress on small crack initiation and propagation paths in coarse-grained FeCrAl alloys. Fatigue Fract. Eng. Mater. Struct. 2023, 47, 728–744. [Google Scholar] [CrossRef]
- Zhan, M.; Dai, Y.; Liu, C.; Wang, X.; Li, L.; Liu, Y.; He, C.; Wang, Q. Effect of rolling on crack behavior of FeCrAl alloys in ultra-long life. Int. J. Struct. Integr. 2023, 14, 827–841. [Google Scholar] [CrossRef]
- Shimizu, S. Weibull distribution function application to static strength and fatigue life of materials. Tribol. Trans. 2012, 55, 267–277. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. Cumulative damage and life prediction models for high-cycle fatigue of metals: A review. Metals 2021, 11, 204. [Google Scholar] [CrossRef]
- Gope, P.C. Determination of sample size for estimation of fatigue life by using Weibull or log-normal distribution. Int. J. Fatigue 1999, 21, 745–752. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons, INC.: New York, NY, USA, 2000; pp. 86–100. [Google Scholar]
- Blacha, Ł.; Karolczuk, A. Validation of the weakest link approach and the proposed Weibull based probability distribution of failure for fatigue design of steel welded joints. Eng. Fail. Anal. 2016, 67, 46–62. [Google Scholar] [CrossRef]
- Yang, K.; He, C.; Huang, Q.; Huang, Z.Y.; Wang, C.; Wang, Q.Y.; Liu, Y.J.; Zhong, B. Very high cycle fatigue behaviors of a turbine engine blade alloy at various stress ratios. Int. J. Fatigue 2022, 99, 35–43. [Google Scholar] [CrossRef]
- Newman, J.C. Fatigue of engineered metallic materials using small-crack theory under constant- and variable-amplitude loading. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2858–2870. [Google Scholar] [CrossRef]
- Palin-Luc, T.; Pérez-Mora, R.; Bathias, C.; Domínguez, G.; Paris, P.C.; Arana, J.L. Fatigue crack initiation and growth on a steel in the very high cycle regime with sea water corrosion. Eng. Fract. Mech. 2010, 77, 1953–1962. [Google Scholar] [CrossRef]
- Pedrosa, F.; Andrade, C. Corrosion induced cracking: Effect of different corrosion rates on crack width evolution. Constr. Build. Mater. 2017, 133, 525–533. [Google Scholar] [CrossRef]
- Woodtli, J.; Kieselbach, R. Damage due to hydrogen embrittlement and stress corrosion cracking. Eng. Fail. Anal. 2000, 7, 427–450. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Wei, Y. Influence of seawater on the carbon steel initial corrosion behavior. Int. J. Electrochem. Sci. 2019, 14, 1147–1162. [Google Scholar] [CrossRef]








| Components | C | Si | Mn | P | S | Cr | Ni | Cu | Mo | W | V |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Values (wt.%) | 0.04 | 0.80 | 1.45 | 0.01 | 0.01 | 13.00 | 5.00 | 0.40 | 0.70 | 0.01 | 0.05 |
| Standard Range (wt.%) | ≤0.05 | ≤1.00 | ≤1.50 | ≤0.03 | ≤0.03 | 12.00–14.00 | 4.00–6.00 | ≤0.50 | 0.30–1.00 | ≤0.05 | ≤0.20 |
| Model | Parameters | Stress Load Level (MPa) | ||||
|---|---|---|---|---|---|---|
| 690.2 | 613.5 | 563.3 | 488.0 | 436.5 | ||
| ND | 34,554 | 103,237 | 365,649 | 1,257,516 | 2,014,203 | |
| 12,688 | 36,754 | 222,574 | 540,972 | 960,250 | ||
| R2 | 0.9804 | 0.9621 | 0.9471 | 0.9715 | 0.9405 | |
| LND | 4.5185 | 4.9959 | 5.5161 | 6.0709 | 6.2708 | |
| 0.1646 | 0.1585 | 0.2486 | 0.2036 | 0.2242 | ||
| R2 | 0.9816 | 0.9586 | 0.9703 | 0.9647 | 0.9441 | |
| Weibull-2 | 38,720 | 115,827 | 421,373 | 1,431,752 | 2,313,912 | |
| 3.1770 | 3.2513 | 2.0328 | 2.5968 | 2.3577 | ||
| R2 | 0.9790 | 0.9421 | 0.9352 | 0.9727 | 0.9515 | |
| Weibull-3 | 13,647 | 60,345 | 188,278 | 248,464 | 902,091 | |
| 24,288 | 49,761 | 170,160 | 1,169,961 | 1,296,626 | ||
| 1.7188 | 1.0443 | 0.6100 | 1.9689 | 0.9463 | ||
| R2 | 0.9849 | 0.9467 | 0.9941 | 0.9733 | 0.9590 | |
| Model | Parameters | Stress Load Level (MPa) | ||||
|---|---|---|---|---|---|---|
| 693.1 | 640.2 | 586.9 | 534.5 | 481.4 | ||
| ND | 53,016 | 103,407 | 135,767 | 295,641 | 585,703 | |
| 38,606 | 79,379 | 102,236 | 176,176 | 610,747 | ||
| R2 | 0.9384 | 0.9337 | 0.9602 | 0.9777 | 0.9093 | |
| LND | 4.6502 | 4.9402 | 5.0464 | 5.4162 | 5.6304 | |
| 0.3242 | 0.3188 | 0.3519 | 0.2754 | 0.4360 | ||
| R2 | 0.9607 | 0.9559 | 0.9702 | 0.9862 | 0.9587 | |
| Weibull-2 | 61,463 | 120,135 | 157,145 | 340,440 | 659,939 | |
| 1.5940 | 1.5820 | 1.4715 | 1.9051 | 1.1671 | ||
| R2 | 0.9466 | 0.9193 | 0.9579 | 0.9868 | 0.9303 | |
| Weibull-3 | 17,133 | 45,033 | 41,344 | 34,737 | 64,737 | |
| 38,950 | 50,822 | 99,720 | 302,116 | 564,228 | ||
| 0.8194 | 0.5247 | 0.7113 | 1.5963 | 0.9877 | ||
| R2 | 0.9773 | 0.9904 | 0.9815 | 0.9882 | 0.9450 | |
| Environment | ND | LND | Weibull-2 | Weibull-3 |
|---|---|---|---|---|
| Air | −0.0132 | 0.0044 | −0.0344 | 0.0432 |
| Water | −0.0174 | 0.0049 | −0.0091 | 0.0216 |
| Environment | S (Mpa) | Inefficient Parameter P | |||
|---|---|---|---|---|---|
| 50% | 10% | 1% | 0.1% | ||
| Air | 690.2 | 33,271 | 20,205 | 15,318 | 14,084 |
| 613.5 | 95,377 | 66,112 | 60,952 | 60,411 | |
| 563.3 | 281,585 | 192,531 | 188,368 | 188,280 | |
| 488.0 | 1,219,705 | 621,536 | 361,570 | 283,506 | |
| 436.5 | 1,782,349 | 1,022,331 | 912,129 | 902,968 | |
| Water | 693.1 | 42,036 | 19,632 | 17,275 | 17,142 |
| 640.2 | 70,309 | 45,730 | 45,041 | 45,033 | |
| 586.9 | 100,911 | 45,559 | 41,499 | 41,350 | |
| 534.5 | 274,875 | 108,518 | 51,667 | 38,727 | |
| 481.4 | 454,043 | 122,536 | 70,091 | 65,255 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, B.; Li, Y.; Yi, W.; Li, W.; Dong, J. Rotational Bending Fatigue Crack Initiation and Early Extension Behavior of Runner Blade Steels in Air and Water Environments. Metals 2025, 15, 783. https://doi.org/10.3390/met15070783
Xue B, Li Y, Yi W, Li W, Dong J. Rotational Bending Fatigue Crack Initiation and Early Extension Behavior of Runner Blade Steels in Air and Water Environments. Metals. 2025; 15(7):783. https://doi.org/10.3390/met15070783
Chicago/Turabian StyleXue, Bing, Yongbo Li, Wanshuang Yi, Wen Li, and Jiangfeng Dong. 2025. "Rotational Bending Fatigue Crack Initiation and Early Extension Behavior of Runner Blade Steels in Air and Water Environments" Metals 15, no. 7: 783. https://doi.org/10.3390/met15070783
APA StyleXue, B., Li, Y., Yi, W., Li, W., & Dong, J. (2025). Rotational Bending Fatigue Crack Initiation and Early Extension Behavior of Runner Blade Steels in Air and Water Environments. Metals, 15(7), 783. https://doi.org/10.3390/met15070783






